A Review of Hot Deck Imputation for Survey Non-response

Summary

Hot deck imputation is a method for handling missing data in which each missing value is replaced with an observed response from a “similar” unit. Despite being used extensively in practice, the theory is not as well developed as that of other imputation methods. We have found that no consensus exists as to the best way to apply the hot deck and obtain inferences from the completed data set. Here we review different forms of the hot deck and existing research on its statistical properties. We describe applications of the hot deck currently in use, including the U.S. Census Bureau’s hot deck for the Current Population Survey (CPS). We also provide an extended example of variations of the hot deck applied to the third National Health and Nutrition Examination Survey (NHANES III). Some potential areas for future research are highlighted.

1 Introduction

Missing data are often a problem in large-scale surveys, arising when a sampled unit does not respond to the entire survey (unit non-response) or to a particular question (item non-response). A common technique for handling item non-response is imputation, whereby the missing values are filled in to create a complete data set that can then be analyzed with traditional analysis methods. It is important to note at the outset that usually sample surveys are conducted with the goal of making inferences about population quantities such as means, correlations and regression coefficients, and the values of individual cases in the data set are not the main interest. Thus, the objective of imputation is not to get the best possible predictions of the missing values, but to replace them by plausible values in order to exploit the information in the recorded variables in the incomplete cases for inference about population parameters (Little & Rubin, 2002). We consider here hot deck imputation, which involves replacing missing values with values from a “similar” responding unit. This method is used extensively in practice, but the theory behind the hot deck is not as well developed as that of other imputation methods, leaving researchers and analysts with limited guidance on how to apply the method. This paper describes various forms of the hot deck, reviews existing research on statistical properties, and highlights some areas for future work.

Hot deck imputation involves replacing missing values of one or more variables for a non-respondent (called the recipient) with observed values from a respondent (the donor) that is similar to the non-respondent with respect to characteristics observed by both cases. In some versions, the donor is selected randomly from a set of potential donors, which we call the donor pool; we call these methods random hot deck methods. In other versions a single donor is identified and values are imputed from that case, usually the “nearest neighbour” based on some metric; we call these methods deterministic hot deck methods, since there is no randomness involved in the selection of the donor. Other methods impute summaries of values for a set of donors, such as the mean, rather than individual values; we do not consider these as hot deck methods, although they share some common features. We note that our use of “deterministic” describes the way in which a donor is selected in the hot deck, and differs from the use of “deterministic” to describe imputation methods that impute the mean or other non-random value.

There are several reasons for the popularity of the hot deck method among survey practitioners. As with all imputation methods, the result is a rectangular data set that can be used by secondary data analysts employing simple complete-data methods. It avoids the issue of cross-user inconsistency that can occur when analysts use their own missing-data adjustments. The hot deck method does not rely on model fitting for the variable to be imputed, and thus is potentially less sensitive to model misspecification than an imputation method based on a parametric model, such as regression imputation. Having said this, it is important to keep in mind that the hot deck makes implicit assumptions through the choice of metric to match donors to recipients, and the variables included in this metric, so it is far from assumption free. Another attractive feature of the hot deck is that only plausible values can be imputed, since values come from observed responses in the donor pool. There may be a gain in efficiency relative to complete-case analysis, since information in the incomplete cases is being retained. There is also a reduction in non-response bias, to the extent that there is an association between the variables defining imputation classes and both the propensity to respond and the variable to be imputed.

Section 2 describes some applications of the hot deck in real surveys, including the original application to the Current Population Survey (CPS). Section 3 discusses methods for finding “similar” units and creating donor pools. Section 4 considers methods for incorporating sampling weights, including weighted hot decks. Section 5 discusses hot decks for imputing multivariate incomplete data with monotone and more complex “swiss cheese” patterns of missingness. Theoretical properties of hot deck estimates, such as unbiasedness and consistency, are the focus of Section 6. Section 7 discusses variance estimation, including resampling methods and multiple imputation. Section 8 illustrates different forms of the hot deck on data from the third National Health and Nutrition Examination Survey (NHANES III), drawing comparisons between the methods by simulation. Some concluding remarks and suggestions for future research are provided in Section 9.

2 Examples of the Hot Deck

Historically, the term “hot deck” comes from the use of computer punch cards for data storage, and refers to the deck of cards for donors available for a non-respondent. The deck was “hot” since it was currently being processed, as opposed to the “cold deck” which refers to using pre-processed data as the donors, i.e. data from a previous data collection or a different data set. At the U.S. Census Bureau, the classic hot deck procedure was developed for item non-response in the Income Supplement of the Current Population Survey (CPS), which was initiated in 1947 and has evolved since then (Ono & Miller, 1969; U.S. Bureau of the Census, 2002).

The CPS uses a sequential adjustment cell method to fill in missing items (U.S. Bureau of the Census, 2002). The main item requiring imputation is the earnings question, but a small fraction (1–4%) missing values of other items relating to demographics, employment status, and occupation are also imputed. Each variable has its own hot deck, and imputation proceeds in a pre-specified order so that items imputed previously may be used to define adjustment cells for later variables. For example, cells to impute labour force items (e.g. employed/not employed) are defined by age, sex, and race. Then industry and occupation is imputed with cells based on age, sex, race, and employment status. Earnings can then be imputed based on age, sex, race, employment status, and industry/occupation. The number of adjustment cells ranges from approximately 100 for employment status to many thousands for earnings estimates. The records within adjustment cell sorted based on geographic location and primary sampling unit, and then values from respondents are used sequentially to impute missing values.

The hot deck is commonly used by other government statistics agencies and survey organizations to provide rectangular data sets for users. For example, the National Center for Education Statistics (NCES) uses different forms of the hot deck and alternative imputation methods even within a survey. Out of twenty recent surveys, eleven used a form of adjustment cell hot deck (sequential or random) while the remaining nine used a form of deterministic imputation (e.g. mean imputation), cold deck imputation, or a Bayesian method for MI. Within the surveys that used the hot deck, many used both random within class imputation and sequential imputation (National Center for Education Statistics, 2002).

The hot deck has been applied in epidemiologic and medical settings, although here parametric imputation methods are more common. Applications of the hot deck and comparisons with other imputation methods include Barzi & Woodward (2004) and Perez et al. (2002) in cross-sectional studies, and Twisk & de Vente (2002) and Tang et al. (2005) in longitudinal studies. The lack of software in commonly used statistical packages such as SAS may deter applications of the hot deck in these settings.

Sequential hot deck methods are the most prevalent in applications, but some recent implementations have used more complex matching metrics and better methods for handling multivariate missingness; these methods are described in the following sections.

3 Methods for Creating the Donor Pool

Hot deck imputation methods share one basic property: each missing value is replaced with an observed response from a “similar” unit (Kalton & Kasprzyk, 1986). Donor pools, also referred to as imputation classes or adjustment cells, are formed based on auxiliary variables that are observed for donors and recipients. We now review the various ways in which donors can be identified. For clarity we initially focus on the use of covariate information x for imputing a single variable Y; the case of multivariate Y is discussed in Section 5.

3.1 Adjustment Cell Methods

The simplest method is to classify responding and non-responding units into imputation classes, also known as adjustment cells, based on x (Brick & Kalton, 1996). To create cells, any continuous covariates are categorized before proceeding. Imputation is then carried out by randomly picking a donor for each non-respondent within each cell. Cross-classification by a number of covariates can lead to many adjustment cells. An example is imputation of income in the Current Population Survey Outgoing Rotation Group (CPS-ORG), which uses seven variables leading to 11,520 adjustment cells (Bollinger & Hirsch, 2006), some of which contain non-respondents but no matching respondents. The usual remedy is to drop or coarsen variables until a suitable donor is found. The choice of variables for creating adjustment cells often relies on subjective knowledge of which variables are associated with the item being imputed, and predictive of non-response. Groups of “similar” donors could also be created empirically using branching algorithms such as CHAID or CART (Kass, 1980; Breiman & Friedman, 1993), though these methods do not seem to be widely used.

Sparseness of donors can lead to the over-usage of a single donor, so some hot decks limit the number of times d any donor is used to impute a recipient. The optimal choice of d is an interesting topic for research—presumably it depends on the size of the sample, and the interplay between gain in precision from limiting d and increased bias from reduced quality of the matches.

The two key properties of a variable used to create adjustment cells are (a) whether it is associated with the missing variable Y, and (b) whether it is associated with the binary variable indicating whether or not Y is missing. Table 1, from Little & Vartivarian (2005), summarizes the effect of high or low levels of these associations on bias and variance of the estimated mean of Y. Table 1 was presented for the case of non-response weighting, but it also applies for hot deck imputation. In order to see a reduction in bias for the mean of Y, the variables x that define the donor pools must be associated both with Y and with the propensity to respond, as in the bottom right cell of the table. If x is associated with the propensity to respond but not with the outcome Y, there is an increase in variance with no compensating reduction in bias, as in the bottom left cell of the table. Using adjustment cells associated with Y leads to an increase in precision, and also reduces bias if the adjustment cell variable is related to non-response. Attempts should thus be made to create cells that are homogeneous with respect to the item or items being imputed, and, if propensity is associated with the outcome, also with the propensity to respond.

Table 1.

Effect of weighting adjustments on bias and variance of a mean, by strength of association of the adjustment cell variables with non-response and outcome (Little & Vartivarian, 2005).

		Association with outcome
		Low	High
Association with non-response	Low	Bias: -	Bias: -
		Var: -	Var: ↓
	High	Bias: -	Bias: ↓
		Var: ↑	Var: ↓

Creating adjustment cells is not the only way of defining groups of “similar” units. A more general principle is to choose donor units that are close to the non-respondent with respect to some distance metric. We now review these methods.

3.2 Metrics for Matching Donors to Recipients

Let x_i = (x_i1, … x_iq ) be the values for subject i of q covariates that are used to create adjustment cells, and let C(x_i ) denote the cell in the cross-classification in which subject i falls. Then matching the recipients i to donors j in the same adjustment cell is the same as matching based on the metric

$$d(i,j)=\{\begin{array}{ll}0\hfill & j\in C(x_i)\hfill \\ 1\hfill & j\notin C(x_i)\hfill \end{array}.$$

Other measures of the “closeness” of potential donors to recipients can be defined that avoid the need to categorize continuous variables, such as the maximum deviation,

$$d(i,j)=\underset{k}{max}\mid x_{ik}-x_{jk}\mid ,$$

where the x_k have been suitably scaled to make differences comparable (e.g. by using ranks and then standardizing), the Mahalanobis distance,

$$d(i,j)={(x_i-x_j)}^T\widehat{\mathit{Var}}{(x_i)}^{-1}(x_i-x_j),$$

where $\widehat{\mathit{Var}}(x_i)$ is an estimate of the covariance matrix of x_i , or the predictive mean,

$$d(i,j)={(\widehat{Y}(x_i)-\widehat{Y}(x_j))}^2,$$ (1)

where $\widehat{Y}(x_i)=x_i^T\widehat{\beta }$ is the predicted value of Y for non-respondent i from the regression of Y on x using only the respondents’ data.

Inclusion of nominal variables using these metrics is not straightforward for all distance measures. It is easiest with the predictive mean metric, which simply requires conversion to a set of dummy variables for inclusion in the regression model. For the other methods more complex approaches are required and different distance measures may be required for nominal variables than (semi-)continuous ones. See for example Bankier et al. (1994) and Bankier et al. (1995) for a discussion of combining qualitative and quantitative variables in distance measures.

If all adjustment variables are categorical and main effects plus all interactions between adjustment variables are included in the regression model, predictive mean matching reduces to the adjustment cell method (Kalton & Kasprzyk, 1986). Subjects with the same x vector will have the same Ŷ, creating identical donor pools as for the cross-tabulation method. One advantage to defining neighbourhoods via the predictive mean is that the variables x that are predictive of Y will dominate the metric, while the Mahalanobis metric may be unduly influenced by variables with little predictive power (Little, 1988). Using generalized linear models such as logistic regression to model the predictive means allow this metric to be used for discrete outcomes as well as continuous ones. The predictive mean neighbourhood method has also been proposed in the context of statistical matching (Rubin, 1986).

Once a metric is chosen there are several ways to define the set of donors for each recipient. One method defines the donor set for non-respondent j as the set of respondents i with d(i, j) < δ, for a pre-specified maximum distance δ. A donor is then selected by a random draw from the respondents in the donor set. Alternatively, if the closest respondent to j is selected, the method is called a deterministic or nearest neighbour hot deck. The widely used Generalized Edit and Imputation System (GEIS) of Statistics Canada uses the nearest neighbour approach, with the maximum deviation metric applied to standardized ranks to find donors (Cotton, 1991; Fay, 1999; Rancourt, 1999). A third method for selecting a donor is developed in Siddique & Belin (2008), where all respondents are eligible as donors but random selection of a donor is with probability inversely proportional to their distance from the recipient, which is defined as a monotonic function of the difference in predictive means.

As previously noted, information about the propensity to respond may help in creating the best adjustment cells. One method is to perform response propensity stratification, whereby the probability of response for a subject p(x) is estimated by the regression of the response indicator on the covariates x, using both respondent and non-respondent data (Little, 1986). As with the predictive mean metric, the predicted probability of response (propensity score, p̂(x)) can be calculated for all subjects, and is itself a type of distance metric. Stratification via predictive means and response propensities are compared in the context of the hot deck in Haziza & Beaumont (2007). They show that either metric can be used to reduce non-response bias; however only the predictive mean metric has the potential to also reduce variance. Similar results were previously described for cell mean imputation in Little (1986). Thus, for a single variable Y, creating cells that are homogeneous with respect to the predictive mean is likely close to optimal; additional stratification by the propensity to respond simply adds to the variance without reducing bias. For a set of Y’s with the same pattern and differing predictive means, a single stratifier compromises over the set of predictive means for each variable in the set, as discussed in Section 5. Additional stratification by the propensity to respond may reduce bias in this setting.

3.3 Redefining the Variables to be Imputed

The natural implementation of the hot deck imputes a missing value y_i of a variable Y with the value y_j of Y from a case j in the donor set. This imputation has the attractive property of being invariant to transformations of the marginal distribution of Y; for example imputing Y yields the same imputations as imputing log Y and exponentiating those values. Improvements may result from imputing a function of Y and x, rather than Y itself. For example, if Y is strongly correlated with an auxiliary variable S measuring size of the unit, then it may be advantageous to treat the missing variable as the ratio R = Y/S. Imputing r̂_i = r _j from a donor j, with the implied imputation ŷ_i = s_i r_j for Y , might be preferable to imputing ŷ = y_j directly from a donor, particularly if donors are chosen within adjustment cells that do not involve S or are based on a crude categorization of S. When missing compositional variables sum to a total that is observed, one might match donor and recipient based on the total and then impute the vector of proportions (Bankier et al., 2000; Little et al., 2008).

3.4 Imputation and Edit Constraints

Hot deck imputation is not used solely for the imputation of missing values. When data are logically inconsistent, for example when a 45-year-old mother is reported to have a 40-year-old son, edit-imputation methods are used to correct contradictory values by deleting inconsistent values and imputing valid values. The hot deck is not necessarily used as the imputation piece of these edit-imputation systems, but it is frequently implemented in concert with editing rules to alter implausible records. What follows is a brief description of edit-imputation methods and discussion of the role of the hot deck; for a more complete treatment see Herzog et al. (2009).

Automated methods for editing and imputation historically relied on complex “if-then-else” rules, which were unique to each survey and could require thousands of lines of complex computer code to implement. In addition, corrections made by one rule could potentially lead to errors under another rule, and many iterations were usually required to obtain a record that met all the logical rules. The methodology for statistical editing was transformed by the work of Fellegi & Holt (1976), who introduced a theoretical model for editing. They provided algorithms for correcting invalid data (“failing records”) that satisfied three criteria: (a) edits should change the fewest possible fields (error localization), (b) imputation rules should follow from editing rules without additional specification, and (c) marginal and joint distributions of variables should be preserved. The Fellegi–Holt (FH) algorithm first determines the minimum number of fields to be imputed and then performs the imputations, customarily but not necessarily by a hot deck procedure with “passing records” as the donors. An example of an FH system that uses the hot deck for imputation is the GEIS system, which uses a deterministic nearest-neighbor hot deck as described in Section 3.2.

An alternative method of editing and imputation is implemented in the Nearest-Neighbour Imputation Methodology (NIM) system of Statistics Canada (Bankier et al., 2000). Unlike the FH systems, NIM first identifies donors from the set of passing records and then determines the minimum change action based on these donors. First the distance between a failing record and each passing record is calculated using a distance metric that allows the incorporation of both discrete and continuous variables; see U.S. Bureau of the Census (2003) for details. For each failing record, a set number of closest passing records (say, 20) are selected as an initial donor pool, and all possible imputation actions are identified for each potential donor. Imputation actions here are ways a passing record could donate values to the failing record such that the failing record would pass the edit constraints. To minimize the number of changes to a failing record, the distance from each of these imputation actions to both the failing record and the donating record is calculated, and a weighted average is used to identify the n (say, 5) closest imputation actions. By adjusting the weighting scheme, more emphasis can be placed on either identifying “close” donors or identifying donors that require the minimum number of changes. Ultimately the imputation action is randomly selected from the n closest actions, so the hot deck used by NIM is a random hot deck that uses complex distance metrics to allow both qualitative and quantitative variables to be imputed within the edit-impute framework.

4 Role of Sampling Weights

We now discuss proposals for explicitly incorporating the survey design weights into donor selection.

4.1 Weighted Sequential Hot Deck

The weighted sequential hot deck procedure (Cox, 1980; Cox & Folsom, 1981) was motivated by two issues: the unweighted sequential hot deck is potentially biased if the weights are related to the imputed variable, and respondent values can be used several times as donors if the sorting of the file results in multiple non-respondents occurring in a row, leading to estimates with excessive variance. The weighted sequential hot deck preserves the sorting methodology of the unweighted procedure, but allows all respondents the chance to be a donor and uses sampling weights to restrict the number of times a respondent value can be used for imputation. Respondents and non-respondents are first separated into two files and sorted (randomly, or by auxiliary variables). Sample weights of the non-respondents are rescaled to sum to the total of the respondent weights. The algorithm can be thought of as aligning both these rescaled weights and the donors’ weights along a line segment, and determining which donors overlap each non-respondent along the line (Williams & Folsom, 1981). Thus the set of potential donors for a given non-respondent is determined by the sort order, the non-respondent’s sample weight, and the sample weights of all the donors. The algorithm is designed so that, over repeated imputations, the weighted mean obtained from the imputed values is equal in expectation to the weighted mean of the respondents alone within imputation strata. “Similarity” of donor to recipient is still controlled by the choice of sorting variables.

The weighted sequential hot deck does not appear to have been widely implemented. For example, the National Survey on Drug Use and Health (NSDUH) used it sparingly in the 2002 survey but has since switched to exclusive use of imputation via predictive mean neighbourhoods (Grau et al., 2004; Bowman et al., 2005).

4.2 Weighted Random Hot Decks

If donors are selected by simple random sampling from the donor pool, estimators are subject to bias if their sampling weight is ignored. One approach, which removes the bias if the probability of response is constant within an adjustment cell, is to inflate the donated value by the ratio of the sample weight of the donor to that of the recipient (Platek & Gray, 1983). However, this adjustment has drawbacks, particularly in the case of integer-valued imputed value Y, since the imputations may no longer be plausible values. An alternative method is to select donors via random draw with probability of selection proportional to the potential donor’s sample weight (Rao & Shao, 1992; Rao, 1996). Assuming the response probability is constant within an adjustment cell, this method yields an asymptotically unbiased estimator for Y. Note that in contrast to the weighted sequential hot deck, the sample weights of non-respondents are not used in determining the selection probabilities of donors.

If the values of Y for donors and recipients within an adjustment cell have the same expected value, then the weighted draw is unnecessary, since unweighted draws will yield unbiased estimates. A similar situation arises in weighting adjustments for unit non-response, where a common approach is to compute non-response weights as the inverse of response rates computed with units weighted by their sampling weights. Little & Vartivarian (2003) argues that this can lead to inefficient and even biased estimates, and suggests instead computing non-response weights within adjustment cells that condition on the design weights and other covariates. The analogous approach to incorporating design weights in the hot deck is to use the design weight variable alongside auxiliary variables to define donor pools. Simulations suggest that that unweighted draws from these donor pools yield better imputations than weighted draws based on donor pools that are defined without including the design weights as a covariate (Andridge & Little, 2009). The caveat in utilizing weights in this manner is that if weights are not related to the outcome, an increase in variance may occur without a corresponding decrease in bias; simulations in Andridge & Little (2009) show only a modest increase, though more investigation is warranted.

5 Hot Decks for Multivariate Missing Data

Often more than one variable has missing values. Let X = (X₁, …, X_q ) denote the fully observed items, including design variables, and let Y = (Y₁, … , Y_p) denote the items with missing values. If the components of Y are missing for the same set of cases, the data have just two missing-data patterns, complete and incomplete cases; we call this the “two-pattern case”. A more general case is “monotone missing data”, where the variables can be arranged in a sequence (Y₁, …, Y_p) so that Y₁, … , Y_j−1 are observed whenever Y_j is observed, for j = 2, … , p. This pattern is often encountered in longitudinal survey data where missing data arise from attrition from the sample. Alternatively, the missing values may occur in a general pattern—Judkins (1997) calls this a “swiss cheese pattern”. We discuss hot deck methods for all three situations, moving from the simplest to the most complex.

5.1 The Two-Pattern Case

Suppose there are just two patterns of data, complete and incomplete cases. The same set of covariate information X is available to create donor sets for all the missing items. One possibility is to develop distinct univariate hot decks for each variable, with different donor pools and donors for each item. This approach has the advantage that the donor pools can be tailored for each missing item, for example by estimating a different predictive mean for each item and creating the donor pools for each incomplete variable using the predictive mean matching metric. However, a consequence of this method is that associations between the imputed variables are not preserved. For example, imputation may result in a former smoker with a current 2-pack per day habit, or an unemployed person with a substantial earned income. This may be acceptable if analyses of interest are univariate and do not involve these associations, but otherwise the approach is flawed.

An alternative method, which Marker et al. (2002) calls the single-partition, common-donor hot deck is to create a single donor pool for each non-respondent, using for example the multivariate analogue of the predictive mean metric (1):

$$d(i,j)={(\widehat{y}(x_i)-\widehat{y}(x_j))}^T\widehat{\mathit{Var}}{(y·x_i)}^{-1}(\widehat{y}(x_i)-\widehat{y}(x_j)),$$ (2)

where $\widehat{\mathit{Var}}(y·x_i)$ is the estimated residual covariance matrix of Y_i given x_i . A donor from this pool is used to impute all the missing items for a recipient. This approach preserves associations within the set. However, since the same metric is used for all the variables, the metric is not tailored to each variable.

Another approach that preserves associations between p variables, which we refer to as the p-partition hot deck, is to create the donor pool for Y_j using adjustment cells (or more generally, a metric) that conditions on X and (Y₁,…, Y_j−1), for j = 2, …, p, using the recipient’s previously imputed values of (Y₁, …, Y_j−1), when matching donors to recipients. Marker et al. (2002) calls this method the n-partition hot deck, here we replace n by p for consistency of notation. This approach allows the metric to be tailored for each item, and the conditioning on previously imputed variables in the metric provides some preservation of associations, although the degree of success depends on whether the distance metrics for each variable Y_j capture associations with X and (Y_1, …, Y_j−1), and the extent to which “close” matches can be found.

The single-partition and p-partition hot deck can be combined by dividing the variables Y into sets, and applying a single partition and shared donors for variables within each set, but different partitions and donors across sets. Intuitively, the variables within each set should be chosen to be homogeneous with respect to potential predictors, but specifics of implementation are a topic for future research.

5.2 Monotone Patterns

Now suppose we have a monotone pattern of missing data, such that Y₁, …, Y_j−1 are observed whenever Y_j is observed, for j = 2, … , n, and let S_j denote the set of cases with X , Y₁, … , Y_j observed. More generally, we allow each Y_j to represent a vector of variables with the same pattern. The p-partition hot deck can be applied to fill in Y₁, … Y_n sequentially, with the added feature that the set S_j can be used as the pool of donors when imputing Y_j . The single-partition hot deck based on a metric that conditions on X has the problem that it fails to preserve associations between observed and imputed components of Y for each pattern. Such associations are preserved if the p-partition method is applied across the sets of variables Y_j , but variables within each set are imputed using a single partition. Again, various elaborations of these two schemes could be envisaged.

5.3 General Patterns

For a general pattern of missing data, it is more challenging to develop a hot deck that preserves associations and conditions on the available information. The cyclic p-partition hot deck attempts to do this by iterative cycling through p-partition hot decks, in the manner of a Gibbs’ sampler (Judkins et al., 1993; England et al., 1994). This approach is a semi-parametric analogue of the parametric conditional imputation methods in the software packages IVEWare (Raghunathan et al., 2001) and MICE (Van Buuren & Oudshoorn, 1999). In the first pass, a simple method is used to fill in starting values for all missing items. Second and later passes define partitions based on the best set of adjustment variables for each item to be re-imputed. Each variable is then imputed sequentially, and the procedure continues until convergence. Convergence in this setting is uncertain, and deciding when to stop is difficult; England et al. (1994) suggest stopping the algorithm when estimates stabilize rather than individual imputations, based on the philosophy that the goal of imputation is good inferences, rather than optimal imputations. The properties of this method remain largely unexplored.

Other approaches to general patterns have been proposed. The full-information common-donor hot deck uses a different single-partition common-donor hot deck for each distinct pattern of missingness in the target vector (Marker et al., 2002). Another method is that of Grau et al. (2004), who extend the idea of neighbourhoods defined by predictive means to multivariate missingness. First, variables to be imputed are placed in a hierarchy, such that items higher in the hierarchy can be used for imputation of items lower in the list. Second, predictive means are determined for each item, using models built using complete cases only. For subjects with multiple missing values, the nearest neighbours are determined using the Mahalanobis distance based on the vector of predictive means for the missing items, and all values are copied from the selected donor to the recipient. All donors within a preset distance Δ are considered to be in the donor pool. Many multivariate methods seem relatively ad hoc, and more theoretical and empirical comparisons with alternative approaches would be of interest.

A slightly different approach is the joint regression imputation method of Srivastava & Carter (1986), which was extended to complex survey data by Shao & Wang (2002). Joint regression aims to preserve correlations by drawing correlated residuals. Srivastava & Carter (1986) suggest drawing residuals from fully observed respondents, and so with the appropriate regression model this becomes a hot deck procedure. Shao & Wang (2002) extend the method to allow flexible choice of distribution for the residuals and to incorporate survey weights. In the case of two items being imputed, if both items are to be imputed the residuals are drawn so they have correlation consistent with what is estimated from cases with all items observed. If only one item is imputed the residual is drawn conditional on the residual for the observed item. This differs from a marginal regression approach where all residuals are drawn independently, and produces unbiased estimates of correlation coefficients as well as marginal totals.

6 Properties of Hot Deck Estimates

We now review the (somewhat limited) literature on theoretical and empirical properties of the hot deck. The simplest hot deck procedure—using the entire sample of respondents as a single donor pool—produces consistent estimates only when data are missing completely at random (MCAR) (Rubin, 1976; Little & Rubin, 2002). The hot deck estimate of the mean equals the respondent mean in expectation, and the respondent mean is an unbiased estimate of the overall mean when data are MCAR. When data are not MCAR, two general frameworks for determining properties of estimates from imputed data have been developed: the imputation model approach (IM) and the non-response model approach (NM) (Shao & Steel, 1999; Haziza & Rao, 2006). Conditions for consistency of hot deck estimates depend on which of these two approaches is adopted.

The IM approach explicitly assumes a superpopulation model for the item to be imputed, termed the “imputation model”; inference is with respect to repeated sampling and this assumed data-generating model. The response mechanism is not specified except to assume that data are missing at random (MAR). In the case of the random hot deck this implies that the response probability is allowed to depend on auxiliary variables that create the donor pools but not on the value of the missing item itself. Brick et al. (2004) show using this framework that the (weighted or unweighted) hot deck applied within adjustment cells leads to an unbiased estimator under a cell mean model; within each cell elements are realizations of independently and identically distributed random variables. For nearest neighbour imputation, Rancourt et al. (1994) claim that estimates of sample means are asymptotically unbiased assuming a linear relationship between the item to be imputed and the auxiliary information, but no theoretical support is offered. Chen & Shao (2000) extend the approach of Rancourt et al. (1994) to show that the relationship between the imputed variable and the auxiliary information need not be linear for asymptotic unbiasedness to hold, with suitable regularity conditions.

Perhaps the most crucial requirement for the hot deck to yield consistent estimates is the existence of at least some donors for a non-respondent at every value of the set of covariates that are related to missingness. To see why, consider the extreme case where missingness of Y depends on a continuous covariate x, such that Y is observed when x < x₀ and Y is missing when x ≥ x₀. A hot deck method that matches donors to recipients using x clearly cannot be consistent when Y has a non-null linear regression on x, since donors close to recipients are not available, even asymptotically as the sample size increases. In contrast, parametric regression imputation would work in this setting, but depends strongly on the assumption that the parametric form of the mean function is correctly specified.

In lieu of making an explicit assumption about the distribution of item values, the NM approach makes explicit assumptions about the response mechanism. Also called the quasirandomization approach (Oh & Scheuren, 1983), the NM approach assumes that the response probability is constant within an imputation cell. Inference is with respect to repeated sampling and the assumed uniform response mechanism within cells. Thus for the random hot deck to lead to unbiased estimates, the within-adjustment-cell response probability must be constant. If sample selection is with equal probability, selection of donors may be by simple random sampling to achieve unbiasedness. For unequal probabilities of selection, selection of donors with probability of selection proportional to the potential donor’s sample weight leads to asymptotically unbiased and consistent mean estimates (Rao & Shao, 1992; Rao, 1996; Chen & Shao, 1999). Applications of both of these approaches to variance estimation can be found in Section 7.

Suppose now that the interest is in estimating either domain means, where a domain is a collection of adjustment cells, or cross-class means, defined as a subset of the population that cuts across adjustment cells (Little, 1986). The hot deck produces consistent estimates of domain and cross-class means if stratification on x produces cells in which Y is independent of response. Since one cannot observe the distribution of Y for the non-respondents, using all auxiliary variables to define the cells would be the best strategy. Often the dimension of x is too large for full stratification, and alternative distance metrics such as the predictive mean, Ŷ(x), or the response propensity, p̂(x), can be useful. Using these metrics to define adjustment cells was discussed by Little (1986). For domain means, predictive mean stratification and response propensity stratification both yield consistent estimates. For estimating cross-class means, predictive mean stratification produces estimates with zero large-sample bias, but response propensity stratification gives non-zero bias. In this case adjustment cells must be formed based on the joint distribution of response propensity and the cross-class variable in order to produce consistent estimates.

Most of the limited work on properties of the hot deck have concerned inferences about means, but properties for other statistics are also of interest. For regression and correlation analysis, it is desirable that imputation methods preserve associations, both within the imputed variables, and between the imputed and observed variables. As discussed above, the single partition common donor hot deck preserves associations between the imputations, since they are all from the same donor. Edit constraints between sets of imputed variables, such as constraints between height and weight, are also preserved by this approach. However, the lack of tailoring of the distance metric to individual imputed variables tends to degrade associations between imputed and observed variables; these tend to be better preserved by the partitioned hot decks, which tailor the distance metric.

Hot decks do not necessarily preserve edit constraints between observed and imputed variables. If it is important to preserve these edit constraints, they need to be checked, and the hot deck imputations adjusted if they are violated. This is clearly useful cosmetically, though it is less clear how important it is for subsequent statistical inferences.

An alternative approach to the hot deck is to generate imputations as draws from the distribution of the missing values based on a parametric model. Examples of this approach include the popular regression imputation, Bayesian MI methods in SAS PROC MI (SAS Institute, Cary, NC) or the sequential MI algorithms implemented in IVEware and MICE (Van Buuren & Oudshoorn, 1999; Raghunathan et al., 2001). Little (1988) points out that the adjustment cell method is in effect the same as imputing based on a regression model that includes all high-order interactions between the covariates, and then adding an empirical residual to the predictions; imputation based on a more parsimonious regression model potentially allows more main effects and low-order interactions to be included (Lillard et al., 1982; Little, 1988).

Several studies have compared parametric methods to the non-parametric hot deck. David et al. (1986) compared the hot deck used by the U.S. Census Bureau to impute income in the CPS to imputation using parametric models for income (both on the log scale and as a ratio) and found that the methods performed similarly. Several authors have compared hot deck imputation using predictive mean matching to parametric methods that impute predicted means plus random residuals (Lazzeroni et al., 1990; Heitjan & Little, 1991; Schenker & Taylor, 1996). The relative performance of the methods depends on the validity of the parametric model and the sample size. When the population model matches the parametric imputation model, hot deck methods generally have larger bias and are less precise. However, the hot deck is less vlunerable to model misspecification. If a model is used to define matches, as in hot deck with predictive mean matching, it is less sensitive to misspecification than models used to impute values directly. The hot deck tends to break down when the sample size is small, since when the pool of potential donors is limited, good matches for non-respondents are hard to find. Also, in small samples the bias from misspecification of parametric models is a smaller component of the mean squared error. Thus, parametric imputation methods become increasingly attractive as the sample size diminishes.

7 Variance Estimation

Data sets imputed using a hot deck method are often analyzed as if they had no missing values (Marker et al., 2002). In particular, variance estimates in the Current Population Survey continue to be based on replication methods appropriate for completely observed data (U.S. Bureau of the Census, 2002). Such approaches clearly understate uncertainty, as they ignore the added variability due to non-response. There are three main approaches to obtaining valid variance estimates from data imputed by a hot deck: (1) explicit variance formulae that incorporate non-response; (2) resampling methods such as the jackknife and the bootstrap, tailored to account for the imputed data; and (3) hot deck multiple imputation (HDMI), where multiple sets of imputations are created, and imputation uncertainty is propagated via MI combining rules (Rubin, 1987; Little, 1988). We now review these three approaches.

7.1 Explicit Variance Formulae

Explicit variance formulae for hot deck estimates can be derived in simple cases; see for example Ford (1983) for simple random sampling from the donor pool and Bailar & Bailar (1978) for the sequential hot deck. These methods make the strong and often unrealistic assumption that the data are missing completely at random (MCAR). Creating adjustment cells, applying one method separately within cells, and pooling the results eliminates bias attributable to differences in response across the cells. Alternatively, if one is willing to make some assumptions about the distribution of Y in the population, several methods have been developed that lead to explicit variance formulae.

The model-assisted estimation approach of Särndal (1992) allows variance estimation under the more realistic assumption that data are missing at random (MAR). By assuming a model for the distribution of Y in the population, the variance of an estimator in the presence of missingness is decomposed into a sampling variance and an imputation variance. Estimators are obtained using information in the sampling design, observed naïive values, and imputation scheme. Brick et al. (2004) extend Särndal’s method to the hot deck, using the assumption that within adjustment cells (g = 1, … , G) values of Y are independent and identically distributed with mean μ_g and variance ${\sigma }_g^2$. They derive a variance estimator that is conditionally unbiased, given the sampling, response, and imputation indicators, and argue that conditioning on the actual number of times responding units are used as donors is more relevant than the unconditional variance which averages over all possible imputation outcomes. Cell means and variances are the only unknown quantities that need estimation to use the variance formula. The authors note that their method covers many forms of hot deck imputation, including both weighted and unweighted imputation and selection with and without replacement from the donor pool.

Chen & Shao (2000) consider variance estimation for nearest neighbour hot deck imputation and derive the asymptotic variance of the mean in the case of a single continuous outcome (Y) subject to missingness and a single continuous auxiliary variable (x). Their formula requires specification of the conditional expectation of Y given x. In practice, one has to assume a model for the mean, such as E(Y | x) = α + βx , fit the model to the observed data, and use the estimates α̂ and β̂in their variance formulas. This method produces a consistent estimate of the variance, assuming the model is correct. Of note, they show that the empirical distribution function obtained from nearest neighbour imputation is asymptotically unbiased, and so quantile estimators are also unbiased.

7.2 Resampling Methods for Single Imputation

Model-assisted methods for variance estimation are vulnerable to violations of model assumptions. A popular alternative is resampling methods. One such method is the jackknife, where estimates are based on dropping a single observation at a time from the data set. Performing a naïve jackknife estimation procedure to the imputed data underestimates the variance of the mean estimate, particularly if the proportion of non-respondents is high. To correct this, Burns (1990) proposed imputing the full sample and then imputing again for each delete-one data set. However, this leads to overestimation when n is large and requires repeating the imputation procedure n + 1 times. To combat this, Rao & Shao (1992) proposed an adjusted jackknife procedure that produces a consistent variance estimate.

Rao and Shao’s jackknife method can be applied to random hot deck imputation of complex stratified multistage surveys; the more straightforward application to inference about means from a simple random sample with replacement is discussed here. Suppose that r units respond out of a sample of size n, and the simple unweighted hot deck is applied, yielding the usual estimate ȳ_HD. First, the hot deck procedure is applied to create a complete data set. The estimator for each jackknife sample is calculated each time a non-respondent value is deleted, but with a slight adjustment when respondents are deleted. Specifically, each time a respondent value is dropped the imputed non-respondent values are each adjusted by $E({\stackrel{\sim }{y}}_i^{(-j)})-E({\stackrel{\sim }{y}}_i)$, where ȳ_i is the imputed value for non-respondent i using the entire donor pool and ${\stackrel{\sim }{y}}_i^{(-j)}$ is the hypothetical imputed value with the j-th respondent dropped, and expectation is with respect to the random imputation. For the random hot deck this reduces to an adjustment of ${\overline{y}}_R^{(-j)}-{\overline{y}}_R$, where ${\overline{y}}_R^{(-j)}$ is the mean of the remaining (r − 1) respondents after deleting the j-th respondent. This adjustment introduces additional variation among the pseudoreplicates to capture the uncertainty in the imputed values that would otherwise be ignored by the naive jackknife. The adjusted jackknife variance estimate is approximately unbiased for the variance of ȳ_HD, assuming a uniform response mechanism and assuming the finite population correction can be ignored.

Extensions of this method to stratified multistage surveys and weighted hot deck imputation involve a similar adjustment to the jackknife estimators formed by deleting clusters; see Rao & Shao (1992) for details. Kim & Fuller (2004) describe application of the jackknife variance estimator to fractional hot deck imputation, first described by Fay (1993). A similar jackknife procedure for imputation in a without-replacement sampling scheme and for situations where sampling fractions may be non-negligible is discussed in Berger & Rao (2006). Chen & Shao (2001) show that for nearest neighbour hot deck imputation the adjusted jackknife produces overestimates of the variance since the adjustment term will be zero or near zero, similar to the difficulty in applying the jackknife to the sample median. They suggest alternative “partially adjusted” and “partially reimputed” methods that are asymptotically unbiased. Other popular resampling techniques for variance estimation include the balanced half sample method and the random repeated replication method. These methods require adjustments similar to those for the jackknife in the presence of imputed data; details are given in Shao et al. (1998) and Shao & Chen (1999).

Though the adjusted jackknife and its variants require only a singly-imputed data set, they are not without limitation. There must be accompanying information that indicates which values were initially non-respondents, a feature that is not often found with public-use data sets imputed via the hot deck (or any other procedure). In addition, the step of adjusting imputed values for each jackknife replicate requires the user to know the precise details of the hot deck method used for the imputation, including how the adjustment cells were formed and how donors were selected. In practice this means that either the end user carries out the imputation himself, or that the end user can be trusted to correctly recreate the original imputation.

The jackknife cannot be applied to estimate the variance of a non-smooth statistic, e.g. a sample quantile. A resampling method that allows for estimation of smooth or non-smooth statistics is the bootstrap (Efron, 1994), and its application to the hot deck was discussed by Shao & Sitter (1996) and Saigo et al. (2001). As with the jackknife, applying a naive bootstrap procedure to a singly-imputed data set leads to underestimation. However, a simple alteration leads to a bootstrap procedure that yields consistent variance estimates. First, the hot deck is used to generate a complete data set. From this a bootstrap sample of size n is drawn with replacement from the imputed sample. Instead of calculating a bootstrap estimate of ȳ at this point, the hot deck must be reapplied and the sampled respondent values used as the donor pool for the sampled non-respondents. Then the usual estimate ȳ ^(b) can be calculated for this b-th bootstrap sample. Bootstrap samples are drawn and the imputation repeated B times, and the usual bootstrap mean and variance formulae can be applied. The extra step of imputing at each bootstrap sample propagates the uncertainty, and thus yields a consistent estimate of variance. In addition, bootstrap estimates can be developed for multistage survey designs, for example by bootstrapping primary sampling units rather than individual units. As with the adjusted jackknife, the bootstrap requires knowledge of which values were imputed, which may not be available in public-use data sets. Chen & Shao (1999) consider variance estimation for singly-imputed data sets when the non-respondents are non-identifiable and derive design-consistent variance estimators for sample means and quantiles. The method only requires a consistent estimator of the response probability, which may be available when more detailed subject-specific response information is not, and produces an adjustment to the usual complete data variance formula (e.g. Cochran, 1977) to account for the uncertainty in imputation.

7.3 Multiple Imputation

First proposed by Rubin (1978), MI involves performing K ≥ 2 independent imputations to create K complete data sets. As before, assume that the mean of the variable y subject to non-response is of interest. Let θ̂_k, W_k denote the estimated mean and variance of ȳ from the k-th complete data set. Then the MI estimator of ȳ is simply the average of the estimators obtained from each of the K completed data sets:

$${\overline{\theta }}_K=\frac{1}{K}\sum _{k=1}^K{\widehat{\theta }}_k.$$ (3)

The averaging over the imputed data sets improves the precision of the estimate, since the added randomness from drawing imputations from an empirical distribution (rather than imputing a conditional mean) is reduced by a factor of 1/K. The variance of θ̂_k is the sum of the average within-imputation variance and the between-imputation variance. Ignoring the finite population correction, the average within-imputation variance is

$${\overline{W}}_K=\frac{1}{K}\sum _{k=1}^K{W}_k$$

and the between-imputation variance is

$$B_K=\frac{1}{K-1}\sum _{k=1}^K{({\widehat{\theta }}_k-{\overline{\theta }}_K)}^2.$$

The total variance of θ̂_k is the sum of these expressions, with a bias correction for the finite number of multiply imputed data sets,

$$\text{Var}({\overline{\theta }}_K)={\overline{W}}_K+\frac{K+1}{K}{B}_K.$$ (4)

When the hot deck procedure is used to create the MI data sets, and the same donor pool is used for a respondent for all K data sets, the method is not a proper MI procedure (Rubin, 1978). The method produces consistent estimates of ȳ as K → ∞ but since the predictive distribution does not properly propagate the uncertainty, its variance is an underestimate, even with an infinite number of imputed data sets. The degree of underestimation becomes important if a lot of information is being imputed.

Adjustments to the basic hot deck procedure that make it “proper” for MI have been suggested, though not widely implemented by practitioners. One such procedure is the Bayesian Bootstrap (BB) (Rubin, 1981). Suppose there are M unique values, d = (d₁, d₂, … d_M) of Y observed among the respondents, with associated probabilities φ = (φ₁, φ₂, … φ_M). Imposing an non-informative Dirichlet prior on φ yields a Dirichlet posterior distribution with mean vector φ̂ = (φ̂₁, … φ̂_M) with φ̂_m = r_m/r, where r_m denotes the number of times that d_m is observed among the respondents. Imputation proceeds by first drawing φ* from the posterior distribution and then imputing values for each non-respondent by drawing from d with vector of probabilities φ*. Repeating the entire procedure K times gives proper multiple imputations.

The Approximate Bayesian Bootstrap (ABB) approximates the draws of φ from the above Dirichlet posterior distribution with draws from a scaled multinomial distribution (Rubin & Schenker, 1986). First an r-dimensional vector X is drawn with replacement from the respondents’ values. Then the n − r non-respondent values are drawn with replacement from X. This method is easy to compute, and repeated applications will yield again yield proper multiple imputations. Variances for the ABB method are on average higher than variances for the BB method by a factor of (r + 1)/r, but confidence coverage for the two methods were very close and always superior to the simple hot deck in simulations in (Rubin & Schenker, 1986). Kim (2002) notes that the bias of the ABB method is not negligible when sample sizes are small and response rates are low. He suggests a modification in which the size of the vector X drawn from the respondents is not r, but instead is a value d chosen to minimize the bias in the variance for small samples. The value of d depends on the total sample size and the response rate and as n → ∞, d → r, so that in large samples the correction is not needed. See Kim (2002) for details.

One of the biggest advantages to parametric multiple imputation is that it allows users to easily estimate variances for sample quantities besides totals and means. To achieve this with the hot deck requires modifying the imputation procedure to be “proper,” via BB or ABB. However, implementation of these methods in sample settings more complex than simple random sampling (i.e. multistage sampling) remains largely unexplored.

8 Detailed Example

With so many variations of the hot deck in use, we set out to compare a subset of these methods using a real data set. The third National Health and Nutrition Examination Survey (NHANES III) is a large-scale survey that has previously been used to compare imputation methods, including parametric and non-parametric and single and multiple imputation methods (Ezzati-Rice et al., 1993a,b; Khare et al., 1993). NHANES III data were also released to the public as a multiply imputed data set (U.S. Department of Health and Human Services, 2001). Details of the survey design and data collection procedures are available in Plan and Operation of the Third National Health and Nutrition Examination Survey (U.S. Department of Health and Human Services, 1994).

8.1 Description of the Data

NHANES III collected data in three phases: (a) a household screening interview, (b) a personal home interview, and (c) a physical examination at a mobile examination center (MEC). The total number of persons screened was 39 695, with 86% (33 994) completing the second phase interview. Of these, only 78% were examined in the MEC. Previous imputation efforts for NHANES III focused on those individuals who had completed the second phase; weighting adjustments were used to compensate for non-response at this second stage. Since the questions asked at both the second and third stage varied considerably by age we chose to select only adults age 17 and older who had completed the second phase interview for the purposes of our example, leaving a sample of 20,050. Variables that were fully observed for the sample included age, gender, race, and household size. We focused on the imputation of diastolic blood pressure measurements (DBP) and selected additional variables from the second and third stages that we hypothesized might be related to this outcome: self-rating of health status (a five-level ordinal variable), an indicator for ever having high blood pressure, and body mass index. To have a “truth” against which to measure each imputation method we selected the cases with fully observed data on all eight selected variables as our population (n = 16 739, 83.5% of total sample).

8.2 Sampling and Non-response Mechanisms

A sample of size 800 was drawn by simple random sampling from the population for an approximate 5% sampling fraction. We created a propensity model to induce missingness in the sample, aiming to induce bias such that a complete case analysis would lead to overestimation of the population average DBP. The following model was used to obtain the probability of non-response for subject i:

$$\text{logit}(P(M_i=1))=-3+1.5\ast I({\text{age}}_i<40)+0.75\ast {\text{female}}_i+0.25\ast \text{Mexican}-{\text{American}}_i$$

where female_i and Mexican-American_i equal one if subject i is female and Mexican-American, respectively, and zero otherwise. The individual probabilities of non-response ranged from 0.10 to 0.75, with an expected percent missing of 33.1%, slightly more than double the observed missingness on DBP in the original NHANES data set (15.4%). We also explored another propensity model that mimicked the propensities in the original data and thus had a lower non-response rate. Results arising with the lower non-response rate had the same general properties as the higher non-response rate but differences among the imputation methods were less pronounced; results from this alternative propensity model are not shown.

Non-response indicators for each unit in the sample were independently drawn from a Bernoulli distribution with probabilities according to the propensity model. Non-respondent values were then deleted from the drawn sample to create the respondent data set. This process of sampling and creating non-respondents was repeated 1 000 times.

8.3 Imputation Methods

The following imputation methods were applied to the incomplete sample: adjustment cell random hot deck, predictive mean random hot deck, propensity cell random hot deck, and parametric regression imputation. All three hot deck methods create donor pools based on a distance metric and use equal probability draws from the donors in each pool to impute for the non-respondents. The adjustment cell hot deck used age, gender, and race to create imputation classes. In comparison, the predictive mean and the response propensity hot decks allowed incorporation of many more variables; Table 2 lists the imputation methods and auxiliary variables used in each method. Because a total of 18 cells were created in the cross-classification of variables in the adjustment cell method we chose to utilize a similar number of cells in the other two methods, 20 equally sized cells for both predictive mean and propensity stratification. Attempts to include more variables when defining adjustment cell strata lead to cells that were too sparse; instead of trying to collapse cells ad-hoc we opted to use the coarser cells. We required a minimum of five respondents in each imputation cell to proceed with hot deck imputation; this minimum was met in all runs. The parametric regression imputation method assumed normality for the outcome and used the same model as that which created the predictive mean strata.

Table 2.

Imputation methods applied to samples drawn from the NHANES III data.

Method	Imputation Cell Variables	Number of Cells
1. Adjustment cells	age (categorical), gender, race	18
2. Predictive Mean cells	age (continuous), gender, race, household size, health status, ever high BP, body mass index	20, equally sized
3. Propensity cells	age (continuous), gender, race, household size	20, equally sized
4. Parametric Model	age (continuous), gender, race, household size, health status, ever high BP, body mass index	n/a

For each method we applied both single and multiple imputation. Single imputation resulted in one estimator of the mean for each of the four imputation methods. A total of three methods for estimating variance for SI after random hot deck imputation were used: a naïve estimator treating the imputed values as if they were observed (SI Naïve), an exact formula (SI Formula), and the jackknife of Rao & Shao (1992) (SI RS Jackknife). For the parametric method there were two variance estimators: a naïve estimator and a bootstrap estimator (SI Bootstrap).

We applied three versions of MI to the incomplete data leading to three separate mean estimators for each imputation method: improper MI with K = 5 data sets (IMI 5), proper MI with K = 5 (PMI 5), and proper MI with K = 20 (PMI 20). The simulation was carried out using the software R with the MICE package for parametric imputation (Van Buuren & Oudshoorn, 1999; R Development Core Team, 2007).

Empirical bias and root mean square error (RMSE) for each imputation method M were calculated as follows,

$$\begin{array}{l}\text{EBias}=\frac{1}{1000}\sum _{i=1}^{1000}({\widehat{\theta }}_{Mi}-\theta )\\ \text{RMSE}=\sqrt{\frac{1}{1000}\sum _{i=1}^{1000}{({\widehat{\theta }}_{Mi}-\theta )}^2}\end{array}$$

where θ̂_Mi is the estimate of the population mean using method M for the i-th replicate and θ is the true population parameter. Variance estimators for each method were evaluated using the empirical variance (defined as the variance of the point estimator observed in the Monte Carlo sample) and the average variance estimate. In addition to evaluating accuracy in point and variance estimators we were interested in coverage properties of the imputation methods, so the actual coverage of a nominal 95% confidence interval and average CI length were also calculated.

8.4 Results

Table 3 displays results from the simulation. All methods performed well in terms of bias, with only the complete case estimate under propensity model 2 demonstrating large bias and thus severe undercoverage (47%). The propensity strata did exhibit higher bias than either the adjustment cell or predictive mean methods but the difference was not significant. Naïve variance estimators always underestimated the empirical variance, leading to empirical coverages for a nominal 95% interval ranging from 81–90%. Improper MI for all hot deck methods underestimated the variance, leading to coverage of only 90–91%. All other methods had near the 95% nominal coverage. Across all hot deck methods MI had lower empirical variance than SI methods, leading to shorter confidence intervals but still adequate coverage. MI with K = 20 showed slight gains in efficiency over K = 5. This simulation failed to demonstrate any major advantage of parametric imputation over the hot deck methods. Performance was very similar, with the parametric imputation having slightly lower RMSE. MI with parametric imputation had shorter confidence intervals than with either adjustment cell or predictive mean strata, however CI length was virtually identical to that of the predictive mean strata.

Table 3.

Results from 1 000 replicates (n = 800).

Method	Variance Estimator	Empirical Bias	RMSE	Empirical Variance	Average Variance	95%Coverage	CI Length
Before Deletion		0.003	0.47	0.22	0.21	95.6	1.8
Complete case		1.13	1.26	0.31	0.31	47.0	2.2
Adjustment cells	SI, Naïve	−0.016	0.67	0.45	0.21	83.1	1.8
	SI, Exact	−0.016	0.67	0.45	0.45	94.5	2.6
	SI, RS Jackknife	−0.016	0.67	0.45	0.47	95.8	2.7
	MI (K = 5), Improper	−0.004	0.63	0.39	0.29	91.5	2.2
	MI (K = 5), Proper	−0.007	0.65	0.42	0.41	94.7	2.7
	MI (K = 20), Proper	−0.007	0.63	0.39	0.39	94.5	2.4
Predictive Mean cells	SI, Naïve	−0.036	0.67	0.45	0.21	82.5	1.8
	SI, Exact	−0.036	0.67	0.45	0.38	91.9	2.4
	SI, RS Jackknife	−0.036	0.67	0.45	0.42	94.2	2.5
	MI (K = 5), Improper	−0.026	0.63	0.39	0.29	90.5	2.1
	MI (K = 5), Proper	−0.031	0.64	0.41	0.36	94.3	2.4
	MI (K = 20), Proper	−0.026	0.62	0.38	0.34	94.1	2.3
Propensity cells	SI, Naïve	−0.060	0.67	0.44	0.22	82.9	1.8
	SI, Exact	−0.060	0.67	0.44	0.45	95.7	2.6
	SI, RS Jackknife	−0.060	0.67	0.44	0.48	96.6	2.7
	MI (K = 5), Improper	−0.048	0.64	0.40	0.30	91.7	2.2
	MI (K = 5), Proper	−0.049	0.65	0.42	0.40	95.0	2.6
	MI (K = 20), Proper	−0.053	0.62	0.39	0.38	94.8	2.4
Parametric Model	SI, Naïve	−0.033	0.69	0.48	0.21	81.2	1.8
	SI, Bootstrap	−0.033	0.69	0.48	0.49	94.5	2.7
	MI (K = 5), Proper	−0.031	0.63	0.39	0.35	93.8	2.4
	MI (K = 20), Proper	−0.030	0.61	0.37	0.33	93.6	2.3

Bolded values are below 1.96 simulation standard errors.

Italicized values are above 1.96 simulation standard errors.

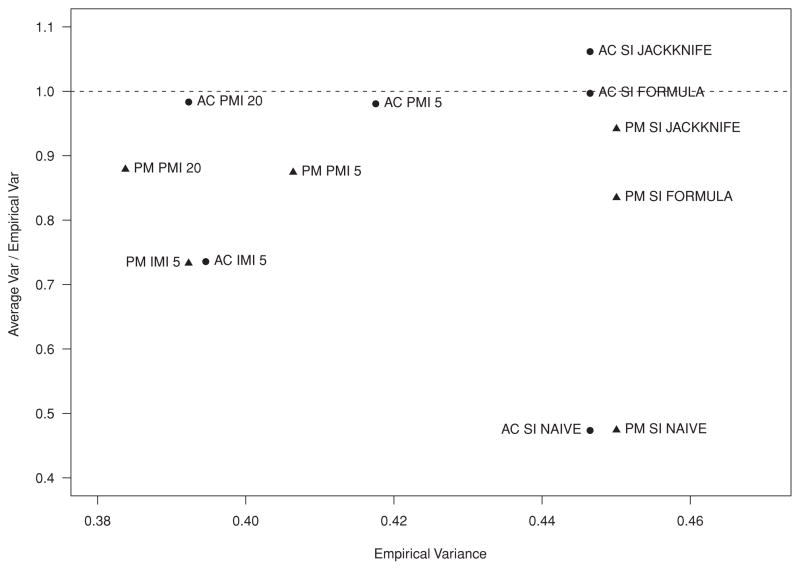
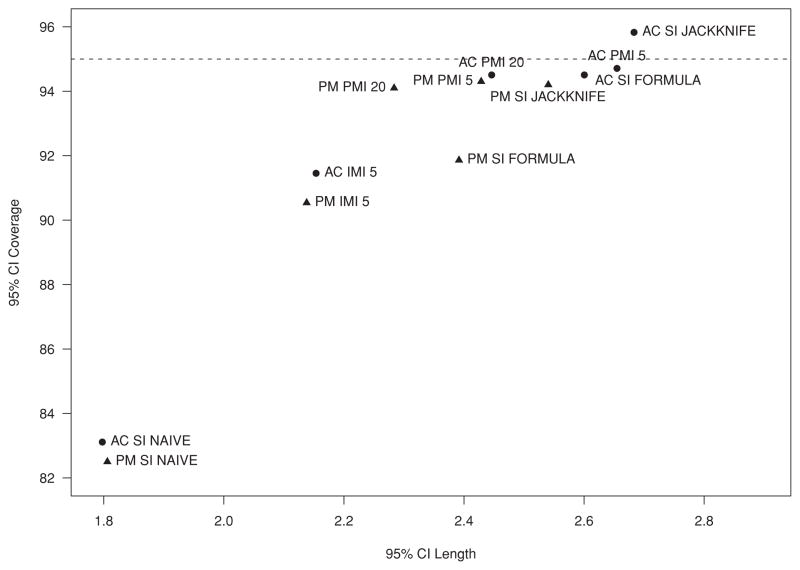
Figure 1 plots the ratio of average to empirical variance against the empirical variance for the adjustment cell (●) and predictive mean cell (▲) methods to give insight into their efficiency. Figure 2 similarly plots CI coverage against CI length. Predictive mean MI demonstrated smaller empirical variance than adjustment cell MI with only slight underestimation of the variance, but coverage was not affected and remained at nominal levels. The jackknife following SI for both methods accurately estimated its empirical variance but was not as efficient; variance estimates were accurate but larger than those of the MI methods and confidence coverage was at nominal levels but with large CI length. Overall the predictive mean method appeared to have a slight advantage over the adjustment cell method as evidenced by a gain in efficiency seen in both single and multiple imputation strategies. We note, however, that the adjustment cell methods were limited to the use of three variables due to sparse cells, while the predictive mean method allowed for the incorporation of all the available variables. Even in this simulation with a limited number of variables, the inability of the adjustment cell methods to include all available auxiliary information may have been a major cause of its poorer performance. More generally, adjustment cell methods may be reasonable when the number of observed predictors is modest, but predictive mean matching seems preferable in settings with more extensive available information.

Figure 1.

Empirical variance and ratio of average to empirical variance for hot deck imputation within adjustment cells (●) and predictive mean cells (▲). Results from 1 000 replicates (n = 800).

Figure 2.

Confidence interval length and coverage for hot deck imputation within adjustment cells (●) and predictive mean cells (▲). Results from 1,000 replicates (n = 800).

This simulation used a variety of random hot deck methods to impute data in a real data set. All hot deck methods performed well and without bias, however the relationship between outcome and predictor variables was not particularly strong in this data set. Applying the predictive mean model to the complete population yielded an R² of 0.20, and this weak association may partially explain why the adjustment cell method that only used three auxiliary variables had similar results to the more flexible methods of creating the donor pools. This simulation also demonstrated the potentially severe effects of treating singly imputed data as if it were observed data, a practice that while unfortunately common in practice cannot be recommended.

9 Conclusion

The hot deck is widely used by practitioners to handle item non-response. Its strengths are that it imputes real (and hence realistic) values, it avoids strong parametric assumptions, it can incorporate covariate information, and it can provide good inferences for linear and non-linear statistics if appropriate attention is paid to propagating imputation uncertainty. A weakness is that it requires good matches of donors to recipients that reflect available covariate information; finding good matches is more likely in large than in small samples.

Our review highlights several issues with the hot deck that we feel deserve consideration. The first issue is the use of covariate information. Adjustment cell methods, while popular in their simplicity, limit the amount of auxiliary information that can be effectively used. Alternative distance metrics are more flexible and should be considered, in particular we feel the predictive mean metric shows promise. When choosing the variables for creating donor pools, the priority should be to select variables that are predictive of the item being imputed, Y. For example, forward selection for the regression of Y on X₁, … , X_k might be used to choose covariates that significantly predict Y and could be the basis for a predictive mean metric for defining donor pools. The response propensity is important for reducing bias, but only if it is associated with Y; traditional covariate selection methods could be used to determine if auxiliary information that is predictive of non-response is also associated with Y. With multiple Y’s, the choice of a single metric (i.e. single partition hot deck) requires compromising matches, whereas partitions for each Y allow tailoring of metrics to each specific item. However, in order to preserve associations among the imputed values, each step should condition on previously imputed Y’s. A topic that apparently has not received attention has been the development of hot-deck approaches that have the property of double robustness, meaning that they yield consistent estimates if either the model for the missing variable or the model for the response propensity are correctly specified (Robins et al., 1994, 1995; Bang & Robins, 2005). Matches based on penalized spline of propensity of prediction (PSPP) (Little & An, 2004; Zhang & Little, 2009) seem one possibility here.

A second issue surrounding the hot deck is how to deal with “swiss cheese” missing data patterns. While some methods have been suggested (e.g. the cyclic p-partition hot deck), we were unable to find much theory to support these methods. More development of their theoretical properties and simulation studies of performance are needed.

The third and final issue that must be taken into consideration is how to obtain valid inference after imputation via the hot deck. As with any imputation method, it is important to propagate error, and with the hot deck this step is often overlooked. In practice, we think that the single most important improvement would be to compute standard errors that incorporate the added variance from the missing information when the fraction of missing information is substantial, by one of the sample reuse methods or MI, as discussed in Section 7. There has been considerable debate among methodologists about the relative merits of these two approaches, particularly under misspecified models (Meng, 1994; Fay, 1996; Rao, 1996; Rubin, 1996; Robins & Wang, 2000; Kim et al., 2006), and more simulation comparisons of the repeated-sampling properties of these approaches would be of interest. However, either approach is superior to assuming the added variance from imputation is zero, which is implied by treating a single imputed data set as if the imputed values are real.

Despite the practical importance of the hot deck as a method for dealing with item non-response, the statistics literature on theory of the method and comparisons with alternative approaches is surprisingly limited, yielding opportunities for further methodological work. Other areas where more development seems possible include better ways to condition on available information in creating donor pools, ways to assess the trade-off between the size of donor pool and quality of matches, and methods for multivariate missing data with a general pattern of missingness. On the theoretical side, consistency of the hot deck has been shown under MCAR, or missing completely at random within adjustment cells, but useful conditions for consistency under MAR when conditioning on the full set of available information seem lacking. Also hot deck methods for situations where non-response is “non-ignorable” (that is, the data are not missing at random) have not been well explored. Hopefully this review will stir some additional methodological activity in these areas.