Movement mechanics as a determinate of muscle structure, recruitment and coordination

Abstract

During muscle contractions, the muscle fascicles may shorten at a rate different from the muscle-tendon unit, and the ratio of these velocities is its gearing. Appropriate gearing allows fascicles to reduce their shortening velocities and allows them to operate at effective shortening velocities across a range of movements. Gearing of the muscle fascicles within the muscle belly is the result of rotations of the fascicles and bulging of the belly. Variable gearing can also occur as a result of tendon length changes that can be caused by changes in the relative timing of muscle activity for different mechanical tasks. Recruitment patterns of slow and fast fibres are crucial for achieving optimal muscle performance, and coordination between muscles is related to whole limb performance. Poor coordination leads to inefficiencies and loss of power, and optimal coordination is required for high power outputs and high mechanical efficiencies from the limb. This paper summarizes key studies in these areas of neuromuscular mechanics and results from studies where we have tested these phenomena on a cycle ergometer are presented to highlight novel insights. The studies show how muscle structure and neural activation interact to generate smooth and effective motion of the body.

1. Prologue

Muscles have a surprising variety of functions during locomotion and can serve as motors, brakes, springs and struts [1]. These muscle functions depend on the arrangement of the muscle fibres within the muscle belly, the length and velocity of the fibres and also on the timing of their activation relative to those length changes. When the muscle fibres undergo substantial length change the muscle can act as a motor if it is active during shortening, or a brake if it is active during lengthening; when the length change is minimal then the muscle can act like a strut if it actively develops force to resist stretch [1]. Muscle fibre velocity may differ from the velocity of the muscle-tendon unit (MTU) in a process known as gearing. Thus, the extent to which the muscle fibres change length during a limb motion depends on how they are geared relative to the MTU. The timing and the level of activation are under neural control. This paper is a synthesis of previous literature on both gearing and activation, with a particular focus on some of the more recent findings in man. We introduce additional findings about structural mechanics in man and propose that some of the features of muscle gearing actually result from the interactions between the structural mechanics and the activation patterns of the muscles.

2. Muscle structure and fascicle gearing

MTUs are comprised of both tendinous structures containing a large proportion of collagen fibres, and skeletal muscle fibres containing the actin- and myosin-rich contractile machinery. The skeletal muscle fibres typically lie parallel to each other and are bundled to form fascicles that combine to form the muscle belly. The mechanics of fibres and fascicles can be assumed to be similar for the purpose of this discussion. Muscle fibres are elongated cells that actively develop force to drive movements. The force that each muscle fibre develops is largely a function of its activation state, length and shortening velocity [2,3]. At fast shortening velocities, the force and the power generated by the muscle fibres are diminished, and so it is important that the fibre shortening velocity does not increase to the very high velocities that can occur in the MTUs during rapid movements. In this study, the ratio between the MTU velocity, V_mtu, and the fibre velocity, V_f, is termed the MTU gearing ratio.

The MTU gearing ratio, V_mtu/V_f, is the product of two components: V_mtu/V_b and V_b/V_f, where V_b is the velocity at which the muscle belly shortens. The contribution of the tendon to the MTU gearing ratio, V_mtu/V_b, can result in an uncoupling of the displacements between the muscle belly and MTU. For a given MTU length change, the muscle belly length change depends on the length and compliance of the external tendon. MTUs that have shorter or stiffer tendons will experience belly length changes more similar to the MTU length changes than will MTUs with longer or more compliant tendons. Additionally, the uncoupling between the MTU and belly displacements depends on the magnitude and phase of the muscle belly force relative to the moments and ranges of motions of the joints over which the MTU spans. Tendon compliance allows the muscle belly length to change at rates appropriate to their optimal muscle fibre velocities even though the MTU may be changing length at a different rate [4].

Muscle fascicles are geared within the muscle belly (V_b/V_f) owing to their structural arrangement [5]. The force vector produced by the muscle belly has a magnitude and direction, and the direction of this force can be considered the line of action of the muscle belly. The longitudinal axes of individual muscle fibres are not necessarily oriented along this line of action of the muscle belly, and the angle between the muscle fibres and the line of action of the muscle belly is known as the pennation angle, β [6]. In some studies, the pennation angle is considered as the angle between the muscle fibres and the superficial aponeurosis [7]. These two definitions of pennation become the same in the mid-region of the muscle belly if the aponeurosis is parallel to the line of action of the muscle and if the fibres are linear. Resting pennation angles in human muscles are typically less than 10°, but can reach about 30° for the biceps femoris, vastus medialis and soleus [8–11]. The role of fascicle pennation to the gearing of the fascicles within the belly is shown in figure 1 and discussed below.

Figure 1.

Schematic diagrams of a muscle fascicle (dashed line) in a block of muscle tissue. As the muscle shortens then it changes its thickness and width, and the fascicle may rotate to a different pennation. Numerical examples for such contractions are given in table 1.

During contraction, the volume of a muscle remains constant [12], which is a property used in models of whole muscle structure [2,13]. This can be combined with simple geometric considerations to predict the effect of fascicle pennation and muscle thickness on the gearing of the fascicles within the muscle belly. If the pennation is kept constant (case A in table 1), then the muscle belly shortening would be less than the fascicle shortening, and so the gearing (V_b/V_f) would be less than one. This would not serve to diminish the fascicle velocity and so this example highlights how pennation alone cannot gear the muscle fascicles down to lower velocities.

Table 1.

Structural parameters for a block of muscle shown in figure 1 before and after shortening. (L_f, fascicle length; L_m, muscle length; β, pennation; t, thickness.)

before shortening	Lf1 (mm)	Lm1 (mm)	β1 (degree)	t1 (mm)	w1 (mm)
	60	56.38	20	20.52	20.52
after shortening	Lf2 (mm)	Lm2 (mm)	β2 (degree)	t2 (mm)	w2 (mm)	gearing ratio
case A, constant pennation	54.00	50.74	20	18.47	25.33	0.94
case B, constant thickness	54.73	50.74	22.02	20.52	22.80	1.07
case C, variable pennation and thickness	56.45	50.74	26	24.75	18.90	1.59

If the muscle thickness is kept constant, then the muscle fascicles must rotate as the belly shortens. This fascicle rotation results in reduced fascicle length change and thus higher gearing (case B in table 1). Muscle fascicle length, pennation and belly thickness are all inter-related (figure 1), and so the assumption of constant thickness has been used to simplify some previous muscle models [14,15]. However, recent studies using ultrasound imaging of muscles have shown that substantial changes in muscle thickness can actually occur during contraction. The thickness of the lateral gastrocnemius may increase by up to 41 per cent during isometric contraction [7,16]. The extent of changes in thickness seem to be muscle-specific with no changes being apparent during contractions of the medial gastrocnemius [7,16].

By relaxing both the pennation angle and thickness constraints, the muscle fascicles can then rotate and the thickness may increase during contraction (case C in table 1). In this example, we have used a modest 6° rotation and 21 per cent increase in thickness, which are at the low end of observed structural changes in vivo: the pennation can increase from 30° to 60° during contraction in the rat gastrocnemius [17]. In man, the pennation angles have been reported to vary between 14° and 21° in the vastus lateralis during shortening [18] and between 11° and 37° in the lateral gastrocnemius during maximal isometric contractions [7]. The data for case C in table 1 show that not only is fascicle gearing within the muscle belly dependent on fascicle rotations, but also it is enhanced by the ability of the muscle to increase in thickness. While some studies have reported changes in muscle thickness with contraction [5,7], and changing thicknesses have been predicted as a consequence of a variety of models [5,13,19,20], we have little theoretical framework to understand the interaction between muscle thickness, fibre rotations and gearing during contractions.

Appropriate gearing of the muscle fibres is important because it allows fibres to change length at rates that result in effective force and power production and good mechanical efficiencies even when the MTU is changing length at very different rates. The gearing of the muscle fibres may even vary according to the mechanical task, and variable gearing can extend the range of velocities over which the muscle fibres can be effective [5]. Gearing of the muscle fibres for a given movement is the result of gearing at a number of different structural levels and mechanisms in the MTU: tendon compliance, pennation angle of the fibres and changes in muscle thickness. Relatively little is known about the role of muscle fibre rotations and muscle belly thickness in the mechanical function of MTUs. Here, we will focus on the role of these structural parameters in the function of the muscle bellies.

This simple model (figure 1 and table 1) highlights that pennation angle alone is not sufficient to gear the fascicles to a lower velocity within the muscle belly. However, the fascicles in pennate muscles do rotate during contractions, and this rotation results in a more substantial belly gearing. During contractions, greater fascicle rotations cause increases to the belly gearing while reduced fascicle rotations result in smaller belly gearings. It is likely that the extent of the fascicle rotations depends on the bulging of the muscle belly. During contraction, the tendon stretches when it is loaded: this will lead to a reduction in the length of the muscle belly that, in turn, results in a bulging of the belly in order to maintain a constant muscle volume. Hence, muscle activation patterns that drive changes in muscle force and consequently tendon loading will also affect the gearing of the fascicles.

If muscle fibres shorten at velocities faster than their maximum intrinsic speed, V_max, then they will be unable to actively develop any force, and such fast contraction speeds yield those fibres mechanically incompetent. Fish axial muscle makes a peculiar example of such a situation, where the gearing of the fast and slow fibres relative to spine flexion is very different [21–23]. During fast-start swimming manoeuvres the slow fibres undergo length changes at rates far greater than their V_max [24], and it has been shown that fast swimming fish barely activate their slow axial muscle [25]. The optimal shortening velocities for a muscle fibre to generate maximum power (typically 0.25–0.36 V_max, [26–28]) and operate at maximum efficiency (0.15–0.29 V_max, [28,29]) are considerably less than V_max. Some rapid movements may thus result in muscle fibres shortening at rates less than V_max, but still faster than the optimal velocity for a given fibre; in these situations those fibres may be able to develop some force and power, but these mechanical outputs would be more effectively achieved by the activation of faster fibre types.

3. Fascicle gearing in the triceps surae in man

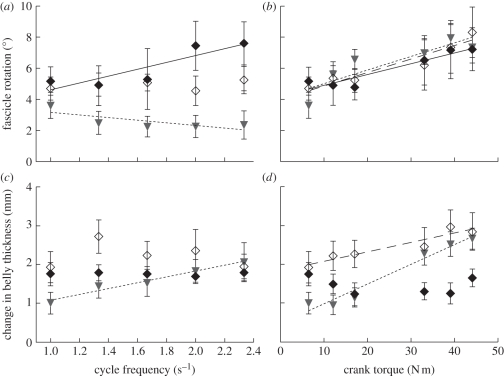
Fascicle gearing in humans is also crucial to limit the muscle fibre shortening and lengthening velocities and to maintain the effective use of the muscles across a range of locomotor tasks. In order to further understand the mechanisms driving muscle fibre gearing we have studied structural parameters in the ankle extensor muscles of the triceps surae in man during the dynamic locomotor task of cycling (figures 2 and 3). During these cyclic contractions, the muscle fascicles underwent cycles of lengthening and shortening that were coupled to cycles of fascicle rotations and changes in muscle thickness. In these studies, the muscle fascicles always changed length at rates slower than those for the MTU or muscle bellies, although there were differences between the muscles in how this was achieved (figure 2). This is to be expected as the gearing is influenced by tendon length, muscle fascicle pennation and belly thickness, and all these parameters differ between these ankle muscles [7,30,31]. At higher crank torques, the velocities of the fascicles, muscle bellies and MTUs showed increases (of about 68% for a 6.9-fold increase in torque), which was related to greater range of motion for the joints. However, a much larger increase in velocity was observed in association with increased cycle frequency (193% for a 2.3-fold increase in frequency) which was due to the shorter period for each contraction cycle. An interesting observation from our study during high-cadence cycling (2.3 cycles s⁻¹) was that two out of the six subjects had soleus muscle fibre shortening velocities that were close to or even exceeded the estimated V_max for slow fibres [32]; furthermore, this cycling cadence can be exceeded by elite trained athletes and so it is possible that the slowest fibres in the soleus can be made to shorten at rates faster than V_max. These results demonstrate that some slow fibres may be mechanically incompetent at the fastest locomotor speeds, despite the gearing mechanisms that occur in the muscles. This issue is discussed in more detail in the next section.

Figure 2.

Fascicle rotations (change of pennation) and changes of belly thickness that occur during cycling in the ankle extensor muscles (medial gastrocnemius: filled diamonds, solid line; lateral gastrocnemius: open diamonds, dashed line; soleus: triangles, dotted line). Points show the mean ± s.e.m. Least-squares regression lines are shown for cases where there was a significant effect of cycle frequency or crank torque on the velocity (p < 0.05, ANCOVA).

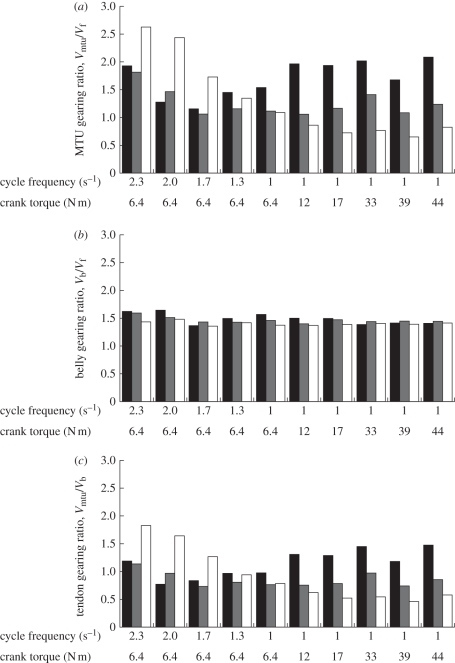
Figure 3.

Gearing ratios in the ankle extensor muscles during cycling at a range of mechanical conditions. Bars show the gearing ratios for the medial gastrocnemius (black), lateral gastrocnemius (grey) and soleus (white). Gearing ratios were calculated from the fascicle and muscle belly velocity measured from six subjects [32], and from the MTU velocities for six subjects measured in this study. For both sets of measurements, the subjects were of similar age, height and cycling experience and an identical cycling protocol was used. (a) V_mtu /V_f ; (b) V_b /V_f ; (c) V_mtu /V_b.

In our study, increases in the required crank torque occurred with increased rotations of the fascicles (main effect across all muscles, table 2). The observed increase in fascicle rotation supports previous findings for the lateral gastrocnemius and soleus during isometric contractions in man [16]. In addition, we show that fascicle rotations significantly covary with the load supported by the limb. However, these results are superficially different to an in situ study of isotonic contractions in the turkey lateral gastrocnemius [5]; reasons for these differences are discussed below. In our study (figure 2 and table 2), there was no consistent relation between fascicle rotation and cycle frequency, with the three tested muscles responding differently to this factor.

Table 2.

Results from ANCOVA for all three ankle extensor muscles. Arrows show where cycle frequency or crank torque showed a significant co-variance with thickness, pennation or gearing (positive relation in all cases, p < 0.05).

	change in thickness Δt (mm)	change in pennation Δβ (degree)	MTU gearing Vmtu/Vf	belly gearing Vb/Vf	tendon gearing Vmtu/Vb
cycle frequency	⇑	—	⇑	⇑	⇑
crank torque	⇑	⇑	—	—	—

The lateral gastrocnemius (LG) and soleus muscles showed greater changes in thickness at the higher crank torques, although this was not observed in the medial gastrocnemius (MG; table 2 and figure 2). This is similar to observations of greater bulging in lateral gastrocnemius and soleus but not medial gastrocnemius that can be calculated using data from isometric contractions [16]. More interestingly, the results showed that similar muscle thicknesses could occur with very different fibre rotations (2.3 s⁻¹ versus 1 s⁻¹ at 6.4 N m for the MG; and 2.3 s⁻¹ at 6.4 N m versus 1 s⁻¹ at 33 N m for the soleus). These results highlight that during dynamic contractions, there is no unique combination of pennation and thickness, but rather a range of β can occur for a given thickness, t, during these dynamic contractions.

The architectural gearing ratio (AGR) has previously been used to define the ratio of the MTU shortening velocity to the muscle fibre shortening velocity [5], but owing to the nature of the protocols in this previous study, the AGR is most similar to our belly gearing ratio. As increases in the MTU gearing ratio at higher speeds would extend the range of velocities over which the muscle would be powerful and efficient, then it would be more effective for the MTU gearing ratio to increase with muscle velocity rather than force. MTU gearing ratio depends on both β and t, and as both these values change with load and velocity (figure 2), it should be expected that the MTU gearing ratio also changes with these mechanical demands. Indeed, our results showed that the MTU gearing ratio increased with increasing pedal cadence, but showed no significant relation with crank torque (table 2). This supports the concept that it is more effective for the MTU gearing ratio to increase with muscle velocity rather than force. These results are again superficially different to those from an in situ study of isotonic contractions in the turkey LG [5]. However, the differences can be attributed to the different protocols used. In this cycling study, we have independently uncoupled the effect of velocity and load on the dynamic architecture in the muscles and the results show that the MTU and belly gearing ratios vary with velocity but not load. The in situ study by Azizi et al. [5] used isotonic contractions where high shortening velocities were associated with low loads: findings that high AGR was related to low load could equally be considered as high AGR being related to high velocity (in agreement with our findings here; figure 3 and table 2).

Increases in MTU gearing ratio at the highest velocities are important as they permit the slowest fascicles in the muscle to contribute useful contractile force during rapid limb movements. We have previously shown that during pedalling at a cycle frequency of 2.3 s⁻¹ the muscle fascicles in the soleus shorten at a strain rate of 1.1 ± 0.4 s⁻¹ [32]. If the MTU gearing ratio was to remain constant at 1.1 (its value at 1 s⁻¹ and 6.4 N m; figure 3) across the range of cadences, rather than increasing to its maximum of 2.6, then the muscle fascicles would have to shorten at a strain rate of 2.6 s⁻¹ at the fastest pedal cadence. The soleus in man contains mainly slow-twitch muscle fibres (88% [33]) that have a maximum shortening strain rate of 6 s⁻¹ [34] or less [35]. Therefore, if the dynamic gearing and increases in MTU gearing ratio had not occurred then the slower muscle fibres, particularly in the soleus, would have shortened at rates too rapid for reasonable force development and so would have been mechanically ineffective and inefficient. However, the increases in MTU gearing ratio that do occur with increased pedal frequency enable the slower fibres to remain competent at the full range of velocities that can be achieved in vivo.

The mechanisms behind gearing can be further understood if the MTU gearing ratio is resolved into the relative contributions of the tendon compliance and the structural properties of the muscle belly. The gearing of the muscle fascicles relative to the muscle bellies showed small but significant increases with increased pedal frequency (figure 3 and table 2), but were in general, remarkably consistent at a value of 1.5. This gearing is similar to that proposed for case C in table 1, and occurred with similar fascicle rotations and changes in muscle belly thickness. Such gearing at the level of the muscle belly would not be possible if the pennation angle was to remain fixed (at its mean level of 16° to 21° [32]), and would necessitate a much higher pennation of 48° that is not observed in these muscles. Therefore, the high gearing observed at the level of the belly in vivo results from fascicle rotations and changes in belly thickness (figure 2), which are important determinants of belly gearing.

Substantial gearing occurred at the level of the muscle belly (figure 3) that was consistent with the simple model of fascicle rotations and muscle bulging (figure 1 and table 1). However, increases in muscle bulging and fascicle rotation occurred with increased crank torque during cycling but not with increased cycle frequency (table 2). Therefore, it is unlikely that changes in the belly gearing were the major factor causing the increases in MTU gearing ratio that occurred at the fast cycle frequencies. Instead, the variable nature of the MTU gearing ratio that occurred with different mechanical demands (table 2 and figure 3) appeared more dependent on the tendon gearing (between the muscle belly and MTU velocities: V_mtu/V_b) than on the belly gearing (between the muscle fascicles and muscle belly: V_b/V_f). Variable tendon gearing depends on the relative phase and magnitude of the displacements of the muscle bellies and MTUs. This could be achieved, for instance, by changes in the timing of muscle activation relative to the MTU stretch-shortening cycle, and we refer to this timing as the coordination. Such changes in the coordination of activation could alter the phase relations between the muscle belly force and the MTU length change, and thus account for differential tendon stretch and variable tendon gearing. The effects of muscle coordination and its dependence on movement mechanics are discussed further in a later section. Finally, it should be noted that the gearing relationships discussed here refer to changes in the relative velocities within the muscle; however, they do not necessarily translate to reciprocal changes in force owing to the nonlinear force–velocity and pennation effects within each fibre, and the series elasticity contribution of the tendon.

In summary, our studies show that the MTU gearing ratio depends on gearing at both the level of the muscle belly and tendon. However, despite the fact that the MTU gearing ratio increases with pedal frequency (table 2), the resultant shortening velocities of the muscle fibres may still reach rates that challenge the mechanical competency of some fibres [32]. To overcome this challenge it would make mechanical sense for the motor unit recruitment patterns to similarly match the mechanical demands of the movements, and this phenomenon is discussed in the next section.

4. Mechanically appropriate recruitment

Different muscle fibre types have different contractile properties, and can vary in both their activation and deactivation rates as well as their shortening rates. The activation state can be considered as the relative amount of Ca²⁺ bound to troponin [36]: faster fibres experience greater flux of Ca²⁺ from the sarcoplasmic reticulum to the sarcoplasm, with faster rates of [Ca²⁺] change [37]. Shortening rates are a function of the myosin-ATPase activities [38]. Both of these rates are coupled, and faster muscle fibres typically have faster activation rates as well as faster intrinsic speeds [39].

Some muscle contractions are better suited to slower fibres that are more efficient at slower speeds. Examples of this are slow movements and maintaining postural muscle tone. Contrarily, some fast muscle contractions are mechanically better suited to faster muscle fibres than slower muscle fibres. Examples of this include damping of soft-tissue vibrations in the leg [40] that requires fast activation and deactivation rates at about 13 Hz, and specialized high-frequency muscles such as the tail-shaker muscle of the rattlesnake, which have specialized fibres with faster calcium transients and a greater proportion of sarcoplasmic reticulum to facilitate even faster activation and deactivation rates up to 90 Hz [41,42]. Fast-starting fish provide an example of muscle contractions that occur at rates faster than the slower fibres can actively develop any force [24] and so faster fibres must be recruited on the basis of their faster contractile speeds.

The excitability of the α-motorneurons in the spine is inversely related to the size of the neurons and results in the slower motor units (with their slower muscle fibres) being more excitable than the faster motor units: this is the basis for motor unit recruitment and is known as orderly recruitment or ‘the size principle’ [43]. The size principle was originally identified using a stretch reflex protocol in the decerebrate cat, a model in which many pathways that would normally influence motor unit recruitment were not left intact and therefore could not influence the results (for review, see [44]). More recent studies have repeated the protocol, but have additionally shown that soleus motor units can be selectively inhibited by stretch in synergistic muscles [45] and so there are some fundamental connections at the spinal level that allow recruitment reversals. Renshaw cells [46] are an example of spinal interneurons that can cause recruitment reversals and recurrent inhibition; in turn, Renshaw cells can be controlled by descending tracts from supraspinal centres (for review, see [47]) and so, differential recruitment of the different types of motor unit can be achieved by both spinal and supraspinal circuits.

For rapid contractions that require low forces not all the muscle fibres need to be activated and potentially only a subset of the motor units may need to be recruited. The base plan of orderly recruitment would predict that only the slower motor units would be recruited, but mechanical arguments would suggest that for rapid contractions the task may be better achieved by preferential recruitment of faster motor units [44]. Our studies on the cycle ergometer show that despite the muscle gearing mechanisms highlighted at the start of this paper, the shortening velocities of the muscle fibres can exceed the optimal velocities of the slower fibres, and may even reach or exceed the maximum intrinsic speed of the slower fibres [32]. Thus, high cadence cycling is a task that would be better achieved by predominantly recruiting faster muscle fibres. When testing the recruitment strategies on a cycle ergometer, we found that the faster fibres were indeed preferentially recruited within the medial gastronemius [32] (figure 4), and these concepts were supported by a parallel study of treadmill running in the rat [48–50]. Identification of motor unit recruitment patterns was made possible by quantifying the time-varying electromyographic (EMG) spectra during the cycles [51–53]. EMG spectra are sensitive to variations in muscle temperature, fatigue and fibre length [54] which emphasizes the need for experimental protocols to minimize and account for these effects. Because higher EMG frequencies can be detected from faster motor units and also from shorter fascicle lengths [55], differences in the fascicle length may obscure information about recruitment patterns in some muscles. When we tested the time-varying frequency spectra from 10 muscles in the leg, the muscles from the upper leg did not show shifts in frequency that were consistent with preferential recruitment of faster fibres for faster contractions [56]. This result may reflect the confounding effects of muscle length on the EMG spectra, or may reflect that preferential recruitment of faster motor units does not occur in muscles of the upper leg. Thus, preferential recruitment may not be a ubiquitous feature from all muscles, but may predominantly occur in the ankle extensors.

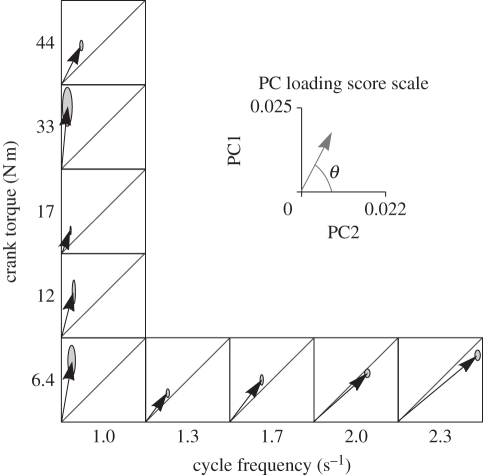
Figure 4.

Principal component (PC) loading score representation of the EMG from the medial gastrocnemius for cycling at a range of mechanical conditions. Data taken from Wakeling et al. [32], and PCs calculated from the EMG for the medial gastrocnemius. Vectors show the PC1–PC2 loading scores for each condition, and ellipses show the s.e.m. for the vectors. Note how the angle θ decreases as the cycle frequency increases and this indicates changes to the spectral properties of the EMG that are consistent with the recruitment of faster motor units.

5. Mechanically appropriate coordination

Mammalian muscles contain a mix of muscle fibre-types and can contain different proportions of faster and slower fibres. Faster muscles are muscles that contain a higher proportion of faster muscle fibres. Arguments that favour the recruitment of faster muscle fibres for faster contractions also apply to the recruitment of faster muscles for faster contractions. Examples of this can be seen in the cat ankle extensor muscles where the faster gastrocnemii are recruited in preference to the slower soleus during rapid paw-shaking [57], but the soleus is predominantly recruited during slower walking [58]. Also, the activation of the faster or slower muscle occurs as a function of the swimming velocity in fish [25]. There are sound mechanical reasons why the relative activity between muscles should be dependent on the velocity requirements of the locomotor task. However, it is commonly suggested that synergistic groups of muscles are activated together for specific movements and that synergies are related to the position of the limb during a gait cycle [59,60] or to the direction of the movement [61,62]. However, the muscles within synergistic groups may have different architectures, mechanical linkages to the skeleton, and biochemical properties, and these put competing demands on the most appropriate way to activate them for different mechanical tasks [56]. In order for velocity-dependent coordination of the muscles to be achieved, the synergies must be modulated in a velocity-dependent fashion. Five major synergies have been shown for walking and running at a range of loads [63,64], and have appeared as robust coordination strategies; however, up to 42 per cent of the coordination patterns remained unexplained by these synergies [63], thus allowing the possibility that considerable modulation of the synergies can occur.

We have tested these ideas about modulating synergies based on the mechanical demands of pedalling on a cycling ergometer [56]. Pronounced changes in the relative activity between the ankle extensor muscles occurs during cycling, with greater activity occurring in the slower soleus muscle for low speed, high-load cycling; however, greater activity occurs in the faster gastrocnemii during high speed but low-load cycling. This suggests that coordination within the ankle extensors occurs in a mechanically sensible fashion. When tested across 10 leg muscles, uncoupling of activity between muscles that share common anatomical arrangements was observed in 69 per cent of the coordination patterns of EMG, and patterns of muscle coordination were independently correlated with the crank torque and with the cycling frequency of the cycle ergometer [56]. These varied coordination patterns included differences in both the timing and level of activation, and such variation in coordination was related to the force and velocity demands of different movement tasks.

Force- and velocity-dependent coordination of the muscles was one of the requirements for variable gearing that was predicted in the first sections of this paper. The large changes in MTU gearing ratio that occurred with different mechanical demands (figure 3) were more dependent on the gearing between the muscle belly and MTU velocities than on the gearing between the muscle fascicles and muscle belly. It was suggested that the variable gearing between the muscle belly and MTU velocities depends on the uncoupling between the phase and magnitude of the displacements of the muscle bellies and MTUs, and these are affected by the relative timing and level of activation between the muscles. It is exactly such force- and velocity-dependent changes to the muscle coordination that have been observed when the cycle ergometer has been used to challenge the mechanical demands of the movements [56].

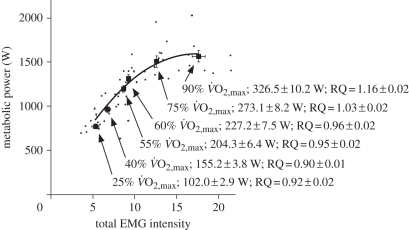
Muscle coordination depends on the mechanics of the movement task, but in turn the mechanics of the limb depend on the muscle coordination. To illustrate this, consider a single muscle that is generating a large power output during a series of cyclic contractions. If an antagonistic muscle were to be contracting at the same time then the net joint power would be smaller than if the first muscle were contracting alone. So, co-contractions can reduce joint moments and powers, but can act to increase the stiffness and thus stability of the joints. Subsequently, the metabolic cost of generating a given joint power is increased. The power output from a limb should thus be expected to depend on the coordination patterns of the muscles. This was supported by our observations during testing of the cycle-by-cycle fluctuations of mechanical power output, efficiency and coordination during cycling [65]. The metabolic cost was estimated from the total intensity of the EMG from all 10 muscles tested, and this simplification has been more recently supported by direct metabolic measurement (figure 5). The results showed that even when a limb is being used to generate maximum power output, not all muscles work at maximal power output. Even muscles that could contribute high power outputs may not be fully activated during maximal power output from the limb. This emphasizes that the muscle coordination patterns limit the maximal performance of a limb in terms of both power output and efficiency [65].

Figure 5.

Metabolic power during cycling is related to the total EMG intensity from 10 muscles in the leg. Small points show individual values for each condition, and least-squares second-order regression is fitted to these points (r² = 0.72). The squares show the mean ± s.e.m. for the 10 subjects for each condition. Text shows the level of effort for each condition; the mechanical power output at the crank; and the respiratory quotient (RQ). Note that the RQ during cycling at levels greater than 60% 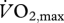was greater than one, indicating a contribution of anaerobic metabolism; therefore, the metabolic power for these conditions has been underestimated. Nonetheless, there was a significant monotonic increase in metabolic power associated with increased EMG intensity (Spearman correlation, r = 0.86.)

6. Conclusions

• — Muscle fascicles are geared to reduce their shortening velocities relative to the MTU velocity and this allows them to generate high power outputs at high efficiencies even at rapid rates of limb movement. Substantial gearing occurs at the level of the muscle belly, and this is the result of rotations of the muscle fascicles and bulging of the muscle belly. Variable gearing occurs at the level of the tendon, and may be due to changes in muscle coordination for different mechanical tasks.

• — The fastest muscle fibres are more mechanically effective than the slower muscle fibres during rapid limb movements, and they can be preferentially recruited in some but probably not all muscles.

• — Coordination patterns of the muscles are related to the mechanical demands of each movement with the appropriate timing and level of activation for each muscle being related to the velocity and load of the movement. Muscle coordination determines the effectiveness of the whole limb mechanics, with poor coordination leading to inefficiencies and loss of power. Optimal coordination is required for high power outputs and high mechanical efficiencies from the limb.

Appendix A. Experimental methods

Participants involved in this study gave informed consent and all procedures were approved by the Ethics Committee of Simon Fraser University.

(a). Muscle gearing

Ultrasound data were reanalysed from a previous study [32]. In brief, B-mode ultrasound images were recorded from the mid belly region from the medial gastrocnemius, lateral gastrocnemius and soleus muscles for six cyclists during cycling on a stationary cycle ergometer at a crank torque of 6.4 N m and a cycle frequency of 1, 1.3, 1.7, 2 or 2.3 s⁻¹ and at a cycle frequency of 1 s⁻¹ and a crank torque of 12, 17, 33, 39 or 44 N m. Two points were digitized on the superficial aponeurosis, deep aponeurosis and muscle fascicle on each ultrasound image. Fascicle lengths, L_f, were calculated as the length of the linear line passing through the fascicle points between the superficial and deep aponeuroses. The pennation angle, β, of the fascicle relative to the superficial aponeurosis and the thickness of the muscle belly that was centred on the digitized fascicle, t, were calculated. The length for (a segment of) the muscle belly, L_b, was calculated as L_f cos β.

In a new study, we recorded the limb kinematics for six male cyclists (age 29.3 ± 5.0 years; mass 73.4 ± 5.7 kg; height 1.86 ± 0.07 m) pedalling under the same conditions on an indoor bike trainer (SRM, Julich, Germany). The segmental motion of the leg and joints (hip, knee and ankle) were recorded using an Optotrak system (Optotrack Certus, Northern Digital Inc., ON, Canada). Three three-marker clusters were used on the thigh, shank, shoe and calcaneus. The calcaneus marker was attached to a custom-made cuff that was secured to the calcaneus with tape and protruded through a pre-cut hole in the shoe. Virtual markers were defined for the origin of the gastrocnemii and soleus (based on anatomical data from [66]). MTU lengths, L_mtu, were calculated from the distance from these muscle origins to the calcaneus.

Functions describing L_f, L_b, L_mtu, t and β as a function of pedal position were described using Fourier series for each muscle and subject. The muscle bulge was defined as the difference between maximum and minimum thickness for each trial, and the fascicle rotation was defined as the difference between maximum and minimum pennation.

(b). Metabolic cost of cycling

Ten male cyclists (age 41.8 ± 2.7 years; mass 77.2 ± 2.2 kg; height 1.81 ± 0.01 m) cycled on the indoor trainer at mechanical power outputs determined to elicit 25, 40, 55, 60, 75 and 90 per cent of maximum oxygen uptake (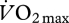), as established by an incremental test to exhaustion one week prior. The conditions were each pedalled for 3 min, and presented twice in a semi-random block design. The EMG intensity from 10 muscles in the right leg was determined using previously described methods [65]. The mean EMG intensity per pedal cycle was normalized to the mean across all conditions. Oxygen and carbon dioxide gas exchange was sampled breath by breath using a metabolic cart (V_max 229, Sensormedics, Yorba Linda, CA, USA). The metabolic power was calculated from the 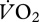and respiratory exchange ratio [67]. The total EMG intensity from the 10 muscles was calculated for 1 min of steady cycling in each condition and correlated with the metabolic power.