Abstract
The purpose of this study was to understand how humans regulate their ‘leg stiffness’ in hopping, and to determine whether this regulation is intended to minimize energy expenditure. ‘Leg stiffness’ is the slope of the relationship between ground reaction force and displacement of the centre of mass (CM). Variations in leg stiffness were achieved in six subjects by having them hop at maximum and submaximum heights at a frequency of 1.7 Hz. Kinematics, ground reaction forces and electromyograms were measured. Leg stiffness decreased with hopping height, from 350 N m−1 kg−1 at 26 cm to 150 N m−1 kg−1 at 14 cm. Subjects reduced hopping height primarily by reducing the amplitude of muscle activation. Experimental results were reproduced with a model of the musculoskeletal system comprising four body segments and nine Hill-type muscles, with muscle stimulation STIM(t) as only input. Correspondence between simulated hops and experimental hops was poor when STIM(t) was optimized to minimize mechanical energy expenditure, but good when an objective function was used that penalized jerk of CM motion, suggesting that hopping subjects are not minimizing energy expenditure. Instead, we speculated, subjects are using a simple control strategy that results in smooth movements and a decrease in leg stiffness with hopping height.
Keywords: leg stiffness, simulation model, optimal control
1. Introduction
Legs behave like compression springs during bouncing gaits such as running and hopping. During the first half of the ground contact phase, leg length (i.e. the distance between hip and toe) decreases while the ground reaction force increases, and during the second half of the ground contact phase, leg length increases while the ground reaction force decreases. In the search for general principles underlying bouncing gaits, biomechanists have modelled the body as a linear massless spring supporting a point mass equivalent to body mass [1,2]. The stiffness of the spring, typically referred to as ‘leg spring’, is determined from the relationship between the magnitude of the ground reaction force and the distance between the centre of mass (CM) and the centre of pressure on the ground [2]. It has been shown abundantly that the stiffness of the leg spring changes when humans change hopping height (e.g. [3]) or frequency (e.g. [3–5]), or when the viscous or elastic properties of the surface underfoot are changed (e.g. [6–9]). In running, where the leg not only changes length but also rotates relative to the support surface, the same principles apply [2,10,11], and the spring-mass system has been shown to provide good predictions of stance time, vertical impulse, contact length, duty factor, relative stride length and relative peak force (e.g. [12]).
It has been suggested in the literature that making the musculoskeletal system behave globally like a linear spring-mass system helps to simplify control (e.g. [13–17]) and/or lower energy expenditure (e.g. [4,13]). However, the simple linear leg spring describes the behaviour of a complicated articulated leg actuated by muscle–tendon complexes (MTCs). Furthermore, while the tendinous tissue in series with muscle fibres may perhaps be considered as a simple (nonlinear) spring, muscle fibre force depends in a complex way on muscle fibre length, velocity and active state. Thus, making the system behave globally like a linear spring-mass system may actually be an extremely challenging task. With respect to lowering energy expenditure, it should be realized that the spring-like behaviour of the leg does not imply that the leg force is a conservative force; while energy stored in tendons during the first half of the ground contact phase can be reutilized during the second half, energy will also be dissipated by muscle fibres during lengthening and hence needs to be regenerated to maintain limit-cycle behaviour. Thus, the spring-like behaviour of the leg should not be confused with the behaviour of a mechanical spring.
The purpose of this study was to understand how humans regulate their ‘leg stiffness’ in hopping, and to determine whether this regulation is intended to minimize energy expenditure. For this purpose, we had subjects hop for maximum and submaximum heights at a frequency at which a large range of hopping heights could be achieved (1.7 Hz) and tried to reproduce the observed spring-mass behaviour with a forward simulation model of the musculoskeletal system using different objective functions. Three objective functions were tested: one for minimization of mechanical energy expenditure, one for maximizing smoothness of vertical motion of the CM by penalizing jerk [18] and one for minimizing the peak vertical ground reaction force. The simulated hops were used to understand how different steady-state hopping heights are realized at a fixed frequency and how the intrinsic properties of MTCs (force–length, force–velocity and force–active state relationships) relate to the global spring-like leg behaviour. Furthermore, the simulation results were used to study energy production and dissipation by muscles and energy storage in elastic elements. Finally, as a first step towards understanding the control of hopping, we used the model to test a simple control strategy to change from hopping at one height to hopping at another height.
2. Material and methods
(a). Outline of experimental procedures
Six male students participated in this study, all of whom practised sports involving jumping at least twice a week. The study received approval of the local ethics committee, and informed consent was obtained from all participants in accordance with the policy statement of the American College of Sports Medicine. Characteristics of the group of subjects were (mean ± s.d.): age 21 ± 2 years, body mass 78 ± 8 kg, height 1.84 ± 0.07 m. The subjects first warmed up on a bicycle ergometer for 10 min and performed various countermovement jumps and squat jumps. Subsequently, they practised hopping barefoot on the beat of a metronome at 1.7 Hz with arms folded across the chest and hands holding the contralateral shoulders, while landing on a force plate of 60 by 40 cm. No instructions were given with respect to landing posture, contact time or any other variables. For the actual data collection, the subjects were instructed to first hop at the maximum height they could reach at 1.7 Hz, then at about 75 per cent of maximum height, subsequently at 50 per cent of maximum height and finally at 25 per cent of maximum height; these conditions will be referred to as HIGH, INTH, INTL and LOW, respectively. We did provide the subjects with online feedback of the height reached by the hip during hopping. However, steady-state hopping on the relatively small force plate turned out to be quite a challenge for the subjects, especially in conditions HIGH and INTH, and we ended up being satisfied when each subject hopped on average lower in INTH than in HIGH, lower in INTL than in INTH and lower in LOW than in INTL. Data were collected over 10 s of hopping in each condition. The hopping trials did not cause any fatigue in the subjects.
As will be detailed below, we measured ground reaction forces, sagittal plane positional data of anatomical landmarks and electromyograms (EMGs) of six muscles of the right lower extremity. Hopping height, defined as the difference between the height of CM at the apex of the hop and the height of CM when the subject was standing upright with heels on the ground, was calculated from the positional data. Net joint moments and joint work were obtained by performing an inverse-dynamics analysis, combining kinematic information and ground reaction forces.
(b). Kinematics and kinetics
Kinematic data were collected using an Optotrak 3020 system (Northern Digital, Waterloo, Ontario, Canada), operating at 200 Hz. Infrared light-emitting diodes were placed on the fifth metatarsophalangeal joint, calcaneus, lateral malleolus, lateral epicondyle of femur, greater trochanter and acromion. Only sagittal plane projections were used in this study. Marker trajectories were smoothed using a bidirectional low-pass Butterworth filter with a cut-off frequency of 8 Hz. The locations of the mass centres of upper legs, lower legs and feet were estimated from the landmark coordinates, in combination with results of cadaver measurements presented in the literature [19]. The location of the mass centre of the upper body relative to the two markers on this segment was determined from two different equilibrium postures of the subjects, as explained elsewhere [20]. With this information, the height of CM (zCM) and the fore-aft location of CM were calculated in all other body postures found during hopping. To obtain linear velocities and accelerations, the smoothed position time histories were differentiated numerically with respect to time using a direct 5-point derivative routine. Angles of body segments with respect to the horizontal were calculated from the smoothed marker position-time histories, and differentiated to obtain angular velocities and accelerations.
Ground reaction forces were measured using a force platform (Kistler 9281B, Kistler Instruments Corp., Amherst, NY, USA). The output signals of the platform were amplified (Kistler 9865E charge amplifier, Kistler Instruments Corp.), sampled at 400 Hz, and processed to determine the fore-aft and vertical components of the reaction force and the location of the centre of pressure.
In the literature, the leg stiffness in hopping is calculated by taking the ratio of the vertical ground reaction force (Fz) to the compression of the leg spring at the instant that this compression is maximal, where the compression of the leg spring is actually the vertical displacement of CM after landing (e.g. [10]). Following Granata et al. [21], in the present study, we calculated leg stiffness as the slope of a line fitted to combinations of the vertical ground reaction force (Fz) and −zCM (we changed the sign of zCM to make the curves comparable to curves of leg-spring compression in the literature).
Net forces, moments and work at the joints were calculated following a standard inverse-dynamics approach [22] using the measured ground reaction force vector in combination with locations of joint axes and segmental mass centres obtained from the positional data, with linear and angular accelerations of segments derived from the positional data, and with segmental masses and moments of inertia calculated from anthropometrical information using regression equations [23].
(c). Electromyography
Pairs of Ag/AgCl surface electrodes (Medicotest, blue sensor, type: N-00-S) were applied to the skin overlying m. soleus, m. gastrocnemius (caput mediale), m. vastus lateralis, m. rectus femoris, m. gluteus maximus and m. biceps femoris (caput longum). The EMG signals were amplified and sampled at 500 Hz (Porti-17t, Twente Medical Systems). Off-line, they were high-pass filtered at 7 Hz to remove any possible movement artefacts, full-wave rectified and smoothed using a bidirectional digital low-pass Butterworth filter with a 7 Hz cut-off frequency, to yield smoothed rectified EMG (srEMG). srEMG signals were normalized for the highest srEMG level found in the maximum height hops to allow for comparison of peak srEMG levels among conditions.
(d). Data analysis and statistics
From each subject we averaged for each condition the results over four hops that best met the following two criteria for steady-state hopping: (i) minimal difference between height reached at the apex of the hop and height reached at the previous apex (i.e. the apex reached in the previous hop), and (ii) minimal difference between the actual cycle duration (i.e. the time between the instants at which the two apices were reached) and 588 ms (i.e. cycle time at 1.7 Hz). The main effects of condition on several dependent variables, including hopping height, leg stiffness and peak srEMG values, were tested to significance using a general linear model ANOVA for repeated measures; when a significant F-value was found, post hoc pairwise comparisons of means were made using the least significant difference post hoc test (SPSS Inc. statistical software). The level of significance for all tests was 0.05.
(e). Computer simulation model
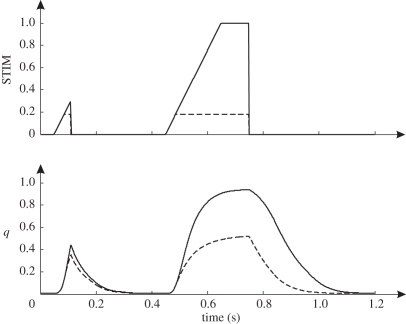
For simulations of hopping, we used the two-dimensional forward dynamic model of the human musculoskeletal system schematically shown in figure 1 (cf. [24]). The model, which had muscle stimulation, STIM, as its only independent input, consisted of four rigid segments representing feet, shanks, thighs and an HAT segment representing head, arms and trunk. These segments were interconnected by hinges representing hip, knee and ankle joints. The ground was rigid, and impact of the foot with the ground was modelled as a completely inelastic collision, i.e. segment angular velocities changed instantaneously. Segment parameters were the same as those used in a model for simulation of vertical jumping, which was previously described in full detail [24]. Nine major MTCs of the lower extremity were embedded in the skeletal model: m. gluteus maximus, biarticular heads of the hamstrings, short head of m. biceps femoris, m. iliopsoas, m. rectus femoris, mm. vasti, m. gastrocnemius, m. soleus and m. tibialis anterior (cf. [25]). Each MTC was represented using a Hill-type unit. The MTC model, which has also been described in full detail elsewhere [26], consisted of a contractile element (CE), a series elastic element (SEE) and a parallel elastic element (PEE). Briefly, behaviour of SEE and PEE was determined by a simple quadratic force–length relationship, while behaviour of CE was complex: CE velocity depended on CE length, force and active state, with the latter being defined as the relative amount of calcium bound to troponin [27]. Following Hatze [28], the relationship between active state and STIM was modelled as a first-order process. STIM, ranging between 0 and 1, was a one-dimensional representation of the effects of recruitment and firing frequency of α-motoneurons.
Figure 1.
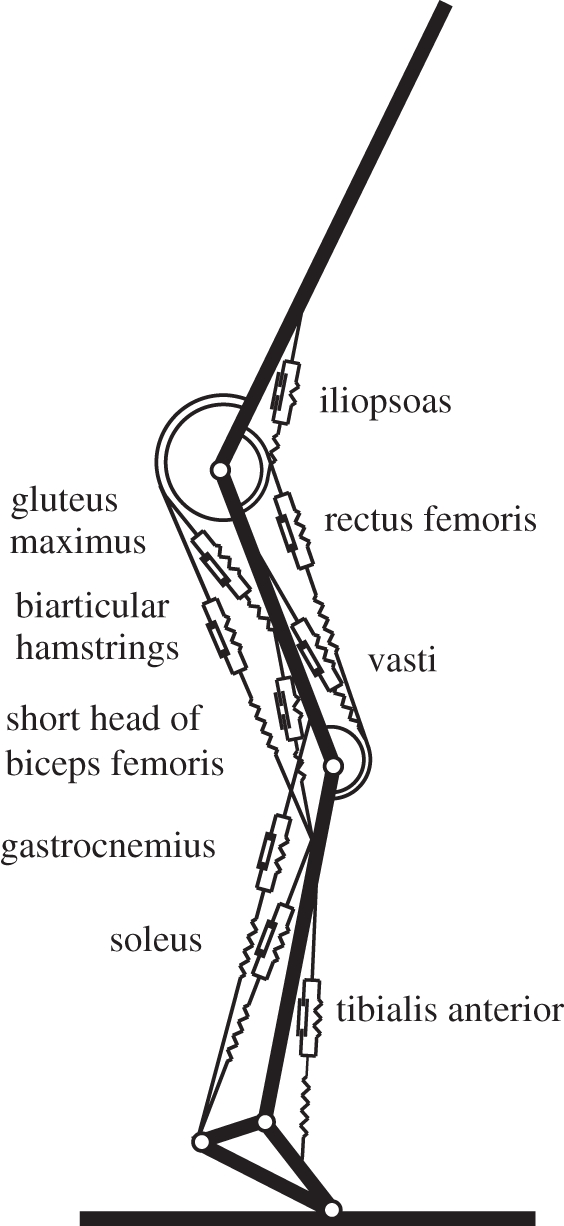
Model of the musculoskeletal system used for forward dynamic simulations. The model consisted of four interconnected rigid segments and nine muscle–tendon complexes of the lower extremity, all represented by Hill-type muscle models. The only input of the model was muscle stimulation as a function of time.
(f). Optimization
At the start of each simulation, the model was put in the average posture observed in the subjects at the apex of the hops. The net joint moments of the subjects were very low in this posture, but we wanted to allow the model to co-contract muscles and therefore made the initial STIM levels part of the parameters to be optimized (see below). We did not actually optimize STIM(t) for steady-state hopping, but rather optimized STIM(t) to achieve single hops in which the state reached at the end of the cycle approximated the state at the start of the cycle. STIM of each muscle was allowed to change at most four times, either towards 0 or to a preselected STIMmax (a value between 0 and 1 that was constant during a particular optimization). By allowing STIM to change four times, it was possible to produce for example two STIM bursts for each muscle. A change towards STIMmax occurred at a rate of 5 s−1, a value previously used to match simulated and experimental curves in maximum height squat jumping [29]; the effect on active state is illustrated for STIMmax values of 1.0 and 0.18 in figure 2. Under these restrictions on STIM(t), the motion of the body segments depended on a set of 54 parameters: nine initial STIM levels (one for each muscle), 36 instants at which STIM started to change (four for each muscle) and the order of STIM changes for each of the nine muscles (initial → 0 → STIMmax → 0 or initial → STIMmax → 0 → STIMmax). These parameters were optimized for different objective functions, composed of a weighted sum of two terms:
Figure 2.
Illustration of the effect of varying muscle stimulation, STIM, on active state, q. A change towards STIMmax occurred at a rate of 5 s−1, a value previously used to match simulated and experimental curves in maximum height squat jumping [29]. Note that the long second burst towards STIMmax of 0.18 leads to higher values of q than the short first burst towards STIMmax of 1.0. Note also that the steady-state relationship between STIM and q is nonlinear.
where w1 and w2 are weight factors, Jerr was an error term that quantified how well the simulated hop approximated steady-state hopping at 1.7 Hz and Jcrit was related to the optimization criterion to be tested. The optimization criteria that we tested in this study were minimum positive work of CEs 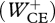 , minimum zCM-jerk (i.e. the square root of the time integral of
, minimum zCM-jerk (i.e. the square root of the time integral of 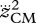 over the contact phase), and minimum Fz,peak. The weight factors themselves depended on the size of Jerr as follows:
over the contact phase), and minimum Fz,peak. The weight factors themselves depended on the size of Jerr as follows:
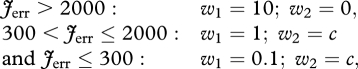 |
where c depended on the criterion of interest in such a way that the magnitude of w2·Jcrit was the same in the optimal solutions (c = 1 when minimizing 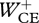 , c = 1.5 when minimizing zCM-jerk and c = 0.1 when minimizing Fz,peak). If the simulated hop approximated steady-state hopping at 1.7 Hz, w1·Jerr was negligible compared with w2·Jcrit.
, c = 1.5 when minimizing zCM-jerk and c = 0.1 when minimizing Fz,peak). If the simulated hop approximated steady-state hopping at 1.7 Hz, w1·Jerr was negligible compared with w2·Jcrit.
Without going into detail, Jerr was a sum of penalties on (i) the magnitude of the steady-state net joint moments at the start of the cycle (which were close to zero in the subjects), (ii) the differences in state variables (segment angles, segment angular velocities, CE-lengths and free calcium concentrations) between the start and the end of the cycle, (iii) the deviation of cycle time from 588 ms (i.e. cycle time at 1.7 Hz), (iv) the difference in zCM at the start and end of the cycle, and (v) the horizontal velocity of CM at take-off (which should be zero for steady-state hopping).
For optimization, we used a genetic algorithm [30] and a simulated annealing algorithm [31]. For the genetic algorithm, the optimization parameters were encoded in discrete bit-strings (‘chromosomes’). The resolution of the instants at which STIM started to change in a chromosome was 1 ms. The population size (i.e. the number of chromosomes in a population) was set to the number of available cores. The genetic algorithm was run overnight on 100–200 cores in parallel, typically for 50 000–100 000 generations, to find a reasonable solution. Instants at which STIM started to change in this solution were then encoded as double-precision floating point values, and the solution was given to the simulated annealing algorithm as initial guess to continue optimizing towards a final solution. By solving each optimization problem several times, we collected a number of solutions in which Jerr was smaller than 300, so that Jtot was mainly determined by the criterion of interest (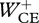 , zCM-jerk or Fz,peak). From these, the solution with the lowest Jtot was selected.
, zCM-jerk or Fz,peak). From these, the solution with the lowest Jtot was selected.
3. Results
(a). Subject experiments
Despite the fact that the task was quite challenging for the subjects, they were able to produce hops for the different conditions that satisfactorily met our steady-state criteria with respect to cycle time and hopping height (table 1). Subjects gradually decreased hopping height over the conditions, on average from 26 cm in HIGH to 12 cm in LOW (table 1). They chose to land and take-off in the same posture in all conditions (figure 3a) and hence had the same CM height at landing and take-off in all conditions (table 1). In the submaximum conditions, they lowered CM on average 2.3–3.4 cm more than in HIGH (table 1), and they had their joints more flexed when reaching the lowest point of CM (figure 3a). The decrease in hopping height obviously led to a decrease in the duration of the airborne phase and hence to an increase in the duration of the contact phase, on average from 218 ms in HIGH to 386 ms in LOW (table 1).
Table 1.
Values for selected variables describing hopping at 1.7 Hz obtained in experiments on subjects (n = 6) at four different heights (means ± s.d.) and in simulations with the musculoskeletal model. Simulation results are for hopping at 20 cm (H20) and 14 cm (H14) with STIMmax set to 1.0, using as the optimization criterion minimal jerk. zCM, apex-pre, height of the centre of mass of the body (CM) at the apex of the previous hop (initial state of the model); zCM, td, zCM, min, zCM, to denote height of CM at touch-down (td), at the lowest point (min) and at take-off (to), respectively; zCM, apex-post, height of CM at the apex following the contact phase; 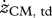 ,
, 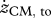 denote vertical velocity of CM at touch-down and take-off, respectively; ECM, td, ECM, min, ECM, to denote the mechanical energy of CM at touch-down, at the lowest point and at take-off, respectively; tcycle, time between reaching zCM, apex-pre and reaching zCM, apex-post; tcontact, duration of ground contact, i.e. from touch-down to take-off; Fz,peak, peak value of the vertical ground reaction force; Pz, net, impulse of (Fz − m · g) over the contact phase; kleg,landing, leg stiffness calculated for the landing phase (i.e. from touch-down to reaching the lowest point of CM); kleg, prop, leg stiffness calculated for the propulsion phase (i.e. from reaching the lowest point of CM to take-off); kankle, landing, ‘ankle joint stiffness’ calculated for the landing phase; kankle, prop, ankle joint stiffness calculated for the propulsion phase. All values for height of CM and energy of CM have been expressed relative to standing upright. Means that do not share subscripts differ at p < 0.05.
denote vertical velocity of CM at touch-down and take-off, respectively; ECM, td, ECM, min, ECM, to denote the mechanical energy of CM at touch-down, at the lowest point and at take-off, respectively; tcycle, time between reaching zCM, apex-pre and reaching zCM, apex-post; tcontact, duration of ground contact, i.e. from touch-down to take-off; Fz,peak, peak value of the vertical ground reaction force; Pz, net, impulse of (Fz − m · g) over the contact phase; kleg,landing, leg stiffness calculated for the landing phase (i.e. from touch-down to reaching the lowest point of CM); kleg, prop, leg stiffness calculated for the propulsion phase (i.e. from reaching the lowest point of CM to take-off); kankle, landing, ‘ankle joint stiffness’ calculated for the landing phase; kankle, prop, ankle joint stiffness calculated for the propulsion phase. All values for height of CM and energy of CM have been expressed relative to standing upright. Means that do not share subscripts differ at p < 0.05.
| variable | subjects |
model |
||||
|---|---|---|---|---|---|---|
| HIGH | INTH | INTL | LOW | H20 | H14 | |
| zCM, apex-pre (m) | 0.26a ± 0.04 | 0.20b ± 0.03 | 0.18b ± 0.04 | 0.12c ± 0.06 | 0.20 | 0.14 |
| zCM, td (m) | 0.07 ± 0.02 | 0.08 ± 0.02 | 0.08 ± 0.03 | 0.07 ± 0.04 | 0.04 | 0.03 |
| zCM, min (m) | −0.07a ± 0.02 | −0.09b ± 0.02 | −0.10b ± 0.03 | −0.10b ± 0.03 | −0.08 | −0.10 |
| zCM, to (m) | 0.10 ± 0.02 | 0.10 ± 0.03 | 0.09 ± 0.02 | 0.08 ± 0.04 | 0.06 | 0.07 |
| zCM, apex-post (m) | 0.26a ± 0.05 | 0.21b ± 0.04 | 0.19b ± 0.04 | 0.12c ± 0.06 | 0.20 | 0.14 |
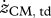 (m s−1) (m s−1) |
−1.9a ± 0.2 | −1.6b ± 0.1 | −1.4c ± 0.3 | −1.0d ± 0.3 | −1.7 | −1.4 |
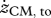 (m s−1) (m s−1) |
1.9a ± 0.2 | 1.5b ± 0.2 | 1.4c ± 0.2 | 1.0d ± 0.3 | 1.6 | 1.2 |
| ECM, td (J kg−1) | 2.6a ± 0.4 | 2.1b ± 0.4 | 1.8b ± 0.5 | 1.2c ± 0.6 | 2.0 | 1.4 |
| ECM, min (J kg−1) | −0.6a ± 0.2 | −0.9b ± 0.2 | −1.0b ± 0.3 | −1.0b ± 0.3 | −0.8 | −1.0 |
| ECM, to (J kg−1) | 2.7a ± 0.5 | 2.1b ± 0.4 | 1.9b ± 0.4 | 1.2c ± 0.6 | 2.0 | 1.4 |
| tcycle (ms) | 589 ± 14 | 591 ± 13 | 595 ± 20 | 576 ± 20 | 590 | 592 |
| tcontact (ms) | 218a ± 26 | 281b ± 27 | 314c ± 47 | 386d ± 63 | 244 | 318 |
| Fz,peak (N kg−1) | 48.5a ± 6.2 | 37b ± 3.9 | 33.7b ± 5.5 | 25.6c ± 4.9 | 34.1 | 28.3 |
| Pz, net (Ns kg−1) | 3.6a ± 0.4 | 3.0 b ± 0.3 | 2.7 c ± 0.4 | 1.8d ± 0.5 | 3.3 | 2.6 |
| kleg, landing (N m−1 kg−1) | 383a ± 103 | 235b ± 34 | 199c ± 49 | 148d ± 30 | 227.7 | 160.0 |
| kleg, prop (N m−1 kg−1) | 316a ± 56 | 213b ± 33 | 194b ± 49 | 153c ± 32 | 181.7 | 121.2 |
| kankle, landing (N m rad−1 kg−1) | 9.1a ± 2.6 | 7.4ab ± 2.6 | 5.6b ± 1.8 | 4.4c ± 1.3 | 8.9 | 6.2 |
| kankle, prop (N m rad−1 kg−1) | 6.6a ± 1.5 | 5.5b ± 0.9 | 4.6bc ± 1.7 | 3.8c ± 1.3 | 5.6 | 3.9 |
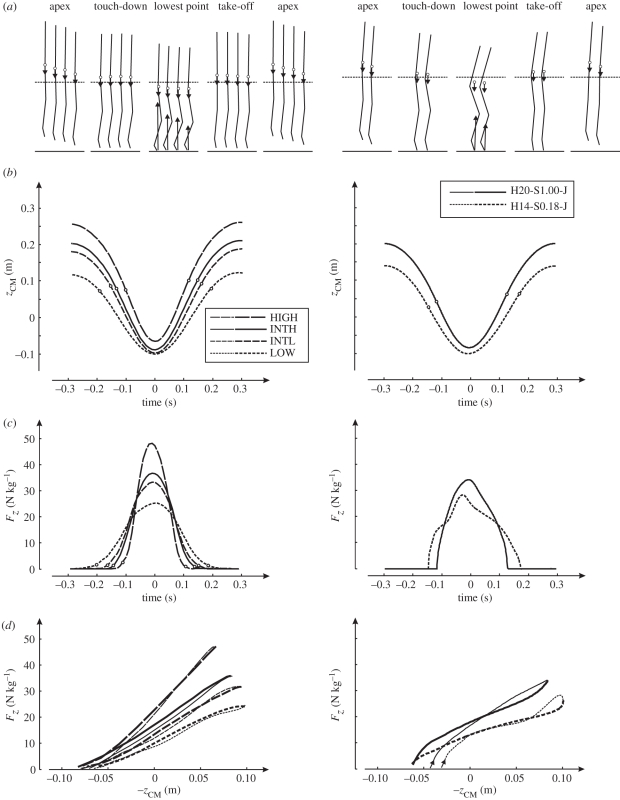
Figure 3.
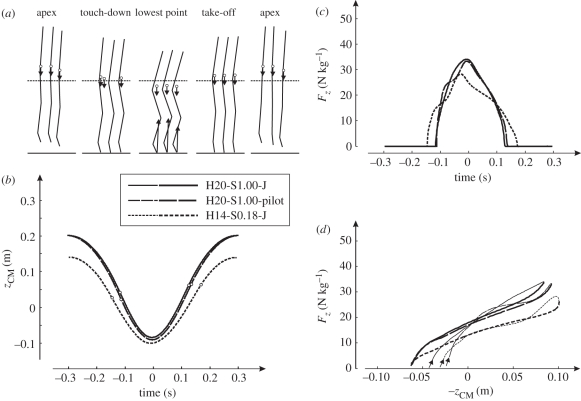
Left panels: mean experimental results obtained in experiments on subjects (n = 6) hopping at 1.7 Hz at four different heights. Right panels: results obtained with the musculoskeletal model. Simulation results are optimal solutions for hopping at 20 cm (H20) with STIMmax set to 1.0 (S1.00) and at 14 cm (H14) with STIMmax set to 0.18 (S0.18), obtained using minimum jerk as the optimization criterion. (a) Stick diagrams of average body postures of the six subjects and of the simulation model at the apex of the previous hop (initial condition for the simulation model), touch-down, lowest point, take-off and apex of the hop. Arrows pointing upward represent the ground reaction force vector plotted with the origin in the centre of pressure; arrows pointing downward represent the force of gravity, plotted with the origin in the centre of mass (CM, open circles). The horizontal dashed line is the height of CM in standing upright. (b) Time history of the height of CM (zCM) relative to upright standing. Time is expressed relative to the instant that CM reached its lowest point. The instants of touch-down and take-off are indicated with open circles. (c) Time history of vertical ground reaction force (Fz). (d) Fz plotted as a function of −zCM; we changed the sign of zCM to make the curves comparable to curves of leg-spring compression in the literature. Curves start at touch-down (arrows) and are thin for the landing phase and thick for the propulsion phase.
The force-time histories of the vertical ground reaction force (Fz) during the contact phase were more or less half-sinusoids; this was not only true for the average Fz curves of the group of subjects (figure 3c) but for all Fz curves of individual hops of the subjects. It follows that the decrease in hopping height and increase in contact phase were accompanied by a decrease in Fz,peak (figure 3c), on average from 49 N kg−1 in HIGH to 26 N kg−1 in LOW. The impulse of (Fz − m · g) over the contact phase corresponded well to the change in the vertical velocity of CM from landing to contact (table 1), which gave us confidence that CM motion was accurately calculated from kinematics. The relationships between Fz and −zCM were indeed more or less linear (figure 3d). Leg stiffness during the landing phase (from touch-down to the instant that CM reached its lowest point) decreased on average from 383 N kg−1 m−1 in HIGH to 148 N kg−1 m−1 in LOW, and leg stiffness during the propulsion phase (from the instant that CM reached its lowest point to take-off) decreased on average from 316 N kg−1 m−1 in HIGH to 153 N kg−1 m−1 in LOW. Note that leg stiffness tended to be slightly lower during the propulsion phase than during the landing phase because CM tended to be higher at take-off than at touch-down (table 1). In line with results of Farley and Morgenroth [3], the reduction in leg stiffness was accompanied by a reduction in ‘ankle stiffness’, i.e. the slope of the regression of ankle moment on ankle angle.
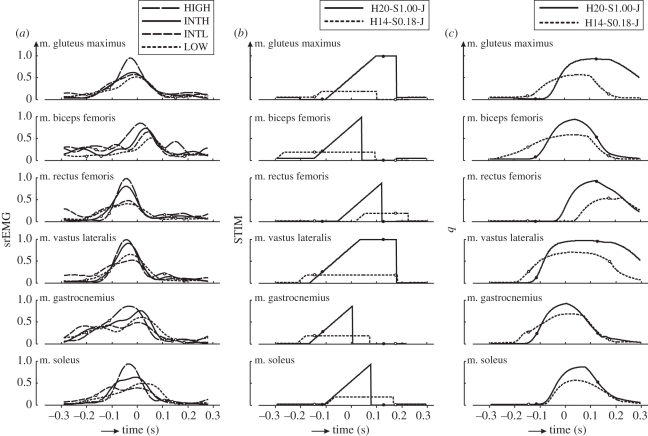
The kinetic and kinematic changes among the conditions are ultimately caused by changes in neural input to the muscles. srEMG is formally one of the results of the neural input to the muscle, but is typically taken to reflect this input. The srEMG time histories suggest that the subjects chose to reduce the rate of increase and the magnitude of the neural input of their muscles to reduce hopping height (figure 4a). Unfortunately, because of the variation in srEMG signals from trial to trial, it was difficult to support this statistically. Suffice it to say that peak srEMG amplitude was lower in LOW than in HIGH in all muscles except m. gluteus maximus (table 2; note that because of differences in the time at which peak srEMG occurred, values reported in this table may be different than peak values of average curves shown in figure 4a).
Figure 4.
(a) Mean time histories of smoothed rectified EMG (srEMG) obtained in experiments on subjects (n = 6) hopping at 1.7 Hz at four different heights. srEMG values have been normalized for the peak value observed when subjects were hopping as high as possible (condition HIGH). Time is expressed relative to the instant that CM reached its lowest point. Small circles indicate the instants of touch-down and take-off. (b) Time histories of optimal STIM solutions for hopping at 20 cm (H20) with STIMmax set to 1.0 (S1.00) and at 14 cm (H14) with STIMmax set to 0.18 (S0.18), obtained using minimum jerk as the optimization criterion. (c) Time histories of active state q corresponding to optimal STIM solutions shown in (b).
Table 2.
Peak values (means ± s.d.) of smoothed rectified EMG (srEMG) observed in subjects (n = 6) hopping at 1.7 Hz at four different heights. Peak srEMG values have been normalized for the peak values observed when subjects were hopping as high as possible (condition HIGH). Means that do not share subscripts differ at p < 0.05.
| muscle | HIGH | INTH | INTL | LOW |
|---|---|---|---|---|
| m. gluteus maximus | 1.0a | 0.7b ± 0.2 | 0.7ab ± 0.4 | 0.6ab ± 0.4 |
| m. biceps femoris | 1.0a | 0.8a ± 0.3 | 0.9a ± 0.2 | 0.6b ± 0.3 |
| m. rectus femoris | 1.0a | 0.8b ± 0.1 | 0.6bc ± 0.2 | 0.4c ± 0.1 |
| m. vastus lateralis | 1.0a | 0.9a ± 0.2 | 0.7ab ± 0.3 | 0.7b ± 0.3 |
| m. gastrocnemius | 1.0a | 0.8a ± 0.2 | 0.7b ± 0.1 | 0.7b ± 0.1 |
| m. soleus | 1.0a | 0.7b ± 0.2 | 0.6b ± 0.2 | 0.6b ± 0.1 |
(b). Computer simulations of hopping
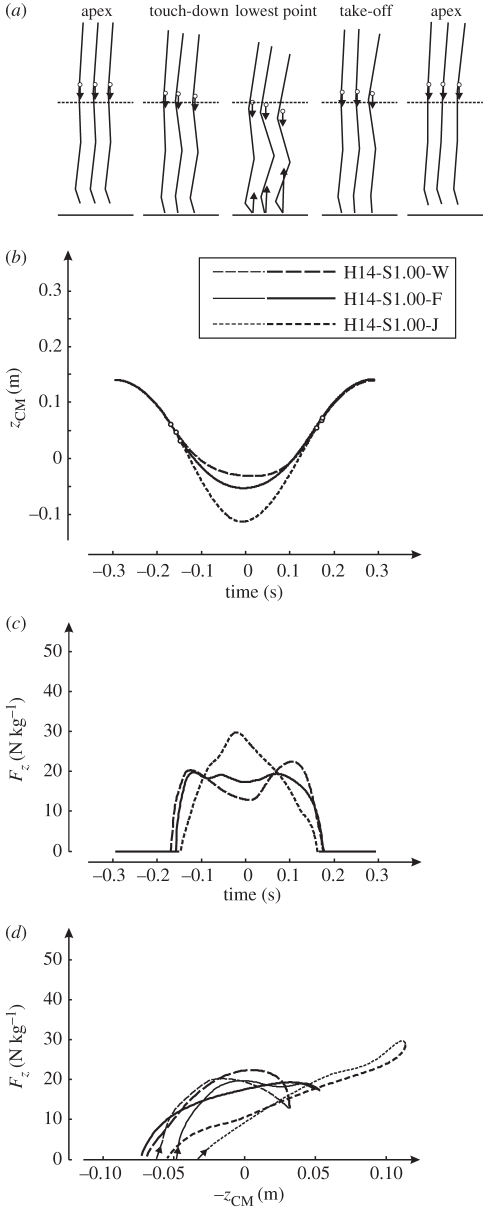
One purpose of performing the simulation study was to try and answer the question which criterion subjects use when asked to hop at 1.7 Hz without further instructions. Obviously, the higher the hopping height required, the smaller the effect that different criteria can have on how the jump is executed. For this reason, it is best to compare solutions obtained with different criteria at a relatively low hopping height. Figure 5 shows kinematics and kinetics of solutions obtained at a hopping height of 14 cm, which is somewhere between the heights at which the subjects hopped in conditions INTL and LOW. When 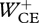 was minimized, Fz(t) was typically a double-humped curve, very different from the single-humped curves observed in the subjects (cf. figure 5c to figure 3c). The system essentially tended to minimize the lowering of CM (and prevent dissipation of energy in eccentric actions of CE) by quickly coming to a stop, waiting and pushing off again. When Fz,peak was minimized, Fz(t) not surprisingly tended towards a block pulse, with a shape very different from the curves observed in the subjects (cf. figure 5c to figure 3c). Only when zCM-jerk was minimized did we find single-humped Fz(t) curves resembling the curves found in the subjects, and simple spring-like leg behaviour in the sense that Fz increased monotonically with ‘leg compression’ (−zCM) during the landing phase and decreased monotonically with ‘leg decompression’ during the propulsion phase (figure 5d). The kinematics of this solution were similar to those observed in the subjects (cf. figure 5a to figure 3a), albeit that hip flexion during landing and subsequent hip extension during propulsion were greater in the simulation model than in the subjects.
was minimized, Fz(t) was typically a double-humped curve, very different from the single-humped curves observed in the subjects (cf. figure 5c to figure 3c). The system essentially tended to minimize the lowering of CM (and prevent dissipation of energy in eccentric actions of CE) by quickly coming to a stop, waiting and pushing off again. When Fz,peak was minimized, Fz(t) not surprisingly tended towards a block pulse, with a shape very different from the curves observed in the subjects (cf. figure 5c to figure 3c). Only when zCM-jerk was minimized did we find single-humped Fz(t) curves resembling the curves found in the subjects, and simple spring-like leg behaviour in the sense that Fz increased monotonically with ‘leg compression’ (−zCM) during the landing phase and decreased monotonically with ‘leg decompression’ during the propulsion phase (figure 5d). The kinematics of this solution were similar to those observed in the subjects (cf. figure 5a to figure 3a), albeit that hip flexion during landing and subsequent hip extension during propulsion were greater in the simulation model than in the subjects.
Figure 5.
Results of the simulation model hopping at 1.7 Hz at a height of 14 cm (H14). Optimal solutions were obtained with STIMmax set to 1.0 (S1.00) using three different optimization criteria: minimum positive work of contractile elements (W), minimum peak force of the vertical ground reaction force (F) and minimum jerk; (a–d) as in figure 3.
A second purpose of performing the simulation study was to try and understand how subjects realize different hopping heights at 1.7 Hz. To study this, we decided to use only minimum zCM-jerk solutions. Unfortunately, our model was unable to hop at the greatest height observed in the subjects, but it was able to hop at the height reached by the subjects in condition INTH, i.e. 20 cm. Figure 3 (right panel) shows kinematics and kinetics of the minimum zCM-jerk solution at 20 cm obtained with STIMmax set to 1.0 (H20-S1.00-J), as well as the solution at 14 cm obtained with STIMmax lowered to 0.18 (H14-S0.18-J), to mimic that the subjects reduced the neural input of their muscles when they reduced hopping height (figure 4a). The corresponding time histories of STIM are shown in figure 4b and those of active state are shown in figure 4c; note that while STIM was allowed to change four times, the solutions involved only one STIM burst in each muscle. In H14-S0.18-J, CM was lowered more during the contact phase, Fz,peak was lower and leg stiffness and ankle stiffness were smaller than in H20-S1.00-J. It may be noted at this point that solution H14-S0.18-J had 10 per cent less zCM-jerk and 5 per cent lower Fz,peak than solution H14-S1.00-J (i.e. the solution found with STIMmax set to 1.0 shown in figure 5), but the hops were kinematically quite similar (cf. figures 3 and 5). Details of H20-S1.00-J and H14-S0.18-J are provided in the two rightmost columns in table 1. Note that the relationship between Fz and −zCM is not perfectly linear in the model (figure 3d, right panel), so that the slope of a line fitted to the relationship, and hence leg stiffness, is not a perfect measure of the behaviour.
The simulation results can now be used to explain how subjects realize different hopping heights at 1.7 Hz, if we make the simplifying assumption that body posture is uniquely coupled to −zCM during landing and propulsion. In figure 6, we have plotted the average active state (q) of four important leg extensors (m. gluteus maximus, mm. vasti, m. gastrocnemius and m. soleus) as a function of −zCM. It can clearly be seen that in H14-S0.18-J, q increases less rapidly with −zCM than in H20-S1.00-J. Hence, under our simplifying assumption, muscle forces will tend to be lower, the positive acceleration of CM will be smaller and CM will reach a lower minimal height at which the joints are more flexed. When the joints are more flexed, the geometrical transfer function from joint moments to vertical acceleration of CM, and hence Fz, is less favourable. The combination of a greater excursion of −zCM and a smaller Fz at the lowest point of CM yields a lower leg stiffness during landing in H14-S0.18-J. During propulsion, q remains lower in H14-S0.18-J than in H20-S1.00-J, and because height of CM at take-off is almost the same, leg stiffness during propulsion is also less in H14-S0.18-J than in H20-S1.00-J.
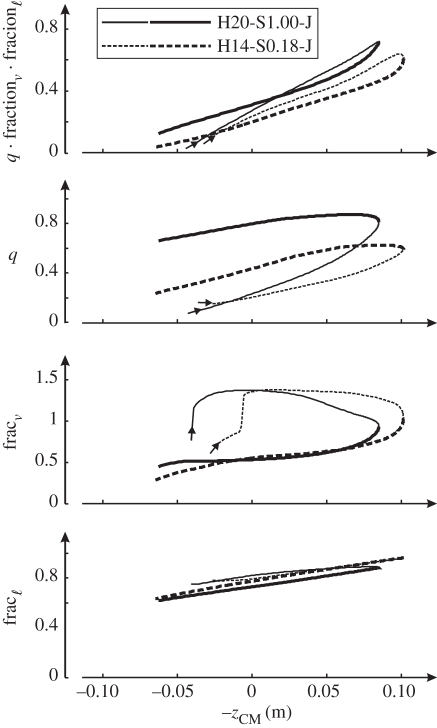
Figure 6.
Heuristic analysis of results of the simulation model hopping at 1.7 Hz. Optimal solutions were obtained for hopping at 20 cm (H20) with STIMmax set to 1.0 (S1.00) and at 14 cm (H14) with STIMmax set to 0.18 (S0.18), in both cases using minimum jerk as the optimization criterion. Muscle force F may be expressed as: F = F0 · q · fractionℓ · fractionv, where F0 is the maximum isometric force, q is active state (a scaling factor between 0 and 1), fractionℓ depends on contractile element length and fractionv depends on contractile element velocity. Values of q, fractionℓ, fractionv and their product were averaged at each point in time over four important leg extensors (m. gluteus maximus, mm. vastii, m. gastrocnemius and m. soleus) and plotted as a function of −zCM. Curves start at touch-down (arrows) and are thin for the landing phase and thick for the propulsion phase.
The reader will have noticed in figure 6 that over most of the range of −zCM, q is much higher during propulsion than during landing, while Fz is almost the same during propulsion and landing (figure 3d, right panel). This is because q is only one of the three factors determining muscle force; the other two factors are CE length and CE velocity. Muscle force F may be expressed as:
where F0 is maximum isometric force, fractionℓ is the force–length relationship describing that the isometric force is lower than F0 at greater and smaller CE lengths than optimum (where fractionℓ is 1.0) and fractionv is the force–velocity relationship describing that CE can produce more force during lengthening than during isometric contraction (where fractionv is 1.0) and less force during shortening than during isometric contraction. We have calculated fractionℓ and fractionv, averaged them over m. gluteus maximus, mm. vasti, m. gastrocnemius and m. soleus and plotted them in figure 6 as a function of −zCM. It becomes immediately clear that the force–velocity relationship has a profound effect on Fz. During landing, the muscles lengthen and fractionv is much greater than 1.0, while during propulsion the muscles shorten and fractionv is much smaller than 1.0. Note that the relationship between fractionℓ and −zCM is almost the same during landing as during propulsion (figure 6). Note also that the relationship between the product q · fractionℓ · fractionv and −zCM is similar during landing and during propulsion as well, and very similar to the relationship between Fz and −zCM (figure 3d, right panel). If we look at the overall behaviour of the system, it will be clear that during landing Fz increases primarily because q increases, while during propulsion Fz decreases primarily because fractionv decreases.
The fact that CE lengthening occurs during the landing phase implies that energy is dissipated during landing and hence underscores what we already knew: the spring-like behaviour of the leg should not be confused with the behaviour of a mechanical spring. We used the simulation results to get an impression of energy dissipation, elastic storage and work production in hopping (table 3). Regardless of which optimization criterion was used, most of the energy that CM lost during landing was dissipated, and only a small fraction (at most some 30%, in H14-S1.00-J) was stored in SEEs (mostly those of m. gastrocnemius and mm. vasti, results not shown) and reutilized during the propulsion phase. Note that net work of the MTCs is positive because it needs to make up for collisional losses and because the rotational energy of segments is greater at take-off than at touch-down.
Table 3.
Work terms summed over all muscle–tendon complexes of the model for hopping at 20 cm (H20) or 14 cm (H14). Solutions were obtained with STIMmax set to 1.0 (S1.00) using as the optimization criterion either minimal jerk (J) or minimal positive work of contractile elements (W). Work terms have been calculated over the total contact phase (Wnet), over the landing phase, i.e. from touch-down to the instant that the centre of mass reached its lowest point (W−), and over the propulsion phase, i.e. from the latter instant to take-off (W+). (MTC, muscle–tendon complexes; CE, contractile elements; SEE, series elastic elements.)
| H20-S1.00-J | H20-S1.00-W | H14-S1.00-J | H14-S1.00-W | |
|---|---|---|---|---|
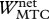 (J kg−1) (J kg−1) |
0.7 | 0.5 | 0.1 | 0.3 |
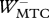 (J kg−1) (J kg−1) |
−2.9 | −2.6 | −2.7 | −1.6 |
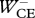 (J kg−1) (J kg−1) |
−2.2 | −2.0 | −1.8 | −1.3 |
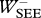 (J kg−1) (J kg−1) |
−0.7 | −0.6 | −0.9 | −0.3 |
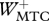 (J kg−1) (J kg−1) |
3.6 | 3.1 | 2.8 | 1.9 |
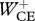 (J kg−1) (J kg−1) |
2.9 | 2.5 | 2.0 | 1.7 |
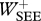 (J kg−1) (J kg−1) |
0.7 | 0.6 | 0.8 | 0.2 |
Finally, as a first step towards understanding the control of hopping, we used the model to test a simple strategy to change from hopping at one height to hopping at another height. We posed the following question: Once optimal control has been found for one hopping height, can it be used to hop at a different height by keeping the pattern of STIM changes the same but adapting STIM amplitude, like the subjects did? We took the pattern of STIM changes corresponding to solution H14-S0.18-J and increased STIMmax from 0.18 to 1.0. We then put the model at an initial height of 20 cm, shifted the whole STIM pattern backward in time to account for the greater fall time and released the model. Figure 7 shows the resulting jump, which is labelled H20-S1.00-pilot. It differs only very little from H20-S1.00-J, albeit that cycle time was a little over 588 ms. Note that the stiffness of the leg spring increased over that in H14-S0.18-J.
Figure 7.
Results of the simulation model hopping at 1.7 Hz at a height of 14 cm (H14) and at 20 cm (H20). The results for hopping at 14 cm correspond to the optimal solution obtained with STIMmax set to 0.18 (S0.18) and using minimum jerk (J) as the optimization criterion (this solution, H14-S0.18-J, was already presented in figure 3, right panel). Results labelled H20-S1.00-J correspond to the optimal solution obtained with STIMmax set to 1.0 (S1.00) and using minimum jerk as the optimization criterion (this solution was also presented in figure 3, right panel). Result labelled H20-S1.00-pilot was not obtained by optimization. Instead of optimizing STIM(t), we took the pattern of STIM changes corresponding to solution H14-S0.18-J and increased STIMmax from 0.18 to 1.0. We then put the model at an initial height of 20 cm, shifted the whole STIM pattern backward in time to account for the greater fall time and released the model. Note that the result differs only very little from those for H20-S1.00-J; (a–d) as in figure 3.
4. Discussion
The purpose of this study was to understand how humans regulate their leg stiffness in hopping, and to determine whether this regulation is intended to minimize energy expenditure. Variations in leg stiffness were achieved in our subjects by having them hop at maximum and submaximum heights at a fixed frequency of 1.7 Hz, without giving instructions with respect to landing posture or contact duration. When the subjects reduced hopping height, they chose to keep the landing and take-off postures unchanged, but lowered CM more and had their joints more flexed when CM reached the lowest point (figure 3a). The leg spring behaved quite linearly and its ‘stiffness’ decreased with hopping height (figure 3d and table 1). The kinematic and kinetic patterns ultimately result from muscle activation patterns. At maximum height, the subjects hopped with a single burst of activity in their major leg extensors and when reducing hopping height, they lowered the rate of increase and the amplitude of these single bursts (figure 4a) rather than, for example, keeping the amplitude unchanged and switching to a double-burst pattern. We attempted to reproduce the experimental results with a forward simulation model of the musculoskeletal system. A poor correspondence between simulated hops and experimental hops was obtained when STIM(t) was optimized using an objective function that minimized mechanical energy expenditure (cf. figures 5 and 3, left panel), but a good correspondence was achieved using an objective function that penalized jerk of CM motion (figure 3 and table 1). Below, we will first compare our experimental results with results reported in the literature. Second, we will discuss a number of limitations of our simulation study. Third, we will address the question whether subjects are minimizing energy expenditure in hopping. Fourth, we will discuss the relationship between the global spring-like behaviour and the behaviour of the elements of the musculoskeletal system. Fifth, we will address the question whether there is any advantage for subjects to make the leg spring linear, and finally we will speculate on why subjects hop at maximum and submaximum heights the way they do.
(a). Comparison of experimental results with results reported in the literature
In previous studies of hopping at maximum height (e.g. [3–5]), it has been shown that leg stiffness becomes lower as frequency decreases. In this study, we chose a relatively low frequency of 1.7 Hz, which is below the preferred hopping frequency (typically around 2 Hz [4]), so that our subjects could produce a large range of hopping heights (on average, a range of 14 cm; table 2). As a consequence, leg stiffness in our subjects at maximum height hopping (of the order of 350 N m−1 kg−1) was lower than that reported by others (up to around 750 N m−1 kg−1 at 2.2 Hz in Farley et al. [4]). Farley et al. [4] reported that below the preferred frequency, their subjects did not behave as much as simple spring-mass systems; in some subjects, Fz dropped before the minimum height of CM was reached or Fz increased during the first part of the propulsion phase. This violates the concept of spring-like behaviour because ‘… in a simple mechanical spring, the force never falls while it is being stretched … ’ and ‘ … the force would never increase as it recoiled’ [4]. However, in the present study, we found no such deviations from spring-like behaviour in any of the trials, and the average behaviour was clearly that of a simple linear spring (figure 3d, left panel). It should be pointed out that body mass in our subjects was 78 kg on average, while that in the subjects participating in the study of Farley et al. [4] was only 63.5 kg on average; differences in body mass have been shown to affect leg stiffness [32] and hence may cause differences in behaviour among subjects. The instruction given to subjects has also been shown to affect leg stiffness [33,34], and some authors have specifically instructed their subjects to hop with as short a contact time as possible (e.g. [5]). However, we were interested in the spontaneous behaviour of subjects and therefore gave no instructions with respect to posture or duration of contact.
(b). Limitations of the simulation study
One of the intriguing questions is why subjects control their musculoskeletal system in such a way that it behaves in a spring-like manner. It has been speculated in the literature that this may help to keep energy expenditure low (e.g. [4,13]). Because mechanical energy expenditure during hopping in subjects cannot be measured, we decided to resort to forward simulations with a model of the musculoskeletal system. Musculoskeletal models are simplifications of the real system and many of the properties of the real system, such as the force–length and force–velocity relationships of individual muscles, cannot be measured in vivo. The parameter values of the model therefore had to be obtained by combining results of experiments on human cadavers, experiments on isolated muscles of animals and dynamometer experiments on human subjects (for details, see [35]), and have the status of educated guesses. Nevertheless, optimization of STIM(t) using only CM height as a criterion has previously allowed us to reproduce various types of jumps of human subjects with the model, not only in terms of kinematics and kinetics but even in activation onset patterns of muscles [29]. Simulating hopping poses an even greater challenge because of the rapid lengthening of MTCs during the landing phase, which increases the involvement of the enigmatic eccentric part of the force–velocity relationship. The question has been raised whether muscle lengthening can be modelled using Hill-type models, or whether cross-bridge models need to be used. Supported by the conclusion of Cole et al. [36] that Hill-type models actually performed better than Huxley-type models in predicting force during isovelocity stretches of cat soleus muscle, we decided to stick to the former. And in fact our model could produce realistic looking hops (figure 3), albeit that it was unable to hop at the greatest height observed in the subjects. We could have easily increased the model's maximum hopping height by changing parameter values. For example, we could have increased the rate of increase of STIM(t) over the value of 5 s−1 based on maximum height squat jumping [29]. However, since the model was able to produce hops that closely resembled the hops of the subjects in terms of kinematic and kinetic patterns, in the case where we optimized STIM(t) for minimum zCM-jerk (figure 3 and table 1), we saw no need to tweak any of its parameters' values.
(c). Are subjects minimizing energy expenditure during hopping?
When we optimized STIM(t) for minimal positive CE work rather than for minimum zCM-jerk, Fz(t) was typically a two-humped curve very different from the single-humped curves observed in the subjects (cf. figure 5c to figure 3c). The optimal solutions for minimum positive CE work in submaximum height hopping involved double-burst STIM(t) patterns of important extensor muscles like mm. vasti (results not shown). Considering the poor resemblance of solutions for minimum mechanical energy expenditure with hops observed in the subjects, we regard it highly unlikely that subjects choose to hop the way they do to minimize mechanical energy expenditure. Would the outcome have been different if we had used metabolic energy consumption as a criterion rather than mechanical energy expenditure? While realizing that this does not provide a decisive answer, we calculated metabolic energy expenditure from our simulation results using the equations provided by Umberger et al. [37]. We confirmed that the solutions obtained for minimum zCM-jerk were not only mechanically more expensive but also had a higher heat production, and hence were also metabolically more expensive than the solutions for minimum 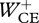 . Interesting in this context is the recent finding that metabolic power is not minimal when subjects hop at their preferred frequency (2 Hz) but rather at frequencies close to 3 Hz [38]. This also suggests that when subjects are hopping, minimization of metabolic power is not their primary concern. The same conclusion was recently reached for making arm movements in complicated force fields [39].
. Interesting in this context is the recent finding that metabolic power is not minimal when subjects hop at their preferred frequency (2 Hz) but rather at frequencies close to 3 Hz [38]. This also suggests that when subjects are hopping, minimization of metabolic power is not their primary concern. The same conclusion was recently reached for making arm movements in complicated force fields [39].
(d). Is the global spring-like behaviour related to the behaviour of elements of the musculoskeletal system?
One of the questions often posed in the literature (e.g. [4,13,17]) is how the global behaviour of the leg spring relates to the behaviour of elements of the musculoskeletal system. It is perhaps tempting to think that the global spring-like behaviour originates from passive elastic elements such as tendons, but this is incorrect. It is true that the Achilles tendon behaves like a linear spring during hopping [40]. Also, the force of the Achilles tendon dominates the ankle joint moment, and ankle stiffness is closely related to leg stiffness [3]. This does not mean, however, that the global spring-like behaviour of the leg originates from the Achilles tendon, because the Achilles tendon is in series with muscle fibres. It is ultimately the activation of the muscle fibres that determines how much force is produced at what position, and hence what the global behaviour will be like. Our simulation results clearly show that with the same musculoskeletal elements, steady-state hopping at 1.7 Hz at a given height can be achieved with very different global behaviour by modifying STIM(t) (figure 5).
(e). Is there any advantage for subjects to make the leg spring linear?
We have shown that the force–velocity relationship has a profound influence on the forces generated during hopping (figure 6). During landing, Fz increases primarily because q increases, while during propulsion, Fz decreases primarily because of the force–velocity relationship. It has been shown in previous studies that the force–velocity relationship helps to stabilize movements [26,41,42], but this stabilization comes at a cost because the force–velocity relationship causes dissipation of energy. During hopping, more than 70 per cent of the energy that CM lost during the landing phase was dissipated and at most 30 per cent could be stored in SEEs (table 3). Clearly, the spring-like behaviour of the leg should not be confused with the behaviour of a mechanical spring and the linearity of the leg spring is not in any way beneficial for energy conservation. Does the linearity of the leg spring perhaps simplify control? It has been shown for hopping that, given a prescribed pattern of STIM(t), leg stiffness passively adjusts to unpredictable changes in surface properties [25]. However, considering that the intrinsic muscle properties play a dominant role in shaping the overall behaviour (figure 6), it seems unlikely that the linearity of the leg spring simplifies adjusting control signals to change the movement. After all, the intrinsic muscle properties need to be taken into account by the central nervous system in preparing control signals to realize any type of behaviour, and why would it be easier to prepare control signals for linear behaviour of the leg spring than to prepare control signals for any other type of behaviour?
(f). Why would subjects hop at maximum and submaximum heights the way they do?
Above, we have argued that the linearity of the leg spring is not a means to an end such as minimizing energy expenditure or simplifying control. More likely, it simply evolves out of the complex interplay between control signals, viscoelastic properties of the elements of the musculoskeletal system and changes in geometry occurring as a result of the forces generated. This brings us back to the question why subjects hop at maximum and submaximum heights the way they do. We speculate that subjects choose a simple control strategy. Let us begin our reasoning by pointing out that hopping at the maximum height at an imposed frequency is a really challenging task, in which performance depends crucially on the timing of muscle stimulation onsets. Humans perform this task with a single burst of activity in each muscle (figure 4a). After optimization, our simulation model also hopped at the maximum height with a single burst of activity in each muscle (figure 4b,c), even though up to four stimulation switches were allowed. It may be concluded that a pattern of well-timed single bursts in each muscle leads to maximum performance. For hopping at submaximum height, there are many possible solutions. Theoretically, the subjects could quickly come to a stop with a first maximal burst of activity, wait and push off with a second maximal burst of activity. However, they chose to basically stick to one burst of activity for each muscle and reduce the burst amplitude (figure 4a). In the simulation model, the use of different optimization criteria for hopping at the submaximum height indeed led to different kinematics and kinetics (figure 5). However, only the solution obtained with minimum zCM-jerk as the criterion involved a single burst of activity in each of the muscles, a single-humped Fz (t) curve, and more or less linear leg-spring behaviour (figure 5). Based on this finding, we could speculate that subjects are trying to make smooth movements, but frankly we see no reason why making smooth movements would be more attractive than making non-smooth movements. Instead, we speculate that when subjects reduce hopping height from maximal to submaximal, they prefer to continue to generate only one burst of activity for each muscle and reduce the burst amplitude, rather than take up the more challenging task of producing multiple bursts in order to minimize energy expenditure or force. The linear behaviour of their leg spring then simply evolves out of the complex interplay between the single-stimulation-burst-per-muscle pattern (figure 4a), the viscoelastic properties of the elements of the musculoskeletal system and the changes in geometry occurring as a result of the forces generated, just like it does in the simulation model (figures 4b,c and 5). In support of this argumentation, we have shown in figure 7 that by adapting STIMmax, a given pattern of STIM changes could be used to produce successful hops at different heights, and that this resulted in different stiffness values of the leg spring. In sum, we speculate that smooth movements and the linear behaviour of the leg spring in hopping are by-products of the need to use single-burst activation patterns and simple control strategies.
Acknowledgements
We would like to thank Erwin Slokker and Chris van Lierop for their valuable help in preparing and carrying out the experiments, and Dinant Kistemaker for his insightful comments on the manuscript.
Footnotes
One contribution of 15 to a Theme Issue ‘Integration of muscle function for producing and controlling movement’.
References
- 1.Blickhan R. 1989. The spring-mass model for running and hopping. J. Biomech. 22, 1217–1227 10.1016/0021-9290(89)90224-8 (doi:10.1016/0021-9290(89)90224-8) [DOI] [PubMed] [Google Scholar]
- 2.McMahon T. A., Cheng G. C. 1990. The mechanics of running: how does stiffness couple with speed? J. Biomech. 23(Suppl. 1), 65–78 10.1016/0021-9290(90)90042-2 (doi:10.1016/0021-9290(90)90042-2) [DOI] [PubMed] [Google Scholar]
- 3.Farley C. T., Morgenroth D. C. 1999. Leg stiffness primarily depends on ankle stiffness during human hopping. J. Biomech. 32, 267–273 10.1016/S0021-9290(98)00170-5 (doi:10.1016/S0021-9290(98)00170-5) [DOI] [PubMed] [Google Scholar]
- 4.Farley C. T., Blickhan R., Saito J., Taylor C. R. 1991. Hopping frequency in humans: a test of how springs set stride frequency in bouncing gaits. J. Appl. Physiol. 71, 2127–2132 [DOI] [PubMed] [Google Scholar]
- 5.Hobara H., Inoue K., Muraoka T., Omuro K., Sakamoto M., Kanosue K. 2009. Leg stiffness adjustment for a range of hopping frequencies in humans. J. Biomech. 43, 506–511 10.1016/j.jbiomech.2009.09.040 (doi:10.1016/j.jbiomech.2009.09.040) [DOI] [PubMed] [Google Scholar]
- 6.Farley C. T., Houdijk H. H., Van Strien C., Louie M. 1998. Mechanism of leg stiffness adjustment for hopping on surfaces of different stiffnesses. J. Appl. Physiol. 85, 1044–1055 [DOI] [PubMed] [Google Scholar]
- 7.Ferris D. P., Farley C. T. 1997. Interaction of leg stiffness and surfaces stiffness during human hopping. J. Appl. Physiol. 82, 15–22, discussion 13–4 [DOI] [PubMed] [Google Scholar]
- 8.Moritz C. T., Farley C. T. 2003. Human hopping on damped surfaces: strategies for adjusting leg mechanics. Proc. R. Soc. Lond. B 270, 1741–1746 10.1098/rstb.2003.2435 (doi:10.1098/rstb.2003.2435) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moritz C. T., Greene S. M., Farley C. T. 2004. Neuromuscular changes for hopping on a range of damped surfaces. J. Appl. Physiol. 96, 1996–2004 10.1152/japplphysiol.00983.2003 (doi:10.1152/japplphysiol.00983.2003) [DOI] [PubMed] [Google Scholar]
- 10.Farley C. T., Gonzalez O. 1996. Leg stiffness and stride frequency in human running. J. Biomech. 29, 181–186 10.1016/0021-9290(95)00029-1 (doi:10.1016/0021-9290(95)00029-1) [DOI] [PubMed] [Google Scholar]
- 11.Blum Y., Lipfert S. W., Seyfarth A. 2009. Effective leg stiffness in running. J. Biomech. 42, 2400–2405 10.1016/j.jbiomech.2009.06.040 (doi:10.1016/j.jbiomech.2009.06.040) [DOI] [PubMed] [Google Scholar]
- 12.Bullimore S. R., Burn J. F. 2007. Ability of the planar spring-mass model to predict mechanical parameters in running humans. J. Theor. Biol. 248, 686–695 10.1016/j.jtbi.2007.06.004 (doi:10.1016/j.jtbi.2007.06.004) [DOI] [PubMed] [Google Scholar]
- 13.Biewener A. A., Daley M. A. 2007. Unsteady locomotion: integrating muscle function with whole body dynamics and neuromuscular control. J. Exp. Biol. 210, 2949–2960 10.1242/jeb.005801 (doi:10.1242/jeb.005801) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Seyfarth A., Geyer H., Gunther M., Blickhan R. 2002. A movement criterion for running. J. Biomech. 35, 649–655 10.1016/S0021-9290(01)00245-7 (doi:10.1016/S0021-9290(01)00245-7) [DOI] [PubMed] [Google Scholar]
- 15.Seyfarth A., Gunther M., Blickhan R. 2001. Stable operation of an elastic three-segment leg. Biol. Cybern. 84, 365–382 10.1007/PL00007982 (doi:10.1007/PL00007982) [DOI] [PubMed] [Google Scholar]
- 16.Auyang A. G., Yen J. T., Chang Y. H. 2009. Neuromechanical stabilization of leg length and orientation through interjoint compensation during human hopping. Exp. Brain Res. Exp. Hirnforsch. 192, 253–264 10.1007/s00221-008-1582-7 (doi:10.1007/s00221-008-1582-7) [DOI] [PubMed] [Google Scholar]
- 17.Yen J. T., Chang Y. H. 2010. Rate-dependent control strategies stabilize limb forces during human locomotion. J. R. Soc. Interface 7, 801–810 10.1098/rsif.2009.0296 (doi:10.1098/rsif.2009.0296) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Flash T., Hogan N. 1985. The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Clauser C. E., McConville J. T., Young J. W. 1969. Weight, volume, and center of mass of segments of the human body. AMRL Technical Report (NTIS No. AD-710-622.), Wright-Patterson Air Force Base, OH, 69–70 [Google Scholar]
- 20.Bobbert M. F., Gerritsen K. G., Litjens M. C., Van Soest A. J. 1996. Why is countermovement jump height greater than squat jump height? Med. Sci. Sports Exerc. 28, 1402–1412 [DOI] [PubMed] [Google Scholar]
- 21.Granata K. P., Padua D. A., Wilson S. E. 2002. Gender differences in active musculoskeletal stiffness. Part II. Quantification of leg stiffness during functional hopping tasks. J. Electromyogr. Kinesiol. 12, 127–135 10.1016/S1050-6411(02)00003-2 (doi:10.1016/S1050-6411(02)00003-2) [DOI] [PubMed] [Google Scholar]
- 22.Elftman H. 1939. Forces and energy changes in the leg during walking. Am. J. Physiol. 125, 339–356 [Google Scholar]
- 23.Yeadon M. R., Morlock M. 1989. The appropriate use of regression equations for the estimation of segmental inertia parameters. J. Biomech. 22, 683–689 10.1016/0021-9290(89)90018-3 (doi:10.1016/0021-9290(89)90018-3) [DOI] [PubMed] [Google Scholar]
- 24.van Soest A. J., Schwab A. L., Bobbert M. F., van Ingen Schenau G. J. 1993. The influence of the biarticularity of the gastrocnemius muscle on vertical-jumping achievement. J. Biomech. 26, 1–8 10.1016/0021-9290(93)90608-H (doi:10.1016/0021-9290(93)90608-H) [DOI] [PubMed] [Google Scholar]
- 25.van der Krogt M. M., de Graaf W. W., Farley C. T., Moritz C. T., Richard Casius L. J., Bobbert M. F. 2009. Robust passive dynamics of the musculoskeletal system compensate for unexpected surface changes during human hopping. J. Appl. Physiol. 107, 801–808 10.1152/japplphysiol.91189.2008 (doi:10.1152/japplphysiol.91189.2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van Soest A. J., Bobbert M. F. 1993. The contribution of muscle properties in the control of explosive movements. Biol. Cybern. 69, 195–204 10.1007/BF00198959 (doi:10.1007/BF00198959) [DOI] [PubMed] [Google Scholar]
- 27.Ebashi S., Endo M. 1968. Calcium ion and muscle contraction. Prog. Biophys. Mol. Biol. 18, 123–183 10.1016/0079-6107(68)90023-0 (doi:10.1016/0079-6107(68)90023-0) [DOI] [PubMed] [Google Scholar]
- 28.Hatze H. 1977. A myocybernetic control model of skeletal muscle. Biol. Cybern. 25, 103–119 10.1007/BF00337268 (doi:10.1007/BF00337268) [DOI] [PubMed] [Google Scholar]
- 29.Bobbert M. F., Casius L. J., Sijpkens I. W., Jaspers R. T. 2008. Humans adjust control to initial squat depth in vertical squat jumping. J. Appl. Physiol. 105, 1428–1440 10.1152/japplphysiol.90571.2008 (doi:10.1152/japplphysiol.90571.2008) [DOI] [PubMed] [Google Scholar]
- 30.van Soest A. J., Casius L. J. 2003. The merits of a parallel genetic algorithm in solving hard optimization problems. J. Biomech. Eng. 125, 141–146 10.1115/1.1537735 (doi:10.1115/1.1537735) [DOI] [PubMed] [Google Scholar]
- 31.Goffe W. L., Ferrier G. D., Rogers J. 1994. Global optimization of statistical functions with simulated annealing. J. Econom. 60, 65–99 10.1016/0304-4076(94)90038-8 (doi:10.1016/0304-4076(94)90038-8) [DOI] [Google Scholar]
- 32.Farley C. T., Korff W. L. 1999. Musculoskeletal basis for the scaling of leg stiffness with body mass in humans. Proc. Am. Soc. Biomech. 230–231 See http://www.asbweb.org/conferences/1990s/1999/ACROBAT/160.PDF
- 33.Arampatzis A., Schade F., Walsh M., Bruggemann G. P. 2001. Influence of leg stiffness and its effect on myodynamic jumping performance. J. Electromyogr. Kinesiol. 11, 355–364 10.1016/S1050-6411(01)00009-8 (doi:10.1016/S1050-6411(01)00009-8) [DOI] [PubMed] [Google Scholar]
- 34.Bobbert M. F., Huijing P. A., van Ingen Schenau G. J., Drop jumping I. 1987. The influence of jumping technique on the biomechanics of jumping. Med. Sci. Sports Exerc. 19, 332–338 [PubMed] [Google Scholar]
- 35.Bobbert M. F. 2001. Dependence of human squat jump performance on the series elastic compliance of the triceps surae: a simulation study. J. Exp. Biol. 204, 533–542 [DOI] [PubMed] [Google Scholar]
- 36.Cole G. K., van den Bogert A. J., Herzog W., Gerritsen K. G. 1996. Modelling of force production in skeletal muscle undergoing stretch. J. Biomech. 29, 1091–1104 10.1016/0021-9290(96)00005-X (doi:10.1016/0021-9290(96)00005-X) [DOI] [PubMed] [Google Scholar]
- 37.Umberger B. R., Gerritsen K. G., Martin P. E. 2003. A model of human muscle energy expenditure. Comput. Methods Biomech. Biomed. Eng. 6, 99–111 10.1080/1025584031000091678 (doi:10.1080/1025584031000091678) [DOI] [PubMed] [Google Scholar]
- 38.Grabowski A. M., Herr H. M. 2009. Leg exoskeleton reduces the metabolic cost of human hopping. J. Appl. Physiol. 107, 670–678 10.1152/japplphysiol.91609.2008 (doi:10.1152/japplphysiol.91609.2008) [DOI] [PubMed] [Google Scholar]
- 39.Kistemaker D. A., Wong J. D., Gribble P. L. 2010. The central nervous system does not minimize energy cost in arm movements. J. Neurophysiol. 104, 2985–2994 10.1152/jn.00483.2010 (doi:10.1152/jn.00483.2010) [DOI] [PubMed] [Google Scholar]
- 40.Lichtwark G. A., Wilson A. M. 2005. In vivo mechanical properties of the human Achilles tendon during one-legged hopping. J. Exp. Biol. 208, 4715–4725 10.1242/jeb.01950 (doi:10.1242/jeb.01950) [DOI] [PubMed] [Google Scholar]
- 41.Blickhan R., Seyfarth A., Geyer H., Grimmer S., Wagner H., Gunther M. 2007. Intelligence by mechanics. Phil. Trans. R. Soc. A 365, 199–220 10.1098/rsta.2006.1911 (doi:10.1098/rsta.2006.1911) [DOI] [PubMed] [Google Scholar]
- 42.Haeufle D. F., Grimmer S., Seyfarth A. 2010. The role of intrinsic muscle properties for stable hopping–stability is achieved by the force–velocity relation. Bioinspir. Biomim. 5, 16004. 10.1088/1748-3182/5/1/016004 (doi:10.1088/1748-3182/5/1/016004) [DOI] [PubMed] [Google Scholar]