Shifts in a single muscle's control potential of body dynamics are determined by mechanical feedback

Abstract

Muscles are multi-functional structures that interface neural and mechanical systems. Muscle work depends on a large multi-dimensional space of stimulus (neural) and strain (mechanical) parameters. In our companion paper, we rewrote activation to individual muscles in intact, behaving cockroaches (Blaberus discoidalis L.), revealing a specific muscle's potential to control body dynamics in different behaviours. Here, we use those results to provide the biologically relevant parameters for in situ work measurements. We test four hypotheses about how muscle function changes to provide mechanisms for the observed control responses. Under isometric conditions, a graded increase in muscle stress underlies its linear actuation during standing behaviours. Despite typically absorbing energy, this muscle can recruit two separate periods of positive work when controlling running. This functional change arises from mechanical feedback filtering a linear increase in neural activation into nonlinear work output. Changing activation phase again led to positive work recruitment, but at different times, consistent with the muscle's ability to also produce a turn. Changes in muscle work required considering the natural sequence of strides and separating swing and stance contributions of work. Both in vivo control potentials and in situ work loops were necessary to discover the neuromechanical coupling enabling control.

1. Introduction

Animals' remarkable locomotor abilities arise from the interaction of neural activity and musculo-skeletal mechanics [1–4]. Muscles mediate this interface, transforming motor activation into forces and work. However, this transformation is complex, tuned by muscles' physiological properties and the mechanics of joints, connective tissue and other associated muscles [5–8]. In our companion paper [9], we quantified a muscle's control potential, the input–output relationship between changes in a specific muscle's activation and its causal effects on body dynamics. We altered motor activation in an intact, behaving animal and measured resulting centre-of-mass impulses and kinematics. We discovered that a single muscle's control potential can be remarkably multi-functional. A graded increase in motor activation could produce graded actuation, a nonlinearly recruited vertical impulse, or generate a turn depending on the animal's behavioural context.

However, understanding how neural and mechanical factors combine to generate these control potentials requires revealing the mechanisms underlying force and work production in the muscle itself. Muscles are already known to be capable of a variety of functions. Predicting their work output solely from activation patterns or isolated muscle physiology experiments can obscure important functional differences [7,8,10–13]. Muscles can act as springs, brakes, struts, actuators or dampers [2,4,8,14,15], and muscle work changes both with changing motor activation (neural feedback) and changes in its mechanical state imposed by limb motion and body orientation (mechanical feedback) [3–5,11,16,17]. We can use the in vivo limb kinematics and patterns of activation from our control potential experiments to specify where in the muscle's vast parameter space it is operating during a perturbation response. In turn, we can test how a muscle's functional capabilities enable specific control responses. Measuring the muscle's control potential is necessary to know its impact on body dynamics in an intact, behaving animal, but measuring its work output is also required for a mechanistic understanding of how the animal generates this control.

In our companion paper [9], we altered the motor activations of intact, running cockroaches (Blaberus discoidalis (L.)) and discovered control potentials for a middle leg control muscle, the ventral femoral extensor muscle 137 [18]. We altered muscle activation in vivo during both static standing (figure 1b(i)) and dynamic running (figure 1c) tasks by adding muscle action potentials (MAPs) with precise timing. We added MAPs at the end of the natural burst of activity to mimic the neural feedback a cockroach provides to this muscle when traversing large obstacles [17]. We also added MAPs at the beginning of the burst to advance activation phase, which was hypothesized to control swing–stance transitions and to generate turns [19,20].

Figure 1.

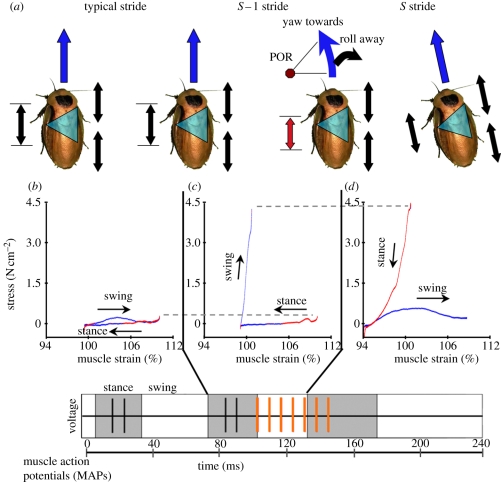
Intact-joint work loop and experimental conditions. We developed (a) a work loop preparation that preserved the physiological environment of the muscle and allowed for stimulus methods more similar to in vivo conditions. We denervated (a(i)) the limb, (a(ii)) enforced realistic patterns of activation and (a(iii)) strain mimicking a standard or (a(iv)) altered stride and recorded the resulting forces around the coxa–femur (CF) joint. Typical stride conditions included two muscle action potentials (MAPs, black dots or lines) a shortening phase when limb extends from its anterior extreme position (AEP; A) to its posterior extreme position (PEP; P) followed by a protraction period with a duty factor of 0.6. Experimental conditions consisted of (b(i)) repeated presentations of isometric twitches, (b(ii)) passive work loops, (b(iii)) a sweep through different levels of activation and (b(iv)) a sweep through phase. We also considered (b(v)) repeated presentations of the stimulated (S) stride and (b(vi)) the following (S + 1) stride. To preserve the appropriate sequence of strides and consider history effects, we played out the S and S + 1 strides with the preceding S − 1 and typical (T) strides while extending (c) the burst of activation or advancing its phase. The trials shown illustrate (c, top) strain and stimulus patterns from seven added MAPs and (c, bottom) a phase onset of −0.5 with seven total MAPs. Black lines or dots, typical stride MAP; orange dots, added MAP.

We can test muscle function with the work loop approach first developed by Boettinger [21] and Machin & Pringle [22], and extended by Josephson [23]. We produce in situ the stress–strain relationships a muscle experiences during locomotion by imposing its observed in vivo strain pattern and stimulation while measuring force. In this paper, we use an intact-joint work loop preparation that differs from the classic approach in two ways (figure 1a). First, instead of direct neural stimulation, we stimulated the muscle with bipolar extracellular electrodes to match the methodology from our in vivo modifications of muscle activation. Secondly, we preserved the mechanical and physiological environment of the muscle. To consider only the work done by the ventral femoral extensor on the coxa–femur (CF) joint, we denervated all leg muscles and accounted for changes in the passive resistance of the joint.

We first compare this work loop preparation to isolated muscle work loops and then test four hypotheses regarding muscle work output in the ventral femoral extensor and its link to the in vivo control potentials. In doing so, we report phase and activation sweep results, consider how work is modulated across multiple sequential strides, and test work output under different patterns of neural stimulation and mechanical strain. We first consider the hypothesis that increasing activation isometrically leads to a graded increase in twitch forces, enabling a linear posture control potential (figure 1b(i); muscle work hypothesis 1). In our companion in vivo paper [9], increasing activation to the ventral femoral extensor in a quasi-static behaviour led to a linear increase in body impulses and rotations around all degrees of freedom of the centre of mass (COM). Previous studies in isolated muscles [11] and detailed musculo-skeletal models [24] indicate that a ventral femoral extensor's force should increase smoothly over this range, although force output has not been considered in the presence of passive joint mechanics.

In our in vivo experiments [9], we found that the same increase in activation in the femoral extensor that leads to multi-directional linear actuation during standing instead produces a nonlinear acceleration restricted to the vertical direction during running. However, while this behaviour suggests a motor-like muscle function, previous work loops on this same muscle suggested that it should instead absorb more energy, acting like a brake as activation increases. This is because the muscle usually does not develop significant stress until the limb has transitioned to its swing phase during which the muscle is actively lengthened. We hypothesized [9] that changes in the limb kinematics and muscle strain that occur along with increases in activation in the locomoting animal can enable significant positive work (muscle work hypothesis 2). Tracking limb kinematics during the in vivo manipulations of motor activation showed nonlinear increases in limb duty factor and extension that paralleled the nonlinear acceleration of the body [9]. To test if these changes are sufficient to alter muscle function, we match work loops to the strain and stimulus parameters of the sequence of strides surrounding changes in muscle activation in the in vivo experiments (figure 1c, top). Alternatively, the muscle may continue to absorb energy and the control potential could arise from coupling its effects to the rest of the musculo-skeletal system.

Changing the activation of the ventral femoral extensor in the running experiments altered body dynamics and limb kinematics for multiple strides [9]. This suggests that stride-to-stride effects may carry over at the level of the muscle's work itself. We hypothesize that the stress and strain developed in one stride could contribute to the work done in subsequent strides (muscle work hypothesis 3). Continued changes in limb kinematics could alter future work production, and the history effects of muscle activation itself can persist for very significant periods, particularly during high-frequency behaviours [6,11,15,16]. This hypothesis predicts that the work output should be significantly different if the muscle's stress and strain is considered for each stride in isolation rather than in the naturally occurring stride sequence. Alternatively, since the ventral femoral extensor's activation is usually early in the stride (figure 1a), effects of muscle stimulation may not persist from one stride to the next. To test this, we compare sequential work loop trials (figure 1c, top) to presentations of isolated stimulated (S) or post-stimulus (S + 1) strides (figure 1b(v)(vi)).

Finally, we test how phase advancing the activation of the ventral femoral extensor leads to a third control potential where vertical acceleration does not change, but the animal accelerates laterally, yaws and rolls in a manner consistent with turning [9,19]. Again, however, the mechanism that enables these control effects remains unclear without studying muscle function, particularly because the yaw and lateral acceleration were towards the stimulated leg, while the roll was away from it. We hypothesize that changing phase of activation leads to greater energy absorption in the muscle, consistent with a turn towards that limb and the muscle's previously known function (muscle work hypothesis 4). Alternatively, the muscle could do positive work while shifting its position and timing to enable a turn. As we will show, incorporating the changes in muscle strain that occur with phase activation does absorb more energy, but only when the limb is off the ground. Instead of directly generating a turn, this allows the muscle to recruit positive work in the subsequent stride, change the timing of work production in the gait cycle, and thereby cause rotation.

Throughout our experiments, we find that the ventral femoral extensor's function is tuned by neural and mechanical feedback to enable the diverse motor control tasks it accomplishes in vivo. Its multi-functional control potential is paralleled by recruitable periods of positive and negative work in the muscle itself.

2. Methods

(a). Animals

We used adult male and non-gravid female cockroaches, B. discoidalis (L.), maintained on a 12 L : 12 D cycle and provided a dog chow and water ad libitum. For the burst extension and phase advance experiments, we used 7 and 18 animals, respectively. Average animal mass was 2.04 ± 0.25 g (s.d.).

(b). Intact-joint work loops

For the intact-joint work loop preparation, it was necessary to first denervate all the limb muscles to prevent spontaneous activation from obscuring the work output of the ventral femoral extensor. Cockroaches were cold anaesthetized and a small incision was made in the soft, non-sclerotized cuticle at the proximal portion of the body–coxa joint. We cut nerves 3, 4, 5 and 6, emanating from the thoracic ganglion, near their origins (figure 1a (i)). These nerves contain all motor neurons projecting to muscles in the middle limb [25,26]. Ablation was monitored through the semi-transparent cuticle and we took care not to sever the central trachea. To test denervation, we confirmed that struggling motions were entirely absent from the denervated limb. We also checked nerve ablation in post-experimentation dissections.

Following denervation, cockroaches were mounted in a custom restraint. We epoxied the coxa to the restraint so that the CF joint was oriented in a horizontal plane and mechanically isolated from the body. No epoxy was allowed to contact the joint. The distal limb segments were removed just below the femur–tibia (FTi) joint. This restraint system allowed the cockroach to be fully awake during measurements. Two 50 µm silver wire stimulus electrodes (California Fine Wire Company, Grover Beach, CA, USA) were inserted through the coxa cuticle above the ventral femoral extensor, mimicking the stimulation used in the in vivo experiments (figure 1a(ii)). Stimulus settings were also the same: 4 V, 0.5 ms long pulses at an interspike interval of 10 ms [9]. Owing to denervation, natural MAPs were necessarily replaced with action potentials provided via the stimulator (figure 1, black dots in all conditions).

A muscle lever (Aurora Scientific Inc. Ontario, Canada) was attached to the femur of the cockroach via a freely rotating insect pin inserted through the femur at one end and through a hole in the lever arm at the other (figure 1a (iii)). Realistic muscle strains were imposed by driving the CF joint with the muscle lever, while monitoring the force produced on the joint. During force measurements, forces were corrected for the relative moment arms of the ventral femoral extensor (estimated at 0.54 mm using data for the hind leg homolog muscle 179 from [24]) and from the joint to the pin insertion, which was measured with micro-calipers for each experiment.

Since work on both ends of a lever is identical, we measured work loops based on the force and length conditions at the pin joint. The necessary strain patterns were determined from the digitized kinematics of the animals in the in vivo experiments [9]. Limb extension is linearly correlated with the angle of the CF joint, which in turn is linearly related to muscle length [11,24]. Because we were interested in how strides varied from steady-state running, we normalized our strain manipulations to a reference stride (figure 1a (iv)). This reference stride was taken from parameters for normal running strides in Full et al. [11], but tuned to a stride frequency (approx. 11 Hz) and number of MAPs (two) typical of strides in our in vivo experiments [9]. The mean muscle length during running strides is slightly (5%) greater than the reported muscle's reference length [11] and both were set via position of the joint again using the relationships from Full et al. [11].

Following experimentation, we carefully exposed the muscle and measured its resting length. The muscle was excised, transferred to a saline bath, and its mass measured using a micro-balance after blotting the muscle dry. Assuming a rectangular prism geometry for the muscle and a density equal to water, we estimated muscle cross-sectional area. This approach has been shown to give comparable results to more extensive fixation procedures [11].

(c). Experimental conditions

(i). Static and control trials

Every experiment began with a series of conditions to characterize the muscle's response properties. We first tested the muscle's isometric responses (figure 1b(i)) to test its change in function to increasing activation in the static standing condition (hypothesis 1) We next established the passive (no activation) energy absorption of the joint during the reference stride (figure 1b(ii)). The next two experimental conditions compared our intact-joint work loop with the classic isolated muscle work loop approach. We first added MAPs to the reference stride without changing strain parameters (figure 1b(iii)). We then performed a phase sweep where the activation burst was kept constant, but onset phase was varied across the full stride (0 to 1) in 1/16th phase increments (21 trials; figure 1b(iv)). We repeated these conditions both for the 8 Hz running from Full et al. [11] and for the 11 Hz running typical of our in vivo trials.

(ii). Burst extension trials for running

To test the effects of neural feedback extending the burst of activation in the femoral extensor (hypothesis 2), we increased the number of spikes in the first modified (S) stride and included the modified strain parameters from our in vivo experiments [9]. The subsequent (S + 1) stride also underwent strain cycles significantly different from a normal stride. We played in a sequence of strain and stimulus cycles mimicking five typical (T) strides followed by one S stride, one S + 1 stride, and then two final typical strides (figure 1c, top). These were repeated 10 times for each neural feedback condition to produce an average muscle response. For every experimental strain pattern, we performed passive, stimulus-free oscillations to correct for changes in the passive absorption of the intact joint.

(iii). Sequential versus non-sequential strides

To test the importance of the multi-stride effects of our stimulation conditions (hypothesis 3), we repeated the S or S + 1 strides in isolation (figure 1b(v)(vi)) rather than in their normal sequence. We conducted the above experiments only for those neural feedback conditions that showed significant effects in our in vivo experiments (+5 and +7 MAPs). Since these strides did not begin and end at the same point, we included slow corrections in position after each stride before continuing the work loops. These were not included in the work results reported.

(iv). Phase advancement trials

Conditions for the phase advancement experiments (figure 1c, bottom) were very similar to those for MAP addition conditions (figure 1c, top). However, since the stimulated stride's MAPs actually preceded the onset of that stride, extending back into the S − 1 stride, we consider the work output for the S − 1, S and S + 1 strides (hypothesis 4; figure 1c, bottom). The S − 1 and S + 1 strides both had normal bursts of MAPs, but different kinematics from the typical stride. We tested a sequence of work loops including five typical (T) strides followed by an S − 1, S and S + 1 stride and culminating in two additional T strides.

In the in vivo phase advancement experiments [9], we performed four manipulations of motor activation, adding one, three, five or seven MAPs to the beginning of the activation burst. However, given variation in timing of these added MAPs and the occasional presence of naturally occurring MAPs, we reclassified the experimental results based on the total number of MAPs (sum of orange and black dots in figure 1c, bottom) and the actual phase when the first MAP occurred (timing of first orange dots). In vivo effects on body dynamics did not depend on the number of MAPs once the actual phase was considered, and so only the latter classification was used in the companion paper [9]. For comparison, we performed work loops for all combinations of spike number and phase bin that occurred at least three times in the in vivo experiments.

(d). Work calculations

We calculated work at each point on the stress–strain curve using numerical integration of the joint torque and joint angle at each sampling interval (10⁻⁴ s). Power was calculated as work divided by the appropriate stride period. Unless otherwise noted, we considered the active work done by the ventral femoral extensor by subtracting out the passive work of the joint (figure 3). Using moment arms around the joint, we converted the joint torque and angle into the stress and strain on the muscle. For mass-specific work, we normalized to muscle mass. Importantly, instead of reporting work as a single value for the entire stride, we found it necessary to consider separately the work done during stance and swing. During stance, muscle work can produce or absorb energy that changes COM momentum via action through the limb's ground contact. During swing, muscle work can act to alter kinematics of the moving leg.

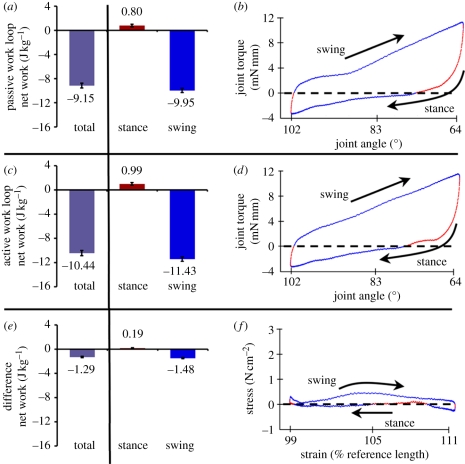
Figure 3.

Swing and stance contributions to intact-joint work loops. We separated the stance and swing components of a typical stride work loop (left column). Red and blue regions in the work loop traces (right plots) indicate respective regions of positive or negative incremental work (joint torque × angular displacement in (b) and (d), or muscle stress × strain in (f)). Incremental work was positive from one sampled point to the next, if the muscle shortened with positive stress or lengthened with negative stress. Net work was negative as evidenced by the clockwise stress–strain curves. The (a) top plots show the passive energy absorption of the joint under a typical strain pattern (figure 1b(ii)). Positive work was due to spring-like return of energy. (b) Active work loops with the typical two MAPs (figure 1a(iv)) produced significantly more positive and negative work (p < 0.01). Removing the passive joint work ((e); subtract (a) from (c)) isolated the effects of the ventral femoral extensor's activation on joint work. Reference length is measured following Full et al. [11].

To control for the effects of individuals and minor differences between preparations, all statistical tests were done comparing the modified strides to the typical stride work from the same trial. Experimental design was also balanced across individuals. All statistics were done with the Jmp platform (SAS Institute, Inc., Cary, NC, USA) or Matlab (Mathworks, Natick, MA, USA). We repeated all statistical tests with non-parametric methods to test for effects of non-normal distributions (e.g. Kruskal–Wallis instead of ANOVAs), but none of our conclusions changed significantly. All data are reported as mean ± s.e.m., unless otherwise noted.

3. Results

(a). Isometric responses

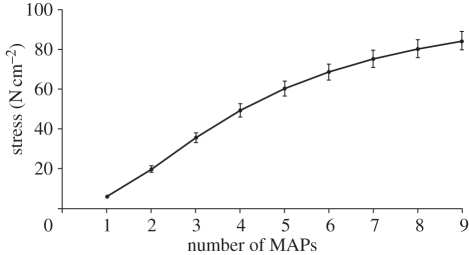
Twitch responses in the intact-joint preparation were similar to those observed in previous isolated muscle experiments for the ventral femoral extensor [11]. Force developed linearly for the first six MAPs and then began to approach tetanus (figure 2). A single MAP produced approximately 5.8 ± 0.47 N cm⁻² stress, which was significantly higher than the peak twitch stress from Full et al. [11] of 3.25 ± 0.19 N cm⁻² (Welch's t-test, p < 0.01). However, this difference was small compared with the difference of increasing activation by a single MAP (approx. 11%, see figure 2). Increasing activation during isometric responses led to a graded increase (p < 0.001) that began to saturate with seven or more added spikes (hypothesis 1; figure 2).

Figure 2.

Isometric force response as a function of the number of MAPs. Graded increases in twitch forces of the ventral femoral extensor resulted from increasing the number of evoked MAPs until they saturated at the highest realistic levels of activation.

We observed rise times to peak stress significantly shorter than the mean rise time for isolated muscle preparations (7.9 ms difference; table 1; [11,14]). Relaxation time constants were not significantly different (table 1). However, the difference in stimulation method should cause significant changes in latency. Since the intact-joint preparation directly stimulates the muscle we can make the isolated muscle preparation more comparable by correcting for approximately 8 ms of conduction time (table 1; row 2). This is estimated from a conduction velocity for non-myelinated, non-giant insect neurons of 1–4 m s⁻¹ and a 2–8 mm length of the innervating nerve [27,28]. This causes the rise times between preparations to be statistically indistinguishable, while the relaxation time constants are significantly shorter (table 1). The larger forces, but shorter twitch times between the two preparations cause their impulses to converge, although lack of impulse values reported for the previously published data makes statistical comparison impossible.

Table 1.

Isometric contraction properties. Values are means ± s.d. Asterisk indicates statistical significance.

	twitch response properties
preparation condition	twitch stress (N cm−2)	rise time (ms)	time to 50% relaxation (ms)	time to 90% relaxation (ms)
isolated musclea	3.25 ± 0.46	26.5 ± 4.8	39.5 ± 6.2	60.2 ± 7.6
w/ 8 ms correctionb	3.25 ± 0.46	18.5 ± 4.8	31.5 ± 6.2	52.2 ± 7.6
intact-joint	5.84 ± 2.27	18.6 ± 1.5	36.1 ± 2.6	60.3 ± 6.0
Welch's t-testc	*p < 0.01	*p < 0.002	p > 0.05	p > 0.05
t-test after correctiond	*p < 0.01	p > 0.05	*p = 0.02	*p < 0.01

^aTwitch stress from Full et al. [11]; twitch time course values from Ahn & Full [14] but from muscle 179, the hind leg serial homolog of muscle 137.

^bSubtracted 8 ms from the isolated muscle values.

^cStatistical comparison of row 1 and row 3.

^dStatistical comparison of row 2 and row 3.

(b). Steady-state work during swing and stance

The ventral femoral extensor shortens as the limb extends during stance and lengthens during swing. During passive oscillations, significant negative work (−9.95 ± 0.35 J kg⁻¹; t-test, p < 0.001) was done during swing, while a very small, but significantly positive, amount of work was done during stance (figure 3a; 0.80 ± 0.21 J kg⁻¹; t-test, p < 0.001). This positive passive work is due to spring-like behaviour in the joint acting to return energy from the more protracted state at the beginning of stance. Both stance and swing periods have positive and negative components of work and the net work loop was negative reflecting joint damping from skeletal structures and non-activated muscles (figure 3b; blue, negative work; red, positive work). Activation of the ventral femoral extensor enhanced the positive and negative components of work in stance and swing, respectively (figure 3c), with the most significant change in stress occurring during the first half of swing (figure 3d). Plotting the difference of the first two work loops (figure 3e) gives us the work output of the ventral femoral extensor without the dissipation of the joint and associated muscles. To isolate the work of just the ventral femoral extensor, all of our subsequent work values are reported as these differential work loops with the passive contribution measured and subtracted for each condition. Despite the fact that energy absorption is significant in the passive joint it does not impact our subsequent conclusions about changes in work output since it varies little compared with the degree of change in the activated ventral femoral extensor.

Even though the onset of MAPs occurs during stance, positive work output during a typical stride was just 0.19 ± 0.05 J kg⁻¹, which is significant, but only slightly above zero net change (figure 3f, t-test, p < 0.05). Work during swing was negative, and seven times larger than the positive stance contribution (−1.48 ± 0.09 J kg⁻¹; t-test, p < 0.001). The net effect was energy absorption across the full stride (−1.29 ± 0.11 J kg⁻¹; t-test, p < 0.001).

(c). Comparison of intact-joint and isolated muscle work loops

(i). Activation sweeps

Intact-joint work loops for typical running conditions at 8 Hz indicate that the muscle still does net negative work (figure 4a, bar marked with §; −3.2 ± 0.7 J kg⁻¹) and power (figure 4b, bar marked with §; −25.3 ± 5.2 W kg⁻¹). These results are not significantly different from those observed in isolated muscle work loops (data from [11]: −3.5 and −23.7 W kg⁻¹; Welch's t-tests, both p > 0.1). Further, increasing the number of MAPs during typical stride cycles, as Full et al. [11] did, showed a very comparable increase in energy absorption up to −28.2 ± 2.2 and −223.3 ± 17.8 W kg⁻¹ at six MAPs (figure 4a,b, six-added MAP condition). Since our experiments included up to nine MAPs, we extended the MAP addition conditions further for the 11 Hz trials (figure 4, dark grey bars). Energy absorption peaked with seven added MAPs (figure 4; −86.9 ± 6.6 and −956.1 ± 72.6 W kg⁻¹). To contrast these results with later conditions based on the in vivo experiments, we emphasize that strain patterns were not altered in these trials, only the degree of activation.

Figure 4.

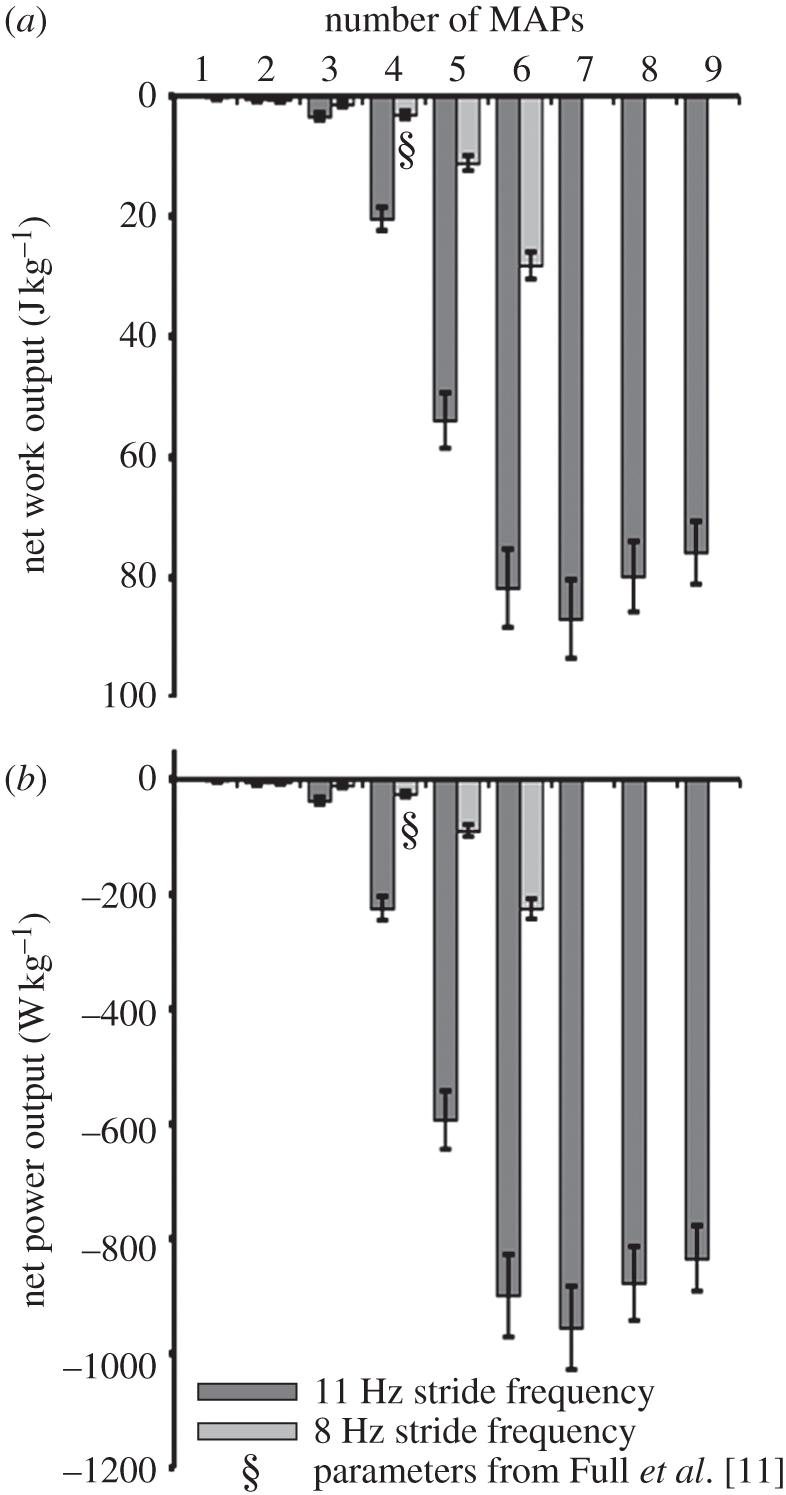
Activation sweep. (a) Work and (b) power outputs from dynamic oscillations of stimulated muscle 137 in the intact-joint work loop preparation showed primarily energy absorbing outcomes as activation was increased. Increasing cycle frequency (8 Hz stride frequency; light grey bars) from those of past studies [11] to the stride frequency observed in our in vivo experiments (11 Hz stride frequency; dark grey bars) increased energy absorption. Intact-joint work loops using the same parameters as previously published [11] isolated muscle work loops produced statistically indistinguishable work and power (bars marked with §).

(ii). Phase sweeps

Phase sweeps of typical activation patterns for both 8 and 11 Hz running reveal a similar phase-dependent pattern of work output (figure 5, grey and black curves, respectively). During our intact-joint experiments, work and power outputs were negative at the typical activation phase of approximately 0.1, where phase is scaled from 0 to 1, with zero at stance initiation in the target limb. At most phases of activation, we observed negative work (figure 5a) with a peak of −17.4 ± 1.4 J kg⁻¹ at a phase of 0.65, which is near the onset of the protraction or swing period (figure 1a(iv)). Work could be positive over a narrow range of phases with a peak at 0.9 (or −0.1) of 2.7 ± 0.4 J kg⁻¹. These results are in close agreement with the phase sweep response from the isolated muscle work loops, where work output followed a similar phase response curve and became positive for a small range of phases centred around −0.15 [11]. Increasing cycle frequency to 11 Hz tended to enhance negative work and power during phases from 0 to 0.6. However, negative work was actually reduced during many swing period activation phases, although the power was constant (figure 5a, compare difference between grey and black lines). At 11 Hz oscillations, work was again positive in a narrow band at slightly negative onset phases and peaked at the same −0.1 phase. The negative work peak was shifted to a phase of 0.6.

Figure 5.

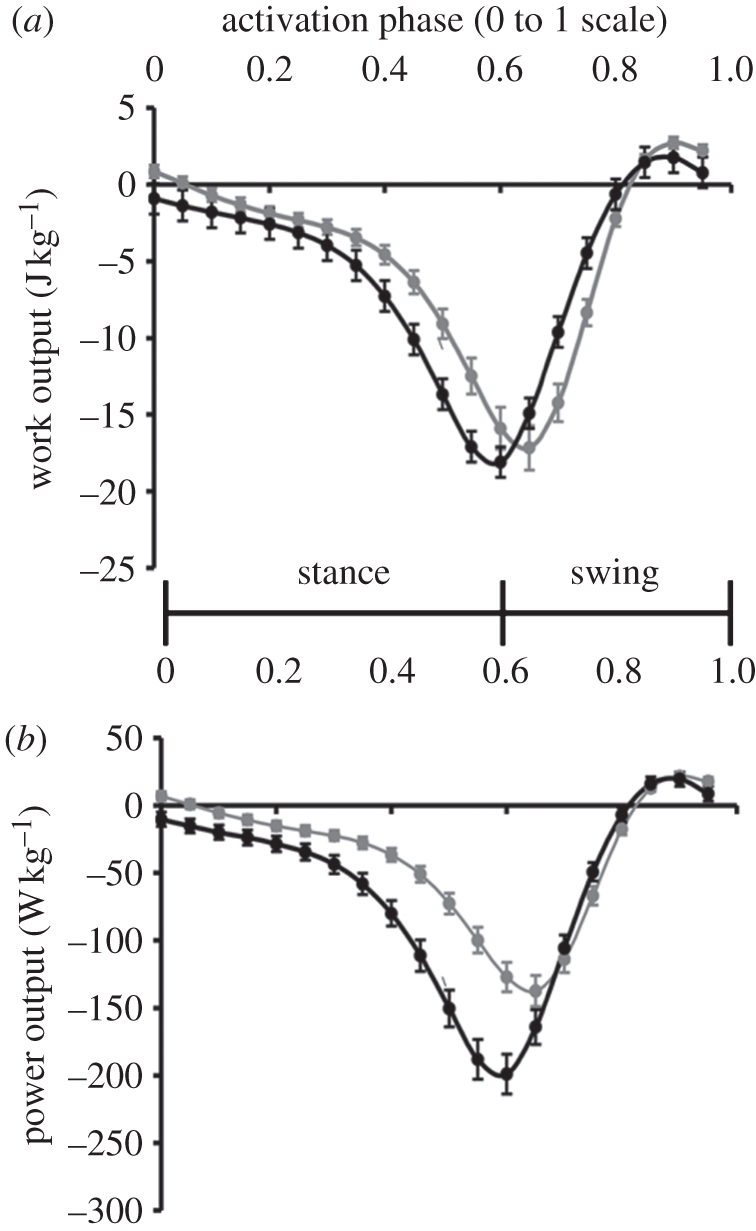
Work loop phase dependency. The ventral femoral extensor (a) work and (b) power outputs depended on phase of activation when the strain parameters remained unchanged (figure 1b(iv)). Typical phase of activation during steady running is approximately 0.05–0.1 [17]. The shape of the phase response curves was comparable to isolated muscle phase responses [11], reaching a minimum when stimulus onset was close to the swing–stance transition at 0.6 (60% duty factor). Increasing stride frequency (11 Hz stride frequency, black lines versus 8 Hz stride frequency, grey lines) had different effects when the stimulus phase was in stance or swing and shifted the peak of energy absorption (curve minima).

(d). Work output under burst extension running conditions

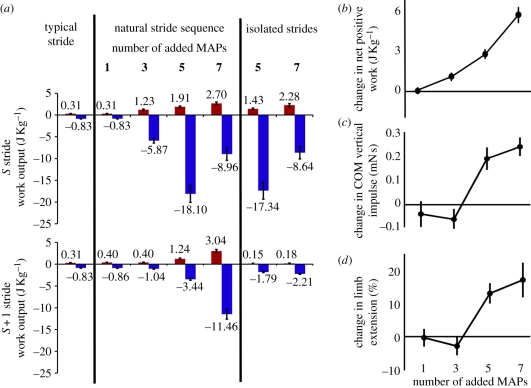
Extending the burst of activation in the ventral femoral extensor revealed significant changes in work during the stimulated (S) and subsequent (S + 1) strides (hypothesis 2; figure 1c). During the initial stance phase where the activity was extended, work output became significantly more positive (figure 6a; ANOVA, p < 0.001). With seven added MAPs, positive work reached 2.7 ± 0.30 J kg⁻¹. Power output was correspondingly large, reaching 27.0 ± 3.0 W kg⁻¹. These values are of greater magnitude than the net negative work typically done during the stride (figure 3e). The increase in work was similar to the increase in COM vertical impulse observed during the in vivo experiments, but the response was graded (figure 6a, top; Tukey Honestly Significant Difference (HSD) for each pair; p < 0.01), unlike the nonlinear change in body and limb kinematics (figure 6b).

Figure 6.

Work output during activation burst extension trials with in vivo strain conditions. (a) Work output for a typical stride (T) is compared with the stimulated (S) and post-stimulation (S + 1) strides where one, three, five or seven MAPs are added. ‘Isolated stride’ conditions represent repeated presentations of the S or S + 1 stride extracted from the sequential presentation of strides. We performed these trials only for five and seven added MAP conditions. These conditions remove the history dependence of the muscle's work. The reduction in positive work between these conditions in the S + 1 strides (a, bottom) indicates that (b) the supralinear increase in net muscle work is due in part to the pre-stressing of the muscle at the transition of the S to S + 1 stride. The overall positive work response contributes to (c) the in vivo body dynamics and (d) limb kinematics control potentials of this muscle. Results in (c) and (d) are taken from in vivo data in our companion paper [9].

Investigating the structure of the work loops more closely reveals that increased force development occurred when limb extension and duty factor increased (figures 1c and 6d). During the S stride swing, the already large force at the end of stance (figure 7b, particularly bottom) increased further, but now acted to resist the motion of the limb, therefore absorbing even more energy than during a normal stride (figures 6a and 7b; ANOVA, p < 0.001). This corresponds to the nonlinear change in limb kinematics (figure 6c). Indeed, owing to increased force production during swing, the initiation of S + 1 stance was advanced in time and shifted posteriorly (figure 1c), such that when five or seven MAPs were added, force was still high at the onset of the next stance phase (greater than 1 N cm⁻²; figure 7, grey dashed lines connecting plots in (b) and (c)). This increased initial force caused an increase in S + 1 stance work output compared with typical strides (figure 6a, bottom; ANOVA, p < 0.001). The negative work done during swing was also increased (figure 6a, bottom; ANOVA, p < 0.001) in part because the recovery swing in this stride was extended in time and distance (figure 7c). Unlike the S stride, stance and swing work enhancement was nonlinear (figure 6a, bottom), and when seven MAPs were added to the S stride, the positive work done during the S + 1 stance was as large as that during the S stride (S stride: 2.7 ± 0.3 J kg⁻¹; S + 1 stride: 3.04 ± 0.34 J kg⁻¹; Welch's t-test, p = 0.4). Combining the positive work done during the two power production phases produced a supralinear increase in total work (figure 6d), although since the positive work done in the S + 1 stride was almost entirely within the first 10 per cent of the cycle, these contributions effectively spanned a single net stride period.

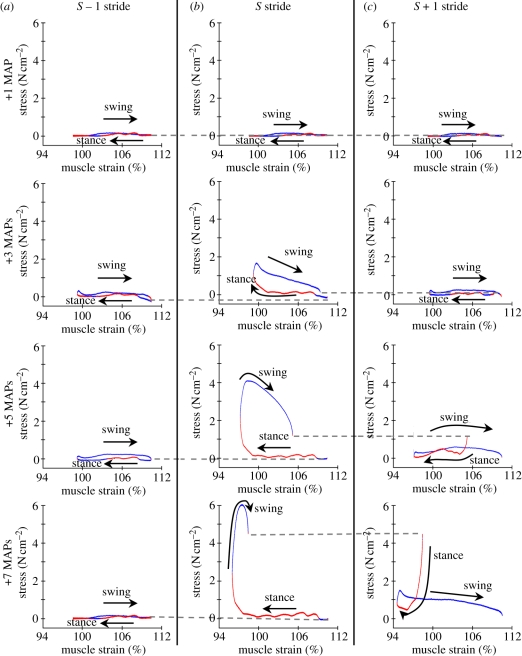
Figure 7.

Work loops from the burst extension trials. Work loop output for (a) S − 1, (b) S and (c) S + 1 strides under each neural feedback condition (one, three, five or seven added MAPs, top to bottom) show how this muscle is recruited to do positive work in addition to enhanced negative work (figure 6). The S − 1 stride was not significantly different from a typical stride because activation only extended forward in time. Adding MAPs resulted in significant stress during the end of S stride stance and persisting through swing (b, bottom plots). This resulted in enhanced positive work production at the very end of S stride stance (rising red line), increased negative work throughout swing (blue line) and the increased positive work at the onset of the S + 1 stride (red line).

(e). Comparison with repeated and sequential work loops

For the five and seven added MAP conditions, we compared the work output from strides occurring in their natural sequence (figure 1c) with isolated presentations of the S and S + 1 stride (hypothesis 3; figure 1b(v)(vi)). Work output was not significantly different during the stance and swing periods of the S stride for either five or seven added spikes (figure 6a, bottom; compare sequential versus isolated S stride results for five and seven added MAPs; Welch's t-tests, p > 0.05 in all cases). However, repeated presentation of the S + 1 stride without the sequential stride progression showed significantly attenuated positive work during stance and negative work during swing (figure 6a, bottom; compare sequential versus isolated S + 1 stride results for five and seven added MAPs; Welch's t-tests, p < 0.001 in all cases). Indeed, the work output during repeated presentations of the S + 1 cycle was not different from a typical stride (figure 6a, bottom; compare typical stride with isolated S + 1 stride results; Welch's t-test, p > 0.05). Thus, taking into account the appropriate history effects and preserving the pre-stressing of the ventral femoral extensor from the S stride was necessary to produce the nonlinear work increase at the beginning of the S + 1 stride.

(f). Work output under phase advancement running conditions

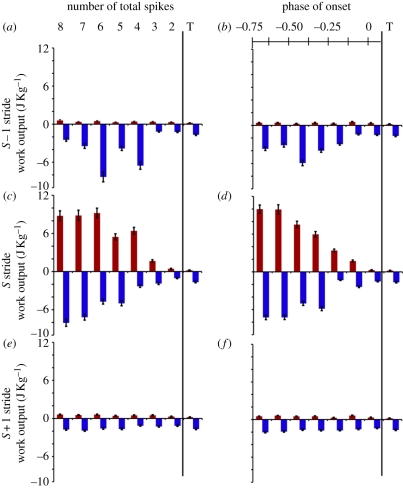
When the phase of activation of the ventral femoral extensor was advanced, activation during the S stride advanced into the S − 1 stride (hypothesis 4; figure 1c). As a result, the ventral femoral extensor produced greater negative work during the swing phase of the S − 1 stride (figure 8a,b; ANOVA, p < 0.001). The magnitude of the negative work increased until the phase was advanced beyond −0.5. Beyond this point there was a small correction (figure 8b). This is probably because swing was shortened to the point where less negative work could occur despite higher muscle stress. Regardless, the negative work remained significantly above the typical stride's value (Welch's t-test, p < 0.01). This increase in negative work resisted limb motion, truncated stance, and as a result pre-stressed the muscle leading into the S stride (figure 9, grey dashed line connecting (c) and (d)). As a result, the stance work output was very large, peaking at 9.98 ± 0.66 J kg⁻¹, which is approximately 50 times the work output during a typical trial and corresponds to a power output of 109.8 ± 7.4 W kg⁻¹ (figure 8c,d). While the increase was graded from phases of −0.625 to 0.125, it showed no significant effect for small phase advances and it saturated at the highest values (figure 8d; Tukey HSD tests, p > 0.1 for extreme conditions). When we consider the number of spikes rather than the phase, the effect was more pronounced, with change only between the three and six added MAP conditions. This is consistent with the nonlinear control potentials (figure 8c). Stress persisted and there was also significantly more negative work during S stride swing (ANOVA, p < 0.001), but not to the degree of the S − 1 stride (figure 8c versus figure 8a). Finally during the S + 1 stride, positive work during stance was still increased, despite the stimulus having occurred more than a full stride prior (figure 8e,f; ANOVA, p < 0.001). However, the differences were small, within 0.4 J kg⁻¹ of the typical stride. Analysis using number of total MAPs (figure 8a,c,e) or actual onset phase (figure 8b,d,f) produced comparable results except where noted.

Figure 8.

Work output during phase advance trials with in vivo strain conditions. Adding MAPs to the beginning of a natural burst advanced the phase of activation in the muscle (figure 1c, bottom). Plots show the effects on the S − 1, S and S + 1 strides divided into stance and swing components (red and blue, respectively). Binning responses either by (a) the number of MAPs or (b) the onset phase resulted in the same statistical conclusions. The ‘T’ condition represents a typical stride work output. Negative work was enhanced during S − 1 swing leading to (c,d) a very large period of positive work in the S stride. The effects of this activation change persisted into the S + 1 strides, where (e,f) positive work was still enhanced.

Figure 9.

Summary figure for phase advancement trials. We previously reported [9] that (a) advancing phase led to a turning control potential. These effects arose primarily during the S to S + 1 stride transition. Using the in vivo strain conditions in conjunction with phase advancement for work loops (b–d) showed that the increased stress that shortened swing movement in the S − 1 stride (c) led to the positive work at the beginning of the S stride. As before, positive incremental work is in red, negative incremental work in blue. The bottom plot shows the timing of evoked MAPs (orange vertical lines) for each stride.

4. Discussion

Exploring the work output of a muscle, here the ventral femoral extensor, provided a mechanistic context for interpreting the control potential of its neural feedback. In turn, the in vivo experiments from our companion paper [9] inform the relevant activation and strain parameters under which this muscle operates. This allowed us to explore the space of muscle function that is realized during tasks involving stability and manoeuvrability. We found under simulated neural feedback conditions, this muscle can both absorb additional energy during swing and be recruited to act as a motor during stance, with its function changing with the task. As predicted from our in vivo experiments, duty factor and limb extension changes are the critical variables underlying this muscle's functional shift during behaviours. Positive work is enhanced by even small changes in duty factor and from stride-to-stride history effects. By exploring the sequential periods of positive and negative work that this muscle generates, we uncover how positive mechanical feedback transformed linear neural feedback into different control potentials.

(a). Intact-joint versus isolated muscle work loops

While there are small differences in twitch mechanics between intact-joint and isolated muscle preparations, they produce similar work loops. The faster, but larger twitch responses (table 1) in intact-joint muscle preparations probably arise from the bipolar stimulation of the muscle causing more uniform depolarization than nerve stimulation. As a result, a larger portion of the contractile fibres may be brought to peak stress in synchrony, increasing peak force and causing stress to increase more rapidly, but also fall off more quickly. Overall, the effects were negligible on the work output of this muscle, because the overall impulses were comparable and their differences were small compared with the differences in work between experimental conditions. Typical stride work loops with a normal phase of activation did negative work comparable to previously published, isolated muscle studies (figures 3e and 4, bars marked with §; [11]) and produced similar phase sweeps (figure 5, grey lines).

Intact-joint preparations can play an important role in understanding the function of the muscle in the context of other mechanical structures. The material properties of joints and skeletal elements can represent significant sources of visco-elastic energy storage and dissipation [29]. They can even dissipate dorso-lateral perturbations to a cockroach leg during a single swing period [30]. While recent studies of muscle work have begun to include realistic loads or impedances [31], the interaction of skeletal passive dynamics with muscle force production remains difficult to assess [4,6,30,32]. Directly comparing intact joint and isolated muscle work loops with characterization of the passive limb material properties can provide a mechanistic understanding of the interaction of active and passive elements. For this study, we were primarily interested in how the ventral femoral extensor's work changes under neural feedback. Passive effects were small (figure 3a) compared with the modulation by changes in activation and strain (figures 6 and 8).

(b). Muscle work has different implications during swing and stance

When considering muscle work during running, we found it necessary to separate the stance and swing components of the stride. In terrestrial locomotion, a femoral extensor typically can do positive work during stance, while the muscle shortens [8,12,16]. It typically does negative work during swing via active lengthening where cross-bridge formation resists the extension of the muscle [11,16,33]. In flight systems, where the work loop was first developed [16,22], work during both protraction and retraction would act on a wing moving through a resistive fluid. During running, stance retraction occurs when the limb is in contact with the ground, resulting in ground reaction forces imposed on the body [34]. However, during swing, the limb is retracted with no contact against a solid surface. In animals like the cockroach, where aerodynamic forces on the limbs are insignificant [35], the limb is not acting against the environment during swing, and so the negative work done is actually resisting the movement of the limb rather than absorbing energy from the motion of the body. Work primarily affects body dynamics during stance, and primarily limb dynamics during swing, so its contributions to control during these phases will be different.

(c). Mechanisms for neuromuscular control: work output during burst extension

(i). Static behaviour

In vivo MAP addition during static control tasks occurred without dynamic oscillation of the ventral femoral extensor. The in situ equivalent is, therefore, most closely matched by the twitch responses observed during isometric MAP addition (figure 2). As the number of MAPs increased to this muscle, it behaved the way its anatomical designation as a femoral extensor would suggest. It produced a moment around the CF joint and accelerated the body up and away from the limb. The linear isometric force production until seven added MAPs supported hypothesis 1 in serving as a mechanism for the graded control potential on body dynamics. These results support the predictability of a muscle's transfer function from motor activation to muscle work and ultimately to body impulse for posture control tasks and slow quasi-static locomotion [36–38].

(ii). Dynamic behaviour

The ventral femoral extensor showed a diversity of functions outside of its normal brake-like role when used to control running. We reject the hypothesis that this muscle only absorbs energy under biologically relevant activation and strain conditions and discover that it can recruit significant positive work supporting hypothesis 2 (figure 6a,b). The ventral femoral extensor transforms a graded increase in muscle activation into changes in positive and negative work over several stance and swing periods. The net supralinear increase (figure 6b) in positive work enables, at least in part, the accelerating control potential it produces in vivo [9].

The mechanical coupling of stress and strain causes force to develop rapidly during the very end of the modified stance phase. This indicates a positive mechanical feedback loop initiated by neural feedback. With three or more added MAPs, activation is sufficient for significant force development in the ventral femoral extensor during the end of stance. This allows greater resistance to antagonistic flexor activity that comes on to initiate swing [20], which in turn causes the limb to continue extending for a longer period (figure 6c). This result keeps the muscle in its shortening phase for longer and provides even more time to develop force. This mechanical coupling makes the muscle work output very sensitive to duty factor, as a small increase in stance extension time and distance results in greatly enhanced positive work. For example, when seven MAPs are added, duty factor increases by 8 per cent and stance extension by 17.5 per cent, while positive work output increases by 870 per cent. As we discussed in the companion paper [9], given the high degree of uncertainty involved in trying to precisely predict dynamics during high-speed behaviours, it is likely advantageous for the animal to recruit additional power through mechanical amplification. This simplifies the control demands placed on neural feedback. Indeed, the inherent delays of neural feedback acting during high-frequency behaviours could lead to instability, if gains are high and precise control is attempted [39,40]. Here, positive mechanical feedback provides a mechanism for altering the effects of neural feedback, allowing it to provide both finely graded control during low-speed behaviours (static and quasi-static behaviours) and the less precise, but high-gain control needed for running dynamics.

While the ventral femoral extensor's own work modulation was consistent with its control potential, the functions of synergist and antagonist muscles could also be modified through changes in kinematics. Other femoral extensors are likely to have enhanced positive work output when stance is extended. Some of these muscles have shorter force development times than the ventral extensor, and are already producing significant force near the end of a stance phase even at the slower 8 Hz running frequencies used in previous experiments [14,15]. The recruitment of work from these muscles may supplement the ventral femoral extensor's own effects in generating the realized control potential.

(d). Multi-stride context: negative work enabled positive work

We support our third hypothesis that the natural sequence of strides during perturbations is critical for capturing the work output underlying these transient behaviours. Here, we find that including the representative history points to a second positive mechanical feedback enhancement of muscle work. Following S stride stance, the ventral femoral extensor does negative work, resisting limb protraction during swing (figure 6a). This truncation was sufficient at the five and seven added spike conditions to cause substantial residual stress to carry through to the S + 1 stride. With this pre-stressing, we observed a nonlinear recruitment of positive work corresponding to acceleration of the body (figure 6a,b). This effect was absent without the stride-to-stride context of sequential work loops (figure 6a, isolated S + 1 stride conditions). The recruitment of additional positive work requires the muscle to develop significant stress while acting against flexors at the end of swing. This strategy is similar to the coactivation of antagonists used in other behaviours demanding high force or power [41,42].

The control consequences of this second period of positive work are distinct from the work done during the end of the S stride stance. In an obstacle traversal experiment, the stride equivalent to S + 1 occurred when at least several legs had gained purchase on the obstacles [17,43]. At this point the cockroach was pulling the COM over the obstacle, consistent with vertical acceleration and positive work. In other slow speed locomotor experiments, increased activity to extensors has been shown to correspond to COM elevation [44]. The multi-stride dependence of muscle work requires interpreting its function in control across the entire transient behaviour until steady-state conditions are regained.

(e). Mechanisms for neuromuscular control: work output during phase advancement

In the in vivo phase advance experiments, the ventral femoral extensor again used a pre-stressing mechanical feedback mechanism to produce a phase of positive work, although its timing was shifted earlier compared with the gait cycle. The high negative work output during S − 1 swing led to the significantly shorter swing period. This shifted the middle leg posterior to its normal placement (figure 9b,c). During walking, where fast motor neuron activity to the ventral femoral extensor is normally absent, Mu & Ritzmann [45] observed changes in activation phase of other femoral extensor muscles innervated by the slow motor neuron (Ds) and corresponding shifts in limb kinematics comparable to our observations. Since turning occurs towards the modified limb (figure 9a), it is tempting to ascribe the energy absorption observed in the S − 1 stride (figure 9c) to directly generating the turn. However, since this occurred during swing phase, it seems unlikely to affect body motion directly. We reject hypothesis 4 suggesting a greater brake-like function on the body, and instead find that this negative work on the limb enabled positive work on the body during stance via the pre-stressing mechanism (figures 8c and 9c,d). This effect persisted into the S + 1 stride's stance phase, modulating work up to two strides later (figure 8e).

While the recruitment of S stride positive work is consistent with the observation that cockroaches roll away from the stimulated limb, it still led to a lateral impulse and yawing rotation in the direction of the limb (figure 9a). A probable explanation is that the posterior shift in the limb and change in timing of the S stride (figure 9c) moves the centre of pressure (COP; the net ground reaction line of action) posterior to the centre of mass, thereby producing a torque in the direction observed. Further, since lateral forces decrease when the limb is in an extended state [34], this limb may no longer resist the opposing force production of the two contralateral legs in the tripod [19]. This suggests that part of the ventral femoral extensor's control potential arises from the muscle enabling the contralateral limbs to contribute significantly to the turn. Current mathematical approaches are beginning to include the effects of posture in multi-legged models of horizontal plane dynamics [46]. Future integration of in vivo and in situ biological experiments with mathematical and physical (e.g. robotic) models may yield design principles for dynamic locomoting systems whose control could be meditated by multi-functional biologically inspired actuators [47,48].

(f). Work modulation across speeds

Under steady-state stride conditions, the ventral femoral extensor typically absorbed more energy at faster speeds (figures 4 and 5), 11 versus 8 Hz, probably because the shorter stride period brought the period of negative work (i.e. swing phase) closer to the normal phase of activation. However, the effect of speed was small compared to the change in work when adding MAPs (figure 4) or changing duty factor (figure 7). Unlike frogs, which show a great deal of power modulation across swimming speeds [49], we find that this putative cockroach control muscle exhibited a greater work and power modulation under patterns of neural feedback in response to perturbations and manoeuvres. This response is more similar to the functional changes observed in guinea fowl limb musculature during recovery from unexpected drops [50]. As we seek more anchored, anatomically detailed models of muscle function [39,51], investigate the functional organization of motor commands [38] and engineer the next generation of biologically inspired actuators [47,48], we must understand the strategies by which organisms combine neural feedback and advantageous mechanical properties to tune muscle function for different control requirements.

5. Conclusions

Understanding the neuromechanical mechanisms for control requires integrating the effects of neural and mechanical feedback at three levels: muscle work, limb kinematics and body dynamics. We must know how particular muscles change in activation under neural feedback, how these changes can contribute to body dynamics, and what physiological mechanisms underlie these transformations. Electrophysiological recordings in intact, behaving animals can reveal relevant patterns of neural feedback. Stimulating specific muscles and measuring dynamics captures the control potential of a specific motor command. Recording limb kinematics demonstrates how the mechanical state of the muscle changes concomitant with neural feedback. Here, we add the mechanistic link, showing how these neural and mechanical determinants combine at the level of muscle work output. We support the hypothesis that the cockroach's ventral femoral extensor changes function from its steady-state energy-absorbing action to facilitate control. Despite extensive previous exploration of this muscle's capabilities in isolated muscle experiments and in simulation [11], it was not until we considered its contributions to control potentials and captured the transient limb kinematics underlying perturbation responses that we discovered that this muscle could do significant positive work. In turn, careful separation of the periods of positive and negative work as well as the sequential stride-to-stride pre-stressing of the muscle uncovered positive mechanical feedback processes. These contribute to the rapid build-up in muscle positive work and ultimately acceleration of the COM. With knowledge of both how an individual muscle can control body dynamics and what neuromechanical processes are critical for the muscle to generate these effects, we can finally quantify the function of the constituent signals of an animal's control strategy.