Assessment of Compositional Heterogeneity Within and Between Eukaryotic Genomes

Abstract

Using large amounts of long genomic sequences, we studied the compositional patterns of eukaryotic genomes. We developed a simple measure, the compositional heterogeneity (or variability) index, to compare the differences in compositional heterogeneity between long genomic sequences. The index measures the average difference in GC content between two adjacent windows normalized by the standard error expected under the assumption of random distribution of nucleotides in a window. We report the following findings: (1) The extent of the compositional heterogeneity in a genomic sequence strongly correlates with its GC content in all multicellular eukaryotes studied regardless of genome size. (2) The human genome appears to be highly compositionally heterogeneous both within and between individual chromosomes; the heterogeneity goes much beyond the predictions of the isochore model. (3) All genomes of multicellular eukaryotes examined in this study are compositionally heterogeneous, although they also contain compositionally uniform segments, or isochores. (4) The true uniqueness of the human (or mammalian) genome is the presence of very high GC regions, which exhibit unusually high compositional heterogeneity and contain few long homogeneous segments (isochores). In general, GC-poor isochores tend to be longer than GC-rich ones. These findings indicate that the genomes of multicellular organisms are much more heterogeneous in nucleotide composition than depicted by the isochore model and so lead to a looser definition of isochores.

Nonuniformity of nucleotide composition within genomic sequences from a variety of taxa ranging from phages to mammals was revealed several decades ago by thermal melting and gradient centrifugation experiments (Inman 1966; Filipski et al. 1973). As this phenomenon was found to be most conspicuous in the genome of warm-blooded vertebrates, G. Bernardi and coworkers (Macaya et al. 1976; Thiery et al. 1976; Bernardi et al. 1985) proposed the isochore model for the genome structure of warm-blooded vertebrates (for review, see Bernardi 2000). In this model, the genome of warm-blooded vertebrates is a mosaic that is composed of isochores, which are long (>300-kb) DNA regions homogeneous in nucleotide composition. Five distinct isochore classes were described for the human genome: GC-poor classes L1 and L2 (∼63% of the genome) and increasingly GC-rich classes H1, H2, and H3 (∼24%, 7.5%, and 4.7%, respectively). These five classes form the so-called typical “genome phenotype”. Birds (chicken) and rodents (mouse and rat) have deviant genome phenotypes: The chicken possesses an additional extremely GC-rich isochore class H4, whereas mouse and rat lack class H3. Various genomic components, such as genes and repetitive elements, are distributed nonrandomly among different isochore classes (Smit 1999; Bernardi 2000; Z. Gu, H. Wang, A. Nekrutenko, and W.-H. Li, in prep.). For example, genes are found predominantly in the GC-richest isochore classes H2 and H3, which comprise only 12% of the human genome (the so-called genome core; Zoubak et al. 1996). Although isochores have also been found in many cold-blooded vertebrates, such as Xenopus, they are fewer in number and less rich in GC content (Bernardi 2000).

The development of the isochore model greatly increased our appreciation of the complexity and compositional variability of eukaryotic genomes. However, the origin and evolution of GC-rich isochores has been a controversial issue (Bernardi et al. 1985; Filipski 1987; Sueoka 1988; Wolfe et al. 1989; Eyre-Walker 1992; for review, see Bernardi 2000). Because gradient centrifugation separates DNA fragments on the basis of their overall (mean) buoyant density, this crude method does not reveal the full extent of compositional variation within a fragment. The first step to resolve the controversy is to understand the heterogeneity of nucleotide composition along the DNA sequence in a genome. The abundance of genomic sequences now allows us to examine whether isochores as identified in Bernardi et al. (1985) are indeed homogeneous in nucleotide composition. The variety of available genomic sequences also allows us to compare the compositional distribution patterns of different genomes ranging from unicellular to multicellular eukaryotes. We use long genomic fragments now available from diverse eukaryotic taxa to address the above questions. We demonstrate that the vertebrate genomes are in fact compositionally even more heterogeneous than postulated by the isochore model and that isochores are not restricted to vertebrate genomes.

RESULTS

Compositional Heterogeneity Index

We developed a measure, the compositional heterogeneity index, that allows the quantification and comparison of compositional differences within and between genomic sequences (see Methods). In this measure, the average difference in GC content between two adjacent windows of length l bp is normalized by the standard error in GC content distribution in a window, i.e.,

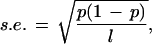where P is the average GC content of the sequence. To see that this is a suitable measure, that is, it fluctuates little with window size and GC content, we performed a series of simple simulations using computer-generated random sequences of varying GC contents and two window sizes (10 and 100 kb, Table 1). Calculations were performed in two ways. First, we calculated the average difference between sequence windows, so that the second window of the current pair is the first window of the next pair (e.g., the average difference is calculated using equation 1, see Methods). Second, to demonstrate that the overlap between window pairs has no effect on the H_gc, we calculated the index using nonoverlapping window pairs (e.g., the average difference is calculated as

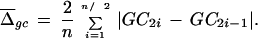From simulations (Table 1) we can see that the H_gc has a baseline value of ∼1.1, regardless of the GC content and window size. In addition, H_gc calculated using overlapping window pairs is not statistically different from the values obtained using nonoverlapping window pairs (Table 1). Therefore, we propose to use H_gc as a simple way of quantifying the extent of compositional heterogeneity. A PERL program for H_gc calculation from large genomic sequences will be available at http://nekrut.uchicago.edu.

Table 1.

Behavior of the Compositional Heterogeneity Index (H_gc) Studied using Two Window Sizes

GC%	10-kb Windows	100-kb Windows
5	1.12/1.14	1.13/1.12
10	1.12/1.14	1.12/1.13
15	1.13/1.14	1.13/1.11
20	1.14/1.14	1.12/1.13
25	1.12/1.14	1.14/1.14
30	1.14/1.14	1.12/1.13
35	1.12/1.12	1.12/1.14
40	1.14/1.13	1.14/1.12
45	1.14/1.13	1.13/1.14
50	1.15/1.12	1.13/1.11

Each simulation was performed using 10,000 computer-generated sequence fragments. Numbers to the right of the slash indicate results of simulations performed using overlapping pairs of windows (e.g., |GC − GC_i − 1|, 2 ⩽ i ⩽ n). Numbers to the left of the slash indicate results of simulation using nonoverlapping window pairs (e.g., |GC_2i − GC_2i − 1|, 2 ⩽ i ⩽ n/2). 

GC Content Versus Compositional Heterogeneity

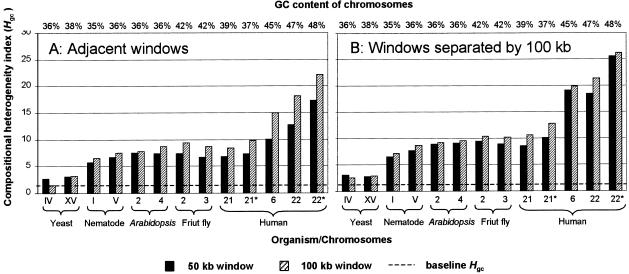
To calculate the heterogeneity index from the genomic data, we compiled a dataset (Table 2) by selecting the longest continuous sequences from the most extensively sequenced eukaryotic genomes. In cases where a chromosome was almost completely sequenced and was deposited into databases as a set of consecutive contigs separated by gaps (e.g., human chromosomes 21 and 22) we selected the longest contig without attempting to concatenate all available data, as this may increase H_gc. Figure 1A compares the heterogeneity index values estimated for the sequences listed in Table 2 using 50-kb and 100-kb windows. From Figure 1A we see that for every organism studied, GC-rich chromosomes have higher heterogeneity indices than do GC-poor ones. Additionally, sequences of taxonomically distant organisms are similar in terms of compositional heterogeneity if they have similar GC contents. For example, nematode chromosome V and Arabidopsis chromosome 2 both have a GC content of 36%, and in spite of the great taxonomic distance separating these two organisms, they have similar heterogeneity indices: 7.51 and 7.89 for 100-kb windows. Furthermore, human chromosome 21 has a GC content lower than that of Drosophila chromosome 2 (39% vs. 42%) and also has a lower compositional heterogeneity value (8.47 vs. 9.46). One exception is the extremely low compositional heterogeneity in the yeast sequences, despite the fact that their GC content is comparable to those of the nematode and Arabidopsis chromosomes. Overall, a strong correlation exists between GC content and compositional variation: For both window sizes the H_gc values correlate strongly with the GC levels of the sequences (r² = 64%, P = 0.002 and r² = 74%, P < 0.0001 for 50-kb and 100-kb windows, respectively).

Table 2.

Genomic Sequences Used in Our Study

Organism	Sequencea	Lengthb	Source
Saccharomyces cerevisiae	chr. IV	1.5	ftp://ncbi.nlm.nih.gov/genbank/genomes/S_cerevisiae/Chr04/
	chr. XV	1.1	ftp://ncbi.nlm.nih.gov/genbank/genomes/S_cerevisiae/Chr15/
Caenorhabditis elegans	chr. I	15.0	ftp://ncbi.nlm.nih.gov/genbank/genomes/C_elegans/CHR_I/
	chr. V	20.5	ftp://ncbi.nlm.nih.gov/genbank/genomes/C_elegans/CHR_V/
Arabidopsis thaliana	chr. 2	19.6	ftp://ncbi.nlm.nih.gov/genbank/genomes/A_thaliana/CHR_II/
	chr. 4	17.5	ftp://ncbi.nlm.nih.gov/genbank/genomes/A_thaliana/CHR_IV/
Drosophila melanogaster	chr. 2 arm L	21.6	http://www.fruitfly.org/
	chr. 3 arm R	27.5	http://www.fruitfly.org/
Homo sapiens	chr. 6, contig NT_001520	3.9	http://www.ncbi.nlm.gov/genome/seq/ctg.cgi?CTG=Hs6_1643&ORG=Hs
	chr. 21, contig NT_002836	28.5	http://www.ncbi.nlm.gov/genome/seq/ctg.cgi?CTG=Hs21_2980&ORG=Hs
	chr. 22, contig NT_001454	23.0	http://www.ncbi.nlm.gov/genome/seq/ctg.cgi?CTG=Hs22_1584&ORG=Hs

For each organism we chose a pair of longest continuous sequences. 

^achr = chromosome 

^bLength is given in millions of base pairs. 

Figure 1.

Heterogeneity index values calculated for each chromosome in our dataset (Table 2) using adjacent windows (A) and windows separated by a 100-kb gap (B). The GC content of every sequence is indicated at the top of each graph. Asterisks signify sequences with all repetitive elements removed (masked). The broken line indicates the baseline H_gc value taken from Table 1.

The longest continuous sequences available for human chromosomes 21 and 22 cover the majority of their lengths: 81% and 68%, respectively. The remaining 19% and 32% are represented by smaller contigs separated by gaps. As mentioned earlier, we excluded shorter sequences from analysis. We now look at the compositional properties of these two human chromosomes in their entirety. To do so we concatenate all contigs available for chromosomes 21 and 22 according to their physical location and calculated the H_gc (Table 3). In both cases the heterogeneity index values for concatenated sequences are slightly higher than for single longest contigs. It is especially evident in the case of chromosome 21 where H_gcfor the entire chromosome increased 18% over the single contig value when a window size of 100 kb is used. The increases can be attributed to two factors. First, sequencing gaps introduce discontinuities between some windows and so increase the overall compositional variation. Second, the telomeric region (e.g., 21q, contig NT_002835, 3,429,800 bp) is relatively GC-rich and therefore contributes to a higher H_gc.

Table 3.

Comparison of H_gc Values for the Largest Continuous Fragments of Human Chromosomes 21 and 22 to the Values Obtained for All Sequences Available for the Two Chromosomes^a

Chromosomeb	Lengthc	Adjacent Windows		Windows 100-kb Apart
Win = 50 kbd	Win = 100 kb	Win = 50 kb	Win = 100 kb
21 contig	28.5	6.800	8.470	8.530	10.630
21 all	35.2	7.990	10.291	10.377	13.371
22 contig	23.0	12.817	10.291	18.479	21.445
22 all	33.5	13.773	10.291	18.276	22.580

^aIndividual contigs were concatenated according to their physical position. 

^bcontig = Longest contiguous fragment available for this chromosome; all = concatenated data. 

^cLength is given in millions of base pairs. 

^dWin = Window size for H_gc calculation. 

To understand how repetitive DNA affects the heterogeneity of nucleotide composition, we analyzed the sequences of human chromosomes 21 and 22 by excluding (masking) all repetitive DNA (interspersed and tandem repeats). Figure 1 shows that the compositional heterogeneity of masked sequences increases, whereas the GC content may go either up or down compared to the original, unmasked sequences. Thus, repetitive DNA actually tends to homogenize the GC content of a chromosome.

Compositional Continuity Within Genomic Sequences

The isochore model predicts a certain degree of compositional continuity within human genomic sequences: Two adjacent DNA fragments (windows) should tend to be more similar in nucleotide composition than a pair of fragments separated by a distance. We used the heterogeneity index to investigate whether this is true, comparing windows separated by a 100-kb gap. Figure 1B shows the results of the calculation. In all organisms some compositional continuity is present as reflected by the fact that the heterogeneity indices for adjacent windows (Fig. 1A) are smaller than those for windows separated by 100 kb (Fig. 1B). The only exception is the yeast genome, which is highly uniform, so that the difference in GC content between two adjacent windows is similar to that between two windows separated by 100 kb. The correlation between the index values and GC levels of the sequences is stronger in Figure 1B than in Figure 1A (for Fig. 1B, r² = 73%, P < 0.0001 and r² = 75%, P < 0.0001 for 50-kb and 100-kb windows, respectively). The difference (ΔH_gc) between the H_gc value calculated using a gap and the value calculated using adjacent windows also correlates positively with the GC level of the sequences (P = 0.002 and P = 0.007 for 50-kb and 100-kb windows, respectively). Note that in Figure 1B, the index values obtained using 50-kb windows do not lag behind the values calculated from 100-kb windows as dramatically as they do in Figure 1A. Altogether, the compositional continuity is present in all sequences, but the scale at which it exists differs between yeast and the other eukaryotes in our dataset. Yeast chromosomes are homogeneous, so that the nucleotide composition does not change significantly across their entire span. For the purposes of this study we can consider each of the yeast chromosomes as a single uniform DNA segment. For the other eukaryotes in our dataset, which possess much larger chromosomes, compositional continuity is restricted to relatively small islands, so the chromosomes in their entirety are highly heterogeneous.

Compositionally Homogeneous Sequence Segments

As described above, although the genomes of multicellular eukaryotes are highly variable in GC content, they still exhibit some compositional continuity. Is it possible to find long compositionally homogeneous segments within each genome? To do so we developed a simple decomposition computer program based on the algorithm described in Methods. The program requires two parameters: the window length and the fluctuation limit. A careful choice of parameters is important. If the window is small, its GC content is subject to strong fluctuations, whereas if the window is large, it may conceal heterogeneity. If we assume that the GC content P_gc in a sequence of length L follows the binomial distribution B (L, p_gc), then the standard error of the GC content in a window of length l is

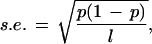which attains the maximum value at P_gc = 0.5. For P_gc = 0.5 the standard errors for l = 1 kb, 10 kb, and 100 kb are 2%, 0.5%, and 0.1%, respectively. In view of the high compositional heterogeneity in eukaryotic genomic sequences, the window size of 1 kb appears to be too small and vulnerable to random fluctuation effects (standard error = 2%). Conversely, a window size of 100 kb is too large to uncover the underlying heterogeneity of genomic sequences (see below). We therefore choose the window size of 10 kb.

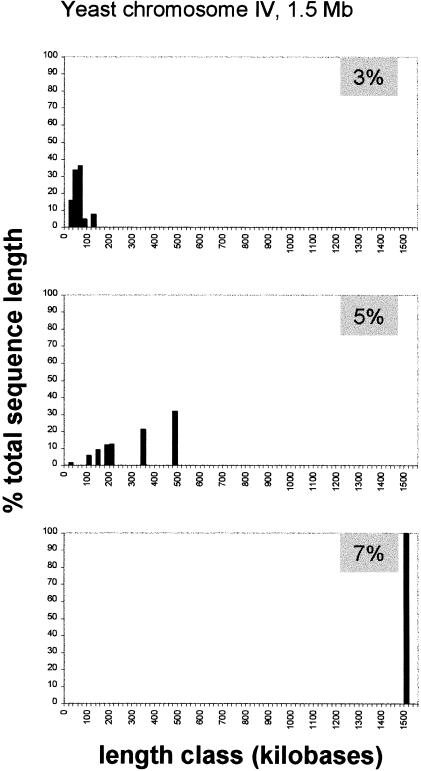
To see what a good fluctuation limit should be, we considered the yeast genome because it was shown to be highly uniform in both statistical and experimental studies (this paper; Macaya et al. 1976). An adequate fluctuation limit should allow us to consider the entire sequence of a yeast chromosome as a single uniform segment. Starting with the 3% limit, which is reasonable because it is much higher than the standard error of 0.5%, we applied the decomposition program to the sequence of chromosome IV, which is the largest yeast chromosome. This procedure was performed several times by incrementing the fluctuation limit value by 0.5% each time until the entire chromosome sequence became a single homogeneous segment (Fig. 2). As we see from Figure 2, when the fluctuation limit is 3% there are many relatively short homogeneous fragments. At the fluctuation limit of 5% chromosome IV can still be divided into seven segments. This suggests that this limit is still too low. For these seven segments the GC contents are within a small range, i.e., 37.6%–39.4%. So there are no segments that differ from each other by >5%. That is, these segments are separated from each other by sudden surges of GC content that may represent “background noise.” Only when the fluctuation limit reaches 7% is the noise completely filtered out. So, we propose to use this value as a standard to delimit compositionally homogeneous sequences within other eukaryotic chromosomes.

Figure 2.

Proportions of the total sequence length of yeast chromosome IV occupied by compositionally uniform sequence segments stratified into length classes using 20 kb as the bin size. The segments were identified using 10-kb window size and fluctuation limits indicated within gray boxes. The purpose of the analysis was to identify a fluctuation limit value at which the entire chromosome IV can be considered as a single uniform segment. This value is 7%.

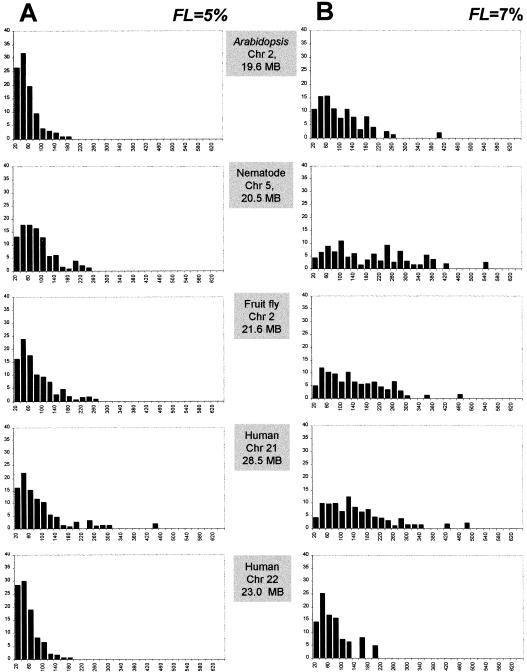
To document the effects of the fluctuation limit on the identification of compositionally uniform segments, we applied the 5% and 7% limits to the genomes of multicellular organisms in our dataset (Table 2). Our goal was to determine the length distribution of homogeneous segments in these sequences. We used the decomposition algorithm to create a list of homogeneous segments for every chromosome using 10-kb window size and the two fluctuation limits. The segments were sorted by size and stratified into 32 classes. For every class we calculated the proportion of sequence length it occupies and plotted the obtained value. The results for selected sequences are given in Figures 3. Comparing Figure 3, A and B, we see that the higher fluctuation limit allows for longer uniform segments and increases overall the spread of distributions. In all organisms both fluctuation limits produced homogeneous segments that are skewed toward the lower end of the distribution, i.e., being shorter than 100 kb. A comparison of these results with the heterogeneity index calculations (Fig. 1) shows that in general the spread of the distribution for a sequence depends on the compositional heterogeneity of that sequence. In other words, the higher the compositional heterogeneity a chromosome displays, the more difficult it is to find homogeneous segments within this chromosome. For example, the nematode and Arabidopsis chromosomes studied exhibit a low compositional heterogeneity (Fig. 1A) and possess many long homogeneous segments, whereas in the extremely variable sequence of human chromosome 22, most of the compositionally uniform fragments are within the 20–100 kb (Fig. 3B).

Figure 3.

Proportions (y axis) of the total sequence length occupied by compositionally uniform sequence segments within chromosomes of multicellular eukaryotes stratified into length classes (x axis) using 20 kb as the bin size. Calculations were performed using 10-kb window size with 5% (A) and 7% (B) FL (fluctuation limits).

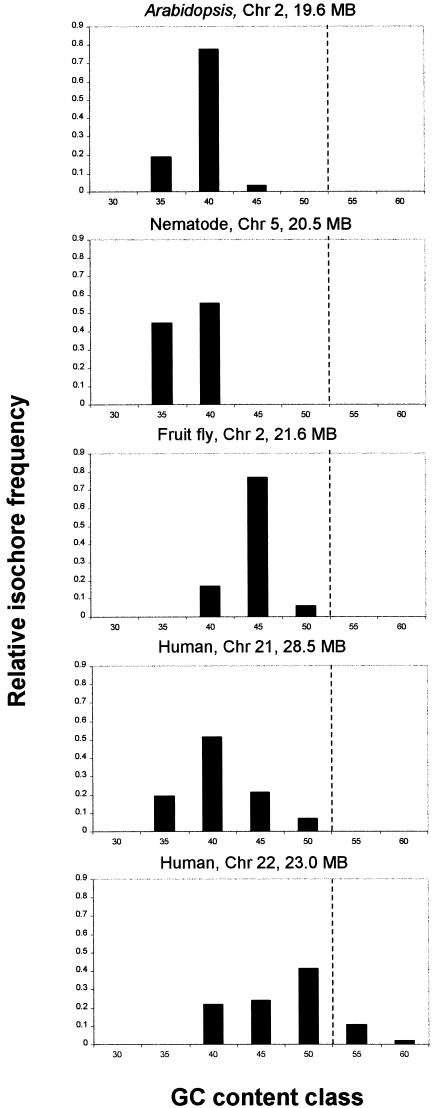
Because the 7% fluctuation limit was calibrated using the homogeneous yeast sequence, we consider the results in Figure 3B to be more realistic. Let us consider what homogeneous segments can be qualified as isochores. Note that according to the original description of isochores by Bernardi et al. (1985), isochores are longer than 300 kb. However, in Figure 3 we see very few homogeneous segments extending past the 300-kb limit. Therefore, we propose using 100 kb as the lower cutoff limit. How do individual isochores differ from each other in terms of average GC content? For each chromosome we calculated the GC content of every isochore. Based on these values we stratified the isochores into several GC level classes ranging from 30% to 60% using 5% as the bin size. Finally, we plotted the relative frequencies of isochores falling in each GC level class. The resulting graph is shown in Figure 4. Nematode chromosome V has the smallest number of classes, only two (35%–40%), whereas human chromosome 22 has the largest number, five (40%–60%). Note that based on our results, all examined eukaryotic genomes contain isochores. However, the diversity of isochores in terms of their GC content varies significantly among taxa.

Figure 4.

The relative frequencies of isochores falling into distinct GC content classes. To construct this figure, all isochores that are ⩾100 kb and are homogeneous at 7% fluctuation level were ordered according to their GC content into seven classes using the 5% GC bin size. The broken line separates GC content classes that are unique for the human genome.

Computational Replication of DNA Sedimentation Profiles

The foundation of the isochore model rests on the observation that the sheared genomic DNA fragments form a distinctive sedimentation profile when analyzed using the gradient centrifugation. Given the high compositional heterogeneity observed above, we expect DNA fragments to form a continuous zone through density gradients instead of several distinct bands. To see how this discrepancy occurred, we downloaded a set of nonoverlapping contigs representing ∼14% (430 million bases) of the human genome from the Oakridge National Laboratory ftp site. All downloaded sequences were divided into a series of nonoverlapping 100-kb fragments. This size was selected because it is similar to the average size of DNA fragments after the DNA purification procedure. The GC content of each fragment was calculated and put into one of the seven GC content classes. Finally, the total length of all fragments in each class was calculated and expressed as the percentage of the total length of all sequences taken together. The results of these calculations are given in Figure 5A. Figure 5B represents genome proportions of five isochore families based on the gradient centrifugation results (Bernardi 2000). The two distribution patterns are similar. The only significant difference at the low end of the distribution (35% GC) is likely a result of “nonrandomness” of the sequencing data: GC-poor regions were avoided in initial sequencing efforts and are, therefore, under-represented. So, like the gradient centrifugation technique, this computational approach does not reveal the high compositional heterogeneity of the genomic sequences. This shows that if a window size of 100 kb is used to search for isochores, the compositional heterogeneity is grossed over and neglected.

Figure 5.

A comparison of results obtained using computational genome fractionation (A) with the results obtained using gradient centrifugation (B). Capital letters above vertical bars in B signify isochore classes as described in Bernardi (2000).

DISCUSSION

Extraordinary Heterogeneity of the Human Genome

The heterogeneity index we developed in this study allows quantitative comparisons of compositional variation among genomic sequences. In Results we demonstrated that the compositional heterogeneity is a function of the GC content: The higher the GC content of a sequence, the higher its compositional heterogeneity. In this view the human genome is peculiar because it contains both GC-rich and GC-poor chromosomes, showing dramatic differences in compositional heterogeneity among them. For example, chromosome 21 is GC poor (39%) and has a compositional heterogeneity only as high as those of Caenorhabditis elegans or Drosophila chromosomes, whereas chromosome 22 is GC rich (47%) and has the highest heterogeneity among all the chromosomes in this dataset. The fact that different chromosomes can be so compositionally different is remarkable. Although chromosomes 21 and 22 account only for a small portion of the genome (∼2%) and may not represent the general case, compositional differences between individual chromosomes have been observed previously through karyotype banding and H isochore hybridization experiments (Saccone et al. 1993, 1999). In addition, the results by H. Wang, A. Nekrutenko, Z. Gu, and W.-H. Li (unpubl.), who computed GC levels for annotated portions of all human chromosomes, also indicate significant differences in the GC content among chromosomes. If the relationship between GC content and compositional heterogeneity holds in general, then these interchromosomal differences in GC content translate into interchromosomal differences in compositional heterogeneity. This is in sharp contrast with the other eukaryotes in our dataset, especially with the yeast genome, where all 16 chromosomes are statistically identical in compositional heterogeneity (Li et al. 1999). These results add a new dimension to the concept of genome complexity. Not only is the human genome complex in terms of size, distribution of genes, repetitive and regulatory elements, and methylation patterns, it is also highly nonuniform in terms of compositional variability within and across chromosomes.

Eukaryotic Genomes Are Mosaic

We see from Figure 3 that genomes of multicellular eukaryotes are composed of large numbers of short homogeneous segments. Therefore, they can be considered as mosaics made of homogeneous segments. If the heterogeneity of a sequence is small, then the “tiles” of the mosaic can be large (e.g., human chromosome 21 and nematode chromosome 5). If the variability is high, the tiles are usually small (e.g., human chromosome 22). In addition to size differences, homogeneous sequences within a genome also differ from each other in terms of mean GC content as illustrated in Figure 4. Using the mosaic analogy, we can refer to the differences in GC content as different colors of tiles used in the mosaic. In this case each color represents a distinct GC content category. Thus, sequences that exhibit low compositional variability are mosaics that have only a few colors (Nematode, Arabidopsis). On the other hand, highly variable sequences can be thought of as very colorful mosaics (human sequences). This analogy brings us to a conclusion that the organization of multicellular eukaryotic genomes is similar throughout the taxonomic levels: They are mosaics, but the size and color of components in these mosaics differ between taxa and depend primarily on the compositional heterogeneity of the genome.

Defining Isochores

Sufficiently long genomic fragments that are uniform in nucleotide composition can be called isochores. This term was coined by Bernardi et al. (1985) largely for the genomes of warm-blooded vertebrates (for review, see Bernardi 2000). These authors, however, did not explicitly define how much compositional heterogeneity is allowed within an isochore. In other words, it is not known what homogeneity criterion one should use to define isochores within a given genomic sequence. In this study we calibrated the homogeneity criterion using yeast sequences. The choice of yeast sequences is justifiable for three reasons: (1) Yeast DNA cannot be separated into separate components using gradient centrifugation (Macaya et al. 1976); (2) yeast chromosomes are sufficiently large, being close to the length requirement imposed by the original isochore model (≫300 kb; for review, see Bernardi 2000); and (3) the statistical analyses described earlier in this study support the notion about the uniformity of yeast sequences. Conversely, as we see from Figure 3B, when the “yeast calibrated” homogeneity criterion is applied to the eukaryotic sequences, only a few homogeneous fragments can be identified that extend beyond 300 kb. Therefore, we propose a new definition of an isochore as any genomic fragment longer or equal to 100 kb such that when it is divided into a series of overlapping 10-kb windows, no two windows can differ by >7% GC. This definition is based on the use of the yeast sequences to find optimal window size and fluctuation limit values. Use of different parameters will change the length and number of isochores. Under this definition, isochores are on average much shorter than those originally described by the gradient centrifugation approach, which did not examine the compositional heterogeneity within a segment. Because the compositional heterogeneity is correlated with the overall GC content of a sequence, GC-rich isochores should tend to be shorter than GC-poor ones. Indeed, GC-rich sequences are more variable, so it is more difficult to find compositionally uniform regions within them. For example, in the case of chromosomes 21 and 22, there is a highly significant (P < 0.0001) negative correlation between the length of the isochores and their GC content. Chromosome 21 is GC poor and contains 97 isochores with the average length of 170 kb, whereas chromosome 22 is GC rich and contains 47 isochores with the average size of 150 kb. Additionally, we expect isochores to occupy a smaller proportion of the total sequence length in GC-rich sequences than in the GC-poor ones. This is because the high variability of GC-rich sequences makes it difficult to find uniform regions that are sufficiently large to be considered isochores. For example, GC-rich chromosome 22 has ∼30% of the total sequence length allocated to isochores, whereas GC-poor chromosome 21 has ∼58%. The same is true for the other multicellular eukaryotes included in this study. These observations suggest that isochores are actually present in all eukaryotic genomes but the majority of isochores are relatively GC poor because GC-rich regions usually do not contain sufficiently long uniform segments. Moreover, the inability of the gradient centrifugation to reveal the high heterogeneity of the human genome is well illustrated in Figure 5, which indicates that the assignment of genome fragments into distinct GC content classes is oversimplified when the internal compositional heterogeneity is not taken into account. Each of the isochore classes described using the gradient centrifugation represents a pool of genomic DNA fragments with the mean GC content falling into one of the five classes (L1, L2, H1, H2, or H3). This, however, does not imply that they are homogeneous.

A caveat for the above discussion is that the definition of isochores that we propose relies solely on the use of the yeast sequences for calibrating the homogeneity criterion. Although we think this is appropriate for the above reasons, the use of different values for the window size and fluctuation limit will inevitably change what one might define as isochores. For example, an increase in window size would result in longer isochores because the fluctuation in the GC content will be smoothened out. Similarly, as Figure 2 suggests, an increase in the fluctuation limit allows for more variation to be tolerated and, hence, will lead to greater lengths of isochores. Although it is difficult to have a precise definition of isochores, the most important conclusion of our analyses is that regardless of the window size/fluctuation limit choice, all genomes of multicellular eukaryotes included in this study behave remarkably similar as indicated by the shape of distributions in Figure 3, A and B.

Yeast versus Multicellular Eukaryotes: A Possible Relationship Between Replication and Genome Composition

This and many other studies show that the yeast genome is compositionally different from their multicellular counterparts. What is the reason for this difference? A possible explanation may lie in the difference between the yeast replication mechanism and that of multicellular eukaryotes. Yeast chromosomes possess discrete replication origins identified as autonomously replicating sequence (ARS) elements having an AT-rich consensus essential for replication initiation (Spradling 1999). Although homologs for the majority of proteins involved in the replication initiation in yeast were identified in taxa as far as mammals (DePamphilis 1999), the nature of replication origins in plants and metazoans remains elusive. It is believed that at least in metazoan genomes there are no preferable initiation sites and this process is driven primarily by the higher order chromatin structure and interactions with the nuclear matrix (Gilbert 1998). Initiation may also take place in different sites in a cell-type-specific manner (Spradling 1999). The same scenario likely holds for plant genomes as well (Van't Hof 1996). Hence, we speculate that the excessive compositional variation in metazoan and plant genomes may be attributable to the possible random nature of the replication origins in these organisms. The lack of stationary replication origins allows constant change of mutational biases resulting in high compositional variability. Conversely, compositional properties of the genome probably dictate the higher order chromatin structure (Ostashevsky 1998) and therefore it is difficult to establish a clear cause/effect relationship between the replication process and compositional properties of the genome. Because these speculations are based largely on the lack of information concerning the mechanism of eukaryotic replication, empirical data is required to test their validity.

METHODS

Data

A list of genomic sequences used in this study along with respective internet sites is given in Table 2. Each sequence was formatted by excising gaps, removing FASTA headers and end-of-the-line characters. In addition, the analyses described in Results were conducted using the sequence data downloaded from the Oakridge National Laboratory depository at ftp://compbio.ornl.gov.

Compositional Heterogeneity Index

We developed a measure to quantify the compositional heterogeneity within a genomic sequence and to compare differences in heterogeneity between sequences. Let us consider a sequence with the GC content P that can be divided into n windows of length l. We first calculate the GC content of each window (e.g., GC₁, GC₂,…, GC_n) and then compute the average GC content difference between two adjacent windows:

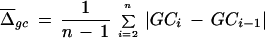1

Although equation 1 is useful for characterizing the compositional heterogeneity within a given sequence, it is not suitable for comparing heterogeneities between sequences because it is not normalized for the overall GC content p. For simplicity, let us assume that nucleotides are distributed randomly within a sequence. In this case we can consider each window as a simple random sample of the entire sequence with the standard error:

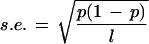2

Now we can normalize the average difference (equation 1) by the standard error (equation 2) and obtain the following equation for the compositional heterogeneity index H_gc:

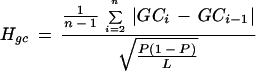3

A PERL program for the H_gc calculation suitable for large genomic sequences will become available at http://nekrut.uchicago.edu.

Decomposition Algorithm

First, we divide a sequence into a series of overlapping windows of length l (overlap = l/2). After calculating the GC content of each window we represent the sequence as an array [gc₁..gc_n] in which the elements gc_i represent the GC contents of consecutive sequence windows, the first element of the array being the 5′-most window. Second, we look for the first pair of adjacent elements (e.g., adjacent sequence windows) whose GC contents do not differ more than a specific fluctuation limit (FL, e.g., |gc_i − gc_i + 1| ≤ FL, where 1 ≤ i < n). When such a pair is found it is considered to be an “isochore seed.” Of the two array elements belonging to the isochore seed we choose the one with greater value and record it as gc_max , and the other element as gc_min. Then we try to extend the isochore seed by looking at the value of the next array element (e.g., toward the 3′ end of the sequence). The isochore will be extended for one more array element if, after including the element under consideration and reassignment of gc_min and gc_max values, the condition gc_max − gc_min ≤ FL holds. There are two possibilities: (1) If gc_max  − gc_min  ≤ FL, the isochore is extended to include the window under consideration, and we then look at the next adjacent element and so on; (2) if gc_max −  gc_min  > FL, the isochore is terminated, and we start to look for the next isochore seed. The algorithm progresses through the array (sequence) and records all identified isochores until the end is reached. A PERL implementation of the algorithm will become available at http://nekrut.uchicago.edu.