Due to intravascular multiple sequential scattering, Diffuse Correlation Spectroscopy of tissue primarily measures relative red blood cell motion within vessels

Abstract

We suggest that Diffuse Correlation Spectroscopy (DCS) measurements of tissue blood flow primarily probe relative red blood cell (RBC) motion, due to the occurrence of multiple sequential scattering events within blood vessels. The magnitude of RBC shear-induced diffusion is known to correlate with flow velocity, explaining previous reports of linear scaling of the DCS “blood flow index” with tissue perfusion despite the observed diffusion-like auto-correlation decay. Further, by modeling RBC mean square displacement using a formulation that captures the transition from ballistic to diffusive motion, we improve the fit to experimental data and recover effective diffusion coefficients and velocity de-correlation time scales in the range expected from previous blood rheology studies.

1. Introduction

Light scattering methods have been used to probe the motion of suspended particles for the last several decades, in either single [1] or multiple scattering regimes [2]. The latter technique, known as diffusing wave spectroscopy (DWS) has been extended to heterogeneous multiple-scattering media by Boas et al. [3, 4] and has gained acceptance as a method to measure perfusion in bulk tissue under the name of Diffuse Correlation Spectroscopy (DCS) [5]. By measuring the intensity fluctuations of light diffusely reflected from tissue, DCS can offer a measure of microvascular blood flow and has been successfully validated against other blood flow measurement techniques, such as arterial spin labeling (ASL) magnetic resonance imaging (MRI) [6–8], Doppler Ultrasound [9, 10], Xenon-CT [11] and fluorescent microspheres [12]. Given the three dimensional micro-topography of vasculature, red blood cell motion has been expected to have the characteristics of ballistic random flow with a uniform spatial velocity distribution [13]. Surprisingly though, the good agreement seen in the validation studies cited above requires modeling particle movement as a diffusion random-walk. Two recent studies have probed the characteristics of DCS signals more deeply, looking at whether the pulsatile nature of blood flow and/or the presence of extravascular tissue shearing contribute to the observed diffusive scatterer dynamics. Using parallel detection of independent speckles Dietsche et al. [14] have measured the auto-correlation of light intensity fluctuations with 26 ms temporal resolution, and noted up to 240% variation in the auto-correlation decay time during one heart pulsation, as well as a somewhat stronger curvature of the decay curve at the systolic maximum flow compared to the diastolic minimum flow. While, this “super-diffusive” decay appears to have a slight ballistic flow quality, the data presented by the authors in Fig. 7 of Ref. [14] indicates the scatterer motion remains predominantly diffusive throughout the pulsation cycle. Further, Ninck et al. [15], using an ex-vivo artificially perfused porcine kidney model has shown that, in the absence of blood, the DCS signal carries the signature of extravascular tissue shearing. Nevertheless, during pulsatile blood perfusion, the correlation decay curves are approximately described by diffusion even as they vary during the pulsation cycle because the contribution of extravascular tissue shearing is small. Taking into account the results of these studies, Ninck et al. [15] conclude in their discussion that the discrepancy between expected red blood cell ballistic flow and diffusion dynamics measured by DCS remains unexplained, but perhaps DCS signals might reflect erythrocyte diffusion in the direction perpendicular to flow, as has been observed through particle tracking experiments [16], with a magnitude proportional to the flow shear rate.

In this paper we revisit the assumptions made in obtaining blood flow estimates from DCS data. In particular we argue that the occurrence of multiple sequential scattering within blood vessels would render the DCS measurements sensitive to relative red blood cell motions. As noted above, these motions are diffusive in nature, and their magnitude scales nearly linearly with blood flow velocity [16], in good agreement with published DCS studies. We also show that an effective hydrodynamic diffusion model capturing the transition between early ballistic and subsequent diffusive motion results in a modest, but significant improvement in the fit to experimental data. In addition to an effective diffusion coefficient proportional to blood flow velocity, this model also provides a measure of the particle velocity randomization time scale, a potentially useful tool for blood rheology studies addressing dynamics faster than the millisecond range currently accessible using video microscopy methods.

2. Methods

2.1. Dynamic light scattering in tissue

In the context of DWS/DCS, the normalized temporal electric field E(t) auto-correlation function g₁(τ) = 〈E(0)E^*(τ)〉/〈|E(0)|²〉 is given by [4]:

$$g_1\hspace{0.17em}(\tau )\hspace{0.17em}=\hspace{0.17em}{\int }_0^{\infty }P(s)\hspace{0.17em}\text{exp}\hspace{0.17em}\left[-1/3\hspace{0.17em}{k}_0^2\hspace{0.17em}\langle \Delta r^2\hspace{0.17em}(\tau )\rangle \hspace{0.17em}\frac{s}{l}\right]\hspace{0.17em}\mathit{\text{ds}}$$ (1)

where τ is the correlation delay time, P(s) is the normalized probability distribution of detected photon path lengths s, k₀ = 2π/λ, with λ the wavelength of the illumination laser, 〈Δr²(τ)〉 is the mean-squared displacement of scattering particles in time τ, and l = 1/μ_s is the photon random-walk step length which is equal to the inverse of the scattering coefficient μ_s (thus s/l gives the average number of scattering events for a pathlength s). The auto-correlation decay in biological tissue has been shown to be nearly completely determined by blood flow-related motion [15, 17]. Thus, given that red blood cells (RBCs) make up over 90% of the corpuscular content of the blood, it is reasonable to assume they represent the dominant source of dynamic scattering events in tissue. In previous DCS investigations, RBC displacement has been modeled as either random flow with 〈Δr²(τ)〉 = V²τ², where V² is the second moment of the velocity distribution, or as Brownian diffusion with 〈Δr²(τ)〉 = 6D_bτ, where D_b is the effective Brownian diffusion coefficient. Unexpectedly, all studies found that the Brownian motion formulation leads to a better fit to experimental data than the random flow formulation. Such an observation may be explained by noting that the random ballistic flow model assumes successive scattering events occur on scattering centers with uncorrelated velocity vectors. This is valid if scattering events from RBCs are always separated by scattering from extravascular, comparatively static tissue, i.e. if the probability of having two or more scattering events in a single blood vessel is low. However, this assumption breaks down if the scattering mean free path l is smaller than the blood vessel dimension. In fact, studies of blood optical properties indicate the scattering length at the common 785–805 nm wavelengths used in DCS instruments is on the order of 12 μm for typical 40% hematocrit [18], while the mean absorption length (1/μ_a) exceeds 3.5 mm. Thus photons entering any blood vessel larger than a capillary most likely undergo multiple scattering before exiting. Note that 70% of the total blood volume (and an even higher percentage of RBCs because of low capillary hematocrit [19]) is contained in such larger vessels [20]. Therefore the majority of intra-vessel scattering events are likely to be part of a sequential scattering chain. In conjunction with the higher flow velocities in these vessels and the additive nature of photon phase change accumulation, we expect sequential within-vessel scattering to dictate the photon decorrelation process. Consequently, the random ballistic flow assumption is invalidated and we must instead consider the relative motions of RBCs within a vessel.

Red blood cell dynamics have been the subject of numerous blood rheology studies. As also noted by Ninck et al. [15], video microscopy has been used ex vivo to track the motion of hemoglobin-depleted ghost RBCs [16] and whole blood [21] in microchannels, as well as in vivo in rat venules [22]. It was found that RBCs undergo shear-induced displacements in the bulk flow frame of reference that can be characterized by an effective diffusion coefficient D_eff on the order of 10⁻⁵ mm²/s, much higher than the Brownian diffusion coefficient expected for the RBCs in plasma ~ 5 × 10⁻⁸ mm²/s [22]. Most importantly, D_eff appears to scale linearly with the shear rate. We postulate that this mechanism underlies the measurement of tissue blood flow using Diffuse Correlation Spectroscopy.

While the simplified Brownian displacement formulation used in DCS literature (〈Δr²(τ)〉 = 6D_bτ) appears to work well, it assumes that the ballistic to random-walk hydrodynamic transition in the RBC diffusion occurs at time scales shorter than those probed by DCS measurements. Since there is no data to support this assumption, we remove it by using the Langevin formulation for RBC mean squared displacement [1]:

$$\langle \Delta r^2\hspace{0.17em}(\tau )\rangle \hspace{0.17em}=\hspace{0.17em}6D_{\text{eff}}\hspace{0.17em}(\tau \hspace{0.17em}-\hspace{0.17em}{\tau }_c(1\hspace{0.17em}-\hspace{0.17em}\text{exp}(-\tau /{\tau }_c)))$$ (2)

where D_eff is the effective diffusion coefficient and τ_c is the time scale for the randomization of velocity vectors associated with RBC scattering events. By Taylor expanding Eq. (2), it can be shown that this formulation of the displacement term describes ballistic motion at short delay times, and diffusive motion at long delay times. Note that we are referring here to the short time scale ballistic motion contained within any diffusive process (including that of erythrocytes in the bulk flow frame of reference), and not to the bulk ballistic motion of erythrocytes in vasculature as seen in the laboratory frame of reference.

2.2. Experimental approach and data analysis

To evaluate the performance of the proposed model, we have applied it to the infant data previously reported by our group in Ref. [10]. Briefly, 11 premature infants, between 28 and 34.5 weeks gestational age were measured several times at weekly intervals, for a total of 66 study visits. At each visit, measurements were obtained in up to seven areas of the head using a handheld multi-distance probe with source detector distances of 1–2.5 cm. Both frequency domain diffuse reflectance as well as diffuse correlation spectroscopy data was acquired. A frequency domain instrument emitting 110 MHz modulated light at 8 wavelengths between 659 and 825 nm was used to estimate absolute optical properties, while the DCS system employed a long-coherence length laser operating at 785 nm (CrystaLaser, Reno, NV, USA) and four photon-counting avalanche photodiodes (Perkin-Elmer, Quebec, Canada) connected to a digital auto-correlator operating at delay times from 200 ns to 1 s (Correlator.com, Bridgewater, NJ, USA). Additional experimental details can be found in Ref. [10].

To analyze the DCS data we used the semi-infinite medium correlation diffusion formulation [5]:

$$G_1\hspace{0.17em}(\rho ,\hspace{0.17em}\tau )\hspace{0.17em}=\hspace{0.17em}\frac{3{\mu }_s^{\prime }}{4\pi }\hspace{0.17em}\left(\frac{\text{exp}(-K{r}_1)}{r_1}\hspace{0.17em}-\hspace{0.17em}\frac{\text{exp}(-K{r}_2)}{r_2}\right)$$ (3)

where $K^2\hspace{0.17em}=\hspace{0.17em}3{\mu }_a{\mu }_s^{\prime }\hspace{0.17em}+\hspace{0.17em}\alpha {\mu }_s^{\prime 2}{k}_0^2\langle \Delta r^2\hspace{0.17em}(\tau )\rangle$, α is the probability of scattering from a moving particle (RBC), ρ is the source-detector separation, $r_1\hspace{0.17em}=\hspace{0.17em}{({\rho }^2\hspace{0.17em}+\hspace{0.17em}{z}_0^2)}^{1/2}$, r₂ = (ρ² + (z₀ + 2z_b)²)^1/2, $z_0\hspace{0.17em}=\hspace{0.17em}{({\mu }_a\hspace{0.17em}+\hspace{0.17em}{\mu }_s^{\prime })}^{-1}$ and $z_b\hspace{0.17em}=\hspace{0.17em}1.76/{\mu }_s^{\prime }$ (assuming the refractive index of tissue to be 1.35). Note that we measure experimentally the normalized temporal intensity auto-correlation function, g₂(τ), related to the normalized field auto-correlation function g₁(τ) through the Siegert relation (β is a factor dependent on the coherence characteristics of the light source and collection system) [1]:

$$g_2\hspace{0.17em}(\rho ,\hspace{0.17em}\tau )\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}+\hspace{0.17em}\beta \hspace{0.17em}{(g_1\hspace{0.17em}(\rho ,\hspace{0.17em}\tau ))}^2;\hspace{0.17em}{g}_1\hspace{0.17em}(\rho ,\hspace{0.17em}\tau )\hspace{0.17em}=\hspace{0.17em}\left|\frac{G_1\hspace{0.17em}(\rho ,\hspace{0.17em}\tau )}{G_1\hspace{0.17em}(\rho ,\hspace{0.17em}0)}\right|$$ (4)

3. Results and discussion

Figure 1 shows a sample intensity auto-correlation curve g₂(τ) that exemplifies the different fits obtained using displacement formulations corresponding to simplified Brownian diffusion, hydrodynamic diffusion (Eq. (2)) and random flow, respectively. For this data, it is clear that only hydrodynamic diffusion provides a good match to the shape of the auto-correlation decay. The decay predicted by the simplified Brownian diffusion appears too “slow”, while the decay predicted by random flow is too “fast”, leading to incorrect estimation of the β factor as well as of the decay rate. To quantify the quality of the fit, we use the statistical metric “fraction of variance unexplained” (FVU), defined as the ratio of the model mean squared error to the variance of the experimental data. For the data in Fig. 1, the hydrodynamic diffusion model has the lowest residuals (FVU=0.04%), followed by Brownian diffusion (FVU=0.48%), and random flow (FVU=0.76%). The average values of FVU over the entire set of experimental measurements are 0.36% for hydrodynamic diffusion, 0.46% for Brownian diffusion, and 2.32% for random flow, respectively. As seen in previous studies, the simplified Brownian diffusion model is found to have significantly lower fit errors compared to random flow. The same direct comparison cannot be made between the simplified Brownian and full hydrodynamic diffusion models because of their different number of parameters. Instead, we perform a statistical F-test to determine if the improvement in the hydrodynamic model exceeds the reduction in unexplained variance expected from adding an additional fitting parameter (τ_c) :

$$F\hspace{0.17em}=\hspace{0.17em}\frac{({\mathit{\text{SSE}}}_{\mathit{\text{Db}}}\hspace{0.17em}-\hspace{0.17em}{\mathit{\text{SSE}}}_{D\text{eff}})}{{\mathit{\text{SSE}}}_{D\text{eff}}}\cdot \frac{{\mathit{\text{DoF}}}_{D\text{eff}}}{({\mathit{\text{DoF}}}_{D\text{eff}}\hspace{0.17em}-\hspace{0.17em}{\mathit{\text{DoF}}}_{\mathit{\text{Db}}})}$$ (5)

where SSE is the sum of the squares of the residuals and DoF is the number of degrees of freedom (number of correlation time bins (137 in our case) minus the number of model parameters (2 for Brownian diffusion (D_b and β), 3 for hydrodynamic diffusion (D_eff, τ_c and β)). For hydrodynamic diffusion to be a better model than Brownian diffusion, the corresponding F-number must exceed a critical F-value, which for p < 0.05 is 3.91 (as calculated using the finv function in Matlab (Mathworks, Natick,MA)). This is true for 80.1% of the individual measurements from our data set, and the whole set F-number is 33.8, corresponding to a highly significant p-value of 4 × 10⁻⁸ (calculated using fcdf in Matlab).

Fig. 1.

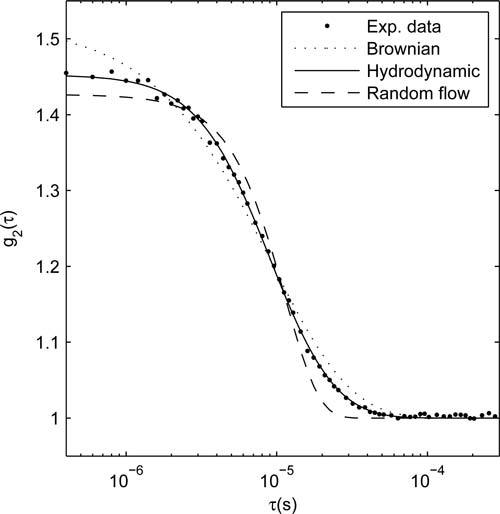
Comparison of data fit errors using the Brownian diffusion (dotted, FVU=0.48%), hydrodynamic diffusion (solid, FVU=0.04%) and random flow (dashed, FVU=0.76%) mean square displacement models.

When Eq. (2) is substituted into Eqs. (3) and (4), a product forms between the probability of scattering from a red blood cell α and the diffusion coefficient. This quantity has been used as a “blood flow index” in DCS studies, because the value of α generally cannot be estimated independently. Figure 2 shows a scatter plot of the αD_eff vs. the αD_b values obtained from each of our measurements. We observe an approximate relationship of αD_eff = 1.07αD_b + 2.1 × 10⁻⁷(mm²/s). αD_eff has a substantially linear relationship with αD_b, with a nearly-zero intercept, indicating both parameters can serve as relative blood flow indices, but αD_eff is expected to provide a more accurate absolute measure. Encouragingly, by assuming α = 0.1 [23] for brain tissue, our estimated effective diffusion coefficients fall within the same range as those determined from video microscopy blood flow studies (10⁻⁵ – 10⁻⁴ mm²/s) [16, 21, 22].

Fig. 2.

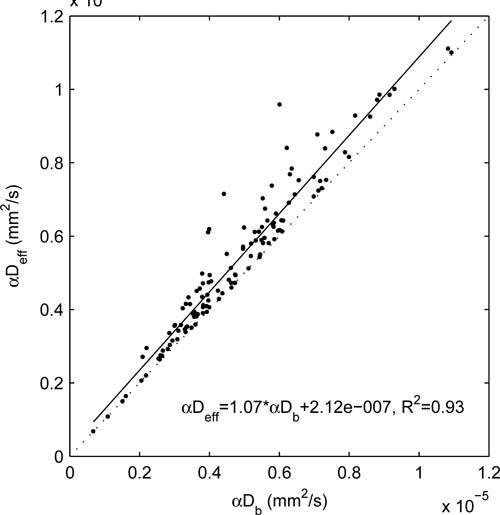
Scatter plot of αD_eff vs. αD_b across the entire data set. The dotted line indicates the diagonal of the plot (ratio=1).

With respect to τ_c, we observed a range between 0.06 and 7.7 μs, with an average of 1.3 μs (however values lower than ~ 0.4μs are not reliable because of the limited time resolution of our correlator). A rough estimation of expected τ_c values may be obtained from hydrodynamic diffusion theory. For a rigid spherical particle the velocity decorrelation characteristic time is on the order of τ_v = ρa²/η, where a is the particle size, ρ is the fluid density and η is the fluid viscosity. Assuming a red blood cell diameter of a = 4 μm, η = 1.2 cP [22] and the density of water, τ_v = 13 μs, within an order of magnitude of our measurements. While the deformable nature of RBCs and the complexity of blood flow make this comparison less meaningful, our results do indicate the ballistic motion time scale (τ < τ_c) of the RBC hydrodynamic diffusion process is observable in most DCS measurements. Thus the full Eq. (2) should be used to reduce variance in the obtained blood flow velocity estimates and to characterize the diffusive transition time scale. To further characterize τ_c we plot in Fig. 3: a) τ_c vs. flow velocity, represented by αD_eff and b) τ_c vs. inter-RBC distance (expected to be proportional to the inverse cube root of the blood hemoglobin concentration HGB^−1/3), for all the measurements where R² of the hydrodynamic fit was greater than 0.999 (giving us confidence in the estimation of τ_c). We observe a weak but statistically significant decrease in τ_c with increased blood flow, as well a weak decrease with increased inter-particle distance that does not reach a p<0.01 significance level. The inverse proportionality between τ_c and D_eff (and hence blood flow) could be explained as an acceleration of the interaction time scale. It is also expected from the short τ Taylor expansion of the mean square displacement expression (Eq. (2)): $\langle \Delta r^2(\tau )\rangle \underset{=}{\tau \ll {\tau }_c}\hspace{0.17em}6(D_{\text{eff}}/{\tau }_c){\tau }^2$. Assuming the short τ ballistic displacement takes the form 〈Δr²(τ)〉 = v²τ², the early ballistic velocity v is proportional to $\sqrt{D_{\text{eff}}/{\tau }_c}$. As a first approximation, one could expect v to be fairly constant (i.e. dependent on blood viscosity and temperature, but not on the speed of the bulk flow), suggesting an inverse-proportional relationship between τ_c and D_eff. A similar intuitive explanation is not apparent for the observed decrease in τ_c with increased inter-particle distance. This trend is likely due to complex blood flow mechanisms. Note though that τ_c is known to be affected by particle deformability in colloids [24], thus it may become a useful tool to monitor RBC mechanical properties. Such changes can occur due to physiological and pathological mechanism, such as the fetal-to-adult hemoglobin replacement, and disease states such as sickle-cell anemia.

Fig. 3.

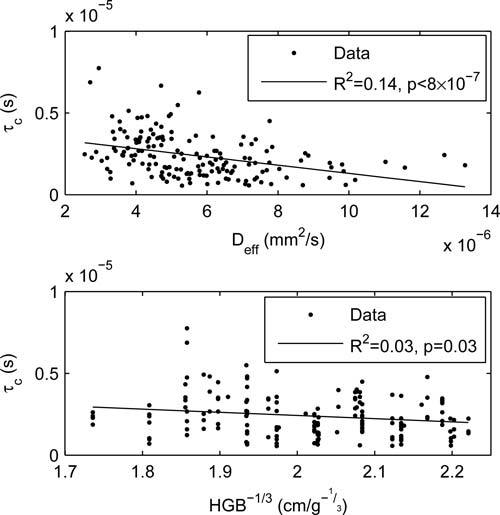
Dependence of τ_c on physiological parameters. (a) dependence on the flow velocity, assumed to be proportional to αD_eff ; (b) dependence on collision length scale, assumed to be inversely proportional to the cubed root of the hemoglobin concentration.

4. Conclusion

In conclusion we have provided a mechanistic explanation for the diffusion-like scatterer dynamics observed in diffuse correlation spectroscopy measurements of biological tissue based on multiple-scattering within individual blood vessels. We have also shown that experimental data is best fit with a hydrodynamic diffusion formulation that includes both ballistic flow at short times and diffusive motion at later times. Both the effective diffusion coefficients and the transition time scale are within an order of magnitude of expected values. Finally, our results imply that, in addition to tissue perfusion measurements, DCS may be a useful tool for blood rheology studies.