Social Capital, Information, and Socioeconomic Disparities in Math Coursework

Abstract

Analysis of the National Education Longitudinal Study revealed that socioeconomically advantaged students persist in high school math at higher rates than their disadvantaged peers, even when they have the same initial placements and skill levels. These disparities are larger among students with prior records of low academic status because students from more privileged backgrounds persist in math coursework even when their prior performance predicts they will not. Among students with low middle school math performance, those from socioeconomically disadvantaged families appear to benefit from having consultants for coursework decisions, so that they make up ground with their socioeconomically advantaged peers.

Biographical Sketches

Robert Crosnoe is Professor of Sociology and, by courtesy, Psychology at the University of Texas at Austin, where is also a faculty associate in the Population Research Center. A life course sociologist, he studies the connections between child/adolescent development and schooling and how these connections contribute to socioeconomic and immigration-related stratification. His books include Mexican Roots, American Schools: Helping Mexican Immigrant Children Succeed (Stanford) and Fitting In, Standing Out: Navigating the Social Challenges of High School to Get an Education (Cambridge).

Barbara Schneider is the John A. Hannah Chair and University Distinguished Professor in the College of Education and Department of Sociology at Michigan State University. Her research focuses on the social context of schools, families, and work. Dr. Schneider is the principle investigator of the College Ambition Program (CAP), a study that tests a model for promoting a STEM college-going culture in two high schools that encourages adolescents to pursue STEM majors in college and occupations in these fields.

In today’s economic climate, persistence in the high school math curriculum provides tangible academic credentials that give young people a competitive edge in college-going in general. It also provides crucial preparation for higher education trajectories into specific sectors of the labor market characterized by growth, stability, and benefits (Adelman 2006; Sadler and Tai 2007). Yet, students at the low end of the socioeconomic spectrum in the U.S. still tend to persist less far in math during high school (Crosnoe and Huston 2007; Schneider and Stevenson 1999), even though economic restructuring has had a negative impact on their traditional routes into secure, well-paying jobs (e.g., the manufacturing sector) and, therefore, increased their need to use higher education to get ahead (Goldin and Katz 2008). Thus, math coursework is an opportunity for social mobility and a vehicle for the intergenerational transmission of socioeconomic inequality.

The give and take between curricular and interpersonal trajectories during secondary school likely plays a role in this paradox. As youth navigate a heavily differentiated curriculum that links their learning and skill development in childhood to their educational attainment in adulthood, their personal traits, proliferating strong and weak social ties, and past experiences come together to shape how short-term decisions match up with long-term goals (Pallas 2003). This link between key trajectories of adolescence offers insights into how to intervene in socioeconomic disparities, depending on whether low socioeconomic status (SES) students or their higher SES peers benefit more from exposure to social networks in which instrumental resources promoting college preparedness are exchanged (Crosnoe and Huston 2007).

Integrating different educational perspectives (Coleman 1988; Erikson and Goldthorpe 2002; Morgan 2005), this study views math coursework as rooted in a process of active and passive decision-making differentiated by the interplay of family SES, prior academic histories, and instrumental social support. The first aim is to identify segments of the high school population in which this interplay likely produces the largest socioeconomic disparities in math coursework for American girls and boys. The second is to assess whether increasing support for academic decision-making in these segments might reduce such disparities. These aims will be pursued with longitudinal, nationally representative data on math coursework and social relations across the transition into high school from the National Education Longitudinal Study (NELS).

Inequality, Secondary Schools, and Math

According to international testing data, SES differences in key academic indicators might be somewhat weaker in the U.S. than in many other industrialized Western nations, at least those with more heavily differentiated educational systems (Buchmann and Park 2009). Yet, even with its more open school organization relative to other nations (e.g., Germany) and strong ideology about meritocracy, the U.S. is still a society in which SES has a profound influence on the educational credentials one attains (Buchmann and Park 2009; Buchmann and Parrado 2006; Fischer and Hout 2006). Indeed, high SES youth tend to do better in elementary, middle, and high school than their peers, which translates into higher rates of college matriculation and graduation. College-educated individuals, in turn, tend to have greater opportunities in the labor market, allowing them to realize advantages in income, job security, and other non-economic domains, such as health (Fischer and Hout 2006; Kingston et al. 2003; Mirowsky and Ross 2003). In this way, education helps to transfer SES across generations. Moreover, even though the shift to a global economy dominated by technology and information places a premium on meritocracy over ascription in job placement and even though income returns to higher education have risen accordingly, this transmission appears to be getting stronger in the U.S. and in other countries (Breen and Goldthorpe 2001; Goldin and Katz 2008).

This SES advantage, however, operates differently across educational systems. As mentioned above, many European countries have highly differentiated systems in which students in early to middle adolescence are sorted into different types of secondary schools (e.g., college preparatory, vocational) depending on their prior performance. In such systems, SES effects are focused on these “branch points”. The American system has fewer distinct branch points and stresses academic training over vocational training more generally, so that SES effects are not focused on specific points but instead filter out more diffusely across the educational career (Buchman and Parrado 2006; Csikszentmihalyi and Schneider 2000).

To be more specific, high school curricula in the U.S. offer many options for enrollment and study within and across time periods. As students navigate this field of choices, therefore, they face numerous points at which decision-making—active or passive, by the student or someone else—about the next move is required, with any one move cumulatively factoring into students’ long-term trajectories (Morgan 2005). SES can then have a primary effect by shaping students’ demonstrated ability at any one point, thereby determining their next opportunities. SES can also have a secondary effect by shaping the decisions students and parents make within existing opportunity structures (Erikson and Goldthorpe 2002). Consequently, high SES students have a primary advantage because their parents’ socioeconomic circumstances grant them access to early childhood cognitive stimulation, high-quality early education, more enriched and better organized elementary and middle schools, and out-of-school programs that, in turn, increase their demonstrated ability as they approach high school (Entwisle et al. 2005; Lareau 2004; Mayer 1997; NICHD Early Child Care Research Network 2005). They then gain a secondary advantage because of their parents’ greater experience navigating the system towards higher education, lower likelihood of being risk averse about academic challenges, and higher levels of status and power in their social networks. These resources allow them to make decisions, or have decisions made for them, in high school that cumulatively increase their chances for college-going (Goldthorpe 2000; Morgan 2005).

Thus, social capital—the resources (e.g., information, support) for getting ahead that flow through relationship ties and provide competitive advantages in settings offering multiple pathways with different rewards (Bourdieu 1987; Coleman 1988)—is a key component in primary and secondary SES effects. Parents with more money, prestige, and education are better able to provide instrumental resources to their children and link them to others with such resources, which increase students’ demonstrated ability and helps them adjudicate among the options available to them as a function of their demonstrated ability (Plank and Jordan 2001).

This process of accumulating primary and secondary SES advantages is writ small in the high school math curriculum. First, it is a heavily differentiated set of course offerings that gradually move from required to elective status over time, so that the math trajectory can be viewed as a sequence of decision-making points with potential for self-propagation (Attewell and Domina 2008; Lee et al. 1997; Riegle-Crumb 2006). Second, SES is a powerful predictor of the math classes that students take, especially when math becomes voluntary, and how well they do in these classes (Attewell and Domina 2008; Gamoran and Hannigan 2000; Plank and Jordan 2001). Third, math coursework factors into socioeconomic attainment by providing academic credentials that are attractive to four-year colleges, especially selective ones, improving college preparedness, reducing the need for remediation once in college (e.g., in intro-level math classes), and channeling students into specific fields of study in college (e.g., engineering) that feed into high-demand professional fields in the new economy (Adelman 2006; National Academy of Sciences 2007; Sadler and Tai 2007).

The math curriculum, therefore, is a complex field of choices in which SES can have both primary and secondary effects with implications for long-term status attainment. Against this backdrop, intervening in high school to reduce socioeconomic disparities in math seems to be an important goal. In that spirit, this study will help to highlight when, to whom, and how such efforts should be targeted.

Points of Vulnerability in the System

Acting at a specific point on a specific group may have a larger long-term impact than a more universal action. Identifying such points is one way for social scientists to inform policy. This study focuses on two stages of high school coursework and then on students of different academic statuses in order to identify who may need special help during these two stages.

First, although American education lacks the official branching points found in many international systems, it does have unofficial branch points in which the primary and secondary effects of SES converge. Consider the transition into high school. Because initial placement in math in high school is largely predicated on middle school math performance, it is a point at which primary SES effects (e.g., on demonstrated ability) are important. Yet, some students are enrolled in math courses either higher or lower than their past math performance would suggest. Thus, this transition is a point at which secondary SES effects (e.g., on choices made among a set of options) are also important (Crosnoe and Huston 2007; Gamoran and Hannigan 2000). At the same time, although initial placement in math powerfully predicts the ultimate progress of students through the math curriculum, even students who start high school in the same math level can persist through the curriculum at unequal rates (Crosnoe and Huston 2007). As math coursework becomes more optional, especially around 11^th/12^th grades, students are faced with the decision to keep going or stop out. Many, especially those with lower prior performance in math, opt for the latter, undermining their marketability to and preparedness for college and work. SES can matter to math trajectories, therefore, by shaping initial math placement (primary effect) and then by influencing the degree to which students build on this initial placement in an environment in which constraints on coursework ease from year to year (Lucas and Berends 2002; Ma and Willms 1999; Riegle-Crumb et al. 2006).

Second, a consideration of the interplay of primary and secondary SES effects in the decision-making model suggests that SES disparities in math coursework at any one point will likely vary across segments of the student population defined by different levels of math progress up to that point. In general, high SES students will have higher levels of demonstrated ability (as defined by test scores and coursework) in middle school and at the start of high school, which will give them an advantage over low SES peers in initial math placement and ultimate math progress. Holding constant this primary SES effect (i.e., looking only at students with same math status at any point), therefore, is when secondary SES effects—how students and parents negotiate available options and opportunities at the start of and then during high school—should matter. This scenario is likely to play out at the low end of the academic hierarchy. There, both high and low SES students have low levels of demonstrated ability, but high SES students have parents who may better understand the value of math coursework for future educational and occupational opportunities and likely have greater standing and power in the school to advocate for their children (Baker and Stevenson 1986; Lareau 1989). Such secondary SES effects, however, could be weaker at the high end of the academic hierarchy. Low SES students with high levels of demonstrated ability might not have the tangible socioeconomic advantages that their high SES peers of the same demonstrated ability enjoy. Yet, their perseverance in math despite the odds against them and the high levels of cognitive and social skills necessary for such perseverance could elicit investment from school personnel and mentors and garner access to high-quality instruction, thereby chipping away at secondary SES effects (Furstenberg et al. 1999; Crosnoe and Huston 2007). If so, disparities in math at any point should be stronger in segments of the student population defined by low academic status prior to that point than in those defined by high academic status (Lucas 1999; Valenzuela 1999).

The first aim of this study, therefore, is to document whether family SES predicts math position at the start of high school and the number of math credits earned by the end of high school. The second aim is to examine whether such disparities vary by students’ prior histories in math; specifically, whether they are largest among students who score low on achievement tests before high school and have low initial course placement in high school.

Social Capital and Secondary SES Effects

If socioeconomic disparities in math coursework are rooted in stronger secondary SES effects among students with histories of lower math performance, then efforts to intervene in these secondary SES effects could reduce socioeconomic disparities in the whole population. In turn, the existence of secondary SES effects even when primary SES effects are held constant may be rooted in high SES students’ greater access to social relations facilitating the flow of instrumental support for making the “right” decisions in an open field of options. If so, increasing the flow of such social capital to low SES students at the low end of the math hierarchy may be one way to reduce socioeconomic disparities in the general student population. This premise, however, rests on whether low SES students accrue the same or greater benefit from social capital than high SES peers (Schneider and Stevenson 1999; Stanton-Salazar 2001).

Consider, for example, information about written and unwritten rules of schooling—what is needed to get ahead, what potential pitfalls to look for, how to game the system. Gathered through network ties, such information provides a competitive edge in a complex system and, compared to other forms of social capital, is more amenable to policy intervention. After all, schools can help set up channels of academic information to students and parents (Gandara 2002; Morgan 2005). This action would have the greatest impact on socioeconomic disparities if low SES students benefit more from the same amount of information than high SES students. In one such scenario, a teacher who understands how important math is to students’ futures may be all that keeps a low SES student from dropping out of math, whereas a high SES student has other protections against dropping out. In this case, socioeconomic disparities would be narrower in information-rich contexts than in others (protection). Yet, if low SES students benefit less from the same amount of information than high SES students, efforts to build information channels would have a weaker impact on disparities. In one such scenario, a teacher’s advice may only make a difference when it is coupled with similar advice from a well-informed parent, so that disparities may be wider in information-rich contexts than in others (cumulative advantage).

In the case of protection, something less than equality in access to social capital may narrow socioeconomic disparities in math. In the case of cumulative advantage, even complete equality may be insufficient. The third aim of this study, then, is to consider whether instrumental resources (e.g., adults with whom adolescents can discuss coursework decisions) condition socioeconomic disparities in the segment of the population with the largest disparities.

Considering Gender

Historically, American girls have persisted less far and posted lower achievement in math than boys (Hyde and Kling 2001). The explanations for this pattern take both demand- and supply-side perspectives, with some highlighting overt or subtle discrimination and others highlighting motivations and self-concepts that undermine performance (Correll 2001; Sandler and Hall 1986). Yet, this gender gap is narrowing considerably (Bae et al. 2000; Riegle-Crumb 2006). Still, even when girls and boys reach similar endpoints, they often get there for different reasons. Indeed, social relations tend to do more to predict the math trajectories of girls than boys. Girls appear to need more support from others to fight the added barriers they face in this curriculum (Catsambis 1994; Crosnoe et al. 2008). Social capital, therefore, is likely a bigger part of the equation for girls in math.

Given the central role of the link between social capital and academic decision-making in our conceptual framework, we pay close attention to gender when pursuing the aims of this study. If social capital has a heightened role among girls, then the variability of socioeconomic disparities in math across the adolescent population and the reactivity of such disparities to the flow of social capital should both be more pronounced for girls than boys.

Methods

Data and Sample

NELS is a nationally representative sample of American students in 1,052 randomly selected high schools (National Center for Education Statistics 1994). Selected students were interviewed in 1988 (base year), when they were all in 8^th grade, and then again in 1990, 1992, and 1994. A fourth follow-up, in 2000, was not analyzed here. These data collections also included interviews with parents, teachers, and school administrators at various stages as well as the collection of high school transcripts in the third follow-up. The analytical sample consisted of the 14,915 students in the 1994 transcript data file release. As explained shortly, missing data were estimated in multivariate analyses to avoid the loss of any cases in this sample. Moreover, sampling weights were employed to correct biases from differential attrition across waves.

NELS students left high school before the major curricular reforms of the mid-1990s and the implementation of No Child Left Behind in 2002 (Gamoran 2007; Gamoran and Hannigan 2000). Focusing on this cohort, therefore, does limit the generalizability of findings to the present day. Yet, NELS increases generalizability to the national context relative to many recent data collections. Moreover, compared to relevant community-based data sources with more recent cohorts, the socioeconomic diversity in NELS also comes with greater heterogeneity (by location, family structure, race, immigrant status) within socioeconomic strata. At the same time, compared to relevant national data sources with more recent cohorts (Educational Longitudinal Study, National Longitudinal Study of Adolescent Health), NELS includes data on middle school academic experiences, which are crucial for dealing with the bias associated with selection into high school trajectories by pre-high school statuses. For these reasons, NELS is still widely used in educational research (Attewell and Domina 2008).

Measures

Math status

Pre-high school status was measured two ways. First, 8^th graders completed standardized tests in math, including items on graphs, equations, and computation, in 1988. To reduce floor and ceiling effects, NCES created Item Response Theory scores that took into account performance on prior tests and the difficulty of each test item. These scores ranged from 15 to 66, with a mean of 36 (see Table 1 for descriptive statistics for most study variables). Second, 8^th graders also reported whether they had taken Algebra I, which is typically part of high school curricula (31%).

Table 1.

Descriptive Statistics for Study Variables

	%	Mean	SD
Academic Factors
Math test score in 8th grade		35.76	11.99
Algebra I enrollment in 8th grade	31.40
Initial math course-taking level		3.76	1.20
Math credits by end of high school		2.88	1.08
Information Factors
Parent discussion of coursework (8th)		2.38	.50
Parent discussion of coursework (10th)		2.01	.53
Number of consultants for coursework (8th)		2.99	1.50
Number of consultants for coursework (10th)		1.04	1.06
Teacher encouragement of math coursework (10th)		1.93	.79
Sociodemographic Factors
Gender (female)	51.34
Age (years)		13.85	.60
Non-Latino/a White	62.02
African-American	9.82
Latino/a	12.46
Asian-American	6.45
Other race/ethnicity	1.17
Two-parent family	62.22
Single parent family	10.90
Stepfamily	15.94
Other family structure	2.51
Family SES		−.13	.79
Middle School Measuresa
Public school	77.20
Catholic school	8.64
Non-Catholic private school	6.84
Suburban school	39.75
Urban school	23.92
Rural school	29.00
Northeast region school	17.20
North central region school	24.36
South region school	32.38
West region school	18.73
Proportion college-educated parents in school (8th)
High School Factorsb
Policy of ability grouping for math	52.05
Degree of movement among tracks		3.11	.62
Number of math classes offered		8.08	5.20
Number of math teachers on staff		1.17	.92
School size		4.77	2.42
Counselor influence on course placement		2.41	.72
Teacher influence on course placement		2.12	.86
Parent influence on course placement		2.28	.86
Test score influence on course placement		1.89	.94
Public school	84.24
Catholic school	5.95
Non-Catholic private school	5.68
Suburban school	37.78
Urban school	28.26
Rural school	30.08
Northeast region school	17.67
North central region school	24.97
South region school	34.32
West region school	19.57
Proportion college-educated parents in school (10th)		.24	.24

n = 14,915

^aMiddle school factors came from 8^th grade data collection.

^bHigh school factors came from 10^th grade data collection.

The measurement of initial math status in high school was based on course completion by 10^th grade, following conventions in NELS and other transcript studies for measuring course enrollment patterns (Riegle-Crumb 2006; Stevenson et al. 1994). These conventions arrange students’ course codes in each grade into sequences based on normative patterns in the student population. The math sequence had nine points: 0 = none, 1 = Remedial Math, 2 = General Math, 3 = Pre-Algebra, 4 = Algebra I, 5 = Geometry, 6 = Algebra II, 7 = Advanced Math (Pre-Calculus, Trigonometry), 8 = Calculus.. On average, sample students completed Pre-Algebra by the start of 10^th grade.

The measurement of final math progress in high school was based on course credits earned by the end of high school for all graduating seniors. Students’ high school transcripts provided the number of credits they had earned in math in Carnegie units. One unit is equivalent to one period per day, five days a week, for an entire school year. The average student took between two and three classes.

Family SES

NELS contains an SES composite based on standardized, averaged parent reports of the educational attainment of father/male guardian, occupational prestige of father/male guardian, educational attainment of mother/female guardian, occupational prestige of mother/female guardian, and family income. Because this measure was an average of z-scores, its values have no intuitive meaning except that larger, positive numbers represent higher statuses. For example, parents who fell one standard deviation below the mean or lower on this composite had, on average, less than a high school diploma and an annual 1987 income below $13,000. Alternatively, parents who fell one standard deviation above the mean or higher on this composite had, on average, a college diploma and an income exceeding $85,000.

Information factors

Three sets of social relations with potential to provide academically relevant information and support were examined in this study (Gandara 2002; Plank and Jordan 2001). First, students estimated in 8^th and 10^th grade the degree to which they discussed their coursework with their parents (1 = never, 2 = sometimes, 3 = often). Second, students reported the people (parents, teachers, counselors, friends) who advised them on what high school programs to enter in 8^th grade and then whether the same people had any influence on their current course program in 10^th grade. In each grade, students’ responses were summed to create a count of the number of coursework “consultants”. Third, in 10^th grade (but not 8^th), students reported whether their math teachers emphasized the importance of being prepared to take more math in the future. This scale tapped teacher encouragement of math persistence.

School factors

To account for the field of constraints placed on “choice” of coursework by school structure and curricular organization (Adelman 2006; Attewell and Thurston 2008; Morgan 2005), we measured several aspects of schools, including region (dummy variables for Northeast, North Central, South, West), urbanicity (rural, urban, suburban), and sector (public, Catholic, non-Catholic private). School administrator reports tapped six aspects of curricular organization. First, reports of whether schools grouped students in math classes by achievement led to a binary marker of ability grouping. Second, the frequency (1 = never to 4 = frequently) with which students changed curricula measured degree of movement among tracks. Third, the sum of the availability of 16 math courses measured course offerings. Fourth, the number of math teachers in school (0 = 0–5 to 3 = 15+) was estimated by administrators. Fifth, total enrollment (1 = 1–199, 2 = 200–399, 3 = 400–599, 4 = 600–799, 5 = 800–999, 6 = 1000–1199, 7 = 1200+) was measured because course offerings and teacher staffing are, in part, a function of school size. Sixth, administrator reports of how much influence various actors/data had in selecting course assignments (1 = none to 4 = a lot) in the school were measured separately, including counselors, teachers, parents, and test scores. Finally, given evidence of how socioeconomic disparities in coursework can vary across schools with different socioeconomic compositions (Crosnoe 2009), the proportion of students in each school with college-educated parents was calculated for 8^th and 10^th grade.

Sociodemographic factors

Analyses took into account gender (1 = female, 0 = male), race/ethnicity (dummy variables for White, African-American, Latino/a, Asian-American, Other), and family structure (two-parent, stepfamily, single parent, other type).

Plan of Analyses

First, initial high school math level was regressed on the sociodemographic controls, school factors, family SES, and 8^th grade math test score and course enrollment. Next, credits in math by the end of high school were regressed on the sociodemographic controls, school factors, family SES, 8^th grade math test score and enrollment, and initial high school math level.

Second, an interaction between family SES and 8^th grade test score was added to the initial level model to determine whether the association between SES and initial level varied by students’ prior test performance. An interaction between SES and initial math level was then added to the final credits model to determine whether the link between SES and credit accumulation varied by students’ initial level. Three-way interactions (SES x math x gender) then allowed the assessment of whether variability in observed SES effects differed by gender.

Third, the model for each outcome was re-estimated for the subsample of students (defined by middle school test scores or initial high school placement) with the largest socioeconomic differences in this outcome. These models included the information factors as predictors as well as two-way interaction terms (information factor x family SES) and then three-way interaction terms (information factor x family SES x gender). Significant interactions indicated that socioeconomic differences in the outcome in the focal group varied as a function of information and support available to girls and/or boys.

Our analytic plan used linear regression in Mplus (Muthen and Muthen 2001). This package allowed for the correction of the NELS design effects (e.g., the clustering of students within schools, the oversampling of some groups) to produce more accurate standard errors. Moreover, it employed full information maximum likelihood to estimate missing data, thereby avoiding the bias associated with listwise deletion.

Results

Basic Socioeconomic Disparities in Math

Table 2 presents descriptive statistics for math, by family SES (low, medium, and high SES categories defined in terms of standard deviation units). As expected, students from high SES families tended to be more advanced in math than those from medium SES families, who tended to be more advanced than those from low SES families. To give a sense of the real world meaning of these statistics, the average student from a high SES family outscored the average student from a low SES family on standardized math tests prior to high school by about 20 points respectively and then, at the start of high school, completed Algebra I (vs. General Math). By the end of high school, the average high SES student had accumulated at least one more math course credit than his/her low SES counterpart. A similar socioeconomic gradient in social information factors (e.g., parent discussion of coursework, number of coursework consultants) was also observed.

Table 2.

Descriptive Statistics for Key Study Variables, by Family Socioeconomic Status

	Mean (SD) for Family SES Groups a
	Low	Medium	High
Academic Factors
Math credits by end of high school	2.36c (1.67)	2.89b (1.03)	3.52a (.71)
Initial math course-taking level	2.87c (2.10)	3.91b (1.94)	4.83a (1.75)
Math test score in 8th grade	28.33c (.74)	35.15b (11.17)	45.48a (11.50)
Algebra I enrollment in 8th grade	.20c (.40)	.31b (.46)	.58a (.49)
Information Factors
Parent discussion of coursework (8th)	2.17c (.54)	2.39b (.49)	2.58a (.43)
Parent discussion of coursework (10th)	1.86c (.52)	2.01b (.52)	2.21a (.48)
Number of consultants for coursework (8th)	2.89c (1.38)	3.23b (1.28)	3.54a (1.18)
Number of consultants for coursework (10th)	.59c (.90)	.90b (1.07)	1.11a (1.16)
Teacher encouragement of math coursework (10th)	1.87b (.83)	1.91b (.78)	2.03a (.73)
n	2,406	9,052	2,362

Note.—Means on the same row with different subscripts differed significantly (p < .001) from each other, as determined by one-way anova. Low SES group included youth with scores on the family SES composite at least one standard deviation lower than the sample mean. Medium SES group included youth with scores between one standard deviation below and one standard deviation above the sample mean. High SES group included youth with scores at least one standard deviation above the sample mean.

On average, therefore, high SES students were ahead of their peers at every step of the math career and also seemed to have greater access to social supports for academic decision-making. The analyses presented in the following sections examined this pattern in a longitudinal, multivariate framework.

Family Status, Prior Academic Status, and Math

Table 3 presents the results of regression models predicting the math outcomes at each time point, controlling for math status at a prior point as well as a host of confounding sociodemographic and school factors. As seen in Initial Level Model 1, higher SES students took higher-level math courses at the start of high school than their lower SES peers with the same middle school test scores and exposure to high school math. According to Final Credits Model 1, higher SES students also accumulated more math credits while in high school than their lower SES peers, even those peers who had the same middle school and initial high school math status. The standardized coefficients indicate that family SES did more to differentiate students on initial math coursework and final math credits than any other aspect of their lives or schools considered except for middle school math status, age, and the number of math classes offered in the high school.

Table 3.

Results from Linear Models Predicting Two Stages of the Math Career

	Unstandardized B (Standardized β)
	Initial Math Level		Final Math Credits
	1	2	1	2
Sociodemographic Factors
Gender (female)	.06	.07	.00	.00
	(.02)	(.02)	(.00)	(.00)
Age (years)	−.41***	−.37***	−.22***	−.21***
	(−.13)	(−.12)	(−.12)	(−.11)
African-American a	−.23*	−.27**	−.21***	−.22***
	(−.04)	(−.05)	(−.07)	(−.07)
Latino/a	.27**	.31**	.19***	.19***
	(.04)	(.05)	(.05)	(.05)
Asian-American	.24**	.24**	.20***	.21***
	(.02)	(.02)	(.03)	(.03)
Other race/ethnicity	−.09	−.03	.10	.11
	(−.01)	(.00)	(.01)	(.01)
Single parent family a	−.26***	−.28***	−.22***	−.22***
	(−.05)	(−.05)	(−.07)	(−.07)
Stepfamily	−.20***	−.20***	−.10*	−.10*
	(−.04)	(−.04)	(−.03)	(−.03)
Other family structure	−.59*	−.60*	−.29*	−.29*
	(−.05)	(−.06)	(−.05)	(−.05)
Family SES	.21***	.78***	.17***	.38***
	(.09)	(.31)	(.12)	(.27)
High School Factorsa
Policy of ability grouping for math	.31***	.30***	.05+	.05
	(.08)	(.08)	(.02)	(.02)
Degree of movement among tracks	−.01	.00	.03	.03
	(.00)	(.00)	(.02)	(.02)
Number of math classes offered	.03***	.03***	.01***	.01***
	(.14)	(.13)	(.07)	(.06)
Number of math teachers on staff	.00	.01	.02	.02
	(.00)	(.01)	(.03)	(.03)
School size	−.03	−.03	−.01	−.01
	(−.03)	(−.03)	(−.03)	(−.03)
Counselor influence on course placement	.06	.06	.05*	.05*
	(.02)	(.02)	(.04)	(.04)
Teacher influence on course placement	−.06	−.07	−.02	−.02
	(−.03)	(−.03)	(−.01)	(−.01)
Parent influence on course placement	.04	.05	.01	.01
	(.02)	(.02)	(.01)	(.01)
Test score influence on course placement	.02	.02	.00	.00
	(.01)	(.01)	(.00)	(.00)
Prop. college-educated parents in school	.18+	.27*	.11+	.14+
	(.02)	(.03)	(.03)	(.03)
Middle/High School Factorsa
Catholic school ab	.35***	.33***	.40***	.40***
	(.05)	(.04)	(.08)	(.08)
Non-Catholic private school	.36***	.38***	.09	.12
	(.04)	(.04)	(.02)	(.02)
Urban school ab	.01	−.01	−.06	−.07
	(.00)	(.00)	(−.03)	(−.03)
Rural school	.21**	.21**	.05	.06
	(.05)	(.05)	(.02)	(.03)
North central region school ab	.27**	.25**	−.06	−.06
	(.06)	(.06)	(−.02)	(−.03)
South region school	.32***	.31***	.12*	.12*
	(.08)	(.08)	(.05)	(.05)
West region school	.15	.14	−.05	−.06
	(.03)	(.03)	(−.02)	(−.02)
Academic Factors
Algebra I enrollment in 8th grade	.54***	.56***	.01	.02
	(.13)	(.13)	(.00)	(.01)
Math test score in 8th grade	.06***	.06***	.02***	.02***
	(.34)	(.35)	(.21)	(.22)
Initial high school math level			.17***	.15***
			(.30)	(.27)
Family x Academic Interactions
Family SES x 8th grade test score		−.02***
		(−.24)
Family SES x initial high school math level				−.06***
				(−.16)
Intercept	6.46***	5.96***	4.19***	4.04***
	(3.30)	(3.05)	(3.75)	(3.61)
R2	.35	.36	.39	.40

⁺p < .10;

^*p < .05;

^**p < .01;

^***p < .001

n = 14,915 (all models)

^aFor individual-level sets of dummy variables, the omitted reference categories were non-Latino/a White (race/ethnicity) and two-parent (family structure). For school-level sets of dummy variables, the omitted reference categories were public (sector), suburban (urbanicity), and Northeast (region).

^bFor school sector, urbanicity, and region, middle school measures used in initial math models and high school measures used in final credit models.

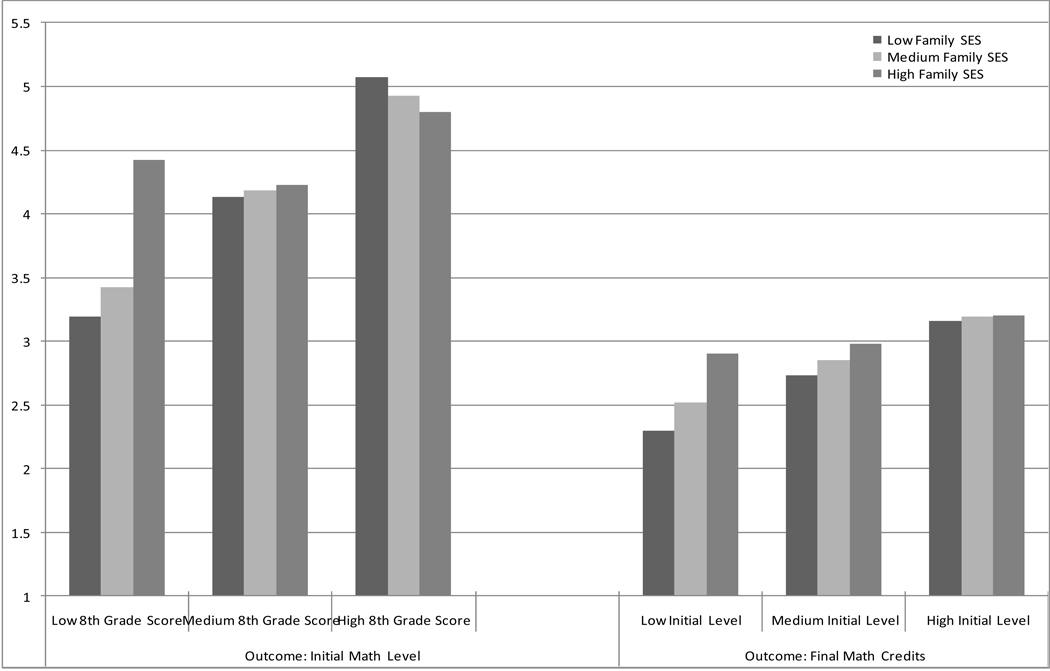
Model 2 for each outcome included a family SES x prior math status interaction term as a way of gauging whether socioeconomic disparities in math coursework at each point varied as a function of math status prior to that point. These interactions were significant and negative in both models. Thus, socioeconomic disparities varied across the student population, within and across schools. To determine what form this variation took, we calculated predicted scores for both math outcomes based on different combinations of family SES and prior math status. In these calculations, family SES and prior math status (either 8^th grade test score or initial high school level) were broken into low (one standard deviation below the mean or lower), medium (between one standard deviation below and above the mean), and high (one standard deviation above the mean or higher) categories, and all other variables in the models were held to their sample means. Figure 1 depicts these predicted values.

Figure 1.

Predicted Math Coursework at Two Stages of the Math Career, by Family SES and Math Status at Prior Stage

The first panel in Figure 1 presents predicted values for initial math level. Among students scoring low on the 8^th grade math test, the high SES students clearly had higher-level math enrollment at the start of high school than their medium or low SES peers. Indeed, the difference between the high and low status groups was a full course level. Among students with average scores on the 8^th grade math test, the differences among the high, medium, and low SES students were much less pronounced, although they still slightly favored the high SES students. Among high scoring students on the 8^th grade test, socioeconomic differences in average initial math level were narrow but slightly favored the low SES students. A similar pattern held when final math credit accumulation was the outcome and initial high school course level the marker of prior status (see second panel in Figure 1): large socioeconomic differences among students with the lowest initial math placement, smaller differences among students with an average initial placement, and even smaller differences among students with the highest initial placement.

A third model was estimated in which a three-way interaction was added to each Model 2: family SES x test score x gender for initial level, family SES x initial level x gender for final credits (along with all possible two-way interactions among the three variables for each model). Selected results from these additional models are presented in Table 4. The three-way interaction was not statistically significant in the Initial Level Model, but it was in the Final Credits Model. The pattern producing this three-way interaction was explored by calculating predicted final math credit values according to the same protocol described above. Basically, girls and boys demonstrated the same pattern (socioeconomic differences in credits larger among students with the lowest initial level), but this pattern was stronger among boys than girls. For example, the difference between low SES and high SES boys was .50 math credits among those who scored one standard deviation below the sample mean on initial high school math level (roughly General Math) but .02 credits among boys who scored one standard deviation above the sample mean on initial high school math level (roughly Geometry). For girls, the corresponding SES differences were .30 and .12.

Table 4.

Selected Results from Models Including Gender Interactions

	Unstandardized B (Standardized β)
	Initial Math Level	Final Math Credits
Gender (female)	.23	−.14+
	(.06)	(−.06)
Family SES	.73***	.49***
	(.29)	(.34)
Math test score in 8th grade	.06***	---
	(.36)
Initial high school math level	---	.14***
		(.25)
Female x SES	.11	−.25*
	(.03)	(.12)
Female x prior math	−.01	.03+
	(−.04)	(.06)
SES x prior math	−.02***	−.08***
	(−.22)	(−.22)
Female x SES x prior math	.00	.05*
	(.00)	(.10)
Intercept	5.89***	4.11***
	(3.00)	(3.68)
R2	.36	.40

⁺p < .10;

^*p < .05;

^**p < .01;

^***p < .001

n = 14,915 (all models)

Note.—All models also controlled for 8^th grade Algebra I enrollment, age, race/ethnicity, family structure as well as several high school variables (policy on ability grouping, number of math classes offered, number of math teachers on staff, school size, counselor influence on course placement, teacher influence on course placement, parent influence on course placement, test score influence on course placement, proportion of students with college-educated parents). The initial level model also controlled for middle school sector, urbanicity, region, and region. The final credit model controlled for high school sector, urbanicity, and region as well as the 8^th grade math test score.

In sum, family SES differentiated students on their starting and ending levels of math in high school, even among students with the same prior history in math attending the same kinds of schools. The socioeconomic difference in initial math level in high school, however, was largest in the segment of the student population scoring poorly on middle school math tests, and the socioeconomic difference in final math credits was largest in the segment starting high school in low-level math. As hypothesized, therefore, prior math status could chip away some of the family-related disadvantages of low SES students at the high end of the math hierarchy, while family-related advantages could chip away at some of the disadvantages related to prior math status of high SES students at the low end.

Social Capital and Math in Specific Groups

The final objective of this study was to assess the extent to which sources of information, a key aspect of social capital, moderated associations between family SES and the math outcomes in the segments of the student population in which these associations were strongest. Table 5 presents selected results from these analyses.

Table 5.

Selected Results from Linear Models Predicting Two Stages of the Math Career in Subsample with Lower than Average Status in Math at Prior Stage

	B (β) for Initial Math Level			B (β) for Final Math Credits
	1	2	3	1	2	3
Family SES	.27**	.23*	.73*	.15*	.10	−.19
	(.10)	(.08)	(.26)	(.09)	(.06)	(−.12)
Information Factorsa
Parent discussion of coursework		.31***	.29+		.25***	.29***
		(.08)	(.08)		(.12)	(.13)
Number coursework consultants		.01	−.09		.30***	.30***
		(.00)	(−.06)		(.20)	(.20)
Teacher encouragement of more coursework					.08+	.09+
					(.05)	(.06)
Family x Information Interactions
SES x parent discussion			−.03			.12
			(−.02)			(.14)
SES x consultants			−.15**			−.02
			(−.18)			(−.02)
SES x teacher encouragement						.03
						(.04)
Intercept	1.65	1.03	1.40	5.18***	3.71***	3.64***
	(.84)	(.53)	(.71)	(3.99)	(2.88)	(2.83)
R2	.20	.21	.22	.48	.52	.52

⁺p < .10;

^*p < .05;

^**p < .01;

^***p < .001

n = 2,459 (initial level models), 2,573 (final credit models)

Note.—All models controlled for 8^th grade math test score, 8^th grade Algebra I enrollment, gender, age, race/ethnicity, and family structure as well as several high school variables (policy on ability grouping, number of math classes offered, number of math teachers on staff, school size, counselor influence on course placement, teacher influence on course placement, parent influence on course placement, test score influence on course placement, proportion of students with college-educated parents). The initial level models also controlled for middle school sector, urbanicity, region, and region. The final credit models controlled for high school sector, urbanicity, and region as well as initial high school math course-level.

^aInformation factors measured in 8^th grade for initial level models and in 10^th grade for final credit models.

The Initial Math Level models were estimated with the subsample of students who scored one standard deviation or lower on the 8^th grade math test. Model 1 established the basic socioeconomic difference in this subsample while controlling for the sociodemographic factors, school factors, and middle school math test score and course enrollment. Note the larger B and β coefficients relative to the coefficients from the corresponding model in Table 3, which would be expected given that the take-home message of Table 3 was that SES mattered more among the subset of students defined by low prior math status (i.e., the sole group of students included in the analyses for Table 5).

Model 2 added the information factors as predictors. Low test-scoring students tended to take higher-level math at the start of high school when they discussed their coursework with parents in middle school. Their initial math course levels, however, did not change as a function of how many coursework consultants they had in middle school. Overall, the inclusion of the information factors did little to attenuate the socioeconomic differences in initial math level in this subsample of students with low prior math status (compare SES coefficient between Model 1 and Model 2). Thus, these socioeconomic differences in math were not mediated, at least not substantially, by corresponding socioeconomic differences in information factors (at least those examined here).

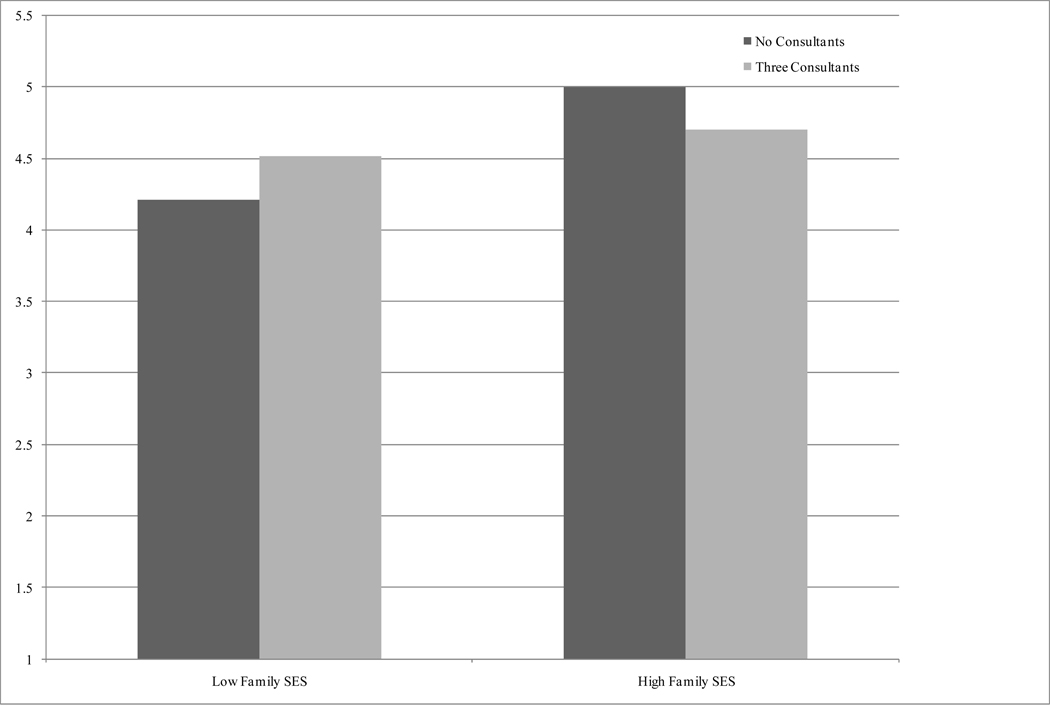
Finally, Model 3 added the full set of interactions between family SES and the information factors. One (family SES x coursework consultants) was significant. To interpret this interaction, we again calculated predicted initial math level values for students with different combinations of low, medium, and high family SES and low, medium, and high numbers of coursework consultants (see Figure 2). Among low SES students, those with a large number of consultants started off high school about one-third of a math course level ahead of those without any consultants. Among high SES students, those without consultants started off just slightly ahead of those with numerous consultants. This latter pattern could have reflected a selection effect, with coursework consultants coming to high SES in the most trouble.

Figure 2.

Predicted Initial Math Coursework Level among Students with Low 8^th Grade Math Test Scores, by Family SES and Number of Coursework Consultants

Also in Table 4, the Final Math Credits models were estimated within the subsample of students who had initial high school math levels one standard deviation below the sample mean or lower. Two information factors predicted the outcome at conventional levels of significance. Students with low initial starting levels in math tended to accumulate more math credits over time when they discussed coursework with parents and had coursework consultants. Examining the standardized coefficients reveals that having coursework consultants in high school had the strongest association with the final number of math credits accumulated. The inclusion of these information factors in the model (Model 2), however, did not substantially attenuate the previously observed SES effect on this outcome. Moreover, no information factor interacted with family SES.

Again, given our interest in gender, we re-estimated Model 3 for each outcome with all possible two- and three-way interactions among family SES, the information factors, and gender. Neither of the three-way interactions was significant.

In sum, the information factors examined did not strongly mediate socioeconomic disparities in math coursework in the groups of students in which these disparities were largest. Some evidence of moderation (e.g., an information factor appearing to condition a link between SES and an outcome in these groups) was detected, but only limited evidence. Among students who scored poorly on 8^th grade math tests, socioeconomic disparities in initial math course level in high school seemed to be weaker when students had access to coursework consultants. These patterns did not differ by gender.

Additional Tests and Considerations

The results generated from our modeling strategy told a more or less consistent story. Yet, two modeling issues need to be addressed to instill more confidence in these results.

First, we used a family SES composite rather than its constituent items because of the theoretical value of taking a holistic profile of family circumstances—exploiting the connections among dimensions of SES in one family rather than focusing on any one while controlling for others. For example, a college degree means something different when it is coupled with high versus low earnings (Crosnoe and Huston 2007; Lareau 2004; McLanahan 2004). Inspecting results for each constituent item in the composite revealed that parent education had consistently bigger coefficients (and interactions) than income or parental occupation. It appeared to drive the observed socioeconomic effects. On a related note, breaking down the continuous SES scale into dummy variables and coupling the continuous scale with a squared term also indicated that the observed SES effects were sufficiently linear.

Second, like all analyses of observational data, making causal inference based on the models presented here was difficult. For example, observed associations between the information factors and math outcomes could have resulted from the effects of access to information on student progress, the selection of certain kinds of students into different kinds of contexts, or spurious factors associated with exposure to information and student progress. Estimating models within subgroups based on prior progress and controlling for a large number of family and school characteristics addressed some of these endogeneity/selection problems, but certainly not definitively so. As an additional check, we drew on propensity scores. We began by estimating regressions with each information factor as the outcome and a host of family and individual characteristics as predictors. Specifically, we included all independent variables from the corresponding analyses presented in Table 3, additional variables tapping adolescent functioning in and out of school (locus of control, self-concept, extracurricular participation, athletic participation, teacher attachment, overall grade point average), a host of family factors in addition to SES measured at the appropriate time points (maternal/paternal work status, home language use, parent age, immigrant status), and interactions between family SES and all other variables. Next, the predicted values for each outcome generated from these models were entered into the primary models for each math outcome. This statistical check produced no meaningful alteration in the main results of this study presented above.

Conclusion and Discussion

In a climate of great educational and economic change, math coursework is important for getting into college, staying in college to get a degree, and entry into fields of study within college that are channels into high-demand sectors of the labor market (Adelman 2006; Goldin and Katz 2008). The link between family SES and this specific educational asset, therefore, helps to translate the socioeconomic stratification of families into long-term socioeconomic disparities in young people’s lives. Conceptual models of academic decision-making suggest that this intergenerational transmission through math is rooted in the ways that young people and their parents navigate a complex field of institutional constraints on and options for high school coursework and how they draw on their own resources and on others in the process (Erikson and Goldthorpe 2002; Morgan 2005). Following this argument, this study attempted to identify when and for whom socioeconomic disparities in math were most pronounced and to gauge the reactivity of these disparities to potential infusions of social capital.

The findings of this study revealed that socioeconomic disparities in math coursework accumulated across the high school career and not just because of differences in prior math experiences and not just because of differences in school settings (e.g., in the extent of math course offerings) likely conflated with family SES. Even when the low and high SES students in NELS had the same observed skill set in middle school, the latter started off high school at a higher curricular level than the former. Moreover, even when low and high SES students had the same starting point in high school and the same observed skill level, the latter persisted through the math curriculum at higher rates. In other words, low SES students started high school behind and then lost ground. Another way of looking at this phenomenon is that slippage (or decoupling) between skill/status and placement in math and then hemorrhaging (for lack of a better word) from math increased as family SES decreased.

In part, these socioeconomic disparities in high school represented an end result of a highly cumulative process of socioeconomic stratification of opportunities to learn and achieve since birth (Entwisle et al. 2005; Heckman 2006). Such advantages built up to allow high SES youth to have higher demonstrable levels of skill by the time they approached high school (i.e., primary SES effect). Yet, evidence that high school appeared to be a period of continued socioeconomic stratification in math, even among youth of similar demonstrable skill levels, indicates the socioeconomic differences in how youth, parents, and others capitalize on options, choices, and opportunities in math to continue to accrue a competitive edge (i.e., secondary SES effects; Erikson and Goldthorpe 2002). Thus, targeting secondary schools is likely to remain an important goal of intervention (Eccles et al. 1993; Rothstein 2004).

Although socioeconomic disparities in the math curriculum appeared to be strong in general, they varied considerably in magnitude across the population. Recall that we expected socioeconomic disparities at any one point of high school to weaken as academic status at the prior point (measured by test scores in middle school and then initial coursework level in high school) increased. The theoretical rationale underlying this hypothesis was that low SES students who were able to neutralize primary SES effects to occupy the same math status as high SES students at any one point likely had high levels of cognitive and social skills that would elicit instrumental support and assistance from others (e.g., teachers, mentors) that could also reduce their disadvantages related to secondary SES effects. Thus, secondary effects would do more to differentiate students of different socioeconomic circumstances at the low end of the math hierarchy. We found consistent evidence for this hypothesis. Low SES students already advanced or at least on track in math at one point managed to keep up with or exceed their high SES peers at the next point. On the other hand, low SES students who had already struggled in math fell behind their high SES peers. As a result, socioeconomic disparities in math were strongest in the segment of the student population characterized by low test scores and low initial coursework levels. These results highlight a key advantage that high SES families enjoy in the American educational system. For students from these families, prior problems are less of an impediment to their future success, so that they can continue to accrue the highly valued academic credentials that can help to get them into college even if their records suggest that they should not (see Lareau 2004 for similar work on younger children).

Identifying where in the student population socioeconomic disparities are biggest is an important step in informing policy because they point to where intervention should go first. The next step is to identify possible means for reducing disparities where they are at a maximum. To think about such means, we focused on a specific aspect of social capital: information and instrumental support for academic decision-making. The few information factors we examined here did not explain (or mediate) socioeconomic differences in math coursework. Recall, however, that our focus was on moderation; in other words, socioeconomic differences in math coursework varying as a function of information factors. Some information factors were associated with higher math coursework in the targeted population groups but typically not in ways that varied by family SES. If the observed associations were indeed causal, then opening up such information channels would result in improvement in the overall level of math coursework but no reductions in the SES gap. Everyone would go up in absolute position, but relative positions would stay the same. Only the association between the number of coursework consultants and initial math level varied by family SES in a way that suggested protection. Again, if these associations were causal, then increasing the number of familial and extra-familial consultants that students had for making coursework decisions would increase the overall math coursework level among students already struggling in math and reduce socioeconomic disparities in this group at the same time. Building mentoring programs and getting out information to low SES parents and students about how important math coursework is for the future would, therefore, seem to be a potentially promising avenue for intervention (Gandara 2002; Plank and Jordan 2001).

Despite expectations to the contrary, the patterns described above did not differ substantially by gender. This lack of evidence of gender differences does not mean that girls and boys had the same experiences in math. What it means is that family SES, math coursework, prior math status, and social capital connected to each other in similar ways for girls and boys.

Of course, more must be done before strong conclusions can be drawn from this line of research. As one example, the connection between these socioeconomic patterns and related race/ethnic patterns must be addressed (Rothstein 2004). The models presented here controlled for race/ethnicity but did not examine it explicitly. Future research needs to determine whether race/ethnic inequality exhibits the same trends as socioeconomic inequality and/or one drives the other. At the same time, qualitative research could be a useful tool for parsing the actual content of information and instrumental support being traded socially in networks, which was only proxied by our social capital measures. Another consideration is that, although this study took many steps (e.g., longitudinal design, propensity scores) to reduce selection effects, it could only take causal inference so far. Indeed, it could not address the many unmeasured or even unknown student, family, and school factors that might be confounded with different aspects of social capital. This research, therefore, should be viewed as a preliminary study with the ultimate goal of informing future quasi-experimental and experimental designs that can do more to tackle both observed and unobserved confounds and provide better evidence of causality. Finally, we relied on NELS, after concluding that the many advantages it offered countered the age of its sample and the relevant changes in educational policy occurring after the sample youth left high school. Clearly, comparing and contrasting results from this study with similar studies drawing on more recent data would help to determine the historical robustness of our results.

These limitations and future needs notwithstanding, this study points to a foundation for socioeconomic disadvantage in America: high schools with large numbers of entering students who are struggling in math without adequate consultation about how to make sense of the options and opportunities in math available to them. This group of students, then, is likely to be the most effective target of policy interventions aimed at reducing SES disparities in math.