Consistent Changes in Intracranial Pressure Waveform Morphology Induced by Acute Hypercapnic Cerebral Vasodilatation

Abstract

Background

Intracranial pressure (ICP) remains a pivotal physiological signal for managing brain injury and subarachnoid hemorrhage (SAH) patients in neurocritical care units. Given the vascular origin of the ICP, changes in ICP waveform morphology could be used to infer cerebrovascular changes. Clinical validation of this association in the setting of brain trauma, and SAH is challenging due to the multi-factorial influences on, and uncertainty of, the state of the cerebral vasculature.

Methods

To gain a more controlled setting, in this articel, we study ICP signals recorded in four uninjured patients undergoing a CO2 inhalation challenge in which hypercapnia induced acute cerebral vasodilatation. We apply our morphological clustering and analysis of intracranial pressure (MOCAIP) algorithm to identify six landmarks on individual ICP pulses (based on the three established ICP sub-peaks; P1, P2, and P3) and extract 128 ICP morphological metrics. Then by comparing baseline, test, and post-test data, we assess the consistency and rate of change for each individual metric.

Results

Acute vasodilatation causes consistent changes in a total of 72 ICP pulse morphological metrics and the P2 sub-region responds to cerebral vascular changes in the most consistent way with the greatest change as compared to P1 and P3 sub-regions.

Conclusions

Since the dilation/constriction of the cerebral vasculature resulted in detectable consistent changes in ICP MOCIAP metrics, by an extended monitoring practice of ICP that includes characterizing ICP pulse morphology, one can potentially detect cerebrovascular changes, continuously, for patients under neurocritical care.

Introduction

Traumatic brain injuries (TBI) is a leading cause of death and disability around the globe especially among young people [1, 2]. Continuous measurement of intracranial pressure (ICP) is a well-established brain monitoring modality used in diagnosing and managing different neurological conditions including TBI and subarachnoid hemorrhage (SAH).

ICP depicts the ability of the craniospinal space to accommodate changes in intracranial volume assuming a non-linear and hyperbolic relationship between the pressure and volume [3]. It has oscillating components at two different frequencies (cardiac and respiratory) [3, 4] and, particularly, consists of three characteristic peaks referred to as P1 (percussion wave), P2 (tidal wave), and P3 (dicrotic wave) in its cardiac component [5, 6], which is also referred in this work as an ICP pulse. A particular form of an ICP pulse is formulated by transforming an incidental arterial pressure pulse under the influences from multiple intracranial compartments. ICP pulse wave morphology represents a complex sum of various components; the pulsations of major arteries and choroid plexus contribute to P1 component, whereas P2 may be dependent upon the intracranial compliance [7], and P3 component might be the result of venous pressure [8, 9]. As a result, the quantitative metrics of ICP pulse morphology may provide additional information regarding the intracranial pathophysiology [10–12] beyond what can be provided by the average value of this complex signal which is the only metric currently offered by the monitoring devices.

The modern signal processing and pattern recognition algorithms could provide the essential tools to extract the subtle patterns of ICP changes influenced by the large brain structural changes. Our recently developed and validated Morphological Clustering and Analysis of Intracranial Pressure (MOCAIP) algorithm [13] is a technical advancement toward a new paradigm of more comprehensive information extraction from ICP. But due to the complexity involved in accurately describing, in mathematical terms, how these ICP morphological metrics reflect changes in the cerebral vasculature, a data-driven engineering approach toward quantifying and assessing this relationship is needed [14–17].

To date, the influence of cerebral vascular changes, including vasoconstriction and vasodilatation, on the ICP has not been well studied in humans. In the setting of brain trauma and SAH, clinical validation of the association of ICP with the cerebrovascular state is challenging due to the multi-factorial influences on, and uncertainty of, the state of the cerebral vasculature [18, 19]. For example, studies have shown that in head injured patients, as the cerebral perfusion pressure (CPP) decreases, the amplitude of pulsatile blood inflow increases [20] and consequently, the exponential shape of the pressure–volume relationship would not be the only factor influencing the magnitude of ICP pulse wave [21, 22].

Considering the implications in TBI and SAH patients, obtaining information with regard to how ICP pulse morphology responds to vasodilatation and vasoconstriction in a more controlled setting, e.g. CO₂ challenge test, seems to be a good solution. Thus, the main objective of the present work is to test the hypothesis that acute hypercapnic cerebral vasodilatation induces consistent changes in ICP waveform morphology. This hypothesis is tested on a dataset of ICP signals of uninjured patients undergoing a CO₂ inhalation challenge in which hypercapnia induced acute cerebral vasodilatation. MOCAIP algorithm [13] were applied to identify six basic landmarks on the individual ICP pulses. In addition, 128 pulse morphological metrics were extracted and quantified based on the identified landmarks. Then the consistency and rate of changes of each individual metric during the hypercapnia were assessed. Finally a binary coding scheme of the contribution of the three individual ICP peaks to each metric was employed to determine the degree of change for each individual sub-peak region during the hypercapnic cerebral vasodilation.

Materials and Methods

An Overview of the MOCAIP Algorithm

MOCAIP is a pulse analysis framework developed for automatic extraction of morphological features of ICP pulses in real time [13]. This integrated and modular framework takes into the consideration the practical problem of handling noises and artifacts that ubiquitously exist in signals collected in an active neurocritical care environment. MOCAIP starts by segmenting the continuous ICP into a sequence of individual ICP pulses using an ICP pulse extraction technique [23] and an ECG QRS detection method [24]. A hierarchical clustering approach [25] is employed to find the main ICP pulse cluster in the sequence, the centroid of which is referred as the dominant pulse (a representative cleaner pulse extracted from a sequence of consecutive ICP pulses). To further avoid signal segments that are heavily contaminated by artifacts, MOCAIP proposes to use a reference library of validated ICP pulses whose construction is treated as a training process that involved data sets from multiple patients. A pulse is judged to be valid if it belongs to a cluster whose average pulse is highly correlated with any of the reference ICP pulses. To avoid false rejection of a valid cluster, due to the incompleteness of the reference library, the rejected pulses by the first step will be further assessed by characterizing the coherence of the pulse cluster to which it belongs. If a pulse fails both tests, it would be declared as a non-valid or noisy pulse.

Once a valid ICP pulse has been extracted from the previous step, MOCAIP detects a set of peak candidates (or curve inflections). Each of them is potentially one of the three peaks or not a peak. The extraction of these candidates relies on the segmentation of the ICP pulse into concave and convex regions which produces a pool of multiple peak candidates. To identify the three peaks from the set of candidates, MOCAIP relies on a Gaussian model to represent the prior knowledge about the position of each peak in the pulse. The assignment is chosen such that it maximizes the probability to observe the peaks given the prior distributions. These priors have been previously learned from the library of valid ICP pulses.

The modular structure of the MOCAIP algorithm facilitates further improvement of each individual processing block as demonstrated in our recent efforts. For example, to improve the performance of recognizing legitimate pulses, a singular value decomposition (SVD)-based signal/noise space separation algorithm has been proposed [26, 27], whereas the performance of the optimal peak designation has been enhanced by applying a nonlinear regression-based [28], an integrated peak recognition technique [29], and a non-parametric Bayesian tracking algorithm [30].

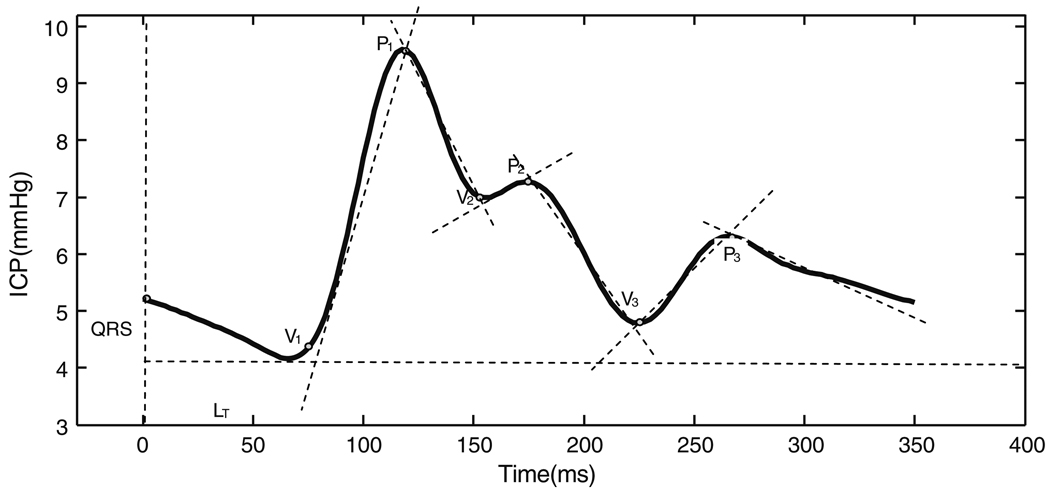
In summary, the MOCAIP algorithm provides a designation of the three sub-peaks and sub-nadirs of dominant ICP pulses. Following the identification of the six landmarks on an individual ICP pulse (Fig. 1), MOCAIP extracts 128 additional pulse morphological metrics based on the identified landmarks (Table 1).

Fig. 1.

Illustration of the six landmarks detected by the morphological clustering and analysis of ICP (MOCAIP) algorithm

Table 1.

128 metrics derived from an ICP pulse-based on the landmarks of Fig. 1

28 Basic metrics extracted from individual landmarks or over all characteristics
dV1, dV2, dV3, dP1, dP2, dP3	Amplitude of landmark relative to the minimum point prior to initial rise
LV1P1, LV1P2, LV1P3, LV2P2, LV3P3	Time delay among landmarks
Curvv1, Curvv2, Curvv3, Curvp1, Curvp2, Curvp3	Absolute curvature of each landmark
K1, K2, K3, RC1, RC2, RC3	K1, K2, K3 are slope of each rising edge and RC1, RC2, RC3 are time-constants of each descending edge
mICP, diasICP	Mean ICP and diastolic ICP
LT	Time delay of V1 to ECG QRS peak
mCurv	Mean absolute curvature of the pulse
WaveAmp	Maximum among dP1–dP3
100 extended metrics calculated as ratios among metrics within each group
dPp1p2,…	Ratio among landmark amplitudes
LV1P1/LT,…	Ratio among time delays
Curvv1/Curvv2,…	Ratio among curvatures
K1/RC1,…	Ratio among slopes/RCs

Calculation of Hourly Rate of Change for each ICP Metric Using a Weighted Least Square Method

The following procedure has been applied to obtain the hourly rate of change for each metric over a specific time segment; first a line has been robustly fitted to the extracted metric values over the segment of interest using weighted least square method and then the slope of this line has been employed to calculate the hourly rate of the metric change.

Furthermore, the sign of the obtained hourly rate of change (negative vs. positive) has been utilized to determine the trend of change (decreasing vs. increasing).

Patient Data

The hypercapnic dataset consists of the ICP and electrocardiograph (ECG) recordings of four female patients (21, 24, 32, and 54-years-old), who were admitted at UCLA medical center for the evaluation of their chronic headaches. They consented for allowing their data to be analyzed under the protocol as approved by the UCLA Internal Review Board.

During their hospitalization, the patients received continuous ICP monitoring for the clinical purpose using Codman intraparenchymal microsensors (Codman and Schurtleff, Raynaud, MA, USA) situated in the right frontal lobe. They also underwent a CO₂ challenge test by inhaling a 5% CO₂ mixture for less than 3 min. Simultaneous cardiovascular monitoring was also performed using the bedside GE monitors. ICP and lead II of ECG signals were recorded at a sampling rate of 400 Hz using a mobile cart at the bedside that was equipped with the PowerLab TM SP-16 data acquisition system (ADInstruments, Colorado Springs, CO, USA).

A data segment including the recorded signals during CO₂ test with few minutes preceding (baseline) and proceeding (post-test) the test was selected for each patient. The ECG-aided pulse detection algorithm [23] was used to delineate each ICP pulse in the segment. Each pulse was saved and visualized using the software developed in-house to screen obvious noise or artifacts, so that only clean beats were further processed. Then, given the good quality of the signal; the MOCAIP was able to work on individual pulses to extract 128 ICP pulse morphological metrics as explained in the previous section.

Data Analysis and Validation Protocol

The duration of the selected data segment for the headache patients was (5.1 ± 0.7 min). This data segment included (1.5 ± 0.5 min) of baseline, (2.5 ± 0.5 min) of CO₂ challenge test and (1.1 ± 0.2 min) of post-test data. Following the procedure described in “Calculation of Hourly Rate of Change for each ICP Metric Using a Weighted Least Square Method” section, the slope of the lines fitted to each of the extracted metrics over the rising edge of ICP signal during CO₂ challenge test and the falling edge of ICP signal during the post-test normal breathing, have been employed to define the hourly rate of change during the test and post-test normal breathing, respectively. For the purpose of comparing the hourly rate of change between different metrics, each metric rate was normalized by the average value of the corresponding metric over either the last 10 beats of the baseline (if the metric is extracted from the rising edge of the ICP signal) or the first 10 beats of the stabilized part of the post-test data (if the metric is extracted from the falling edge of the ICP signal).

By comparing the results of data processing from baseline, test, and post-test, we assessed (1) the consistency of changes of individual metrics; (2) differences in rate of metric changes; and (3) which of the sub-peak regions (P1, P2, and P3) has a more dramatic change during the cerebral vasodilation. For the later purpose, we calculated the region-weighted relative hourly rate of change averaged over the subset of consistent metrics as the following; a binary coding scheme was used to quantify the contribution of the three individual sub-peak regions to each individual metric. In this scheme, each metric is represented by a three bit binary word where the least significant bit indicates the possibility of the contribution of the first peak to that metric (1 vs. 0). For example, the binary word for the metric dP_P1P2 (which represents the peak ratio of the first and second peak, Table 1) is 011. Note that since the third peak does not contribute to this metric, the most significant bit in the corresponding word is set to 0.

Now suppose that W_128×3 is a matrix whose rows represent the binary word of each individual metric and R_128×1 is a column vector of the normalized hourly rate of change. The total hourly rate of change for the sub-peak regions P3, P2, and P1 could be obtained by C = W^T × R = [c₃ c₂ c₁]^T. Then the region-weighted relative hourly rate of change could be easily calculated by dividing each c_i, i = {1, 2, 3} by the total number of metrics whom sub-peak region P_i contributes to.

Results

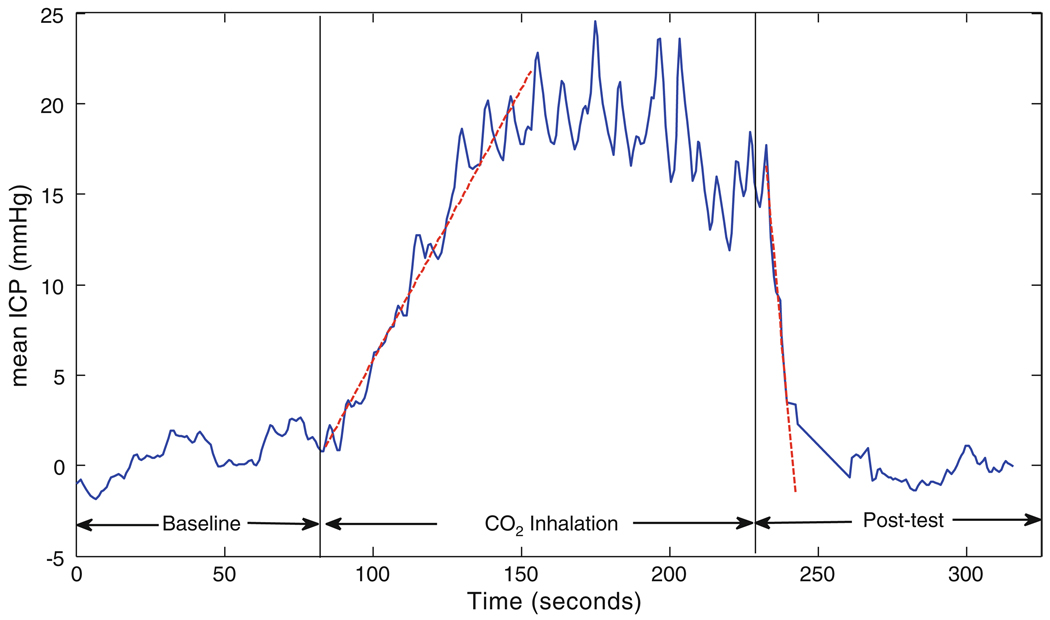
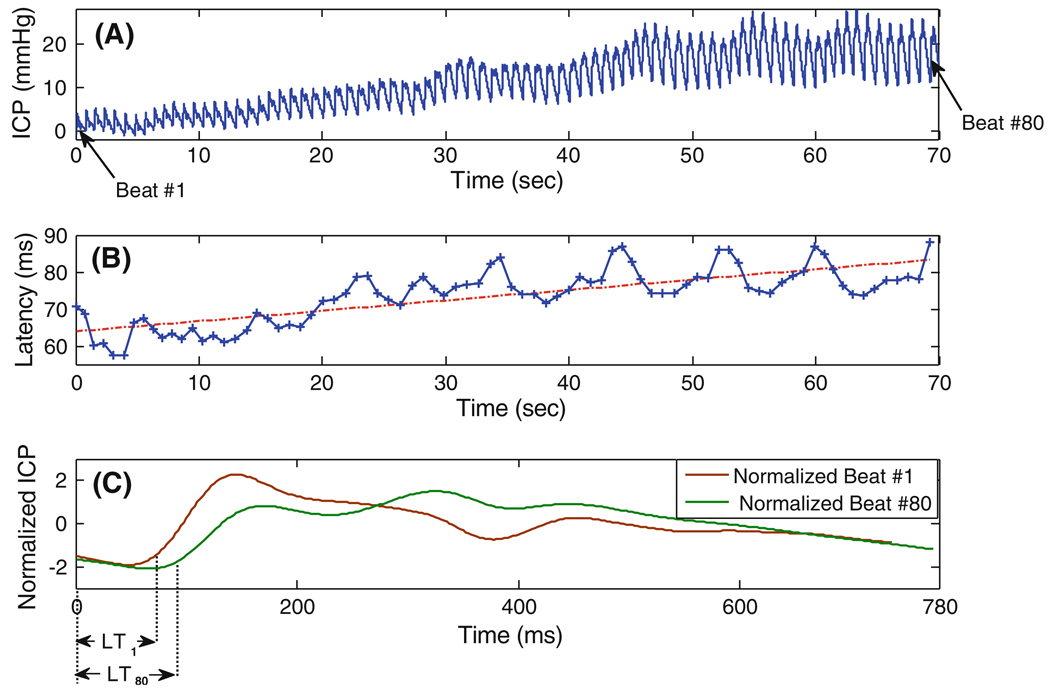
Figure 2 depicts the mean ICP value for one of the headache patients (Patient #4) during the baseline, CO₂ challenge test and post-test normal breathing. As the figure illustrates, when the patient inhales the 5% mixture of CO_2, the mean ICP increases over time, reaches to a saturation level and then stabilizes. When the patient starts to breathe the normal air again, the mean ICP falls down and goes back to the baseline level in less than 1 min. Figure 3a and b demonstrates the rising ICP signal and the extracted latency metric obtained during the CO₂ inhalation of the same subject. The slope of the fitted line (using the weighted least square method described in “Calculation of Hourly Rate of Change for each ICP Metric Using a Weighted Least Square Method” section) equals to 0.28. This means that the pulse latency increases during the CO₂ inhalation with the hourly rate of (0.28) × (60 × 60) ≅ 1 s. Figure 3c depicts the plot of the normalized ICP pulses from the first (beat #1) and the last beat (beat #80) of the segment of interest. The normalization process (normalized by the mean and standard deviation of each beat) has been solely employed to facilitate the comparison of the pulse latencies on the same plot. As the figure shows, the latency of the last beat is greater than that of the first beat and this observation is consistent with the increasing trend of latency derived from the slope of the fitted line.

Fig. 2.

Mean ICP during baseline, CO₂ challenge test and post-test normal breathing for a headache patient. The dashed lines are the robustly fitted lines to the rising and falling edge of ICP employed to define the direction of the mean ICP change

Fig. 3.

a The rising segment of the ICP signal, b the extracted pulse latency and the robustly fitted line to define the hourly rate of change, c the normalized ICP pulses from the first and last beat of the segment, obtained during CO₂ inhalation of the subject of Fig. 2

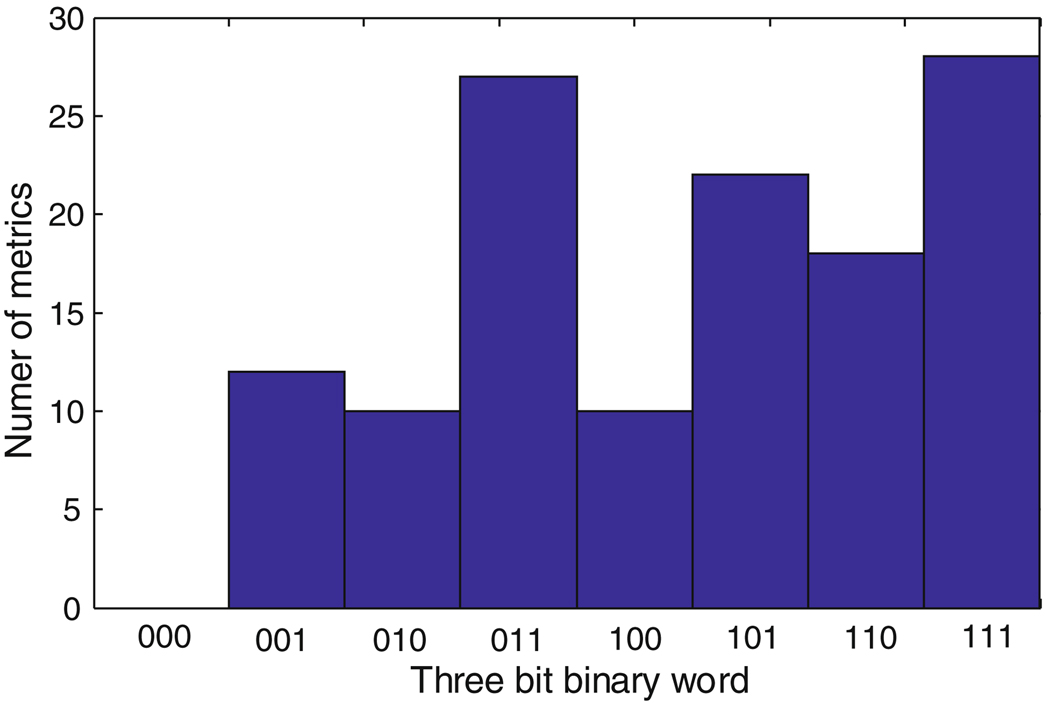
Figure 4 shows a histogram of the eight possible 3 bit binary words over all the 128 metrics. As the plot shows, only less than 10% of the 128 metrics are exclusively related to each of the three sub-peak regions. As a result, most of the metrics are related to two or more sub-peak regions. Note that the total percentage of the P1, P2, and P3 sub-peak region contribution to the metrics are 69, 64, and 60%, respectively.

Fig. 4.

The histogram of the three bit binary words based on the contribution of the three sub-peak regions to the 128 MOCAIP metrics

Further study of the hourly rate of change for all the 128 ICP metrics during the hypercapnic and normal breathing post-test data, reveal that; out of 128 ICP metrics, 72 metrics had consistent changes in association with CO₂ changes for all four subjects. Table 2 summarizes the trend of change during the test for these 72 consistent metrics. We observe that for all subjects, no metrics had the same trend during both the hypercapnic and normal breathing post-test data. This observation is coherent with our expectation that if a variable has a specific trend of change (decreasing/increasing) in one condition (e.g. vasodilation resulted from hypercapnia), the change would be in the opposite direction (increasing/decreasing) as the condition is reversed (e.g. vasoconstriction resulted from post-test normal breathing).

Table 2.

Distribution of the 72 ICP metrics (out of 128 total metrics) with a consistent change for all four subjects during the CO₂ inhalation and post-test normal breathing

	CO2 Inhalation
	Metrics with Increasing trend	Metrics with decreasing trend
Post-test normal breathing
Metrics with Increasing trend	0	50 (named as “+” metrics)
Metrics with decreasing trend	22 (name as “−”metrics)	0

We also observe that for all subjects, 50 metrics consistently increased during hypercapnia and decreased when patients switched back to room air (“+” metrics) and 22 metrics consistently decreased during CO₂ inhalation phase and increased during post-test normal breathing (“−” metrics).

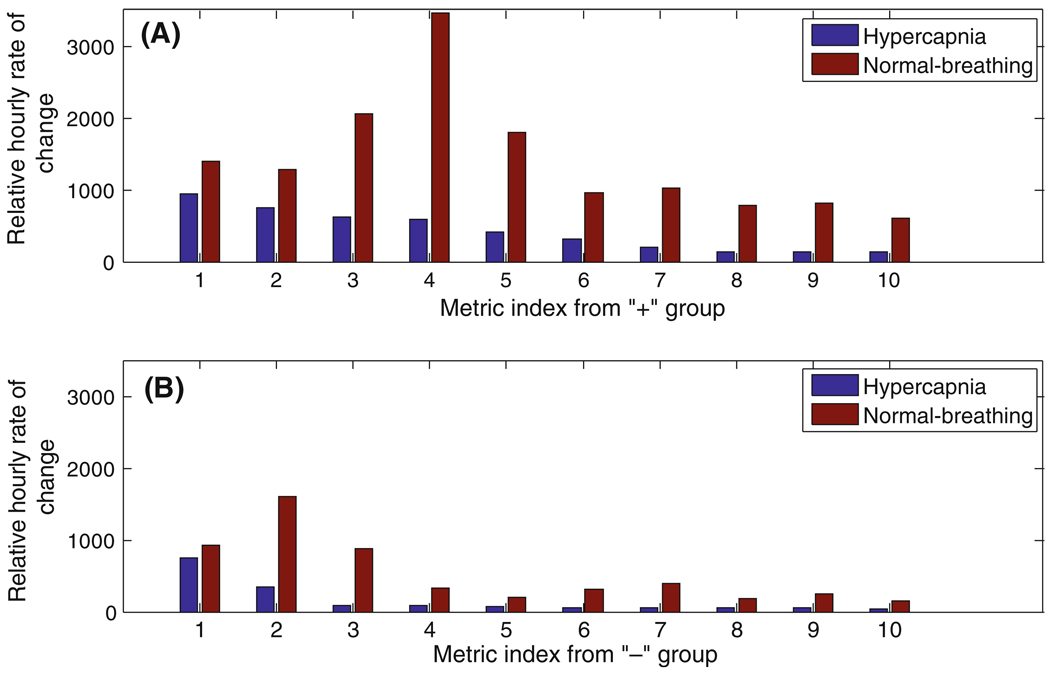
Figure 5a depicts the 10 metrics among the 50 “+” metrics with the highest absolute value of the relative hourly rate of change during both hypercapnic and normal breathing. We observe that these group of metrics include only one metric related to the first sub-peak (P1) region and have much larger relative hourly rate of change during normal breathing than the hypercapnia (t test, P = 0.001).

Fig. 5.

The relative hourly rate of change during hypercapnia and normal breathing post-test for the 10 metrics with the highest relative rate of change from a the “+” group, b the “−” group. The 10 metrics from “+” group in the ascending order of index (1,…,10) are (‘RCurvp2Curvp3’, ‘diasP’, ‘Curvp2’, ‘mICP’, ‘k2’, ‘RCurvp2Curvv3’, ‘dV3’, ‘RC3’, ‘dP3’, ‘dP2’). The 10 metrics from “−” group in the ascending order of index are (‘RCurvp3Curvv2’, ‘RCurvp1Curvv2’, ‘RCurvv1Curvp2’, ‘RLv3p3Lp1p2’, ‘Lv3p3’, ‘RP1V3’, ‘RV1V3’, ‘RLv1p3Lv2p2’, ‘RV2V3’, ‘RLv3p3Lp1p3’)

Among 22 “−” metrics, the 10 metrics with the highest absolute value of relative hourly rate of change are demonstrated in Fig. 5b. A t test on the rate of the changes shows that, similar to “+” metrics; the relative hourly rate of change during normal breathing is significantly higher than the hypercapnia (P = 0.006). We also observe that the “+” metrics change more dramatically, during both hypercapnic and normal breathing; comparing to “−” metrics. In fact, the mean of the hourly rate of change for the “+” metrics is 2.6 times of that for the “−” metrics.

The region-weighted (P1, P2, P3) relative hourly rate of change of the 50 “+” metrics calculated following the procedure described in Sect. 2.4 were (0.518, 1.076, and 0.976), respectively. And finally the region-weighted relative hourly rate of change averaged over 22 “−” metrics were (0.20, 0.32, and 0.27), respectively.

Discussion

The management of many neurological disorders relies on the continuous measurement of ICP. Dynamics of ICP reflect the brain’s compensatory capability to intracranial volumetric changes and pathophysiological changes of the cerebral vasculature. Despite this importance, signal processing capabilities in existing commercial ICP monitoring devices remain poor providing clinicians with limited amount of information that is confined to mean ICP. As a consequence, clinical decisions related to treating ICP related abnormalities are typically made solely based on mean ICP although raw continuous waveform data are usually available.

One very desirable way of characterizing ICP dynamics is through the extraction of morphological features of ICP. Our group’s MOCAIP related work, a technical advancement toward this direction, is a new paradigm of more comprehensive information extraction. However, revelation/validation of what these morphological metrics mean and how to use them is still under way.

It has long been recognized that pulsatile ICP originates mostly from cerebral arterial pulsations with some contributions of venous origin. Now given the vascular aspect of MOCAIP metrics, a basic question is what kind of morphological changes are associated with the dilation/constriction of the cerebral vasculature. In other words, if the ICP pulse could indeed provide information related to cerebral vascular changes, one would expect to observe consistent changes in ICP MOCIAP metrics during the dilation/constriction of the cerebral vasculature. One ideal test that can offer the data to investigate such hypothesis is CO₂ challenge test which is the main motivation behind this work.

Our results showed that out of 128 ICP metrics, 72 metrics had consistent changes in association with CO₂ changes for all four subjects. 50 metrics (including mean ICP, pulse latency and diastolic pressure) showed increasing/decreasing pattern during the rising/falling edge of ICP signal. The increase/decrease of mean ICP and diastolic pressure is in agreement with the fact that the ICP signal makes a plateau wave as increases gradually with the onset of hypoventilation, reaches a saturated level and then starts to decrease when the subject resumes inhaling the normal air [31]. The increase/decrease of pulse latency during the rising/falling edge of ICP signal is related to the dilation/constriction of the vessels. As the cerebrovasculature dilates/constricts, the pulse wave velocity decreases/increases and this results in an increase/decrease in the latency (Fig. 3a) [23, 32].

The comparison of relative hourly rates of change for different metrics revealed that the morphological features of the ICP signal changes more rapidly during the post-test normal breathing than that of CO₂ inhalation. An explanation could be that while the ICP signal increases gradually to the maximum level (average time duration of ICP rising is 56.5 s), it decreases rapidly as the subjects resume breathing in the normal air (average time duration of ICP falling is 16.5 s).

The average rate of change for the “+” metrics were 2.6 times of that of the “−” metric. This means that the ICP MOCAIP metrics whose pattern of change is in accordance to that of the mean ICP signal, changes more dramatically than the metrics whose pattern of change is in the opposite direction of the mean ICP. This may be attributed to the inherent hysteresis property of the system.

The majority of the metrics with the highest rate of change were not related to P1 sub-peak. Also the calculated region-weighted relative hourly rate of change indicated that P2 and P3 regions experienced larger degree of changes during hypercapnic cerebral vasodilation. Considering the origins of the sub-peaks, this observation may suggest that, during the hypercapnia, the intracranial compliance and venous pressure are more affected than the choroid plexus pressure.

In summary, this work provides positive preliminary results related to the hypothesis that the dilation/constriction of the cerebral vasculature result in detectable consistent changes in ICP MOCIAP metrics. Our future plan could include further validation of these findings in a larger study group of uninjured patients or in a setting where cerebral vasoreactivity is disturbed (SAH or traumatic brain injury). We conclude that, by an extended monitoring practice of ICP that includes characterizing ICP pulse morphology, one can potentially detect cerebrovascular changes of interest including cerebral vasospasm.

Conclusion

Acute vasodilatation caused consistent changes in a total of 72 ICP pulse morphological metrics. In addition, it appears that the P2 sub-region responded to cerebral vascular changes in the most consistent way with the greatest changes as compared to P₁ and P3 sub-regions. Information with regard to how ICP pulse morphology responds to vasodilatation and vasoconstriction may allow surrogate, continuous monitoring of the cerebral vasculature.