The Comparison of Gene Expression from Multiple cDNA Libraries

Abstract

We describe a method for comparing the abundance of gene transcripts in cDNA libraries. This method allows for the comparison of gene expression in any number of libraries, in a single statistical analysis, to identify differentially expressed genes. Such genes may be of potential biological or pharmaceutical relevance. The formula that we derive is essentially the entropy of a partitioning of genes among cDNA libraries. This work goes beyond previously published analyses, which can either compare only two libraries, or identify a single outlier in a group of libraries. This work also addresses the problem of false positives associated with repeating the test on many thousands of genes. A randomization procedure is described that provides a quantitative measure of the degree of belief in the results; the results are further verified by considering a theoretically derived large deviations rate for the test statistic. As an example, the analysis is applied to four prostate cancer libraries from the Cancer Genome Anatomy Project. The analysis identifies biologically relevant genes that are differentially expressed in the different tumor cell types.

The introduction of high throughput sequencing and robotics technology has transformed the field of molecular biology. In the field of gene expression, the introduction of array technology has made it possible to monitor the expression of thousands of genes in single experiments (Phimister 1999) This approach is playing a fundamental role in the quantitative analysis of gene expression. However, it is limited by the propensity for cDNA clones and oligos to generate hybridization artifacts, especially the cross-hybridization of highly related family members. Complementary approaches use the frequency of a gene in a cDNA library as a measure of its tissue-specific expression. One approach, termed serial analysis of gene expression (SAGE) relies on high throughput sequencing of 14-bp gene-specific sequence tags to enumerate the expression of individual genes in a cell (Velculescu et al. 1995). A different approach uses EST counts to infer the relative level of expression of a gene (Okubo et al. 1992; Lee et al. 1995; Franco et al. 1997). Both methods, with their own advantages and limitations, can identify novel genes differentially expressed in a biological sample. Microarray-based gene expression analysis relies on an existing DNA sequence being present on the array and therefore can detect only expression of a predefined set of genes.

There are a growing number of cDNA library databases available both commercially and in the public domain. These include the BodyMap project (Okubo et al. 1992; http://www.imcb.osaka-u.ac.jp/bodymap/) and Incyte's LifeSeq database (http://www.incyte.com). Recently, the NCBI has launched the Cancer Genome Anatomy Project (O'Brien 1997; http://www.ncbi.nlm.nih.gov/ncicgap/). This project aims to understand the molecular bases of the transformation of specific normal epithelial cells into pre-malignant populations, and their further transformation into invasive and metastatic cancer. To circumvent the problem of tissue heterogeneity, different cell types are first dissected out of the tumor mass by use of a laser-based technology (Emmert-Buck et al. 1996) and then converted into cDNA libraries.

One of the uses of cDNA libraries is to identify genes whose expression differs between the tissue sources of the libraries (Lee et al. 1995; Franco et al. 1997; Bortoluzzi and Danieli 1999). Such genes may be of potential biological or pharmaceutical relevance. Thus, as this type of data is becoming more widely available, analysis techniques are now being developed to identify differentially expressed genes.

The Cancer Genome Anatomy Project use Fisher's Exact Test (see for example, Kanji et al. 1993) to compare the abundance of genes in cDNA libraries in their Digital Differential Display tool (DDD). Audic and Claverie (1997) raised a number of valid criticisms of the use of Fisher's exact test for this type of data, and developed their own statistical test to compare the expression of a gene in two cDNA libraries. Their test also allows for the construction of confidence intervals about a gene expression level.

However, both Audic and Claverie's test, and Fisher's exact test, can only be used to compare gene expression between precisely two libraries. When comparing more than two libraries, both groups use their test repeatedly to compare all possible pairs of libraries. In particular, Audic and Claverie performed multiple comparisons between libraries to construct Table 3 in their paper — a procedure that is statistically invalid. CGAP's DDD analysis provides a heuristic approximation to compensate for this procedure, by multiplying the P-values by the number of comparisons made. However, this is only a first order approximation, which ignores the correlation between all of the P-values derived. As a result, the P-values generated consistently underestimate the true probabilities of the events.

In addition to the problem of testing the same gene in many libraries, these tests will typically also be used repeatedly on many genes to identify those genes that are most differentially expressed between the libraries. In such situations, some genes would have significant P-values, even if the data were truly random. Again, CGAP's analysis multiplies the P-values by the number of genes tested.

More recently, Greller and Tobin (1999) developed a technique to compare the expression of a gene in more than two libraries. However, their analysis only identifies genes whose expression in a single library is markedly different from their expression in the others. It does not extend to more general patterns of differing gene expressions.

In this work, a more general test is developed that compares the abundance of a gene in any number of cDNA libraries by use of a single statistical test. The extent to which a gene is differentially expressed between the libraries is described by a log likelihood ratio statistic that we derive; this statistic tends asymptotically to a χ² distribution.

Because the test is to be used repeatedly on many thousands of genes, we deliberately do not ascribe a P-value to the test statistic. Instead, two procedures are described that can verify that the genes found with high levels of the test statistic do not represent random noise. The first procedure is to use a randomization procedure that gives a quantitative measure of the degree to which the genes associated with a particular level of the statistic represent true differential expression. The second procedure is to use a theoretically derived large deviations rate.

RESULTS

This section starts with an informal description of the basis of the statistic used for comparing gene expressions. A formal derivation is given in the Methods section. Consider a gene expressed in a set of cDNA libraries that have been constructed, using the same protocol, from a collection of tissues. The differences in abundance of that gene between the libraries can arise via two factors. First, it might be that the true frequency of the gene is the same in all of the tissues. In this case, the differences in gene transcript abundance between the cDNA libraries are simply sampling errors, arising by chance when the clones are selected. This is referred to as the Null Hypothesis.

Alternatively, the differences in transcript abundance may reflect genuine differences in the gene expressions in the different libraries. These differences may be due to any biological or pharmaceutical mechanism, for example, heterogeneities between tissues, patients, pathologies, or drug treatments. This is referred to as the Alternative Hypothesis.

In most cases, the differences in abundance will arise through a combination of these factors. The aim of the test we develop is to identify the extent to which the differenc es in expression represent true heterogeneity as opposed to sampling variability. This is possible because the distribution of the sampling errors can be quantified. The test works by considering each of the two situations in turn, and, in each case, calculating the likelihood of seeing the observed data. The two likelihoods are compared by subtracting the logs of the likelihoods, generating a log likelihood ratio. This ratio gives a measure of the extent to which the differences in gene expression correspond to heterogeneity of the libraries as opposed to random sampling variability.

The statistic, denoted R_j for gene j, is derived in the Methods section, and is given by the expression

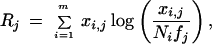1

where m is the number of cDNA libraries, x_i,j is the number of transcript copies of gene j in the ith library and N_i is the total number of cDNA clones sequenced in the ith library. f_j is the frequency of gene transcript copies of gene j in all of the libraries, given by the formula

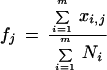2

In a library in which there are no observed copies of the gene, that is, x_i,j = 0, its contribution to R_j is zero.

The formula is only valid if at least 50 ESTs have been sequenced from each library, and no single gene contributes >20% of the ESTs in a library. However, such libraries are unlikely to be encountered in real-life examples.

Example Analysis

As an example, the analysis is performed on four prostate cancer libraries from the Cancer Genome Anatomy Project database. The four libraries are derived from the same patient. They have been constructed by use of the same protocol, from populations of micro-dissected cells representing different levels of pathology, varying from normal epithelium to invasive prostatic tumor. Details of the libraries used are shown in Table 1.

Table 1.

Details of the Four cDNA Prostate Libraries Used as Example Data for the Analysis

Library ID	Tissue ID	Type	Number of ESTs sequenced	Number of UniGene clusters
Pr1	46.1	Normal epithelium	5689	1441
Pr2	46.2	PIN low grade	5688	1692
Pr3	46.3	Invasive prostatic tumor	5173	1396
Pr4	46.4	PIN high grade	649	276

Note. The four libraries used for the example analysis are all from the Cancer Genome Anatomy Project database (http://www.ncbi.nlm.nih.gov/ncicgap/). They have all been prepared from the same patient, using microdissection and plasmid cloning techniques (Krizman et al. 1996). Each library represents a different level of prostate pathology ranging from normal epithelium, prostatic intraepithelial neoplasia (PIN) to invasive prostatic tumor. Note that library Pr4 had fewer clones sequenced than the other libraries. 

The top hits, with R > 8, are shown in Table 2. The table shows the UniGene Hs cluster ID, a brief description of the protein, the value of the test statistic R and the abundance of the gene in each of the four prostate cancer libraries.

Table 2.

Top Hits with R > 8

UniGene	Description	R	Pr1	Pr2	Pr3	Pr4
Hs.6179	mRNA for cDNA DKFZp586K2322	27.57	4	2	4	13
Hs.171995	Prostate Specific Antigen	24.12	69	138	54	2
Hs.183752	Prostatic Secretory Protein	24.01	55	11	50	0
Hs.173554	Ubiquinol-Cytochrome C Reductase	12.18	11	0	0	0
Hs.194329	ESTs	11.07	10	0	0	0
Hs.200539	ESTs	10.96	0	12	1	0
Hs.184014	Ribosomal Protein L31	10.93	27	6	24	0
Hs.234726	α1 Antichymotrypsin	10.91	0	13	2	0
Hs.5417	150KD Oxygen-Regulated Protein	10.82	0	0	9	0
Hs.75344	Ribosomal Protein S4	10.44	16	10	0	1
Hs.193434	ESTs	9.79	0	0	0	3
Hs.112259	T-cell Receptor γ Cluster	9.78	1	0	10	0
Hs.184109	Ribosomal Protein L37a	9.50	7	31	10	2
Hs.236561	Interferon α Inducible Protein	9.49	5	1	2	5
Hs.55296	HLA-B Associated Transcript	8.95	3	0	0	3
Hs.183826	ESTs	8.41	0	0	7	0
Hs.172603	ESTs	8.41	0	0	7	0
Hs.169241	SRF Accessory Protein 1A	8.41	0	0	7	0
Hs.5662	Guanine Binding Protein	8.33	2	8	3	5
Hs.2953	Ribosomal Protein S15a	8.29	4	2	15	0
Hs.181350	Glandular Kallikrein 2 Precursor	8.15	18	33	10	0

Note. This table lists the 21 genes for which R > 8. The first column is the UniGene Hs cluster ID. The second coluymn is a description of the gene product. The third column gives the likelihood statistic R. The next four columns show the number of ESTs in each of the four libraries that belong to the Unigene cluster. The total number of clones sequenced in each of the libraries are 5689, 5688, 5173, and 659. 

There are 21 genes with R > 8. The majority of these clusters are annotated; four clusters are unclassified ESTs. Among the annotated clusters are a number of genes whose products are associated with the prostate, inflammation or proliferation.

Two genes belonging to the kallikreinin family, kallikreinin 2 and prostate-specific antigen (PSA), are differentially expressed in the micro-dissected tumor cell types. Both are known markers for prostate cancer (Daher and Beaini 1998; Nelson et al. 1998). Interestingly, these genes appear to be over-expressed in low-grade prostatic intraepithelial neoplasia (PIN) compared with normal, high-grade PIN and invasive tumor cells. This finding is in accordance with in-situ hybridization studies in which it was found that the level of PSA expression in the prostate tumor mass is inversely proportional to the tumor grade (Qiu et al. 1990). α-1-antichymotrypsin, a protein known to bind PSA (Borchert et al. 1999), shows a similar expression pattern.

The analysis also identifies four genes up-regulated only in invasive tumor cells. Among these genes, human 150-kD oxygen-related protein is involved in the mechanisms that protect cells from hypoxia damage (Ikeda et al. 1997), and may play a role in the development of tumor metastasis.

The ribosomal genes S4, S15a, L31, and L37a are all found to be differentially regulated between the four tissue types. However, these genes do not behave consistently. The genes for S4, L37, and L37a are under-expressed in tumor tissue compared with the normal or hyperplastic cells. This appears to be contrary to the findings of Vaarala et al. (1998), who have found that a number of ribosomal mRNAs, including L37, are over-expressed in prostatic cancer cell lines and tumor samples. We do not have any explanation for these discrepancies.

Inflammatory genes, as well as a number of novel genes, were also identified as differentially regulated within the four cell types. One of the unannotated EST clusters, Hs.172603, consists of ESTs almost entirely derived from prostatic cDNA libraries. These results, far from being conclusive, would need to be confirmed by further experimental research.

Verification

In these analyses, many thousands of genes are separately tested to identify those genes that are most differentially expressed. Intrinsic to this type of analysis is the problem that even with totally random data, it is likely that some genes would achieve significant levels of the test statistic R. This is the reason that we have not associated P-values with the likelihood ratio statistic, and only used it to rank the genes.

Therefore, two verifications of these results are provided. The first is to generate random data sets conforming to the null hypothesis and identify the number of genes achieving each level of R, as described in the Methods section. The second is to assess the results in the context of the theoretical considerations of the large deviations rate associated with the test statistic R.

The results of the randomization are detailed in Table 3. As the log likelihood ratio decreases, becoming more significant, the proportion of true positives among the real data increases.

Table 3.

Results of the Data Randomization

R	Number of genes from CGAP libraries log likelihood at least R	Mean number of genes from randomized libraries LogLik at least R	Believability
13	3	0.003	99.9%
12	4	0.005	99.9%
11	5	0.009	99.8%
10	10	0.03	99.7%
9	14	0.1	99.0%
8	21	0.4	98.2%
7	36	1.1	97.0%
6	74	6.3	91.5%
5	120	16	86.3%
4	275	49	82.2%
3	997	421	57.8%
2	1840	1347	26.8%
1	9947	5294	46.8%

Note. This table shows the results of the randomization procedure to test the believability of the genes for a given log likelihood ratio. The number of genes from the CGAP data set with log likelihood at least the value given in the first column is shown in the second column. The third column is the same, but averaged over 1000 runs of randomized data. The final column is a heuristic measure of believability, which is one minus the ratio of the number of genes from the randomized data to the number of genes from the CGAP data with at most the given log likelihood; this heuristic is only valid when the number of genes from the real data set is much greater than the number of genes from the randomized data. The 21 genes with log likelihood ratio at least 8 are listed in Table 2. 

For the threshold selected for Table 2, R > 8, the mean number of false positives is 0.4, compared with 21 real genes found at this threshold. This corresponds to a true positive rate of ∼98%. Therefore, according to this analysis, it is likely that all of the 21 genes listed in Table 2 are genuine results. As the threshold value of R is decreased, both the number and the proportion of false positives increases. For example, of the 74 genes with R > 6, there may be 6 false positives. Only 90% of these genes are likely to be true positives and correspond to genuine biological effect.

It is important to note that the results of these simulations are entirely data dependent. With different data, simulations would need to be repeated, and the numbers and thresholds derived would be different.

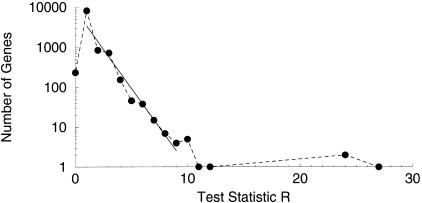
The second verification uses the theory of large deviations described in the Methods section. If the data were truly random, then the number of genes achieving levels of the statistic R should fall exponentially as a function of R. If there are more genes than predicted by this exponential decline, then this would be an indication that these genes represent true effect. In Figure 1, the number of genes at each level of the test statistic R is plotted as a function of R. It can be seen that there are two distinct regions of behavior. For 1 ⩽ R ⩽ 9, the number of genes decreases exponentially. The gradient in this region is −0.9, with standard error 0.7. This is not significantly different from the theoretically derived value of −1 for random data. Thus, according to this analysis, the number of genes achieving values of R in this region is not distinguishable from the number that would be expected when comparing a large number of genes. However, for R > 9, the number of genes is much above the exponential curve. This indicates that for R > 9, the number of genes observed is much greater than would be expected from random data. Therefore, we can be confident that these genes represent true variation, and are not false positive results.

Figure 1.

The number of genes for a given value of the test statistic R is plotted as a function of R. It can be seen that the data falls into two regions. For 1 ⩽ R ⩽ 9, the number of genes decreases exponentially with R. The solid line is the regression in this interval. The slope is −0.9 with standard error 0.07, and is therefore not significantly different from −1 at 5% significance. This is in accordance with the large deviations calculation described in the Methods section. When R > 9, the number of genes is above this exponential curve, and is much greater than predicted by the large deviations calculation.

DISCUSSION

This work has described a likelihood ratio method for comparing the abundance of a gene in any number of cDNA libraries. The statistic can be used to identify those genes whose expression most varies across a set of cDNA libraries. The analysis method was tested on example prostate library data. It identified a number of genes that appear to be biologically relevant, as well as a number of unannotated EST clusters. That many of the top hits are known to be important in the prostate and associated pathology provides confidence that the analysis produces meaningful results. It also gives confidence that the unannotated EST clusters identified by the test warrant further investigation.

Because this method is used for comparing expression data for large numbers of genes, it is essential to quantify the number of false positives associated with an analysis. A method was described for randomizing the data, which assesses the extent to which results can be believed. The randomization was used to demonstrate that ∼98% of the genes identified from the example libraries, at the threshold level chosen, are likely to constitute genuine biological effect. The results were further verified by considering the large deviations rate for the test statistic. The number of highly differentially expressed genes was shown to be much greater than predicted by this rate.

In a sense, Figure 1 is incomplete in that it does not include those genes that are expressed, but which have not been sampled in any of the libraries. As a gene becomes more differentially expressed, we expect to find more copies of the gene in the tissue, and thus have a higher chance of capturing it in one of the libraries. Consequently, the smaller the value of R, the more genes are missing from the analysis. Examining Figure 1, we see that this effect when 0 < R < 1 and the histogram drops below the linear fit. The intercept of the linear regression could be used as an estimate of the total number of genes that are expressed in the tissue. However, this would only be true if the libraries were prepared from identical tissue; in our case, the estimate would be invalid.

Both cDNA sequencing and hybridization-array-based methods are now being increasingly used to quantify gene expressions in tissues and cell lines, and to make comparisons between healthy, pathological, and drug-treated states. The study of gene expression alone, however, does not give the complete picture of cellular activity. Studies comparing gene expression with protein abundance (Anderson and Seilhamer 1997; Gygi et al. 1999) have shown little correlation between the two. There are several reasons why this might be the case, including differences in translational control and RNA and protein turnover rates (Hargrove and Schmidt 1989; Rivett 1990). Thus, this type of analysis can only give an indication of genes whose products may be of biological or pharmaceutical relevance. Any results of this type of analysis would have to be confirmed by further research.

METHODS

Derivation of the Test Statistic

Consider the expression of gene j in all of the cDNA libraries. Denote the number of clones sampled for each library i as N_i, and the observed number of copies of the gene as x_i,j. Let m be the number of cDNA libraries. We will compare two hypotheses relating to the frequency of this gene using a likelihood ratio. Under the null hypothesis, the gene is not differentially expressed, so the frequency of the gene is the same in all libraries. Under the alternative hypothesis, the gene is differentially expressed, so the frequency of the gene in each of the libraries is different.

In both cases, as long as the abundance of the gene is small relative to the total mRNA content of the cell (20% is the usual heuristic, Hays 1994), the distribution of the gene, denoted X_i,j, will be well approximated by a Poisson distribution, with

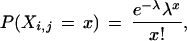3

λ will be determined below and will have a different value for the two hypotheses. The same Poisson approximation is also made by Audic and Claverie (1997).

The null hypothesis is that the frequency of the gene is the same in each library. For a gene with transcript frequency f, the number of transcripts in library i is approximately distributed as a Poisson variable with parameter fN_i. Therefore, the likelihood of the observed data, under the null hypothesis, is given by

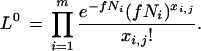4

The maximum likelihood estimate of the common gene frequency is the solution to the equation

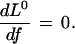5

The solution, f_j, is given by

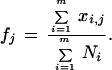6

This is just the proportion of the mRNA for the gene of interest among all mRNA transcripts in all of the libraries. Observe that this is also the general solution that maximizes the likelihood of the entire data set under the null hypothesis. Thus, the maximum estimate of the likelihood of the observed data under the null hypothesis, L_j⁰, is given by

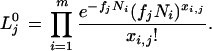7

Under the alternative hypothesis, the frequency of gene transcripts in each library is different. The maximum likelihood estimate of gene frequency in each library i is x_i,j/N_i. Therefore, the gene abundance in library i is approximately distributed as a Poisson variable with parameter x_i,j. (When x_i,j = 0, the Poisson distribution is well defined, with the event x = 0 having probability 1, and events x > 0 having probability 0). Note that for the Poisson approximation to hold, each library must have at least 50 ESTs sequenced (Hays 1994). Thus, the maximum estimate of the likelihood of the observed data under the alternative hypothesis is given by

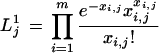8

The null hypothesis is compared with the alternative hypothesis by taking the log of the ratio of the two likelihoods, that is, log (L¹_j/L⁰_j). This gives the test statistic R_j

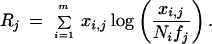9

Application of Method to CGAP Data

For each sequence in the CGAP libraries, we identified the Unigene cluster to which the sequence has been allocated; this was acheived by searching for the accession number of the EST in the Unigene database (Hs Build 96; Boguski and Schuler 1995; http://www.ncbi.nlm.nih.gov/ncicgap/). The number of ESTs from each library that belong to each Unigene cluster were used as the input into the statistical test. The test was applied to each gene in turn. The genes were then ordered according to their value of the test statistic R.

Verification

For the first verification, the number of false positives is assessed by generating random data sets satisfying the null hypothesis, and performing the analysis on these data. This is used to provide a quantitative measure of the extent to which the results of the original analysis can be believed. For each gene, the common gene transcript frequency, f_j (eqaution 2) is calculated. Then, for each library, a random gene abundance is generated from a Poisson distribution whose parameter is equal to the expected number of gene transcripts for that library(equal to N_if_j for library i).

One-thousand random data sets were generated in this way. The analysis was performed on each data set. For each level of the log likelihood test statistic R, the mean number of genes across the 1000 analyses with at most that log likelihood was calculated. This was compared with the number of genes from the true data set with at most the same level of R. For each log likelihood threshold, the proportion of the genes from the true data set likely not to be false positives was calculated.

Theoretical Considerations of the Test Statistic

When the null hypothesis is correct, there are a number of theoretical considerations that can be made about the test statistic. Under the null hypothesis, the true frequency of each gene j, in every library, is f_j, as given in equation 6.

Firstly, under Wilke's theorem (De Groot 1986), as all of the N_i → ∞, the distribution of 2R_j for each R_j tends to a χ² distribution with m – 1 degrees of freedom.

Secondly, for each library, the probabilities of the observed gene frequencies, {x_ij/N_i ∶ 1 ⩽ j ⩽ k} deviating from the actual frequencies {fj ∶ 1 j ⩽ k} can be determined. These are denoted P_i. When N_i is large, the theory of large deviations (Ellis 1985) estimates that P_i decays exponentially, so that

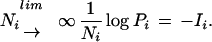10

I_i is the large deviations rate function for a multinomial distribution and is given by

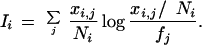11

This function is also know as the Kullback-Leibler distance between the two frequencies and measures the relative entropy between them. Because there are m (independent) libraries, the joint probability of observing {x_i,j: 1 ≤ i ≤ m, 1 ≤ j ≤ k} is Π_iP_i, which is proportional to

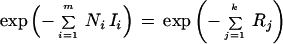12

Equation 12 gives the duality under which we may think of the probability of observing the expression of gene j in each of the libraries as proportional to e^−R_j.

There is an alternative way to view R_j as an appropriate test statistic. Consider the distribution of the number of mRNAs for gene j, in all libraries, {x_i,j: 1 ≤ i ≤ m}, conditioned on the total number of mRNAs for gene j seen in all of the libraries. We denote this total as x_j = Σ_ix_i,j. If each of the x_i,j are drawn from Poisson random variables, then, according to the divisibility property of the Poisson distribution, the variables {x_i,j|x_j: 1 ≤ i ≤ m} are drawn from a multinomial distribution, with x_j events, and m outcomes, with probabilities N₁/N, … , N_m/N. N is the total number of observed mRNAs in all of the libraries, equal to Σ_i N_i. When x_j is large, the large deviations rate function for the multinomial distribution (equation 11) can be used directly to deduce that the probability of observing {x_i,j: 1 ≤ i ≤ m |x_j} is proportional to

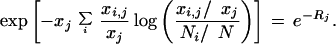13

Therefore, with k genes, the expected number of genes for which the test statistic R is approximately r will decrease exponentially as a function of r, with gradient −1. Thus, a logarithmic plot of the number of genes with R approximately r, as a function of r, can be used to determine the extent to which the number of observed genes with a given value of R is greater than one would expect by random chance.