Longitudinal functional principal component analysis

Abstract

We introduce models for the analysis of functional data observed at multiple time points. The dynamic behavior of functional data is decomposed into a time-dependent population average, baseline (or static) subject-specific variability, longitudinal (or dynamic) subject-specific variability, subject-visit-specific variability and measurement error. The model can be viewed as the functional analog of the classical longitudinal mixed effects model where random effects are replaced by random processes. Methods have wide applicability and are computationally feasible for moderate and large data sets. Computational feasibility is assured by using principal component bases for the functional processes. The methodology is motivated by and applied to a diffusion tensor imaging (DTI) study designed to analyze differences and changes in brain connectivity in healthy volunteers and multiple sclerosis (MS) patients. An R implementation is provided.

87

1. Introduction

Scientific studies now commonly collect functional or imaging data at multiple visits over time. In this paper we introduce a class of models and inferential methods for the analysis of longitudinal data where each repeated observation is functional.

Our motivating data set comes from a diffusion tensor imaging (DTI) study, which was designed to analyze cross-sectional and longitudinal differences in brain connectivity in healthy volunteers and multiple sclerosis (MS) patients. For each of 112 subjects and each visit, we have fractional anisotropy (FA) measurements along the corpus callosum in the brain. Figure 1 shows an image of the corpus callosum with 7 biological landmarks (denoted 1, 20, 40, 60, 80, 100, 120) used for registration of measurements across subjects. Each visit’s data for a subject is a finely sampled function across the corpus callosum, with the argument of the function being the spatial distance along the tract. For illustration, the FA data is displayed for 2 subjects, one with 5 and one with 6 complete visits. Although change over time may be subtle in comparison with measurement error, accurate quantification of that change is crucial for applications ranging from powering clinical trials to understanding brain development. This data structure is not unique to this study. In fact, the tractography data is an example of many new data sets containing functions or images that are observed repeatedly over time (longitudinal functional data).

Fig 1.

Top: Sagittal image of the corpus callosum in one of the study subjects, a healthy 33-year-old man, showing the segmentation used [following 46] for construction of the tract profile. Values denote the bin number at the boundary point from the splenium (back of the head) to the genu/rostrum (closer to the eyes). Bottom: Two example subjects (both MS patients) from the tractography data with 5 and 6 complete visits, respectively. Shown are the fractional anisotropy along the corpus callosum, measured at the 120 sample points. Different visits for the same subject are indicated by color and overlaid.

The common structure of these studies can be understood using an analogy with classical longitudinal data [8]. Longitudinal data is commonly analyzed using the very flexible class of linear mixed models [22, 44], which explicitly decompose the variation in the data into between- and within- subject variability. Similarly, we decompose the dynamic behavior of functional data into a time-dependent population average, baseline (or static) subject-specific variability, longitudinal (or dynamic) subject-specific variability, subject-visit-specific variability and measurement error. Technically this is achieved by replacing random effects with random functional effects.

We propose an estimation procedure that is based on an eigenanalysis and extends functional principal component analysis (FPCA) to the longitudinal setting. Computation is very efficient, even for very large data sets. The estimation procedure performed well both in an extensive simulation study and in the DTI application, where it uncovered subtle but potentially important subject-specific changes over time in a specific region of the corpus callosum, the isthmus. The character of these changes could conceivably be used as an early gauge of disease progression or response to neuroprotective therapies.

Our approach is different from functional mixed models based on the smoothing of fixed and random curves using splines or wavelets [3, 15, 16, 29]. In contrast to these methods focusing on the estimation of fixed and random curves, our approach is based on functional principal component analysis. In addition to the computational advantages of such an approach [compare also 19], we are able to extract the main differences between subjects in their average profiles and in how their profiles evolve over time. Such a signal extraction, which is not possible using smoothing methods alone, allows the relation of subject-specific scores to other variables such as disease status, age or disease progression. Our approach can be seen as an extension of functional principal component analysis for multilevel functional data [7]. Our methods apply to longitudinal data where each observation is functional, and should thus not be confused with nonparametric methods for the longitudinal profiles of scalar variables [17, 30, 31, 37, 41, 48, 50, 51]. For good introductions to functional data analysis in general, please see [10, 34].

The remainder of the paper is organized as follows. Section 2 introduces the longitudinal functional model and explains how dimension reduction via longitudinal functional principal component analysis (LFPCA) is achieved. Section 3 develops our estimation procedure and provides computational efficiency results. Section 4 shows the performance of our procedure in an extensive simulation study. Section 5 provides the application of LFPCA methods to the tractography data, while Section 6 concludes with a discussion. Theoretical results and proofs are given in the appendix. Supplementary material [13] providing an R function implementing LFPCA, simulation code and additional graphs is available in the archive that the Electronic Journal of Statistics maintains on Project Euclid.

2. The longitudinal functional model

In this section we introduce models for data sets where functional data are recorded at multiple time points or visits for the same observational unit or subject. The observed data are {Y_ij(d), d ∈ , T_ij, Z_ij, V_ij}, where Y_ij(·) is a random function in L²[0, 1] observed at arguments d in some set , T_ij is the time of visit j for subject i, and Z_ij and V_ij are vectors of covariates for subject i = 1, …, I at visit j = 1, …, J_i, where the number of visits J_i can vary with the subject, i. We assume that at least some subjects i have at least 3 visits, that is J_i ≥ 3. The multi-level case when J_i ≤ 2 for all i was fully addressed by [7] and [6].

2.1. The functional random intercept and random slope model

The data structure in this paper is similar to that of standard longitudinal data, with the exception that instead of observing scalars, Y_ij, one observes functions, Y_ij(d), over time. We use this analogy to build up intuition and to introduce the functional equivalent of the standard longitudinal model. For simplicity we first extend the random intercept and slope model [35]. The functional analog is

$$Y_{ij}(d)=\eta (d,T_{ij})+X_{i,0}(d)+X_{i,1}(d)T_{ij}+U_{ij}(d)+{\epsilon }_{ij}(d),$$ (2.1)

where η(d, T_ij) is a fixed main effect surface, X_i,0(d) is the random functional intercept for subject i, X_i,1(d) is the random functional slope for subject i, T_ij is the time of visit j for subject i, U_ij(d) is the random subject and visit-specific functional deviation, and ε_ij(d) is random homoscedastic white noise. We make the following assumptions:

• A.1X_i(d) = {X_i,0(d), X_i,1(d)}, U_ij(d) and ε_ij(d) are zero-mean, square-integrable, mutually uncorrelated random processes on [0, 1],
• A.2X_i,0(d) and X_i,1(d) have auto-covariance functions K₀(d, d′) and K₁(d, d′), respectively, and cross-covariance function K₀₁(d, d′),
• A.3U_ij(d) has covariance function K_U (d, d′), and
• A.4ε_ij(d) is white noise measurement error with variance σ².

There are several parallels between the scalar random intercept-random slope model and model (2.1). First, Y_ij(d) is now a functional observation. Second, X_i,0(d) and X_i,1(d) replace the scalar random effects b_i0 and b_i1 as functional random intercept and random slope, respectively, capturing subject-to-subject variation. Third, the cross-covariance function K₀₁(d, d′) replaces the covariance between b_i0 and b_i1. Fourth, the subject- and visit-specific deviation now consists of two parts. U_i,j(d) is a visit-specific functional deviation from the subject-specific functional trend, capturing visit-to-visit functional variation on the same subject. ε_ij(d) is additional white noise measurement error, capturing random uncorrelated variation within each curve. The overall mean trend is allowed to be a smooth surface η(d, T_ij), which generalizes the linear mean β₀ + β₁T_ij often assumed in the scalar model.

Model (2.1) encompasses several simpler models that can be obtained as special cases. For example, visits may be of equal number J_i = J per subject or equally spaced, T_ij = j for all i and j. The mean function η(d, T_ij) may be time constant, η(d), additive or linear in T, η(s, T_ij) = η₁(d) + η₂(T_ij), or η(d, T_ij) = η₀(d) + T_ijη₁(d). The latter formulation is a direct extension of the linear population trend typically assumed in the scalar model.

Model (2.1) allows the decomposition of the variation in the observed curves into a) differences in subject’s baseline functions; b) differences in subjects’ average changes over time; c) visit-specific variation around these average trends; and d) measurement error. This decomposition is of interest in many applications. For example, in the tractography application we describe in Section 5, it is of interest to study both the population cross-sectional and the dynamic behavior of various measurements along neuronal tracts.

2.2. The general functional mixed model

While model (2.1) is rich enough for our application, it lends itself well to generalization, which could be useful in other applications. A more general form of the longitudinal functional model is

$$Y_{ij}(d)=\eta (d,{\mathit{Z}}_{ij})+{\mathit{V}}_{ij}^{\prime }{\mathit{X}}_i(d)+U_{ij}(d)+{\epsilon }_{ij}(d),$$ (2.2)

where we assume that

• B.1X_i(d), U_ij(d) and ε_ij(d) are zero-mean, square-integrable, mutually uncorrelated random processes on [0, 1],
• B.2X_i(d) is a vector-valued random process with auto-covariance functions for the p components K₁₁(d, d′), …, K_pp(d, d′), and cross-covariance functions K₁₂(d, d′), …, K_1,p(d, d′), …, K_p−1,p(d, d′),
• B.3U_ij(d) is a random process with covariance function K_U (d, d′), and
• B.4ε_ij(d) is white noise measurement error with variance σ².

Model (2.1) and its assumptions A.1 to A.4 are obtained as a special case of (2.2) and B.1 to B.4 by setting p = 2, Z_ij = T_ij and V_ij = (1, T_ij)′. Note that model (2.1) counts the components of X from 0 to 1 rather than from 1 to 2 to stress the analogy to the scalar random intercept-random slope model. The functional mixed-effects ANOVA model [7] results if we set p = 1, Z_ij = j, V_ij = 1, and η(d, Z_ij) = μ(d) + η_j(d). More generally, Z_ij and V_ij are vectors of known covariates for subject i at time T_ij. η(d, Z_ij) is the fixed main effect surface, which can depend parametrically, semi-parametrically or non-parametrically on the covariates Z_ij = (Z_ij,1, …, Z_ij,m). The simplest parametric form is a linear mean $\eta (d,{\mathit{Z}}_{ij})={\alpha }_0+{\alpha }_{1}d+{\mathit{Z}}_{ij}^{\prime }\mathit{\beta }$, while the most complex nonparametric form is a (p+1)-dimensional smooth function η(d, Z_ij). Intermediate semi-parametric models such as η(d, Z_ij) = η₁(d, Z_ij,1) + ···+ η_m (d, Z_ij,m) or $\eta (d,{\mathit{Z}}_{ij})={\eta }_0(d)+{\mathit{Z}}_{ij}^{\prime }\mathit{\beta }$ could also be useful in particular applications.

Model (2.2) is the functional analog of the linear mixed model for longitudinal data [22]. It is similar to models used by [15, 29], but we do not assume Gaussianity and allow for more general fixed effects. The model of [15] also does not admit correlated random functional effects, as are present in (2.1). In addition, we follow quite a different modeling approach, using longitudinal functional principal component analysis instead of smoothing splines or wavelets for nested curves. This has large computational advantages compared to [29], especially when the number of random effects is large, see Section 4.3 and [19]. We are at the same time able to extract the main differences between subjects in how their profiles evolve over time, something not possible in these other approaches.

For notational simplicity in the remainder of the paper we will focus on model (2.1). In Appendix B we point out the small technical differences for fitting the more general model (2.2).

2.3. Dimension reduction via longitudinal FPCA

While models (2.1) and (2.2) are intuitive generalizations of linear mixed effects models, their computational feasibility is not obvious, especially for large numbers of subjects, visits and observations. We here propose an efficient modeling approach, Longitudinal Functional Principal Component Analysis (LFPCA). LFPCA is the longitudinal generalization of functional principal component analysis (FPCA) [34] and multilevel functional principal component analysis (MFPCA) [7]. The main idea of LFPCA is to extract the main directions of variation of the X and U processes using an eigen decomposition of their respective covariance operators on the basis of Mercer’s theorem [27]. The Karhunen-Loève expansion [20, 26] is then used to obtain parsimonious expansions of X and U.

In the notation of model (2.1), we expand the covariance operator of the bivariate process X_i(d) = {X_i,0(d), X_i,1(d)} as

$$K_X(d,d^{\prime })=\left(\begin{array}{cc}{K}_0(d,d^{\prime })& K_{01}(d,d^{\prime })\\ K_{01}(d^{\prime },d)& K_1(d,d^{\prime })\end{array}\right)=\sum _{k=1}^{\infty }{\lambda }_k{\phi }_k^X(d){\phi }_k^X{(d^{\prime })}^{\prime },$$

where ${\phi }_k^X(d)={\{{\phi }_k^0(d),{\phi }_k^1(d)\}}^{\prime }$ are the ordered eigenfunctions of K_X(d, d′) corresponding to the eigenvalues λ₁ ≥ λ₂ ≥ ··· ≥ 0. Similarly, let $K_U(d,d^{\prime })={\displaystyle \sum _{k=1}^{\infty }}{\nu }_k{\phi }_k^U(d){\phi }_k^U(d^{\prime })$, where ${\phi }_k^U(d)$ are the ordered eigenfunctions of K_U (d, d′) corresponding to the eigenvalues ν₁ ≥ ν₂ ≥ ··· ≥ 0. The eigenfunctions { ${\phi }_k^U$, k ∈ IN} form an orthonormal basis of L²[0, 1] with respect to the usual L²[0, 1] scalar product. The eigenfunctions { ${\phi }_k^X$, k ∈ IN} form an orthonormal basis of L²[0, 1] × L²[0, 1] with respect to the additive scalar product

$$<(f_0,f_1),(g_0,g_1)>={\int }_0^1{f}_0(s)g_0(s)ds+{\int }_0^1{f}_1(s)g_1(s)ds.$$

The function pairs $({\phi }_k^0,{\phi }_j^1),({\phi }_k^0,{\phi }_j^U)$ or ( ${\phi }_k^1,{\phi }_j^U$) are not required to be orthogonal in L²[0, 1], nor will ( ${\phi }_k^0,{\phi }_j^0$) or ( ${\phi }_k^1,{\phi }_j^1$) be orthogonal in general for k ≠ j. The Karhunen-Loève expansions of the random processes are

$${\mathit{X}}_i(d)=\sum _{k=1}^{\infty }{\xi }_{ik}{\phi }_k^X(d)\text{and}{U}_{ij}(d)=\sum _{k=1}^{\infty }{\zeta }_{\mathit{ijk}}{\phi }_k^U(d),$$

where the principal components scores

$${\xi }_{ik}={\int }_0^1{X}_{i,0}(s){\phi }_k^0(s)ds+{\int }_0^1{X}_{i,1}(s){\phi }_k^1(s)ds\text{and}{\zeta }_{\mathit{ijk}}={\int }_0^1{U}_{ij}(s){\phi }_k^U(s)ds$$

are uncorrelated random variables with mean zero and variances λ_k and ν_k, respectively. Assumption A.1. is ensured by assuming that {ξ_ik, i = 1, …, I, k ∈ IN} and {ζ_ijk, j = 1, …, J_i, i = 1, …, I, k ∈ IN} are mutually uncorrelated. Because working with infinite expansions is impractical, we consider the finite-dimensional approximations of the X and U processes

$${\mathit{X}}_i(d)=\sum _{k=1}^{N_X}{\xi }_{ik}{\phi }_k^X(d)\text{and}{U}_{ij}(d)=\sum _{k=1}^{N_U}{\zeta }_{\mathit{ijk}}{\phi }_k^U(d),$$

where N_X and N_U will be estimated, as described in Section 3.4. Conditional on N_X and N_U the finite approximation to model (2.1) is

$$\begin{array}{lll}{Y}_{ij}(d)\hfill & =\hfill & \eta (d,T_{ij})+\sum _{k=1}^{N_X}{\xi }_{ik}{\mathit{V}}_{ij}^{\prime }{\phi }_k^X(d)+\sum _{k=1}^{N_U}{\zeta }_{\mathit{ijl}}{\phi }_k^U(d)+{\epsilon }_{ij}(d),\hfill \\ {\xi }_{ik}\hfill & \stackrel{\mathit{unc}}{\sim }\hfill & (0,{\lambda }_k),{\zeta }_{\mathit{ijl}}\stackrel{\mathit{unc}}{\sim }(0,{\nu }_l),{\epsilon }_{ij}(d)\stackrel{\mathit{unc}}{\sim }(0,{\sigma }^2),\hfill \end{array}\}$$ (2.3)

V_ij = (1, T_ij)′, which is a linear mixed model [see also 7]. Here, $x_l\stackrel{\mathit{unc}}{\sim }(0,a)$ denotes uncorrelated variables with mean 0 and variance a. We are neither assuming normality of the processes in (2.1) nor of the scores in (2.3). LFPCA extends similarly to the more general model (2.2).

3. Estimation

For reasons of simplicity, we focus the presentation on model (2.1), but estimation is done similarly for model (2.2). The minor adjustments for fitting (2.2) are described in Appendix B. We assume that the mean, covariance operators and eigenfunctions are smooth. For presentation purposes, we assume that all functions Y_ij(d) are measured at a finite number, D, of grid points ⊂ [0, 1]. However, the method can easily handle missing data, both in terms of visits per subject or observations per visit. Estimation can be done using a few simple steps, which will be described in more detail in the following.

• Step 1
  The fixed effect surface η is estimated using the working independence model

  $$Y_{ij}(d)=\eta (d,T_{ij})+{\epsilon }_{ij}(d).$$

  Smoothness selection is by REML, which is more robust to neglecting the correlations in the errors than prediction error methods [21].

• Step 2The autocovariance functions for the random processes X_i = (X_i,0, X_i,1) and U_ij are estimated from the residuals Y_ij(d) − η̂ (d, T_ij), using a linear regression step.
• Step 3The ‘raw’ autocovariance function estimates from step 2 are subjected to bivariate smoothing, yielding also an estimate for σ².
• Step 4Eigen decompositions of the smoothed autocovariance functions provide bases for representing X = (X_i,0, X_i,1) and U_ij, which are truncated to achieve parsimony.
• Step 5Estimated BLUPs then provide estimates for the subject- and visit-specific scores, which summarize the main differences in the dynamics of functions over time.

3.1. Estimation of the mean

The fixed effect population mean surface η(d, T) can be estimated using a bivariate smoother in d and T under a working independence assumption. For discussions of smoothing for correlated data, see [21, 24]. Possibilities for smoothers include penalized splines [39], smoothing splines [11] and local polynomials [9]. Choice of a smoother and of the smoothing parameter or bandwidth is discussed extensively in the literature and is not the main focus here. It is our experience that most reasonable smoothers used judiciously will provide similar results. For simplicity and efficiency of the implementation for large data sets, we use penalized spline smoothing with REML estimation of the smoothing parameter. This choice has also been found to be relatively robust to misspecification of the error correlation structure in [21].

A bivariate smoother is appropriate when the collection of observations across visits and subjects is relatively dense. This need not be the case in general, and simpler choices might be more sensible. For example, η(d, T_ij) = η₀(d) + T_ijβ might be more appropriate if the T_ij form a sparser collection. In the case of equally spaced visits, T_ij = T_j, [7] used η(d, T_ij) = η_j(d). Choices will depend on the particular application, available data and scientific problem. In most applications, estimating the mean function is quite easy and, even, routine. Once a consistent estimator of the mean function is available, data can be centered as follows Y_ij(d) − η̂(d, T_ij) for all i, j and d. In the following we assume that the Y_ij(d) are mean zero.

3.2. Estimation of the covariance operators

A crucial point of our proposed methodology is estimating the covariance operators K_X(·, ·) and K_U (·, ·). To estimate the covariance functions, we focus on the cross-products Y_ij(d)Y_ik(d′). Because Y_ij(d) has zero mean, each product Y_ij(d)Y_ik(d′) is an estimator of the covariance between the function observed at time T_ij evaluated at location d, and the function observed at time T_ik evaluated at location d′. Every subject thus contributes an estimator each for every available pair of observations at time T_ij evaluated at location d, and at time T_ik evaluated at location d′. Available pairs of observations may vary between subjects in their (d, d′) and (T_ij, T_ik) combinations. The method described in the following can thus easily handle missing data, both in terms of visits per subject or observations per visit.

Under the assumptions of model (2.1),

$$\text{E}\{Y_{ij}(d)Y_{ik}(d^{\prime })\}=\text{Cov}\{Y_{ij}(d),Y_{ik}(d^{\prime })\}=K_0(d,d^{\prime })+T_{ik}{K}_{01}(d,d^{\prime })+T_{ij}{K}_{01}(d^{\prime },d)+T_{ij}{T}_{ik}{K}_1(d,d^{\prime })+[K_U(d,d^{\prime })+{\sigma }^2{\delta }_{d{d}^{\prime }}]{\delta }_{jk},$$ (3.1)

for all d, d′, i, j and k, where δ_jk is Kronecker’s delta. Equation (3.1) suggests a straightforward solution for estimating the covariance operators: regress linearly the “outcome” Y_ij(d)Y_ik(d′) on the “covariates” (1, T_ik, T_ij, T_ikT_ij, δ_jk), where the “parameters” are {K₀(d, d′), K₀₁(d, d′), K₀₁(d′, d), K₁(d, d′), K_U (d, d′); d, d′ ∈ ; σ²}.

While the intuition behind the method is simple, there are two potential pitfalls that should be carefully avoided. First, σ² is identifiable only under the assumption that K_U (d, d′) is a bivariate smooth function in d and d′. Second, in a straightforward implementation of the linear regression on the basis of (3.1), there are $D^2{\sum }_{i=1}^I{J}_i^2$ observations and 4D² + 1 variables. In our moderately sized tract data, this would correspond to 19 million observations and 57, 500 variables. In larger data sets the problem would be even more serious. Thus, careful implementation is required to ensure computational feasibility. We propose the following 3-step estimation procedure that avoids these problems.

• Step A{K₀(d, d′), K₀₁(d, d′), K₀₁(d′, d), K₁(d, d′), K_U (d, d′)+ σ²δ_dd′} is estimated for each pair d ≤ d′ ∈ using least squares estimation based on (3.1). Symmetry constraints yield K₀(d, d′) = K₀(d′, d), K₁(d, d′) = K₁(d′, d) and K_U (d, d′) = K_U (d′, d) for d > d′. Denote estimates by K̃₀(d, d′), K̃₀₁(d, d′), K̃₁(d, d′) and K̃_U (d, d′).
• Step BBivariate smoothing in d and d′ over K̃₀(d, d′), K̃₀₁(d, d′) and K̃₁(d, d′) yields smooth estimates K̂₀(d, d′), K̂₀₁(d, d′) and K̂₁(d, d′). Bivariate smoothing over K̃_U (d, d′), leaving out the diagonal elements as proposed by [41, 50], also yields estimates K̂_U (d, d′).

  Please see Section 3.1 for a discussion of bivariate smoothing.

• Step Cσ² can be estimated as ${\widehat{\sigma }}^2=\frac{1}{D}{\displaystyle \sum _{d=1}^D}\{{\stackrel{\sim }{K}}_U(d,d)-{\widehat{K}}_U(d,d)\}$, if positive, and as zero otherwise.

Estimation in Step A can be done using efficient matrix-vector computations as detailed in Theorem 1 in Appendix A. The following is a consequence of that theorem.

Corollary 1

The computational effort for estimation of the covariance functions in Step A for the general model (2.2) is of the order O{max(p⁶, p²D²g)}, where $g=\sum J_i^2$ and p is the dimension of the vector-valued random process X_i(d) in (2.2).

All proofs can be found in Appendix A. For model (2.1), p = 2 is small. Note that p²D² is the order of the number of unknown parameters in the covariance functions, and g is the number of observation pairs contributing to the estimation. The effort thus is linear in both. Our software implementation is so efficient that the computational effort is dominated by the bivariate smoothing of the mean and covariance functions; see Section 4.3 for a detailed investigation of efficiency.

Our procedure does not guarantee that K̂_X(·, ·) and K̂_U (·, ·) are positive definite. We correct this problem by trimming the eigenvalue-eigenvector pairs corresponding to negative eigenvalues, a method that has been found to increase the L² accuracy [17] and has been shown to work well in practice [51].

3.3. Estimation of the eigenfunctions and scores

In the previous section we showed how to obtain the estimated covariance matrices K̂₀ = {K̂₀(d, d′)}_{d;d′ ∈} , K̂₀₁ = {K̂₀₁(d, d′)}_{d;d′ ∈} , K̂₁ = {K̂₁(d, d′)}_{d;d′ ∈} , and K̂_U = {K̂_U (d, d′)}_{d;d′ ∈} . Estimates of the eigenvalues and of the eigenfunctions ${\phi }_k^X(·)$, k = 1, 2, …, D, and ${\phi }_k^U(·)$, k = 1, 2, …, D, at the grid points can then be obtained using the spectral decomposition of K_X and K_U, ${\widehat{\mathit{K}}}_X={\displaystyle \sum _{k=1}^{2D}}{\widehat{\lambda }}_k{\widehat{\phi }}_k^X{\{{\widehat{\phi }}_k^X\}}^{\prime }$ and ${\widehat{\mathit{K}}}_U={\displaystyle \sum _{k=1}^D}{\widehat{\nu }}_k{\widehat{\phi }}_k^U{\{{\phi }_k^U\}}^{\prime }$, where ${\widehat{\phi }}_k^X=\{({\widehat{\phi }}_k^0(d),{\widehat{\phi }}_k^1(d));d\in \mathcal{D}\}$ and ${\widehat{\phi }}_k^U=\{{\widehat{\phi }}_k^U(d);d\in \mathcal{D}\}$, are orthonormal vectors in IR^2D and IR^D, respectively. The estimation of the number of eigenfunctions retained for further analysis, N_X and N_U, is described in Section 3.4.

In Section 2.3, equation (2.3), we showed that for fixed N_X and N_U, model (2.1) is a linear mixed model. Thus, we can use best linear unbiased prediction (BLUP) to obtain predictions of the subject- and subject/visit-specific scores, ξ_ik and ζ_ijk, respectively. BLUP calculation does not require a normality assumption and is a generalization of the conditional expectations used by [50].

For given eigenfunctions, mean function η(d, T), and variances λ_k, k = 1, …, N_X, ν_k, k = 1, …, N_U, the BLUP for b = (ξ₁₁, …, ξ_1NX, …, ξ_I1, …, ξ_INX ζ₁₁₁, …, ζ_11NU, …, ζ_IJI1, …, ζ_IJINU) in model (2.3) is given in the usual form by

$$\widehat{\mathit{b}}={\mathit{DZ}}^{\prime }{({\sigma }^2\mathit{I}+{\mathit{ZDZ}}^{\prime })}^{-1}(\mathit{Y}-\mathit{\eta }),$$ (3.2)

where Z = [Z_X|Z_U], Z_X = E_I ⊗ Φ⁰ + T ⊗ Φ¹, Z_U = I_n ⊗ Φ^U, E_I = (δ_ih)_ij=11,_…,_IJI;_h=1,…,I, T = (T_ijδ_ih)_ij=11,_…,_IJI;_h=1,…,I, ${\mathbf{\Phi }}^{\mathbf{0}}={\{{\phi }_k^0(d)\}}_{d\in \mathcal{D};k=1,\dots ,N_X},{\mathbf{\Phi }}^{\mathbf{1}}={\{{\phi }_k^1(d)\}}_{d\in \mathcal{D};k=1,\dots ,N_X},{\mathbf{\Phi }}^{\mathit{U}}={\{{\phi }_k^U(d)\}}_{d\in \mathcal{D};k=1,\dots ,N_U}$, D = blockdiag(D_X, D_U ) = blockdiag{I_I ⊗ diag(λ₁, …, λ_NX), I_n ⊗ diag(ν₁, …, ν_NU)}, Y = {Y₁₁(1), …, Y₁₁(D), …, Y_1J1(1), …, Y_1J1 (D), …, Y_IJI(1), …, Y_IJI(D)}, and η = {η(1, T₁₁), …, η(D, T₁₁), …, η(D, T_1J1), …, η(1, T_IJI), …, η(D, T_IJI)}. Here, ⊗ denotes the Kronecker product of matrices, and (a_ijh)_ij=11,_…,_IJIh=1,…,I denotes a matrix with entries a_ijh, rows ij, j = 1, …, J_i, i = 1, …, I, and columns h = 1, …, I.

We can obtain estimated BLUPs (EBLUPs) using the estimated functions and variances η̂(·, ·), σ̂², ${\widehat{\phi }}_k^0(·),{\widehat{\phi }}_k^1(·)$, λ̂_k, k = 1, …, N_X, and ${\widehat{\phi }}_k^U(·)$, ν̂_k, k =1, …, N_U, from Sections 3.1 and 3.2. This does not require fitting the model (2.3), which greatly increases computational efficiency. While straightforward implementation of (3.2) requires inverting nD × nD matrices, which would result in computational effort of the order O(n³D³), we make use of common matrix rules and of the model structure to obtain a more efficient representation, as detailed in Theorem 2 in Appendix A. The following result of Theorem 2 confirms the manageable computational effort even for very large data sets.

Corollary 2

Computational effort for calculation of the estimated BLUPs in (3.2) is of the order $O\{max(\mathit{nDf},I{N}_X^3)\}$, where $n={\sum }_{i=1}^I{J}_i$ and f= N_U + N_XI/n.

The proofs are provided in Appendix A. N_X and N_U are typically small, and much smaller than either D or the number of observed curves n. These results and efficient block matrix manipulation make the models proposed here feasible even for very large data sets. For example, one of the simulation examples in Section 4 uses 1, 000 subjects, who were observed at 8 visits and had 200 observations per visit.

3.4. Decomposition of variance and choice of the number of components

There are several possible ways to choose the numbers of eigenfunctions N_X and N_U. Two alternatives that have been used before are leave-one-curve-out cross validation [38] and an AIC-type criterion [50]. Alternatively, one can make use of the fact that (2.3) is a linear mixed model, with N_X and N_U corresponding to the number of random effects. The conditional Akaike information criterion (cAIC), proposed for the selection of random effects in linear mixed models [12, 23, 43] could thus be employed. [40] and [6] point out that choosing the number of eigenfunctions corresponds to step-wise testing for zero variance components. They propose using a Restricted Likelihood Ratio Test (RLRT) for this zero variance. The null distribution can be easily approximated using methods introduced by [14] based on the null distribution derived in [5].

Here we follow a simpler approach based on the proportion of variance explained. This approach has several advantages: a) popularity; b) simplicity and interpretability; c) quantification of the contribution of the different processes to the variability in Y_ij(d).

To better understand variance partitioning, we give the following result.

Lemma 1

Let Y_ij(d) ∈ L²[0, 1] be a process that follows model (2.1) with zero mean, η(d, T_ij) ≡ 0. Let T_ij be independently distributed as T for all i and j, where E(T ²) < ∞, and let T_ij be independent of X_i, U_ij and ε_ij(d), d ∈ . Then, the average variance of Y_ij(d) can be written as

$${\int }_0^1\mathit{Var}\{Y_{ij}(s)\}ds={\int }_0^1(\sum _{k=1}^{\infty }{\lambda }_k[{\{{\phi }_k^0(s)\}}^2+2\text{E}(T_{ij}){\phi }_k^0(s){\phi }_k^1(s)+\text{E}(T_{ij}^2){\{{\phi }_k^1(s)\}}^2]+\sum _{k=1}^{\infty }{\nu }_k{\{{\phi }_k^U(s)\}}^2+{\sigma }^2)ds.$$

The proof can be found in Appendix A. Given the usual interpretation of eigenvalues as variance explained in FPCA, one could be tempted to interpret λ_k similarly in the longitudinal context. The variance decomposition that we just described indicates that in LFPCA, λ_k can be interpreted as a variance component only if the time variable is standardized to have zero mean and unit variance. In this case, the two components of the ${\phi }_k^X$ eigenfunction, ${\phi }_k^0$ and ${\phi }_k^1$, will be on the same scale. We can then directly discuss λ_k as the “variance explained” by the eigenfunction ${\phi }_k^X$ of K_X. Thus, we recommend standardizing the time variable. The variation in Y_ij(d) then has the following simple additive decomposition.

Corollary 3

In the case when E(T_ij) = 0 and Var(T_ij) = 1, the expression in Lemma 1 reduces to

$${\int }_0^1\mathit{Var}\{Y_{ij}(s)\}ds=\sum _{k=1}^{\infty }{\lambda }_k+\sum _{k=1}^{\infty }{\nu }_k+{\sigma }^2.$$

Thus, for standardized T_ij, the variation in Y_ij(d) can be decomposed additively into the contributions from the random intercept and random slope process, ${\sum }_{k=1}^{\infty }{\lambda }_k$, from the visit-specific deviation process, ${\sum }_{k=1}^{\infty }{\nu }_k$, and from the additional random noise, σ². This leads to a simple decision rule for N_X and N_U: choose ${\phi }_k^X$ and ${\phi }_k^U$ corresponding to λ_k and ν_k in decreasing order, until

$$\{\sum _{k=1}^{N_X}{\lambda }_k+\sum _{k=1}^{N_U}{\nu }_k+{\sigma }^2\}/\{\sum _{k=1}^{\infty }{\lambda }_k+\sum _{k=1}^{\infty }{\nu }_k+{\sigma }^2\}\ge L,$$

where L is a pre-specified proportion of explained variation, such as L = 0.95. ${\sum }_{k=1}^{\infty }{\lambda }_k$ and ${\sum }_{k=1}^{\infty }{\nu }_k$ provide quantifications of the relative importance of the X and U processes.

4. Simulations

4.1. Simulation design

To investigate the performance of our estimation procedure, we conduct an extensive simulation study. The design combines and extends scenarios used by [7] and [50]. For all settings, we generate 1000 data sets from model (2.3), where N_X = N_U = 4. We set the mean function to η(d, T ) = 0.5(T/4 − d)². The unequally spaced time points T_ij are simulated such that the mean for each subject is zero, and increments T_ij − T_ij−1 are independent draws from a uniform distribution on [0, 1]. The time variable is then standardized to have unit variance. The curves Y_ij(d) are taken to be observed for d ∈ = {(k −0.5)/D, k = 1, …, D}, D = 120, as in the tract data. We set the variances to be λ_k = ν_k = 2^1−k, k = 1, …, 4, and σ = 0.05. This choice corresponds to 0.07% of the overall average variance explained by the error variance σ², higher than in the tract data (0.02%, please see Table 2).

Table 2.

Average variance ${\int }_0^1\mathit{Var}\{Y_{ij}(s)\}ds$ explained by the different model components in percent.

To obtain the variance explained by ${\phi }_k^0$ and ${\phi }_k^1$, the corresponding λ_k is multiplied by $\int {({\phi }_k^0(s))}^{2}ds$ and $\int {({\phi }_k^1(s))}^{2}ds$, respectively. The cumulative variance explained for row k is the sum of the row entries up to and including row k. The last row gives the cumulative variance explained for the respective column.

k	${\phi }_k^0$	${\phi }_k^1$	${\phi }_k^U$	σ 2	cumulative
1	37.97	0.21	22.81	0.02	61.01
2	6.76	0.55	5.41		73.73
3	3.33	0.32	2.96		80.34
4	2.11	0.43	2.07		84.95
5	1.50	0.28	1.51		88.24
6	0.98	0.19	1.32		90.73
	52.65	1.98	36.08	0.02	90.73

We consider all possible combinations of the following scenarios:

1. number of subjects (a) I = 50 (b) I = 100 (c) I = 200 and (d) I = 500, including both smaller and larger numbers than in the tract data,

2. 1. balanced design with J_i = 4 for all i,

   2. unbalanced design with J_i ∈ {1, …, 9}, (a multiple of 8, 8, 9, 6, 5, 5, 4, 3, 2 times, respectively), giving 4 observations per subject on average,

3. 1. normal scores ξ_ik ~ (0, λ_k) and ζ_ijk ~ (0, ν_k) for all i, j and k,

   2. non-normal scores; ξ_ik drawn from a mixture of two normals, with equal probability from either $\mathcal{N}(\sqrt{{\lambda }_k/2},{\lambda }_k/2)$ or from $\mathcal{N}(-\sqrt{{\lambda }_k/2},{\lambda }_k/2)$; ζ_ijk drawn with equal probability from either $\mathcal{N}(\sqrt{{\nu }_k/2},{\nu }_k/2)$ or $\mathcal{N}(-\sqrt{{\nu }_k/2},{\nu }_k/2)$,

4. 1. eigenfunctions ${\phi }_k^X=({\phi }_k^0,{\phi }_k^1)$ with ${\phi }_k^0$ and ${\phi }_k^1$ orthogonal and of equal norm $\sqrt{1/2};{\phi }_k^U$ are not orthogonal to either ${\phi }_k^0$ or ${\phi }_k^1$,

   2. eigenfunctions ${\phi }_k^X=({\phi }_k^0,{\phi }_k^1)$ with ${\phi }_k^0$ and ${\phi }_k^1$ non-orthogonal and of unequal norms $\sqrt{3/4}$ and $\sqrt{1/4}$. ${\phi }_k^U$ are equal to ${\phi }_j^0$ or ${\phi }_j^1$ for some j for all k,

5. 1. estimation does not include bivariate smoothing of the covariance functions. In this case, smoothing is only used to obtain an estimate of the diagonal K_U (d, d), d ∈ , and of σ²,

   2. estimation includes bivariate smoothing of the covariance functions.

This gives 64 different combinations overall. The eigenfunctions for setting 4. (a) are

$$\begin{array}{lll}{\phi }_1^0(d)=sin(2\pi d)\hfill & {\phi }_1^1(d)=1/\sqrt{2}\hfill & {\phi }_1^U(d)=1\hfill \\ {\phi }_2^0(d)=cos(2\pi d)\hfill & {\phi }_2^1(d)=sin(6\pi d)\hfill & {\phi }_2^U(d)=\sqrt{3}(2d-1)\hfill \\ {\phi }_3^0(d)=sin(4\pi d)\hfill & {\phi }_3^1(d)=cos(6\pi d)\hfill & {\phi }_3^U(d)=\sqrt{5}(6d^2-6d+1)\hfill \\ {\phi }_4^0(d)=cos(4\pi d)\hfill & {\phi }_4^1(d)=sin(8\pi d)\hfill & {\phi }_4^U(d)=\sqrt{7}(20d^3-30d^2+12d-1).\hfill \end{array}$$

Note that while ${\phi }_k^0$ and ${\phi }_k^1$ are orthogonal, they are not orthogonal to ${\phi }_j^U$ for all k and j ≠ 1. The eigenfunctions for setting 4. (b) are

$$\begin{array}{ll}{\phi }_1^0(d)=sin(2\pi d)\sqrt{2/3}\hfill & {\phi }_1^1(d)=1/2\hfill \\ {\phi }_2^0(d)=cos(2\pi d)\sqrt{2/3}\hfill & {\phi }_2^1(d)=\sqrt{3}(2d-1)/2\hfill \\ {\phi }_3^0(d)=sin(4\pi d)\sqrt{2/3}\hfill & {\phi }_3^1(d)=\sqrt{5}(6d^2-6d+1)/2\hfill \\ {\phi }_4^0(d)=cos(4\pi d)\sqrt{2/3}\hfill & {\phi }_4^1(d)=\sqrt{7}(20d^3-30d^2+12d-1)/2\hfill \\ {\phi }_1^U(d)=\sqrt{4}{\phi }_1^1(d)\hfill & \hfill \\ {\phi }_2^U(d)=\sqrt{4/3}{\phi }_1^0(d)\hfill & \hfill \\ {\phi }_3^U(d)=\sqrt{4/3}{\phi }_2^1(d)\hfill & \hfill \\ {\phi }_4^U(d)=\sqrt{4/3}{\phi }_3^1(d).\hfill & \hfill \end{array}$$

Note that now ${\phi }_k^0$ and ${\phi }_j^1$ are non-orthogonal, and ${\phi }_k^0$ has a larger norm than ${\phi }_k^1$. Also, ${\phi }_k^U$ is equal to one of the ${\phi }_j^0$ or ${\phi }_j^1$, j = 1, …, 4, for each k, making separation of the two processes X and U much more difficult. For bivariate smoothing of the mean and covariance functions, we use tensor product penalized cubic regression splines with 10 knots per dimension, where the smoothing parameters are estimated using REML estimation, as implemented in the R package mgcv [47].

To investigate the sensitivity of our results to our choices for η and σ, we also consider four variations on the balanced design with I = 100 and J_i = 4 for all i (1b and 2a), non-orthogonal ${\phi }_k^0,{\phi }_k^1$ and ${\phi }_k^U$ with unequal weight on ${\phi }_k^1$ and ${\phi }_k^0$ (4b), a mixture distribution for the scores ξ_ij and ζ_ijk (3b), and bivariate smoothing of the covariance functions (5b). For these four settings, we vary η(d, T ) = (T/4 − d/D + 1/2)(T/4 + d/D − 1/2), η(d, T) = sin(πT/2)d/D, σ = 0.5 (corresponding to 6.25% of the overall average variance explained by the error variance σ²) or σ = 1 (21.05%), respectively.

For each of the 1000 replications and for each of the 68 settings, our estimation procedure from Section 3 with N_X = N_U = 4 is used to obtain estimates of the mean function, the covariance functions, the eigenfunctions, the scores, and all variances.

4.2. Simulation results

We now discuss results for one of the 68 settings in detail, and point out differences across settings. The complete simulation results can be found in the supplementary material.

Figure 2 and Table 1 show the main results of simulations based on a balanced design with I = 100 and J_i = 4 for all i (1b and 2a), non-orthogonal ${\phi }_k^0,{\phi }_k^1$ and ${\phi }_k^U$ with unequal weight on ${\phi }_k^1$ and ${\phi }_k^0$ (4b), a mixture distribution for the scores ξ_ij and ζ_ijk (3b), and no bivariate smoothing of the covariance functions (5a). A plot of the true and estimated mean functions can be found in the supplementary material, illustrating that the mean is well and unbiasedly estimated.

Fig 2.

True and estimated eigenfunctions ${\phi }_k^X=({\phi }_k^0,{\phi }_k^1)$ and ${\phi }_k^U$, k = 1, …, 4. The left column gives results for the part ${\phi }_k^0$ corresponding to the random functional intercept X_i,0, the middle column for the part ${\phi }_k^1$ corresponding to the random functional slope X_i,1, and the right column for the component ${\phi }_k^U$ corresponding to the visit-specific functional deviation U_ij. Shown are the true function (thick black line), the mean of the estimated functions over 1000 simulations (dashed red line), the pointwise 5th and 95th percentiles of the estimated functions (blue), and the estimated functions from the first 50 simulations (grey). Simulations were based on model (2.3) with N_X = N_U = 4, a balanced design with I = 100 and J_i = 4 for all i, non-orthogonal ${\phi }_k^0,{\phi }_k^1$ and ${\phi }_k^U$ with unequal weight on ${\phi }_k^1$ and ${\phi }_k^0$, a mixture distribution for the scores ξ_ij and ζ_ijk, and no bivariate smoothing of the covariance functions.

Table 1.

True and estimated subject-specific and visit-specific scores ξ_ik and ζ_ijk. Given are summary statistics of the scaled differences $({\widehat{\xi }}_{ik}-{\xi }_{ik})/\sqrt{{\lambda }_k}$ (top) and $({\widehat{\zeta }}_{\mathit{ijk}}-{\zeta }_{\mathit{ijk}})/\sqrt{{\nu }_k}$ (bottom), k = 1, …, 4. Simulations were based on model (2.3) with N_X = N_U = 4, a balanced design with I = 100 and J_i = 4 for all i, non-orthogonal ${\phi }_k^0,{\phi }_k^1$ and ${\phi }_k^U$ with unequal weight on ${\phi }_k^1$ and ${\phi }_k^0$, a mixture distribution for the scores ξ_ij and ζ_ijk, and no bivariate smoothing of the covariance functions.

Minimum	1st Quantile	Median	Mean	3rd Quantile	Maximum
−2.39	−0.31	0.00	0.00	0.30	2.56
−2.52	−0.24	0.00	0.00	0.23	3.13
−3.42	−0.31	0.00	0.00	0.31	3.39
−4.17	−0.20	0.00	0.00	0.20	4.58
−2.80	−0.18	0.00	0.00	0.18	3.11
−3.68	−0.39	0.00	0.00	0.39	4.26
−2.77	−0.30	0.01	0.01	0.31	2.54
−3.38	−0.34	0.00	0.00	0.34	4.16

Figure 2 shows the true and estimated eigenfunctions ${\phi }_k^X=({\phi }_k^0,{\phi }_k^1)$ and ${\phi }_k^U$, k = 1, …, 4. Results for ${\phi }_k^0,{\phi }_k^1$ and ${\phi }_k^U$ are displayed in the left, middle and right panels, respectively. Shown are the true function (thick black line), the mean of the estimated functions over 1000 simulations (dashed red line), the pointwise 5th and 95th percentiles of the estimated functions (blue), and the estimated functions from the first 100 simulations (grey). Note that the covariance functions, and thus the eigenfunctions, are not smoothed in this setting.

For all functions, the mean of the estimated functions is very close to the true function, and the variability around it is small. It can be noted that the ${\phi }_k^U$ are slightly better estimated. This is due to the fact that estimation of the covariance function K_U (d, d′) is based on n = ΣJ_i visits, while estimation of the covariance function K_X(d, d′) is based on only I subjects, with I = n/4 in this setting. In this case, ${\phi }_k^0$ has a larger norm than ${\phi }_k^1$, making estimation of this component easier. This is noticeable in a smaller variance for ${\phi }_k^0$. Nevertheless, estimation of the ${\phi }_k^1$ is also remarkably good. Overall, estimation of all functions is very good, even though: a) ${\phi }_k^0$ and ${\phi }_k^1$ are not mutually orthogonal; and b) each ${\phi }_k^U$ is actually identical to either ${\phi }_j^0$ or ${\phi }_j^1$ for some j. Our estimation procedure effectively separates the X and U processes, even in the most difficult of circumstances and with a moderate sample size.

Table 1 provides results for the scores ξ_ik and ζ_ijk, k = 1, …, 4. Shown are summary statistics for the scaled differences between estimated and true scores, $({\widehat{\xi }}_{ik}-{\xi }_{ik})/\sqrt{{\lambda }_k}$ and $({\widehat{\zeta }}_{\mathit{ijk}}-{\zeta }_{\mathit{ijk}})/\sqrt{{\nu }_k}$, k = 1, …, 4. The table illustrates that the majority of estimates lies close to the true scores, relative to the standard deviation of the score in question, even if the distribution of the estimates is more heavy tailed than in a normal distribution. This might be expected from the fact that the principal components ${\phi }_k^X$ and ${\phi }_k^U$ in model (2.3) are estimated and not observed.

Further figures in the supplementary material show results for the estimation of the variances, σ², λ_k and ν_k, k = 1, …, 4. The ν̂_k are centered at the true values ν_k, with about 70% within 10% and more than 95% within 20% of the true value. The λ̂_k show a slight downward bias and somewhat larger variation, reflecting the smaller effective sample size for estimation of these variance components. σ² is estimated almost as well as the ν_k.

Overall, the estimation procedure performed very well in a wide range of scenarios. Across simulations, we found the following similarities and differences. First, results improve for an increasing number of subjects I. As expected, a larger I decreases the variability of the estimated eigenfunctions, mean function, scores and variances. The slight downward bias in the λ̂_k disappears with increasing I. Second, a balanced design (2a) improves results compared to an unbalanced design (2b) with the same number of subjects and visits. A balanced design leads to a) decreased variability in the estimated mean η̂(d, T ), as we estimate the mean under a working independence assumption before estimating the complex covariance structure b) decreased variability in the estimated eigenfunctions ${\widehat{\phi }}_K^X$ and decreased variability and small sample bias in the variances λ̂_k, k = 1, …, N_X. This is similarly due to the fact that we estimate the covariance functions using least squares under a working independence assumption. Estimation of the ${\phi }_k^U$ is not much affected by how balanced the design is, although there is some indication that small estimates λ̂_k are compensated for by a slight increase in the ν̂_k. Third, results for normal scores (3a) and non-normal scores (3b) where virtually identical. This is expected, as BLUPs do not rely on a normality assumption and are thus robust to departures from normality. Still, it is reassuring to see this confirmed in practice. Forth, non-orthogonality of ${\phi }_k^0$ and ${\phi }_k^1$ (4b) does not affect results compared to orthogonality (4a). Even though in (4b), each ${\phi }_k^U$ is equal to either ${\phi }_j^0$ or ${\phi }_j^1$ for some j, estimation of the ${\phi }_k^U$ is equally good in both cases. The only consistent difference between the two designs is, that as in (4b) ${\phi }_k^0$ has a larger part in the norm of ${\phi }_k^X$, estimation of ${\phi }_k^0$ improves somewhat, while estimation of ${\phi }_k^1$ deteriorates slightly. Fifth, results excluding (5a) and including (5b) bivariate smoothing of the covariance functions were very similar, with the smooth version more effective at filtering out the measurement errors ε_ij(d) and obtaining smooth eigenfunctions ${\phi }_k^X$ and ${\phi }_k^U$.

Our sensitivity analyses indicate that results are not very sensitive to the choice of the mean function, with all three considered mean functions estimated well and unbiasedly. Large error variances increase the variability of all estimates. When signal-to-noise ratios become small due to very large error variances and small variances λ_k or ν_k, this leads to some underestimation of the magnitude (but not shape) of the eigenfunctions. This is due to the unbiasedness of estimation for the covariance functions, which are quadratic in the eigenfunctions, and the attenuation resulting from large variances in $\mid \text{E}(X)\mid =\sqrt{\text{E}(X^2)-\text{Var}(X)}<\sqrt{\text{E}(X^2)}$.

4.3. Computational efficiency

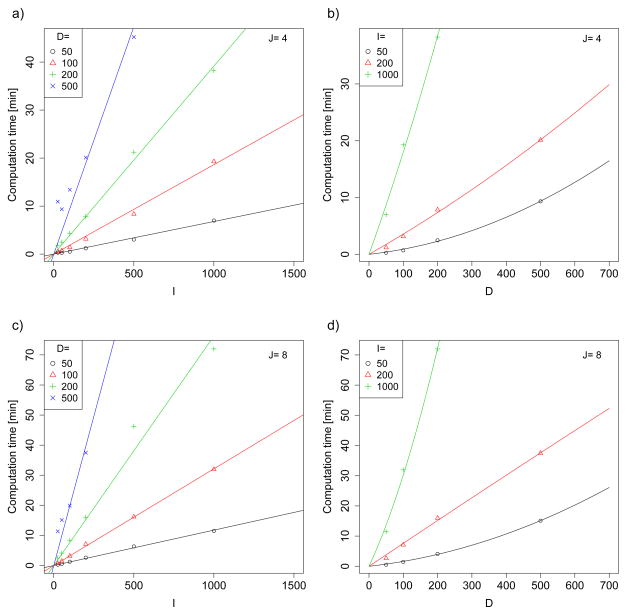
To investigate computation time we considered different combinations of number of subjects I ∈ {25, 50, 100, 200, 500, 1000}, number of observations per subject J ∈ {4, 8}, and number of sample points per curve D ∈ {50, 100, 200, 500}. All other parameters were chosen as for the simulations described in Section 4.1, settings combination 2(a), 3(a), 4(a), 5(a).

Figure 3 provides the computation times. System times were (for practical reasons) measured on three different cluster nodes running 64-bit Red Hat Linux, with 2.3/2.6/3.0 GHz AMD Opteron Processors and 32 GB random access memory. Figures 3 a) and c) for J = 4 and J = 8 display computation time versus the number of subjects I, stratified by D. For example, computation time for I = 100 subjects with J = 4 visits and D = 100 points per curve was just 1.4 minutes, while computation for I = 1, 000, J = 8 and D = 200 took 72 minutes. Figures 3 b) and d) display computation times versus sample points per curve, D, stratified by I. As suggested by Corollaries 1 and 2, computation time is roughly linear in I and between linear and quadratic in D. A linear regression of the log computation time log(C) on log(I), log(J) and log(D) yields $\widehat{log(C)}=-7.12+0.93log(I)+1.38log(D)+0.82log(J)$. The coefficient for log(D) is indeed between 1 and 2, as expected from Corollaries 1 and 2. The coefficients for log(I) and log(J) are close to 1, but somewhat lower, reflecting that there are some parts of the estimation procedure not depending on I and J. The adjusted R² for the model is a high 0.98, indicating that good estimates of computation time on comparable machines can be obtained from this regression equation also for parameter combinations not considered here. Note, however, that for very large I and, especially, D, memory might be more of a concern than computational efficiency. In that case, one can replace our efficient matrix computations by less efficient methods that optimize memory usage.

Fig 3.

Computation time for LFPCA for a simulated data set with the given number of subjects I and number of observations per subject J, and with D sample points per curve. Specifics of how computation time was measured are given in Section 4.3.

5. Application

In this section, we use LFPCA to decompose the variability in the tractography data. We first provide the scientific background.

5.1. Background and scientific questions

Multiple sclerosis (MS) is a disorder of the central nervous system (CNS) [e.g. 4]. MS causes typical abnormalities on magnetic resonance imaging (MRI) scans of the brain and spinal cord, and consequently MRI has become the primary diagnostic tool for MS. MRI scanning is increasingly used to monitor disease progression and response to therapy and has become an important surrogate outcome measure in clinical trials.

Diffusion tensor imaging (DTI), in contrast to conventional MRI techniques, is able to resolve individual functional tracts within the CNS white matter, the primary target of MS. DTI is sensitive to diffusion anisotropy, which, in the brain and spinal cord, corresponds to the tendency of water to diffuse along axonal tracts [1]. A focus on one or several tracts with specific functional correlates can then help in understanding the neuroanatomical basis of disability in MS. Quantitative measures derived from DTI data include fractional anisotropy (FA), measuring the degree of anisotropy between 0 and 1 [2]. FA can be decreased in MS due to lesions, loss of myelin and axon damage [42, 45].

Measurement of tract-specific MRI indices has traditionally worked with averages along tracts, ignoring the spatial variation of those indices within tracts [25, 32, 36]. However, that spatial variation can be considerable. The extent to which accounting for this spatial variation can improve detection of abnormality, correlation with disability, or sensitivity to change across time, remains uncertain. The last of these is particularly relevant for monitoring individual patients in the clinic and for the design and powering of clinical trials of new drugs.

We are interested in using the full spatial information to gain a better understanding of differences between subjects both with respect to their mean tract profiles over time (static behavior) and to the changes in those tract profiles over time (dynamic behavior). Our data set includes measurements for 84 MS patients and 28 controls with 1 to 8 complete visits, giving 308 visits overall. At each visit, we have measurements of FA and the diffusivities along several tracts in the brain, which were reconstructed using the tract finding algorithm of [28]. We will focus here on the corpus callosum, a tract connecting the two hemispheres of the brain. The 120 sample points - from the splenium (back of the head) to the genu/rostrum (closer to the eyes) - were chosen equidistantly between certain landmarks on the tract used for registration of curves between subjects [33]. The corpus callosum and its segmentation are illustrated in Figure 1 (top). Figure 1 (bottom) shows example profiles from two MS patients, illustrating the variability of profiles between subjects and within subjects over time. Visual examination of these tract profiles reveals variation within subjects across both space and time but no clear and consistent trend over time.

5.2. Application of LFPCA to the tractography data

As changes in MRI hardware over the five years of the study caused some variation in the measured MRI indices, we use a preprocessing step to remove differences due to variation in scanning technique. For each of the five scanning epochs, we estimate a mean profile for cases alone, using one visit per subject. This avoids confounding of disease status with epoch due to uneven distribution of cases and controls among epochs, and confounding by disease progression. We then subtract the difference of the epoch mean profile to the overall mean profile from all functional observations.

We obtain a decomposition of the variance using LFPCA. The time variable is centered by subject and standardized. For bivariate smoothing of the mean and covariance functions, we use tensor product penalized cubic regression splines with 30 knots per dimension, with smoothing parameters estimated using REML. A graph of the mean function η(d, T) is given in the supplementary material. The mean profile is roughly constant over time, with some variation near areas of high curvature.

For a pre-specified level L = 90% of explained average variance ${\int }_0^1\text{Var}\{Y_{ij}(s)\}ds$, LFPCA gives N_X = N_U = 6 principal components ${\phi }_k^X$ and ${\phi }_k^U$ for the X and U processes. The decomposition of the average variance is given in Table 2. 38% of the variation is explained by the first principal component for X, ${\phi }_1^X$, another 23% by the first principal component for U, ${\phi }_1^U$. Overall, the first six components ${\phi }_k^X$, k = 1, …, 6, explain 55% of the average variance, indicating that the X process captures most of the variation in the data. Within X, most of the variation is explained by the random functional intercept X_i,0, but the variance due to the subject-specific random slope is still large compared to the measurement error. Note also that the study period is much shorter than the disease duration for some of the patients, such that X_i,1 might still be of large practical relevance over many years. Within-curve measurement error is negligible due to a smoothing step during profile construction, explaining only 0.02%. Estimated variances were λ̂_k = 0.316, 0.060, 0.030, 0.021, 0.015, 0.010, k = 1, …, 6, ν̂_k = 0.189, 0.045, 0.025, 0.017, 0.012, 0.011, k = 1, …, 6, and σ̂² = 0.0002.

Figure 4 shows the first three estimated principal components for the random intercept and slope process X. The left column gives estimates for the ${\phi }_k^0$, corresponding to the random functional intercept X_i,0. Depicted are estimates for the overall mean η(d) (solid line), and for $\eta (d)\pm 2\sqrt{{\lambda }_k}{\phi }_k^0$, k = 1, 2, 3 (+ and −, respectively). The middle column gives the corresponding results for the random functional slope X_i,1. The right column shows boxplots for the estimates of the scores ξ_ik corresponding to ( ${\phi }_k^0,{\phi }_k^1$), k = 1, 2, 3, by case/control group. Estimated scores for the two example patients with tract profiles shown in Figure 1 are indicated by A and B, respectively.

Fig 4.

The first three estimated principal components for the random intercept and slope process X. The left column gives estimates for the ${\phi }_k^0$, corresponding to the random functional intercept X_i,0. Depicted are estimates for the overall mean η(d) (solid line), and for $\eta (d)\pm 2\sqrt{{\lambda }_k}{\phi }_k^0$, k = 1, 2, 3 (+ and −, respectively). The middle column gives the corresponding results for the random functional slope X_i,1. The right column shows boxplots for the estimates of the scores ξ_ik corresponding to ( ${\phi }_k^0,{\phi }_k^1$), k = 1, 2, 3, by case/control group. Estimated scores for the two example patients with tract profiles shown in Figure 1 are indicated by A and B, respectively.

Positive loadings ξ̂_i1 > 0 on the first component correspond to a lower mean function with a particularly deep FA dip in the isthmus (around 20), but only to small changes of profiles over time. For example, patient A with a much lower dip than B loads positively on this component, while B’s loading is roughly zero. The second component is a mean contrast, with positive scores corresponding to a lower dip around 20 and a higher plateau around 60. The corresponding change over time is similar, if smaller in magnitude, and could explain how the differences in mean profiles evolved over time. The large positive score ξ̂_i2 in patient A corresponds to the large contrast between low dip and high plateau in this patient, which is very unpronounced in patient B (roughly zero score). The third component shows a shift of the location of the dip, which might reflect differences in anatomy that affect the tractography. This goes hand in hand with a slight further shifting and deepening (for negative scores) of the dip over time. For example, patient A, in contrast to patient B, exhibits more of a deepening of the dip and a shift to the left, with corresponding negative score ξ̂_i3. As mentioned above, these consistent changes over time are not immediately apparent from an examination of the tract profiles in Figure 1 but are clearly revealed by loadings on the principal components derived from the LFPCA analysis. In future work, we plan to examine whether these changes can portend disease course.

Figure 5 shows the corresponding results for the visit-specific functional deviation U. ${\widehat{\phi }}_1^U$ is similar in shape to ${\widehat{\phi }}_1^0$. Patient A at visit 8, for example, shows a lower profile than would be expected from the average evolution in this patient over time, and consequently has a positive score ζ̂_ij1, with the converse being true for patient B at visit 2. Components ${\widehat{\phi }}_2^U$ and ${\widehat{\phi }}_3^U$ seem to pick up variation at the ends of the tract as well as visit-to-visit shifts of the location of the dip, which might be due to measurement error. Note that the U process captures both measurement error and true biological fluctuations, which are impossible to separate without additional subject-matter insight. Filtering out these processes allows us to study the systematic trends modeled by X.

Fig 5.

The first three estimated principal components for the visit-specific deviation process U. The left column gives results for the principal components ${\phi }_k^U$, depicting estimates for the overall mean η(d) (solid line), and for $\eta (d)\pm 2\sqrt{{\nu }_k}{\phi }_k^U$, k = 1, 2, 3 (+ and −, respectively). The right column shows boxplots for the estimates of the scores ζ_ik corresponding to ${\phi }_k^U$, k = 1, 2, 3, by case/control group. Estimated scores for example visits of the two patients with tract profiles shown in Figure 1 are indicated by A (visit 8) and B (visit 2), respectively.

Our model allows straightforward inclusion of additional covariates such as case/control status, disease severity, medication or age in the mean function η. In this study, however, we were interested in how the main variations in tract profiles and their changes over time differed by case/control group, i.e. in the covariance part of the model. When fixed effect group specific means are the target of inference, our approach could be used to improve the confidence band estimators on the group-specific mean difference. For example, the group-specific means could be estimated first under independence, then the covariances can be estimated using LFPCA, and then estimates of the group-specific mean differences can be further improved using the estimated covariance structure. The process can even be iterated until convergence.

Focusing on the covariances, we find a statistically significant difference in the distribution of the estimated scores ξ̂_i1 between MS patients and controls (p=0.0056 in a Mann-Whitney-Wilcoxon test; also in a linear regression adjusting for age and sex). The patient group in particular seems to have a higher mean and a heavier right tail. This could be an indication of a mixture in this group of patients who are more or less affected by MS along this particular tract. Potential loading-based clustering into patient subgroups will be of interest in future work. Interestingly, FA for this component is not decreased uniformly along the tract, but only posterior to the genu (ca. 1–100), with the decrease being especially pronounced in the area of the isthmus (ca. 20). Our results thus identify the region of the corpus callosum (the isthmus) where MS seems to take its greatest toll and also define the ways in which that portion of the tract changes from one year to the next. In future work, we plan to examine whether these changes can portend disease course. This result could not have been obtained by using the average FA instead of our functional approach.

6. Discussion

We have introduced methods for functional data that is observed at multiple time points for the same subject. Our methods can be viewed as extending longitudinal mixed effects models by replacing the random effects with random processes. Models are designed to decompose the longitudinal functional data into a time-dependent population average, baseline (or static) subject-specific variability, longitudinal (or dynamic) subject-specific variability, subject/visit-specific variability and measurement error. We propose an estimation procedure based on an eigen expansion that is highly computationally efficient and performs well in a wide range of simulations and in our application.

Our work is different from functional data methodology applied to the analysis of longitudinally observed scalar data [41, among others], but builds on methods from both functional and longitudinal data analysis [8, 34]. While the considered model shares similarities with models used by [15, 29], we do not assume Gaussianity and our approach is based on functional principal component analysis. In addition to computational advantages (compare Section 4.3 and [19]), this allows the extraction of the main differences between subjects in the dynamics of their profiles over time, something of interest in many applications including our tractography study. Also, our work is different from methods for the 3-D analysis of subject-specific DTI studies [see for example 18]. It takes a functional data approach to tract data, as has recently been done for non-longitudinal DTI tractography data in [52].

Our approach can serve as a stepping-stone for further developments in the field of longitudinally observed functional data, and lends itself well to extensions. As our estimation procedure performs best when the number of time points per subject is balanced, it might be interesting to investigate further improvements, such as via iterations between mean and covariance estimation. Using an iterative approach, [49] find improvements to the integrated mean squared errors that are most pronounced for sparse functional data, where the number of sample points per curve is small. We will pursue such an approach in the future, in particular if dealing with sparse longitudinal functional data. While the functional random intercept-random slope model was sufficient for our application, it would also be interesting to apply our general model in more complex settings. And as our methods extract the main modes of variation in longitudinal functional data, including differences in mean curves and changes in curves over time, the associated scores could be of interest for further use in regression or classification.

Supplementary Material

Supplementary materials to “Longitudinal functional principal component analysis” by S. Greven, C. Crainiceanu, B. Caffo and D. Reich (doi: 10.1214/10-EJS575SUPP).

Appendix A: Theoretical results and proofs

Theorem 1

Estimates of the covariance functions in Step A can be expressed as ${\widehat{\mathit{\beta }}}_1={({\mathit{X}}_1^{\prime }{\mathit{X}}_1)}^{-1}{\mathit{X}}_1^{\prime }{\mathit{c}}_1$ and ${\widehat{\mathit{\beta }}}_2={({\mathit{X}}_2^{\prime }{\mathit{X}}_2)}^{-1}{\mathit{X}}_2^{\prime }{\mathit{c}}_2$. Here, β₁ is the 5×{D(D−1)/2} matrix with column {K₀(d, d′), K₀₁(d, d′), K₀₁(d′, d), K₁(d, d′), K_U (d, d′)} corresponding to d < d′ ∈ , and β₂ is the 4 × D matrix with column {K₀(d, d), K₀₁(d, d), K₁(d, d′), K_U (d, d) + σ²} corresponding to d ∈ . X₁ is the $({\sum }_{i=1}^I{J}_i^2)\times 5$ matrix with rows (1, T_ik, T_ij, T_ijT_ik, δ_jk), j, k = 1, …, Ji, i = 1, …, I, and X₂ is the $\{{\sum }_{i=1}^I{J}_i(J_i+1)/2\}\times 4$ matrix with rows (1, T_ik + T_ij, T_ijT_ik, δ_jk), j ≤ k = 1, …, J_i, i = 1, …, I. c₁ is the $({\sum }_{i=1}^I{J}_i^2)\times \{D(D-1)\}/2)$ matrix with column (Y_ij(d)Y_ik(d′), j, k = 1, …, J_i, i = 1, …, I) corresponding to d < d′ ∈ , and c₂ the $\{{\sum }_{i=1}^I{J}_i(J_i+1)/2\}\times D$ matrix with column (Y_ij(d)Y_ik(d), j ≤ k = 1, …, J_i, i = 1, …, I) corresponding to d ∈ .

Proof

Consider least squares estimation of (K₀(d, d′), K₀₁(d, d′), K₀₁(d′, d), K₁(d, d′), K_U (d, d′) + σ²δ_dd′; d ≤ d′ ∈ ) on the basis of (3.1). First, note that the design matrix in the corresponding linear regression is block diagonal, with blocks corresponding to (d, d′), d < d′, containing entries (1, T_ik, T_ij, T_ijT_ik, δ_jk) in the row corresponding to Y_ij(d)Y_ik(d′), and blocks corresponding to (d, d) containing entries (1, T_ik +T_ij, T_ijT_ik, δ_jk) in the row corresponding to Y_ij(d)Y_ik(d). Second, note that the blocks are identical for all pairs (d, d′), d < d′, respectively all pairs (d, d). Least squares estimates thus can be expressed as ${\widehat{\mathit{\beta }}}_1\equiv {({\mathit{X}}_1^{\prime }{\mathit{X}}_{\mathbf{1}})}^{-1}{\mathit{X}}_1^{\prime }{\mathit{c}}_1$ and ${\widehat{\mathit{\beta }}}_2={({\mathit{X}}_2^{\prime }{\mathit{X}}_2)}^{-1}{\mathit{X}}_2^{\prime }{\mathit{c}}_2$, where ${\mathit{X}}_1^{\prime }{\mathit{X}}_1$ and ${\mathit{X}}_2^{\prime }{\mathit{X}}_2$ are 5 × 5 and 4 × 4 matrices, respectively.

Proof of Corollary 1

From Theorem 1 and the analogous argument for the general model, only (p²+1)×(p²+1) matrices need to be inverted. Matrix inversion thus is of order O(p⁶). Matrix multiplication is of order O(p²D²g), giving overall computational effort of order O(max(p⁶, p²D²g)).

Theorem 2

The estimated BLUPs in (3.2) can be expressed as

$$\widehat{\mathit{b}}=\left(\begin{array}{ll}{\mathit{I}}_{{\mathit{N}}_{\mathit{X}}\mathit{I}}\hfill & -{\mathit{BC}}^{\prime }\hfill \\ \mathbf{0}\hfill & {\mathit{I}}_{{\mathit{N}}_{\mathit{U}}\mathit{n}}\hfill \end{array}\right)\left(\begin{array}{ll}\mathit{B}\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathit{R}\hfill \end{array}\right)\left(\begin{array}{ll}{\mathit{I}}_{{\mathit{N}}_{\mathit{X}}\mathit{I}}\hfill & \mathbf{0}\hfill \\ -\mathit{CB}\hfill & {\mathit{I}}_{{\mathit{N}}_{\mathit{U}}\mathit{n}}\hfill \end{array}\right){\mathit{Z}}^{\prime }(\mathit{Y}-\mathit{\eta }),$$

with C = E_I ⊗ φ^U′ φ⁰ + T ⊗ φ^U′ φ¹, R = I_n ⊗ diag(ν_k/(ν_k + σ²)) + GFG′, G = E_I ⊗ diag(ν_k/(ν_k + σ²)) φ^U′ φ⁰ + T ⊗ diag(ν_k/(ν_k + σ²)) φ^U′ φ¹, and where B and F are block-diagonal with blocks

$$\begin{array}{l}{\mathit{B}}_i={[J_i{{\mathbf{\Phi }}^0}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+T_{i•}({{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}})+T_{i•}^2{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+\text{diag}({\sigma }^2/{\lambda }_1,\dots ,{\sigma }^2/{\lambda }_{N_X})]}^{-1},\\ {\mathit{F}}_i={[J_i{{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{0}}+T_{i•}({{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{1}}+{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{0}})+T_{i•}^2{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{1}}+\text{diag}({\sigma }^2/{\lambda }_1,\dots ,{\sigma }^2/{\lambda }_{N_X})]}^{-1},\end{array}$$

i = 1, …, I, denoting $T_{i•}={\sum }_{j=1}^{J_i}{T}_{ij},T_{i•}^2={\sum }_{j=1}^{J_i}{T}_{ij}^2$, and L = I_D − Φ^U diag(ν_k/(ν_k + σ²)) Φ^U′. Here, diag(a_k) denotes a diagonal matrix with entries a_k, k = 1, …, N_U, and we suppress for simplicity hat notation that indicates estimated quantities.

Proof

For simplicity, we suppress hat notation that indicates estimated quantities in the computation of the EBLUPs. Using the Woodbury formula, we obtain

$$\widehat{\mathit{b}}={({\mathit{Z}}^{\prime }\mathit{Z}+{\sigma }^2{\mathit{D}}^{-1})}^{-1}{\mathit{Z}}^{\prime }(\mathit{Y}-\mathit{\eta }).$$

Using the Schur complement S, write

$$\begin{array}{c}{({\mathit{Z}}^{\prime }\mathit{Z}+{\sigma }^2{\mathit{D}}^{-1})}^{-1}={\left(\begin{array}{cc}\hfill {\mathit{Z}}_X^{\prime }{\mathit{Z}}_X+{\sigma }^2{\mathit{D}}_X^{-1}\hfill & \hfill {\mathit{Z}}_X^{\prime }{\mathit{Z}}_U\hfill \\ \hfill {\mathit{Z}}_U^{\prime }{\mathit{Z}}_X\hfill & \hfill {\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1}\hfill \end{array}\right)}^{-1}\\ =\left(\begin{array}{cc}\hfill {\mathit{I}}_{{\mathit{N}}_{\mathit{X}}\mathit{I}}\hfill & \hfill -{\mathit{A}}^{-1}{\mathit{Z}}_X^{\prime }{\mathit{Z}}_U\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_{{\mathit{N}}_{\mathit{U}}\mathit{n}}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\mathit{A}}^{-1}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{S}}^{-1}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\mathit{I}}_{{\mathit{N}}_{\mathit{X}}\mathit{I}}\hfill & \hfill \mathbf{0}\hfill \\ \hfill -{\mathit{Z}}_U^{\prime }{\mathit{Z}}_X{\mathit{A}}^{-1}\hfill & \hfill {\mathit{I}}_{{\mathit{N}}_{\mathit{U}}\mathit{n}}\hfill \end{array}\right),\end{array}$$

where $\mathit{A}={\mathit{Z}}_X^{\prime }{\mathit{Z}}_X+{\sigma }^2{\mathit{D}}_X^{-1}$ and $\mathit{S}=({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})-{\mathit{Z}}_U^{\prime }{\mathit{Z}}_X{\mathit{A}}^{-1}{\mathit{Z}}_X^{\prime }{\mathit{Z}}_U$.

Using properties of the Kronecker product, we have

$$\mathit{A}=\text{diag}(J_1,\dots ,J_I)\otimes {{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+\text{diag}(T_{1•},\dots ,T_{I•})\otimes ({{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}})+\text{diag}(T_{1•}^2,\dots ,T_{I•}^2)\otimes {{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+{\mathit{I}}_{\mathit{I}}\otimes \text{diag}({\sigma }^2/{\lambda }_1,\dots ,{\sigma }^2/{\lambda }_{N_X}).$$

Thus, A is a block-diagonal matrix with I blocks A_i of size N_X × N_X, and B = A⁻¹ can be computed as a block-diagonal matrix with the ith block of size N_X × N_X of the form

$${\mathit{B}}_i=[J_i{{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+T_{i•}({{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}})+T_{i•}^2{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}{+\text{diag}({\sigma }^2/{\lambda }_1,\dots ,{\sigma }^2/{\lambda }_{N_X})]}^{-1}.$$

Analogously,

$$\begin{array}{l}{({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}={({\mathit{I}}_{\mathit{n}}\otimes {{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}+{\mathit{I}}_{\mathit{n}}\otimes \text{diag}({\sigma }^2/{\nu }_1,\dots ,{\sigma }^2/{\nu }_{N_U}))}^{-1}\\ ={\mathit{I}}_{\mathit{n}}\otimes \text{diag}({\nu }_1/({\nu }_1+{\sigma }^2),\dots ,{\nu }_{N_U}/({\nu }_{N_U}+{\sigma }^2))\end{array}$$

can be computed explicitly, as the columns of Φ_U are orthonormal by construction. And finally, using the Woodbury formula again, the Schur complement S can be inverted as

$$\begin{array}{l}\mathit{R}={\mathit{S}}^{-1}={({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}+{({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}{\mathit{Z}}_U^{\prime }{\mathit{Z}}_X\times [\mathit{A}-{\mathit{Z}}_X^{\prime }{\mathit{Z}}_U{({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}\times {{\mathit{Z}}_U^{\prime }{\mathit{Z}}_X]}^{-1}{\mathit{Z}}_X^{\prime }{\mathit{Z}}_U{({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}\\ ={\mathit{I}}_{\mathit{n}}\otimes \text{diag}({\nu }_k/({\nu }_k+{\sigma }^2))+{\mathit{GFG}}^{\prime },\end{array}$$

where

$$\begin{array}{l}\mathit{C}={\mathit{Z}}_U^{\prime }{\mathit{Z}}_X={\mathit{E}}_{\mathit{I}}\otimes {{\mathit{\phi }}^U}^{\prime }{\mathit{\phi }}^0+\mathit{T}\otimes {{\mathit{\phi }}^U}^{\prime }{\mathit{\phi }}^{\mathbf{1}},\\ \mathit{G}={({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}\mathit{C}\\ ={\mathit{E}}_{\mathit{I}}\otimes \text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathit{\phi }}^U}^{\prime }{\mathit{\phi }}^{\mathbf{0}}+\mathit{T}\otimes \text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathit{\phi }}^U}^{\prime }{\mathit{\phi }}^{\mathbf{1}},\end{array}$$

and

$$\begin{array}{l}\mathit{H}={\mathit{Z}}_X^{\prime }{\mathit{Z}}_U{({\mathit{Z}}_U^{\prime }{\mathit{Z}}_U+{\sigma }^2{\mathit{D}}_U^{-1})}^{-1}{\mathit{Z}}_U^{\prime }{\mathit{Z}}_X\\ =({{\mathit{E}}_{\mathit{I}}}^{\prime }\otimes {{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}+{\mathit{T}}^{\prime }\otimes {{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}})\times ({\mathit{I}}_{\mathit{n}}\otimes \text{diag}({\nu }_k/{\nu }_k+{\sigma }^2))({\mathit{E}}_{\mathit{I}}\otimes {{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+\mathit{T}\otimes {{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}})\\ =\text{diag}(J_i)\otimes {{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}\text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+\text{diag}(T_{i•})\otimes {{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}\text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}+\text{diag}(T_{i•})\otimes {{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}\text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{0}}+\text{diag}(T_{i•}^2)\otimes {{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }{\mathbf{\Phi }}^{\mathit{U}}\text{diag}({\nu }_k/({\nu }_k+{\sigma }^2)){{\mathbf{\Phi }}^{\mathit{U}}}^{\prime }{\mathbf{\Phi }}^{\mathbf{1}}\end{array}$$

is again block-diagonal with N_X × N_X blocks, as is A, such that F = [A−H]⁻¹ can be computed by inverting each block

$${\mathit{A}}_i-{\mathit{H}}_i=[J_i{{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{0}}+T_{i•}({{\mathbf{\Phi }}^{\mathbf{0}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{1}}+{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{0}})+T_{i•}^2{{\mathbf{\Phi }}^{\mathbf{1}}}^{\prime }\mathit{L}{\mathbf{\Phi }}^{\mathbf{1}}+\text{diag}({\sigma }^2/{\lambda }_1,\dots ,{\sigma }^2/{\lambda }_{N_X})],$$

with L = I_D − Φ^U diag(ν_k/(ν_k + σ²))Φ^U′, separately.

Proof of Corollary 2

From Theorem 2, only matrices of size N_X × N_X need to be inverted to compute the EBLUPs, giving computational effort of order $O(I{N}_X^3)$. Usage of the block structure for all matrices reduces computation for the matrix multiplications. For example, multiplication of the (nN_U + IN_X) × nD and nD × 1 matrices Z′ and (Y − η), usually an O(nD(nN_U + IN_X)) operation, here reduces to I multiplications of N_X × D with D × 1 matrices and n multiplications of N_U × D with D × 1 matrices. Similarly bookkeeping for the other operations leads to the overall effort of order O(nD(N_U + N_XI/n)).

Proof of Lemma 1 and Corollary 3

Iterated expectations give us

$$\text{Var}\{Y_{ij}(s)\}=\text{E}\{\text{Var}[Y_{ij}(s)\mid T_{ij}]\}+\text{Var}\{\text{E}[Y_{ij}(s)\mid T_{ij}]\}.$$

As E{Y_ij(s)|T_ij} = 0,

$$\begin{array}{l}\underset{0}{\overset{1}{\int }}\text{Var}\{Y_{ij}(s)\}ds=\underset{0}{\overset{1}{\int }}\text{E}\{\sum _{k=1}^{\infty }{\lambda }_k{[{\phi }_k^0(s)+T_{ij}{\phi }_k^1(s)]}^2+\sum _{k=1}^{\infty }{\nu }_k{({\phi }_k^U(s))}^2+{\sigma }^2\}ds\\ =\underset{0}{\overset{1}{\int }}\sum _{k=1}^{\infty }{\lambda }_k[{({\phi }_k^0(s))}^2+2\text{E(}{T}_{ij}){\phi }_k^0(s){\phi }_k^1(s)+\text{E}(T_{ij}^2){({\phi }_k^1(s))}^2]+\sum _{k=1}^{\infty }{\nu }_k{({\phi }_k^U(s))}^2+{\sigma }^{2}ds.\end{array}$$

Now consider the case where E(T_ij) = 0 and Var(T_ij) = 1. In this case, we have

$$\begin{array}{l}\underset{0}{\overset{1}{\int }}\text{Var}\{Y_{ij}(s)\}ds=\sum _{k=1}^{\infty }{\lambda }_k\underset{0}{\overset{1}{\int }}{({\phi }_k^0(s))}^2+{({\phi }_k^1(s))}^{2}ds+\sum _{k=1}^{\infty }{\nu }_k\underset{0}{\overset{1}{\int }}{({\phi }_k^U(s))}^{2}ds+{\sigma }^2\\ =\sum _{k=1}^{\infty }{\lambda }_k+\sum _{k=1}^{\infty }{\nu }_k+{\sigma }^2\end{array}$$

due to the orthonormality of the eigenfunctions.

Appendix B: Estimation of the general functional mixed model

Estimation for model (2.2) proceeds in the same way as for model (2.1). In this section, we briefly point out the necessary minor adjustments. An estimate of the mean function η(d, Z_ij) can again be obtained under a working independence assumption and under the specified model. For example, under the specification η(d, Z_ij) = η₁(d, Z_ij,1) + ···+ η_m(d, Z_ij,m), bivariate smoothing in an additive model can be used.

In the estimation of the covariance functions, equation (3.1) now becomes

$$\begin{array}{l}\text{E}\{Y_{ij}(d)Y_{ik}(d^{\prime })\}={\mathit{V}}_{ij}^{\prime }{\mathit{K}}_X(d,d^{\prime }){\mathit{V}}_{ij}+[K_U(d,d^{\prime })+{\sigma }^2{\delta }_{d{d}^{\prime }}]{\delta }_{jk}\\ =\sum _{l=1}^p\sum _{m=1}^p{V}_{ij}{V}_{\mathit{ijm}}{K}_{lm}(d,d^{\prime })+[K_U(d,d^{\prime })+{\sigma }^2{\delta }_{d{d}^{\prime }}]{\delta }_{jk},\end{array}$$

where V_ij = (V_ij1, …, V_ijp), and the three step estimation procedure for the covariance functions extends straightforwardly. The size of the matrix to be inverted during step 1 increases from 5 × 5 to (p² + 1) × (p² + 1).

Similarly, estimation of the eigenfunctions using the spectral decomposition, and estimation of the scores using best linear unbiased prediction, proceeds completely analogously, keeping in mind that { ${\phi }_k^X(·)=({\phi }_k^1(·),\dots ,{\phi }_k^p(·)$, k = 1, 2, …} now form an orthonormal basis for the (L²[0, 1])^p.

Choice of N_X and N_U can again proceed using the proportion of variance explained. Standardization of variables in V_ij is recommended. Note, however, an additional complication in the higher-dimensional case. If some of the covariates in V_ij are correlated, corresponding additional terms will appear in the expansion of ∫Var{Y_ij(d)}. The eigenvalues λ_k might then somewhat over- or underrepresent the relative importance of the corresponding component ${\phi }_k^X$ in explaining the variation in Y_ij(d). If strong correlations are a concern, additional measures, such as the use of orthogonal polynomials in the case of polynomial V_ij, should be taken.