LOGISMOS—Layered Optimal Graph Image Segmentation of Multiple Objects and Surfaces: Cartilage Segmentation in the Knee Joint

Abstract

A novel method for simultaneous segmentation of multiple interacting surfaces belonging to multiple interacting objects, called LOGISMOS (layered optimal graph image segmentation of multiple objects and surfaces), is reported. The approach is based on the algorithmic incorporation of multiple spatial inter-relationships in a single n-dimensional graph, followed by graph optimization that yields a globally optimal solution. The LOGISMOS method’s utility and performance are demonstrated on a bone and cartilage segmentation task in the human knee joint. Although trained on only a relatively small number of nine example images, this system achieved good performance. Judged by dice similarity coefficients (DSC) using a leave-one-out test, DSC values of 0.84 ± 0.04, 0.80 ± 0.04 and 0.80 ± 0.04 were obtained for the femoral, tibial, and patellar cartilage regions, respectively. These are excellent DSC values, considering the narrow-sheet character of the cartilage regions. Similarly, low signed mean cartilage thickness errors were obtained when compared to a manually-traced independent standard in 60 randomly selected 3-D MR image datasets from the Osteoarthritis Initiative database—0.11 ± 0.24, 0.05 ± 0.23, and 0.03 ± 0.17 mm for the femoral, tibial, and patellar cartilage thickness, respectively. The average signed surface positioning errors for the six detected surfaces ranged from 0.04 ± 0.12 mm to 0.16 ± 0.22 mm. The reported LOGISMOS framework provides robust and accurate segmentation of the knee joint bone and cartilage surfaces of the femur, tibia, and patella. As a general segmentation tool, the developed framework can be applied to a broad range of multiobject multisurface segmentation problems.

I. Introduction

Substantial effort has been devoted to developing automated or semi-automated image segmentation techniques in 3-D [1]. Recently, we have reported a layered graph approach for optimal segmentation of single and multiple interacting surfaces of a single n-dimensional object [2], [3]. Despite a pressing need to solve multiobject segmentation tasks that are common in medical imaging (e.g., multiple organ segmentations), the literature discussing such methods is limited and mainly based on multiobject shape models. Examples include a method employing multiobject statistical shape models, in which a parametric model is derived by applying principal component analysis to the collection of multiple signed distance functions. Application examples included pelvic and/or brain structures [4]. A multiobject prior shape model for use in curve evolution-based image segmentations was introduced in [5] and applied to segmentation of deep neuroanatomical structures. Sequential deformation of a pair of pubic bones using medial representation-based statistical multiobject shape model was reported in [6]. Two-hand gesture recognition in image sequences by incorporating temporal coupling information into hidden Markov models and level sets was presented in [7].

We report a novel approach called LOGISMOS (layered optimal graph image segmentation of multiple objects and surfaces). While our method is motivated by the clinical need to accurately segment multiple bone and cartilage surfaces in osteoarthritic joints, including knees, ankles, hips, etc., the LOGISMOS approach is general, and its applicability is broader than orthopaedic applications. Therefore, the paper first introduces the LOGISMOS method in general terms while avoiding application-specific details. This is followed by the example application of knee joint cartilage segmentation, in which detailed description is provided of all aspects that need to be considered when using LOGISMOS for a specific segmentation task. In the orthopaedic application, a typical scenario includes the need to segment surfaces of the periosteal and subchondral bone and of the overlying articular cartilage from MRI scans with high accuracy and in a globally consistent manner (Fig. 1). Other examples include simultaneous segmentation of the prostate—bladder surfaces for radiation oncology guidance [8], [9] (including the rectum is also desirable), segmentation of two or more cardiac chambers from volumetric image data, segmentation of brain structures [10], or other segmentation tasks requiring segmentation of multiple objects positioned in close proximity, each of the objects possibly exhibiting more than one surfaces of interest.

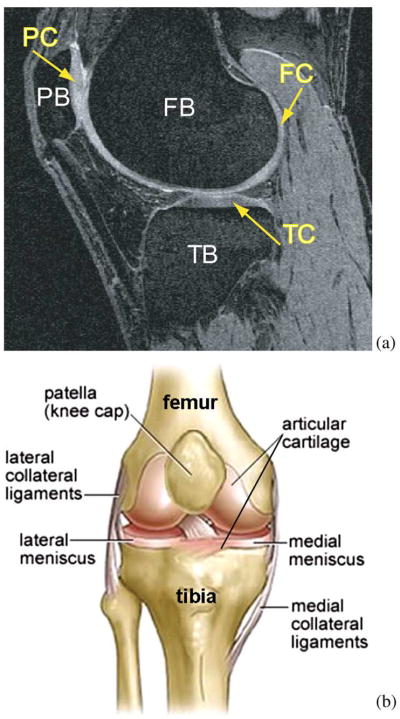
Fig. 1.

Human knee. (a) Example MR image of a knee joint—femur, patella, and tibia bones with associated cartilage surfaces are clearly visible. FB = femoral bone, TB = tibial bone, PB = patellar bone, FC = femoral cartilage, TC = tibial cartilage, PC = patellar cartilage. (b) Schematic view of knee anatomy (adapted from http://www.ACLSolutions.com).

II. LOGISMOS—Method

The reported multiobject multisurface segmentation method is a general approach for optimally segmenting multiple surfaces that mutually interact within individual objects and/or between objects. The problem is modeled by a complex multilayered graph in which solution-related costs are associated with individual graph nodes. Intrasurface, intersurface, and interobject relationships are represented by context-specific graph arcs. The multiobject multisurface segmentation reported here is a nontrivial extension of our previously reported method for optimal segmentation of multiple interacting surfaces [3].

The LOGISMOS approach starts with an object pre-segmentation step, after which a single graph holding all relationships and surface cost elements is constructed, and in which the segmentation of all desired surfaces is performed simultaneously in a single optimization process. While the description given below specifically refers to 3-D image segmentation, the LOGISMOS method is fundamentally n-dimensional.

A. Object Pre-Segmentation

The LOGISMOS method begins with a coarse pre-segmentation of the image data, but there is no prescribed method that must be used. The only requirement is that pre-segmentation yields robust approximate surfaces of the individual objects, having the same (correct) topology as the underlying objects and being sufficiently close to the true surfaces. The definition of “sufficiently close” is problem-specific and needs to be considered in relationship with how the layered graph is constructed from the approximate surfaces. Note that it is frequently sufficient to generate a single pre-segmented surface per object, even if the object itself exhibits more than one mutually interacting surfaces of interest. Depending upon the application, level sets, deformable models, active shape/appearance models, or other segmentation techniques can be used to yield object pre-segmentations.

B. Construction of Object-Specific Graphs

To represent a single or multiple interacting surface segmentation as a graph optimization problem, the resulting graph must be a properly-ordered multicolumn graph, so that the segmentation task can be represented as a search for a V-weight net surface as defined in [2].

A graph G = (V, E) is a collection of vertices V and arcs E. If an arc e₁ ∈ E connects a vertex v₁ ∈ V with v₂ ∈ V, v₁ and v₂ are called adjacent and the arc can be written as 〈v₁, v₂〉. In a graph with undirected arcs, 〈v₁, v₂〉 and 〈v₂, v₁〉 are equivalent.

In a multicolumn graph, an undirected graph B = (V_B, E_B) in (d − 1) − D is called the base graph and represents the graph search support domain. An undirected graph G = (V, E) in d − D is generated by B and a positive integer K, where each vertex v_i ∈ V_B has a set V_i of K vertices in V. V_i is also called the i-column of G. An i-column and a j-column are adjacent if v_i and v_j are adjacent in B. Intuitively, a net surface in G is a subgraph of G defined by a height function that maps the (d − 1)−D base graph B to the d-D graph G, such that 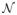intersects each column of G at exactly one vertex and 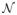preserves all topologies of B. For exact definition, see [2] and [3]. If each node in G was assigned a cost value, then finding a net with minimum cost is called a V-weight net problem. The construction of a directed graph G̃ = (Ṽ, Ẽ) from G was reported in [2], where lemmas were presented showing that a V-weight net 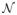in G corresponds to a nonempty closed set 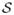in G̃ with the same weight. An example of this process can be seen in Fig. 2. Consequently, an optimal surface segmentation problem can be converted to solving a minimum closed set problem in G̃. Especially, when G is properly-ordered, the optimal V-weight net in G can be computed in T(n, m_BK), where n is the number of vertices in V, m_B is the number of arcs in E_B, and T is the time for finding a minimum s − t cut in an edge-weighted directed graph.

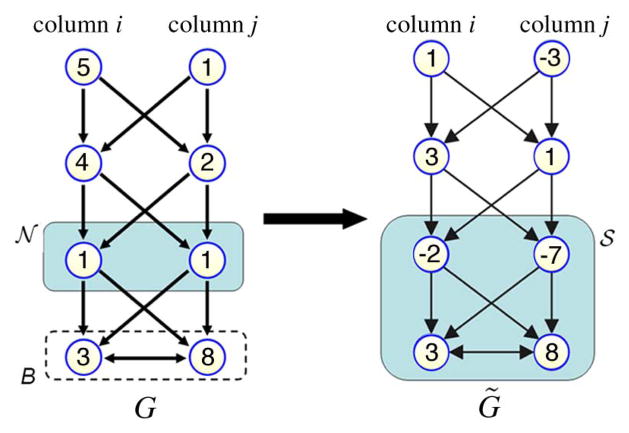
Fig. 2.

The process of converting finding V-weight net 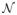in G problem into finding nonempty closed set 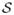in G̃ with the same weight. Here K = 4.

If the object-specific graph is constructed from a result of object pre-segmentation as described above, the approximate pre-segmented surface may be meshed and the graph columns constructed as normals to individual mesh faces. The lengths of the columns are then derived from the expected maximum distances between the pre-segmented approximate surface and the true surface, so that the correct solution can be found within the constructed graph. The present approach to multisurface graph construction for multiple closed surfaces was introduced in [11]. Maintaining the same graph structure for individual objects, the base graph is formed using the pre-segmented surface mesh 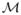. V_B is the vertex set on 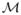and E_B is the edge set. A graph column is formed by equally sampling several nodes along normal direction of a vertex in V_B. The base graph is formed by connecting the bottom nodes by the connection relationship of E_B. In the multiple closed surface detection case, a duplication of graph G base graph is constructed each time when searching for an additional surface. The duplicated graphs G are connected by undirected arcs to form a new base graph which ensures that the interacting surfaces can be detected simultaneously. Additional directed intracolumn arcs, intercolumn arcs and intersurface arcs incorporate surface smoothness Δ and surface separation δ constraints into the graph.

C. Multiobject Interactions

When multiple objects with multiple surfaces of interest are in close apposition, a multiobject graph construction is adopted. This begins with considering pairwise interacting objects, with the connection of the base graphs of these two objects to form a new base graph. Note however, that more than one surface may need to be detected on each object, with such surfaces being mutually interacting as described above. Object interaction is frequently local, limited to only some portions of the two objects’ surfaces. Here we will assume that the region of pairwise mutual object interaction is known. A usual requirement may be that surfaces of closely-located adjacent objects do not cross each other, that they are at a specific maximum/minimum distance, or similar. Object-interacting surface separation constraints are implemented by adding interobject arcs at the interacting areas. Interobject surface separation constraints are also added to the interacting areas to define the separation requirements that shall be in place between two adjacent objects. The interobject arcs are constructed in the same way as the intersurface arcs. The challenge in this task is that no one-to-one correspondence exists between the base graphs (meshes) of the interacting object pairs. To address this challenge, corresponding columns i and j need to be defined between the interacting objects. The corresponding columns should have the same directions. Considering signed distance offset d between the vertex sets V_i and V_j of the two objects, interobject arcs A^o between two corresponding columns can be defined as

$$\begin{array}{l}{A}^o=\{\langle V_i(k),V_j(k-d+{\delta }^l)\rangle \mid \forall k:\\ max(d-{\delta }^l,0)\le k\le \\ min(K-1+d-{\delta }^l,K-1)\}\\ \cup \{\langle V_j(k),V_i(k+d-{\delta }^u)\rangle \mid \forall k:\\ max({\delta }^u-d,0)\le k\\ \le min(K-1+d-{\delta }^u,K-1)\}\end{array}$$ (1)

where k is the vertex index number; δ^l and δ^u are interobject separation constraints with δ^l ≤ δ^u.

Nevertheless, it may be difficult to find corresponding columns between two regions of different topology. The approach presented below offers one possible solution. Since more than two objects may be mutually interacting, more than one set of pairwise interactions may co-exist in the constructed graph.

1) Electric Lines of Force

Starting with the initial pre-segmented shapes, a cross-object search direction must be defined for each location along the surface. The presently adopted method for defining corresponding columns via cross-object surface mapping relies upon electric field theory for a robust and general definition of such search direction lines [12]. Recall Coulomb’s law from basic physics

$$E_i=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}\widehat{\mathbf{r}}$$ (2)

where E_i is the electric field at point i. Q is the charge of point i; r is the distance from point i to the evaluation point; r̂ is the unit vector pointing from the point i to the evaluation point. ε₀ is the vacuum permittivity. Since the total electric field E is the sum of E_i’s

$$E=\sum _i{E}_i$$ (3)

the electric field has the same direction as the electric line(s) of force (ELF). When an electric field is generated from multiple source points, the electric lines of force exhibit a nonintersection property, which is of major interest in the context of finding corresponding columns.

When computing ELF for a computer generated 3-D triangulated surface, the surface is composed of a limited number of vertices that are usually not uniformly distributed. These two observations greatly reduce the effect of charges located in close proximity. To cope with this undesirable effect, a positive charge Q_i is assigned to each vertex v_i. The value of Q_i is determined by the area sum of triangles t_j where v_i ∈ t_j. When changing r² to r^m (m > 2), the non-intersection property still holds. The difference is that more distant vertices will be penalized in ELF computing. Therefore, a slightly larger m will increase the robustness of local ELF computation. Discarding the constant term, the electric field is defined as

$$\widehat{E}=\sum _i\frac{{\sum }_j\mathit{AREA}(t_j)}{r_i^m}{\widehat{\mathbf{r}}}_i$$ (4)

where v_i ∈ t_j and m > 2.

Assuming there is a closed surface in an n-D space, the point having a zero electric field is the solution of equation Ê = 0. In an extreme case, the closed surface will converge to the solution points when searching along the ELF. Except for these points, the non-intersecting ELF will fill the entire space. Since ELF are non-intersecting, it is easy to interpolate ELF at non-vertex locations on a surface. The interpolation can greatly reduce total ELF computation load when upsampling a surface. In 2-D, linear interpolation from two neighboring vertices and their corresponding ELF can be implemented. In 3-D, use of barycentric coordinates is preferred to interpolate points within triangles.

When a closed surface is used for ELF computation, iso-electric-potential surfaces can be found. Except for the solution points Ê = 0, all other points belong to an iso-electric-potential surface and the ELF passing through such a point can be easily interpolated. The interpolated ELF intersects the initial closed surface. Consequently, this technique can be used to create connections between a point in space and a closed surface, yielding cross-surface mapping.

2) ELF-Based Cross-Object Surface Mapping

The nonintersection property of ELF is useful to find one-to-one mapping between adjacent objects with different surface topologies. Interrelated ELF of two coupled surfaces can be determined in two steps.

• Push forward—regular ELF path computation using (4).

• Trace back—interpolation process to form an ELF path from a point in space to a closed surface as outlined above.

The general idea of mapping two coupled surfaces using ELF includes defining an ELF path using the push forward process, identifying the medial-sheet intersection point on this path, generating a constraint point on the opposite surface, and connecting the constraint point with already existing close vertices on this surface—so called constraint-point mapping [12]. Fig. 3(a) shows ELF pushed forward from a surface and traced back from a point to that surface. Fig. 3(b) shows an example of mapping two coupled surfaces in 3-D.

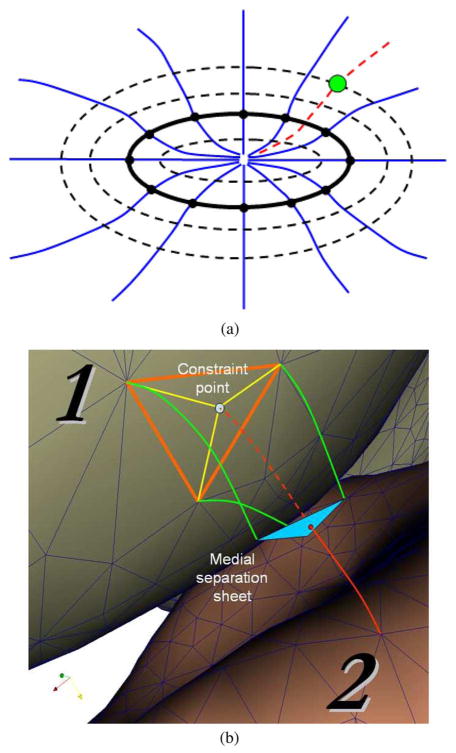
Fig. 3.

Cross-object surface mapping by ELF (a) The ELF (blue lines) are pushed forward from a surface composed of black vertices. The dashed black surfaces indicate the location of iso-electric-potential contours. The red-dashed ELF is the traced-back line from a green point to the solid black surface. The traced-back line is computed by interpolating two neighboring pushed-forward ELF. (b) Constraint-point mapping of coupled 3-D surfaces is performed in the following 5 steps: i) Green and red ELF are pushed forward from surface 1 and 2, respectively. ii) The intersections between the ELF and medial separating sheet form a blue triangle and a red point. iii) The red point is traced back along dotted red line to surface 1. iv) When the dotted red line intersects surface 1, it forms a light-blue constraint point on surface 1. v) The constraint point is connected at surface 1 by yellow edges.

Note that each vertex in the object-interaction area can therefore be used to create a constraint point affecting the coupled surface. Importantly, the corresponding pairs of vertices (the original vertex and its constraint point) from two interacting objects in the contact area identified using the ELF are guaranteed to be in a one-to-one relationship and all-to-all mapping, irrespective of surface vertex density. As a result, the desirable property of maintaining the previous surface geometry [e.g., the orange triangle in Fig. 3(b)] is preserved. Therefore, the mapping procedure avoids surface regeneration and merging [13] (which is usually difficult) and enhances robustness with respect to local roughness of the surface, when compared with our previously introduced nearest point based mapping techniques [14], [15].

D. Cost Function and Graph Optimization

The resulting segmentation is driven by the cost functions associated with the graph vertices. Design of vertex-associated costs is problem-specific and costs may reflect edge-based, region-based, or combined edge—region image properties [16], [17]. After the step of cost translation, guaranteeing that the cost of a surface is identical to the cost of a minimum closed set enveloped by this surface—see [2] and [3] for details, the constructed interacting graph reflecting all surface and object interactions is a directed graph G̃ derived from a properly-ordered multicolumn graph G. As stated before, a V-weight net problem in G can be converted to finding the minimum nonempty closed set in G̃. This can be done by an s − t cut algorithm, e.g., [18]. As a result of the single optimization process, a globally optimal solution provides all segmentation surfaces for all involved interacting objects while satisfying all surface and object interaction constraints.

III. LOGISMOS-Based Segmentation of Bone and Cartilage Surfaces in the Knee Joint

Following the general outline of our LOGISMOS approach, a method for simultaneous segmentation of bone and cartilage surfaces in the femur, tibia, and patella, which all articulate in the knee joint, is reported. Problem-specific details of the individual processing steps outlined above are given in the next sections.

Three bones articulate in the knee joint: the femur, the tibia, and the patella. Each of these bones is partly covered by cartilage in regions where individual bone pairs slide over each other during joint movements. For assessment of the knee joint cartilage health, it is necessary to identify six surfaces: femoral bone, femoral cartilage, tibial bone, tibial cartilage, patellar bone, and patellar cartilage. In addition to each connected bone and cartilage surface mutually interacting on a given bone, the bones interact in a pairwise manner—cartilage surfaces of the tibia and femur and of the femur and patella are in close proximity (or in frank contact) for any given knee joint position. Clearly, the problem of simultaneous segmentation of the six surfaces belonging to three interacting objects is well suited for application of the LOGISMOS method.

A. Bone Pre-Segmentation

Figs. 4 and 5 show the flowchart of our method. As the first step, the volume of interest (VOI) of each bone, together with its associated cartilage, is identified using an Adaboost approach in 3-D MR images [Fig. 4(a), Fig. 5(a)]. Following application of a 3-D median filter (radius one voxel) to remove local noise, image intensities are normalized as suggested in [19], the values between the image-intensity minimum and maximum are linearly stretched to cover the range of 0–1000. Inspired by the facial recognition work of Viola and Jones [20], their idea was extended to 3-D. Nine types of 3-D Haar features were designed as shown in Fig. 6, in which the total voxel intensity sum in the white area is subtracted from the total voxel intensity sum in the gray area. It is efficient to compute these features in an integral image [20] using 12, 16, and/or 18 index references (types a ~ c, d ~ f, and g ~ i, respectively). Furthermore, computing the Haar features in multiple resolutions can be achieved by rescaling the box sizes shown in Fig. 6, which avoids re-sampling the entire image and thus leads to a single cross-scale classification process. The goal of the bone localization is to determine three VOIs per knee joint image within which the individual bones (femur, tibia, patella) are located.

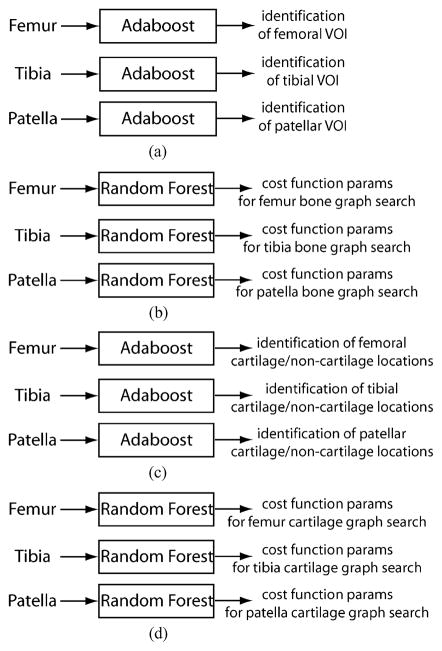
Fig. 4.

The flowchart of LOGISMOS based segmentation of articular cartilage for all bones in the knee joint. (a) Detection of bone volumes of interest using Adaboost approach. (b) Approximate bone segmentation using single-surface graph search. (c) Generation of multisurface interaction constraints. (d) Construction of multiobject interaction constraints. (e) LOGISMOS-based simultaneous segmentation of six bone and cartilage surfaces in 3-D.

Fig. 5.

Summary of classifier-learning stages of LOGISMOS based segmentation of articular cartilage for all bones in the knee joint. A total of 12 classifiers was trained and utilized. Complete expert-defined VOIs are available for TRAIN-1 (25 MR images). Complete tracings of bone and cartilage surfaces are available for TRAIN-2 (9 MR images) dataset. Note that individual steps are separately validated. The TEST dataset is large and consists of 60 MR datasets, for which dense but not complete tracing of bone and cartilage surfaces is available. (a) Learning of VOI properties in TRAIN-1 dataset, Adaboost localization of individual bones VOIs, leave-one-out validation in TRAIN-1. (b) Learning of bone surface properties in TRAIN-2 dataset, leave-one-out validation in TRAIN-2. (c) Learning of cartilage/non-cartilage location properties in TRAIN-2 dataset, Adaboost classification of cartilage/non-cartilage regions, (also leave-one-out validation in TRAIN-2). (d) Learning cartilage regional properties in TRAIN-2 dataset, final validation in TEST dataset, (also leave-one-out validation in TRAIN-2).

Fig. 6.

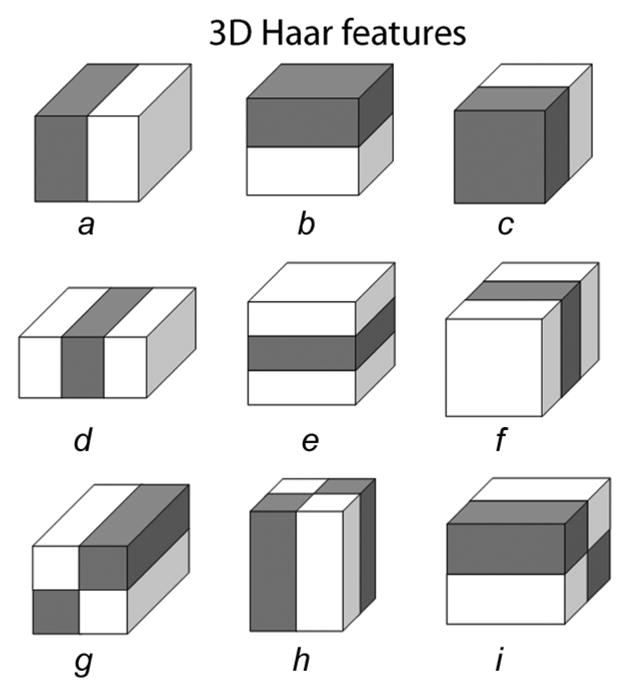
Nine types of 3-D Haar features, employed in a multiscale manner.

To learn VOI-related 3-D Haar features from a training set of images, example VOIs were manually identified in a TRAIN-1 dataset (Section IV-B) that was completely separate from any testing image sets used later. The example VOIs included the femoral, tibial, and patellar bone and cartilage structures [Fig. 4(a)]. After scaling to the mean size for each bone, the bone VOIs were used as representative bone class (foreground) samples. A large number of 3-D Haar features (~ 150 000) of different types and sizes were computed inside the foreground VOI location in each training image. The mean± standard deviation (std) of the VOI sizes were computed for each bone, as well. To determine VOI-related features for non-bone (background) VOI locations, these VOI positions were perturbed—randomly shifted nine times for each axis and each training image within an experimentally set 2.8–21 mm range—to produce background class samples. In the course of Adaboost training, the 500 most appropriate features were identified. Three Adaboost classifier results were obtained separately for each of the three bones.

To detect the femur, tibia, and patella bones in 3-D MR images, the selected 500 features are computed within each VOI in all possible VOI positions in a multiresolution fashion (VOI sizes ranging within mean±3 std of the learned VOI size). Detection of the three bones is sequential and starts with the femur, since it has the most recognizable appearance. The tibia is then localized as inferior to the femur, and the patella anterior to the femur as shown in Fig. 4(a).

After localizing the object VOIs, approximate surfaces of the individual bones must be obtained [Fig. 4(b) and Fig. 5(b)]. For the purpose of accurate delineation of knee bone and cartilage structures as imaged by MR, the bone surfaces alone provide an initial approximation of the pair of inter-related bone and cartilage surfaces. Using a separate training set TRAIN-2 (Section IV-B) for which complete manual tracings of all three bones were available in all image slices, mean shapes of the three bones were constructed and represented as closed surfaces, of about 2000 mesh vertices each. Using the volumetric bone surface meshes, a random forest classifier [21] was trained to distinguish the bone surface from the rest of the image. The utilized features included intensity, intensity gradient, and second order intensity derivatives calculated in Gaussian-smoothed images constructed using 0.5 mm, 1.0 mm, and 2.0 mm smoothing kernels. Additional features were derived from the distances between the geometric center of the bone VOI and the true bone surface, and served as shape-bearing information. All these features formed the input to the random forest classifier.

The approximate bone surfaces were identified in previously unseen images by first roughly fitting the mean bone shape models obtained from the TRAIN-2 training set directly to the automatically-identified VOIs [upper panels of Fig. 4(b)]. A single surface detection graph was constructed based on the fitted mean shapes—graph columns were built along nonintersecting electric lines of force to increase the robustness of the graph construction (Section II-C-1). The surface costs were associated with each graph node based on the inverted surface likelihood probabilities provided by the random forest classifiers. After repeating this step iteratively until convergence (usually 3–5 iterations were needed), the approximate surfaces of each bone were automatically identified, without considering any bone-to-bone context, see lower panel of Fig. 4(b).

B. Multisurface Interaction Constraints

Image locations adjacent to and outside of the bone may belong to cartilage, meniscus, synovial fluid, or other tissue, and they thus exhibit different image appearance [Fig. 4(c)]. For example, the cartilage and noncartilage regions along the knee bone surface differ dramatically in texture. Features utilized in a respective cartilage/noncartilage tissue classifier include those used previously (intensity, intensity gradient, and second-order derivatives of Gaussian-smoothed images). Additional features were added, including the physical distances of a location from the bone surface [19] and three eigenvalues of the Hessian image. To reveal the cartilage shape properties in different locations, each graph node was mapped back to the mean bone shape along a given search direction. The original vertex coordinates of the corresponding vertex on the mean bone shape were used as yet another feature [22].

Using the cartilage features collected from the training dataset TRAIN-2 for all cartilage/non-cartilage locations, a new Adaboost classifier was trained for each bone [Fig. 5(c)]. When segmenting the bone surface, these Adaboost classifiers quickly classify the graph nodes into one of the cartilage/non-cartilage classes. If any node along a search direction is identified as cartilage, the search path is identified as passing through the cartilage region.

The goal is to extract from MR images the bone and cartilage surfaces of each of the three bones forming the knee joint (six surfaces in total). Since the cartilage generally covers only those parts of the respective bones which may articulate with another bone, two surfaces (cartilage and bone) are defined only at those locations, while single (bone) surfaces are to be detected in noncartilage regions. This also reflects the distinction between truly external bone surfaces versus the subchondral bone surface, which marks the interface between bone and cartilage where they are joined. To facilitate a topologically robust problem definition across a variety of joint shapes and cartilage disease stages, two surfaces are detected for each bone, and the single-double surface topology differentiation reduces into differentiation of zero and nonzero distances between the two surfaces. In this respect, the noncartilage regions along the external bone surface were identified as regions in which zero distance between the two surfaces was enforced so that the two surfaces collapsed onto each other, effectively forming a single bone surface. In the cartilage regions, the zero-distance rule was not enforced, providing for both a subchondral bone and articular cartilage surface segmentation.

C. Multiobject Interaction Constraints

In addition to dual-surface segmentation that must be performed for each individual bone, the bones of the joint interact in the sense that cartilage surfaces from adjacent bones cannot intersect each other, cartilage and bone surfaces must coincide at the articular margin, the maximum anatomically feasible cartilage thickness shall be observed, etc. The regions in which adjacent cartilage surfaces come into contact are considered the interacting regions [Fig. 4(d)]. In the knee, such interacting regions exist between the tibia and the femur (tibiofemoral joint) and between the patella and the femur (patellofemoral joint). It is also desirable to find these interacting regions automatically.

For this purpose, an iso-distance medial separation sheet is identified in the global coordinate system midway between adjacent pre-segmented bone surfaces. If a vertex is located on an initial surface while having a search direction intersecting the sheet, the vertex is identified as belonging to the region of surface interaction. The separation sheet can be identified using signed distance maps even if the initial surfaces intersect. Following the ELF approach described above, femoral and tibial initial surfaces were up-sampled to approximately 8000 vertices each in order to increase the surface resolution. Then, one-to-one and all-to-all corresponding pairs are generated between femur-tibia contact area as well as femur-patella contact area by constraint-point mapping technique. The corresponding pairs and their ELF connections are used for inter-object graph link construction [14], [15].

D. Knee Joint Bone-Cartilage Segmentation

After completion of the above steps, the segmentation of multiple surfaces of multiple mutually interacting objects can be solved as previously presented in [15]. Consequently, all surfaces are segmented simultaneously and globally optimally subject to the interaction constraints [Fig. 4(e), Fig. 5(d)]. Specifically, double surface segmentation graphs were constructed individually for each bone using that bone’s initial surface. The three double surface graphs were further connected by inter-object graph arcs between the corresponding columns identified during the previous step as belonging to the region of close-contact object interaction. The minimum distance between the interacting cartilage surfaces from adjacent bones was set to zero to avoid cartilage overlap.

After the step of cost translation [3], the constructed interacting graph is a directed graph G̃ derived from a properly-ordered multicolumn graph G. As stated before, a V-weight net problem in G can be converted to finding the minimum nonempty closed set in G̃. This can be done by an s − t cut algorithm, e.g., [18], as a result of which all six surfaces (femoral bone-cartilage, tibial bone-cartilage and patellar bone-cartilage) are detected simultaneously.

E. Cost Functions

Pattern recognition can substantially aid image segmentation. Due to the flexibility of the cost function design, pattern recognition techniques can be embedded directly in the optimal surface detection framework as summarized in Fig. 5.

Inspired by the work of Folkesson and Fripp [19], [23], a random forest classifier [21] was trained for each bone using voxels surrounding the corresponding bone boundaries [Fig. 5(b)]. Intensity, gradient and second order intensity derivatives under Gaussian smoothed images with 0.5 mm, 1.0 mm, 2.0 mm smoothing kernels were used as features. Furthermore, 3-D distances from the center of the VOI were utilized as shape-information-bearing features, yielding a more robust behavior than using global 3-D location as features [23]. All these features have already been described in Section III-A. The surface cost was associated with each graph node based on the inverted surface probabilities provided by the random forest classifiers.

Three additional binary random forest classifiers were trained based on the training samples (labeled as either cartilage or other). For this training, only samples from the cartilage-present bone regions were utilized, obtained from the TRAIN-2 set [Fig. 5(d)]. The same features as previously used for cartilage/noncartilage detection were used (Section III-B).

Once trained and applied to previously unseen to-be-segmented images, the classifiers provide information for each location of the graph nodes about the likelihood that this location belongs to a given tissue class (cartilage or other). Inverted tissue probabilities are therefore associated with each graph node and represent regional cost terms.

IV. Experimental Methods

A. Image Data

The goal of the performance assessment was to determine the surface segmentation accuracy obtained when simultaneously segmenting six bone and cartilage surfaces in the knee joint (femoral bone and cartilage, tibial bone and cartilage, patellar bone and cartilage) in full 3-D. MR images utilized in this study were randomly selected from the publicly available Osteoarthritis Initiative (OAI) database, which is available for public access at http://www.oai.ucsf.edu/.

The knees of subjects in the OAI study exhibit differing levels of joint degeneration. By study design, subjects are enrolled into one of two cohorts, based on whether they have symptomatic knee osteoarthritis (OA) at the time of entry into the study (progression cohort) or they do not (incidence cohort). The MR images used were acquired with a 3T scanner following a standardized procedure. A sagittal 3-D dual-echo steady state (DESS) sequence with water-excitation and the following imaging parameters: image stack of 384 × 384 × 160 voxels, with voxel size 0.365 × 0.365 × 0.70 mm.

B. Independent Standard

The initial bone segmentation relied upon the TRAIN-1 training set, which consisted of 25 randomly selected OAI image datasets in which bone VOIs were manually identified (11 incidence and 14 progression subjects in TRAIN-1). The remaining training steps were performed using a training set (TRAIN-2) that consisted of nine image datasets (four incidence and five progression subjects). Complete volumetric bone and cartilage tracing was manually performed for the three bones of the knee joint in the TRAIN-2 datasets. The performance of the LOGISMOS method was tested in the TEST dataset of 60 OAI subjects for which volumetric tracings were available either in coronal orientation (1618 traced slices, 40.5 ± 4.7 traced slices per dataset), or in sagittal orientation (2266 traced slices, 113.3 ± 9.8 per dataset). The TEST set included 48 (80%) incidence and 12 (20%) progression subjects, roughly reflecting the overall distribution of progression and incidence subjects in the OAI dataset (70.3% incidence and 29.7% progression cases). In 20 of the 60 datasets, the femoral, tibial and patellar bone and cartilage borders were expert-traced in all sagittal-view slices by one observer. In the remaining 40 datasets, femoral and tibial bone and cartilage borders were expert-traced in all of the coronal-view slices by two other observers. Expert observers were either orthopedics residents or trained technologists at the University of Iowa. The independent standard thus resulted from fully manual tracing with no automated or semi-automated segmentation tool assistance, and expected interobserver variability.

C. Parameters of the Method

For preliminary segmentation, the surface smoothness was set as Δ = 3 vertices. Due to anisotropic voxel sizes, Δ ranged from 1.04 to 2.1 mm based on the direction in the 3-D volume. Similar directionality-caused ranges apply to other parameters. Following the bone pre-segmentation, the femoral and tibial surfaces were upsampled from about 2000 vertices to 8000 vertices each.

For the final-segmentation graph construction, vertices were sampled in a narrow band of [−5, 20] voxels (−3.5–14 mm) along the ELF direction around the pre-segmented surface (up-sampled to K = 51). The range of this narrow band is determined by the observed inaccuracies of the preliminary segmentation (−5 voxels allows the final surface to be up to five voxels “inside” of the preliminary surface) and by the maximum thickness of segmented cartilage (7 mm—combined with pre-segmentation inaccuracies resulted in the outer limit of +20 voxels). The surface smoothness parameters were set to Δ = 3 vertices (1.04–2.1 mm) for both the bone and cartilage surfaces. During the ELF computation, m = 4 was experimentally identified as the least computationally demanding option from those offering a good trade-off between local accuracy and regularity of the ELF line set (4 ≤ m ≤ 6 were identified as good options) and was used in (4). The inter-surface distance constraint values were set to δ_lower = 0 to allow for denuded bone and δ_upper = 0 at noncartilage area to create coincident bone and cartilage surfaces. The inter-object surface smoothness parameter was δ^l = 0 to prevent cartilage surface overlapping.

D. Quantitative Assessment Indices

To provide a detailed assessment of the cartilage segmentation accuracy, signed and unsigned surface positioning errors were assessed in each of the 60 images from the TEST set, and they are reported as mean ± standard deviation in millimeters. Surface positioning errors were defined as the shortest 3-D distances between the independent standard and computer-determined surfaces. Similarly, local cartilage thickness was measured as the closest distance between the cartilage and bone surfaces and compared to the independent standard.

To determine dice similarity coefficients (DSC) of cartilage segmentation performance, complete volumetric tracings of the entire joint must be available, as in the TRAIN-2 dataset. Therefore, DSC analysis of the cartilage volume was performed in the TRAIN-2 dataset following a leave-one-out training/testing strategy to maintain full training/testing separation.

V. Results

All testing datasets were segmented using the described fully automated framework. No user-interaction was allowed in any of the segmentation steps and no resulting surfaces were manually edited. The segmentation required roughly 20 min on average to segment one knee joint dataset, on a PC with Intel Core 2 Duo 2.6-GHz processor and 4 GB of RAM (single thread). Out of the 20 min, the bone VOI locating process takes about 6 min per dataset on average (all three bones) with no location errors observed. The subsequent step of presegmenting one bone surface requires about 2 min each and can be performed in parallel. All remaining steps of the multiobject multisurfaces simultaneous segmentation need about 8 min to complete. Fig. 7 shows an example of a knee joint contact area slice from the 3-D MR dataset. Note the contact between the femoral and tibial cartilage surfaces, as well as the contact between the femoral and patellar cartilage surfaces. Furthermore, there is an area of high intensity synovial fluid adjacent to the femoral cartilage that is not part of the cartilage tissue and should not be segmented as such. Similarly, notice the low-intensity inner band within the central femoral cartilage. The right panel of Fig. 7 shows the resulting segmentation demonstrating very good delineation of all six segmented surfaces and correct exclusion of the synovial fluid from the cartilage surface segmentations. Since the segmentations are performed simultaneously for all six bone and cartilage surfaces in the 3-D space, computer segmentation directly yields the 3-D cartilage thickness for all bone surface locations. Typical segmentation results are given in Fig. 8.

Fig. 7.

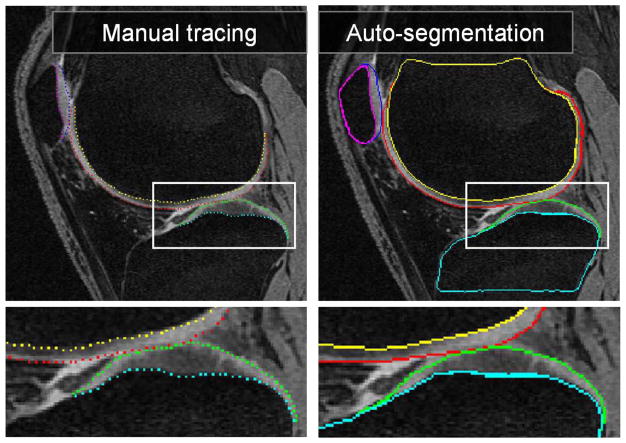
MR image segmentation of a knee joint—a single contact-area slice from a 3-D MR dataset is shown. Segmentation of all six surfaces was performed simultaneously in 3-D. (left) Original image data with expert-tracing overlaid. (right) Computer segmentation result. Note that the double-line boundary of tibial bone is caused by intersecting the segmented 3-D surface with the image plane.

Fig. 8.

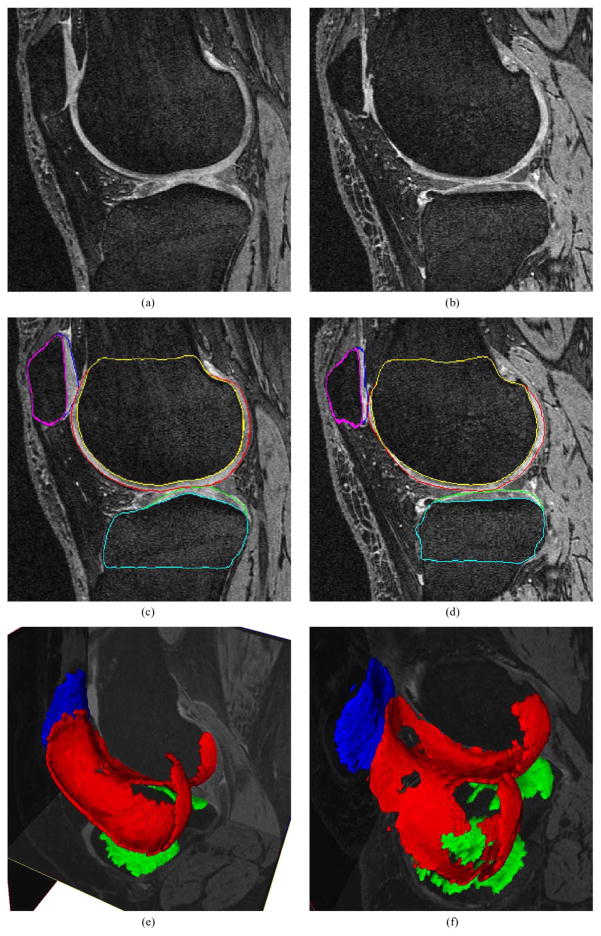
3-D segmentation of knee cartilages. Images from a knee minimally affected by osteoarthritis shown on the left. Severe cartilage degeneration shown on the right. (a), (b) Original images. (c), (d) The same slice with bone/cartilage segmentation. (e), (f) Cartilage segmentation shown in 3-D, note the cartilage thinning and “holes” in panel (f).

The signed and unsigned surface positioning errors of the obtained cartilage segmentations were quantitatively measured over the cartilage regions, and they are presented in Table I. For these results, the femoral bone and cartilage errors, as well as tibial bone and cartilage errors, were evaluated in each of the 60 testing datasets. The patellar bone and cartilage errors were evaluated in the 20 testing datasets for which sagittal patellar tracings were available. The average signed surface positioning errors for the six detected surfaces ranged from 0.04 to 0.16 mm, while the average unsigned surface positioning error ranged from 0.22 to 0.53 mm. Positive values of the signed error in Table I represent that the computer surface is “inside” of the closed bone or cartilage surfaces. The close-to-zero signed positioning errors attest to a small bias of surface detection. The unsigned positioning errors show that the local fluctuations around the correct location are much smaller than the longest face of MR image voxels (0.70 mm). Our results therefore show virtually no surface positioning bias and subvoxel local accuracy for each of the six detected surfaces. Signed positioning error maps for femoral and tibial bone and cartilage surfaces and for calculated cartilage thickness are shown in Fig. 9 demonstrating that the mean errors are small for all three cartilage areas across all central regions of greatest functional significance.

TABLE I.

Mean Signed and Unsigned Error of Computer Segmentation in Comparison With the Independent standard in Millimeters

ERRORS (mm)	Signed Bone Positioning	Signed Cartilage Positioning	Unsigned Bone Positioning	Unsigned Cartilage Positioning	Signed Mean Cartilage Thickness
Femur	0.04 ±0.12	0.16 ±0.22	0.22 ±0.07	0.45 ±0.12	0.11 ±0.24
Tibia	0.05 ±0.12	0.10 ±0.19	0.23 ±0.06	0.53 ±0.11	0.05 ±0.23
Patella	0.09 ±0.09	0.12 ±0.21	0.23 ±0.11	0.53 ±0.14	0.03 ±0.17

Fig. 9.

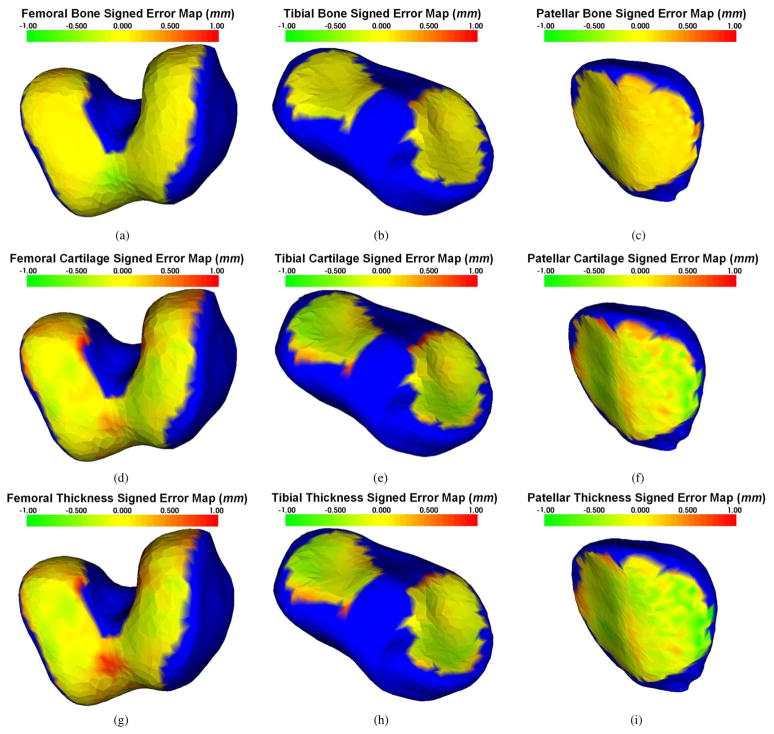
Distribution of mean signed surface positioning errors superimposed on mean shapes of the three bones forming the knee joint. In all panels, blue color corresponds to bone areas not covered by cartilage when mapped to mean shape. The range of colors from green to red corresponds to surface positioning errors ranging from −1 to +1 mm. Panels (a)–(c) show bone surface positioning errors, (d)–(f) show cartilage surface positioning errors, and (g)–(i) mean signed errors of computed cartilage thickness. Note that the yellowish color corresponds with zero error, visually demonstrating only a small systematic segmentation and thickness assessment bias across all cartilage regions.

When assessing the performance using Dice coefficients, the obtained DSC values were 0.84, 0.80, and 0.80 for the femoral, tibial, and patellar cartilage surfaces, respectively, as shown in Table II.

TABLE II.

Volume Measurement in Comparison With the Independent Standard

	DSC	Sensitivity	Specificity
Femoral cartilage	0.84 ±0.04	0.80 ±0.07	1.00 ±0.00
Tibial cartilage	0.80 ±0.04	0.75 ± 0.08	1.00 ±0.00
Patellar cartilage	0.80 ±0.04	0.76 ± 0.08	1.00 ±0.00

VI. Discussion

In this section, we overview previous approaches to cartilage segmentation and then focus on three issues associated with the reported multiobject multisurface segmentation framework: overall properties, novelty and generality of the presented method; its limitations; and causes and locations of errors in the knee cartilage segmentation.

A. Previous Cartilage Segmentation Approaches

Automated segmentation of articular cartilage in the knee has been researched for decades. Many MR image analysis approaches have been developed with varying levels of automation. An excellent overview of previously reported approaches to articular cartilage MR image acquisition and quantitative analysis is given in [24].

Lynch used region growing segmentation with manual initialization [25], [26]. Carballido–Gamio developed a semi-automated approach based on Bezier splines [27]. Similarly, Raynauld and König both selected active contour approaches [28], [29]. These methods generally depend upon user interactive processes to select initial contours and frequently require human–expert correction of the final results.

A higher level of automation has been achieved using statistical shape models (SSMs) or active shape models (ASMs). For instance, Solloway reported cartilage segmentation based on ASM [30], [31]. Kapur adopted the strategy to first segment the more easily identifiable femur and tibia bones by region growing, and then detect cartilage voxels using a Bayesian classifier [32]. Pirnog combined ASM and Kapur’s strategy to produce a fully automated segmentation of patellar cartilage [33].

Fripp designed an automated segmentation system based on SSM [34]. In this work, when given a pre-segmented bone-cartilage interfaces, it took about an hour to segment the cartilage surface on an MR image with size 512 × 512 × 70. More recently, Fripp et al. [19] employed atlas-based bone registration and bone-cartilage interfaces (BCI) were segmented by ASMs. The cartilage surfaces were detected along BCIs using active surface models. This system achieved very good segmentation results but required optimization of a large set of parameters and suffered from long segmentation times. Based on similar statistical shape modeling principles, a method for defining anatomical correspondence enabling regional analysis of cartilage morphology was reported in [35].

Folkesson’s fully automatic voxel classification method used two KNN classifiers to distinguish femoral and tibial cartilage regions [23]. The results established that multiple binary classifiers performed better than a multiple-class classifier, and it illustrated the importance of different features for cartilage segmentation. However, like other pure pattern recognition based segmentation systems, their method suffered from slow performance. Dam et al. accelerated the process with sample-expand and sample-surround algorithms [36]. His method required about 15 min to segment femoral and tibial cartilages in a 170 × 170 × 110 MR image with so called sample-expand and sample-surround algorithms. Warfield’s template moderated (ATM), spatially varying statistical classification (SVC) algorithm combined nonlinear registration and KNN classification [37]. Other employed approaches include Watershed Transform by Grau or Ghosh [38], [39].

B. Method Properties, Novelty and Generality

To the best of our knowledge, this is the first paper in the archival literature to report the simultaneous segmentation of multiple objects with multiple surfaces per object. In the present application, the framework was applied to segment knee joint cartilage via simultaneous segmentation of the bone and cartilage surfaces of the femur, tibia, and patella. We have previously reported a general outline of this approach which required interactive initialization, used simplified cost functions, and lacked any validation [40]. The method is based on a layered-graph optimal image segmentation [3] that was extended to handle multiple interacting objects. This is a nontrivial extension that facilitates utilization of the optimal layered graph approach for segmentation of multiple objects for which the interaction properties may be based on surface proximity (as in the present application) as well as on any other general mutual relationships (e.g., relative distances of object centroids, orientation of the interacting objects in space, relative orientation of the interacting surfaces, etc.). The method can be directly extended to n-D, and the interobject relationships can include higher-dimensional interactions, e.g., mutual object motion, interactive shape changes over time, and similar. Overall, the presented framework is general and represents a new level of complexity that can be addressed using the layered surface graph optimization paradigm.

C. Limitations of the Reported Approach

Our framework is general but not free of limitations. First, optimal layered surface graph segmentation approaches require availability of a meaningful preliminary segmentation (or localization) of the objects of interest prior to the optimal segmentation (or accurate delineation) step. Clearly, the quality of pre-segmentation can affect the ability of the final graph-search segmentation to identify the desired borders. For example, if the pre-segmentation surfaces are too distant from the desired surfaces, their shape is inappropriate, or if the pre-segmentation fails for a variety of other reasons, the final graph may not contain the desired solution. In the multiple interacting object case, the pre-segmentation must be reasonable for all mutually interacting objects since it affects the cross-object context incorporated in the framework. Note however, that the reasonability requirement may allow substantial inaccuracy. For example, if segmenting 3-D objects, all that may be required as a pre-segmentation result may be a topologically correct surface that is positioned within a range of possible distances from this pre-segmentation surface to the desired surface. As long as the desired surface occurs within the overall graph constructed from the pre-segmentation surfaces, the final simultaneous segmentation step may still yield the correct final segmentation—although with a dependency on the quality of the employed cost functions, surface smoothness constraints, possible shape priors, etc. In our knee joint segmentation application, the Adaboost localization followed by an iterative graph search approach for pre-segmentation of the individual bone surfaces was sufficiently robust and performed without any need for interaction or editing.

While ably solving the column-crossing problem, the ELF calculation utilized is computationally demanding for surfaces with high vertex density [12]. In our experiment, computing 40 points along each ELF for 2000 vertices consumed 13 s on our PC, which is comparable to computing Danielsson distance transform [41] for a 200 × 200 × 200 volume. However, ELF computation time increases exponentially with the increase in the numbers of vertices. One possible way to address this potential limitation would be to merge multiple distant vertex charges to one “larger” vertex charge when computing local ELF, thereby greatly decreasing the total amount of vertices involved in the computation.

The current implementation does not specifically deal with osteophytes, which can cause difficulties in the preliminary segmentation steps. This problem is left open for future work.

D. Cartilage Segmentation Errors

Complete 3-D cartilage segmentation is a difficult problem. Our current method, while performing very well overall, exhibited local surface positioning inaccuracies as reflected in the reported unsigned surface positioning errors (Fig. 9). The difficult character of the cartilage MR segmentation task can be appreciated when assessing the interobserver variability of bone and cartilage surface definition by human experts—manual tracings suffered from interobserver variability of 0.5 ± 0.5 mm assessed on a set of 16 MR 3-D datasets, with 10 slices manually traced per dataset by each of four expert observers. The interobserver variability of cartilage thickness was 1.0 ± 0.8 mm and was computed as the mean closest distance measured from all points marked by one observer to the mean curve fitted to all points identified by the remaining three observers. These closest distances were averaged over the entire marked dataset and served as an indicator of interobserver variability, thus calculated individually for each of the four observers. Clearly, the performance of the presented segmentation system compares well with the interobserver variability and is generally the same for all three bone and cartilage surfaces.

When considering the segmentation inaccuracy with respect to its location and underlying cause, a clear pattern can be observed, with errors mostly contained within the noncartilage regions and therefore of less functional importance. Short of implementing better MR imaging sequences, interactive user guidance may be incorporated resulting in semi-automated multiobject multisurface layered surface graph segmentation. Fig. 10 shows the case with the worst segmentation performance from the TEST set. Despite its locally incorrect surface segmentation caused by MR signal voids, interactive user guidance can very efficiently correct these errors in a semi-automated fashion and yield an accurate segmentation.

Fig. 10.

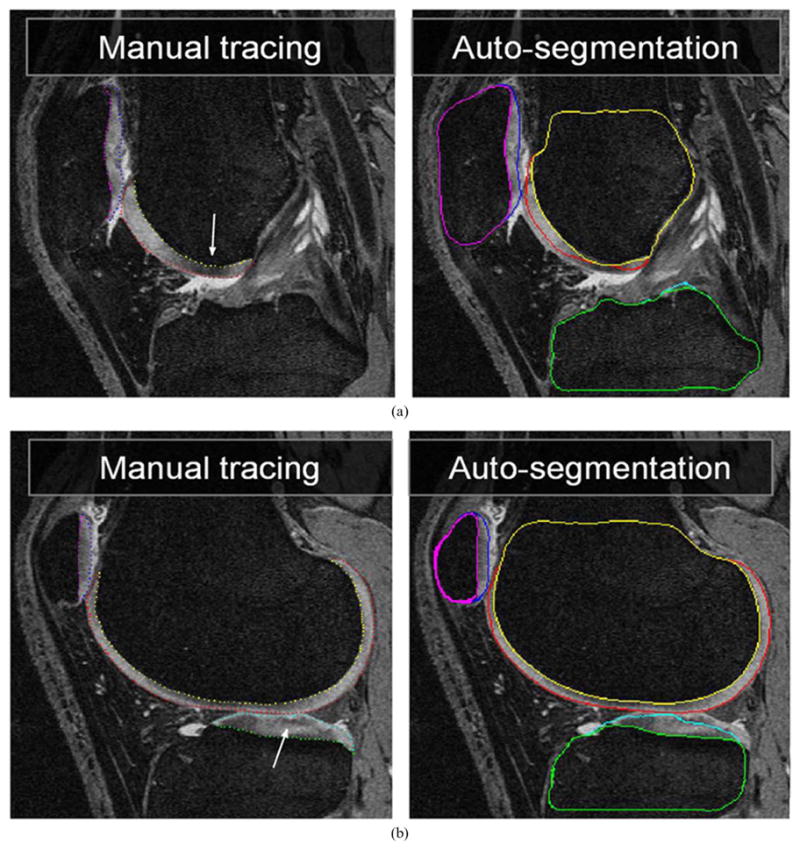
Worst TEST-set segmentation case. Two MR image slices from the 3-D volume shown with expert contours (left panels). Computer segmentation result shows local inaccuracies caused by signal void regions in the femoral and tibial cartilages, marked by arrows and by unexpectedly large cartilage thickness that has not appeared in the training set.

When assessing segmentation performance, it may be difficult to compare DSC-based segmentation performance directly with published results of others, since each study uses different images, training data sizes, and disease conditions. Note that the OA images are substantially more difficult to segment than images of healthy joints utilized in most published cartilage segmentation studies. The presented method obtains the segmentation relatively quickly and is much faster compared to the two previously reported methods of Dam and Fripp [19], [36]. Our approach required 20 min, compared with one to several hours of the earlier approaches on a comparable hardware when images of the same size are considered. Importantly, our novel approach offers comparable if not better performance than the earlier approaches. For example, Folkesson achieved DSC values of 0.78 and 0.81 for the femoral and tibial cartilage based on 51 healthy and 63 OA low-field MR images [23]. Fripp reported DSC values of 0.85, 0.83, and 0.83 for the femoral, tibial, and patellar cartilages from 20 healthy SPGR MR images [19].

The presented validation has been performed in several datasets using either leave-one-out or full-set approach. When setting up the validation scheme, it was imperative that the training and testing sets be completely disjoint—which asked for a somewhat complicated scheme of validation in different datasets and using different strategies. Not being able to get complete 3-D manual segmentations from the full set of 60 knees due to a large labor intensity, we needed to find a compromise. We have made a decision that it was more important to increase the number of subjects in our testing environment than having fully-traced knee surfaces. Therefore, we have performed partial validations in TRAIN-1, TRAIN-2, and TEST datasets. The advantage is our ability to present results in 60 datasets for which independent standard was created. However, a drawback of this decision was that we could not obtain DSC values from the large TEST set.

It is interesting to study whether the segmentation performance differed in the two OAI subgroups—incidence and progression. The signed and unsigned surface positioning errors for femoral and tibial bone and cartilage segmentations were compared using t-test. With p-value of 0.05 representing statistical significance, the signed and unsigned surface positioning errors for all six bone/cartilage surfaces were not significantly different in the two subgroups (p = NS for all six tests). The same outcome was obtained when comparing cartilage thickness errors—no statistical difference in femoral and tibial cartilage thickness errors (p = NS in both tests, patellar cartilage thickness comparison was not meaningful since the progression subgroup had only three subjects among the patellar cases for which independent standard was available.

The embedding of pattern recognition techniques within an optimal surface detection framework is the key new contribution of the presented methods. Notably, the presented approach has only one sensitive parameter to be determined—the surface smoothness constraint, and the selection of this parameter is intuitive. Too-small constraint values will make the algorithm insensitive to sharp discontinuities of bone and cartilage surfaces while too-large values will contribute to surface noise, roughness, and loss of the a priori shape information. In the work reported here, a smoothness constraint of three voxels was utilized, based on empirical determination. Although trained only on a small training set, the algorithm segmented complicated knee bone and cartilage structures well. As more training data becomes available in the future, we believe that the performance of the system can be expected to further improve.

VII. Conclusion

The presented LOGISMOS framework yields globally optimal segmentation of multiple surfaces and multiple objects, that are obtained simultaneously for all objects and all surfaces involved in the segmentation task. This novel approach extends the utility of our optimal layered surface approach reported in [3] by allowing the respective constraints and a priori information to be incorporated in the searched graph. The final segmentation is achieved in a single optimization step. A proof-of-concept application for knee joint cartilage segmentation was reported, successfully demonstrating the applicability of the novel method to the difficult and previously unsolved task of complete 3-D bone and cartilage segmentation from 3-D MR image data.