I. Introduction
The Karplus equation has had a long association with carbohydrates. Apparently, in 1958, while Martin Karplus was in the process of completing his seminal 1959 paper on the theoretical dependence of vicinal NMR coupling constants on the dihedral angle of the coupled protons,1 he attended a lecture by the late Raymond Lemieux at the University of Illinois in May, 1958 and recognized that Lemieux’s new experimental data for such couplings in carbohydrates2 and cyclohexenes3 fitted his theoretical results very well.4 It was not long before a number of other sugar chemists started exploiting this angular dependence of coupling constants in the conformational and configurational analysis of carbohydrates and their derivatives,5–7 and the Karplus equation has found wide acceptance and utility throughout organic and inorganic chemistry.
In many instances, however, it has been sufficient merely to be aware of the angular dependence, and to use the experimental fact that the coupling constant is large or small, depending on whether the coupled nuclei are trans or gauche, an approach which Karplus himself recommended.8 Responding to some criticism of the accuracy of dihedral angles calculated from coupling constants, Karplus published a second paper on the subject in 1963, in which the dependence of the couplings on substituent electronegativity and on bond length and bond angle were addressed.8 Since that time, the original Karplus equation has been modified, extended, generalized, and reparametrized to include a large number of different nuclear pairs, and more-finely tuned dependences on a host of molecular properties, in addition to dihedral angle and electronegativity.
Because of the very large number of applications of the Karplus equation in chemistry, an effort has been made to restrict the scope of this chapter to the more fundamental investigations of the Karplus equation and the coupling constants that support it. Also, coupling constants over one and two bonds do not have dihedral angles between the coupled nuclei and so have largely not been included, even though they depend on the orientation of substituents.9 Couplings over two bonds also have the practical disadvantage of a change in sign,9 depending on structure, and are not as highly used as three-bond couplings for structural determination. On the other hand, following Perlin and Casu’s discovery that one-bond 1H–13C coupling constants depend on anomeric configuration,10 its detailed elaboration by Bock and Pedersen,11–14 and angular dependence studies by Tvaroška, Taravel, and coworkers,15–18 these couplings have constantly been used as a method for determination of anomeric configuration that complements the use of three-bond 1H–1H coupling constants from the anomeric center. Indeed, the use of 1JCH is better in some cases than the use of 3JH-1,H-2, for example in α- and β-mannopyranose derivatives, where the 3J1,2 values are very similar.
II. The Impact of Improved NMR Instrumentation
In 1959, NMR spectroscopy was still in the primitive state of relying on continuous-wave, RF techniques, with magnetic field sweeps, and analogue spectral output on chart paper, from which coupling constants were determined by manual measurements of peak separations on the chart. Spectra were calibrated by the relatively crude procedure of placing audio modulation sidebands on the charts, which defined the frequency separations needed for measurements of coupling constants. Within 10 years, there were to be revolutions in both the practice of NMR spectroscopy and the computer field. The transition from continuous-wave techniques to Richard Ernst’s pulse-FT NMR method19,20 occurred rapidly, but the computer systems that were required for this new experimental procedure were at first slow, awkward, and suffered from extremely limited storage for data and programs; for example, 4 Kb for data and 4 Kb for program space, with no permanent storage for data, except on punched, paper tape.
Fortunately, there have been enormous improvements in computer technology resulting in cheap memory and storage, with the result that the number of digital points that can be used to define a spectrum is now limited only by the decay rate 1/T2★ of the FID, which is given by the sum of the real, transverse relaxation rate 1/T2 and the rate 1/T2(inhomo) due to magnetic field inhomogeneity. As a result, data tables of 256 Kb are now routinely possible for the 1D 1H and 13C NMR methods that are most commonly used to measure spin–spin coupling constants, as long as the FID does not decay to noise first.
Along with the computer revolution and digitization of data, there have been constant, iterative improvements in spectrometer and NMR probe performance. Competitive pressures have led to increasingly accurate phase and frequency synthesis, the adoption of more stable, digital lock systems for field–frequency regulation, and very large gains in NMR detection sensitivity, particularly from the development of cryoprobes (cold probes) that afford a sensitivity improvement of ~4 over normal probes, corresponding to a reduction in acquisition time by a factor of 16.
By using the trade off of sensitivity versus resolution that is inherent in most spectral apodization methods, the improved sensitivity has allowed much more vigorous resolution enhancement to be used, allowing spectral multiplets to be split easily to the baseline, thus enhancing the measurement accuracy for the coupling constants.
Because the spacings used to measure the coupling constants are calculated as the difference of two frequencies, it is important that the spectra have adequate digital resolution, otherwise the experimental errors in the coupling constants could possibly be doubled. The larger data sets that are possible with modern equipment certainly allow this, together with such data extension methods as zero-filling and linear prediction, and the digital output of the peak positions by sophisticated algorithms that take into account several points near the top of the peak, and not just its maximum value. Enhanced computer processing speed has also been important for rapid computations of the Fourier transform and for other digital signal processing, which became essential once multidimensional NMR techniques were adopted.
III. The Impact of Molecular Modeling
When the Karplus equation was first developed, few methods were in use for the specification of molecular geometry, and correlations of coupling constants with atomic dihedral angles were perforce often based on approximate methods such as measurement of Dreiding molecular models (±10°) or on assumptions that carbohydrate rings have dihedral angles that are similar to the “idealized” angles in related alicyclic molecules.21 The wider use of X-ray crystal structure data has had the advantage that the dihedral angles that may be calculated from such data are obtained by experiment, but the disadvantage that they refer to the solid state, which may exhibit a different conformation from that present in solution. Other methods for the determination of molecular geometry such as high-quantum, local field solid-state NMR spectroscopy22 suffer from the same disadvantage, if comparisons with the solution state are desired. A number of authors have clearly assumed, without proof, that the conformations in the solid and solution states are the same. Over the past 50 years, a number of powerful computational methods for the determination of molecular geometry have been adopted, including ab initio MO methods (such as Hartree–Fock), VB calculations, semiempirical (CNDO, INDO, and others), DFT (GAUSSIAN94, GAUSSIAN98, GAUSSIAN03), and MD/MM (such as Accelrys Insight/Discover, CHARMM, GROMOS96, PCMODEL, and others). VB methods are largely out of date at this point and do not always correctly reproduce the magnitudes and signs of coupling constants. Programs such as Insight/Discover that display values of dihedral angles merely by clicking on four atoms of a structure displayed on a computer monitor are particularly useful, since they avoid tedious manual calculations based on atomic coordinates. Of course, many of the methods of computational chemistry are based on approximations to a varying degree, but a realistic goal for the computation of dihedral angles appears to be ±0.5°.
IV. Vicinal Coupling Constants
Vicinal 1H–1H coupling constants comprise the vast majority of coupling data that have been reported, and as the simplest case, substituted ethanes, have been exhaustively studied. These studies are described here because sugar chains may be regarded as a series of ethanic fragments, albeit with transannular stereoelectronic and anomeric effects, flanking group interactions, and other phenomena superimposed.
1. Proton–Proton Couplings
a. Proton–Proton Couplings, 3JHCCH
Initially, VB theory was used by Karplus to calculate 3JHCCH in ethane,1 which could be fitted approximately by the equations:
| (1) |
where ϕ is the dihedral angle between the hydrogen atoms (also known as the projected valency angle, the torsion angle, or the torsion). For unsaturated systems, additional contributions from π-electrons were found to provide a quantitative explanation of the experimental results.23 Later,8 the results of the VB σ-electron calculation were restated in the equation:
| (2) |
For a C–C bond length of 1.543 Å, sp3 hybridized carbon atoms, and an average energy, ΔE of 9 eV, the calculated constants were A = 4.22, B = −0.5, and C = 4.5 Hz.
A trigonometrically identical form of Eq. (2) has generally been used, namely,
| (3) |
because its quadratic form21 allows an explicit calculation of ϕ from the coupling constant, despite a warning from Karplus.8 In Eq. (3), the values of the constants A, B, and C are 9.0, −0.5, and −0.3 Hz, respectively. Dependences on substituent electro-negativity, and on bond angle and length were also calculated,8 although the latter two molecular properties have proved to have minor effects.
Efforts were soon made to incorporate an explicit electronegativity dependence. For example, Abraham and Pachler derived the expression
| (4) |
where ΣΔχi is the sum of the electronegativity differences between the substituents i attached to the ethane molecule and hydrogen.24 From data for tetrasubstituted aldopentopyranose derivatives, Durette and Horton formulated the expression:25
| (5) |
This equation was modified by Streefkerk et al.26 and used for calculation of 3JHCCH values for 14 ideal conformations (two chair, six boat, and six skew forms) of per-O-trimethylsilyl derivatives of 6-deoxyhexoses,27 and for structural studies of glycopeptides:28
| (6) |
where ϕ is the dihedral angle between the protons in the fragment H–C–C′–H′, and where the electronegativity factor fi = 0.15 when the torsion angle θ between R and H in H–C–C′–R is > 90°, and fi = 0.05 when θ < 90°. In effect, Eq. (6) includes an approximate dependence of 3JHCCH on the angular orientation θ of the substituent R, a subject that is discussed next.
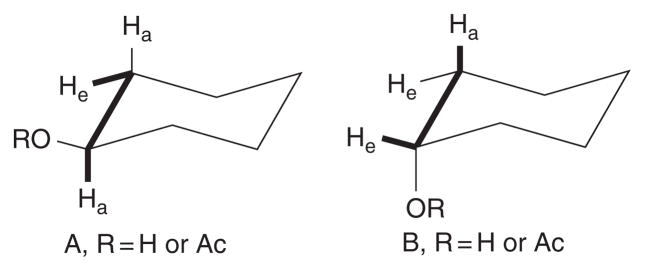
It was recognized as early as 1964 that there is a dependence of 3JHCCH on substituent electronegativity orientation. In a study of steroid molecules, Williams and Bhacca found that Jae 5.5 ± 1.0 Hz was about twice as large when there was an equatorial electronegative substituent attached to the coupling pathway, as the value Jea 2.5–3.2 Hz measured when the substituent was attached axially.29 These orientations correspond to a gauche relationship of the substituent to one of the coupled protons, and a trans arrangement, respectively (Fig. 1).
Fig. 1.
Differing orientations of the electronegative substituent RO on the 3JHCCH coupling pathway in steroid fragments. In type A, Jae was observed to be 5.5 ± 1.0 Hz, whereas type B showed Jea 2.5–3.2 Hz, thus illustrating enhancement of the coupling constant when the electronegative substituent is gauche to one of the coupled protons.
This significant dependence was also noted by others,30,31 but was not fully addressed until 1979, when Haasnoot, Altona, and coworkers commenced the publication of a series of papers32–34 in which the 3JHCCH values of substituted ethanes and other molecules were investigated with great attention to accuracy and detail; studies that were assisted by the increasing sophistication of NMR instrumentation.
Meanwhile, Pachler calculated 3JHCCH values for substituted ethyl derivatives using the Pople–Santry LCAO-MO method, a variant of EHT, and found (a) a linear dependence of the vicinal couplings on substituent electronegativity, and (b) that the couplings were described35 well by the expression:
| (7) |
This relationship has been described as a truncated Fourier series containing a fundamental and one overtone.33 Addition of the sine terms to the original Karplus equation was required to represent the asymmetry of the curves at ϕ = 0°.
Pachler subsequently accounted for the dependence of the coupling on electronegativity and its orientation using equations36 which were interpreted by Haasnoot et al.33 as:
| (8) |
where Σ′Δχi is a sum of the electronegativity differences that is given a positive or negative sign, depending on the gauche or trans orientation of the electronegative substituent just mentioned above. This reflects experimental observations that the gauche orientation of this substituent increases the magnitude of the coupling,29 whereas the trans orientation decreases it.37
For reasons that have been described in detail,33 it was proposed that Eq. (8) be replaced by a new relationship, now known as the Haasnoot or Altona equation:
| (9) |
in which the sign parameter ζ takes the value +1 or −1, depending on the orientation of the electronegative substituent, which was now defined more carefully33 to cover all possible values of ϕ (Fig. 2). By least-squares fitting of 315 coupling constants obtained from 109 compounds to dihedral angles calculated by molecular mechanics using Allinger’s MM1 force field, the parameter values P1 13.88, P2 −0.81, P3 0 (assumed), P4 0.56, P5 −2.32, and P6 17.9 Hz were determined. A Macintosh desktop calculator program, SWEET J is available for Eqs. (3) and (9), which solves the equations both numerically and graphically.38 The program features include display of the fragment under consideration as a Newman projection, the dihedral angle can be changed with the mouse device, and the absolute configuration of stereogenic centers is determined by the computer.38 An alternative PC desktop calculator program, ALTONA, has been written39 for Eq. (9).
Fig. 2.
Definition of positive and negative orientations of substituents R-1–R-4 with respect to the vicinally coupled protons in tetrasubstituted ethanes.
Although the first atom of the electronegative substituent has the greatest effect on the coupling constant (and also on 1H and 13C chemical shifts in general), the data and EHT-MO calculations of Haasnoot et al. and other data in the literature indicated the need for another parameter P7 that would describe the moderating effect of the β-part of a substituent on its electronegativity, namely, a reduction in the electronegativity of the entire substituent, as the electronegativity of the β-part increased.33 Therefore, an additional equation was introduced:
| (10) |
where the summation extends over all of the substituents attached to the α-substituent. Small values of P7 were found, 0.14, 0.24, 0, and 0.19, depending on whether Eq. (10) was used with only the β-effect, or two, three, or four substituents, respectively.33
Equations (9) and (10) were applied initially to monosubstituted cyclohexanes with reasonable success,33 and later to proline derivatives,40 together with the ribose ring in nucleosides and nucleotides.32,34 These equations readily allow the computation of a coupling constant from a torsion angle and the electronegativity factors, but do not offer an explicit solution for the reverse computation, namely the calculation of a torsion angle from a coupling constant.33 For the latter computation, iterative, trial-and-error methods or graphical determination can be used, assisted by a computer program CAGPLUS.33
The conformations of five-membered rings have long been interpreted in terms of a classical equilibrium of North (N) and South (S) conformers, where these terms refer to the regions of conformational space at the top and bottom of the pseudorotational cycle, respectively.34,40–42 While the cyclopentane conformation moves freely around the pseudorotational cycle, the placement of substituents on either homocyclic or heterocyclic five-membered rings raises the energy barriers between certain conformers, generally restricting them to the N and S regions.34 By applying Eq. (9) to the sugar ring in a range of nucleoside and nucleotide derivatives, Haasnoot et al. demonstrated that, depending on substituent pattern and structure, the equilibrium can be biased toward either the N or S type.34 For example, the 2′-deoxyribose ring with O-3′ pseudoaxial favors the S-type conformation, whereas the 3′-deoxy compound with O-2′ quasiaxial favors the N-form.34
Following the recognition that 3JHCCH depends on both the group electronegativity value and its orientation, and the availability of a set of additive constants (ΔJ values) proposed for prediction of Jgauche in trisubstituted (CH2CH) fragments of polypeptides,43 Altona and Haasnoot developed a simple additivity rule for prediction of anti and gauche 3JHCCH values in pyranose rings.44 This represents an alternative approach to the use of Eqs. (9) and (10). Good quality 1H NMR data were tabulated or measured mostly at 270, 300, or 360 MHz for a large number of hexopyranoses, pentopyranoses, and 2-deoxy-pentopyranoses, and a few 4,6-O-benzylidene derivatives.44 Analysis of the data allowed a table of additivity constants, ΔJ(X) for substituents X in pyranose rings to be constructed.44 These constants clearly demonstrate the incremental effect of Xgauche on 3Jae and 3Jee, and the decremental effect of Xanti on 3Jae and 3Jee, and of Xgauche on 3Jaa. The agreement between experimental and calculated coupling constants was characterized by a standard deviation σ = 0.29 Hz, so that in 95% of the cases, the experimental value would not deviate from the predicted value by more than ±0.6 Hz. It was predicted that, for pyranose systems that bear an axial substituent at C-2 (e.g., mannosides, altrosides, and rhamnosides), the difference in 3J1,2 of the α and β anomers will be determined exclusively by the electronegativity of this axial substituent.44 The results also encompass Booth’s rule that an electronegative substituent attached to an HCCH fragment exerts a maximum negative effect on 3Jgauche when positioned in an anti-periplanar orientation to one of the coupled protons,37 and the observation of Abraham and Gatti that, in 1,2-disubstituted ethanes,30 the coupling of two gauche protons flanked by two gauche electro-negative substituents obeys Eq. (11):
| (11) |
where the electronegativity difference Δχi = χi − χH.
Colucci et al. proposed the equation:
| (12) |
where ϕHX(i) is the dihedral angle between the interacting proton and the substituent Xi, and Δsi is a single, empirically determined constant of the substituent.45 This equation was constructed on the premise that the torsional dependence of 3JHCCH could be described as a simple perturbation of the ethane system. Torsion angles were determined from X-ray crystal structure data and MM2 molecular mechanics. If perfect tetrahedral geometry is assumed for the ethanic fragment, then ϕHX(i) = ϕ ± 120° can be used, leading to a more useful expression:
| (13) |
The values of Δsi were obtained from experimental coupling constants for mono-substituted ethanes,45 and the values tabulated for 39 substituents covered a range from −0.92 Hz for a lithium substituent (electron donating), through 0.00 Hz for H, to 13.9 Hz for (electron withdrawing). However, the authors commented that the variation of the Δsi values defied a consistent explanation, and at that time had not been totally correlated with any other set of substituent constants or properties of the groups.45
In the foregoing discussion, the electronegativity values χi referred to are those of Huggins,46 which are modifications of Pauling electronegativities.47 In later work, Altona et al.48 studied the electronegativity dependence of the torsion angle-independent term A in equations such as (7). They measured 3JHCCH values for substituted ethanes even more carefully, with an estimated data-point accuracy of ≤ 0.02 Hz. Attempts to fit these data led to the conclusion that none of the existing χ tables would correlate well with the observed couplings.48 On this basis, it was proposed that the use of χ electro-negativities for coupling-constant correlations be abandoned in favor of a new electro-negativity scale of λi values, derived from the data set at hand.48 A least-squares fit was applied to the J values of 55 mono- and 38 1,1-di-substituted ethanes, including 22 isopropyl derivatives. Altona et al. also proposed that any nonadditivity or interaction effect on the coupling constants could be described well by the introduction of cross terms, including the product of either the electronegativity differences, ΔχiΔχj, or of the substituent constants, λiλj. To correspond approximately to the Huggins electronegativity scale, the new λi values were scaled so that λH = 0, and λOR = 1.40, values that were part of a series for some 50 substituents, including many carbon-bound groups, and nitrogen, oxygen, halogen, phosphorus, silicon, and sulfur-containing groups.48 It was proposed that the electronegativity dependence of the couplings of the substituted ethanes could be described by the expression:
| (14) |
where λ1 and λ2 are the new electronegativity values of up to two substitutents. A striking difference between the new λi scale and other empirical, electronegativity scales was found to be the inverse correlation of λi with the electronegativity of the β substituent, whereas in Δχ scales, the reverse obtains.48 Equation (14) was found to fit 84 experimental couplings with an rms deviation of 0.018 Hz, and a maximum deviation of 0.06 Hz, but the parent ethane and monohalo- and 1,1-dihalo-ethanes were exceptions that had to be parametrized differently. The λ electronegativity approach was supported by theoretical calculations of 1404 coupling constants using a reparametrized EHT method for ethane and its derivatives, singly or multiply substituted with Cl, F, Me, and OH.49 Pairwise interactions between substituents were accounted for by using specific quadratic cross terms to describe the electronegativity dependence of the coefficients in a truncated Fourier series, with simultaneous least-squares optimization of the Fourier coefficients and the electronegativity values.49 The theoretical coupling constants generated in this study were fitted by expanding Pachler’s equation [Eq. (7)] to include a cos 3ϕ term, and additional coefficients for the electronegativity cross terms, giving:
| (15) |
where
and
Definitions and values for the coefficients are given in the original publication.49
The rms deviation of the total set of couplings was reduced to 0.124 Hz, which was stated to be markedly improved over that for the Pachler and earlier Haasnoot–Altona studies.49
The non-bonded, through-space transmission of spin information, known as the Barfield transmission effect, has been investigated theoretically for five-membered rings by the FPT-INDO-SCF-MO method.50 An early observation of this effect was the non-equivalence of Jendo-endo and Jexo-exo in norbornanes,51,52 which was also predicted to occur in cyclopentane, tetrahydrofuran, and in 7-hetero-substituted nor-bornanes,50 and also explains50 the observed non-equivalence of cisoid H–Cβ–Cγ–H and H–Cγ–Cδ–H couplings in prolines.53,54 This effect is not described by the typical basic or generalized Karplus equations, and the computations of de Leeuw et al.50 suggested that it could be approximated by the function:
| (16) |
where ΔJ is a decrease in the size of the coupling due to the transmission effect, P is the phase angle of pseudorotation in the five-membered ring, Pb is the phase angle of the envelope form for which a maximum effect is reached, and T depends strongly on the nature of the atom through whose orbitals the effect is transmitted. T was estimated to be ~0.5 Hz for a furanose ring oxygen, and ~2 Hz for a carbon atom. Correction by Eq. (16) needs to be applied only to cisoidal coupling constants in five-membered rings calculated from a Karplus-like equation.50 The correction is thought to be negligible for ribofuranose systems, where the maximum decreasing effect is small (~0.5 Hz) and occurs in a forbidden region of P ~270°. In 2-deoxyribose systems, the correction is more important, because the South-type conformer predominates.50 The Barfield correction term has been incorporated in the PSEUROT program, with the assumption of a two-state, North–South equilibrium.55 Transoid couplings are not affected by this Barfield effect.50
In an empirical tour de force, the Karplus equation has been expanded to contain 13 mutually independent structural terms and 22 adjustable parameters.56 The terms were selected and evaluated individually, with the assumption of a linear additivity. A standard set of 198 vicinal coupling constants determined from 104 compounds dissolved in nonpolar solvents was selected from the literature, including mostly alkanes and halides, but with a number of other substituent types represented, and four sugars. An interesting, arbitrary assessment of coupling constants measured in different decades was made by assigning a precision of 0.2 Hz for data reported before 1969, 0.1 Hz for those from 1970–1979, and 0.05 Hz for those reported after 1980. In fitting data to the modified equation, the experimental coupling constants were weighted by the reciprocals of the assigned precisions. A number of group-electronegativity scales were considered, and that of Mullay was selected as being most suitable.56 Plotting of Mullay’s group electronegativities, χsub against 26 3JHCCH values for substituted ethanes revealed a good linear relationship:
| (17) |
with A = 7.520 and B = −0.2088. Optimum molecular geometries were determined by Allinger’s MM2/MMP2(85) program, and the consideration and rejection of many different molecular properties led to the equation:
| (18) |
where the summation with respect to i refers to all substituents on the H–C–C–H system, the summation pertaining to j to all β substituents, and ω1 and ω2 are the C–C–H bond angles.56 The cos3ϕ and cos22ϕ terms represent testing of logical extensions of the series of terms in the original Karplus equation [Eq. (2)], and in Eq. (18), the angle θi subtended by the electronegative substituent with respect to a coupled proton has been parametrized separately from the HCCH dihedral angle ϕ, or the cos (ϕ + 120°) and cos (ϕ − 120°) terms used in other studies. As is evident in Eq. (18), combinations containing both ϕ and θi were also tested for the electronegativity terms, and the orientation of the β-part of the α-substituent to a coupled proton is described by a new torsion angle, ψ. The H term in Eq. (18) represents an average deviation of the C–C–H bond angles from the tetrahedral angle, and the Barfield transmission effect, which reflects the proximity effect of non-bonded substituent atoms to the coupled protons, is characterized by the Lr−4 term. The exponent in the latter term was tested exhaustively in the range −1 to −12, but was found to be meaningful only when the proximal atom was carbon or oxygen at a distance r < 3.3 Å. Fitting of Eq. (18) to the 198 values of 3JHCCH led to the optimum parameters A = −1.2246, B = 5.0935, C = −0.1055, D = 0.5711, E = 0.8319, F = 0.0433, G = 0.0345, H = −0.2058, I = −8.9222, K = 0.1438, L(carbon) = −8.9395, and L(oxygen) = 6.9202. The parameter M took values of 7.5075, 7.0306, 6.4793, 6.5432, or 5.5319, depending on whether the compounds were mono-, 1,1-di-, 1,2-di-, tri-, or tetra-substituted, respectively.56 Similarly, the W values found for these substitution patterns were 1.00, 2.55, 1.16, 2.29, and 1.40, respectively. The units used in Eq. (18) are Å for distances, degrees for valence and dihedral angles, and Hz for coupling constants.
This comprehensive study also tested the relative importance of the various terms in Eq. (18), and its relative performance when compared with modified Karplus equations of the Pachler, Haasnoot, and Colucci et al. types. Based on standard deviations of errors, the ranking of the four most important terms was found to be cos2ϕ, cosϕ ΣΔχi cos θi, cos ϕ, and (ω1 + ω2)/2. Thus, the second most important term is the combined electronegativity/electronegativity orientation term, and the fourth most significant one is the bond angle term, the first- and third-ranked terms being present in the original Karplus expression. An alternative equation containing these top four terms was proposed:
| (19) |
which can be used with little loss of precision, if a computer program for Eq. (18) is unavailable.56 However, Eq. (18) was found to have the lowest standard deviation (0.3255 Hz) of the four equations tested, when they were applied to the 3JHCCH values of single conformation molecules in the standard set.56
Some 14 years after publication of the original Haasnoot equation, it was reparametrized to include a λi group electronegativity scale and specific parameters for substituted ethane derivatives,57 regardless of degree of substitution:
| (20) |
where the sign parameter is now si = ± 1. A slightly modified λi scale was constructed from the couplings to methyl in substituted ethanes and isopropyl derivatives, which were represented by the equation:
| (21) |
The parent ethane and its dihalo derivatives were now included, but norbornanes and molecules suspected to be conformationally inhomogeneous were excluded.57 Molecular geometries were recalculated using the MM2-85 force field. By this means, the overall rms error for the 3JHCCH values was lowered from 0.48 to 0.36 Hz. The λi values derived previously were found to be still valid for common organic solvents, but a slightly different λi scale was constructed for solutions in D2O,57 for compounds where the α-substituent carries one or two non-conjugated lone pairs of electrons that readily act as hydrogen-bond acceptors, so that Δλ = −0.11 ± 0.03 for NH2, NHR, NR2, OH, OR, and R = alkyl. The λi values for the nucleic acid bases A, C, G, T, and U, as determined from N-isopropyl derivatives, were found to be 0.56 ± 0.01, irrespective of solvent.57 The Pachler equation and equations such as (20) were stated to be valid for saturated HCCH fragments with approximately tetrahedral bond angles, but not for strained molecules such as norbornanes, in which large deviations from tetrahedral geometry occur.57
Various models for the interaction between pairs of substituents in ethanes have been discussed.58,59 MCSCF ab initio calculations of 3JHCCH in ethane have given the contributions from the Fermi contact, spin dipolar, orbital paramagnetic, and orbital diamagnetic mechanisms, of which only the Fermi contact contribution was found to be significant.60
In a different approach,61 3JHCCH values (and also 1JCH and 2JHCH) have been computed by DFT methods for exocyclic hydroxymethyl groups on aldopyranosyl rings, and the values compared with experiment and correlated with the O-5–C-5–C-6–O-6 torsion angle ω, according to the equations:
| (22) |
| (23) |
These relationships have been confirmed by DFT calculations on hydroxymethylte-trahydropyran analogues of aldohexopyranosides,62 using a set of staggered and eclipsed geometries, which on least-squares fitting of the theoretical coupling constants yielded:
| (24) |
| (25) |
This study62 also led to the equation:
| (26) |
reflecting the dependence of this geminal coupling on both of the torsion angles ω and θ, about C-5–C-6 and C-6–O-6, respectively, and the more significant dependence on θ.
Experimental values of 3JHCCH were redetermined for the methyl α- and β-pyranosides of D-glucose and D-galactose, and were found to agree well with the results of the DFT computations.62
b. Proton–Proton Couplings, 3JHCNH
Barfield and Karplus63 combined a theoretical VB bond-order formulation of contact nuclear spin–spin coupling with a semiempirical approach based on Whiffen’s measurements of proton hyperfine splitting data for π-electron radicals and radical ions of the form •C-CHR2, •C-NHR, and •C-OH, leading to the equation:
| (27) |
However, equations such as this one were thought to have the limitation that because they were derived from the hyperfine interaction, which is symmetric about ϕ = 90° no account was given of the asymmetry in the coupling constant.63 3JHCNH is commonly observed to be 8.0–9.5 Hz in acetamidodeoxy sugars, and in secondary amines, such as N-2,4-dinitrophenyl derivatives of amino sugars.64–66 For a long time, an explicit Karplus equation for 3JHCNH in amino sugars was not available, and an equation with coefficients derived from model peptides by Bystrov et al.67 was sometimes used. It has often been assumed that the 8.0–9.5 Hz coupling represents a trans arrangement of the coupled protons, for example H-2 and NH in the 2-acetamido-2-deoxy sugars. However, molecular dynamics simulations of tetrasaccharide fragments of hyaluronan suggested that a cis arrangement of the coupled protons sometimes occurs, and, therefore, that high values of 3JHCNH cannot always be used to infer a purely trans form of the acetamido group.68
More recently, a very detailed theoretical study of 2-acetamido-2-deoxy-D-glucose and 2-acetamido-2-deoxy-D-galactose has been reported, in which DFT was used to calculate 3JH-2,NH values of the pyranose anomers.69 Karplus coefficients were then derived by least-squares fitting of the theoretical coupling constants to Eq. (3). The fitted Karplus parameters were found to be similar to those derived previously for peptide amide groups,67 but were consistently larger. An implicit solvation model consistently lowered the magnitude of the calculated values, improving the agreement with experiment. However, an explicit solvation model worsened the agreement with the experimental data.69 A detailed study of the effect of libration of the acetamido group on 3JH-2,NH values was also performed.69 The dynamical spread of the rotation of the acetamido group in free α-GlcNAc, β-GlcNAc, and α-GalNAc was estimated to be 32°, 42°, and 20°, with corresponding dihedral angles of 160°, 180°, and 146°, respectively. From DFT calculations containing mainly the important Fermi contact coupling term (but sometimes other interactions, too), the Karplus coefficients found for a 3JH-2,NH version of Eq. (3) were A = 9.45–10.02 ± 0.21–0.26, B = −1.51 to −2.08 ± 0.10–0.13, and C = 0.49–0.99 ± 0.12–0.16, depending on which GlcNAc or GalNac anomer was calculated. It was suggested that Karplus equations derived for proteins no longer be used for these sugars.69
c. Proton–Proton Couplings, 3JHCOH
The VB bond-order–proton hyperfine splitting combination of Barfield and Karplus63 also led to the equation:
| (28) |
However, this equation was considered to have the same failing as Eq. (27) in Section IV.1.b, in that the couplings for torsion angles of 0° and 180° are expected to be and are most commonly observed to be different.63
Based on two values of 3JHCOH obtained by an exact analysis of the ABC system in the hydroxymethyl group of 3β-acetoxy-5β,6β-oxidocholestan-19-ol and three other literature values, Fraser et al.70 formulated the expression:
| (29) |
However, the published spectrum of the steroid had significant noise on the peak maxima, and inspection of the 1H shifts reported from an ABC analysis at 60 MHz revealed that this system would undoubtedly be AMX at current 1H NMR frequencies of 500–950 MHz and would benefit from redetermination of the 3JHCOH values. Until recently, this type of coupling had not been investigated in detail for sugars, despite many reported values, and the detection of such couplings in supercooled, aqueous solutions of carbohydrates.71–73 For methyl β-D-gluco- and β-D-galactopyranosides, the latter studies reported averaging of the 3JHCOH values (4.75–6.24 Hz), which was attributed to free rotor, hydroxyl groups.72 However, other studies, for example, methyl 2,6-anhydro-3-deoxy-3-phthalimido-α-D-mannopyranoside in chloroform solution, have shown more extreme values (3J4,HO-4 11.6 Hz) that probably represent an anti arrangement of the coupled protons.74
A very detailed study of 3JHCOH and other related coupling constants has recently been conducted.75 Zhao et al. performed DFT calculations on a series of aldopyranosyl model structures, many of which were deoxygenated at C-3, C-4, and/or C-6, so as to eliminate any undesired hydrogen bonding.75 DFT calculations were carried out with (a) only the Fermi contact contribution included and (b) non-Fermi contact terms included as well. For non-anomeric protons, inclusion of only the Fermi contact term resulted in a generalized Karplus equation:
| (30) |
which is similar to Eq. (29) of Fraser et al. The results from inclusion of all four contributions showed that the spin–dipolar term is negligible, whereas the paramagnetic spin–orbital and diamagnetic spin–orbital terms have comparable magnitudes, but opposite signs, thus leading to a slightly modified equation:
| (31) |
The situation is more complicated for 3JHCOH involving the C-1–O-1 bond, because in one of the rotamers about this bond, HO-1 is anti to O-5, which (by Booth’s effect) reduces the value of 3JHCOH in this rotamer, causing the magnitudes of the two gauche couplings to be non-equivalent, and the derived Karplus curve to be phase-shifted relative to that predicted from Eq. (31). Because of this phenomenon, separate equations (Fig. 3A) are required for α- and β-pyranoses:
| (32) |
| (33) |
Fig. 3.
(A) DFT calculated, four-quadrant plots of dependence of 3JH-1,HO-1 on the torsion angle about C-1–O-1, for 3,4,6-trideoxy mimics of α-D-glucopyranose and α-D-mannopyranose (Eq. (32), blue triangles) and β-D-glucopyranose and β-D-mannopyranose (Eq. (33), black squares). The data are superimposed on a plot of Eq. (31), (red circles). (B) DFT dependence of 3JC-2,HO-1 on the C-1–O-1 torsion angle in 3,4,6-trideoxy mimics of α-D-glucopyranose (Eq. (57), green circles), β-D-glucopyranose (Eq. (59), blue triangles), α-D-mannopyranose (Eq. (58), black squares), and β-D-mannopyranose (Eq. (60), purple diamonds).
The theoretical studies of 3JHCOH were supported by experimental measurements on methyl β-D-glucopyranoside, methyl β-galactopyranoside, methyl β-lactoside, methyl β-D-(4-13C)glucopyranoside, methyl β-D-(1-13C)galactopyranoside, and methyl β-(1,4′-13C2)lactoside at 600 MHz, using solutions of the sugars in a mixture of acetone-d6 and highly purified water at −20 °C, to reduce the rate of hydroxyl-proton exchange.75
d. Proton–Proton Couplings, 3JHCSiH
The angular dependence of 3JHCSiH has been investigated by NMR studies of cis- and trans-3,5-dimethyl-1-silacyclohexanes, and 3-silabicyclo-[3.2.1]octane, the 1H spectra of which afforded eight values of the coupling.76 Torsion angles for the 1-silacyclohexane derivatives were assumed on the basis of electron-diffraction data for 1,1-dichloro- and 1,1-dimethoxy-1-silacyclohex-ane in the gas phase, and for 3-silabicyclo-[3.2.1]octane from literature data obtained by force-field methods, which together yielded ϕ values in the range 25°–165°. Least-squares fitting of the couplings to the angles resulted in the equation:
| (34) |
An interesting corollary of this study was that the conformational free energy of the methyl group in 1-methyl-1-silacyclohexane is ~1.45 kJ mol−1 in favor of the axial orientation of this group.76
2. Proton–Carbon Couplings
The most important coupling constant of this type in carbohydrates is undoubtedly 3JHCOC, because this coupling occurs up to two times in the interglycosidic linkage, and, therefore, offers information on the transglycosidic angles ϕ and ψ. 13C substitution is helpful in the measurement of these couplings, but is not mandatory, as a large number of NMR methods have been developed for measurements at natural abundance. Early data measured by Lemieux et al.77 on uridine analogues substituted with 13C at C-2 of the uracil residue and on 3,4,6-tri-O-acetyl-α-D-glucopyranose 1,2-(methyl 1-13C-orthoacetate) suggested the existence of a Karplus relationship for 3JHCOC and 3JHCNC, but no attempt was made to define any equations.
a. Proton–Carbon Couplings, 3JHCOC
The early history of this coupling has been the subject of previous reviews, in which the Karplus-type relationship was illustrated graphically,78,79 and later interpreted80 by the equation:
| (35) |
A Karplus equation of the three-parameter type was proposed by Tvaroška et al.81 based on the precise measurement of 3JHCOC in a series of conformationally rigid carbohydrate derivatives having known X-ray structures:
| (36) |
The compounds studied included 1,6-anhydro-aldohexo- and ketohexo-pyranoses, which contained X-ray defined dihedral angles in the range 86°–279° and 3JHCOC 0–5.9 Hz. Literature data for cyclomaltohexaose, phenyl 3-O-acetyl-β-D-xylopyrano-side, and 1,2-O-ethylidene-β-D-glucopyranoside, provided coupling values for estimated dihedral angles of 10° and 60°. The 3JHCOC values were measured on natural-abundance 13C by selective, 2D J-resolved spectroscopy, or by a modified, selective 2D INEPT experiment. Seventeen data pairs were used to construct 17 simultaneous equations which were solved for the values of A, B, and C in Eq. (3). In this study, the possible influence of electronegativity factors on the couplings was avoided by keeping the sum of the substituent electronegativities constant.81
A very similar study was submitted at almost the same time, but published sooner.82 Mulloy et al. used the glycosidic linkages of cyclomaltohexaose and -heptaose as the best source of data for dihedral angles in the range 0°–20°, and several H–C–O–C pathways in 1,6-anhydro-β-D-glucopyranose for angles of 100°–170°. The 3JH-1,C-5 values measured for β-D-Glc and β-D-Gal residues provided points for dihedral angles of ~60°, and the same coupling pathway for α-D-Glc residues gave data on dihedral angles of ~180°. Values of dihedral angles were obtained from X-ray crystal structures of the subject compounds, or from those of analogues. The resulting Eq. (37) obtained82 by least-squares fitting of 3JHCOC values measured by the 2D heteronuclear J-resolved method is very similar to that of Tvaroška et al.,81 and these two studies confirm one another:
| (37) |
The resulting curve differed from that proposed by Hamer et al.78 most significantly near 180°, where several J values were too large to be accommodated by their results or Eq. (35). The results of Mulloy et al.82 suggested that for the interglycosidic bond angles ϕ and ψ, the prediction of 3JHCOC from angles may be made to ±1 Hz, and the calculation of angles from 3JHCOC to ±10°. These techniques were used to compare the conformations of sucrose, raffinose, and stachyose in solution and the solid state. The discrepancies between experimental values of 3JHCOC and those predicted from the crystal structures indicated that sucrose and its homologous oligosaccharides do not exist in D2O or Me2SO-d6 solutions in the conformation found in the solid state. Data from this study were also used to reassign the 13C NMR spectrum of melezi-tose.82 The general form of the equation is also supported by FPT-INDO calculations for the model compound 2-methoxytetrahydropyran, which when formulated as a superposition of dependences on ϕ and ψ yielded83 the equation:
| (38) |
DFT calculations have been used to investigate the structures and conformations of four β-[1→4]-linked disaccharide mimics,84 the method being used to compute both optimized geometries, and values of 3JHCOC (and 3JCOCC, see below) as a function of the interglycosidic torsion angles ϕ and ψ. The 3JHCOC values computed by DFT were fitted by least squares to Eq. (3) giving:
| (39) |
A comparison of the theoretical 3JHCOC values with Eq. (36) of Tvaroška et al.81 indicated good agreement (Fig. 4), except for the extremes of the curve at ϕ = 0°–20° and 160°–180°, where the computed couplings were larger, as implied by the larger A constant in Eq. (39). Re-measurement of the couplings for these angles was suggested.84 Sufficient confidence was expressed in the theoretical computations of the coupling constants to suggest that the application of such computations to specific bonding structures might supersede the construction of generalized Karplus curves from experimental data for model compounds.84
Fig. 4.
Variation of trans-O-glycoside 3JHCOC values (corrected) with dihedral angle ϕ, computed by DFT for four β-[1→4]-linked disaccharide mimics. The dashed line is a plot of the Karplus equation (Eq. (36)) defined experimentally by Tvaroška et al.,81 and the solid line is the computed relationship (Eq. (39)), where ■ represents 3JH-4′,C-1 data, and ○ is 3JH-1,C-4′ data.84
Interglycosidic 3JHCOC values have also been measured by non-selective, 2D J-resolved 1H NMR of tri-, tetra-, and penta-saccharide fragments of the O-specific polysaccharide of Shigella dysenteriae type 1 substituted with 13C at C-1 of the galactopyranose residues.85
More advanced NMR methods have also been used. Höög and Widmalm86 measured transglycosidic 3JHCOC of α-D-Manp-(1→3)-β-D-Glcp-OMe by selective excitation of 13C resonances, followed by evolution of the heteronuclear couplings, and detection of 1H resonances by two-site, Hadamard spectroscopy.87,88 The 3JHCOC values across the glycosidic linkage were extracted by a J-doubling procedure and were correlated with the interglycosidic angles ϕ and ψ by molecular dynamics/molecular mechanics using the CHARMM force field and Eqs. (36) and (39). The results indicated that the disaccharide adopts a preponderant conformation and has limited flexibility on a short timescale of less than the rotational correlation time τM, but on a timescale > τM, excursions to other conformational states are required to obtain agreement between simulation and experiment.86 In related work, trans-glycosidic 3JHCOC values have been measured for eight α- or β-linked disaccharides by gradient-enhanced, multiple 13C site-selective excitation, with 1H decoupling after polarization transfer.89 In most cases, good agreement was obtained between the experimental 3JHCOC values and those calculated by application of Eq. (36) of Tvaroška et al.81 to dihedral angles obtained by molecular-dynamics computations, with explicit water and the Amber–Homans forcefield.89
DFT calculations have been used to construct new Karplus curves for 2JHH, 3JHH (as mentioned before) 2JCH, 3JCH, 3JHCCC, 3JHCOC, and 3JHCSC. A major focus of this investigation62 was DFT computations for the exocyclic hydroxymethyl group of aldohexopyranoside derivatives, particularly in methyl α- and β-D-gluco- and -galactopyranosides, for which coupling constants were also determined experimentally by 2D 1H–13C heteronuclear zero- and double-quantum, phase-sensitive J-HMBC NMR. DFT on methyl β-D-glucopyranoside yielded 3JHCOC values that fitted the equation:
| (40) |
in which the coefficient of the important cos2 ϕ term lies in between the values in Eqs. (36) and (39). However, the DFT computations agree better with each other, than with the experimental data, possibly owing to solvation effects, basis set limitations in the DFT, and the use of a small set of geometries.62
Improved Karplus equations have been developed for 3JC-1,H-4 in aldopentofuranosides90 by extension of the Haasnoot–Altona equation for 3JHCCH, to 3JHCOC. DFT calculations were performed for the eight methyl aldopentofuranosides using the GAUSSIAN98 program in the gas phase at the B3LYP/6–31G★ level, thus generating 30 conformers for each structure. 3JC-1,H-4 values were then calculated for each optimized geometry by using the DEMON-KS program augmented by the DEMON-NMR code. These calculations furnished a data set of 240 3JC-1,H-4 values comprised of 120 with the α configuration, and 120 with the β configuration. A three-step procedure was used to construct a Haasnoot–Altona equation. First, 240 scaled values of 3JC-1,H-4 were fitted to a three-parameter Karplus equation, giving:
| (41) |
The need for scaling of the values of 3JHCOC calculated by the ab initio, DEMON-NMR procedure was assessed by comparison of the theoretical and experimental values of four 1,6-anhydro-aldohexopyranose derivatives, which disclosed that the theory overestimated the couplings by an average of 16.7%, thus leading to a scaling factor of 0.833.
Secondly, by using the A, B, and C values from Eq. (41), the effect of anomeric configuration was accounted for by fitting the data for the α-furanosides to the full Haasnoot–Altona equation:
| (42) |
where G and H are the electronegativities of the substituents at C-1, thereby giving:
| (43) |
In the same manner, an equation was constructed for the β-glycosides:
| (44) |
Thirdly, the D–F values from the 3JC-1,H-4 (α) and (β) equations were averaged to give:
| (45) |
The curve from this equation was similar to that from Eq. (39) of Cloran et al.,84 the curve for the α-glycosides lying just below, and the curve for the β-glycosides slightly above, the curve from Eq. (39). The combination equation for α- and β-furanosides was used to investigate their conformational preferences further and could also be used to clarify the results of PSEUROT analyses based only on 3JHCCH values.90
b. Proton–Carbon Couplings, 3JHCCC
Bock and Pedersen performed a complete analysis of the 1H-coupled 13C spectrum of 1,6-anhydro-β-D-galactopyranose and some other sugars and found evidence of a Karplus dependence of 3JHCCC and 3JHCOC, although only a limited range of dihedral angles (from Dreiding models) could be tested.91 The complex 1H-coupled 13C spectra were simplified by selective, 1H spin decoupling.
An unusual, indirect method was used by Aydin and Günther to determine 13C, 1H couplings over one, two, and three bonds in norbornanes.92 They measured the corresponding 13C, 2H couplings in 1H-decoupled, 13C NMR spectra of deuterated isotopomers of norbornane-d, fenchane-2-d, and a number of deuterated, alkylada-mantanes, thus avoiding the complexity of analyzing 1H-coupled 13C spectra.92 The 13C, 1H couplings were calculated by multiplying the 13C, 2H couplings by the ratio of the magnetogyric constants, γH/γD = 6.5144. Dihedral angles were derived from MM2 force field calculations, and when substituent effects from branching and methyl substitution in the norbornanes were taken into account, the following equation was obtained:
| (46) |
which may be rewritten as
| (47) |
Corrections to the coupling-constant measurements because of quadrupolar relaxation by deuterium were employed, and one disadvantage of this indirect method is that the 3JDCCC values measured may be too small to be resolved, since they are a factor of 6.5 smaller than the corresponding 3JHCCC values.92 In sugars, the 13C resonance of a deuterium-substituted carbon may disappear,93 due either to quadrupolar relaxation by deuterium, and/or to saturation caused by lengthening of the 13C T1 on replacement of dipolar relaxation by a proton with the weaker effect of a deuteron.
The pendant hydroxymethyl group in sugars has been a popular vehicle for experimental and theoretical studies of coupling constants, and the application of FPT-INDO calculations to both anomers of the eight aldohexopyranoses yielded an equation for the dependence of 3JC-4,H-6:
| (48) |
where ω is the torsion angle of C-4 and H-6 about the C-5–C-6 bond.94,95 The agreement of the calculated values and the experimental values available for mono- and oligo-saccharides was found to be satisfactory.94
Separate dependences have recently been computed62 for H-6R and H-6S in 1,2,3-trideoxy analogues of D-gluco- and D-galactopyranose:
| (49) |
| (50) |
c. Proton–Carbon Couplings, 3JHCSC
The application of a modified, 2D heteronuclear J-resolved NMR method to a set of eight conformationally rigid, thio sugar derivatives provided 17 values of 3JHCSC that were used to define96 the equation:
| (51) |
A crystal structure was available for one of the thio sugars studied, but for the others, no structural data were available, and dihedral angles for the H–C–S–C fragments were computed by the PCILO quantum chemical method. These angles covered the range −155° to 179°, with a gap from −60° to 35°. The experimental 3JHCSC values spanned 0.3–8.1 Hz, but the latter value was rejected because its magnitude was thought to be enhanced by the π-electrons of a neighboring C=O group. Equation (51) was tested by application to methyl 4-thio-α-maltoside, for which it was found that the values 3JC-1,H-4′ 5.15 Hz and 3JC-4′,H-1 2.95 Hz measured for the H-1–C-1–S-4′–C-4′–H-4′ moiety differed from those, 3.8 and 3.1 Hz, respectively, predicted from the conformation in the crystal.96 This discrepancy was rationalized by using the PCILO method to calculate a relaxed (ϕ, ψ) conformational energy surface for the thio disaccharide in aqueous solution, which revealed the existence of 15 conformers having five main minima for rotation about the glycosidic C–S bonds. Conformational averaging based on the populations computed for the five stable conformers and the 3JHCSC values calculated from Eq. (51) yielded the values 3JC-1,H-4′ 5.2 Hz and 3JC-4′,H-1 2.6 Hz.96
Taffazoli and Ghiasi performed DFT computations62 on methyl 1-thio-β-D-glucopyranoside, yielding values of 3JHCSC, which fitted the equation:
| (52) |
which is in reasonable agreement with the experimental data of Tvaroška et al.96
d. Proton–Carbon Couplings, 3JHOCC
These couplings had previously been little studied,97,98 but have recently been investigated in detail by DFT and experimental NMR.75 Using the same deoxy-aldohexopyranoside models already described for 3JHCOH, Zhao et al. used DFT results (Fig. 5) to construct the equation:
| (53) |
which was derived by averaging the coefficients obtained from three model structures.
Fig. 5.
Dependence of 3JC-1,HO-2 on the glycosidic torsion angle ω and the C-1/HO-2 dihedral angle θ, as calculated by DFT for methyl α- and β-D-glucopyranoside mimics (curves (A) and (B), respectively) and. methyl α- and β-D-mannopyranoside mimics (curves (C) and (D), respectively), all having deoxy functions at C-3, C-4, and C-6. The curves display a strong dependence of 3JCCOH on θ, and a minimal dependency on ω.
Fitting of the DFT data for a fourth structure generated an equation containing somewhat smaller coefficients:
| (54) |
This result was interpreted75 in terms of the absence of a terminal, in-plane electronegative substituent in the fourth structure, as compared with the other three models, in each of which, the magnitude of 3JC-1,HO-2 was enhanced by the presence of an in-plane O-1, or O-5. Calculations using the GAUSSIAN03 program indicated that non-FC contributions to 3JC-1,HO-2 were negligible. The applicability of Eqs. (53) and (54) to similar coupling pathways was investigated for 3JC-2,HO-1, 3JC-3,HO-2, 3JC-5,HO-4, and 3JC-1,HO-2 in additional model structures, using only staggered H–O–C–C torsion angles. Consideration of the presence or absence of terminal in-plane electronegative substituent effects led to a further equation for pathways without these effects:
| (55) |
which on averaging with Eq. (54) gave
| (56) |
Similar considerations for 3JC–2,HO–1 led to non-symmetric equations (Fig. 3B) for specific configurations:
| (57) |
| (58) |
| (59) |
| (60) |
The latter two equations are very similar and were averaged75 to give a combination:
| (61) |
3JH-6R,HO-6 and 3JH-6S,HO-6 were calculated in GAUSSIAN03 by using appropriate torsion angles in a model structure, and the couplings were found to be consistent with Eq. (31). 3JC-5,HO-6 values were found to be influenced by the O-5–C-5–C-6–O-6 and C-5–C-6–O-6–H torsion angles, and by the orientation of O-5. The computed couplings were consistent with Eq. (59) for gg and gt rotamers, and Eq. (53) for the tg rotamer.75 2JHOC values were also examined, but were found to be small (−2 to −4 Hz), and showed non-systematic dependences on C–C and C–O torsion angles, suggesting that these couplings are not useful indicators of C–O conformation.75
3. Proton–Nitrogen Couplings
a. Proton–Nitrogen Couplings, 3JHCCN
Coxon has measured the scalar 15N–1H NMR coupling constants of amino sugars over one to four bonds by three methods: (a) 1D 1H NMR, (b) 1D and 2D 1H–15N HSQMBC99,100 using an HCN cryoprobe,66 and (c) 1D 1H–15N CPMG-HSQMBC101 using a normal broadband probe. Method (a) was applied to organic-soluble, 15N-substituted amino sugar derivatives synthesized by addition of phthalimide-15N to carbohydrate epoxides,74,102–103 method (b) to similar, unsubstituted derivatives, and method (c) to the 2-amino-2-deoxy-sugars common in biological systems, namely glucosamine, mannosamine, and galactosamine, as their N-acetyl and hydrochloride pyranose derivatives in D2O and/or Me2SO-d6 solutions.104 The precision of coupling constants measured by method (a) is probably better than ± 0.1 Hz, whereas methods (b) and (c) afford ± 0.3 Hz. The common amino sugars were usually present in the original crystal principally as a single pyranose anomer, either α or β, which underwent tautomeric interconversion to as many as four other forms on dissolution. The organic-soluble group included a number of aminodeoxy–hexopyranose derivatives that were conformationally restricted to chair, boat, or skew forms by the attachment of anhydro or 4,6-O-benzylidene rings.74,102–103
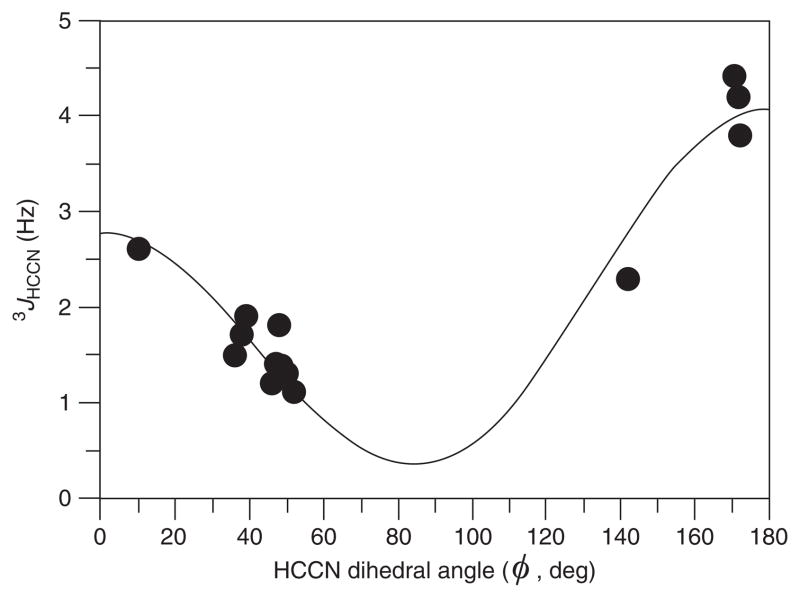
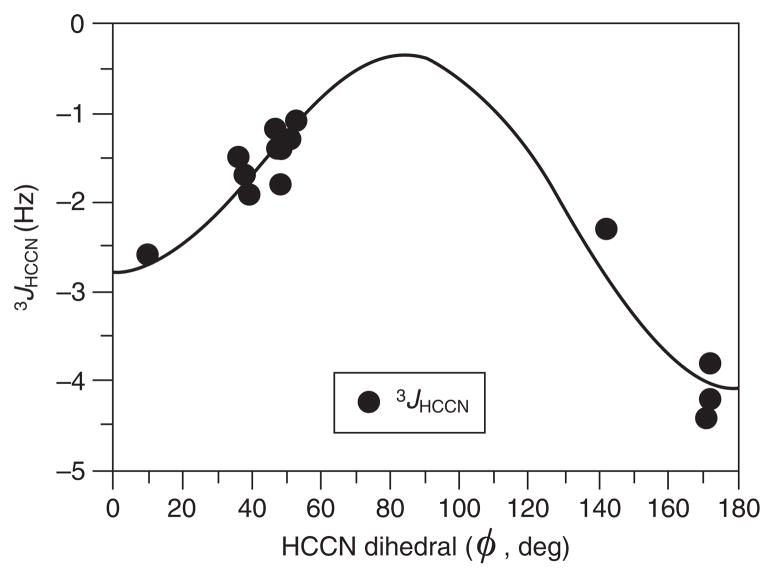
Dihedral angles ϕHCCN for the amino sugars were defined by molecular dynamics and mechanics calculations using either implicit solvent or explicit chloroform-d. Least-squares fitting of the angles of the organic-soluble derivatives in the range ϕHCCN = 10°–172°, to experimental 3JHCCN data with the assumption of positive values for the couplings allowed formulation66 of a Karplus equation (Fig. 6) of the three-parameter type:
| (62) |
Fig. 6.
Two-quadrant plot of Karplus equation 3JHCCN = 3.1 cos2 ϕ − 0.6 cos ϕ + 0.4 derived by fitting of experimental values of 3JHCCN to the dihedral angle ϕ, with the assumption of positive values for 3JHCCN.
However, because of the negative magnetogyric ratio of the 15N nucleus, these couplings are likely to be negative, in which case Eq. (62) becomes
| (63) |
This equation (Fig. 7) is quite similar to the one developed105 for 3JHCαC′N in peptides:
| (64) |
except that the magnitudes of the A, B, and C coefficients for the peptides appear to be enhanced by p-orbital contributions from the carbonyl group C′ in the coupling pathway.
Fig. 7.
Two-quadrant plot of Karplus equation 3JHCCN = −3.1 cos2 ϕ + 0.6 cos ϕ − 0.4 derived by fitting of experimental 3JHCCN values to the dihedral angle ϕ, with the supposition of negative values for 3JHCCN.
The 4C1 chair conformations of the water-soluble amino sugars that were defined by their 3JHCCH values and molecular modeling provided a more restricted set of ϕHCCN angles (nominally 60° or 180°) than the conformationally limited, organic-soluble amino sugar derivatives. However, the 3JHCCN values measured for the water-soluble ones are in reasonable agreement with Eq. (62). These couplings are potentially useful for characterization of amino sugar-containing, bacterial polysaccharides of interest in vaccine development, and for structural analysis of aminoglycoside antibiotics.
4. Phosphorus Couplings
a. Proton–Phosphorus Couplings, 3JHCOP and Carbon–Phosphorus Couplings, 3JCCOP
Reparametrized Karplus equations for these couplings were developed simultaneously using a data set of 17 such couplings measured experimentally106 for oligoribonucleotides:
| (65) |
| (66) |
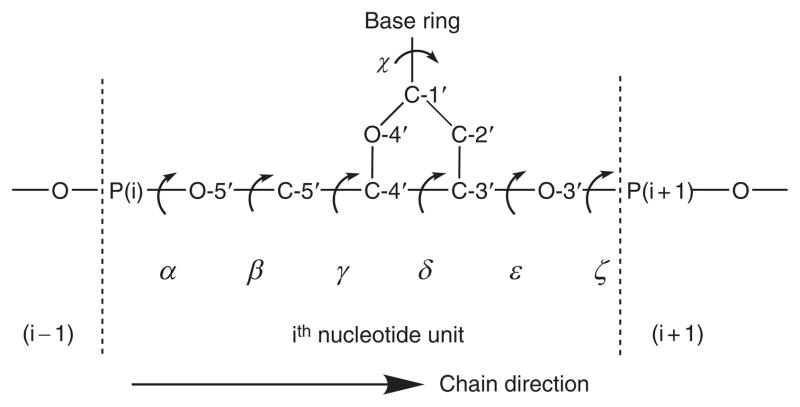
The 3JHCOP values were determined by direct extraction of splittings or by subtraction of the widths of multiplets in 31P-decoupled, 1H NMR spectra from those of the corresponding multiplets in 31P-coupled spectra. 3JCCOP values were measured directly from the 31P splittings in 1H-decoupled 13C spectra. Other parametrizations had been developed earlier for these couplings, but were limited to one- or two-parameter equations by being based on too few values of the dihedral angle. For example, only parameters A and B in Eq. (3) could be derived from a data set containing only J(60) and J(180). These cases have been discussed in detail.106 A study of the deoxyribonucleotide d(TpA), 3′,5′-cyclic AMP, and 3′,5′-cyclic dAMP showed that the different substitution of C-2′ in deoxyribonucleotides versus ribonucleotides does not change 3JC-2′–C-3′–O-3′–P to a measurable extent, so that the same Karplus parameters may be used for such couplings in ribonucleotides and deoxyribonucleotides.107 Backbone conformations of oligonucleotides have been characterized by six torsional angles, α, β, γ, δ, ε, and χ (Fig. 8), representing rotations about the P(i)–O-5′, O-5′–C-5′, C-5′–C-4′, C-4′–C-3′, C-3′–O-3′, and O-3′–P(i+1) bonds, respectively.106 The results showed that the torsion angle ε(t) of the trans conformer of right-handed ribo helices is confined to the range 214°–226°, the average of which (219°) is in excellent agreement with the average value (218°) from single-crystal, X-ray studies, in contrast to that (208°) deduced from previous NMR data. Vicinal proton–phosphorus and carbon–phosphorus couplings have also been used to calculate the torsion angle ε (C-4′–C-3′–O-3′–P), in d(TpA), which was 195° in the trans conformer ε(t), and 261° in the gauche form ε(−). A two-state equilibrium of ε(t) and ε(−) was assumed in this study. Variable-temperature experiments demonstrated that the ε(t) form predominates at 1.5°–92 °C, and increases as the temperature is lowered.107
Fig. 8.
Torsion angle descriptors α–ζ and χ for oligonucleotides.
In an extension of this study to the oligodeoxynucleotides d(CT), d(CC), d(TA), d(AT), d(CG), d(GC), d(AG), d(AAA), d(TATA), and d(GGTAAT), the three coupling constants 3JC-4′–P, 3JC-2′–P, and 3JH-3′–P that are related to the backbone angle ε were analyzed in terms of a three-state equilibrium that took into account the N and S forms of the deoxyribose ring.108 Depending on the N or S conformation of the deoxyribose ring, two ε(t) values occurred: ε(t, N) = 212° and ε(t, S) = 192°. The third rotamer was gauche and was associated exclusively with the S-type sugar ring, with the value ε(−, S) = 266°. Within experimental error, the magnitudes of these three angles were found to be independent of base sequence, with one exception: d(CG), which had ε(t, S) = 197°. Excellent agreement of the coupling constants was obtained with the three-state model, but poor agreement with a two-state analysis.108
Later, the application of more-sophisticated NMR experiments to a 10 base pair DNA duplex, uniformly 13C,15N-substituted in only one of the two strands was demonstrated:
Zimmer et al.109 measured JHH in the deoxyribose ring by 2D and 3D HCCH-E. COSY, JCH couplings across the glycosidic torsion angle χ (see Fig. 8) by refocused HMBC, and 2JCP and 3JHP about the backbone torsion angle ε by a P-FIDS-CT-HSQC experiment. Using these experiments, a number of coupling constants in duplex DNA could be measured. Following the assumption by Lankhorst et al.106 of trigonal projection symmetry about the ε torsion angle, their Karplus equations (Eqs. (65) and (66)) were expressed directly in terms of this angle:
| (67) |
| (68) |
A dependence of 3JH-3′,P on position in the DNA sequence was noted, with the minimum value occurring at the 3′-end of the dA–dT tract.109
For the circular trinucleotide cr(GpGpGp), Mooren et al.110 measured the value 3JC-4′–C-5′–O-5′–P 11.1 Hz, and similar values 3JC-4′–C-5′–O-5′–P = 3JC-4′–C-3′–O-3′–P = 10.9 Hz had been observed earlier for the circular dinucleotide cd(ApAp). These large values did not fit the equations of Lankhorst et al.,106 which were then reparametrized again according to 26 experimental calibration points based on dihedral angles obtained by molecular-mechanics energy minimization with the CHARMM force field.110 The fitting of the coupling constant/dihedral angle pairs was achieved by least-squares optimization using a conjugate gradient minimization method, giving:
| (69) |
| (70) |
As expected, the main difference is in the A parameter (8.0 Hz) for 3JCCOP, but since these equations were constructed in tandem, there is a small influence on 3JHCOP. On the basis of this reparametrization,110 seven equations were presented that related the populations of the β and γ conformers to the values of 3JH,P and 3JC,P. It was recognized that the parametrization is a little weak in the 0°–60° region, as only one indirectly estimated value of 3JC,P was available, for ϕ = 60°.
The A, B, and C parameters were modified again by Plavec and Chattopadhyaya111 based on 17 values of 3JC,P and the corresponding X-ray derived torsion angles for 3′,5′-cyclonucleotides, giving:
| (71) |
Inclusion of the coupling constants of “strained” cyclonucleotides had been criticized earlier. Stating that the three-parameter Karplus equation applies only to a limited class of compounds, Plavec and Chattopadhyaya then accounted for the effects of the electronegativity of α-C and α-H attached to the second carbon atom of the CCOP pathway by constructing a five-parameter Karplus equation, according to the method used by Haasnoot and Altona for 3JHCCH (Eq. (9)). Least-squares, conjugate gradient minimization using 17 3JC,P values, torsion angles, and electronegativities of α-substituents on the “middle” carbon yielded the equation:
| (72) |
The first three terms describe the dependence of 3JCCOP on torsion angle, whereas the summation term reflects the dependence on substituent electronegativity and its orientation. Δχi is the difference in electronegativity between the α-substituent and hydrogen on the Huggins scale and, as before, ζ is the “sign” parameter that takes values of +1 or −1, depending on the orientation of the substituent (see Fig. 2). 3JCCOP input values were reproduced within ΔJ ≤ 0.4 Hz, with an rms deviation of 0.2 Hz between experimental and back-calculated 3JCCOP values. This deviation was slightly smaller than that achieved with the three-parameter Eq. (3), but it was acknowledged that a larger range of electronegativities and more data points are needed to give a more widely applicable relationship.111
5. Carbon–Carbon Couplings
Due to NMR sensitivity constraints, these coupling constants have most often been measured by use of selectively or uniformly 13C-substituted compounds. The early, observational history of these couplings has been reviewed previously.79 Sucrose and methyl α- and β-D-fructofuranoside have been prepared by chemical and/or enzymic methods with single sites of 13C substitution at C-1, C-2, C-3, and C-6 of the fructofuranosyl rings.112 Complete sets of 1JCC, 2JCC, and 3JCC couplings constants were measured for sucrose and the methyl D-fructofuranosides by 1D 13C NMR, with assistance from 1D 13C INADEQUATE, for which various mixing times were used to observe selectively, carbon nuclei coupled to the 13C-substituted site. Values for 13C,1H and 1H,1H couplings were also reported. The values of 13C–1H and 13C–13C couplings across the glycosidic linkage of sucrose suggested a ψ glycosidic torsion angle that was different from that in the crystal, although ϕ appeared to be similar.112
The signs of 3JC-1,C-6 and 3JC-3,C-6 coupling constants have been assumed to be positive and were used to determine the relative signs of 2JC-1,C-3 and 2JC-1,C-5 by application of a 13C–13C COSY-45 method to triply 13C-substituted, D-aldopyranoses.113 These sign determinations provided experimental confirmation of the relative signs of 2JCCC and 2JCOC predicted by an empirical, projection resultant method.114,115
Xu and Bush measured the 2JCC and 3JCC coupling constants of a cell-wall lectin-receptor polysaccharide from Streptococcus mitis J22, uniformly substituted with 13C to the extent of 96%.116,117 The couplings were measured by 2D quantitative coherence transfer correlation spectroscopy,118 the validity of which was confirmed by application of the method to the u-13C-D-glucose growth precursor for the polysaccharide. The 2JCC and 3JCC values measured for the α and β anomers of the latter substrate were in good agreement with those reported by Serianni and coworkers, on the basis of direct, 1D 13C NMR of single-site, 13C-enriched glucoses.119,120 Correlation of the 3JCC couplings of the J22 polysaccharide was made by reference to the geometries of a three-conformation model determined by CHARMM molecular modeling.117 Xu and Bush did not distinguish 3JCCOC and 3JCCCC, but instead formulated116 a combination equation:
| (73) |
a. Carbon–Carbon Couplings, 3JCCOC
Milton et al. synthesized 13C-enriched α-Neu5Ac-(2→3)-β-Gal-(1→4)-Glc by enzymatic sialylation of a 13C-enriched β-Gal-(1→4)-Glc acceptor using Trypanosoma cruzi trans-sialidase with p-nitrophenyl (u-13C)Neu5Ac as a donor.121 The 1H NMR spectrum of this trisaccharide derivative is extremely complex because of substantial resonance overlap within a 0.4 ppm chemical-shift range, so that the interpretation of conventional 2D 1H–1H ROESY spectra is difficult. Therefore, the 3D ROESY-HSQC technique was used to separate the ROESY cross peaks according to their 13C chemical shifts. This led to seven trans-glycosidic ROEs that were used in restrained MD with simulated annealing, using as input 10 pseudo-random geometries generated by a dynamical quenching procedure. Three families of structures that differed principally in the conformation about the α-Neu5Ac-(2→3)-Gal linkage resulted from the computations. The lowest-energy conformer in each family was selected as input for 5 ns restrained MD simulations in vacuo. Back calculation of theoretical ROEs from the global energy minimized MD simulation using a full relaxation matrix approach produced very good agreement with experiment.121
In this study, carbon–carbon coupling constants were found to be particularly valuable for additional validation of the predicted motional behavior, because only one 13C–1H coupling is available across the α-Neu5Ac-(2→3)-Gal linkage. Parametrization of the Karplus equation was implemented using only four 3JCCOC/ϕCCOC pairs, obtained from 13C-substituted β-D-glucose (3JC-1–O-5–C-5–C-6 = 3.8 Hz/ϕ = 180°), methyl 4,6-O-(1-methylbenzylidene)-α-D-glucopyranoside, uniformly 13C-substituted in the glucose moiety (3JMe–C–O-4–C-4 2.4 Hz/60°, 3JMe–C–O-6–C-6 1.9 Hz/60°), and (1-13C)-1,6-anhydro-2,3-O-isopropylidene-β-D-mannopyranose (3JC-1–C-2–O-2–C-7 0.6 Hz/109°, the latter dihedral angle being determined from a crystal structure). Fitting of these data to the three-parameter Eq. (3) yielded121 the equation:
| (74) |
which was thought to be semi-quantitative at best, due to the limited number of data points, and neglect of electronegativity effects.121 Because α-Neu5Ac-(2→3)-β-Gal-(1→4)-Glc suffers from poor spectral dispersion in critical regions of its 13C spectrum, 3D LRCC was used to measure six values of 3JCCOC for the trisaccharide, which agreed very well with those calculated for the MD-simulated structure by use of Eq. (74). Two trans-glycosidic values of 3JHCOC were also measured for the trisaccharide by heteronuclear, CT COSY and were in excellent agreement with those calculated using the equations of Tvaroška et al.81 and Mulloy et al.82 (Eqs. (36) and (37), respectively).
In a comprehensive study, Bose et al.122 synthesized a large number of aldose derivatives selectively substituted with 13C at C-1 or C-6, and ketoses similarly substituted at C-1, C-2, C-3, C-4, C-5, or C-6. Various 13C–13C coupling constants were measured for these derivatives by 1D 13C/1H decoupled NMR at 151/600 MHz. Many of the couplings were also calculated by DFT methods and were found to be mostly in close agreement with the experimental values, although some significant deviations (14%) of 1JC-1,C-2 values were thought to be due to such possible limitations in the theoretical method as (a) the appropriateness of the functional procedure adopted, (b) the incompleteness of the chosen basis set, and (c) the omission of solvent effects from the computation. The types of coupling pathways were analyzed in detail, including such multiple pathways as 3+3JC-1,C-4 and 3+3JC-2,C-5, which in most ring configurations are observed to be very small or zero, leading to the conclusion that the coupling along each constituent pathway in these cases must be small or zero.122 Dihedral angles for the atoms of interest were derived from geometrical optimizations using a modified GAUSSIAN94 program, with the B3LYP functional, and 6–31G basis set. Many of the aldo- and ketopyranoses contained only ϕCCOC dihedral angles of ~180°, and so data for other values of ϕCCOC were measured or compiled from methyl 3,6-anhydro-α- and β-D-(1–13C)glucopyranosides (~45°), methyl β-D-ribofuranoside (ab initio MO gave ϕC-1–O-4–C-4–C-3 ~123° for both forms), α-D-erythro- and -threo-2-pentulofuranoses (ϕC-1–C-2–O-5–C-5 ~154°), methyl α- and β-D-fructofuranosides (ϕC-1–C-2–O-5–C-5 ~164° and ~156° in the respective South (E2) and North (2E) conformations of these anomers), and sucrose, in which the 4T3 form of the β-D-fructofuranosyl ring has ϕC-1–C-2–O-5–C-5 = ϕC-2–O-5–C-5–C-6 ~133° in the crystalline state.122 Theoretical calculations of coupling constants were also performed for three structural models, including one for a disaccharide as a function of the interglycosidic angle ψ. Careful attention was paid to the effects of rotameric populations about the C-1–O-1, O-1–C-4′, and C-5–C-6 bonds in the models.
An important result from this study was that the 3JCCOC coupling constant is influenced by geometrical factors in addition to dihedral angle, the most critical being the orientation of terminal electronegative substituents on the coupling pathway.122 For example, for HO–C–C–O–C–OH pathways, the magnitude of coupling between the terminal carbon nuclei is enhanced when the terminal oxygen atoms lie in the C–C–O–C plane (ϕCCOC = 180°). Similar effects were observed for ϕCCOC = 60° when the terminal oxygen was in-plane (HO–C–O–C or O–C–C–OH plane). Out-of-plane terminal oxygen substituents and oxygen substituents on internal carbon atoms appeared to exert little effect on the magnitude of the coupling. For example, 3JCC in a H3C–C–O–C–OH was found to be virtually identical to 3JCC in a HO–H2C–C–O–C–OH pathway, when the hydroxymethyl oxygen atom in the latter moiety was oriented outside the C–C–O–C plane.122 Similar phenomena had been reported earlier by Marshall et al. for 3JCCCC couplings in C–C–C–CH2OH pathways in butanol derivatives, although the effect of terminal substitution for eclipsed C–C–C–C fragments appeared to be smaller than expected from theoretical considerations.123
By excluding 3JC-1,C-6 in ketopyranoses and also couplings enhanced by in-plane oxygen atoms, least-squares fitting of the 3JCCOC data yielded the equation:
| (75) |
This equation yields a larger 3JCCOC value for ϕ = 0° than for ϕ = ± 180°, which mirrors the behavior suggested for 3JCCCC in HO–CH2–C–C–C pathways,123,124 with couplings of 3.5–6 Hz expected122 for ϕCCOC = 0° and 2–4 Hz for ϕCCOC = 180°. In most Karplus equations of the three-parameter type, the B coefficient (of the cosϕ term) for positive coupling constants is negative, which leads to an increased value of the coupling for ϕ = 180° over that for ϕ = 0°. Because of this anomaly and the paucity of data for ϕ < 100°, as an afterthought, Bose et al.122 excluded the cos ϕ term from Eq. (75) and refitted their data to give a simplified equation:
| (76) |
which they stated was better supported by the available data, and which corresponds to identical maxima for ϕ = 0° and 180°. It was pointed out that 3JC-1,C-6 values in aldohexopyranosyl and ketohexopyranosyl rings do not obey the same Karplus relationship, that for the latter rings appearing to have decreased amplitude.122
The shortage of experimental data for ϕCCOC < 100° was soon addressed by a purely theoretical study of the four β-(1→4)-linked disaccharide mimics mentioned earlier.84 DFT-calculated 3JCCOC couplings for ϕCCOC 0°–100°, together with geometries calculated likewise, suggested that the first Eq. (75) may be the more accurate relationship, namely, one where the couplings at ϕCCOC = 0° are somewhat larger than those at ϕCCOC = 180°, at least in the absence of an in-plane electronegative substituent effect.84 The latter effect was considered to be significant for the C-1–O-1–C-4′–C-5′ coupling pathway, where for some linkage geometries, O-5′ lies in the plane of this pathway. This led to the development of three parametrizations by least-squares fitting of the theoretically calculated coupling constants and geometries.84 One used only 3JC-1,C-5′ data (Eq. (77)), another used just 3JC-1,C-3′ and 3JC-2,C-4′ (Eq. (78)), and one more employed all coupling data (Eq. (79)).
| (77) |
| (78) |
| (79) |
Interestingly, the first Eq. (77) contains a sign reversal for the B coefficient, which would indicate that for a possible in-plane oxygen atom, the coupling for ϕCCOC = 180° would be larger than that for ϕCCOC = 0°.
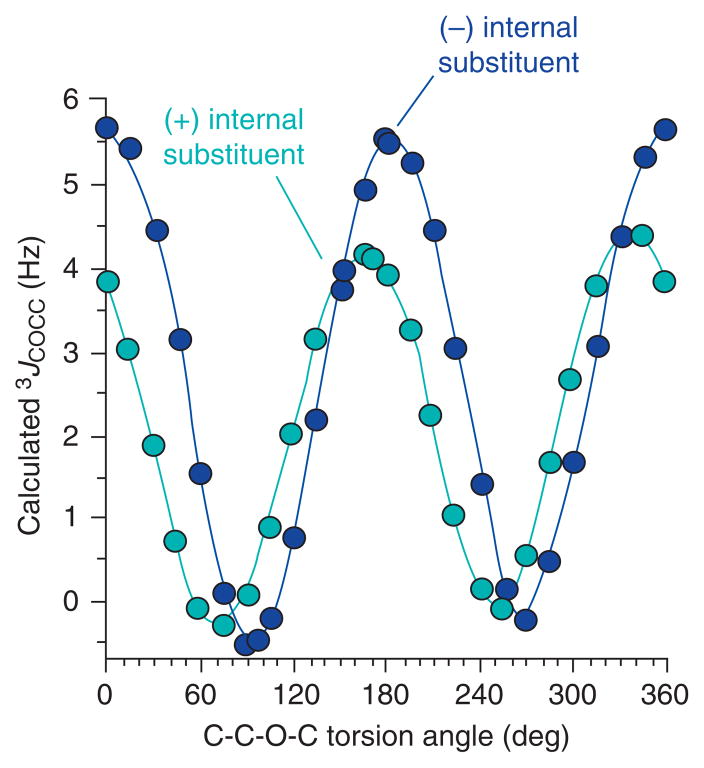
Recent preliminary DFT calculations have shown that the two trans-glycosidic 3JCCOC couplings in oligosaccharide linkages are not equivalent.125 By using the GAUSSIAN03 program with structures that modeled the glycosidic linkage, Zhao et al. demonstrated that internal electronegative substituents in the coupling pathway cause a −15° phase shift of the Karplus curve (Fig. 9), so that the maximum coupling occurs at 165° instead of at 180°. This effect will need to be considered in the evaluation of linkage geometries by quantitative interpretation of 3JCCOC.125
Fig. 9.
Four-quadrant plots of DFT results for an ethyl β-D-glucopyranoside mimic of a disaccharide, showing phase shifting of 3JCCOC Karplus curves for C–C–O–C coupling pathways bearing an internal electronegative substituent. The mimic has deoxy functions at C-3, C-4, and C-6.
Six spin-coupling pathways are subtended by typical glycosidic linkages, and in the structural analysis of oligo- and polysaccharides, it would clearly be advantageous to use as many of these coupling constants as possible for the definition of molecular geometry, particularly in view of the limited number of NOEs observed in these systems.
b. Carbon–Carbon Couplings, 3JCCCC
Early observations of the 3JCCCC couplings of carbohydrates have been summarized previously.79 The experimental determination and theoretical interpretation of such couplings in alicyclic compounds have been studied extensively by Barfield, Marshall, and coworkers.123,124,126–129 For example, VB and MO studies of 13C-substituted, 1-substituted butyl derivatives, 11-substituted 1-methyladamantane compounds, and methylcyclohexane indicated that a large number of direct (electron-mediated) and indirect coupling pathways contribute to vicinal 13C–13C coupling constants. The calculated Fermi-contact contributions for trans arrangements of carbon atoms in butane, methylcyclohexane, and 1-methyladamantane being 4.27, 3.72, and 3.32 Hz, respectively.128,129 Coincidentally, the monotonic decrease in the magnitude of the coupling constant was found to parallel the increase in the number of impinging rear orbital lobes on carbon, the effect of which, may however, be small, and the observed decrease may be related to an increasing number of β methylene substituents in these systems.131 With a cautionary note, Barfield et al.128 suggested the equation:
| (80) |
on the basis of INDO-FPT calculations with a number of overlap integrals set to zero. The A coefficient of this equation is very similar to that in Eq. (79) of Cloran et al.84 for 3JCCOC. According to a VB bond-order formulation of Barfield et al.,128 there is a connection between 3JCCCC and 1H–1H coupling constants that is not implied by any of the foregoing Karplus equations. Consideration of the direct and indirect contributions to 3JCCCC in the all-trans arrangement in butane led to a 16-term expression,128 containing one term that corresponded to 3JHCCH, six to long-range 1H–1H coupling over four bonds, and nine terms to long-range coupling over five bonds
| (81) |
where ϕ is the dihedral angle about the C-2–C-3 bond in butane, and the fixed values of the angles in parentheses are the dihedral angles around the C-1–C-2 and C-3–C-4 bonds. This type of relationship has never been explored in carbohydrate chemistry, perhaps because of its complexity. In most studies of sugars, homo- and heteronuclear coupling constants have been considered in isolation.
Multiple coupling pathways are important for vicinal 13C–13C couplings in sugars (for example, 3+3JC-1–C-4 and 3+3JC-2–C-5), and in relevant work on dual-path couplings 2+3JCCCC in 13C-substituted 1-methylcyclopentanol, 1-methylcyclopentene, and polycyclic hydrocarbons, it has been proposed that the individual contributions of such pathways are algebraically additive, that is, the sum must take into account the relative signs of the couplings.130 Evidently, the resultant of two simultaneous coupling pathways can be unexpectedly large, or anomalously small, as in the 3+3JC-1–C-4 values of many aldohexopyranoses.122
Berger measured the 3JCCCC values of 22 compounds, including 13C-substituted derivatives of adamantane, bicyclo[2.2.2]octanes, bicyclo[3.2.1]octanes, cis-bicyclo [3.2.0]octanes, and bicyclo[2.2.1]heptanes, and fitted the values to ideal angles of 0°, 60°, 90°, 120°, and 180° that were close to angles obtained from force-field calculations, or from X-ray structure determinations.132 His experimentally determined equation was determined by use of the additivity principle, if there was more than one pathway, giving
| (82) |
which may be rewritten as
| (83) |
Equation (82) was compared with one obtained from a different set of Barfield’s theoretical data:
| (84) |
which can be reformulated as the alternative:
| (85) |
The agreement between experimental data and INDO-calculated couplings was thought to be rather good, within the error limits for both.132
3JCCCC values have been measured for the bicyclic monoterpenes, 3-carene, α-pinene, and camphene by selective 1D INADEQUATE, with 13C at natural abundance, but the agreement between experimental data and the results of SCPT-INDO calculations was not satifactory.133
Wu et al. synthesized eight aldohexoses, four aldopentoses, and two aldotetroses, all substituted with 13C at the terminal hydroxymethyl carbon atom.120 Interpretation of the 13C NMR spectra measured at 75 and 125 MHz was assisted by 1D INADEQUATE 13C spectra, which can sometimes alleviate problems of spectral overlap, and enhance the detection of small 13C–13C couplings.120 In the aldohexopyranoses, the dihedral angle ϕC-3–C-4–C-5–C-6 has a relatively fixed value of ~180°, and, therefore, these compounds provide a good model for the study of substituent effects along the coupling pathway. On the other hand, the interior dihedral angles of the pyranose ring are ~60°, thus offering alternative angles for studies of the angular dependence of 3JCCCC (and 3JCCOC). The results of this study for 3JCCCC mirror those obtained for 3JCCOC. Coupling is maximal when O-3 and O-4 are equatorial (3.6–4.4 Hz in glucopyranoses and mannopyranoses) or when O-3 is equatorial and O-4 is axial (3.4–4.1 Hz in galactopyranoses and talopyranoses), and minimal when these substituents are axial (1.8 Hz in gulopyranoses). Intermediate values were observed when O-3 is axial and O-4 equatorial (2.6–3.0 Hz in allopyranoses and β-altropyranose). Therefore, 3JC-3,C-6 values may differ by a factor of 2 for coupled carbon nuclei having the same 180° dihedral angle, depending on the configuration of the hydroxyl groups attached to the terminal and intervening carbon atoms in the coupling path-way.120 In the pentopyranoses, 3+3JC-2,C-5 coupling (1.8 Hz) was observed in only one example,120 behavior that is similar to that of 3+3JC-1,C-4 in the aldohexopyranoses.122
An elaborate experimental and theoretical study of 3JCCCC and many related coupling constants has recently been carried out. Thibaudeau et al.134 prepared methyl α- and β-pyranosides of D-glucose and D-galactose containing single 13C atoms at C-4, C-5, and C-6 (12 compounds) and measured complete sets of 1J, 2J, and 3J couplings between the 13C-substituted carbon, and nearby protons and carbons within the exocyclic hydroxymethyl group.134 At the same time, these couplings were also computed by DFT methods by using a special basis set to obtain reliable Fermi-contact contributions. Complete hypersurfaces were calculated for 1JC-5,C-6, 2JC-5,H-6R, 2JC-5,H-6S, 2JH-5,C-6, 2JC-4,C-6, 3JC-4,H-6R, 3JC-4,H-6S, 3JH-4,C-6, 2JH-6R,H-6S, 3JH-5,H-6R, and 3JH-5,H-6S.
The results were used to parametrize new equations correlating these couplings with the C-5–C-6 and C-6–O-6 dihedral angles ω and θ, respectively. Couplings computed by DFT were also tested by measuring them experimentally for 13C-substituted 4,6-O-ethylidene derivatives of D-glucose and D-galactose, in which the values of ω and θ were constrained. Effects of substituents were also assessed by using DFT calculations for tetrahydropyran models containing a hydroxymethyl group, or this group plus a vicinal hydroxyl group in either an axial or an equatorial orientation. Favored rotamer populations about ω and θ in the methyl glycosides just mentioned were determined by use of a new computer program, CHYMESA, which was designed to analyze multiple J-couplings sensitive to exocyclic CH2OH conformation. Due to the sensitivity of some couplings, especially 2JH-6R,H-6S, 2JC-5,H-6R, and 2JC-5,H-6S to both ω and θ, important information on correlated conformation about both torsion angles was obtained, which provides a method of evaluating such conformations in (1→6)-linked oligosaccharides, since ψ and θ are identical in these linkages.134 The new equations for vicinal coupling constants included:
| (86) |
| (87) |
but several other equations reflecting the dependence of two-bond C–C and C–H couplings on the orientation of the hydroxymethyl gtoup were also developed. Both 3JC-4,H-6R and 3JC-4,H-6S display a Karplus dependence, as expected, but the curves are mutually phase-shifted by ~20°. Based on the good agreement between experimental and computed couplings, it was concluded that DFT provides an almost quantitative tool for the calculation of JHH, JCH, and JCC values in saccharides, without the use of empirical scaling adjustments.134
V. Other Types of Vicinal Couplings
1. Fluorine Couplings
a. Proton–Fluorine Couplings, 3JHCCF
Studies of the dependence of 3JHCCF couplings on electronegativity have been a subject in their own right. Hall and Jones measured 3JHCCF for 16 geometrically constrained 1,2-disubstituted, fluorohaloace-naphthene derivatives, and, contrary to expectations based on 3JHCCH, found that plots of the couplings against Huggins electronegativity values were described better by an exponential relationship than by a linear one.135 Also, the dependences of cis and trans couplings were quite different,135 according to
| (88) |
| (89) |
However, Hamman et al.136 analyzed the rotameric populations of 2-fluoro-1,2-disubstituted ethanes and found that transoid 3JHCCH and 3JHCCF couplings could be described by linear fits
| (90) |
| (91) |
whereas 3JHCCF (gauche) displayed an exponential fit
| (92) |
where Σ(Δχ) is the sum of the differences in Huggins electronegativity between hydrogen and the six atoms or groups on the HCCF fragment.136
An elaborate study of the dependence of 3JHCCF on molecular properties was conducted by Thibaudeau et al.137 who also summarized the early history of these couplings in which the three-parameter Karplus equation was used to describe the couplings. By using experimental values of 3JHCCH in the Haasnoot–Altona equation, these authors calculated the corresponding 1H–1H torsion angles, from which endo-cyclic torsion angles ν0–ν4 were obtained from a detailed analysis of the temperature-dependent North–South equilibria of the pentofuranose rings in 11 monofluorinated nucleosides, by use of the PSEUROT program.137 The equilibria were used to calculate the phase angle and pucker values that characterized the major conformers. These values were used to calculate the proton–fluorine torsion angle ϕHF from the linear relationship
| (93) |
where j = 0–4, and the AF and BF parameters were obtained from a series of ab initio geometry optimizations on eight of the monofluorinated nucleosides, by means of the GAUSSIAN94 program at the HF/3–21G level.137 Values of 3JHCCF were measured for the nucleosides by 1D 1H NMR, and the values were supplemented by literature values for four fluorocyclohexane derivatives, six geometrically constrained fluoro-bicycloalkanes, and a fluoro-cis-decalin, giving a data set of 57 3JHCCF/ϕHF pairs. This data set could not readily be fitted to a Karplus equation of the three-parameter type, nor could an accurate fit to a six-parameter, generalized Haasnoot–Altona equation be achieved. Finally, the introduction of bond-angle terms aFCC and aHCC led to a seven-parameter equation:
| (94) |
The difference between experimental and back-calculated 3JHCCF values was <2.9 Hz, with an overall rms deviation of 1.38 Hz. Graphical analysis of the conformational preferences of the 11 fluronucleosides indicated that the use of 3JHCCF and 3JHCCH values gave qualitatively similar results. These two types of coupling constants were combined in a modified version of the PSEUROT program: PSEUROT + JHF in which 3JHCCH values can be used alone or in combination with 3JHCCF. The application of the seven-parameter Eq. (94) in conjunction with the PSEUROT + JHF program was tested further on two more fluoronucleosides, on four difluorinated nucleosides, and on a fluoro-trans-decalin derivative, giving reasonable results in each case.137
b. Proton–Fluorine Couplings, 3JHCNF and 4JHCC′NF
As models for peptides, Hammer and Chandrasegaran138 synthesized a series of nine N-fluoroamide derivatives by reaction of trifluoromethyl hypofluorite with the corresponding amides and measured their 3JHCNF values by 1D 1H and 19F NMR. However, the observation of 3JHCNF < 5 Hz in the 19F NMR spectra was not feasible, because of quadrupolar broadening by the 14N nucleus. The compounds were chosen partly for their rigidity (as in four bicycloalkanes), expected dihedral angles, or ease of preparation. Dihedral angles were taken either from X-ray data for NH analogs, or with the assumption of a planar amide group, were estimated from “carefully straightened” Dreiding models, with a suggested accuracy of ±5°. Nonlinear, least-squares fitting of the coupling constants using the MLAB implementation of the PROPHET program yielded138 the equation:
| (95) |
In these N-fluoroamides, the coupling pathway differs from those previously discussed in that it contains an sp2-hybridized carbonyl carbon atom, which may enhance the magnitude of the coupling. The shape of the fitted curve is highly skewed, apparently reflecting the fact that the values estimated for 3JHCNF (180°) are approximately five times as large as those measured for 3JHCNF (0°), thus producing comparable values of the A and B constants.138 By using similar methods, this study also yielded a Karplus equation for 4JHCC′NF:
| (96) |
where ψ is the dihedral angle about the C–C′ (Cα–CO) bond. Presumably, only one torsion angle is required to describe this four-bond coupling, because of restricted rotation about the amide bond. The best fit to the experimental data generated a highly skewed, inverted Karplus curve in which 4JHCC′NF = ~−5 Hz for ψ = 0° and 4JHCC′NF = ~−23 Hz for ψ = 180°, with the curve crossing zero twice.138
c. Carbon–Fluorine Couplings, 3JCCCF and 3JCOCF
In a study of glycosyl fluorides, Bock and Pedersen found evidence of a Karplus dependence of 3JCCCF, since the 3JC-3,F-1 values (4–10 Hz) of β-pyranosyl fluorides in which C-3 and F-1 are trans are larger than those (0–6 Hz) of the α-fluorides, in which these coupling nuclei are gauche.139 However, the same could not be said for 3JCOCF, because in all pyranosyl fluorides, 3JC-5,F-1 was found to be in the range 2–5 Hz, regardless of anomeric configuration.139 Additional examples of the 3JCF couplings of fluorinated carbohydrates have been reviewed.140
d. Fluorine–Fluorine Couplings, 3JFCCF
These couplings have been found not to obey a simple dependence on dihedral angle, as noted by Hall et al. on the basis of measurements on the anomeric 3,4,6-tri-O-acetyl-2-deoxy-2-fluoro-D-gluco- and D-manno-pyranosyl fluorides, and 7,7,8-trifluoro-2(3),5(6)-dibenzobicyclo[2.2.2] octane and its 7-chloro derivative.141 Thus, approximate 19F–19F dihedral angles of 0°, 60°, 120°, and 180° showed 3JFCCF values in the ranges +9.4 to +11.4, −13.5 to −18.8, −1.2 to −2.2, and −20.0 Hz, respectively. The reversal in sign was unexpected, and various attempts have been made to explain these and similar observations theoretically. Kurtkaya et al.142 performed DFT computations for 1,2-difluoroethane in which the four Ramsey contributions, Fermi contact, spin–dipolar, diamagnetic spin–orbit, and paramagnetic spin–orbit to the spin coupling were characterized separately. The positive region of the curve from 0° to 40° was determined by a Fermi-contact term, but the negative section from 40° to 180° originated from reinforcing negative Fermi-contact and paramagnetic spin–orbit terms. More importantly, the Fermi-contact term in the range 90°–180° was found to contain an extremely strong negative contribution from the three non-bonded lone pairs of electrons on the fluorine atoms.142
Various theoretical treatments, including DFT and two high-level ab initio methods, MCSCF and SOPPA, have been tested recently by San Fabián and Westra Hoekzema.143 These authors represented contributions to the angular dependence of 3JFCCF in 1,2-difluoroethane by a truncated Fourier series:
| (97) |
where this general expression could be used to describe either the total contributions or any of the component Fermi contact, spin–dipolar, diamagnetic spin–orbit, or paramagnetic spin–orbit terms. Owing to the symmetry in unsubstituted 1,2-difluoroethane, 3JFCCF (+ϕ) = 3JFCCF (−ϕ), and so sine coefficients were not included in Eq. (97). When m = 2, this equation simplifies to the familiar Karplus equation, which suggests that the latter equation is a subset of a more complex relationship. The lack of a traditional Karplus dependence for 3JFCCF values of saturated fluorocarbons is reflected in the interpretation that (a) higher order Fourier coefficients are needed in Eq. (97) to reproduce these couplings correctly and (b) the values of the first three coefficients differ from the usual large C0 and C2 coefficients, and small C1 value.143 It was concluded that the deviation of 3JFCCF from the Karplus equation arises mainly from through-space interaction in the Fermi-contact contribution, and that the description of this contribution by Eq. (97) requires at least six coefficients (that is, m = 5 in Eq. (97)). As a result, an explicit, analytical expression is not available for the dependence of 3JFCCF on torsion angle. Moreover, the dependence of the 3JFCCF coupling on substituents is generally complex and not well understood.
2. Carbon–Tin Couplings
a. Carbon–Tin Couplings, 3JCCCSn
Vicinal 13C–119Sn couplings have been measured for geometrically constrained, exo- and endo-2-norbornyl-, 1- and 2-adamantyl-, and 3-nortricyclyl-trimethylstannane.144 Fitting of the 3JCCCSn values to a three-parameter Karplus equation using CCCSn torsion angles 35°, 70°, 85°, 120°, 160°, 170°, and 180° obtained from Dreiding models of the stannane derivatives gave the equation:
| (98) |
which may be rewritten as
| (99) |
VI. Couplings Over Four Bonds
These couplings may certainly be described as long range, but two definitions of long-range coupling constants have been used. Some authors refer to long-range couplings as those transmitted over more than one bond, while others mean the couplings over more than three or even four bonds. In sugars, this group of couplings includes those over pathways containing four saturated bonds, or three saturated and one unsaturated bond (allylic couplings), which have different dependences on dihedral angle.
1. Proton–Proton Couplings
a. W and non-W Couplings, 4JHCCCH
W-type couplings are rather common in saturated, carbohydrate structures, occurring whenever the coupling pathway has a near planar W shape,145 as in pyranose and furanose rings having a 1,3-diequatorial arrangement of protons, or of different pairs of magnetically active nuclei.66 4JHCCCH couplings were first observed in carbohydrates by Hall and Hough, who found 4J1,3 1.3, 1.4, and 1.8 Hz for three 2,3,4-tri-O-acetyl-1,6-anhydro-β-D-hexopyranoses in which H-1 and H-3 were both equatorial.146 At that time, the long-range coupling was not observable in 1,6-anhydro derivatives in which H-3 was axial, thus indicating a stereochemical dependence. Other early examples were 4J1,3 0.7–0.9 Hz in 4C1 chair conformations of methyl 4,6-O-benzylidene-α-D-altropyranoside derivatives,64 and 4J2,4 0.8–1.0 Hz in 3S5 skew conformations of 1,2-O-alkylidene-α-D-glucopyranosides147,148 and similar derivatives having a five-membered ring fused to C-1 and C-2.149 On the basis of a semi-empirical VB theory, Barfield soon indicated that the maximum long-range coupling (if positive) should correspond to a planar zigzag (that is, W) arrangement in which the relevant dihedral angles ϕ1 and ϕ3 are both 180°, with a sharp decrease in magnitude expected as either proton H-1 or H-3 is moved out of the plane.150 For the 4J1,3 couplings in the 1,6-anhydrohexopyranoses, ϕ1 and ϕ3 are subtended by H-1–C-1–C-2–C-3 and C-1–C-2–C-3–H-3, respectively.
At the time of our report on the observation of an unusually large coupling 4J2,4 +2.45 Hz in the 1H NMR spectrum of 3-O-benzoyl-1,2,4-O-benzylidyne-α-D-ribopyr-anose,151 the theoretical interpretation of these couplings was somewhat inexplicit, and rather confusing. Barfield’s early VB theory150 did not account satisfactorily for the variation of the sign of 4JHCCCH with the 1,3-diequatorial or 1,3-equatorial-axial orientations of ring protons in the chair conformations of pyranose sugars152 The theory was interpreted153 either in terms of the equation:
| (100) |
or an alternative:
| (101) |
where B = 0.35, and A = 0.31 for 0° ≤ ϕ1, ϕ3 ≤ 90°, 1.07 for 0° ≤ ϕ1 ≤ 90° ≤ ϕ3 ≤ 180°, or 3.61 for 90° ≤ ϕ1, ϕ3 ≤ 180°. The latter equation agreed more closely with 4JHCCCH = +2.45 Hz of the 1,2,4-O-benzylidyne-α-D-ribopyranose derivative,151 whereas the former equation predicts the couplings more accurately for 4J1,3 +1.6 Hz and 4J3,5 +1.5 Hz in 1,6-anhydro-β-D-mannopyranose triacetate, and other similar derivatives.152 However, 4JHCCCH couplings in conformationally locked ring-systems have frequently been observed to be abnormally large, for example, reaching 4J1,3 18.2 Hz in bicyclo[1.1.1]pentane.154 In this derivative, H-1 and H-3 are collinear and may be expected to couple strongly through overlap of the rear lobes of their H–C bonding orbitals.
In a reprise, almost 40 years later, Barfield has clarified the situation by a study of the structural dependencies of 4JHCCCH in propanic and allylic systems by DFT/FPT methods, which were used to obtain the Fermi-contact contributions to the couplings.154 The theoretical contributions to the coupling constants were dissected according to dependences on various molecular properties, including the ϕ1 and ϕ3 torsion angles, the central C-1–C-2–C-3 bond angle θ2, and the C-1–C-3 distance rC-1,C-3. Barfield has published a very revealing 3D plot of 4JHCCCH as a function of both ϕ1 and ϕ3 (Fig. 10).
Fig. 10.
3D plot and contour map for 4JHCCCH in propane, calculated as a function of the dihedral angles ϕ1 and ϕ3 by DFT/FPT at 30° intervals of the angles. 3D spline interpolations were used to create the graphs, which illustrate how the coupling constant changes sign, depending on the values of ϕ1 and ϕ3. A maximum positive value is seen for ϕ1 = ϕ3 = 180°.
The data for this plot were calculated by DFT/FPT for 30° intervals of ϕ1 and ϕ3 and show that 4JHCCCH reaches a maximum of +2.11 Hz for ϕ1 = ϕ3 = 180°, and a minimum value of −0.73 Hz for ϕ1 = ϕ3 = 0°, thus adequately interpreting the variation of the signs of the experimental couplings with geometrical factors.154 For propane, the following expression was proposed:
| (102) |
Unfortunately, the choice of trigonometric functions still seems a little arbitrary, perhaps reflecting the difficulty of translating the theory into practical equations.
The dependence of 4JHCCCH on ϕ1, ϕ3, θ2, and rC-1,C-3 was investigated by a DFT/FPT procedure in which ϕ1 and ϕ3 were stepped by 60° increments, and θ2 by 10° intervals in the range 70–130°. Fitting of the theoretical results for the trans–trans (tt) conformation of propane (W-form, ϕ1 = ϕ3 = 180°) yielded154 the equation:
| (103) |
where r(0)C-1,C-3 is the smallest value (1.978 Å) in the series, occurring for θ2 = 70°.
A simple alternative to Eq. (102) was formulated to represent W-couplings in bicycloalkanes:
| (104) |
For example, using rC-1,C-3 = 1.872 Å in this equation leads to a computed value 4J1,3 20.6 Hz in bicyclo[1.1.1]pentane, which may be compared with its experimental value of 18.2 Hz.154
The 4JHCCCH values of 28 cyclopentane and cyclohexane derivatives have been subjected to PCA, by using the couplings, the corresponding torsion angles, and the cos2 ϕ1 cos2 ϕ3 product as variables in a multivariate data analysis.155 The torsion angles were calculated by use of three different molecular-mechanics packages, PC MODEL (MMX), CS MOPAC PRO (AM1), and GAUSSIAN98 [HF/6–31g(d,p)]. PCA was performed by using the PIROUETTE software package, the application of which to GAUSSIAN98 data yielded seven clusters of compounds, where the clustering reflected structural similarities in the compounds. Two significant principal components were described by the equations:
| (105) |
| (106) |
The most important variables in the separation of the seven clusters were found to be the coupling-constant values and the calculated products, cos2 ϕ1 cos2 ϕ3, which together had the highest modeling-power indices, and the largest coefficients in PC1 and PC2.155 Two trends in clustering were observed, one owing to similarities in torsion angle (four groups of samples) and another to values of the four-bond coupling, including the small or zero couplings resulting from 1,3-diaxial arrangements of protons. It was proposed that substituents positioned on the same side of the ring as the coupled protons have a greater influence in diminishing the W-coupling than does the orientation of these protons,155 a somewhat surprising result, in view of the known dependence of 4JHCCCH values of carbohydrates on the stereochemistry of the protons.
As the resolution of NMR spectrometers has improved and resolution enhancement by such methods as Gaussian multiplication of the FID has been more widely used, non-W values of 4JHCCCH have been detected more frequently.156 For example, 4J1,5 0.5–0.7 Hz in a series of methyl 4,6-O-benzylidene-α-D-hexopyranosides, in which ϕ1 and ϕ3 have values of ~180° and ~60°, respectively.66 In partially protected galactopyranosides, the observation of 4JHO-4,H-5 1.0 Hz was more reasonably interpreted by a W coupling to a hydroxyl proton,157 than by a through-hydrogen-bond-coupling hJ involving a pathway via the ring oxygen,158 as supported by DFT calculations.157
b. Allylic Couplings, 4JHC=CCH
The early history of these couplings has been reviewed before.21,145 Fermi-contact contributions to the transoid and cisoid allylic couplings in propene have recently been calculated by DFT/FPT and fitted154 to the equations:
| (107) |
| (108) |
These couplings are theoretically expected to have largest numeric magnitudes of approximately −4 Hz for ϕ = 90°, although the experimental values have been found to be 1–2 Hz smaller.154
VII. Couplings Over Five Bonds
1. Proton–Proton Couplings
a. Extended W Couplings, 5JHCCCCH
An especially favorable geometry for the detection of these couplings is when the protons are separated by five bonds in a planar, zigzag (extended W) arrangement.145 For example, methyl 4,6-O-benzyli-dene-α-D-altropyranosides having the pyranose ring in a 4C1 form (Fig. 11) exhibited values 5J3e,6e 0.5–0.7 Hz, whereas in similar derivatives in which H-3 and H-6 were not in a planar, extended W, the 5J3,6 coupling was not detectable.66 However, couplings of 0.4–1.3 Hz have also been measured for chair forms of 1,3-dioxanes and pyranoid compounds in which the 1,4-protons are diequatorial, but not precisely in an extended W orientation.159 According to Barfield et al.,128 5JHCCCCH couplings may be expected to have a functional dependence on cos ϕ1,2, cos ϕ2,3, and cos ϕ3,4, where ϕ1,2, ϕ2,3, and ϕ3,4 are the dihedral angles about C-1–C-2, C-2–C-3, and C-3–C-4, respectively.
Fig. 11.
A planar, extended W coupling pathway (heavy bonds) in methyl N-2′,4′-dinitrophenyl-3-amino-4,6-O-benzylidene-3-deoxy-2-O-methyl-α-D-altropyranoside, which results in a long-range coupling constant of 5J3,6 0.5 Hz.
b. Biallylic Couplings, 5JHCC=CCH
These couplings have been reviewed previously66,145 Based on measurements of the magnitudes and relative signs of 5J1,4 in methyl 3,4-dichloro-4-deoxy-D-glycero-pent-2-enopyranosides,160 Eq. (109) was proposed
| (109) |
where ϕ1 and ϕ4 are the torsion angles of the terminal protons with respect to the coupling pathway.66 For the important π-electron contribution to homoallylic (biallylic) couplings, Barfield and Sternhell suggested161,162 Eq. (110) on the basis of VB formalism:
| (110) |
However, σ-electron contributions were not included because the size of the secular determinants increases enormously with the size of the basis set, and it was difficult to find suitable empirical parameters for the σ-electron system.162
VIII. Online Calculators for Coupling Constants and Torsions
Stenutz has provided a number of useful tools for the online calculation of homo-and heteronuclear coupling constants, torsion angles, rotameric populations, and puckering phase. Two calculations of 3JHCCH are available, using either the Haasnoot,163 or Pachler164 relationships. Both implementations depend on the relative orientation of the substituents, and turning a molecular model so that the proton on the near side is pointing up is recommended. Each online program requires four substituents to be selected from drop-down menus of atom types. The implementation of the Haasnoot procedure automatically selects one of three equations, depending on the number of attached hydrogen atoms. Entry of a ϕHCCH value then allows the corresponding 3JHCCH to be calculated, or conversely, the insertion of a coupling constant value results in the computation of one to four torsion angles, depending on the size of the coupling.
A generalized online calculation of the three-parameter Eq. (3) is also available, which can be used to compute either homo- or heteronuclear coupling constants from given dihedral angles.165 Users of this calculation either type in new values of the A, B, and C coefficients or select these coefficients automatically by choosing a literature reference from a list, many of which have been discussed in this chapter. Conversely, the entry of a coupling constant permits the calculation of four solutions for a torsion angle, which are comprised of ± a smaller angle, and ± a larger angle. If there are only two torsions that will reproduce the coupling constant, or if the 3J value lies outside the range of the Karplus equation, then “not a number” is displayed.
Another online module allows the calculation of 3JHCCH values specifically for β-ribofuranosides (or nucleosides/nucleotides) from the puckering phase or determines the puckering phase from experimental coupling constants.166 There may be more than one phase that reproduces the experimental couplings, but only one is found by the program. An rmsd > 0.5 suggests that there is an equilibrium of two conformers, namely, N ↔ S, and for comparison purposes, such an equilibrium is calculated. If the ribofuranose ring is rigid, then the rmsd for the fitted pseudorotation angle (P) should be lower than for the two-state model. To calculate the coupling constant, either the pseudorotation angle is entered in degrees or a conformer, such as 3T2 and the like, is selected by clicking on a button.166 The program output displays the calculated values of J1,2, J2,3, and J3,4, as well as the best P, the rmsd values, and the best N ↔ S equilibrium in terms of the %N conformer (3E).
A module for unsubstituted 2-deoxy-erythro-β-pentofuranose permits the calculation from the pseudorotation angle of all the 1JCH, 2JCH, and 3JCH couplings around the furanose ring, except that, in some cases, the relative proportions of the two dominant C-4–C-5 rotamers (gg and gt) are required.167 In nucleic acids, the gg rotamer is the only one present.
Yet another module can be used to calculate hydroxymethyl coupling constants related to the ω torsion angle, O-5–C-5–C-6–O-6 in hexopyranoses. By entering this angle together with a value for the θ torsion, C-5–C-6–O-6–HO-6, the magnitudes of 1JC-5,C-6, 2JC-4,C-6, 1JC-6,H-6R, 1JC-6,H-6S, 2JC-5,H-6R, 2JC-5,H-6S, 2JC-6,H-5, 3JC-4,H-6R, 3JC-4,H-6S, 2JH-6R,H-6S, 3JH-5,H-6R, and 3JH-5,H-6S can be estimated.168
Two useful tables of rotameric populations for the hydroxymethyl groups in hexopyranoside derivatives are available online. In the first,169 two protocols have been used to calculate rotameric distributions from experimental values of 3JH-5,H-6R and 3JH-5,H-6S, using either application of the Haasnoot equation to the data of Bock and Duus,170 or the results of the quantum-mechanical calculations of Stenutz et al.61 The populations of the gt rotamer obtained by the two methods are in good agreement, but those of the gg and tg rotamers agree less well. In the second table,171 a single set of populations of the gt, gg, and tg rotamers has been calculated from the experimental 3JH-5,H-6R and 3JH-5,H-6S values of a larger collection of both hexopyranoside and disaccharide derivatives, by using the limiting values of Stenutz et al.61
An online calculator is available that relates 13C chemical shifts on glycosylation to the 1H–1H distance rH,H across the glycosidic linkage, and the ψH torsion angle.172 The method applies to α-linked disaccharides containing galacto, gluco, and manno residues, and is based on the work of Bock et al.173 Entry of the glycosylation shifts (ppm) for the non-reducing end, ΔδC-1 and for the reducing end, ΔδC-n into the calculator gives estimates of ψH (in degrees) and rH,H (in Å). Examples of results are given for 11 α-linked disaccharide methyl glycoside derivatives.172
An interactive plotting program for Eq. (2) is available online which allows the entry of different sets of the parameters A, B, and C and then displays up to five plots simultaneously, together with the parameters for each plot. The values of J and ϕ at any value of ϕ on each plot can be inspected by moving the cursor to the location, followed by clicking and holding the left mouse button at that location.174,175
A free graphical tool, MestRe-J for Windows-32 platforms, is available for the prediction of 3JHCCH from torsion angles176,177 using either the Haasnoot–Altona equation33 with Huggins electronegativities Δχ, the Colucci–Jungk–Gandour equation,45 or the more recent and precise Díez–Altona–Donders equations with λ electro-negativities.58 The latter equations include the effects of nonadditive interactions between substituents, and the equations for 3JHCCH can also be solved for the torsion angles. This graphical application works with a Newman projection of the molecular fragment and displays a plot of J values versus the torsion angle. Computation of the Barfield–Smith equation178,179 has also been implemented,177 for which a significant erratum has been published.180 Other programs are also available for the calculation of torsion angles from NMR data, including the MULDER program,181 and a module in the AURELIA program.182
IX. Summary
Karplus equations of varying complexity are available for most of the three- and four-bond spin–spin coupling constants that are commonly measured for carbohydrates. Similar equations have also been developed for one- and two-bond couplings between pairs of nuclei that are not directly connected by a dihedral angle, but instead depend on the relative torsion angles of substituents either inside, or outside the coupling pathway. The coefficients in the equations have in most cases been determined by fitting of experimental data and are specific for particular pairs of nuclei separated by various coupling pathways. These coefficients are summarized in Table I for Karplus equations of the three-parameter type that describe vicinal couplings, for which the important A coefficient varies from a maximum value of 70.8 Hz for 3JHCNF, to a minimum of 3.1 Hz for 3JHCCN. Many of the three-parameter equations have been constructed from quite small experimental data sets, especially for the heteronuclear couplings. A notable exception is the work of Serianni and coworkers, who have generated vast quantities of coupling-constant data, experimentally from 13C-substituted sugars, and theoretically by DFT methods. The inclusion, in the Karplus equation, of other admittedly important molecular properties such as atomic or group electronegativity, electronegativity orientation, valence-bond angle, and bond length requires large experimental (or theoretical) data sets and has not been performed for all combinations of nuclei, and of coupling pathway.
Table I.
Coefficientsa in Selected Three-Parameter Karplus Equations, 3J = A cos2 ϕ + B cos ϕ + C, for Vicinal NMR Coupling Constants, Ranked According to the Magnitude of A
| 3J | A | B | C | References |
|---|---|---|---|---|
| 3JHCNF | 70.8 | −44.1 | −7.2 | 138 |
| 3JCCCSnb | 50.4 | −7.6 | 5.2 | 144 |
| 3JHCOP | 15.3 | −6.2 | 1.5 | 110 |
| 3JHCOH | 13.56 | −2.05 | −1.02 | 75 |
| 10.4 | −1.5 | 0.2 | 70 | |
| 3JCCOP | 9.1 | −1.9 | 0.8 | 111 |
| 3JHCCH | 9.0 | −0.5 | −0.3 | 8 |
| 3JHCαNC′ | 9.0 | −4.4 | −0.8 | 105 |
| 3JHOCC | 8.36 | −1.41 | −0.69 | 75 |
| 3JHCCC | 8.06 | −0.87 | 0.47 | 92 |
| 3JHCSiH | 5.83 | −2.59 | 0.84 | 76 |
| 3JHCOC | 5.7 | −0.6 | 0.5 | 81 |
| 5.5 | −0.7 | 0.6 | 82 | |
| 3JCCCC | 4.48 | 0.18 | −0.57 | 132 |
| 3JHCSC | 4.44 | −1.06 | 0.45 | 96 |
| 3JCCOC | 4.4 | 1.1 | 0.5 | 121 |
| 3.70 | 0.18 | 0.11 | 122 | |
| 3JHCCNc | 3.1 | −0.6 | 0.4 | 66 |
| 3JHCαC′Nc | −4.6 | 3.0 | 0.8 | 105 |
The entries in the table are illustrative, rather than comprehensive, and do not take into account the recent trend to develop multiple Karplus equations for different structural elements. The main text or original publications should be consulted for full details.
119Sn.
15N.
As the quantity of available experimental and theoretical data has increased, there has been a trend towards parametrization of multiple Karplus equations for various structural elements, especially for different coupling pathways, and anomeric configurations.
As an alternative to the use of these empirically derived equations, Serianni et al. have suggested that spin couplings could instead be calculated for molecules of interest by DFT, which with the correct choice of basis sets, now seems to give theoretical coupling values that agree well with experimental measurements, often without the need for scaling adjustments.
Interactive, online programs are available for the calculation of coupling constants, dihedral angles, and the 1H–1H distance across thr α-linkages of some disaccharides, as well as a program for plotting up to five Karplus curves.
Abbreviations
- 1D
one-dimensional
- 2D
two-dimensional
- 3D
three-dimensional
- AMP
adenosine monophosphate
- CNDO
complete neglect of differential overlap
- COSY
correlation spectroscopy
- CPMG
Carr-Purcell–Meiboom–Gill NMR pulse sequence
- CT
constant time
- dAMP
deoxyadenosine monophosphate
- DFT
density functional theory
- EHT
extended Hückel theory
- FID
free induction decay
- FPT
finite perturbation theory
- FT
Fourier transform
- HMBC
heteronuclear multiple bond correlation
- HSQC
heteronuclear single quantum correlation
- HSQMBC
heteronuclear single quantum multiple bond correlation
- INADEQUATE
incredible natural abundance double quantum transfer experiment
- INDO
intermediate neglect of differential overlap
- INEPT
insensitive nuclei enhancement by polarization transfer
- Kb
kilobyte
- LCAO
linear combination of atomic orbitals
- LRCC
long-range carbon–carbon correlation spectroscopy
- MCSCF
multi-configurational self-consistent field
- MD
molecular dynamics
- MM
MM1, MM2, MMP2(85), MM2–85, MMX, various versions of Allinger’s molecular-mechanics program
- MO
molecular orbital
- NOE
nuclear Overhauser effect
- PCA
principal component analysis
- PCILO
perturbative configuration interaction with localized orbitals
- PFIDS
phosphorus fitting of coupling constants from doublets and singlets
- PMR
proton magnetic resonance
- RF
radio frequency
- ROE
rotating-frame Overhauser effect
- ROESY
rotating-frame Overhauser effect spectroscopy
- SCF
self-consistent field
- SCPT
self-consistent perturbation theory
- SOPPA
second-order polarization propagator approximation
- T1
spin–lattice relaxation time
- T2
spin–spin relaxation time
- VB
valence bond
Single-letter abbreviations for ribonucleoside or ribonucleotide base-containing components depending on context
- A
adenosine
- C
cytosine
- G
guanosine
- T
ribosylthymine
- U
uridine
References
- 1.Karplus M. Contact electron–spin coupling of nuclear magnetic moments. J Chem Phys. 1959;30:11–15. [Google Scholar]
- 2.Lemieux RU, Kullnig RK, Bernstein HJ, Schneider WG. Configurational effects on the proton magnetic resonance spectra of six-membered ring compounds. J Am Chem Soc. 1958;80:6098–6105. [Google Scholar]
- 3.Lemieux RU, Kullnig RK, Moir RY. The configuration of the 3-methoxycyclohexene oxides. A novel application of proton magnetic resonance spectroscopy to the determination of structure and configuration. J Am Chem Soc. 1958;80:2237–2242. [Google Scholar]
- 4.Dalton L. Karplus equation. Theoretical calculation links NMR coupling constant to molecular geometry. Chem Eng News. 2003;81:37–39. [Google Scholar]
- 5.Lenz JW, Heeschen JP. The application of nuclear magnetic resonance to structural studies of carbohydrates in aqueous solution. J Polymer Sci. 1961;51:247–261. [Google Scholar]
- 6.Abraham RJ, Hall LD, Hough L, McLauchlan KA. A proton resonance study of the conformations of carbohydrates in solution. Part I. Derivatives of 1,2-O-isopropylidene-α-D-xylo-hexofuranose. J Chem Soc. 1962:3699–3705. [Google Scholar]
- 7.Hall LD. Nuclear magnetic resonance. Adv Carbohydr Chem. 1964;19:51–93. doi: 10.1016/s0096-5332(08)60279-9. [DOI] [PubMed] [Google Scholar]
- 8.Karplus M. Vicinal proton coupling in nuclear magnetic resonance. J Am Chem Soc. 1963;85:2870–2871. [Google Scholar]
- 9.Tvaroška I, Taravel FR. Carbon–proton coupling constants in the conformational analysis of sugar molecules. Adv Carbohydr Chem Biochem. 1995;51:15–61. doi: 10.1016/s0065-2318(08)60191-2. [DOI] [PubMed] [Google Scholar]
- 10.Perlin AS, Casu B. Carbon-13 and proton magnetic resonance spectra of D-glucose-13C. Tetrahedron Lett. 1969:2921–2924. [Google Scholar]
- 11.Bock K, Lundt I, Pedersen CM. Assignment of anomeric structure to carbohydrates through geminal 13C-H coupling constants. Tetrahedron Lett. 1973:1037–1040. [Google Scholar]
- 12.Bock K, Pedersen CM. A study of 13CH coupling constants in hexopyranoses. J Chem Soc Perkin II. 1974:293–297. [Google Scholar]
- 13.Bock K, Pedersen CM. A study of 13CH coupling constants in pentopyranoses and some of their derivatives. Acta Chem Scand, B. 1975;29:258–264. [Google Scholar]
- 14.Bock K, Pedersen CM. Determination of one-bond carbon–proton coupling constants through 13C-satellites in 1H-n.m.r. spectra. Carbohydr Res. 1985;145:135–140. [Google Scholar]
- 15.Hricovini M, Tvaroška I. Conformational dependence of the one-bond carbon–proton coupling constants in oligosaccharides. Magn Reson Chem. 1990;28:862–866. [Google Scholar]
- 16.Tvaroška I, Taravel FR. One-bond carbon–proton coupling constants: Angular dependence in α-linked oligosaccharides. Carbohydr Res. 1991;221:83–94. doi: 10.1016/0008-6215(91)80050-w. [DOI] [PubMed] [Google Scholar]
- 17.Tvaroška I. Theoretical aspects of structure and conformation of oligosaccharides. Curr Opin Struct Biol. 1991;2:661–665. [Google Scholar]
- 18.Tvaroška I, Taravel FR. One-bond carbon–proton coupling constants: Angular dependence in β-linked oligosaccharides. J Biomol NMR. 1992;2:421–430. doi: 10.1016/0008-6215(91)80050-w. [DOI] [PubMed] [Google Scholar]
- 19.Ernst RR. Sensitivity enhancement in magnetic resonance. Advan Magn Reson. 1966;2:1–135. [Google Scholar]
- 20.Ernst RR, Anderson WA. Application of Fourier transform spectroscopy to magnetic resonance. Rev Sci Instrum. 1966;37:93–102. [Google Scholar]
- 21.Coxon B. Conformational analysis via nuclear magnetic resonance spectroscopy. Methods Carbohydr Chem. 1972;6:513–539. [Google Scholar]
- 22.Edén M, Brinkmann A, Luthman H, Eriksson L, Levitt MH. Determination of molecular geometry by high-order multiple-quantum evolution in solid-state NMR. J Magn Reson. 2000;144:266–279. doi: 10.1006/jmre.2000.2042. [DOI] [PubMed] [Google Scholar]
- 23.Karplus M. Theory of proton coupling constants in unsaturated molecules. J Am Chem Soc. 1960;82:4431–4432. [Google Scholar]
- 24.Abraham RJ, Pachler KGR. The proton magnetic resonance spectra of some substituted ethanes. The influence of substitution on CH–CH coupling constants. Mol Phys. 1964;7:165–182. [Google Scholar]
- 25.Durette PL, Horton D. Conformational studies on pyranoid sugar derivatives by NMR spectroscopy. Correlations of observed proton–proton coupling constants with the generalized Karplus equation. Org Magn Reson. 1971;3:417–427. [Google Scholar]
- 26.Streefkerk DG, De Bie MJA, Vliegenthart JFG. Conformational studies on pertrimethyl-silyl derivatives of some mono- and disaccharides by 220 MHz PMR spectroscopy. Tetrahedron. 1973;29:833–844. [Google Scholar]
- 27.Streefkerk DG, De Bie MJA, Vliegenthart JFG. Conformational studies of pertrimethyl-silyl derivatives of some 6-deoxyaldohexopyranoses and four less-common aldohexopyranoses by 220-MHz P.M.R. spectroscopy. Substituent and configurational effects on the chemical shifts of the ring protons. Carbohydr Res. 1974;38:47–59. [Google Scholar]
- 28.Dorland L, Schut BL, Vliegenthart JFG, Strecker G, Fournet B, Spik G, Montreuil J. Structural studies on 2-acetamido-1-N-(4-L-aspartyl)-2-deoxy-β-D-glucopyranosylamine and 2-acetamido-6-O(α-L-fucopyranosyl)-1-N-(4-L-aspartyl)-2-deoxy-β-D-glucopyranosylamine. Eur J Biochem. 1977;73:93–97. doi: 10.1111/j.1432-1033.1977.tb11294.x. [DOI] [PubMed] [Google Scholar]
- 29.Williams DH, Bhacca NS. Dependency of vicinal coupling constants on the configuration of electronegative substituents. J Am Chem Soc. 1964;86:2742–2743. [Google Scholar]
- 30.Abraham RJ, Gatti G. Rotational isomerism. Part VII. Effect of substituents on vicinal coupling constants in XCH2-CH2Y fragments. J Chem Soc (B) 1969:961–968. [Google Scholar]
- 31.Phillips L, Wray V. The structural dependence of the inductive effect. Part VI. The calculation of vicinal proton–proton spin–spin coupling constants in substituted ethanes. J Chem Soc Perkin II. 1972:536–539. [Google Scholar]
- 32.Haasnoot CAG, de Leeuw FAAM, de Leeuw HPM, Altona C. Interpretation of vicinal proton–proton coupling constants by a generalized Karplus relation. Conformational analysis of the exocyclic C-4′–C-5′ bond in nucleosides and nucleotides. Recueil, J Roy Netherlands Chem Soc. 1979;98:576–577. [Google Scholar]
- 33.Haasnoot CAG, de Leeuw FAAM, Altona C. The relationship between proton–proton NMR coupling constants and substituent electronegativities-I. An empirical generalization of the Karplus equation. Tetrahedron. 1980;36:2783–2792. [Google Scholar]
- 34.Haasnoot CAG, de Leeuw FAAM, de Leeuw HPM, Altona C. The relationship between proton–proton NMR coupling constants and substituent electronegativities. II-Conformational analysis of the sugar ring in nucleosides and nucleotides in solution using a generalized Karplus equation. Org Magn Reson. 1981;15:43–52. [Google Scholar]
- 35.Pachler KGR. Extended Hückel theory MO calculations of proton–proton coupling constants-II. The effect of substituents on vicinal couplings in monosubstituted ethanes. Tetrahedron. 1971;27:187–199. [Google Scholar]
- 36.Pachler KGR. The dependence of vicinal proton–proton coupling constants on dihedral angle and substituents. J Chem Soc Perkin II. 1972:1936–1940. [Google Scholar]
- 37.Booth H. The variation of vicinal proton–proton coupling constants with orientation of electronegative substituents. Tetrahedron Lett. 1965:411–416. [Google Scholar]
- 38.Balacco G. A desktop calculator for the Karplus equation. J Chem Inf Comput Sci. 1996;36:885–887. [Google Scholar]
- 39.Cerda-Garcia-Rojas CM, Zepeda LG, Joseph-Nathan P. A PC program for calculation of dihedral angles from 1H NMR data. Tetrahedron Comput Methods. 1990;3:113–118. [Google Scholar]
- 40.Haasnoot CAG, de Leeuw FAAM, de Leeuw HPM, Altona C. Relationship between proton–proton NMR coupling constants and substituent electronegativities. III. Conformational analysis of proline rings in solution using a generalized Karplus equation. Biopolymers. 1981;20:1211–1245. [Google Scholar]
- 41.Altona C, Sundaralingam M. Conformational analysis of the sugar ring in nucleosides and nucleotides. A new description using the concept of pseudorotation. J Am Chem Soc. 1972;94:8205–8212. doi: 10.1021/ja00778a043. [DOI] [PubMed] [Google Scholar]
- 42.Altona C, Sundaralingam M. Conformational analysis of the sugar ring in nucleosides and nucleotides. Improved method for the interpretation of proton magnetic resonance coupling constants. J Am Chem Soc. 1972;95:2333–2344. doi: 10.1021/ja00788a038. [DOI] [PubMed] [Google Scholar]
- 43.Abraham RJ, Loftus P, Thomas WA. Rotational isomerism-XXI. The conformation of 2-amino-3-fluoropropanoic acid (2AFP) and 2-fluoro-3-aminopropanoic acid (3-AFP) as the zwitterion, cation, and anion, an NMR and MO study. Tetrahedron. 1977;33:1227–1234. [Google Scholar]
- 44.Altona C, Haasnoot CAG. Prediction of anti and gauche vicinal proton–proton coupling constants in carbohydrates: A simple additivity rule for pyranose rings. Org Magn Reson. 1980;13:417–429. [Google Scholar]
- 45.Colucci WJ, Jungk SJ, Gandour RD. An equation utilizing empirically derived substituent constants for the prediction of vicinal coupling constants in substituted ethanes. Magn Reson Chem. 1985;23:335–343. [Google Scholar]
- 46.Huggins ML. Bond energies and polarities. J Am Chem Soc. 1953;75:4123–4126. [Google Scholar]
- 47.Pauling L. The nature of the chemical bond. IV. The energy of single bonds and the relative electronegativity of atoms. J Am Chem Soc. 1932;54:3570–3582. [Google Scholar]
- 48.Altona C, Ippel JH, Westra Hoekzema AJA, Erkelens C, Groesbeek M, Donders LA. Relationship between proton–proton NMR coupling constants and substituent electronegativities. V. Empirical substituent constants derived from ethanes and propanes. Magn Reson Chem. 1989;27:564–576. [Google Scholar]
- 49.Donders LA, de Leeuw FAAM, Altona C. Relationship between proton–proton NMR coupling constants and substituent electronegativities. IV. An extended Karplus equation accounting for interaction between substituents and its application to coupling constant data calculated by the extended Hückel method. Magn Reson Chem. 1989;27:556–563. [Google Scholar]
- 50.de Leeuw FAAM, van Beuzekom AA, Altona C. Through-space effects on vicinal proton spin–spin coupling constants mediated via hetero atoms: Nonequivalence of cis-couplings in five-membered rings. J Comput Chem. 1983;4:438–448. [Google Scholar]
- 51.Marchand AP, Marchand NW, Segre AL. NMR studies of rigid bicyclic systems. II. Evidence for the nonequivalence of exo–exo and endo–endo coupling constants in 7-substituted-1,4-dichloro-2,2,3,3-tetradeuterionorbornanes. Tetrahedron Lett. 1969;59:5207–5210. [Google Scholar]
- 52.Marshall JL, Walter SR, Barfield M, Marchand AP, Marchand NW, Segre AL. Reasons for the nonequivalence of the exo–exo and endo–endo vicinal NMR coupling constants in norbornanes. Tetrahedron. 1976;32:537–542. [Google Scholar]
- 53.Kessler H, Friedrich A, Hull WE. Peptide conformation. 12. Conformation of cyclo-(L-Pro3) in solution. J Org Chem. 1981;46:3892–3895. [Google Scholar]
- 54.Kessler H, Bermel W, Friedrich A, Krack G, Hull WE. Peptide conformation. 17. cyclo(L-Pro-L-Pro-D-Pro). Conformational analysis by 270- and 500-MHz one- and two-dimensional 1H NMR spectroscopy. J Am Chem Soc. 1982;104:6297–6304. [Google Scholar]
- 55.de Leeuw FAAM, Altona C. Computer-assisted pseudorotation analysis of five-membered rings by means of proton spin–spin coupling constants: Program PSEUROT. J Comput Chem. 1983;4:428–437. [Google Scholar]
- 56.Imai K, Ôsawa E. An empirical extension of the Karplus equation. Magn Reson Chem. 1990;28:668–674. [Google Scholar]
- 57.Altona C, Francke R, de Haan R, Ippel JH, Daalmans GJ, Westra Hoekzema AJA, van Wijk J. Empirical group electronegativities for vicinal NMR proton–proton couplings along a C–C bond: Solvent effects and reparameterization of the Haasnoot equation. Magn Reson Chem. 1994;32:670–678. [Google Scholar]
- 58.Díez E, San-Fabián J, Guilleme J, Altona C, Donders LA. Vicinal proton–proton coupling constants. I. Formulation of an equation including interactions between substituents. Molec Phys. 1989;68:49–63. [Google Scholar]
- 59.Guilleme J, San-Fabián J, Díez E, Bermejo F, Esteban AL. Vicinal proton–proton coupling constants. II: Analysis of the effect of interaction between geminal substituents upon vicinal couplings to methyl groups. Molec Phys. 1989;68:65–85. [Google Scholar]
- 60.Guilleme J, San-Fabián J, Casanueva J, Díez E. Vicinal proton–proton coupling constants: MCSCF ab initio calculations of ethane. Chem Phys Lett. 1999;314:168–175. [Google Scholar]
- 61.Stenutz R, Carmichael I, Widmalm G, Serianni AS. Hydroxymethyl group conformation in saccharides: Structural dependencies of 2JHH, 3JHH,and 1JCH spin–spin coupling constants. J Org Chem. 2002;67:949–958. doi: 10.1021/jo010985i. [DOI] [PubMed] [Google Scholar]
- 62.Tafazzoli M, Ghiasi M. New Karplus equations for 2JHH, 3JHH, 2JCH, 3JCH, 3JCOCH, 3JCSCH,and 3JCCCH in some aldohexopyranoside derivatives as determined using NMR spectroscopy and density functional theory calculations. Carbohydr Res. 2007;342:2086–2096. doi: 10.1016/j.carres.2007.05.032. [DOI] [PubMed] [Google Scholar]
- 63.Barfield M, Karplus M. Valence-bond bond-order formulation for contact nuclear spin–spin coupling. J Am Chem Soc. 1969;91:1–10. [Google Scholar]
- 64.Coxon B. Conformations and proton coupling constants in some methyl 4,6-O-benzylidene-α-D-hexopyranosides. Tetrahedron. 1965;21:3481–3503. [Google Scholar]
- 65.Coxon B. Deuterium isotope effects in carbohydrates revisited. Cryoprobe studies of the anomerization and NH to ND deuterium isotope induced 13C NMR chemical shifts of acetamidodeoxy and aminodeoxy sugars. Carbohydr Res. 2005;340:1714–1721. doi: 10.1016/j.carres.2005.04.022. [DOI] [PubMed] [Google Scholar]
- 66.Coxon B. A Karplus equation for 3JHCCN in amino sugar derivatives. Carbohydr Res. 2007;342:1044–1054. doi: 10.1016/j.carres.2007.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bystrov VF, Ivanov VT, Portnova SL, Balashova TL, Ovchinnikov YA. Refinement of the angular dependence of the peptide vicinal NH-C(alpha)H coupling constant. Tetrahedron. 1973;29:873–877. [Google Scholar]
- 68.Almond A, Brass A, Sheehan JK. Dynamic exchange between stabilized conformations predicted for hyaluronan tetrasaccharides: Comparison of molecular dynamics simulations with available NMR data. Glycobiology. 1998;8:973–980. doi: 10.1093/glycob/8.10.973. [DOI] [PubMed] [Google Scholar]
- 69.Mobli M, Almond A. N-Acetylated amino sugars: The dependence of NMR 3J(HNH2)-couplings on conformation, dynamics, and solvent. Org Biomol Chem. 2007;5:2243–2251. doi: 10.1039/b705761j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fraser RR, Kaufman M, Morand P, Govil G. Stereochemical dependence of vicinal H–C–O–H coupling constants. Can J Chem. 1969;47:403–409. [Google Scholar]
- 71.Poppe L, van Halbeek H. Nuclear magnetic resonance of hydroxyl and amido protons of oligosaccharides in aqueous solution. Evidence for a strong intramolecular hydrogen bond in sialic acid residues. J Am Chem Soc. 1991;113:363–365. [Google Scholar]
- 72.Poppe L, van Halbeek H. NMR spectroscopy of hydroxyl protons in supercooled carbohydrates. Nature Struct Biol. 1994;1:215–216. doi: 10.1038/nsb0494-215. [DOI] [PubMed] [Google Scholar]
- 73.van Halbeek H. NMR developments in structural studies of carbohydrates and their complexes. Curr Opin Struct Biol. 1994;4:697–709. [Google Scholar]
- 74.Coxon B. Boat conformations: Synthesis, NMR spectroscopy, and molecular modeling of methyl 2,6-anhydro-3-deoxy-3-phthalimido-α-D-mannopyranoside and its 15N-labeled analog. Carbohydr Res. 1999;322:120–127. [Google Scholar]
- 75.Zhao H, Pan Q, Zhang W, Carmichael I, Serianni AS. DFT and NMR studies of 2JCOH, 3JHCOH, and 3JCCOH spin-couplings in saccharides: C–O torsional bias H-bonding in aqueous solution. J Org Chem. 2007;72:7071–7082. doi: 10.1021/jo0619884. [DOI] [PubMed] [Google Scholar]
- 76.Carleer R, Anteunis MJO. Angular dependence of the vicinal interproton spin–spin coupling in silacyclohexanes. The conformational energy term of the methyl group in 1-methyl-1-silacyclohexane. Org Magn Reson. 1979;12:673–678. [Google Scholar]
- 77.Lemieux RU, Nagabhushan TL, Paul B. Relationship of 13C to vicinal 1H coupling to the torsion angle in uridine and related structures. Can J Chem. 1972;50:773–776. [Google Scholar]
- 78.Hamer GK, Balza F, Cyr N, Perlin AS. A conformational study of methyl β-cellobioside-d8 by 13C nuclear magnetic resonance spectroscopy: Dihedral angle dependence of 3JC-H in 13C–O–C–1H arrays. Can J Chem. 1978;56:3109–3116. [Google Scholar]
- 79.Coxon B. Carbon-13 Nuclear magnetic resonance spectroscopy of food-related disaccharides and trisaccharides. In: Lee CK, editor. Developments in Food Carbohydrate-2. Applied Science Publishers Ltd; Barking, Essex, England: 1980. pp. 351–390. [Google Scholar]
- 80.Tvaroška I, Václavík L. Stereochemistry of nonreducing disaccharides in solution. Carbohydr Res. 1987;160:137–149. [Google Scholar]
- 81.Tvaroška I, Hricovíni M, Petráková E. An attempt to derive a new Karplus-type equation of vicinal proton–carbon coupling constants for C–O–C–H segments of bonded atoms. Carbohydr Res. 1989;189:359–362. [Google Scholar]
- 82.Mulloy B, Frenkiel TA, Davies DB. Long-range carbon–proton coupling constants. Application of conformational studies of oligosaccharides. Carbohydr Res. 1988;184:39–46. doi: 10.1016/0008-6215(88)80004-1. [DOI] [PubMed] [Google Scholar]
- 83.Tvaroška I. Dependence on saccharide conformation of the one-bond and three-bond carbon–proton coupling constants. Carbohydr Res. 1990;206:55–64. [Google Scholar]
- 84.Cloran F, Carmichael I, Serianni AS. DFT calculations on disaccharide models: Studies of molecular geometries and trans-O-glycoside 3JCOCH and 3JCOCC spin-couplings. J Am Chem Soc. 1999;121:9843–9851. [Google Scholar]
- 85.Pozsgay V, Sari N, Coxon B. Measurement of interglycosidic 3JCH coupling constants of selectively 13C-labeled oligosaccharides by 2D J-resolved 1H NMR spectroscopy. Carbohydr Res. 1998;208:229–238. doi: 10.1016/s0008-6215(98)00047-0. [DOI] [PubMed] [Google Scholar]
- 86.Höög C, Widmalm G. Conformational flexibility of the disaccharide α-D-Manp-(1→3)-β-D-Glcp-OMe employing molecular dynamics simulations and trans-glycosidic 3JC,H from NMR experiment. J Phys Chem. 2000;104:9443–9447. [Google Scholar]
- 87.Nishida T, Widmalm G, Sandor P. Hadamard long-range proton–carbon coupling constant measurements with band-selective proton decoupling. Magn Reson Chem. 1995;33:596–599. [Google Scholar]
- 88.Rundlöf T, Kjellberg A, Damberg C, Nishida T, Widmalm G. Magn Reson Chem. 1998;36:839–847. [Google Scholar]
- 89.Cheetham NWH, Dasgupta P, Ball GE. NMR and modelling studies of disaccharide conformation. Carbohydr Res. 2003;338:955–962. doi: 10.1016/s0008-6215(03)00069-7. [DOI] [PubMed] [Google Scholar]
- 90.Houseknecht JB, Lowary TL, Hadad CM. Improved Karplus equations for 3JC1,H4 in aldopentofuranosides: Application to the conformational preferences of the methyl aldopentofuranosides. J Phys Chem. 2003;107:372–378. [Google Scholar]
- 91.Bock K, Pedersen CM. Two- and three-bond 13C–1H couplings in some carbohydrates. Acta Chem Scand B. 1977;31:354–358. [Google Scholar]
- 92.Aydin R, Günther H. 13C,1H spin–spin coupling. X.-Norbornane: A reinvestigation of the Karplus curve for 3J(13C,1H) Magn Reson Chem. 1990;28:448–457. [Google Scholar]
- 93.Koch HJ, Perlin AS. Synthesis and 13C NMR spectroscopy of D-glucose-3-d. Bond-polarization differences between the anomers of D-glucose. Carbohydr Res. 1970;15:403–410. [Google Scholar]
- 94.Tvaroška I, Gajdoŝ J. Angular dependence of vicinal carbon–proton coupling constants for conformational studies of the hydroxymethyl group in carbohydrates. Carbohydr Res. 1995;271:151–162. [Google Scholar]
- 95.Taravel FR, Durier V, Gouvion C, Mazeau K, Tvaroška I. Conformational analysis of carbohydrates inferred from carbon–proton coupling constants. J Chim Phys. 1994;91:798–805. [Google Scholar]
- 96.Tvaroška I, Mazeau K, Blanc-Muesser M, Lavaitte S, Driguez H, Taravel FR. Karplus-type equation for vicinal carbon–proton coupling constants for the C–S–C–H pathway in 1-thioglycosides. Carbohydr Res. 1992;229:225–231. [Google Scholar]
- 97.Carmichael I, Chipman DM, Podlasek CA, Serianni AS. Torsional effects on the one-bond 13C–13C spin coupling constant in ethylene glycol: Insights into the behavior of 1JCC in carbohydrates. J Am Chem Soc. 1993;115:10863–10870. [Google Scholar]
- 98.Batta G, Kövér KE. Heteronuclear coupling constants of hydroxyl protons in a water solution of oligosaccharides: Trehalose and sucrose. Carbohydr Res. 1999;320:267–272. [Google Scholar]
- 99.Williamson RT, Márquez BL, Gerwick WH, Kövér KE. One- and two-dimensional gradient-selected HSQMBC NMR experiments for the efficient analysis of long-range heteronuclear coupling constants. Magn Reson Chem. 2000;38:265–273. [Google Scholar]
- 100.Márquez BL, Gerwick WH, Williamson RT. Survey of NMR experiments for the determination of nJ(C,H) heteronuclear coupling constants in small molecules. Magn Reson Chem. 2001;39:499–530. [Google Scholar]
- 101.Kövér KE, Batta G, Fehér K. Accurate measurement of long-range heteronuclear coupling constants from undistorted multiplets of an enhanced CPMG-HSQMBC experiment. J Magn Reson. 2006;181:89–97. doi: 10.1016/j.jmr.2006.03.015. [DOI] [PubMed] [Google Scholar]
- 102.Coxon B, Reynolds RC. Synthesis of nitrogen-15-labeled amino sugar derivatives by addition of phthalimide-15N to a carbohydrate epoxide. Carbohydr Res. 1982;110:43–54. [Google Scholar]
- 103.Coxon B, Reynolds RC. Boat conformations. Synthesis, NMR spectroscopy, and molecular dynamics of methyl 4,6-O-benzylidene-3-deoxy-3-phthalimido-α-D-altropyranoside derivatives. Carbohydr Res. 2001;331:461–467. doi: 10.1016/s0008-6215(01)00036-2. [DOI] [PubMed] [Google Scholar]
- 104.Coxon B. unpublished. [Google Scholar]
- 105.Bystrov VF, Gavrilov YD, Solkan VN. Stereochemical dependence of the vicinal 13C′–NCα–1H and 1H–CαC′–15N proton–heteroatom coupling constants in the NMR spectra of peptides. Comparison of experimental and theoretical data. J Magn Reson. 1975;19:123–129. [Google Scholar]
- 106.Lankhorst PP, Haasnoot CAG, Erkelens C, Altona C. Carbon-13 NMR in conformational analysis of nucleic acid fragments. 2. A reparametrization of the Karplus equation for vicinal NMR coupling constants in CCOP and HCOP fragments. J Biomol Struct Dyns. 1984;1:1387–1405. doi: 10.1080/07391102.1984.10507527. [DOI] [PubMed] [Google Scholar]
- 107.Lankhorst PP, Haasnoot CAG, Erkelens C, Altona C. Carbon-13 NMR in conformational analysis of nucleic acid fragments. 3. The magnitude of torsional angle ε in d(TpA) from CCOP and HCOP coupling constants. Nucleic Acids Res. 1984;12:5419–5428. doi: 10.1093/nar/12.13.5419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Lankhorst PP, Haasnoot CAG, Erkelens C, Westerink HP, van der Marel GA, van Boom JH, Altona C. Carbon-13 NMR in conformational analysis of nucleic acid fragments. 4. The torsion angle distribution about the C3′-O3′ bond in DNA constituents. Nucleic Acids Res. 1985;13:927–942. doi: 10.1093/nar/13.3.927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Zimmer DP, Marino JP, Griesinger C. Determination of homo- and heteronuclear coupling constants in uniformly 13C,15N-labeled DNA oligonucleotides. Magn Reson Chem. 1996;34:S177–S186. [Google Scholar]
- 110.Mooren MMW, Wijmenga SS, van der Marel GA, van Boom JH, Hilbers CW. The solution structure of the circular trinucleotide cr(GpGpGp) determined by NMR and molecular mechanics calculation. Nucleic Acids Res. 1994;22:2658–2666. doi: 10.1093/nar/22.13.2658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Plavec J, Chattopadhyaya J. Reparametrization of Karplus equation relating 3JCCOP to torsion angle. Tetrahedron Lett. 1995;36:1949–1952. [Google Scholar]
- 112.Duker JM, Serianni AS. (13C)-Substituted sucrose: 13C–1H and 13C–13C spin coupling constants to assess furanose ring and glycosidic bond conformations in aqueous solution. Carbohydr Res. 1993;249:281–303. doi: 10.1016/0008-6215(93)84096-o. [DOI] [PubMed] [Google Scholar]
- 113.Zhao S, Bondo G, Zajicek J, Serianni AS. Two-bond 13C–13C spin-coupling constants in carbohydrates: New measurements of coupling signs. Carbohydr Res. 1998;309:145–152. [Google Scholar]
- 114.Church T, Carmichael I, Serianni AS. Two-bond 13C–13C spin coupling constants in carbohydrates: Effect of structure on coupling magnitude and sign. Carbohydr Res. 1996;280:177–186. [Google Scholar]
- 115.Serianni AS, Bondo PB, Zajicek J. Verification of the projection resultant method for two-bond 13C–13C coupling sign determinations in carbohydrates. J Magn Reson, B. 1996;112:69–74. doi: 10.1006/jmrb.1996.0111. [DOI] [PubMed] [Google Scholar]
- 116.Xu Q, Bush CA. Measurement of long-range carbon–carbon coupling constants in a uniformly enriched complex polysaccharide. Carbohydr Res. 1998;306:335–339. doi: 10.1016/s0008-6215(97)10099-4. [DOI] [PubMed] [Google Scholar]
- 117.Xu Q, Bush CA. Molecular modeling of the flexible cell wall polysaccharide of Streptococcus mitis J22 on the basis of heteronuclear NMR coupling constants. Biochemistry. 1996;35:14521–14529. doi: 10.1021/bi961262+. [DOI] [PubMed] [Google Scholar]
- 118.Bax A, Max D, Zax D. Measurement of long-range 13C–13C J couplings in a 20-kDa protein–peptide complex. J Am Chem Soc. 1992;114:6923–6925. [Google Scholar]
- 119.King-Morris MJ, Serianni AS. 13C NMR studies of [1-13C]aldoses: Empirical rules correlating pyranose ring configuration and conformation with 13C chemical shifts and 13C–13C spin couplings. J Am Chem Soc. 1987;109:3501–3508. [Google Scholar]
- 120.Wu J, Bondo PB, Vuorinen T, Serianni AS. 13C–13C Spin coupling constants in aldoses enriched with 13C at the terminal hydroxymethyl carbon: Effect of coupling pathway structure on JCC in carbohydrates. J Am Chem Soc. 1992;114:3499–3505. [Google Scholar]
- 121.Milton MJ, Harris R, Probert MA, Field RA, Homans SW. New conformational constraints in isotopically (13C) enriched oligosaccharides. Glycobiology. 1998;8:147–153. doi: 10.1093/glycob/8.2.147. [DOI] [PubMed] [Google Scholar]
- 122.Bose B, Zhao S, Stenutz R, Cloran F, Bondo PB, Bondo G, Hertz B, Carmichael I, Serianni AS. Three-bond C–O–C–C spin-coupling constants in carbohydrates: Development of a Karplus relationship. J Am Chem Soc. 1998;120:11158–11173. [Google Scholar]
- 123.Marshall JL, Conn SA, Barfield M. Vicinal 13C–13C spin-spin coupling constants of 1-butanols. Org Magn Reson. 1977;9:404–407. [Google Scholar]
- 124.Marshall JL. Methods in Stereochemical Analysis. Vol. 2. Verlag Chemie International; Deerfield Beach, FL: 1983. Carbon–carbon and carbon–proton NMR couplings. Applications to organic stereochemistry and conformational analysis. [Google Scholar]
- 125.Zhao H, Carmichael I, Serianni AS. Oligosaccharide trans-glycoside 3JCCOC Karplus curves are not equivalent: Effect of internal electronegative substituents. J Org Chem. 2008;73:3255–3257. doi: 10.1021/jo702288h. [DOI] [PubMed] [Google Scholar]
- 126.Doddrell D, Burfitt I, Grutzner JB, Barfield M. Experimental and theoretical studies of vicinal 13C–13C coupling oonstants. J Am Chem Soc. 1974;96:1241–1243. [Google Scholar]
- 127.Barfield M, Burfitt I, Doddrell D. Conformational and substituent dependencies of 13C–13C coupling constants. J Am Chem Soc. 1975;97:2631–2634. [Google Scholar]
- 128.Barfield M, Conn SA, Marshall JL, Miiller DE. Experimental and theoretical studies of the conformational and substituent dependencies of vicinal 13C–13C coupling constants. Impinging multiple rear-lobe effects. J Am Chem Soc. 1976;98:6253–6260. [Google Scholar]
- 129.Barfield M, Marshall JL, Canada ED, Willcott MR., III γ-Methyl substituent effect on vicinal coupling constants involving carbon-13. J Am Chem Soc. 1978;100:7075–7077. [Google Scholar]
- 130.Marshall JL, Faehl LG, Kattner R. The additivity of NMR carbon–carbon spin–spin coupling constants. Org Magn Reson. 1979;12:163–168. [Google Scholar]
- 131.Wray V. An INDO MO study of substituent effects upon 3JCC. J Am Chem Soc. 1978;100:768–770. [Google Scholar]
- 132.Berger S. The conformational dependence of vicinal 13C13C spin–spin coupling constants in alicyclic compounds. Org Magn Reson. 1980;14:65–68. [Google Scholar]
- 133.Denisov AY, Tkachev AV, Mamatyuk VI. Vicinal 13C–13C coupling constants in bicyclic monoterpenes. Magn Reson Chem. 1992;30:95–100. [Google Scholar]
- 134.Thibaudeau C, Stenutz R, Hertz B, Klepach T, Zhao S, Wu Q, Carmichael I, Serianni AS. Correlated C–C and C–O bond conformations in saccharide hydroxymethyl groups: Parametrization and application of redundant 1H–1H, 13C–1H, and 13C–13C NMR J-couplings. J Am Chem Soc. 2004;126:15668–15685. doi: 10.1021/ja0306718. [DOI] [PubMed] [Google Scholar]
- 135.Hall LD, Jones DL. Observations on the electronegativity dependence of vicinal 19F-1H coupling constants. Can J Chem. 1973;51:2925–2929. [Google Scholar]
- 136.Hamman S, Béguin C, Charlon C, Luu-Duc C. Conformational studies on 2-fluoro-1, 2-disubstituted ethanes by NMR spectroscopy. Influence of electronegativity on vicinal proton–proton and fluorine–proton coupling constants. Org Magn Reson. 1983;21:361–366. [Google Scholar]
- 137.Thibaudeau C, Plavec J, Chattopadhyaya J. A new generalized Karplus-type equation relating vicinal proton–fluorine coupling constants to H–C–C–F torsion angles. J Org Chem. 1998;63:4967–4984. [Google Scholar]
- 138.Hammer CF, Chandrasegaran S. Determination of 3JHF and 4JHF Karplus relationships for the ϕ and ψ angles of peptides using N-fluoroamides as models. J Am Chem Soc. 1984;106:1543–1552. [Google Scholar]
- 139.Bock K, Pedersen CM. A study of 13C–19F coupling constants in glycosyl fluorides. Acta Chem Scand B. 1975;29:682–686. [Google Scholar]
- 140.Michalik M, Hein M, Frank M. NMR spectra of fluorinated carbohydrates. Carbohydr Res. 2000;327:185–218. doi: 10.1016/s0008-6215(99)00323-7. [DOI] [PubMed] [Google Scholar]
- 141.Hall LD, Johnson RN, Adamson J, Foster AB. Observations on the angular dependence of vicinal 19F–19F coupling constants. Chem Commun. 1970:463–464. [Google Scholar]
- 142.Kurtkaya S, Barone V, Peralta JE, Contreras RH, Snyder JP. On the capriciousness of the FCCF Karplus curve. J Am Chem Soc. 2002;124:9702–9703. doi: 10.1021/ja0269136. [DOI] [PubMed] [Google Scholar]
- 143.San Fabián J, Westra Hoekzema AJA. Vicinal fluorine–fluorine coupling constants: Fourier analysis. J Chem Phys. 2004;121:6268–6276. doi: 10.1063/1.1785141. [DOI] [PubMed] [Google Scholar]
- 144.Doddrell D, Burfitt I, Kitching W, Bullpitt M, Lee C-H, Mynott RJ, Considine JL, Kuivila HG, Sarma RH. Karplus-type dependence of vicinal 119Sn–13C coupling. J Am Chem Soc. 1974;96:1640–1642. [Google Scholar]
- 145.Sternhell S. Correlation of interproton spin–spin coupling constants with structure. Quart Rev. 1969;23:236–270. [Google Scholar]
- 146.Hall LD, Hough L. Proton magnetic resonance spectra of 2,3,4-tri-O-acetyl-1,6-anhydro-D-hexopyranoses: A long-range coupling. Proc Chem Soc. 1962:382. [Google Scholar]
- 147.Coxon B, Hall LD. The conformations of cyclic compounds in solution-II. Some 1,2-O-alkylidene-pyranose derivatives. Tetrahedron. 1964;20:1685–1694. [Google Scholar]
- 148.Heitmann JA, Richards GF, Schroeder LR. Carbohydrate orthoesters. III. The crystal and molecular structure of 3,4,6-tri-O-acetyl-1,2-O-[1-(exo-ethoxy)ethylidene]-α-D-glucopyranose. Acta Cryst. 1974;B30:2322–2328. [Google Scholar]
- 149.Ito T. Synthesis and nuclear magnetic resonance spectrum of 3′,4′,6′-tri-O-acetyl-2-(methylthio)-D-glucopyrano[2′,1′:4,5]-2-thiazoline. Can J Chem. 1966;44:94–97. [Google Scholar]
- 150.Barfield M. Angular dependence of long-range proton coupling constants across four bonds. J Chem Phys. 1964;41:3825–3832. [Google Scholar]
- 151.Coxon B. Model parameters for the analysis of skew conformations of carbohydrates by PMR spectroscopy. Carbohydr Res. 1970;13:321–330. [Google Scholar]
- 152.Hall LD, Manville JF. Studies of carbohydrate derivatives by nuclear magnetic double-resonance. Part II. A determination of the signs of proton–proton coupling-constants of saturated and unsaturated carbohydrates. Carbohydr Res. 1968;8:295–307. [Google Scholar]
- 153.Bystrov VF, Stepanyants AU. The stereochemical significance of the long-range proton spin coupling constant of the σ-fragment H–C–C–C–H. J Mol Spectrosc. 1966;21:241–248. [Google Scholar]
- 154.Barfield M. DFT/FPT studies of the structural dependencies of long-range 1H,1H coupling over four bonds 4J(H,H′) in propanic and allylic systems. Magn Reson Chem. 2003;41:344–358. [Google Scholar]
- 155.Constantino MG, Lacerda V, Jr, da Silva GVJ, Tasic L, Rittner R. Principal component analysis of long-range ‘W’ coupling constants of some cyclic compounds. J Mol Struct. 2001;597:129–136. [Google Scholar]
- 156.Ramey KC, Messick J. Stereospecific long range couplings in the NMR spectra of substituted 1,3-dioxanes. Tetrahedron Lett. 1965:4423–4428. [Google Scholar]
- 157.Larsson EA, Ulicny J, Laaksonen A, Widmalm G. Analysis of NMR J couplings in partially protected galactopyranosides. Org Lett. 2002;4:1831–1834. doi: 10.1021/ol0200347. [DOI] [PubMed] [Google Scholar]
- 158.Kwon O, Danishefsky SJ. Synthesis of asialo GM1. New insights in the application of sulfonamidoglycosylation in oligosaccharide assembly: Subtle proximity effects in the stereochemical governance of glycosylation. J Am Chem Soc. 1998;120:1588–1599. [Google Scholar]
- 159.Jochims JC, Taigel G, Meyer zu Reckendorf W. Fernkopplungen bei glucopyranosen in der 1-C-konformation. Tetrahedron Lett. 1967:3227–3234. [Google Scholar]
- 160.Coxon B, Jennings HJ, McLauchlan KA. Structures and conformations of some D-glycero-pent-2-enopyranosyl derivatives and determination of the relative signs of some associated long-range proton coupling constants. Tetrahedron. 1967;23:2395–2412. [Google Scholar]
- 161.Barfield M, Spear RJ, Sternhell S. Interproton spin–spin coupling across a dual path in five-membered rings. J Am Chem Soc. 1971;93:5322–5327. [Google Scholar]
- 162.Barfield M, Sternhell S. Conformational dependence of homoallylic H–H coupling constants. J Am Chem Soc. 1972;94:1905–1913. [Google Scholar]
- 163.Stenutz R. Scalar coupling constants – 3JHH Haasnoot, 3JHH calculation. http://www.stenutz.eu/conf/jhh.html.
- 164.Stenutz R. Scalar coupling constants – 3JHH Pachler, 3JHH calculation. http://www.stenutz.eu/conf/pachler.html.
- 165.Stenutz R. Scalar coupling constants, hetero- and homo-nuclear coupling constant calculation. http://www.stenutz.eu/conf/karplus.html, http://www.casper.organ.su.se/ke3690/karplus.html. The latter format does not require an active network connection, as it can be saved to the computer desktop, and run from there.
- 166.Stenutz R. Scalar coupling constantsβ-ribose. http://www.stenutz.eu/conf/rib2.html.
- 167.Stenutz R. Scalar coupling constants, β-2-deoxyribose (2-deoxy-erythro-pentose) http://www.stenutz.eu/conf/rib.html.
- 168.Stenutz R. Scalar coupling constants, coupling constants related to the ω torsion. http://www.stenutzeu/conf/hm_rscalc.html.
- 169.Stenutz R. Hydroxymethyl groups, conformation of hydroxymethyl groups determined from 3JH-5,H-6. http://www.stenutz.eu/conf/hm_bock.html.
- 170.Bock K, Duus JØ. A conformational study of hydroxymethyl groups in carbohydrates investigated by 1H NMR spectroscopy. J Carbohydr Chem. 1994;13:513–543. [Google Scholar]
- 171.Stenutz R. Hydroxymethyl groups, conformation of hydroxymethyl groups from 3JH-5,H-6. http://www.stenutz.eu/conf/hm_div.html.
- 172.Stenutz R. Chemical shifts, 13C glycosylation shifts and conformation. http://www.stenutz.eu/conf/hm_div.html.
- 173.Bock K, Brignole A, Sigurskjold BW. Conformational dependence of 13C nuclear magnetic resonance chemical shifts in oligosaccharides. JCS Perkin Trans II. 1986:1711–1713. [Google Scholar]
- 174.Atkins P, de Paula J. Living graphs, Karplus equation. http://www.oup.com/uk/orc/bin/9780199280957/01student/graphs/graphs/lg_14.14.html.
- 175.Atkins P, de Paula J. Physical Chemistry for the Life Sciences. Chapter 14. Oxford University Press; Oxford: 2005. [Google Scholar]
- 176.Navarro-Vázquez A, Cobas JC, Sardina FJ. A graphical tool for the prediction of vicinal proton–proton 3JHH coupling constants. J Chem Inf Comput Sci. 2004;44:1680–1685. doi: 10.1021/ci049913t. [DOI] [PubMed] [Google Scholar]
- 177.Cobas JC. MestReJ: A free tool for the prediction of vicinal proton–proton 3J(HH) coupling constants. doi: 10.1021/ci049913t. http://nmr-analysis.blogspot.com/2008/10/mestrej-free-tool-for-prediction-of.html (includes a link to download the program) [DOI] [PubMed]
- 178.Barfield M, Smith WB. Internal H–C–C angle dependence of vicinal 1H–1H coupling constants. J Am Chem Soc. 1992;114:1574–1581. [Google Scholar]
- 179.Smith WB, Barfield M. Predictions of 3J(HH) near 180° – Reparameterization of the sp3–sp3 equation. Magn Reson Chem. 1993;31:696–697. [Google Scholar]
- 180.Smith WB, Barfield M. Predictions of 3J(HH) near 180° – Reparameterization of the sp3–sp3 equation, erratum. Magn Reson Chem. 1996;34:740. [Google Scholar]
- 181.Padrta P, Sklenář V. Program Mulder – A tool for extracting torsion angles from NMR data. J Biomol NMR. 2002;24:339–349. doi: 10.1023/a:1021656808607. [DOI] [PubMed] [Google Scholar]
- 182.Neidig KP, Geyer M, Goerler A, Antz C, Saffrich R, Beneicke W, Kalbitzer HR. Aurelia, a program for computer aided analysis of multidimensional NMR spectra. J Biomol NMR. 1995;6:255–270. doi: 10.1007/BF00197807. [DOI] [PubMed] [Google Scholar]