Estimating Disease Prevalence Using Inverse Binomial Pooled Testing

Abstract

Monitoring populations of hosts as well as insect vectors is an important part of agricultural and public health risk assessment. In applications where pathogen prevalence is likely low, it is common to test pools of subjects for the presence of infection, rather than to test subjects individually. This technique is known as pooled (group) testing. In this paper, we revisit the problem of estimating the population prevalence p from pooled testing, but we consider applications where inverse binomial sampling is used. Our work is unlike previous research in pooled testing, which has largely assumed a binomial model. Inverse sampling is natural to implement when there is a need to report estimates early on in the data collection process and has been used in individual testing applications when disease incidence is low. We consider point and interval estimation procedures for p in this new pooled testing setting, and we use example data sets from the literature to describe and to illustrate our methods.

1. INTRODUCTION

Pooled testing, also known as group testing, arises naturally as a means of data collection in agricultural and other infectious disease applications; see, e.g., Swallow (1985), Block, Hill, and McGee (1999), Tebbs and Bilder (2004), Hepworth (2005), Katholi and Unnasch (2006), Peck (2006), and Biggerstaff (2008). The underlying premise is that individuals (e.g., insect vectors, ear notch samples, seed kernels, urine/fecal specimens, etc.) are first pooled together into groups (pools), and the groups are then tested for the presence of infection. When the infection rate is low, there is overwhelming evidence that pooled testing can confer substantial benefits when compared to testing subjects individually.

Statistical research in pooled testing has a rich history, dating back to Dorfman (1943). Since this seminal work, pooled testing has been applied to problems in blood bank screening, genetics, drug discovery, epidemiology, veterinary medicine, and other areas; see Hughes-Oliver (2006) for a review. In the estimation problem, the primary goal is to estimate p, the individual probability of infection. A large majority of research in the estimation problem has presumed a binomial model. However, other models have been used to achieve this goal, including the hypergeometric (Bhattacharyya, Karandinos, and DeFo-liart 1979), the beta binomial (Turechek and Madden 2003), and, in the related application of limiting dilution assay, the Poisson (see, e.g., Chick 1996). Bayesian and empirical Bayesian approaches have been proposed (see, e.g., Bilder and Tebbs 2005), and when individual covariate information is available, regression models for pooled response have been developed to produce covariate-adjusted estimates; see Vansteelandt, Goetghebeur, and Verstraeten (2000), Xie (2001), Huang and Tebbs (2009), and Chen, Tebbs, and Bilder (2009).

In this paper, we consider the problem of estimating disease prevalence from pooled samples collected using inverse binomial sampling (Haldane 1945). Our interest in this sampling model (applied to pooled testing) arises from Katholi and Unnasch (2006), who suggested that inverse sampling may be more appropriate when there is a need to report estimates early on in the data collection process. One can easily envision experimental situations where this would be the case, particularly if the pathogen under investigation is subject to constant surveillance and/or is very serious. Under the inverse sampling model, unlike the standard binomial, the number of positive pools n is fixed in advance, and testing is complete when the nth positive pool is observed. Because the binomial model presumes a fixed number of pools to be observed, inverse sampling may be preferred if the occurrence of one or a few positive pools triggers an immediate response; e.g., initiating appropriate disease intervention efforts. In addition, in emergency situations such as natural disasters, there would naturally be a need to quickly measure the amount of risk and to eliminate the spread of infection (Foppa et al. 2007). We now discuss two situations where our methods are potentially applicable.

1.1. West Nile Virus

West Nile Virus (WNV) is an arthropod-borne pathogen transmitted predominantly by mosquito vectors and is the leading cause of arboviral encephalitis in the United States. In 2002, there were about 3,500 documented cases of WNV in humans, resulting in 200 fatalities in the US (Solomon et al. 2003). WNV detection becomes critical after natural disasters, such as hurricanes and floods, due to a potential increase in the mosquito population. For this and other viral diseases vectored by mosquitos, surveillance is an important part of public health risk assessment and rapid detection is critical (Lanciotti and Kerst 2001).

1.2. Foot and Mouth Disease

Foot and mouth disease (FMD) has been described as one of the most economically important diseases (Callahan et al. 2002) because of the devastating effects an outbreak can have on the meat and milk industry. It has also been suggested that FMD could be used as a biological weapon (Zilinskas 1997; Koda 2002). FMD is extremely contagious, and although vaccinations do exist, it is common to slaughter all animals on or near infected premises if the outbreak is severe. In 2001, an outbreak occurred in Essex County, England, which led to the slaughter of six million animals, mostly cattle, sheep, and pigs (Bush et al. 2005). After this disaster, there was major incentive to develop assays to screen for FMD rapidly and reliably (Reid et al. 2002). Early detection of infection could limit the severity of an outbreak, and countermeasures could be taken to prevent further infection.

1.3. Assumptions and Related Work

We assume that individual statuses are independent and identically distributed Bernoulli random variables with mean p and that tests are performed on pools of individuals until the nth positive pool is found. Also, we assume that the testing process is perfect (i.e., pools are not misclassified). This may be reasonable for applications in arbovirus surveillance and FMD detection with assays based on nucleic acid technology (NAT). Investigators have shown empirically that NATs are extremely sensitive and specific (Lanciotti and Kerst 2001; Reid et al. 2002; Callahan et al. 2002). For imperfect testing, one could modify our methods in a manner similar to that of Tu, Litvak, and Pagano (1995) in the binomial model.

Katholi (2006) considered the negative binomial model for pooled testing estimation but examined the maximum likelihood estimator (MLE) only in the equal pool size case. In our survey of the arbovirus literature, for example, we found that pools are often of unequal size. We thus relax this assumption and treat equal pool sizes (which gives rise to the negative binomial model) as a special case. When equal sized pools are used, we also present alternative estimators that are shown to be far superior to the MLE. We examine interval estimation for p, and we use a WNV data example from the literature to illustrate the potential use of our methods.

2. POINT ESTIMATION

2.1. Maximum Likelihood

Suppose that Y = y pools are tested until the first positive is observed; i.e., n = 1. For j = 1, 2, …, y, we let s_j denote the fixed pool size for the j th pool. The probability that pool j is positive is 1 − (1 − p)^s_j so that the log-likelihood is

$$l(p\mid y)=log\{1-{(1-p)}^{s_y}\}+\sum _{j=1}^{y-1}{s}_{j}log(1-p).$$

A closed-form expression for the MLE exists and is given by

$$\widehat{p}=1-{\left(\frac{s_{+}}{s_y+s_{+}}\right)}^{1/s_y},$$ (2.1)

where $s_{+}={\sum }_{j=1}^{y-1}{s}_j$. When the pool sizes are equal, i.e., when s_j = s for all j, Y follows a geometric distribution with success probability θ = 1 − (1 − p)^s, and (2.1) reduces to

$$\widehat{p}=1-{\left(1-\frac{1}{Y}\right)}^{1/s}.$$

Now suppose that testing continues until the nth positive pool is found, where n > 1. In this case, we can envision the observed data as Y₁, Y₂, …, Y_n, where Y_i plays the role of Y above. For i = 1, 2, …, n and for j = 1, 2, …, y_i, let s_ij denote the size for the j th pool in the sequence of pools tested to obtain the ith observation Y_i so that s_iyi denotes the size of the ith positive pool. The log-likelihood is

$$l(p\mid \mathbf{y})=\sum _{i=1}^n\left[log\{1-{(1-p)}^{s_{{iy}_i}}\}+\sum _{j=1}^{y_i-1}{s}_{ij}log(1-p)\right],$$

where y = (y₁, y₂, …, y_n), and the score function, obtained through differentiation, is

$$S(p\mid \mathbf{y})=\frac{\partial l(p\mid \mathbf{y})}{\partial p}=\sum _{i=1}^n\frac{s_{{iy}_i}{(1-p)}^{s_{{iy}_i}-1}}{1-{(1-p)}^{s_{{iy}_i}}}-\sum _{i=1}^n\sum _{j=1}^{y_i-1}\frac{s_{ij}}{1-p}.$$ (2.2)

The MLE for p, p̂, is the solution to S(p|y) = 0 and must be obtained iteratively, except when pools are of equal size, say s, in which case the MLE reduces to

$$\widehat{p}=1-{\left(1-\frac{n}{T}\right)}^{1/s},$$ (2.3)

where $T={\sum }_{i=1}^n{Y}_i$. In the equal pool size case, T follows a negative binomial distribution with waiting parameter n and success probability θ = 1 − (1 − p)^s; i.e., T ~ nib(n, θ). The estimator in (2.3) is the only (non-Bayesian) estimator considered by Katholi (2006). In the equal pool size case, Jensen’s Inequality can be used to show that E(p̂) > p; i.e., p̂ is positively biased. However, p̂ enjoys the usual large sample properties of MLEs, specifically, consistency and asymptotic normality.

We have performed simulation studies to assess the point estimate properties of p̂ using equal and unequal pool sizes for small n. Because of limitations on space, we do not present the results. However, it suffices to mention that the MLE p̂ is severely biased upwards, especially if n is small. 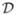For example, when n = 5, p = 0.10, and s_ij are sampled from a discrete uniform distribution from 5 to 15, 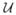(5, 15), the positive bias in p̂ is approximately 0.10 and the mean squared error (MSE) is approximately 0.08! Our simulations suggest that the bias and MSE do converge to 0 as n → ∞, as expected, but at a very slow rate, much too slow for the MLE to be used in application. This motivates us to find improved small sample estimators.

2.2. Alternative Estimators Using Equal Sized Pools

In the binomial model, the MLE for p is also positively biased (see, e.g., Swallow 1985). This has prompted a large literature on ways to reduce the bias; see Hepworth and Watson (2009) for an excellent review. In the negative binomial model, however, the number of pools observed is not fixed; rather, the number of observed positive pools is fixed. From a practical point of view, this complicates things significantly. For example, depending on the level of infection (and the pool size), thousands of pools may be needed to observe, say, n = 2 or 3 positives. In other words, in situations where inverse binomial pooled testing might be used, n may not be large enough for asymptotic considerations to apply. This makes Taylor series expansions, commonly used in the binomial problem to reduce bias (Burrows 1987), somewhat vacuous. This notwithstanding, our desire to reduce the bias in p̂ has led us to examine four alternative estimators when equal group sizes are used. Each estimator is motivated by the work of Colón, Patil, and Taillie (2001), who examined alternative pooled testing estimators in the binomial case.

Because p̂= 1 − {1 − (n/T)}^1/s is positively biased, one way to reduce the bias is to shrink the fraction of positive pools n/T towards 0. We define the “shrinkage” estimator by

$${\widehat{p}}_{\alpha }=1-{\left\{1-\alpha \left(\frac{n}{T}\right)\right\}}^{1/s},$$

where 0 < α ≤ 1. Instead of using a multiplicative constant, one can also shrink n/T by adding a positive constant to T in the denominator. We define the “shift” estimator by

$${\widehat{p}}_{\beta }=1-{\left(1-\frac{n+1}{T+\beta }\right)}^{1/s},$$

where β ≥ 1. Using n + 1 in the numerator of p̂_β is motivated by a Bayesian approach described in the Ph.D. dissertation of N. Pritchard. Briefly, an estimator similar to p̂_β arises from using a beta(1, ξ) prior on p and a squared-error loss function on θ = 1 − (1 − p)^s, the probability of observing a positive pool. By combining the attributes of the shrinkage and shift estimators, we also investigated a “combined” estimator

$${\widehat{p}}_C=1-{\left\{1-{\alpha }_C\left(\frac{n+1}{T+{\beta }_C}\right)\right\}}^{1/s},$$

where 0 < α_C ≤ 1 and β_C ≥ 1. Choosing α, β, α_C, and β_C has yet to be discussed. Finally, we also examined the jackknife estimator

$${\widehat{p}}_J=\frac{1}{n}\sum _{i=1}^n\{n\widehat{p}-(n-1){\widehat{p}}_{(i)}\},$$

where p̂_(i) is the MLE of p when Y_i is omitted. When n = 1, p̂_J simplifies to the MLE.

2.3. Comparisons

We compare the four alternative estimators and the MLE in the equal pool size case. Because T ~ nib(n, θ), where θ = 1 − (1 − p)^s, the exact bias and MSE of a generic estimator p̃ can be expressed as an infinite sum. Because these sums do not reduce to anything tractable, we tried to approximate the bias and MSE using asymptotic expansions similarly to Colón, Patil, and Taillie (2001) in the binomial case. Unfortunately, this approach was not successful for the reasons mentioned in Section 2.2. We therefore approximate the bias and MSE of an estimator p̃ by

$$B(\stackrel{\sim }{p})\approx \sum _{t=n}^{t^{\ast }}(\stackrel{\sim }{p}-p)\left(\begin{array}{c}t-1\\ n-1\end{array}\right){\{1-{(1-p)}^s\}}^n{(1-p)}^{s(t-n)}$$

and

$$\text{MSE}(\stackrel{\sim }{p})\approx \sum _{t=n}^{t^{\ast }}{(\stackrel{\sim }{p}-p)}^2\left(\begin{array}{c}t-1\\ n-1\end{array}\right){\{1-{(1-p)}^s\}}^n{(1-p)}^{s(t-n)},$$

respectively, where pr(T ≤ t*) ≥ 1 − ν for ν small. We take ν = 0.000001 throughout, making these approximations very close to the true values of bias and MSE.

To use the alternative estimators, one must specify the additional values of α, β, α_C, and β_C. For p̂_α, we define

$${\alpha }^{\ast }=arg\underset{0<\alpha \le 1}{min}\text{MSE}({\widehat{p}}_{\alpha };p),$$

the value of α that minimizes MSE(p̂_α) for fixed n, s, and p, and we call this the “optimal” choice of α. Optimal values β^* and ( ${\alpha }_C^{\ast },{\beta }_C^{\ast }$) are defined similarly for p̂_β and p̂_C, respectively. Of course, by this definition, optimal selection is not possible in application since each depends on the unknown p. We discuss this momentarily.

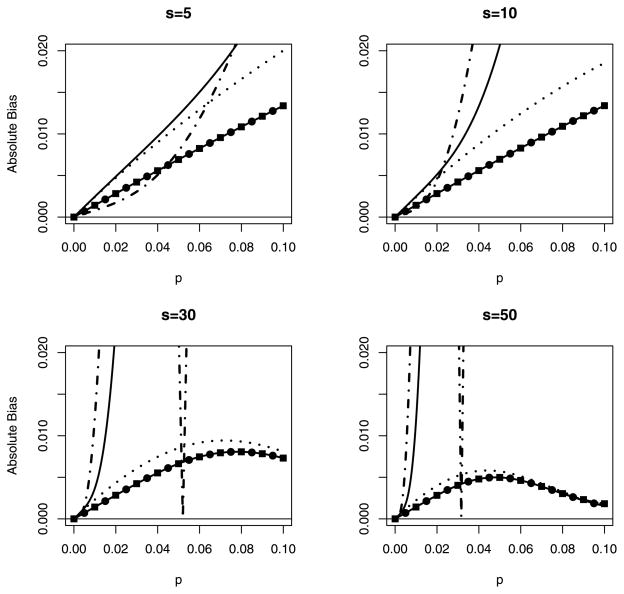
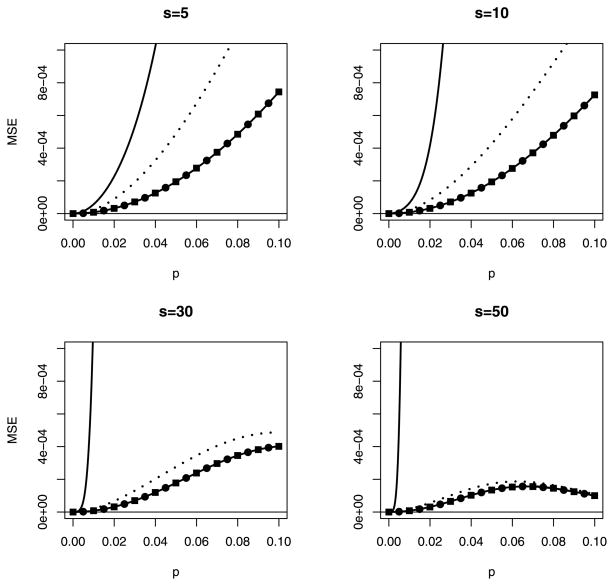
Figures 1 and 2 display the absolute bias and MSE of the five estimators, respectively, when n = 5 for pool sizes s = 5, 10, 30, and 50. For p̂_α, p̂_β, and p̂_C, optimal choices of α, β, α_C, and β_C are used. We use absolute bias in Figure 1 for cosmetic reasons only; otherwise, it is difficult to display the results. It should suffice to note that the MLE p̂ is the only estimator that is always positively biased, the jackknife estimator p̂_J is negatively biased for small p, and p̂_α, p̂_β, and p̂_C are always negatively biased. For the settings in Figs. 1 and 2, ${\alpha }_C^{\ast }\approx 1$ and ${\beta }_C^{\ast }\approx {\beta }^{\ast }$ for most values of p, making it difficult to distinguish p̂_β from p̂_C. Overall, the adjusted estimators p̂_α, p̂_β, and p̂_C are clearly better choices, and the latter two are favored slightly. The jackknife estimator is not shown in Figure 2, because its absolute bias, shown in Figure 1, renders it impractical for use.

Figure 1.

Absolute bias for p̂ (—), p̂_α (···), p̂_β (—●—), p̂_C (—■—), and p̂_J (–·–) for different pool sizes s when n = 5. Optimal values of α, β, α_C, and β_C are used. B(p̂_β) and B(p̂_C) are indistinguishable.

Figure 2.

MSE for p̂ (—), p̂_α (···), p̂_β (—●—), and p̂_C (—■—) for different pool sizes s when n = 5. Optimal values of α, β, α_C, and β_C are used. MSE(p̂_β) and MSE(p̂_C) are indistinguishable. The jackknife estimator is not depicted.

A concern arises with using the alternative estimators p̂_α, p̂_β, and p̂_C because their optimal versions are not known. In practice, we recommend choosing the additional parameters α, β, α_C, and β_C to minimize MSE using an upper bound for p, say, p₀ > p. This is the same recommendation given by Swallow (1985) when choosing pool sizes in the binomial case and is not unrealistic in the applications we consider. We now illustrate with two examples.

Example 1

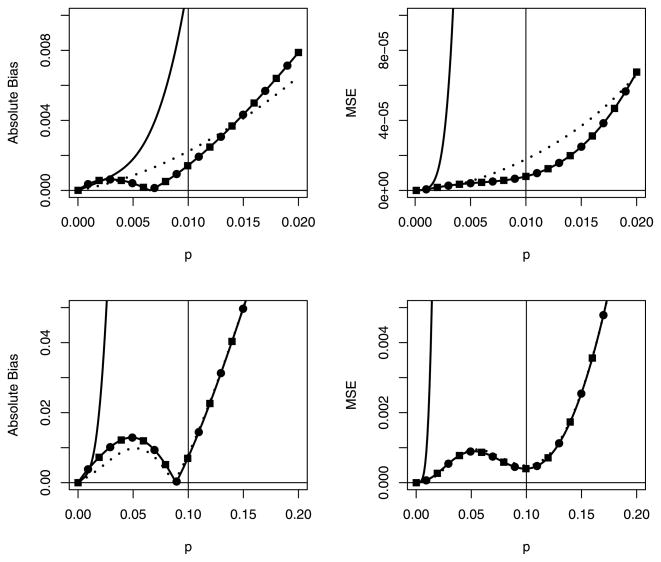
Data from two separate studies, Rutledge et al. (2003) and Godsey et al. (2005), suggest that an upper bound for the prevalence of WNV is around 0.01, and both studies use pool sizes rarely greater than 50 mosquitos. For illustration, we take n = 5, s = 50 and p₀ = 0.01, which provide α^* = 0.7050, β^* = 5.6868, ${\alpha }_C^{\ast }=1$, and ${\beta }_C^{\ast }=5.6868$. Figure 3 displays the absolute bias (top left) and MSE (top right) with a vertical line at p₀ = 0.01 in each. Two important points are to be made. First, the adjusted estimators p̂_α, p̂_β, and p̂_C, each based on the upper bound of p₀ = 0.01, outperform the MLE p̂ when p < p₀. Second, the bias and MSE of the adjusted estimators are much smaller for values of p < p₀ than the bias and MSE when p > p₀, supporting our recommendation to choose the adjusted estimators using an upper bound for p. However, the upper bound should be chosen carefully; for p > 0.01, the absolute biases of p̂_α, p̂_β, and p̂_C increase until they eventually become larger than that of the MLE (not displayed in Figure 1). That is, choosing p₀ < p could lead to adjusted estimators that are worse than the MLE.

Figure 3.

Absolute bias and MSE of p̂ (—), p̂_α (···), p̂_β (—●—), and p̂_C (—■—). Top: n = 5, s = 50, and optimal values of α, β, α_C, and β_C are based on the upper bound p₀ = 0.01. Bottom: n = 5, s = 30, and optimal values of α, β, α_C, and β_C are based on the upper bound p₀ = 0.10. In both cases, p̂_β and p̂_C are indistinguishable.

Example 2

Data from the 2001 outbreak of FMD in England suggest that the individual prevalence does not exceed 0.10 (Anderson 2002). While it has been envisioned using polymerase chain reaction assays on pools of blood or serum in FMD settings (Reid et al. 2002), pooling has not been empirically evaluated. For verisimilitude, we thus take n = 5, s = 30 and p₀ = 0.10. These choices give α^* = 0.9603, β^* = 1.2495, ${\alpha }_C^{\ast }=1$, and ${\beta }_C^{\ast }=1.2495$. Figure 3 displays the absolute bias (bottom left) and MSE (bottom right) with a vertical line at p₀ = 0.10 in each. The same discoveries are revealed; namely, the adjusted estimators are much better than the MLE when p < p₀ and choosing p₀ carefully is important to avoid estimators with high bias and MSE.

We have evaluated the performance of the MLE p̂, the jackknife estimator p̂_J, and the alternative estimators using many other settings for n, s, and p; more extensive results are available from the authors. We have consistently observed that p̂_β and p̂_C are the best choices and have nearly the same bias and MSE, except when the pool size s or the waiting parameter n is very large. In these cases, p̂_C provides the largest reduction in bias and the smallest MSE when an upper bound for p is correctly specified. As a special case, when n = 1, it is worth mentioning that the MLE is abhorrently bad and that the adjusted estimators p̂_β and p̂_C offer substantial improvements.

3. INTERVAL ESTIMATION

In this section, we derive (large sample) Wald, score, and likelihood ratio confidence intervals for p when inverse pooled testing is used. An exact interval is also presented for the equal pool size case. We focus on two-sided intervals herein; one-sided intervals are formed by making appropriate modifications.

3.1. Likelihood-Based Intervals

When n is large, the MLE p̂ is approximately normal with mean p and variance equal to I (p)⁻¹, where I (p) = E_p {−∂²l(p|y)/∂p²} is the Fisher information. When pools of equal size s are used, l(p|y) simplifies considerably (see Section 2.1) and it can be shown that

$$I(p)=\frac{{ns}^2{(1-p)}^{s-2}}{{\{1-{(1-p)}^s\}}^2}.$$

Applying the Weak Law of Large Numbers, continuity of convergence, and Slutsky’s Theorem, we have $I{(\widehat{p})}^{-1/2}(\widehat{p}-p)\stackrel{d}{\to }\mathcal{N}(0,1)$, as n → ∞, so that

$$\widehat{p}\pm z_{\gamma /2}I{(\widehat{p})}^{-1/2}$$

is an approximate 100(1 − γ) percent Wald confidence interval for p. The symbol z_γ/2 denotes the upper γ/2 quantile from the 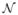(0, 1) distribution. When pools are of unequal size, the distribution of $T={\sum }_{i=1}^n{Y}_i$ is not negative binomial and I (p) is not tractable. In this case, we instead calculate the observed information (Efron and Hinkley 1978) given by

$$\begin{array}{l}J(p)=-\frac{{\partial }^{2}l(p\mid \mathbf{y})}{\partial p^2}\\ =\sum _{i=1}^n\frac{s_{{iy}_i}{(1-p)}^{s_{{iy}_i}-2}\{s_{{iy}_i}-1+{(1-p)}^{s_{{iy}_i}}\}}{{\{1-{(1-p)}^{s_{{iy}_i}}\}}^2}+\sum _{i=1}^n\sum _{j=1}^{y_i-1}\frac{s_{ij}}{{(1-p)}^2},\end{array}$$ (3.1)

and use p̂ ± z_γ/2 J (p̂)^−1/2 instead.

The score interval for p arises from the fact that the score function in (2.2), when viewed as random, is approximately normal with zero mean and variance I (p) when n is large. Thus, when pools are of equal size, the solutions to

$$\frac{S(p\mid \mathbf{y})}{\sqrt{I(p)}}=\pm z_{\gamma /2}$$

delimit an approximate 100(1 − γ) percent confidence interval. When pools are of unequal size, we replace I (p) with J (p) in (3.1). The likelihood ratio (LR) interval is based on the fact that 2 {l(p̂|y) − l(p|y)} is distributed approximately as a central ${\chi }_1^2$ random variable when n is large. Thus, the solutions to

$$2\{l(\widehat{p}\mid \mathbf{y})-l(p\mid \mathbf{y})\}=2\sum _{i=1}^n\left[log\left\{\frac{1-{(1-\widehat{p})}^{s_{{iy}_i}}}{1-{(1-p)}^{s_{{iy}_i}}}\right\}-\sum _{j=1}^{y_i-1}{s}_{ij}log\left\{\frac{1-p}{1-\widehat{p}}\right\}\right]={\chi }_{1,\gamma }^2$$

form an approximate 100(1 − γ) percent confidence interval for p, where ${\chi }_{1,\gamma }^2$ is the upper γ quantile of the ${\chi }_1^2$ distribution.

3.2. An Exact Interval

When equal pool sizes s are used, T ~ nib(n, θ), where θ = 1 − (1 − p)^s. Using the relationship between the negative binomial distribution and the incomplete beta function, Lui (1995) derived an exact interval for θ. The lower and upper confidence limits are θ_L = B_{1 − γ/2,n,t−n+1} and θ_U = B_γ/2,n,t−n, respectively, where $t={\sum }_{i=1}^n{y}_i$ and B_γ,a,b denotes the upper γ quantile of the two-parameter beta(a, b) distribution. Thus, an exact 100(1 − γ) percent confidence interval for p can be obtained by suitably transforming the endpoints of the θ interval; i.e., p_L = 1 − (1 − B_{1− γ/2,n,t−n+1})^1/s and p_U =1 − (1 − B_γ/2,n,t−n)^1/s. To the best of our knowledge, exact intervals for p are not available when pool sizes are unequal. This is in stark contrast to the binomial case, as demonstrated by Hepworth (1996).

3.3. Discussion

There are a myriad of other large sample approaches one could use for interval estimation. We did examine variance stabilized and suitably transformed logit-type intervals, used by Tebbs and Bilder (2004) and Hepworth (2005), respectively, in the binomial problem. Both, surprisingly, were not better than the Wald interval. When unequal pool sizes are used, Hepworth (2005) showed that the LR interval outperformed the standard score interval, while, in the equal pool size case, Tebbs and Bilder (2004) showed that the score interval was preferred in terms of coverage probability.

The lower limit of the Wald and score intervals can be negative when n is small and/or when p̂ is close to 0; on the other hand, LR endpoints cannot be negative. All large sample intervals have complications when p̂ = 1; i.e., every pool tests positive. In this case, I (p̂) is undefined and the Wald interval cannot be computed; additionally, when equal sized pools are used, the score function is zero, and the upper limit for the LR interval cannot be computed. Observing p̂ = 1 would not be likely in practice, unless n is small and/or the pool size is inappropriately large. However, when it does occur, we set the Wald interval equal to the uninformative (0, 1) and make similar adjustments for the score and LR intervals.

3.4. Comparisons

We first consider the equal pool size case. For each of the confidence intervals (Wald, score, LR, and exact), the true coverage probability, for a given prevalence p, waiting parameter n, and pool size s, can be approximated in the same manner as the bias and MSE were in Section 2.3. Specifically, the exact coverage probability is approximated by

$$C(p,n,s)=\sum _{t=n}^{t^{\ast }}\mathcal{I}(\widehat{p})\left(\begin{array}{c}t-1\\ n-1\end{array}\right){\{1-{(1-p)}^s\}}^n{\{{(i-p)}^s\}}^{t-n},$$

where 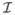(p̂) = 1 if the interval contains p, 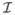(p̂) = 0 otherwise, and t^* satisfies pr(T ≤ t^*) ≥ 1 − ν, where we take ν = 0.000001. The exact mean length is approximated by using the same expression as C(p, n, s), except that D(p̂) replaces 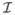(p̂), where D(p̂) represents the length of the interval for a particular realization of p̂.

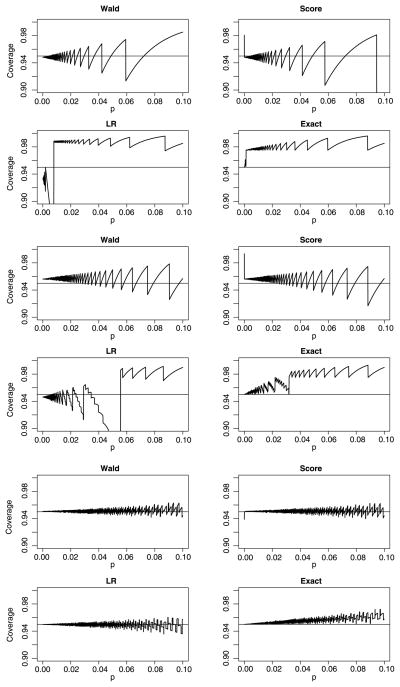
Figure 4 displays the exact coverage probabilities for the four intervals when γ = 0.05, s = 20 (common pool size), n = 1, 5, and 100, and values of p ranging from 0.00005 to 0.10 by increments of 0.00005. The distinct jagged pattern in the plots is due to the discrete nature of the negative binomial distribution. For example, if n = 1, t = 5, and s = 20, 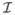(p̂) for the Wald interval switches from 1 to 0 when p becomes greater than 0.0327, which, in turn, corresponds to a drop in the coverage probability function. When n = 1, we find it unusual that the Wald and score intervals are somewhat centered around the nominal level, although the variability increases as the prevalence does. The LR interval is generally conservative as long as the prevalence is not small. The same general patterns hold for the n = 5 case, and our depiction when n = 100 is visual evidence that the asymptotic properties are taking hold.

Figure 4.

Exact coverage probability for 95 percent Wald, score, LR, and exact confidence intervals when s = 20. Top four: n = 1; Middle four: n = 5; Bottom four: n = 100. Within each block of four, the intervals are arranged as Wald (upper left), score (upper right), LR (lower left), and exact (lower right).

To accompany Figure 4, we also calculated the exact mean length for the four intervals with equal pool sizes (results available from the authors). The exact interval, not surprisingly, possesses the greatest length, but it is generally not too much larger than the large sample intervals. The latter intervals, in turn, are comparable, with the Wald interval being slightly shorter on average. We also constructed plots of the distal and mesial non-coverage probabilities corresponding to Figure 4; these plots are available from the authors. Distal (mesial) non-coverage measures the probability content for all values of y in the support producing intervals that miss p on the left (right) side. Some would argue that a desirable interval possesses symmetry in the non-coverage tails; i.e., that the distal and mesial non-coverage probabilities are approximately γ/2 (Newcombe 1998). Not surprisingly, for n = 1 and n = 5, mesial non-coverage almost exceeds distal non-coverage. In addition, for small n, it should be noted that the Wald and score lower endpoints are often negative when p is close to zero. In this situation, suitable adjustment may be warranted (e.g., use an exact interval, construct a one-sided Wald interval, etc.). When n = 100, the large sample intervals’ non-coverage is nearly perfectly symmetrical.

For unequal pool sizes, we used simulation to compare the large sample intervals for γ = 0.05 using different n and p. The results in Table 1 are based on 10,000 Monte Carlo data sets so that the margin of error (assuming a 99 percent confidence level) is 0.006. Pool sizes were generated from a discrete uniform distribution from 20 to 50, 10 to 30, and 5 to 15, for p = 0.001, p = 0.01, and p = 0.1, respectively. Perhaps most interesting is that, in terms of coverage probability, the large sample intervals are all quite good for small n, even when n = 1. The LR interval is notably conservative when n = 1, but this behavior diminishes for larger n. When n = 20, the estimated coverages for all procedures are all mostly within the margin of Monte Carlo error. The performance of the intervals is, of course, dependent on the pool size, and inappropriately large pool sizes can lead to very bad results. For example, when n = 5 and p = 0.1, using 50 ≤ s_ij ≤ 100 produced an average coverage probability of greater than 0.99 for all three methods. This is likely due to the fact that p̂ = 1 with high probability when the pool size is large (this occurs in 99.5 percent of the simulated confidence intervals for the setting just described). However, using pool sizes smaller than those seen in Table 1 does not greatly alter the procedures’ coverage properties.

Table 1.

Coverage probabilities for likelihood-based confidence intervals when pool sizes are unequal. The nominal level is 1 − γ = 0.95. Coverage probabilities are approximated based on 10,000 Monte Carlo data sets. The margin of error, assuming a 99 percent confidence level, is 0.006.

# positive pools	p	Pool sizes	Wald	Score	LR
n = 1	0.001	20 ≤ sij ≤ 50	0.951	0.948	0.967
	0.01	10 ≤ sij ≤ 30	0.950	0.951	0.990
	0.1	5 ≤ sij ≤ 15	0.951	0.957	0.988
n = 5	0.001	20 ≤ sij ≤ 50	0.956	0.956	0.945
	0.01	10 ≤ sij ≤ 30	0.959	0.960	0.946
	0.1	5 ≤ sij ≤ 15	0.958	0.958	0.982
n = 20	0.001	20 ≤ sij ≤ 50	0.950	0.951	0.953
	0.01	10 ≤ sij ≤ 30	0.950	0.954	0.948
	0.1	5 ≤ sij ≤ 15	0.951	0.957	0.949

4. APPLICATION TO WNV PREVALENCE ESTIMATION

Rutledge et al. (2003) describe a public health study involving WNV surveillance. Immediately following a 2001 outbreak in Jefferson County, Florida, researchers set out to estimate the WNV prevalence in the mosquito population. Pools of mosquitos, formed from 11,948 individuals captured, were tested for the presence of WNV using reverse-transcription polymerase chain reaction assays, which resulted in 14 WNV positive pools. Variable pool sizes were used in the study, but nearly all of the pool sizes were less than 50. The study described by the authors was the first documented field study of WNV vectored by the North American mosquito, Culex nigripalpus Theobald, which is also believed to vector the St. Louis and eastern equine encephalitis viruses. WNV had been detected in Florida in early 2001; later that year, 12 human cases of WNV meningoencephalitis had been confirmed.

Inverse sampling was not used by Rutledge et al. (2003), but we use this investigation as a basis to illustrate our methodology. The authors only presented the complete results from the pools that tested positive; based on these data, the estimated prevalence was reported to be approximately 0.005 (likely an upper bound because some negative pools were ignored). We henceforth assume that 0.005 is the true value of p and simulate data sets for waiting parameters n = 1, 5, 10, and 20, using equal and unequal pool sizes. In the unequal pool size case, the authors reported using various sizes ranging mostly from 15 to 50 mosquitos. We thus use 15 ≤ s_ij ≤ 50 when considering those methods based on unequal pool sizes; we use s = 50 in the equal pool size case.

Table 2 provides the averaged point estimates (with estimated standard errors in parentheses), based on 10,000 Monte Carlo data sets. For equal pool sizes, we present results for the MLE and the three adjusted estimators p̂_α, p̂_β, and p̂_C using p₀ = 0.01 as an upper bound. The jackknife estimator is not reported because of its poor performance. 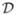The MLE from using unequal pool sizes is also reported; pool sizes s_ij were simulated from a 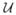(15, 50) distribution, endpoints consistent with Rutledge et al. (2003). The results from Table 2 reaffirm our discovery that the adjusted estimators in the equal pool size case are preferred, especially when n is small. For n = 1, the MLE is exorbitantly biased in both the equal and unequal pool size cases. For larger n, all (averaged) estimates are generally on target, with standard errors generally being larger for unequal pool sizes.

Table 2.

Mean prevalence estimates for WNV infection using the data from Rutledge et al. (2003). Equal pool size estimates use s = 50. Unequal pool size estimates use 15 ≤ s_ij ≤ 50. Estimates are based on 10,000 Monte Carlo data sets assuming p = 0.005. Estimated standard errors are in parentheses.

n	Equal pool sizes				Unequal pool sizes
	p̂	p̂α	p̂β	p̂C	p̂
1	0.229 (0.064)	0.005 (0.006)	0.007 (0.005)	0.007 (0.005)	0.163 (0.060)
5	0.007 (0.015)	0.004 (0.004)	0.005 (0.006)	0.005 (0.006)	0.006 (0.010)
10	0.006 (0.004)	0.005 (0.004)	0.005 (0.003)	0.005 (0.003)	0.006 (0.004)
20	0.005 (0.003)	0.005 (0.003)	0.005 (0.003)	0.005 (0.003)	0.005 (0.003)

Using the same simulated data, we computed 10,000 confidence intervals for p using the likelihood-based and exact methods from Section 3 and have reported in Table 3 the average confidence limits (lower and upper). The Wald and score intervals are the only ones that can return negative lower limits; when n = 1, 77, and 100 percent of Wald and score lower limits, respectively, were negative. The averaged upper and lower limits are not symmetrical about the average value of p̂, because we assign noninformative intervals when p̂ = 1 (e.g., about 15 percent of the data sets produced p̂ = 1 when n = 1). When this realization is not likely, we found that all interval procedures produce roughly the same averaged endpoints. Furthermore, using the actual (binomial) data reported in the article, a 95 percent logit transformed confidence interval, suggested by Hepworth (2005), was found to be (0.003, 0.009). Most of the averaged intervals in Table 3, excluding the n = 1 case, are consistent with this estimate.

Table 3.

Mean confidence interval limits for the prevalence of WNV infection using negative binomial type sampling. Equal pool size intervals use s = 50. Unequal pool size intervals use 15 ≤ s_ij ≤ 50. Lower and upper limits are averaged over 10,000 Monte Carlo confidence intervals constructed assuming p = 0.005.

n	Equal pool sizes
	W	S	LR	E
1	(−0.005, 0.239)	(−0.011, 0.239)	(0.001, 0.247)	(0.001, 0.248)
5	(0.001, 0.012)	(0.001, 0.012)	(0.002, 0.014)	(0.002, 0.014)
10	(0.002, 0.009)	(0.002, 0.009)	(0.003, 0.010)	(0.003, 0.010)
20	(0.003, 0.008)	(0.003, 0.008)	(0.003, 0.008)	(0.003, 0.008)

n	Unequal pool sizes
	W	S	LR	E
1	(−0.007, 0.177)	(0.000, 0.177)	(0.001, 0.188)	–
5	(0.001, 0.012)	(0.001, 0.012)	(0.002, 0.014)	–
10	(0.002, 0.009)	(0.002, 0.009)	(0.003, 0.010)	–
20	(0.003, 0.008)	(0.003, 0.008)	(0.003, 0.008)	–

5. DISCUSSION

We have presented a new way of viewing the usual pooled testing prevalence estimation problem, considering situations that employ inverse binomial sampling. As we have discussed, this type of data collection procedure might be reasonable when sampling and testing occurs sequentially and when positive results instigate the need for immediate analysis. The usual binomial model requires that a fixed number of pools be used. This requirement seems to be incongruous with those applications where it is potentially critical to have timely intervention. To disseminate our work, we have written user-friendly R programs to calculate all point and interval estimates in this paper; these are located at the R-Forge website http://r-forge.r-project.org/ under the name invbingroup.

It is important to note that the methods proposed herein may not be appropriate when there is a delay between the acquisition of individuals, such as mosquitos, and the actual testing of them in pools. In some research investigations, it is not uncommon for individual specimens to be stored for long periods of time before testing begins. On the other hand, an anonymous reviewer has described how mosquito testing for WNV and for other ar-boviruses occurs almost weekly in nearly every state. In addition, continuous monitoring for pathogens in livestock, such as bovine viral disease, is now a requirement to maintain healthy herds (Peck 2006). In these and related situations, our methods are applicable and may be more natural to implement because of the sequential nature of the data collection process.

Within an inverse sampling context, we have investigated point and interval estimation for p, the probability of individual infection. Future research could involve finding improved techniques in each area. For example, in the point estimation problem, Hepworth and Watson (2009) describe an iterative correction strategy to nearly remove the bias in the binomial pooled testing MLE; it may be possible to implement similar corrections in the inverse binomial problem. There may also be benefits to considering other confidence interval procedures, such as the skew-corrected score interval (Hepworth 2005) or an interval based on the mid-p correction (Hepworth 2004). The development of multiple population methods, similar to those of McCann and Tebbs (2007), Tebbs and McCann (2007), and Biggerstaff (2008) in the binomial case, would also be worthwhile extensions.

Especially when n is small, so that action is desirable early on in the data collection process, one would naturally conjecture that the development of Bayesian estimators might be a useful pursuit. Bayesian techniques could also prove to be useful in applications where there are no observed positive pools. A manuscript is currently in progress that examines these questions. We are also working on developing regression methodology, similar to that proposed by Xie (2001) in the binomial case, that can be used to incorporate covariate information on individual subjects. For example, in testing for FMD, the prevalence may be affected by animal gender, species, type of farm, and the distance from an infected premises. Early results suggest that regression estimators possess good statistical properties when the waiting parameter n is large and the prevalence is moderate.