Entropic effects in channel-facilitated transport: Inter-particle interactions break the flux symmetry

Abstract

We analyze transport through conical channels due to the difference in particle concentration on the two sides of the membrane. Because of the detailed balance, fluxes of non-interacting particles through the same channel, inserted into the membrane in two opposite orientations, are equal. We show that this flux symmetry is broken by particle-particle interactions, so that one of the orientations can be much more efficient for transport under the same external conditions. The results are obtained analytically using 1-D diffusion model and confirmed by 3-D Brownian dynamics simulations.

Water-filled pores of biological channels usually have complex geometry that only rarely can be approximated by a cylinder. For example, high-resolution crystallography of bacterial porins and other large channels demonstrates that their pores can be envisaged as tunnels whose cross-sections change significantly along the channel axis. For some of them, variation in cross-section area exceeds an order of magnitude [1,2]. This leads to the so-called entropic wells and barriers [3–9] in theoretical description of transport through such structures. In addition to biological channels, entropic effects are also important for understanding transport in nano-fluidic devices [10] and synthetic nanopores [11–13]. As the above mentioned theoretical studies deal with single particles, their results are limited to transport of non-interacting particles. Here we consider the effect of particle-particle interaction on transport through membrane channels of varying cross-section. Note that the effects of inter-particle interactions have been studied in the context of diffusion through narrow pores where the solute and solvent molecules move as a single file. However, the theory of single-file transport does not address the entropic effect analyzed below.

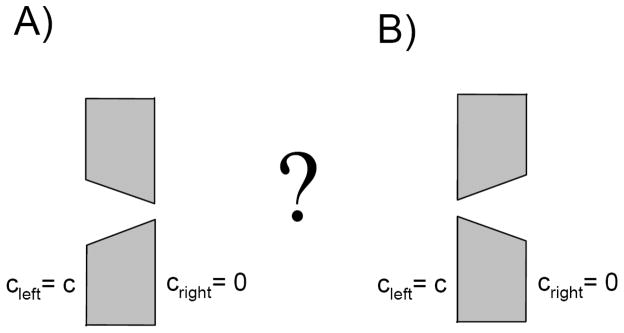
Consider two membranes separating empty and particle-containing reservoirs connected by the single channels shown in Fig. 1. The channel on the right is a truncated cone facing particle-containing reservoir with its wider opening; the channel on the left is identical to its right counterpart but has the opposite orientation. Which channel orientation is more efficient in facilitating transport of particles driven by the same concentration difference between the two reservoirs?

Figure 1.

Which one of these two identical but oppositely oriented channels is more efficient in transporting particles? The particles strongly repel each other, so that the channel can not be occupied by more than one particle at a time. In both cases the transport is driven by the same difference in particle concentrations on the two sides of the membrane.

The channel on the left has larger entry area, but to translocate a particle has to climb up the entropy barrier. At the same time, although the channel on the right has smaller entry area, translocating particles slide down the entropy hill. In spite of these distinctions, both channels are equally efficient in transporting non-interacting particles. If not, then for a given orientation of the channel there would be a net flux between the reservoirs at equilibrium when the particle concentrations in the reservoirs are equal. This violates the condition of detailed balance. In this Letter we show that particle-particle interaction breaks the symmetry of the fluxes driven by the difference in the particle concentrations on the two sides of the membrane. We demonstrate that, contrary to one’s intuition, configuration B is more efficient for transport of strongly repelling particles. This is shown analytically in the framework of a one-dimensional diffusion model of particle dynamics in the channel and supported by three-dimensional Brownian dynamics simulations.

We use the Smoluchowski equation to describe the particle motion in the channel, i.e., we assume that the Green function G ≡ G (x, t|x₀) – the probability density of finding the particle at point x at time t on condition that it was at x₀ at t = 0 and has not escaped from the channel during time t – satisfies

$$\frac{\partial G}{\partial t}=\frac{\partial }{\partial x}\left\{D_{ch}(x)exp\left(-\frac{U(x)}{k_{B}T}\right)\frac{\partial }{\partial x}\left[exp\left(\frac{U(x)}{k_{B}T}\right)G\right]\right\}.$$ (1)

Here U (x) is the potential of mean force acting on the particle in the channel, D_ch (x) is a position-dependent particle diffusion coefficient in the channel, and k_B and T have their usual meanings of the Boltzmann constant and absolute temperature. The propagator satisfies the initial condition, G (x, 0|x₀) = δ(x − x₀), and the radiation boundary conditions [14,15] at the channel ends located at x = x _L and x = x _R,

$$\begin{array}{l}{D_{ch}(x_L)exp\left(-\frac{U(x_L)}{k_{B}T}\right)\frac{\partial }{\partial x}\left\{exp\left(\frac{U(x)}{k_{B}T}\right)G\right\}|}_{x=x_L}={\kappa }_{L}G{\mid }_{x=x_L},\\ {-D_{ch}(x_R)exp\left(-\frac{U(x_R)}{k_{B}T}\right)\frac{\partial }{\partial x}\left\{exp\left(\frac{U(x)}{k_{B}T}\right)G\right\}|}_{x=x_R}={\kappa }_{R}G{\mid }_{x=x_R}.\end{array}$$ (2)

The rate constants κ _L and κ _R entering into the boundary conditions are related to the rate constants $k_{on}^{(L,R)}$, which characterize the rate of the particle entrance into the channel from the left and right reservoirs. The relations are

$${\kappa }_I=\frac{k_{on}^{(I)}}{A(x_I)},I=L,R,$$ (3)

where A (x) is the channel cross section area at a given value of the coordinate x. For a conical channel of radius r (x) this area is A (x) = π r² (x) and the rate constants $k_{on}^{(L,R)}$ are given by the Hill formula [16]

$$k_{on}^{(I)}=4D_{b}r(x_I),I=L,R,$$ (4)

where D_b is the particle diffusion coefficient in the bulk solutions in the reservoirs.

We assume that the particles strongly repel each other. When analyzing the effect of inter-particle repulsion on channel-facilitated transport, one has to deal with the many-body problem. This is true for both intra-channel dynamics of the particles and their entrance into the channel from the reservoirs. Unfortunately, the many-body problem is too complicated to be solved analytically. Therefore, here we consider a toy model, in which we assume that (i) the inter-particle repulsion is described by the requirement that the channel cannot be occupied by more than one particle and (ii) the effect of the repulsion on the entrance is neglected. This allows us to find analytical solutions for the fluxes J _A and J _B, Eqs. (12) and (13), in the two orientations of the channel shown in Fig. 1. Thus, the price we have to pay for the analytical solution is to accept the two simplifying assumptions mentioned above.

We consider the case of no specific interactions between the particles and the channel walls. As a consequence, the potential of mean force, U (x), is purely entropic. It arises naturally when reducing the three-dimensional diffusion problem to an effective one-dimensional problem to account for the deviations of the channel geometry from that of a cylinder [3]. For single point particles the entropy potential can be written in terms of the channel cross sectional area, A(x), and its minimum value, A_min, as

$$U(x)=-k_{B}Tln\frac{A(x)}{A_{min}},$$ (5)

so that the one-dimensional equilibrium concentration of non-interacting particles is proportional to the channel cross section area,

$$c(x)\propto exp(-U(x)/k_{B}T)\propto A(x).$$ (6)

The potential U (x) vanishes at x = x_R for the channel orientation shown in Fig. 1A, and at x = x_L for the opposite orientation of the channel shown in Fig. 1B. For all other values of x the potential is negative.

As follows from Eq. (5), in order to translocate, particles entering the channel through the wide opening have to climb up the entropy barrier, while particles entering through the narrow opening slide down the entropy hill. This, however, is not enough to answer the question which channel orientation is more efficient in transporting the particles between the two reservoirs, because one also has to account for the differences in the on-rates: the wide opening receives more particles per unit time than the narrow one. Therefore, a detailed analysis of the problem is required.

Non-cylindrical geometry of the channel also manifests itself in the position dependence of the effective diffusion coefficient [3–5, 17]. The expression for D_ch (x) was first derived by Zwanzig [3] assuming that the channel radius r (x) is a slowly varying function of x, |dr (x)/dx| ≪ 1. Later, based on heuristic arguments, Zwanzig’s result was generalized by Reguera and Rubi [4] to read

$$D_{ch}(x)=\frac{D_{\mathit{cyl}}}{\sqrt{1+{(dr(x)/dx)}^2}},$$ (7)

where D_cyl is the particle diffusion constant in a cylindrical channel. Detailed analysis of this question was performed in a series of papers by Kalinay and Percus (see Ref. 5 and references therein). Recently we carried out a numerical study of diffusion of single particles in conical channels [17] with the goal to test the applicability of different approximate expressions for D_ch (x). We found that the approximate formula in Eq. (7) works reasonably well when the growth rate of the channel radius, λ = dr (x)/dx, is not too large, specifically, |λ| ≤ 1. Note that for the conical channels shown in Fig. 1 the growth rate of the channel radius, λ, is a constant, and, therefore, the diffusion coefficient in Eqs. (1) and (2) is independent of x and given by $D_{\mathit{cyl}}/\sqrt{1+{\lambda }^2}$.

Eventually Eq. (1) reduces to the conventional Fick-Jacobs equation [18] with the renormalized diffusion coefficient

$$\frac{\partial G}{\partial t}=\frac{D_{\mathit{cyl}}}{\sqrt{1+{\lambda }^2}}\frac{\partial }{\partial x}\left\{A(x)\frac{\partial }{\partial x}\left[\frac{G}{A(x)}\right]\right\}$$ (8)

and the boundary conditions in Eq. (2) take the form

$$\begin{array}{l}{\frac{D_{\mathit{cyl}}}{\sqrt{1+{\lambda }^2}}A(x_L)\frac{\partial }{\partial x}\left\{\frac{G}{A(x)}\right\}|}_{x=x_L}=k_{on}^{(L)}G{\mid }_{x=x_L},\\ {-\frac{D_{\mathit{cyl}}}{\sqrt{1+{\lambda }^2}}A(x_R)\frac{\partial }{\partial x}\left\{\frac{G}{A(x)}\right\}|}_{x=x_R}=k_{on}^{(R)}G{\mid }_{x=x_R}.\end{array}$$ (9)

To find the fluxes J _A (λ) and J _B (λ) we use general relations derived in Ref. 15, which, for conical channels shown in Fig. 1 lead to

$$J_A(\lambda )=\frac{k_{on}^{(L)}{k}_{on}^{(R)}c}{k_{on}^{(L)}+k_{on}^{(R)}(1+{cV}_{ch})+\frac{k_{on}^{(L)}{k}_{on}^{(R)}\sqrt{1+{\lambda }^2}}{D_{\mathit{cyl}}}\underset{x_L}{\overset{x_R}{\int }}\left[1+c\underset{x}{\overset{x_R}{\int }}A(y)dy\right]\frac{dx}{A(x)}},$$ (10)

and

$$J_B(\lambda )=\frac{k_{on}^{(L)}{k}_{on}^{(R)}c}{k_{on}^{(L)}(1+{cV}_{ch})+k_{on}^{(R)}+\frac{k_{on}^{(L)}{k}_{on}^{(R)}\sqrt{1+{\lambda }^2}}{D_{\mathit{cyl}}}\underset{x_L}{\overset{x_R}{\int }}\left[1+c\underset{x_L}{\overset{x}{\int }}A(y)dy\right]\frac{dx}{A(x)}},$$ (11)

where V_ch is the channel volume. Carrying out the integrations and assuming that D_cyl =D_b = D we arrive at

$$J_A(\lambda )=\frac{4\pi a(a+\mid \lambda \mid L)Dc}{\pi (2a+\mid \lambda \mid L)+4L\sqrt{1+{\lambda }^2}+\pi (a+\mid \lambda \mid L)c\left[f(\mid \lambda \mid )+\frac{2}{3}\mid \lambda \mid L^3\sqrt{1+{\lambda }^2}\right]},\lambda \le 0$$ (12)

and

$$J_B(\lambda )=\left\{1+\frac{\pi \lambda Lc\left[f(\lambda )+\frac{2L^2}{3}(a+\lambda L)\sqrt{1+{\lambda }^2}\right]}{\pi (2a+\lambda L)+4L\sqrt{1+{\lambda }^4}+\pi \mathit{acf}(\lambda )}\right\}{J}_A(-\lambda ),\lambda \ge 0$$ (13)

with function f (λ) defined as $f(\lambda )=V_{ch}+2L^2(a+\lambda L/3)\sqrt{1+{\lambda }^2}$, where L and a are the channel length and the radius of its small opening, respectively. The results in Eqs. (12) and (13) are exact in the sense that no additional assumptions were made on the way to these expressions.

One can see that J_B (λ) > J _A (λ) except for the cases when either L, or λ, or c tend to zero. The cases of L = 0 and λ = 0 correspond to symmetric systems, in which J_B = J _A. When the system is asymmetric, L >0 and λ ≠ 0, but the particle concentration is small, c → 0, the particle-particle interaction can be neglected (channel occupancy tends to zero), and therefore the flux symmetry is restored, J_B (λ) = J _A (λ).

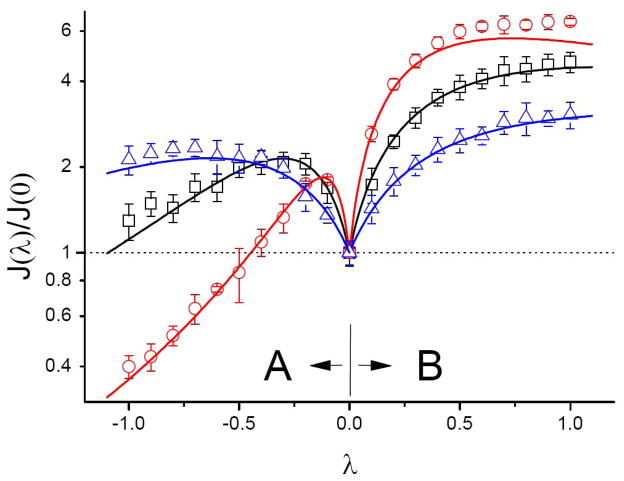
The λ -dependence of the fluxes, Eqs. (12) and (13), for channels of different length is illustrated in Fig. 2. In this figure we also compare our analytical predictions based on the one-dimensional diffusion model, Eqs. (1) and (2), with the results of three-dimensional Brownian dynamics simulations. The results are given for the three channel lengths (L = 25, 50, and 100) and normalized to the fluxes through the corresponding cylindrical channels of radius a. It can be seen that the difference between the two orientations of the channel may lead to significant flux asymmetry. The strength of the effect depends on the geometric parameters, |λ| and the channel length, namely, the larger |λ| and/or the longer the channel, the stronger the effect.

Figure 2.

Fluxes J _A (λ), λ <0, and J_B (λ), λ >0, through the conical channels of different lengths as functions of λ = dr (x)/dx normalized to the fluxes at λ = 0. Solid lines are theoretical predictions while symbols represent results of Brownian dynamics simulations. The channel lengths are L = 25 (triangles), 50 (squares), and 100 (circles). Other parameters are: a = 5, D _cyl =D_b = D = 0.02, c =2.5 · 10⁻⁵. The fluxes are asymmetric and their asymmetry at fixed λ grows with the channel length.

This can be understood if one takes into account the fact that the main parameter characterizing the effect of inter-particle interaction on transport is the average channel occupancy. For a singly occupied channel the occupancy is given by the probability of finding a particle in the channel. When this probability is small, the system should exhibit symmetric behavior independently of its structural asymmetry. At fixed concentration of the particles the probability of finding a particle in the channel grows with the channel length. At c =2.5 · 10⁻⁵ the occupancy of the relatively short channel of length L = 25 is low, and the fluxes in Fig. 2 are nearly symmetric in λ within the whole range of its variation. The channel occupancy is much higher in the longest channel (L = 100). As a result, the particle-particle interaction breaks the flux symmetry, and the orientation shown in Fig. 1B proves to be more than 10-fold more efficient for the transport than the orientation in Fig. 1A at λ =±1.

It is also interesting to note that for small deviations of the channel shape from a cylinder, |λ| ≪1, the fluxes are almost symmetric in λ. Both fluxes first grow with |λ|. However, as |λ| is getting larger, the role played by entropic effects becomes more and more important. Indeed, for the longest channel at λ = −1 the effect of climbing the entropy barrier is so strong that the flux through this channel is well below the flux through its cylindrical counterpart of radius a. This happens in spite of the fact that the radius of the channel opening facing the particle-containing reservoir, a + L, is much larger than a.

Thus, comparison with the numerical results shows that the one-dimensional diffusion model of particle dynamics in the channel provides an accurate description of channel-facilitated transport in the presence of entropy potentials which are due to the deviation of the channel pore geometry from that of a cylinder. In Fig. 2 small deviations of the simulation results from the analytical predictions at |λ| > 0.5 are due to the limitations of the approximation given by Eq. (9), which were studied recently in Ref. 17. Importantly, our analysis is based only on given geometric parameters of the channel, a, L, and λ, and does not use any adjustable parameters.

In summary, earlier studies of entropic effects in transport [3–9] were focused on transport of single particles. Here, for the first time, we analyze how particle-particle interaction affects the transport in the presence of entropy potentials. We demonstrate that mutual repulsion of the particles breaks the flux symmetry inherent in transport of non-interacting particles. Finally, we note that the flux asymmetry discussed here should be distinguished from the asymmetry that underlies current rectification in charged synthetic conical nanopores [13, 19] or asymmetric diffusion through these structures [20]. While the subject of the present study is a purely entropic effect due to the asymmetry in the channel geometry (Fig. 1), the current rectification is due to the asymmetry in the volume charge density [13], and is a purely energetic effect. The asymmetric diffusion [20] is not of the entropic origin either. Rather, it is related to the salt concentration effect on the thickness of the electric double layer within the nanopore [20]. This, in turn, changes the effective aperture of the narrow opening of the channel and, therefore, controls transport in a concentration-dependent manner.