A dynamical model of ommatidial crystal formation

Abstract

The crystalline photoreceptor lattice in the Drosophila eye is a paradigm for pattern formation during development. During eye development, activation of proneural genes at a moving front adds new columns to a regular lattice of R8 photoreceptors. We present a mathematical model of the governing activator–inhibitor system, which indicates that the dynamics of positive induction play a central role in the selection of certain cells as R8s. The “switch and template” patterning mechanism we observe is mathematically very different from the well-known Turing instability. Unlike a standard lateral inhibition model, our picture implies that R8s are defined before the appearance of the complete group of proneural cells. The model reproduces the full time course of proneural gene expression and accounts for specific features of the refinement of proneural groups that had resisted explanation. It moreover predicts that perturbing the normal template can lead to eyes containing stripes of R8 cells. We observed these stripes experimentally after manipulation of the Notch and scabrous genes. Our results suggest an alternative to the generally assumed mode of operation for lateral inhibition during development; more generally, they hint at a broader role for bistable switches in the initial establishment of patterns as well as in their maintenance.

Regular patterns of cell fate appear widely in biology, and it has long been a major challenge to explain how such de novo patterning occurs during development. The R8 photoreceptor lattice in the Drosophila melanogaster eye is a particularly striking example. The adult Drosophila eye comprises ∼750 ommatidia, each composed of photoreceptors and support cells, packed in a crystalline array (1). These ommatidia are founded by R8 photoreceptors, whose orderly alignment takes shape in the wake of the morphogenetic furrow (MF) that moves from posterior to anterior across the eye imaginal disc during the third larval instar (Fig. 1) (2). The emergence of a solitary R8 from within a proneural group of competent cells has parallels in many examples of neural and neuronal fate specification (3, 4). This selection of a neural precursor through lateral inhibition is generally believed to involve an instability whereby feedback loops reinforce random fluctuations to choose one among a collection of equivalent cells (5–7). Here, we present a mathematical model of R8 selection and spacing that suggests a different scenario. This model turns out to generate patterns through a “switch and template” mechanism at whose heart is a cell-autonomous, bistable switch that takes one state in the R8s and another in the surrounding, undifferentiated cells. Whether a cell switches from undifferentiated to R8 depends primarily on the balance between inductive and inhibitory signals emanating from more mature cells to its posterior; direct inhibitory interactions among neighboring cells play a secondary role, preventing the appearance of superfluous R8s after the initial R8 specification. This mechanism implies that R8s are chosen earlier than previously thought, during the initial process of induction. Unlike previous scenarios (8, 9), the switch and template mechanism predicts that genetically identical tissue can readily sustain different patterns depending on initial conditions, as we verify experimentally.

Fig. 1.

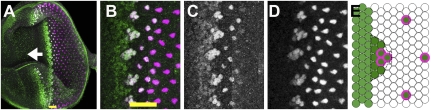
Specification of R8 cells. In all figures, anterior is to the left. (A) In the eye imaginal disc epithelium, precisely constructed ommatidia each differentiate around a single R8 cell. R8 specification is accompanied by a transient contraction of disc cells in the “morphogenetic furrow” (MF) that sweeps anteriorly across the disc (arrow gives MF direction). Posterior to the furrow are vertical columns of R8s. Ato protein (green) appears just ahead of the furrow and is accompanied, then replaced, by Sens (magenta), expressed stably in R8 cells. (B) Ato expression evolves from a low uniform stripe into periodic intermediate groups (IGs) that then resolve into single R8 cells. Sens tracks Ato from the IGs. [Because the eye disc epithelium is pseudostratified, there are more unstained cells between R8s than it might appear from the size of the stained R8 nuclei (2, 4).] (C) Ato expression in intermediate groups and R8 cells. (Ato is lost in R8s posterior to the MF through a regulatory mechanism not discussed in this paper; ref. 33). (D) Sens expression. (E) Schematic of Ato (green) and Sens (magenta rings) expression in the furrow. Black dotted lines outline an IG, which has higher Ato expression than the stripe to its anterior. Yellow scale bars indicate the extent of the MF. (Scale bars: A and B, 18 μm.)

The earliest markers of R8 fate are the transcription factors Atonal (Ato) and Senseless (Sens). ato expression is first detected in a low uniform band directly anterior to the MF (Fig. 1). As cells enter the MF, regularly spaced intermediate groups (IGs) of ∼10 cells raise their ato level, and ato expression is lost in the other cells. Sens can first be detected soon after the appearance of the IGs. Over ∼2 h, Ato and Sens progressively disappear from the IG until only a single cell, usually near the IG posterior, is left expressing both genes.

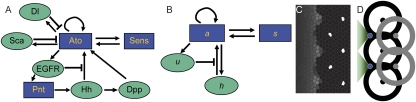
R8 patterning has hitherto been analyzed primarily by identifying mutations that affect the pattern (3, 4). Such studies define at least three kinds of regulatory interaction: nonautonomous induction of initial ato expression, cell-autonomous autoregulation by ato, and nonautonomous repression of ato (Fig. 2A). Induction is exemplified by Hedgehog (Hh), which is secreted by differentiating photoreceptors posterior to the MF; because ato expression is required for neural differentiation, one can think of hh as being indirectly activated by ato, creating a loop that drives the MF forward across the eye disc (3, 4, 10, 11). Cell-autonomous ato self-activation, in part through a positive feedback loop with sens, sustains ato expression once it reaches a critical level. Ato also activates signals that repress ato expression in nearby cells and contribute to lateral inhibition. These include the ligand Delta (Dl) for the Notch (N) receptor, the secreted factor Scabrous (Sca), which can diffuse at least a few cell diameters and affects Notch signaling (12–16), and signals that interfere with Hh signaling posterior to the MF (3, 4, 17, 18). Notch signaling plays an additional role in ato induction, in combination with the nonautonomous signal Decapentaplegic (Dpp) (19, 20).

Fig. 2.

R8 determination network. (A) Interactions regulating the expression of Ato in the MF. Pointed arrows, activation; blunt arrows, inhibition. Green ellipses, nonautonomous signals; blue boxes, transcription factors acting cell autonomously. EGFR is known to block Hh signals (18); Dl and Sca are shown acting directly on Ato because it is not certain which mode of ato activation they inhibit. Pointed (Pnt) is activated in the photoreceptor differentiation pathway that eventually leads to hh transcription posterior to the MF (46). (B) Simplified mathematical model of the interactions in A. All inhibitory signals are condensed into the variable u, and all long-range activation into h. (C) Simulated a expression in the model; compare Fig. 1C. (Parameters are in Table S1.) (D) The patterning mechanism in the model. Each R8 (dots) inhibits a within a certain radius (circles). As the MF progresses, the first cell reached by the activator h that is free of this inhibition (blue) is strongly favored to become the next R8. a expression extends outward from this cell to transiently form the IG (green triangles).

These genetic studies have established that inhibition of ato expression in IGs depends on Notch signaling, as in other proneural groups. Beyond this outline, however, many questions remain. No fully satisfactory picture exists for the initial spacing of IGs, for example. The scabrous mutation that affects IG spacing also affects selection of R8 cells within IGs, suggesting a relationship between these patterning phases, whereas other results suggest that spacing and resolution of IGs occur independently. Mutations in further genes, such as the EGF receptor (EGFR) pathway, also affect R8 patterning, but their role is incompletely understood. Although it is currently believed that, in some other proneural groups, all cells are equally likely to emerge as the neuron (7), multiple lines of evidence indicate differences among IG cells tied to their spatial positions; how such differences arise in, for example, the level and duration of Ato expression (21–23) or the apical–basal position of nuclei (23) is not known (3, 4, 24).

In this paper, we first abstract the known genetic interactions into a mathematical model of R8 fate specification (Fig. 2B). We then delineate the parameter regime where this model can replicate the dynamics of wild-type R8 patterning, from the initial stripe of proneural gene expression through IGs to isolated R8s, and examine in detail the pattern formation mechanism at work in this regime. This mechanism offers explanations for several puzzling features of pattern formation in the eye disc and makes experimentally testable predictions. The most striking of these—the appearance of a stripe pattern when inhibition is slow and a template of well-separated R8s is lacking—is verified by transiently perturbing pattern formation in a sca mutant background.

Model

Because the details of molecular interactions are not completely known, our approach is based on identifying key functional elements of the circuit and modeling them in enough generality that unknown molecular details can be effectively parameterized (Fig. 2B). We condense the known players into several lumped variables, each of which can be thought of as representing a given type of regulatory interaction rather than a specific gene: The variable u takes the place of all nonautonomous inhibition and h of the several nonautonomous activators that drive the MF; s implements delayed, cell-autonomous positive feedback; and a self-activates and is a marker of the R8 fate. Both h and u are allowed to move from cell to cell; our mathematical formulation is sufficiently broad to encompass both simple molecular diffusion and more general forms of nondirectional transport (25–27). Because the R8 pattern is ultimately defined on a single-cell level, we use a disordered array of discrete cells rather than a continuum model. We thus translate the interactions of Fig. 2B into ordinary differential equations on a lattice, with each site representing a single cell and irregular spacing between sites mimicking the disordered packing of cells in the eye disc. The dimensionless variables a_j, s_j, h_j, and u_j, where j indexes the lattice sites, then obey

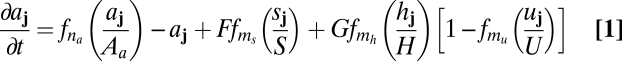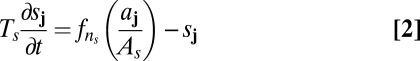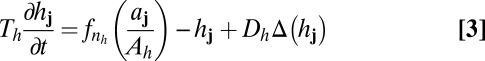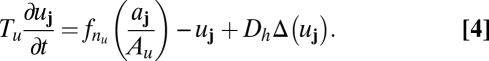Here uppercase letters (e.g., A_u, D_h, or F) denote dimensionless parameters, and Δ represents the discretized diffusion operator, which encodes the random cell packing (SI Text). The Hill function f_n, where f_n(x) = xⁿ/(1 + xⁿ), is a convenient way to represent sigmoidal functions, and parameters of the form n_x or m_y are thus exponents. We nondimensionalize the model so that the variables a_j, s_j, h_j, and u_j vary between zero and a maximum value of order unity, and we take the linear decay rate of a_j, which sets its characteristic time scale, to be 1.

After initially finding, through interactive searches, parameter sets where the model of Eqs. 1–4 could mimic the experimentally observed evolution of ato and sens expression, we explored the neighborhood of one preferred set (Table S1) in a more systematic two-step numerical screen (SI Text). In the interests of computational efficiency, we first simulated each randomly chosen parameter set in one dimension, and we then examined the 2D behavior only of those sets able to produce a moving front and a periodic pattern in one dimension. For these latter tests, we used a variant of our model (SI Text) that decouples pattern formation on the scale of a few ommatidia from the front motion on much larger scales, thus allowing us to focus on the essentials of 2D pattern formation and greatly speeding up simulations.

Results

Our preferred “wild-type” parameter set (Table S1) was chosen to make a hexagonal lattice of s expression, with transient a expression in IGs, for arbitrarily many successive R8 columns (Fig. 2C, Movie S1, and SI Text). This pattern was robust both to parameter variation and to quenched disorder (SI Text and Figs. S1 and S2). In particular, of 10,000 sets with all parameters (except Hill coefficients) varied within a factor of 2 of the preferred set, 1,462 were able to generate a one-dimensional pattern, and a significant fraction of these were capable of at least minimal 2D patterning, albeit often with a higher frequency of twinned R8s (text below, SI Text, and Table S2). In retrospect, this robustness seems a natural consequence of the switch and template mechanism, which, we argue, requires little more than cell-autonomous bistability and an appropriate separation of length and time scales.

The majority of the parameter sets that gave the correct pattern were biologically plausible, with decay lengths (i.e., the typical distance over which morphogen concentration drops by 1/e) and time scales for concentration changes consistent with the known properties of the proteins (3, 4, 27–29). Working parameter sets shared several characteristics. The nonautonomous activator h had to be longer ranged than the nonautonomous inhibitor u; u’s decay length was usually no more than a typical intercellular distance. Together with u’s highly cooperative, noncompetitive inhibition of h, these features allow for sharp boundaries between spatial domains of strong repression, where the action of h is effectively blocked by u, and of weak repression, where h can influence a. In the working parameter sets, the cell-autonomous positive feedback made a bistable even without any input from h, and moderate h levels were sufficient to force a toward the higher of its two stable states (SI Text and Fig. S3). We identify this high or R8 steady state with cells that will become R8s; cells at the steady state with the lower a value, the low state, do not differentiate at this stage. Finally, a separation of time scales was needed, with h changing more slowly than s and a, and u responding faster than the s–a feedback loop. This rapid relaxation of u to steady state was balanced by a relatively high threshold for activation of u by a. Thus, cells did little to inhibit their neighbors until their a levels neared the high steady-state value characteristic of R8s, but once a cell reached this point, it was able to quickly prevent its neighbors from attaining the same state. It is likely that repression in actual flies targets both activation by h, as in our model, and a’s self-activation (22, 30). In SI Text, section S7A, we show that a model variant in which u instead inhibits a self-activation can also sustain switch and template pattern formation.

Strikingly, although we did not preselect for this, the model reproduced features of observed ato patterns that had been difficult to understand. For example, our model selects R8s near the posterior of the IG (Fig. 2D) and generates intermediates characteristic of the resolution of an IG to single R8s (Fig. S4A). In the model, these differences among IG cells are straightforward consequences of differences in the timing of initial induction and in the strength of the inhibitory signal cells receive from the previous column.

Fig. 2D outlines how the successful parameter sets lead to R8 patterning (31). Every step relies on mechanisms distinct from previous notions of R8 specification. Each R8 defines a roughly circular region where activation of a in other cells is prevented. As the MF progresses and the long-ranged activator h builds up to the anterior of the existing R8s, the first cells it is able to flip to the high a state are located halfway between the R8s of the previous column, as far to the posterior as possible without being strongly inhibited. These cells, chosen by their position relative to the cells of the previous column, will become the R8s of the new column and block this fate in their neighbors. There is, however, a delay between their initial induction and when they can produce enough u to inhibit nearby cells effectively. During this time, h levels continue to increase, so that a rises transiently in other cells immediately to the anterior of the presumptive R8s, making the IGs. The cells fated to become R8s have, however, already been chosen by the time the full IGs are observed. In effect, the combination of a high threshold for u production and the ability of cells beyond this threshold to quickly repress their neighbors creates a race for the neural fate: Whereas a is increasing in the IG cells, they make little u and thus barely interact with each other. However, as soon as one cell has enough a to produce significant u it forces all of the others down, becoming the sole R8. The posteriormost cells that are induced first have a large head start and have effectively been chosen as R8s before other IG cells really begin to be activated.

The R8 selection process is thus strongly dependent on the distribution of inhibitor u coming from the previous column. This template ensures that only one cell is initially induced at the back of the IG. Although u provides a strong enough signal to place the single founding R8, its profile becomes more uniform more anteriorly, so that the location and shape of the larger and more diffuse IG are considerably more variable. Because the cells of the eye disc are not packed in an ordered lattice at this stage (32), sometimes the template allows two R8 candidates to be induced almost simultaneously; both then reach the R8 state before either can repress the other. Even the best parameter sets in our model lead to a low frequency of such R8 twinning; interestingly, twinned R8s are indeed observed experimentally posterior to the resolving IGs in ∼6% of ommatidia (33). That twins always resolve in wild-type discs, but not in our model, likely indicates some slower, ancillary inhibitory process in vivo (SI Text).

Because templating plays a central role in our pattern formation mechanism, the form of the final pattern is strongly dependent on the initial template (Fig. S5 and SI Text, section S6B). [In this light, it is interesting that a separate regulatory circuitry specifies the first column of ommatidia at the far posterior of the eye disc (2, 11).] Fig. 3B shows how, for our preferred parameters, an initial condition in which all cells in a column express a and s results in a poorly ordered assortment of isolated and twinned R8 cells. This result is in agreement with long-lasting disturbances observed after R8 patterning is perturbed in vivo. For example, conditional reduction or elevation of Notch activity that leads to a transient increase or decrease in R8 numbers disrupts subsequent patterning even after normal Notch function is restored (Fig. 4B) (22).

Fig. 3.

R8 model patterns depend on initial conditions. Sens (s) expression in the model is shown. (See Fig. S6 for other model variables.) (A) Wild-type parameters (Table S1) with an ordered template yield the usual hexagonal pattern. (B) With a stripe-like template, the same wild-type parameter set generates poorly ordered isolated and twinned R8s, as seen after a perturbation of Notch function (Fig. 4B). (C) With a template of single R8s, the slower u (“sca”) parameters (Table S1) lead to a disrupted pattern with some twinned R8s (compare Fig. 4C). (D) With a stripe template, the sca parameter set maintains stripe-like R8 patterning. Such patterns have now been observed experimentally (Fig. 4D). Magenta boxes in A, B, and D enclose the initial template (Fig. S4B); the template in C is the same as in A but is omitted to leave more space for the full sca pattern.

Fig. 4.

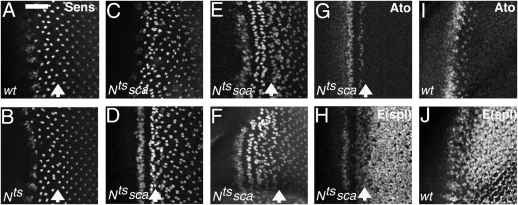
R8 patterns after experimental perturbations. (A–F) Projections of confocal images of Sens labeling. (A–H) Ommatidia near the arrow were at the IG stage at the higher (restrictive) temperature. (A) Normal patterning in wild type, exposed to 31.5 °C for 2 h and 18 °C for 14 h. Scale bar gives MF extent at fixation. (Scale bar, 17 μm.) (B) N^ts (temperature-sensitive allele) exposed to the restrictive temperature of 31.5 °C for 2 h and returned to the permissive 18 °C for 14 h before fixation. R8 patterning is haphazard anterior to the arrow indicating ommatidia that were IGs at the restrictive temperature. (C) Disordered ommatidial development and sporadic R8 twinning in the sca mutant phenotype (N^ts; sca at the permissive temperature). (D–F) N^ts; sca exposed to 31.5 °C for 2 h and 18 °C for 6 h (D), 20 h (E), or 30 h (F). The disordered sca phenotype is replaced by a propagating stripe pattern. (G) Same specimen as D, colabeled for Ato expression (Fig. S7). (H) Same specimen as D, labeled for E(spl) expression, reflecting N signaling activity. Stripes of of high N activity alternate with stripes of Ato expression. (I) Ato expression in wild type. (J) E(spl) expression in wild type reflects the complex pattern of N activity (22, 23).

Unexpectedly, for some parameter sets, the model produced an alternative pattern of continuous stripes of R8 cells from the same uniform initial template as in Fig. 3B (Fig. 3D and Fig. S4D). No striped pattern of ommatidia has ever been reported previously. Stripes developed when the parameters were such that a newly created R8 could not inhibit its neighbors as quickly and as sharply as with the wild-type parameters of Table S1. This outcome is seen most cleanly when T_u (Eq. 4) is increased (by a factor of 5 for Fig. 3 C and D), adjusting the response time of the inhibitor u without affecting its steady-state profile, but other parameter changes affecting the speed of inhibition can have similar effects (SI Text). The inhibitor signal from a uniform template lacks the indented profile of Fig. 2D, leading to the near-simultaneous activation of many cells as the MF moves forward. If the cells in the eye disc were packed in a perfectly regular lattice, an unbroken line of cells would be induced at the same instant, and all would reach the R8 state together, without having repressed each other. A stripe of R8s would result. Because cell packing is disordered, however, some cells in the new column will in fact be induced before others. The stripe will break up, as in Fig. 3B, if inhibition is fast enough that the first cells to be induced can reach the high state and repress their neighbors before these cells have crossed the threshold to become R8s. If, on the other hand, inhibition is slower, and the first cells are not able to repress the laggards before these also reach the high state, a stripe pattern will result, as in Fig. 3D.

We now report corresponding striped patterns in vivo (Fig. 4). When Notch function is briefly inhibited (with a temperature-sensitive allele) in a scabrous mutant disc, atonal expression persists in almost all cells, creating a near-uniform template of presumptive R8s. After Notch function returns, the eye disc then produces stripes of R8 cells to the anterior of this template. The sca gene encodes a secreted protein that is produced in cells expressing Delta and endocytosed into cells where Notch is active (13, 34). It has been reported to bind both of these proteins and is thought to modulate Notch signaling, although the precise mechanism remains uncertain (14–16). The known properties of Sca are thus consistent with a role in the speed of inhibition, although there has been no experimental study of this possibility.

Without the transient Notch inhibition, the sca mutant exhibits haphazard R8 patterning (Fig. 4C) (12, 32). If stripe-producing parameter sets model the sca mutation (and thus the system's evolution after it has been returned to the permissive temperature, to the anterior of the arrows in Fig. 4), then these parameters should lead to a sca mutant-like pattern when the template consists of isolated R8s. This was indeed the case (compare Fig. 3C with Fig. 4C).

It is significant that genetically identical tissue is able to support two distinct patterns, as predicted by the switch and template mechanism. Our preferred wild-type parameters accurately predict the result of removing the template from otherwise normal tissue. In addition, the same parameters that generate stripes with a uniform template also reproduce the spacing defects and the twinned R8s characteristic of the sca phenotype when the template is nonuniform. Taken together, these observations show the predictive value of the model and demonstrate a hidden connection between the normal R8 spacing pattern and stripes.

Discussion

The model introduced here suggests that the patterns of proneural gene expression and R8 photoreceptor determination seen in vivo arise from a patterning mechanism that differs from previous notions at many steps. This mechanism is the one most readily compatible with the interactions shown in Fig. 2A. In this alternative picture, single R8 photoreceptor cells provide the template that positions other single cells as R8 precursors, and the proneural intermediate groups are not precursors but arise secondarily, although they do provide a pool of potential replacement R8 cells. This mechanism naturally explains features of R8 patterning that previously had no ready interpretation and predicts a distinct, unexpected, striped pattern that we observed experimentally. It thus yields important insights beyond what has been gleaned from informal models based on developmental genetic studies (3, 4, 24). Other examples of neural fate specification through lateral inhibition may merit reexamination in light of these conclusions.

Mathematically, our mechanism is distinguished from most earlier descriptions of lateral inhibition by the presence of a bistable switch in each cell; this feature, in turn, emerges over a large region of parameter space as a natural consequence of the strictly cell-autonomous positive feedbacks involving a and s. In contrast, whether because they were concerned with systems where no analog of the proneural genes is known or for other reasons, previous models often focused entirely on regulatory interactions involving Notch and Dl (6, 35–39) (but see refs. 29 and 40–42). In such models, no cell-autonomous bistability is possible, and patterns are instead generated through a Turing instability (9, 43, 44); the same is true of an abstract activator–inhibitor model of R8 spacing featuring a diffusible activator (9). Models based on the Turing mechanism face several hurdles in reproducing the full time course of ato and sens expression seen in the eye disc, from the transient appearance of IGs to the emergence of a single R8 toward the IG posterior. For example, when positive feedback is cell autonomous, such descriptions cannot yield both compact IGs and the correct final R8 spacing. More importantly, models centered on Turing instabilities generally support more than one pattern for given parameter values only in narrow parameter ranges and then only at low amplitude (44), whereas we have experimentally observed the robust coexistence of patterns (Fig. 4). The switch and template mechanism, in contrast, can meet all of these challenges.

Our model deliberately elides molecular details, but a few of the simplifications embodied in Eqs. 1–4 deserve further comment. Most obviously, our only inhibitor is the secreted factor u, but it is known that juxtacrine (i.e., mediated by direct cell–cell contact) Delta–Notch signaling also plays an inhibitory role in eye discs. Juxtacrine interactions avoid the self-inhibition possible when a diffusible signal can act on the same cell that secretes it. This phenomenon is unimportant in our model, however, because cells secrete appreciable u only after they reach the R8 state and, through bistability, become relatively refractory to inhibition. Similarly, a picture of planar cells communicating only with their nearest neighbors likely underestimates the range of Notch signaling. For example, more cells might be in contact across the entire depth of the epithelium than can be represented in a planar model, whether through filipodia (25, 27) or through other complex packing geometries. Indeed, genetic mosaic studies suggest that Dl's nonautonomy extends beyond obviously adjacent cells (19, 45). Our model can approximate all of these possibilities through lattice diffusion and degradation. Similarly, our model subsumes into direct activation of h by a the long chain of events from the specification of R8 photoreceptors to the secretion of Hh by cells behind the MF. This choice emphasizes the feedback between photoreceptor differentiation and MF motion that propagates the MF as a self-sustained front. Neglecting the facts that differentiating photoreceptors other than R8s secrete the majority of Hh (46) and that Dpp is expressed uniformly in the MF (4), however, likely makes the MF speed too sensitive to local a concentrations, suggesting that our description may understate the robustness of the real patterning system.

Conversely, one might ask whether our model can be further simplified without jettisoning essential features. It is difficult to imagine how the experimentally determined network diagram (Fig. 2A) could be reduced beyond Fig. 2B without assuming a favored pattern formation mechanism. Now that we have identified the switch and template mechanism, however, it is possible to take limits that remove some free parameters while retaining the mechanism's basic elements. We have already alluded to one such limit: The separation of time and length scales between the long-ranged activator h and the a–s–u subsystem can be exploited to study pattern formation on short scales without explicit h dynamics; if desired, the speed of the h front can then be determined self-consistently from a knowledge of the small-scale pattern (47). Similarly, because the inhibitor u is usually fast in working parameter sets, pattern formation survives slaving u to the other variables by allowing T_u → 0. Finally, the best results are obtained when activation and inhibition are highly cooperative, so the model performs well in the step function limit of infinite cooperativity.

Although its most striking success is its ability to account for the striped pattern of R8 cell specification, our model provides insights into several other real-world observations. In the model, R8 cells that are already isolated are found to be the important patterned source of u; this result may explain why mosaic analysis defines the R8 cells as uniquely important for sca function, even though more Sca protein is produced from IGs (12). Our simulations show that loss of a and u expression from IGs coincides with the appearance of individual R8s whose inhibitor u serves as a template for the next column. This result may explain the temporal correspondence observed between the appearance of a periodic IG pattern in a new column and the resolution to single R8 cells of the preceding column (22, 23). Whereas it has been difficult to explain why the loss of sca, which seems primarily to space IGs, should also cause twinning (32), in our model twinning is a natural consequence of spacing defects that weaken the bias in favor of one particular cell provided by an ordered template (Fig. 3C). Most importantly, the model predicts that the positioning of R8 cells is essentially a geometric effect (depending on the location of cells in the previous column) and that the selection of the individual R8s precedes the appearance of the full IGs even though this is not visible from inspection of the expression pattern. The choice of the R8 is thus not primarily a result of interactions among proneural IG cells, the mechanism thought to select single neural precursors from proneural groups in many other contexts (3–5). This conclusion may explain why selection of R8 cells is not dependent on moderate differences in N levels between IG cells (3). Some previous authors have suggested that a static prepattern may bias the competition to assume the neural fate in some proneural groups (7, 23, 24, 48); our model differs in identifying the timing of initial activation of the proneural gene, rather than the strength of activation from a prepattern per se, as an essential variable.

In the half century since biological patterns were first modeled, it has become clear that the cell-autonomous autoregulation central to our model—and with it, a tendency toward bistable, switch-like behavior—is widespread in cell determination networks and probably essential if cells are not to remain perpetually dependent on extracellular signals (49, 50). The ubiquity of such complex feedbacks within individual cells requires models that treat cells as discrete objects (51). The switch and template mechanism described here arises naturally in the presence of just such discreteness and feedbacks. It provides a flexible and robust route to a variety of biological patterns.

Methods

Except as noted (SI Text), Eqs. 1–4 were solved by a custom-written Matlab program that treats the diffusive and degradation terms implicitly but the production terms explicitly. Eye discs were dissected from late third-instar larvae, fixed, and subjected to indirect immunolabeling as described (52). Confocal images were z-projected to include labeled nuclei. Normal culture was at 25 °C; culture vials were immersed in water baths to achieve the restrictive treatment for N^ts1. See SI Text for strains.