Diffusion model for one-choice reaction-time tasks and the cognitive effects of sleep deprivation

Abstract

One-choice reaction-time (RT) tasks are used in many domains, including assessments of motor vehicle driving and assessments of the cognitive/behavioral consequences of sleep deprivation. In such tasks, subjects are asked to respond when they detect the onset of a stimulus; the dependent variable is RT. We present a cognitive model for one-choice RT tasks that uses a one-boundary diffusion process to represent the accumulation of stimulus information. When the accumulated evidence reaches a decision criterion, a response is initiated. This model is distinct in accounting for the RT distributions observed for one-choice RT tasks, which can have long tails that have not been accurately captured by earlier cognitive modeling approaches. We show that the model explains performance on a brightness-detection task (a “simple RT task”) and on a psychomotor vigilance test. The latter is used extensively to examine the clinical and behavioral effects of sleep deprivation. For the brightness-detection task, the model explains the behavior of RT distributions as a function of brightness. For the psychomotor vigilance test, it accounts for lapses in performance under conditions of sleep deprivation and for changes in the shapes of RT distributions over the course of sleep deprivation. The model also successfully maps the rate of accumulation of stimulus information onto independently derived predictions of alertness. The model is a unified, mechanistic account of one-choice RT under conditions of sleep deprivation.

In a one-choice reaction-time (RT) task, a subject must detect the onset of a stimulus and respond to the onset as quickly as possible. Tasks like this are performed every day. For example, a driver has to slow when he or she detects a car ahead slowing (1). One-choice RT tasks are also used extensively in animal research because it is easier to train animals on one-choice tasks than on multiple-choice tasks (2). Despite the ubiquity of one-choice RT tasks (e.g., over 200 published papers on the effects of sleep deprivation), there has been no theory that successfully explains what components of cognitive processing underlie performance on these tasks, nor how the components are affected individually and in combination by experimental variables (the closest attempt for sleep deprivation is the model described in ref. 3). Intuition suggests that processing in one-choice tasks should be closely related to processing in two-choice tasks when the stimuli are similar. RT distributions and accuracy on a wide range of two-choice decision tasks are successfully described by the diffusion model (4, 5). Extending the diffusion model to one-choice RT tasks was the goal of the research presented here.

There are three types of one-choice RT tasks that have been in common use. First, for a classic “vigilance” task, the onsets of stimuli are widely spaced in time: for example, 12 events every 20 min (6). Vigilance was a mainstream area of study in information processing psychology (6–8) that arose out of practical issues of fatigue in World War II. Theories of vigilance were not quantitative, but instead tried to identify global factors responsible for declines in vigilance: factors such as motivation, expectancy, blocking, signal-detection criterion movement, activation, and arousal (8). Second, for a “psychomotor vigilance test” (PVT) (9, 10), the stimuli appear more frequently, on the order of several per minute. Over the past 25 y, the PVT has become a standard assay of the clinical and behavioral effects of sleep deprivation (11). Third, for “simple RT” tasks, stimuli are presented at an even higher rate, every few hundred milliseconds (12). Simple RT tasks have been the focus of seminal research on RT distributions (13).

For all three tasks, the dependent variable is RT, and the RT distribution provides the data for modeling. A successful model must produce the correct shape for the RT distribution and, in particular, must capture the behavior of the distribution's right tail. An insightful way of describing the RT distribution and the right tail is through the hazard function (13), which is defined as h(t) = f(t)/(1 − F(t)), where f(t) is the probability density function and F(t) is the cumulative density function. The function expresses the probability of the one-choice decision process terminating in the next instant of time, given that it has survived to that time.

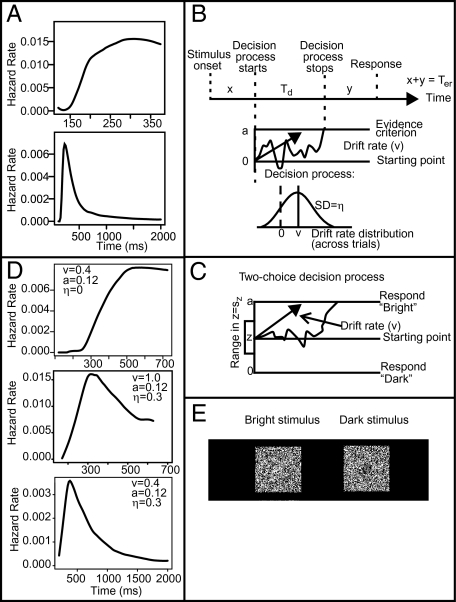
Fig. 1A shows two possible shapes for hazard functions in one-choice RT tasks. Burbeck and Luce (14) reported hazard functions, like the one in Fig. 1A, Upper (both with and without the slight fall in the right-most end of the function). Green and Smith (15) found the same shapes, but in addition, when stimulus presentation duration was short, hazard functions like the one in Fig. 1A, Lower were obtained (a function that rises to a peak and then falls to near zero). Below, we show that our model accounts for both patterns and that it explains how performance can transition from one to the other (Fig. 1).

Fig. 1.

(A) Two hazard functions taken from one subject in a sleep deprivation experiment. (Upper) A nondeprived condition; (Lower) a sleep-deprived condition. (B) Illustration of the one-choice diffusion model. Evidence is accumulated at a drift rate v with SD across trials η, until a decision criterion at a is reached after time T_d. Additional processing times include stimulus encoding time x and response output time y; these sum to nondecision time T_er, which has uniform variability across trials with range s_t. (C) Illustration of the well-established two-choice diffusion model (4, 5, 18). Boundary separation is a, starting point is z, and range of variability in the starting point is s_z. The other components of the model are the same as the one-choice model. (D) Sample hazard functions from the model, with parameters varied as shown. Compare with A. (E) Sample single frames of the stimuli for experiment 1.

Consistent with recent theoretical work on two-choice decision making, we model one-choice RT performance with a diffusion process. Fig. 1B illustrates the model. The RT for a stimulus is made up of encoding time (x), decision time (T_d), and response execution time (y). The decision process is a one-boundary diffusion process in which evidence is accumulated from a starting point 0 to a decision criterion a. The rate of accumulation of evidence [i.e., drift rate (v)], for nominally equivalent stimuli is assumed to vary across trials according to a normal distribution with SD η: that is, a continuous mixture (16). Encoding time and response execution time are not separately identifiable from behavioral data and so they are summed into a single nondecision parameter with mean time T_er. Nondecision time is assumed to vary from trial to trial according to a uniform distribution with range s_t (17). In applying the model to two experiments presented below, we found that both sources of variability are necessary to fit data (i.e., that goodness of fit is worse if either source is removed). In the two-choice diffusion model (4), variability in starting point of the process is assumed (Fig. 1C), but in the one-choice model, including variability in starting point does not improve goodness of fit.

The assumption of across-trial variability in drift rate allows the one-choice diffusion model to explain the various shapes of hazard functions. If there was no across-trial variability in drift rate (i.e., η = 0), drift rate was positive or zero, and there was no variability in nondecision time, then the RT distribution would be an inverse Gaussian (14, 18–20), as in Fig. 1D (Top), and all processes would be guaranteed to terminate (see, for example, Fig. 1A, Upper). However, with across-trial variability in drift rate, some proportion of drift rates are negative (to the left of the dashed line in Fig. 1B, Bottom). Some proportion of these processes never terminate, and the distribution of those that do terminate is not known (21). The middle and bottom panels of Fig. 1D show two such cases, both with SD of drift rate η = 0.3. With a mean drift rate of 0.4, the result is a long-tailed hazard function (Fig. 1D, Bottom; see also, Fig. 1A, Lower), whereas with mean a drift rate of 1.0, the result (Fig. 1D, Middle) is a hazard function that is transitional between Fig. 1D, Top and Bottom. The ratio v/η is an index of the form of the hazard function for one-choice tasks. The ratio is comparable to the d′ index traditionally derived from accuracy measures in two-choice tasks.

Results

Experiment 1.

Experiment 1 (55 subjects) showed that the one-choice diffusion model can explain simple RT data, and demonstrated the theoretical correspondence between one-choice and two-choice tasks. Blocks of trials from a one-choice brightness-discrimination task were mixed with blocks of trials from a two-choice brightness-discrimination task (22). The stimulus in both tasks was a 20 × 20 patch of pixels centered on a larger 100 × 100-pixel background (Fig. 1E). At the beginning of a trial for the one-choice task, the proportions of black and white pixels in both the background and stimulus patches were equal. Then after a variable time, the proportion of black and white pixels in the 20 × 20 patch changed so that it became brighter or darker than the background. The stimulus was dynamic; on every frame of the video display, a different random sample of pixels in both the stimulus and background was presented. Subjects were required to respond as quickly as possible when the brightness changed. For the two-choice task, at the beginning of a trial, the 20 × 20 patch was made up of either more black than white pixels (“dark”) or more white than black pixels (“bright”). Subjects were required to decide as quickly as possible between dark and bright.

Mean RTs for the one-choice task, and accuracy and mean correct and error RTs for the two-choice task are shown in Table 1. For both tasks, responses to bright stimuli were combined with responses to equivalent dark stimuli to produce data for three conditions: easy, medium, and difficult. As the proportion of black-to-white pixels approached 0.5 (from easy to difficult), mean RT increased and, in the two-choice task, accuracy decreased.

Table 1.

Results from experiment 1

	One-choice (simple RT)		Two-choice
Difficulty	Proportion of black or white pixels	Mean RT (ms)	Proportion of black or white pixels	Proportion correct	Correct mean RT (ms)	Error mean RT (ms)
Difficult	0.56	949	0.52	0.76	852	932
Medium	0.59	571	0.54	0.89	765	877
Easy	0.62	477	0.56	0.94	692	767

The two-choice task was included to allow comparison between model components for the one-choice diffusion model and the standard two-choice diffusion model (4, 17, 18). In the two-choice model (Fig. 1C), information from a stimulus (drift rate) drives an accumulation-of-evidence process that results in a response when a criterial amount of evidence is reached. Evidence begins at a starting point z, which varies across trials uniformly with range s_z, and accumulates toward one of two criteria, 0 or a. The one-choice and two-choice diffusion models are alike in all other respects.

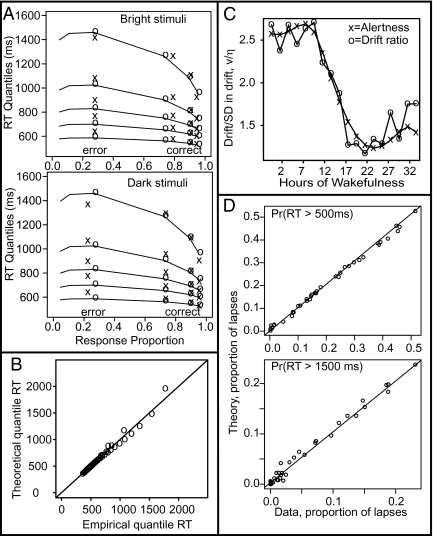
The two-choice model fit the two-choice data well, with only drift rate varying between levels of difficulty (with a single value of SD in drift rate across trials). Table 2 shows the parameter estimates and the χ² value. Fig. 2A shows fits of the two-choice model to the 0.1, 0.3, 0.5, 0.7, and 0.9 quantile RTs, with quantile RTs stacked vertically and response proportions on the abscissa (4).

Table 2.

One-choice and two-choice diffusion model parameter estimates for experiment 1

					Easy	Medium	Difficult	Easy	Medium	Difficult
Task	Value	a	Ter	st	v1	v2	v3	η1	η2	η3	χ2
Simple (one-choice)	Mean	0.136	253	136	0.777	0.567	0.321	0.262	0.209	0.153	47.9
	SD	0.017	34	37	0.191	0.122	0.068	0.076	0.049	0.047	9.6
Two-choice	Mean	0.155	466	160	0.352	0.250	0.118	0.150			64.3
	SD	0.031	59	68	0.105	0.086	0.047	0.072			22.4

Note: χ², df = 50 for the simple RT task (critical value 71) and, df = 56 for the two-choice task (critical value 79). Variability in starting point (s_z) across trials in the two-choice task has estimated range 0.054 with SD 0.035. a, boundary setting; T_er, nondecision component of response time; η, SD in drift across trials; s_t, range of the distribution of nondecision times, and v₁, v₂, and v₃ are drift rates.

Fig. 2.

(A) Quantile probability plots for the two-choice data from experiment 1. The “x” symbols denote the data and the “o” symbols and lines represent the model predictions (see ref. 4 for further explanation). The plots show the 0.1, 0.3, 0.5, 0.7, and 0.9 quantile RTs (stacked curves) plotted against response proportion. Error data are shown for only one of the three levels of difficulty, because several subjects had zero errors in the other conditions (so quantiles cannot be computed). (B) Experimental and theoretical RT quantiles averaged over subjects for the one-choice data from experiment 1. The diagonal line has slope 1 and intercept 0. (C) Ratio of drift rate to SD in drift rate (v/η) plotted against independently derived alertness predictions for the data from experiment 2. (D) Proportion of performance lapses with RTs > 500 ms (Upper) and RTs > 1,500 ms (Lower) for the data from experiment 2, and corresponding model predictions. Each point represents data from a single subject for either the sleep-deprived or nondeprived conditions. The diagonal lines have slope 1 and intercept 0.

For the one-choice model, difficulty was assumed to affect only drift rate and SD of drift rate: that is, the drift ratio v/η. The nondecision time, the variability in the nondecision time, and the decision criterion were held constant across the three levels of difficulty. The drift ratio decreased with difficulty of the stimulus. The model fit the one-choice RT distributions well. To compare model predictions with data, a plot of the 19 0.05-step quantile RTs (from 0.05 to 0.95) for the three stimulus difficulty levels is displayed in Fig. 2B. The correspondence between predictions and data are good. Table 2 shows the parameter estimates and the χ² value.

Because the models were fit to the data at the level of individual subjects, correlations between the one-choice and two-choice parameter estimates can be examined. For the mean drift rates (averaged across the three stimulus difficulty levels), the correlation was 0.48; the critical value with n = 55 is 0.26. This result is not a priori obvious. In the two-choice diffusion model, drift rate is most highly correlated with accuracy, not RT (23), but in the one-choice case, there is no measure of accuracy and drift rate is thus determined solely by the RT distribution.

The correlations between the one-choice and two-choice estimates for other model parameters were small: decision criterion, 0.09; nondecision time, −0.04; range in nondecision time, 0.05; and SD of drift rate across trials, 0.12. Moreover, the difference in the nondecision times between the one- and two-choice trials was large, 204 ms on average. These findings suggest that the cognitive processes involved in the components of processing differed between the one- and two-choice tasks but, in agreement with the goal of our research, there was a shared decision process that generalized from the two-choice diffusion model to the one-choice diffusion model.

Experiment 2.

Experiment 2 showed that the one-choice diffusion model accounts for changes in the shapes of PVT RT distributions over the course of sleep deprivation, and that changes in drift ratios map to an independently derived measure of predictions of alertness. Nineteen subjects were tested on a 20-min PVT for two replications of 36 h of total sleep deprivation. Sleep deprivation responses were highly stable within subjects (24), so the two replications were combined for data analyses. For each replication, PVT performance was tested every 2 h for a total of 18 test bouts. On each trial, a millisecond counter was displayed on a computer screen. Subjects were instructed to respond immediately, by pressing a response key, when the counter appeared and began counting up. When the key was pressed, the counter stopped, the RT in milliseconds was displayed for 1 s, and then there was an interval that varied from 2 to 10 s before the next trial.

In a first analysis, the model was fit to the data from the 18 test bouts for the 19 individual subjects (i.e., 342 RT distributions), with about 350 observations per bout per subject. The one- choice diffusion model fit the RT distributions well; Table 3 (Bottom) shows the parameter estimates and the χ² value. The drift ratio v/η changed significantly across test bouts [F(17,306) = 16.92, P < 0.05]. Nondecision time increased slightly but significantly across test bouts by about 12 ms [F(17,306) = 2.08, P < 0.05], and the range of the distributions of nondecision times increased significantly by about 20 ms [F(17,306) = 2.82, P < 0.05]. Parameter estimates varied modestly from test bout to test bout. Average correlations between each test bout and the next were 0.427 for T_er, 0.508 for s_t, 0.614 for a/v, and 0.646 for v/η.

Table 3.

Results and one-choice diffusion model parameter estimates from experiment 2

Condition	Value	Mean RT (ms)	a	Ter	st	v	η	χ2
Nondeprived	mean	368	0.092	175	103	0.770	0.292	20.7
	SD		0.019	31	40	0.282	0.164	7.9
Deprived	mean	876	0.096	187	123	0.500	0.331	19.3
	SD		0.018	31	48	0.162	0.160	17.7
Averaged over all 18 sessions	mean	697	0.085	187	114	0.527	0.260	14.1

Note: χ², df = 14, critical value 26.1.

Fig. 2C shows a plot of the drift ratio v/η and a plot of independently predicted alertness as a function of the number of hours of continuous wakefulness. The values of alertness were derived from a biomathematical model of fatigue (25) in which alertness declines near-linearly over time awake modulated by a 24-h circadian cycle. The drift ratio closely tracked the nonmonotonic alertness function, indicating that alertness changes across the sleep-deprivation experiment were reflected in drift rate changes, and thereby in the shapes of the hazard functions associated with the fitted RT distributions.

In a further analysis to examine the hazard functions, test bouts were grouped across approximately equivalent levels of performance: the first 10 bouts were combined into a nondeprived condition and the last 10 bouts were combined into a sleep-deprived condition (Fig. 2C), giving over 2,000 observations per condition per subject. The model fit the RT distributions well (Table 3). As would be expected, mean RT increased between the two conditions and the drift ratio decreased. The other parameters did not differ significantly between the two conditions. The mean χ² value was 20.0, and 85% of the χ² values were below the critical value of 26.1.

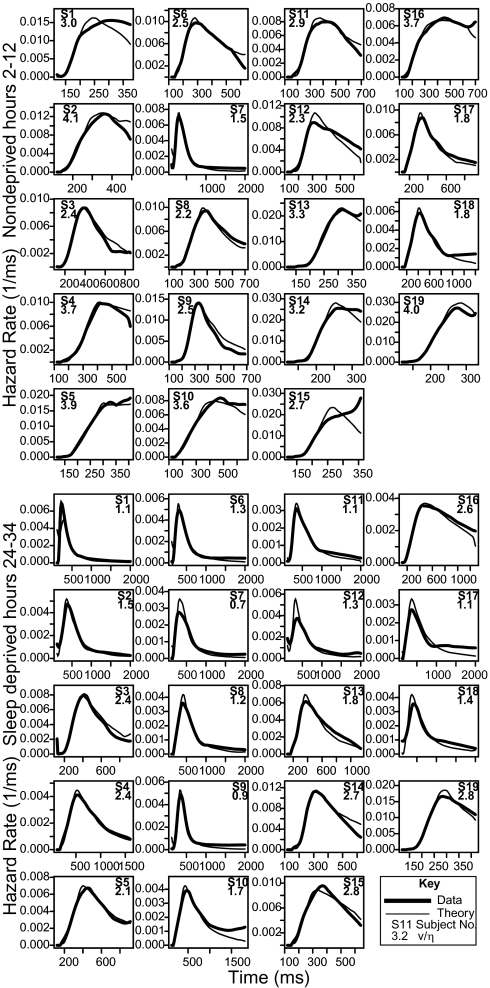
Given that the model fit the data well, the question was whether it captured the variety of shapes of hazard functions for individual subjects, as shown in Fig. 3 (histograms are shown in SI Appendix). In the model, whether the hazard function levels off at a relatively high value or has a long tail near zero is determined by the drift ratio. The larger this ratio, the more the hazard function falls toward zero. As Fig. 3 reveals, there were large individual differences among subjects. Some subjects showed a high hazard-function tail when nondeprived, which transitioned to a much lower tail after sleep deprivation. The other subjects showed a lower tail initially that, for most subjects, became even lower after sleep deprivation. However, in all cases the model captured the shape of the hazard function and the transition between the nondeprived and sleep-deprived conditions.

Fig. 3.

Hazard functions for individual subjects’ data from experiment 2 (narrow lines) and predicted hazard functions from fits of the one-choice diffusion model (thick lines) for sleep-deprived and nondeprived conditions. The legend in each figure shows the subject number, as well as the model-derived ratio of mean drift rate to SD in drift rate (v/η). The latter provides an index of the length of the right tail of the RT distribution.

The drift ratio v/η is shown below the subject number in each plot in Fig. 3. If the ratio is greater than 3, less than 0.1% of the drift rate distribution is negative, and the function has a high right tail. A value of 2 means that 2.3% of drift rates are negative, and a value of 1 means 15.8% of drift rates are negative. Fig. 3 shows that, as a rule of thumb, if v/η is less than 2, the hazard function decreases to a low right tail.

A measure typically used as an index of behavioral impairment on the PVT is the number of lapses: that is, the number of RTs greater than some cutoff, conventionally 500 ms (11). The model fit the RT distributions well, and the hazard functions (Fig. 3) indicate it also captured the right tails of the distributions well. Thus, it should accurately predict the proportions of lapses. Fig. 2D plots the proportions of lapses for the 500 ms cut-off as well as a 1,500-ms cut-off. The plots show excellent correspondence between model and data. For the 500-ms cut-off, the correlation between the proportion of lapses and the drift ratio is −0.71, which confirms that v/η indexes the spread in the tail of the RT distribution.

Discussion

Despite hundreds of studies and real-world applications in many domains, there has been no cognitive model that satisfactorily explains how one-choice decisions are made. It has not been possible to know what the components of processing are or which components are affected by such variables as stimulus difficulty or sleep deprivation. The one-boundary diffusion model presented here captures the full data (RT distributions and hazard functions) for one-choice decision tasks. It assigns effects of difficulty and sleep deprivation to the quality of the information on which a decision is made (i.e., drift rates) and its across-trial variability, not to stimulus-encoding processes or the decision criterion. The drift rates determined from the data have external validity, tracking an independently derived measure of alertness across 36 h of sleep deprivation.

Smith (12) presented a model for one-choice RTs based on two processes, a change-detector and a level-detector (i.e., a system that responds to a transient change in visual stimuli and a system that responds to steady-state or sustained intensity levels, respectively). The combination was designed to produce peaked hazard functions with long tails, with the change-detector producing a highly peaked function and the level-detector producing a sustained longer tail. Model parameters include rate constants representing the growth of evidence in stages for each system, parameters representing visual contrast sensitivity, and decision-process variables. These parameters are not constrained by the data from experiment 1, and especially from experiment 2, when considering the millisecond counter stimulus of the PVT (as it is not a perceptual luminance stimulus). The model of Smith (12) could conceivably be refined to explain RT distributions from the PVT, but in its published form it is overdetermined and has a more restricted range of applicability than our model.

In experiment 1, the quality of the information on which decisions were made was significantly correlated across individuals between the one- and two-choice tasks. This finding indicates that the combination of the diffusion models provides a unified explanation of behavior in the two types of tasks, with the same assumptions about components of processing operating in the same ways and the same diffusion decision process. The correlations also show that the evidence extracted from stimuli as instantiated in the models is similar between the two task types.

In sum, diffusion models provide a unified and comprehensive account of simple decision making. The model presented here supports this claim by extending diffusion decision models that have been applied to two-choice and multichoice tasks (26) to one-choice tasks. What is special about the one-choice model is that the data provide a RT distribution and the model extracts a d′-like measure, v/η. The results from experiment 1 provide quantitative evidence to support the view that one- and two-choice tasks use a common underlying decision mechanism, and the results from experiment 2 also give unique insight into the effects of sleep deprivation on components of cognitive processing.

Methods

Experiment 1.

Method.

For both the one-choice and two-choice tasks, each stimulus was a 20 × 20 square of pixels (Fig. 1E). It was centered in a 100 × 100 square of randomly placed black and white pixels, an equal number of each, on a gray background (the whole display was 640 × 480 pixels on a 17-inch monitor). The 20 × 20-pixel array subtended an angle of 0.6° when subjects were seated at a normal viewing distance of 57 cm. The stimulus was dynamic; on every frame of the video display, a different random sample of pixels for both the background and the stimulus was presented. There were six blocks of one-choice trials, 96 trials per block, and six blocks of two-choice trials, 96 trials per block. The blocks were presented in random order and subjects were cued with the type of task at the beginning of every block.

Each one-choice trial began with the gray background for 835 ms, and then the 100 × 100 background was displayed. After a delay of 500 ms plus an exponentially distributed amount of time with a mean of 750 ms (implemented as a discrete exponential function with 100 distinct durations), the 20 × 20 stimulus patch changed brightness (the total delay ranged from 500 to 3,454 ms). There was a 2,000-ms time-out after stimulus onset if a response had not been made. After the subject's response, or time-out, the screen returned to the gray background. Difficulty was manipulated with three levels of brightness and three levels of equivalent darkness, that is, 62%, 59%, and 56% of black and 62%, 59%, and 56% of white pixels.

Each two-choice trial also began with the gray background for 835 ms. Then, the 100 × 100-background array and the 20 × 20 stimulus appeared simultaneously. The levels of brightness/darkness were 56%, 54%, or 52% of black or white pixels. Note that the most difficult conditions in the one-choice trials had the same stimulus pixel proportions as the easiest conditions in the two-choice trials. The other proportions were different because pilot results had shown that, if subjects could detect the stimulus in the one-choice task, they performed at ceiling in the two-choice task (see the experiment described in the SI Appendix, where the pixel proportions were the same in one-choice and two-choice tasks and there was variable onset in the two-choice task).

Subjects.

Undergraduate students from Ohio State University participated in the experiment for credit in an introductory psychology class. Fifty-five subjects were tested, each for one 45-min session. Informed consent was obtained from all subjects in accordance with the guidelines and approval of the Ohio State University Institutional Review Board.

Experiment 2.

Method.

On each trial, a millisecond counter was displayed on a computer screen. Subjects were instructed to respond immediately by pressing a response key when the stimulus was presented: that is, when the millisecond counter appeared and began counting up from zero. When the key was pressed, the counter stopped, and the RT in milliseconds was displayed on the screen; it remained on the screen for 1 s. The interval between a response and the next stimulus presentation varied randomly from 2 to 10 s (uniformly distributed in steps of 1 s). The maximum response time was 30 s, at which time the trial timed out and the computer beeped to alert the subject (this occurred very rarely, less than 0.5% of trials). For further details, see ref. 9.

The PVT is a sensitive, validated, and widely used assay of the fatiguing effects of sleep deprivation, with minimal aptitude differences and no significant learning curve (see refs 11, 27, and 28.). PVT responses to sleep deprivation vary substantially among subjects, yet are highly replicable within subjects (24).

Subjects.

As part of a larger study, 19 healthy subjects (ages 21–38; 11 men, 8 women) took part in two experimental sessions, each of which involved 36 h of total sleep deprivation (from 1000 hours until 2200 hours the next day). Every 2 h—that is, for a total of 18 test bouts in each of the two experimental sessions—subjects were tested on the PVT for 20 min. For data analyses, the raw data from the two experimental sessions were combined by test bout by subject. Laboratory conditions (ambient temperature, light, meals, activities, interactions, continuous wakefulness, and prior night's sleep) were strictly controlled. The sleep deprivation sessions were each preceded by a week of sleep satiation, by requiring subjects to spend 12 h in bed for sleep daily (24). The study was approved by the Institutional Review Board of the University of Pennsylvania, and all subjects gave written informed consent.

Model Fitting.

For the one-choice model, there is no explicit mathematical solution for a RT distribution with negative drift rate (which results from across-trial variability). The model was therefore implemented as a simulation using a random walk approximation to the diffusion process with 20,000 iterations per distribution at 0.5-ms step size (29). To fit the model to data, the 0.05, 0.10, …, 0.95 quantiles of the RT distribution were generated from the data. These quantile RTs were used to find the proportion of responses in the RT distribution from the model lying between the data quantiles and these were multiplied by the number of observations to give the expected values (E). The proportions of responses between the data quantiles were 0.05 and these were multiplied by the number of observations to give the observed values (O). RTs greater than 2,000 ms in experiment 1 and 3,000 ms in experiment 2 in both theory and data were pooled to produce a single proportion (in the simulations, if a process had not terminated by this time, it was stopped and 2,000 or 3,000 ms, respectively, was assigned as the RT). This procedure reduced the degrees of freedom in some cases because it reduced the number of quantile bins. However, in experiment 1 the reduction totaled only 67 across all 55 subjects, which means on average the degrees of freedom were reduced by 1.2. For experiment 2, for the individual subject-session analysis, the reduction was 0.8 degrees of freedom and for the grouped analysis, the reduction was 0.4 degrees of freedom.

A χ² statistic Σ(O − E)²/E was computed, and the parameters of the model were adjusted by a simplex minimization routine to minimize the χ² value. A Markov-Chain Monte Carlo algorithm was used to obtain starting values for the simplex minimization routine to achieve robustness to local minima. The model was fit to the data for each individual subject, which allowed individual difference analyses.

For the one-choice data in experiment 1, we also fit the model with variability in drift rate constant across the three levels of difficulty, with the result that the χ² value was a little worse (53.4 as opposed to 47.9 in Table 2). Additionally, we fit the model with nondecision time and the variability in it varying with difficulty, but the overall χ² value did not improve so we did not adopt these variants.

We also fit the one-choice model to the sleep-deprived and nondeprived data from experiment 2 with drift rates constrained to be zero or positive. If the drift rate from the normal distribution of drift rates across trials was selected to be negative in the fitting program, it was set to zero. The result was that the fits and parameter values were quite similar to those in Table 3, and so having zero drift rate instead of negative drift rate produced a long enough tail to allow fits to the observed RT distributions. This result means that it is not necessary to allow negative drift rates, which have the property that some proportion of processes do not terminate in the experimentally allowed time.

The two-choice model was fit to the two-choice data from experiment 1 in the standard way (18), using a χ² minimization routine. The only parameter that was allowed to vary across stimulus difficulty was drift rate. Because “dark” responses to dark stimuli were symmetric with “bright” responses to bright stimuli, the mean starting point of the diffusion process (z) was set to half the distance between the criteria. The data entered into the routine for each level of difficulty were the 0.1, 0.3, 0.5, 0.7, and 0.9 quantile RTs for correct and error responses and the corresponding response proportions. The quantile RTs and the diffusion model were used to generate the predicted cumulative probability of a response by each quantile RT. Subtracting the cumulative probability for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For the χ² computation, these are the expected values, to be compared with the observed proportions of responses between the quantiles. Summing over (O − E)²/E for all conditions gave a single χ² value to be minimized.

Variability in drift rate across trials causes a parameter identifiability issue in the one-choice diffusion model that is not encountered in the two-choice diffusion model. Without across-trial variability in drift rate, generating simulated RTs from the one-choice diffusion model and fitting the model back to the simulated data leads to accurate recovery of the parameter values. With across-trial variability, however, parameters v, η, and a are not uniquely identified; different starting values in the fitting program produce the same goodness of fit but with parameter values that can differ by as much as 2:1. However, the ratios v/η and a/v remain invariant, as demonstrated in the SI Appendix. Furthermore, the nondecision time is not uniquely determined. However, the range of values of the nondecision time when a and v differ by 2:1 is not large and the value of T_er can be determined to within plus or minus 20 ms in these experiments.