Multiscale approach to link red blood cell dynamics, shear viscosity, and ATP release

Abstract

RBCs are known to release ATP, which acts as a signaling molecule to cause dilation of blood vessels. A reduction in the release of ATP from RBCs has been linked to diseases such as type II diabetes and cystic fibrosis. Furthermore, reduced deformation of RBCs has been correlated with myocardial infarction and coronary heart disease. Because ATP release has been linked to cell deformation, we undertook a multiscale approach to understand the links between single RBC dynamics, ATP release, and macroscopic viscosity all at physiological shear rates. Our experimental approach included microfluidics, ATP measurements using a bioluminescent reaction, and rheology. Using microfluidics technology with high-speed imaging, we visualize the deformation and dynamics of single cells, which are known to undergo motions such as tumbling, swinging, tanktreading, and deformation. We report that shear thinning is not due to cellular deformation as previously believed, but rather it is due to the tumbling-to-tanktreading transition. In addition, our results indicate that ATP release is constant at shear stresses below a threshold (3 Pa), whereas above the threshold ATP release is increased and accompanied by large cellular deformations. Finally, performing experiments with well-known inhibitors, we show that the Pannexin 1 hemichannel is the main avenue for ATP release both above and below the threshold, whereas, the cystic fibrosis transmembrane conductance regulator only contributes to deformation-dependent ATP release above the stress threshold.

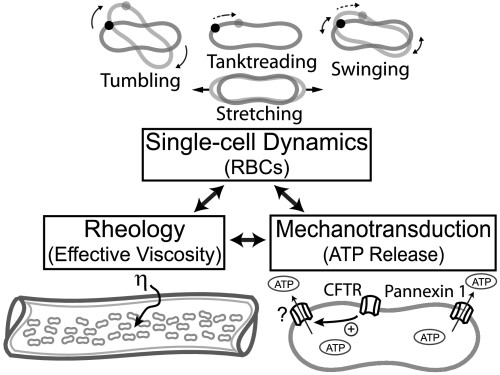
Red blood cells participate in blood flow through chemical signaling and contribute to blood viscosity through their individual motion. For example, RBCs release ATP, which acts as a signaling molecule in the blood plasma, and triggers the release of nitric oxide from endothelial cells, producing vasodilation (1–3). This idea indicates that RBCs are not just inert bags of hemoglobin, but rather are paracrine signaling the vessel wall (4). On the other hand, the traditional characterization of blood flow is through hemorheology, which is the study of the relationship of stress to strain rate and quantifies the blood’s resistance to flow. From such macroscopic studies, it is generally accepted that blood viscosity is affected by hematocrit, plasma viscosity, cell aggregation, and cell deformability (5). As a third pillar of the ideas we integrate, the biophysics literature contains physical models and experiments that give insights into single-cell dynamics in flow (6–8). In this paper, we utilize an experimental approach to elucidate the links between macroscale shear viscosity, microfluidic observations of single cells in flow, and ATP release (Fig. 1). These three topics are generally treated pairwise at most, though are linked in reality, and have not been fully explored to obtain a multiscale view of RBCs, connecting rheology, cell dynamics, and mechanotransduction.

Fig. 1.

A multiscale view of the links between RBC dynamics, shear viscosity, and ATP release. RBC dynamics including tumbling, tanktreading, swinging, and stretching are descriptions of the cell’s mechanical response to flow. ATP release from RBCs through transmembrane channels is a chemical signaling mechanism, which induces vasodilation in the circulation. Shear viscosity η is a macroscale measurement of the blood’s resistance to flow and a contributor to shear stress on the vessel walls.

Unraveling the links between ATP release from RBCs and cellular-scale mechanical responses may provide insight into cardiovascular pathology and therapeutics. ATP is a well-established vasodilator (9). In vivo work has shown that RBCs are required for nitric oxide production in the endothelium, cerebral arteriole vasodilation in hypoxic conditions, and can contribute to reduced pulmonary vascular resistance (1–3). In vitro, RBCs forced to flow through filter paper were found to release ATP proportional to the pore size of the paper, which suggested the importance of cell deformation to ATP release (10). Subsequently, the dependence of ATP release on deformation of individual cells was confirmed by high-speed imaging in microfluidic channels (11). Moreover, many cardiovascular diseases have been linked to reduced RBC deformability, and blood storage has been shown to cause RBC stiffening and reduced ATP release (12, 13). The correlation between deformation and chemical signaling suggests that ATP release may play a role in disease mechanisms and patient outcomes following blood transfusion. For example, cystic fibrosis and type II diabetes have both been linked to reduced release of ATP from RBCs (10, 14, 15). In addition, atherosclerotic plaques tend to localize in regions of low and oscillatory shear stress (16), which is directly controlled by vessel caliber and viscosity, and the earliest manifestations of these plaques are a reduction of nitric oxide (17). Therefore, ATP release, or the lack thereof, may be important in understanding the manifestation of atherosclerosis, but much work remains to be done to understand the role of ATP release in the context of disease.

In order to understand possible links of macroscale rheology and chemical signaling to the dynamics of individual cells, we give a short summary of the several modes of RBC dynamics. Cells have been shown to tumble, which is an end-over-end rigid body rotation, whereas tanktreading is the rotation of the cell membrane around the center of mass of the cell. During tanktreading, an oscillatory movement known as swinging has been observed experimentally, in which the cell’s inclination angle changes periodically, relative to the direction of flow, with an amplitude that decreases with increasing shear rates (6). RBCs are also capable of large-scale deformations or stretching in flows with large shear rates, where the membrane surface area remains constant, and the long axis of the cell extends as the shape changes from an oblate to a prolate ellipsoid. An early model of fluid ellipsoids concluded that tanktreading and tumbling were controlled by the viscosity ratio λ, where λ is the viscosity inside the cell relative to the viscosity of the suspending solution (7). It is now recognized that an elastic component also contributes to the transitions in dynamic modes from tumbling, to swinging, and finally to tanktreading (6, 8). Although these cellular dynamic modes have been implicated as contributing to bulk viscosity (18, 19), experimental evidence unraveling the link between cell dynamics, bulk viscosity, and ATP release is still lacking.

On the subcellular scale, the RBC has a membrane skeleton comprised of a spectrin–actin network that is located just beneath the membrane. Gov and Safran proposed a model that links the ATP release mechanism with cell deformation at this scale (20). The model predicts that cell deformation or large changes in local membrane curvature cause the spectrin proteins to dissociate from actin, and that these topological defects in the network can reduce the shear modulus of the cell. The partially dissociated actin at these defect sites are then free to bind with and activate the cystic fibrosis transmembrane conductance regulator (CFTR) (21), which has been implicated in the ATP release cascade (4, 10). However, the mechanism through which ATP is released from the cell has not been clearly established. Several candidates have been proposed, such as a volume-regulated channel that may act in conjunction with CFTR and Pannexin 1 hemichannels (Px1). More specifically, the CFTR protein has been shown to enhance ATP release and is thought to activate another volume-regulated channel rather than release ATP itself (22). In addition, RBCs express Px1 hemichannels, which have been shown to release ATP when exposed to osmotic stress (23). We investigate Px1 and CFTR in the context of shear stress triggered ATP release.

In this paper, we report that (i) in contrast to the accepted belief that RBC deformation is a major contributor to shear thinning (5), we observe that the tumbling-to-tanktreading transition alters viscosity, whereas significant cell deformation does not begin until shear thinning has ceased. (ii) ATP release has previously been reported to be deformation dependent (10, 11), however, we find that ATP release occurs both in deformation-dependent and independent regimes. We also show that tanktreading does not increase ATP release. (iii) Px1 is involved in both deformation-dependent and independent ATP release, whereas the CFTR plays a larger role in ATP release during deformation. In summary, our ATP measurements, macroscale viscosity measurements, and single-cell observations provide direct evidence for spectrin–actin network topological remodeling, which can apply to cell deformation and ATP release (20, 24).

Results

For all of our experiments, we suspended 10 μL of blood [approximately 40% hematocrit (Hct)] in 430 μL of physiological salt solution (PSS) to produce approximately a 1% Hct solution. Some solutions were mixed with 20 or 40 g/L Dextran (2 × 10⁶ M_r) to produce viscosities ranging from 0.9–7.0 mPa. Assuming that the viscosity inside the cell is 12 mPa (7, 8), the solutions correspond to viscosity ratios λ = 11.1, 3.8, and 1.6, which are the ratio of the viscosity inside the cell to the viscosity of the suspending solution measured at 50 s^-1. Shear rates in the human vascular system have typical values 130 s^-1 in the aorta, 1,000 s^-1 in a typical capillary, and 8,000 s^-1 in the arterioles (25). Therefore, to more closely represent physiological shear rates, our experiments were performed between 50–5,000 s^-1.

Viscosity and ATP Release.

We first study the correlation between the viscosity of the RBC solution and ATP release at varying levels of shear stress. Samples were sheared on a cone-plate viscometer for 30 s at a constant rate between 50 and 5,000 s^-1. The change in viscosity was calculated as η/η_o, where η is the measured effective viscosity of the RBC solution and η_o is the viscosity of the suspending media at the same shear rate (Fig. 2A). The shear stress σ is the shear rate multiplied by the measured effective viscosity η. Following shearing, we gently mixed blood samples with a bioluminescent luciferase/luciferin solution and we used a photomultiplier tube to count photons emitted from the solution. This photon count, which is proportional to the concentration of extracellular ATP, was averaged over five measurements (I). A zero-shear control was taken for each prepared solution (I_o). Consequently, the relative ATP release is reported as (I-I_o)/I_o (Fig. 2B).

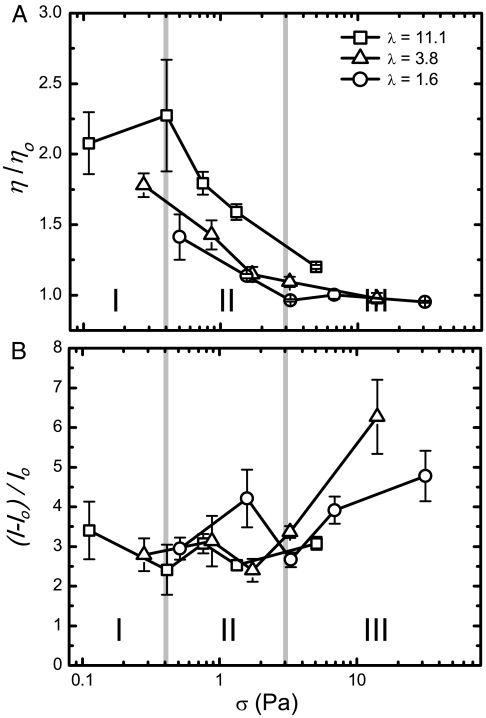
Fig. 2.

Relating the bulk viscosity with ATP release from RBCs. (A) Viscosity parameter η/η_o versus shear stress σ for RBCs in λ = 11.1, 3.8, and 1.6 solutions, where λ is the viscosity contrast. (B) Relative ATP release versus shear stress. Changes between regimes I and II and between II and III identified as approximately 0.4 and 3 Pa, respectively, are labeled with vertical lines. Error bars =  ± 1 SEM; N = 3–7.

The viscosity parameter η/η_o and the change in relative ATP release (I-I_o)/I_o as a function of shear stress σ are reported (Fig. 2). We recognize that the effective viscosity η values are somewhat larger than those reported elsewhere (26), and we believe this is due to a confinement effect, which is consistent throughout our experiments. Hence, our conclusions about the influence of changing shear stress are self-consistent and representative of the stress levels indicated. In particular, we identify a shear-thinning regime in Fig. 2A when σ = 0.4–3 Pa. At shear stresses larger than 3 Pa, we find that the viscosity parameter approaches one. At lower shear stress, σ < 0.4 Pa, the viscosity parameter appears to be unchanged. Based on the changes in η/η_o and (I-I_o)/I_o, we delineate regimes I–III, and in forthcoming sections we will link these regimes to single-cell deformation and dynamics. Specifically, regime II is identified by a sharp decrease in the viscosity parameter (Fig. 2A), but shows no steady increase in relative ATP release. Regime I, which we define as σ < 0.4 Pa, has the largest value of the viscosity parameter. Finally, in regime III at σ > 3 Pa, the ATP release increases above its basal level. In regime III, the viscosity parameter also approaches unity, η/η_o → 1, which means that the solution viscosity is comparable to that of the solvent.

The results in Fig. 2 show that, at lower stress levels (σ < 3 Pa), the ATP released from RBCs is about threefold greater than that found in the solution of the zero-shear control. This observation implies that flow is necessary to produce this basal level of ATP release, but that the level of stress does not make a significant difference on how much ATP is released. The amount of ATP released by the RBCs only increases once the threshold to regime III is reached, at approximately 3 Pa, which coincides with the viscosity parameter approaching one.

Single-Cell Dynamics and Deformation.

In order to better understand the role that cell dynamics play in these viscosity and ATP trends, we developed a second experiment to observe single cells in microfluidic channels, such as tanktreading, tumbling, swinging, and stretching of cells. The channels were 45 μm (h) × 100 μm (w) and cells traveled approximately 300 μm from the channel inlet before reaching the region where we performed high-speed imaging. One micrometer carboxylate microspheres, which randomly adhere to cell membranes, were mixed in solution to identify the dynamics of tanktreading and tumbling. Only cells in the focal plane, away from the wall and not interacting with other cells, were measured. In order to characterize modes of RBC dynamics, we calculate a tumbling ratio as the number of cells tumbling N_tb to the total number of measured cells N_cell at varying shear rates (see Materials and Methods). Given the single view available to us to characterize cell deformation, which we define as the stretch of the cell while constant surface area is maintained, we calculated a stretch ratio L/L_o by measuring the length of each cell L and then averaged the data from all the cells for a given set of conditions; this value was normalized by the average length L_o at the lowest shear rate.

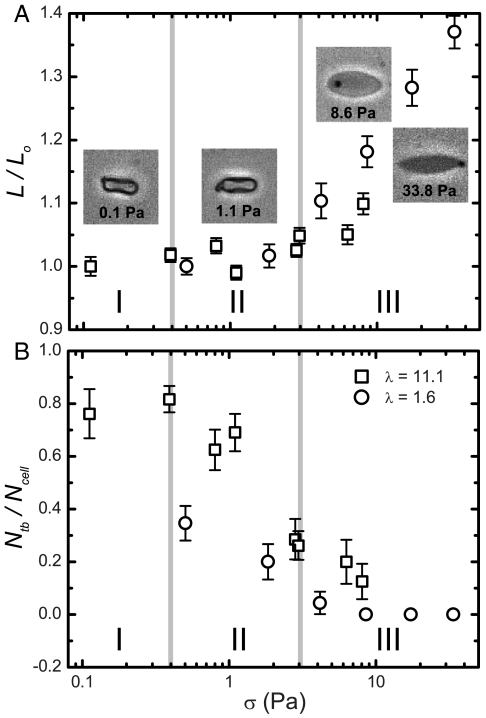
The three regimes relating viscosity and ATP release to shear stress, which were delineated in Fig. 2, are also distinguishable in the microfluidic experiments for RBC stretching and dynamics (Fig. 3). In regime I, there was no cellular-scale deformation (i.e., stretch), and in regime II, the stretch ratios vary only a small amount; λ = 1.6, 1.00 < L/L_o < 1.02 and λ = 11.1, 0.99 < L/L_o < 1.03. In regime III, the deformation increases significantly to L/L_o = 1.37 at 33.8 Pa for λ = 1.6 and L/L_o = 1.10 at 8.0 Pa for λ = 11.1 (Fig. 3A). This deformation is accompanied by a large increase in curvature at the ends of the cell, and the transition from an oblate to a prolate ellipsoid also appears to correspond with the onset of regime III for the λ = 11.1 data (images in Fig. 3A). The stretch ratios do not appear to vary between the two solutions and therefore only depend on shear stress.

Fig. 3.

Microfluidic observations of single cells in flow. (A) The stretch ratio versus shear stress for λ = 11.1 and 1.6 solutions. Images display typical cells and their corresponding shear stress level. (B) The ratio of the number of cells tumbling N_tb to the total number of cells N_cell versus the shear stress. Regimes I, II, and III are as identified in Fig. 2. Error bars =  ± 1 SEM; N = 21–65.

In regime I, more than 75% of the cells are tumbling (Fig. 3B). Not surprisingly, the highest viscosity is found in regime I (Fig. 2A) because tumbling cells disturb a larger volume of fluid, leading to a larger viscosity. Regime II is marked by a decrease in the instances of tumbling; the tumbling ratio decreased from 0.35 to 0.20 for λ = 1.6 and from 0.82 to 0.29 for λ = 11.1. The decreasing viscosity parameter in Fig. 2A is caused by the recruitment of more cells to tanktreading, which has been shown to decrease viscous energy losses (27, 28). However, this effect does not result in an increase in ATP release (Fig. 2B). In regime III, the tumbling ratio for λ = 1.6 reaches zero and, at this point, ATP release levels increase (Fig. 2B).

The transition from tumbling to tanktreading has been described physically as the point when the stress exerted by the flow is sufficient to drive the membrane through a maximum of elastic energy, which is identified with the spectrin–actin network (6, 8, 29). Detailed calculations show that the transition is dependent on the combination of the viscosity contrast and the shear stress normalized by the effective elasticity of the cell (6, 8). Our results are consistent with the idea that shear stress and viscosity contrast are both factors that influence this transition, as evidenced by the disparity between the tumbling ratios for λ = 11.1 and 1.6 (Fig. 3B).

It is widely believed that deformation of RBCs is a major factor in the shear thinning of blood (5). Indeed, over many years, much emphasis in hemorheology has been put on measuring the deformation of RBCs (13, 30–32). However, our results indicate that shear thinning of the RBC solution actually occurs in regime II, where the cells are beginning to tanktread, before cell deformation starts to increase in regime III (Figs. 2A and 3A). Thus, we conclude that, for our flows, shear thinning is due to the reduction in the number of tumbling cells characteristic of regime II and that deformation of individual cells occurs once shear thinning is complete. This result agrees with simulation results, for vesicles, which found that the transition from tumbling to tanktreading was a major contributor to shear thinning (18). This conclusion is an important distinction because both the viscosity contrast and elasticity of the cell contribute to the tumbling-to-tanktreading transition (8), whereas deformability is dominated by the elasticity of the cell membrane with internal viscosity being neglected (33).

Tanktreading and Swinging Analysis.

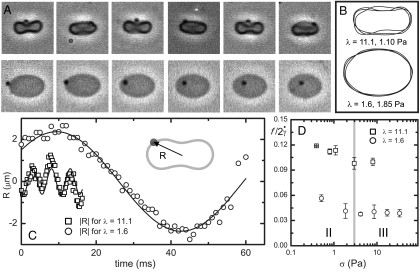
To gain more insight into single-cell dynamics, we investigate the tanktreading frequency of RBCs by tracking beads attached to the cell membrane. Time-lapse images show tanktreading cells for λ = 11.1 and λ = 1.6 (Fig. 4A, Upper and Lower). Using image processing, the cells’ perimeters are scaled up by 200% and overlapped (Fig. 4B). It is clear that the cell for λ = 11.1 is wobbling or swinging, whereas the cell for λ = 1.6 is not. This behavior was typically observed at the lower stress levels found in regime II. The swinging phenomenon is thought to be due to the dissipation of elastic energy stored in the spectrin–actin network during tanktreading (6), which helps to rationalize the lack of deformation in regime II (Fig. 3A). Next, the distance R between the cell’s center of area and a bead attached to the membrane was tracked as a function of time. The data were fit with a sinusoidal function sin(ωt + φ), where ω = 2πf, in order to extract the frequency f in sec^-1 (Fig. 4C). This tanktreading frequency f was then divided by two to represent one full revolution of the bead around the cell and normalized by the shear rate (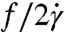). We find 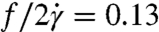for λ = 11.1 and 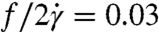for λ = 1.6 for the example cells in Fig. 4 A–C.

Fig. 4.

Analysis of tanktreading of single cells. (A, Upper) Time-lapse images showing tanktreading cell in λ = 11.1 and (A, Lower) for comparison a λ = 1.6 cell. (B, Upper) Multiple outlines of both cell perimeters scaled up and overlapped showing the cell in λ = 11.1 solution swinging or wobbling; in contrast (B, Lower), the λ = 1.6 cell holds a constant orientation. (C) The radial distance to a bead on the membrane is denoted as R. Data corresponding to the images in A, R values versus time for single cells in λ = 11.1 σ = 1.10 Pa and λ = 1.6 σ = 1.85 Pa. Solid curves are fits of sin(ωt + φ). (D) Nondimensional tanktreading frequency, 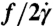, where f = ω/2π, versus shear stress. Error bars =  ± 1 SEM; N = 3–8.

We made measurements on 57 cells to extract average tanktreading frequencies. We found that λ = 11.1 cells tanktread faster than cells for λ = 1.6 (Fig. 4D), which supports the concept that viscosity contrast plays a role in determining RBC dynamics. At larger stresses in regime III, our nondimensional tanktreading frequency levels off to approximately 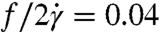for λ = 1.6 and 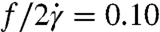for λ = 11.1. The value for the λ = 1.6 data is similar to earlier RBC experimental results in the literature, which range from 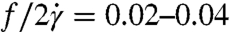for λ = 0.12–1.2 (34). At smaller stress levels (regime II), where the cells are still swinging (Fig. 4D), our nondimensional frequency is slightly larger than in regime III. Larger tanktreading frequencies for swinging cells have also been reported in numerical simulations (35). In contrast to our result that 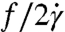is larger for large viscosity contrasts, earlier reports find that this frequency is actually smaller for large viscosity contrasts (34). However, the earlier experimental data (34) were measured at smaller viscosity contrasts. Further, the Keller-Skalak model (KS) does predict larger frequencies for more oblate ellipsoid shapes (7), which may explain the discrepancy because we see oblate cell shapes for λ = 11.1 in regimes I and II. We also observe a different orientation in the λ = 11.1 cells, orthogonal to that described in KS (Fig. 4A).

Regime-Dependent ATP Release Mechanism.

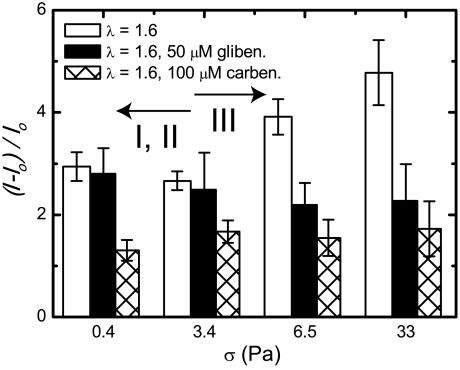
We studied the regime-dependent ATP release (Fig. 2A) by inhibiting two different components of the RBC ATP signaling pathway. In this way, we can identify their contributions to both deformation-dependent (regime III) and independent (regimes I and II) ATP release. Px1, a vertebrate hemichannel, has been identified as one possible pathway for osmotic stress-induced ATP release (23, 36). We chose to use carbenoxolone to block Px1 because carbenoxolone has been shown to selectively block Px1 over other hemichannels with high sensitivity (36). We returned to our cone-plate viscometer and bioluminescent ATP measurements, but now we inhibit Px1 with carbenoxolone; see Materials and Methods. We found that carbenoxolone reduced ATP release, to the same magnitude relative to the zero-shear control, regardless of the stress level or regime (Fig. 5). These results indicate that, under mechanical stress generated by flow, Px1 is the predominant ATP release channel. However, the relative ATP release was not fully inhibited by carbenoxolone, which implies either that carbenoxolone does not completely block Px1 or that another channel is responsible for this additional release found in all regimes. Finally, we observe that carbenoxolone prevents the additional deformation-dependent ATP release characteristic of regime III (σ > 3 Pa), and therefore Px1 is likely the sole channel responsible for deformation-dependent ATP release.

Fig. 5.

Inhibition of ATP release mechanism components. Relative ATP release versus shear stress for RBC solutions in λ = 1.6, controls, 100 μM carbenoxolone thought to inhibit Px1, and 50 μM glibenclamide thought to inhibit CFTR. Regimes I, II, and III are marked with arrows. Error bars =  ± 1 SEM; N = 4–7.

Next, we inhibited the CFTR using glibenclamide; see Materials and Methods. CFTR has been shown to enhance ATP release and is thought to activate another volume-regulated channel rather than release ATP itself (22). We found that, in regimes I and II, CFTR inhibition had little effect on ATP release. However, in regime III, ATP release was greatly reduced to a level similar to that found in Px1 inhibition. From this result, we conclude that CFTR plays a role in deformation-dependent ATP release found in regime III, but not regimes I and II. This conclusion agrees with current models of deformation-dependent ATP release, which find that topological defects in the spectrin–actin network, caused by deformation and curvature changes, lead to CFTR activation (20). Comparing the relative ATP release results in regime III, we hypothesize that CFTR somehow up-regulates Px1 to cause deformation-dependent ATP release, which suggests that Px1 is the volume-regulated channel previously described to interact with CFTR (22).

Discussion

We have shown that shear thinning of RBC solutions is the result of the transition from tumbling to tanktreading, and that RBC deformation (i.e., stretching) does not contribute to the change in solution viscosity. Deformation does, however, play a role in ATP release, whereas the transition from tumbling to tanktreading does not alter ATP release levels. Previously, RBC dynamics such as tumbling had been observed in aged and glutaraldehyde treated cells (19, 37). Other reports have concluded that stiffened RBCs increase viscosity (30), and we believe it is likely that the viscosity was increased because the instances of tumbling were increased, rather than reduced deformation altering the blood viscosity. We find this distinction important because both the viscosity contrast and membrane elasticity of the cell contribute to the tumbling dynamics (6, 8, 37), whereas deformability is dominated by the cell membrane with internal viscosity being neglected (33).

Previous reports on ATP release from RBCs have found that ATP release was proportional to shear stress (10, 11). We find that only in the third regime (σ > 3 Pa), once the cells begin to deform, is ATP release proportional to shear stress. We note that we are measuring cellular deformation or stretching at the scale of the whole cell as L/L_o. It is possible that local shear deformations in the membrane are responsible for the constant ATP release in regimes I and II. We also show that tanktreading does not increase ATP release, because we see no increase in ATP release in regime II where the cells transition from tumbling to tanktreading. In this investigation (always at 1% Hct), the total ATP release for λ = 11.1, taken at a shear rate of 1,000 s^-1, was 0.31 μM, where 0.076 μM was the contribution to the total from the zero-shear control. These values agree with previous reports when corrected for Hct; for example, in filter paper experiments, extracellular ATP concentrations of 1–3 μM were measured (10), whereas microfluidic experiments at similar shear rates reported 0.2–1.4 μM ATP (both at 10% Hct) (11). ATP release values for zero-shear controls at λ = 11.1 are also reported (Fig. S1).

At the subcellular level, it has previously been reported that the ability of RBCs to undergo large deformation cannot be explained by static connectivity between the spectrin–actin network and the membrane; as such, topological remodeling has been proposed (20, 24). From a physical viewpoint, the unity-level viscosity parameter (Fig. 2A), increased stretching, and change in membrane curvature (Fig. 3A) all reported in regime III, support the hypothesis that topological defects in the spectrin–actin network reduce the cell’s modulus with increasing shear. These defects could free actin proteins to bind with CFTR, which has been reported to increase ATP release (10), and which we also report in regime III where ATP release is enhanced by cell stretching (Fig. 5). The involvement of Px1 in ATP release for all three regimes (Fig. 5) suggests that this hemichannel may be the volume-regulating channel predicted to interact with CFTR (22). Further, the inhibition of Px1 did not eliminate ATP release relative to the zero-shear control, which implies that there could be another ATP channel; it is also possible that the inhibitor did not block completely all of the Px1 channels.

In order to reach higher shear stresses to cause larger cell deformation, we increased the RBC solution viscosity with dextran. However, we observed rouleaux formation of the RBCs in the presence of this long chain polymer. This aggregation was not observed in PSS (λ = 11.1) and was reduced by increasing the dextran concentration from 2% (λ = 3.8) to 4% (λ = 1.6). Viscosity versus shear rate curves of the 2% dextran-RBC solution showed a hysteresis when comparing increasing and decreasing shear. This hysteresis was negligible for PSS and 4% dextran solutions and is evidence that aggregation forces under these conditions are minimal, and not responsible for the increase in ATP release found in regime III (Fig. S2). As further evidence that the increased ATP release was not due to rouleaux breakup, we repeated experiments in Fig. 2 with 12.5% albumin (λ = 6.7) and 5% glycerol (λ = 9.0), which do not form rouleaux. Both results show the same trends we report here (Fig. S3).

In conclusion, we have linked viscosity, ATP release, cell stretching, and cell dynamics at varying physiological shear rates. With this knowledge, we are in a better position to understand shear stress, its regulation throughout the vasculature, and possible links of shear stress and RBCs to disease states. RBC deformation, which produces increased ATP release at σ > 3 Pa, is known to be reduced in cardiovascular disease, diabetes, and stored blood. Because ATP is a potent vasodilator, the participation of RBCs in flow through ATP signaling, dynamics, and viscosity, which directly affects wall shear stress, may lead to further understanding of essential hypertension and the enhanced efficacy of blood transfusions.

Materials and Methods

RBC and Solution Preparation.

A 10 μL volume of blood was extracted via a pinprick from healthy human donors and was used within 1 h. The blood was diluted to approximately 1% Hct in PSS: 4.7 mM KCl, 2.0 mM CaCl2, 1.2 mM MgSO₄, 140.5 mM NaCl, 21.0 mM tris(hydroxymethyl)aminomethane, and 11.1 mM dextrose; the pH was adjusted to 7.4. The blood suspension was then centrifuged at 135 × g for 4 min and the buffy coat was removed. This procedure was repeated twice to obtain washed RBCs. Blood samples were kept at 25 °C throughout preparation and experiments.

A luciferin/luciferase solution, which was used to detect extracellular ATP in the solution, was prepared by adding 50 μL of 2 mg/mL luciferase and 1.5 mg D-luciferin sodium salt into 5 mL of N₂-quenched PSS buffer. The luciferin/luciferase mixture was used within 6 h of preparation. Ten micromolar carbenoxolone disodium salt stock solution was mixed in distilled water and diluted in 4% dextran PSS. Ten micromolar glibenclamide stock solution was prepared following procedures in ref. 10; it was then diluted to 50 μM in 4% dextran PSS and filtered before mixing with RBCs.

Viscosity and ATP Measurements.

Prepared RBC solutions were slowly rotated for 20 min at 8 rpm on an in-house mixing device to prevent sedimentation during incubation. Samples were sheared on a 25 mm, 0.99°, cone-plate viscometer (MCR 301, Anton Paar), which includes software corrections for inertial effects. To confirm there was no hemolysis in the RBC samples at all stress levels, we tested the supernatant of the samples using a photospectrometer (DU 730, Beckman Coulter) to determine light adsorption at 430 nm.

Immediately following shearing on the viscometer, blood samples were removed from the viscometer and were mixed 50/50 with the luciferase/luciferin solution. A photomultiplier tube (Model R1527P, Hamamatsu) installed in a housing with a high-voltage supply (Model 814, Photon Technology International) was attached to the microscope with a 5× objective. Five measurements of 20 s each were performed on each sample. The background intensity, in the absence of RBCs, was approximately 25 photons per second, 2–5 orders of magnitude below the intensity of signals with RBCs.

Microfluidic Experiments.

Standard soft photolithographic techniques were used to fabricate microchannels of polydimethylsiloxane and glass. For the visualization of tanktreading and tumbling RBCs, 1 μm carboxylate microspheres (Polybead, Polysciences, Inc.) were mixed in solution. Flow was controlled with a syringe pump (PHD 2000, Harvard Apparatus) and a 0.38-mm i.d. tubing connected the syringe to the inlet hole in the device. The cells were visualized using a 40× objective on a light microscope. Video was acquired at 500–4,300 frames per second with a 10–20 μs exposure time using a high-speed camera (Phantom V9.1, Vision Research).

To calculate the average fluid velocity in the microfluidic channel, we identified the fastest free bead in the channel for each experiment and used its velocity as an estimate of the maximum velocity of the flow (u_max). With this observed maximum velocity, the average flow velocity in the channel was estimated as 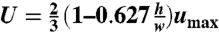, which is a good average velocity estimate for pressure-driven flow through a rectangular cross-section in which 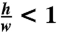. An average shear rate 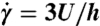was multiplied by the blood sample effective viscosity (η), at the same shear rate, to get an average shear stress (σ).