Abstract
Spindle oscillations are commonly observed during stage 2 of non-rapid eye movement sleep. During sleep spindles, the cerebral cortex and thalamus interact through feedback connections. Both initiation and termination of spindle oscillations are thought to originate in the thalamus based on thalamic recordings and computational models, although some in vivo results suggest otherwise. Here, we have used computer modeling and in vivo multisite recordings from the cortex and the thalamus in cats to examine the involvement of the cortex in spindle oscillations. We found that although the propagation of spindles depended on synaptic interaction within the thalamus, the initiation and termination of spindle sequences critically involved corticothalamic influences.
Introduction
Spindle oscillations, a hallmark of slow-wave sleep, have been linked to a wide spectrum of physiological and cognitive processes, such as synaptic plasticity and memory reconsolidation (Born and Fehm, 1998; Stickgold, 2005). In the human electroencephalogram (EEG), these waves are grouped in short 0.5–3 s periods of 7–15 Hz oscillations, forming a waxing-and-waning envelope that recurs periodically every 5–15 s. These oscillations typically appear during the light stages of slow-wave sleep (stage 2). Spindle waves of similar characteristics also appear during slow-wave sleep in cats and have been observed with the highest occurrence in motor, somatosensory, and associative cortical areas (Morison and Basset, 1945).
Spindles have been recorded from the cat thalamus after in vivo decortication (Morison and Basset, 1945; Contreras et al., 1996; Timofeev and Steriade, 1996). Spindle-like activity has also been found in slices of the dorsal lateral geniculate nucleus of the ferret thalamus that included the perigeniculate nucleus (Bal and McCormick, 1993; von Krosigk et al., 1993; Kim et al., 1995). These observations suggest a thalamic origin for spindle oscillation and raise the possibility that the neocortex is neither needed for the initiation nor the termination of spindles.
It was proposed that a shift of the voltage activation curve of a hyperpolarization-activated nonspecific cation current, Ih (Soltesz et al., 1991; Lüthi and McCormick, 1998a)—found in thalamic relay cells—toward more positive membrane potentials with increasing intracellular Ca2+ concentration is responsible for terminating spindles (Destexhe and Babloyantz, 1993; Destexhe et al., 1993, 1996; Lüthi and McCormick, 1998b). However, in vivo data have suggested a possible involvement of the neocortex (Andersen et al., 1968, Contreras and Steriade, 1996, Timofeev et al., 2001).
We used electrographic in vivo recordings in the cat and a realistic thalamocortical network model of spindle activity to explore the hypothesis that neocortical feedback actively regulates spindle termination in intact thalamocortical networks and have characterized a new mechanism for spindle termination involving the desynchronization of firing between thalamic and cortical neurons. We conclude that the interaction of thalamic and cortical mechanisms underlies sleep spindle termination.
Materials and Methods
We used a computational model of the thalamocortical circuitry (see Fig. 1C) to investigate the interaction between the thalamus and the cortex during spindle generation (Bazhenov et al., 2002). The predictions of the model were tested using multisite in vivo field potential, as well as extracellular and intracellular recordings from thalamic and cortical neurons in the cat.
Figure 1.
Basic spindle properties and model topology. A, Field potential and simultaneous recordings from cortical and thalamocortical neurons. A recording from reticular thalamic neuron was obtained in a different experiment [modified from Timofeev and Bazhenov (2005)]. B(1), [Ca2+]i-dependent shift in the activation curve of the hyperpolarization-activated h-type current, Ih. T-type current, IT, allows Ca2+ ions to enter the cell, bind to the mixed Na+/K+ channel Ih, and modify its voltage-dependent properties. B(2), Binding of Ca2+ ions to Ih channels shifts the voltage dependence of the current toward positive membrane potentials. C, Model topology and structure of the thalamocortical network distributed into four different layers. The TC (thalamocortical relay) neurons and the thalamic RE (reticular) neurons formed two of the layers, strongly interacting with each other. The two cortical layers contained PY (pyramidal excitatory) neurons and IN (inhibitory) neurons. Connections between layers were stochastically distributed. Heterogeneity in the same layer was achieved through a random distribution of parameters for intrinsic properties (see Materials and Methods for details).
In vivo experiments.
All experiments were carried out in accordance with National Institutes of Health Guidelines for the Care and Use of Laboratory Animals, and protocols were approved by the institutional care and use committee at Laval University (Quebec, Canada). All efforts were made to minimize the number of animals used.
The electrophysiological experiments were performed on male cats (n = 5) under general anesthesia with pentobarbital (35 mg/kg) artificially ventilated and paralyzed with 2% gallamine triethiodide. Stability of recordings was insured by draining the cisterna magna and filling the hole made on the skull with 4% agar.
Two tungsten electrodes were inserted 1.5 mm deep in the motor cortex to record depth EEG and monitor spindles occurrence. Juxtacellular recordings were performed from the motor cortex (area 4) with micropipettes filled with 0.5 m potassium acetate. We obtained local field potential recordings with tungsten electrodes from cortical areas simultaneously with dual intracellular recordings with pipettes filled with 2 m potassium acetate from the motor cortex and the thalamic ventral lateral (VL) nucleus. Neuronal activities were recorded by a high-impedance amplifier with active bridge circuitry.
All electrographical recordings were acquired on Nicolet Vision 2.0 data recorder and segments displaying clear spindles were analyzed using IGOR Pro (version 4.0). Spindles were identified on juxtacellular recordings filtered at 7–15 Hz. Initiation and termination of spindles were respectively defined as the first and last cycles for which the amplitude was higher than +1.5 standard deviation of the amplitude of the filtered recording. Spikes were detected from the same original recordings, but the traces were bandpass filtered at 100–10,000 Hz. Spike counts were collected in a time window of 1000 ms around the initiation and termination of spindles and were displayed in perihistograms (time bins set to 5 ms).
Computational model.
Conductance-based models have been used to reveal the neural correlates underlying sleep spindles (Destexhe et al., 1994a, 1996, 1998; Bazhenov et al., 1998, 2000, 2002). These models confirmed that the interactions between reticular and thalamocortical cells were sufficient to account for the main features of sleep spindles, that the low-threshold Ca2+ current, IT, was critical for sustaining the oscillation, and that the cortex influenced spatial and temporal synchronizations.
However, these models relied on in vitro thalamic studies (i.e., in the absence of the cortex), in which calcium (Ca2+) upregulation was the only termination mechanism. To identify how cortical feedback could affect spindles in vivo, we modified a previous thalamocortical model (Bazhenov et al., 2002) by increasing the strength of corticothalamic connections and reducing Ca2+ upregulation to more physiological values.
The thalamocortical network model had four layers: The thalamic model had a layer of thalamocortical relay (TC) neurons and a layer of thalamic reticular (RE) neurons, and the two cortical layers had an excitatory pyramidal neuron (PY) layer and a layer of inhibitory interneurons (INs). The models for the TC and RE cells had a single compartment. Cortical neuron models were based on reduced equivalent models with an axosomatic and dendritic compartments (Pinsky and Rinzel, 1994; Mainen and Sejnowski, 1996) and adequately reproduced the relevant electrophysiological aspects of spindle generation in thalamocortical circuits (Bazhenov et al., 1999; 2000). The ion channels in each compartment are given below.
The spatial patterns of afferents and efferents to these neurons were stochastically distributed according to biological measurements. Network heterogeneity was introduced by stochastically varying the intrinsic cell parameters around the standard values.
Model of intrinsic currents.
Each TC, RE, IN, and PY cell was modeled with voltage- and/or Ca2+-dependent currents described by Hodgkin–Huxley kinetics (Hodgkin and Huxley, 1952),
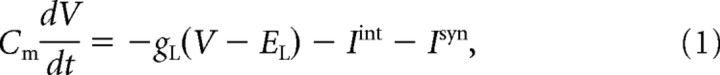 |
where V is the membrane potential, Cm is the membrane capacitance, gL is the leakage conductance, EL is the reversal potential, Iint is a sum of active intrinsic currents of neuron j (Ijint), and Isyn is a sum of synaptic currents (Ijsyn). For the PY and IN neurons, Equation 1 described dendritic membrane voltages; the right side of Equation 1 also included the current from adjacent (axosomatic) compartment, e.g., Id = −gc(Vd − Vs), where Vd (resp. Vs) is the voltage of the dendritic (resp. axosomatic) compartment. The axosomatic and dendritic compartments were coupled by an axial current with conductance gc.
The TC and RE cell models had a fast sodium (Na+) current, INa, a fast potassium (K+) current, IK (Traub and Miles, 1991), a low-threshold Ca2+ current, IT [see Huguenard and McCormick (1992) for TC cells and Huguenard and Prince (1992) for RE cells], and a potassium leak current. A hyperpolarization-activated cation current, Ih, was also included in TC cells (McCormick and Pape, 1990; Destexhe et al., 1996).
The equations and parameters for the ion channels and intracellular calcium dynamics used in this model were taken from Bazhenov et al. (2000, 2002), as summarized below, with the exception of the maximal conductance for Ih, which was varied from gh = 0.02 mS/cm2 to 0.009 mS/cm2.
The cortical PY and IN cell models included a fast Na+ current, INa, with a high density in the axosomatic compartment and a low density in the dendritic compartment. A fast delayed rectifier K+ current, IK, was present in the axosomatic compartment and persistent Na+ current, INa(P), was included in the axosomatic and dendritic compartments (Alzheimer et al., 1993; Kay et al., 1998). A slow voltage-dependent noninactivating K+ current, IKm, a slow Ca2+-dependent K+ current, IKCa, a high-threshold Ca2+ current, IHVA, and a K+ leak current, IKL, were included in the dendritic compartment.
The equations for the voltage- and Ca2+-dependent transition rates for all currents were based on those given in Timofeev et al. (2000) and Bazhenov et al. (2000, 2002) and are summarized here. All the voltage-dependent ionic currents Ijint had the same general form,
where gj is the maximal conductance, m(t) is the activation variable, h(t) is the inactivation variable, and (V − Ej) is the difference between membrane potential and reversal potential. The maximal conductances and passive properties were Ssoma = 1.0 · 10−6 cm2, gNa = 3000 mS/cm2, gK = 200 mS/cm2, gNa(P) = 0.07 mS/cm2 for axosomatic compartments, and Cm = 0.75 μF/cm2, gL = 0.033 mS/cm2, gKL = 0.0025 mS/cm2, Sdend = Ssoma · r, gHVA = 0.01 mS/cm2, gNa = 1.5 mS/cm2, gKCa = 0.3 mS/cm2, gKm = 0.01 mS/cm2, and gNa(P) = 0.07 mS/cm2 for dendritic compartments; EL = −68 mV and EKL = −95 mV. The resistance between compartments was r = 10 MΩ. The reversal potential for low-threshold Ca2+ current was calculated according to the Nernst equation,
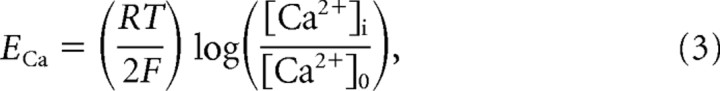 |
where r = 8.31441 J/(mol · K), T = 309.15 K, F = 96,489 C/mol, and [Ca2+]0 = 2 mm.
The intracellular Ca2+ concentration was updated based on Ca2+ currents and pump,
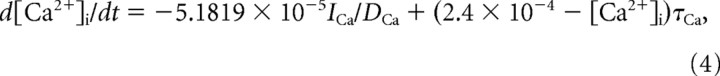 |
where τCa = 300 ms and DCa = 0.85. The gating variables 0 ≤ m(t), h(t) ≤1 satisfied
where a dot implies the time derivative and m∞(V), h∞(V), τ∞(V) are nonlinear functions of V derived from experimental recordings of ionic currents, which can be found in Bazhenov et al. (2000).
Network geometry and simulation.
The thalamocortical model consisted of 325 cells segregated in a four-layer array of 100 PYs, REs, and TCs, and 25 INs (see Fig. 1C). Similar to previously studied network configurations, the intrathalamic and intracortical connections in the model were local and topographically organized, following a stochastic distribution of synaptic weights. Synaptic connections for PY cells included AMPA and NMDA receptors. Connections from TC to RE neurons had AMPA receptors, and connections from RE to TC neurons had GABAA and GABAB receptors. Corticothalamic and thalamocortical connections were wider and mediated by AMPA; corticothalamic connections with AMPA receptors were stronger in reticular neurons than in relay cells.
Postsynaptic receptors were modeled with a simplified first-order kinetic scheme of binding and unbinding of a neurotransmitter described by instantaneous rise and exponential decay of synaptic conductances (Destexhe et al., 1994b). The values for the maximal conductances (for each synapse) were taken from Bazhenov et al. (2002) and listed in detail therein. The total synaptic strengths from the cortex to the thalamus (feedback) and from the thalamus to the cortex (feedforward) were varied over a range of values (see Results for more details). These maximal synaptic conductances were divided by the number of synapses targeting a given cell to determine the unitary conductances. AMPAergic synapses between PYs included short-term depression with a constant of U = 0.073 per action potential and exponential recovery and a time constant of τ = 700 ms (Tsodyks and Markram, 1997). The spontaneous synaptic activity was modeled by Poisson-distributed synaptic events at dendrites of all PY neurons and interneurons.
Reduction of calcium upregulation.
The model for the hyperpolarization-activated cation current, Ih, in the TC neurons was taken from McCormick and Pape (1990) and included both voltage and Ca2+ dependencies (Destexhe et al., 1996). The voltage dependence followed first-order kinetics for transitions between closed (C) and open (O) states of the channels without inactivation:
 |
where α(V) and β(V) are the voltage-dependent transition rates [see Huguenard and McCormick (1992) and McCormick and Pape (1990) for the equations of α(V) and β(V)].
The Ca2+ dependence was based on higher-order kinetics: The binding of Ca2+ molecules with an unbound form of the regulation factor P0 led to the bound form of P1. Then, P1 bound to the open state of channel O that produced the locked form OL:
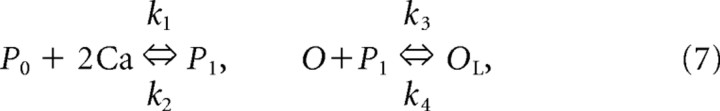 |
Both open and locked states of the channels contributed to the h-current,
where Eh = −40 mV and k is a parameter that was varied to modulate the contribution of Ca2+ dependence to the strength of the current. Initially, we set k = 2.0 based on previous studies [see Destexhe et al. (1996), in which there was a strong [Ca2+]i dependence on the channel dynamics]. This parameter was progressively reduced to the value k = 0.9, because we observed at this value a transition in the spindling dynamics to continous spindle-like activity. The fractions of the channels in the open [O] and locked [OL] forms were calculated according to Equations 6 and 7 (where k1 = 2.5 × 107 mm−4 ms−1, k2 = 4 × 10−4 ms−1, k3 = 0.1 ms−1, and k4 = 0.001 ms−1 are the rate constants).
Data analysis.
All simulations were performed using custom C++ code that implemented a fourth-order Runge–Kutta integration method with a time step of 0.02 ms. The source code was compiled using GCC compilers. Modeling data were analyzed, processed, and displayed using MATLAB R14 (MathWorks). Data obtained in vivo were analyzed using IGOR Pro (WaveMetrics).
Results
A typical in vivo intracellular recording of a sleep spindle in the cat, shown in Figure 1A, has three distinct phases: (1) a waxing (beginning) phase; (2) a middle (main) phase; and (3) a waning (end) phase (Timofeev et al., 2001; Timofeev and Bazhenov, 2005).
In the waxing phase, spindles started with a series of IPSPs in TC (thalamocortical relay) neurons, but these IPSPs were not followed by rebound spike bursts in TC cells (Fig. 1Ai). In the middle phase of the spindle epoch, rebound bursts and Na+ spikes cyclically recurred in many TC cells due to the mutual interaction between RE and TC cells (Fig. 1Aii). These rebound spike bursts in TC neurons excited both RE and cortical neurons. In this phase, the firing of cortical, RE, and TC neurons were phase locked.
Finally, the waning phase of the oscillation and its termination were characterized by less regular spiking of thalamic and cortical neurons (Fig. 1Aiii). In vitro, the primary mechanism underlying the waning phase has been tied to the upregulation of the nonspecific h-type current, Ih. Intracellular calcium concentration ([Ca2+]i) increases in TC cells during spindles because of Ca2+ entry through several types of Ca2+ channels, primarily low-threshold Ca2+ channels [Fig. 1B(1)]. An increase of [Ca2+]i causes a shift in the activation curve of Ih [Fig. 1B(2)]. Progressive increase of [Ca2+]i in TC cells during spindles leads to a persistent Ih activation that depolarizes TC cells and may inactivate the low- threshold Ca2+ current, IT, during the late phases of a spindle sequence (Bal and McCormick, 1996; Budde et al., 1997; Lüthi and McCormick, 1998a).
We used a combination of modeling, juxtacellular, and dual intracellular recordings to explore the possible involvement of the cerebral cortex in spindle initiation and termination in vivo.
The model reproduces waxing-and-waning spindle oscillations
The thalamocortical network model based on Bazhenov et al. (2002) reproduced the basic properties of spindle oscillations (Fig. 1C). On average, six recurring isolated spindle sequences could be identified from the voltage traces of individual model neurons during a 50 s simulation, an example of which is shown in Figure 2A. The spindles showed typical waxing-and-waning deflection of the membrane potential accompanied with rebound spike bursts in the simulated voltage traces of TC neurons (Fig. 2A, TC trace). The waning phase in the model was mediated by the Ca2+-dependent upregulation of Ih, which led to the depolarization of TC neurons and terminated the oscillation. Immediately following termination, [Ca2+]i remained elevated in TC cells. This residual upregulation of Ih determined the inter-spindle lull duration during which the thalamic network failed to initiate new spindles despite cortical drive.
Figure 2.
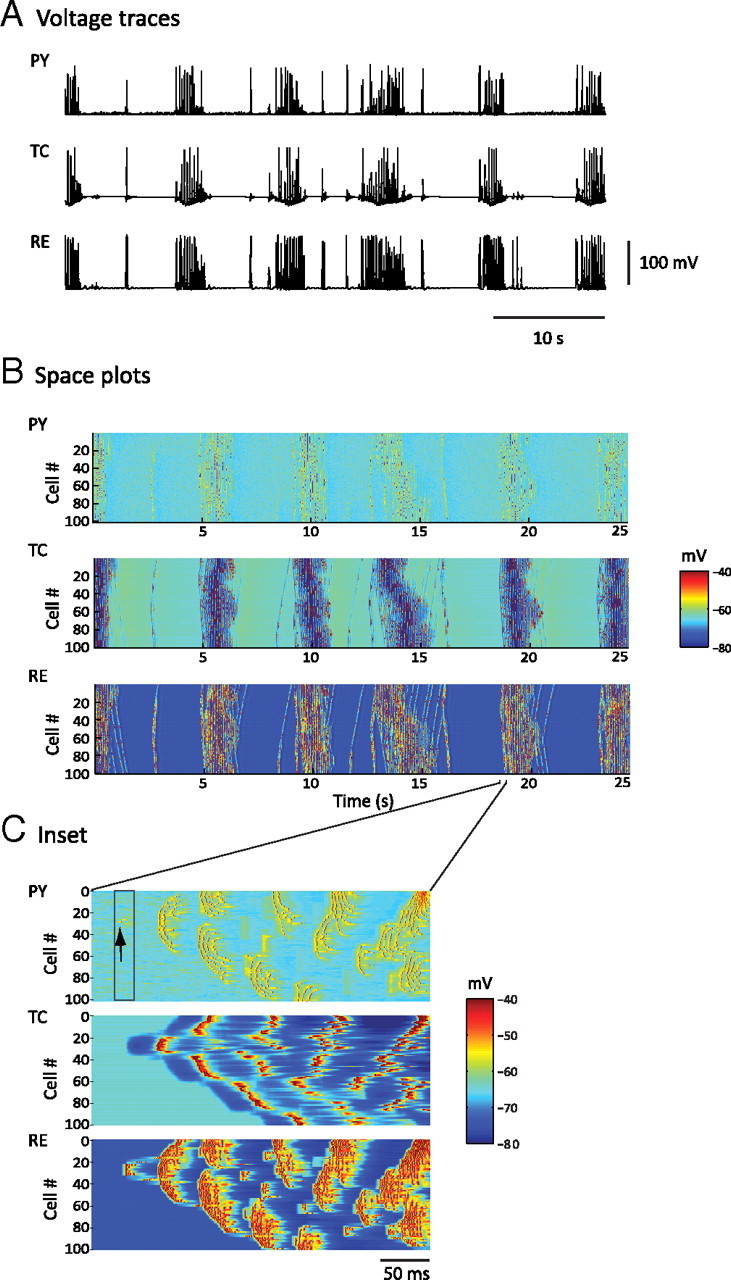
Simulated spindle oscillations. A, Voltage traces of individual neurons [PY (cortical pyramidal), TC (thalamocortical), and RE (reticular thalamic)] in each layer of the thalamocortical network during a 50 s simulation of spindle activity. B, Space–time plot representing the activity of the whole network for 25 s, showing the pattern of wave propagation within the network. Individual membrane potential activity from A corresponds to the cell in the middle of each respective layer (Cell #50 of TC, RE, and PY) of B. The value of the membrane potential for each neuron is coded by the false color scale. C, Enlargement for 350 ms of the space plot in B showing a spontaneous initiation of a spindle cycle. A small subset of PY cells accounted for the genesis of the cycle (black arrow), and RE cells were then recruited. TC cells exhibited far less bursting than RE cells at the beginning of this spindle sequence, and the level of synchrony was lower than that for the middle phase of a sequence.
The spindles also appeared in an isolated thalamus model, consistent with in vitro findings. The synchrony of spindle oscillations was, however, reduced. Adding cortical feedback to the thalamic model enhanced the temporal and spatial synchronizations of spindle discharges within the network, in agreement with in vivo and modeling studies (Contreras et al., 1996; Destexhe et al., 1998). The global phase-locked synchrony between PY, TC, and RE cell populations was apparent on spatiotemporal maps (Fig. 2B).
Cortical mini-EPSPs may initiate spindle oscillations
In the spatiotemporal maps, the spindle wave originated from PY and RE cells (Figs. 2B,C). Thus, cortical volleys were a powerful trigger for spindle initiation in the thalamus. In the model, each spindle sequence started by a random summation of spontaneous mini-EPSPs that triggered spikes in one or a small number of PY neurons (Fig. 2C). These PY cells in turn recruited RE and TC cells through corticothalamic projections, as in previous models (Destexhe et al., 1998). Other mechanisms of spontaneous cortical firing would lead to the same effect. Powerful bursts in RE cells, which received the strongest cortical input, led to hyperpolarization and rebound bursts in some TC cells. These TC afferents then activated more PY neurons, which in turn recruited a larger number of RE and TC neurons. After a few cycles, the entire thalamocortical network was engaged in the spindle sequence, much more quickly than in models of the isolated thalamus, in which spindles propagate slowly by local thalamic recruitment (Destexhe et al., 1996).
Large-scale synchrony was achieved within a few hundreds of milliseconds because of the wide radius of the corticothalamic inputs in the thalamus, consistent with in vivo observations of near simultaneous spindling over widespread cortical and thalamic areas (Contreras et al., 1996, 1997). The corticothalamic feedback was also effective in increasing the global synchrony of TC rebounds and decreasing the local jitter of TC bursts during the middle phase of spindle activity. Invariantly, the firing of cortical neurons initiated spindle sequences.
Once initiated by cortical discharge, the spindles were sustained through reciprocal interactions between TC and RE neurons by means of the interplay between Ih and IT currents in TC cells. As in a previous thalamic model (Destexhe et al., 1996), a burst of spikes in RE neurons led to the hyperpolarization of TC cells, which deinactivated the low-threshold Ca2+ T-channels. Released from the IPSPs, TC neurons produced a low-threshold Ca2+ spike (LTS) rebound crowned by Na+ spikes. This rebound burst in TC neurons then triggered another burst in RE cells and firing of cortical neurons, starting another cycle.
Corticothalamic feedback mediates spindle termination with weak calcium upregulation
Do corticothalamic neurons also participate in terminating spindle sequences together with the Ca2+-dependent upregulation mechanism? We investigated the role of corticothalamic feedback in spindle termination to determine whether corticothalamic feedback could terminate the oscillation when the Ih upregulation failed to do so.
In the absence of cortical input to the model, only one spindle sequence was initiated by a brief external stimulus of the thalamus (at t = 1500 ms) (Fig. 3A). The duration of the spindle in the isolated thalamus increased to 3.66 ± 0.84 from 2.67 ± 0.79 s in the network with intact corticothalamic feedback. Although individual traces of neurons appeared to be phase locked, the spatiotemporal pattern of spindle activity changed substantially. In the absence of the cortical feedback, the oscillation was a traveling wave that propagated from the site of initiation through local connectivity between thalamic RE and TC neurons (data not shown).
Figure 3.
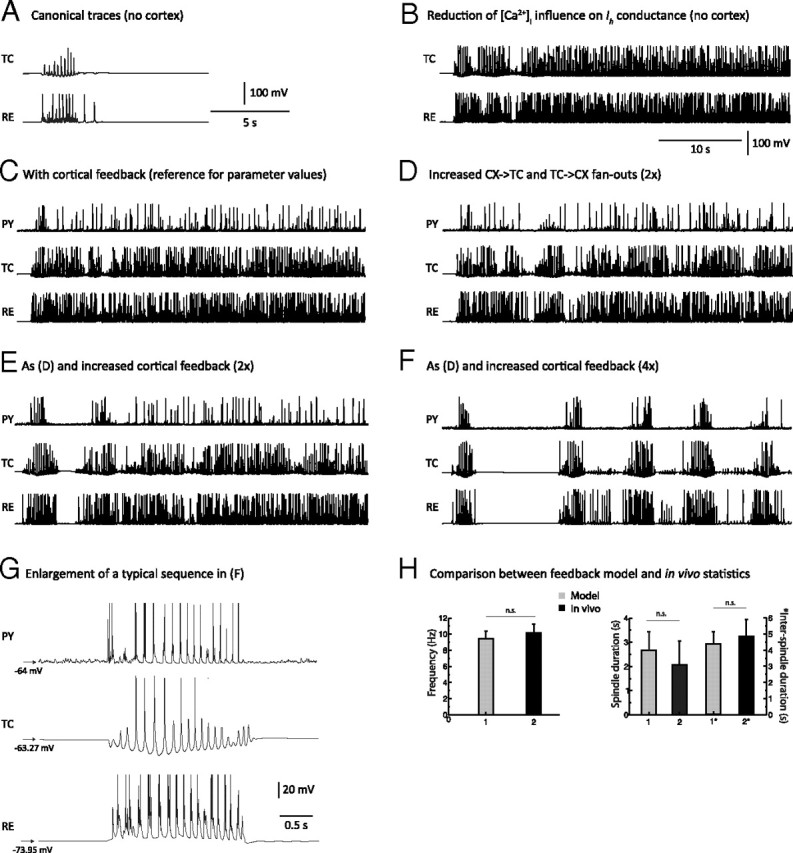
Network mechanisms leading to spindle termination. A, Membrane potentials of TC and RE cells during a 10 s simulation of spindles generated in the thalamic model in absence of the cortex. One occurrence of a spindle sequence with waxing-and-waning properties was initiated by an external stimulation to the RE network. B, The [Ca2+]i influence on h-type current conductance (upregulation) was reduced by ∼55% compared to the value used in A, below the threshold that terminates spindles. The oscillation became continuous. C, The cortical network was added to the model used in B. The total synaptic strength of cortical feedback per cell was identical to the value used in Figure 2A and was sufficient to elicit synchronization of the network but unable to cause spindle termination in presence of a weak Ca2+ upregulation. D, Radii of the corticothalamic (PY→TC) and thalamocortical (TC→PY) afferent projections were doubled from the value used in C. Keeping Ca2+ upregulation low caused a few spontaneous spindle terminations to occur sporadically, but the duration of spindles remained excessively long. E, The total synaptic strength of cortical feedback per cell (PY→{TC,RE}) was doubled from the strength level used in C, while the radius of cortical afferents was the same as that in D. A few spindle epochs are apparent with evidence of a waxing-and-waning pattern (mostly at the beginning of the simulation). F, The total synaptic strength of cortical feedback per cell was quadrupled compared to the value used in C, while the radius of cortical afferents was kept constant from D. The waxing-and-waning envelope of the spindle has shape and duration comparable to the simulation in Figure 2. This demonstrates that a sufficiently strong cortical feedback coupled to a weak Ca2+ upregulation was sufficient for spindle termination and could control the duration of each spindle sequence. G, Membrane potential traces of PY, TC, and RE neurons during a typical waxing-and-waning spindle sequence obtained from a simulation using parameters as described for F. Compare this panel with in vivo data from Figure 1A. H, Statistical comparison of modeling and in vivo data: Left, frequency; right, average spindle sequence duration (1 and 2) and average inter-spindle interval duration (1* and 2*). All differences are statistically nonsignificant, showing that the modeling results agree well with in vivo data.
Reducing the [Ca2+]i dependence of Ih decreased the upregulation and led to a spindle of longer duration. When the [Ca2+]i dependence was reduced to 55% of the baseline, the oscillation became continuous at the spindle frequency (∼10 Hz) because the Ca2+ upregulation of Ih was no longer able to terminate the spindle (Fig. 3B). This threshold value of [Ca2+]i dependence of Ih current was used as the new baseline value for all subsequent simulations.
We then investigated the effects of cortical afferents on the duration and the pattern of these nonterminating sequences. Weak and topographically limited cortical afferents, as found in Bazhenov et al. (2002), only marginally affected persistent thalamocortical oscillation (Fig. 3C). In this configuration, a cortical presence did not contribute to the termination of the oscillatory activity.
These results would appear to support the upregulation of the h-type channel as the main factor underlying spindle termination. However, when the radii of the thalamocortical (feedforward) and corticothalamic (feedback) afferents were doubled, leaving the total synaptic strength per cell unaffected, (1) the continuous oscillation was disrupted, and (2) sporadic terminations occurred (Fig. 3D). Although this oscillation had an abnormally long duration, the waxing-and-waning pattern of the spindle oscillation reappeared sporadically. When the total strength of corticothalamic synaptic input from both TC and RE neurons was doubled and the radius of cortical afferents was also doubled, the temporal segregation of the resulting oscillatory sequences was improved (Fig. 3E), and the waxing-and-waning of the spindle sequence became clearly identifiable at the beginning of the simulation.
If changing the synaptic connection strengths can cause a disruption of the oscillation, then further increasing the strengths might lead to a regime in which cortical feedback can control spindle termination. Indeed, when the total synaptic strength per corticothalamic cell was quadrupled compared to control, five well segregated spindle sequences of finite duration were obtained, interleaved with subthreshold oscillations (Fig. 3F). Thus, despite weak Ca2+ upregulation, spindle epochs were well segregated and became similar to in vivo recordings in frequency, duration, and shape. A typical voltage trace for each cell type in the simulation with a temporal scale similar to that in Figure 1A is displayed in Figure 3G. Sequence duration, inter-spindle lull, and waxing-and-waning properties of the oscillation were comparable to that observed experimentally in vivo (Fig. 3H). The following compares the model versus in vivo values: frequency, 9.43 ± 0.98 versus 10.15 ± 1.12 Hz (p > 0.1, n.s.); average spindle duration, 2.67 ± 0.79 versus 2.06 ± 0.99 s (n.s.); inter-spindle interval: 4.36 ± 0.78 versus 4.88 ± 1.04 s (n.s.). Ca2+ upregulation was itself unable, ceteris paribus, to cause spindle waning unless a moderately strong corticothalamic feedback (measured by a relatively large radius and a high conductance strength) was applied, which supports the involvement of cortical feedback in the waning and termination of spindle sequences. Cortical feedback also enhanced both large-scale spatial and temporal synchronizations of spindles in the model.
Relative impact of corticothalamic feedback on RE and TC neurons
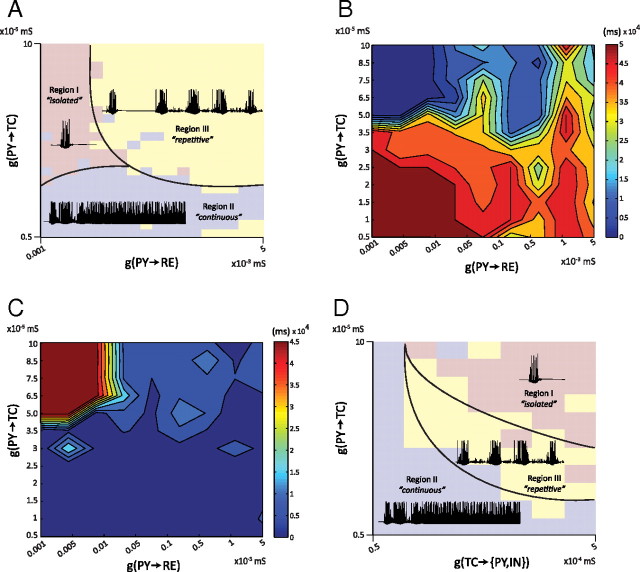
Knowing that cortical feedback can mediate spindle termination and duration, we systematically investigated whether the relative strengths of cortical feedback onto TC cells and RE cells had a differential impact on spindle patterns. A total of 625 different spindle sequences were simulated in the model with the low upregulation of Ih, and the results are summarized on a space-time diagram (Fig. 4A). These simulations were obtained under different combinations of parameters, where the maximal conductances for corticothalamic (gPY→TC) and corticoreticular (gPY→RE) synapses were independently varied from low (5 · 10−6 and 10−6 mS, respectively) to high (10−4 and 5 · 10−3 mS, respectively). In so doing, three qualitative distinct regions of oscillatory activity were observed, herein referred to as follows: (1) “isolated spindle”; (2) “continuous oscillation”; and (3) “repetitive spindles.”
Figure 4.
Differential impact of cortical feedback on spindle pattern. A, Spindle pattern generation for a range of corticothalamic conductances (PY→TC and PY→RE). The Ca2+ upregulation was low and kept constant in all simulations. Three qualitatively distinct regions (Region I, isolated; Region II, continuous; Region III, repetitive) of spindle pattern activity can be distinguished depending on the strength of the cortical feedback. A typical pattern behavior of the TC membrane potential illustrates each of these regions. The borders separating these regions depended on several factors, and the solid lines are smoothed and stylized. B, Total spindling time shown in false color for a range of corticothalamic conductance strengths. Compare to the three regions identified in A. C, Inter-spindle duration in false color, averaged across each simulation, for each point in the diagram of corticothalamic conductance strengths. The longest and shortest inter-spindle durations occurred for isolated spindle patterns and nonterminating oscillations at spindle frequency, respectively. D. Generation of spindle pattern for a range of synaptic conductances (feedforward TC→PY/IN and feedback PY→TC). The thalamocortical (TC→PY/IN) feedforward connection strengths strongly influence spindle pattern. Repetitive spindle patterns were observed only for a narrow range of connection strengths.
The isolated spindle region was defined by only a single spindle sequence occurring during the 50 s simulation. With stronger cortical synaptic inputs onto TC cells and weaker inputs onto RE cells, the network had a low probability to spontaneously generate a spindle sequence; the cortical feedback failed to recruit enough RE cells to entrain a repetitive pattern of oscillation. A single isolated spindle sequence was then followed by a period of quiescence (Fig. 4A, Region I). The continuous oscillation region was characterized by the presence of nonterminating oscillations at spindle frequency (∼10 Hz) that were not temporally segmented and neither waned nor terminated. These nonterminating oscillations appeared when the cortical feedback onto TC cells was too weak to induce a waning of the oscillation (Fig. 4A, Region II). Finally, the repetitive spindle region was characterized by several spindle sequences of finite duration, interleaved by periods of quiescence and exhibiting all of the properties of spindle oscillations that occurred only when the activity of cortical inputs to both TC and RE cells were above a threshold shown in (Fig. 4A, Region III).
The total spindle duration for each simulation (Fig. 4B) and the average inter-spindle lull duration (Fig. 4C) also depended on the strengths of the cortical synaptic feedback onto TC and RE cells, and three regions could be identified corresponding to the qualitatively distinct regions previously described. The isolated spindle region had the shortest total spindle duration (Fig. 4B) and the longest average inter-spindle duration (Fig. 4C). In contrast, the continuous oscillation region had the longest total spindle duration (Fig. 4B) and the shortest average inter-spindle duration (Fig. 4C). Intermediate durations of both spindle sequence and inter-spindle interval characterized the repetitive spindle region (Figs. 4B,C).
We then explored the effects of changing the synaptic strength of the feedforward TC projections on spindle duration. Using the same simulation parameters as the control condition, 625 simulations lasting 50 s each were generated independently varying the strengths of corticothalamic (gPY→TC) and thalamocortical (gTC→PY) inputs. Regions with isolated, continuous, and repetitive spindling were identified (Fig. 4D). As in previous simulations, strong cortical feedback was required to terminate the spindle. When either gTC→PC/IN or gPY→TC inputs were weak, there were nonterminating oscillations at ∼10 Hz (Fig. 4D, Region II). The generation of biologically plausible recurrent spindle sequences only occurred when both the feedforward and feedback connection strengths were strong (Fig. 4D, Region III). Further increasing the strengths of these projections led to solitary, isolated spindles (Fig. 4D, Region I).
Corticothalamic feedback contributes to spindle termination by desynchronizing of thalamic neurons
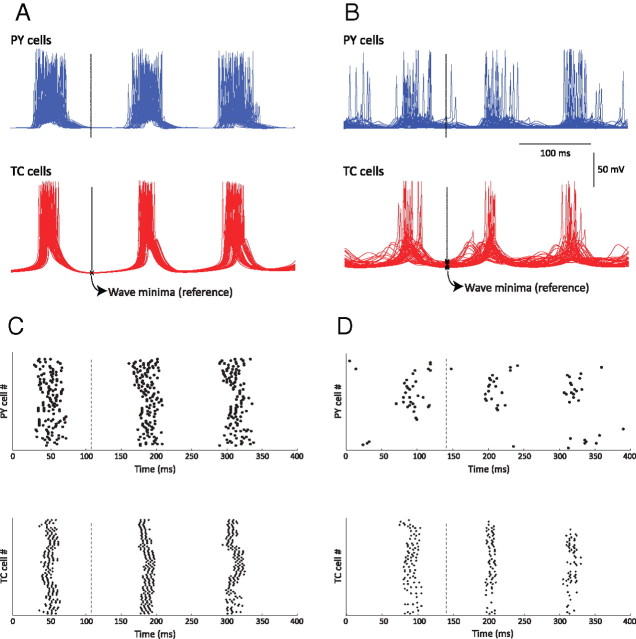
The relative timing of the bursting of TC and PY cells within a single spindle sequence may provide insights into spindle termination. A spindle epoch has three phases: waxing, middle, and waning (Timofeev et al., 2001; Timofeev and Bazhenov, 2005). The spike distributions between thalamic and cortical cells were analyzed during the middle and waning phases. The middle phase of a spindle epoch was defined as a period of relatively stable distribution of TC membrane voltage (∼ −79.17 mV) at the minima between bursts, whereas the waning phase lasted from the first significant depolarization of the minimum membrane voltage between bursts (>−75.8 mV) to the end of bursting (cf. Fig. 1A). The activity of cortical neurons was less synchronized and less periodic during the waning phase than the middle phase. In event-triggered averages aligned by minima of thalamic neuron membrane potential, cortical (PY) population activity was phase locked with TC neurons during the middle phase of a spindle epoch (Fig. 5A,C) but became more desynchronized during the waning phase (Fig. 5B,D).
Figure 5.
IPSP-triggered analysis of spindles in the model. Traces are aligned by minima of TC cell voltage (arrows) to show that cortical population activity is phase locked with TC neurons for each cycle of the spindle oscillation during the middle phase of a spindle. A, Middle phase of a spindle. B, Waning phase (end) of a spindle. C, Raster plots of TC and PY spikes corresponding to the activity in A, showing that TC and PY activities are phase locked in the middle of a spindle sequence. D, Raster plots of TC and PY spikes corresponding to the activity in B, showing that TC and PY activities are more desynchronized at the end of a spindle sequence.
We calculated the time lags between cortical activity and TC membrane potential.
Time lags were calculated as the delay between a wave minimum of TC membrane potential (maximum of IPSP) and the occurrence of the following PY spike for the middle (Fig. 6A) and waning phases (Fig. 6B). The histogram of the time lags for PY spikes was characterized by (1) shorter latencies and (2) a significantly smaller standard deviation for spikes occurring during the middle phase of the spindle epoch (Fig. 6A) compared to spikes fired during the waning phase (Fig. 6B, mean ± SD: 91.2 ± 14.8 vs 114.3 ± 20.2, p < 0.005). The cortical activity became irregular during the waning phase compared to the middle phase, with a distribution of time lags during waning phase ∼25% wider than the middle phase.
Figure 6.
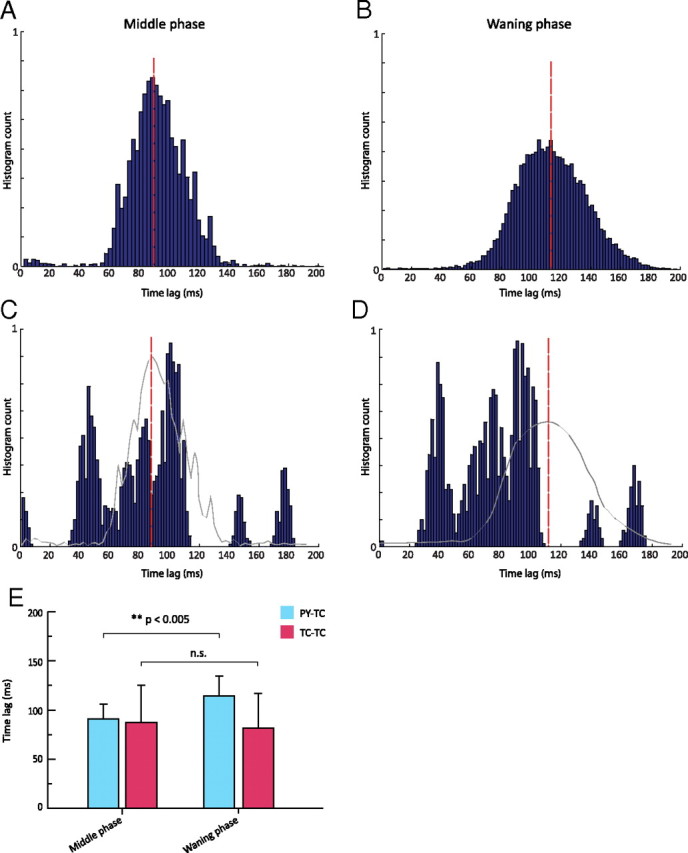
Firing distribution triggered by IPSP in model TC neurons. A, B, Time lag between TC and PY cells firing during the middle of a spindle (A) and during the waning phase (B). The envelope of the histogram in B has a lower amplitude and a wider distribution than that in A, suggesting great variance in the time lag differences between the IPSP before the TC burst and the onset of a spike in an afferent PY cell. The synchronization between cortical and thalamic cells during the middle of a spindle epoch is greater than during the waning phase. C, D, Time lag between TC cells during the middle of a spindle (C) and during the waning phase (D). The red bars show the mean values of the histogram in (A) and (B), respectively. The envelope of the histograms in A and B are superimposed in gray in C and D, respectively. E, Bar plot of mean time lag differences. There was a significant difference between the means for A (91.2 ± 14.8) and B (114.3 ± 20.2) (p < 0.005) (left), but there was no significant difference between the means for C (87.1 ± 38.2) and D (81.5 ± 35.3) (right).
Similar time lags were calculated between wave minima of TC membrane potential and the occurrence of a rebound spike in the same TC cell for the middle (Fig. 6C) and waning phases (Fig. 6D). In contrast to the distribution of cortical firing with the same time reference (Fig. 6A,B), there was no significant difference between the middle and waning phases (mean ± SD: 87.1 ± 38.2 vs 81.5 ± 35.3, n.s., p > 0.05), confirming that the firing of thalamic cells generally preserves its regularity throughout the spindle sequence. The statistical analysis is summarized in Figure 6E.
We conclude that during the waning phase of a spindle, the asynchronous firing of cortical neurons imposes a steady depolarization on TC neurons, preventing the deinactivation of IT and, therefore, inhibiting the generation of rebound bursts. This shows that cortical asynchronous firing (1) begins before the termination of spindles, and (2) contributes to or triggers the termination of spindles generated in the thalamus.
Role of corticothalamic feedback in spindle termination in vivo
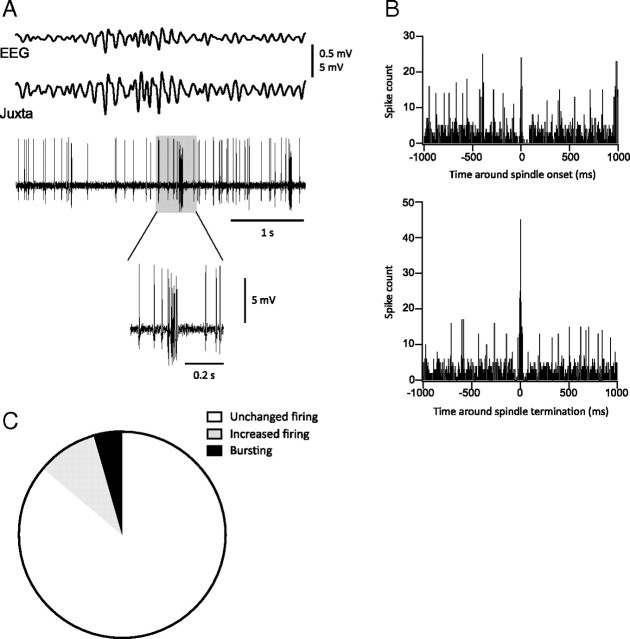
Our model predicted that the precision of neuronal firing is a critical parameter for spindle progression; therefore, we performed juxtacellular recordings in the motor (n = 22) area of the neocortex that neither shunted currents nor affected the firing rates. Spikes were counted around the initiation and termination of spindles. An example of electrophysiological recordings of a neuron (located at a cortical depth of 2000 μm) that fired bursts of action potentials at spindle termination is shown in Figure 7A. There was a higher incidence of spikes at the termination of spindles compared to their initiation (Fig. 7B). Of the 22 neurons recorded, three of them (13.64%) showed a higher incidence of firing at spindle termination, and among these, one was found to burst (4.55%). An increase of the cortical firing rate that is desynchronized with respect to thalamic activity is likely to terminate the spindle. Although such an increase was not a necessary condition for spindle termination in the model, we also observed slightly increased firing rates in a few but not in a majority of the neurons. In the model, desynchronization of cortical firing, even with no increase of the firing rate, was sufficient to terminate spindles.
Figure 7.
Action potential firing in neurons from motor cortex (area 4) during spindles. A, Example of typical simultaneous field potentials and juxtacellular recordings (bottom traces) illustrating bursting at termination of spindles compared to EEG recordings (top traces). The shaded box on the juxtacellular trace is expanded below. B, Histograms of spikes count occurring 1000 ms (bins of 5 ms) around spindles onset (top) and waning (bottom). Note that spikes count is higher at termination than at onset. C, Proportion of neurons that fire at spindle termination: 86.36% (white area) had unchanged firing rate, while 9.09% (gray area) increased their firing rate without bursting and 4.55% (black area) increased their firing rate while bursting.
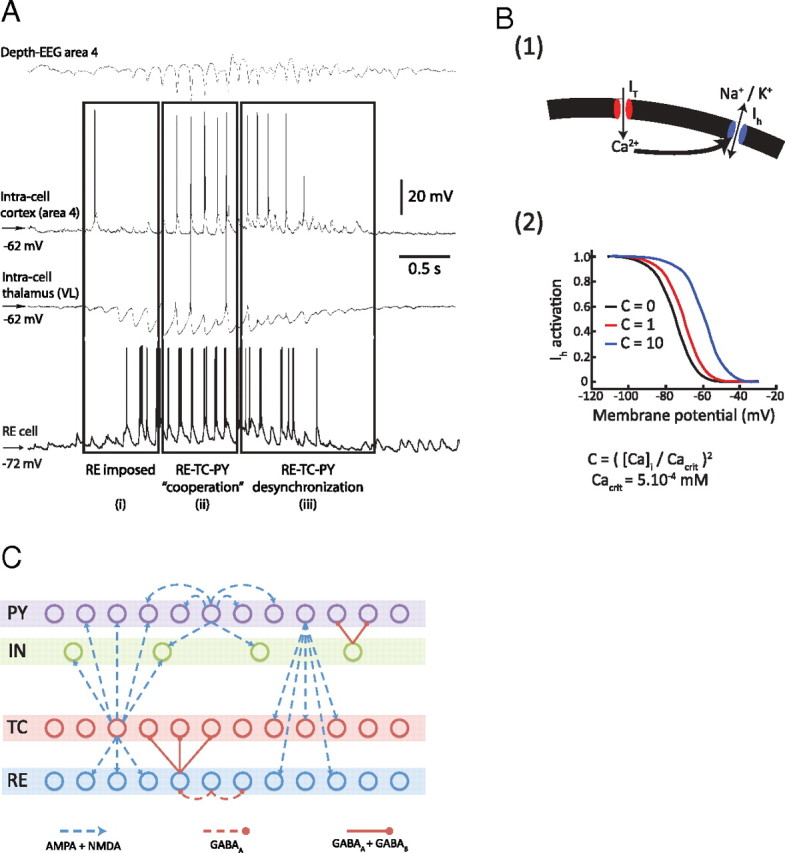
To further test the prediction of the model that a decrease of thalamocortical synchronization contributes to the termination of spindle events, simultaneous dual intracellular recordings (Contreras and Steriade, 1995; Contreras et al., 1996; Timofeev et al., 1996) were performed from thalamic relay neurons (VL nucleus) and cortical cells (motor cortex) during spindle activity (n = 7). In these recordings, TC neurons never displayed rebound spike bursts at the initiation of a spindle sequence—defined as the first IPSP in TC neurons (Fig. 8A). The first rebound spike in TC cells usually occurred after the fourth or fifth IPSP. In cortical neurons, the first EPSPs in a spindle epoch were recorded only when TC neurons started to fire rebound spikes during the middle phase (Fig. 8A,B). At the end of a spindle sequence, the cortical neurons became more depolarized and some started to fire more action potentials, most likely due to recurrent cortical excitation. In these recordings during the waning phase of the spindle oscillation: (1) the cortical firing was no longer phase-locked with the IPSPs in TC neurons (Fig. 8C); (2) the overall hyperpolarization level of TC neurons was reduced; and (3) TC cells rarely exhibited rebound spike bursts. These results confirm the predictions of the model and support the hypothesis that cortically driven depolarization of TC cells during the waning phase of a spindle prevents rebound burst generation in thalamic neurons.
Figure 8.
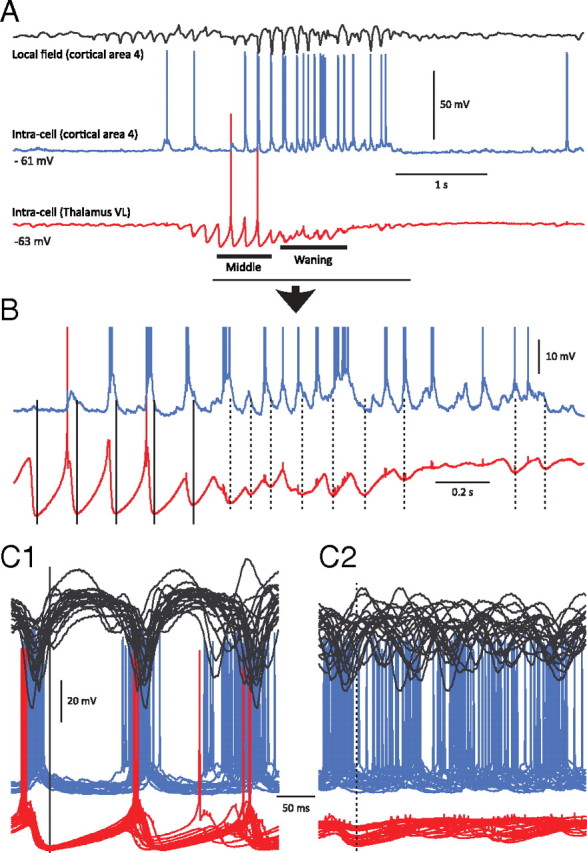
Thalamocortical synchronization at the early, middle, and late portions of spindles in motor cortex and thalamus. A, Simultaneous intracellular recordings during spindles from area 4 of the motor cortex (blue) and the VL nucleus of the thalamus (red). Top trace, Local field potential from motor cortical area 4. Middle trace, Intracellular recording from the same cortical area. Bottom trace, Intracellular recording from the corresponding thalamic VL nucleus. Note that at spindle onset, the thalamocortical neuron exhibits rhythmic IPSPs without rebound action potentials, and the cortical neuron does not show rhythmic EPSPs. B, Expanded from A as indicated by the horizontal line. During waxing but not waning phases, the cortical neuron has rhythmic depolarizing potentials in synchrony with oscillations in the thalamocortical neuron. C1, Superposition of segments of local field potentials and intracellular activities of cortical and thalamocortical neurons during an early phase of spindles. Zero time is set at the maximal hyperpolarization achieved by thalamocortical neurons during a particular cycle of spindle (vertical line). C2, The same arrangement as in C1 but for the waxing phase of the spindle, showing desynchronization between thalamic and cortical firing.
Discussion
It is generally thought that sleep spindles are generated in the thalamus, which then recruits cortical circuits. The evidence presented here, from both intracellular and extracellular unit recordings of cortical and thalamic neurons and from thalamocortical models, gives the cortex a more central role in initiating spindles through corticothalamic AMPA-mediated synaptic feedback to RE cells and in terminating spindle through feedback to TC cells.
Mechanisms for spindle initiation
This study supports the hypothesis that the cortex is actively involved in the initiation of spindle sequences, consistent with the mechanism proposed by Destexhe et al. (1998). In the model, the spontaneous spiking of PY cells triggered bursts of spikes in RE cells at spindle onset. When the cortical feedback to RE cells was reduced, external thalamic stimulation was required to initiate a spindle and the thalamic network was unable to sustain repetitive spindle activity on its own. Cortical feedback was also critical during the first few cycles of normal spindle oscillations when the involvement of TC cells was minimal. Later in the spindle progression, the thalamic network alone could only sustain the oscillation when many TC cells were active.
When an input to the thalamus was sufficiently strong, powerful bursts could be triggered in RE cells, and an immediate LTS response in TC neurons could initiate a spindle sequence even without cortical involvement. However, early cortical involvement was essential for spindle progression when there were only relatively weak bursts in the RE cells during the waxing phase of the spindle and the responses of TC cells were minimal.
Mechanisms for spindle termination
The presence of waning at the end of a spindle, followed by its termination in the deafferented thalamus, supports the idea that the thalamus has properties that can sufficiently mediate spindle termination. This hypothesis has also been supported by computational studies in which the strength of thalamocortical feedback was usually kept weak, leading to a dominant—if not exclusive—role of the aforementioned Ca2+-dependent upregulating mechanism (Destexhe et al., 1998; Bazhenov et al., 2000). Based on in vitro studies, it has been proposed that the progressive depolarization undergone by TC cells during a spindle sequence—caused by an activation shift of Ih toward more depolarized potentials (McCormick and Pape, 1990)—prevents TC neurons from reaching a sufficient level of hyperpolarization required to deinactivate IT, thus mediating the termination of spindles.
In vivo studies have suggested, however, that cortical feedback may significantly shorten spindle duration and possibly contribute to its termination (Timofeev et al., 2001). In our model, weak Ca2+ upregulation of Ih channels was unable by itself to terminate spindle sequences but nonetheless reduced the strength of TC rebounds, leading to larger spike delays and less synchronous spiking in all cortical cells during the last phase of a spindle. The influence of the neocortex on spindle termination depended both on the strengths and patterns of connectivity in the thalamocortical and corticothalamic projections and was primarily mediated by the desynchronizing impact of cortical spikes on thalamic relay neurons. The spiking activities in the cortex and the thalamus were phase locked during the middle part of the spindle, but as the spindle waned the cortical activity fell out of step with activity in the thalamus. This desynchronization between thalamic and cortical structures caused the cortical feedback to depolarize both RE and TC neurons, which prevented the deinactivation of the low threshold T-type Ca2+ channels in TC cells normally involved in spindle generation and eventually led to the termination of the spindle sequence.
Simultaneous intracellular recordings from the thalamus and the neocortex further confirmed the prediction from the model regarding the loss of coordinated TC spiking during waning. Both our computational and in vivo data therefore provide compelling evidence that corticothalamic input effectively desynchronizes the thalamic network during waning and indeed contributes to termination. In conclusion, our model predicts that spindle termination depends on both Ih upregulation and corticothalamic feedback.
Dual role of cortical synchronization and desynchronization
Although cortical feedback may contribute to spindle termination by desynchronization, this is not its unique function. We have also shown that cortical inputs initiate spindles (Fig. 2C) consistent with experimental results (Steriade et al., 1972; Contreras and Steriade, 1996) and previous computational studies (Destexhe et al., 1998). We have also found that cortical feedback can enhance synchronization during the middle phase, when the TC-PY discharges are phase-locked (Figs. 5A,C, 6, 8C1).
These conclusions are consistent with previous experimental reports on the role of corticothalamic volleys in the synchronizing spindles (Contreras and Steriade, 1996; Contreras et al., 1996, 1997; Destexhe et al., 1998), and thus cortical feedback may have a dual role in synchronizing and desynchronizing spindles. In our model, the thalamo-corticothalamic loop synchronized spindles when thalamocortical input was strong (i.e., during the middle phase of spindle), but then became desynchronizing when rebound bursts in TC cells were weakened as a result of the membrane voltage depolarization—and associated with this inactivation of IT—triggered by even weak Ih upregulation near the end of the spindle epoch.
Functional role of sleep spindles: implications of our study
Sleep spindles have been linked to synaptic plasticity and memory consolidation (Steriade and Timofeev, 2003). Because there is no other sleep oscillation that has been linked to a wider spectrum of cognitive, physiological, and pathological processes than spindles, the possible involvement of the neocortex in actively regulating spindle duration has far reaching implications.
There is a growing literature on how different phases of sleep may affect the consolidation of different types of memories (Born and Fehm, 1998; Stickgold, 2005). Sleep spindle density has been found to be positively correlated with performance on various psychometric scales for intelligence assessment (Bódizs et al., 2005; Schabus et al., 2006; Fogel et al., 2007) and has also been positively correlated with different forms of memory retention (Gais et al., 2002; Clemens et al., 2005). In rodents, induction of long-term potentiation (LTP) causes increased reliability of evoked sleep spindles (Werk et al., 2005) and, conversely, sleep spindle-like activity can produce LTP in preparations of rat somatosensory cortex in vitro (Rosanova and Ulrich, 2005). Similarly, in vivo studies have demonstrated that sleep spindle density increased following reward learning in rats (Eschenko et al., 2006). Spindles are not only present during stage 2 of non-rapid eye movement (nonREM) sleep, but also occur during deeper stages of non-REM sleep [slow-wave sleep (SWS), stages 3 and 4] in concomitance with the slow oscillation. As such, they may be involved in hippocampal-neocortical dialogue, which takes place during SWS (Siapas and Wilson, 1998) and could be important for sleep-dependent memory consolidation (Fogel et al., 2010).
The exact mechanisms by which spindles and sleep oscillations in general participate in memory consolidation remain largely elusive (Sejnowski and Destexhe, 2000; Tononi and Cirelli, 2003) because of several independent mechanisms facilitating TC responses during stimulation in the spindle frequency range. In vivo and computational studies (Bazhenov et al., 1998b; Steriade et al., 1998; Houweling et al., 2002; Timofeev et al., 2002) found that spindle activity could induce an augmentation of neocortical responses and may have a profound impact on intracellular and synaptic plasticity. Massive Ca2+ entry in cortical pyramidal neurons during spindle oscillations may activate the molecular “gate” mediated by protein kinase A, thus opening the door for gene expression over hours (Sejnowski and Destexhe, 2000). Spindles in the prefrontal cortex are coordinated with sharp waves in the hippocampus (Siapas and Wilson, 1998), which raises further questions about the nature of the hippocampal-neocortical dialogue and memory consolidation. This study explored some of the neural mechanisms possibly taking part in these changes.
Conclusion
Spindle oscillations are a complex dance that arise from interactions between neurons in the thalamus and cortex: (1) initiation of spindle sequence depends on random activities of cortical PY neurons, which recruit bursts in RE cells; (2) very few TC cells contribute to the initial phase of the sequence, consistent with the absence of rebound bursts during most early IPSPs; (3) the middle phase of a sequence results from synchronizing interactions in the RE-TC-RE loop (Steriade et al., 1993; von Krosigk et al., 1993); and (4) the termination of spindles is due to the depolarizing action of Ih (Bal and McCormick, 1996) in combination with the depolarizing action of corticothalamic inputs, which is caused by the lack of precise coordination of thalamic and cortical firing during the later phase of spindles. Thus, corticothalamic activity is involved not only in the long-range synchronization of spindles but also in the initiation and termination of individual spindle sequences, thereby controlling spindle duration. The active involvement of the cortex in determining spindle duration could influence cognitive processes during sleep, including memory consolidation as well as pathological states such as nocturnal seizures.
Footnotes
This study was supported by National Institutes of Health (NIH)-National Institute of Biomedical Imaging and Bioengineering Grant 1R01 EB009282 (T.S., M.Ba., and M.Bo.), Howard Hughes Medical Institute (T.S.), Crick Jacobs Center for Theoretical and Computational Biology, Salk Institute (T.B.), NIH-National Institute of Neurological Disorders and StrokeGrant 1R01 NS060870 (M.Ba. and I.T.), Canadian Institutes of Health Research Grants MOP-37862 and MOP-67175 (I.T.), and National Science and Engineering Research Council of Canada Grant 298475 (I.T.). I.T. is a Scholar with the “Fonds de la Recherche en Santé du Québec.” M.Bo. thanks Drs. Jay Coggan, Samat Moldakarimov, and Jeffrey Kwong for valuable comments on the manuscript.
The authors declare no competing financial interests.
References
- Alzheimer C, Schwindt PC, Crill WE. Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. J Neurosci. 1993;13:660–673. doi: 10.1523/JNEUROSCI.13-02-00660.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen P, Andersson S, Lomo T. Thalamo-cortical relations during spontaneous barbiturate spindles. Electroencephalogr Clin Neurophysiol. 1968;24:90. [PubMed] [Google Scholar]
- Bal T, McCormick DA. Mechanisms of oscillatory activity in guinea-pig nucleus reticularis thalami in vitro: a mammalian pacemaker. J Physiol. 1993;468:669–691. doi: 10.1113/jphysiol.1993.sp019794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bal T, McCormick DA. What stops synchronized thalamocortical oscillations? Neuron. 1996;17:297–308. doi: 10.1016/s0896-6273(00)80161-0. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Computational models of thalamocortical augmenting responses. J Neurosci. 1998;18:6444–6465. doi: 10.1523/JNEUROSCI.18-16-06444.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Self-sustained rhythmic activity in the thalamic reticular nucleus mediated by depolarizing GABAA receptor potentials. Nat Neurosci. 1999;2:168–174. doi: 10.1038/5729. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski T. Spiking-bursting activity in the thalamic reticular nucleus initiates sequences of spindle oscillations in thalamic networks. J Neurophysiol. 2000;84:1076–1087. doi: 10.1152/jn.2000.84.2.1076. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Model of thalamocortical slow-wave sleep oscillations and transitions to activated States. J Neurosci. 2002;22:8691–8704. doi: 10.1523/JNEUROSCI.22-19-08691.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bódizs R, Kis T, Lázár AS, Havrán L, Rigó P, Clemens Z, Halász P. Prediction of general mental ability based on neural oscillation measures of sleep. J Sleep Res. 2005;14:285–292. doi: 10.1111/j.1365-2869.2005.00472.x. [DOI] [PubMed] [Google Scholar]
- Born J, Fehm HL. Hypothalamus-pituitary-adrenal activity during human sleep: a coordinating role for the limbic hippocampal system. Exp Clin Endocrinol Diabetes. 1998;106:153–163. doi: 10.1055/s-0029-1211969. [DOI] [PubMed] [Google Scholar]
- Budde T, Biella G, Munsch T, Pape HC. Lack of regulation by intracellular Ca2+ of the hyperpolarization-activated cation current in rat thalamic neurones. J Physiol. 1997;503:79–85. doi: 10.1111/j.1469-7793.1997.079bi.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens Z, Fabó D, Halász P. Overnight verbal memory retention correlates with the number of sleep spindles. Neuroscience. 2005;132:529–535. doi: 10.1016/j.neuroscience.2005.01.011. [DOI] [PubMed] [Google Scholar]
- Contreras D, Steriade M. Cellular basis of EEG slow rhythms: a study of dynamic corticothalamic relationships. J Neurosci. 1995;15:604–622. doi: 10.1523/JNEUROSCI.15-01-00604.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contreras D, Steriade M. Spindle oscillation in cats: the role of corticothalamic feedback in a thalamically generated rhythm. J Physiol. 1996;490:159–179. doi: 10.1113/jphysiol.1996.sp021133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contreras D, Destexhe A, Sejnowski TJ, Steriade M. Control of spatiotemporal coherence of a thalamic oscillation by corticothalamic feedback. Science. 1996;274:771–774. doi: 10.1126/science.274.5288.771. [DOI] [PubMed] [Google Scholar]
- Contreras D, Destexhe A, Sejnowski TJ, Steriade M. Spatiotemporal patterns of spindle oscillations in cortex and thalamus. J Neurosci. 1997;17:1179–1196. doi: 10.1523/JNEUROSCI.17-03-01179.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Babloyantz A. A model of the inward current Ih and its possible role in thalamocortical oscillations. Neuroreport. 1993;4:223–226. doi: 10.1097/00001756-199302000-00028. [DOI] [PubMed] [Google Scholar]
- Destexhe A, McCormick DA, Sejnowski TJ. A model for 8–10 Hz spindling in interconnected thalamic relay and reticularis neurons. Biophys J. 1993;65:2473–2477. doi: 10.1016/S0006-3495(93)81297-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Sejnowski TJ, Steriade M. A model of spindle rhythmicity in the isolated thalamic reticular nucleus. J Neurophysiol. 1994a;72:803–818. doi: 10.1152/jn.1994.72.2.803. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J Comput Neurosci. 1994b;1:195–230. doi: 10.1007/BF00961734. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Bal T, McCormick DA, Sejnowski TJ. Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices. J Neurophysiol. 1996;76:2049–2070. doi: 10.1152/jn.1996.76.3.2049. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Steriade M. Mechanisms underlying the synchronizing action of corticothalamic feedback through inhibition of thalamic relay cells. J Neurophysiol. 1998;79:999–1016. doi: 10.1152/jn.1998.79.2.999. [DOI] [PubMed] [Google Scholar]
- Eschenko O, Mölle M, Born J, Sara SJ. Elevated sleep spindle density after learning or after retrieval in rats. J Neurosci. 2006;26:12914–12920. doi: 10.1523/JNEUROSCI.3175-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogel SM, Smith CT, Cote KA. Dissociable learning-dependent changes in REM and non-REM sleep in declarative and procedural memory systems. Behav Brain Res. 2007;180:48–61. doi: 10.1016/j.bbr.2007.02.037. [DOI] [PubMed] [Google Scholar]
- Fogel SM, Smith CT, Beninger RJ. Too much of a good thing? Elevated baseline sleep spindles predict poor avoidance performance in rats. Brain Res. 2010;1319:112–117. doi: 10.1016/j.brainres.2010.01.026. [DOI] [PubMed] [Google Scholar]
- Gais S, Mölle M, Helms K, Born J. Learning-dependent increases in sleep spindle density. J Neurosci. 2002;22:6830–6834. doi: 10.1523/JNEUROSCI.22-15-06830.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houweling AR, Bazhenov M, Timofeev I, Grenier F, Steriade M, Sejnowski TJ. Frequency-selective augmenting responses by short-term synaptic depression in cat neocortex. J Physiol. 2002;542:599–617. doi: 10.1113/jphysiol.2001.012759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard JR, Prince DA. A novel T-type current underlies prolonged Ca2+-dependent burst firing in GABAergic neurons of rat thalamic reticular nucleus. J Neurosci. 1992;12:3804–3817. doi: 10.1523/JNEUROSCI.12-10-03804.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. J Neurophysiol. 1992;68:1373–1383. doi: 10.1152/jn.1992.68.4.1373. [DOI] [PubMed] [Google Scholar]
- Kay AR, Sugimori M, Llinás R. Kinetic and stochastic properties of a persistent sodium current in mature guinea pig cerebellar Purkinje cells. J Neurophysiol. 1998;80:1167–1179. doi: 10.1152/jn.1998.80.3.1167. [DOI] [PubMed] [Google Scholar]
- Kim U, Bal T, McCormick DA. Spindle waves are propagating synchronized oscillations in the ferret LGNd in vitro. J Neurophysiol. 1995;74:1301–1323. doi: 10.1152/jn.1995.74.3.1301. [DOI] [PubMed] [Google Scholar]
- Lüthi A, McCormick DA. Periodicity of thalamic synchronized oscillations: the role of Ca2+-mediated upregulation of Ih. Neuron. 1998a;20:553–563. doi: 10.1016/s0896-6273(00)80994-0. [DOI] [PubMed] [Google Scholar]
- Lüthi A, McCormick DA. H-current: properties of a neuronal and network pacemaker. Neuron. 1998b;21:9–12. doi: 10.1016/s0896-6273(00)80509-7. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature. 1996;382:363–366. doi: 10.1038/382363a0. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Pape HC. Properties of a hyperpolarization-activated cation current and its role in rhythmic oscillation in thalamic relay neurones. J Physiol. 1990;431:291–318. doi: 10.1113/jphysiol.1990.sp018331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morison RS, Basset DL. Electrical activity of the thalamus and basal ganglia in decorticate cats. J Neurophysiol. 1945;8:309–314. [Google Scholar]
- Pinsky PF, Rinzel J. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. J Comput Neurosci. 1994;1:39–60. doi: 10.1007/BF00962717. [DOI] [PubMed] [Google Scholar]
- Rosanova M, Ulrich D. Pattern-specific associative long-term potentiation induced by a sleep spindle-related spike train. J Neurosci. 2005;25:9398–9405. doi: 10.1523/JNEUROSCI.2149-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schabus M, Hödlmoser K, Gruber G, Sauter C, Anderer P, Klösch G, Parapatics S, Saletu B, Klimesch W, Zeitlhofer J. Sleep spindle-related activity in the human EEG and its relation to general cognitive and learning abilities. Eur J Neurosci. 2006;23:1738–1746. doi: 10.1111/j.1460-9568.2006.04694.x. [DOI] [PubMed] [Google Scholar]
- Sejnowski TJ, Destexhe A. Why do we sleep? Brain Res. 2000;886:208–223. doi: 10.1016/s0006-8993(00)03007-9. [DOI] [PubMed] [Google Scholar]
- Siapas AG, Wilson MA. Coordinated interactions between hippocampal ripples and cortical spindles during slow-wave sleep. Neuron. 1998;21:1123–1128. doi: 10.1016/s0896-6273(00)80629-7. [DOI] [PubMed] [Google Scholar]
- Soltesz I, Lightowler S, Leresche N, Jassik-Gerschenfeld D, Pollard CE, Crunelli V. Two inward currents and the transformation of low-frequency oscillations of rat and cat thalamocortical cells. J Physiol. 1991;441:175–197. doi: 10.1113/jphysiol.1991.sp018745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Timofeev I. Neuronal plasticity in thalamocortical networks during sleep and waking oscillations. Neuron. 2003;37:563–576. doi: 10.1016/s0896-6273(03)00065-5. [DOI] [PubMed] [Google Scholar]
- Steriade M, Wyzinski P. Cortically elicited activities in thalamic reticularis neurons. Brain Res. 1972;42:514–520. doi: 10.1016/0006-8993(72)90552-5. [DOI] [PubMed] [Google Scholar]
- Steriade M, McCormick DA, Sejnowski TJ. Thalamocortical oscillations in the sleeping and aroused brain. Science. 1993;262:679–685. doi: 10.1126/science.8235588. [DOI] [PubMed] [Google Scholar]
- Steriade M, Timofeev I, Grenier F, Dürmüller N. Role of thalamic and cortical neurons in augmenting responses and self-sustained activity: dual intracellular recordings in vivo. J Neurosci. 1998;18:6425–6443. doi: 10.1523/JNEUROSCI.18-16-06425.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stickgold R. Sleep-dependent memory consolidation. Nature. 2005;437:1272–1278. doi: 10.1038/nature04286. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Bazhenov M. Mechanisms and biological role of thalamocortical oscillations. In: Columbus F, editor. Trends in chronobiology research. New York: Nova; 2005. pp. 1–47. [Google Scholar]
- Timofeev I, Steriade M. Low-frequency rhythms in the thalamus of intact-cortex and decorticated cats. J Neurophysiol. 1996;76:4152–4168. doi: 10.1152/jn.1996.76.6.4152. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Grenier F, Bazhenov M, Sejnowski TJ, Steriade M. Origin of slow cortical oscillations in deafferented cortical slabs. Cereb Cortex. 2000;10:1185–1199. doi: 10.1093/cercor/10.12.1185. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Bazhenov M, Sejnowski TJ, Steriade M. Contribution of intrinsic and synaptic factors in the desynchronization of thalamic oscillatory activity. Thal Relat Syst. 2001;1:53–69. [Google Scholar]
- Timofeev I, Grenier F, Bazhenov M, Houweling AR, Sejnowski TJ, Steriade M. Short- and medium-term plasticity associated with augmenting responses in cortical slabs and spindles in intact cortex of cats in vivo. J Physiol. 2002;542:583–598. doi: 10.1113/jphysiol.2001.013479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Cirelli C. Sleep and synaptic homeostasis: a hypothesis. Brain Res Bull. 2003;62:143–150. doi: 10.1016/j.brainresbull.2003.09.004. [DOI] [PubMed] [Google Scholar]
- Traub RD, Miles R. Neuronal networks of the hippocampus. Cambridge, UK: Cambridge UP; 1991. [Google Scholar]
- Tsodyks M, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci U S A. 1997;94:719–723. doi: 10.1073/pnas.94.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Krosigk M, Bal T, McCormick DA. Cellular mechanisms of a synchronized oscillation in the thalamus. Science. 1993;261:361–364. doi: 10.1126/science.8392750. [DOI] [PubMed] [Google Scholar]
- Werk CM, Harbour VL, Chapman CA. Induction of long-term potentiation leads to increased reliability of evoked neocortical spindles in vivo. Neuroscience. 2005;131:793–800. doi: 10.1016/j.neuroscience.2004.12.020. [DOI] [PubMed] [Google Scholar]