Evolution of restraint in a structured rock–paper–scissors community

Abstract

It is not immediately clear how costly behavior that benefits others evolves by natural selection. By saving on inherent costs, individuals that do not contribute socially have a selective advantage over altruists if both types receive equal benefits. Restrained consumption of a common resource is a form of altruism. The cost of this kind of prudent behavior is that restrained individuals give up resources to less-restrained individuals. The benefit of restraint is that better resource management may prolong the persistence of the group. One way to dodge the problem of defection is for altruists to interact disproportionately with other altruists. With limited dispersal, restrained individuals persist because of interaction with like types, whereas it is the unrestrained individuals that must face the negative long-term consequences of their rapacity. Here, we study the evolution of restraint in a community of three competitors exhibiting a nontransitive (rock–paper–scissors) relationship. The nontransitivity ensures a form of negative feedback, whereby improvement in growth of one competitor has the counterintuitive consequence of lowering the density of that improved player. This negative feedback generates detrimental long-term consequences for unrestrained growth. Using both computer simulations and evolution experiments with a nontransitive community of Escherichia coli, we find that restrained growth can evolve under conditions of limited dispersal in which negative feedback is present. This research, thus, highlights a set of ecological conditions sufficient for the evolution of one form of altruism.

Wisely and slow; they stumble that run fast.

William Shakespeare

The conflict between individual and group interests is a common element in many social dilemmas. Consider the rate at which an organism consumes shared resources. Prudent use of common resources promotes the longevity or fecundity of the group; however, any individual that exhibits restraint suffers in competition with those using resources rapidly. Rapacity is selectively favored and the displacement of prudent types by their unrestrained contemporaries occurs despite harmful consequences for the group (1, 2). Restraint in the use of common resources is a form of altruism: behavior that is self-sacrificial and prosocial. Like other types of altruistic behavior, restraint faces a fundamental problem of subversion (3, 4). How can restrained types persist in the midst of would-be cheaters—individuals that have a competitive edge because they are unrestrained? In this article, we address this question directly by outlining ecological conditions sufficient to favor the evolution of restraint.

One ingredient found in most explanations for the evolution of altruism, and thus relevant to the evolution of restraint, is positive assortment. Altruism stands a better chance when altruistic individuals disproportionately help those possessing the genes for altruism (5–9). One of the most obvious ways to achieve positive assortment is through interactions between genetic relatives (10). In such a case, altruistic individuals disproportionately experience beneficial social environments (engineered by their kin), whereas selfish individuals tend to face a milieu lacking prosocial behavior (because their kin tend to be less altruistic). Interaction with kin can occur actively through the choice of relatives as social contacts or passively through the interaction with neighbors in a habitat with limited dispersal. There is now a large body of literature on the effect of active and passive assortment on the evolution of altruism (5, 11–18). At a fundamental level, this research focuses on the distribution of interactions among altruistic and selfish individuals. However, in many systems, these individuals are also interacting with other members of their community (e.g., competing species, predators, prey, mutualists, etc.). It is less common to consider the role of broader ecological interactions on the evolution of various forms of altruism.

Here, we consider the evolution of restraint in communities where ecological interactions generate a type of negative feedback. One of the simplest communities with this property involves three members engaged in nontransitive competition. A simple scenario entails one player incurring a significant cost to harm a second player (e.g., through parasitism or allelopathy) and a third player possessing mildly costly resistance to the harm. Reminiscent of the children's game rock–paper–scissors, the harmer outcompetes the sensitive player, who outcompetes the resistant player; in turn, the resistant player outcompetes the harmer. Such nontransitivity has been reported in plant systems (19, 20) and as we see below, bacterial systems. More generally, in rock–paper–scissors games, each strategy beats one of the other two and is beaten by the third (e.g., paper covers rock but is cut by scissors). Imagine a nontransitive community in which, for convenience, we call the players Rock, Paper, and Scissors. Each type has a rate at which it displaces its victim (e.g., Rocks crush Scissors at some rate). Next, imagine a less-restrained variant of Rock, called Rock*, that displaces Scissors at a faster rate. In a Rock*–Paper–Scissors community, the abundance of Scissors decreases because of the increased prowess of Rock*. As a consequence, Scissors’ victim (Paper) is liberated, which can displace Rock*. In an ironic twist, the improved Rock* decreases in abundance because of the expansion of its victim's victim. This form of negative feedback ensures that a higher displacement rate results in decreased abundance (21–24). Thus, more restrained players may be less prone to extinction, a phenomenon termed “survival of the weakest” (21). A complication arises when considering a community with multiple variants present simultaneously (e.g., Rock and Rock* with Paper and Scissors). The same traits that allow Rock* to displace Scissors faster may render Rock* a better competitor against Rock. In this case, restraint has a selective disadvantage, despite its positive effects on abundance. How then can restraint evolve in a nontransitive community?

Spatial structure can play a critical role promoting restraint in nontransitive systems. Returning to our Rock–Paper–Scissors community, limitation of dispersal results in a patchwork of the three players. A patch of any one player chases its victim and is chased by its enemy (25, 26). Within any patch, an unrestrained variant (Rock*) will replace its restrained counterpart (Rock). However, patches of unrestrained variants are more likely to go extinct. This difference in patch viability favors restraint. Limited dispersal ensures a type of positive assortment where restrained and unrestrained individuals tend to be surrounded by like types. This means that the long-term negative consequences of faster displacement are visited disproportionately on the less-restrained type. Consequently, restraint can be maintained evolutionarily in a structured nontransitive community. This outcome has been shown theoretically in nontransitive triplets and larger communities (27, 28), but there is little empirical work on this topic. This is despite the fact that nontransitive dynamics have been described in natural communities ranging from microbes to animals to plants (19, 20, 29–36).

One well-studied nontransitive system involves strains of Escherichia coli that produce antimicrobial proteins termed colicins (37, 38). Colicin-producing cells possess a plasmid housing the colicin gene as well as a gene coding for a colicin-specific immunity protein. Cells that lack the plasmid, and thus lack immunity, are sensitive to the colicin. However, sensitive cells can experience mutations yielding resistance to colicins. Resistance is caused by alteration or loss of membrane proteins that bind or translocate the colicin. Because these same membrane components are involved in nutrient acquisition, resistance is often costly in the absence of colicins (measured by a reduced growth rate relative to sensitive cells) (39, 40). However, in some cases, the producer incurs even greater costs to carry the colicin plasmid and express immunity constitutively. Thus, these three players constitute a nontransitive community: the sensitive strain outgrows the resistant strain, the resistant strain outgrows the producer, and the producer kills the sensitive strain. Previous work with the three members of the colicin E2 system has shown nontransitivity both in vitro (25) and in vivo (41). Nevertheless, there have been no experimental studies of the evolution of restraint in this system.

In this article, we describe experiments with bacteria that explore how positive assortment and negative ecological feedback influence the evolution of restraint. Of the three players (sensitive, resistant, and producer), we focus on the resistant strain. The mutations that define the resistant strain are costly, and there is evidence from numerous systems that secondary mutations can compensate for the initial costs of antimicrobial resistance (42–46). Thus, we predict that this strain is the most likely to increase its growth rate, making it the most attractive candidate to study factors that would hinder such increase. We place the community in a metapopulation, structured into many subpopulations. We manipulate the pattern of migration within the metapopulation, which affects the degree of positive assortment. Migrations are either restricted to occur between neighboring subpopulations (Restricted treatment) or could occur between any subpopulations (Unrestricted treatment). The evolution of the resistant strain can be compared across migration treatments to gauge the effect of population structure on the evolution of restraint. To identify the role of negative feedback, the evolution of the resistant strain in the full community is compared with the evolution of the resistant strain evolving alone (Community and Alone treatments, respectively). By monitoring the resistant strain in three different types of metapopulations (Restricted Community, Unrestricted Community, and Restricted Alone), we assess the impact of both positive assortment and negative ecological feedback on the evolution of restraint.

Results

Presence of Nontransitivity.

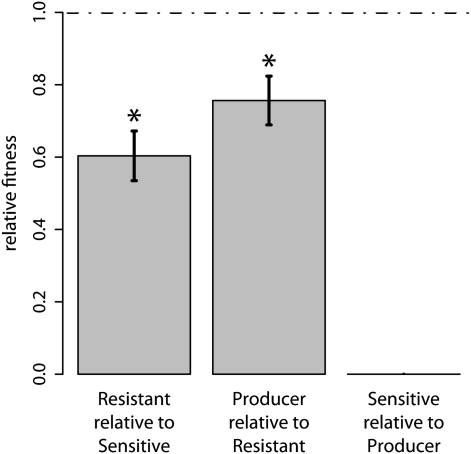
As detailed in Methods, we constructed a strain that produced two colicins (Producer), a strain sensitive to both colicins (Sensitive), and a strain resistant to both colicins (Resistant). The double colicin producer was used to decrease the likelihood of de novo resistance arising from the sensitive population during the evolution experiment. These three constructed strains are henceforth referred to as the ancestors. To confirm the nontransitive relationship, we performed pair-wise competitions among the ancestral strains. Each competition was initiated with a ratio matching the proportions of two competitors when they first meet through migration within the metapopulation. The resistant ancestor was outcompeted by the sensitive ancestor (one-sample t test; t₅ = −5.78, P = 0.0022). The producer ancestor was outgrown by the resistant ancestor (one-sample t test; t₅ = −3.62, P = 0.015). The sensitive ancestor was always driven to extinction when mixed with the producer (giving a relative fitness of zero in all five replicates). Because each player was competitively inferior to the second player (but superior to the third player), these three strains form a nontransitive system (Fig. 1).

Fig. 1.

Pair-wise competitions between the ancestral bacterial strains show nontransitivity. Asterisks signify that relative fitness is significantly less than one, and the error bars show the SEM. The resistant ancestor is dominated by the sensitive ancestor, and the ancestral producer is outgrown by the resistant ancestor. The sensitive strain is killed by the producer in all replicates, yielding a uniform relative fitness of zero. As each strain outcompetes one other strain but is outcompeted by the third strain, a nontransitive relation holds.

Ecological Dynamics.

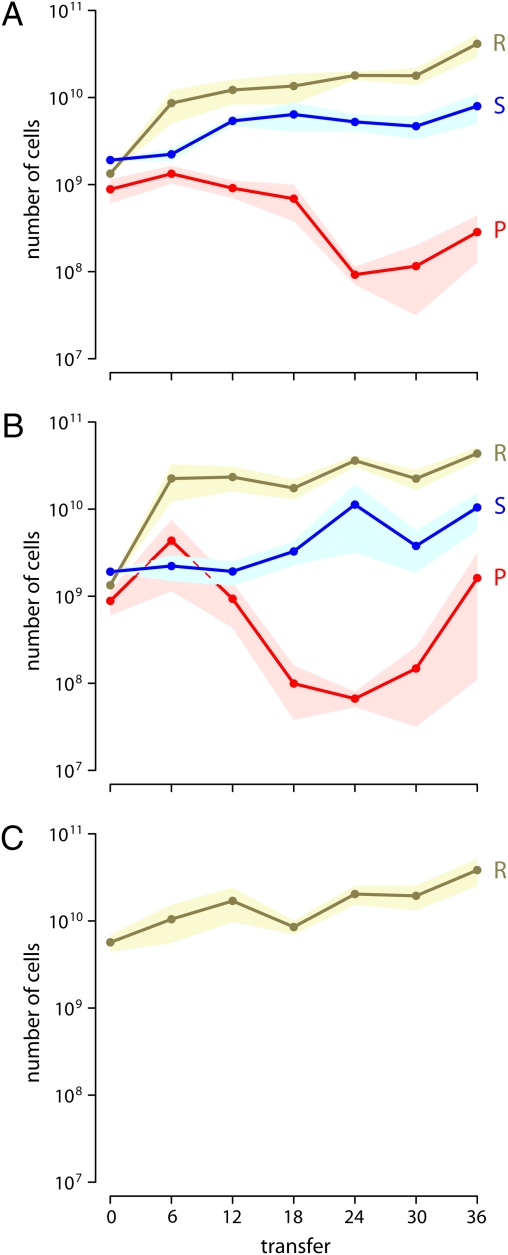
We propagated our bacteria as metapopulations using 96-well microtiter plates, where each well constituted a distinct subpopulation. We initialized the metapopulations with the nontransitive community (Community treatment) or the resistant strain alone (Alone treatment). Every 12 h, each subpopulation was diluted into fresh growth medium, and migrations between subpopulations occurred. Within each metapopulation, migrations occurred between neighboring wells (Restricted treatment) or among any wells (Unrestricted treatment). We measured the abundances of all strains every six transfers. All three players were maintained in the Restricted Community and Unrestricted Community treatments for the duration of the experiment (Fig. 2 A and B). The resistant strain persisted at a constant level in the Restricted Alone treatment for the length of the experiment (Fig. 2C).

Fig. 2.

Bacterial abundance in (A) the Restricted Community treatment, (B) the Unrestricted Community treatment, and (C) the Restricted Alone treatment. Points represent mean abundance of the sensitive strain (S; blue), resistant strain (R; yellow), and producer strain (P; red). Shading gives the SEM. All three players coexisted in the Community treatments for the duration of the experiment, and the density of the resistant strain was comparable across all three treatments.

Evolution of the Resistant Strain.

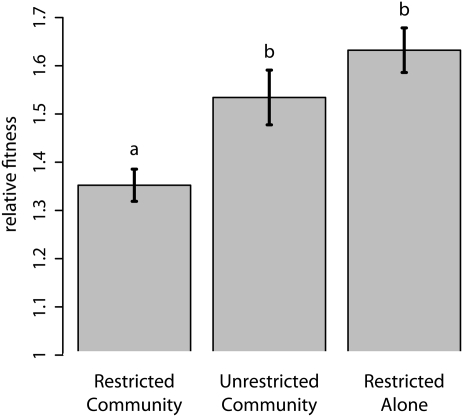
We randomly sampled eight resistant isolates from the last transfer of the experiment. Each of these isolates was competed against a marked variant of the common resistant ancestor. To avoid pseudoreplication, we averaged relative fitness across isolates within each of five replicates of each treatment. We found that isolates from the Restricted Community treatment had the lowest competitive ability [single-factor ANOVA; F_2,12 = 9.36, P = 0.0036, multiple comparisons by Tukey's Honestly Significant Difference (HSD)]. This is consistent with the evolution of a restrained growth rate. Resistant cells in a full community evolved a significantly higher competitive ability under unrestricted migration than under restricted migration (Unrestricted Community vs. Restricted Community in Fig. 3). Resistant cells propagated alone evolved a significantly higher competitive ability than resistant cells in a nontransitive community (Restricted Alone vs. Restricted Community in Fig. 3). Thus, both population structure and the presence of the full community were important to the evolution of competitive restraint.

Fig. 3.

The fitness of evolved resistant isolates relative to their common ancestor. Mean relative fitness of each treatment is shown, and error bars give the SEM. The fitness of isolates from the Restricted Community treatment was significantly lower than the fitness of isolates from the other treatments. Letters distinguish treatments significantly different using posthoc comparisons. This pattern is consistent with the evolution of restrained growth in the Restricted Community treatment.

Simulation of Ecoevolutionary Dynamics.

To better understand the evolutionary behavior of our system, we modeled the bacterial metapopulations using a lattice-based simulation (details in Methods, SI Methods, Table S1, and Figs. S1 and S2). Each metapopulation was initialized with the three ancestral strains in a spatially clumped pattern. The basic algorithm consisted of a cycle of three stages: (i) growth/competition within wells, (ii) dilution of wells, and (iii) migration among wells. Thus, a simulated cycle corresponds to a transfer within our experiment. Every cycle, mutations to growth rate were permitted in resistant subpopulations. We simulated evolution within metapopulations in each of the three treatments described above (Restricted Community, Unrestricted Community, and Restricted Alone).

Although diversity was maintained in the Restricted Community treatment, the community tended to lose players in the Unrestricted Community treatment in the long run (e.g., after 100 transfers). Consequently, the Unrestricted Community treatment was excluded from analysis. The loss of diversity was robust to changes in several different parameters of the model and suggests that the Unrestricted Community treatment in the laboratory may have lost strains if it had been run for more transfers. This result is also consistent with previous work on the importance of limited dispersal to coexistence in this system (25, 26). After evolving the metapopulations in each treatment, we determined the mean relative fitness of the resistant population. Consistent with our empirical results, we found the average growth rate of resistant strains from the Restricted Community treatment to be significantly lower than the average growth rate from the Restricted Alone treatment (Fig. S3).

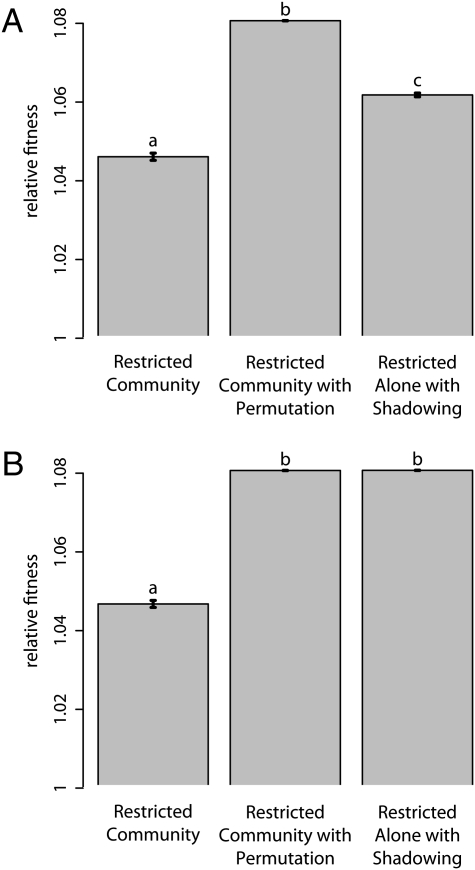
To confirm the importance of positive assortment in the evolution of restraint, we ran an additional treatment: Restricted Community with Permutation. This treatment was identical to the Restricted Community treatment except that, at the beginning of each cycle, wells containing only resistant cells (ancestor or mutants) were randomly permuted. This operation allowed for mixing between the patches of resistant wells (capturing an element from the Unrestricted treatment). The average growth rate of resistant strains from the Restricted Community treatment was significantly lower than the average growth rate from the Restricted Community with Permutation treatment (Fig. 4).

Fig. 4.

The mean resistant fitness relative to the resistant ancestor after simulated evolution in multiple treatments. Fitness values after (A) 100 and (B) 400 cycles are shown. Mean relative fitness of each treatment is shown, and error bars give the SEM. Letters distinguish significantly different treatments by posthoc comparisons. The fitness of resistant populations from the Restricted Community treatment was significantly lower than that of the other treatments at both time points. This pattern is consistent with the evolution of restrained growth in the Restricted Community treatment.

The rate of displacement by fitter variants within any population will be slowed by population subdivision. We were curious if the lower growth rate of our Restricted Community treatment could be explained entirely by the fact that the evolving resistant population was divided into semi-isolated patches. To explore this possibility, we ran an additional simulation treatment: Restricted Alone with Shadowing. In this treatment, a Restricted Alone metapopulation evolved alongside a standard Restricted Community metapopulation, with the caveat that the Restricted Alone metapopulation's migrations and spatial distribution were forced to match the resistant portion of its paired Restricted Community metapopulation. In this way, the Restricted Alone shadowed the Restricted Community. This meant that the Restricted Alone metapopulation was divided into patches. However, because mutation occurred independently in the Restricted Alone shadow and its Restricted Community master, mutations within a given patch in the shadow world had no effect on the survival of the patch in that world. We found that division into semi-isolated patches accounted for some but not all of the effect of lowering growth rate in the short term (Fig. 4A) (single-factor ANOVA; F_2,331 = 829.6, P < 0.001, multiple comparisons by Tukey's HSD). However, simulations that ran for longer (Fig. 4B) show that the Shadowing treatment converges to the Permutation treatment (single-factor ANOVA; F_2,331 = 1,421, P < 0.001, multiple comparisons by Tukey's HSD). We find the same patterns when we run simulations that exactly match the metapopulation size and number of transfers used in our experiment (Figs. S4 and S5). Thus, apparently, the connection between the presence of fast-growing variants within a patch and a greater probability of patch extinction was an important ingredient in explaining the evolution of restraint in the Restricted Community treatment.

Discussion

For the resistant isolates considered here, the evolution of the lowest competitive ability occurred in the treatment in which migration was restricted and all three members of the nontransitive community were present (Fig. 3). If either migration was unrestricted or the resistant strain evolved alone, final competitive ability was significantly higher. The low competitive ability in the Restricted Community treatment presumably reflects a relatively low growth rate. There are a few possible explanations for this outcome. One explanation is that if the number of resistant cell divisions in the Restricted Community treatment was less than the number of divisions in the other treatments, isolates from the Restricted Community treatment might not have had enough opportunity to evolve a higher growth rate. However, we find no significant difference among the treatments in the total number of resistant cell divisions (SI Methods and Fig. S6). A second explanation is that restricted migration slows the spread of any advantageous mutant (47). In this case, resistant mutants with a higher growth rate reach a lower frequency in the Restricted Community treatment than in the Unrestricted Community treatment by the end of the experiment. However, the resistant isolates with the highest growth rate came from Restricted Alone treatment; thus, a restriction to migration does not uniformly hinder the advent of fast-growing resistant mutants. A third explanation is that the presence of producers constrains the manner in which a resistant strain can compensate for the cost of resistance (e.g., reversion to sensitivity is not an option). This would limit the set of evolutionary options for resistant cells in the Restricted Community treatment relative to the Restricted Alone treatment. However, the growth rate of isolates from the treatment with the highest level of interaction between resistant cells and producers (Unrestricted Community) was similar to that of the treatment without producers (Restricted Alone). Additionally, not a single resistant isolate from any treatment reverted to sensitivity; thus, reversion did not explain competitive differences. Finally, the Restricted Community treatment's resistant population was divided into discontinuous regions by barriers consisting of the other strains (illustrated in Fig. 5), and such barriers would inhibit the spread of advantageous mutants. Our simulation-based treatment, Restricted Alone with Shadowing, where the resistant type was restricted to the patchy spatial distribution of Restricted Community evolved a lower growth rate, indicating that population subdivision may contribute to the low growth rate in the Restricted Community. Nonetheless, subdivision does not fully account for the restraint found in the Restricted Community treatment (Fig. 4 and Fig. S5). Thus, we do not find complete support for any of these explanations and instead, favor the following alternative.

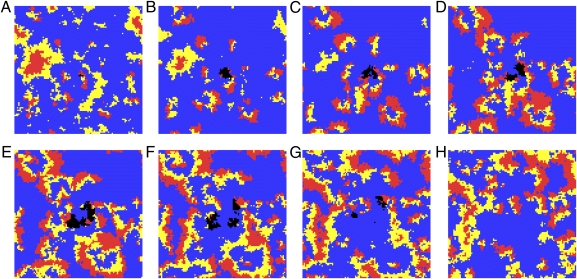
Fig. 5.

Snapshots of a metapopulation from an illustrative Restricted Community simulation recorded every 20 cycles (A–H). The metapopulation was initialized with the three bacterial strains sensitive (blue), resistant (yellow), and producer (red) in addition to a small patch of a mutant resistant strain (black) with an increased growth rate. The mutant initially outcompetes nearby ancestor patches (A–E) but is extinguished after outcompeting neighboring patches of the producer (F–H).

In the Restricted Community treatment, the nontransitivity of the full community provides a form of negative feedback, and the restricted migration ensures a form of positive assortment. We suggest that it is these two factors, negative feedback and positive assortment, that set the stage for the evolution of restraint. In the Restricted Community treatment, we have a set of patches chasing each other (Fig. 5). A faster-growing resistant mutant has a competitive advantage within a resistant patch, but a fast-growing resistant patch is more likely to burn through its victim (the producer) and consequently, face its enemy (the sensitive strain). This sequence of events is shown in Fig. 5 for a Restricted Community simulation in which wells with a faster-growing resistant mutant are labeled in black. Limited migration ensures that it is the unrestrained mutants that reap the negative long-term consequences (patch extinction) of their myopic strategy. When assortment is eradicated by shuffling the contents of multiple patches (as in the simulation-based treatment Restricted Community with Permutation), restraint is not maintained (Fig. 4). Without the negative feedback of the full community (e.g., in the Restricted Alone treatment) or the positive assortment resulting from limited migration (e.g., in the Unrestricted Community treatment), the evolution of restraint is not expected.

We have explored a model system under laboratory conditions, but our findings carry potential implications for other systems. In general, allelopathy permits nontransitivity, and allelopathic bacteriocins are widely distributed across bacterial taxa (48). Nontransitive relationships have also been described in other ecological contexts. For instance, nontransitivity in male mating systems has been reported in common side-blotched lizards (31) and viviparous lizards (36), wherein the males exist in three color morphs: an aggressive morph can displace a less aggressive morph, which displaces a nonaggressive morph. The nonaggressive male is a female mimic, which disproportionately mates with females on the most aggressive male's territory. It has been argued that similar nontransitive mating systems are likely present in other animals, including some reptiles, fish, birds, and insects (36, 49), and nontransitive sperm competition has been reported in fruit flies (32) and domestic fowl (33). Another situation resulting in nontransitivity involves types differing in their colonization and competitive abilities. An overgrower (the best competitor) can displace a fugitive (the best colonizer), which displaces a preemptor (an intermediate colonizer that is resistant to overgrowth); then, the preemptor can displace the original overgrower (50). This type of system was described for a rocky subtidal community (35, 50), and nontransitivity in overgrowth patterns has also been reported in coral reef communities (51). Another instance of nontransitivity involves a victim–exploiter relationship. This situation was reported in a grassland community in which grasses outcompete forb species but are disproportionately parasitized by a root hemiparasitic plant (20). More broadly, many studies have proposed that nontransitive relations may be more prevalent than currently appreciated in systems with frequency-dependent selection or ecological tradeoffs (49, 52, 53).

Although the prevalence of nontransitivities in natural ecosystems remains to be determined (54), the ubiquity of spatial structure is widely recognized. Indeed, spatial structure is a component of many of the nontransitive systems described above. Structure may be most pronounced in sessile organisms (e.g., plants, some marine invertebrates, and microbes in biofilms); however, even populations of motile organisms can possess some degree of structure because of spatial limitations to dispersal and interaction. The spatial scale of ecological processes has been shown to be an important factor in the invasion of rare types (55, 56), coexistence of multiple types (57), stability of communities (58), and evolutionary trajectories of community members (59). We have shown that limited migration in a nontransitive community can promote the evolution of restraint. However, spatial structure can be important for the evolution of restraint in other types of communities as well.

As an example, limited dispersal can promote restraint within victim–exploiter communities (60, 61). An inherent form of negative feedback exists when one species (e.g., predator, parasite, or herbivore) exploits another for critical resources (e.g., prey, host, or plant). To see this, consider a simple version of the Lotka–Volterra model, where the dynamics of exploiters (at density E) and victims (at density V) are described by (Eqs. 1)

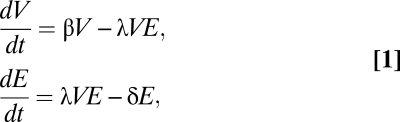where β is the birth rate of victims, λ measures the attack rate of the exploiter, and δ is the death rate of the exploiter (we assume a conversion efficiency of unity). The nontrivial equilibrium for this community is 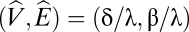. As the exploiter reduces its attack rate, its equilibrium abundance increases (as λ drops, 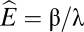grows). Nonetheless, an exploiter with a higher attack rate will displace a second exploiter exercising restraint (62). Selection for rapacious exploitation that results in community collapse constitutes an example of the tragedy of the commons (63). Limited dispersal ensures that any tragedy of the commons that results from overexploitation primarily befalls the unrestrained exploiters. Several theoretical studies have explored the role of spatial structure in promoting restraint in victim–exploiter interactions (64, 65). There have also been experimental demonstrations that limited dispersal favors restraint in host–parasite communities in the form of reduced parasite virulence and/or infectivity (60, 61, 66).

A second example involves the role of structure in promoting restraint in hypercycle communities. A hypercycle is a series of self-replicative molecules cyclically linked, where each molecule catalyzes the replication of the next molecule in the cycle. Unstructured hypercycles are plagued by parasitic molecules, which receive greater catalytic activity from the previous molecule in the cycle while withholding catalytic support for the next molecule in the cycle. Boerlijst and Hogeweg (67) showed theoretically that hypercycles in an incompletely mixed medium could keep parasitic molecules at bay. In a structured habitat, the hypercycle community organizes into a collage of rotating spirals. A parasitic molecule originating at the center of a spiral can lead to spiral demise and replacement by other spirals. Thus, short-term payoffs to the parasite (displacement within a spiral) can generate negative long-term consequences (spiral extinction) in a structured world. This favors the evolution of restrained molecules that avoid the immediate gains of parasitism.

Spatial structure and ecological feedback can also favor mutualistic behavior between species (68). Recently, Harcombe (69) studied a case of bacterial cross-feeding. In lactose medium, Salmonella enterica consumes the acetate waste products of a mutant strain of E. coli. The E. coli mutant was a methionine auxotroph and could grow if S. enterica excreted methionine. Harcombe (69) showed that, although methionine excretion was intrinsically costly, a mutant of S. enterica that exported an excess of methionine was able to displace WT S. enterica (which did not excrete methionine) when these types were grown on lactose plates with E. coli. The cooperative excretion by S. enterica was favored through a combination of ecological feedback (acetate was produced when E. coli obtained methionine) and spatial structure (ensuring that excreting cells had disproportionate access to acetate). When Harcombe (69) destroyed either feedback (by growing the community on acetate plates so that S. enterica did not rely on E. coli) or structure (by growing the community in lactose flasks), the excreting S. enterica mutant was outcompeted by WT. This work shows that ecological feedback and positive assortment can be important ingredients in other forms of cooperation.

In all of the communities described above, a form of altruism exists. The elements that we have underlined as important to the evolution of restraint connect readily to prominent theoretical frameworks used to understand the evolution of altruism. In our nontransitive system, limited dispersal results in a preponderance of interaction between relatives. Kin selection arguments often focus on the coefficient of relatedness between interacting individuals (70, 71). In our system, limited dispersal results in higher coefficients of relatedness than in conditions of unlimited dispersal, a form of positive assortment (72). The multilevel selection framework describes altruism as a behavior opposed by within-group selection but favored by between-group selection (73, 74). In the patchwork of a structured community, a restrained variant is at a local disadvantage (e.g., within its patch), but patches of restrained types may persist longer because of the negative feedback from rapid growth. We propose that multiple frameworks have relevance for understanding restraint in our system, because each framework focuses on (different) important elements underlying the evolution of altruism (75).

Overall, we observe that a form of altruism can evolve in microbial metacommunities. With limited migration, similar types associate into patches that chase one another. The negative feedback resulting from the nontransitivity in our system means that patches filled with unrestrained variants are more prone to extinction. Thus, we see that altruistic restraint is favored precisely when those that run fast tend to stumble.

Methods

Community Players.

The bacterial community consisted of three players: a toxin-producing strain (P), a toxin-sensitive strain (S), and a toxin-resistant strain (R). P expressed two toxins (colicin E2 and colicin D). This strain was constructed by transforming the Col E2 and Col D plasmids sequentially into BK10 (E. coli K-12) cells followed by selecting for resistance to phage T5. S was constructed by transforming the pACYC184 plasmid encoding tetracycline (Tet) resistance into BK10 cells. R was constructed by a series of sequential selections on BK10—resistance to colicin E2, colicin D, and phage T6. Before marker additions (T5, Tet, and T6 resistance), these strains exhibited a rock–paper–scissors relationship. However, the growth inhibition of P and R by a low concentration of Tet (and the cost of T6 resistance in R) magnified the nontransitivity in our growth medium (LB + 0.25 μg/mL Tet).

Experimental Treatments.

The evolution experiments involved propagating metapopulations of bacteria with two factors manipulated. The first experimental factor was the identity of the players in the metapopulation. Either the full community (S-R-P) was used or the resistant strain (R) was propagated alone (the Community or Alone treatments, respectively). In the Community treatments, each metapopulation consisted of two microtiter plates (192 wells with 200 μL growth medium each). In the Alone treatments, each metapopulation consisted of a single microtiter plate (96 wells with 200 μL growth medium each). The difference in the number of wells reflected our attempt to balance the total number of resistant cells across treatments (Fig. 2). The second factor manipulated was the pattern of migration within the metapopulations. Migration was either restricted to occur between wells directly bordering each other along cardinal directions or unrestricted (the Restricted or Unrestricted treatments, respectively). In both treatments, each well had a 1/3 probability of experiencing an immigration event from one random well in its neighborhood. In the Restricted treatment, this neighborhood included the wells directly north, east, south, or west of the focal well (using periodic boundaries to eliminate edge effects). In the Unrestricted treatment, the neighborhood included all wells minus the focal well. Migration events directly followed dilution of the entire metapopulation in fresh growth medium. Every 12 h, 40-fold dilution was accomplished using a 96 slot-pin multiblot replicator (5 μL in 200 μL). Immediately after dilution, a BioRobot 8000 liquid-handling robot (Qiagen) executed the migrations, where each migration involved transferring 5 μL from the source well within the exhausted plate into the destination well within the fresh plate. Between transfers, plates were incubated (37 °C) and shaken (350 rpm using a microtiter shaker, Bellco Glass). For the Alone treatment, the metapopulation was initiated with the resistant strain in each well. For the Community treatment, the initial spatial arrangement of strains was obtained from the 100th transfer of a 192-point lattice-based simulation with a restricted neighborhood (SI Methods). Each metapopulation was propagated for a total of 36 transfers. The abundance of each strain was gauged every six transfers by selective plating (using Tet, T5, and T6). There were five replicates of each of three treatments: (i) Restricted Community, (ii) Unrestricted Community, and (iii) Restricted Alone.

Competition Assay.

We picked eight random resistant isolates from the last transfer of each metapopulation (we denote any one of these strains as R_E). We marked our ancestral resistant strain (denoted R_A) with resistance to phage T5. Before the competition, R_E and R_A are grown separately in 200 μL growth medium for two 12-h cycles (with 40-fold dilution at transfer). After this acclimation phase, we added 5 μL R_E and 5 μL R_A to a well containing 200 μL growth medium. The titer of each strain was assessed (by plating with and without phage T5) immediately after the competition was initiated and again after 12 h. If R_i(t) is the titer of strain R_i at time t, then the fitness of the evolved strain relative to its ancestor is given by (Eq. 2)

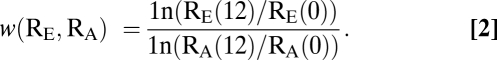The same competitive assay was used to establish the nontransitive dynamic between the three ancestral players (simply with different selective plating schemes).

Simulation.

We model the metapopulation as an L × W regular square lattice with periodic boundaries subjected to a cycle of three phases: (i) growth, (ii) dilution, and (iii) migration. Each lattice point i at time t is described by the vector (Eq. 3)

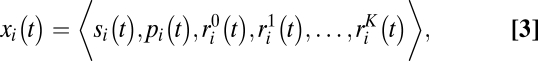where s_i(t), 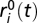, and p_i(t) are the abundances of sensitive, resistant, and producer ancestors, respectively. The variables 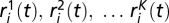are the abundances of each of K types of mutant resistant strains. These abundances are expressed in units of the limiting nutrient concentration (SI Methods).

During the growth phase, the dynamics of each strain (y) of each lattice point (i) are described by the following differential equation (SI Methods) (Eq. 4):

where 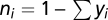, μ_Y is the maximum growth rate, and κ_Y is the Monod constant (nutrient concentration yielding one-half maximum growth rate) of player Y. Each growth phase lasts T time units.

Dilution at time t is given by (Eq. 5)

where ϕ is the dilution factor and t′ marks the postdilution state.

Migration happens with a uniform probability α. If a migration event occurs, a point within the focal point's neighborhood is chosen at random. For the Restricted treatment, the neighborhood is the four nearest lattice points (von Neumann neighborhood). For the Unrestricted treatment, the neighborhood is the entire lattice minus the focal point. In the case of migration, let the chosen neighbor of the focal point i be designated j. The state after migration (signified by t″) is given by (Eq. 6)

Removal occurs next. At point i, any player whose abundance is less than or equal to a critical value (a_crit) is removed. Also, the sensitive player is removed if the producer is present. In the simulation, the dilution, migration, and removal are assumed to be instantaneous and followed by a new growth phase. Lastly, mutation can occur with probability π. In the case of a mutational event, a fraction γ of the total abundance of the resistant players (ancestral and mutant) of a point is converted to a random resistant type.

We initialize lattice point i with the starting abundances of each ancestral player [s_i(0), 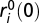, and p_i(0)] using the same method as in the bacterial experiment (SI Methods). After C growth cycles, we measured the expected fitness of a randomly chosen resistant cell relative to the resistant ancestor. This mean fitness is (Eq. 7)

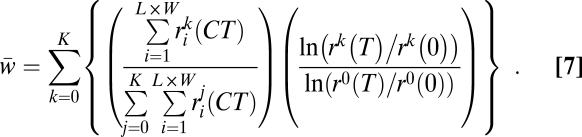In Table 1, we give values for all of the simulation parameters, which are tailored to our bacterial experiment or estimated from assays (SI Methods). For Figs. 4 and 5 and Fig. S3, we assume L = 100 and W = 100. For Figs. S4 and S5, we assume L = 16, W = 12, and C = 36, which are the values corresponding to our laboratory experiment.

Table 1.

Simulation parameters

Parameter	Description (units)	Value(s)
L	Length of the lattice (points)	16 or 100
W	Width of the lattice (points)	12 or 100
T	Duration of growth phase (hours)	12
C	Number of growth cycles (unitless)	36, 100, or 400
K	Number of mutant resistant strains (unitless)	7
μY	Maximum growth rate (abundance per hour)	0.61
{KS,KP,KR0,KR1,KR2,KR3,KR4,KR5,KR6,KR7}	Monod constant of ancestral strains and resistant mutants (abundance)	{0.165, 0.93, 0.341, 0.27, 0.28, 0.29, 0.30, 0.31, 0.32, 0.33}
{ rk(0), r0(0) }	Initial competition amount (abundance)	{1/40, 1/40}
ϕ	Dilution factor (unitless)	1/40
α	Probability of migration (unitless)	1/3
acrit	Critical abundance for persistence (abundance)	0.00275
π	Mutation probability per transfer per well (unitless)	1/100
γ	Fraction of resistant subpopulation converted to a random mutant given a mutation event (unitless)	1/2