Expanded social fitness and Hamilton's rule for kin, kith, and kind

Abstract

Inclusive fitness theory has a combination of simplicity, generality, and accuracy that has made it an extremely successful way of thinking about and modeling effects on kin. However, there are types of social interactions that, although covered, are not illuminated. Here, I expand the inclusive fitness approach and the corresponding neighbor-modulated approach to specify two other kinds of social selection. Kind selection, which includes greenbeards and many nonadditive games, is where selection depends on an actor's trait having different effects on others depending on whether they share the trait. Kith selection includes social effects that do not require either kin or kind, such as mutualism and manipulation. It involves social effects of a trait that affect a partner, with feedback to the actor's fitness. I derive expanded versions of Hamilton's rule for kith and kind selection, generalizing Hamilton's insight that we can model social selection through a sum of fitness effects, each multiplied by an appropriate association coefficient. Kinship is, thus, only one of the important types of association, but all can be incorporated within an expanded inclusive fitness.

Hamilton's rule and the associated concept of inclusive fitness (1) have provided an extremely successful way of thinking about and modeling social evolution (2). There are a number of reasons why this is true. It is simple, and therefore, users can apply its logic with ease; nevertheless, it is quite general. In some versions, it is exact, and even less exact versions are not necessarily a strong concern for field or comparative studies, where we can only measure crudely anyway. Crucially, it is often sufficiently independent of the genetic details, such as dominance and recessiveness, the number of genes, and their allele frequencies. This allows it to become an important tool of the phenotypic gambit (3) and optimality approaches. It can be used for traits where we do not understand the underlying genetics, and, in fact, we never fully understand the genetics. It also conveniently separates selection into two kinds of summary terms: effects on fitness (costs and benefits) and population structure (relatedness). This separation makes the process easy to think about and the equations easy to apply. Inclusive fitness points to cause–effect relations, specifically to the various effects caused by the actor's behavior. This focus on what the actor can control allows us to tie into the long biological tradition of thinking of actors, or their genes, as agents. Additionally, it tells us that these agents should appear to be trying to maximize inclusive fitness.

Inclusive fitness is not perfect. It does not provide the most natural way to handle explicit dynamics. It usually takes population structure as a given, and when it does this, it may not yield insight into how population structure emerges. Although, in principle, it covers everything, its summary parameters may sometimes conceal interesting complexity. Even its treatment of social causation is incomplete. For example, although it would include any benefits from mutualism in with other effects on the actor's direct fitness, it does not usually separate out these effects or provide a causal treatment of them. Many or all of these deficits are fixable, although sometimes at the cost of making the models more complex and therefore, losing some of the advantages of the approach. In this paper, I will try to expand the types of social causation covered explicitly, while trying to maintain reasonable simplicity. For example, I will show how to specify mutualistic social effects in a category that I call kith selection, named after the largely archaic word for acquaintances, friends, and neighbors.

I will also argue that it is often worth distinguishing kin and kith selection from what I call kind selection, partly to properly capture social causality and partly because these forms of social selection act in very different ways. Inclusive fitness, developed by Hamilton (1), is closely associated with the process of kin selection, named by Maynard Smith (4). However, they are not the same thing. Inclusive fitness is an accounting method and maximand. Kin selection is a process, and it can be described by other kinds of accounting. The obvious example is the neighbor-modulated approach that uses the same fitness partition as inclusive fitness but groups by effects received rather than effects given (5). However, models with other fitness partitions, such as multilevel selection models, also often describe kin selection (6–9). Another reason is that inclusive fitness includes standard selection where there are no kin effects at all. Finally, kin selection, when interpreted as resulting from genome-wide genealogical relatedness, does not cover all indirect effects. The most commonly cited examples are greenbeard genes (10), which act based on their own identities rather than pedigree kinship. These are commonly grouped under kin selection, but I will argue that greenbeards are one example of the distinct phenomenon that I will call kind selection.

Specifically, I derive an expanded Hamilton's rule (1) or inclusive fitness effect (and neighbor-modulated fitness effect) as

The first two terms look like the standard Hamilton's rule but are not exactly the same, because some social effects have been split off into additional terms. Here, −c is nonsocial direct fitness but does not include some social components of direct fitness. These fitness effects, m (for mutualism or manipulation), are multiplied by a feedback coefficient f to give the kith selection term. Also, kind effects d (deviation from additivity) multiplied by a kind coefficient s (synergism) are split off. These include greenbeard effects that are normally in indirect fitness and some frequency-dependent effects that are usually placed in direct fitness. This is an expanded form in two senses. First, it covers more kinds of social selection or at least, it covers more in a causal manner. Second, it expands out into the number of terms needed to describe this causation with two kinds of distinct terms: selection terms relating social actions to fitness components and association coefficients that essentially describe the relative heritability of those effects. I continue to call this a version of Hamilton's rule because of this key similarity.

In introducing kith and kind selection, I am not claiming to have discovered new forms of social selection. All of the social situations that I discuss have been explored in other ways. Nor should this treatment be viewed as invalidating the standard inclusive fitness approach; it can be viewed as a more detailed version of that approach. My goal here is to present a useful classification of social behaviors and derive a common theoretical framework that partakes of the many advantages of the inclusive fitness approach.

Modeling Social Effects

In this section, I illustrate the method I use to partition different kinds of selection using the methods of Queller (6, 11). The approach closely parallels the causal modeling approach pioneered by Lande and Arnold (12), which is further developed for social traits in the indirect genetics effects approach (13–15). I begin with Price's (16) equation 9 for the change in the average some quantity—here, the average breeding value for a trait, 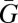, which can be for a single gene or multiple loci affecting a trait. Price's (16) equation is an identity that always holds, but additional assumptions are often made. Here, I follow the common practice of ignoring its second term, which can incorporate effects like meiotic drive or change in environment, to focus on organismal selection and adaptation. Price's (1) equation can then be written as

showing that breeding value is expected to increase if it covaries positively with fitness. Now, consider a social trait where an individual's fitness is affected by both his own trait and the trait of a partner. For the moment, we will assume that we know each individual's genes for the trait, with a breeding value of G for the focal individual and G′ for its partner. Fitness can be written in the form of a regression

The α is the intercept, and it can be conceived of as the base fitness before any social actions. The β symbols are partial regression coefficients for the effect of the focal individual's genes and the partner's genes on the focal individual's fitness, each holding the effect of the other individual constant. The ε is the residual or remainder, including the effects of any other causes and any truly random effects. The regression equation might make it seem that we are interested purely in estimation, but it is also gives us a model of fitness which, depending on the predictors, can be useful, useless, or even misleading.

Substituting Eq. 2 into expression 1 yields

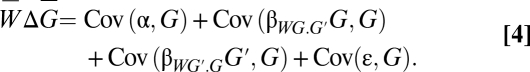The first covariance drops out, because a constant has zero covariance. The last term drops out, because the residuals of a regression are uncorrelated with the predictor variables. If we are thinking in terms of a model, we assume that ε and G are uncorrelated. Next, we can pull the constant β outside of the covariance terms to give

Average breeding value will increase when β_WG.G′Cov(G,G) + β_WG′.GCov(G′,G) > 0. Dividing through by the first covariance gives β_WG.G′ + β_WG′.GCov(G′,G)/Cov(G,G) > 0 or

This is Hamilton's rule, with the direct effect on fitness β_WG.G′, the indirect effect of a partner β_WG′.G, and a regression coefficient of relatedness β_GG′. It is a neighbor-modulated fitness form of Hamilton's rule, which totes up effect on each individual, but it can be rearranged under quite general conditions to an inclusive fitness form that switches all of the primes and nonprimes in the second term and thus, totes up the effects of each individual (17).

Because we assumed we knew the genes, this form is extremely general. It belies the claim that is occasionally made that inclusive fitness requires many assumptions (18). Those claims are usually made about phenotypic versions that are used when we do not assume that we know the genetic basis of the traits, and the same limitations would generally apply to alternative models faced with that assumption. Therefore, proponents of inclusive fitness can rightly refute the claim of limited generality. However, one of the main appeals of inclusive fitness is that it can often be used without knowledge of the genes, and therefore, we will consider the phenotypic gambit shortly.

I have dwelled a bit on already published math (6, 11), because every subsequent derivation in this paper, for which I will not show the math, follows an exactly parallel procedure consisting of the following steps:

• i) Write a regression model for the actor's fitness.

• ii) Substitute that expression for fitness into the abbreviated Price's (16) equation.

• iii) Divide the covariance into separate terms, one for each term of the regression.

• iv) Drop out the α (intercept) term.

• v) Drop out the ε (residual) term provided that Cov(G,ε) = 0.

• vi) Extract the regression coefficients from the covariances.

• vii) Ask when > 0.

• viii) Divide through by the covariance associated with actor's fitness.

We could stop at step vi to preserve a more general equation that predicts actual change in , but I will follow the customary step in inclusive fitness analysis of asking the more restricted question of when 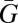increases. Either way, the crucial step turns out to be step v. This is the only step that invokes an assumption, which is Cov(G,ε) = 0. This condition will, therefore, determine whether an exact Hamilton-type (1) result can legitimately be obtained. When it does drop out, we end up with an equation with the desired neat separation between fitness and structure terms, and therefore, I have called this the separation condition (6).

Causality

There is nothing preordained about the predictors used in the derivation above. We could attempt to get a result from any equation predicting or describing fitness. Indeed, it was technically unnecessary to include the partner's breeding value. If we use only the focal individual's breeding value (W = α + β_WGG + ε) and follow steps ii–viii above, we show that 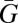> 0 when β_WG > 0. This does not take us far from Price's (16) equation, but it has exactly the same level of validity and accuracy as the inclusive fitness result derived above. Why then do we prefer the inclusive fitness result? The first reason, to be treated shortly, is that leaving out the partner does not work when we try to play the phenotypic gambit. The other reason is that including the partner can provide some additional causal explanation. We are no longer just saying certain genes are associated with fitness; we are giving a breakdown of how that association is caused. It is this causal feature that I want to expand to include more than kin effects.

To illustrate the point about causality, consider another model of fitness based on the individual's breeding value G and the phase of the moon, represented by M. If we substitute W = α + β_WG.MG + β_WM.GM + ε into Price's (16) equation, steps ii–viii lead us to the conclusion that 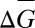> 0 when β_WG.M + β_WM.G β_GM > 0. The first term remains the effect of the actor's genes on its fitness, but the second term is now the effect of the moon phase and is multiplied by β_GM, a sort of moony relatedness linking breeding value and phase of the moon. This model is just as correct as the first two that we considered (the ε term must drop out, because G is one of the predictors); however, no one would consider it very useful, because moon phase is unlikely to have any causality. Even if the phase of the moon had some effect on fitness (in which case, we would need to take it into account for a full evolutionary explanation of the trait), the actor would still be a passive player. There is nothing the actor can do to alter the phase of the moon, and therefore, for optimality arguments, we can ignore it.

Any causes can be included (11, 17). In this respect, my approach is similar to that taken by the indirect genetic effects (IGE) school of social evolution, which can recover versions of Hamilton's rule (1) in very similar ways (13–15). IGE is an extension of quantitative genetics to social evolution, and quantitative genetics has always engaged in partitioning evolution into causal components. My interest here is not in all possible causes but in those that most clarify the role of selection on an actor's social behavior. Thus, in the same way that I exclude the moon phase from the model, I will not generally explore byproduct social effects. A lion that kills a zebra benefits local vultures, and this can influence their traits and fitness; therefore, the killing has a social aspect. However, the vultures do not influence the killing, and the evolution of that killing behavior (as opposed to the incidental effects on vulture traits) does not need to take vultures into account. An important exception is when there are byproducts with feedbacks on the actor's fitness.

Phenotypes and Social Causes

Much of the value of inclusive fitness stems from its use in the phenotypic gambit (3). If we know costs, benefits, and relatedness, we can usually make good predictions about what kinds of traits will be favored, even if we do not understand the underlying genetics. Such approaches are sometimes denigrated by theoreticians, who prefer precision and mathematical rigor over all else, but for understanding the real world, it is essential. To deny this is to deny that Darwin understood anything about adaptation, because all he had to work with was the fit of phenotypes to their environments and a knowledge that some form of heredity exists.

When kin are affected, the phenotypic gambit requires indirect effects. If we use only the actor's phenotype P to model its fitness (W = α + β_WPP + ε) and follow steps ii–viii, we predict that 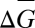> 0 when β_WP > 0. This predicts that altruism cannot evolve, because a cost to self means a negative β_WP. However, we know that altruism can evolve. Mathematically, the reason that the phenotypic gambit fails here is step v, the separation condition (6). After the effect of the actor's behavior on its own fitness is removed, the residual ε is correlated with genotype G if the interaction involves relatives. The partner's fitness W is affected by the partner's behavior P′, which is correlated with G′, that, in turn, is correlated with G when the individuals are relatives.

The solution of inclusive fitness theory is to include the partner's phenotype in the fitness model: W = α + β_WP.P′P + β_WP′.PP′ + ε. Following steps ii–viii now yields

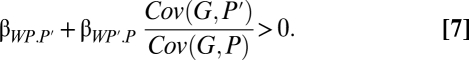Here, the two regression terms represent the cost and benefit like in 6, except that we now use phenotypes instead of breeding values. The relatedness coefficient is now a more complicated ratio of covariances (19). The ratio makes intuitive sense, however, particularly if we think of phenotype being one for performing the behavior and zero for not performing. Then, relatedness is essentially the ratio of the actor's breeding value when the partner performs the behavior to its breeding value when the actor performs the behavior. Switching this neighbor-modulated version to inclusive fitness gives

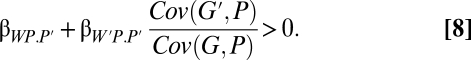Seger (20) discusses the relationship among these regression coefficients.

Kith Selection

Hamilton's rule (7) is normally applied to kin selection, with the relatedness covariances arising from common descent (1). However, there is nothing in the derivations that limits it to this case. The primary limitation, as I will show, is additivity of the two fitness components β_WP.P′ and β_WP′.P. Within that constraint, the gene–phenotype associations represented in the covariance ratio could have any cause. Queller (21) pointed out that the phenotypic covariance ratio could also be used to describe reciprocity. Frank (17, 22) argued that mutualism or indeed, any correlated interaction could be described by a version of Hamilton's rule, and argued for a general informational view of relatedness coefficients. Fletcher and Doebeli (23) further developed these themes and argued for abandoning genetic relatedness as the main key to cooperation in favor of correlated interactions. I will develop those themes here, grouping the mechanisms under the heading of kith selection—selection involving neighbors who need not be kin or similar in kind.

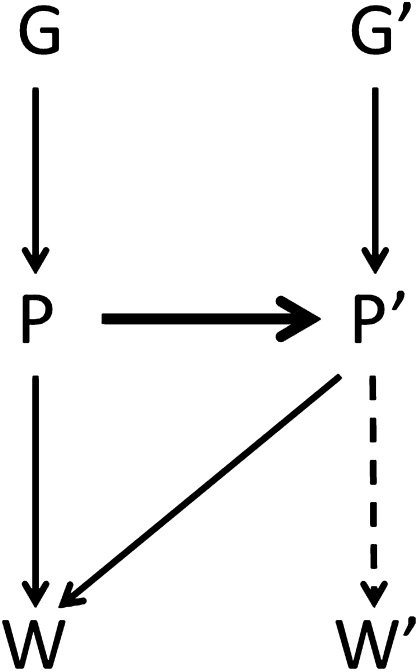
Fig. 1 illustrates the connections. Under kin selection, an arrow would connect G and G′. However, even if there is no kinship, P′ and P can still be used to model or predict the focal individual's fitness W, resulting in expression 7 or 8. If the actor's phenotype predicts its partner's phenotype P′ (heavy arrow), this generates a covariance between G and P′ (or G′ and P), making the relatedness coefficient in expressions 7 and 8 nonzero. However, we now allow P′ to represent an entirely different behavior than P, coded for by different kinds of genes that possibly belong to different species. P could be carbon production by an alga in a lichen, and P′ could be nitrogen production by its fungal partner. The link between P and P′ could come through several means, including the two kinds of mechanisms that can be involved in reciprocity and mutualism: partner choice and partner fidelity feedback (24). If cooperators choose to associate with cooperators and reject noncooperators, this situation will generate a correlation between P and P′. The same will be true if individuals join at random, but those who give larger benefits induce their partners to return larger benefits. Finally, the actor could influence the partner's phenotype through pure manipulation.

Fig. 1.

Kith selection. An actor's phenotype P can influence P′, its partners phenotype (often for a different trait), by manipulation, partner choice, and partner fidelity feedback (heavy arrow). These components create an association between phenotypes P and P′ and therefore, also between P′ and G required in Eq. 7 (or P and G′ in Eq. 8).

Kin selection occurs through genetic identity, and can occur even if the partner does not express the behavior. Indeed, conditional helping of partners who do not help underlies some of the most important manifestations of kin selection, such as social insect workers helping queens. Kith selection, in contrast, requires phenotypic expression by the partner. The focal individual can affect its own fitness in kith interactions only through feedbacks. It affects the phenotype of the partner—whether by manipulation, partner fidelity, or partner choice—and the partner's phenotype feeds back on the actor's fitness. The essential role of phenotypes is brought out by modeling the partner's phenotype as P′ = α + β_P′PP + ε and substituting it into the covariance ratio of expression 7:

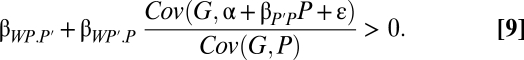Splitting the covariance, dropping the α and ε terms, and extracting the β coefficient yields

We now have Hamilton's rule with the usual effect on fitness of self (β_WP.P′) and partner (β_WP′.P), but instead of genetic relatedness, there is a structural feedback coefficient β_P′P that tells how much the actor's behavior influences or is correlated with the relevant behavior of its partner. Remember that the phenotypes may be entirely different things (perhaps cooperative carbon production by an alga and cooperative nitrogen production by a fungus) but that a correlation can still exist between the two forms of cooperation. The actor's cooperation can pay, even if it pays a cost (β_WP.P′ < 0), if its behavior causes or is associated with (β_P′P > 0) partner behaviors with positive benefits (β_WP′.P > 0).

If the partner is unrelated or in a different species, the standard Hamilton's rule (1) would simply require β_WP > 0, where β_WP includes any effects of the actor's behavior that operate by feedback through partners. That result is perfectly correct and does not need to be altered, but it does not capture the social causation. With expression 10 we can see that the actor increases its own fitness by a pathway that, like kin selection, involves social benefits and some kind of association.

Expression 10 is an expanded version of Hamilton's rule that captures kith selection, but it is a neighbor-modulated form, with effects on a focal actor rather than an inclusive fitness form that attributes all effects to a focal actor. Neighbor-modulated forms are often better for modeling (5), whereas inclusive fitness forms are often better for intuition and insight. To obtain an inclusive fitness form that tells how actors value a partner's fitness, we need to include the partner's fitness.

I distinguish two cases. In the first case, the partner's fitness is incidental for the actor, affected only as a side effect of the actor's effect on the partner's phenotype (dashed arrow in Fig. 1). The effect of the actor's behavior on partner fitness is the product of its effect on the partner's phenotype β_P′.P and the effect of the partner's phenotype on the partner's fitness β_W′.P = β_P′.P β_W′P′. Therefore, β_P′.P = β_W′.P/β_W′P′, which can be substituted into expression 10 to give 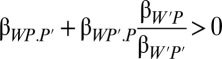or, shifting the denominator,

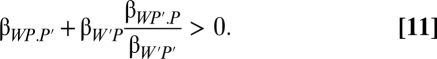Now, we have the actor's nonsocial effect on its own fitness and its kith effect on its partner's fitness β_W′.P through its effect on the partner phenotype. The latter is multiplied by a regression ratio that tells how the actor values those fitness effects on the partner. This kith or feedback coefficient shows that the actor values effects on its partner's fitness (by P and P′) only to the degree that they are associated with fitness returns to itself. This makes sense as a scaling factor for the actor, when it acts through affecting the partner's phenotype. The effect on the partner's fitness is incidental, but when the feedback coefficient is positive, the actor gets a positive feedback by aiding its partner. The feedback need not be positive. We could use the equation to describe manipulation that harms the partner but benefits the actor.

A second possibility is that the actor gains not so much by affecting some particular cooperative trait of the partner but by affecting its fitness in general. That is, effects on the partner's fitness are necessary for the feedback to the actor, not just an incidental effect. In a lichen, an alga that produces more carbon may make its fungal partner fitter, and fitter fungi may make more nitrogen that benefit the alga. Here, we write fitness as W = α + β_WP.W′P + β_WW′.PP′ + ε and follow steps ii–viii to get a simpler result (12):

Here, the actor affects its own fitness (β_WP.W′) and the fitness of its partner (β_W′P), with the latter multiplied by a feedback coefficient of β_WW′.P that describes how much partner's fitness affects the actor's fitness, partialling out the nonsocial effects of the actor's behavior (which are included in the first term). This is a more intuitive result than expression 11, but it is really just a special case of it, where P′ = W′. In both cases, the actor values its partner's fitness according to how it affects its own fitness, but in one case, it is mediated through some intermediate trait. The difference may be important for the evolution of complex mutualisms, which may be much easier to evolve when any benefits to partner's fitness feed back to the actor than if it occurs through only one or a few traits.

Expressions 10–12 provide Hamilton's rule forms to handle kith selection. As suggested previously, both reciprocity (21, 25) and mutualism (17, 22, 25, 26) can be addressed using such results. The analysis here adds at least three features. First, manipulation can be added to the kinds of interactions treated. Second, the results can be expressed not just in terms of neighbor-modulated fitness but also in terms of inclusive fitness. Third, I have put these kinds of results into the common language of regressions and covariances used by quantitative geneticists. The regressions of phenotype on fitness are selection differentials. The coefficient that scales the second regression has to do with heritability; it is actually a ratio of the heritability of the nonsocial effect on self and the heritability of the social effect of, or on, one's partner. This has been shown previously for relatedness in the kin selection form, where the heritability of the indirect selection effect is lowered, because the partner is less likely to pass on the trait (6). For kith selection, the heritability through social effects is lowered by the fact that the actor's phenotype does not perfectly predict the partner's phenotype.

Kind Selection

Another type of selection that is usefully considered separately from the other two is what I call kind selection (27). The first example is the greenbeard gene, which has three effects: it produces a cue (like a greenbeard), perceives that cue in others, and directs some special action to those cue bearers (1). Once viewed more as a thought experiment than as a real possibility (10), real greenbeards are being identified with increasing frequency (27–31). There are greenbeards that help others with the same trait, and there are greenbeards that harm others with different traits. There are both facultative greenbeards that take special actions to like or unlike interactants and obligate greenbeards that perform a general action that has different effects on like and unlike (32).

Table 1 shows many differences between greenbeard or kind selection relative to kin selection (and also, for completeness, to kith selection). I will focus on greenbeards for the moment and come to other forms of kind selection later. The key difference is that, where kin selection works through genealogical kin of the actor, kind selection operates on those who specifically possess the same trait as the actor. Those two features can be correlated of course; kin tend to have similar genes that will tend to produce similar traits. However, in one case kinship is fundamental, and in the other case, phenotypic similarity is fundamental. Greenbeards can be favored even among nonkin. Conversely, kin selection can operate even in the absence of having actual traits in common; often, one kind of individual will express the trait, such as a worker bee's behavior, to benefit others who specifically do not express the trait (queens and males) but are nevertheless kin.

Table 1.

Kin and kind discrimination

	Kin	Kind	Kith
Behavior	Action to partner	Interaction with partner	Feedback from partner
Key partner feature	Possession of same allele	Expression of same trait	Expression of other trait
Beneficiaries	Genealogical kin	Same trait or kind	Any
Role of genetic identity	By descent only	All identities (but really trait identity)	None
Kinship required	Yes	No	No
Genes	Often multigenic	Often one or linked complex	Often multigenic
Relatedness or genetic correlation	Same across genome	Higher at kind locus	None
Complex cooperation	Possible	Unlikely	Possible
Additive fitness effects	Yes	Usually no	Possible
Frequency dependence	Usually no	Usually yes	Possible

Where kin selection operates through cues that correlate with identity by descent, kind selection operates based on all identities (both by descent and by state). Indeed, identity by trait might be a better description; two separate loci producing the same greenbeard trait could work just as well as one. Because identity by descent is normally the same across the genome, kin-selected genes across the genome agree, and complex cooperation can easily be built. The situation with greenbeards is more complex. An altruistic greenbeard allele is related by r = 1 to its beneficiaries and therefore, may give more aid compared with what would be favored at other loci not related to that degree. There has been some debate over whether greenbeards are outlaws with respect to the rest of the genome (32, 33). However, the important point here is that no other locus, unless very closely linked, would build on a greenbeard's identification of beneficiaries. More precisely, if it did build on this identification, it would only be to the extent that the greenbeard cue identified kin. As a result, we do not expect a lot of complexity from greenbeards—they are generally limited to simple traits.

The last two rows in Table 1 require a bit more explanation. Greenbeard traits depend on all identities, not just identity by descent, and therefore, they usually depend on the frequency of the trait in the population (facultative helping greenbeards can be an exception) (32). Kin selection is typically frequency-independent; the condition −c + rb > 0 includes no allele frequencies, because the fraction of alleles identical by descent is independent of gene frequency. However, kin selection models with costs and benefits that are nonadditive typically show frequency dependence. I will argue below that this is because these nonadditive models include a form of kind selection.

I will begin by comparing facultative and obligate greenbeards and then build an argument (34) that obligate greenbeards are insensibly different from more general forms of kind selection. In facultative greenbeards, the actor first classifies its partners and then performs the appropriate behavior. Fire ant workers identify queens lacking their greenbeard allele and then attack them (30). Obligate greenbeards, in contrast, perform a behavior to all interactants without prior identification, but the behavior has different effects on partners who are greenbeards versus those who are not. Bacteriocins provide many examples of obligate harming greenbeards (32, 35). Many bacteria have several tightly linked genes that make a poison, which some cells release at times of stress, and also make an antidote to the poison, which they keep private (35). Cells lacking the complex are killed by the poison, freeing up resources for those who have it. This greenbeard is obligate, because the cells produce the poison and antidote independently of who their partners are; however, the poison adversely affects only those that lack the gene complex (32).

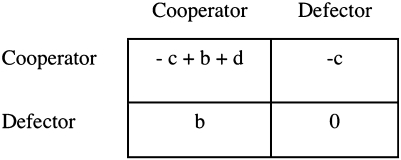
The key feature of a greenbeard is that it gives some fitness benefit to partners who share the trait that it does not give to partners who lack the trait. In a two-interactant payoff matrix, this can be represented as in Fig. 2. The simplest greenbeard effect does not require this full complexity. It could be represented with the d parameter alone. d is what a greenbeard cooperator gets when playing another greenbeard cooperator, and it is generally the sum of the cost of greenbeard cooperation and the benefit of being helped. These are not the c and b variables in the matrix, which instead represent any general costs and benefits, not specific greenbeard ones. Consider the Ti plasmid of Agrobacterium tumefaciens, an obligate helping greenbeard (32). It harbors a number of genes that induce its plant host to produce a tumor and produce a food source in the form of opines (36, 37). The costs of these behaviors are represented by c in Fig. 2—they apply whether there are nonbearers present or not. Any benefits that are public goods benefiting bearers and nonbearers alike—perhaps tumor production—are represented by b. However, the gains from opine production are a greenbeard effect, because opine catabolism is also coded on the Ti plasmid; nonbearers do not benefit. This targeted benefit must be represented by d. Thus, greenbeard effects may be superimposed on nongreenbeard effects, and they can be viewed as nonadditive fitness parts. When you are both an actor and a recipient, the payoff is not the −c + b that would come from adding the separate effects, but −c + b + d.

Fig. 2.

General payoff matrix for the two persons expressed in terms of general effects on self (c), general effects on partner (b), and an extra effect (d) that applies only when both partners perform the behavior.

The payoff matrix in Fig. 2, required to represent greenbeard effects, is actually the general payoff matrix for two interactants (34). With three parameters plus zero, it covers exactly the same ground as any four-parameter matrix. Every such game can be expressed as a general effect on self c, a general effect on partners b, and a specific effect that applies only when both actor and partner perform the behavior d. That means that any nonadditive two-person game, one that requires the complexity of a d parameter, has the greenbeard-like character of giving some fitness gain (or loss) to those who share the trait but not to others (34). Additionally, most of the games that have occupied the interests of evolutionary theorists over the years are nonadditive. Long ago, I noted this similarity and toyed with the idea that all these games represent forms of greenbeard selection (34). That had the problem of subsuming the larger familiar category under the smaller—then nearly nonexistent—category of greenbeard. It might be more palatable to do the opposite (subsume greenbeard effects under the other type), but the problem here is that there really is no name for the process that underlies selection in these games. They are frequency-dependent and nonadditive, but those terms do not capture the reason why the process works (the way kin selection does for affecting relatives). Kind selection does capture the feature, common with greenbeards, that an actor has different effects on its own kind than on different kinds.

Although I motivated this kind selection grouping using nonadditivity and frequency dependence, the similarities extend throughout Table 1. Most notably, the fitness increment (or decrement) represented by d depends on expression of the trait by one's partner. This involves all identities rather than just identity by descent, and kinship is not required. The similarity between partners receiving the d effect is generally higher than genealogical relatedness at the loci causing the behavior, but not at the rest of the genome. Cooperation that results from this single-trait similarity is expected to be relatively simple cooperation and not the highly complex cooperation that can lead to major transitions.

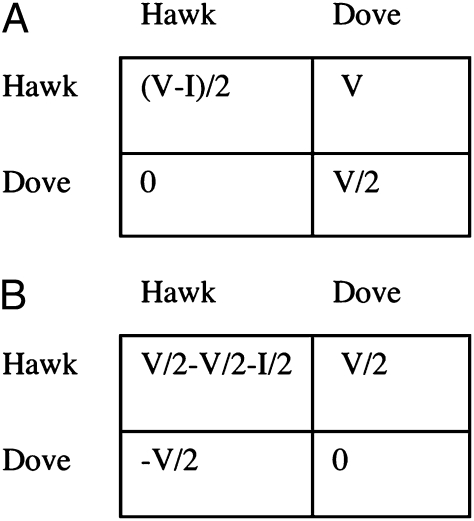
As an example, consider the Hawk–Dove game (Fig. 3A) (38). There is some contested resource worth V fitness units at stake. Hawks fight, gaining all of the fitness units against doves, whereas two doves divide them peaceably. Two hawks will fight each other; a random one of them gets the resource, and the other gets injured, suffering fitness loss I. We can convert to the form of Fig. 3B by subtracting V/2 from all entries to get Fig. 3B. We can now see that being a hawk adds V/2 to your own fitness, subtracts V/2 from your partner's fitness, and subtracts an additional I/2 only when both partners are hawks. Thus, the d term here is negative, representing an antigreenbeard effect of harming one's own type. A negative d means negative frequency dependence, with strategies being more favored when rare, leading to the possibility of polymorphism.

Fig. 3.

Payoffs for the Hawk–Dove game in (A) conventional form and (B) the form of Fig. 2, emphasizing that there is a nonadditive effect of both partners performing the behavior, d = I/2.

An example of a positive d would be two ant foundresses cooperating in colony establishment. Groupers pay a cost of searching for other groupers (c term in Fig. 2) and may also impose a general cost on all potential partners as they negotiate or figure out who is a grouper and who is a loner (the b term, likely negative in this case). However, there are also synergisms that can apply to two groupers that associate. For example, if one dies before the first workers hatch out, the other inherits those workers, getting a double brood, an advantage that loners never get. Many such group effects, such as selfish-herd defense (39), can be viewed in this way.

Warning coloration in distasteful insects provides a more elaborate example (34, 40). A bright individual is more likely to be seen by a predator (c term). If eaten, it will teach the predator that insects like this taste bad. That might provide some general benefit b to both bright and dull forms, but warning coloration will not evolve for that reason. It is favored if an eaten bright bug teaches the predator specifically about bright bugs being bad. This is a positive d, a benefit that bright bugs confer only on other bright bugs.

I do not include all game theory under kind selection, only games between individuals with the same trait options, with nonadditive effects. Games between individuals with different roles, such as male and female, that express different traits are better considered as kith selection. Also excluded from kind selection are some frequency-dependent effects in multiinteractant games if the effects of an individual's behavior are the same on both like and unlike partners (41).

How should we model kind effects? There are many ways, with game theory having been the most popular. Even within the inclusive fitness approach, there are multiple options. Frequency-dependent effects are often incorporated into direct fitness. Greenbeard effects, in contrast, are usually attributed to indirect fitness through the partner. This is odd given that these two kinds of effects are so similar, but it is because d effects are really joint effects of the pair, and the two different historical traditions that attributed them to one partner happened to choose differently. A third alternative is often better. If the effect comes from the joint behavior of both partners, the best causal representation would be joint one (21, 34).

This can be accomplished, for the two-person game, by adding the joint phenotype P × P′ as a part in the model (6, 21). This has a particularly clear interpretation when the trait is dichotomous and assigned values of 1 and 0. P × P′ then equals zero unless both partners express the trait, and therefore, it becomes a variable indicating when that happens. Specifically, let W = α + β_WPP + β_WP′P′ + β_WPP′PP′ + ε (here, I omit the extra regression subscripts showing the partialled-out variables, but let it be understood that these are still partial regression coefficients). Now, follow steps ii–viii from earlier in the paper to find that 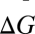increases when

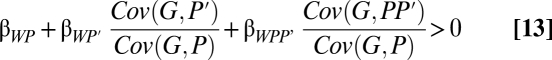from the neighbor-modulated point of view or

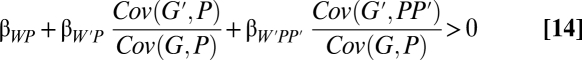for inclusive fitness with indirect effects on partners (6). I have termed the second covariance ratio, which depends on when both partners perform the behavior, a synergism coefficient (6, 21, 34).

There are two reasons for preferring these forms to simpler versions of Hamilton's rule (1) that bundle nonadditive effects into one of the other terms. The main reason is the same one that applies to the kith selection forms; it captures the social causality better. Instead of an undifferentiated average direct fitness that implicitly combines two kinds of direct fitness (some individuals get −c and some get −c + d), the new forms split out those two effects and make the frequency dependence more explicit. It distinguishes true kin effects from effects that result from being similar in kind.

A secondary reason for preferring these forms is that they are sometimes more accurate than the simpler Hamilton's rule. As noted above, the strictly genetic version of Hamilton's rule (6) is always valid, but much of the value of Hamilton’s rule lies in being able to apply the phenotypic gambit. The two phenotypic predictors in expressions 7 and 8 successfully capture the complexity of an additive game. Together, the two predictors define a plane as do the four fitness values in the two-person additive game. However, a plane cannot fit four nonadditive points. Adding P × P′ as a predictor allows us to fit those points and explain more of the variance. However, more importantly, the simpler versions can sometimes be incorrect, biased in the same way that caused us to reject the simple direct fitness model in favor of inclusive fitness. Specifically, the crucial step v of our derivation procedure, dropping Cov(G, ε), is not always possible for a model with only P and P′. Suppose, for example, that cooperation is multigenic. Cooperators all perform the behavior, but they can vary in their breeding values for the trait. Then, if partners are at least sometimes related, those actors with the highest breeding values will be more likely to have partners who also perform the behavior and therefore, are more likely to get the d effect. Thus, the average G differs for actors who get −c + b + d and those who get −c + b. One cannot simply average the two types any more than one could average eight fitness units given to a sibling and one unit given to a third cousins. In short, there are cases in phenotypic models where we cannot get away with two predictors. Synergism can be more complex than in the simple two-person game. When interactions occur in larger groups, additional terms may be needed to capture higher-order interactions (41).

Conclusions

Although I have worked through kin, kith, and kind selection separately, the results can be combined in the expanded version of Hamilton's rule in expression 1. It covers more kinds of social selection in a causal manner. The inclusive fitness form would use terms from expression 8 for kin, expressions 11 or 12 for kith, and expression 14 for kind, whereas the neighbor-modulated form would use expressions 7, 10, and 13, respectively. These expanded social fitness results, like the traditional ones, separate out two kinds of distinct terms: selection terms relating social phenotype to fitness components and relative heritability terms that derive from associations of genes and phenotypes, or just phenotypes.

The model suggested here stakes out a middle position between standard inclusive fitness theory and more complex models (for example, from population genetics). The goal has been to extend the advantages of inclusive fitness theory to a more explicitly causal analysis of social effects other than kin selection. I have chosen to still call the result Hamilton's rule because of the way both separate fitness terms from association or currency translation terms that measure relative heritability. This approach makes the phenotypic gambit a plausible strategy; we can ask how phenotypes affect fitness and then separately assess or measure the associations implied by relatedness, synergism, or feedback coefficients. Like standard inclusive fitness, these high-level summary variables can cut through much of the complexity of population genetic models, where often, a new model must be constructed and solved for a small change in assumptions. The result is, like standard inclusive fitness, an individual-centered analysis that allows us to use the intuition that comes from a simple model and viewing individuals as agents.

This model probably does not much change the view that standard inclusive fitness is maximized, although it does change it to some extent. Kith effects are simply cleaved off of the standard direct fitness term, and therefore, they do not alter total inclusive fitness. Kind effects are a bit more complex. The strictly genetic form of standard inclusive fitness (6) is always valid. However, the phenotypic form (8), which is often more useful in practice, is not always exactly valid under kind selection, and therefore, the expanded inclusive fitness with kind selection can differ somewhat from standard inclusive fitness. More work needs to be done on when these two forms differ and by how much, but I suspect that standard inclusive fitness will usually be a good approximation.

I have framed this paper largely in terms of the problem of cooperation, with positive costs to the actor and positive benefits to partners, that has intrigued biologists for the last several decades. However, of course, as with inclusive fitness, the equations here also apply when they have fitness terms of the opposite sign. If c is negative, we have selfish effects. If b is negative, harm falls on relatives. If d is negative, two actors together have more negative effects than one acting alone. If m is negative, the actor is harming its partner, which can be favored if it is coupled with a negative feedback coefficient—if negative effects on partners generate positive effects back to the actor. Predation is an extreme example.

One complication that I have not treated explicitly is kith selection with multiple partners. For example, mutualisms often involve a large partner of one species and many smaller (often microbial) partners in another species. Actions of one of the smaller partners may then feed back onto kin, so extra terms, with both feedback and relatedness, may be required (17, 22, 25, 26). There could also be an interaction with kind selection if the fitness feedbacks affect actors and nonactors differently. For example, the A. tumefaciens Ti plasmid works this way, with the opine greenbeard effects operating through influence on the host plant.

No social model will perform all possible functions. There are tradeoffs in precision, realism, and generality (42) as well as in simplicity and elegance. Inclusive fitness does pretty well on most of these scores, but it does not tell us everything in either the standard or expanded forms. There is, for example, an increasing interest in how genetic relatedness patterns are generated in the course of selection, migration, and drift. Inclusive fitness typically (although not always) takes the relatedness pattern as given. This is true as well for the associations that underlie kith and kin selection. It is certainly useful to have more detailed models of how these associations are built up, and the paths may sometimes be too complex for such simple models to fully illuminate. However, the history of inclusive fitness suggests that it is also extremely useful to have summary models that cut through much of the complexity to illuminate crucial similarities and differences. Such models are especially useful to empiricists who do not usually know the genetics underlying their trait and prefer to work with a small number of parameters rather than many. These advantages should apply to the expanded social fitness model that includes and distinguishes kin, kith, and kind.