Strong gene flow and lack of stable population structure in the face of rapid adaptation to local temperature in a spring-spawning salmonid, the European grayling (Thymallus thymallus)

Abstract

Gene flow has the potential to both constrain and facilitate adaptation to local environmental conditions. The early stages of population divergence can be unstable because of fluctuating levels of gene flow. Investigating temporal variation in gene flow during the initial stages of population divergence can therefore provide insights to the role of gene flow in adaptive evolution. Since the recent colonization of Lake Lesjaskogsvatnet in Norway by European grayling (Thymallus thymallus), local populations have been established in over 20 tributaries. Multiple founder events appear to have resulted in reduced neutral variation. Nevertheless, there is evidence for local adaptation in early life-history traits to different temperature regimes. In this study, microsatellite data from almost a decade of sampling were assessed to infer population structuring and its temporal stability. Several alternative analyses indicated that spatial variation explained 2–3 times more of the divergence in the system than temporal variation. Over all samples and years, there was a significant correlation between genetic and geographic distance. However, decomposed pairwise regression analysis revealed differing patterns of genetic structure among local populations and indicated that migration outweighs genetic drift in the majority of populations. In addition, isolation by distance was observable in only three of the six years, and signals of population bottlenecks were observed in the majority of samples. Combined, the results suggest that habitat-specific adaptation in this system has preceded the development of consistent population substructuring in the face of high levels of gene flow from divergent environments.

Introduction

When colonizing a new habitat, organisms are often faced with novel and potentially fluctuating environmental conditions that exert strong selection pressures (Schluter, 2000). The ability to adapt to these novel conditions may be critical for population persistence in these new environments (Chevin and Lande, 2009). Adaptive diversification may, however, be constrained by gene flow (Garcia-Ramos and Kirkpatrick, 1997; Lenormand, 2002; Garant et al., 2007; Räsänen and Hendry, 2008). Genetic models show that gene flow can be a strong force that can inhibit local populations from evolving to their optima, whereas rapid divergence can occur in the absence of gene flow (Garcia-Ramos and Kirkpatrick, 1997; Lenormand, 2002). On the other hand, gene flow mitigates negative effects of genetic drift in small populations by replenishing genetic variation and reducing the negative effects of inbreeding, and may thus facilitate adaptive evolution under certain circumstances (Alleaume-Benharira et al., 2006; Garant et al., 2007). Several recent studies have shown that adaptive divergence can occur despite gene flow (for example, Hemmer-Hansen et al., 2007; Nadachowska and Babik, 2009; Richter-Boix et al., 2010). Hence, the relationship between local adaptation and gene flow can be complex (see Garant et al., 2007). The relationship between genetic drift and adaptive divergence is also often complex, as genetic drift can aid divergence but might oppose adaptation because of its random nature. When either genetic drift or gene flow is able to overpower selection, local adaptation can be inhibited.

One way of investigating the importance of the different processes influencing population divergence and adaptation is to study the early phases when a species invades a set of new environments. By doing this, it may be possible to better understand the relative roles of genetic drift and selection, together with the opposing effect of gene flow for divergence. One important question is whether population structuring is required before adaptive divergence can proceed or whether adaptive divergence can occur simultaneously with or even precede the development of isolation (see Dieckmann et al., 2004).

Salmonid fishes are an economically and culturally important group of fishes. Accordingly, they are often translocated and introduced into novel environments (Hendry and Stearns, 2004). As a consequence, a number of examples of rapid adaptation to novel environments have been reported in salmonids (for example, Haugen and Vøllestad 2001; Hendry, 2001; Kinnison et al., 2001; Koskinen et al., 2002a; for a review on the genetics of local adaptation in salmonids see Fraser et al. (submitted)).

We, herein, use a unique system for studying the early phases of divergence in a spring-spawning salmonid, the European grayling (Thymallus thymallus). In the late 1880s, grayling colonized the lake ‘Lesjaskogsvatnet' in Norway from a downstream river-dwelling population (∼20–25 grayling generations ago, Haugen and Vøllestad, 2001). Subsequent dam construction restricted migration into the lake but individuals can still move out of the lake into the river. The lake has therefore been isolated from the river populations since the initial colonization. Since the colonization, spawning populations have been established in more than 20 tributaries of the lake (see Figure 1). A weak ‘isolation by distance' (IBD) population structure was detected in a previous study that assessed samples collected during a single spawning season (Barson et al., 2009). The young age of this system implies that it may not be in equilibrium, and hence the signals detected at a single point in time may be transitory. Accordingly, an analysis of changes in demographic signals through time may provide a more complete picture, not, in the least, because of the potentially important interactions between genetics and demography in newly colonized populations (Ronce and Kirkpatrick, 2001). Overall, very low genetic diversity has been observed in the system (Koskinen et al., 2002b), which is probably a result of serial bottlenecks caused by the founding of the original lake population as well as previous upstream translocations within the ancestral river system (see Barson et al. (2009) for details).

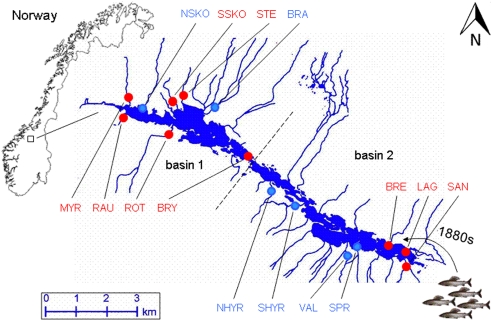
Figure 1.

The Lesjaskogsvatnet lake system (elevation 411 m above sea level, area 4.52 km²) in mid Norway (after Gregersen et al. 2008). It contains two major outlets draining into two of the largest Norwegian rivers, the river Gudbrandsdalslågen in the south and the river Rauma in the north. The dashed line indicates the two basins, basin 1 north and basin 2 south, separated by distinct stream-like straits. Sampling locations are abbreviated and labeled in blue for ‘cold' and red for ‘warm' (see Table 1). For more details of the lake system see Gregersen et al. (2008).

Large variations in water flow and temperature are found among the different Lesjaskogsvatnet tributaries because of a variable topography, along with the presence of small glaciers. This leads to significant variation in spawning time among spawning tributaries (for details see Gregersen et al., 2008). Fish spawning in ‘warm' tributaries typically spawn 3–4 weeks earlier than those in ‘cold' tributaries, and their eggs and larvae develop at higher temperatures (Gregersen et al., 2008; Barson et al., 2009; Kavanagh et al., 2010). Following hatching and subsequent emergence from the gravel in late July, the juvenile grayling develop in the tributaries for some weeks before migrating into the lake by early September for feeding and maturation. All grayling then live in sympatry within the lake until first maturation, after 4–6 years, only returning to the streams, thereafter, to spawn (Haugen and Vøllestad, 2001). The timing of fertilization and subsequent development is critical, as for juvenile freshwater fish in temperate areas, large body size and hence large energy reserves increase winter survival (see Kavanagh et al., 2010, and references therein). Therefore, late hatchers, that is, from cold-spawning populations, are likely to be at a disadvantage without compensatory local adaptation.

Interestingly, there is strong evidence for local variation and adaptation in various life-history traits for grayling spawning in cold and warm tributaries of Lesjaskogsvatnet. Gregersen et al. (2008) showed that grayling spawning in warm, small streams have larger eggs compared with females, with the same body size, spawning in cold, large streams. Furthermore, Kavanagh et al., 2010 demonstrated differential embryo- and larvae development pattern between offspring derived from parents spawning in cold versus warm streams when reared in a common-garden environment. Offspring from cold streams grew faster and had a higher yolk-to-body mass conversion efficiency than those from warm streams. All of this is as predicted for countergradient variation (Conover and Schultz, 1995). Thus, it appears that grayling that recently invaded these new environments have already diverged and adapted, despite experiencing a history of serial bottlenecks and potentially in the face of strong gene flow. Studies on salmonids have shown that life-history traits may evolve within contemporary timescales, which can lead to local adaptation on small spatial scales (Haugen and Vøllestad, 2001; Hendry, 2001; Kinnison et al., 2001). Herein, only about 20–25 generations, assuming a generation time for grayling of about 5–6 years (Haugen and Vøllestad, 2001), have passed since the colonization. The combination of environmentally dependent adaptive differences and ongoing gene flow makes this system well suited for investigating whether a scenario of ‘isolation by adaptation' or ‘adaptation by isolation' (see Dieckmann et al., 2004) can better explain the development of local adaptation in the very early stages of adaptive divergence. To investigate this question we analyzed neutral genetic structure and its stability over time in this very young system, using microsatellite markers. Theoretically, if isolation has been important in facilitating the development of adaptive differences found among populations (‘adaptation by isolation'), then we would expect to find stable population structure with reduced gene flow among the populations. Whereas if adaptation is driving the development of isolation, which in turn facilitates further divergence (‘isolation by adaptation'), then isolation based on habitat types should be evident. A lack of stability and consistent population structure in equilibrium could therefore indicate adaptive divergence in the face of persistent gene flow in this system. Furthermore, we use the analysis of temporal stability to assess the strength of temporal stochasticity in comparison with fluctuations in gene flow using a decomposed pairwise regression (DPR) analysis (Koizumi et al., 2006) to investigate whether the system is more influenced by drift or gene flow.

Materials and methods

Sampling and microsatellite genotyping

Collection

Samples of mature grayling were collected from 15 spawning populations from two basins in Lesjaskogsvatnet (Figure 1) during spawning runs in May/June between 2001 and 2008. Those local populations included two lake-spawning populations (BRY and LAG), seven ‘warm' stream populations (MYR, BRE, RAU, ROT, SAN, SSKO and STE) and six ‘cold' stream populations (BRA, NHYR, SHYR, NSKO, SPR and VAL); some were sampled only once and others for up to 7 years (see Table 1). Fish were either sampled using gillnets at the spawning locations of the lake-spawning populations (BRY and LAG) and in the outlet area of three streams (NSKO, SPR and BRE), or using fish traps and fyke nets in the streams. At capture, all fish were anesthetized in either clove oil or benzocaine (5 ml per 10 l), measured (fork length) and sexed, and fin clips were excised from the adipose fin and stored in 96% ethanol. The fish were then allowed to recover from the anesthesia before being released into the stream to complete spawning.

Table 1. Sampling details, genetic diversity indices and bottleneck test results.

					Genetic diversity			BOTTLENECK:
Location	Popcode	Temp	Year	N	AR	Uhe	Ho	P-valuesa
Raubekken	RAU	w	2004	19	3.7	0.54	0.55	0.166
Myribekken	MYR	w	2004	36	3.7	0.56	0.60	0.007
Skotteå Nordre	NSKO	c	2001	43	3.6	0.55	0.56	0.001
Skottåe Søre	SSKO	w	2001	69	3.6	0.54	0.55	0.000
			2004	43	3.6	0.55	0.61	0.006
			2006	43	3.6	0.55	0.58	0.004
			2007	38	3.7	0.55	0.54	0.013
			2008	59	3.6	0.55	0.57	0.005
Steinbekken	STE	w	2001	41	3.7	0.56	0.56	0.005
			2004	40	3.6	0.55	0.57	0.052
			2005	32	3.6	0.56	0.60	0.014
			2006	42	3.6	0.54	0.54	0.018
			2007	44	3.8	0.56	0.58	0.009
			2008	44	3.7	0.54	0.57	0.048
Brandliåe	BRA	c	2001	45	3.5	0.55	0.58	0.005
			2006	22	3.8	0.55	0.56	0.030
Rota	ROT	w	2006	26	3.8	0.55	0.56	0.030
Bryggeosen	BRY	w	2001	32	3.7	0.54	0.56	0.105
Hyrion Nordre	NHYR	c	2001	28	3.7	0.55	0.56	0.004
Hyrion Søre	SHYR	c	2003	19	3.7	0.56	0.61	0.048
			2006	30	3.7	0.54	0.56	0.013
			2008	42	3.5	0.55	0.56	0.003
Valåe	VAL	c	2001	53	3.8	0.56	0.58	0.009
			2003	41	3.7	0.56	0.56	0.010
			2004	19	3.7	0.55	0.55	0.027
			2005	21	3.4	0.54	0.60	0.025
			2006	37	3.8	0.56	0.54	0.011
			2007	43	3.7	0.55	0.57	0.091
			2008	43	3.7	0.54	0.54	0.040
Sprela	SPR	c	2005	25	3.7	0.55	0.55	0.057
Breidbekken	BRE	w	2005	21	3.8	0.57	0.61	0.030
Sandbekken	SAN	w	2005	20	3.6	0.52	0.56	0.176
			2007	38	3.4	0.50	0.46	0.054
			2008	44	3.5	0.52	0.51	0.166
Lågenoset	LAG	w	2001	17	3.7	0.53	0.58	0.176

Abbreviations: A_R, allelic richness; Ho, observed heteozygosity; N, number of individuals sampled; Temp, broad classification of the thermal profile of the tributary; UHe, unbiased expected heterozygosity; Year, year of sampling.

^aP-values from the Wilcoxon signed rank test for heterozygote excess. Non-significant results (P>0.05) are marked bold.

Genotyping

DNA was extracted using the DNeasy Blood & Tissue Kit (Qiagen, Hilden, Germany) for the 2003–2008 samples, and in addition, previously extracted DNA from the 2001 samples (see Barson et al., 2009) was used. All samples were genotyped for a set of 19 loci (Supplementary Table 1), comprising 7 of those previously used (see Barson et al. 2009) plus an additional 12 recently developed markers (Junge et al., 2010). Methodological details can be found in Supplementary Table 1. Briefly, seven multiplex PCRs (using 1 × Qiagen Multiplex PCR Master Mix), with annealing temperatures between 58 and 60 °C, were run and subsequently combined for electrophoresis on an ABI3730xl Genetic Analyzer, Applied Biosystems (ABI, Foster City, CA, USA). Genotypes were scored using GeneMapper 4.0 software (ABI) and genotype data were converted for further analysis using GenAlEx 6.2 (Peakall and Smouse, 2006). The complete dataset included a total of 1259 individuals collected from 15 sampling sites across different years (35 population-year samples in total).

Statistical analysis

Genetic diversity and equilibrium

Descriptive statistics of microsatellite diversity, that is, unbiased expected and observed heterozygosity, allele frequencies and mean number of alleles per locus were calculated in GenAlEx 6.2 (Peakall and Smouse, 2006). Allelic richness was estimated in FSTAT 2.9.3.2 (Goudet, 2001), assuming a sample size of 14 individuals.

GENEPOP version 4.0.7 (Rousset, 2007) was used to test significant deviations from Hardy–Weinberg and linkage equilibrium with Markov chain parameters set at maximum dememorization number and maximum number of iterations per batch (10 000) for 1000 batches. We corrected for multiple tests by applying sequential Bonferroni corrections (Rice, 1989), and also the Bernoulli method (Moran, 2003) that is less vulnerable to type II errors.

Population differentiation and statistical power

We tested for population differentiation by performing exact G-tests, implemented in GENEPOP, to estimate the P-values for genic differentiation between each population pair at every locus and over all loci. We used the same Markov chain parameter settings and multiple test correction procedures as described above. To estimate the degree of differentiation, pairwise F_ST values and a global F_ST were calculated (Weir and Cockerham, 1984, GENEPOP, FSTAT). Additionally, we used the computer program CHIFISH (Ryman, 2006) to test the hypothesis of no difference at any locus using the actual genotype data.

To assess the statistical power when testing for genetic differentiation, we conducted several simulations using the computer program POWSIM (Ryman and Palm, 2006). The program mimics sampling from populations at a predefined level of expected divergence through random number computer simulations under a classical Wright–Fisher model without migration or mutation (Ryman and Palm, 2006). We simulated scenarios assuming different local population sizes, levels of divergence and sample sizes, including our actual sample sizes, our smallest ones (<30) and up to highly skewed sampling regimes when year-samples of respective local populations were pooled. Significance estimates were based on 1000 independent simulations.

Spatial versus temporal structuring

To assess how much of the total genetic variation is explained by either spatial or temporal variation, a hierarchical analysis of molecular variance was performed using the locus-by-locus procedure in Arlequin 3.11 (Excoffier et al., 2005). The significance of the variance components (VCs) was also tested. As all individuals were sampled during the spawning runs in their respective spawning habitat, we could partition the VCs into the variance (i) among streams (spatial component), (ii) among years within streams (temporal component) and (iii) among individuals within samples (that is, of the same stream and year). The analysis was conducted for the complete data set, including all 35 population-year samples, and for the temporal dataset, that included data from only those local populations that were sampled in more than one year (26 population-year samples, see Table 1).

Spatial

Under migration-drift equilibrium, populations are expected to exhibit a significant correlation between their genetic and geographic distance, termed IBD (Wright, 1943). This means that populations in close proximity to each other should be genetically less differentiated, because of ongoing gene flow among them, than populations geographically further apart. The occurrence of IBD was tested by correlating genetic distances (F_ST/(1-F_ST); Rousset, 1997) with geographic distances (km), measured as the shortest water distance between tributary mouths (see Supplementary Table 3). The association of the matrices was assessed using a Mantel test as implemented in the ‘ecodist 1.1.3' (Goslee and Urban, 2007) package for R 2.6.2 software (R Development Core Team, 2008). The level of significance was evaluated by performing 10 000 permutations. All 35 population-year samples were analyzed.

By using standard regression analysis on all pairwise plots, information on local specialties is lost, that is, sub-population-specific characters (for example, population size, degree of isolation), which are in turn responsible for the relative strengths of genetic drift and gene flow (Koizumi et al., 2006). This information is important for characterizing complex population systems like metapopulations, which can exhibit complex extinction–recolonization dynamics (Hanski and Gaggiotti, 2004). Although a metapopulation may be in regional migration-drift equilibrium, it is still possible that local populations are not in equilibrium, because of either genetic drift or gene flow being locally dominant. Such local disequilibria could potentially mask either the presence or absence of an overall IBD relationship (Koizumi et al., 2006). We applied the DPR approach introduced by Koizumi et al. (2006) to detect such ‘outlier' populations and to estimate the relative strengths of genetic drift and gene flow for each local population (for method details see Koizumi et al., 2006). Briefly, after regressing genetic against geographic distance for all pairwise comparisons, putative outlier populations are detected (and removed) based on systematic bias of the regression residuals. The true outlier populations are then identified by choosing the best model based on the corrected Akaike information criteria. For each of the true outlier populations, pairwise genetic and geographic distances are regressed separately against all non-outlier populations, and each non-outlier population is further regressed against all other non-outlying populations to investigate the relative patterns of gene flow and drift (Koizumi et al., 2006).

We used a principal component analysis (PCA) to visualize potential groupings of individuals according to population, year, or basin and/or habitat (see Figure 1). For this purpose, allele frequencies were analyzed using a PCA based on the correlation matrix to consider all frequency variables (populations) equally important. Because of the large presence of (double) zero frequencies (see Supplementary Table 2), the data set was standardized by allele (that is, subtracting the mean and dividing by the s.d.) before running the PCA. Another clustering approach, implemented in STRUCTURE (Pritchard et al., 2000), was also tested and is described in the Supplementary Information.

Temporal

To assess the stability of spatial structuring, that is, IBD pattern (as described above), the data set was partitioned into years and Mantel tests were conducted, as described previously, separately for each of the six years in which four or more local populations were sampled (2001, 04, 05, 06, 07 and 08). We furthermore conducted the same DPR procedure for the years that included previously identified outlier populations, where it seemed appropriate.

Additionally, to test for ‘isolation by time' within years (following the analysis from Barson et al. (2009)), we performed Mantel tests between genetic distances, that is, F_ST/(1-F_ST) and spawning time differences (days). The data were likewise partitioned into years, and the test was conducted for each year as described above. The spawning time difference was based on direct observations and/or trap catch data from the respective streams. The first day that a spawner was observed was assigned as the spawning time. For streams in which no observations or catches of ascending spawners were available, the spawning times were estimated from a binomial GAM function (see Barson et al., 2009 for details) using the water temperature and date as predictor variables. Water temperatures were available from submerged temperature loggers. However, for streams without temperature data for a given year, the water temperature was accessed from the nearest stream that had highly correlated (that is, r>0.9) water temperatures with the stream of interest in other years.

Population bottlenecks, effective population sizes (N_e) and immigration rates (m)

In a recently bottlenecked population, the level of heterozygosity expected under Hardy–Weinberg equilibrium (observed H_E) exceeds that expected in a population at mutation-drift equilibrium (H_EQ) (Piry et al., 1999). The program BOTTLENECK 1.2.02 (Cornuet and Luikart, 1996; Piry et al., 1999) tests whether a population exhibits a significant number of loci with such heterozygosity excess. We used the two-phase model of mutation with 95% stepwise mutation model, 5% infinite allele model and a 12% variance, as recommended for microsatellites (Piry et al., 1999). Statistical significance was tested with a Wilcoxon signed rank test (one tailed) to calculate the probability of heterozygosity excess, as for fewer than 20 loci, it has been suggested to be generally the most useful of all bottleneck tests because it is the most powerful and robust (Piry et al., 1999). Corrections for multiple tests were performed by applying the Bernoulli method (Moran, 2003).

Short-term effective population sizes (N_e) were estimated where feasible, based on short-term allelic frequency changes between sampling periods using a method that allows for migration (MNe 1.0; Wang and Whitlock, 2003). Waples and Yokota (2007) noted; however, that these standard temporal estimates of N_e should be interpreted with extreme caution, when applied to species with overlapping generations, and when samples are closely spaced in time. The estimation bias, based on Waples and Yokota (2007), is thus largest for short time intervals and small sample sizes. Fortunately, in our lake system, we expect low-effective population sizes of the respective local populations, a situation in which the temporal method could be used most effectively because the signal from genetic drift is large relative to sampling error (see Waples and Yokota, 2007). In general, failing to account for age structure tends to bias N_e estimates downward (see Waples, 2010), which is the same direction shown by Waples and Yokota (2007) for species with life histories comparable with grayling. Overall, however, we do not expect the bias to be particularly large especially when compared with the effect of migration herein. Not accounting for migration in this system would upward bias estimations of N_e, most likely to a much larger extent than the downward bias caused by age structure. For this reason, we chose this temporal method, which allows for migration, despite its known limitations in species with overlapping generations (for a review of N_e estimation methods and their performances in taxa with overlapping generations, see Fraser et al., 2007). When accounting for migration, MNe furthermore calculates the immigration rate (m) for the respective local population. As it requires allele frequency data on the source population(s), we always pooled genotype data for all other populations except the population in question. This temporal N_e estimation was only possible for five populations that had samples one generation apart—BRA, SHYR, SSKO, STE and VAL (see Table 1). The maximum effective population size was initially set to 1000 for each population and further extended, if necessary. We additionally conducted estimations of N_e not accounting for migration to evaluate its effect and found the expected severe overestimation we predicted above (up to 20-fold, data not shown), clearly showing that migration outweighs the influence of age structure in our system.

Results

Genetic diversity and equilibrium

The average number of alleles per locus within a sampling site varied between 3.5 and 4.4 (Supplementary Table 2), and allelic richness ranged from 3.4 to 3.8 (Table 1). Observed and expected heterozygosities ranged from 0.46 to 0.61, and 0.50 to 0.57, respectively (Table 1). Over all loci, a total of 104 alleles were observed with Tth-445 being the most variable with 13 alleles and Tth-309, Tth-207, BFRO9, BFRO11 and 419a the least variable with two alleles each (Supplementary Table 2). Two sampling years from Sandbekken (SAN07 and SAN08) showed an across loci deviation from Hardy–Weinberg equilibrium. After correction for multiple testing, only one population-year sample (SAN07) deviated significantly from HWE and all locus pairs were in linkage equilibrium.

Population differentiation and statistical power

Out of 595 pairwise population comparisons for genic differentiation, a total of 217 showed significant differentiation, which is significant given the Bernoulli method (that is, the probability of getting this result with α=0.05 by chance alone is very small, P<0.001). These included 6 of the 53 tests (11%) that were purely temporal in nature (that is, comparisons between years within the same stream) and 27 of the 80 tests (34%) that were purely spatial in nature (that is, between streams within the same year), both significantly higher proportions than expected purely by chance according to the Bernoulli method (P<0.05 and P<0.001, respectively). Of the remaining 462 pairwise comparisons, 184 were significantly differentiated. The global F_ST (jackknifed over loci) was 0.006 (95% confidence interval (CI): 0.005–0.008, 99% CI: 0.005–0.009), and pairwise F_ST-values varied between −0.006 and 0.036 (Supplementary Table 4). Furthermore, using CHIFISH, the null hypothesis of genetic homogeneity was rejected by the χ² approach as well as the Fisher method (P<0.001 in both cases).

Power simulations conducted in POWSIM indicated that given the number of loci, their polymorphism and the sample sizes used in the study, the probability of detecting F_ST values as low as 0.005 was over 99%. This also held true when testing very small or drastically skewed sample sizes. The detection probability of an F_ST as low as 0.001 still resulted in a reasonable probability, above 63%, to detect a true F_ST this small. Given that the smallest F_ST value between two significantly diverged populations in our study was 0.0038, we are confident that the small but significant F_ST values observed in our study are indeed real.

Spatial versus temporal structuring

The analysis of molecular variance revealed a similar pattern to the tests for genic differentiation, with 0.45% (VC: 0.024, F_ST=0.007, P<0.001) of the variation being explained by spatial variation and 0.20% (VC: 0.010, F_SC=0.002, P<0.001) by temporal variation, leaving more than 99% (VC: 5.200, F_CT=0.005, P<0.001) to within sample variation. The results were almost identical when only the streams sampled in more than one year were included (0.42% spatial, 0.20% temporal and >99% within sample variation; all significant).

Spatial

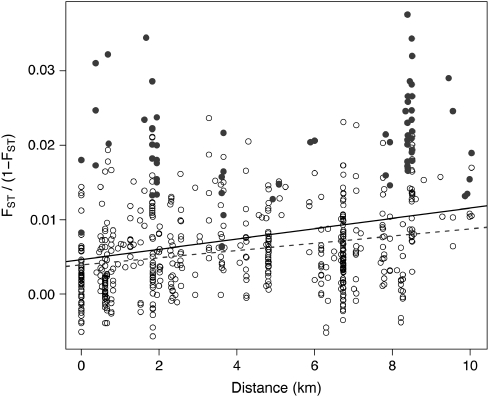
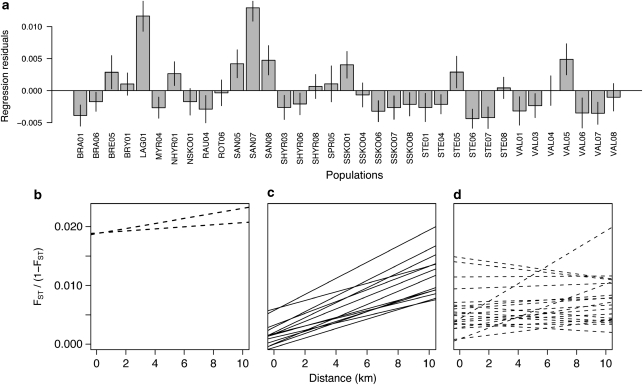
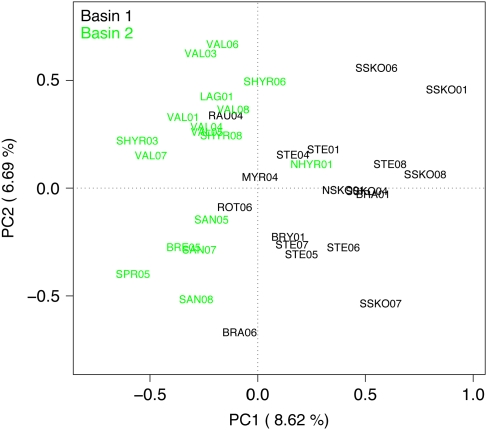
There was a significant correlation between genetic and geographic distance for the complete dataset (P_Mantel <0.001; Figure 2). Putative outlier populations were identified (Figure 3a). The best model, based on the DPR approach, included 33 population-year samples (r²=0.066); two population-year samples (SAN07 and LAG01) were identified as ‘true outliers' (Supplementary Table 5). These two outliers were then separately regressed against all 33 non-outliers (Figure 3b; Table 2) and subsequently categorized as belonging to pattern 1, that is, genetic drift ≫ gene flow (Koizumi et al. 2006). These populations do not exhibit a significant correlation between genetic and geographic distance and are, furthermore, significantly diverged even from very close populations. The DPR approach also revealed two different patterns among non-outlier population-year samples (Figures 3c and d; Table 2), with 13 out of 33 showing significant IBD relationships (Figure 3c), whereas the other 20 do not (Figure 3d). The PCA showed a clustering of populations by basin, with PC1 explaining 8.6% and PC2 6.7% of the variation (Figure 4; see Supplementary Table 6 for the scores of each population in the x, y space). There was no clear grouping by habitat and no grouping by population or year at all.

Figure 2.

Relationship between genetic (F_ST/(1-F_ST)) and geographic distance (km) for all 35 population-year combinations (all dots, black line: —; Mantel r=0.29, P<0.0001) and excluding two outlier populations (SAN07 and LAG01) identified by the DPR analysis (excluding filled dots, dashed line: - - - -; Mantel r=0.26, P<0.0001).

Figure 3.

DPR analyses. (a) Average residuals and 95% CIs from the regression in Figure 2. (b–d) DPR of genetic (F_ST/(1-F_ST) versus geographic distance (km) for each of the 35 population-year combinations. Each of the two ‘true' outlier populations was regressed with the 33 non-outlier populations (b), whereas each of the 33 non-outlier populations was regressed with the other 32 populations showing statistically significant (c) and non-significant (d) regressions.

Table 2. Intercepts and slopes of the decomposed pairwise regressions for each population.

Population	Intercept (±standard error)a	Slope (±standard error)a	r2	Groupb
Outlier populations
SAN07	1.88e–2 (1.20e–3)***	4.31e–4 (3.05e–4)	0.061	B
LAG01	1.89e–2 (2.29e–3)***	1.79e–4 (3.54e–4)	0.008	B
Non-outlier populations
RAU04	5.41e–3 (1.82e–3)**	–1.44e–4 (3.16e–4)	0.007	D
MYR04	2.84e–3 (1.44e–3)	4.16e–4 (2.48e–4)	0.085	D
NSKO01	1.65e–3 (1.29e–3)	7.27e–4 (2.39e–4)**	0.235	C
SSKO01	5.72e–3 (1.42e–3)***	1.37e–3 (3.09e–4)***	0.395	C
SSKO04	1.76e–3 (9.10e–4)	1.06e–3 (1.98e–4)***	0.488	C
SSKO06	–2.35e–5 (1.09e–3)	9.26e–4 (2.37e–4)***	0.337	C
SSKO07	5.26e–4 (9.58e–4)	8.37e–4 (2.08e–4)***	0.349	C
SSKO08	4.22e–5 (8.98e–4)	1.12e–3 (1.95e–4)***	0.523	C
STE01	1.15e–3 (1.24e–3)	6.16e–4 (2.70e–4)*	0.148	C
STE04	1.80e–3 (7.39e–4)*	6.50e–4 (1.60e–4)***	0.353	C
STE05	5.98e–3 (1.16e–3)***	7.30e–4 (2.51e–4)**	0.220	C
STE06	1.99e–3 (1.27e–3)	1.27e–3 (2.77e–4)***	0.412	C
STE07	9.34e–4 (9.59e–4)	3.06e–4 (2.08e–4)	0.067	D
STE08	3.23e–3 (1.02e–3)**	1.00e–3 (2.21e–4)***	0.407	C
BRA01	–5.53e–4 (8.71e–4)	8.03e–4 (2.05e–4)***	0.338	C
BRA06	4.16e–3 (1.09e–3)***	1.77e–4 (2.58e–4)	0.016	D
ROT06	5.17e–3 (1.05e–3)***	1.44e–4 (2.29e–4)	0.013	D
BRY01	2.87e–3 (2.27e–3)	1.33e–3 (6.46e–4)*	0.124	C
NHYR01	4.33e–3 (3.45e–3)	1.49e–3 (9.61e–4)	0.074	D
SHYR03	9.01e–4 (2.24e–3)	9.33e–4 (5.66e–4)	0.083	D
SHYR06	3.88e–3 (1.64e–3)*	1.22e–4 (4.16e–4)	0.003	D
SHYR08	6.48e–3 (1.96e–3)**	1.78e–4 (4.96e–4)	0.004	D
VAL01	3.37e–3 (1.40e–3)*	2.78e–6 (2.69e–4)	0.000	D
VAL03	4.84e–3 (1.04e–3)***	–1.17e–4 (1.99e–4)	0.011	D
VAL04	6.07e–3 (1.83e–3)**	1.75e–4 (3.52e–4)	0.008	D
VAL05	1.14e–2 (1.73e–3)***	1.62e–5 (3.33e–4)	0.000	D
VAL06	3.51e–3 (1.31e–3)*	–1.42e–4 (2.52e–4)	0.011	D
VAL07	2.72e–3 (1.20e–3)*	1.46e–4 (2.32e–4)	0.013	D
VAL08	6.57e–3 (1.42e–3)***	–2.06e–4 (2.73e–4)	0.019	D
SPR05	7.15e–3 (1.78e–3)***	6.54e–5 (3.26e–4)	0.001	D
BRE05	9.44e–3 (1.88e–3)***	9.08e–5 (3.13e–4)	0.003	D
SAN05	1.39e–2 (1.83e–3)***	–2.85e–4 (2.75e–4)	0.035	D
SAN08	1.47e–2 (1.55e–3)***	–3.49e–4 (2.34e–4)	0.069	D

^*P<0.05; ^**P<0.001; ^***P<0.0001.

^aThe significance of each relationship was assessed by ordinary least squares regression.

^bLetters (B–D) indicate the observed regression pattern (see Figure 3).

Figure 4.

Correlation biplot of PC1 (8.62% of the total variance) versus PC2 (6.69% of the total variance) showing the loadings of each population sampled in a given year on both PCs and color coded according to basin (PC, principal component).

Temporal

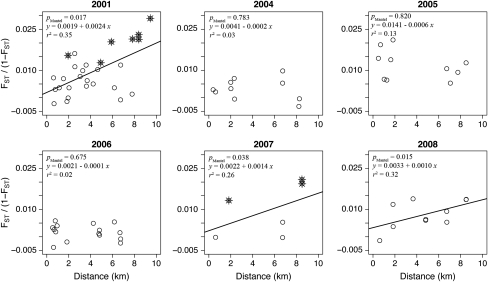
Three out of the six single years assessed for IBD, 2001, 2007 and 2008, showed a significant correlation (Figure 5). The DPR analysis for 2001 revealed that the full model, that is, including the putative outlier LAG01 (see Supplementary Figure 1), is the best model (see Supplementary Table 7). No correlation between genetic and spawning time distance, that is, isolation by time, could be detected in any of the years analyzed (see Supplementary Figure 2).

Figure 5.

Relationship between genetic (F_ST/(1-F_ST) and geographic distance (km) in each sampling year. The linear regression model and P-value of the Mantel test are also shown in each panel. For 2001 and 2007, pairwise comparisons involving the two previously identified ‘overall' outlier populations (LAG01 in 2001 and SAN07 in 2007) are indicated by asterisks.

Population bottlenecks, effective population sizes (N_e) and immigration rates (m)

The heterozygosity expected under Hardy–Weinberg equilibrium (observed H_E) exceeded that expected in a population at mutation-drift equilibrium (H_EQ) in 26 out of the 35 population-year samples, suggesting that they are recently bottlenecked (Table 1). Among those that did not show bottleneck signatures are the two lake-spawning sites, BRY and LAG, as well as all three sampling years from Sandbekken (2005, 07 and 08).

Short-term N_e estimates obtained by applying the temporal method in MNe resulted in estimates between approximately 60 and 150, with mostly reasonable 95% CIs (SSKO: 63 (CI: 40–126), SHYR: 80 (CI: 44–306), BRA: 83 (CI: 52–147), STE: 130 (CI: 76–>3000) and VAL: 147 (CI: 77–>3000)). The same analysis also revealed immigration rates (m) per generation of around 0.4 but with fairly wide 95% CIs (VAL: 0.37 (CI: 0.01–0.93), SHYR: 0.42 (CI: 0.09–0.87), SSKO: 0.43 (CI: 0.18–0.74) and STE: 0.48 (CI: 0.01>1) but up to 0.78 (CI 0.30>1) in BRA).

Discussion

In this study, we used neutral genetic markers to better understand the demographic processes that occur during the early phase of adaptive differentiation of grayling in a Nordic lake, Lesjaskogsvatnet. Across all years, we found a weak but significant signal of genetic structuring based on geographic distance. However, this signal seemed to be subjected to temporal fluctuation, possibly related to environmental variation among years that through its influence on spawning time could affect the level of among-stream migration. This indicates that the system is not in migration-drift equilibrium. Among-year differences in environmental conditions may influence the potential for dispersal and thus gene flow. Therefore, the population structure is still weak, questioning isolation as the main driver of divergence in this system. The small amount of structuring detected may nevertheless allow adaptive divergence to be initiated.

The small local population sizes, together with the recent colonization that could have been associated with initial maladaptation and the potential environmental stochasticity, could have increased the role of genetic drift. The results of the DPR analysis, however, suggest that the influence of drift is in fact secondary to that of gene flow. Caution needs to be exercised in interpreting patterns of IBD in such a non-equilibrium system in which fluctuations in population size are likely (Björklund et al., 2010). Nevertheless, an IBD signal was observed in several single-year analyses spanning the entire 8-year period of the study.

Gene flow versus genetic drift in Lesjaskogsvatnet

The overall significant correlation between genetic and geographic distance in this system suggests a regional migration-drift equilibrium, allowing for divergence despite ongoing gene flow. The DPR analysis (Koizumi et al., 2006) additionally revealed differing patterns among local populations that can be divided into three groups:

1. The majority of the population-year samples (20/35) did not show increasing genetic distance with increasing geographic distance (Figure 3d), and showed a generally low level of genetic differentiation, indicating that gene flow overrides the effects of genetic drift in most of these local populations. It should be noted, however, that the very steep slope of one population-year sample, NHYR01, suggests that the lack of significance in this case might be because of a lack of close population comparisons (Figure 1 and Table 2).

2. Thirteen out of the 35 population-year samples revealed a significant IBD pattern representing an increasing contribution of genetic drift together with less gene flow among more distant populations (Figure 3c), that is, a pattern that most closely resembles a migration-drift equilibrium. All populations that showed this pattern (BRA, BRY, NSKO, SSKO and STE) are found in basin 1 (see Figure 1), as they exhibited the largest genetic differentiation when compared with more distant populations from basin 2. Thus, it seems that the two basins are weakly separated, despite the absence of any obvious physical barriers and all tributaries being within easily attainable swimming distance of grayling (see also Figure 4). In fact, grayling individuals at any location in the lake can easily access any stream in less than 24 h, even at very low swimming velocities. At an average swimming speed of 0.5 body lengths per second, which is slow compared with typical grayling values (for example, Nykänen et al., 2004), individuals larger than 22 cm can swim from one end of the lake to the other within that time. Preliminary results from an acoustic telemetry study conducted in 2009/10 reveal high site fidelity for most individuals tracked. Individuals from one sub-population (SSKO) seem to be more prone to interbasin movements (50% visited other basins during the cause of a year) than those from three other sub-populations (7%). However, all but one individual (from SSKO) came back to the original basin within a couple of weeks (unpublished data). In future, a landscape genetic approach aimed at investigating how genetic variation is affected by landscape and environmental variables would be useful to disentangle the effects of evolutionary forces interacting with landscape characteristics within and also across basins.

3. Two ‘outlier' population-year samples (LAG01 and SAN07), not in migration-drift equilibrium, appeared to be significantly diverged even from very nearby populations, indicating that genetic drift might dominate in these cases. From fishermen catch reports, we know that fishes belonging to the lake-spawning LAG population spawn much earlier than any non-lake-spawning population, and the year-to-year stability in spawning temperature is likely to be greater in the lake than in the rivers. SAN is a small, warm stream that not only shows a high contribution of genetic drift but is also the only spawning stream (with more than one sampling year, see Table 1) that consistently did not exhibit signatures of a population bottleneck. Some, so far unknown, factor(s) isolate these populations from the others, and further investigations are required to understand why.

The immigration rates estimated for five of the populations (m>0.4) are high, especially when compared with more stable systems (see, for example, Fraser et al. (2007) for a comparison of two contrasting population systems). For selection to outweigh this level of immigration to sufficiently enable adaptive divergence (Kavanagh et al., 2010), the difference in fitness optima between the habitat types and/or the additive genetic variance for the divergent traits would need to be high (Hendry et al., 2001; Bolnick and Nosil, 2007). In addition, gene flow measured at the neutral loci assessed in this study may not reflect the degree of isolation at loci under selection. F_ST values for loci under selection, and loci tightly linked to them, can be significantly higher than for neutral loci (for example, O'Malley et al., 2007). In earlier studies, selection on specific regions of the genome has been identified through the detection of soft selective sweeps (for example, Pritchard et al., 2010) and outlier loci under directional selection (for example, Novembre and Di Rienzo, 2009; Whitehead and Crawford, 2006). Within Lesjaskogsvatnet, the early life-history traits that have been shown to diverge among habitat types display plastic responses to developmental temperature (for example, Haugen and Vøllestad, 2000). The impacts of adaptive plasticity on interactions between selection, adaptation and gene flow are complex but are likely to be both positive and negative depending on the nuances of the system under consideration (Crispo, 2008). Fitzpatrick et al. (2008) suggest that ‘divergence with gene flow' is likely to be the most common form of divergence in nature. As such, gaining a more detailed understanding of this process and its limitations needs to be a future focus of both theoretical and empirical research (Fitzpatrick et al., 2008).

Temporal stability and signals of bottlenecks

The evolution of specializations can be very vulnerable to demographic perturbations, and hence it is important to study the early phase in which a system might not be in equilibrium yet to understand the development of the type of local adaptation for which salmonids are famous (see for example, Ronce and Kirkpatrick, 2001). One of the main questions that we aimed to address was, therefore, whether or not this system is at equilibrium, which would assume a stable population structure. We tested for both migration-drift equilibrium, that is, IBD, and mutation-drift equilibrium, as evidenced by an absence of bottleneck signatures. None of the performed tests to detect these equilibria convincingly revealed a stable system. That being said both pairwise genetic differentiation tests and analysis of molecular variance analysis indicated that spatial variation explained 2–3 times more of the divergence in the system than temporal variation. Signals indicative of recent population bottlenecks were found for ∼2/3 of the 35 population-year samples (Table 1). Given the young age of populations in the system (approximately 20–25 generations), it is unclear whether the bottleneck signals result from the original founding events or reflect more recent demographic instability, as the timing of the founding event is still within the detection time span of the bottleneck test (Cornuet and Luikart, 1996). We might therefore detect the original lake colonization bottleneck signal still evident in most spawning populations, which seems to disappear from time to time and in some local populations because of, for example, demographic fluctuations.

In the year-by-year analysis, a positive correlation between genetic and geographic distance was found for three out of the six years; 2001, 2007 and 2008 (Figure 5). Although the detection of a potential signal is more difficult in some years because of the low number of sampled populations, we can nevertheless draw some conclusions. The DPR analysis indicated that most 2001 populations (all except VAL and LAG) showed a positive correlation between genetic and geographic distance (although this relationship was not statistically significant for NHYR01, as explained above). Why then do we not find this migration-drift equilibrium in the following years and find it reappearing in 2007 and 2008?

A possible explanation for such a temporal pattern is that IBD may be unstable during the initial phase of its establishment. For instance, in a study of brook charr, Castric and Bernatchez (2003) found highly variable levels of IBD in the very youngest of populations that developed into strong IBD quite rapidly and then slowly decayed over time owing to fragmentation. However, our sampling regime is not ideal for explicitly testing for such a scenario, as we have varying numbers of pairwise population comparisons in each year and the populations that are compared differ. It is nevertheless interesting to observe that neither the absolute number nor any particular population can be directly associated with the appearance or non-appearance of an IBD signal. A combination of sampling issues, fluctuating environmental conditions and possibly fluctuating population dynamics could result in the observed pattern in this very young and thus yet unstable system. In our study, a lack of temporal stability was furthermore suggested by (i) the non-grouping of temporal samples in the PCA and (ii) the analysis of molecular variance that showed that a significant amount of the overall variance was accounted for by temporal variance in addition to the underlying spatial variation. Thus, both temporal and spatial genetic variations are evident in this initial phase following colonization of Lesjaskogsvatnet.

Isolation by adaptation or adaptation by isolation?

The overall significant correlation between genetic and geographic distance suggests a regional equilibrium, allowing for divergence despite ongoing gene flow. This trend, however, does not seem to be associated with the temperature-dependent divergence previously observed in the system (see Kavanagh et al., 2010). Thus, it seems that habitat-specific adaptation in this system has preceded the development of consistent population substructuring in the face of high levels of gene flow from divergent environments. More detailed assessment of specific local populations indicated that they may in fact be affected differently by gene flow and drift, and possibly also by extinction–recolonization dynamics, but for the majority of populations and years, gene flow appears to be dominant to drift.

It is conceivable, however, that even the low level of population structuring detected may be sufficient for adaptive divergence to be initiated. Once adaptive divergence proceeds to a sufficient level, selection against immigrants would become an important factor, which could lead to further selection, promoting isolation. The dominance of gene flow over drift observed in the majority of local populations in this system suggests that selection against immigrants may not currently be strong enough to significantly curtail gene flow, as does the lack of a pattern of ‘isolation by time'. On the other hand, even a very slight deviation from panmixia can sometimes be sufficient to permit divergence at specific traits, provided the traits in question have high levels of additive genetic variance and provided selection is sufficiently strong (for example, Hendry et al., 2001). Obvious next steps include investigation of the population genetics of loci potentially affecting traits under divergent selection and investigating the role of environmental fluctuations on the stability of the system.

The authors declare no conflict of interest.