Sound scattering from two concentric fluid spheres (L)

Abstract

The solution to the problem of plane wave and point source scattering by two concentric fluid spheres is derived. The effect of differences in sound speed, density, and absorption coefficient is taken into account. The scattered field is then found in the limit as the outer sphere becomes an infinitely thin shell and compared to the solution for a single fluid sphere for verification. A simulation is then performed using the concentric fluid sphere solution as an approximation to the human head and compared to the solution of a single fluid sphere with the properties of either bone or water. The solutions were found to be similar outside of the spheres but differ significantly inside the spheres.

INTRODUCTION

The concentric sphere geometry can be used to approximate many applications. For example, scattering from single cells could be modeled with the concentric sphere model with the inner sphere having the properties of the nucleus and the outer sphere the properties of the cytoplasm.¹ Ultrasound contrast agents are composed of microbubbles enclosed in a polymer, protein, or lipid shell which could also be analyzed using the concentric sphere model.² The finite element method is also currently being applied to model sound wave propagation into the human head.³ It is important to validate the model with geometries that have analytical solutions to test the accuracy of the model. One such geometry is that of two concentric fluid spheres, where the outer sphere has the bulk fluid properties of bone (neglecting the presence of shear waves) and the inner sphere has the properties of water.

Past publications have dealt with situations similar to this but are limited in their application. For example, Goodman and Stern⁴ derived the solution to plane wave scattering from an elastic shell in a fluid medium but the medium and inner sphere were assumed to have identical properties. Kakogiannos’ and Roumeliotis’⁵ solution is limited to spheres whose radii are small relative to a wavelength. The present work combines Sinai and Waag’s solution to plane wave scattering from concentric fluid cylinders⁶ and Anderson’s solution to plane wave scattering from a single fluid sphere⁷ to derive the solution to plane wave scattering from two concentric fluid spheres. These solutions are also extended to include attenuation and point sources.

Other publications have solved more general problems involving concentric spheres. For example, Gerard and co-workers^8,9 used resonant scattering theory as a framework to derive solutions to scattering by spherical elastic layers. Martin¹⁰ derived the solution to concentric fluid spheres when the properties of the outer sphere are specific functions of the distance from the center of the sphere. In both cases, the solution to scattering from two concentric fluid spheres can be synthesized but require significant manipulation of the provided results. The contribution of the present work is to provide simple expressions that can be readily used to calculate fields scattered by concentric fluid spheres when shear waves can be neglected.

II. ABBREVIATIONS

The following abbreviations are used in this paper.

• P_m=Legendre polynomial

• j_m=spherical Bessel function

• $h_m^{(k)}=\text{spherical Hankel function}$

III. THEORY

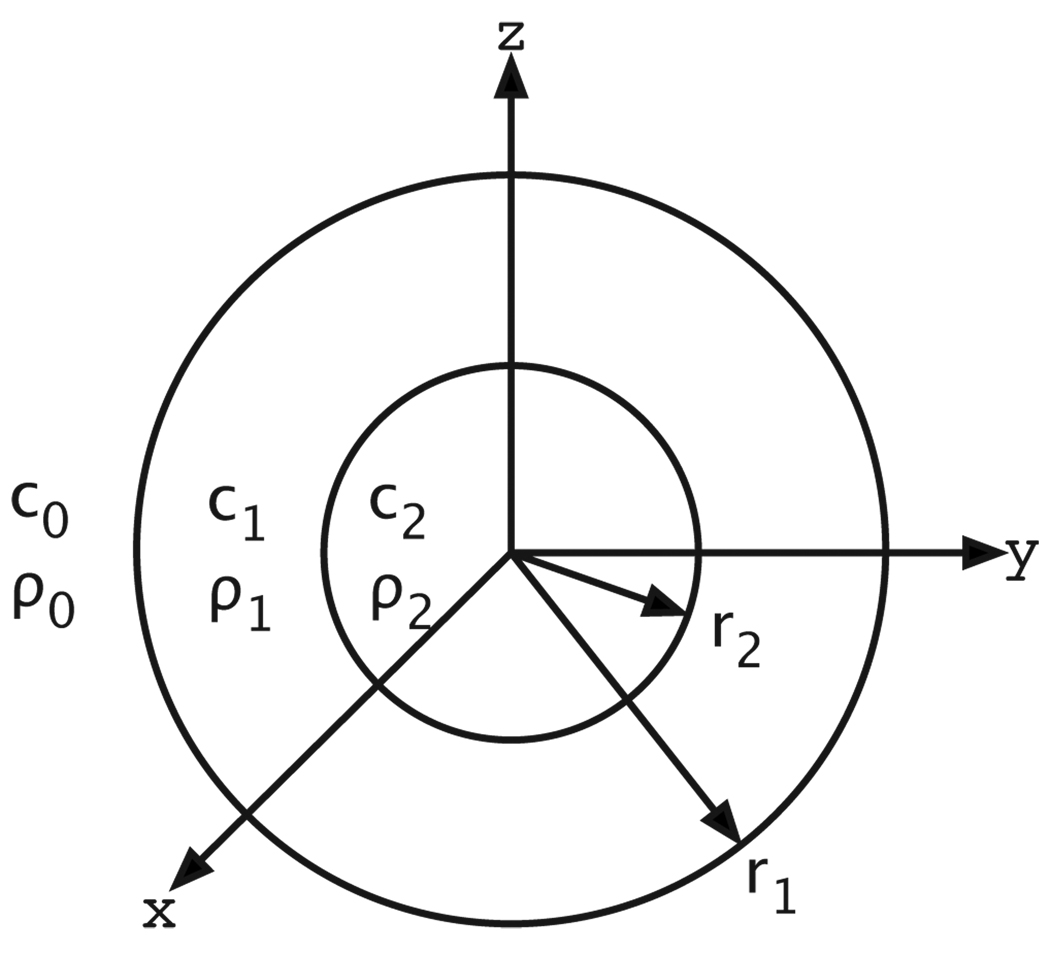
For computational simplicity, the spheres are placed at the origin of a spherical coordinate system (r, θ, ϕ), as shown in Fig. 1. The source is either a plane wave propagated in the −z direction or a point source located on the positive z-axis at a distance R from the origin which eliminates any dependence on ϕ.

FIG. 1.

Physical properties. Infinite medium with density ρ₀, sound speed c₀, and absorption coefficient α₀. The outer sphere has density ρ₁, sound speed c₁, absorption coefficient α₁, and radius r₁. The inner sphere has density ρ₂, sound speed c₂, absorption coefficient α₂, and radius r₂. The spheres are centered at the origin of a spherical coordinate system (r,θ,ϕ), where r is the radial coordinate, θ is the azimuthal coordinate, and ϕ is the polar coordinate.

The pressure in the infinite medium p₀ is the sum of the incident pressure p_0i and the scattered pressure p_0r.¹¹

$$p_0=p_{0i}+p_{0r}$$ (1)

$$p_{0i}={𝒫}_0{\displaystyle \sum _{m=0}^{\mathrm{\infty }}}(2m+1){ℒ}_m{P}_m(\mu )j_m((k_0+i{\alpha }_0)r)e^{-i\omega t},$$ (2)

$$p_{0r}={\displaystyle \sum _{m=0}^{\mathrm{\infty }}}{A}_m{P}_m(\mu )h_m^{(1)}((k_0+i{\alpha }_0)r)e^{-i\omega t},$$ (3)

where μ=cos(θ) and ℒ_m is given by¹²

$${ℒ}_m=\{\begin{array}{cc}{(-i)}^m\hfill & \text{plane wave}\hfill \\ h_m^{(1)}((k_0+i{\alpha }_0)R)\hfill & \text{monopole}.\hfill \end{array}$$ (4)

The pressure in the outer sphere p₁ is the sum of a standing wave, p_1r, and a traveling wave, p_1i.

$$p_1=p_{1i}+p_{1r},$$ (5)

$$p_{1i}={\displaystyle \sum _{m=0}^{\mathrm{\infty }}}{B}_m{P}_m(\mu )h_m^{(1)}((k_1+i{\alpha }_1)r)e^{-i\omega t},$$ (6)

$$p_{1r}={\displaystyle \sum _{m=0}^{\mathrm{\infty }}}{C}_m{P}_m(\mu )j_m((k_1+i{\alpha }_1)r)e^{-i\omega t}.$$ (7)

The pressure in the inner sphere can be written as

$$p_{2i}={\displaystyle \sum _{m=0}^{\mathrm{\infty }}}{D}_m{P}_m(\mu )j_m((k_2+i{\alpha }_2)r)e^{-i\omega t}.$$ (8)

Applying the boundary conditions of continuity of pressure and radial velocity at the two interfaces, a system of four equations with four unknowns results. This system can be written in the matrix form:

$$\left(\begin{array}{cccc}\hfill \frac{h_m^{(1)}\prime ({\tilde{k}}_0{r}_1)}{Z_0}\hfill & \hfill \frac{h_m^{(1)}\prime ({\tilde{k}}_1{r}_1)}{-Z_1}\hfill & \hfill \frac{j_m^{\prime }({\tilde{k}}_1{r}_1)}{-Z_1}\hfill & \hfill 0\hfill \\ \hfill -h_m^{(1)}({\tilde{k}}_0{r}_1)\hfill & \hfill h_m^{(1)}({\tilde{k}}_1{r}_1)\hfill & \hfill j_m({\tilde{k}}_1{r}_1)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{h_m^{(1)}\prime ({\tilde{k}}_1{r}_2)}{Z_1}\hfill & \hfill \frac{j_m^{\prime }({\tilde{k}}_1{r}_2)}{Z_1}\hfill & \hfill \frac{j_m^{\prime }({\tilde{k}}_2{r}_2)}{-Z_2}\hfill \\ \hfill 0\hfill & \hfill h_m^{(1)}({\tilde{k}}_1{r}_2)\hfill & \hfill j_m({\tilde{k}}_1{r}_2)\hfill & \hfill -j_m({\tilde{k}}_2{r}_2)\hfill \end{array}\right)\times \left(\begin{array}{c}\hfill A_m\hfill \\ \hfill B_m\hfill \\ \hfill C_m\hfill \\ \hfill D_m\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \frac{-{𝒫}_0}{Z_0}(2m+1){ℒ}_m{j}_m^{\prime }({\tilde{k}}_0{r}_1)\hfill \\ \hfill {𝒫}_0(2m+1){ℒ}_m{j}_m({\tilde{k}}_0{r}_1)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right).$$ (9)

where k̃_n is the complex wave number, k̃_n=k_n+iα_n, and

$$Z_n=\frac{{\rho }_n{c}_n}{1+i\frac{\alpha c_n}{\omega }}.$$ (10)

The coefficients can then be solved for analytically using Cramer’s rule or numerically using LU decomposition.

Often, only the scattered pressure needs to be computed so the values of B_m, C_m, and D_m do not need to be calculated. One can show that by direct manipulation of Eq. (9), the value of A_m is

$$A_m={𝒫}_0(2m+1){ℒ}_m\{[Z_{r2}{j}_m({\tilde{k}}_1{r}_2)j_m^{\prime }({\tilde{k}}_2{r}_2)-Z_{r1}{j}_m^{\prime }({\tilde{k}}_1{r}_2)j_m({\tilde{k}}_2{r}_2)]\times [Z_{r1}{h}_m^{\prime (1)}({\tilde{k}}_1{r}_1)j_m({\tilde{k}}_0{r}_1)-h_m^{(1)}({\tilde{k}}_1{r}_1)j_m^{\prime }({\tilde{k}}_0{r}_1)]-[Z_{r1}{h}_m^{\prime (1)}({\tilde{k}}_1{r}_2)j_m({\tilde{k}}_2{r}_2)-Z_{r2}{h}_m^{(1)}({\tilde{k}}_1{r}_2)j_m^{\prime }({\tilde{k}}_2{r}_2)]\times [j_m({\tilde{k}}_1{r}_1)j_m^{\prime }({\tilde{k}}_0{r}_1)-Z_{r1}{j}_m^{\prime }({\tilde{k}}_1{r}_1)j_m({\tilde{k}}_0{r}_1)]\}÷\{[Z_{r1}{h}_m^{\prime (1)}({\tilde{k}}_1{r}_2)j_m({\tilde{k}}_2{r}_2)-Z_{r2}{h}_m^{(1)}({\tilde{k}}_1{r}_2)j_m^{\prime }({\tilde{k}}_2{r}_2)]\times [h_m^{\prime (1)}({\tilde{k}}_0{r}_1)j_m({\tilde{k}}_1{r}_1)-Z_{r1}{h}_m^{(1)}({\tilde{k}}_0{r}_1)j_m^{\prime }({\tilde{k}}_1{r}_1)]-[Z_{r1}{j}_m^{\prime }({\tilde{k}}_1{r}_2)j_m({\tilde{k}}_2{r}_2)-Z_{r2}{j}_m({\tilde{k}}_1{r}_2)j_m^{\prime }({\tilde{k}}_2{r}_2)]\times [h_m^{\prime (1)}({\tilde{k}}_0{r}_1)h_m^{(1)}({\tilde{k}}_1{r}_1)-Z_{r1}{h}_m^{(1)}({\tilde{k}}_0{r}_1)h_m^{\prime (1)}({\tilde{k}}_1{r}_1)]\},$$ (11)

where

$$Z_{r1}=\frac{{\rho }_0{c}_0}{{\rho }_1{c}_1}\left[\frac{1+\frac{i{\alpha }_1{c}_1}{\omega }}{1+\frac{i{\alpha }_0{c}_0}{\omega }}\right]$$ (12)

and

$$Z_{r2}=\frac{{\rho }_0{c}_0}{{\rho }_2{c}_2}\left[\frac{1+\frac{i{\alpha }_2{c}_2}{\omega }}{1+\frac{i{\alpha }_0{c}_0}{\omega }}\right].$$ (13)

IV. VERIFICATION

One method of verifying the solution is to take the limit as the radius of the inner sphere, r₂, approaches the radius of the outer sphere, r₁. It can be shown that the coefficient for the scattered pressure in the infinite medium, A_m, takes on the following value as r₁→r₂:

$$A_m=\frac{(2m+1){𝒫}_0{ℒ}_m[j_m^{\prime }({\tilde{k}}_2{r}_1)j_m({\tilde{k}}_0{r}_1)Z_0-j_m^{\prime }({\tilde{k}}_0{r}_1)j_m({\tilde{k}}_2{r}_1)Z_2]}{-j_m^{\prime }({\tilde{k}}_2{r}_1)h_m^{(1)}({\tilde{k}}_0{r}_1)Z_0+h_m^{\prime (1)}({\tilde{k}}_0{r}_1)j_m({\tilde{k}}_2{r}_1)Z_2}.$$ (14)

If loss is no longer considered, k̃_n becomes k, and Z_n becomes ρ_nc_n. Making these substitutions,

$$A_m=\frac{(2m+1){𝒫}_0{ℒ}_m[j_m^{\prime }(k_2{r}_1)j_m(k_0{r}_1){\rho }_0{c}_0-j_m^{\prime }(k_0{r}_1)j_m(k_2{r}_1){\rho }_2{c}_2]}{-j_m^{\prime }(k_2{r}_1)h_m^{(1)}(k_0{r}_1){\rho }_0{c}_0+h_m^{\prime (1)}(k_0{r}_1)j_m(k_2{r}_1){\rho }_2{c}_2},$$ (15)

which is identical to Anderson’s solution for the single fluid sphere⁷ after some algebraic manipulation.

V. SIMULATION

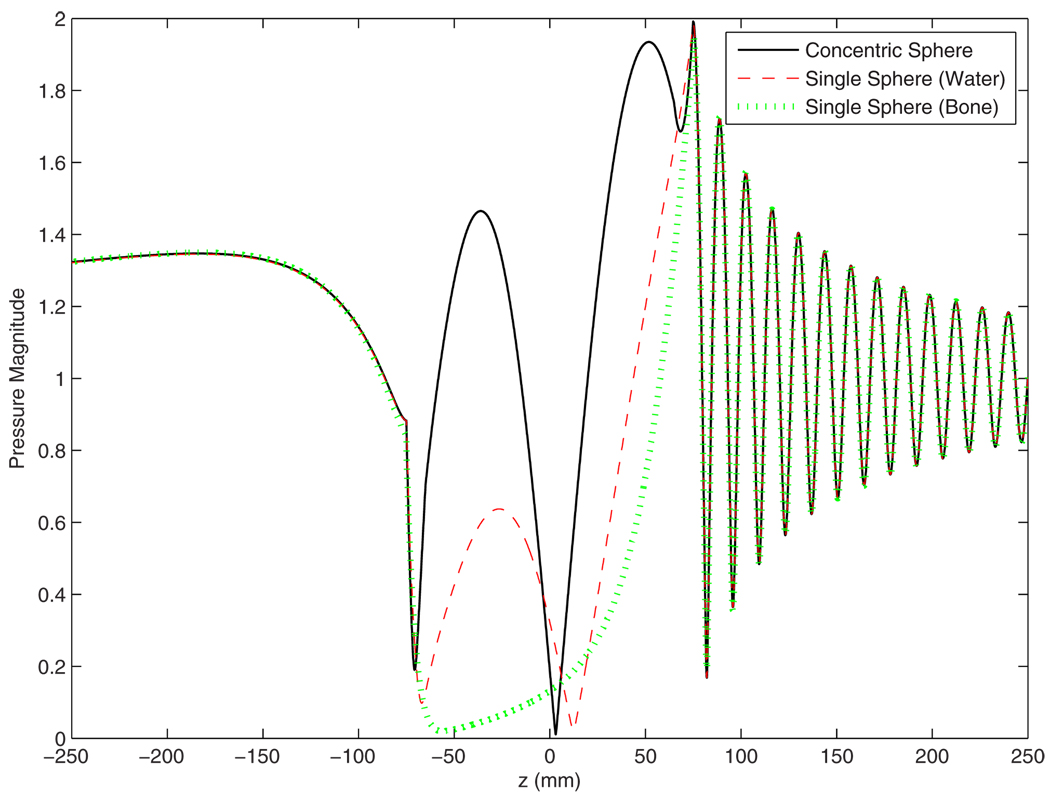
Three simulations were performed to compare the solution found using the concentric fluid sphere model to the single fluid sphere model using a frequency of 12.5 kHz. The first simulation approximated the human head as an outer sphere of bone (r₁=75 mm, ρ₁=2000 kg/m³, and c₁=2900 m/s) surrounding an inner sphere of water (r₂=65 mm, ρ₂=1000 kg/m³, and c₂=1500 m/s) placed in an infinite medium of air (ρ₀=1.21 kg/m³ and c₀=343 m/s). The second simulation used Anderson’s single fluid sphere solution to simulate a fluid sphere of bone (a=75 mm, ρ′=2000 kg/m³, and c′=2900 m/s) placed in an infinite medium of air (ρ=1.21 kg/m³ and c=343 m/s). The third simulation used Anderson’s single fluid sphere solution to simulate a fluid sphere of water (a=75 mm, ρ′=1000 kg/m³, and c′=1500 m/s) placed in an infinite medium of air (ρ=1.21 kg/m³ and c=343 m/s). The magnitude of the pressure along the z-axis is plotted in Fig. 2.

FIG. 2.

(Color online) Pressure magnitude along the z-axis for concentric fluid sphere and single fluid sphere solutions.

As can be seen in Fig. 2, the pressure outside of the spheres is nearly identical for all three solutions. This is expected because for all cases the impedance mismatch between the scatterer and the background medium is very large, and therefore the scattered field approaches the limiting rigid sphere case. Inside of the spheres, however, the three solutions differ significantly.

VI. CONCLUSIONS

The solution to plane wave and point source scattering from two concentric fluid spheres was derived. The effects of differences in speed of sound, density, and attenuation coefficient were included. The coefficient required to solve for the scattered pressure was explicitly computed for cases only requiring the scattered pressure. The limit as the outer sphere becomes a thin shell is found and found to agree with Anderson’s solution to a single fluid sphere. Finally, the solution is found to a concentric sphere approximation of the human head and compared to approximations of the human head as a single fluid sphere. It was found that outside of the scatterer, the solutions are similar but differ significantly inside the scatterer.