Abstract
The frequency-dependent ultrasound backscatter from tissues contains information about the microstructure that can be quantified. In many cases, the anatomic microstructure details responsible for ultrasonic scattering remain unidentified. However, their identification would lead to potentially improved methodologies for characterizing tissue and diagnosing disease from ultrasonic backscatter measurements. Recently, three-dimensional (3D) acoustic models of tissue microstructure, termed 3D impedance maps (3DZMs), were introduced to help to identify scattering sources [J. Mamou, M. L. Oelze, W. D. O’Brien, Jr., and J. F. Zachary, “Identifying ultrasonic scattering sites from 3D impedance maps,” J. Acoust. Soc. Am. 117, 413–423 (2005)]. In the current study, new 3DZM methodologies are used to model and identify scattering structures. New processing procedures (e.g., registration, interpolations) are presented that allow more accurate 3DZMs to be constructed from histology. New strategies are proposed to construct scattering models [i.e., form factor (FF)] from 3DZMs. These new methods are tested on simulated 3DZMs, and then used to evaluate 3DZMs from three different rodent tumor models. Simulation results demonstrate the ability of the extended strategies to accurately predict FFs and estimate scatterer properties. Using the 3DZM methods, distinct FFs and scatterer properties were obtained for each tumor examined.
I. INTRODUCTION
There has been a clear need for developing methodologies to better understand how ultrasonic waves are scattered by tissue microarchitecture. Developing a strategy to identify and quantify scattering sites could lead to significant advances in ultrasonic imaging because it would connect ultrasound-derived parameters with histopathologic properties of tissues. Consequently, medical diagnoses could possibly be drawn without the need for invasive biopsies.
The goal of quantitative ultrasound (QUS) is to identify, quantify and display tissue features that are related to histopathologic properties. Many QUS techniques rely on the frequency-dependent information contained in the radio-frequency backscattered signals to estimate tissue properties.1,2 From the frequency-dependent information, QUS methods quantify tissue properties based on assumptions about the nature of scattering structures. Because in many tissues the actual structures responsible for scattering remain unknown, there is no scientific basis for validating current hypotheses or choosing a model. However, the limitations in understanding ultrasonic scattering sites in tissue have not deterred QUS progress. Our group conducted several studies using a Gaussian scattering model because it led to efficient estimation schemes3–5 and also developed a new scattering model that took into account the cell’s internal structure.6 Other groups have successfully demonstrated that QUS parameters of extravascular matrix patterns (EMPs) correlated with histologic EMP, thus allowing for the discrimination between lethal and less lethal primary malignant melanoma of the choriod and ciliary body.7
For more than two decades, QUS methods have been developed to ultrasonically quantify ocular, liver, prostate, renal, and cardiac tissues.8–11 As this work progressed, the need for a more fundamental understanding of ultrasonic scattering became evident. Thus, QUS studies were conducted on simpler biological media wherein cells in pellets or in suspension were characterized.12,13 These studies had some success at quantifying cell apoptosis and more generally at suggesting which structures might be responsible for scattering in specific cell types.
Recently, we proposed an original method to predict ultrasonic scattering from complex tissue structures.14–17 Based on an aligned set of adjacent and stained histologic sections, a three-dimensional (3D) acoustic computational model, termed the three-dimensional impedance map (3DZM), was constructed and utilized to obtain quantitative information about tissue scattering. A 3DZM is a 3D matrix whose elements are acoustic impedance values corresponding spatially to tissue structures. These preliminary studies demonstrated the feasibility of the 3DZM method, and also assisted in the identification of advanced methodologies to further investigate and fundamentally understand ultrasonic scattering. The aim of this paper is to introduce and evaluate these advanced 3DZM methodologies.
The paper is organized as follows. Section II briefly reviews the theoretical background of 3DZMs and discusses their effectiveness as tools for understanding tissue scattering by ultrasound. The processing strategies to derive 3DZMs in an automatic fashion from the adjacent set of two-dimensional (2D) histologic sections were improved and are presented in Sec. III. Section IV presents advanced methodologies based on 3DZMs to help in identifying the anatomic structures responsible for ultrasonic tissue scattering. Section V presents results from simulated and experimentally derived 3DZMs. Finally, Sec. VI proposes possible extensions of the methodologies.
II. THEORETICAL MOTIVATION
A. Weak scattering in an inhomogeneous medium
The theory of scattering of a propagating acoustic wave in a heterogeneous medium is briefly reviewed (see Refs. 15, 18, and 19 for more details). In the theory, weak scattering is defined as the case where the inhomogeneities that cause scattering have tissue property values (density, ρ, and compressibility, κ) very close to those of the rest of the medium. For plane wave incidence, the backscattered acoustic pressure from a weakly scattering medium is18
| (1) |
where bs denotes backscattered, k is the propagation constant (k=ω/c where ω is the angular frequency and c is the propagation speed) and the angle distribution function, which describes the frequency dependence of the backscatter, is
| (2) |
where Δz(r0)/z(r0) is the relative change in acoustic impedance at spatial location r0.
From Eq. (2), the final expression for the backscattered intensity is
| (3) |
where
| (4) |
and
| (5) |
and where A is a proportionality constant. S′(2k) and S(2k) are the power spectrum and normalized power spectrum of the medium, respectively. (Details about this derivation can be found in Ref. 15.)
B. Form factor
Form factors (FFs) are functions of frequency that describe the amplitude of the backscattered intensity from an inhomogeneous medium. FFs are defined as the ratio of the medium’s backscatter cross section to that of the same medium but under the Rayleigh scattering assumption.1 Following that definition, FFs can be interpreted as the ultrasonic signature of a stochastic medium under ultrasonic interrogation.
Theoretical FFs can be deduced from 3D spatial correlation models by assuming some form or shape for the scattering tissue structures.1,19 Usually simple scattering shapes are assumed and in most cases they have a spherical symmetry. Specifically, the FF is the Fourier transform of the 3D spatial autocorrelation function of a 3D medium containing a single scattering structure, that is, the magnitude squared of the Fourier transform of the single scatterer’s shape. The normalization to Rayleigh scattering removes the k4 dependence from the backscattered intensity [see Eq. (3)] and consequently FFs are normalized to a value of 1 when k=0 and their derivative usually vanishes when k=0.19 Therefore, FFs are readily comparable to the normalized power spectrum S(2k) [Eq. (4)].
C. Relationships between scattering, FF and 3DZM
The previous sections have introduced the theoretical background needed to use the 3DZMs as a powerful tool to understand ultrasonic scattering. In what follows, it is assumed that an accurate 3DZM of a specific tissue type exists. This assumption means that each impedance value at each 3DZM voxel is the correct impedance value for the underlying tissue type.
Based on Eqs. (1)–(5), the backscattered intensity resulting from a plane wave incident on a scattering volume is
| (6) |
where the superscript denotes the 3DZM-deduced intensity (as opposed to that ultrasonically measured), FT[•] denotes the Fourier transform operator, B is a proportionality constant and SAF(3DZM) is the spatial autocorrelation function of the 3DZM. The second equality is obtained using the Wiener–Khintchine theorem. Equation (6) reveals that the 3DZM can be used as an independent estimator of the backscattered intensity at any frequency. This frequency-independent property of the 3DZM will be exploited in Sec. IV A.
The FF of the inhomogeneous medium can be deduced by
| (7) |
where a is the mean scatterer radius and is often a parameter to be estimated. Equation (7) provides a unique means of estimating the FF for a given medium from its 3DZM. This is a powerful tool to identify ultrasonic structures responsible for scattering because of the intimate relationship that exists between scatterers and FFs. (Section IV B presents an algorithm that exploits Eq. (7) to estimate the FF of a medium from its 3DZM.)
III. ADVANCED 3DZM CONSTRUCTION METHODS
A 3DZM is an acoustic computational phantom, i.e., a 3D matrix whose elements are the values of the acoustic impedance of the medium. The 3DZMs are derived from a 3D histologic dataset. The tissue is fixed in 10% neutral-buffered formalin, embedded in paraffin, sectioned, mounted on glass slides, and stained with H&E (Hematoxylin and Eosin). Hematoxylin stains nucleic acids (chromatin in nuclei and ribosomes) blue; the greater the nucleic acid density, the darker the blue color. Eosin stains proteins such as cell cytoplasm, connective tissue, muscle, etc. pink; the greater the protein concentration, the darker the pink color. Each stained section is photographed with a light microscope [Nikon (Nikon Corporation, Tokyo, Japan) Optiphot-2 optical microscope], and the photographs are digitized with a Sony (Sony Corporation, Tokyo, Japan) charge coupled device, Iris/RGB color video camera as a bitmap image.
The 3D reconstruction of a 3DZM from two-dimensional (2D) histologic sections involves several processing steps. Since initially presenting the 3DZM strategy,15 three significant improvements of the processing strategies to construct 3DZMs from adjacent photomicrographs of histologic sections have occurred. These improvements include contrast equalization, fine-tune registration, and interpolation of missing sections. First, the contrast of the thin sections is equalized because the uptake of stain, in general, is not uniform from section to section; nor is the video capture intensity necessarily the same from section to section. Second, a fine-tuning registration is conducted. Third, after registration, the sections lost during sectioning are interpolated. Finally, each voxel in the 3D histologic volume is assigned an acoustic impedance value. The resulting 3D matrix is the final 3DZM.
A. Contrast adjustment
Image contrast of each H&E stained bitmap image is equalized prior to registration in order to increase the robustness of the registration algorithm. Contrast equalization leads to more similar images increasing the likelihood for correct convergence of the registration algorithm.
Equalization is conducted for each of the three color components (i.e., red, green, and blue) of each image. Specifically, let denote the cumulative histogram of image I (for one of the color components). Thus, is the number of pixels with intensity level ≤α in the image (α is assumed to be an integer in the range 0–255 because of the 8 bit precision for each color component). If I(i, j) represents the intensity level of pixel (i, j) in image I, then the new pixel intensity in the equalized image I′ at (i, j) is given by20
| (8) |
where N is the total number of pixels in the image and the factor 255 has been added so that the new pixel intensity is in the range 0–255 (because ).
B. Registration
Registration or alignment is an essential step in the 3D reconstruction of the tissue model from serially sectioned photomicrographs. If the consecutive sections are not aligned correctly, then the resulting 3D model yields misleading or incorrect results that lead to potentially serious artifacts. The goal is to determine the best transformation to apply to an image I2 so that it is the most similar to the original and adjacent image I1. Hence, the registration algorithm is composed of three parts: a set of transformations, a similarity measure and an optimization process.
1. Set of transformations
The goal of this part of the registration algorithm is to transform I2 using a transformation T such that T(I2) is as similar as possible to I1 (I1 and I2 are adjacent histologic section images). Several types of transformations T can be used. The set of transformations, S, usually falls into two main categories: rigid and nonrigid transformations.21,22 The rigid transformations set, Sr, consists of three degrees of freedom (DOFs) (two translational and one rotational). The non-rigid transformations set, Snr, is composed of just about any conceivable adjustable parameter.
In the present work, Sr is used because it is a reasonable choice considering the error sources in the initial manual alignment of the images. A subset of Snr limited to the affine transformations (Saf) is used because this class of transforms can compensate for the small (likely in the 2–5% range), but unknown and inherent tissue shrinkage that occurs during tissue preparation. The shrinkage could affect the predicted form factor by preferentially shrinking some components more than others. However, because water comprises a majority of the molecules in the cells in these tumors and all of the tumors were processed under identical conditions, it is reasonable to assume that shrinkage, if it occurred, was evenly distributed throughout the entire tissue including tumor cells and other extracellular matrix components. At this stage of 3DZM development, even if a 2–5% shrinkage occurred, it would not significantly affect the quantitative measures; however, this is an area that will need to be investigated further.
The affine transform has six DOFs that consist of a rotation, a scaling along both axes, a shearing parameter, and a 2D translation vector.23 Basically, an affine transformation is the composition of a translation with any invertible linear transformation. Therefore, Saf is the set of all the transforms that conserves parallelism. It is also important to notice that the set of rigid transforms is strictly included into affine transforms.
When the pathologist performs the initial manual registration, only a rigid registration is performed. Therefore, when rigid registration is considered herein, it is a fine-tuning registration. Affine transforms include DOFs (stretching and shearing) that are not available to the pathologist when aligning adjacent sections.
2. Similarity measure
Once the image I2 is transformed, the similarity of T(I2) to I1 must be quantified. Define G(I,J) as a function that quantifies the similarity between image I and image J. Many choices are possible for G,24 but the functions G based on information theory concepts are usually very robust.25,26 A robust response is also observed in the present study. Therefore, the normalized mutual information (NMI), based on entropy concepts, is used as a similarity measure.21,23,27
For a gray-level image I, the probability distribution, pI, is defined as the normalized histogram of I. Specifically, pI(i) is equal to the number of pixels with intensity level i in image I divided by the total number of pixels in image I. The notation H(I) denotes the entropy of an image I using the above definition for the underlying probability distribution of the image. H(I) is defined by:
| (9) |
Given two images, the joint probability distribution of images I and J (where I and J are assumed to have the same dimensions), PI,J(i, j), is equal to the number of pixels that have intensity level i in I and j in J divided by the total number of pixels of image I (or J). Consequently, the joint entropy of images I and J is defined by
| (10) |
| (11) |
The images are assumed to be aligned when the NMI value is maximum. In the present work, the NMI is evaluated on intensity (gray-level) images derived from the color images by averaging the color components. The resulting gray-scale image is coded using 24 bits per pixel.
3. Optimization process
The next step is to update the transform (T→T′) so that NMI(I1, T′(I2)) ≥ NMI(I1, T(I2)), where T and T′ belong to the set of transforms. Many algorithms (e.g., gradient, Newton’s method, Levenberg–Marquardt method) rely on the possibility of estimating the gradient and/or the Hessian of the similarity function (with respect to the transformation’s DOFs).28 These techniques are not readily applicable to the NMI measure even though expressions exist for the gradient of the mutual information.29 Popular algorithms that bypass the need for derivatives are Powell’s algorithm and the simplex method.30,31 Powell’s algorithm optimizes each of the transformation’s DOFs one by one. The simplex method considers all DOFs simultaneously and is, therefore, used in the present work.32
C. Interpolation
Interpolation is required in two different steps of the 3D reconstruction: registration and missing sections.
1. Registration interpolation
When an image is transformed, there is a high probability that the new grid does not line up with a Cartesian grid. Therefore, an interpolation is needed to sample the transformed image onto the Cartesian grid to permit computer implementation. During registration optimization, nearest-neighbor interpolation is used to interpolate the transformed images. Once the best transform is found, a more accurate 2D bi-cubic interpolation algorithm is used for the reconstruction of the registered sections.33
2. Missing section interpolation
During the histologic preparation procedures of sectioning, mounting and staining, some of the sections are lost or destroyed. Therefore, interpolation is necessary to replace the missing sections to avoid further artifacts in the 3D tissue model. After alignment, the missing sections are interpolated. To interpolate the missing sections, cubic Hermite interpolating polynomials are used. Specifically, a third-degree polynomial (four unknowns) is found to match slope and values of the signals (images) on each side of a “hole.” This process yields four equations from which four unknowns are determined. The Hermite polynomials are chosen because they are shape preserving, i.e., extrema present in the available data are also extrema in the reconstructed signal. This property is of particular interest when dealing with images, because it guarantees that the reconstructed signals will remain within the range 0–255, thus avoiding the need for postprocessing to compress values into the range 0–255.
D. Acoustic impedance assignment
After completion of the previous steps, a 3D histologic map (3DHM) is obtained. The last step is to convert each 3DHM voxel to an adequate impedance value. To accomplish this task a color-threshold algorithm is carefully designed under the supervision of a board-certified pathologist, with each color representing a specific impedance value, to yield the final 3DZM. This part of the algorithm has not been changed and has been extensively discussed previously.15
IV. 3DZM-BASED IDENTIFICATION OF ULTRASONIC SCATTERING SITES
A. Estimation of scatterer properties
After the 3DZM is divided into smaller volumes called regions of interest (ROIs), the scatterer size and acoustic concentration are estimated for each ROI by an estimation routine that fits a chosen FF to the power spectrum of each individual ROI (see Sec. II C). A frequency-independent optimization routine has been implemented and tested previously15 and is used in the present study.
B. 3DZM-based form factor extraction
A strategy is proposed to extract a tissue-specific FF from 3DZMs. The theoretical model is first introduced, then the methodology is described and finally the implementation is demonstrated.
1. Theory
Assume that a given 3DZM contains a single type of scatterer but with variations in size and local number density. The 3DZM is divided into N ROIs. Each ROI is large enough to contain a number of random-sized scatterers of the same type from which the FF is deduced (assuming the largest scatterer is much smaller than the ROI).
The power spectrum of the lth ROI is denoted by PSl (where 1 ≤ l ≤ N). Assume further that the scatterers are isotropic and described by the to-be-determined form factor F*(ka) and that the lth ROI contains nl scatterers with random spatial locations within this ROI. The scatterers are assumed to have an acoustic impedance of z and the background impedance is z0. Using Eq. (7) and Fourier transform arguments, one obtains
| (12) |
where E[•]denotes the expected value; ap and Vs(ap) are the radius and the volume of the pth scatterer in the lth ROI, respectively; xp, yp, and zp describes the random location of the pth scatterer in the lth ROI; and kx, ky, and kz are the spatial frequency variables of the 3D Fourier transform ( ). The term inside the absolute value bars is the 3D Fourier transform of the lth ROI. To expand and simplify this term, assume that the scatterer radii inside the lth ROI have a narrow distribution, i.e., ∀pap ≈ 〈a〉l, where 〈a〉l denotes the mean radius of the scatterers contained in the lth ROI. This approximation also yields ∀p Vs(ap) ≈ Vs(〈a〉l). Thus, Eq. (12) reduces to
| (13) |
where the double sum term can be further reduced to
| (14) |
where was used. The first term of Eq. (14) is the incoherent scattering and the second term represents the amount of coherence between the scatterers. For a large number of randomly located scatterers, the expected value of the second term of Eq. (14) is zero (i.e., the sum of cosines is a random process with a zero expected value when k>0). Thus, when k>0, Eq. (12) reduces to
| (15) |
Equation (15) suggests that PSl can be approximated by the to-be-determined FF of the unknown variable k〈a〉l scaled by the unknown factor .
2. Methodology
Based on the theory, the function F* can be estimated from the 3DZM. Assume that the 3DZM is divided into N ROIs for which the assumptions of Sec. IV B 1 are valid over a spatial frequency range defined from k1 to k2. F* will then be estimated from PSl for every l (1 ≤ l ≤ N).
Each PSl is transformed to Tl(PSl) using a transformation (Tl) with two DOFs (magnitude and frequency axis scaling) to account for the two unknowns and k〈a〉l. In the ideal case where Eq. (15) is valid, it should then be possible to determine a set of N transforms such that the transformed power spectra are all the same. F* is deduced by normalizing the common power spectrum to unity when k=0.
Based on the theoretical assumptions, it is unrealistic to expect that the transformed power spectra fit perfectly. Therefore, a fitting criterion is introduced to quantify with a single number the similarity of the N transformed power spectra. This criterion is the mean standard deviation (MSTD) of the transformed power spectra over the chosen spatial frequency range. The quantity that needs to be minimized is
| (16) |
where 〈T(PS)(k)〉 is the mean of the transformed power spectra and is defined by
| (17) |
The algorithm is complete when the N transforms (i.e., T1, …, TN) that minimize the MSTD, i.e., Eq. (16), are determined.
3. Implementation
The implementation is not straightforward because the fitting algorithm is attempting to optimize simultaneously 2N unknowns. To reduce the number of unknowns, the power spectra are first log transformed. The log of Eq. (15) transforms the magnitude scaling term to a magnitude shift . The effect of this unknown magnitude shift is mitigated after the mean of each PSl is removed. Specifically, each log power spectra is modified according to the following:
| (18) |
Matching the mean values reduces the optimized DOFs to the N spatial frequency scaling coefficients that are defined by Tl(PSl)(k) = PSl(kαl). From Eq. (15) if {αl, for 1 ≤ l ≤ N} is a set of optimal scaling parameters, then so is {χαl, for 1 ≤ l ≤ N} for χ arbitrary, thus allowing for the further reduction of the DOFs by enforcing a mean value of unity for the set of scaling coefficients. This N−1 parameter optimization problem is finally implemented using the simplex algorithm.32
Once the MSTD is minimized, 〈T*(PS)(k)〉 (asterisk denotes the optimal transforms) is a scaled version of the to-be-determined FF, F*, over the chosen spatial frequency range. However, to obtain the actual FF one also needs to transform 〈T*(PS)〉 that is a function of k into a function of ka. The question is how to chose a; an heuristic approach of doing this consists, for example, of picking a such that
| (19) |
An alternate approach is to assume that the chosen spatial frequency range is such that k2 =4k1, thus leading to a value of a such that the ka range is 0.5–2.0. Specifically, a would be deduced from k1a =0.5 or equivalently k2a =2.0. Nevertheless, unless prior information is known regarding the average size of the scattering structures, no perfect way exists to choose a. One way to establish bounds for the possible ranges of a is to limit the frequency analysis bandwidth to 0.5<ka<2.0. In this study, a was chosen to be the value found with Gaussian FF for the same 3DZM (i.e., simulated or experimental). Denote the resulting function by F(ka)=〈T*(PS)(k)〉. This function of ka is now a magnitude-scaled estimate of F*(ka), that is, F(ka) ≈ BF*(ka) for some unknown constant B.
F(ka) is not expected to be a smooth curve, because it is a mean of N random processes (the N transformed power spectra) and for any 3DZM, the second term of Eq. (14) does not exactly go to zero. Several possible approaches exist to deduce a usable FF from F.
The simplest approach consists of keeping F(ka) as it is; even though noisy, F(ka) should be a curve with a fairly high signal-to-noise ratio (SNR) because it is the mean of the transformed power spectra that minimizes the MSTD. Each of these power spectra represents independent samples from a random process with the same statistics.
The next option is to conduct a smoothing of F* by either linear filtering (e.g., low-pass filtering) or nonlinear filtering (e.g., median filtering). The problem with these filtering approaches is that the resulting estimate of F* yields a function that is known only at the discrete locations where ka is sampled in the first place, which is a problem, for example, for the estimation step described in Sec. IV A. To avoid the need for interpolation, an approach is to model F* as a function, P(ka), that has a certain number of DOFs and find the DOF parameters that minimize the mean-squared error between F* and P. Because the expression for the function P is closed form, it can be evaluated at any spatial frequency exactly without the need for interpolation. Furthermore, because the ultimate goal is to fit this to-be-determined FF to the available spectra, an advantageous model for fast optimization is the 2-parameter (i.e., α and n) exponential model
| (20) |
The exponential model reduces to the Gaussian FF when α =0.827 and n=2. The choice for this model was motivated by our experience from simulations, ultrasound data and also because the model reduces to the Gaussian FF for specific values of α and n. In particular, mean-squared errors smaller than 3×10−5 were found when we modeled the fluid-filled, spherical shell, glass sphere, or fat sphere FF with Eq. (20).34 Furthermore, this model has been previously used to model FFs over a given frequency range.35 The 2-parameter exponential model is used in the remainder in this study. Therefore, the outputs of the FF-estimation algorithm are estimates of parameters α and n.
C. 3DZM Simulation methods
Each simulation was conducted in the same fashion: we simulated the actual power spectrum of each 3DZM. We did not simulate the 3DZM and then compute its spectrum. Both of these approaches are rigorously equivalent from a mathematical standpoint, but using the power spectrum of each 3DZM was much faster to implement.
In each simulation, the scatterers were modeled with the Gaussian FF. The spatial coordinates of the center of each scatterer were obtained from a realization of a uniform probability distribution function. The scatterer size was Gaussian distributed and quantified in terms of the mean radius or diameter and standard deviation. After all the spatial locations and sizes were obtained, the simulated power spectra were obtained by summing in the Fourier domain the contribution of each scatter as in Eq. (12). This summation could be performed because the FF of each scatterer is known and because spatial shifts become phase shifts in the Fourier domain.
Two sets of simulation studies were conducted as described below.
1. Simulation A
Previous simulation studies evaluated 3DZMs that contained either a single population of scatterers of the same size or contained two populations of scatterers of two different sizes for which the fluid-sphere FF was used.15 The purpose of this simulation study is to evaluate further how the presence of a size distribution affects the estimates. The previous work is extended to a set of simulations involving 3DZMs containing single populations of Gaussian FF scatterers whose sizes follow a Gaussian distribution with a mean diameter of 40 μm. Nineteen 3DZMs are generated, each with a different standard deviation, σ, for Gaussian size distribution that varied between 2 and 20 μm in 1 μm increments. The scatterers have an impedance of 1.51 Mrayl with a background of 1.50 Mrayl, the same as the previous simulations.15 The number density of the scatterers was 4 ×103/mm3 for the 19 simulated 3DZMs. Each 3DZM was a cube with a side length of 500 μm.
2. Simulations 1–4
The purpose of these simulation studies is to assess the methodology to extract a FF from a 3DZM. Each of the four simulations consists in the generation of 25 ROIs (i.e., N =25). We found that using 25 ROIs yields adequate results and is not too computationally extensive for simplex optimization. Each of the 25 spectra of each simulation was generated using the parameters listed in Table I. Each ROI was a cube with a side length of 250 μm.
TABLE I.
Simulation parameters and results. For each simulation the size distribution and number density listed were used for each ROI, G and D denotes for Gaussian and deduced, respectively. The range values (i.e., symbol “–”) mean that for each ROI, the corresponding parameter was chosen randomly and uniformly within this range.
| Simulation Number | FF | Number density 103/mm3 | G size distribution
|
N | Results
|
||||
|---|---|---|---|---|---|---|---|---|---|
| 〈diameter〉 (μm) | σ (μm) | α | n | G FF Mean error (%) | D FF Mean error (%) | ||||
| 1 | G | 4–8 | 32 | 0 | 25 | 0.796 | 2.08 | 2.5 | 2.4 |
| 2 | G | 4–8 | 32 | 8 | 25 | 1.46 | 1.66 | 15 | 2.5 |
| 3 | G | 4–8 | 16–48 | 0 | 25 | 0.796 | 2.07 | 3.2 | 3.5 |
| 4 | G | 4–8 | 16–48 | 0–48 | 25 | 3.24 | 1.04 | 27 | 19 |
Each ROI is populated spatially by uniformly distributed scatterers. For each ROI the number density of scatterers is random and ranges between 4×103/mm3 and 8×103/mm3. The sizes of the scatterers within a given ROI follow a Gaussian distribution whose parameters for some simulations are constant and for others have a range indicated in Table I. The scatterers have an impedance of 1.51 Mrayl with a background of 1.50 Mrayl. The analysis frequency band is 7.66–30.7 MHz, from ka=0.5 to ka=2 when c=1540 m/s for a radius a=16 μm.
Each set of simulations consists of a three-step process: (1) 25 random ROIs are generated to model the 3DZM. (2) A 3DZM-deduced FF is extracted from the power spectra of each of the 25 ROIs using the 2-parameter exponential law, Eq. (20), yielding values for α and n. (3) The extracted FF is then used with the 25 power spectra to obtain estimates following the methodology presented in Sec. IV A. Estimates using the Gaussian FF (often used for QUS studies3) are also obtained, allowing for comparison of the estimates between the deduced FF and the Gaussian FF. Four different simulations assess quantitatively the FF-extraction methodology.
V. RESULTS
Simulated and experimental results obtained using the advanced methodologies are presented. Simulations evaluate the FF-estimation algorithm. The advanced 3DZM reconstruction strategies are illustrated with a mouse sarcoma dataset. Finally, results from three experimental 3DZMs are presented. The three experimental 3DZMs are a rat mammary fibroadenoma, a mouse mammary carcinoma, and a mouse sarcoma.
A. Simulation results
1. Simulation A: Gaussian size simulations
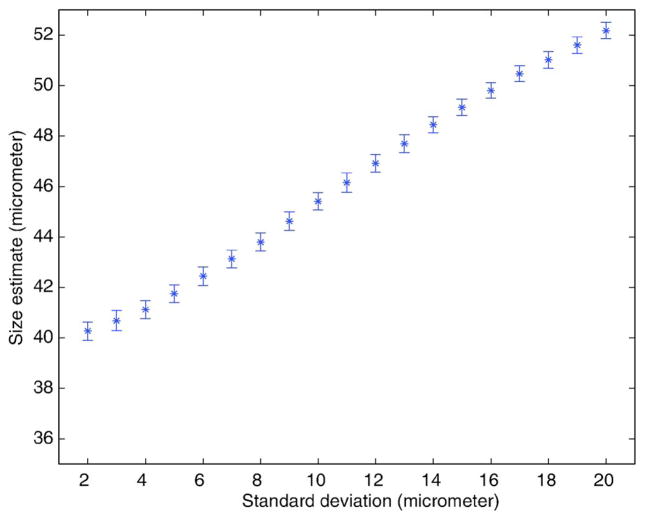
The larger scatterers in the distribution of sizes cause a bias in the estimates towards a larger value than the mean scatterer size when a Gaussian FF is used as the scattering model. This is observed in Fig. 1 by the increasing mean diameter estimate as a function of the increasing standard deviation. Even though biased, the estimates are precise because the standard deviation of the estimates is always small (<0.5 μm). The bias of the estimates is a problem if the absolute (mean) sizes of scattering structures are of importance. The size estimates represent a weighted average of the distribution of scatterer sizes in the population of scatterers. Scatterers with larger size distributions will have a volume-weighted average estimate of size that is much larger than the actual average size compared to smaller size distributions.
FIG. 1.
(Color online) Size estimates obtained using a Gaussian FF. The simulated 3DZM contained Gaussian scatterers whose size distribution was Gaussian with a mean diameter of 40 μm. The STD of the size distribution varied from 2 to 20 μm by 1 μm increments. For each STD value, 64 3DZMs were generated. Error bars represent STDs of estimates.
2. Simulations 1–4: Validation of the 3DZM-FF estimation
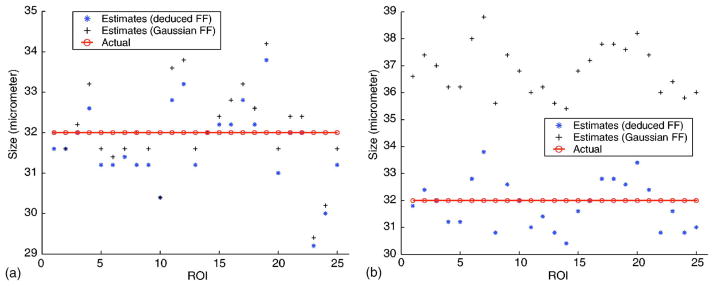
a. Simulation 1
This simulation tests the FF-extraction methodology because in this case the optimal FF is the Gaussian FF [Fig. 2(a)]. The accuracy of the estimates is good; all the size estimates (Gaussian FF and deduced FF) are in the range 29–35 μm (i.e., within 10%). There is no visible difference between the Gaussian FF and the deduced FF estimates. The mean errors are 2.5% and 2.4% for the Gaussian and deduced FFs (Table I), respectively. These results validate that for this simulation the FF-extraction algorithm is capable of deriving an accurate FF. Specifically, the parameters found from the FF-extraction algorithm are α =0.796 and n=2.08, which are near (within 4%) the Gaussian values (α=0.827 and n=2).
FIG. 2.
(Color online) Estimates obtained from 25 ROIs using the Gaussian and the 3DZM-deduced FF. (a) Each ROI was filled with a random number of randomly located Gaussian scatterers. Each ROI contained scatterers of diameter 32 μm. (b) Each ROI was filled with a random number of randomly located Gaussian scatterers. Each ROI contained scatterers following a Gaussian size distribution with mean diameter of 32 μm and standard deviation of 8 μm.
b. Simulation 2
The estimation routine using a Gaussian FF is expected to overestimate the mean size because of the non-zero standard deviation [Fig. 2(b)]. The Gaussian estimates are greater than the actual mean scatterer size; the mean Gaussian error is 15%. The deduced FF estimates do not show any bias and the deduced FF mean error is 2.5%. The FF-extraction algorithm estimates α=1.46 and n=1.66. These values are within 7% of the theoretical values (α =1.54 and n=1.57) for this Gaussian distribution of Gaussian scatterers.34 This agreement demonstrates the ability of the FF-extraction algorithm to estimate the correct FF.
c. Simulation 3
This simulation tests the ability of the algorithm to find the correct spatial frequency axis scaling coefficients (Table II). Furthermore, in this simulation (σ=0 for each ROI) the assumptions of Sec. B are valid [e.g., the transition from Eq. (12) to Eq. (13)]. The optimal FF for this simulation is the Gaussian FF because there is no variance in the size of the scatterers within a given ROI. Both FFs yield accurate estimates even though the actual diameters are randomly selected in the large range 16–48 μm. The mean errors are 3.2% and 3.5% for the Gaussian and deduced FFs, respectively. The FF-extraction algorithm estimates α=0.796 and n=2.07, values that are within 4% of the actual Gaussian values. Thus, this simulation demonstrates the ability of the FF-extraction algorithm to determine accurate spatial frequency scaling coefficients.
TABLE II.
Actual (A), Gaussian (G) FF, and deduced (D) FF mean size estimates (μm) for each of the 25 ROIs of Simulations 3 and 4.
| ROI number | Simulation 3
|
Simulation 4
|
||||
|---|---|---|---|---|---|---|
| A | G FF | D FF | A | G FF | D FF | |
| 1 | 18.2 | 20.1 | 19.5 | 38.0 | 41.8 | 37.8 |
| 2 | 20.8 | 17.9 | 18.1 | 46.5 | 45.0 | 45.0 |
| 3 | 16.9 | 14.8 | 14.9 | 37.8 | 42.5 | 39.9 |
| 4 | 30.1 | 29.9 | 29.9 | 28.1 | 38.8 | 34.1 |
| 5 | 29.4 | 29.4 | 29.4 | 19.5 | 36.5 | 29.8 |
| 6 | 42.1 | 42.1 | 41.7 | 42.5 | 41.5 | 37.5 |
| 7 | 37.5 | 37.0 | 36.9 | 29.1 | 39.1 | 34.1 |
| 8 | 36.0 | 36.0 | 35.9 | 20.8 | 31.8 | 20.6 |
| 9 | 24.9 | 22.1 | 23.1 | 28.0 | 32.0 | 30.0 |
| 10 | 25.9 | 24.9 | 24.9 | 38.5 | 43.1 | 40.2 |
| 11 | 42.0 | 41.0 | 40.5 | 18.9 | 33.8 | 26.9 |
| 12 | 25.3 | 25.2 | 25.2 | 24.9 | 41.9 | 36.9 |
| 13 | 23.9 | 27.1 | 27.1 | 30.0 | 39.0 | 34.0 |
| 14 | 42.1 | 42.3 | 42.1 | 20.8 | 24.9 | 12.9 |
| 15 | 35.6 | 34.9 | 34.8 | 22.2 | 28.1 | 16.8 |
| 16 | 33.8 | 34.8 | 34.7 | 23.2 | 27.1 | 16.4 |
| 17 | 42.5 | 42.4 | 41.6 | 33.8 | 38.9 | 33.8 |
| 18 | 26.1 | 24.9 | 24.9 | 21.1 | 38.1 | 33.2 |
| 19 | 36.5 | 36.7 | 36.5 | 45.2 | 45.5 | 45.6 |
| 20 | 22.5 | 21.5 | 21.2 | 22.5 | 31.2 | 20.8 |
| 21 | 45.1 | 46.1 | 46.2 | 42.5 | 43.3 | 42.0 |
| 22 | 32.0 | 31.8 | 31.8 | 23.1 | 23.7 | 12.1 |
| 23 | 29.1 | 29.1 | 29.1 | 26.1 | 27.8 | 18.2 |
| 24 | 25.1 | 24.9 | 24.9 | 33.7 | 40.0 | 25.5 |
| 25 | 44.8 | 44.4 | 44.1 | 30.0 | 37.2 | 30.5 |
d. Simulation 4
This simulation tests whether the FF-extraction algorithm is capable of extracting a FF from 25 ROIs that have different size distributions but contain the same (Gaussian FF) scatterers (Table II). For this simulation, the Gaussian estimates of size should be greater than the actual mean values, with a bias that depends on the (random) standard deviation of each ROI. From the results, the Gaussian estimates of size are greater than the actual mean values in all except one ROI. The deduced FF estimates of size are sometimes greater and sometimes smaller than the actual mean values. The mean errors are 27% and 19% for the Gaussian and deduced FFs, respectively. These larger errors indicate that neither of the two FFs are accurate scattering models. The FF-extraction algorithm estimates α=3.24 and n=1.04. The fact that the Gaussian FF produces inaccurate estimates was expected. However, the fact that the deduced FF produces inaccurate estimates is unexpected. The problem may be due to the two-parameter exponential model that may not be capable of tracking the three DOFs: the random mean radius, the random standard deviation, and the random ROIs. One suggestion to mitigate this problem is to fit the extracted FF to a model with three or more DOFs. A three-parameter FF can be derived theoretically by extending further the theory of Sec. IV B.
These four simulations demonstrate the ability of the FF-extraction algorithm to accurately model complex scattering media. In particular, the 3DZM-deduced FF greatly outperformed the Gaussian FF for these advanced media in terms of estimate bias even though the media contain only Gaussian scatterers.
B. Experimental results
1. Sarcoma 3DZM reconstruction
The 3D reconstruction strategies are developed and demonstrated with a murine sarcoma tumor model. The EHS (Englebreth–Holm–Swarm) tumor cell line (CRL-2108, American Type Culture Collection, Manassas, VA) is a transplantable sarcoma in C57BL/6 mice. This tumor produces extracellular matrix (ECM) components such as laminin, collagen IV, entactin, and heparan sulfate proteoglycan. The cells are injected subcutaneously and the tumor was allowed to grow until it was approximately 1 cm in diameter. Details of cell maintenance and tumor growth with this animal model have been published.36 The experimental protocol was approved by the Institutional Animal Care and Use Committee, University of Illinois, Urbana-Champaign, and satisfied all University and NIH rules for the humane use of laboratory animals.
Sections of the sarcoma are fixed in 10% neutral-buffered formalin, embedded in paraffin, sectioned at 3 μm thickness, mounted on glass slides, and stained with H&E for evaluation. These processes cause a minor degree of inherent tissue shrinkage that is small, but indeterminate for each section. In addition, it is not possible to obtain 200 serial sections (one section after another) without the loss of some sections due to technical difficulties.
The sarcoma sections are examined and captured (see Sec. III). The optical (bitmap) images measure laterally 400 μm (640 pixels) by 300 μm (480 pixels) with 8 bit accuracy for each red, green and blue component. The EHS dataset contains 200 sections of which 54 sections (27%) were lost during tissue preparation.
The 3D reconstruction strategies are then applied to the EHS dataset. These 43 consecutive sections (Fig. 3) are 218 by 156 μm (i.e., 350 by 250 pixels) subimages of the original 400 by 300 μm EHS images. Among these 43 consecutive sections, seven are missing (including four consecutive sections). The sections are misaligned, and the contrast between sections is also slightly different. The misalignment can be observed by following the pink quasicircular structure (muscle) from one section to the next. In addition, sections 8 and 17 have slightly better contrast than the neighboring sections. In each section of the EHS dataset, the histopathologic characteristics of the tissue that are diagnostically consistent with an EHS sarcoma, that is, the islands of tumor cells intermixed with ECM, are clearly visible.
FIG. 3.
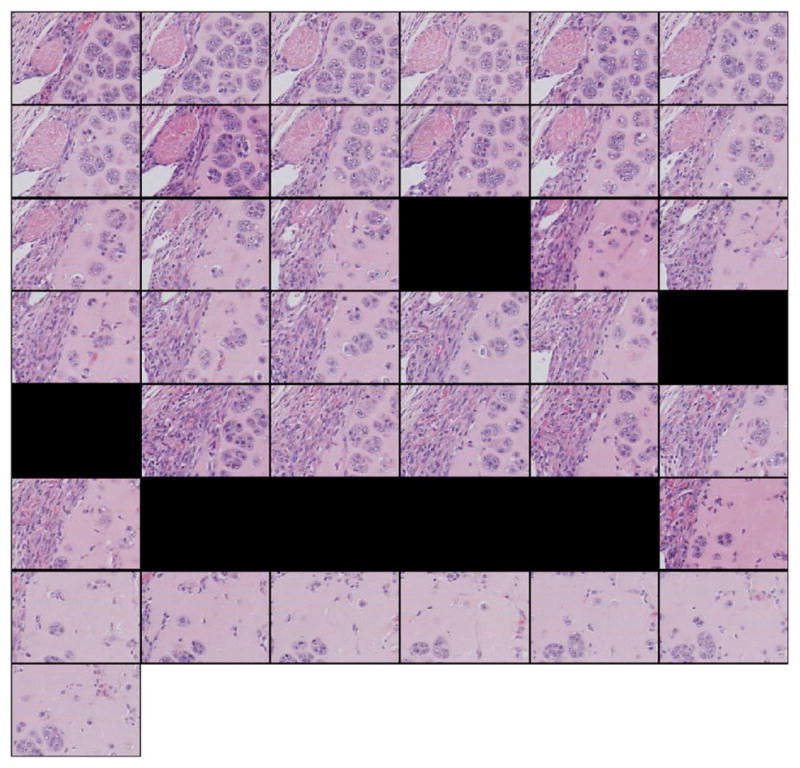
(Color online) Forty-three-section dataset from the EHS dataset. Sections are of size 218×156 μm (i.e., 350×250 pixels). Sections are sub-images of size 218×156 μm (i.e., 350×250 pixels) of the original 400×300 μm EHS sections. Subimages were extracted from the same location in each of the 43 original EHS sections. The sections were consecutive from left to right and top to bottom. Black fields symbolize missing sections.
Figure 4 shows the reconstructed 43-section dataset. To align the images, affine registration was used. The reconstructed images have a similar contrast. The alignment can be observed by following the oblique structures in the top left corner. The interpolated missing sections are of lower quality than the others because the interpolated missing sections are not as sharp and contained some edge artifacts. This is particularly true for the four reconstructed images of the four consecutive missing sections in which the purple background in the bottom-right corners of the interpolated images is not as uniform as in the other sections. In addition, the background appears to be “noisy” and to contain random small structures with blurry edges. Except for the artifacts noted, in each section of the EHS dataset, the histopathologic characteristics of the tissue are diagnostically consistent with an EHS sarcoma.
FIG. 4.
(Color online) Reconstruction of the 43-section EHS dataset of Fig. 3. The contrast of the available sections was equalized. Each section was affine registered with the next available section. Missing sections were Hermite interpolated.
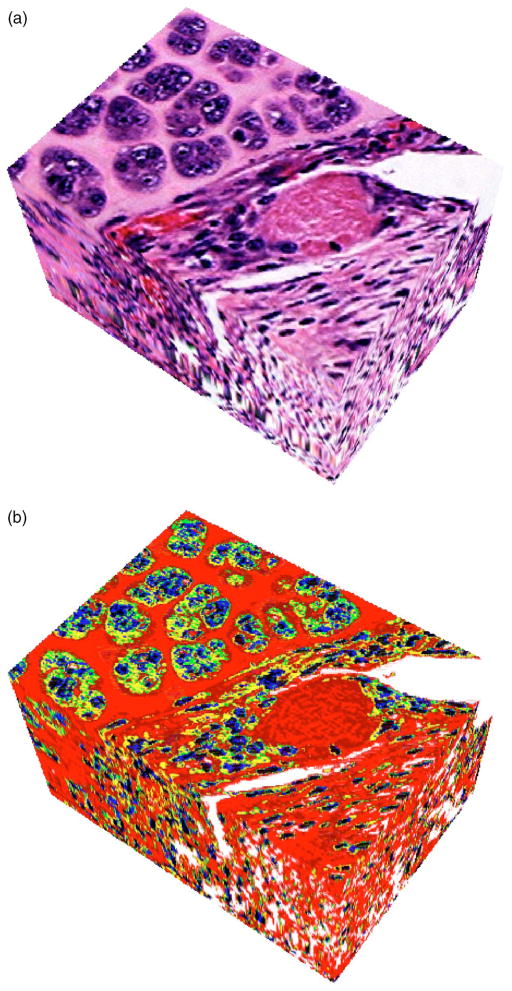
Figure 5(a) shows a 3D rendering from the 43-section reconstructed EHS dataset. The interpolated section artifacts are noticeable on the bottom half of the left side of the volume where the rendering is blurry. To obtain a 3DZM of the EHS sarcoma, seven distinct impedance values are used: 2.00 Mrayl for the nuclear heterochromatin [black on Fig. 5(b)], 1.85 Mrayl for the nuclear euchromatin (blue), 1.70 and 1.65 Mrayl for the extracellular matrix (dark red/red), 1.60 for the vascular space/whole blood (white), and 1.58 and 1.55 for the cytoplasm (green/yellow). The 3DZMs and impedance values for the fibroadenoma and carcinoma were published previously.15
FIG. 5.
(Color online) (a) Three-dimensional rendering from the 43-section dataset (Fig. 4). (b) Derived 3D impedance map. The volumes shown in (a) and (b) are of size 218×156×129 μm (depth).
2. Scatterer property estimates
The frequency-independent estimation algorithm is conducted on four ROIs on the three 3DZMs (fibroadenoma, carcinoma and sarcoma) using the Gaussian FF and the 3DZM-deduced FF. The use of four ROIs was to reduce estimate variance through averaging. The dimensions of the 3DZMs and of the ROIs are displayed in Table III. We chose to use only four ROIs because if we decided to further divide the 3DZM, then each individual ROI would have been too small to possibly contain a sufficient number scatterers in the size range being investigated. For each experimental 3DZM, the 3DZM-deduced FF was obtained using 25 overlapping ROIs (i.e., N=25, adjacent ROI overlap by 75%). We use 25 ROIs because the same number was chosen for the simulation and yields acceptable results. Going beyond N=25 would increase further the redundancy of the data within two adjacent ROIs.
TABLE III.
The 3DZM and ROI dimensions in μm used for scatterer property estimation and FF extraction.
| Rat fibroadenoma | Mouse carcinoma | Mouse sarcoma | |
|---|---|---|---|
| 3DZM width | 800 | 200 | 218 |
| 3DZM length | 600 | 150 | 156 |
| 3DZM depth | 390 | 330 | 129 |
| ROI width | 400 | 100 | 109 |
| ROI length | 300 | 75 | 78 |
| ROI depth | 390 | 330 | 129 |
The 3DZM results along with the independent ultrasonic estimates are summarized in Table IV. Ultrasonic results were obtained by using standard in vivo backscattered methodology.4 (Some of the results presented in Table IV were reported before and are indicated by the superscript *,15 and a topic for future research.)
TABLE IV.
The 3DZMs and ultrasound estimates. Ultrasound (US) estimates were obtained using the Gaussian FF. The 3DZM estimates were obtained using the Gaussian (G.) and the 3DZM-deduced (D.) FF.
| Rat fibroadenoma
|
Mouse carcinoma
|
Mouse sarcoma
|
||||
|---|---|---|---|---|---|---|
| Diameter μm | Conc. dB mm−3 | Diameter μm | Conc. dB mm−3 | Diameter μm | Conc. dB mm−3 | |
| US | 105±25 | −15.6±5 | 30.0±9.6 | 10.6±6.9 | 33.0±8.0 | 9.9±5.3 |
| 3DZM G. | 91.5±25* | −21.9±6.1* | 31.5±2.5* | −1.4±6.1* | 32.9±6.1* | −0.59±4.3* |
| 3DZM D. | 96.5±14 | −21.8±5.1 | 56.0±19 | −6.9±7.2 | 37.0±12 | 0.46±5.5 |
Experimentally derived estimates were obtained by measuring the ultrasonic backscatter from the tumors using a Gaussian FF.4 The experimentally derived estimates represent an independent measure from those of the 3DZM estimates. The mean scatterer size and acoustic concentration 3DZM-based estimates (Table IV) are obtained by computing the mean and standard deviation of the estimates over the four ROIs for each of the three 3DZMs. Results have good agreement (difference less than 10%) between ultrasonic and 3DZM estimates of size estimates for three tumors. However, the acoustic concentration values are significantly different (difference greater than 6 dB mm−3). The difference in acoustic concentration has already been observed and discussed previously.15
The deduced FF study has yielded interesting results. (1) The exponential fit FFs deduced using the FF-extraction methodology are different for each tumor (Table V). This difference may indicate that each tumor has its own unique ultrasonic scattering signature (i.e., FF) that is not detected using a Gaussian FF. The results suggest that the tumor-specific FF may be used to characterize, distinguish and possibly diagnose disease with QUS techniques. (2) Using the deduced FF the mean diameter estimate is now statistically different for each of the three tumors (Table IV). The specificities of the estimates are potentially significant for diagnosing (classifying) tissue.
TABLE V.
Parameters and frequency range of the exponential fit obtained using the FF extraction methodology. Exponential fit parameters were extracted from the three experimental 3DZMs.
| Frequency range (MHz) | α | n | |
|---|---|---|---|
| Rat fibroadenoma | 0.5–15 | 1.501 | 0.6145 |
| Mouse carcinoma | 1–25 | 2.359 | 0.4054 |
| Mouse sarcoma | 1–25 | 1.070 | 1.580 |
VI. DISCUSSION
The purpose of this study has been to report on continued developments of strategies to identify and characterize ultrasonic scattering sites in biological tissue. In our previous contribution,15 a novel approach to identify the anatomical scattering sources was introduced. This approach uses volume sections (3D histologic maps) that correspond to in vivo scanned tumor volumes to generate a 3D impedance map (3DZM). In the previous contribution, 3DZMs were created by manually aligning serial photomicrographs of tumor sections. In this contribution, an automated capability is presented that enhances, aligns and interpolates serial photomicrographs. In the previous contribution, 39 10-μm-thick rat fibroadenoma sections were assigned three impedance values and 66 5-μm-thick mouse mammary carcinoma sections were assigned five impedance values. In this contribution, 200 3-μm-thick mouse sarcoma sections were assigned seven impedance values. In the previous contribution, the Gaussian FF was used to estimate QUS parameters (size and acoustic concentration) from the fibroadenoma and carcinoma 3DZMs. In this contribution, a tissue-specific FF using a two-parameter exponential model [Eq. (20)] is developed, validated, and used to estimate QUS parameters from the 3DZMs of all three tumors. Each of these incremental improvements represents a significant advance to yield an accurate tissue macrostructure- and microstructure-based computational phantom for identifying and quantifying the anatomical scattering sources. Thus, accurate 3DZMs enable several important issues to be resolved or better understood: (1) The comparison between tumor 3DZMs and ultrasound scatterer property estimates of the same tumors will allow precise connections to be made between the microanatomical and ultrasound echo features. (2) The 3DZMs will allow FFs to emerge directly from histological analyses by assigning impedance values to candidate structures and calculating the corresponding spatial autocorrelation. (We already have developed a “new cell model” based on this idea.6) (3) Tissue anisotropy can be deduced by examination of the 3DZMs. Determining the anisotropy of a tissue (deduced from 3DZMs) will be important for understanding the interaction of ultrasound with the tissue and formulation of models. (4) Periodicities in the tissue structures can be quantified through the 3DZMs because current backscatter models assume scattering from randomly located structures.
A. 3DZM validation
Within this paper, theories relating 3DZMs to scatterer property estimates are presented and tested through improved 3DZM construction, simulations, and experimental data. Both qualitative and quantitative assessments of the 3D reconstruction strategies have been conducted, but they extend beyond the scope of this paper.34 In particular, on well-controlled cases it was quantitatively demonstrated that the registration algorithm was robust. Furthermore, interpolated sections were evaluated by a board-certified pathologist who was able to diagnose the tumor.
Nevertheless, work is still needed to explicitly validate 3DZMs. In particular, acoustic impedances were empirically assigned.15 These assignments were conducted jointly between a board-certified pathologist (who described the tissue constituent and its amount) and an ultrasonic tissue property expert (who conducted and published many ultrasonic tissue measurements). Because scattering properties depend significantly on the assigned impedance values, efforts should be pursued to acquire independent and reliable ultrasonic tissue property measurements at the micron-scale level.
An alternate technique to be considered is to deduce ultrasonic tissue property values by iteration. The 3DZMs could be used as computational phantoms to simulate backscattered signals to be compared with real experimental backscatter data. At each step, the 3DZM would be updated until the simulated backscattered signals matched the signals obtained by ultrasonic measurements.
B. Gaussian FF limitations
Estimating scattering properties using a Gaussian FF can be misleading even in the case of Gaussian scatterers (Sec. IV A 1). Therefore, while the Gaussian FF allows fast optimization schemes,15 the results might not be useful for identifying and quantifying the actual scattering structures.
The size estimates of the tumors do not allow for statistical distinction between the carcinoma and sarcoma (Table IV) using the Gaussian FF over the analysis bandwidth. The three tumors were chosen because they contained distinct histopathologic features (Fig. 6), features that are used by pathologists for diagnosis. An explanation may be that the Gaussian FF is an inadequate scattering model and is unable to track the specific ultrasonic scattering properties expected from these two tumors over the chosen bandwidth. Over the same bandwidth, improved FFs may yield greater sensitivities to the differences between the carcinoma and sarcoma using characterization techniques, as demonstrated successfully in Refs. 6 and 36.
FIG. 6.
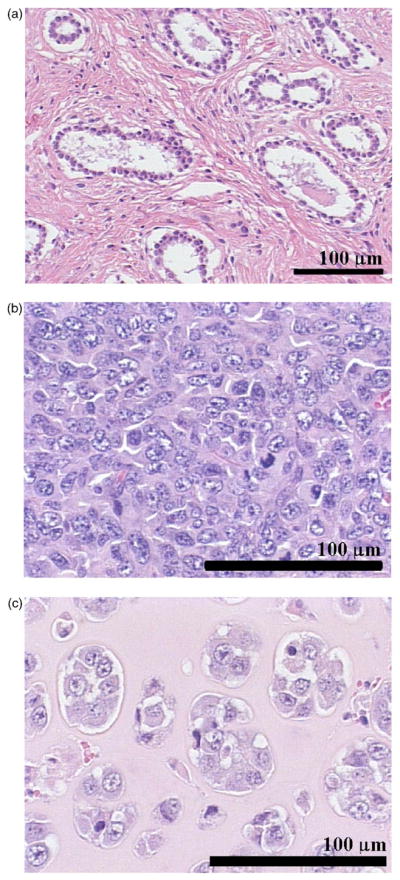
(Color online) Typical H&E stained tissue sections for a rat mammary fibroadenoma (a), a 4T1 mouse mammary carcinoma (b), and a EHS mouse sarcoma (c). This figure demonstrates that the histopathologic properties of the tumor tissue investigated are very different.
C. Identification of the ultrasonic scattering sites
The initial motivation in the development of the 3DZMs was that they represent accurate morphological models of tissue microstructure that can aid in identifying and quantifying scattering sites. Identifying and quantifying the ultrasonic scattering sites would lead to significant improved capabilities for diagnosing pathologies using QUS techniques. Parameters estimated could then be chosen that actually describe histologic features of tissue microstructures.
1. Identification using size estimates
One approach to identify anatomic scattering sites is to utilize the information from the histologic images. For the fibroadenoma, all the size estimates are near 100 μm (Table IV). The circular white structures, acini with neighboring epithelial cells, have diameters near 100 μm [Fig. 6(a)]. Thus, it is likely that for the fibroadenoma the anatomic structures responsible for scattering are the acini.
The carcinoma size estimates obtained with either the Gaussian or the deduced FF (Table IV) do not correspond to any specific histologic structures. The histology is very dense with a lot of tumor cells (nuclei around 10 μm in diameter) and very little ECM [Fig. 6(b)]. These structures are much smaller than those obtained via QUS estimation techniques. Thus, the estimates suggest that the Gaussian FF and the deduced FF are not good scattering models for this tumor. A recent study also demonstrated that carcinoma cells in pellet form had the same ultrasonic size estimates using a Gaussian FF.36 Thus, it is likely that individual cells combined with their inner constituents (e.g., cytoplasm, nuclei, organelles, and cytoskeleton) are significantly responsible for ultrasonic scattering.
For the sarcoma, all the size estimates (Table IV) are in the range 30–40 μm in diameter. This range is consistent with the diameters of the islands of tumor cells [Fig. 6(c)]. Furthermore, the ECM background is quite uniform, which adds confidence that the anatomic structures responsible for scattering may be the islands of tumor cells.
Figure 6 also raises the concern for having periodic scattering structures. Periodic structures would in particular violate the uniform random spatial locations assumption of scatterers used for the simulation and estimation methods. Our previous experience in which ultrasonic backscatter analysis of these tumors matched the 3DZM approach15 and more recent study37 reveal that the assumption of randomness was most likely not violated.
2. Identification using form factors
Another approach to identify anatomic scattering structures is to consider the computational phantom capability (3DZMs) to deduce FFs. The 3DZM-deduced FFs could be iteratively compared to ultrasound backscatter signatures from either the same tissues from which in vivo ultrasonic echo data were acquired or from computational echo data acquired for the 3DZM, or both. When the ultrasonic echo data converges with the 3DZM-deduced FFs, the FF-SAF duality (Sec. III B) would help to identify the scattering sources. Further, from the inverse Fourier transform of the 3DZM-deduced FF, a 3D acoustic model of the SAF of a scattering structure can be determined. Then, it might be possible to identify the scattering sites by comparison of the SAF characteristics with the histology.
Acknowledgments
The authors would like to acknowledge the support by NIH Grant No. CA111289 and by the University of Illinois Research Board. J.M. thanks the Riverside Research Institute and the Lizzi Center for Biomedical Engineering for its support in enabling the preparation of this paper.
Contributor Information
Jonathan Mamou, Bioacoustics Research Laboratory, Department of Electrical and Computer Engineering, University of Illinois, 405 North Mathews, Urbana, Illinois 61801.
Michael L. Oelze, Bioacoustics Research Laboratory, Department of Electrical and Computer Engineering, University of Illinois, 405 North Mathews, Urbana, Illinois 61801
William D. O’Brien, Jr., Bioacoustics Research Laboratory, Department of Electrical and Computer Engineering, University of Illinois, 405 North Mathews, Urbana, Illinois 61801
James F. Zachary, Department of Pathobiology, University of Illinois, 2001 South Lincoln, Urbana, Illinois 61802
References
- 1.Insana MF, Wagner RF, Brown DG. Describing small-scale structure in random media using pulse-echo ultrasound. J Acoust Soc Am. 1990;87:179–192. doi: 10.1121/1.399283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Feleppa EJ, Lizzi FL, Coleman DJ, Yaremko MM. Diagnostics spectrum analysis ophthalmology: A physical perspective. Ultrasound Med Biol. 1986;12:623–631. doi: 10.1016/0301-5629(86)90183-3. [DOI] [PubMed] [Google Scholar]
- 3.Oelze ML, Zachary JF, O’Brien WD., Jr Characterization of tissue microstructure using ultrasonic backscatter: Theory and technique for optimization using a Gaussian form factor. J Acoust Soc Am. 2002;112:1202–1211. doi: 10.1121/1.1501278. [DOI] [PubMed] [Google Scholar]
- 4.Oelze ML, Zachary JF, O’Brien WD., Jr Parametric imaging of rat mammary tumors in vivo for the purposes of tissue characterization. J Ultrasound Med. 2002;21:1201–1210. doi: 10.7863/jum.2002.21.11.1201. [DOI] [PubMed] [Google Scholar]
- 5.Oelze ML, O’Brien WD, Jr, Zachary JF. Differentiation and characterization of rat mammary fibroadenomas and 4tl mouse carcinomas using quantitative ultrasound imaging. IEEE Trans Med Imaging. 2004;23:764–771. doi: 10.1109/tmi.2004.826953. [DOI] [PubMed] [Google Scholar]
- 6.Oelze ML, O’Brien WD., Jr Application of three scattering models to characterization of solid tumors in mice. Ultrason Imaging. 2006;28:83–96. doi: 10.1177/016173460602800202. [DOI] [PubMed] [Google Scholar]
- 7.Coleman DJ, Silverman RH, Rondeau MJ, Boldt HC, Lloyd HO, Lizzi FL, Weingeist TA, Chen X, Vangveeravong S, Folberg R. Noninvasive in vivo detection of prognostic indicators for high-risk uveal melanoma: Ultrasound parameter imaging. Ophthalmology. 2004;111:558–564. doi: 10.1016/j.ophtha.2003.06.021. [DOI] [PubMed] [Google Scholar]
- 8.Perez JE, Miller JG, Barzilai B, Wickline S, Mohr GA, Wear K, Vered Z, Sobel BE. Quantitative characterization of myocardium with ultrasonic imaging. J Nucl Med Allied Sci. 1988;32:149–157. [PubMed] [Google Scholar]
- 9.Lizzi FL, Greenebaum M, Feleppa EJ, Elbaum M, Coleman DJ. Theoretical framework for spectrum analysis in ultrasonic tissue characterization. J Acoust Soc Am. 1983;73:1366–1373. doi: 10.1121/1.389241. [DOI] [PubMed] [Google Scholar]
- 10.Lizzi FL, Ostromogilsky M, Feleppa EJ, Rorke MC, Yaremko MM. Relationship of ultrasonic spectral parameters to features of tissue microstructure. IEEE Trans Ultrason Ferroelectr Freq Control. 1986;33:319–329. doi: 10.1109/t-uffc.1987.26950. [DOI] [PubMed] [Google Scholar]
- 11.Insana MF, Wood JG, Hall TJ. Identifying acoustic scattering sources in normal renal parenchyma in vivo by varying arterial and ureteral pressures. Ultrasound Med Biol. 1991;17:613–626. doi: 10.1016/0301-5629(92)90073-j. [DOI] [PubMed] [Google Scholar]
- 12.Baddour RE, Sherar MD, Hunt JW, Czarnota GJ, Kolios MC. High-frequency ultrasound scattering from microspheres and single cells. J Acoust Soc Am. 2005;117:934–943. doi: 10.1121/1.1830668. [DOI] [PubMed] [Google Scholar]
- 13.Kolios MC, Czarnota GJ, Lee M, Hunt JW, Sherar MD. Ultrasonic spectral parameter characterization of apoptosis. Ultrasound Med Biol. 2002;28:589–597. doi: 10.1016/s0301-5629(02)00492-1. [DOI] [PubMed] [Google Scholar]
- 14.Mamou J, Oelze ML, Zachary JF, O’Brien WD., Jr Ultrasound scatterer size estimation technique based on a 3D acoustic impedance map from histologic sections. Proceedings of the 2003 IEEE Ultrasonics Symposium; Honolulu, HI. 2003. pp. 1022–1025. [Google Scholar]
- 15.Mamou J, Oelze ML, O’Brien WD, Jr, Zachary JF. Identifying ultrasonic scattering sites from 3D impedance maps. J Acoust Soc Am. 2005;117:413–423. doi: 10.1121/1.1810191. [DOI] [PubMed] [Google Scholar]
- 16.Mamou J, Oelze ML, O’Brien WD, Jr, Zachary JF. Ultrasound characterization of three animal mammary tumors from three-dimensional acoustic tissue models. Proceedings of the 2005 IEEE Ultrasonics Symposium; Rotterdam, Netherlands. 2005. pp. 866–869. [Google Scholar]
- 17.Mamou J, Oelze ML, O’Brien WD, Jr, Zachary JF. A view on quantitative biomedical ultrasound imaging. IEEE Signal Process Mag. 2006;23:112–116. [Google Scholar]
- 18.Morse PM, Ingard KU. Theoretical Acoustics. McGraw–Hill; New York: 1968. [Google Scholar]
- 19.Shung KK, Thieme GA. Ultrasonic Scattering in Biological Tissues. CRC; Boca Raton, FL: 1993. [Google Scholar]
- 20.Caselles V, Lisani JL, Morel JM, Sapiro G. Shape preserving local histogram modification. IEEE Trans Image Process. 1999;8:220–230. doi: 10.1109/83.743856. [DOI] [PubMed] [Google Scholar]
- 21.Pluim JPW, Maintz JBA, Viergever MA. Mutual-information-based registration of medical images: A survey. IEEE Trans Med Imaging. 2003;22:986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- 22.Kybic J, Unser M. Fast parametric elastic image registration. IEEE Trans Image Process. 2003;12:1427–1442. doi: 10.1109/TIP.2003.813139. [DOI] [PubMed] [Google Scholar]
- 23.Hajnal JV, Hill DLG, Hawkes DJ. Medical Image Registration. CRC; Boca Raton, FL: 2001. [Google Scholar]
- 24.Penney GP, Weese J, Little JA, Desmedt P, Hill DLG, Hawkes DJ. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Trans Med Imaging. 1998;17:586–595. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
- 25.Cole-Rhodes AA, Johnson KL, LeMoigne J, Zavorin I. Multi-resolution registration of remote sensing imagery by optimization of mutual information using a stochastic gradient. IEEE Trans Image Process. 2003;12:1495–1511. doi: 10.1109/TIP.2003.819237. [DOI] [PubMed] [Google Scholar]
- 26.Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recogn. 1999;32:71–86. [Google Scholar]
- 27.Zhu YM. Volume image registration by cross-entropy optimization. IEEE Trans Med Imaging. 2002;21:174–180. doi: 10.1109/42.993135. [DOI] [PubMed] [Google Scholar]
- 28.Bertsekas DP. Nonlinear Programming. Athena Scientific; Belmont, MA: 1999. [Google Scholar]
- 29.Maes F, Vandermeulen D, Suetens P. Comparative evaluation of multiresolution optimization strategies for multimodality image registration by maximization of mutual information. Med Image Anal. 1999;3:373–386. doi: 10.1016/s1361-8415(99)80030-9. [DOI] [PubMed] [Google Scholar]
- 30.Powell MJD. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput J. 1964;7:155–162. [Google Scholar]
- 31.Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16:187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- 32.Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–313. [Google Scholar]
- 33.Dodgson NA. Quadratic interpolation for image resampling. IEEE Trans Image Process. 1997;6:1322–1326. doi: 10.1109/83.623195. [DOI] [PubMed] [Google Scholar]
- 34.Mamou J. PhD Dissertation. University of Illinois; Urbana-Champaign: 2005. Ultrasonic characterization of three animal mammary tumors from three-dimensional acoustic tissue models. [Google Scholar]
- 35.Bigelow TA, Oelze ML, O’Brien WD., Jr Estimation of total attenuation and scatterer size from backscattered ultrasound waveforms. J Acoust Soc Am. 2005;117:1–10. doi: 10.1121/1.1858192. [DOI] [PubMed] [Google Scholar]
- 36.Oelze ML, Zachary JF. Examination of cancer in mouse models using quantitative ultrasound. Ultrasound Med Biol. 2006;32:1639–1648. doi: 10.1016/j.ultrasmedbio.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 37.Oelze ML, O’Brien WD, Jr, Zachary JF. Quantitative ultrasound assessment of breast cancer using a multiparameter approach. Proceedings of the 2007 IEEE Ultrasonics Symposium; New York City, NY. 2007. [Google Scholar]