Internal organization of large protein families: relationship between the sequence, structure and function based clustering

Abstract

The protein universe can be organized in families that group proteins sharing common ancestry. Such families display variable levels of structural and functional divergence, from homogenous families, where all members have the same function and very similar structure, to very divergent families, where large variations in function and structure are observed. For practical purposes of structure and function prediction, it would be beneficial to identify sub-groups of proteins with highly similar structures (iso-structural) and/or functions (iso-functional) within divergent protein families. We compared three algorithms in their ability to cluster large protein families and discuss whether any of these methods could reliably identify such iso-structural or iso-functional groups. We show that clustering using profile-sequence and profile-profile comparison methods closely reproduces clusters based on similarities between 3D structures or clusters of proteins with similar biological functions. In contrast, the still commonly used sequence-based methods with fixed thresholds result in vast overestimates of structural and functional diversity in protein families. As a result, these methods also overestimate the number of protein structures that have to be determined to fully characterize structural space of such families. The fact that one can build reliable models based on apparently distantly related templates is crucial for extracting maximal amount of information from new sequencing projects.

Introduction

The size of the known protein universe is expanding rapidly, driven by the ongoing technical advances in DNA sequencing. While this may suggest that whatever we know about proteins today may be dwarfed by upcoming discoveries, the consequences of this growth are partly mitigated by the fact that the majority of newly discovered proteins can be reliably classified into a hierarchical system of already known and characterized protein families. Because of the complex relations between protein amino-acid sequence, three-dimensional structure and function, typically three levels of family classification are used. The most intuitive concept – protein family, which groups proteins whose relation is manifested in strong sequence similarity, forms the core of this classification. Proteins in the same family are expected to have very similar (or identical) function and some level of divergence in their structures. The increased sensitivity of sequence comparison methods and the growing amount of structural information has allowed us to recognize distant evolutionary relations leading to the definition of a higher classification level, - superfamily grouping distantly related proteins with similar structures and detectable homology. Proteins whose structures share overall shape and connectivity of the secondary structures in the domain core ¹ form fold groups - the highest level of classification. At this level of structural hierarchy proteins may or may not be homologous.

Besides these three levels, for practical purposes, protein families are often split into smaller groups called modeling families (iso-structural groups), grouping together very closely related and structurally very similar proteins (that would add one more level below family level).

The difference between family and modeling family classification levels seems to be very superficial, but it is related to a very practical problem: if the structure of at least one protein from a modeling family has been solved experimentally, structures of others can be easily and accurately predicted using tools of comparative modeling. This leads to an important question: how can we define modeling families, or in other words, can we recognize groups of proteins with highly similar structures solely from sequence information? Historically, a threshold of 30% sequence identity was used for this purpose. This is a conservative choice minimizing the number of potentially wrong models. Unfortunately, at the same time it leads to a gross overestimate of structural diversity in protein families, suggesting that only a relatively small percentage of all known proteins can be accurately modeled^2,3 and leading to a picture of a universe of protein structures that expands almost linearly with the number of known proteins⁴. Both these statements are at least partially incorrect, as they ignore a significant number of strong structural similarities between distantly related proteins⁵ that could be recognized using more sophisticated strategies.

Any sequence based threshold or criteria of accurate structure prediction are based on a general observation that proteins with more similar sequences tend to fold into more similar structures. We have to underscore the fact that this is a statistical correlation and, no threshold of sequence similarity can give us absolute certainty that two structures reach certain level of similarity as both very similar ⁵ and very divergent ⁶ pairs of structures can be found at any sequence identity level. Because of that, in our analysis we present average accuracies, which can be compared between different clustering strategies. For instance, profile-profile alignments (and corresponding models) above the threshold of 20% sequence identity reach average accuracy comparable to those based on Blast alignments with sequence identity higher than 30%).

Sizes of protein families, superfamilies, and fold groups follow a power-law distribution⁷, with some being very large, containing thousands and, in some cases, hundreds of thousands proteins. The 2000 largest protein families account for 70% of non-singleton protein sequences⁸ and a similar distribution is observed in the genomes of even the most exotic species and in never before studied environments recently sampled by metagenomics. At the higher hierarchy levels a few hundred superfamilies or fold groups account for over 50% of proteins in fully sequenced genomes⁸. For such superfamilies or folds, estimates of their structural diversity based on simple sequence identity threshold suggest that they could contain hundreds and, in some cases, even tens of thousands of modeling families. Thus, to provide accurate models for all or even for a significant percentage of proteins in such groups, we would have to solve unrealistically large number of representatives. However, we suggest here that this picture is incorrect and that the real structural diversity in protein families is much smaller than suggested by estimates based on simple sequence identity similarity thresholds. In fact, at least for some proteins, high quality models can be built from very distant templates^5,9 (also see reviews of the field of remote homology detection by Dunbrack¹⁰ and Xu¹¹) and hundreds of examples of very strong structural similarity between apparently distant homologs can be found ⁵.

To address these issues, we tested three popular sequence comparison methods as distance measures for clustering five very large CATH protein topologies (fold groups). We start from this very high level of the hierarchy to make sure that the group being analyzed is very diverse and to avoid any a priori filtering of these proteins by sequence similarity that is used to define protein superfamilies and families. In each case, we used structure-based clustering as a “standard of truth” and asked to what extent clusters of structurally similar proteins can be reproduced by sequence-based clustering. Since sequence is usually the first, and often the only, information that we have about a protein, any improvement in using sequence-only information to recognize iso-structural groups could have a significant practical impact on classifying novel proteins. We also try to use a similar approach to identify iso-functional groups, a task that is somewhat more difficult because of lack of unique measure of functional similarity between proteins.

By using sequences from SCOP and CATH databases in all our benchmarks we were able to test clustering accuracy independently from the question of dividing proteins into domains. In reality the latter problem is often nontrivial for proteins without detectable similarity to known structures. However, since our study is focused on large protein families that include proteins with solved structures, boundaries of these domains can be identified in proteins based on the alignment with their structural templates. This allowed us to focus on the question of optimal clustering without tackling the problem of identifying and determining domains and their boundaries.

In all our tests we used three popular sequence alignment methods: Blast¹² (a standard sequence-sequence comparison algorithm), PSI Blast¹³ (profile-sequence comparison method) and FFAS¹⁴ (profile-profile method). It is well established that profile based methods perform better than sequence based methods in recognizing remote homologies and in alignment accuracy ^14-19. However, this does not imply how well these algorithms can be used to predict the level of structural divergence and therefore to reproduce internal structure of protein families and, if yes, what is the extent of that improvement. Answering these questions is the objective of our analysis.

Materials and Methods

Terminology

In our analyses, we used data from several public databases. Here we clarify how we used terminologies adopted from these databases:

• CATH²⁰: We most often referred to the two levels of CATH hierarchy:

  • superfamily – “groups together protein domains that are thought to share a common ancestor and can, therefore, be described as homologous”²¹. This level is similar to SCOP superfamily level.
  • topology (fold) – groups superfamilies that “share the same overall shape and connectivity of the secondary structure elements in the domain core”²¹. This level is similar to SCOP fold level.

• PFAM²²: we use PFAM families as a proxy for iso-functional groups of proteins (these families are initially created based on sequence similarity but then usually curated by experts).

• SCOP²³: this database was used only to prepare the general Benchmark of alignment accuracy (described in the next section). In order to avoid confusion with CATH hierarchy, we explicitly refer to SCOP domains, SCOP superfamilies, etc if different from CATH domains, CATH superfamilies etc.

We use the term ‘protein family’ to refer to a set of proteins identified by sequence-only based tools, which employ mostly HMMs, which implies common ancestry of all proteins in the family. We sometimes also use the term ‘protein group’ for the highest levels of protein classification (topology, fold), where homology between proteins is typically not established.

Benchmarks

In this manuscript, we compared different alignment and clustering methods using sets of proteins with known structures and functional assignments as benchmarks. Benchmarks make it possible to evaluate accuracy of alignments by calculating structural similarity of aligned regions or to evaluate different sequence clustering methods by comparing their results to structure-based clusters or to groups of proteins with the same function.

Benchmark of alignment accuracy

Sequences and structures of protein domains clustered at 40% identity sequence identity were downloaded from ASTRAL resource of SCOP database (ver. 1.73). (In this benchmark set we used 40% sequence identity threshold in order to include pairs with similarities below and above standard threshold of 30% sequence identity). Domains consisting of more than one chain fragment and domains with missing residues were removed. Since the purpose of this benchmark was to test alignment accuracy and not the detection of very weak homology, we also removed sequences of domains whose similarity could not be reliably detected using the most sensitive alignment program used here, the profile-profile algorithm FFAS¹⁴. The remaining pairs were further filtered by aligning them with FATCAT flexible structural alignment algorithm²⁴ and removing pairs with C_αRMSD higher than 3Å and pairs where structural alignment covered less than 75% of any of two structures (in order to eliminate cases where even structural alignment was not accurate or complete). Finally, to avoid bias toward the largest superfamilies in SCOP database, the number of pairs accepted from each SCOP superfamily was limited to 30. This procedure yielded 4561 protein pairs representing 607 SCOP superfamilies.

Clustering benchmark

We used five very large topologies selected from CATH database to test the agreement between sequence clusters, structural clusters and functional categories. (By using CATH topology level instead of CATH superfamily level, we avoided any a priori filtering of these sequences by sequence similarity since CATH topology level is based only on structural similarity. However, in order to reduce the calculation time, we downloaded sequences from CATH database that were already clustered at 60% sequence identity cutoff assuming that above that threshold significant structural differences between protein are very rare (numbers of structures given below refer to already clustered sequences).

The following five CATH topologies were included in the benchmark:

1. Topology 3.20.20, “TIM Barrel-like”, 27 superfamilies, 493 structures

2. Topology 2.60.40, “Immunoglobulin-like”, 83 superfamilies, 723 structures

3. Topology 3.40.50, “Rossmann fold”, 105 superfamilies, 1500 structures

4. Topology 3.30.70, “Alpha-Beta Plaits”, 77 superfamilies, 341 structures

5. Topology 3.10.450, “NTF2-like”, 13 superfamilies, 80 structures

Benchmarks of modeling coverage

We evaluated a practical impact of using profile based method by calculating modeling coverage of the following sets of proteins:

• the proteomes representing four different Kingdoms of life (A.fulgidus, E.coli, A.thaliana, and H.sapiens). Protein sequences from these organisms were downloaded from REFSEQ FTP site (ftp://ftp.ncbi.nih.gov/genomes/).

• selected superfamilies from CATH database. We used 56 CATH superfamilies that were systematically targeted by the Protein Structure Initiative (PSI) ²⁵ to test the practical impact of using optimized alignment methods on the modeling coverage of large families whose overall structure is known. Sequences of proteins from CATH superfamilies were downloaded and clustered at 30% sequence identity to reduce redundancy. Only superfamilies containing at least 10 non-redundant structures and more than 30% of those structures determined by the PSI were included in the benchmark. The resulting benchmark contains 56 CATH superfamilies with number of proteins ranging from 1,979 to 196,906 and the total number of protein sequences included in the benchmark is about 1.5 million. The number of proteins with known structures in these families ranges between 17 and 1331.

Sequence-based clustering

Blast, PSI-Blast and FFAS method were used to cluster sequences from each of the five very large protein topologies included in the Clustering benchmark. Sequences pre-clustered at 60% sequence identity level were aligned pair-wise (one-to-one) by each of the three alignment methods. Any pair of aligned sequences was put in the same cluster if the alignment covered at least 50% of the query sequence and the normalized sequence identity was above the cutoff value. In the case of Blast, we tested two methods of calculating sequence identity: the standard method provided by Blast and the sequence identity normalized by the length of the query sequence.

Structure-based clustering

A rigid option for FATCAT structure alignment algorithm²⁴ was used to perform pairwise comparison of all structural domains from five CATH topologies included in the Clustering benchmark. Any pair of structures was placed in the same cluster if the alignment covered at least 70% of residues of any of two compared domains and C_αRMSD of the alignment was below 2.5Å. C_αRMSD of 2.5Å is often used as the threshold of close structural similarity. For instance, it is usually possible to use molecular replacement method to solve structure using a model with that level of similarity to the target. We decided to use a relatively high alignment coverage requirement of 70% in order to eliminate additional complications related to partial structural similarities. We used higher threshold for structural alignments than for sequence alignments (where we used 50%) since structural alignments usually tend to be longer and are not limited to regions of high sequence conservation.

Identifying functional categories in large CATH topologies

Sequences of CATH domains were compared with the PFAM database version 23 using the HMMER program (ver. 2.3.2)²⁶. We used an e-value cutoff of 0.01 for HMMER hits. In cases where multiple hits were found, only the hit with the lowest e-value was accepted. In comparison with sequence clusters (generated by Blast, PSI-Blast, and FFAS), we only used proteins for which such PFAM hits were found. Proteins with Pfam hits to the same family were grouped in one functional group. Such functional groups were then compared with sequence-based clusters.

Comparison of sequence-based clusters, structure-based clusters, and functional categories for 5 large CATH topologies

Blast, PSI-Blast and FFAS were used to perform pair-wise alignments of all sequences and then clusters were calculated with single linkage algorithm using different sequence identity cutoffs. The resulting clusters were then compared with structure-based clusters calculated with FATCAT algorithm (as described above) and with functional categories based on Pfam.

The accuracy of predicting structural clusters from sequence clusters was evaluated by counting the number of cases when structural clusters contain proteins from two or more sequence clusters (“split” clusters) and the number of cases when proteins from two or more structural clusters belong to the same sequence cluster (“merged” clusters). In order to avoid arbitrarily selected clustering cutoffs, the analysis was performed for a wide range of sequence identity values. If the number of split and merged clusters is zero for a given sequence identity cutoff, then it indicates exact prediction of sequence clusters by structural clusters. This is usually not the case, but we assess the quality of prediction of structural clusters from sequence clusters by the number of split and merged structural clusters at the point where the graphs intersect (i.e., the point where number of merged clusters is equal the number of split clusters). This number can be used to compare the agreement between different clustering methods and structure-based clustering independently from the exact scoring schemes they use. One can also assume that X coordinate of this intersection point corresponds to an optimal sequence identity cutoff for clustering of a protein family.

An analogous method was used to evaluate the prediction of functional categories from sequence clusters when, instead of structural clusters, sequence clusters were compared with functional categories based on Pfam assignments.

Selection of sequence identity cutoff values for accurate comparative modeling with different methods

Widely used criteria of accurate comparative modeling are 30% sequence identity and 50% alignment coverage in Blast alignment algorithm. We have used Blast alignments fulfilling these criteria as a reference for other clustering methods and parameters.

We calculated the alignments of all sequence pairs from the benchmark described in the previous section using Blast, PSI-Blast, and FFAS methods and calculated C_αRMSD of these alignments. (C_αRMSD value of the alignment is known to be closely correlated with accuracy of the model that is built using this alignment).

We created a ‘reference set’ of accurate Blast alignments by selecting sequence pairs from the benchmark where at least 50% of the first sequence (a ‘query’) was aligned with the second sequence (a template) and sequence identity of the alignment exceeded 30%. The average C_αRMSD of these alignments was 2.6Å.

We then selected subsets of aligned pairs where at least 50% of the query sequence was aligned with the template, and further narrowed down these subsets by applying increasing sequence identity cutoffs and, for each of the resulting subsets calculated the average C_αRMSD of alignments remaining in the set. These steps were repeated separately for PSI-Blast and FFAS. The sequence identity cutoff that corresponded to average alignment C_αRMSD of 2.6Å, was 26% and 20% of normalized sequence identity for PSI-Blast and FFAS, respectively. These cutoff values were then used to calculate percentage of modeling coverage for in the Benchmark of modeling coverage consisting of large superfamilies from CATH database (see the next Section). Since the Benchmark of alignment accuracy consists of filtered protein pairs linked by high structural similarity, one can expect that the average model's accuracy might be lower for the alignment of more remotely related proteins. However, we assume here that the same average alignment accuracy of tested methods over the benchmark would translate into comparable (albeit, possibly lower) average alignment accuracy in more difficult modeling problems. It means that normalized sequence identity cutoffs of 26% and 20% for PSI-Blast and FFAS alignments, respectively, correspond to alignment accuracy achieved by Blast with 30% sequence identity threshold.

Testing the percentage of modeling coverage by different alignment methods

Sequences of proteins with and without structures were downloaded from Gene-3D²⁷ resource associated with CATH database for each of 56 protein superfamilies included in the Benchmark of modeling coverage. Proteins within each superfamily from this benchmark were clustered at 30% sequence identity using Blast implemented in PSI-CD-HIT script²⁸. For each superfamily, its internal clusters were divided into 2 groups: clusters without structural coverage, where none of the proteins had any experimentally determined structure and clusters with structural coverage, containing at least one such protein. This clustering corresponds to “standard” modeling coverage by Blast method with fixed thresholds of 30% sequence identity and 50% alignment completeness. Modeling coverage by PSI-Blast and FFAS was calculated by aligning proteins from clusters with no structural coverage (obtained in the previous step) to proteins with known structures from that superfamily. If more than 50% of residues from any protein could be aligned with a known structure and the percentage of identity was above a cutoff specific for this method, this protein was counted as having an accurate structural model (normalized sequence identity cutoffs used for PSI-Blast and FFAS equal 26% and 20%, respectively were calculated as described in one of the earlier sections).

Results and Discussion

Comparing sequence-based clusters with structure-based clusters

To address the question of predicting clusters of structurally similar proteins by using sequence only information, we assessed the agreement between protein clusters identified with the structure comparison FATCAT algorithm^24,29 with a set of sequence-based clusters generated with different sequence comparison methods. Such agreement can be assessed by calculating the “confusion” index; namely, counting the number of false negatives, i.e. structural clusters “split” between different sequence clusters where sequence-based clustering falsely predicted structural divergence, and the number of false positives, i.e. structural clusters “merged” in one sequence cluster where sequence-based clustering falsely predicted structural similarity. These two numbers were plotted as a function of the sequence identity cutoffs used in sequence-based clustering. If both numbers reach zero for a certain sequence identity threshold, sequence-based clustering would exactly reproduce the structure clusters. But even if this does not happen, the height (Y-coordinate) of the point where the false positive and false negative plots intersect can be used to compare the accuracy of different clustering procedures. Also, the X-coordinate at the intersection is a good estimate of the optimal threshold for a specific sequence-based clustering approach.

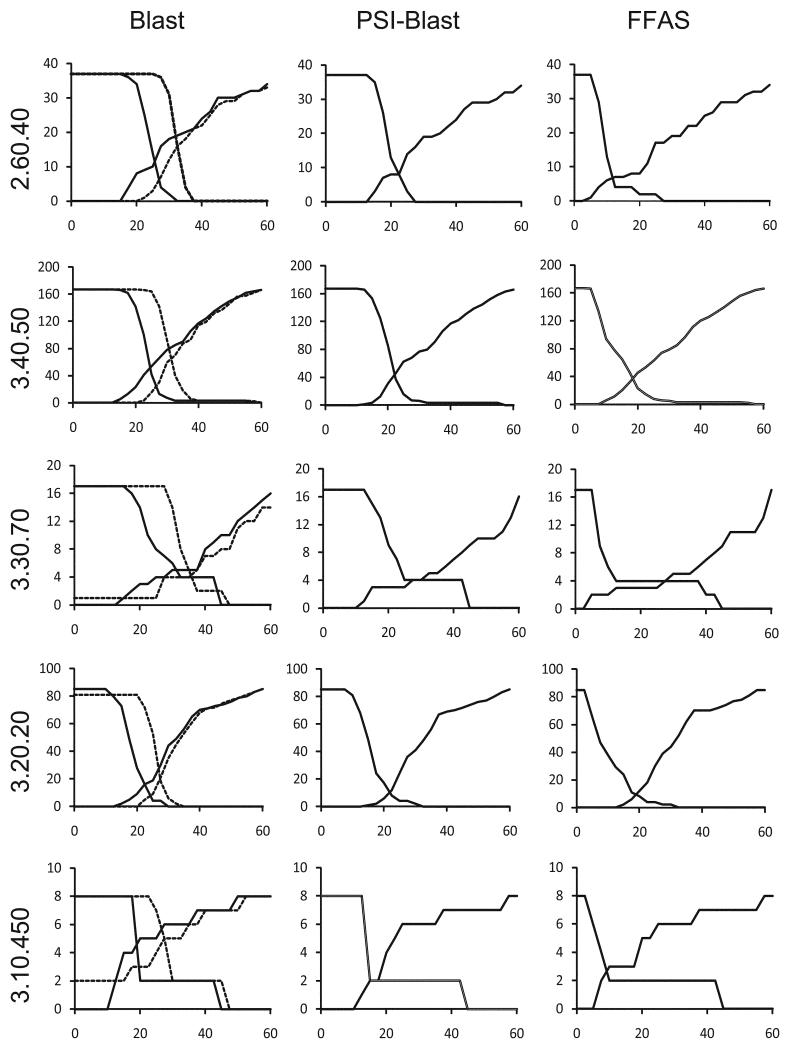
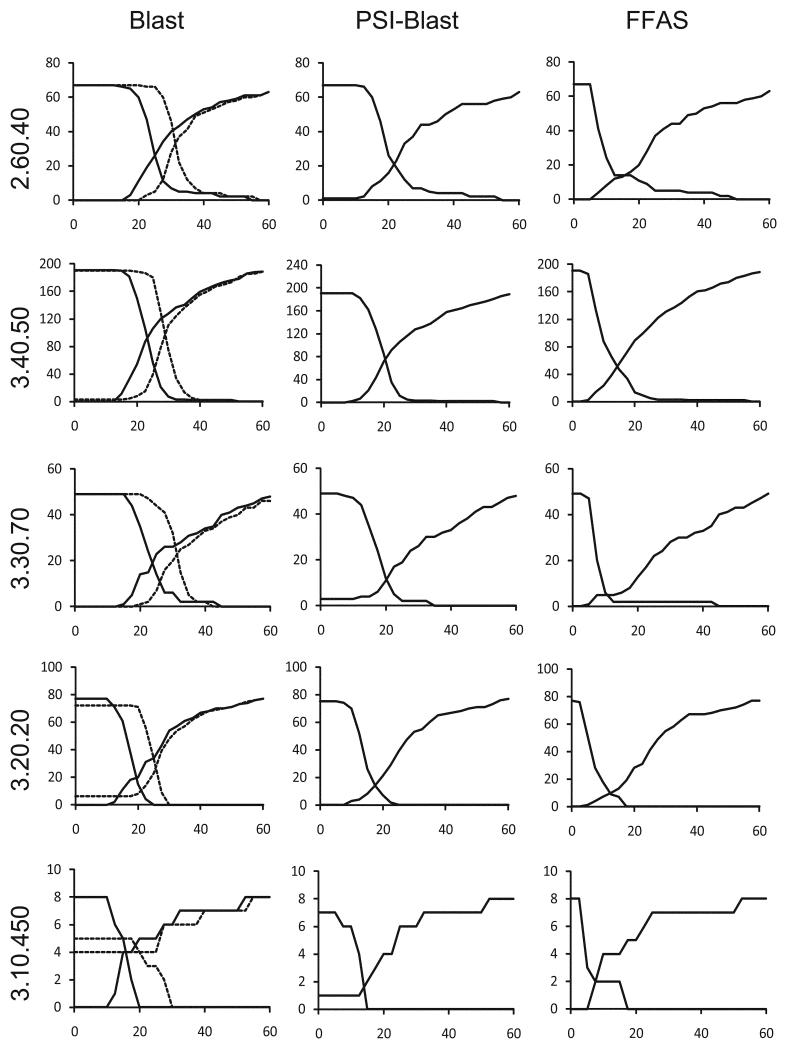
First, we used the criteria described above to assess the agreement between structure and sequence-based clusters calculated using two different methods of normalizing sequence identity values. Then, we compared clustering performed with three sequence alignment methods: Blast¹², PSI-Blast¹³, and FFAS¹⁴. These programs use sequence-sequence, profile-sequence and profile-profile alignment algorithms, respectively. The results of these comparisons performed for five CATH topologies included in Clustering benchmark described in the Methods section are shown in Figure 1 and discussed in detail in the next two sections.

Figure 1.

Predicting structure-based clusters from sequence-based clustering in five large topologies defined in the CATH database. The number of structure-based clusters ‘split’ between different sequence-based clusters and the number of structure-based clusters ‘merged’ into the same sequence-based clusters (Y-axes) are shown as function of sequence identity cutoff used in sequence clustering (X-axes). The number of ‘merged’ structure-based clusters is decreasing with increasing sequence identity cutoff and the number of ‘split’ structure-based clusters is increasing. The intersection of these two curves corresponds to the most accurate prediction of structure-based clusters by sequence-based clusters. Y coordinate of this point provides an assessment of the agreement between sequence-based clusters and structure-based clusters and allows comparison of the accuracy of different sequence clustering algorithms. The corresponding X coordinate gives an optimal sequence identity cutoff for this protein topology (see Methods section for more details). The analysis was performed for Blast, PSI-Blast and FFAS methods. In case of Blast method we tested two ways of normalizing sequence identity. Results obtained with sequence identity normalized by query sequence length (globally normalized sequence identity) and by alignment length (standard sequence identity) are shown as continuous and dashed curves, respectively. The name of CATH topology used in calculations is shown on the left side for each set of graphs.

Normalizing sequence identity

The standard Blast algorithm calculates sequence identity as the number of identical residues pairs divided by the length of the alignment. In this method, very short alignments with only a few identical residues may have very high values of sequence identity. These values may indicate short and accurate alignments, but not necessarily global similarity. Thus, alignment completeness requirement is usually added to the sequence identity cutoff. For instance, an often-used threshold for accurate homology model requires the Blast alignment to have sequence identity higher than 30% and to cover more than 50% of the sequence. However, for predicting structural clusters, it may be better to use a clustering procedure based on a single similarity measure that can be tested for several cutoff values. We have used a simple method of normalizing sequence identity by the length of the query sequence (which we term ‘globally normalized’ or ‘normalized’ sequence identity). Short alignments with only a few identical residues are scored very low when using such normalization. As illustrated by graphs shown in the ‘Blast’ column of Figure 1, sequence clustering with normalized sequence identity (without any additional criterion related to alignment completeness) led to better agreement with structure-based clusters than clustering by standard sequence identity. In four out of five CATH topology groups used in our tests, the number of ‘split’ and ‘merged’ clusters based on normalized sequence identity was lower at the intersection than the analogous number for clusters obtained with the standard sequence identity provided by Blast. The numbers were comparable in Alpha-Beta Pleat CATH topology (3.30.70). Therefore, we decided to use normalized sequence identity for clustering by Blast, PSI-Blast, and FFAS.

Profile-based alignment methods allow more accurate prediction of structure-based clusters

It has been shown that profile-based algorithms surpass sequence-based methods in predicting remote similarities and in the accuracy of the alignment^14,30. However, this does not automatically mean that these algorithms would allow more accurate prediction of the closest structural similarities (i.e., clusters of similar structures) between proteins from the same family, superfamily, or topology (fold)).

A comparison of three sequence alignment methods (Figure 1) clearly shows that sequence clusters calculated with PSI-Blast and FFAS more accurately reproduce structural clusters than clusters based on Blast sequence alignments, and that clustering based on profile-profile FFAS performs better than clustering based on PSI-Blast. In addition, the identity values corresponding to the intersection of FFAS ‘split’ and ‘merged’ graphs are lower than analogous values for PSI-Blast and Blast, suggesting that the traditional and widely used 25%-30% limit of ‘twilight zone’ similarity for sequence-sequence alignments may be lowered for profile-sequence or profile-profile alignments. This result opens the possibility of improving modeling coverage of the proteins in the ‘twilight zone’ of sequence similarities.

Improving modeling coverage in twilight zone

One can expect that more sensitive and accurate alignment methods can extend the limits of accurate comparative modeling beyond the “traditional” threshold of 25%-30% sequence identity. To test this notion, we used the Benchmark of alignment accuracy described in the Methods section to find sequence identity cutoffs for PSI-Blast and FFAS such that the alignments (and the corresponding models) with sequence identities above these cutoffs would be as accurate as the alignments (and the models) calculated by Blast and fulfilling standard criteria (normalized sequence identity higher than 30% and more than 50% of residues covered by the alignment - see Methods section for details). This procedure yielded cutoffs of 26% and 20% for normalized sequence identity for PSI-Blast and FFAS, respectively (for all three methods, only alignments with completeness higher than 50% were taken into account). The suggestion that sequence identity threshold defining strong structural similarity may be lower than 25%-30% has been made earlier³¹. Interestingly, the author also concluded that “no sound structure similarity is statistically expected below 20% identity”, which is close to the threshold estimated for FFAS in this study.

We assessed differences in the percentage of proteins that can be accurately modeled with different methods using two benchmarks of modeling coverage (see Methods section) which included: proteomes representing four different Kingdoms of life and selected superfamilies from CATH database.

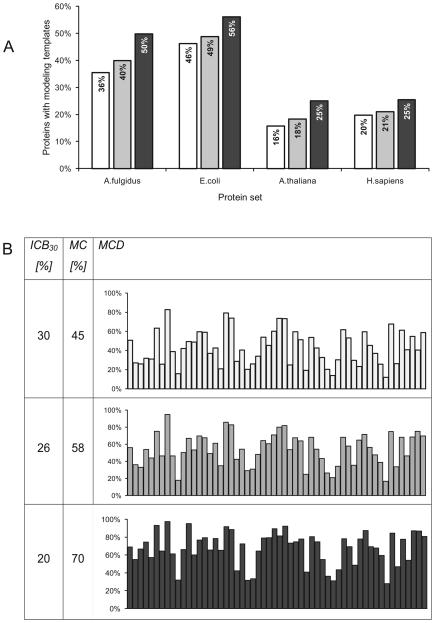
As expected, profile based methods provide higher modeling coverage than sequence based methods but there are significant differences between different sets of proteins (see Figure 2). Modeling coverage of eukaryotic proteomes with accurate models is about two times lower than prokaryotic proteomes (25% versus 50%). This big difference is partly an effect of higher percentage of structural disorder in eukaryotic proteins. For instance, “long (>30 residue) disordered segments are found to occur in 2.0% of archaean, 4.2% of eubacterial and 33.0% of eukaryotic proteins” ³². The differences in modeling coverage of representative proteomes provided by three methods were quite large with FFAS enabling modeling of 20% to 50% more proteins as compared to Blast (see Figure 2A).

Figure 2.

Modeling coverage of representative sets of proteins calculated with three methods: Blast (white), PSI-Blast (grey), and FFAS (black). Sequence identity cutoffs used to determine the percent of accurately modeled proteins or protein domains were selected to provide the same average model accuracy of 2.6Å (these thresholds are 30%, 26% and 20% for Blast, PSI-Blast and FFAS, respectively; see Methods section).

A) Modeling coverage of proteomes representing Archaea, Bacteria, Plants, and Animals.

B) Modeling coverage of 56 protein superfamilies targeted by the PSI. Horizontal axis on each chart corresponds to 56 protein superfamilies sorted by size.

Columns:

ICB30: globally normalized sequence identity cutoff for each method giving average CαRMSD of 2.6Å in alignments covering at least 50% residues in the Benchmark of alignment accuracy (see Methods section for benchmark description). MC: percent of proteins from superfamilies targeted by the PSI where more than 50% residues are included in the alignment and sequence identity is above the ICB30 cutoff. MCD: distribution of modeling coverage in large protein superfamilies targeted by the PSI.

Differences in modeling coverage of very large protein families which contain several known structures were evaluated on 56 CATH superfamilies targeted by PSI (see Benchmark of modeling coverage in the Methods section). Overall, 45% proteins from these 56 CATH superfamilies were covered by accurate BLAST alignments and models as measured by the standard criteria of 30% sequence identity and 50% completeness of alignment. Using PSI-Blast resulted in the coverage of 58% of proteins, whereas FFAS allowed modeling coverage of 70% of proteins from these superfamilies (Figure 2B).

In summary, the largest improvement of modeling coverage resulting from using profile based methods is observed for large protein families. It translates into relatively large differences observed for full proteomes which usually contain several representatives of large protein superfamilies.

The significant improvement in accurate modeling coverage described above could be anticipated, since both a higher accuracy of the alignments and a better selection of structural template contribute to lower sequence identity cutoffs in profile-based methods and, thus, enable significantly higher modeling coverage.

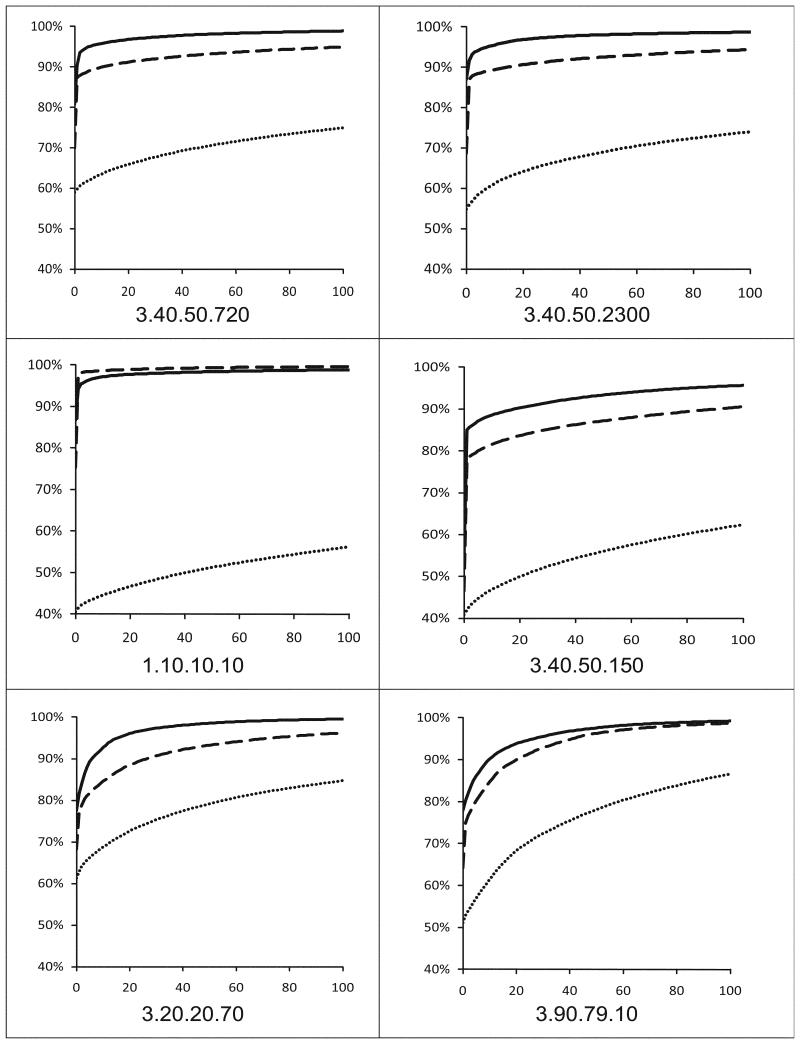
Besides calculating current modeling coverage of protein families, it is also possible to estimate how many structures still need to be solved to reach certain percent of modeling coverage. We calculated such projections of modeling leverage for the six largest families from our set of 56 assuming an optimal scenario where the structure providing most coverage is solved first. As it can be expected, modeling coverage increases faster with each solved structure if one uses FFAS or PSI-Blast alignments as a base for modeling, instead of Blast (Figure 3).

Figure 3.

The “modeling coverage graphs” calculated for the six largest protein superfamilies systematically targeted by the PSI. Each curve shows the percentage of sequences from a superfamily with available models (Y-axis) as a function of the number of proteins whose structures would have to be determined experimentally (X-axis). The graphs were extended only to 100 potential targets for structure determination. Dotted curves represent modeling coverage based on Blast results with 30% sequence identity cutoff, dashed curves represent modeling coverage with PSI-Blast with 26% normalized identity cutoff, and solid curves represent modeling coverage based on FFAS results with 20% normalized identity cutoff (all three thresholds correspond to average models’ accuracy of 2.6Å as calculated using the Benchmark of modeling accuracy).

It is important to note that, while profile methods are now already widely used in comparative modeling, estimates of modeling coverage of protein families in literature ^33,34 typically still rely on simple sequence-sequence and, sometimes, profile-sequence alignment methods. This is easily understood because of the higher computational cost, time and effort involved in applications of profile-based methods but, nevertheless, it leads to large overestimates of the number of structures that still need to be solved to provide accurate homology models for many protein families.

Limits of accurate comparative modeling depend on the models' completeness and accuracy that can be adjusted by algorithm parameters

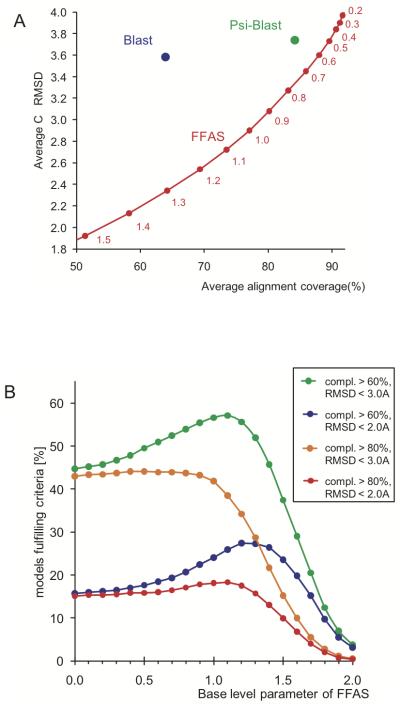
In the previous sections, we discussed the problem of the accuracy of predicting structural clusters from sequence clusters where sequence clusters were defined by an identity cutoff. The problem of predicting structural similarity from sequence similarity is related (albeit, not equivalent) to the problem of the accuracy of comparative modeling. However, the question of the accuracy of models is not one-dimensional, despite the fact that it is often addressed by a single sequence identity cutoff. In fact, in most cases, even for the same query-template pair, one can choose between greater coverage, but less accurate alignment (and the resulting model), or shorter coverage, but more accurate alignment. Such shorter alignment (and corresponding model) would cover only the most conserved structural core of a family, and would have lower errors as measured by C_αRMSD and higher sequence identity. We show that the balance between a model's completeness and its accuracy can be adjusted by changing the ‘base level’ (or average value) of the matrix used to calculate the alignment with dynamic programming. This method has been used previously to adjust average length of FFAS profile-profile alignments to enable direct comparison with PSI-Blast alignments³⁰. The Benchmark of alignment accuracy described in the Methods section makes it possible to calculate average coverage and C_αRMSD for any alignment method or set of parameters. For instance, Figure 4A illustrates the balance between model completeness and accuracy for two popular alignment methods, Blast and PSI-Blast, and for the FFAS algorithm with a wide range of values of the base level parameter. The figure shows the average values of model completeness and C_αRMSD calculated over all pairs of proteins from the Benchmark of alignment accuracy. The figure clearly indicates that one can improve model completeness at the cost of lowering accuracy by using lower values of the base level or one can increase modeling accuracy at the cost of completeness by increasing the base level. It also confirms that, at the same modeling coverage as Blast or PSI-Blast, FFAS alignments reach higher accuracy and, at the same average modeling accuracy as Blast or PSI-Blast, FFAS would produce more complete models.

Figure 4.

A) Balance between model completeness and accuracy for different alignment methods. Average completeness and accuracy of Blast and PSI-Blast algorithms with standard parameters are represented as blue and green circles, respectively, while FFAS results are shown as a curve representing a wide range of ‘base level’ values used in the dynamic programming algorithm (‘base level’ values are shown as labels below the curve describing FFAS results). The results were obtained using a comprehensive Benchmark for alignment accuracy (see Methods section for more details). B) The percentage of models from the alignment accuracy benchmark fulfilling different criteria of completeness and accuracy depending as a function of the ‘base level’ parameter of FFAS (see Methods). Green curve shows the percentage of models with completeness higher than 60% and C_αRMSD to the real structure below 3.0Å, blue - models with completeness > 60% and C_αRMSD < 2.0Å, orange - models with completeness > 80% and C_αRMSD < 3.0Å, and red - models with completeness > 80% and C_αRMSD < 2.0Å.

In Figure 4B, the percentages of alignments (and corresponding models) from the alignment accuracy benchmark fulfilling different completeness and accuracy criteria are shown as function of the ‘base level’ parameter of FFAS. The fact that percentages of models fulfilling specific completeness and accuracy criteria reach maxima for different base level values indicates that there is no single ‘optimal set’ of parameters for FFAS alignments. As expected, the percentage of highly accurate, but shorter alignments can be improved by using higher base level values and the percentage of less accurate, but longer alignments is maximized by using lower base level values. We expect that similar ‘calibration’ can be done for other alignment algorithms.

Profile-based alignment methods allow more accurate prediction of functional categories

The problem of the agreement between function and sequence-based clustering of large protein families can be addressed in a similar way as the question about predicting structural clusters from sequence-based clusters. However this issue is complicated by the fact that there are no universally accepted measures of function similarity between proteins. Therefore here we use a specific, curated set of protein families as a proxy for functional clustering of proteins. The Pfam database²² is the oldest and most used collection of annotated protein families. We used the Pfam database to assign functional categories to sequences from five large CATH topology groups and then compared these functional groupings with sequence clusters calculated as described in the previous section.

We observed a tendency similar to one observed for structural clustering - the accuracy of predicting functional categories from sequence clusters was also improved when we moved from sequence-based to profile-based alignment methods. At the intersection of these two graphs, i.e. the number of ‘split’ and ‘merged’ functional categories in PSI-Blast and FFAS clusters, is lower than the corresponding number from Blast clustering; the corresponding number for FFAS is also slightly lower than for PSI-Blast. The sequence identity value corresponding to the intersection of the two graphs is also lower for FFAS compared to PSI-Blast or Blast (see Figure 5).

Figure 5.

Predicting functional categories (based on Pfam database) by sequence-based clustering in five large topologies defined by CATH database. Blast, PSI-Blast and FFAS were used to perform all-to-all alignment of sequences and then clusters were calculated with single linkage algorithm using different sequence identity cutoffs. The resulting clusters were compared with Pfam families. The number of Pfam families ‘split’ between different sequence-based clusters and the number of Pfam families clusters ‘merged’ into the same sequence-based clusters (Y-axes) are shown as function of sequence identity cutoff used in calculations (X-axes). The number of ‘merged’ Pfam families is decreasing with increasing sequence identity cutoff and the number of ‘split’ Pfam families is increasing. The intersection of these two curves corresponds to the most accurate prediction of Pfam families by sequence-based clusters. Y coordinate of this point provides an assessment of the agreement between sequence-based clusters and Pfam families and allows comparison of the accuracy of different sequence clustering algorithms (see Methods section for more details). Results obtained with sequence identity normalized by query sequence length (globally normalized sequence identity) and by alignment length (standard sequence identity) were shown as continuous and dashed curves, respectively.

Conclusions

The general problem of understanding the evolution of proteins and, specifically, the issue of structural and functional similarity of homologous proteins, is very important for interpreting massive amounts of data from sequencing projects. We can often classify a new protein into an already known protein family, but we cannot reliably predict how its structure and function would differ from that of the already characterized members of this family. Here we address this question by looking at the internal structure of very large protein families and, in particular, we asked to what extent can sequence only information be used to predict clusters based on similarity of experimentally determined three-dimensional structures. This question also translates into the practical problems of estimating the quality of protein models and predicting protein function. We show that profile-based alignment methods are not only more sensitive and produce more accurate alignments, but also allow more accurate prediction of structural and functional sub-groups in large protein families. Moreover, a higher accuracy of alignments produced by these methods makes it possible to lower the sequence identity threshold for accurate comparative modeling while maintaining the same average accuracy of models as those based on ‘traditional’ criteria of 30% sequence identity and 50% completeness. Higher alignment accuracy and better prediction of structural clusters increases the accuracy of the resulting models and the application of comparative modeling. In other words, a researcher who in the past may have been discouraged from using comparative modeling to seek structural insights for specific question because of low sequence identity to a potential modeling template, may now reconsider doing so. A big impact of profile based methods on modeling coverage of very large protein families translates into significant improvement of modeling coverage of proteomes from different Kingdoms of life which contain large number of representatives of such families.

Our analysis showed that approximate threshold of accurate modeling (30% seq id) can be lowered if one uses profile based alignment methods instead of direct sequence similarity based ones. At the same time, it also confirms that the relationship between protein sequences and protein structures is not uniform and, thus, the approximation of using a single criterion of accurate modeling for all protein families can be improved. The solution to that problem is suggested by analyses illustrated by Figures 1 and 5. The intersection points in graphs shown in these figures for different CATH topologies correspond to ‘balanced’ clustering level where the number of structural (or functional) clusters unnecessarily ‘split’ between two sequence clusters and the number of distinct structural (or functional) clusters ‘merged’ into the same sequence clusters are comparable. These thresholds vary substantially between different topologies ranging approximately from sequence identity of 10% to sequence identity of 30%. For most protein superfamilies and topologies we still don't have enough structural data to propose statistically valid ‘customized’ thresholds of accurate homology modeling but we are planning to explore this direction in the future.

Additional analysis suggests that the problem of accuracy of comparative modeling is better described as a balance between expected model's completeness and its accuracy. This balance varies among popular alignment methods and can be controlled by changing parameters of alignment algorithms to obtain less accurate, but more complete models, or vice versa.

In summary, significant progress in homology detection and alignment methods makes it possible to assess the internal structure of protein families from sequence data and could lead to significant changes in the strategy of applying comparative modeling to answer specific questions about proteins from a given family. It is important to stress that the results presented here do not focus on improving modeling or function predictions methods, but rather, on the estimates of what level of accuracy can be expected using standard and other available methods. Further improvements could come from improving the modeling methods, a field that is undergoing continuous development^35-37.