Approaching the molecular origins of collective dynamics in oscillating cell populations

Abstract

From flocking birds, to organ generation, to swarming bacterial colonies, biological systems often exhibit collective behaviors. Here, we review recent advances in our understanding of collective dynamics in cell populations. We argue that understanding population-level oscillations requires examining the system under consideration at three different levels of complexity: at the level of isolated cells, homogenous populations, and spatially structured populations. We discuss the experimental and theoretical challenges this poses and highlight how new experimental techniques, when combined with conceptual tools adapted from physics, may help us overcome these challenges.

Introduction

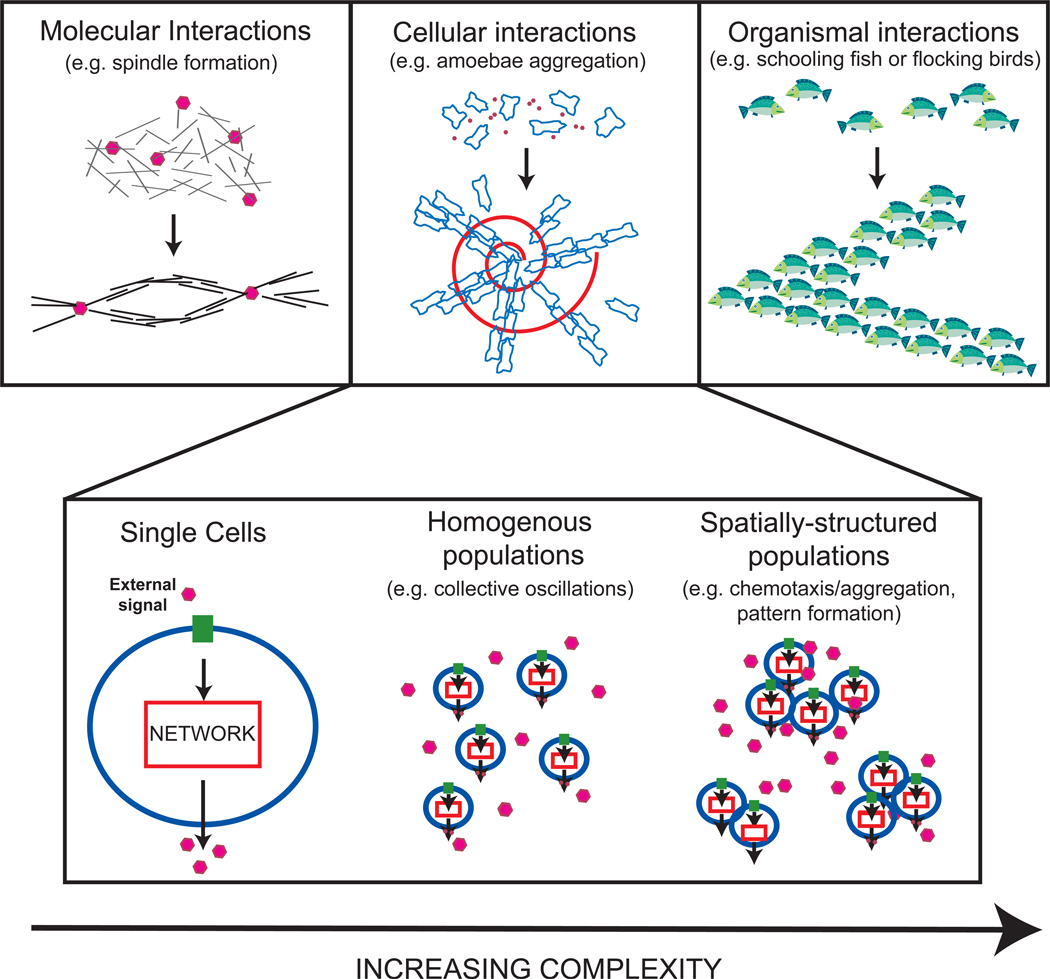
Collective behaviors are ubiquitous in biological systems. At the molecular level, proteins often aggregate into self-organized structures such as spindles [1]. At the cellular level, unicellular organisms often form structured communities composed of many individuals [2–4]. At the level of organisms, birds and fish colonies exhibit dramatic emergent behaviors such as flocking [5–7] and schooling [8–10] (see Figure). Our understanding of collective behaviors in biological systems, however, is still in its infancy, highlighting the crucial need to study systems where the link between macroscopic behavior and the microscopic components that make up the system can be probed directly through experiments. This review focuses on one class of systems where such an approach is possible: the collective dynamics in cellular populations.

Figure 1. Collective behaviors in biology at different levels of complexity.

Top: Collective behaviors in biology exist at the molecular (mitotic spindle formation [1]), the cellular (social amoebae aggregation [4]) and the organismal (schooling fish [8]) levels. This review focuses on systems at the cellular level. Cellular organism retain many of the interesting phenomena found in higher-order organisms such as information processing and collective decision making, with the added advantage that behavior can be directly linked to processes at the molecular level.

Bottom: Cellular systems can be analyzed at three different levels of complexity, at the level of isolated cells, homogenous cell populations, and spatially-structured populations [77]. Understanding behavior requires systematic examination of these systems at all three levels of complexity. The main challenge faced when examining these systems is to link behavior at the single cell level to that of populations and vice versa.

In their natural environments, cells often undertake complex collective behaviors in response to environmental and population cues [11,12]. Thus, understanding how cells behave in the wild requires characterizing not only the behavior of isolated cells but also how environmental signals combine with cell-to-cell communication (such as quorum sensing [13] and autocrine signaling [14]) to give rise to observed behaviors at the population level. Doing so requires us to examine how the cooperative behaviors of cell colonies differ from those of isolated cells and conversely, how the properties of single cells generate and explain the observed communal behavior.

The challenges inherent in this research program are summarized by Phil Anderson’s famous declaration “More is Different” [15] - namely, systems composed of many interacting components will exhibit new emergent behaviors that cannot be understood simply by looking at the behavior of the individual components that make up the system. Whereas Anderson largely had in mind physical systems, biological systems pose additional challenges not encountered in physics. The collective behavior of cellular populations often require cells to integrate information from a wide variety of sources in order to perform a desired task such as cellular aggregation or cellular differentiation [16,17]. These challenges highlight the critical need to simultaneously observe the behavior of individual cells within a population, the behavior of the population as a whole, and to measure the relevant signaling and environment induced interactions between cells.

Oscillations in communicating cell populations

A particularly attractive system to study collective behaviors is provided by communicating cell populations that display rhythmic activities in the form of intracellular oscillations of signaling molecules or gene expression. Collective cellular oscillations play an important role in a wide variety of biological systems [18], ranging from neural systems [19] to the social amoebae Dictyostelium discoideum, where synchronized oscillations lead starved cells to aggregate [20–25], to glycolytic and non-glycolytic oscillations in yeast populations [26–32], to oscillations in the pancreatic islets which control insulin secretion [33,34]. Recently, even bacteria have been synthetically engineered to exhibit collective oscillations [35]. Oscillations represent an especially tractable example of collective behavior because the link between macroscopic behavior and molecular interactions can be readily experimentally tested. Oscillations are easy to observe experimentally, can be unmasked even in noisy data using analytical tools such as Fourier transforms, and there exist a large body of theoretical work to help interpret existing and guide new experiments. In addition, such systems are amenable to theoretical analysis using ideas from theory of dynamical systems [36–38].

Understanding collective oscillations requires disentangling behaviors at three different levels of complexity (see Figure). At the cellular level, it is necessary to characterize how cellular networks of genes and proteins allow single cells to respond to external signals (such as environmental cues and signaling molecules) as well as how these signals control the production of secreted molecules that are involved in cell-to-cell communication. The behavior of single cells must then be related to the behavior of cellular populations by exploring how system parameters, such as cell-density, change the collective dynamics. Finally, one must understand the spatial dynamics of these cellular oscillation processes. The main challenge faced when studying such systems is to understand how behaviors at lower levels of complexity shape and give rise to the behaviors seen at higher levels of complexity [15].

Recently, this program has been carried out with some success in two systems, one natural and the other synthetic. Gregor et al. [25] used a FRET-sensor to measure internal levels of the signaling molecule cAMP [39,40]. They showed that isolated Dictoystelium amoeba behave like an excitable system, with individual cells capable of generating sustained oscillations in response to elevated levels of external cAMP. They then related these single-cell oscillations to the synchronized, cell-density-dependent oscillations exhibited by homogeneous cell populations and mapped out a phase diagram indicating under what conditions collective oscillations occur. The external cAMP level was identified as the control parameter that determines the oscillatory state of the system. Finally, they observed small populations of Dictoystelium cells on agar where they showed that the first cell that randomly pulses entrains the rest of the population in rhythmic activity. The ensuing synchronized oscillations gave rise to spatial, concentric waves, with cells eventually aggregating at the wave origin, the spatial center from which the first oscillation pulse was emitted. What was notable about these series of experiments was that Gregor et al. were able to show that the system undergoes a collective transition from a non-oscillatory state where all cells are quiescent to a state where all cells oscillate synchronously. Furthermore, they showed that the transition does not result from specialized pacemaker cells, but is a direct consequence of the excitable nature of individual cells.

Using tools from synthetic biology, Danino et al. [35] engineered a genetic circuit in E. coli capable of generating synchronized oscillations in growing populations. One of the unique features of the system is that a population of cells, that in isolation is incapable of oscillating, exhibits collective oscillations when coupled using a quorum-sensing molecule. The genetic circuits utilized components of the naturally occurring quorum-sensing machinery in other bacterial species to induce a global coupling between cells [41,42]. Using cleverly designed microfluidic chambers (networks of micro-channels that house cells in fluid flow) that allow bacteria to grow naturally while simultaneously holding the cell density fixed, Danino et al were able to control the density of cells, and consequently the external concentration of signaling molecules, to induce synchronized oscillations in cell colonies. The experiments were then repeated in larger microfluidic chambers where spatial inhomogeneities resulted in a multitude of fascinating phenomena such as traveling waves and front propagation. What is groundbreaking about this work is that it provides proof of principle that one can engineer the properties of a system at the level of a single cell to control behavior at the level of cellular populations.

Both systems discussed above exhibit a cell-density dependent transition to collective oscillations that has been termed “dynamical quorum sensing” [43,44]. This phenomenon was first explicated in the context of glycolytic oscillations in yeast through a successful combination of theory and experiment [43]. Dynamical quorum sensing relies on the mutual synchronization of cells through the exchange of chemicals (metabolites in yeast, cAMP in Dictyostelium, quorum sensing molecules for the engineered circuits discussed above). Since the cells themselves produce the chemicals, the external concentration of the chemicals reflects the local cell-density of the population. Collective oscillations emerge when the external concentration, or equivalently cell-density, exceeds some critical threshold. Thus, in dynamical quorum sensing, cell density information is encoded in the collective intracellular dynamical state of the entire population. Finally, it is worth noting that the term “dynamical quorum sensing” is used by various authors to refer to qualitatively different types of density-dependent transitions. This highlights the need for a better theoretical understanding of the qualitatively different ways that density-dependent transitions to synchronized oscillations can occur.

Challenges in understanding collective behaviors

Understanding and manipulating collective behaviors in cellular systems poses a number of new experimental and theoretical challenges. On the experimental side, the advent of fluorescent markers has resulted in tremendous progress [45–47]. These markers include derivatives of various fluorescent proteins that can be genetically encoded and directly tag signaling proteins [48–53], as well as reporter constructs for smaller signaling molecules such as ions (Ca2+) [54,55] and nucleotides (ATP, cAMP, cGMP) [56,57]. These markers and sensors work very well inside cells where they are synthesized. However, understanding the signaling that underlies collective behavior also requires measuring signaling molecule concentrations in the extracellular space. This is particularly challenging when the individual cells are not packed together but free floating in solution. Possible techniques that may allow for the measurement of the extracellular, spatio-temporal dynamics of signaling molecules include engineering cells to artificially release sensors into the environment, as well as tagging the outside of the cell membranes with sensor molecules. For example in cortical astrocytes extracellular ATP release has been reported by both real-time imaging using bioluminescence [58] as well as using chemiluminescence with cell surface-tagged beads [59]. Extreme care has to be taken with these methods because genetically altering cells, generally, can simply give rise to collective behaviors that differ from those exhibited by wild-type cells. Alternatively, the experimenter could supply sensors externally by coating the walls of the experimental setup or by continuous flow in solution. Both require the highly controllable environments of miniature size provided by microfluidics [60–63]. Microfluidics refers to fluid flow in a network of micro-channels that houses cells and can be integrated on disposable, low-cost Lab-on-a-Chip cartridges [64,65]. Cells can survive in these environments, be easily tracked and still retain most of the natural characteristics necessary to probe collective behaviors. The ability to perform live-cell imaging while simultaneously measuring the spatio-temporal dynamics of both intra- and extra-cellular signaling molecules is likely to greatly expand our understanding of collective behaviors in cellular colonies over the next decade.

Mathematical and computational modeling will also likely play an important role in expanding our understanding of cellular oscillations. Mathematical models have helped shape our current understanding of Dictyostelium by pointing out important connections with the theory of excitable systems – systems like neurons where a small change in inputs/parameters can elicit large responses such as a spike [66,67] or the stochastic release of the second messenger molecule Calcium which can give rise to sustained oscillations [68,69]. Mathematical models have also highlighted the importance of feedback loops and balancing time scales for oscillations [70] as well as aiding the design of genetic circuits capable of oscillations [35,71,72].

Despite these considerable achievements, theory has not kept pace with the rapid experimental advances of the last decade. The need for new conceptual and theoretical approaches to collective behavior in biological systems becomes even more clear when we contrast our current level of understanding of biological systems to their physics counterparts [15,73]. The major theoretical challenge is to understand how the microscopic details of a system shape collective behaviors at larger scales. Though this theoretical program seems daunting, we can draw on inspiration from the study of collective behavior in physics. A unifying theme in the study of collective phenomenon in physics is the idea of “universality” – the idea that many collective properties depend only on a few “relevant” microscopic details of the system under consideration [74]. The role of theory is to identify these relevant details and understand how they give rise to the observed behaviors at macroscopic scales. Recent work suggests that universality is also likely to be relevant to biological systems. For example, recent experiments demonstrate that despite its vast complexity, the yeast cell-cycle network exhibits phase locking in response to a periodic driving force, much like an idealized oscillator [75].

Another important implication of universality is that, often, there are only a few qualitatively different collective behaviors a system can exhibit. For example, tools from dynamical systems such as bifurcation theory allow for a classification of the qualitatively different behaviors that can be exhibited by a neuron. Theoretical considerations also suggest that there are likely only a few different ways that cells can undergo a density-dependent, dynamical quorum sensing transition to synchronized collective oscillations [36,38]. The accompanying table summarizes four common routes to synchronized oscillations seen in nature. A key challenge facing researchers studying cellular rhythms is to relate the type of dynamical quorum sensing transition exhibited by a system to relevant microscopic details such as cell coupling. For example, Ref. [34] utilized ideas from percolation theory to show that altering the gap-junction couplings between cells can qualitatively affect the emergence of collective calcium oscillations in the pancreatic islet.

A final theoretical challenge is that, in contrast with physical systems, biological systems often use oscillations to perform a desired task in response to environmental and cellular signals. The classical example being the aggregation of Dictyostelium cells in response to starvation [24]. Thus, fully understanding biological rhythms requires integrating conceptual tools from statistical physics and dynamical systems with tools for understanding signal processing such as information theory [17,76].

Conclusion and Outlook

Collective oscillations in cellular systems represent a rich avenue of research for both biology and the physical sciences. It is now clear that the behavior of cellular populations arises from a complex interplay of components at the molecular and cellular levels. Understanding this behavior will require us to develop new theoretical and experimental tools linking the properties of single cells to those of cell populations. Ultimately, this knowledge should allow us to control the behavior of entire cell populations simply by manipulating the properties of isolated cells.

Table 1. Four roads to synchronized oscillations.

1. Specialized pacemaker cells such as in the heart [78]. 2. Phase-locking and frequency-locking of individually oscillating cells [79–82]. 3. Oscillator death in oscillators coupled with time delays [83,84]. 4. Dynamic quorum sensing such as in the social amoebae [20] and yeast [36]

Type of transition	Below the transition	Mechanism
Pacemaker	Cells are excitable. Pacemakers do not fire.	Firing of specialized pacemaker cells trigger oscillations.
Kuramoto (phase-locking)	Individual cells oscillate at their natural frequencies	An increase in the coupling strength results in phase and/or frequency locking.
Oscillator Death	Isolated cells oscillate at a wide range of frequencies. However, when cells are coupled, individual cells do not oscillate.	A decrease in the strength of the coupling between oscillators leads to collective oscillations.
Dynamic Quorum Sensing	Cells do not oscillate but can become oscillatory in response to an external signal they themselves produce.	An increase in cell density leads to a larger concentration of the external signaling molecules. When the concentration increases beyond the critical concentration (i.e. bifurcation point), the cells start collectively oscillating.