Hypothesis testing, power and sample size determination for between group comparisons in fMRI experiments

Abstract

Modern methods for imaging the human brain, such as functional magnetic resonance imaging (fMRI) present a range of challenging statistical problems. In this paper, we first develop a large sample based test for between group comparisons and use it to determine the necessary sample size in order to obtain a target power via simulation under various alternatives for a given pre-specified significance level. Both testing and sample size calculations are particularly critical for neuroscientists who use these new techniques, since each subject is expensive to image.

1. Introduction

Functional neuroimaging – the use of advanced imaging techniques such as functional magnetic resonance (fMRI) and positron emission tomography (PET) – to study the working human brain represents a major advance in our ability to understand brain function, and how that function differs among groups (men versus women, patients versus controls, children of different ages, stroke patients at different stages of recovery, and so forth). The data obtained from a typical fMRI study are large and complex, providing many statistical challenges. For a detailed discussion of the data collection process in fMRI, see Lange [17], Lazar et al. [18].

Our goal in this article is to develop a large sample based multivariate proportion testing procedure to compare two groups, in order to examine issues of power and sample size for fMRI studies. Sample size considerations are important due to the cost (in time and money) of scanning a subject. Recently, researchers have been moving in the direction of larger studies, with dozens of subjects, and power calculations have become more relevant. While power considerations have been studied to some extent for PET (see for example [28]), relatively little has been done in fMRI. Friston et al. [11] compared the number of subjects needed in two different modeling approaches to fMRI data. More recently Desmond and Glover [9] performed an explicit power analysis for fMRI, by first estimating and obtaining the distributions of typical effect size, and between and within subject variances from real studies. They then looked at the effects of varying those components on the number of subjects needed to maintain power at a given level, for a given level of significance. In this paper, we take a more theoretical approach than Desmond and Glover [9]. As in any statistical analysis, in the analysis of fMRI data there are choices and assumptions that are made, and these will have implications for testing and sample size calculations that ensue. It is important to state these in advance. In particular, we focus on the following issues: nature of the outcome (dichotomous or continuous); extent of the analysis (particular regions only or the whole brain) and the role of independence.

To the first point, we consider binary outcomes. The data are by nature continuous, giving levels of activation or percent signal change at a voxel (volume element, the three-dimensional version of a pixel) over time (for the many thousands of voxels in the brain), so this choice might seem contrary to expectations. However, researchers are often interested in determining which voxels are active in response to a given task. A voxel is deemed either active or inactive; there are no intermediate levels. Hence, this decision is a binary one. Before proceeding further, let us provide a brief review of the literature in connection to classification of active voxels.

Some classification based procedures have been proposed in the literature to determine whether voxels are active or not. For example, in block design fMRI experiment, with two conditions (baseline and an experimental condition), the analysis involves calculating t tests on all of the individual voxels in the brain (or perhaps in a region of interest in the brain). Voxels with t-statistic values above a certain pre-specified threshold are then classified as being active. Though this procedure is simple to implement, the main concern regarding this technique is that it does not take into account correlations between voxels that are close to each other, or between voxels that may be separated physically, but assume similar (or related) functionality. It relies on adjustments for multiple testing: when thousands of tests are carried out on the same data, it is misleading to conduct each one at standard significance levels of α = 0.05 or α = 0.01. As a result, this method suffers from high false positive and false negative rates. Forman et al. [10], Holmes et al. [15], Worsley [30], Genovese et al. [12] have introduced various alternative techniques in order to address these concerns in connection to block design fMRI experiments. Several authors have used model-oriented approaches for block designs to refine the classification available from simple t-tests (see for example [29,33]). These authors use random fields of different types (Gaussian, t, χ²) to model the observed patterns of activation in the brain incorporating some of the spatial correlations in the data and determining regions of activity areas in the random field where a given threshold value is exceeded. Bandettini et al.’s [1] “correlation method”, uses a reference function, r(t), and correlates it with each voxel data time series v(t). At each voxel, the correlation coefficient is calculated and is used to select active voxels. Different types of reference functions such as simple square waves, sine waves and other parametric functions can be used resulting in several different analyses.

Another type of design that is being frequently used in fMRI experiments is known as “event-related” design. In event-related design a stimulus is presented for a short period of time (instead of for a relatively prolonged period of time, as in a block design). Event-related studies allow researchers to learn about the hemodynamic responses in addition to detecting areas of activation [4,24]. Buckner and colleagues [8,25,5] present a methodology based on selective averaging to get hemodynamic response curves, and t-tests to locate areas of activation for event-related studies with rapid presentation of stimuli and with mixed trials. Postle et al. [23] propose a general linear model (multiple regression) for their event-related study of working memory. The authors use least squares technique to estimate the coefficients of the covariates of interest, and generate statistical maps by computing t-statistics. This review is not comprehensive; we have provided an outline of some of the major techniques for classification of active voxels, for both block design and event-related design studies. Gibbons et al. [13] proposed a random effects approach for modeling fMRI data by combining hierarchical polynomial models, Bayes estimation, and clustering. The methodology requires fitting cubic polynomials to the voxel time courses of event-related design experiments. The coefficients of the polynomials are then estimated using empirical Bayes procedures in a two-level hierarchical model. The empirical Bayes cubic fit for each voxel is designed to borrow strength from all voxels. The voxel-specific Bayes polynomial coefficients are then transformed to the times and magnitudes of the minimum and maximum points on the hemodynamic response curve, which are in turn used to classify the voxels as being activated or not. Thus, the final output of the procedure is a binary number for each voxel indicating the activation level of the voxel.

Second, we build tests that work on the whole brain, as well as tests that focus on specified regions of interest. Typically, statistical analysis is done on all of the voxels in the brain (on a voxel-by-voxel basis). There are situations, on the other hand, where the experimental task is very robust and well understood (for example, some visual processing tasks), and it makes little sense to test all voxels for activation. Some are known a priori, on the basis of neurological and psychological theory and experience, to be irrelevant; for example, if a voxel in a language processing area of the brain were to be picked out as active in response to a visual stimulus, such as a flashing checkerboard, the researcher would probably deem that finding to be spurious and uninteresting. Furthermore, activation should only be observed in the gray matter of the brain, not in other tissue types, allowing a further reduction in the regions under test, should this be desired.

Finally, it is common in the analysis of fMRI data to assume that the observations at different voxels are independent. Thus, as mentioned above, analysis is on a voxel-by-voxel basis. While it is clear in an intuitive sense that voxels cannot be independent (since they are all in the brain of the same individual, who is reacting to a particular stimulus), it is a great simplification to act as if they are. Indeed, since the correlation among voxels is complicated and not entirely understood, it would be hard to proceed at all without some such simplifying assumption. In the procedures described below, some mild forms of dependence are possible.

We assume a binary (“on/off”) response at each voxel, for pre-specified regions of interest. The research question of interest is whether or not two subject groups differ in the proportion of active voxels in the region. We address this issue under the assumption that the voxel within a region of interest are dependent but the regions are independent.

Section 2 discusses the general problem of working with the proportion of active voxels in regions of interest (ROI). In Section 3, we present large sample tests for equality of proportions. Section 4 introduces a common thresholding method and the control of the False Discovery Rate (FDR), which are used in this paper to compare ROIs of two groups. In Section 5 we develop the methodology, which is illustrated by a real life data set in Section 6. The methodology is demonstrated by a simulated data set in Section 7. We conclude with a discussion of our results in Section 8.

2. Proportions in regions

In this section we discuss how to work with the proportion of active voxels in ROIs in a general way. The scenario we consider here is the following: the brain is divided into ROIs, which are areas of the brain defined by anatomy, function, or both. For a given task, such as processing a visual stimulus, certain ROIs will be deemed to be relevant, while others are irrelevant. Our goal is to determine whether the proportion of activation for voxels in a pre-specified region is the same for two groups, for instance, normal controls compared to autistic patients. To distinguish between the two groups, we test equality of the underlying population proportions. We assume that all subjects within a given group have the same underlying proportion of active voxels, and any observed differences are simply the result of random variation. However, practical experience indicates that some individuals are “high activators” (that is, they show extensive and intense activation in response to the stimulus), whereas others are “low activators” (that is, they show limited activation, both in terms of pervasiveness and level, to the same stimulus). In that situation there is no particular reason to assume the same underlying parameter for each individual in a group, and testing a hypothesis about the group parameters will only be feasible when multiple observations are available for each subject in each group. We do not address this case, as it is rare in fMRI studies to have repetitions of the type required for this more sophisticated model.

Working with proportions in ROIs raises two additional issues. First, there is the question of spatial normalization as brains differ in size, shape and configuration. In order to carry out any group analysis, including the definition of regions of interest, the brain maps of different subjects need to be warped onto a common reference. To date there is no ideal way of doing this, but one of the common solutions is to transform individual brains into Talairach coordinates [27]. This is accomplished using a small number of reference points and an interpolation scheme (often linear or cubic). By transforming all images into Talairach space, we guarantee that the ROIs for each individual contain the same number of voxels and are located in the same place (in Talairach coordinates). Neither of these statements would be true in original data space. For purposes of group statistical analysis, it is essential to do such a warping, although the true data become distorted and lose spatial resolution as a result.

The second issue concerns thresholding, that is, how to decide that a given voxel is active (or inactive). This is, in essence, a question of statistical hypothesis testing, with thousands, or even millions of tests, and lies at the heart of many neuroimaging research problems. Traditional approaches to multiple testing, such as the Bonferroni correction, are too conservative when the number of tests is as large as in the current context. Various other methods have been proposed in the literature, such as contiguity thresholding, which builds on the idea that active voxels should occur in clumps [10]; random field theory, which looks for “excursions” or peaks of activity that are above what would be expected for a field of a given type (Markov, Gaussian, etc.) [29–32]; the use of FDR procedures [2,12]; random-effect models with clustering [13].

We take as our starting point that brain space has been transformed into Talairach coordinates using the widely used software package AFNI, ROIs have been defined, and the p-threshold has been applied, so that voxels are classified as either active or inactive [27,6,7].

Our methodology is based on two technical concepts: large sample tests for equality of proportions and control of the FDR. Therefore, for the convenience of the reader first we include some details on these two topics before formally introducing our methodology.

3. Large sample tests for equality of proportions

In this section we present large sample tests for equality of proportions that we discussed in the previous section. Let X₁, X₂, …, X_n1 be a random sample from a K-dimensional binary distribution, where each component of X_i = (X_i,₁, X_i,2, … X_i,_K)′ is either 0 or 1. Here the parameters of the multivariate binary distribution are E(X₁) = Π₁, Var (X₁) = Σ₁. Let Y₁, Y₂, …, Y_n2 be another random sample from a K-dimensional binary distribution with E(Y₁) = Π₂, Var (Y₁) = Σ₂. The covariance matrices Σ₁ and Σ₂ are functions of the parameters Π₁ and Π₂, respectively, but also depend on unknown parameters that determine the correlation structure between the components of the X_is and the Y_is. Assume the two samples to be mutually independent. Let n = n₁ + n₂. In our large sample framework we assume the following conditions on the sample sizes.

Assumption SS: min (n₁, n₂) → ∞ and n⁻¹n₁ → c for some c ∈ [0, 1].

Suppose that we are interested in testing the equality of the marginal proportions in the two populations. More specifically, we want to test H₀: Π₁ = Π₂ = Π. Let ${\widehat{\mathrm{\Pi }}}_1=n_1^{-1}{\sum }_{i=1}^{n_1}{X}_i$ and ${\widehat{\mathrm{\Pi }}}_2=n_2^{-1}{\sum }_{i=1}^{n_2}{Y}_i$ be the respective sample means. If we assume that the correlation structure of the components of the X_is and the Y_is are the same, under the null hypothesis, then the two groups have a common covariance matrix, say Σ. Let $\widehat{\mathrm{\sum }}=n^{-1}\{{\sum }_{i=1}^{n_1}(X_i-\widehat{\mathrm{\Pi }}){(X_i-\widehat{\mathrm{\Pi }})}^{\prime }+{\sum }_{j=1}^{n_2}(Y_j-\widehat{\mathrm{\Pi }}){(Y_j-\widehat{\mathrm{\Pi }})}^{\prime }\}$, where Π̂ = n⁻¹ (n₁Π̂₁ + n₂Π̂₂). Then a natural test statistic is a Wald type statistic given by

$$T_n=\frac{n_1{n}_2}{n}{({\widehat{\mathrm{\Pi }}}_1-{\widehat{\mathrm{\Pi }}}_2)}^{\prime }{\widehat{\mathrm{\sum }}}^{-1}({\widehat{\mathrm{\Pi }}}_1-{\widehat{\mathrm{\Pi }}}_2).$$ (3.1)

Note that, for sufficiently large n, Σ̂ is nonsingular and hence in the large sample framework the test statistic is well defined. The following theorem gives the large sample distribution of T_n under the null hypothesis.

Theorem 1

Let T_n be the test statistic as defined in (3.1) and let Assumption SS hold. Then under the null hypothesis H₀: Π₁ = Π₂ we have

$$T_n\stackrel{\mathcal{L}}{\to }{\chi }_K^2,$$

where ${\chi }_K^2$ is a chi-square random variable with K degrees of freedom and the $\stackrel{\mathcal{L}}{\to }$ denotes convergence in distribution.

Proof

Under the null hypothesis, E (Π̂) = Π the common value of Π₁ and Π₂. By standard results, the sample variance matrices ${\widehat{\mathrm{\sum }}}_1=n_1^{-1}{\sum }_{i=1}^{n_1}(X_i-\widehat{\mathrm{\Pi }}){(X_i-\widehat{\mathrm{\Pi }})}^{\prime }$ and ${\widehat{\mathrm{\sum }}}_2=n_2^{-1}{\sum }_{j=1}^{n_2}(Y_j-\widehat{\mathrm{\Pi }}){(Y_j-\widehat{\mathrm{\Pi }})}^{\prime }$ converge in probability to Σ. Then

$$\widehat{\mathrm{\sum }}=\frac{n_1}{n}{\widehat{\mathrm{\sum }}}_1+\frac{n_2}{n}{\widehat{\mathrm{\sum }}}_2\stackrel{p}{\to }\mathrm{\sum }.$$

Also, by continuity of convergence in probability the unique symmetric square root Σ̂^−1/2, of Σ̂⁻¹, converges in probability to the unique symmetric square root Σ^−1/2, of Σ⁻¹. By the multivariate Central Limit Theorem,

$$W_i:=\sqrt{n_i}({\widehat{\mathrm{\Pi }}}_i-\mathrm{\Pi })\stackrel{\mathcal{L}}{\to }{N}_K(0,\mathrm{\sum }),i=1,2,$$

where N_K (0, Σ) denotes the K-dimensional normal distribution with mean zero and variance matrix Σ. Here W₁ and W₂ are independent. Let $Z_n=\sqrt{\frac{n_1{n}_2}{n}}({\widehat{\mathrm{\Pi }}}_1-{\widehat{\mathrm{\Pi }}}_2)$. Then by Slutsky’s theorem and the multivariate CLT,

$$\begin{array}{l}{Z}_n={\widehat{\mathrm{\sum }}}^{-1/2}\left[\sqrt{\frac{n_2}{n}}\sqrt{n_1}({\widehat{\mathrm{\Pi }}}_1-\mathrm{\Pi })-\sqrt{\frac{n_1}{n}}\sqrt{n_2}({\widehat{\mathrm{\Pi }}}_2-\mathrm{\Pi })\right]\stackrel{\mathcal{L}}{\to }{\mathrm{\sum }}^{-1/2}N(0,(1-c)\mathrm{\sum }+c\mathrm{\sum })\\ =N(0,I).\end{array}$$

By continuity of convergence in distribution, we get the following result.

$$T_n=Z_n^{\prime }{Z}_n\stackrel{\mathcal{L}}{\to }{\chi }_K^2.$$

The test statistic T_n can be used to define a large sample critical region as { $T_n>{\chi }_{\alpha ,k}^2$} where ${\chi }_{\alpha ,K}^2$ is the upper α percentile for the ${\chi }_K^2$ distribution.

4. False discovery rate

Let us now introduce a common thresholding method, the control of the FDR, which we use in this article to compare ROIs of two groups. We assume that the voxels nested within a particular ROI are correlated and we have incorporated an unstructured correlation matrix while developing our test. On the other hand, our assumption is that the correlation among voxels across different ROIs is not significant. However, as multiple ROIs are involved in the study controlling the type I error rate is inevitable. It is true that the total number of ROIs in any study of this type will not be huge, most likely the number of ROIs will not exceed 25–30. A simple Bonferroni correction or an approach proposed by Meinshausen and Rice [21] can suffice in this case. When the number of significance tests to be performed in the course of a single study is large, it is crucial to correct for multiple testing error rates. If every test, out of possibly tens of thousands of tests, is evaluated at traditional levels of α = 0.05 or even α = 0.01, the aggregate error rate will be considerably higher than the nominal level and many false positives will be detected. Let m denote the number of hypotheses being tested. The general technique is as follows:

1. Select a desired FDR bound q between 0 and 1. This is the maximum proportion of false discoveries that the researcher is willing to tolerate, on average. While q of 0.15–0.20 is reasonable in many cases (Benjamini, personal communication), for our illustration we have used values of q starting 0.1–0.5.

2. Order the p-values from smallest to largest:

   $$p_{(1)}\le p_{(2)}\le \cdots \le p_{(m)}.$$

   H_(i) is the hypothesis corresponding to p-value p_(i).

3. Let r be the largest i for which

   $$p_{(i)}\le \frac{i}{m}q.$$

4. Reject the hypotheses H₍₁₎, …, H_(r).

Aside from ease of implementation, FDR has other advantages over alternative approaches. Benjamini and Hochberg [2,3] show that the FDR procedures have good power compared to the Bonferroni correction. The method is adaptive, in the sense that the thresholds that are chosen are automatically adjusted to the strength of the signal in the data. The parameter q has a definite and clear meaning that is comparable across studies. Finally, since the procedures work with p-values, and not test statistics, FDR methods can be applied with any valid statistical test, with equal ease.

5. Methodology

In this section we assume that our data (i.e. pre-processed and p-thresholded) are binary with a score of “one” indicating that the voxel has been classified as active and “zero” if it has been classified as inactive. Our response probability model is based on the following assumptions:

• Subjects under study are independent. They are nested within two groups, called “Treatment (or Patient)(1)” and “Control(2)”.

• The K voxels nested within an anatomical ROI in a particular subject are possibly dependent.

The region (or the set of K voxels) over which the testing of equality of proportion is performed deserves some discussion. The power of the test can be greatly enhanced by accurate identification of regions of activation (ROA) specific to a task. Such regions can be thought of as the collection of all voxels with reasonably high activation probability. As explained in Section 2, for a given task one generally concentrates on ROI that are obtained based on anatomical or functional considerations. However, such regions may still be quite conservative in the sense that they may be a large superset of the regions of activation. The voxels where the activation probability is uniformly low across groups and across subjects within groups will curtail the power of any test that is trying to detect a differential activation pattern between the groups. More specifically, let ${\mathrm{\Pi }}_i^{\prime }={({\pi }_{i1},{\pi }_{i2},\dots ,{\pi }_{iK})}^{\prime }$ denote the overall activation probability of the ith group for the ROI. The activation probabilities depend on the task performed. Let the set of all possible tasks be 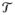and let the voxel space for the ROI be denoted by 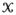. For a specific task T ∈ 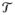, let A_T ⊂ 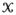denote the ROA. For notational convenience we suppress the task dependence of the activation probabilities. Then instead of testing

$$H_0:{\pi }_{1,k}={\pi }_{2,k}\forall k\in \mathcal{X},vs{H}_A:{\pi }_{1,k}\ne {\pi }_{2,k}\text{for}\text{some}k\in \mathcal{X},$$

considerable power can be gained by reducing the dimension of the test space to

$$H_0:{\pi }_{1,k}={\pi }_{2,k}\forall k\in A_T,vs{H}_A:{\pi }_{1,k}\ne {\pi }_{2,k}\text{for}\text{some}k\in A_T.$$

However, one can potentially fail to identify group differences if the ROA is identified inaccurately and the test is restricted only to the ROA. The test of equality should be performed solely on the basis of the voxels in the ROA only if one strongly believes that such regions contain all possible active voxels for the given task. Thus, depending upon the situation, the number of voxels K will be either the total number of voxels in the ROI or that in the smaller ROA.

Let us denote the binary response variable from the kth voxel nested within the jth subject belonging to the ith group by x_ijk, where i = 1, 2, j = 1, 2, …, n_i, and k = 1, 2, …, K. Then for a single voxel in a single subject in one of the groups, P(x_ijk = 1) = π_ik, E(x_ijk) = π_ik, and V (x_ijk) = π_ik(1 − π_ik). We also define, for two distinct voxels belonging to the same subject P(x_ijk = 1, x_ijk′ = 1) = π_ikk′, Cov(x_ijk, x_ijk′) = π_ikk′ − π_ikπ_ik′(= δ_ikk′, where k ≠ k′). Write Σ_i = ((δ_ikk′)). Finally, let ${\widehat{\mathrm{\Pi }}}_{ik}=n_i^{-1}{\sum }_{j=1}^{n_i}{x}_{\mathit{ijk}}$ be an estimate of π_ik, and ${\widehat{\pi }}_{{\mathit{ikk}}^{\prime }}=n_i^{-1}{\sum }_{j=1}^{n_i}{x}_{\mathit{ijk}}{x}_{{\mathit{ijk}}^{\prime }}$ be an estimate of π_ikk′. Denote the corresponding estimate of Π_i by Π̂_i. Hence E(Π̂_i) = Π_i, and $\text{Cov}({\widehat{\mathrm{\Pi }}}_i)=n_i^{-1}{\mathrm{\sum }}_i$. We estimate Σ_i by Σ̂_i = ((δ̂_ikk′)). The null hypothesis is

$$H_0:{\mathrm{\Pi }}_1={\mathrm{\Pi }}_2.$$ (5.1)

Note that the dimension of the hypothesis for standard fMRI experiments is typically much larger than the sample size available, since even small ROIs have hundreds of voxels, and most studies comprise fewer than twenty subjects in total. This makes it infeasible to test the multivariate hypothesis without assuming some structure for the voxel-to-voxel dependence of the binary data. We did not assume any parametric structure for the correlation of the voxels as it is not well accepted by the experts in the field.

Note that H₀ defined in (5.1) can also be tested by using the following collection of univariate hypotheses.

$$H_{0,k}:{\pi }_{1k}={\pi }_{2k},k=1,2,\dots ,K.$$ (5.2)

In that case, the error rate that is controlled is the FDR. We will reject (5.1) if at least one of the hypotheses in (5.2) is rejected. The simplest FDR controlling methods assume a certain dependence structure among the hypotheses. Clearly, the p-values obtained in an fMRI example need not conform to this dependence structure. The number of hypotheses tested simultaneously is high, making the bias due to dependence possibly even higher. Thus, applying FDR to the collection of K hypotheses may lead to loss of power. We want to strike a balance between loss of efficiency in estimation of parameters due to small sample sizes relative to parameter dimension and lack of power due to application of FDR to a collection of possibly dependent p-values.

Suppose that we partition the region of interest into smaller regions, i.e., let 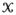= B₁ ∪ B₂ ∪ · · · ∪B_R. Let ${\mathrm{\Pi }}_i^{(r)}$ denote the probability response vector corresponding to the voxels in the subregion B_r. The partition is such that the number of voxels in each of the subregions is large enough to ensure efficient estimation of Σ_r, the variance–covariance matrix of the voxels in B_r. This makes it feasible to test each of the multivariate hypotheses

$$H_0^{(r)}:{\mathrm{\Pi }}_1^{(r)}={\mathrm{\Pi }}_2^{(r)},r=1,2,\dots ,R.$$ (5.3)

Let $T_n^{(r)}$, r = 1, 2, …, R be the test statistic (3.1) computed for each of the subregions and let p₁, p₂, …, p_R be the corresponding p-values. The p-value for the rth region is obtained as

$$p_r=P({\chi }_{k(r)}^2>T_n^{(r)}),$$

where k(r) is the number of voxels in B_r. Let W be the number of subhypotheses (5.3) rejected when the Benjamini–Hochberg FDR procedure is applied to the sorted p-values, p₍₁₎ ≤ p₍₂₎ ≤ · · · ≤ p_(R). Then we will reject the hypothesis (5.1) if W is greater than zero, i.e., at least one of the subhypotheses is rejected based on the FDR procedure.

6. Illustration

As an illustration of our methodology, we consider the following experiment. The experiment used a visually guided saccade task to compare autistic and normal children. This is a simple visual task, in which the subject fixates on a crosshair in the middle of a screen, until a light appears in peripheral vision. The subject then needs to guide her eyes to the spot where the light appears. Saccade tasks are used in the study of diseases such as autism and schizophrenia since patients with these pathologies often exhibit disturbances in performance compared to healthy controls [20,22,19,14,26].

We chose the supplementary eye field of the left hemisphere of the brain as the ROI. This is one of the regions known to be involved in the performance of the visually guided saccade task. Data were collected using a standard block design, alternating periods of rest with periods of task. The study consisted of 24 subjects, 10 in the control group and 14 in the autistic group. The original dataset consisted of a section of the brain divided in a three-dimensional grid of voxels. There were in all 27 × 21 × 9 = 5103 voxels. Each of the 5103 voxels was classified as either 1 (active) or 0 (inactive), using a p-threshold of 0.001. The data obtained at the resolution of the 5103 voxels contained too many zero voxels and was mostly uninformative. Thus, the analysis was done on a coarser resolution and the three-dimensional grid was reduced by a factor of 3 in each direction. That is, 27 voxels in 3 × 3 × 3 grid of voxels were merged to construct larger voxels which we refer to as “supervoxels”. Suppose that the original voxels are indexed in a three-dimensional cube as V_ijk, i = 1, …, 27, j = 1, …, 21, k = 1, …, 9, Then we define the supervoxels as ${\stackrel{\sim }{V}}_{\mathit{lmn}}={\cup }_{i=3(l-1)+1}^{3l}{\cup }_{j=3(m-1)+1}^{3m}{\cup }_{k=3(n-1)+1}^{3n}{V}_{\mathit{ijk}}$ where l = 1, …, 9, m = 1, …, 7, n = 1, …, 3. Combining voxels into supervoxels helps us to avoid the problem of excessive zero that we encounter in most of the original voxels and also simplifies computation. Thus, there were 5103/27 = 189(9 × 7 × 3) supervoxels. Each supervoxel was classified as 1 (active) if at least one of its 27 voxels had a score of 1. Otherwise the supervoxel was classified as 0 (inactive). Thus, if the value of the binary response at V_ijk was x_ijk then the value of the binary variable on the ‘supervoxel’ was defined as

$${\stackrel{\sim }{x}}_{\mathit{lmn}}=max\{x_{\mathit{ijk}}:3(l-1)+1\le i\le 3l;3(m-1)+1\le j\le 3m;3(n-1)+1\le k\le 3n\}.$$

The idea of supervoxel reduces the dimension of ROA that helps in implementing a chi-square test even for small samples. The resolution of 189 supervoxels is used to generate a framework for simulation in the next section. Before we present results from our simulation study on power properties of the proposed testing procedure, we end this section with an application of the proposed methodology to the given data. Following the description in Section 5, we subdivided the 189 supervoxels in a contiguous fashion into 63 subregions, each consisting of 3 supervoxels. Following the notation of Section 5, the subregions were B₁ = {Ṽ₁₁₁, Ṽ₁₁₂, Ṽ₁₁₃}, B₂ = {Ṽ_121, Ṽ₁₂₂, Ṽ₁₂₃}, …, B₆₃ = {Ṽ₉₇₁, Ṽ₉₇₂, Ṽ₉₇₃}. The chi-square test, based on the binary values of the three supervoxels, was applied in each subregion and the values of the test statistic and the corresponding p-values for the 63 subregions are reported in Table 1. If the FDR methodology is applied to the 63 p-values, then the procedure fails to reject the hypothesis of equal activation probability in all of the 63 subregions for any reasonable value of the FDR control and hence fails to reject the overall hypothesis of equal activation profile. The values of the test statistic or p-values at these 63 regions are likely to be spatially correlated. The Benjamini–Hochberg FDR control procedure is known to be conservative for dependent data. This could be the reason for the procedure being not able to detect the significant difference. A more refined FDR control procedure which can take into account the dependence among the p-values is more likely to yield significance in some of the subregions. Table 1 shows the chi-square test statistic values, and their corresponding p-values for each of the 63 subregions. All of the p-values are quite large (>0.05), and so we fail to reject the null hypothesis in any location (with or without the FDR mechanism).

Table 1.

Chi-square test statistic and the corresponding p-values for testing control and autistic group for 63 subregions

Subregion χ2-test statistic	p-value	Subregion χ2-test statistic	p-value
1.4400	0.6962	2.4686	0.4810
1.3714	0.7122	2.5019	0.4750
2.4332	0.4875	0.9375	0.8164
3.7034	0.2953	4.2514	0.2356
4.6945	0.1956	4.3337	0.2276
2.9727	0.3958	4.1646	0.2442
0.8687	0.8330	4.5426	0.2085
0.9301	0.8181	0.0000	1.0000
2.8726	0.4117	2.3808	0.4972
4.0962	0.2513	4.3680	0.2244
3.1543	0.3684	3.0677	0.3813
6.8571	0.0766	5.9468	0.1142
1.4338	0.6976	3.2262	0.3580
1.4338	0.6976	1.6000	0.6594
2.2664	0.5190	4.1546	0.2452
2.7664	0.4291	2.6057	0.4565
1.6124	0.6566	1.9830	0.5759
3.4412	0.3285	2.5412	0.4679
0.7945	0.8508	3.2229	0.3585
2.6416	0.4502	6.3552	0.0956
3.1657	0.3668	3.8741	0.2754
1.9228	0.5886	2.7318	0.4349
3.4433	0.3282	1.5889	0.6619
5.0449	0.1685	1.9714	0.5784
7.5624	0.0560	0.8874	0.8285
6.2707	0.0992	6.1714	0.1036
6.3059	0.0976	3.2229	0.3585
6.5049	0.0895	3.2816	0.3502
1.5095	0.6801	2.2015	0.5317
1.0955	0.7782	1.6000	0.6594
2.0875	0.5545	1.6000	0.6594
6.2948	0.0981

7. Statistical power

In order to compute the simulated power, we preserved this layout of 189 supervoxels for the simulation experiment and generated binary data for each of the supervoxels for 24 subjects. To generate realistic data, we needed to designate some of the 189 supervoxels as more likely to generate active response. First we estimated which supervoxels were more likely to be active for the control group. In order to do this, the average activation proportion over the ten subjects in the control group was calculated for each supervoxel. Thus, for the kth supervoxel, the population activation probability was estimated as π̂_k = s(k)/10, where s(k) ∈ {0, 1, 2, …, 10} denotes the number of subjects in the control group with a 1 for the kth supervoxel and k = 1, 2, …,189. After computing π̂_k for each supervoxel, those with high (estimated) activation probability, i.e., where π̂_k exceeded a given threshold, were considered active for the simulation experiment. For a threshold of 0.3, there were in all 34 supervoxels that were classified as active (which matches with expert experience).

For convenience, the numbers of subjects in the control group and in the patient group are taken to be the same, say n. The premise of our simulation model is that the nature of the voxels outside the region of activation is the same for both groups. By contrast, the activation probability for the voxels in the region of activation is not the same. For both groups, a model for the “on” voxels in the inactive region is

$$x_{i,j,k}\sim \text{Bernoulli}(\delta ),k\in \mathcal{X}\backslash A_T,$$

where δ is a small probability that captures the random noise in the inactive region and 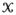\A_T is the collection of all inactive voxels in the ROI. Thus, according to our model each voxel in the inactive region gets a small probability of activation. Therefore, the number of active voxels, U, in the complement of the region of activation is distributed as a Binomial (K_I, δ) where K_I is the number of voxels in 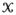\A_T. Given U, the locations of the active voxels are distributed uniformly over 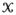\A_T.

The number of active voxels in the region of activation for the control group, V₁, is distributed as Binomial (K_A, p₁) where K_A is the number of voxels in the region of activation. Given V₁ the locations of the active voxels are distributed uniformly over the region of activation. Thus, for the control group

$$x_{i,j,k}\sim \text{Bernoulli}(p_1),k\in A_T.$$

Similarly, the number of active voxels in the region of activation for the patient group, V₂ is distributed as Binomial (K_A, p₂) and given V₂ the locations of the active voxels are distributed uniformly over A_T.

Therefore, for the treatment group

$$x_{i,j,k}\sim \text{Bernoulli}(p_2),k\in A_T.$$

Finally, we partition the region of interest, 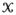into B₁ ∪ B₂ ∪ · · · ∪ B_R. In our simulation study, the total number of voxels in 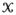, K, is 189 and that in the ROA, K_A, is 34. We choose a regular grid of 21 disjoint three-dimensional cubes as our partition where each cube contains 9 voxels. Of course in practice if natural partitions are known (for example, groups of voxels that are anatomically close and not necessarily contiguous in space) then one can choose such partitions to potentially improve the performance of the tests. We compute R(=21) test statistics for testing equality of the nine-dimensional probability vectors for each cube across the two groups. The large sample χ² null distributions are used for computing the p-values and then FDR is applied to the sorted p-values. Thus, in our case, the number of hypotheses, m, is 21. One may argue that for such a small number of tests, controlling the family wise error rate (FWER) with Bonferroni or similar procedures is more reasonable. However, in practice, the number of tests can be considerably larger, making FDR the more appropriate measure for control. For our simulation, we set 0 < p₁, p₂ ≤ 0.5 at an increment of 0.02, δ ∈ {0.05, 0.1}, n ∈ {20, 25, 30} and q ∈ {0.10, 0.15,…, 0.60} where q is the control level in the FDR procedure.

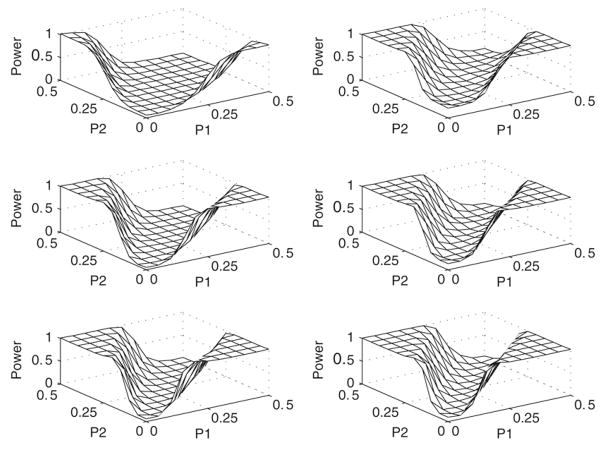
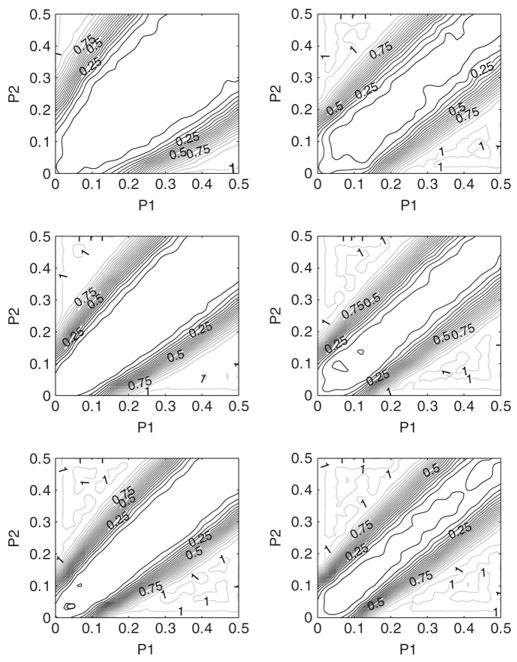
Figs. 1 and 2 both show the power surfaces as a function of p₁ and p₂ for different sample sizes and different values of δ. The general findings are that the power is an increasing function of the sample size and a decreasing function of the noise parameter δ. Note that power is also an increasing function of the critical difference |p₁ − p₂|. This can be used for sample size determination when a certain level of power is desired for a given parameter combination. To this end, we tabulated the critical difference |p₁ − p₂| required for attaining a desired power γ for different values of n, q and for δ = 0.05.

Fig. 1.

Power surface plots for δ = 0.05: Left column: R = 9; Right column: R = 63: First row: n = 20; Second row: n = 25; Third row: n = 30.

Fig. 2.

Power contour plots for δ = 0.05; Left column: R = 9; Right column: R = 63: First row: n = 20; Second row: n = 25; Third row: n = 30.

Tables 2, 4 and 6 show that the critical difference |p₁ − p₂| required for a fixed power level γ = (0.60, 0.80, 0.90) is a decreasing function of both n and α for all the regions (denoted by R in equation 5.3) 9, 21 and 63. The critical difference values are averages over the range 0 < p₁ < 1. The values have a slight increasing trend for 0 < p₁ < 1/2 and a slight decreasing trend for 1/2 < p₁ < 1. However, as evident in the standard errors reported at the bottom of the table, the variability of the critical difference is not severe. Thus, the power for a fixed n, α and δ can be taken as a function of the difference |p₁ − p₂| rather than a bivariate function of p₁ and p₂. Tables 3, 5 and 7 report the control level q required for attaining the pre-fixed size of the test for number of ROIs 9, 21and 63 respectively. Tables 2, 4 and 6 reveal that as the number of regions increase the corresponding critical differences |p₁ − p₂| decreases. However, we do not see this kind of monotonicity property of q in Tables 3, 5 and Specifically, we looked at the control level q needed to maintain the size of the tests at 1%, 5% or 10%. For smaller sample sizes, the control level cannot be too stringent, otherwise the tests will be undersized.

Table 2.

Critical difference, |p₁ − p₂| forgiven power level, γ, at different sample sizes, n, type I error, α, δ = 0.05 and number of ROIs R = 9

α	γ= 0.60			γ = 0.80			γ= 0.90
	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30
0.01	0.352	0.205	0.163	0.416	0.255	0.186	0.437	0.266	0.203
0.05	0.203	0.148	0.125	0.264	0.174	0.155	0.231	0.203	0.175
0.10	0.151	0.120	0.117	0.175	0.151	0.143	0.220	0.178	0.151

Standard errors of entries in the table range between 5% and 50% of the entries.

Table 4.

Critical difference, |p₁ − p₂| for given power level, γ, at different sample sizes, n, type I error, α, δ = 0.05 and number of ROIs R = 21

α	γ = 0.60			γ = 0.80			γ = 0.90
	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30
0.01	0.214	0.172	0.142	0.240	0.191	0.166	0.262	0.206	0.180
0.05	0.137	0.120	0.111	0.174	0.148	0.136	0.188	0.162	0.151
0.10	0.119	0.110	0.097	0.149	0.132	0.120	0.176	0.150	0.142

Standard errors of entries in the table range between 5% and 50% of the entries.

Table 6.

Critical difference, |p₁ − p₂| for given power level, γ, at different sample sizes, n, type I error, α, δ = 0.05 and number of ROIs R = 63

α	γ = 0.60			γ = 0.80			γ = 0.90
	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30	n = 20	n = 25	n = 30
0.01	0.199	0.162	0.138	0.227	0.184	0.163	0.242	0.191	0.172
0.05	0.136	0.131	0.130	0.168	0.152	0.146	0.177	0.165	0.150
0.10	0.118	0.116	0.103	0.139	0.126	0.126	0.150	0.146	0.139

Standard errors of entries in the table range between 5% and 50% of the entries.

Table 3.

Control level q required for attaining prescribed type I error rates for different sample sizes (n), δ = 0.05 and number of ROIs R = 9

α	n = 20	n = 25	n = 30
0.01	0.15	0.15	0.15
0.05	0.35	0.30	0.30
0.10	0.50	0.50	0.40

Table 5.

Control level q required for attaining prescribed type I error rates for different sample sizes (n), δ = 0.05 and number of ROIs R = 21

α	n = 20	n = 25	n = 30
0.01	0.15	0.10	0.05
0.05	0.45	0.40	0.30
0.10	0.55	0.50	0.40

Table 7.

Control level q required for attaining prescribed type I error rates for different sample sizes (n), α = 0.05 and number of ROIs R = 63

α	n = 20	n = 25	n = 30
0.01	0.05	0.05	0.05
0.05	0.40	0.20	0.15
0.10	0.55	0.50	0.45

Discussion

We have presented a methodology for performing between group comparisons in fMRI, based on the proportions of active voxels in a region of interest for a group of control subjects and a group of patients. The test is based on certain simplifying assumptions, such as being able to partition the region of interest into a set of subregions, and having a constant proportion of active voxels across subjects in a group. These constraints are due to characteristics of the data; for instance, having many more voxels than subjects makes it impossible to get good estimates of the correlation structure across voxels, hence some “parcelling” of voxels and subdividing of regions are necessary. Similarly, without having multiple repetitions of the same experiment for each subject, something that is not currently routine in fMRI studies, it is impossible to get individual estimates of the activation parameter, and we need to assume constancy of the probability of activation.

Using this test we have investigated its power depending on various sample sizes. Not surprisingly, the power of the test increases as sample size increases, and decreases as the probability of activation in supposedly “inactive” parts of the studied region goes up. The latter indicates that the test loses power in the presence of noise, a sensible finding. Finally, even for small sample size (e.g. n = 10 per group) we can achieve quite good power, of the order of 80% or 90%, if the probabilities of activation in the two groups are sufficiently separated (e.g. 15%–20% difference between p₁ and p₂). Lower thresholds, as determined by the FDR procedure (but presumably similar findings would hold for other thresholding methods), require more separation of the base probabilities, as do smaller sample sizes. For the sample sizes common in fMRI (where it is usually not feasible to have even as few as 20 subjects per group), and the generally low q-thresholds that are used by fMRI researchers, the degree of separation would have to be that much clearer for high levels of power to be attained. Our test therefore behaves as we would expect a “reasonable” test of the equality of proportions to behave.

The study of power and sample size is relatively new in this application area, and the current work is just one of the first steps necessary for providing fMRI researchers with guidance on this aspect of their experimental design. Our basic strategy can, and should be, expanded to explore some of the other comparisons of interest [16].