Reduction of the virtual space for coupled-cluster excitation energies of large molecules and embedded systems

Abstract

We investigate how the reduction of the virtual space affects coupled-cluster excitation energies at the approximate singles and doubles coupled-cluster level (CC2). In this reduced-virtual-space (RVS) approach, all virtual orbitals above a certain energy threshold are omitted in the correlation calculation. The effects of the RVS approach are assessed by calculations on the two lowest excitation energies of 11 biochromophores using different sizes of the virtual space. Our set of biochromophores consists of common model systems for the chromophores of the photoactive yellow protein, the green fluorescent protein, and rhodopsin. The RVS calculations show that most of the high-lying virtual orbitals can be neglected without significantly affecting the accuracy of the obtained excitation energies. Omitting all virtual orbitals above 50 eV in the correlation calculation introduces errors in the excitation energies that are smaller than 0.1 eV . By using a RVS energy threshold of 50 eV , the CC2 calculations using triple-ζ basis sets (TZVP) on protonated Schiff base retinal are accelerated by a factor of 6. We demonstrate the applicability of the RVS approach by performing CC2∕TZVP calculations on the lowest singlet excitation energy of a rhodopsin model consisting of 165 atoms using RVS thresholds between 20 eV and 120 eV. The calculations on the rhodopsin model show that the RVS errors determined in the gas-phase are a very good approximation to the RVS errors in the protein environment. The RVS approach thus renders purely quantum mechanical treatments of chromophores in protein environments feasible and offers an ab initio alternative to quantum mechanics∕molecular mechanics separation schemes.

INTRODUCTION

Mechanistic experimental studies of biological systems often rely on spectroscopic characterization of the chemical intermediates. However, establishing a molecular interpretation from the spectroscopic information is very challenging. Theoretical spectroscopy aims at establishing such a link between the chemical structure and the spectra by employing the methodology of quantum chemical theory. This requires highly accurate computational approaches within the 1 kcal∕mol limit of chemical accuracy.

The accuracy of calculated excitation energies is determined by the level of electron correlation treatment and the size of the basis set. Accurate electron-correlation methods, such as high-order configuration interaction (CI) or coupled-cluster (CC) schemes, yield excitation energies in close agreement with experiment when using large basis sets.^{1, 2, 3, 4, 5} However, high-order CI and CC calculations are limited to very small molecules,⁶ often comprising no more than a few tens of atoms, and therefore not applicable for studying biological systems. Using too small basis sets results in inaccurate excitation energies despite a sophisticated treatment of electron correlation. Density functional theory (DFT) and low-order ab initio electron correlation methods, such as the coupled-cluster approximate singles and doubles (CC2) model,^{7, 8, 9, 10} can be employed in combination with large basis sets yielding results close to the basis-set limit. For many biochromophores, CC2 calculations are computationally at the limit of the feasible with today's computational resources. The popular linear-response time-dependent DFT (TDDFT) method provides accurate excitation energies at a much lower cost than ab initio correlation calculations.^{11, 12, 13} However, a number of problematic cases exists, where today's functionals are not able to provide accurate excitation energies.^{2, 5, 14, 15, 16, 17, 18} Thus, alternative methods to assess the accuracy of the TDDFT calculations on large molecules are needed.

A popular approach to speed up quantum chemical methods is the partial neglect of molecular orbitals in the correlation calculation. The orbitals most commonly neglected are those lowest in energy, the core orbitals. The idea of omitting high-lying virtual orbitals in ab initio correlation calculations is simple and not new.^{19, 20, 21, 22, 23, 24, 25} A similar approach has recently been used to study ionized states of small molecules at the equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) level.²⁶ A frozen natural orbital approach has recently been implemented in the MOLCAS program.²⁸ However, to our knowledge a reduced-virtual-space (RVS) approach has not previously been employed in excitation energy calculations of large molecules at ab initio correlation levels.

In this work, we employ the RVS approach for the lowest excitation energies of photoactive yellow protein (PYP), green fluorescent protein (GFP), and rhodopsin chromophore models at CC2 level. Using differently sized virtual spaces, the present CC2 calculations show that a large fraction of the virtual orbitals barely contributes to the two lowest excitation energies. At the CC2 level, the uncertainty introduced by the electron correlation treatment is about 0.3 eV,¹ depending on the benchmark set.²⁷ This is larger than the error caused by the omission of a large part of the virtual space. Due to the significant computational savings, RVS calculations at the CC2 response theory level can be performed on large systems in combination with sufficiently converged basis sets.

The central novelty in our work is that the RVS error determined for chromophores in the gas-phase is a very good approximation to the RVS error of the same chromophore in a protein environment. This allows fully quantum mechanical calculations on protein models and even offers a scheme for extrapolating the result obtained without reduced orbital space. The RVS CC2 approach thus offers a fully quantum mechanical alternative to the combined quantum mechanical∕molecular mechanics (QM∕MM) calculations, in which the boundary region between the classical and quantum regions can be a source of significant errors.²⁹ We demonstrate the efficiency of our approach on a rhodopsin model with 165 atoms, for which we calculate the excitation energy at RVS CC2 level.

This article is structured as follows. The computational methods and the studied chromophores are described in Secs. 2, 3. An analysis of the RVS approach and the results of the RVS calculations are given in Secs. 4, 5. The main conclusions are summarized in Sec. 6.

COMPUTATIONAL DETAILS

The Karlsruhe basis sets of triple-ζ quality augmented with polarization functions (def2-TZVP) were employed in this work.³⁰ The ground state structures of the biochromophores were optimized at the second-order Møller-Plesset perturbation (MP2) level employing TZVP basis sets and the resolution-of-the-identity (RI) approximation.^{31, 32, 33} The excitation energies were calculated at the approximate second-order coupled-cluster level using the RI approximation.^{7, 8, 9, 10} In the basis-set studies, the Karlsruhe basis sets of double-ζ and quadruple-ζ quality (def2-SVP and def2-QZVP), as well as the triple-ζ basis set augmented with diffuse functions from Dunning's aug-cc-pVTZ basis set (aug-TZVP) were also employed.^{30, 34, 35} We neglect the def2 prefix in the basis set abbreviations throughout this work. The ground-state structure of a rhodopsin model, consisting of retinal and its nearest rhodopsin residues, was optimized at the DFT level using the B3LYP functional and the Karlsruhe SVP basis sets.^{34, 36, 37} All calculations were done with TURBOMOLE.³⁸

STUDIED MOLECULAR SYSTEMS

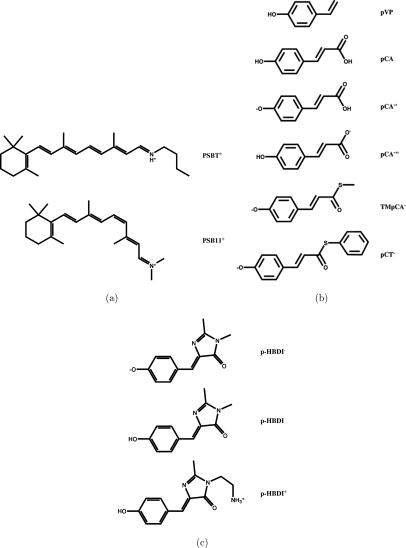
Protonated Schiff-base (PSB) retinals are the chromophores of the rhodopsin proteins found in eyes and photosensitive spots from humans to bacteria.^{39, 40} The all-trans protonated Schiff base retinal (PSBT⁺) studied here has a proton and a butyl group connected to the nitrogen of the retinyl chain forming a positively charged Schiff base. The 11-cis-retinal chromophore (${\mathrm{PSBMe}}_2^{+}$) has a positive charge with two methyl groups attached to the retinyl nitrogen. The molecular structures of the retinals are shown in Fig. 1a.

Figure 1.

The molecular structures of the studied molecules: (a) the rhodopsin chromophore models; (b) the photoactive yellow protein chromophore models; and (c) the green fluorescent protein chromophore models.

The PYP is a blue-light photoreceptor consisting of a p-hydroxycinnamic acid chromophore embedded in the protein.⁴¹ The studied PYP chromophore models comprise trans-p-coumaric acid (pCA), deprotonated trans-p-coumaric acid (pCA⁻′), trans-p-coumarate (pCA^−′′), p-vinyl phenol (pVP), thiomethyl-p-coumarate (TMpCA⁻), and thiophenyl p-coumarate (pCT⁻). The molecular structures of the PYP model chromophores are shown in Fig. 1b.

Three different GFP model chromophores were investigated, namely, p-hydroxybenzylideneimidazolinone (pHBDI) and the anionic and cationic forms pHBDI⁻ and pHBDI⁺, respectively. pHBDI and pHBDI⁻ are identical except that pHBDI⁻ has a deprotonated hydroxyl group. pHBDI⁺ differs from pHBDI by having an ethyl amine (–CH₂CH₂${\mathrm{NH}}_3^{+}$) substituent instead of the methyl group at the nitrogen of the imidazolinone ring.^{42, 43} The molecular structures of the GFP chromophores are shown in Fig. 1c.

The 11 chromophore models depicted in Figs. 1a, 1b, 1c have been carefully benchmarked with respect to their basis-set requirements, and the calculated CC2 excitation energies were compared to experimental values and other computational results.⁴⁴ The excited states of all chromophores show a complex character that has been extensively discussed in previous studies. The oscillator strengths given as supporting information can be used to identify the most important states.⁴⁵ For further discussion of the excited state character see Ref. 44 and references therein.

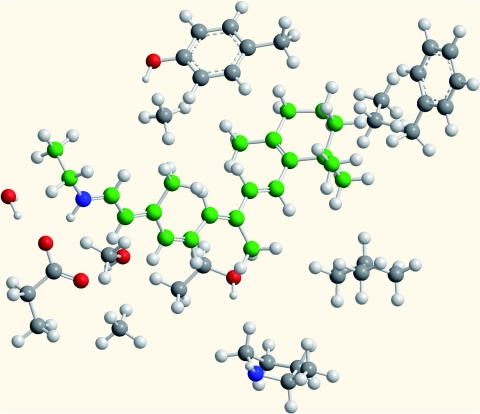
An 11-cis-retinal chromophore surrounded by the most relevant adjacent parts of rhodopsin residues has also been studied. The structural model was built based on the homology model for the human bluecone pigment 1KPN.⁴⁶ The rhodopsin chromophore model comprises 165 atoms including Gly-114, Thr-118, Glu-113, Ser-186, Phe-212, Leu-207, Tyr-265, Ala-269, Lys-296, in addition to the retinal chromophore. Amino-acid residues were terminated at their β-carbons, which were fixed in the structure optimizations. The Schiff base proton was restrained to reside on the retinyl moiety during structure optimization.⁴⁶ The molecular structure of the rhodopsin model is shown in Fig. 2.

Figure 2.

The molecular structure of the model used for retinal embedded in a protein environment. The rhodopsin model consists of 165 atoms.

REDUCED-VIRTUAL-SPACE APPROACH

Idea

The Hartree-Fock orbital space can be divided into occupied core orbitals, occupied valence orbitals, unoccupied anticore orbitals, and other unoccupied virtual orbitals. In the frozen core approximation (FCA), all electrons are correlated except the occupied core orbitals and the corresponding electrons. As the idea behind the FCA is very intuitive, it is uncertain when the approach was first introduced.⁴⁸ Moreover, the highest virtual orbitals are energetically separated from the lower virtual orbitals in a similar way as the core orbitals are separated from the rest of the occupied orbitals. We denote these high-lying virtual orbitals as anticore.

In the RVS approach, we employ the FCA and additionally omit (freeze) all virtual orbitals above a certain energy threshold in the CC2 calculation. For the studied molecules, the orbital energies of the anticore orbitals lie typically 400 eV above the rest of the virtual orbitals. As for the core orbitals, the anticore hardly contributes to relative energies and can thus be omitted in the correlation calculation without significantly affecting the obtained excitation energies. However, since the number of anticore orbitals is relatively small, freezing them has a limited influence on the computing time. For example, a CC2∕TZVP calculation on the retinal model PSBT⁺ with frozen anticore orbitals is only 10% faster.

The energies of the virtual orbitals below the anticore extend 0-200 eV for the molecules studied here. One can expect that the remaining high-lying virtual orbitals also have a small contribution to the lowest excitation energies, and that the omission of virtual orbitals at the CC2 level leads to significantly faster calculations. The uncertainties introduced by the RVS approach are assessed in the following by calculations on the two lowest excited singlet states, demonstrating that a large fraction of the virtual orbitals can be ignored in the correlation calculations without introducing significant errors in the excitation energies.

Error dependence

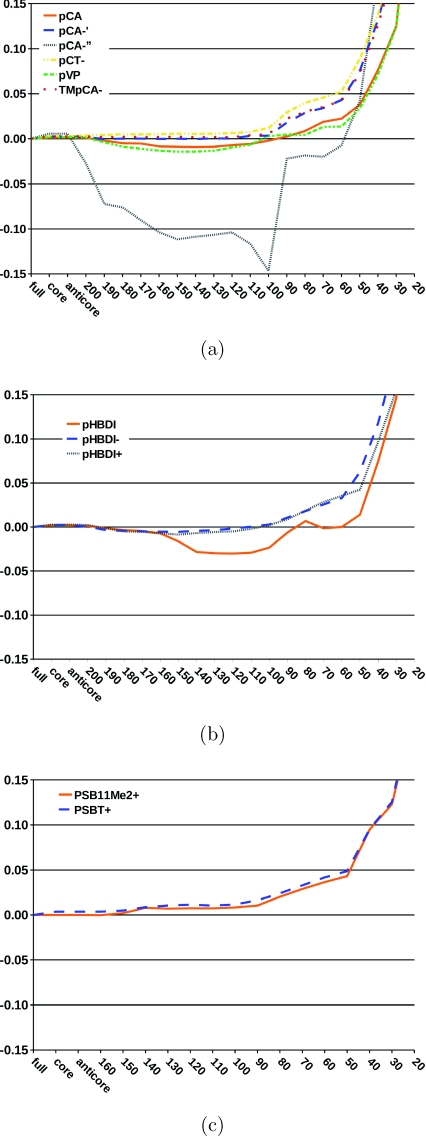
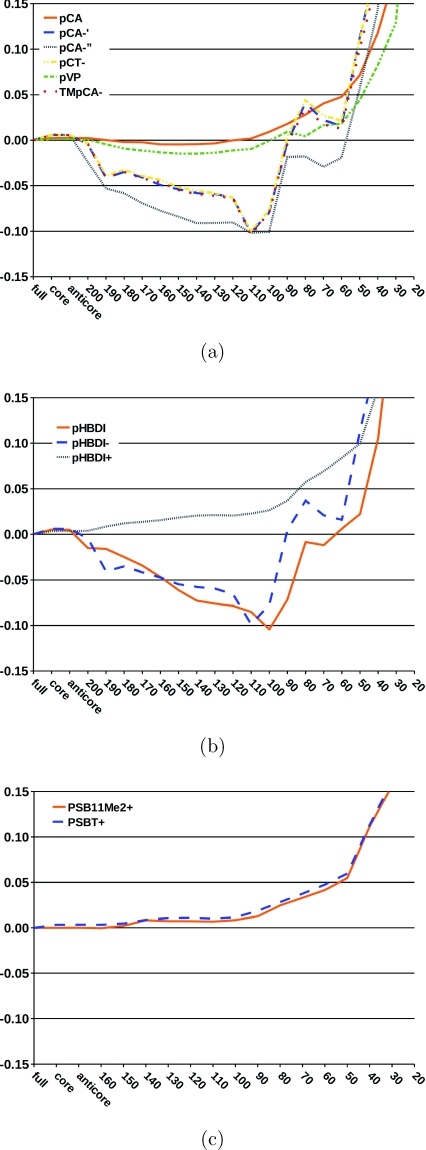
The dependence of the excitation energies on the size of the virtual space is investigated by systematically omitting high-lying virtual orbitals in the CC2 calculations using the TZVP basis sets. The deviations of the two lowest excitation energies from those obtained without frozen orbitals are shown in Figs. 34. The truncation of the virtual space has in general little effect on the excitation energies until one reaches an energy threshold of about 50 eV. Below 50 eV, the errors become significant as also found in a previous EOM-CCSD study.⁴⁹ Omission of the virtual orbitals above 50 eV reduces the size of the virtual space of the CC2∕TZVP calculation by about 35% for the studied chromophores.

Figure 3.

The relative error (in eV) of the first singlet excitation energy is given as a function of the energy threshold (in eV) used in the reduction of the virtual space. No orbitals were frozen in the reference CC2 calculation. (a) photoactive yellow protein chromophore models; (b) green fluorescent protein chromophore models; and (c) rhodopsin chromophore models.

Figure 4.

The relative error (in eV) of the second singlet excitation energy is given as a function of the energy threshold (in eV) used in the reduction of the virtual space. No orbitals were frozen in the reference CC2 calculation. (a) photoactive yellow protein chromophore models; (b) green fluorescent protein chromophore models; and (c) rhodopsin chromophore models.

For all studied states and chromophores, the errors of the RVS approach are small when the energy threshold is larger than 50 eV. The largest truncation errors for the first excited state were obtained for pCA⁻, for which the excitation energies have a maximum error of 0.15 eV at a truncation threshold of 100 eV. For smaller energy thresholds, the excitation energy of pCA^−′′ is more accurate, before the error rapidly increases at a threshold of about 50 eV. For the remaining PYP chromophore models, the RVS truncation errors are smaller than 0.05 eV until an energy threshold of 50 eV. The first excitation energies of the GFP and retinal chromophores are also very insensitive to the reduction of the virtual space as long as the RVS threshold is larger than 50 eV.

The deviations are slightly larger for the second excited state relative to the lowest one. The negatively charged GFP chromophores, pHBDI⁻, and pHBDI have a maximum RVS truncation error of 0.1 eV at a threshold of 100–120 eV. For pHBDI⁺, the neutral PYP chromophores, and the retinals, the errors introduced by the RVS approach are similar to the first and second excited states. For these systems, the RVS error is less than 0.03 eV up to a threshold of around 100 eV, the error at an energy threshold of 50 eV is still below 0.1 eV. For all studied systems, the uncertainties in the excitation energies with a RVS threshold of 50 eV are smaller than the general accuracy of ±0.3 eV for the CC2 model.

The character of the excitation is not significantly changed upon reduction of the virtual space. We conclude this from comparing oscillator strengths calculated using the full orbital space with oscillator strengths calculated at an energy threshold of 50 eV (see supporting information).

Basis-set dependence

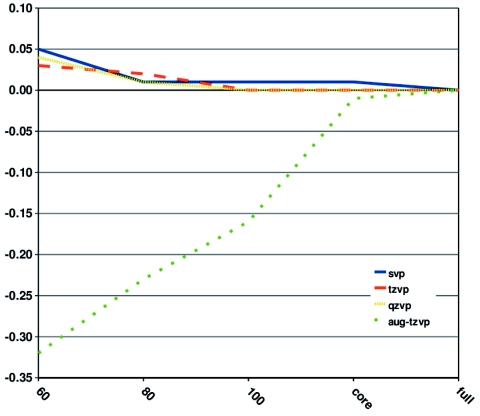
The uncertainty in the excitation energies caused by the omission of virtual orbitals is rather basis-set independent when diffuse basis functions are unnecessary to describe the excited state. The error in the first excitation energy of pHBDI⁻ is given as a function of the RVS threshold for different basis sets in Fig. 5. The calculations employing SVP, TZVP, and QZVP basis sets yield errors smaller than 0.05 eV up to a RVS threshold of 60 eV, whereas the excitation energy is much more sensitive to the RVS threshold when diffuse functions are included in the basis set. The largest RVS error of 0.32 eV was obtained in the CC2∕aug-TZVP calculation when a threshold of 60 eV is used.

Figure 5.

The relative error (in eV) of the first singlet excitation energy of pHBDI⁻ as a function of the energy threshold (in eV) used in the reduction of the virtual space is shown for different sizes of the basis set.

The RVS approach allows the use of larger basis sets in the CC2 calculations. For example, the CC2∕QZVP calculation on pHBDI⁻ using a RVS threshold of 60 eV demands less than half of the computing time of the full CC2∕TZVP calculation. Thus, larger relative computational savings are obtained with increasing basis-set size.

Efficiency

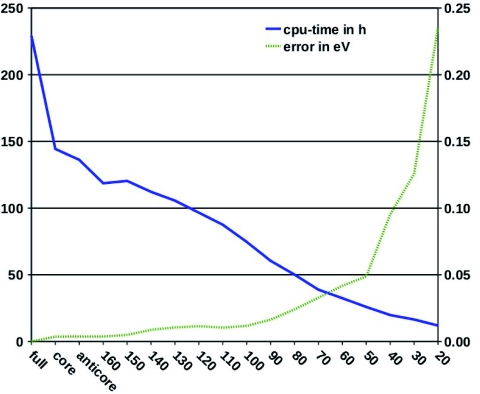
In Fig. 6, the balance between efficiency and speed-up is illustrated with CC2∕TZVP calculations on the first excited state of PSBT⁺. In the graph, the central processing unit (CPU) time decreases roughly linearly with decreasing RVS energy threshold, whereas the truncation error stays almost constant until a threshold of about 100 eV. Below 100 eV, the error rises almost linearly to 0.05 eV at a RVS threshold of 50 eV. For thresholds smaller than 50 eV, the truncation error increases fast. For PSBT⁺, the RVS error approaches the general CC2 uncertainty of 0.3 eV at an energy threshold of 20 eV. The increased computational efficiency for the above mentioned thresholds is very promising. At a threshold of 100 eV, we obtain a speed-up factor of 3.5 with a RVS error of 0.01 eV. At a threshold of 50 eV, we obtain a speed-up factor of 6 with an error of 0.05 eV.

Figure 6.

The computing time (in CPU hours) and the error of the first singlet excitation energy of PSBT⁺ (in eV) as a function of the energy threshold (in eV) used in the reduction of the virtual space. The TZVP basis set was employed.

Limitations

Excitation energies are energy differences, profit from error cancellation, and are thus less liable to certain errors than absolute energies and properties derived from these. The RVS approach is thus likely to be less successful in calculating absolute energies and absolute energy derivatives. It is an open question whether the RVS approach leads to significant errors in geometry optimizations and excited state properties but this is beyond the scope of the present work. However, the oscillator strengths calculated at an energy threshold of 50 eV show only minor deviations from those calculated using the full orbital space (see supporting information). This is a promising result concerning applications of the RVS approach to excited state properties.

Size-intensivity is not guaranteed by the RVS approach. However, in the calculation of excitation energies, especially for biological systems, this can be considered a minor problem. The errors introduced by the RVS approach are much smaller than the error bars introduced by the choice of method. The errors discussed for excited states of biological systems are generally larger than the 1 kcal ∕ mol chemical accuracy.

The present approach does not alter the scaling of the method. The number of basis-functions is not reduced, and the number of integrals resulting from these is not reduced either. The cost reduction results from the reduced size of occupied-virtual molecular orbital matrices, which in the end reduces the prefactor of the method. In the case of CC2, the scaling with the number of basis functions N is N⁵, with and without the RVS approach.

The lowest excited states are well described using the RVS approach, and these are the states relevant in biological systems. For higher excited states and excitations without valence character, higher lying orbitals will be more relevant and the lowest possible RVS threshold will be higher in energy. Further studies are necessary to judge the transferability of the method to high-lying non-valence excited states, but this is beyond the scope of this work since high-lying excited states are a general challenge to ab initio methods.⁵

REDUCED-VIRTUAL-SPACE APPROACH FOR EMBEDDED SYSTEMS

Embedded systems

The RVS approach renders excited state studies of biochromophores in their protein environment feasible and fully quantum mechanical treatments become a realistic alternative to QM∕MM approaches.²⁹ The challenge of studying chromophores in a protein environment is to obtain the correct treatment of the chromophore and to consider the polarization of the protein due to the excitation of the chromophore.⁵⁰ An accurate treatment of polarization effects necessitates a sophisticated modeling including through-shell interactions. Using our RVS approach, the protein model and the chromophore are treated at quantum mechanical level. The excitation energies are obtained without creating a bias between the chromophore and its surroundings, where the coupling region can introduce a significant source of errors.

High-lying orbitals are dispensable for the description of excitations in the studied isolated chromophores, and thus expected to have a similar significance for the chromophore embedded in its native protein surroundings. The excitation energies of the surrounding protein fragments are much higher in energy than those of the retinal-chromophore. Thus, a smaller threshold can be used for the surrounding protein provided that the corresponding orbitals can be identified. The orbital localization method suggested by Ziolkowski et al. could be used to identify the occupied and virtual orbitals that are of relevance for the lowest excited states of the chromophore,⁵¹ whereas a larger fraction of the virtual orbitals located on the surroundings could be omitted in the excited state calculation. Such a computational approach would make ab initio electron correlation calculations on even larger embedded systems computationally feasible.

The RVS approach is thus a powerful alternative to QM∕MM approaches. Faster CC2 methods, such as the scaled-opposite-spin CC2 method,⁵² which can be made to scale as N⁴ with number of basis functions N, can be combined with the RVS approach to further increase efficiency and to treat even larger systems. The RVS approach is not limited to CC2 calculations but can also be used at more accurate correlation levels, in the second-order algebraic diagrammatic construction approximation (ADC(2)),⁵³ and also in TDDFT calculations as long as the uncertainty in the electron correlation treatment is larger than the RVS truncation error.

Retinal embedded in a rhodopsin environment

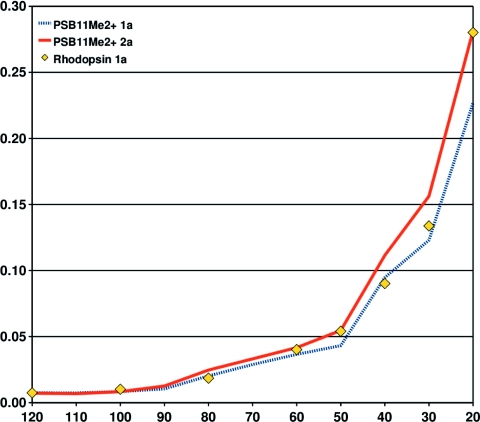
We demonstrate the applicability of the RVS approach on biochromophores embedded in the protein with CC2∕TZVP calculations on a rhodopsin model consisting of 165 atoms. The central question is whether the RVS truncation error determined for the isolated chromophore applies for the chromophore within the protein environment. To show this, we have calculated the lowest excitation energy of our rhodopsin model using several RVS energy thresholds from 120 eV to 20 eV. The truncation errors for the protein and the isolated chromophores are compared in Fig. 7.

Figure 7.

The relative error (in eV) of the first singlet excitation energy of ${\mathrm{PSB}11\mathrm{Me}}_2^{+}$ in the gas phase and of the rhodopsin model as a function of the energy threshold (in eV) used in the reduction of the virtual space. It is assumed that the excitation energy error for the rhodopsin and retinal states are identical at a RVS threshold of 120 eV. The TZVP basis set was employed.

Figure 7 shows that the RVS truncation errors of the protein and the isolated chromophores depict an almost identical growth below 120 eV. Assuming that the rhodopsin and ${\mathrm{PSB}11\mathrm{Me}}_2^{+}$ RVS truncation errors are identical at 120 eV, the figure shows that the rhodopsin RVS error for the first singlet excitation energy lies between the RVS errors for the first and second singlet excitation energies of ${\mathrm{PSB}11\mathrm{Me}}_2^{+}$ . This is not unexpected, as the first excitation energy of rhodopsin is higher than that of the isolated chromophore. The first excited state of rhodopsin is a mixture of the two lowest excited states of the retinal chromophore in the gas phase.

For a RVS energy threshold of 60 eV, the truncation error is below 0.05 eV, whereas a RVS energy threshold of 40 eV yields a truncation error of less than 0.10 eV. This uncertainty is smaller than the errors introduced by limited feasibility in basis-set size and below the errors introduced by QM∕MM separation schemes.²⁹ In fact, our RVS approach allows for the first time an ab initio estimate of the errors introduced by QM∕MM separation schemes in large systems.

The RVS approach allows extrapolation of the excitation energies to the limit of full virtual space. Accurate extrapolated values can be obtained by subtracting the RVS error of the isolated chromophore from the excitation energy of the protein. Figure 7 shows that such an extrapolation scheme works well even for RVS energy thresholds as low as 20 eV.

Comparison to experiment

Our rhodopsin model yields an extrapolated CC2 excitation energy of 2.92 eV, which lies close to the experimental value of 2.99 eV.⁵⁴ The non-extrapolated result at a RVS threshold of 120 eV is 2.93 eV. A QM∕MM calculation with CC2∕TZVPP employed for the QM part yielded 2.90 eV (Ref. ⁵⁵) in close agreement with our result. The comparison of the above RVS and QM∕MM results does not allow a direct estimation of the errors introduced by the QM∕MM separation, since the employed models of the protein environment are not identical. However, the small deviation between the two approaches suggests that errors are far below the standard deviation of the CC2 method. Our results thus confirm the choice of the QM∕MM separation in Ref. 55.

The CC2∕TZVP value of 2.17 eV obtained for the chromophore in the gas phase is only 0.14 eV larger than the corresponding experimental value.⁵⁶ One would thus expect a similar overestimation for the excitation energy in the protein. However, the computed value for the protein environment lies 0.07 eV below the experimental value. Possible reasons for this might be that the protein environment must be further extended or that long-range interactions between the protein environment and the chromophore are not properly described. The CC2 results for the gas-phase and the protein environment lie close to the experimental value and well within the statistical error bars of the CC2 method. A systematic improvement within these error bars is not impossible but demands further assumptions.

CONCLUSIONS

We assess and carefully benchmark the reduced virtual space approach for CC2 excitation energies of biochromophores. This approach leads to a large speed up of the calculations, while its error may be kept smaller than the expected deviation of CC2 excitation energies from experimental values and within the range of the basis-set truncation error. For isolated biochromophores, freezing virtual orbitals with energies larger than 50 eV introduces errors below 0.15 eV in the CC2 excitation energies. For most chromophores in this study, the error is even below 0.05 eV. The speed up in computing time is a factor of 6 in the case of retinal, and it strongly increases with basis-set size. The reduced virtual space approach thus makes it possible to use sufficiently large basis sets in the CC2 calculation, by reducing the prefactor of the N⁵ scaling with basis-set size N.

The rhodopsin protein environment is efficiently treated using the (RVS) approach. The energy thresholds and errors determined on isolated chromophores can be used in the rhodopsin protein environment alike. We demonstrate this using a 165 atom rhodopsin model, for which we determine the lowest excitation energy with varying truncation energy thresholds. The RVS errors in gas-phase and protein are almost identical, and the gas-phase RVS errors may be used to extrapolate the CC2 excitation energies in the protein. The increase in efficiency and the controlled introduction of errors makes the RVS approach a powerful ab initio alternative to QM∕MM methods for the description of proteins. Future studies will show whether these findings can be confirmed in other proteins as well.

The present RVS benchmark of CC2 excitation energies is only a first step in exploring possible applications of the RVS approach. It can be extended to different excited-state coupled-cluster or configuration-interaction methods, or even to time-dependent density functional theory. Its applicability in geometry optimizations, excited state dynamics, and in studies of other properties needs to be explored. The simple approach used here to reduce the virtual space by an energy threshold is not the first approach to do this, and one with little sophistication. We hope that the applicability and efficiency demonstrated here will stimulate the development of more sophisticated models for virtual space reduction and encourage the use in examples that have so far been limited to QM∕MM treatments.