Simulation via direct computation of partition functions

Abstract

In this paper, we demonstrate the efficiency of simulations via direct computation of the partition function under various macroscopic conditions, such as different temperatures or volumes. The method can compute partition functions by flattening histograms, through, for example, the Wang-Landau recursive scheme, outside the energy space. This method offers a more general and flexible framework for handling various types of ensembles, especially ones in which computation of the density of states is not convenient. It can be easily scaled to large systems, and it is flexible in incorporating Monte Carlo cluster algorithms or molecular dynamics. High efficiency is shown in simulating large Ising models, in finding ground states of simple protein models, and in studying the liquid-vapor phase transition of a simple fluid. The method is very simple to implement and we expect it to be efficient in studying complex systems with rugged energy landscapes, e.g., biological macromolecules.

In recent years, methods for Monte Carlo (MC) simulation have been dramatically improved over the traditional Metropolis algorithm [1]. A large class of MC methods are those based on the flat energy histogram, such as the multi-canonical ensemble method [2], the entropic sampling method [3], the density of states (DOS) method [4], and the statistical temperature method [5]. In this study, we demonstrate the efficiency of an alternative sampling method, which simultaneously and directly computes the partition function at various values of a certain macroscopic variable, e.g., T or V. Since one does not know the partition function in advance, the partition function at different values of a chosen variable is initially set to unity and continuously modified throughout the simulation until convergence.

We first demonstrate the case of sampling based on a number of discrete values of temperature. In this case, a number of sampling temperatures are set over the temperature range of interest. Similar to the expanded ensemble method or the simulated tempering method [6], two types of MC moves are used: an energy move under a fixed temperature and a temperature move under a fixed energy. Before each MC step, a fixed probability is used to determine which type of move the system takes. For the energy move, the Metropolis algorithm is performed at the present (reciprocal) temperature β. For the temperature move, another temperature β′ is randomly chosen, and the following acceptance probability is used to accept the move:

$$\text{Acc}(\beta \to \beta \prime )=\text{min}\left\{1,\frac{\text{exp}(-\beta \prime E)/{\tilde{Z}}_{\beta \prime }}{\text{exp}(-\beta E)/{\tilde{Z}}_{\beta }}\right\}.$$ (1)

Here E is the present energy; Z̃_β and Z̃_β′, are the values of the estimated partition function at temperatures β and β′, respectively. The partition function is “estimated” because it is unknown in advance. After each MC step, the estimated partition function at the present temperature is multiplied by a factor f> 1 [4]. This can be written as,

$$\text{ln}{\tilde{Z}}_{\beta }\to \text{ln}{\tilde{Z}}_{\beta }+\text{ln}f.$$ (2)

Similar to the WL algorithm, it is shown that by repeating the above procedure for a fixed f, the estimated partition function can eventually converge within certain fluctuations proportional to $\sqrt{\text{ln}f}$ [7,8]. Moreover, due to the frequently modified acceptance probability, the additional errors in the estimated partition function (due to violation of the detailed balance condition) are larger in a stage with a larger ln f. Therefore, the value of ln f should be gradually decreased to improve the accuracy of the estimated partition function. In practice, the whole simulation is separated into several stages, each marked by a different value of ln f [4]. In passing from one stage to the next, ln f is modified to (ln f)/n [4]. We use $n=\sqrt{10}$ in this study so that ln f is decreased by an order of magnitude every two stages (the procedure for optimizing the ln f of each intermediate stage will be given in a forthcoming presentation [8]). At the end of the simulation, ln f is reduced to a tiny number such that violation of the detailed balance condition is negligible. For each f stage, if the simulation runs for sufficient number of steps, each temperature receives on average an equal number of visits, i.e., a flat temperature histogram is achieved. Here the term “temperature histogram” refers to the number of visits to each discrete temperature instead of to a temperature interval. The simulation is allowed to enter the next f stage when the histogram fluctuation falls below a cutoff percentage [4].

An alternative approach is to fix the number of simulation steps by $C/\sqrt{\text{ln}f}$ for an f stage. It can be shown that the two approaches are equivalent for sufficiently long simulations [8]. The constant C can be estimated from a few initial f stages. The second approach ensures a better convergence for a stage with a smaller ln f.

In principle, any set of sampling temperatures of interest can be used. However, two consecutive temperatures must be close enough to allow sufficiently frequent temperature transitions. This requires a certain overlap between the energy distributions of two neighboring temperatures. This condition can be expressed as $\mathbf{\Delta }T\sim \sqrt{\langle \mathbf{\Delta }{E}^2\rangle }/C_V\sim T/\sqrt{C_V}$, where C_V and $\sqrt{\langle \mathbf{\Delta }{E}^2\rangle }$ are the heat capacity and energy fluctuation at temperature T, respectively. Therefore, the number of sampling temperatures is roughly proportional to $\sqrt{N}$ (except around the critical region), where N is the system size. This feature is advantageous for larger systems, which is also a merit of the parallel tempering method [9], but the latter does not deliver the partition function quickly.

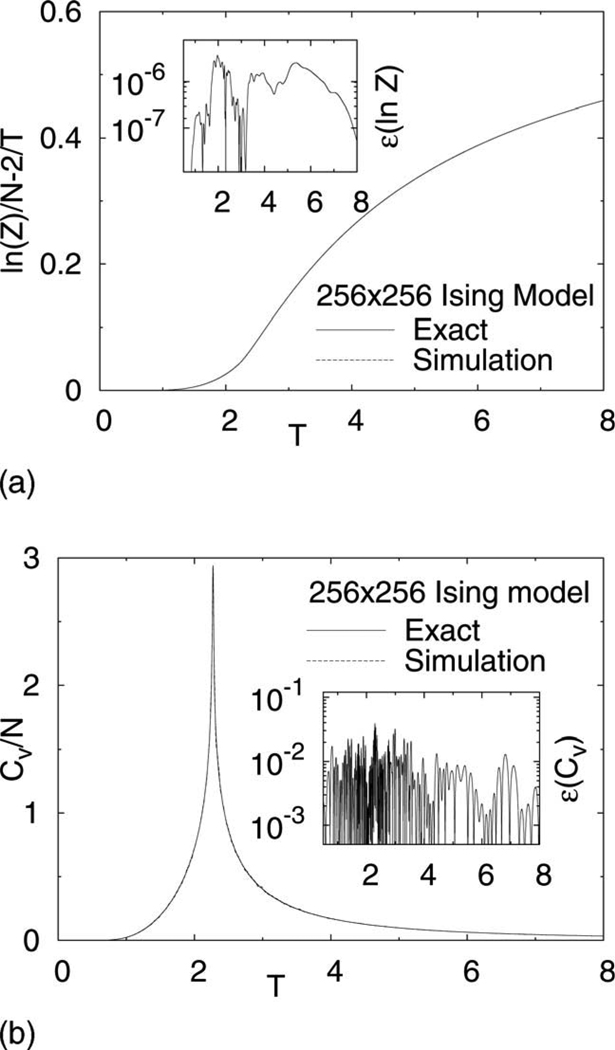
The algorithm was first tested on the 256×256 square lattice Ising model. A wide temperature range, T ∈ [0,8], was simulated in a single simulation. Since the sampling temperature increment of an efficient simulation should be inversely related to the heat capacity as discussed above (nonuniform temperature setup is known to be advantageous [10]), for this large system, sampling temperatures were distributed based on the roughly estimated heat capacity (e.g., that from simulation of a smaller system). Accordingly, the entire temperature range was partitioned into 13 subranges. Sampling temperatures were linearly distributed inside each subrange with a different increment. The temperature subranges and their increments were (0.1, 1.0|0.1), (1.0, 1.8|0.04), (1.8, 2.0|0.02), (2.0, 2.2|0.005), (2.2, 2.25|0.0025), (2.25, 2.3|0.002), (2.3, 2.35|0.005), (2.35, 2.5|0.01), (2.5, 2.7|0.02), (2.7, 3.6|0.05), (3.6, 5.0|0.07), (5.0, 6.0|0.1), and (6.0, 8.0|0.2). Here the notation for each subrange is (beginning temperature, ending temperature | increment). In total, there were 218 sampling temperatures. Each time the probability of choosing temperature over energy moves was 0.1% (this number should be larger for smaller systems). The modification factor ln f was decreased from 1.0 to 10⁻⁹, the number of MC steps for stage f was $100/\sqrt{\text{ln}f}$ sweeps, so the whole simulation took 7.2×10⁶ sweeps. Thermodynamic quantities at temperatures other than the sampled temperatures can be calculated using the multiple histogram method [11]. Histograms from the last f stage were used. The exact results of the Ising model were also calculated using the method by Ferdinand and Fisher [12]. The relative errors of the partition function, energy, entropy, and heat capacity were no larger than 0.000 64%, 0.071%, 1.1%, and 3.9%, respectively. Figure 1 shows the results for the partition function and heat capacity. For comparison, the WL algorithm was applied to the same system using 15 independent simulations, and the maximum relative errors of the free energy, energy, entropy, and heat capacity were 0.0008%, 0.09%, 1.2%, and 4.5%, respectively [4]. The simulation cost of the WL algorithm was 6.1×10⁶ sweeps [4]. However, the acceptance probabilities for energy moves can be precalculated to avoid expensive exponential computation in our case. The above simulation was finished in 10 h on a single Intel Xeon processor (2.8 GHz).

FIG. 1.

Results for the 256×256 Ising model. (a) shows the partition function as a function of temperature. The curve is shown for ln Z per spin with the contribution of the two ground states subtracted. (b) shows the heat capacity per spin as a function of temperature. The relative errors are shown in the insets for both panels.

Next, we introduce a variation of the above algorithm that tries to find the transition temperature automatically and to spend more effort sampling around that. This feature is desirable if the transition temperature is not roughly estimated in advance. This can be achieved by using a modified updating scheme, to let the system visit each temperature with a different frequency ζ_β. In the acceptance probability Eq. (1), the values Z̃_β and Z̃_β′ of the estimated partition function are replaced by Z̃_β/ζ_β and Z̃_β′/ζ_β′, respectively, whereas the updating scheme Eq. (2) is changed to ln Z̃_β→ln Z̃_β+ln f/ζ_β. The temperature histogram is constructed in such a way that the total number of visits to a particular temperature β is now divided by its associated frequency ζ_β. To focus sampling around the transition temperature, the frequency ζ_β can be specified as an increasing function of the heat capacity. Since the values of the heat capacity are unknown in advance, they are updated at the end of each f stage and are used in the next stage. The modified algorithm was tested on the same 256×256 Ising system. The frequency ζ_β at temperature β was set as the square of the heat capacity per spin. Sampling temperatures were uniformly distributed over the whole range T ∈ [0,8], with a fixed increment ΔT=0.002. The probability of choosing temperature over energy moves was raised to 10%. The value of ln f was lowered from 1.0 to $\sqrt{10}\times {10}^{-9}$. The simulation was kept running at each f stage until the temperature histogram fluctuation was lowered below 50%. The last stage was purposely extended to 5.0×10⁶ MC sweeps to accumulate more statistical data. Totally, 9.8×10⁶ sweeps were used. The relative errors of the free energy, the energy, and the heat capacity were no larger than 0.000 45%, 0.055%, and 4.0%, respectively.

It is also possible to realize rejection-free, and hence more efficient, temperature transitions. First, the relative probability at each temperature β_i, P_i=exp(−β_iE)/Z̃_βi, is calculated for the present energy E. Next, the accumulated probability for each temperature, Q_i=∑_j≤iP_j/∑_jP_j, is also calculated, to form a series of brackets, [Q_i−1,Q_i), i=1,2,…, with Q₀=0. If a uniform random number r ∈ [0, 1) falls in the ith bracket, β_i will be chosen as the next temperature. This type of temperature move is analogous to the heat bath algorithm for energy moves [13]. It is relatively expensive because of the many exponential calculations. However, this expense is negligible if a more expensive non-Metropolis algorithm is used for the energy move. As an example, the Swendsen-Wang cluster algorithm [14] was used as the energy move on large two-dimensional Ising models. To improve the efficiency, the energy and temperature moves were merged in such a way that each energy move was immediately followed by a rejection-free temperature move. Simulations were performed on critical temperature windows estimated by |T − T_c|~ L^−ν. Here ν=1 is the critical exponent, and T_c is the critical temperature. About 10–20 sampling temperatures were distributed in each window. Parameters and results are listed in Table I. The efficiency is clear in terms of the number of simulation steps required to reach the desired accuracy.

TABLE I.

Results for L×L Ising models using the Swendsen-Wang cluster algorithm [14] as the energy move. Maximum relative errors were calculated by assuming the errors at the left boundary to be zeros. Here, T₋ and T₊ define the temperature window, and ΔT defines the increment.

L	(T−,T+ |ΔT)	MC steps	ε(ln Z)	ε(CV)
64	(2.0, 2.9|0.1)	0.7×106	4.0×10−6	1.6%
128	(2.1, 2.6|0.05)	2.0×106	1.2×10−6	1.1%
256	(2.2, 2.42|0.02)	2.9×106	3.6×10−7	1.4%
512	(2.2, 2.34|0.01)	3.1×106	1.0×10−7	1.0%
1024	(2.24, 2.30|0.005)	3.1×106	6.9×10−8	1.4%

Molecular dynamics (MD) can be used as an energy move as well. In this case, the probability of taking temperature over energy moves is 50%. Constant-temperature MD (a length-5 Nosé-Hoover chain [15] with force scaling [16]) is used as a (potential-)energy move [5]. The thermostat temperature T₀ was set to be 0.5. The simulations were used to find ground states of AB protein models [17]. We were able to find all known ground states [5,18–20], and several new ones with lower energies. Table II lists the new ground-state energies, and Fig. 2 shows the corresponding configurations. Comparing our results (for model I [17]) with those from the statistical temperature method [5], the new ground state of the two-dimensional (2D) 55mer, Fig. 2(a), has a different topology in the two inner strands; the new ground state of the three-dimensional (3D) 55mer, Fig. 2(c), has a more compact configuration. In both cases, our ground states have black-black clusters (strong attractions) that are more favorably packed with no exposed black beads.

TABLE II.

Lowest energies of AB proteins with Fibonacci sequences. Results were compared with those from the annealing contour Monte Carlo (ACMC) [18], the energy landscape paving (ELP) [19], the conformational space annealing (CSA) [20], and the statistical temperature molecular dynamics (STMD) [5].

Protein	ACMC	ELP	CSA	STMD	This work
2D, 55mer, model I	−18.7407		−18.9110	−18.9202	−19.2570
3D, 55mer, model I		−42.438	−42.3418	−42.5789	−44.8765
3D, 34mer, model II	−94.0431	−92.746	−97.7321		−98.3571
3D, 55mer, model II	−154.5050	−172.696	−173.9803		−178.1339

FIG. 2.

Lowest-energy configurations of AB proteins (black, A; white, B). (a) 2D, 55mer, model I. (b) 3D, 55mer, model I. (c) 3D, 34mer, model II. (d) 3D, 55mer, model II.

The WL-type algorithms have also been applied to Lennard-Jones simple liquid systems [21], for computing the multidimensional DOS. Here, we demonstrate that the simulation can be carried out using volume, instead of temperature, as the sampling variable, where the temperature and particle number are held constant. Each volume move can be implemented as a change of the scale of the system. Therefore, it is convenient to adopt reduced coordinates $\mathbf{s}=\mathbf{r}/\sqrt[3]{V}$. The partition function is factorized to the ideal gas part, Z_ig, and a potential part, Z_V, i.e., Z=Z_igZ_V, where Z_V ≡ (1/V^N) ∫ dr^N exp[−βU(r^N)]=∫ ds^N exp[−βU(s^N;V)]. Thus, we can dynamically compute the potential part of the partition function Z_V, instead of Z, in the acceptance probability Eq. (1). This method was used to study the liquid-vapor transition of a 108-particle Lennard-Jones system with half-box truncation and periodic boundary conditions. After the simulation, the Helmholtz free energy can be obtained through F=F_ig − ln Z_V/β, and the Gibbs free energy profile under pressure p can be derived through G=F+pV, at each sampling volume (or density). For each simulation under a fixed temperature, the transition pressure was first determined by equalizing the two minima on the Gibbs free energy curve; the values of liquid density ρ₊ and vapor density ρ₋ were also determined correspondingly. Simulations were performed under different temperatures T ∈ [0.85, 1.20], with increment ΔT=0.01. To accurately determine the position of coexistence densities, the sampling density increments Δρ were 0.002 and 0.0005 around the roughly estimated liquid and vapor coexistence densities, respectively, whereas the transition region was filled with a larger increment Δρ=0.005. Typically, about 300 volume sampling points were used in a single simulation. The computed vapor-liquid coexistence curve is shown in Fig. 3. The relation ρ_±−ρ_c~a|T_c−T|±b|T_c−T|^β (the critical exponent β=0.3258 [22]) was used to extrapolate the critical temperature T_c and the critical density ρ_c based on the corresponding power-law regions. The estimated critical temperature T_c and critical density ρ_c were 1.304 and 0.315, respectively. The results for this small system are consistent with those of the infinite system (e.g., T_c=1.3123 and ρ_c=0.3174 [23]).

FIG. 3.

Phase diagram for the 108-particle Lennard-Jones system. The empty circles are results of simulations, the solid line is from power-law fitting, and the solid circle represents the estimated critical point for this small system.

In summary, we have demonstrated the efficiency of simulations via direct computation of the partition function. The method has a range of advantages. An important one is in the ground-state-oriented applications, such as in the protein folding problem, in which case the WL algorithm suffers from lack of efficient sampling around the ground state. This is because the location of the ground state, and hence the proper energy range over which the sampling should be performed, is not known in advance. The efficiency of the WL algorithm will be further reduced if the energy landscape in the last energy bin (near the ground state) is continuous and rugged [24]. By contrast, sampling in the temperature space does not require a priori information about the ground state and can sample the vicinity of the ground state with desired accuracy.

Our method can be viewed as a generalization of the original DOS-based WL algorithm [4] since the DOS is indeed the partition function of the microcanonical ensemble. In the case of canonical versus microcanonical ensembles, for example, the partition functions are related by an expression $Z(N,V,T)={\displaystyle {\int }_0^{\infty }}g(N,V,E)\text{exp}(-\beta E)\mathit{\text{dE}}$ where Z(N,V,T) is the canonical partition function and g(N,V,E) is the density of states or microcanonical partition function. It is easy to see that, in the canonical ensemble, one can fix any pair of thermodynamic parameters and change the third one for sampling, while in the microcanonical ensemble, it is hard to do so, e.g., one cannot fix N and E to change V. This indicates that there are inherent advantages in performing simulations (such as flattening the histogram) outside the energy space. We thus expect that the general framework to be more flexible in handling other types of ensembles, especially the ones in which computation of the DOS is not convenient.