Improving the power of chronic disease surveillance by incorporating residential history

Abstract

We present a global test for disease clustering with power to identify disturbances from the null population distribution which accounts for the lag time between the date of exposure and the date of diagnosis. Location at diagnosis is often used as a surrogate for the location of exposure, however, the causative exposure could have occurred at a previous address in a case’s residential history. We incorporate models for the incubation distribution of a disease to weight each address in the residential history by the corresponding probability of the exposure occurring at that address. We then introduce a test statistic which uses these incubation-weighted addresses to test for a difference between the spatial distribution of the cases and the spatial distribution of the controls, or the background population. We follow the construction of the M statistic to evaluate the significance of these new distance distributions. Our results show that gains in detection power when residential history is accounted for are of such a degree that it might make the qualitative difference between the presence of spatial clustering being detected or not, thus making a strong argument for the inclusion of residential history in the analysis of such data.

1. Introduction

Our goal is to study the effect long incubation periods have on the power of a test for global clustering, as defined in [1]. Tests for global clustering attempt to detect the presence of clustering process throughout a study region, without necessarily attempting to locate or identify the actual clusters. For several examples of tests for global clustering, see [2, 3, 4, 5, 6, 7, 8, 9]. Cluster detection techniques have been criticized [10] and, in 1990, researchers claimed that there had been no cancer clusters found in the prior 22 years [11]. But, if one accepts the fact that cancers have non-auto-induced causes, whether they be environmental or infectious, then some form of clustering among cases should be expected. Indeed, the National Cancer Institute cancer mortality maps [12] show that several cancers have a regional prevalence distribution that is clearly nonuniform. So it is puzzling why more clusters have not been discovered on a smaller geographic scale. In this paper, we suggest that one possible reason current statistical techniques do not provide adequate evidence of cancer clusters is that lengthy incubation periods combined with residential mobility render addresses at diagnosis almost non-informative as to where a disease causing exposure may have occurred. We propose a test for global clustering that uses more informative address histories, which has more power to detect the presence of possible disease clustering.

Disease clusters have been found in the past, and their detection has led to informative results, especially regarding their etiologic explanations. The most famous of these has to be the work by John Snow and his famous cholera study [13], but others have been found such as the anthrax cluster located downwind of a Russian weapons factory [14]. The investigators’ brilliant use of the correct addresses accounted for the ability to identify the most likely cause of exposure, despite the official governmental pronouncements to the contrary.

What these two successful cluster studies share is the immediacy of the disease; there is no significant lag between the exposure and disease onset. When this lag time is extended, as with some chronic diseases, cancers for example, the linkage may become more tenuous. The substantial amount of time between a possible exposure and subsequent diagnosis, combined with a mobile population, will mask the true spatial relationship between cases and exposure. This is why we must incorporate the incubation period of the disease in our calculations.

That is not to say that an anticipated effect cannot be studied in a prospective manner, no matter how long the incubation period. For example, the survivors of the Hiroshima bombing have been followed and their subsequent health studied [15]. So, as happened, an increase in the incidence of leukemia was observed over several years; an association that one would not attribute to chance; as defined in [10].

Another example in which a cancer’s long incubation period might have affected the detection of an informative cluster is the group of young women with adenocarcinoma of the vagina, in Boston, Massachusetts between 1966 and 1969[16]. Had the investigators just focused on the cases presenting with disease and their recent exposures, the true relationship may never have been found.

As most spatio-temporal analyses are performed to find a link between exposure location and disease, typical surveillance data involve a time component, usually date of diagnosis, together with a spatial component; usually some indicator of residence at the time of diagnosis [9, 17]. However, critical information regarding the relationship between location and disease would be the location where the exposure occurred, which is not always collected, analyzed, known, or even considered. If we are interested in studying the spatial patterns of a disease such as leukemia or breast cancer, the current locations of the cases could be irrelevant to our study. According to census estimates, the median duration of residence for Americans is 4.7 years. For children under 18 years old, the median duration of residence is 3.8 years [18]. If there is a substantial lag between the exposure of interest and the detection of this disease, then by using the address at diagnosis the spatial relationship is usually lost. Recommendations published by the Mortality and Morbidity Weekly Report remind investigators of the importance of accounting for the incubation period of a disease when investigating clusters[19]. Following a meeting of national experts with backgrounds in statistics, epidemiology and geography the council agreed that residential history information is a crucial aspect in the analysis of cancer registry data [20, 21].

For example, the incubation period associated with mesothelioma has been estimated at almost 40 years[22], and 20 years for breast cancer [23], thus those individuals who are diagnosed with this disease, are likely to have been exposed decades prior to diagnosis. The effects of this are two-fold. First, a large proportion of individuals exposed to asbestos, for example, are likely to have moved to other areas, adding additional cases to the background rate and thus attenuating the contrast, and making subsequent signal detection that much more difficult. Second, those cases currently living at the location of interest, are perhaps unlikely to have been living there when their cancer causing exposure occurred.

We propose a novel method that summarizes the spatial and temporal distributions of a group diagnosed with a chronic disease, and compares that distribution to the distribution of controls. If the cases are distributed differently from the controls then an explanation of this discrepancy is necessary. We seek to evaluate the relationships between cases using a measure of distance between them that incorporates information specific to the disease of interest. The additional information which we combine with the physical distances between cases is the incubation distribution of the disease. The incubation distribution is the probability distribution of the time between exposure and diagnosis. This in turn yields information regarding the spatial relationships between the cases. We extend the M statistic [8] to evaluate the significance of this new “distance” distribution, building on the work of Sartwell, Armenian and Lillienfeld[24, 25, 26] to define and describe the incubation distributions. This method attempts to answer the question, “Are the spatial distributions of the cases and the controls the same?” This question can arise from evidence-based reports from concerned citizens, or via routine collection and analysis of disease surveillance data. If the the spatial distributions are not the same, then one can attempt to identify potential clusters. We envision this method being used as a first step in the identification of a chronic disease cluster.

While residential history collection may not currently be the norm in disease surveillance, with the adoption of person based surveillance systems, and electronic health records, this information will be compiled and more widely accessible in the near future. We feel it is important to develop methods which utilize this information, both to lend weight to the importance of its collection, and to be able to use this important information once collected.

2. The Incubation Distribution

The lognormal incubation distribution model has been tested for non-infectious, chronic diseases by Armenian and Lillienfeld[26] who study incubation periods associated with six neoplastic diseases. They find that the incubation periods for the neoplastic diseases also closely follow the lognormal distribution. But, because there is no obvious “infection” time involved with these chronic diseases, the authors define the incubation period as, “the interval between exposure to an etiologic factor and the onset of symptoms or disease detection.” In this paper, we refer to time from exposure to diagnosis as the incubation period, though because this is a simulation study, one could easily replace ”address at diagnosis” with ”address of symptom onset” and arrive at the same conclusions. Also, to focus our discussion we refer to this first exposure as the time of the “disease causing exposure.”

In addition to how to define the start of the incubation period, another difference between an infectious disease and a chronic disease, is the question of a possible dose-response relationship between the intensity of the exposure and the outcome. In [27], an early study of skin tumors in mice induced by UV light exposure, the lognormally distributed incubation period was observed, with no systematic variability due to either intensity or frequency of dose, or age of subject. Lack of a dose-response relationship is also evident in the aftermath of the atomic bomb drops in Hiroshima. While incidence of leukemia was influenced by individuals’ proximity to the bomb site, there was no significant difference between the incubation periods between distances considered close enough to the blast to be “exposed” [15]. Other studies have shown similar relationships between the intensity of exposure, the incidence and the incubation period [28, 29]. More recently, researchers show that while there is a strong positive dose-response between baseline alcohol intake and the risk of breast cancer, including most recent alcohol intake diminished the relationship [23], which may indicate the lack of an affect of cumulative exposure. Thus, for the remainder of this work we assume that given a cancer is diagnosed, reversing time and looking back to determine when the exposure occurred should not be affected by the distance from the source, or intensity of the exposure.

3. Methods

3.1. Complete Residential History

To truly detect if cases of a disease cluster together, we need to measure the spatial distribution of the cases at the moment of infection, or in the case of chronic disease, when the disease causing exposure occurred. We can then compare this spatial distribution to the distribution of a suitably defined control group, to look for differences in the two distributions. Unfortunately, in practice we fall short in two ways: (i) we do not know when the disease causing exposure occurred, and (ii) as a result, we do not measure the spatial distribution accurately.

Suppose our data consist of N individuals, with each individual having a residential history: person i lived at location A_ik for a duration of P_ik, k in 1, …, n_i and i in 1, …, N. We scale the durations such that Σ_k P_ik = 1, and consider P_ik as the proportion of time person i is living at location A_ik. The set 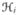= {(A_i1, P_i1), (A_i2, P_i2), …, (A_ini, P_ini)} is the complete residential history of individual i.

To overcome the problem of not knowing which address is the informative location, we can weight each known addresses by the relative probability that it is the address of exposure. A naive approach might be to use a uniform prior; i.e. weight each address by the length of time resided at that address, given above as P_ik. A more refined approach, which we suggest, is to define each weight as the probability of that address being the address of exposure. We use the incubation distribution to estimate these probabilities. With this approach, each address for a given case has attached to it, the probability that the disease causing exposure occurred at that location. Let C_ik be the incubation based weight, which we can calculate as C_ik =∫_Aikf(t)dt, k = 1, …, n_i, where f(·) is the density function for the estimated incubation distribution, and integrating over A_ik is to be taken as the integral over the period of time individual i lived at address A_ik. Following the work of Sartwell, Armenian, and Lillienfeld [25, 26, 30], we use the lognormal distribution to model the incubation distribution.

For each individual in our study population, we have a set of addresses, and each address has an associated weight. We use these addresses and weights to summarize the difference between the spatial locations of the cases and the controls, by examining the distribution of the distances between the cases and the distribution of the distances between the controls. To test the difference between the spatial distributions of the cases and the controls, we use an adapted form of the M-statistic [8]. The M-statistic is a nonparametric test that quantifies the difference between two sets of locations by examining the differences of the distributions of the distances between those locations. The distances between the locations are called the interpoint distances, and the distribution of these distances is the interpoint distance distribution. The M-statistic has typically been used to summarize differences based on Euclidean distances, but in this work, we generalize this statistic to handle a new distance metric.

Specific to chronic illnesses, such as leukemia or breast cancer, we formulate a distance metric that has power to detect a point-source environmental exposure. This point-source could be a contaminated well (as in the cholera outbreak), or a source of aerosolized release (as in the anthrax cluster). In those settings, we are concerned with the spatial proximity between cases more so than with their temporal proximity. Consider the John Snow Cholera setting: it is informative to know that two people visited the same well, not necessarily that those two people visited at the same (or different) times. If two cases happen to occupy the same residence but at different times, we are still interested in this spatial relationship. For this reason, the metric we choose to consider is the ‘all possible distances’ measure. This metric weights the physical distances between individual’s locations by the time each person spends at each respective address.

We represent this random distance between individuals i and j by the random variable D_ij whose distribution we define as,

$$D_{ij}=\{\begin{array}{ccc}d(A_{i1},A_{j1})& \text{with}\text{probability}& C_{i1}{C}_{j1}\\ d(A_{i1},A_{j2})& \text{with}\text{probability}& C_{i1}{C}_{j2}\\ ⋮& ⋮& \\ d(A_{{in}_i},A_{{jn}_j})& \text{with}\text{probability}& C_{{in}_i}{C}_{{jn}_j},\end{array}$$

where d(X, Y) is the Euclidean distance between locations X and Y. Although we use the Euclidean distance, if the scale of the study region is especially large, other distances such as the Harvesine distance can be used [31]. Summarize this non-negative random variable, D_ij, by constructing its distribution function F_ij (·). The steps of F_ij are at the possible distance values and the step sizes are determined by the probability associated with those values. Thus the cumulative distribution function for the random variable representing all possible distances between individuals i and j is given by,

$$F_{ij}(d)=P(D_{ij}\le d)=\sum _{k,l}{C}_{ik}{C}_{jl}·1(d(A_{ik},A_{jl})\le d),\forall d\ge 0,$$ (1)

where 1(X) is the indicator function, with values 1 if X is true, zero otherwise. Once we calculate each distribution function corresponding to the $\left(\begin{array}{c}N\\ 2\end{array}\right)$ pairs of individuals, we define the overall empirical distribution function for our sample as,

$$\mathbf{F}(d)=\frac{1}{\left(\begin{array}{c}\begin{array}{c}N\\ 2\end{array}\end{array}\right)}\sum _{\left(\begin{array}{c}\begin{array}{c}N\\ 2\end{array}\end{array}\right)}{F}_{ij}(d),\forall d\ge 0$$ (2)

where scaling by $1/\left(\begin{array}{c}N\\ 2\end{array}\right)$ ensures that F(+∞) = 1 and F(·) is thus a proper distribution function.

This summary measure associated with the spatial distribution is not usually invertible (it is translation and rotation invariant) and thus does not uniquely identify the contemporaneous spatial distribution, but it does have advantages: One, a general advantage, is that it is univariate and thus much easier to manipulate and comprehend. Two, it has been shown to be powerful in detecting the presence of clusters[32, 33, 8]. And, three, it lends itself easily to the problem at hand when we actually do not know with certainty which address we wish to consider. The details of the proposed method follows.

3.2. Incomplete Residential History

Consider a situation where individual i has the complete residential history 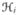, as above, but the data consist of only a subset of these values. Let the subset be ${\mathcal{H}}_i^{\prime }=\{(A_{i1},C_{i1}),(A_{i2},C_{i2}),\dots ,(A_{{im}_i},C_{{im}_i})\}$ where m_i < n_i.

In this situation, the property Σ_kC_ik = 1 no longer holds, instead Σ_kC_ik = p_i, the proportion of the residential history known for individual i. The individual CDFs, F_ij (·), are constructed in the same manner as outlined in Section 3.1, except now F_ij (+∞) = p_i p_j. When we sum across the $\left(\begin{array}{c}N\\ 2\end{array}\right)$ CDFs, the resultant function F is such that F(+∞) = Σ_ij p_i p_j. To obtain a proper empirical CDF (ECDF), the increment of the step function that the missing information would have contributed must be appropriately accounted for.

This missing information is analogous to a censored observation in the survival setting. However, with right censored survival times, the minimum time is known (the time at which the observation is censored) and the maximum likelihood solution, as shown in [34], distributes the observation’s mass equally to all remaining event times greater than the censoring time. Here, in the distance based setting, there is no directional information regarding the missing distances, therefore we distribute the missing distance’s mass equally among all observed distances. Thus, we assume a missing distance is equally likely to be any distance which we observe. In practice, this is achieved by a proper scaling factor applied to F,

$$\mathbf{F}(·)=\frac{{\displaystyle \sum _{\left(\begin{array}{c}N\\ 2\end{array}\right)}}{F}_{ij}(·)}{{\displaystyle \sum _{\left(\begin{array}{c}N\\ 2\end{array}\right)}}{F}_{ij}(+\infty )},$$ (3)

and thus F(·) is now a proper distribution function. In the complete residential history setting, ${\displaystyle \sum _{\left(\begin{array}{c}N\\ 2\end{array}\right)}}{F}_{ij}(+\infty )=\left(\begin{array}{c}N\\ 2\end{array}\right)$. Note that this method of scaling F is not equivalent to scaling each F_ij individually, as we use all observed distances to determine the proper weighting factor.

4. Constructing the two-sample test statistic

Suppose the data consist of the N couplets, ((X₁, G₁), (X₂, G₂), …, (X_N, G_N)), where X_i = {(A_i1, C_i1), (A_i2, C_i2), …, (A_ini, C_ini)} and G_i is a group indicator variable with values, G_i = 1 if subject i is in Group 1 and G_i = 0 if subject i is in Group 2. Let N₁ and N₂ be the number of subjects belonging to Group 1 and Group 2, respectively. The cumulative distribution function corresponding to the distance between individuals i and j is given by F_ij in Equation 1. If there is a relationship between location and disease, then we expect the distribution function of the interpoint distances between the cases to be different from the distribution function of the interpoint distances between the controls.

To compare two distribution functions, we first select a vector d = (d₁, d₂, …, d_m), spanning the range of observed values of the weighted distances between individuals. We then define two vectors, F̂_j (d) = {F̂_j (d₁), F̂_j (d₂), …, F̂_j (d_m)}, j = 1, 2, to construct the test statistic,

$$M_R({\widehat{\mathbf{F}}}_1,{\widehat{\mathbf{F}}}_2)={\left({\widehat{\mathbf{F}}}_1(\mathbf{d})-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right)}^t{S}_R^{-}\left({\widehat{\mathbf{F}}}_1(\mathbf{d})-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right),$$ (4)

where $S_R^{-}$ is the generalized inverse of the estimated covariance matrix for the weighted distances.

Note that (F̂₁ − F̂₂) is indeed a U-statistic[35], and thus will allow us to appeal to the appropriate asymptotic results[36], to define the covariance between F̂₁ and F̂₂ evaluated at any two interpoint distances, d_a, d_b as

$$\widehat{\mathit{Cov}}\left({\widehat{\text{F}}}_1(d_a)-{\widehat{\text{F}}}_2(d_a),{\widehat{\text{F}}}_1(d_b)-{\widehat{\text{F}}}_2(d_b)\right)=\left(\frac{N_1{N}_2}{N_1+N_2}\right)\frac{1}{\left(\begin{array}{c}N\\ 3\end{array}\right)}\sum _{m,n,p}\left({\phi }_1(m,n,p,d_a,d_b)+{\phi }_0(m,n,p,d_a,d_b)\right).$$

Where φ_g(m, n, p, d_a, d_b) =Σ_i,j,k,l(C_mi C_nj C_mk C_pl 1d(X_mi, X_nj) ≤ d_a, d(X_mi, X_pk) ≤ d_b |G_m = G_n = G_p = g).

This test is analogous to a χ² goodness-of-fit test, where the choice of the vector d represents the binning of the data. For a more complete discussion of the bin selection procedure, see [33]. When the interpoint distance distribution of the cases differs from the distribution of the controls, M_R will have larger values. To calculate a p-value, one could rely on the asymptotic theory available from U-statistic theory, or generate the null permutation distribution for M_R using the random labeling hypothesis and randomly switching the case and control status of the subjects in the sample[37].

We also note the simplifying assumptions made in the construction of this test statistic. In this paper a common incubation distribution is considered for each individual. While this assumption may not be ideal in practice, modeling a different incubation distribution for each subject is a straightforward extension, as this distribution just influences the weights assigned to each address. For example, one could parameterize the incubation distribution and introduce personal covariates for each individual. We also assume uniformity of exposure conditions through time. If there is a clustering mechanism, such as a point-source of exposure, then this assumption means that mechanism will be present throughout the study. This assumption will often be satisfied when studying patients diagnosed within a relatively short time of each other. We also note that calendar time does not enter into our model, as each person’s time origin is their time of diagnosis.

4.1. Properties of the test statistic

Incorporating weights into the residential histories through the incubation distribution results in greater power for the M statistic to detect a difference between F₁(·) and F₂(·), than simply using the address at diagnosis.

Proposition 4.1 (Increased weight)

On average, the weighting scheme which accounts for residential history will give more weight to the address of exposure than the method which only uses the address at diagnosis.

Proof

For each case i = 1, …, N₁, let {(A_i1, C_i1), …, (A_ie, C_ie ), …, (A_ini, C_ini)} be the complete residential history, where A_ie is the address of exposure, and C_ie is the corresponding weight given to that address. Note, if the address at diagnosis is in fact the address of exposure, then e = n_i. Considering only the address at diagnosis is equivalent to forcing C_ini = 1.

When considering only the address at diagnosis, the expected weight given to the address at exposure, C_ie, is equal to the probability that the address of exposure is also the address at diagnosis. Let t^* be the time at which the exposure occurred, and t be the duration of residence at the address at diagnosis, A_ini, which we assume follows an exponential distribution, with mean λ. The expectation of the weight given to the address of exposure is then,

$$E[C_{ie}]=E[E[C_{ie}\mid t^{\ast }]]=E_{t^{\ast }}[P(t\ge t^{\ast })]=E_{t^{\ast }}[1-P(t\le t^{\ast })]=1-E_{t^{\ast }}[\frac{1}{\lambda }{e}^{-t^{\ast }/\lambda }]=1-{\int }_0^{\infty }\frac{1}{\lambda }{e}^{-t^{\ast }/\lambda }f(t^{\ast }){dt}^{\ast }.$$

Assuming t^* ~ LogNormal(μ, σ) gives the form of f(t^*), and allows us to evaluate this probability for a given set of parameters, μ and σ. We call this expectation, $E[C_{ie}^{\mathit{DDx}}]$.

Using the residential history weighting scheme outlined above, we can calculate the expected weight given to A_ie, and compare this to $E[C_{ie}^{\mathit{DDx}}]$. Using the residential history method, the expected weight each address is given is defined as the probability that the exposure occurred at that address, E[C_ik] = Pr{A_ik = A_ie}. Thus, under this scheme, E[C_ini] = E_t^*[P (t ≥ t^*)], which is equivalent to the expected weight from the method only incorporating the address at diagnosis. So, if the exposure occurred at the address at diagnosis, the expected weight given to that address, E[C_ini], is the same in both methods.

However, if A_ie is not the address at the time of diagnosis, then the address at diagnosis method will result in C_ie = 0, whereas the residential history weighting method will still assign a non-negative weight. Thus, the residential history weighting scheme will always result in the address at exposure having an expected weight that is greater than or equal to the expected weight resulting from the address at diagnosis method.

Proposition 4.2 (Increased power)

Assuming a constant covariance matrix for the different weighting schemes, the M statistic which accounts for residential history will have more power to detect a difference between the distributions of the cases and the controls.

Proof

Assume that each case in our study population was exposed to a causative agent at exactly one location in their residential history, then the interpoint distances described by F̂₁(·) come from three possible categories: (i) the distances between two addresses of exposure, (ii) the distances between one address of exposure and one non-exposure address, and (iii) the distances between two non-exposure addresses. Because we expect the clustering to only occur among the addresses of exposure, the third group of distances, should be indistinguishable from the interpoint distance distribution for the controls, estimated by F̂₂(·). By examining how each category of interpoint distances contributes to F̂₁(·), one can compare the performance of the proposed test statistic under two different weighting schemes.

Let us decompose F̂₁(·) into a mixture of ${\widehat{\mathbf{F}}}_1^{\prime }(·)$, the distribution from interpoint distances (i) and (ii), and F̂₂(·), as

$${\widehat{\mathbf{F}}}_1(\mathbf{d})=\alpha {\widehat{\mathbf{F}}}_1^{\prime }(\mathbf{d})+(1-\alpha ){\widehat{\mathbf{F}}}_2(\mathbf{d}).$$

We can expand the M statistic as,

$$M={\left({\widehat{\mathbf{F}}}_1(\mathbf{d})-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right)}^t{S}^{-}\left({\widehat{\mathbf{F}}}_1(\mathbf{d})-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right)={\alpha }^2{\left({\widehat{\mathbf{F}}}_1^{\prime }(d)-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right)}^t{S}^{-}\left({\widehat{\mathbf{F}}}_1^{\prime }(d)-{\widehat{\mathbf{F}}}_2(\mathbf{d})\right)={\alpha }^2{M}^{\prime }$$

Larger values of α result in larger values of M. Because $NM\sim {\chi }_{\mathit{rank}(S)}^2$, larger values of M result in increased power to reject the null hypothesis. From Proposition 4.1, we see that the incubation based weighting scheme gives increased weight to the correct address, which in turn, increases α, thus yielding greater power.

Despite our simplifying assumption of a constant covariance matrix in Proposition 4.2, all of the simulations presented in the following section are consistent with both of these results, even when the covariance matrix does vary.

5. A Simulation Study

To assess the validity and performance of our proposed methods in controlled situations, we simulate case control data with complete residential histories. The design of the current simulation gives us control over several important factors. First, we decide on the source(s) of exposure, as well as a radius of influence of exposure for each source. Second, we control the percent of cases whose infection we attribute directly to these point-sources (to vary the strength of the signal in the noise), and these in turn determine the magnitude of the cluster. Third, we control the residential mobility, imposing a model on the number of years the subjects spend at each address throughout the designated time span, as well as the total length of time for which we keep a history.

For the results presented, we simulate situations with both one and two point-sources located in the unit square, our study region. We impose an exposure radius of 0.1 units around each point-source. This exposure radius defines which cases are part of the clusters. Of the N_c cases generated, we designate a proportion p of these cases as “exposed cases”, meaning that these individuals are part of a cluster induced on the background population, the signal in the noise, the remainder of the cases are part of the background. We vary the proportion of cases considered to be exposed: p = {0.00, 0.10, 0.25, 0.35, 0.50, 0.75, 1.00}. Each of the pN_c, “exposed cases” are guaranteed to have at least one address from their residential history located within the exposure radius of a point-source: this is our definition of an “exposed case”. The remaining (1 − p)N_c cases may have an address within the exposure radius as well, but are not part of the cluster. These would be the naturally occurring background cases. A control may also have an address within the exposure radius, but never develop disease.

For both the one-source and two-source settings, we generate individual residential histories under two scenarios. To study the influence residential mobility has on our statistic, we vary the mean number of moves per year, m, from m = 0.25 (roughly corresponding to an estimated median duration of residence of 3.8 to 4.7 years, the current mean in the United States) to m = 0.10 (to model the effect on less mobile populations). The length of time each individual spends at each address is modeled as a Poisson process where the inter-arrival times are distributed exponentially with mean μ = 1/m. Using a 20 year history length, we generate a set of n_i times, T_i = {T_i0, T_i1, …, T_ini} for each individual, i = 1, …, N. These n_i times represent when an individual’s address changes.

An address for each time in an individual’s residential history, is randomly generated on the uniform square. Though we assume a homogeneous population density, the M-statistic is effective at identifying the presence of clustering in situations involving heterogeneous population structures [38]. Here we make the simplifying assumption of a closed population with no movement into, or out of, the study region. Thus the address history for individual i is listed as A_i = {A_i1, A_i2, …, A_ini }, where A_ij = (x_ij, y_ij), the coordinates of address A_ij. If individual i is an “exposed case,” then one of these addresses will be guaranteed to be located within the exposure radius of a point-source. This guaranteed address is selected according to the incubation distribution we use in this simulation, and the address location is randomly generated within the exposure radius of the point-source.

Consider an incubation distribution, lognormally distributed with a median of 6.4 years and a dispersion factor of 1.71 years, the estimates from a leukemia study presented by Court Brown and Doll [39]. To determine which address will be the “exposed address” we use multinomial selections with probabilities associated with picking each address equal to the weights under the incubation distribution, C_ik. For the example, if the residential history of individual i is comprised of three addresses, we would select the cluster address based on a realization of the multinomial random variable taking the values (A_i1, A_i2, A_i3) with the respective probabilities (C_i1, C_i2, C_i3). Using the multinomial distribution to select which address should be restricted to a cluster site insures that the method of weighting by the incubation distribution is being evaluated fairly.

In practice, cluster investigations are not conducted on an on-going basis, but are generally only performed when there is sufficient cause for alarm, often when a concerned citizen notices an abundance of cases within a close proximity to each other. We also consider the power of using the incubation weighted residential histories versus just the address at diagnosis in these potential cluster situations, to further examine the benefit of incorporating this additional information. We define two distinct potential cluster situations, both determined by the spatial distributions of the cases’ addresses at diagnosis, and simulated in the single point-source setting.

In summary the process described above simulates a closed sample of cases and controls on the unit square. Each individual in the sample has a random number of addresses, and spends a random amount of time at each address. Of the simulated cases, a proportion of them, which we vary, are guaranteed to have at least one address in their residential history located within a pre-specified radius of a point-source of exposure. Our simulation varies the parameters governing the average length of time an individual lives at an address, and the percent of the cases considered exposed. We present the performance of the weighted M-statistic under these different scenarios. We compare the performance of the incubation-weighted M-statistic to the performance of the M-statistic in the currently more accepted situation when one simply uses the address at the time of diagnosis (as is done in [8], for example).

To further demonstrate the information contained in the residential histories, we also calculate a uniformly-weighted M-statistic. This uniform-weighted M-statistic is constructed similarly to the incubation-weighted M-statistic, except each address in an individual’s residential history is given weight proportionate to the corresponding residential duration. This statistic is useful in situations where residential addresses are collected, but the incubation distribution is unknown. Thus we consider the three weighting schemes: (i) known incubation distribution based weights (fully informed), (ii) uniform weights (partial information), and (iii) address at diagnosis (uninformed).

6. Simulation results

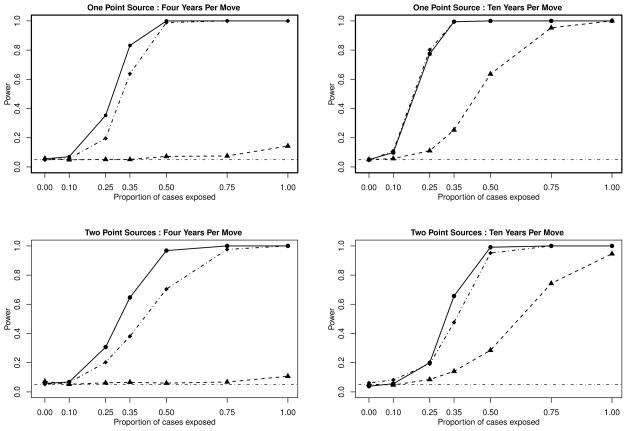
We present the results of several simulations, each of which are considered at the α = 0.05 significance level. For each scenario described, we create a null distribution for the M-statistic, which is calculated by randomly permuting the case/control status of the individuals in the data set, following the method presented in [37]. A test is considered significant when the value of the M-statistic obtained is greater than the 95^th percentile of the null distribution. First, consider the situation where a single point-source is generated on the unit square, and the population has an average residential duration of 4 years, m = 0.25. Figure 1, top left, shows the dramatic gain in power one achieves by incorporating residential histories, through the incubation based weighting scheme, compared to simply using the address at the time of diagnosis. Because this population is so mobile, using the address at diagnosis time results in a power level which is only marginally better than the type-1 error rate as the percentage of cases exposed, p, reaches 100%. Clearly, as an individual’s number of addresses increases, the chance that the exposure occurred at the address of diagnosis decreases.

Figure 1.

Power curves for simulations of 100 cases and 100 controls on the unit square. Top left and top right assume a single point-source. Bottom left and bottom right assume two point-sources. Top left and bottom left assume an average residential duration of 4 years. Top right and bottom right assume an average residential duration of 10 years. These plots present the power curves for the M-statistic using the incubation based weighting system (–●–) compared to the M-statistic with uniform weights (–·◆–·)and the M-statistic using just the address at diagnosis (–▲–).

Next, we examine the one point-source scenario on a less mobile population, with an average residential duration of 10 years, m = 0.10, in Figure 1, top right. We see that in the less mobile population, that as the proportion of cases exposed approaches 1, the power when using the address at diagnosis also reaches 1, but at a much slower rate and in fact, the method incorporating incubation based weights results in higher power for all p > 0.

When we consider two point-sources of exposure, the results are similar to the single point-source setting. From Figure 1, bottom left, we see that in a more mobile population, when m = 0.25, the power of the address at diagnosis method hovers at the alpha level for all values of p. However, the power of the incubation based weights method rises sharply with p, dominating the address at diagnosis method. When m = 0.10, again with two point-sources, Figure 1, bottom right, shows that the incubation based weighting scheme is consistently more powerful. These four figures give evidence of the potential power gains when the residential history is incorporated into the M-statistic to test for differences between two spatial distributions.

In the scenarios we investigate, the power curves for the uniformly-weighted M-statistic are bounded above by the incubation-weighted statistic and below by the address-at-diagnosis method, with the exception of the 10 year duration, single point-source setting. In this situation, the uniformly-wieghted M-statistic power curve lies approximately on top of the power curve for the incubation-weight scheme.

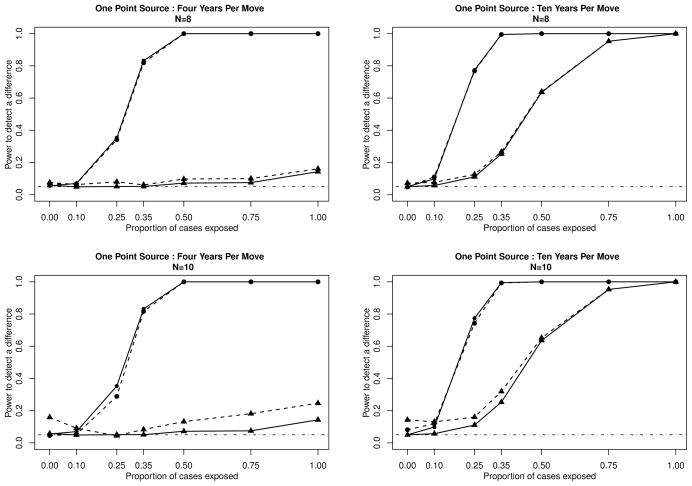
In the first potential cluster scenario, we perform both tests when at least eight of the 100 cases have addresses of diagnosis within a distance of 0.1 units of each other. From the results of this subset of tests, which are shown on the top row of Figure 2, we see slight power gains for the standard address at diagnosis tests. While one would expect to observe power gains for the address at diagnosis test, the incubation weighting scheme still dominates.

Figure 2.

Power curves for simulations of 100 cases and 100 controls on the unit square, assuming one point-source. Plots on the left assume an average residential duration of 4 years, while the plots on the right assume an average residential duration of 10 years. We only test for a difference between the cases and the controls when we have a large enough signal to sound an alarm. For the top row of plots, we define that signal as 8 cases within 0.1 units of each other, while with the bottom row of plots we define that signal as 10 cases within 0.1 units of each other. Power of the M-statistic using the incubation based weighting system is plotted as (●), power of the M-statistic using address at diagnosis is plotted as (▲). The solid lines (—) represent the calculated power for all simulations, while the dashed lines (– – –) represent the calculated power for those simulations with N cases (N= 8 or 10) within 0.1 units of each other.

In Scenario 2, we only test for spatial differences when ten or more cases reside at addresses within 0.1 units of each other at the time of diagnosis. We present the results of these tests on the bottom row of Figure 2. Again, while there are slight gains for the address at diagnosis method, the incubation weighted statistic still outperforms it. It is clear from these power comparison plots that, even in these circumstances, the residential history and the incubation distribution are crucial factors in the detection of the imposed clusters. Even when one only investigates if an alarm is raised, here defined as either eight or ten cases within a 0.1 units of each other, the conventional test underperforms our proposed test.

7. Discussion

We argue that using the location at the time of diagnosis, though informative for a disease with a short incubation period, is much less desirable when considering diseases that have long incubation periods. Most cancers, for example, have long incubation periods and combining that with the relatively brief time that the average American resides in their residence, might contribute to why we have not been successful in describing the obvious non-uniform geographical distribution of cancer cases. To overcome this predicament we propose a method for the incorporation of residential history into existing methods to detect the difference between two sets of spatial data, with an eye to disease surveillance. The information contained in a subject’s residential history can readily be incorporated into the distance based framework of the M-statistic. The inclusion of residential history allows an investigator to more accurately assess spatial differences between affected populations and background populations when the disease of interest may have a long incubation period. These methods are also useful in situations involving mobile populations, where despite short lag times, the address at exposure may be different from the address at diagnosis. This method can also be extended to stationary populations, where individuals remain at the same address but visit several locations throughout a day–such as work address, home address, gym address, etc.

Through several simulations, we demonstrate the power gains possible from using the methods presented. As expected, across all the studied scenarios, the tests that incorporate incubation based weights outperform the tests that rely solely on the address at the time of diagnosis. The effects of residential mobility and the incubation distribution of the disease of interest are significant factors in the detection of spatial differences between study populations, especially when dealing with a disease with a long incubation period. Even when the tests are only performed in situations with cause for alarm, the incubation weighted statistic is much more powerful. This adds evidence to the importance of collecting (as suggested by the CDC [40]), and using, residential history when attempting to study the relationships between exposure and chronic disease. The performance of the uniformly-weighted statistic serves to further enhance the argument that residential histories must be collected to gain a more complete summary of exposure, even in the situation where an incubation distribution is unknown.

Enhancing cluster modeling by accounting for residential mobility has begun to appear in the literature. Jacquez et al. and Meliker et al. present a k-nearest neighbor method for incorporating residential histories and exposure traces [41, 42]. Their work concentrates on combining nearest neighbor statistics over varying exposures. Han et al. use kernel density estimation methods to identify clustering of breast cancer using residential histories [43]. Sabel et al. examine clustering of Amyotrophic Lateral Sclerosis in Finland based on place of birth and place of death [44]. Gallagher et al. use residential history to asses the affect of drinking water exposure to breast cancer [45], by examining any previous address where a study participant was exposed to public drinking water impacted by wastewater. In this work, we include a model for the incubation period distribution to assign weights to all available addresses in the residential history. We prefer to look at the spatial distribution in this manner because it incorporates the likelihood of the time when the disease causing exposure occurred via the incubation distribution.

We have made several simplifying assumptions. We assume a single-hit model for the exposure, similar to the Hiroshima example. This has allowed us to consider the incubation period as starting at a single time point. However, this assumption can be relaxed by convolving the incubation period distribution with a specific disease’s exposure curve. Similarly, we have used the work of [27, 15, 28, 29] to justify our assumption of the independence of exposure intensity and incubation period. One could remove this assumption by allowing different incubation period distributions for different subjects, determined by each specificc exposure history. One could relax both of these stated assumptions simultaneously, and allow differential exposure intensities to affect the course of disease development. Also, within each presented simulation, we assume a constant residential mobility processes. In actuality, residential mobility is affected by several factors such as age, socio-economic group, and population density [18]. However, we feel this work shows that incorporating both residential histories and incubation period distributions, even in these simplified settings, is a worthwhile practice.