Abstract
The EPOXI Discovery Mission of Opportunity reused the Deep Impact flyby spacecraft to obtain spatially and temporally resolved visible photometric and moderate resolution near-infrared (NIR) spectroscopic observations of Earth. These remote observations provide a rigorous validation of whole-disk Earth model simulations used to better understand remotely detectable extrasolar planet characteristics. We have used these data to upgrade, correct, and validate the NASA Astrobiology Institute's Virtual Planetary Laboratory three-dimensional line-by-line, multiple-scattering spectral Earth model. This comprehensive model now includes specular reflectance from the ocean and explicitly includes atmospheric effects such as Rayleigh scattering, gas absorption, and temperature structure. We have used this model to generate spatially and temporally resolved synthetic spectra and images of Earth for the dates of EPOXI observation. Model parameters were varied to yield an optimum fit to the data. We found that a minimum spatial resolution of ∼100 pixels on the visible disk, and four categories of water clouds, which were defined by using observed cloud positions and optical thicknesses, were needed to yield acceptable fits. The validated model provides a simultaneous fit to Earth's lightcurve, absolute brightness, and spectral data, with a root-mean-square (RMS) error of typically less than 3% for the multiwavelength lightcurves and residuals of ∼10% for the absolute brightness throughout the visible and NIR spectral range. We have extended our validation into the mid-infrared by comparing the model to high spectral resolution observations of Earth from the Atmospheric Infrared Sounder, obtaining a fit with residuals of ∼7% and brightness temperature errors of less than 1 K in the atmospheric window. For the purpose of understanding the observable characteristics of the distant Earth at arbitrary viewing geometry and observing cadence, our validated forward model can be used to simulate Earth's time-dependent brightness and spectral properties for wavelengths from the far ultraviolet to the far infrared. Key Words: Astrobiology—Extrasolar terrestrial planets—Habitability—Planetary science—Radiative transfer. Astrobiology 11, 393–408.
1. Introduction
After an initial decade dominated by the discovery of Jupiter-mass planets, the next frontier of exoplanet research will be the detection and characterization of Earth-mass planets. Within the next few years, NASA's Kepler spacecraft will make the first comprehensive estimates of the prevalence and nature of extrasolar terrestrial planets (Borucki et al., 2003), while searching for Earth-mass planets in the habitable zones of their parent stars (Basri et al., 2005). In the coming decades, more ambitious planet detection and characterization missions for habitable Earth-mass planets are planned, such as NASA's Terrestrial Planet Finder (TPF) mission (Beichman et al., 1999). These missions will be designed to detect and characterize nearby habitable planets, with the capability to obtain direct imaging and photometric and spectroscopic data for extrasolar terrestrial planets.
The observational challenges inherent in characterizing a terrestrial exoplanet are significant, and carefully considered trade-offs must be made to maximize the science return. Even with the most ambitious telescopes planned, terrestrial exoplanets will remain faint, spatially unresolved point sources. The principal challenge is to determine the minimum and optimum sets of observational parameters that can best characterize the environment of an unresolved planet, which may be spatially inhomogeneous, cloud covered, and temporally variable. For example, the combination of temporal resolution and multiwavelength photometry could disentangle phase- or rotation-dependent differences in surface properties from variable cloud cover. The resulting maps could discriminate between large-scale surface inhomogeneities such as continents and oceans (Pallé et al., 2008; Cowan et al., 2009; Kawahara and Fujii, 2010; Fujii et al., 2011). Disk-integrated spectroscopy can potentially determine globally averaged atmospheric and surface composition to verify habitability and to search for global evidence of life in the planetary environment (Seager et al., 2005; Meadows, 2006; Montañés-Rodríguez et al., 2006).
New tools are needed to obtain quantitative information about the environments of terrestrial planets that can only be studied as unresolved point sources. A typical approach to understanding a world from disk-integrated observations consists of a “forward model,” an “instrument model,” and an “inverse model.” The forward model is typically a radiative transfer model designed to generate a synthetic spectrum, given an assumed surface-atmospheric state and viewing geometry. The instrument model simulates the spectral and spatial resolution and other properties of the observing system. The inverse model adjusts surface or atmospheric state to yield a better fit to the observations. Given a candidate observing system design, refinements in both forward models and inverse methods are needed to fully exploit the information content of disk-integrated observations of terrestrial planets. Most existing forward models are designed to analyze soundings taken with adequate spatial resolution to yield spatially homogeneous sounding footprints. Forward models designed for surface or “clear sky” remote sensing applications rarely perform well with cloudy soundings. Those designed for land remote sensing observations rarely simulate the reflection from the ocean surface. In short, few if any forward models have been designed to yield accurate observations over the full range of solar illumination angles, observation angles, or surface and atmospheric properties present in a single, integrated, full disk observation of an extrasolar planet. Here, we describe a forward model designed specifically to simulate disk-integrated observations of Earth, which can serve as a theoretical “laboratory” for the accurate simulation of Earth's appearance at arbitrary viewing geometries and phases. These simulations can be used to explore and identify the best conditions under which to search for planetary characteristics of habitability and life, such as the presence of an ocean or a photosynthetic biosphere, and can also be used to generate test data to challenge proposed observational and retrieval techniques for extrasolar planet characterization.
Remote sensing observations provide a glimpse of Earth's appearance from space. Our planet is well studied by an armada of satellites that cover several wavelength regions from the UV through microwave with high temporal and spatial sampling of Earth's photometry and spectroscopy (Hearty et al., 2009). However, these data sets are often not ideal for studying Earth as an astronomical target because of the sheer data volume that must be manipulated to produce a global, or disk-integrated, view and because most satellites are in Sun-synchronous low-Earth orbits, which view Earth over a limited range of viewing geometries and times of day. By comparison, spatially and/or spectrally resolved forward models can readily simulate the full-disk Earth from observing geometries, solar illuminations, and wavelengths that may not be accessible to existing Earth-observing satellites.
Existing Earth models for exoplanet characterization studies are largely dominated by computationally inexpensive specular reflectance models (e.g., Ford et al., 2001; Williams and Gaidos, 2008). These models do not include atmospheric absorption and scattering and are most effective at visible light wavelengths, where they can be used to model the photometric variability of the rotating Earth and determine the detectability as a function of phase of specular reflection or “glint” from the ocean surface. Similar models (Pallé et al., 2003; Oakley and Cash, 2009) utilize bi-directional reflectance functions that are designed to match data that have been measured by Earth-observing satellites (e.g., Manalo-Smith et al., 1998). Spectral Earth models that include absorption by some atmospheric species and simulate Earth spectra by using weighted averages of independent, one-dimensional component spectra representing cloudy and clear sky scenes have also been developed (Woolf et al., 2002; Turnbull et al., 2006; Stam, 2008). Montañés-Rodríguez et al. (2006) modeled Earth's spectrum, using a line-by-line radiative transfer model that was limited to simulating Earth's environment in one dimension by using globally averaged atmospheric, surface, and cloud properties. In their model, standard atmospheric composition and temperature profiles were assumed, and Earth's spectrum was obtained by averaging different component spectra based on data from the International Satellite Cloud Climatology Project. The primary limitation associated with one-dimensional approaches to modeling Earth's disk-integrated spectrum is that these models do not capture latitudinal and longitudinal variations in the composition and temperature of Earth's atmosphere and thus cannot be used to quantify the impact of spatial variations in temperature and composition on the information content of simulated observations.
The EPOXI mission, a reuse of the Deep Impact flyby spacecraft, has recently provided a very rigorous data set for validating full-disk forward models of Earth's spectrum prior to predictive use. The EPOXI observations of distant Earth (Livengood et al., 2008) provide several days of time-resolved, multiwavelength visible photometry and near-infrared (NIR) spectroscopy of Earth's disk through a full 24-hour rotation period. Previously, disk-integrated spectra and photometry of Earth had been obtained from limited, often single, measurements of Earthshine and from planetary spacecraft. Earthshine is reflected light from Earth that illuminates the night side of the Moon (Goode et al., 2001; Arnold et al., 2002; Woolf et al., 2002; Montañés-Rodríguez et al., 2006; Turnbull et al., 2006), and it is constrained by viewing geometry to restricted phases and temporal durations. Snapshot or flyby observations of Earth have also been obtained from spacecraft en route to other planets, for example from the Galileo spacecraft (Sagan et al., 1993) or from Mars Global Surveyor (Christensen and Pearl, 1997).
Using the new EPOXI data set, we validate and present the most comprehensive spectral Earth model to date for the prediction of the photometric and spectroscopic characteristics of Earth-like exoplanets. This model is a forward model, which is used to simulate the appearance of Earth to an observer, for the purpose of exploring the detectability of Earth's planetary characteristics as a function of observational geometry and time. Forward models, such as the model presented in this work, are distinct from, but complementary to, retrieval models designed to retrieve atmospheric characteristics from observations of extrasolar planets (e.g., Madhusudhan and Seager, 2009). In particular, it is important that forward models are as realistic as possible so that they accurately represent the appearance of a planet and, as a result, do not bias the observed planetary properties inferred when using the model as a predictive tool.
A previous, more limited version of this model, published by Tinetti et al. (2006a, 2006b), has been corrected and significantly updated and improved to allow accurate predictions of Earth's time-dependent photometric and spectroscopic brightness, on hourly to yearly timescales, through realistic modeling of the radiative effects of a surface ocean, atmosphere, and clouds. The previous model allowed for an arbitrary scaling of its input cloud coverage data, and it also used the optical thickness of clouds as free parameters. By tuning the previous model, snapshot observations of Earth could be reproduced, and the model could then be used to explore certain characteristics of Earth, such as how the planet's brightness changes with phase. Time-resolved data were not used for validation.
In the process of validating the model against the time- and phase-resolved EPOXI observations, we have significantly upgraded the model to self-consistently utilize satellite-derived cloud data. Cloud coverage is now taken from observations by Earth-observing satellites and is no longer scaled in order to reproduce observations. The optical thickness of clouds in our new model is also provided by Earth-observing satellites, rather than being tunable free parameters. We have also corrected an error in the model presented by Tinetti et al. (2006a, 2006b), which effectively confused forward scattering with backward scattering and thus caused the model to produce unphysical simulated observations of Earth. Our Earth model is based on a fully multiple-scattering, line-by-line radiative transfer model, SMART (Meadows and Crisp, 1996; Crisp, 1997), which is at the core of the exoplanet simulations generated by the NASA Astrobiology Institute's Virtual Planetary Laboratory. The new, self-consistent treatment of clouds in our model has allowed us to match the EPOXI Earth observations, which span almost 3 months in time and a variety of phases without tuning from one data set to the next [for validation against Earthshine data over a wider range of phases, see Robinson et al. (2010)]. Our validated model is capable of simulating Earth's wavelength-dependent temporal variability and absolute brightness, for any given viewing geometry and phase, over wavelengths from the UV to the far IR.
2. Description of EPOXI Earth Observations
The EPOXI Earth data sets used for our model validation were acquired with the High Resolution Instrument (HRI) on board the Deep Impact flyby spacecraft and were described by Livengood et al. (2008). The HRI is a 0.3 m f/35 telescope with nine square-bandpass filters and a NIR spectrometer (Hampton et al., 2005). Seven filters are ∼100 nm wide and are centered at 350, 450, 550, 650, 750, 850, and 950 nm, segmenting the visual spectral range. The NIR spectrometer covers the wavelength range from 1.05 to 4.5 μm with a maximum resolution (R = λ/Δλ) of 750 at the shortest wavelengths, a minimum resolution of 200 at about 2.6 μm, and a resolution of 350 at the longest wavelengths (Klaasen et al., 2008).
Earth was observed with the HRI in three separate 24-hour periods: 2008-Mar-18 18:18 UT to 2008-Mar-19 18:18 UT; 2008-May-28 20:05 UT to 2008-May-29 20:05 UT; and 2008-Jun-4 16:57 UT to 2008-Jun-5 16:57 UT. The star-planet-telescope angle (phase angle) for the three sets of observations was 57.7°, 75.1°, and 76.6°, respectively. NIR spectra of Earth were taken every 2 hours (30° rotation), a total of 13 times, to cover a full rotation of Earth from the viewpoint of the spacecraft. The NIR spectrometer slit was oriented perpendicular to the terminator, due to spacecraft constraints. To avoid saturation and obtain globally averaged spectra, rapid scans were made alternating between south to north and north to south across Earth to limit the amount of time any part of Earth was within the slit of the spectrometer. Photometry in the 450, 550, 650, and 850 nm filters was taken every 15 minutes (∼4° rotation) and every hour (15° rotation) for the 350, 750, and 950 nm filters. Note that a subset of the March and June data sets were published by Cowan et al. (2009), who treated the data in a retrieval sense and performed a principal component analysis of the lightcurves to map the latitudinally averaged distribution of land and ocean on Earth.
3. Description of Model
The comprehensive Earth model presented in this paper uses input data from Earth-observing satellites and a radiative transfer model to create spatially and temporally resolved spectra of Earth. Our model is a new and improved version of the Virtual Planetary Laboratory's spectral Earth model (Tinetti et al., 2006a, 2006b). The model uses date-specific information on spatially resolved atmospheric composition and cloud and surface properties to derive a spatially and spectrally resolved datacube. This datacube can be used to generate both images of Earth over a given wavelength range and spatially resolved or disk-integrated spectra.
In our new model, the surface of Earth is divided into a number of pixels of equal area according to the Hierarchical Equal Area isoLatitude Pixelization (HEALPix) model (http://healpix.jpl.nasa.gov) (Górski et al., 2005). HEALPix partitions a sphere into a number of equal area pixels, which is ideal for a planetary model where the exoplanet may be viewed at arbitrary viewing geometries. The resolution of the HEALPix model is defined by an integer N, and the number of pixels used to cover a sphere is then equal to 12N2, which is a behavior inherent to the HEALPix scheme. A set of surface pixels are nested beneath a set of atmospheric pixels, which are also defined according to the HEALPix scheme. Our new model allows the surface resolution and the atmospheric resolution to vary independently, which provides improved surface resolution at minimum computational cost.
For each surface type (see Section 3.1) lying beneath each atmospheric pixel, we run a one-dimensional, line-by-line radiative transfer model—the Spectral Mapping Atmospheric Radiative Transfer (SMART) model developed by D. Crisp (Meadows and Crisp, 1996; Crisp, 1997)—over a grid of solar zenith angles and observer zenith and azimuth angles, and for wavelengths from the UV to the far IR, to create a look-up table of synthetic spectra. For a given subsolar and sub-observer latitude and longitude, spectra from each atmospheric pixel are taken from the look-up table, interpolated over solar and observer azimuth and zenith angles, and combined at the surface resolution of the model to create a three-dimensional spectral map of Earth. The spectral map can be integrated over a given wavelength range and used to create images of Earth, as shown in Fig. 1, or the three-dimensional spectral map can be integrated over solid angle to create a disk-integrated spectrum of Earth. Note that SMART is the same radiative transfer model used as the core to the Earth model presented by Tinetti et al. (2006a, 2006b). The following subsections describe the input data to our Earth model.
FIG. 1.
A true color image of Earth taken from the EPOXI data set (left) and from our model (right). Using date-specific cloud coverage and optical depth data allows us to match cloud features in the model to cloud features in the data.
3.1. Surface properties
We determine the spatial distribution of Earth's surface types from a yearly averaged map obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) instruments (Salomonson et al., 1989) aboard NASA's Terra and Aqua satellites (http://www-modis.bu.edu/landcover). In general, the largest seasonal variability in surface reflectivity will be due to snowfall or advancing/retreating sea ice, so the yearly averaged data is tailored to a specific date of observation by using 8-day-averaged snow cover (Hall et al., 1995) and sea ice cover (Riggs et al., 1999) from MODIS observations (http://modis-snow-ice.gsfc.nasa.gov).
The wavelength-dependent surface reflectivity was characterized by five surface types: ocean, forest, grassland, desert, and snow. Specular reflectance from liquid water surfaces in our model is simulated by the Cox-Munk glint model (Cox and Munk, 1954), which allows for the calculation of the bidirectional reflectance distribution function of a wave-covered ocean, given wind speed and direction, which are provided by the QuikSCAT satellite (http://winds.jpl.nasa.gov/missions/quikscat/index.cfm). Other surfaces are assumed to be Lambertian and reflect isotropically. Wavelength-dependent albedos for non-ocean surfaces are taken from the USGS Digital Spectral Library (http://speclab.cr.usgs.gov/spectral-lib.html) and the ASTER Spectral Library (http://speclib.jpl.nasa.gov). The Cox-Munk formalism is an improvement in our new model over the model presented by Tinetti et al. (2006a, 2006b), which assumed that oceans scatter as Lambertian surfaces with an albedo near 5–6% at most wavelengths.
3.2. Atmospheric properties
To simulate molecular absorption in Earth's visible and NIR disk-integrated spectra and predict planetary brightness temperature in the mid-IR, we require the three-dimensional distribution of atmospheric gases and temperatures as input to the model. The model includes both Rayleigh scattering by air molecules as well as absorption from H2O, CO2, O3, N2O, CO, CH4, and O2. Spatially resolved mixing ratio profiles for atmospheric gases are obtained from the Microwave Limb Sounder (MLS) (Waters et al., 2006), the Tropospheric Emission Spectrometer (TES) (Beer et al., 2001) (both aboard NASA's Aura satellite), and the Atmospheric Infrared Sounder (AIRS) (Aumann et al., 2003) aboard NASA's Aqua satellite (http://mls.jpl.nasa.gov/data, http://tes.jpl.nasa.gov/data, http://airs.jpl.nasa.gov). An abridged list of the species investigated by these instruments and the valid ranges for profile retrievals are shown in Table 1 (Livesey et al., 2007; Payne et al., 2009). Data from Aqua/AIRS and Aura/MLS are combined to produce spatially resolved temperature profiles. These atmospheric properties are averaged over each atmospheric pixel and resolved into 40 vertical layers prior to input to our one-dimensional radiative transfer model. Absorption cross sections for gases are generated by using the HITRAN 2004 line list database (Rothman et al., 2005) (http://www.cfa.harvard.edu/hitran). Line profiles are simulated by a line-by-line absorption coefficient model developed by D. Crisp (Meadows and Crisp, 1996).
Table 1.
Summary of Trace Gas Input Data
| |
|
|
Typical Mass Mixing Ratio |
||
|---|---|---|---|---|---|
| Species | Instrument | Valid range (Pa) | Surface | Tropopause | Stratopause |
| CH4 | Aura/TES | 1 × 105 to 5 × 102 | 1 × 10−6 | 1 × 10−6 | 2 × 10−7 |
| CO | Aura/MLS | 1 × 104 to 1 × 102 | 10−8 to 10−7 | 10−8 to 10−7 | 1 × 10−7 |
| H2O | AIRS | 1 × 105 to 1 × 104 | 10−3 to 10−2 | 3 × 10−6 | 3 × 10−6 |
| H2O | Aura/MLS | 3 × 104 to 2 × 10−1 | |||
| N2O | Aura/MLS | 1 × 104 to 1 × 101 | 5 × 10−7 | 4 × 10−7 | 2 × 10−8 |
| O3 | Aura/MLS | 2 × 104 to 2 × 100 | 10−8 to 10−7 | 10−7 to 10−6 | 5 × 10−6 |
3.3. Clouds
The reflectivities, optical depths, and spatial and vertical distribution of clouds have a profound effect on Earth's time-variable spectrum. In our model, the spatial distribution of clouds is straightforwardly obtained from cloud coverage maps provided by the MODIS instruments (http://modis-atmos.gsfc.nasa.gov). MODIS provides only cloud phase assignments (liquid, ice, and undetermined), optical depth measurements, and cloud-top pressure. MODIS does not directly report cloud altitude or reflectivity. Other data sets (e.g., CloudSat or the International Satellite Cloud Climatology Project) can provide more detailed information about cloud distribution but suffer from either poor spatial coverage or a large lag time between data acquisition and release, which makes these data sets a poor choice for the date-dependent simulations presented in this work.
Not all locations on the planet have MODIS data recorded within a given 24-hour period. We interpolate cloud coverage and optical depths to the times of EPOXI observations by using the closest Aqua/MODIS and Terra/MODIS data that bracket the observation times (Wolfe, 2006). The spectral model has been improved to allow for an arbitrary number of cloud varieties, where a cloud variety is defined according to its phase (liquid or ice), altitude, and optical thickness, whereas the previous model (Tinetti et al., 2006a, 2006b) used a fixed number of cloud varieties. The previous model used simulated as well as satellite-observed cloud locations but allowed the global coverage and optical thickness of each cloud type to be a free parameter. Our new model now fixes cloud coverage and optical depth based purely on satellite measurements, instead of allowing these to be free parameters that can be tuned to fit an observation.
To model the clouds, we used the MODIS cloud phase identification to categorize a cloud at a given spatial location as either liquid or ice. MODIS has a third category, “undetermined,” which covers ∼1% of the planet and is neglected in our simulations. Model ice clouds were placed near 8.5 km (0.331 bar) altitude, and model water clouds were placed near 1.5 km (0.847 bar). The average cloud-top pressure in our model agrees with the average cloud-top pressure reported by MODIS. Liquid and ice clouds were then subdivided with MODIS optical depth measurements into two subcategories, for a total of four cloud varieties. These subcategories allow us to resolve different cloud thicknesses in the model and can be thought of as moderately optically thick and optically thick cloud categories. The subdivision occurs at an optical depth of 10 for both liquid and ice clouds, since roughly half of all liquid and ice clouds within the MODIS data have optical depths smaller than this value. A weighted average of the cloud data within these subcategories yields best-fit optical depths of 5 and 15 for our two liquid cloud types and optical depths of 5 and 20 for our ice cloud types. This approach and the derived values held for all three dates of EPOXI observations. Wavelength-dependent optical properties for liquid clouds were derived by a Mie theory model (Crisp, 1997), and ice clouds were parameterized with geometric optics (Muinonen et al., 1989). The cloud-scattering properties were assumed to be defined strictly by cloud phase (i.e., liquid or ice).
3.4. Comparison to previous model
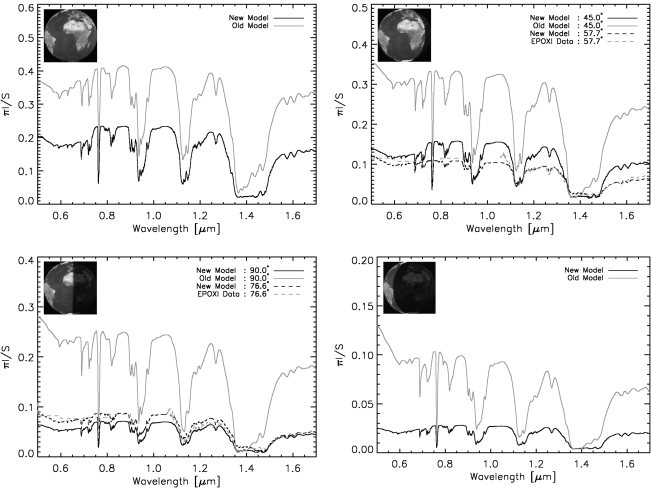
To demonstrate the significant improvements made in our new model, we compared spectral, phase-dependent results from our model to the model described by Tinetti et al. (2006a) as well as to EPOXI observations in Fig. 2. In this figure, we show Earth's wavelength-dependent reflectivity at visible and NIR wavelengths for a variety of different phases (full, gibbous, half illuminated or quadrature, and crescent). Both models assume realistic clouds. In general, the model described by Tinetti et al. (2006a) is significantly brighter than our new model, with the most extreme discrepancy occurring at 0.5 μm in the crescent view, where the Tinetti et al. model is about 400% brighter than our new model. Also, the old model is distinctly bluer than our new model at phases between half illumination and crescent. EPOXI observations taken at gibbous phase and near half illumination (phase angles of 57.7° and 76.6°, respectively) and our model of the observations are shown as dashed lines in the gibbous and quadrature plots, which demonstrates our ability to reproduce Earth's brightness and reflectivity at these phases. Robinson et al. (2010) presented further validation of our model against measurements of Earth's phase-dependent brightness and reflectivity from Earthshine observations.
FIG. 2.
Comparison between the Tinetti et al. (2006a, 2006b) model (old model, gray) and our new model (black). A measure of Earth's reflectivity, taken as π times the disk-integrated radiance (in W/m2/μm/sr) divided by the solar flux at 1 AU (in W/m2/μm), is shown for the planet viewed at full phase, gibbous phase, quadrature (i.e., half illuminated), and crescent phase, or, alternatively, phase angles of 0°, 45°, 90°, and 135°, respectively. Both models use realistic cloud cover, and the data for the old model is taken from the left column of Fig. 6 in Tinetti et al. (2006b). EPOXI observations taken at phase angles of 57.7° and 76.6° (dashed gray) and our model of the observations (dashed black) are shown in the gibbous and quadrature cases, demonstrating that our model correctly reproduces the brightness and spectral shape of the data at these phases. In general, the Earth model from Tinetti et al. (2006a, 2006b) is about 100–400% too bright and is too blue at phases near quadrature and crescent. Earth views generated by the Earth and Moon Viewer, first implemented by J. Walker (http://www.fourmilab.ch/cgi-bin/Earth).
Some of the differences between the two models shown in Fig. 2 can be accounted for by an error in the model described by Tinetti et al. (2006a), which rotated the angle between the Sun and the observer by 180°, effectively confusing forward scattering with backward scattering. Inserting this error into our model allows us to reproduce the excess brightness in the old model near full phase and also allows us to reproduce the incorrect blue nature of the old model near quadrature and crescent phases. We have not, however, been able to reproduce the excess brightness in the old model at phases away from full phase, which indicates that other problems exist in the model described by Tinetti et al. (2006a). It is important to note that the confusion between forward and backward scattering in the Tinetti et al. model compromises the phase-dependent, reflected light brightnesses and reflectivities presented by Tinetti et al. (2006b).
4. Results
4.1. Validation with lightcurves and spectra
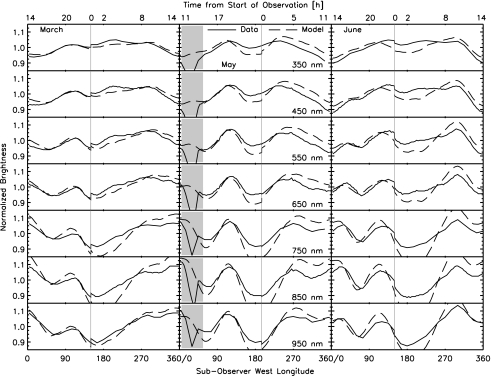
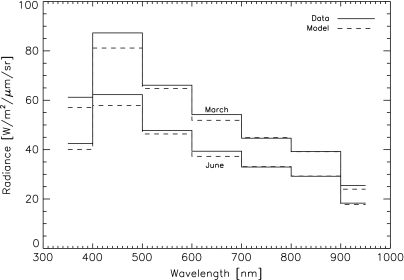
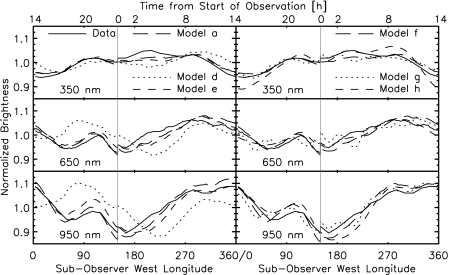
Comparisons between EPOXI observations and our model for all three epochs of observation are shown in Fig. 3. These plots demonstrate the brightness of Earth through seven EPOXI bandpasses over the duration of the 24-hour observation. Both the data and the model have been normalized to their respective 24-hour averages through these filters. The vertical gray line marks the beginning and end of the observations. The discontinuity in normalized intensity between beginning and end is real and is due to Earth's time-varying cloud formations, which typically produce a 3–5% change in the lightcurve over all wavelengths (relative errors for an individual bandpass are typically much less than 1%). The model generally reproduces the sign and magnitude of this discontinuity. The shaded region of the lightcurves for the May set of observations marks a lunar transit of Earth's disk, which is an effect not included in our model. The comparison between the 24-hour averaged radiance from the data and our model for the March and June epochs of observation is shown in Fig. 4. Table 2 shows the percent difference between the 24-hour average radiance data and the standard March, May, and June models (Models a, b, and c, respectively). The model reproduces the data on an absolute scale of radiance to within the ∼10% uncertainty in EPOXI/HRI calibration accuracy (Klaasen et al., 2008). Root-mean-square (RMS) errors for the lightcurve comparisons are also shown in Table 2. These errors measure the goodness of fit of the model lightcurves and are computed by comparing the data to the model for each bandpass at each observation within the 24-hour observing sequence. Our model reproduces the time-dependent variability to within 3% in most cases. Note the trend in the data of larger peak-to-trough variability with increasing wavelength, with roughly 10–15% variability at shorter wavelengths and over 20% variability (in some cases) at longer wavelengths.
FIG. 3.
Lightcurves of data (solid) and our new and improved model (dashed) for EPOXI observations from March (left), May (center), and June (right). March observations begin at 2008-Mar-18 18:18 UT, May observations begin at 2008-May-28 20:05 UT, and June observations begin at 2008-Jun-4 16:57 UT. The filter center wavelength is noted in the central column. Model values and data have been normalized to their respective 24-hour averages. The shaded region in the central column marks a lunar transit of Earth's visible disk, which is an effect not included in our spectral model. The vertical gray line indicates where the observations begin and, 24 hours later, end. The discontinuity here is a real effect due to time-varying cloud structure and is of order 2–3% in March. The discontinuity tends to be smaller in the May observations and larger in the June observations. The model generally reproduces the scale and sense of these discontinuities.
FIG. 4.
Comparison of the 24-hour averaged signal for the model (dashed) with the EPOXI data (solid) for the March (upper) and June (lower) dates of observation, demonstrating our fit to the data on an absolute scale. Note that the June observations are overall dimmer than the March observations due to Earth phase. The largest discrepancies are typically in the 450 nm filter and are ∼8% for both observations, within the 10% absolute error in the HRI calibration (Klaasen et al., 2008). The average spectrum of the May observations is similar to that of the June observations (i.e., within a few percent) and was omitted for clarity.
Table 2.
Sensitivity Test Results
| Model | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| Observation Month | March | May | June | March | March | March | March | March |
| Atm. Res. (pixels) | 48 | 48 | 48 | 48 | 48 | 1 | 48 | 0 |
| Srf. Res. (pixels) | 192 | 192 | 192 | >3000 | 192 | 192 | 48 | 192 |
| Cloud Cat. | 4 | 4 | 4 | 3 | 1 | 4 | 4 | 1 (Lambert) |
| Filter Center (nm) | 24-hour Avg. Rad. Errora (%) : Lightcurve RMS Errorb (%) | |||||||
| 350 | 6.7 : 1.4 | 8.1 : 3.4 | 5.5 : 3.3 | 3.1 : 4.5 | 4.8 : 1.7 | 6.5 : 1.4 | 1.0 : 1.6 | 31 : 3.1 |
| 450 | 7.0 : 2.0 | 8.1 : 3.4 | 7.1 : 3.5 | 1.3 : 5.3 | 3.2 : 2.3 | 6.7 : 1.9 | 0.9 : 2.1 | 13 : 1.6 |
| 550 | 2.1 : 2.3 | 4.0 : 3.8 | 2.9 : 3.8 | 9.8 : 5.1 | 3.6 : 2.6 | 0.8 : 2.2 | 4.8 : 2.5 | 19 : 1.4 |
| 650 | 4.2 : 2.0 | 5.8 : 3.7 | 5.3 : 3.7 | 7.6 : 4.2 | 2.8 : 2.3 | 3.0 : 1.9 | 2.5 : 2.6 | 27 : 1.7 |
| 750 | 0.5 : 4.3 | 0.5 : 5.7 | 0.5 : 5.8 | 5.7 : 5.1 | 8.7 : 3.8 | 0.5 : 4.1 | 6.6 : 2.9 | 34 : 2.3 |
| 850 | 0.2 : 5.5 | 1.3 : 7.2 | 0.3 : 7.2 | 2.6 : 6.6 | 8.4 : 4.6 | 0.4 : 5.4 | 5.2 : 3.7 | 27 : 2.7 |
| 950 | 5.7 : 2.1 | 6.3 : 4.2 | 3.3 : 4.0 | 13.5: 5.1 | 7.2 : 2.8 | 7.3 : 2.2 | 0.1 : 2.3 | 56 : 3.0 |
Percent error for 24-hour average radiance, a measure of ability to reproduce visible radiance of Earth; compare to ∼10% instrument absolute calibration uncertainty.
Root-mean-square error for normalized model lightcurves, a measure of ability to reproduce lightcurve shape.
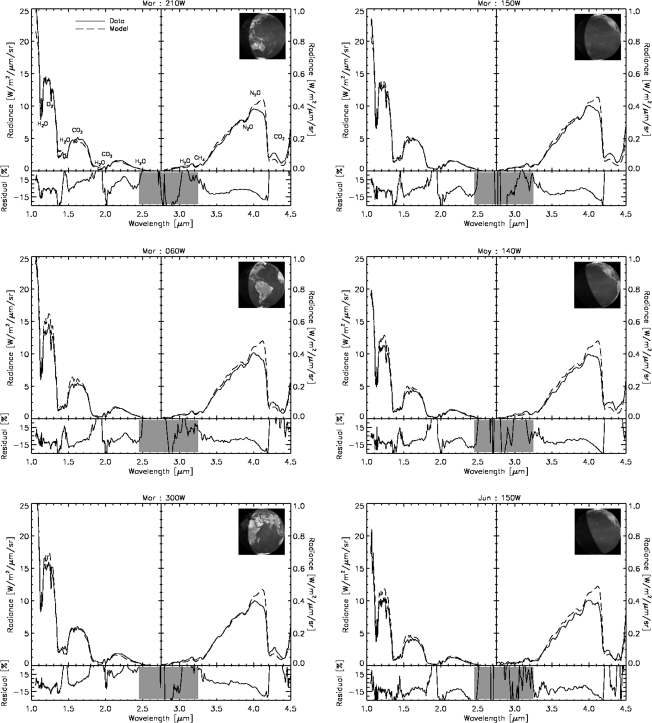
In addition to fitting lightcurve time variability and absolute brightness in the visible, our model simultaneously reproduces the EPOXI NIR spectral data, shown in Fig. 5. This figure shows comparisons between our model and the EPOXI data for a variety of viewing geometries from the March set of observations as well as for data from the May and June sets of observations, which are dimmer in reflected light due to Earth phase. Residuals from the data-model comparison are also shown and are typically less than about 15%, which demonstrates the ability of the model to reproduce spectral observations on timescales from hours to months. Notable disagreements occur near the center of the 1.4 and 1.9 μm water bands and near 4.1 μm, in the short wavelength wing of the 4.3 μm CO2 feature. The absolute magnitude of the 4.1 μm defect is much smaller than the 1.4 and 1.9 μm defects. Instrument calibration uncertainties are typically 10% and tend to increase below 2.0 μm and above 4.3 μm (Klaasen et al., 2008).
FIG. 5.
Near-infrared spectral comparison of the model (dashed) with EPOXI data (solid) for a variety of observations, demonstrating the ability of the model to reproduce moderate spectral resolution observations on timescales from hours to months. Note the different scales used for the y axes on the left and right sides of the spectral plots and also note that the model has not been scaled to match the data. Date indicators and sub-observer longitudes are given at the top of each plot. Prominent absorption features have been labeled in the upper-left plot. May (middle-right) and June (lower-right) observations are dimmer in reflected light due to Earth phase. Residuals for the data-model comparison are shown below each plot and are typically less than about 15%. Stronger disagreements tend to occur between 1.1 and 1.2 μm (water), between 1.35 and 1.5 μm (water), and between 3.9 and 4.15 μm (N2O, wing of CO2 feature). Extremely low signal levels and instrument artifacts lead to large residuals in the 2.5–3.25 μm range. Instrument calibration uncertainties are typically 10%, and tend to increase below 2.0 μm and above 4.3 μm (Klaasen et al., 2008). Earth views generated by the Earth and Moon Viewer.
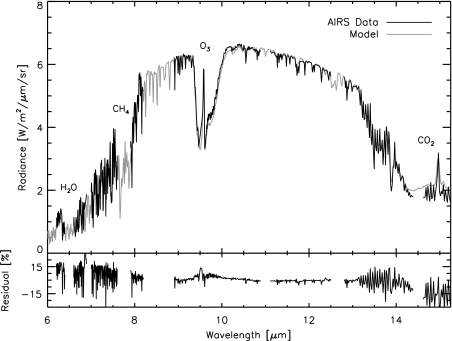
In Fig. 6 we show a comparison between the 24-hour average mid-IR spectrum from our March model and a mid-IR spectrum of Earth generated from AIRS observations taken over the same timeframe (Hearty et al., 2009). The AIRS instrument does not record full disk observations of Earth, so the AIRS spectrum is assembled from multiple scenes recorded over the observational period. The fact that many observations must be combined to produce a disk-integrated spectrum implies that this technique cannot provide the same time resolution as the EPOXI data set. In general, the model reproduces the AIRS observations quite well, with residuals being, on average, about 7%, and with brightness temperature errors less than 1 K in the atmospheric window.
FIG. 6.
Mid-infrared, 24-hour average spectra of Earth from our March model (gray) and as generated from AIRS observations (black) (Hearty et al., 2009). In general, the agreement is quite good, with residuals (lower panel) being typically ∼7%. Large gaps are regions where the instrument does not return data. Note that the AIRS instrument does not record full disk observations, so disk-integrated observations are generated from multiple scenes recorded over a 24-hour period. Thus, this technique cannot achieve the same time resolution as the EPOXI data set.
For comparison, we ran the original Virtual Planetary Laboratory Earth model (Tinetti et al., 2006a, 2006b), which was only validated with single snapshots of Earth, using input cloud coverage maps as well as atmospheric composition and temperature data for the appropriate dates of EPOXI observation. As the core radiative transfer model is the same in both Earth models, this experiment primarily tested the cloud parameterization in the two models. The comparisons between EPOXI data from March and the 2006 model are shown in Fig. 7 (Model d). Discrepancies in the 24-hour average radiance and the RMS errors for the lightcurves are also shown in Table 2. The inability of the model to reproduce the lightcurves indicated that a new cloud parameterization was needed and demonstrated the importance of validating spectral Earth models against time- and phase-resolved data.
FIG. 7.
Comparison between the EPOXI data and a variety of models considered in this work through a subset of the EPOXI filters for the March set of observations. Filter center wavelength is noted on each plot. The details of the models shown are outlined in Table 2. Model a: standard model; Model d: 2006 version of model Tinetti et al. (2006a, 2006b); Model e: single-cloud category; Model f: single atmospheric pixel; Model g: 48 surface pixels; Model h: reflectance model. Filters were selected to demonstrate the effects of Rayleigh scattering (350 nm) and water absorption (950 nm). The 650 nm filter is relatively free of atmospheric extinction.
4.2. Model sensitivity
Our selected atmospheric and surface resolution (48 pixels and 192 pixels, respectively) and our set of four cloud categories represent our standard model. The following set of investigations aims to determine the level of detail required in the model to reproduce both the visible and NIR EPOXI observations while remaining consistent with the input data. The parameters used in these studies and a summary of the results are shown in Table 2. Lightcurves for a subset of the studies through three EPOXI filters are shown in Fig. 7. Results are presented and discussed in greater depth below.
4.2.1. Cloud categories: the importance of spectra
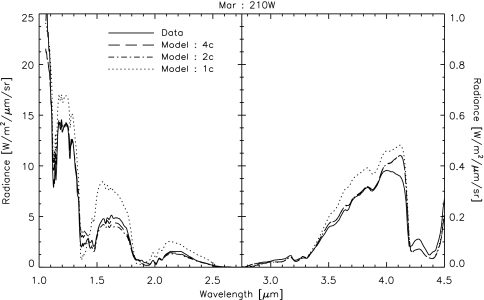
The characteristics that define our selected cloud subcategories are based on MODIS data, but the number of cloud varieties in our model is arbitrary. While our standard model utilizes four cloud subcategories, it is useful to know how sensitive the model is to the chosen number of cloud subcategories. To test this, the model was run with only a single cloud subcategory (Model e in Table 2) and with two cloud subcategories. The single-cloud model uses a cloud extinction optical depth of 10 and places the cloud in the middle of the troposphere, while the two-cloud model uses liquid water clouds with an extinction optical depth of 5 and ice clouds with an extinction optical depth of 15, placed at the same altitudes as the liquid and ice water clouds in the standard model. In all cases, the characteristics of the cloud subcategories were derived from MODIS observations. Example NIR spectra from these low “cloud resolution” models are compared to the EPOXI data and our standard model in Fig. 8. In general, the models with less than four cloud subcategories are poorer fits to the NIR data. The single-cloud model is too bright in the continuum regions, underestimates water vapor absorption near 1.4 μm, and overestimates water vapor absorption near 1.1 μm. Furthermore, this model cannot reproduce the shape of the continuum region near 1.6 μm, where water ice absorbs. Thus, the EPOXI disk-integrated NIR spectra contain evidence for the presence of both liquid and ice water clouds. The two-cloud model is an improved fit but struggles to reproduce the measured intensity within the 1.1 and 1.4 μm water features. A six-cloud model was run (not shown here) and did not offer significant improvements over the four-cloud model when compared to the EPOXI data set.
FIG. 8.
Comparison between the EPOXI data (solid), our standard model (dashed), a model run with a single cloud category (dotted), and a model run with two cloud categories (dot-dashed) for a view over the Pacific Ocean on 2008-Mar-18 UT. Note the different scales used for the y axes on the left and right sides of the spectral plots. While the single-cloud model and the two-cloud model can reproduce the visible EPOXI lightcurves, they cannot reproduce the NIR data.
The visible EPOXI lightcurves are less of a challenge to models due to their broadband nature and the fact that these data are relatively insensitive to atmospheric absorbers. Thus, the single-cloud model can still reproduce the absolute brightness and temporal variability seen in the low spectral resolution; visible EPOXI data, as shown in Table 2; and in the filters presented in Fig. 7 (the two-cloud model can reproduce the visible data and is not shown for clarity). These results emphasize the crucial role that spectra play in disentangling the effects of clouds; the EPOXI visible, broadband data can be fit with a single cloud category, while four cloud varieties were required to fit the NIR data. It may also be possible to tweak the optical depths of the clouds in the two-cloud or the four-cloud model to improve the fit to the NIR spectra while remaining consistent with MODIS data.
4.2.2. Sensitivity to atmospheric and surface resolution
The atmospheric resolution determines the scale at which temperature and gas mixing ratio profiles are resolved, while the surface resolution determines the scale at which surface features are resolved. To test our sensitivity to these parameters, we ran a model with a single atmospheric pixel as well as a model with 48 surface pixels (Models f and g in Table 2, respectively). Using a single atmospheric pixel amounts to assuming there is no spatial variability in the temperature and composition of Earth's atmosphere. Earth's surface exhibits large variations in both water vapor mixing ratios and surface temperatures, which makes a single atmospheric pixel a poor choice for a model that aims to simulate these variations. For example, a model with a single atmospheric pixel would incorrectly produce polar and equatorial thermal IR spectra that are nearly identical, even though, in reality, these regions can differ in temperature by over 100 K. In general, though, the model with a single atmospheric pixel can still reproduce the visible EPOXI data reasonably well since the visible data is relatively insensitive to atmospheric/surface temperature as well as water vapor distribution. Regarding surface resolution, the coarse resolution of the 48-pixel model (surface pixels are several thousand kilometers in size) leads to a poor reproduction of the longitudinal variations in brightness in the lightcurves at all wavelengths, which is shown in Fig. 7. The visible disk of Earth in this low-resolution model is dominated by ∼10 pixels, which leads to unrealistic periodicities in the lightcurves as relatively bright surface pixels rotate into and out of view.
4.3. Comparison to reflectance models
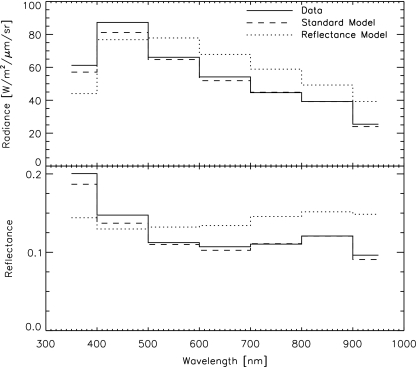
To mimic previously published reflectance models (e.g., Williams and Gaidos, 2008), we removed atmospheric absorption and scattering from our model and replaced the Mie scattering clouds in our model with a Lambertian surface with a visible reflectance of 0.60, which is a typical value assumed in reflectance models (Model h in Table 2). By definition, a reflectance model cannot reproduce spectral data, like the NIR EPOXI data, because such models explicitly ignore atmospheric absorption. The 24-hour average radiance is shown for the reflectance model, the EPOXI data, and our standard model in Fig. 9. The reflectance model clearly struggles to reproduce the radiance data (quantified in Table 2), especially in the 350 nm and 950 nm filters, which are strongly affected by extinction due to Rayleigh scattering and water vapor, respectively. However, the reflectance model can reproduce the relative variations in brightness in the EPOXI lightcurves, as shown in Table 2 and in Fig. 7.
FIG. 9.
Comparison of the 24-hour averaged signal (top) for the EPOXI data (solid), our standard model (dashed), and a model where atmospheric absorption and scattering has been removed and clouds have been treated as a Lambertian surface with an albedo of 0.60 (dotted). The data and models have been converted to a measure of reflectance (bottom) in the same fashion as in Fig. 2. The effects of ignoring Rayleigh scattering can be seen in the shortest wavelength filters, while the lack of atmospheric absorption is especially apparent in the 950 nm filter, which includes a strong water absorption feature. Data and models are all for the March observations.
5. Discussion
Earth is a complex system, and as a result any model that aims to simulate Earth's appearance to a distant observer should reflect this complexity. Our spectral Earth model aims to accurately simulate Earth's disk-integrated spectrum at any arbitrary viewing geometry and wavelength, which necessitates a comprehensive and rigorous treatment of a large number of physical processes (e.g., ocean glint, realistic cloud scattering, vertically and spatially resolved temperature, and gas mixing ratio profiles). However, as we have shown, this does not necessarily imply that more simplified models cannot reproduce specific details of Earth's appearance [e.g., ocean glint in Williams and Gaidos (2008)]. In either case, any model of Earth's appearance should be validated against observational data, which ensures its accuracy as a predictive or interpretive tool.
Our new model is capable of reproducing the time variable color and absolute brightness of Earth, as observed in the visible and NIR EPOXI data, and can do so for multiple dates of EPOXI observations. Typical RMS errors for the model lightcurves are within 3–4%, and the 24-hour average visible radiance for the model matches the EPOXI observations to within calibration uncertainties. The model also simultaneously provides a good fit to the shape and absolute brightness of the high-resolution AIRS mid-IR observations.
Although our fit to the lightcurves is generally good (Fig. 3), the largest RMS errors are seen for the 750 and 850 nm filters, which indicates that our poorest match to the shapes of the EPOXI lightcurves occurs at these wavelengths. These filters are relatively clear of atmospheric absorbers and are largely unaffected by the strong Rayleigh scattering seen in bluer filters. As a result, these filters are the most sensitive to the surface, and mismatches in these filters may indicate that more than five surface types are needed to better reproduce the EPOXI data at these wavelengths.
Even though our model reproduces the 24-hour average visible radiance of Earth to within instrument uncertainties (Fig. 4), discrepancies at short wavelengths are typically in the sense of the data being brighter than the model, which suggests either a systematic calibration error or residual minor defects in the model. The difference in the 24-hour average brightness between the data and the model is largest in the 350 and 450 nm filters. A small fraction of the light incident on an ocean surface actually enters the water and is scattered back out (Cox and Munk, 1954), which is an effect not accounted for in our model. Adding this ocean “volume scattering” behavior to our simulations could improve our fits to Earth's radiance, as water is most transparent in the 350 and 450 nm filters.
Notable disagreements between the model and data in the NIR spectra occurred near 1.4, 1.9, and 4.1 μm. The 1.4 and 1.9 μm discrepancies occur at the base of water vapor absorption features, which indicates problems with the input MODIS water vapor distribution data, the HITRAN line lists, and/or the vertical placement of clouds in our model. The height of clouds in the atmosphere controls the column depth of water vapor that is available to absorb radiation incident on the top of the atmosphere. For this reason, low clouds allow a longer column through the atmosphere and more absorption by water vapor in the spectrum than high clouds. MODIS data does not contain a complete description of the full three-dimensional distribution of clouds in Earth's atmosphere, and we must estimate standard altitudes for our liquid and ice clouds. While the altitudes that we assumed seem to offer a reasonably good fit overall to the NIR data, these fits could be improved by allowing our clouds to have a varying vertical distribution that is determined by CloudSat data (Stephens et al., 2002).
The disagreement near 4.1 μm is in the wing of a CO2 absorption feature. Efforts to fit this shape by altering cloud coverage and thickness were unsuccessful. N2O has a weak absorption feature between 4.0 and 4.1 μm, but altering atmospheric N2O levels also failed to reproduce the observed shape. SO2 absorbs in this region, but the strength of this feature is even less than the N2O feature. It is possible that we are missing a trace gas that absorbs in this region, or that our CO2 linelist is incomplete, although a test in which the more recent HITRAN 2008 database (Rothman et al., 2009) was used did not improve our fit in this region.
The original version of the model (Tinetti et al., 2006a, 2006b) failed to reproduce the observed lightcurves primarily because this version of the model required a less rigorous parameterization of clouds to reproduce limited Earth-observing data sets. Most importantly, this earlier version of the model assumed that all ice clouds were quite thin with an extinction optical depth of order unity, which is true for only ∼10% of all ice clouds in the MODIS data. The model presented in this work has a much improved treatment of spatially and temporally varying clouds, and parameterizes them based solely on input data collected from the MODIS instruments. Our cloud parameterization technique is rigorous and versatile, allowing us to reproduce all three sets of EPOXI observations, which span almost three months in time, without needing to tune model parameters to each data set.
In summary, our model is designed to be comprehensive and versatile enough to model Earth's appearance over a very large wavelength range and at arbitrary viewing angle and phase. The level of model complexity required to simulate Earth's spectrum simultaneously over a large wavelength range, where different physical processes dominate, may at first appear daunting, especially if considering the reverse problem of retrieval of the correct planetary characteristics from a limited data set. However, the more optimistic view is that, in cases where a more comprehensive model is required to fit Earth data accurately, this indicates that the data contained enough information to allow us to discriminate the more complex environmental characteristics from more simplistic models. This would be a desirable circumstance when attempting to learn about extrasolar planetary environments from observations. Additionally, in the process of fitting the EPOXI data, we have been able to quantify when model complexity is and is not required for a particular application or wavelength range subset.
For example, modeling moderate resolution NIR spectra does require multiple categories of clouds, providing cloud altitude, phase, and optical thickness resolution. As demonstrated in Fig. 8, a single cloud category produces a disk integrated spectrum that is too bright in the NIR continuum and underestimates water vapor absorption in some regions (near 1.4 μm) while overestimating water vapor absorption at other wavelength regions (near 1.1 μm). The lack of ice clouds leads to discrepancies near 1.5 μm where ice particles absorb. A model with two cloud categories reproduces the spectral data more accurately than the single-cloud model but struggles with the shape of the 1.1 and 1.4 μm water features. Residuals for the two-cloud model can be over 40% larger than the residuals for the four-cloud model in these regions. The four-cloud model therefore appears to be optimal for simultaneously fitting both the visible and NIR spectral regions and would be most useful for studying the detectability of Earth's globally averaged characteristics for TPF-like designs that span both the visible and NIR.
The absolute brightness and temporal variability of the EPOXI lightcurves can be reproduced by models without a large number of cloud categories due to the broadband nature of these data and the fact that observations at these wavelengths are relatively insensitive to atmospheric absorption. In essence, the broadband lightcurves provide evidence for white, highly reflective structures that vary in time on the planet, and observations in the 950 nm filter demonstrate an absorption feature from water vapor. The higher spectral resolution NIR data provide information regarding the phase and vertical distribution of these structures. Furthermore, insofar as both liquid water and ice clouds are required to reproduce the observations near 1.5 μm, the broadband data and moderate resolution spectra demonstrate that water is found in the atmosphere as vapor, liquid, and ice.
Sensitivity tests indicate that high atmospheric resolution is not needed to reproduce the EPOXI visible photometric data. This is not surprising, as at visible the temperature structure and distribution of trace gases within the atmosphere should have only small effects on the lightcurves. Even data in the 950 nm filter, which contains a large water vapor absorption feature, can still be fit due to variations in the brightness of the continuum outside the absorption feature and the fact that clouds control the column depth of water vapor that is available to absorb radiation. Earth exhibits large variations in both water vapor mixing ratios and surface temperatures, which indicates that models with low atmospheric resolution are poor choices for modeling high-resolution spectral data or mid-IR data, especially if the model aims to generate observations for arbitrary viewing geometries (e.g., polar versus equatorial views).
Reflectance models that ignore scattering and absorption in the atmosphere and treat clouds as Lambertian reflectors cannot reproduce the 24-hour averaged brightness of Earth. The short-wavelength filters have lower reflectivity than the data because Rayleigh scattering has been ignored, while longer-wavelength filters (e.g., the 950 nm filter, which contains a strong water feature) show enhanced reflectivity because atmospheric absorption has been ignored. Reflectance models can, however, reproduce the shapes of the EPOXI lightcurves as these models are designed to reproduce relative brightness variations due to structures (e.g., clouds, continents) rotating into and out of view. While simple, computationally inexpensive models, like reflectance models, may be useful as retrieval tools in scenarios where observational data are limited or of poor quality, these models are not optimal when compared to more rigorous and comprehensive spectral models for applications that require accurate predictions.
Our validated model has a variety of applications. Robinson et al. (2010) used the model to demonstrate that surface oceans on Earth-like extrasolar planets may be detectable, even after considering the confusing effects of forward scattering from clouds. The Tinetti et al. (2006a, 2006b) model could not perform such a study, as it did not simulate specular reflection from ocean surfaces; and reflectance models, while excellent at reproducing glint, could not address the important issue of phase-dependent aerosol scattering when investigating the detection of ocean glint in the presence of clouds (Williams and Gaidos, 2008). Cowan et al. (2011) used the model presented here to simulate observations of a distant Earth to validate and better understand a retrieval method for exoplanets.
Our comprehensive model is uniquely capable of investigating a variety of Earth's traits over wavelength ranges, synoptic views, and vantage points that are unavailable to Earth-observing spacecraft or satellites. For example, future applications could include model-generated disk-integrated, UV, visible, or IR spectra of Earth for a variety of sub-observer points and phases. These simulated data sets could be used, among other applications, to investigate the wavelength-dependent effect of clouds on our ability to measure thermal radiation from the surface or to simulate Earth as seen from a lunar vantage point over a complete lunar orbit. We could also investigate the effects of an unresolved, airless satellite on the spectrum of its host by pairing our simulations with a model of the spectrum of the Moon. Finally, our Earth model could also be used to generate synthetic observations for “blind” tests of retrieval models, where other individuals or teams attempt to retrieve planetary characteristics without knowing the input to our Earth model (e.g., season, viewing geometry, phase). In general, simulated data can be used to test techniques aimed at characterizing habitable planets that may be employed by TPF-class missions.
6. Conclusion
We have developed and validated a three-dimensional spectral model of Earth that is capable of reproducing the temporal variability and absolute brightness of observations in both the visible, NIR, and mid-IR. Earth's visible lightcurves are strongly dependent on cloud spatial distribution and reflectivity. To simultaneously reproduce the EPOXI visible and NIR observations of Earth, we used four categories of water clouds defined by using data from the MODIS instruments. Smaller amounts of cloud categories can reproduce the visible EPOXI data (which is at a very low spectral resolution, R ∼ 6), but cannot reproduce the moderate resolution (R ∼ 500) NIR data. Our simulations are relatively insensitive to variations in the surface resolution and can also reproduce the EPOXI lightcurves at a very low atmospheric resolution. The model can now be used as a forward model to explore the detectability of planetary characteristics by generating synthetic observations of Earth from the far UV to the far IR at a variety of spectral, spatial, and temporal resolutions.
Acknowledgments
This work is supported by the NASA Discovery Program and the EPOXI mission. The authors gratefully acknowledge the contributions of the Deep Impact/EPOXI operations team at the Jet Propulsion Laboratory/California Institute of Technology, without whom Earth observations could not have been accomplished. T.R and V.M. gratefully acknowledge the support of the NASA Astrobiology Institute, without which the original Earth model would not have been developed. We would like to thank Jeff Pedelty for his work designing the EPOXI Earth observation program as well as Tom Ackerman and Gwyn Fireman for assistance with MODIS data interpretation. Some of the results in this paper have been derived using the HEALPix (Górski et al., 2005) package.
Author Disclosure Statement
The authors of this work have no competing financial interests.
Abbreviations
AIRS, Atmospheric Infrared Sounder; HEALPix, Hierarchical Equal Area isoLatitude Pixelization; HRI, High Resolution Instrument; MLS, Microwave Limb Sounder; MODIS, Moderate Resolution Imaging Spectroradiometer; NIR, near-infrared; RMS, root-mean-square; SMART, Spectral Mapping Atmospheric Radiative Transfer; TES, Tropospheric Emission Spectrometer; TPF, Terrestrial Planet Finder.
References
- Arnold L. Gillet S. Lardière O. Riaud P. Schneider J. A test for the search for life on extrasolar planets: looking for the terrestrial vegetation signature in the Earthshine spectrum. Astron Astrophys. 2002;392:231–237. [Google Scholar]
- Aumann H.H. Chahine M.T. Gautier C. Goldberg M.D. Kalnay E. McMillin L.M. Revercomb H. Rosenkranz P.W. Smith W.L. Staelin D.H. Strow L.L. Susskind J. AIRS/AMSU/HSB on the Aqua mission: design, science objectives, data products, and processing systems. IEEE Trans Geosci Remote Sens. 2003;41:253–264. [Google Scholar]
- Basri G. Borucki W.J. Koch D. The Kepler Mission: A wide-field transit search for terrestrial planets. New Astronomy Review. 2005;49:478–485. [Google Scholar]
- Beer R. Glavich T.A. Rider D.M. Tropospheric emission spectrometer for the Earth Observing System's Aura satellite. Appl Opt. 2001;40:2356–2367. doi: 10.1364/ao.40.002356. [DOI] [PubMed] [Google Scholar]
- Beichman C.A., editor; Woolf N.J., editor; Lindensmith C.A., editor. The Terrestrial Planet Finder (TPF): a NASA Origins program to search for habitable planets. Jet Propulsion Laboratory; Pasadena, CA: 1999. [Google Scholar]
- Borucki W.J. Koch D.G. Lissauer J.J. Basri G.B. Caldwell J.F. Cochran W.D. Dunham E.W. Geary J.C. Latham D.W. Gilliland R.L. Caldwell D.A. Jenkins J.M. Kondo Y. The Kepler mission: a wide-field-of-view photometer designed to determine the frequency of Earth-size planets around solar-like stars. Proc SPIE. 2003;4854:129–140. [Google Scholar]
- Christensen P.R. Pearl J.C. Initial data from the Mars Global Surveyor thermal emission spectrometer experiment: observations of the Earth. J Geophys Res. 1997;102:10875–10880. [Google Scholar]
- Cowan N.B. Agol E. Meadows V.S. Robinson T. Livengood T.A. Deming D. Lisse C.M. A'Hearn M.F. Wellnitz D.D. Seager S. Charbonneau D. the EPOXI team. Alien maps of an ocean-bearing world. Astrophys J. 2009;700:915–923. [Google Scholar]
- Cowan N.B. Robinson T.D. Livengood T.A. Deming D. Agol E. A'Hearn M.F. Charbonneau D. Lisse C.M. Meadows V.S. Seager S. Shields A.L. Wellnitz D.D. Rotational variability of Earth's polar regions: implications for detecting snowball planets. Astrophys J. 2011;731:76. [Google Scholar]
- Cox C. Munk W. Measurement of the roughness of the sea surface from photographs of the Sun's glitter. J Opt Soc Am. 1954;44:838–850. [Google Scholar]
- Crisp D. Absorption of sunlight by water vapor in cloudy conditions: a partial explanation for the cloud absorption anomaly. Geophys Res Lett. 1997;24:571–574. [Google Scholar]
- Ford E.B. Seager S. Turner E.L. Characterization of extrasolar terrestrial planets from diurnal photometric variability. Nature. 2001;412:885–887. doi: 10.1038/35091009. [DOI] [PubMed] [Google Scholar]
- Fujii Y. Kawahara H. Suto Y. Fukuda S. Nakajima T. Livengood T.A. Turner E.L. Colors of a second Earth II: effects of clouds on photometric characterization of Earth-like exoplanets. 2011. arXiv:1102.3625v1.
- Goode P.R. Qiu J. Yurchyshyn V. Hickey J. Chu M. Kolbe E. Brown C.T. Koonin S.E. Earthshine observations of the Earth's reflectance. Geophys Res Lett. 2001;28:1671–1674. [Google Scholar]
- Górski K.M. Hivon E. Banday A.J. Wandelt B.D. Hansen F.K. Reinecke M. Bartelmann M. HEALPix: a framework for high-resolution discretization and fast analysis of data distributed on the sphere. Astrophys J. 2005;622:759–771. [Google Scholar]
- Hall D.K. Riggs G. Salomonson V.V. Development of methods for mapping global snow cover using Moderate Resolution Imaging Spectroradiometer (MODIS) data. Remote Sensing of Environment. 1995;54:127–140. [Google Scholar]
- Hampton D.L. Baer J.W. Huisjen M.A. Varner C.C. Delamere A. Wellnitz D.D. A'Hearn M.F. Klaasen K.P. An overview of the instrument suite for the Deep Impact mission. Space Sci Rev. 2005;117:43–93. [Google Scholar]
- Hearty T. Song I. Kim S. Tinetti G. Mid-infrared properties of disk averaged observations of Earth with AIRS. Astrophys J. 2009;693:1763–1774. [Google Scholar]
- Kawahara H. Fujii Y. Global mapping of Earth-like exoplanets from scattered light curves. Astrophys J. 2010;720:1333–1350. [Google Scholar]
- Klaasen K.P. A'Hearn M.F. Baca M. Delamere A. Desnoyer M. Farnham T. Groussin O. Hampton D. Ipatov S. Li J. Lisse C. Mastrodemos N. McLaughlin S. Sunshine J. Thomas P. Wellnitz D. Invited article: Deep Impact instrument calibration. Rev Sci Instrum. 2008;79 doi: 10.1063/1.2972112. [DOI] [PubMed] [Google Scholar]
- Livengood T.A. A'Hearn M.F. Deming D. Charbonneau D. Hewagama T. Lisse C.M. McFadden L.A. Meadows V.S. Seager S. Wellnitz D.D. EPOXI-EPOCh Science Team. EPOXI Empirical Test of Optical Characterization of an Earth-like Planet. (Abstract no. 1.03) Bull Am Astron Soc. 2008;40:385. [Google Scholar]
- Livesey N.J. Read W.G. Lambert A. Cofield R.E. Cuddy D.T. Froidevaux L. Fuller R.A. Jarnot R.F. Jiang J.H. Jiang Y.B. Knosp B.W. Kovalenko L.J. Pickett H.M. Pumphrey H.C. Santee M.L. Schwartz M.J. Stek P.C. Wagner P.A. Waters J.W. Wu D.L. Aura Microwave Limb Sounder Level 2 data quality and description document. Jet Propulsion Laboratory; Pasadena, CA: 2007. [Google Scholar]
- Madhusudhan N. Seager S. A temperature and abundance retrieval method for exoplanet atmospheres. Astrophysical Journal. 2009;707:24–39. [Google Scholar]
- Manalo-Smith N. Smith G.L. Tiwari S.N. Staylor W.F. Analytic forms of bidirectional reflectance functions for application to Earth radiation budget studies. J Geophys Res. 1998;103:19733–19752. [Google Scholar]
- Meadows V.S. Modelling the diversity of extrasolar terrestrial planets. In: Aime C., editor; Vakili F., editor. Direct Imaging of Exoplanets: Science & Techniques. Proceedings of the IAU Colloquium #200. Cambridge University Press; Cambridge: 2006. pp. 25–34. [Google Scholar]
- Meadows V.S. Crisp D. Ground-based near-infrared observations of the Venus nightside: the thermal structure and water abundance near the surface. J Geophys Res. 1996;101:4595–4622. [Google Scholar]
- Montañés-Rodríguez P. Pallé E. Goode P.R. Martín-Torres F.J. Vegetation signature in the observed globally integrated spectrum of Earth considering simultaneous cloud data: applications for extrasolar planets. Astrophys J. 2006;651:544–552. [Google Scholar]
- Muinonen K. Lumme K. Peltoniemi J. Irvine W.M. Light scattering by randomly oriented crystals. Appl Opt. 1989;28:3051–3060. doi: 10.1364/AO.28.003051. [DOI] [PubMed] [Google Scholar]
- Oakley P.H.H. Cash W. Construction of an Earth model: analysis of exoplanet light curves and mapping the next Earth with the New Worlds Observer. Astrophys J. 2009;700:1428–1439. [Google Scholar]
- Pallé E. Goode P.R. Yurchyshyn V. Qiu J. Hickey J. Montañés-Rodríguez P. Chu M. Kolbe E. Brown C.T. Koonin S.E. Earthshine and the Earth's albedo: 2. Observations and simulations over 3 years. J Geophys Res. 2003;108:4710. [Google Scholar]
- Pallé E. Ford E.B. Seager S. Montañés-Rodríguez P. Vazquez M. Identifying the rotation rate and the presence of dynamic weather on extrasolar Earth-like planets from photometric observations. Astrophys J. 2008;676:1319–1329. [Google Scholar]
- Payne V.H. Clough S.A. Shephard M.W. Nassar R. Logan J.A. Information-centered representation of retrievals with limited degrees of freedom for signal: application to methane from the Tropospheric Emission Spectrometer. J Geophys Res. 2009;114 doi: 10.1029/2008JD010155. [DOI] [Google Scholar]
- Riggs G. Hall D.K. Ackerman S.A. Sea ice extent and classification mapping with the Moderate Resolution Imaging Spectroradiometer Airborne Simulator. Remote Sensing of Environment. 1999;68:152–163. [Google Scholar]
- Robinson T.D. Meadows V.S. Crisp D. Detecting oceans on extrasolar planets using the glint effect. Astrophys J. 2010;721:L67–L71. [Google Scholar]
- Rothman L.S. Jacquemart D. Barbe A. Chris Benner D. Birk M. Brown L.R. Carleer M.R. Chackerian C. Chance K. Coudert L.H. Dana V. Devi V.M. Flaud J.M. Gamache R.R. Goldman A. Hartmann J.M. Jucks K.W. Maki A.G. Mandin J.Y. Massie S.T. Orphal J. Perrin A. Rinsland C.P. Smith M.A.H. Tennyson J. Tolchenov R.N. Toth R.A. Vander Auwera J. Varanasi P. Wagner G. The HITRAN 2004 molecular spectroscopic database. J Quant Spectrosc Radiat Transf. 2005;96:139–204. [Google Scholar]
- Rothman L.S. Gordon I.E. Barbe A. Benner D.C. Bernath P.F. Birk M. Boudon V. Brown L.R. Campargue A. Champion J.P. Chance K. Coudert L.H. Dana V. Devi V.M. Fally S. Flaud J.M. Gamache R.R. Goldman A. Jacquemart D. Kleiner I. Lacome N. Lafferty W.J. Mandin J.Y. Massie S.T. Mikhailenko S.N. Miller C.E. Moazzen-Ahmadi N. Naumenko O.V. Nikitin A.V. Orphal J. Perevalov V.I. Perrin A. Predoi-Cross A. Rinsland C.P. Rotger M. Simecková M. Smith M.A.H. Sung K. Tashkun S.A. Tennyson J. Toth R.A. Vandaele A.C. Vander-Auwera J. The HITRAN 2008 molecular spectroscopic database. J Quant Spectrosc Radiat Transf. 2009;110:533–572. [Google Scholar]
- Sagan C. Thompson W.R. Carlson R. Gurnett D. Hord C. A search for life on Earth from the Galileo spacecraft. Nature. 1993;365:715–721. doi: 10.1038/365715a0. [DOI] [PubMed] [Google Scholar]
- Salomonson V.V. Barnes W.L. Maymon P.W. Montgomery H.E. Ostrow H. MODIS—advanced facility instrument for studies of the Earth as a system. IEEE Trans Geosci Remote Sens. 1989;27:145–153. [Google Scholar]
- Seager S. Turner E.L. Schafer J. Ford E.B. Vegetation's red edge: a possible spectroscopic biosignature of extraterrestrial plants. Astrobiology. 2005;5:372–390. doi: 10.1089/ast.2005.5.372. [DOI] [PubMed] [Google Scholar]
- Stam D.M. Spectropolarimetric signatures of Earth-like extrasolar planets. Astron Astrophys. 2008;482:989–1007. [Google Scholar]
- Stephens G.L. Vane D.G. Boain R.J. Mace G.G. Sassen K. Wang Z. Illingworth A.J. O'Connor E.J. Rossow W.B. Durden S.L. Miller S.D. Austin R.T. Benedetti A. Mitrescu C. the Cloudsat science team. The Cloudsat mission and the A-Train. Bulletin of the American Meteorological Society. 2002;83:1771–1790. [Google Scholar]
- Tinetti G. Meadows V.S. Crisp D. Fong W. Fishbein E. Turnbull M. Bibring J.-P. Detectability of planetary characteristics in disk-averaged spectra. I: The Earth model. Astrobiology. 2006a;6:34–47. doi: 10.1089/ast.2006.6.34. [DOI] [PubMed] [Google Scholar]
- Tinetti G. Meadows V.S. Crisp D. Kiang N.Y. Kahn B.H. Fishbein E. Velusamy T. Turnbull M. Detectability of planetary characteristics in disk-averaged spectra II: Synthetic spectra and light-curves of Earth. Astrobiology. 2006b;6:881–900. doi: 10.1089/ast.2006.6.881. [DOI] [PubMed] [Google Scholar]
- Turnbull M.C. Traub W.A. Jucks K.W. Woolf N.J. Meyer M.R. Gorlova N. Skrutskie M.F. Wilson J.C. Spectrum of a habitable world: Earthshine in the near-infrared. Astrophys J. 2006;644:551–559. [Google Scholar]
- Waters J.W. Froidevaux L. Harwood R.S. Jarnot R.F. Pickett H.M. Read W.G. Siegel P.H. Cofield R.E. Filipiak M.J. Flower D.A. Holden J.R. Lau G.K. Livesey N.J. Manney G.L. Pumphrey H.C. Santee M.L. Wu D.L. Cuddy D.T. Lay R.R. Loo M.S. Perun V.S. Schwartz M.J. Stek P.C. Thurstans R.P. Boyles M.A. Chandra K.M. Chavez M.C. Chen G.S. Chudasama B.V. Dodge R. Fuller R.A. Girard M.A. Jiang J.H. Jiang Y. Knosp B.W. Labelle R.C. Lam J.C. Lee A.K. Miller D. Oswald J.E. Patel N.C. Pukala D.M. Quintero O. Scaff D.M. Vansnyder W. Tope M.C. Wagner P.A. Walch M.J. The Earth Observing System Microwave Limb Sounder (EOS MLS) on the Aura satellite. IEEE Trans Geosci Remote Sens. 2006;44:1075–1092. [Google Scholar]
- Williams D.M. Gaidos E. Detecting the glint of starlight on the oceans of distant planets. Icarus. 2008;195:927–937. [Google Scholar]
- Wolfe R.E. MODIS Geolocation. In: Qu J.J., editor; Gao W., editor; Kafatos M., editor; Murphy R.E., editor; Salomonson V.V., editor. Earth Science Satellite Remote Sensing, Vol. 1 of Science and Instruments. Springer; Berlin: 2006. pp. 50–73. [Google Scholar]
- Woolf N.J. Smith P.S. Traub W.A. Jucks K.W. The spectrum of Earthshine: a pale blue dot observed from the ground. Astrophys J. 2002;574:430–433. [Google Scholar]