New variable selection methods for zero-inflated count data with applications to the substance abuse field

Abstract

Zero-inflated count data are very common in health surveys. This study develops new variable selection methods for the zero-inflated Poisson regression model. Our simulations demonstrate the negative consequences which arise from the ignorance of zero-inflation. Among the competing methods, the one-step SCAD method is recommended because it has the highest specificity, sensitivity, exact fit, and lowest estimation error. The design of the simulations is based on the special features of two large national databases commonly used in the alcoholism and substance abuse field so that our findings can be easily generalized to the real settings. Applications of the methodology are demonstrated by empirical analyses on the data from a well-known alcohol study.

1. Introduction

Health surveys commonly inquire about participants’ symptoms of target diseases. The resulting symptom count is an important indicator of the severity of a particular disease. Identifying risk factors for a disease can provide invaluable guidance for policy making and prevention programming. Our methodological research has been motivated by the challenges we encountered when building a multilevel model of individual, familial, and neighborhood influences on the symptomatology of alcohol use disorder (AUD). Although being the most distal among the three levels of influence, many risk factors involving the neighborhood environment, such as high poverty rate and unemployment rate, have been found to be associated with residents’ alcohol or other substance use (e.g. [1, 2, 3, 4, 5]). The neighborhood environment is usually characterized by descriptive statistics at the census tract level. Through geocoding, study participants’ symptom count data and potential individual and familial risk factors can be merged with potential risk factors at the neighborhood level (i.e. the census tract level). However, there are many candidate variables in the census data and some of them are highly correlated. Our goal is to select a subset of important neighborhood risk factors for AUD symptomatology that can be used for model building purposes.

When health surveys are conducted on the general population or a community sample, the symptom count measure tends to have a high frequency of zero values. In the context of alcohol research, such excess zeros in the data come from nondrinkers or drinkers who have not developed AUD symptoms. Because zero-inflated count data are very common in health surveys, a statistical method that can model such highly skewed discrete distributions is highly desirable in practice. Classic variable selection criteria (e.g. AIC [6] and BIC [7]) and traditional variable selection procedures, including stepwise and best subset selection, may be adapted to analysis of zero-inflated count data. However, traditional variable selection procedures are unstable – that is, small changes in the data may result in very different models [8]. Furthermore, when the pool of candidate variables is large, the best subset selection procedure becomes infeasible since it is computationally expensive.

Variable selection has been an active research area in the recent statistical literature. The Least Absolute Shrinkage and Selection Operator (LASSO) [9] and the Smoothly Clipped Absolute Deviation penalty (SCAD) [10] are two well-known variable selection procedures developed in the past decade. Both methods have desirable properties and both have been extended to generalized linear models that can handle binary, categorical, and count data [11, 12]. The aim of this paper is to develop new variable selection procedures for the zero-inflated Poisson regression model (ZIP) [13] using LASSO and one-step SCAD techniques. In order to better assess the applicability of these new variable selection methods in the area of alcoholism and substance abuse research, we conduct simulations to evaluate their performance based on the data features of the U.S. census and a national health survey on alcohol and related conditions. We also demonstrate the use of our methodology by analyzing data from a well-known alcohol study.

This paper is organized as follows. In Section 2, we develop new variable selection methods for the ZIP model using LASSO and one-step SCAD techniques and we address issues related to the practical implementation of the proposed procedures. In Section 3, we conduct simulation studies to assess the performance of the proposed procedures, and investigate the impact of the ignorance of zero-inflation. In Section 4, we conduct an empirical analysis on the data from a community sample using the proposed procedures. Discussion and concluding remarks are presented in Section 5. The technical details and key derivation of the statistical property related to the proposed methods are given in the appendices.

2. The Model and Variable Selection Methods

2.1. Zero-inflated Poisson Regression Model

Suppose that {w_i, y_i}, i = 1, …, n, is an independent and identically distributed sample from a population (w, y}. Let x_i and z_i be d₁- and d₂-dimensional sub-vectors of w_i, respectively. Here x_i and z_i may contain the same elements. Conditioning on w_i, y_i follows a zero-inflated Poisson (ZIP) distribution

$$y_i\sim {\pi }_i\text{Poisson}(0)+(1-{\pi }_i)\text{Poisson}({\lambda }_i),$$ (1)

where ${\pi }_i=exp({\mathit{z}}_i^{\prime }\mathit{\gamma })/\{1+exp({\mathit{z}}_i^{\prime }\mathit{\gamma })\}$ and ${\lambda }_i=exp({\mathit{x}}_i^{\prime }\mathit{\beta })$ with unknown regression coefficient vectors β = (β₁, …, β_d1)′ and γ = (γ₁, …, γ_d2)′. Here Poisson(0) stands for a degenerate distribution with the support point at 0. To include an intercept, we set x_i1 = 1 and z_i1 = 1. Thus, β₁ and γ₁ are the corresponding intercepts. Model (1) is referred to as the ZIP model. From (1), the conditional probability mass function for y_i is

$$P(y_i=0\mid {\mathit{w}}_i)={\pi }_i+(1-{\pi }_i)e^{-{\lambda }_i};P(y_i=m\mid {\mathit{w}}_i)=(1-{\pi }_i)e^{-{\lambda }_i}{\lambda }_i^m/m!,\text{for}m=1,2,\dots .$$

The logarithm of the likelihood function is

$$\ell (\mathit{\beta },\mathit{\gamma })=\sum _{y_i=0}log[exp({\mathit{z}}_i^{\prime }\mathit{\gamma })+exp\{-exp({\mathit{x}}_i^{\prime }\mathit{\beta })\}]+\sum _{y_i>0}\{y_i{\mathit{x}}_i^{\prime }\mathit{\beta }-exp({\mathit{x}}_i^{\prime }\mathit{\beta })\}-\sum _{i=1}^{n}log\{1+exp({\mathit{z}}_i^{\prime }\mathit{\gamma })\}-\sum _{y_i>0}log(y_i!).$$ (2)

Lambert [13] proposed the ZIP to model zero-inflated count data collected from a quality control study, in which the response typically is the number of defective products in a sample unit. The major strength of the ZIP model is that it can simultaneously accommodate one set of factors x_i that contribute to fewer defects in the imperfect state and another set of factors z_i that make the perfect state more likely. The model has been applied in many fields including medicine (e.g. [14]). An alternative model, the hurdle model [15], originated in the economic literature that postulates a two-stage decision structure in the demand process: the first stage involves a selection process leading to zero or non-zero outcomes (a logit model); the second stage models the distribution of non-zero outcomes (a truncated Poisson model). The ZIP model is more intuitive when the population consists of a group of people who can only have zero symptoms (e.g. nondrinkers) and another group who may have zero symptoms (e.g. drinkers). Thus, the logic behind the ZIP model fits better with our practical setting that does not involve a clear choice between zero and non-zero outcomes (symptoms). For this reason, we adopted the ZIP model in this paper.

2.2. Variable Selection

Health surveys commonly collect many variables that can potentially be included in the model. In practice, it is desirable to select important variables and have a parsimonious model in order to improve prediction accuracy and model interpretability [9]. Here we propose new variable selection procedures for the ZIP model using the penalized likelihood method.

The penalized likelihood for the ZIP model is defined to be

$$Q(\mathit{\beta },\mathit{\gamma })=\ell (\mathit{\beta },\mathit{\gamma })-n\sum _{j=1}^{d_1}{p}_{a_j}(\mid {\beta }_j\mid )-n\sum _{k=1}^{d_2}{p}_{b_k}(\mid {\gamma }_k\mid ),$$ (3)

where p_aj(·) and p_bk (·) are penalty functions with tuning parameters a_j and b_k. The regression coefficients, β_j and γ_k, are allowed to have different penalties. In particular, we may set p_a1 (|β₁|) = p_b1 (|γ₁|)= 0 in order not to penalize the intercepts β₁ and γ₁. Fan and Li [10] studied the choice of penalty function in depth. In this paper, we consider only the most commonly used penalties developed in the recent literature: the L₁ penalty, defined by p_τ (α) = τ|α|, and the SCAD penalty, defined by

$$p_{\tau }(\mid \alpha \mid )=\{\begin{array}{lll}\tau \mid \alpha \mid ,\hfill & \text{if}\hfill & 0\le \mid \alpha \mid <\tau \hfill \\ -({\mid \alpha \mid }^2-2c\tau \mid \alpha \mid +{\tau }^2)/[2(c-1)],\hfill & \text{if}\hfill & \tau \le \mid \alpha \mid <c\tau \hfill \\ (c+1){\tau }^2/2,\hfill & \text{if}\hfill & \mid \alpha \mid \ge c\tau ,\hfill \end{array}$$

where the value of c = 3.7, as suggested in Fan and Li [10].

For linear regression models, the penalized least squares with the L₁ penalty leads to the LASSO proposed by Tibshirani [9]. The advantage of the penalized least squares with the L₁ penalty is that the entire solution path of the LASSO estimator can be constructed by using the Least Angle Regression (LAR) [16]. As demonstrated in Fan and Li [10], the penalized least squares with the SCAD penalty possess good theoretical properties, particularly, the oracle property (i.e. the resulting estimator asymptotically performs as well as if we knew the true submodel). For this reason, we consider only the L₁ and SCAD penalties.

The likelihood function for the ZIP model is, however, much more complicated than the least squares function for linear regression models or the likelihood function for generalized linear models. To maximize the penalized likelihood function (3), we adapt the one-step sparse estimator strategy proposed in Zou and Li [12].

Set the initial values (β⁽⁰⁾, γ⁽⁰⁾) to be the un-penalized maximum likelihood estimates (β̂, γ̂). The log-likelihood function ℓ(β, γ) can be locally approximated by

$$\ell ({\mathit{\beta }}^{(0)},{\mathit{\gamma }}^{(0)})+\frac{1}{2}[{(\mathit{\beta }-{\mathit{\beta }}^{(0)})}^{\prime },{(\mathit{\gamma }-{\mathit{\gamma }}^{(0)})}^{\prime }][{\nabla }^2{\ell }^{\prime }{\mathit{\beta }}^{(0)},{\mathit{\gamma }}^{(0)})]\left[\begin{array}{c}\mathit{\beta }-{\mathit{\beta }}^{(0)}\\ \mathit{\gamma }-{\mathit{\gamma }}^{(0)}\end{array}\right],$$ (4)

where Δ² ℓ(β⁽⁰⁾, γ⁽⁰⁾) is the Hessian matrix of the log-likelihood function, since the gradient of the log-likelihood function at the initial value Δℓ(β⁽⁰⁾, γ⁽⁰⁾) = 0. The penalty functions can be locally linear approximated by

$$p_{a_j}(\mid {\beta }_j\mid )\approx p_{a_j}(\mid {\beta }_j^{(0)}\mid )+p_{a_j}^{\prime }(\mid {\beta }_j^{(0)}\mid )(\mid {\beta }_j\mid -\mid {\beta }_j^{(0)}\mid ),\mathit{for}{\beta }_j\approx {\beta }_j^{(0)};$$

and

$$p_{b_k}(\mid {\gamma }_k\mid )\approx p_{b_k}(\mid {\gamma }_k^{(0)}\mid )+p_{b_k}^{\prime }(\mid {\gamma }_k^{(0)}\mid )(\mid {\gamma }_k\mid -\mid {\gamma }_k^{(0)}\mid ),\mathit{for}{\gamma }_k\approx {\gamma }_k^{(0)}.$$

Thus, the one-step sparse estimator for the ZIP model is defined to be

$$({\widehat{\mathit{\beta }}}^{(1)},{\widehat{\mathit{\gamma }}}^{(1)})={\text{argmin}}_{\mathit{\beta },\mathit{\gamma }}\{\frac{1}{2}[{(\mathit{\beta }-{\mathit{\beta }}^{(0)})}^{\prime },{(\mathit{\gamma }-{\mathit{\gamma }}^{(0)})}^{\prime }][-{\nabla }^2\ell ({\mathit{\beta }}^{(0)},{\mathit{\gamma }}^{(0)})]\left[\begin{array}{c}\mathit{\beta }-{\mathit{\beta }}^{(0)}\\ \mathit{\gamma }-{\mathit{\gamma }}^{(0)}\end{array}\right]+n\sum _{j=1}^{d_1}{p}_{a_j}^{\prime }(\mid {\beta }_j^{(0)}\mid )\mid {\beta }_j\mid +n\sum _{k=1}^{d_2}{p}_{b_k}^{\prime }(\mid {\gamma }_k^{(0)}\mid )\mid {\gamma }_k\mid \}$$

When the SCAD penalty is employed, this one-step sparse estimator is referred to as one-step SCAD that can be viewed as an adaptive LASSO with weights obtained from the SCAD penalty. Since the first term in the objective function is a quadratic function of (β′, γ′), and the penalty function is a weighted L₁ penalty, we employ the LARS algorithm to obtain the one-step sparse estimator. See Appendix I for the technical details related to the implementation of the LARS algorithm. Using the same techniques employed in Zou and Li [12], it can be shown that the one-step SCAD possesses an oracle property (see Appendix II for the key derivation). The local quadratic approximation (4) of the logarithm of the likelihood function indeed is the same as the least squares approximation in Wang and Leng [17], in which the authors emphasized the adaptive LASSO penalty in comparison to the SCAD penalty used in this article.

Automatic selection of the tuning parameters a_j and b_k using data-driven methods is desirable and yet computationally expensive because one has to search over a (d₁ + d₂)-dimensional grid for the proposed one-step sparse estimator. To save computation cost, we follow the strategy of Fan and Li 18] and set $a_j=\tau \text{SE}({\widehat{\beta }}_j^{(0)})$ and $b_k=\tau \text{SE}({\widehat{\gamma }}_k^{(0)})$, where $\text{SE}({\widehat{\beta }}_j^{(0)})$ and $\text{SE}({\widehat{\gamma }}_k^{(0)})$ are the standard errors of the unpenalized maximum likelihood estimate of β_j and γ_k, respectively. This procedure reduces the search for τ to a set of one-dimensional grid points. In our simulation studies and our empirical analysis using a real data set, τ is determined from a modification of the BIC tuning parameter selector [19]. Our simulation results show that this strategy for determining the tuning parameters works well.

3. Simulation Study

Most simulation studies in the variable selection literature employ covariates that are idealistically distributed (e.g. multivariate normal) and parameters that are arbitrarily determined. However, as pointed out by Burton et al. [20], simulated data should closely represent the structure of real data so that the results can be generalizable to real situations and thus have credibility. One unique strength of this study is that our simulation experiments are based on the special features of two large national databases: the 2000 U.S. census and the National Epidemiologic Survey on Alcohol and Related Conditions (NESARC) [21]. For this reason, our results can be used to guide future applications of the proposed methods in the field of alcoholism and substance abuse research. In Experiment 1, we used a census database as a pseudo-population from which to draw covariate values in varied sample sizes. We determined parameter values by fitting a ZIP model to census and NESARC data. In order to evaluate the performance of competing methods under different correlation structures, we conducted Experiment 2 that employed the same set of parameter values as in Experiment 1 but drew random samples from multivariate normal distributions with varied levels of correlation and sample sizes. In Experiment 3, the other two factors were manipulated while holding the correlation and sample size at the medium values: the proportion of non-zero coefficients and the proportion of zero outcome.

3.1. Experiment 1: Sampling from Census Data with Varied Sample Sizes

This experiment aims to evaluate the performance of the following four competing methods, when the true model is a ZIP model with two different sets of covariates in the Poisson component and the zero component:

1. Poisson regression with LASSO (PR-LASSO)

2. Poisson regression with SCAD (PR-SCAD)

3. ZIP regression with LASSO (ZIP-LASSO)

4. ZIP regression with SCAD (ZIP-SCAD).

In order to construct covariates with real data properties, we obtained the statistical characteristics of 66,304 census tracts from the official 2000 U.S. census website and from these derived the twenty composite variables which have been used in the substance abuse literature to indicate neighborhood risk (listed in Table 1). These variables were standardized (with sample means and standard deviations) and used as candidates for variable selection in the Poisson and zero components of the model. Not surprisingly, some of these variables are highly correlated (Pearson’s r = 0.01 – 0.80). By combining these covariates along with the AUD symptom counts from the NESARC database (i.e. the outcome), we were able to conduct exploratory analyses and determine the following set of true parameter values:

$$\begin{array}{c}\mathit{\beta }={(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0)}^{\prime }\\ \mathit{\gamma }={(0.30,-0.48,0,0,0,0.40,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0)}^{\prime }.\end{array}$$

Table 1.

The covariates derived from the 2000 U.S. census data.

1	Proportion of male residents
2	Proportion of residents aged 25+ who dropped out of high school
3	Proportion of residents aged 16+ who are unemployed
4	Proportion of residents aged 16+ with professional or managerial occupations
5	Proportion of residents aged 16+ who are not in labor force
6	Resident per capita income
7	Proportion of residents with public assistance income in 1999
8	Proportion of households with public assistance income in 1999
9	Proportion of residents under poverty line in 1999
10	Proportion of residents who are black
11	Proportion of residents who are Hispanic or Latino
12	Proportion of residents born outside the U.S.
13	Proportion of households with husband, wife and children under age 18
14	Proportion of households that are female-headed and have children under age 18
15	Average household size
16	Proportion of housing units not owned by occupants
17	Proportion of vacant housing
18	Proportion of residents aged 5+ who did not live at the same address 5 years earlier
19	Proportion of disabled residents aged 5+
20	Proportion of urban area

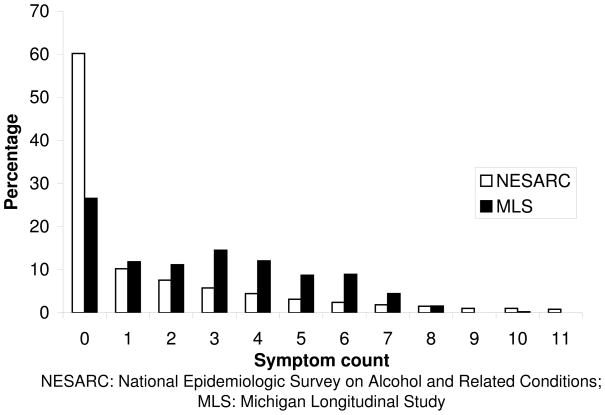
Applying this set of ZIP regression parameters to the covariates x_i(=z_i) from the ith census tract, we generated the outcome Y_i (i = 1, …, 66304). The resulting outcome distributes like the AUD symptom count in the NESARC database (see Figure 1). We randomly drew a sample of size n from the resulting 66,304 covariates-outcome pairs and applied the four statistical methods to analyze the data. Three sample sizes, small (n = 300), medium (n = 600) and large (n = 900), were chosen based on our survey of existing studies in the substance abuse field (e.g. [22, 23, 24, 25, 26, 27]). This experiment was replicated 1,000 times.

Figure 1. Distributions of DSM-IV alcohol use disorder symptom counts.

In Table 2, the performance of the four competing statistical methods are evaluated based on several criteria. For each replication, we computed the mean squared error (MSE) for both the reduced model and the full ZIP model, then computed the ratio of these two MSE values. The median of the ratios from 1,000 replications is reported under the column “MRMSE.” A smaller value indicates a better performance in terms of parameter estimation. We also calculated the specificity and sensitivity for each replication. Specificity is defined as the proportion of zero coefficients that were correctly estimated to be zero; sensitivity is the proportion of nonzero coefficients that were correctly estimated to be nonzero. The averages of both indices over 1,000 replications are listed under the columns with corresponding headings in the table. “Under fit” is defined as the probability of excluding any significant coefficients in 1,000 replications, whereas “exact fit” is the probability of selecting the exact sub-model. The probabilities of including all significant variables and some noise variables (1, 2, ≥ 3) are also reported in the columns under “over fit.”

Table 2.

Simulation results for Experiment 1: census data.

The Poisson Component
Method	MRMSEa	Specificityb	Sensitivityc	Under fitd	Exact fite	Over fitf
						1	2	≥ 3
n = 300
PR-LASSO	0.923	0.465	0.771	0.419	0.000	0.000	0.000	0.581
PR-SCAD	1.716	0.575	0.686	0.532	0.000	0.000	0.003	0.465
ZIP-LASSO	0.218	0.808	0.760	0.366	0.010	0.050	0.103	0.471
ZIP-SCAD	0.201	0.891	0.740	0.452	0.154	0.163	0.118	0.113
n = 600
PR-LASSO	2.060	0.425	0.921	0.157	0.000	0.000	0.000	0.843
PR-SCAD	3.112	0.581	0.858	0.273	0.000	0.000	0.000	0.727
ZIP-LASSO	0.336	0.774	0.973	0.050	0.010	0.044	0.142	0.754
ZIP-SCAD	0.101	0.903	0.964	0.073	0.247	0.279	0.197	0.204
The Zero Component
n = 300
ZIP-LASSO	0.280	1.000	0.002	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	0.210	0.983	0.315	0.978	0.008	0.010	0.004	0.000
n = 600
ZIP-LASSO	0.746	0.997	0.074	0.952	0.026	0.019	0.001	0.002
ZIP-SCAD	0.292	0.981	0.670	0.785	0.159	0.046	0.010	0.000

^aMRMSE = Median of the ratio of the reduced model MSE to the full model MSE.

^bSpecificity = Mean of the proportion of zero coefficients that were correctly identified.

^cSensitivity = Mean of the proportion of nonzero coefficients that were correctly identified.

^dUnder fit = Probability of excluding any significant coefficients.

^eExact fit = Probability of selecting the exact sub-model.

^fOver fit = Probabilities of including all significant variables and some noise variables (1, 2, ≥ 3).

Table 2 summaries the simulation results for the Poisson component (top of table) and the zero component (bottom of table) of the ZIP model. In order to save space, we omit the results of the n = 900 condition from the table. Interested readers may request the technical report with a complete table from the first author. For the Poisson component, the Poisson regression methods (i.e. PR-LASSO and PR-SCAD) tended to have higher values of MRMSE, low specificity, and never fit the model exactly because they did not take into account the excess zeros in the data. Their lower levels of specificity (0.4–0.6) stemmed from their greater tendency to over fit the model (i.e. select noise variables). Between the ZIP regression methods, the SCAD outperformed the LASSO on MRMSE, specificity, and exact fit across all sample sizes. ZIP-LASSO tended to over fit to a large degree and thus performed poorly. In terms of the zero component, we only compared the two ZIP methods because the Poisson regression methods did not employ the zero component. ZIP-SCAD outperformed ZIP-LASSO on MRMSE, sensitivity, and exact fit across all sample sizes. The performance of both methods on sensitivity and exact fit tended to improve as the sample size increased.

3.2. Experiment 2: Manipulating Correlations and Sample Sizes

In Experiment 1, we drew random samples from the census data that served as a pseudo-population having a given correlation structure. In order to evaluate the performance of the competing methods under different correlation structures, we conducted Experiment 2 by manipulating the levels of correlation while employing the same set of parameter values and sample sizes as in Experiment 1. We drew random samples from a multivariate normal distribution N₂₀(0, Σ), where the diagonal element σ_ii = 1 and the off-diagonal element σ_ij = ρ^|i–j| (i, j = 1, …, 20). Because the correlation coefficients for the covariates in census data range from 0.01 to 0.80, three levels of correlation were used in this experiment: small (ρ = 0), medium (ρ = 0.4), and large (ρ = 0.8).

The results of Experiment 2 are depicted in Tables 3–4. In order to save space, we omit the results of the n = 900 and ρ = 0.8 conditions from the tables. Interested readers may request the technical report with complete tables from the first author. Some of the general trends observed in Experiment 1 are also observed in Experiment 2. The Poisson regression methods had high MRMSE, low specificity, and zero exact fit across the three levels of correlation due to their tendency to over fit the model. Between the two ZIP methods, the SCAD tended to have lower MRMSE in both the Poisson and the zero components, higher sensitivity in the zero component, and higher exact fit in the zero component. As the sample size increased or the correlation decreased, the ZIP-SCAD had a noticeable improvement in performance in the zero component. The ZIP-LASSO’s performance, on the other hand, followed a clear pattern of improvement in the Poisson component as the correlation decreased.

Table 3.

Simulation results for Experiment 2: multivariate normal data with ρ = 0.0.

The Poisson Component
Method	MRMSEa	Specificityb	Sensitivityc	Under fitd	Exact fite	Over fitf
						1	2	≥ 3
n = 300
PR-LASSO	2.421	0.477	0.994	0.012	0.001	0.001	0.006	0.980
PR-SCAD	3.321	0.609	0.988	0.025	0.002	0.007	0.012	0.954
ZIP-LASSO	0.375	0.955	0.996	0.008	0.502	0.286	0.124	0.080
ZIP-SCAD	0.094	0.971	0.999	0.002	0.664	0.208	0.084	0.042
n = 600
PR-LASSO	5.381	0.479	1.000	0.000	0.000	0.000	0.000	1.000
PR-SCAD	6.932	0.641	1.000	0.001	0.000	0.000	0.000	0.999
ZIP-LASSO	0.508	0.968	1.000	0.000	0.617	0.247	0.094	0.042
ZIP-SCAD	0.154	0.921	1.000	0.000	0.288	0.304	0.223	0.185
The Zero Component
n = 300
ZIP-LASSO	1.470	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	1.192	1.000	0.185	0.983	0.015	0.002	0.000	0.000
n = 600
ZIP-LASSO	3.516	1.000	0.001	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	0.642	0.998	0.793	0.516	0.462	0.020	0.002	0.000

^aMRMSE = Median of the ratio of the reduced model MSE to the full model MSE.

^bSpecificity = Mean of the proportion of zero coefficients that were correctly identified.

^cSensitivity = Mean of the proportion of nonzero coefficients that were correctly identified.

^dUnder fit = Probability of excluding any significant coefficients.

^eExact fit = Probability of selecting the exact sub-model.

^fOver fit = Probabilities of including all significant variables and some noise variables (1, 2, ≥ 3).

Table 4.

Simulation results for Experiment 2: multivariate normal data with ρ = 0.4.

The Poisson Component
Method	MRMSEa	Specificityb	Sensitivityc	Under fitd	Exact fite	Over fitf
						1	2	≥3
n = 300
PR-LASSO	1.965	0.521	0.997	0.007	0.000	0.000	0.003	0.990
PR-SCAD	2.698	0.629	0.986	0.028	0.000	0.005	0.027	0.940
ZIP-LASSO	0.281	0.941	0.998	0.004	0.380	0.325	0.181	0.110
ZIP-SCAD	0.086	0.961	1.000	0.000	0.570	0.251	0.109	0.070
n = 600
PR-LASSO	4.107	0.517	1.000	0.000	0.000	0.000	0.000	1.000
PR-SCAD	5.388	0.637	1.000	0.001	0.000	0.000	0.003	0.996
ZIP-LASSO	0.361	0.956	1.000	0.000	0.494	0.310	0.139	0.057
ZIP-SCAD	0.125	0.909	1.000	0.000	0.234	0.291	0.229	0.246
The Zero Component
n = 300
ZIP-LASSO	1.103	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	0.902	0.999	0.224	0.973	0.026	0.001	0.000	0.000
n = 600
ZIP-LASSO	2.673	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	0.536	0.997	0.781	0.557	0.411	0.028	0.003	0.001

^aMRMSE = Median of the ratio of the reduced model MSE to the full model MSE.

^bSpecificity = Mean of the proportion of zero coefficients that were correctly identified.

^cSensitivity = Mean of the proportion of nonzero coefficients that were correctly identified.

^dUnder fit = Probability of excluding any significant coefficients.

^eExact fit = Probability of selecting the exact sub-model.

^fOver fit = Probabilities of including all significant variables and some noise variables (1, 2, ≥ 3).

3.3. Experiment 3: Manipulating Proportions of Non-zero Coefficients & Proportions of Zero Outcome

In Experiment 3, we evaluated the performance of the competing methods when the proportion of non-zero coefficients and the proportion of zero outcome were varied. Since the effects of correlation and sample size on the performance were tested in Experiment 2, we fixed both factors at their medium values: ρ = 0.4, n = 600. The proportion of non-zero coefficients was manipulated at three levels: 15%, 30%, and 45%. The proportion of zero outcome was also varied at three levels: 30%, 45%, and 60%. The following are the parameter values that generated these 3 × 3 settings: 15% non-zero coefficients with 30% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0)}^{\prime }\\ \mathit{\gamma }={(-1.20,-0.48,0,0,0,0.40,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0)}^{\prime }\end{array}$$

15% non-zero coefficients with 45% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0)}^{\prime }\\ \mathit{\gamma }={(-0.35,-0.48,0,0,0,0.40,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0)}^{\prime }\end{array}$$

15% non-zero coefficients with 60% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0)}^{\prime }\\ \mathit{\gamma }={(0.30,-0.48,0,0,0,0.40,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0)}^{\prime }\end{array}$$

30% non-zero coefficients with 30% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.50,0,0,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0,0,0.20,0,0,0)}^{\prime }\\ \mathit{\gamma }={(-1.05,0,0.45,0,-0.3,0,0,0,0,0,-0.33,0,-0.39,0,0,0.3,0,0,0,0.36,0)}^{\prime }\end{array}$$

30% non-zero coefficients with 45% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.10,0,0,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0,0,0.20,0,0,0)}^{\prime }\\ \mathit{\gamma }={(-0.41,0,0.45,0,-0.3,0,0,0,0,0,-0.33,0,-0.39,0,0,0.3,0,0,0,0.36,0)}^{\prime }\end{array}$$

30% non-zero coefficients with 60% zero outcome

$$\begin{array}{c}\mathit{\beta }={(0.10,0,0,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0,0,0.20,0,0,0)}^{\prime }\\ \mathit{\gamma }={(-0.3,0,0.45,0,-0.3,0,0,0,0,0,-0.33,0,-0.39,0,0,0.3,0,0,0,0.36,0)}^{\prime }\end{array}$$

45% non-zero coefficients with 30% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.8,0,0.28,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0.21,0,0.20,0,-0.28,0)}^{\prime }\\ \mathit{\gamma }={(-1.14,0,0.45,0,-0.3,0,-0.45,0,-0.54,0,-0.33,0,-0.39,0,0,0.3,0.6,0,0,0.36,0)}^{\prime }\end{array}$$

45% non-zero coefficients with 45% zero outcome

$$\begin{array}{c}\mathit{\beta }={(1.1,0,0.28,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0.21,0,0.20,0,-0.28,0)}^{\prime }\\ \mathit{\gamma }={(-0.6,0,0.45,0,-0.3,0,-0.45,0,-0.54,0,-0.33,0,-0.39,0,0,0.3,0.6,0,0,0.36,0)}^{\prime }\end{array}$$

45% non-zero coefficients with 60% zero outcome

$$\begin{array}{c}\mathit{\beta }={(0.5,0,0.28,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0.21,0,0.20,0,-0.28,0)}^{\prime }\\ \mathit{\gamma }={(-0.09,0,0.45,0,-0.3,0,-0.45,0,-0.54,0,-0.33,0,-0.39,0,0,0.3,0.6,0,0,0.36,0)}^{\prime }\end{array}$$

Tables 5–6 summarize the results of Experiment 3. In order to save space, we omit the results of the 60% zeros and 45% non-zero coefficients conditions from the table. Interested readers may request the technical report with complete tables from the first author. The Poisson regression methods performed poorly across all the 9 settings due to their tendency to over fit the model. This tendency was also observed in the other two experiments. While the two ZIP methods had comparable performance in the Poisson component, the ZIP-LASSO performed poorly (i.e. almost zero sensitivity and exact fit) across all the settings in the zero component. As the proportion of non-zero coefficients increased, the ZIP-LASSO’s performance became worse in the Poisson component while the ZIP-SCAD’s performance was mostly affected in the zero component. When there were 15 or 30% non-zero coefficients, the two ZIP methods tended to perform worse in the Poisson component as the proportion of zero outcome increased.

Table 5.

Simulation results for Experiment 3: 15% non-zero coefficients, ρ = 0.4, n = 600.

The Poisson Component
Method	MRMSEa	Specificityb	Sensitivityc	Under fitd	Exact fite	Over fitf
						1	2	≥3
30% zeros
PR-LASSO	1.344	0.655	1.000	0.000	0.000	0.001	0.026	0.973
PR-SCAD	1.439	0.723	1.000	0.000	0.014	0.043	0.088	0.855
ZIP-LASSO	0.391	0.961	1.000	0.000	0.538	0.290	0.121	0.051
ZIP-SCAD	0.080	0.948	1.000	0.000	0.652	0.092	0.084	0.172
45% zeros
PR-LASSO	2.864	0.568	1.000	0.000	0.000	0.000	0.001	0.999
PR-SCAD	3.647	0.652	1.000	0.000	0.000	0.001	0.015	0.984
ZIP-LASSO	0.372	0.953	1.000	0.000	0.479	0.316	0.126	0.079
ZIP-SCAD	0.147	0.876	1.000	0.000	0.202	0.183	0.209	0.406
The Zero Component
30% zeros
ZIP-LASSO	1.832	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	1.508	1.000	0.192	0.950	0.049	0.001	0.000	0.000
45% zeros
ZIP-LASSO	2.640	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	0.794	0.998	0.655	0.680	0.309	0.009	0.002	0.000

^aMRMSE = Median of the ratio of the reduced model MSE to the full model MSE.

^bSpecificity = Mean of the proportion of zero coefficients that were correctly identified.

^cSensitivity = Mean of the proportion of nonzero coefficients that were correctly identified.

^dUnder fit = Probability of excluding any significant coefficients.

^eExact fit = Probability of selecting the exact sub-model.

^fOver fit = Probabilities of including all significant variables and some noise variables (1, 2, ≥ 3).

Table 6.

Simulation results for Experiment 3: 30% non-zero coefficients, ρ = 0.4, n = 600.

The Poisson Component
Method	MRMSEa	Specificityb	Sensitivityc	Under fitd	Exact fite	Over fitf
						1	2	≥3
30% zeros
PR-LASSO	4.088	0.437	1.000	0.000	0.000	0.000	0.004	0.996
PR-SCAD	4.395	0.596	1.000	0.000	0.001	0.016	0.046	0.937
ZIP-LASSO	0.936	0.828	1.000	0.000	0.101	0.214	0.245	0.440
ZIP-SCAD	0.340	0.917	1.000	0.000	0.535	0.222	0.079	0.164
45% zeros
PR-LASSO	4.024	0.438	0.988	0.070	0.000	0.000	0.002	0.928
PR-SCAD	4.880	0.636	0.973	0.157	0.000	0.014	0.054	0.775
ZIP-LASSO	0.903	0.818	1.000	0.000	0.085	0.221	0.237	0.457
ZIP-SCAD	0.336	0.897	1.000	0.001	0.368	0.214	0.192	0.225
The Zero Component
30% zeros
ZIP-LASSO	2.428	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	2.256	0.999	0.100	0.993	0.007	0.000	0.000	0.000
45% zeros
ZIP-LASSO	2.529	1.000	0.000	1.000	0.000	0.000	0.000	0.000
ZIP-SCAD	1.477	0.997	0.357	0.961	0.035	0.004	0.000	0.000

^aMRMSE = Median of the ratio of the reduced model MSE to the full model MSE.

^bSpecificity = Mean of the proportion of zero coefficients that were correctly identified.

^cSensitivity = Mean of the proportion of nonzero coefficients that were correctly identified.

^dUnder fit = Probability of excluding any significant coefficients.

^eExact fit = Probability of selecting the exact sub-model.

^fOver fit = Probabilities of including all significant variables and some noise variables (1, 2, ≥3).

4. The Michigan Longitudinal Study Example

The Michigan Longitudinal Study (MLS) is an ongoing multi-wave prospective study of people at high risk for substance use disorders [27]. The study recruited participants using drunk driving conviction records and door-to-door community canvassing in a four-county area surrounding Michigan’s capital city, Lansing. All participants received extensive in-home assessments of their psychiatric symptoms at baseline, and thereafter at 3-year intervals. In order to identify risk factors for alcohol use disorder (AUD) at the neighborhood level, we geocoded the residential addresses of the participants and merged the twenty potential covariates derived from census data (listed in Table 1) into the MLS database. In our analysis, we included 448 young adult participants (72% male), having a mean age of 22 years.

The following is a brief list of the 11 DSM-IV symptom criteria for AUD [28]:

• Abuse symptom 1: Failure to fulfill major role obligations

• Abuse symptom 2: Hazardous use

• Abuse symptom 3: Legal problems

• Abuse symptom 4: Social or interpersonal problems

• Dependence symptom 1: Tolerance

• Dependence symptom 2: Withdrawal

• Dependence symptom 3: Taken in larger amounts or over a longer period

• Dependence symptom 4: Persistent desire or unsuccessful efforts to cut down

• Dependence symptom 5: A great deal of time spent

• Dependence symptom 6: Important activities given up or reduced

• Dependence symptom 7: Physical or psychological problems

The symptom count (ranges 0–11) serves as an important indicator for AUD severity. As shown in Figure 1, this community sample has fewer zero symptom counts (27%) than the national sample (60%) due to the recruitment protocol targeting the high risk population. There is also a higher proportion of people with multiple AUD symptoms in this sample. Overall, the zero values in the data are still more than would be predicted from a Poisson regression model.

The four competing methods compared in the simulations were used to analyze the MLS data. Table 7 shows the estimated regression coefficients. While the Poisson regression methods selected 7–8 covariates, the ZIP methods only selected 1–5 covariates. This may reflect a general finding from the simulations: the Poisson regression methods have a great tendency to over fit the model. Under the SCAD penalty, the Poisson regression model and the ZIP model both identified the high school drop out rate, the unemployment rate, and the disability rate to be associated with the severity of AUD symptomatology. However, the Poisson regression model selected four additional covariates: the proportion of residents with public assistance income, the poverty rate, the proportion of Hispanic residents, and the proportion of residents who did not live at the same address 5 years earlier. Since the primary purpose of involving the variable selection technique for this project was to reduce the neighborhood level covariates, it may not be desirable to adopt the Poisson regression model that resulted in a larger set of covariates some of which were highly correlated. Furthermore, the Poisson regression model would not have the capacity to specify that the unemployment rate was also associated with the probability of being a drinker.

Table 7.

The estimated regression coefficients for the models on MLS data.

	PR-LASSO	PR-SCAD	ZIP-LASSO	ZIP-SCAD
The Poisson Component
Intercept	0.9788	0.9583	1.2916	1.2575
Covariate #1	0.0022	0	0	0
Covariate #2	0.1554	0.2558	0	0.2205
Covariate #3	0.1028	0.2153	0.0691	0.0878
Covariate #4	0	0	0	0
Covariate #5	−0.0192	0	0	−0.0440
Covariate #6	0	0	0	0
Covariate #7	−0.0789	−0.0884	0	0
Covariate #8	0	0	0	0
Covariate #9	0	−0.2333	0	0
Covariate #10	0	0	0	0
Covariate #11	0.0313	0.0210	0	0
Covariate #12	0	0	0	0
Covariate #13	0	0	0	0
Covariate #14	0	0	0	0
Covariate #15	0	0	0	0
Covariate #16	0	0	0	0
Covariate #17	0	0	0	0
Covariate #18	0.1224	0.2483	0	0
Covariate #19	−0.0676	−0.1607	0	−0.1926
Covariate #20	0	0	0	0
The Zero Component
Intercept			−0.7179	−1.0583
Covariate #3				−0.9225

In order to assess the goodness-of-fit of the ZIP model, we conducted a series of tests to compare it against alternative models. First, a score test [29] was employed to compare the ZIP model with the Poisson regression model. The result shows that the Poisson regression model is not sufficient to fit the data with excess zeros (χ² = 12.37, df = 1, p < .001). We also compared the ZIP model against the saturated model using the Pearson’s chi-square statistics implemented in the SAS PROC GENMOD [31] and found the ZIP model fits the data as well as the saturated model (χ² = 436, df = 406, p > .05). Moreover, the likelihood ratio test was adopted to compare the reduced ZIP model fitted by each variable selection method against the full ZIP model with all the 20 covariates in both the Poisson and Zero components. The result shows that the reduced ZIP model with only one covariate selected by the ZIP-LASSO may be oversimplified (χ² = 55.06, df = 39, p < .001). On the other hand, the reduced ZIP model with the covariates selected by the ZIP-SCAD is sufficient to interpret the neighborhood impact on AUD symptomatology (χ² = 28.08, df = 35, p ≈ .05).

In this example, the ZIP model fits the particular data set well. However, in some situations, the ZIP model might not be sufficient to fit the real data. We refer interested readers to recent work by Deng and Paul [30] that developed a series of score tests to facilitate selection among a class of generalized linear models with different link functions, zero-inflation components, and over-dispersion features.

5. Discussion

This study has extended two dominant methods in the recent variable selection literature, the LASSO and the SCAD, to deal with zero-inflated count data that are very common in health surveys. Our simulations demonstrate the danger of using Poisson regression methods to conduct variable selection when excess zeros exist in the data: the methods have a great tendency to over fit the model. The design of our simulations is unique because it preserves the special features of two national databases that have been commonly used in the alcoholism and substance abuse field. As a result, our findings can be easily generalized to the real settings. Our empirical analyses on the data from a community sample not only demonstrate the applications of the methodology but also reflect some trends observed in the simulations.

Based on the results of our simulation on the census data, we recommend the use of ZIP-SCAD in the field of alcoholism and substance abuse research because (I) it can maintain both the specificity and sensitivity at the highest level (mostly over .90), (II) it has the lowest MRMSE, and (III) it has the highest value of exact fit. It demonstrates this high level of performance not only in the Poisson component but also in the zero component. In general, its performance improves as the sample size increases, the correlation between covariates decreases, the proportion of non-zero coefficients decreased, and the proportion of zero outcome decreased.

The choice of penalty functions in penalized likelihood has been studied by Fan and Li [10] in depth. They demonstrated that the SCAD penalty improves the LASSO penalty by reducing estimation bias due to the L₁ penalty, although the LASSO and SCAD share the same spirit in terms of simultaneous variable selection and parameter estimation. The tuning parameter selection is crucial in the penalized likelihood methods. Zhang, Li and Tsai [19] suggested using the BIC tuning parameter in order for the SCAD to achieve the oracle property. The LASSO with the BIC tuning parameter selector likely yields an estimate with non-ignorable bias. This explains that the MRMSEs of ZIP-LASSO are systematically greater than those for ZIP-SCAD. The BIC tuning parameter selector is a data-driven method. In order to avoid larger estimation bias due to the L₁ penalty, the BIC tuning parameter selector tends to select a smaller tuning parameter for the ZIP-LASSO than for the ZIP-SCAD. This explains that the ZIP-SCAD estimator has better specificity than the ZIP-LASSO.

Like other variable selection methods [32], the methods proposed in this paper do not work well with small sample sizes. The results of the simulation based on the census data show that for the sample size of 300, the sensitivity level of the ZIP-SCAD only reaches .70 in the Poisson component and .30 in the zero component. Our simulation with the sample sizes of 100 and 200 (unreported results available upon request) resulted in up to 50% replications failing to converge. Thus, for the case of 40 candidate covariates (20 in the Poisson component and 20 in the zero component), a sample size of 600 would be required for the ZIP-SCAD to perform well. Future studies may evaluate the performance of these variable selection methods under different ratios of the number of candidate covariates to the sample size.

Appendix I: Technical Details of Implementation of LARS

For ease of presentation, we write θ = (β^′, γ^′)^′. That is, θ_j = β_j, for j = 1, …, d₁ and θ_j = γ_j−d1, for j = d₁ + 1, …, d₁ +d₂. Similarly, θ⁽⁰⁾ = (β^(0)′, γ^(0)′)^′. Denote

$${\mathrm{\sum }}_0=-{\nabla }^2\ell ({\mathit{\beta }}^{(0)},{\mathit{\gamma }}^{(0)})=-{\nabla }^2\ell ({\mathit{\theta }}^{(0)}).$$

In what follows, we give the details on how to employ the LARS algorithm [16] to the one-step sparse estimator θ⁽¹⁾, given the initial value θ⁽⁰⁾.

• Step 1:
  Define index sets

  $$U=\{j:p_{a_j}^{\prime }(\mid {\beta }_j^{(0)}\mid )=0\}\cup \{d_1+k:p_{b_k}^{\prime }(\mid {\gamma }_k^{(0)}\mid )=0\},$$
  and

  $$V=\{j:p_{a_j}^{\prime }(\mid {\beta }_j^{(0)}\mid )\ne 0\}\cup \{d_1+k:p_{b_k}^{\prime }(\mid {\gamma }_k^{(0)}\mid )\ne 0\}.$$
• Step 2:
  Find the Cholesky decomposition of Σ₀. That is, to find a (d₁ + d₂) × (d₁ + d₂) matrix L, such that,

  $${\mathrm{\sum }}_0=L^{\prime }L.$$
  Create working data by

  $$Y^{\ast }=L{\mathit{\theta }}^{(0)},$$
  let ${\mathit{x}}_j^{\ast }=\frac{\tau }{{np}_{{\tau }_j}^{\prime }(\mid {\theta }_j^{(0)}\mid )}{\ell }_j^{\ast }$ for j ∈ V, where ${\ell }_j^{\ast }$ is the j-th column of L, τ_j = a_j for j ≤ d₁ and τ_j = b_j−d1 for j > d₁. Further write

  $$X^{\ast }=[X_U^{\ast },X_V^{\ast }],{\mathit{\theta }}^{(1)}={({\mathit{\theta }}_U^{{(1)}^{\prime }},{\mathit{\theta }}_V^{{(1)}^{\prime }})}^{\prime }.$$
• Step 3:
  Let H_U be the projection matrix in the space of $X_U^{\ast }$, i.e., $H_U=X_U^{\ast }(X_U^{{\ast }^{\prime }}{X}_U^{\ast })-X_U^{{\ast }^{\prime }}$. Compute

  $$Y^{\ast \ast }=Y^{\ast }-H_U{Y}^{\ast },X_V^{\ast \ast }=X_V^{\ast }-H_U{X}_V^{\ast }$$
• Step 4:
  Apply the LARS algorithm to solve

  $${\widehat{\mathit{\theta }}}_V^{\ast }={\text{argmin}}_{\mathit{\theta }}\{\frac{1}{2}||Y^{\ast \ast }-X_V^{\ast \ast }\mathit{\theta }||+\tau \sum _{j=1}^{d_1+d_2}\mid {\theta }_j\mid \}.$$
• Step 5:

  Compute ${\widehat{\mathit{\theta }}}_U^{\ast }={(X_U^{{\ast }^{\prime }}{X}_U^{\ast })}^{-1}{X}_U^{{\ast }^{\prime }}(Y^{\ast }-X_V^{\ast }{\widehat{\mathit{\theta }}}_V^{\ast })$.

It follows that the one-step LLA estimator is:

$${\widehat{\mathit{\theta }}}_U^{(1)}={\widehat{\mathit{\theta }}}_U^{\ast }\text{and}{\widehat{\theta }}_j^{(1)}=\frac{\tau }{n{p}_{{\tau }_j}^{\prime }(\mid {\theta }_j^{(0)}\mid )}{\widehat{\theta }}_j^{\ast }\text{for}j\in V.$$

Appendix II: Regularity Conditions and Key Derivation of Oracle Property of ZIP with One-step SCAD

We will need the following regularity conditions, under which the oracle property of the one-step SCAD for ZIP may be established.

Regularity Conditions

1. The observations v_i = {w_i, y_i}, i = 1, …, n, is an independent and identically distributed sample from the ZIP model (1). Denote θ = (β^′, γ^′)^′ and ℓ(θ, v_i) to be the log-likelihood function of the ith observation v_i. Assume that the first and second partial derivatives ℓ(θ, v_i) of with respect to θ_j satisfies the equations

   $$E_{\mathit{\theta }}\left[\frac{\partial \ell (\mathit{\theta },{\mathit{v}}_i)}{\partial {\theta }_j}\right]=0$$
   and

   $$I_{jk}(\mathit{\theta })=E_{\mathit{\theta }}\left[\frac{\partial }{\partial {\theta }_j}\ell (\mathit{\theta },{\mathit{v}}_i)\frac{\partial }{\partial {\theta }_k}\ell (\mathit{\theta },{\mathit{v}}_i)\right]=E_{\mathit{\theta }}\left[-\frac{{\partial }^2}{\partial {\theta }_j\partial {\theta }_k}\ell (\mathit{\theta },{\mathit{v}}_i)\right].$$

   for j = 1, …, d₁ + d₂.

2. The Fisher information matrix

   $$I(\mathit{\theta })=E\left\{\left[\frac{\partial }{\partial \mathit{\theta }}\ell (\mathit{\theta },{\mathit{v}}_i)\right]{\left[\frac{\partial }{\partial \mathit{\theta }}\ell (\mathit{\theta },{\mathit{v}}_i)\right]}^{\prime }\right\}$$

   is finite and positive definite at θ = θ₀.

3. There exists an open subset ω of Ω containing the true parameter point θ₀ such that for almost all v_i, ℓ(θ, v_i) admits all third derivatives $\frac{\partial \ell (\mathit{\theta },{\mathit{v}}_i)}{\partial {\theta }_j\partial {\theta }_k\partial {\theta }_l}$

   for all θ ∈ ω. Further there exist functions M_jkl such that

   $$\left|\frac{{\partial }^3}{\partial {\beta }_j\partial {\beta }_k\partial {\beta }_l}\ell (\mathit{\theta },{\mathit{v}}_i)\right|\le M_{\mathit{jkl}}({\mathit{v}}_i)\text{for}\text{all}\mathit{\theta }\in \omega ,$$

   where m_jkl = E_θ0[M_jkl(v_i)] < ∞ for j, k, l.

These regularity conditions guarantee asymptotic normality of the ordinary maximum likelihood estimate of the ZIP model. See, for example, Lehmann and Casella [33].

Key derivation of oracle properties of the one-step SCAD estimator

Under Conditions (A)—(C), we can show that the maximum likelihood estimate of θ in the ZIP model, denoted by θ̂ (mle), is root n consistent,

$$-\frac{1}{n}\sum _{i=1}^n\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}\ell (\mathit{\theta },{\mathit{v}}_i){\mid }_{\mathit{\theta }-\widehat{\mathit{\theta }}(\text{mle})}\to I({\mathit{\theta }}_0)$$

in probability as n → ∞, and

$$\sqrt{n}(\widehat{\mathit{\theta }}(\text{mle})-{\mathit{\theta }}_0)\to N(0,I^{-1}({\mathit{\theta }}_0))$$

in distribution as n → ∞. As a direct application of Theorem 5 of Zou and Li [12], if λ_n → 0 and $\sqrt{n}{\lambda }_n\to \infty$, then the one-step SCAD estimator for the ZIP model possesses the oracle property: with probability tending to one, the estimate for zero coefficients equals 0, and the estimate for nonzero coefficient has an asymptotic normal distribution. with mean being the true value of nonzero coefficient and variance $I_1^{-1}({\mathit{\theta }}_0)$, where I₁(θ₀) is the submatrix of the Fisher information matrix corresponding to the nonzero coefficients.