Kinetic Mechanism of the ssDNA Recognition by the Polymerase X From African Swine Fever Virus. Dynamics and Energetics of Intermediate Formations

Abstract

Kinetic mechanism of the ssDNA recognition by the polymerase X of African Swine Fever Virus (ASFV) and energetics of intermediate formations have been examined, using the fluorescence stopped-flow method. The association is a minimum three-step process

$$\text{Pol}\text{X}+\text{ssDNA}\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\rightleftarrows }}{(\text{P}-\text{ssDNA})}_1\underset{{\text{k}}_{-2}}{\overset{{\text{k}}_2}{\rightleftarrows }}{(\text{P}-\text{ssDNA})}_2\underset{{\text{k}}_{-3}}{\overset{{\text{k}}_3}{\rightleftarrows }}{(\text{P}-\text{ssDNA})}_3$$

The nucleic acid makes the initial contact through the C-terminal domain, which generates most of the overall ΔG°. In the second step the nucleic acid engages the N-terminal domain, assuming the bent structure. In equilibrium, the complex exists in at least two different states. Apparent enthalpy and entropy changes, characterizing formations of intermediates, reflect association of the DNA with the C-terminal domain and gradual engagement of the catalytic domain by the nucleic acid. The intrinsic DNA-binding steps are entropy-driven processes accompanied by the net release of water molecules. The final conformational transition of the complex does not involve any large changes of the DNA topology, or the net release of the water molecules.

INTRODUCTION

The African Swine Fever Virus (ASFV) is the etiological agent responsible for acute hemorrhagic fever of domestic pigs (see accompanying paper) [1–6]. Besides the replicative DNA polymerase, the DNA genome of the virus encodes another ~20 kDa DNA polymerase, a member of the pol X family referred to as the ASFV pol X [1–3]. The major physiological role of the ASFV pol X is to repair the damaged viral DNA [5,6]. The pol X family comprises several polymerases with different and specialized functions in the cell [7–9]. The well-known member of the family is the mammalian pol β, which plays a very specialized function in the DNA repair processes [8–12]. The structure of pol β shows a typical polymerase fold, containing a thumb, palm, and fingers domains, due to its resemblance to the human hand [12–16]. It also possesses an additional, N-terminal 8-kDa domain, which is the primary DNA-binding site of the enzyme with a significant degree of functional autonomy and spatial separation from the rest of the enzyme molecule [13–17].

The NMR studies of ASFV pol X revealed a structure, which is very different from pol β and other DNA replicative or repair polymerases [18,19]. The enzyme is built only of the N-terminal domain, which includes the first 105 amino acids from the N-terminus of the protein and the C-terminal domain, which encompasses the remaining 69 amino acid residues (see accompanying paper) [18,19]. Both the N-terminal domain and the C-terminal domain contains highly positively charged helices, αC and αE, respectively, which do not have their counterparts in pol β. Nevertheless, the entire molecule of the ASFV pol X corresponds to the palm domain of the typical DNA replicative or repair polymerase. Nevertheless, in spite of the simplified structure, thermodynamic studies have already shown very complex characteristics of the ASFV pol X interactions with the ssDNA (see accompanying paper) [20–22].

The total DNA-binding site of the enzyme encompasses 16 ± 1 nucleotides and possesses a heterogeneous structure, which includes the strong and the weak ssDNA-binding subsites (see accompanying paper) [20–22]. The strong ssDNA-binding subsite engages only 7 ± 1 nucleotides and generates the predominant part of the free energy of binding. Studies described in the accompanying paper indicated that the strong DNA-binding subsite is the primary DNA-binding site of the enzyme, independent of the nucleic acid conformation and is located on the C-terminal domain of the enzyme. With the longer DNA oligomers, the enzyme additionally engages the weak DNA-binding subsite on the catalytic N-terminal domain in interactions with the nucleic acid, although the efficiency of the engagement depends on the length of the nucleic acid [20]. The intrinsic affinity of the total DNA-binding site is not a simple sum of contributions from the intrinsic affinities of strong and the weak DNA-binding subsites. Moreover, the affinities of the subsites differ by at least two orders of magnitude. This large affinity difference results from specific conformational changes, induced by the engagement of the weak DNA-binding subsite in interactions with the DNA and characterized by a large positive enthalpy change. The intrinsic affinities of the strong DNA-binding subsite and the total DNA-binding site are mostly driven by large entropy changes, predominantly resulting from the release of water molecules (see accompanying paper).

Elucidation of the kinetics of the ASFV pol X association with the nucleic acid is a prerequisite for understanding the recognition processes of the nucleic acid. This is of particular importance in the case of the DNA repair polymerases, which must recognize specific structure of the damaged DNA. Moreover, dynamics of the DNA recognition are of paramount significance for understanding the dynamics of DNA synthesis, as the recognition processes precede and determine the overall efficiency of the catalysis. In spite of the importance of the ASFV pol X in the DNA metabolism of the ASFV virus, the kinetic mechanisms of the enzyme interactions with the ssDNA, as well as the energetics of the intermediate formations, have never been quantitatively addressed.

In this communication, we examine the kinetic mechanisms of interactions of the strong DNA-binding subsite and the total DNA-binding site of the ASFV pol X with the ssDNA, and energetics of the intermediate formations. The DNA makes initial contact through the strong DNA-binding subsite. The first binding step is very close to the diffusion-controlled reaction, although it generates most of the overall ΔG° of binding. The second step is also very fast and occurs within ~1 ms of the reaction time. The DNA engages the weak DNA-binding subsite and the bound nucleic acid assumes the bent structure. In equilibrium, the polymerase - ssDNA complex exists in at least two different states. The intrinsic DNA-binding steps to the strong and the weak subsite are entropy-driven processes and accompanied by the release of similar numbers of water molecules from each subsite.

MATERIALS & METHODS

Reagents and Buffers

All solutions were made with distilled and deionized >18 MΩ (Milli-Q Plus) water. All chemicals were reagent grade. Buffer C is 10 mM sodium cacodylate adjusted to pH 7.0 with HCl, 1 mM MgCl₂, 50 mM NaCl, 1 mM DTT, and 10% glycerol (w/v). The temperature in the buffer is indicated in the text.

ASFV Pol X

Isolation and purification of the protein was performed as previously describe (see accompanying paper) [20–22].

Nucleic Acids

All nucleic acids were purchased from Midland Certified Reagents (Midland, Texas). Concentrations of all ssDNA oligomers have been spectrophotometrically determined, as previously described by us [20–25].

Stopped-Flow Kinetics

All fluorescence stopped-flow kinetic experiments were performed using SX.MV18 stopped-flow instrument (Applied Photophysics Ltd. Leatherhead, UK) [26–35]. The reactions were monitored using the fluorescence of the etheno-derivatives of the ssDNA oligomers, dε(pεA)₉ and dεA(pεA)₁₉, with λ_ex = 325 nm, or, in the case of 5′Fl-dT (pT)₁₉-CP-3′, with λ_ex = 425 nm, with the excitation monochromator slits at 1 mm (band pass ~4.5 nm). The emission intensity was observed through the emission monochromator set at 410 nm or 520 nm, for the etheno-derivatives and 5′Fl-dT(pT)₁₉-CP-3′ respectively, Usually, 11–15 traces were collected and averaged for each sample [26–35]. The kinetic curves were fitted to extract relaxation times and corresponding amplitudes, using nonlinear least-squares software provided by the manufacturer, with the exponential function defined as

$$\text{F}(\text{t})=\text{F}(\infty )+\sum _{\text{i}=1}^{\text{n}}{\text{A}}_{\text{i}}exp(-{\lambda }_{\text{i}}\text{t})$$ (1)

where F(t) is the fluorescence intensity at time t, F(∞) is the fluorescence intensity at t = ∞, A_i is the amplitude corresponding to ith relaxation process, λ_i is the time constant (reciprocal relaxation time) characterizing ith relaxation process, n is number of relaxation processes. All analyses of the data were performed using Mathematica (Wolfram, Urbana, IL) and Kaleida Graph (Synergy Software, PA) [26–35].

Analysis of Stopped-Flow Kinetic Experiments

Quantitative examinations of both the relaxation times and the amplitudes of the observed kinetic processes have been performed using the matrix projection operator approach, as previously described by us [26–35]. Briefly, the most complex mechanism of the ASFV pol X (P) binding to the ssDNA (D), which encompass the total DNA-binding site of the enzyme, includes the bimolecular step, which is followed by two, first-order conformational transitions as

$$\text{P}+{\text{D}}_1\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\leftrightarrow }}{\text{D}}_2\underset{{\text{k}}_{-2}}{\overset{{\text{k}}_2}{\leftrightarrow }}{\text{D}}_3\underset{{\text{k}}_{-3}}{\overset{{\text{k}}_3}{\leftrightarrow }}{\text{D}}_4$$ (2)

The reaction is monitored by the fluorescence change of the DNA. Under pseudo-first-order conditions, the total concentration of the protein is much larger than the total concentration of the nucleic acid, i.e., [P]_T ≫ [D]_T, the time-dependence of different nucleic acid species is expressed, using matrix projection operators, Q_i, as [26,27,36,37]

$$\mathbf{N}={\mathbf{Q}}_{\mathbf{0}}{\mathbf{N}}_{\mathbf{0}}+{\mathbf{Q}}_{\mathbf{1}}{\mathbf{N}}_{\mathbf{0}}exp({\lambda }_1\text{t})+{\mathbf{Q}}_{\mathbf{2}}{\mathbf{N}}_{\mathbf{0}}exp({\lambda }_2\text{t})+{\mathbf{Q}}_{\mathbf{3}}{\mathbf{N}}_{\mathbf{0}}exp({\lambda }_3\text{t})$$ (3)

where λ₁, λ₂, and λ₃ are eigenvalues of coefficient matrix, M, of the reaction, and N₀ is the vector of initial concentrations. The projection operators, Q_i, are defined, using the original coefficient matrix M of the reaction and its eigenvalues, λ_i as

$${\mathbf{Q}}_{\mathbf{i}}=\frac{{\displaystyle \prod _{\text{j}\ne \text{i}}^{\text{n}}}(\mathbf{M}-{\lambda }_{\text{j}}\mathbf{I})}{{\displaystyle \prod _{\text{j}\ne \text{i}}^{\text{n}}}({\lambda }_{\text{i}}-{\lambda }_{\text{j}})}$$ (4)

where n is the number of eigenvalues and I is the identity matrix. In the considered reaction, there are four eigenvalues λ₀, λ₁, λ₂, and λ₃, with λ₀ = 0 because of the mass conservation in the system. Eq. 3 becomes

$$\left(\begin{array}{c}{\text{D}}_1\\ {\text{D}}_2\\ {\text{D}}_3\\ {\text{D}}_4\end{array}\right)=\left(\begin{array}{c}{\text{P}}_{01}\\ {\text{P}}_{02}\\ {\text{P}}_{03}\\ {\text{P}}_{04}\end{array}\right)+\left(\begin{array}{c}{\text{P}}_{11}\\ {\text{P}}_{12}\\ {\text{P}}_{13}\\ {\text{P}}_{14}\end{array}\right)exp({\lambda }_1\text{t})+\left(\begin{array}{c}{\text{P}}_{21}\\ {\text{P}}_{22}\\ {\text{P}}_{23}\\ {\text{P}}_{24}\end{array}\right)exp({\lambda }_2\text{t})+\left(\begin{array}{c}{\text{P}}_{31}\\ {\text{P}}_{32}\\ {\text{P}}_{33}\\ {\text{P}}_{34}\end{array}\right)exp({\lambda }_3\text{t})$$ (5)

where P_ij is the jth element of the projection of the vector of the initial concentrations N₀ on the eigenvector, corresponding to the ith eigenvalue of matrix M. The three normal modes of the reaction characterized by the amplitudes, A₁, A₂, and A₃, have corresponding relaxation times τ₁ = −1/λ₁, τ₂ = −1/λ₂, and τ₃ = −1/λ₃. The analysis of the relaxation times, as a function of [P]_T, allows us to extract all rate constants of the system [26–35]. Using eq. 5, the experimentally observed individual amplitudes, A₁, A₂, and A₃, are

$${\text{A}}_1=\left(\begin{array}{ccc}{\text{P}}_{12}& {\text{P}}_{13}& {\text{P}}_{14}\end{array}\right)\left(\begin{array}{c}{\text{F}}_1-{\text{F}}_2\\ {\text{F}}_1-{\text{F}}_3\\ {\text{F}}_1-{\text{F}}_4\end{array}\right){\text{A}}_2=\left(\begin{array}{ccc}{\text{P}}_{22}& {\text{P}}_{23}& {\text{P}}_{24}\end{array}\right)\left(\begin{array}{c}{\text{F}}_1-{\text{F}}_2\\ {\text{F}}_1-{\text{F}}_3\\ {\text{F}}_1-{\text{F}}_4\end{array}\right){\text{A}}_3=\left(\begin{array}{ccc}{\text{P}}_{32}& {\text{P}}_{33}& {\text{P}}_{34}\end{array}\right)\left(\begin{array}{c}{\text{F}}_1-{\text{F}}_2\\ {\text{F}}_1-{\text{F}}_3\\ {\text{F}}_1-{\text{F}}_4\end{array}\right)$$ (6)

where four molar fluorescence intensities F₁, F₂, F₃, and F₄, characterize D₁, D₂, D₃, and D₄ states of the nucleic acid [26–35].

RESULTS

Dynamics of the ssDNA Binding to the Strong DNA-Binding Subsite of the ASFV Pol X

The intrinsic affinity of the strong DNA-binding subsite of the ASFV pol X is at least ~2 orders of magnitude higher than the intrinsic affinity of the weak DNA-binding subsite (see accompanying paper) [20–22]. Such a large difference in the affinities allows us to examine the kinetics of the enzyme binding to the ssDNA exclusively through its strong subsite, independent of the weak subsite. To examine the mechanism of the DNA association with the strong DNA-binding subsite, we used the ssDNA 10-mer, dεA(pεA)₉, which can only engage the strong subsite (see below).

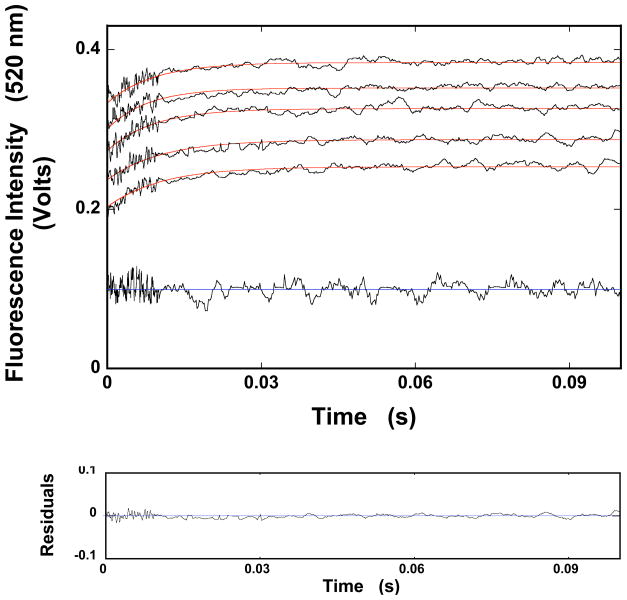
All stopped-flow experiments described in this work have been performed under pseudo-first-order conditions with respect to the protein concentration, by mixing the ssDNA oligomer with a large excess of the ASFV pol X (see above) [26–35]. The stopped-flow kinetic traces of the dεA(pεA)₉ fluorescence, after mixing 2 × 10⁻⁷ M (oligomer) with different total concentrations of the ASFV pol X (final concentrations) in buffer C (pH 7.0, 10°C), are shown in Figure 1. The solid lines in Figure 1 are nonlinear least-squares fits of the experimental curves, using a single exponential function (Materials and Methods) [26–37]. As indicated by the included deviations from the fit for one of the experimental curves, the single-exponential function provides an adequate description of the experimentally observed kinetics. However, the process is clearly more complex, as the amplitude of the observed relaxation step is significantly smaller than the total amplitude of the relaxation process (Figure 1). In other words, there is a fast step, which is beyond the resolution of the stopped-flow instrument and which precedes the observed relaxation step [26–35,38].

Figure 1.

a. The fluorescence stopped-flow kinetic traces after mixing the ssDNA 10-mer, dεA(pεA)₉, with the ASFV pol X in buffer C (pH 7.0, 10°C) (λ_ex = 325 nm, λ_em = 410 nm). The final concentration of the 10-mer is 2 × 10⁻⁷ M (oligomer). The traces were recorded at two time bases, 10 and 100 ms. The concentrations of the polymerase are: 4 × 10⁻⁷ M, 6 × 10⁻⁷ M, 8 × 10⁻⁷ M, 1 × 10⁻⁶ M, and 1.2 × 10⁻⁶ M. The solid red lines are the single-exponential, nonlinear leastsquares fits of the experimental curves using eq. 1. The low horizontal trace is the nucleic acid mixed with the buffer alone with the blue line indicating the average value of the signal. The lower panel shows the deviations of the experimental curve, recorded at [ASFV pol X]_T = 6 × 10⁻⁷ M, from the fit.

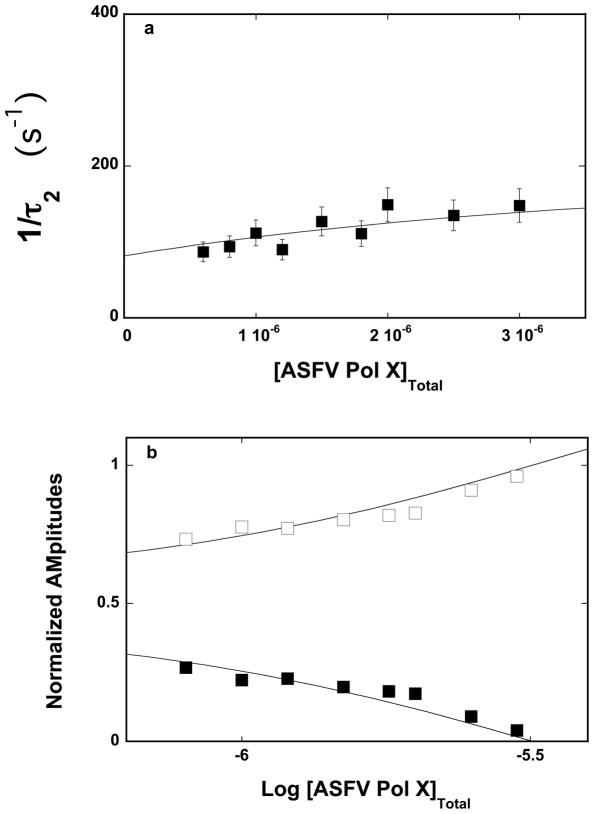
The dependence of the reciprocal relaxation time, 1/τ₂, characterizing the observed kinetic step, as a function of the total ASFV pol X concentration, [ASFV pol X]_T, is shown in Figures 2a. The values of 1/τ₂ show little dependence upon [ASFV pol X]_T, providing the first indication that it characterizes an intramolecular step [26–35,38]. Thus, in the case of the ssDNA 10-mer, dεA(pεA)₉, the simplest minimum mechanism, which can account for the observed dependence of the relaxation time upon the ASFV pol X concentration, is a two-step, sequential binding process, in which the bimolecular association is followed by the isomerization step, as described by the equation

Figure 2.

a. The dependence of the reciprocal of the relaxation time, 1/τ₂, for the binding of the ssDNA 10-mer, dεA(pεA)₉, to the strong DNA-binding subsite of the ASFV pol X in buffer C (pH 7.0, 10°C), upon the total concentration of enzyme. The solid line is the nonlinear least-squares fit according to the two-step sequential mechanism defined by eq. 7, with the rate constants included in Table 1 (details in text). The error bars are standard deviations obtained from 3 – 4 independent experiments. b. The dependence of the normalized, individual relaxation amplitudes of the corresponding relaxation processes, A₁ and A₂, upon the logarithm of the total concentration of the polymerase. The solid lines are nonlinear least-squares fits, according to the two-step sequential mechanism, defined by eq. 7, with the relative fluorescence intensities included in Table 1. The rate constants are the same as obtained from the relaxation time analysis (Table 1); A₁ (❑), A₂ (■).

$$\text{Pol}\text{X}+\text{ssDNA}\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\leftrightarrow }}{(\text{P}-\text{ssDNA})}_1\underset{{\text{k}}_{-2}}{\overset{{\text{k}}_2}{\leftrightarrow }}{(\text{P}-\text{ssDNA})}_2$$ (7)

Although we cannot determine the relaxation time of the fast step, we can obtain its amplitude, which is determined by

$${\text{A}}_1={\text{A}}_{\text{T}}-{\text{A}}_2$$ (8)

where A_T and A₂ are the total amplitude and amplitude of the observed relaxation step, respectively [26–35]. The dependence of the individual amplitude, A₁ and A₂ upon the total concentration of the ASFV pol X is shown in Figure 2b. The individual amplitudes are normalized. i.e., expressed as fractions of the total amplitude, A_i/ΣA_T. The contribution of the amplitude, A₁ of the fast relaxation step dominates the total observed amplitude, A_T, over the entire range of the examined enzyme concentration. The values of A₁ steadily increase while the values of A₂ strongly diminish as the [ASFV Pol X]_T increases. Such behavior of the individual amplitudes is in complete agreement with the proposed kinetic mechanism (eq.7) (see below) [26–35]. Nevertheless, an alternative model where the protein can undergo a transition prior to the nucleic acid binding is addressed in Discussion section.

To extract the partial equilibrium constants and rate constants from the relaxation time data in Figures 2a and 2b, we utilized the fact that the value of the overall binding constant, K₁₀ = (5.8 ± 0.9) × 10⁵ M⁻¹, has been independently obtained in the same solution conditions by the equilibrium fluorescence titration method (see accompanying paper). The overall binding constant K₁₀ is related to the partial equilibrium constants, K₁ and K₂ for each step of the reaction (eq. 7), as

$${\text{K}}_{10}={\text{K}}_1(1+{\text{K}}_2)$$ (9)

where K₁ = k₁/k₋₁ and K₂ = k₂/k₋₂. Expression 9 reduces the number of fitting parameters by one [26–35].

Because the individual amplitudes have been determined, we can address the molar fluorescence intensities characterizing each intermediate of the reaction (Materials and Methods) [26–35]. To achieve this, we used the maximum, fractional increase of the nucleic acid fluorescence, ΔF_max ≈ 0.8, obtained in independent equilibrium studies (see accompanying paper). The value of ΔF_max is analytically expressed as

$$\mathrm{\Delta }{\text{F}}_{max}=\frac{\mathrm{\Delta }{\text{F}}_1+{\text{K}}_2\mathrm{\Delta }{\text{F}}_2}{1+{\text{K}}_2}$$ (10)

where ΔF₁ and ΔF₂ are fractional fluorescence intensities of the corresponding intermediates in the association reaction of the 10-mer with the ASFV pol X, relative to the fluorescence of the free nucleic acid, F₁, i.e., ΔF_i = (F_i – F₁)/F₁. The value of F₁ can be taken as 1. Expression 10 furnishes an additional relationship among the fluorescence parameters, with the value of ΔF_max playing the role of a scaling factor [26–35].

The solid lines in Figures 2a and 2d are nonlinear least-squares fits of the experimentally determined relaxation times and fractional individual amplitudes of the reaction, defined by eq. 7, using a single set of binding and spectroscopic parameters, and using the matrix projection operator methods together with eqs. 9 and 10 (Materials and Methods) [26–37]. The numerical analysis was first performed by nonlinear least-squares fitting of the relaxation time data to extract K₁, k₂, and k₋₂. Subsequently, the nonlinear least-squares fitting was performed for the individual amplitudes, using the partial equilibrium constant and the rate constants obtained from the relaxation time analysis and allowing the values of K₁, k₂, and k₋₂ to float between ± 10% of the determined values. Finally, global fitting, with the simultaneous analysis of all relaxation times and individual amplitudes, refines the parameters [26–35]. The obtained partial equilibrium constants, rate constants, and spectroscopic parameters characterizing the intermediates of the reaction are included in Table 1.

Table 1.

Kinetic, thermodynamic, and spectroscopic parameters characterizing the binding of ASFV pol X to the ssDNA oligomers differing by the number of nucleotides, in buffer C (pH 7, 10 °C), containing 50 mM NaCl

ssDNA N	KN* (M−1)	K1	K2	k2 (s−1)	k−2 (s−1)	ΔF*	F2**	F3**	ΔH1 kcal/mol	ΔS1 cal/mol deg	ΔH2 kcal/mol	ΔS2 cal/ mol deg
10	(5.8 ± 0.9) × 105	2.0 ± 0.7) × 105	1.9 ± 0.6	155 ± 31	83 ± 16	0.8 ± 0.05	2.30 ± 0.02	1.50 ± 0.05	2.6 ± 0.8	33.3 ± 11	−0.13 ± 0.10	1.7 ± 1.1
14	(1.4 ± 0.3) × 106	5.4 ± 1.8) × 105	1.6 ± 0.5	135 ± 27	84 ± 15	0.7 ± 0.05	1.9 ± 0.05	1.6 ± 0.05	8.6 ± 2.8	59 ± 19	0.10 ± 0.10	1.3 ± 0.6
16	(1.8 ± 0.3) 106	7.2 ± 1.4) × 105	1.1 ± 0.3	105 ± 21	95 ± 19	0.9 ± 0.05	2.1 ± 0.05	1.7 ± 0.05	8.3 ± 2.8	56 ± 18	0.10 ± 0.10	0.5 ± 0.3
20	(4.4 ± 1.1) × 106	(2.5 ± 0.8) × 106	0.8 ± 0.3	80 ± 16	105 ± 21	0.85 ± 0.05	1.78 ± 0.05	1.94 ± 0.05	14.4 ± 4.8	80 ± 27	0.24 ± 0.10	0.40 ± 0.20

^*Determined in independent fluorescence titrations.

^**Values relative to the fluorescence, F₀ = 1 of the free DNA oligomers (details in text).

Dynamics of the ssDNA Binding to the Total DNA-Binding Subsite of the ASFV Pol X

The mechanism of the DNA binding to the total DNA-binding site of the ASFV pol X has been addressed using the ssDNA 20-mer, dεA(pεA)₁₉, which can engage both the strong and the weak DNA-binding subsites of the enzyme (see accompanying paper) [20–22]. Similar to the experiments with the 10-mer, the stopped-flow kinetic traces obtained for the 20-mer require only a single-exponential function to adequately represent the experimental curves (data not shown). Nevertheless, analogously to the 10-mer, the amplitude of the observed relaxation step is significantly smaller than the total amplitude of the relaxation process, indicating that there is an additional fast step in the binding reaction (see above). Therefore, the association of the 20-mer with the total ssDNA-binding site of the ASFV pol X, also includes at least two steps.

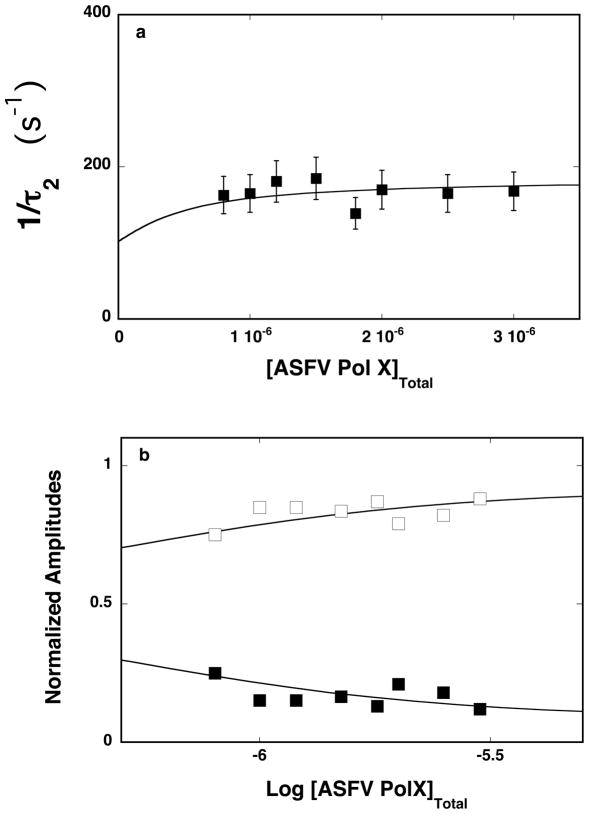
The reciprocal relaxation time, 1/τ₂, characterizing the observed relaxation step, as a function of the total ASFV pol X concentration, is shown in Figure 3a. The values of 1/τ₂ show only a little dependence upon [ASFV pol X]_T, i.e., as mentioned above, the behavior of 1/τ₂ indicates that it characterizes an intramolecular step [26–35,38]. Moreover, the values of 1/τ₂ are similar to the values of the corresponding 1/τ₂ observed for the 10-mer, pointing to similar dynamics of the observed relaxation step for the oligomer, which engages the total DNA-binding site of the enzyme and the oligomer that engages only the strong DNA-binding subsite (see Discussion). Thus, the minimum mechanism of the 20-mer binding to the total DNA-binding subsite of the ASFV pol X is a two-step, sequential binding process, as described by eq. 7. The dependence of the normalized individual amplitudes, A₁ and A₂ of the observed relaxation processes, in the binding of the 20-mer to the polymerase, upon the total protein concentration, is shown in Figure 3b. The behavior of the amplitudes is different from the behavior observed in the case of the 10-mer (Figure 2b), indicating different partial equilibria among the intermediates when the oligomer engages the total DNA-binding site (see below). Amplitude, A₁, of the fast relaxation step, dominates the total amplitude, A_T, over the entire examined enzyme concentration range. However, instead of clearly increasing, as observed for the 10-mer (Figure 2b) it depends very little on the polymerase concentrations. The amplitude of the slow observed relaxation step, A₂, has significantly lower values than A₁, and only gradually decreases with increasing [ASFV pol X]_T. Nevertheless, the observed behavior of the individual amplitudes is in excellent agreement with the proposed kinetic mechanism, as defined by eq. 7 [26–35,38].

Figure 3.

a. The dependence of the reciprocal of the relaxation time, 1/τ₂, for binding of the ssDNA 20-mer, dεA(pεA)₁₉, to the total DNA-binding site of the ASFV pol X in buffer C (pH 7.0, 10°C) upon the total concentration of enzyme. The solid line is the nonlinear least-squares fit according to the two-step sequential mechanism, defined by eq. 7, with the rate constants included in Table 1 (see text for details). The error bars are standard deviations obtained from 3 – 4 independent experiments. b. The dependence of the normalized, individual relaxation amplitudes of the corresponding relaxation processes, A₁ and A₂, upon the logarithm of the total concentration of the polymerase. The solid lines are nonlinear least-squares fits according to the two-step sequential mechanism, defined by eq. 7, with the relative fluorescence intensities included in Table1. The rate constants are the same as obtained from the relaxation time analysis (Table 1); A₁ (❑), A₂ (■).

The strategy of the numerical analysis of the data was the same as described above for the 10-mer (see above). The solid lines in Figures 3a and 3b are nonlinear least-squares fits of the experimentally determined relaxation time and normalized individual amplitudes of the reaction, defined by eq. 7, using a single set of kinetic and spectroscopic parameters. Analogous stopped-flow and numerical analyses have been carried out for the 14- and the 16-mer, dεA(pεA)₁₃ and dεA(pεA)₁₅, which bind to the strong DNA-binding subsite and can only partially engage in interactions with the weak DNA-binding subsite of the ASFV pol X (see accompanying paper) [20–22]. The obtained partial equilibrium constants, rate constants, and spectroscopic parameters characterizing the intermediates of the reaction for all examined oligomers are included in Table 1.

The values of the partial equilibrium constant, K₁, show that for all examined oligomers, the predominant part of the free energy of binding is generated in the formation of the intermediate (P-ssDNA) ₁ (Table 1). Nevertheless, in the case of the 10-mer, which exclusively associates with the strong DNA-binding subsite, K₁ is ~one order of magnitude lower, as compared to the value of the same parameter for the 20-mer that efficiently encompasses the total DNA-binding site. Thus, the additional engagement of the weak DNA-binding subsite, in the case of the 20-mer, provides a favorable contribution to the overall free energy of binding (see below). Contrary, the value of the partial equilibrium constant, K₂, which characterizes the transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, are ~1.9 and ~ 0.8 for the 10- and 20-mer, respectively, i.e., the observed second reaction step has very modest if any, contribution to the overall ΔG° of binding, particularly, in the case of the 20-mer. Comparison with the 14- and 16-mer indicates diminishing values of the partial equilibrium constant, K₂, with the length of the nucleic acid (Table 1). Moreover, the lower values of K₂ for the longer oligomers result chiefly from the systematically diminishing values of the forward rate constant, k₂. In other words, it is more difficult for the oligomer, which encompasses the total DNA-binding site, to enter the (P-ssDNA)₂ intermediate. Nevertheless, the transition, (P-ssDNA)₁ <-> (P-ssDNA) ₂, is fast and occurs within ~10 ms for all examined oligomers.

In the case of the 10-mer, which exclusively binds to the strong DNA-binding subsite, amplitude analysis indicates that the major fluorescence change of the nucleic acid occurs in the formation of the intermediate, (P-ssDNA)₁, with F₂ ≈ 2.30 (Table 1). The subsequent conformational transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, diminishes the emission of the bound oligomer, with F₃ ≈ 1.50. Nevertheless, there is a clear trend in the observed emission intensity changes with the increasing length of the bound oligomer, i.e., with the increasing efficiency of engaging the weak DNA-binding subsite by the nucleic aid. The value of F₂ diminishes for the 10-, 14-, 16-, and 20-mer, from ~2.30 to ~1.78, while the value of F₃ increases for the same oligomers from ~ 1.50 to ~1.94 (Table 1) (see Discussion).

Temperature Effect On the ssDNA Binding Dynamics To the Strong DNA-Binding Subsite and To the Total DNA-Binding Site of the ASFV Pol X

The nature of different intermediates in the ASFV pol X binding to the ssDNA has been addressed by examining the temperature effect on the dynamics of the DNA association with the strong DNA-binding subsite and the total DNA-binding site of the polymerase, as a function of the nucleic acid length. The stopped-flow studies were carried out at four different temperatures (data not shown). In general, the temperature increase from 10°C to 25°C does not affect the major features of the observed kinetic mechanism, which at all examined temperatures, is the two-step sequential process, described by eq. 7. However, the effect of the temperature on internal equilibria differs among the reaction intermediates and is different for the strong DNA-binding subsite, as compared to the total DNA-binding site.

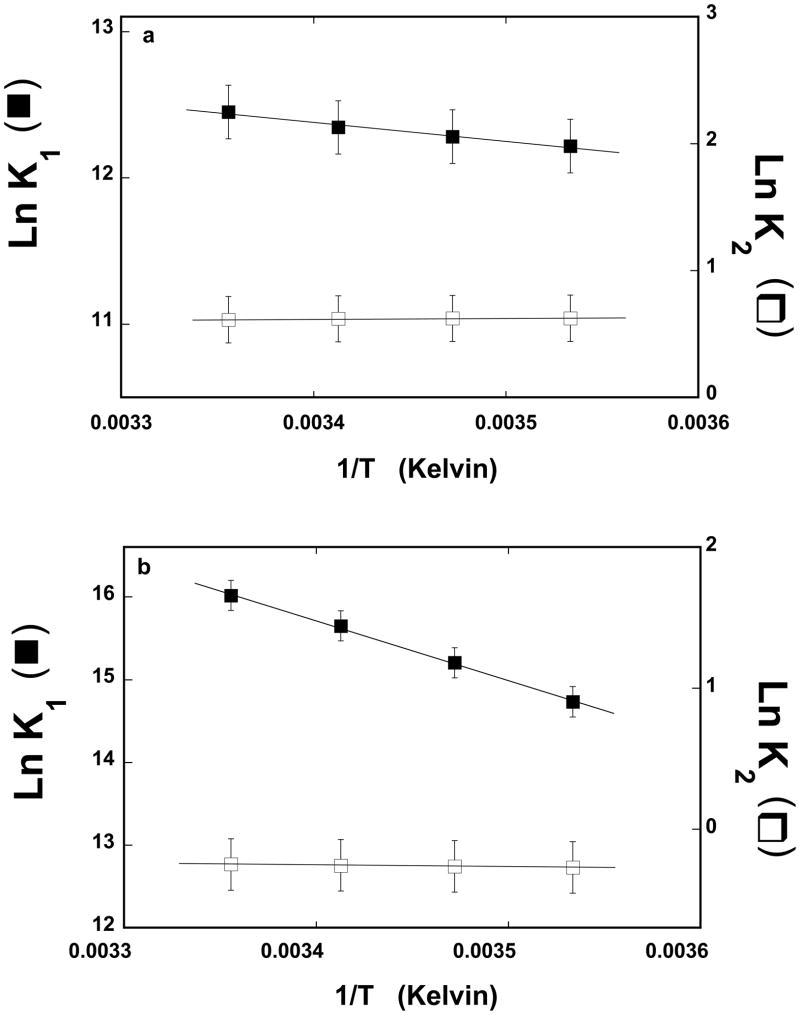
The dependence of the natural logarithms of the partial equilibrium constant, K₁ and K₂ upon the reciprocal of the temperature (Kelvin), for the association of the 10-mer, dεA(pεA)₉, with the strong DNA-binding subsite, is shown in Figure 4a. Within experimental accuracy, the plots are linear in the examined temperature range. The values of the partial equilibrium constant, K₁, characterizing the first binding step, ASFV pol X + ssDNA <-> (P-ssDNA) (eq. 7) modestly increases with the temperature increase, changing from ~2 × 10⁵ M⁻¹ at 10°C to ~2.6 × 10⁵ M⁻¹ at 25°C. This step is too fast to address its dynamics in the stopped-flow experiment. The partial equilibrium constants, K₂ characterizing the transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, remains unaffected by the temperature, resulting from the negligible effect of the temperature on the rate constants, k₂, and k₋₂ (data not shown). Analogous dependence of the natural logarithms of the partial equilibrium constant, K₁ and K₂ upon the reciprocal of the temperature, for the 20-mer, dεA(pεA)₁₉, which encompasses the total DNA-binding site of the ASFV pol X, is shown in Figure 4b. Unlike in the case of the 10-mer (see above), the values of K₁ characterizing the first binding step strongly increases with the temperature increase, changing from ~2.5 × 10⁶ M⁻¹ at 10°C to ~9 × 10⁶ M⁻¹ at 25°C. However, similar to the 10-mer, the partial equilibrium constant, K₂ characterizing the intramolecular transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, remains unaffected by the temperature, as a result of the lack of any pronounced effect of the temperature on k₂, and k₋₂ (data not shown).

Figure 4.

a. The dependence of the natural logarithm of the partial equilibrium constants, K₁ (■) and K₂ (❑), upon the reciprocal of the temperature (Kelvin) (van’t Hoff plot) for binding of the ssDNA 10-mer, dεA(pεA)₉, to the strong DNA-binding subsite of the ASFV pol X, as defined by the two-step kinetic mechanism (eq, 7). The solid lines are the linear least-squares fits of the experimental plot (eq. 11), which provide ΔH₁ = 2.6 ± 0.8 kcal/mol and ΔH₂ = −0.1 ± 0.1 kcal/mol. b. The dependence of the natural logarithm of the partial equilibrium constants, K₁ (■) and K₂ (❑), upon the reciprocal of the temperature (Kelvin) (van’t Hoff plot) for the binding of the ssDNA 20-mer, dεA(pεA)₁₉, to the total DNA-binding subsite of the ASFV pol X, as defined by the two-step kinetic mechanism (eq, 7). The solid lines are the linear least-squares fits of the experimental plot (eq. 11), which provide ΔH₁ = 14.4 ± 4.8 kcal/mol and ΔH₂ = −0.24 ± 0.10 kcal/mol (details in text).

The temperature dependence of the partial equilibrium constant, K_i, for each ith transition in the process of the ssDNA binding to the ASFV pol X is described by van’t Hoff’s equation [39]

$$\frac{\partial {\text{lnK}}_{\text{i}}}{\partial (\frac{1}{\text{T}})}=-\frac{\mathrm{\Delta }{\text{H}}_{\text{i}}}{\text{R}}$$ (11)

where K_i and ΔH_i are the partial equilibrium constant and the enthalpy change accompanying the ith transition, respectively. The obtained values of the thermodynamic function, ΔH_i and ΔS_i, characterizing the partial equilibria among the intermediates for all examined oligomers, are included in Table 1. The errors in the determined parameters are inherently large. Nevertheless, the observed differences are larger than the errors and provide an important insight about the nature of the observed transitions.

In the case of the 10- and 20-mer, which exclusively bind to the strong DNA-binding site and efficiently encompass total DNA-binding site of the enzyme, respectively, the first step, is characterized by positive enthalpy and entropy changes. However, the value of ΔH₁ ≈ 2.6 kcal/mol and ΔS₁ ≈ 33 cal/(mol deg), obtained for the 10-mer, are dramatically lower from ΔH₁ ≈ 14.4 kcal/mol and ΔS₁ ≈ 80 cal/(mol deg), obtained for the 20-mer (Table 1), indicating that processes of different natures are observed in the first binding step, exclusively to the strong subsite, as compared to the total DNA-binding site, which involves the engagement of the weak DNA-binding subsite of the polymerase in interactions with the nucleic acid. In the case of the 14- and 16-mers, which can only inefficiently associate with the weak DNA-binding subsite, the values of ΔH₁ are ~ 8.3 – 8.6 kcal/mol and ΔS₁ ~ 59 – 56 cal/(mol deg) (Table 1). On the other hand, the values of ΔH₂ and ΔS₂ are very small for all examined oligomers, indicating that the next transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, is very different from the binding steps and, at the same time, that the final transition of the complex has a similar nature whether or not it occurs when the DNA associates with the strong DNA-binding subsite or the total DNA-binding site (see Discussion).

Solvent Effect On the Kinetics of the ssDNA Association With the Strong DNA-Binding Subsite and With the Total DNA-Binding Site of the ASFV Pol X

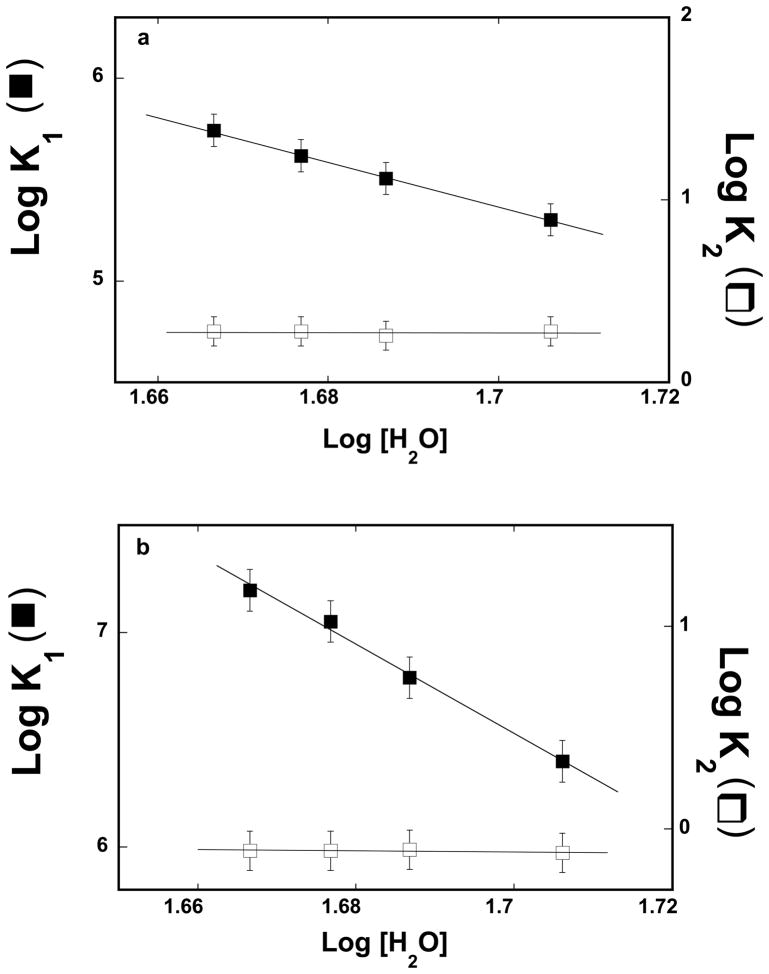
As in the case of the thermodynamic studies described in the accompanying paper, we have further addressed the nature of different intermediates in the ASFV pol X binding to the ssDNA, by examining the solvent effect on the kinetics of the DNA association with the strong DNA-binding subsite and the total DNA-binding site, as a function of the nucleic acid length. The stopped-flow experiments were performed at four different concentrations of glycerol (data not shown). Similar to the temperature effect, changing glycerol concentration does not affect the major character of the observed kinetic mechanism, which is the two-step sequential process (eq. 7).

Analysis described in the accompanying paper, indicates that glycerol affects the nucleic acid binding to the ASFV pol X, predominantly, through the changes of the water concentration, i.e., through the osmotic stress effect [40,41]. The dependence of the logarithms of the partial equilibrium constants, K₁ and K₂, upon the logarithm of water concentration (log-log plots) for the association of the 10-mer, dεA(pεA)₉, exclusively with the strong DNA-binding subsite, is shown in Figure 5a [42–44]. The plots are linear in the examined glycerol concentration range. The values of the partial equilibrium constant, K₁, strongly decreases with the increase of [H₂O], while K₂ remains unaffected by changes in [H₂O], with both rate constants, k₂, and k₋₂ being unaffected by glycerol concentrations (data not shown). In the case of K₁, the slope of the log-log plot is ∂logK₁/∂Log[H₂O] = −11.1 ± 3.0 indicating that ~11 water molecules are released in the first binding step, Pol X + ssDNA <-> (P-ssDNA)₁, upon the 10-mer binding to the strong subsite. Corresponding dependence of the logarithms of the partial equilibrium constants, K₁ and K₂, upon the logarithm of [H₂O], for the 20-mer, deA(peA)₁₉, which encompasses the total DNA-binding site, is shown in Figure 5b. Similar to the 10-mer, the partial equilibrium constants, K₂, remains unaffected by [H₂O], as a result of the lack of any pronounced effect of glycerol on the rate constants, k₂, and k₋₂ (data not shown). However, the slope of the log-log plot is ∂logK₁/∂Log[H₂O] = −20.7 ± 6.0, significantly larger than in the case of the 10-mer, indicating that ~21 water molecules are released in the first binding step of the 20-mer association with the total DNA-binding site (see accompanying paper) (see Discussion).

Figure 5.

a. The dependence of the logarithm of the partial equilibrium constants, K₁ (■) and K₂ (❑) upon the logarithm of the water concentration for binding of the ssDNA 10-mer, dεA(pεA)₉, to the strong DNA-binding subsite of the ASFV pol X, as defined by the two-step kinetic mechanism (eq, 7), in buffer C (pH 7.0, 10°C) containing different concentrations of glycerol. The solid lines are the linear least-squares fits of the experimental plots, which provide the slopes ∂LogK₁/∂Log[H₂O] = −11.1 ± 3.0 and ∂LogK₂/∂Log[H₂O] = −0.10 ± 0.20. b. The dependence of the logarithm of the partial equilibrium constants, K₁ (■) and K₂ (❑), upon the logarithm of the water concentration for the binding of the ssDNA 20-mer, dεA(pεA)₁₉, to the total DNA-binding site of the ASFV pol X, as defined by the two-step kinetic mechanism (eq, 7), in buffer C (pH 7.0, 10°C) containing different concentration of glycerol. The solid lines are the linear least-squares fits of the experimental plots, which provide the slopes ∂LogK₁/∂Log[H₂O] = −20.7 ± 6.0 and ∂LogK₂/∂Log[H₂O] = −0.2 ± 0.20 (details in text).

Dynamics of the 5′Fl-dT(pT)-CP-3′ Binding to the Total DNA-Binding Subsite of the ASFV Pol X

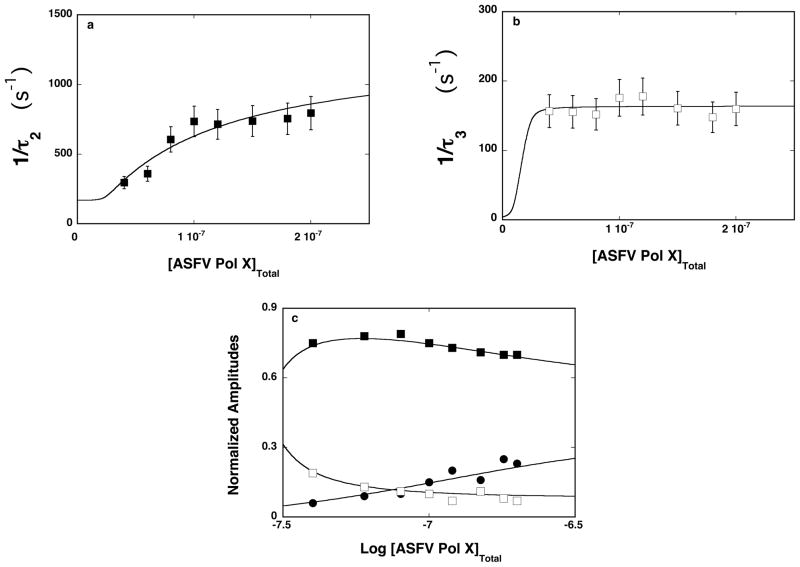
Experiments described so far, were performed with the etheno-derivatives of the homo-adenosine ssDNA oligomers corresponding to the oligomers, which were used in our equilibrium studies (see accompanying paper) [20]. However, due to the low quantum yield of the etheno-derivatives, the stopped-flow experiments require rather high concentrations of nucleic acids [45]. Correspondingly, higher concentrations of the protein were required to maintain pseudo-first-order conditions, which limit the resolution of the stopped-flow data. To get insight into the initial fast step(s) of the association reaction between the ASFV pol X and the ssDNA, we performed stopped-flow experiments with the ssDNA oligomer, 5′-Fl-dT(pT)₁₉-CP-3′, which contains the fluorescence acceptor (Fl), and the donor (CP). This is the same oligomer, which we applied in the fluorescence energy transfer studies of the enzyme - ssDNA complex (see accompanying paper). The dynamics of the reaction was monitored using the sensitized emission of the acceptor, Fl (see accompanying paper). The samples were excited in the donor (CP) absorption band (λ_ex = 425 nm) and the fluorescence emission was monitored in the acceptor emission band (520 nm) [46]. Very high quantum yields of the markers allowed us to apply significantly lower nucleic acid and protein concentrations, as compared to studies with the etheno-derivatives (see below). Moreover, the affinity of the thymine homo-oligomers is a factor of ~30 higher than the affinities of corresponding etheno-derivatives [20]. Unlike in the case of the etheno-derivatives, the stopped-flow kinetic traces of the 5′-Fl-dT(pT)₁₉-CP-3′ fluorescence required a two-exponential function to adequately represent the experimental data, indicating the presence of two relaxation steps (data not shown) [26–35]. Nevertheless, the amplitudes of the observed relaxation steps did not account for the total amplitude of the relaxation process, indicating the presence of an additional fast step beyond the resolution of the experimental system.

The dependence of the reciprocal relaxation time, 1/τ₂ and 1/τ₃, characterizing the observed kinetic steps, as a function of the total ASFV pol X concentration are shown in Figures 6a and 6b. The values of 1/τ₂, show hyperbolic dependence upon [ASFV pol X]_T, tending to plateau and indicating that 1/τ₂ characterizes an intramolecular step [26–35,38]. The plot reaches plateau at ~1000 s⁻¹. It is evident that the transition is beyond the resolution of the stopped-flow experiment, using the etheno-derivatives of the nucleic acid, as experimentally observed (see above). In other words, it is a part of the first, fast-unresolved step in the mechanism defined by eq. 7. The values of 1/τ₃ are within experimental accuracy, independent of the [ASFV pol X]_T, also indicating that it characterizes an intramolecular step. Moreover, they are very similar to the values of 1/τ₂, observed using etheno-derivatives, strongly suggesting that 1/τ₃ describes the same intramolecular transition as 1/τ₂, in the case of the etheno-derivatives (Figures 2a and 3a). Thus, the simplest minimum mechanism, which can account for the observed dependence of the relaxation times upon the ASFV pol X concentration, is a three-step, sequential binding process, described by equation

Figure 6.

a. The dependence of the reciprocal of the relaxation time, 1/τ₂, for the binding of the ssDNA 20-mer, 5′Fl-dT(pT)-CP-3′, to the total DNA-binding site of the ASFV pol X in buffer C (pH 7.0, 10°C) upon the total concentration of enzyme. The solid line is the nonlinear least-squares fit according to the three-step sequential mechanism, defined by eq. 12 (details in text). The error bars are standard deviations obtained from 3 – 4 independent experiments. b. The dependence of the reciprocal of the relaxation time, 1/τ₃, for binding of the ssDNA 20-mer, 5′Fl-dT(pT)-CP-3′, to the total DNA-binding site of the ASFV pol X in buffer C (pH 7.0, 10°C), upon the total concentration of enzyme. The solid line is the nonlinear least-squares fit according to the three-step sequential mechanism, defined by eq. 12. The error bars are standard deviations obtained from 3 – 4 independent experiments. c. The dependence of the normalized, individual relaxation amplitudes of the corresponding relaxation processes, A₁, A₂, and A₃, upon the logarithm of the total concentration of the polymerase. The solid lines are nonlinear least-squares fits according to the three-step sequential mechanism, defined by eq. 12; A₁ (●), A₂ (■), A₃ (❑) (details in text).

$$\text{Pol}\text{X}+\text{ssDNA}\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\leftrightarrow }}{(\text{P}-\text{ssDNA})}_1\underset{{\text{k}}_{-2}}{\overset{{\text{k}}_2}{\leftrightarrow }}{(\text{P}-\text{ssDNA})}_2\underset{{\text{k}}_{-3}}{\overset{{\text{k}}_3}{\leftrightarrow }}{(\text{P}-\text{ssDNA})}_3$$ (12)

The dependence of the normalized individual amplitude, A₁, A₂, and A₃ upon the total concentration of the ASFV pol X is shown in Figure 6c. Amplitude, A₂ of the resolved fast relaxation step dominates the total amplitudes of the relaxation process over the examined range of the enzyme concentration and, after reaching a maximum, gradually decreases with increasing [ASFV pol X]_T. The values of A₃, characterizing the slowest relaxation step, steadily decreases while the amplitude of the fast unresolved process, A₁, increases with the increase of [ASFV pol X]_T. The behavior of the individual relaxation times and amplitudes is in complete agreement with the proposed kinetic mechanism (eq. 12) (see below) [26–35,38].

The numerical analysis to extract the partial equilibrium constants and rate constants from the relaxation data in Figures 6a, 6b, and 6c, was the same as described above for the etheno-derivatives (see above). We also utilize the fact that the value of the overall binding constant, K₂₀ = (2.8 ± 0.9) × 10⁹ M⁻¹, has previously been independently obtained in the same solution conditions by the equilibrium fluorescence titration method [20]. The overall binding constant K₂₀ is related to the partial equilibrium constants for each step of the reaction (eq. 12), as

$${\text{K}}_{20}={\text{K}}_1(1+{\text{K}}_2+{\text{K}}_2{\text{K}}_3)$$ (13)

with K₁ = k₁/k₋₁, K₂ = k₂/k₋₂, and K₃ = k₃/k₋₃ [26–35]. Individual amplitudes were analyzed using the maximum, fractional increase of the nucleic acid fluorescence, ΔF_max ≈ 1.65, obtained in independent FRET equilibrium studies (see accompanying paper). The values of ΔF_max is analytically expressed as

$$\mathrm{\Delta }{\text{F}}_{max}=\frac{\mathrm{\Delta }{\text{F}}_2+{\text{K}}_2\mathrm{\Delta }{\text{F}}_3+{\text{K}}_2{\text{K}}_3\mathrm{\Delta }{\text{F}}_4}{1+{\text{K}}_2+{\text{K}}_2{\text{K}}_3}$$ (14)

where ΔF₂, ΔF₃, and ΔF₄ are fractional fluorescence intensities of the corresponding intermediates in the association reaction of 5′-Fl-dT(pT)₁₉-CP-3′, with the ASFV pol X relative to the fluorescence of the free nucleic acid, F₁ (see above) [26–35]. The solid lines in Figures 6a, 6b and 6c are nonlinear least-squares fits of the relaxation times and fractional individual amplitudes of the reaction, defined by eq. 12, using a single set of binding, kinetic, and spectroscopic parameters, which provide: K₁ = (1.2 ± 0.2) × 10⁷ M⁻¹, K₂ = 125 ± 27, K₃ = 0.9 ± 0.2, k₂ = 1250 ± 200 s⁻¹, and k₋₂ = 10 ± 2 s⁻¹, k₃ = 80 ± 16 s⁻¹, k₋₃ = 85 ± 17 s⁻¹, F₂ = 1.6 ± 0.2, F₃ = 2.5 ± 0.1, and F₄ = 2.8 ± 0.1 (see Discussion).

The first unresolved step, characterized by K₁, contributes most to the overall free energy of binding, ΔG°. The second step, unresolved in experiments with etheno-derivatives of the nucleic acids, also favorably contributes ΔG°. The value of k₂ indicates that the ASFV pol X - ssDNA complex reaches the (P-ssDNA)₂ intermediate in less than ~1 ms. On the other hand, the values of k₃ and k₋₃ are, within experimental accuracy, the same as, k₂ and k₋₂, observed for the etheno-derivatives. As pointed out above, these data indicate that the intramolecular step, (P-ssDNA)₂ <-> (P-ssDNA)₃, is identical to the step, (P-ssDNA)₁ <-> (P-ssDNA)₂, observed for the etheno-derivatives, and is the same for all examined ssDNA oligomers. The large value of F₃ indicates that the nucleic acid undergoes a major, topological conformational transition in the complex as a result of the transition, (P-ssDNA)₁ <-> (P-ssDNA)₂ and preserves the same conformation in the (P-ssDNA) ₃ intermediate, as indicated by the similar values of F₃ and F₄ (see Discussion).

The Fractional Distributions of the Intermediates of the ASFV Pol X in the Complex With the ssDNA Which Encompasses the Total DNA-Binding Site

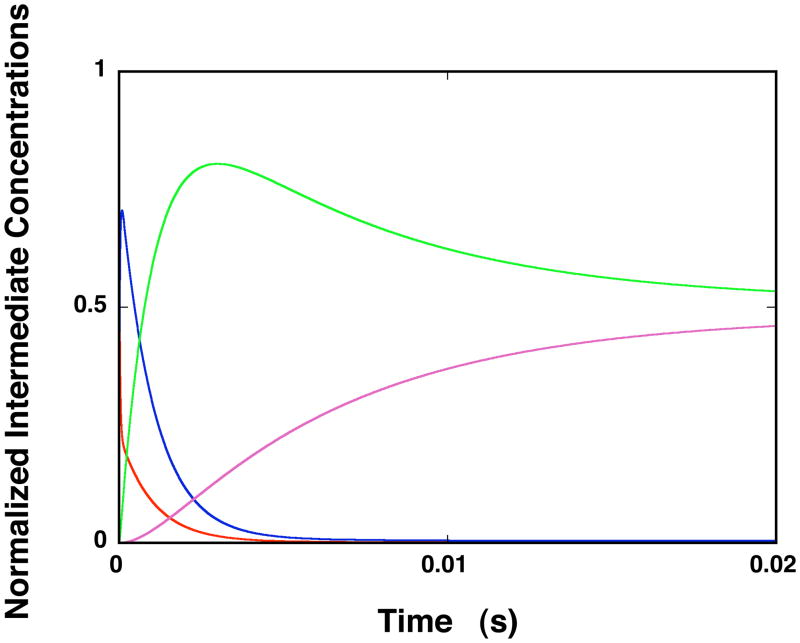
The fractional distributions of the ssDNA intermediates, for the ssDNA oligomer, which encompasses the total DNA-binding site of the ASFV pol X, as a function of time, are shown in Figure 7. The plots were generated using the rate constants obtained for 5′Fl-dT(pT)₁₉-CP-3′ (see above) and assuming that the first unresolved step is closed to the diffusion-controlled reaction. The concentrations of the intermediates are normalized as molar fractions of the total concentration of the DNA oligomer. At the selected protein concentration, the nucleic acid is predominantly saturated with the enzyme. The first intermediate, (P-ssDNA)₁, does not significantly contribute to the total population of the nucleic acid states beyond the first ~5 ms of the reaction, as its fractional contribution strongly diminishes with time and becomes negligible at equilibrium. The fractional contribution of the second intermediate, (H-ssDNA)₂, initially dominates the distribution. At equilibrium, (H-ssDNA)₂, constitutes ~52%, of the total population of the DNA. The contribution of (H-ssDNA)₃ becomes significant after ~10 ms of the reaction and constitute ~48% of the nucleic acid population at equilibrium. The final equilibrium of the ASFV pol X - ssDNA complex is achieved after ~30 ms of the reaction time (see Discussion).

Figure 7.

Computer simulation of the time courses of the fractional concentration distribution of different ssDNA species in the binding of the ssDNA 20-mer, which engages the total DNA-binding site of the enzyme, using the mechanism defined by eq. 12, obtained for 5′Fl-dT(pT)-CP-3′, and the determined partial equilibrium, and rate constants, in buffer C (pH 7.0, 10°C). The first step of the reaction has been modeled as diffusion-controlled reaction with the determined K₁; free ssDNA oligomer ( ), (P-ssDNA)₁ ( ), (P-ssDNA)₂ ( ), (P-ssDNA)₃ ( ). The concentration of the nucleic acid and the protein are 1 × 10⁻⁸ M (oligomer) and 3 × 10⁻⁷ M polymerase, respectively (details in text).

DISCUSSION

Sequential, Multiple-Step Kinetic Mechanism of the ssDNA Binding To the Total DNA-Binding Site and To the Strong DNA-Binding Subsite of the ASFV Pol X

Energetics and dynamics of interactions of the DNA polymerase with the ssDNA play a fundamental role in enzyme activities [9–17,47–50]. This includes the specific recognition of the ssDNA conformation, which constitutes the template for the synthesis of the complementary strand, as well as the mechanism of the free energy transduction by the enzyme. Binding of the etheno-derivatives of the ssDNA oligomers, encompassing the total DNA-binding site and the ssDNA oligomers, which exclusively bind to the strong DNA-binding subsite, occurs through the same two-step sequential mechanism, i.e., fast bimolecular association followed by a significantly slower isomerization process (eq. 7). This seemingly simple relaxation process results from the fact that the association reaction is very fast and partly beyond the resolution of the stopped-flow experiments at applied protein and nucleic acid concentrations. Large fluorescence changes of the etheno-derivatives reflect significant immobilization and separation of the nucleic acid bases (see accompanying paper) [45,51]. The changes occur in the first step of the reaction and provide the first indication that the binding step (eq. 7) cannot be a purely diffusion-controlled reaction, even in the case of the 10-mer that exclusively associates with the strong subsite. The unresolved relaxation step must contain at least another very fast step(s), which lead to the changed conformation of the nucleic acid.

In the case of the longer oligomers, which can additionally engage the weak DNA-binding subsite, the presence of the additional relaxation step has been confirmed by kinetic experiments with the sensitized emission of the 20-mer, containing the fluorescence acceptor and the donor. These experiments allowed us to directly identify another relaxation step, unresolved in etheno-adenosine oligomers studies (see below). In the case of the etheno-derivatives, the complexity of the binding step in eq. 7 was also indicated by the effect of the temperature, as well as the solvent on the energetics of the observed intermediates, as function of the nucleic acid length (see below). Furthermore, the observed number of the relaxation steps does not changes under pseudo-first-order conditions with respect to the nucleic acid, when the DNA is in large excess over the protein (data not shown) [52]. Such behavior indicates that the enzyme does not undergo a kinetically relevant conformational transition prior to the nucleic acid binding. i.e., the binding process is sequential, as described by eq. 7 and, with higher resolution by eq. 12.

The Nucleic Acid Makes the Initial Contact With the ASFV Pol X Through the Strong DNA-Binding Subsite of the Enzyme

As mentioned above, equilibrium studies provide the first indication that the nucleic acid initiates contact with the total DNA-binding site through the strong DNA-binding subsite (see accompanying paper). Kinetic data using the analogous etheno-derivatives of the ssDNA oligomers indicate that the first reaction step generates the predominant part of the overall free energy of binding, ΔG°. This is true for both the ssDNA oligomer, which exclusively associates with the strong DNA-binding subsite and the oligomers that engage the total DNA-binding site. Such a large free energy of binding is only available at the strong DNA-binding subsite of the enzyme [20–22]. Although kinetic data, where the association was monitored using the sensitized emission, indicate the presence of an additional fast step (eq. 12), unresolved in the experiments with etheno-derivatives, this energetically favorable step only accounts for a small fraction of the overall ΔG°. The major part of the free energy of binding is still generated in the first step of the reaction, as defined by eq. 12 (see above).

Binding of the ssDNA to the Total DNA-Binding Site of the ASFV Pol X Occurs Through Sequential Engagement of the Strong and the Weak DNA-Binding Subsites of the Enzyme, Without an Intervening Conformational Transition of the Protein

Equilibrium FRET analyses described in the accompanying paper showed that the nucleic acid, which encompasses the total DNA-binding site of the enzyme, is strongly bent in the complex with the ASFV pol X. Stopped-flow studies using the same ssDNA oligomer containing the fluorescence donor and the acceptor indicate the lack of a major change of the sensitized emission of the acceptor in the first binding step of the reaction. These data provide strong support for the conclusion (see above) that the first step, as defined by the more complex eq. 12, is the initial association of the nucleic acid with the strong DNA-binding subsite, with local, but not global, topological changes of the nucleic acid structure. The major increase of the sensitized emission of the acceptor occurs in the second reaction step, (P-ssDNA)₁ <-> (P-ssDNA)₂, resolved using 5′Fl-dT(pT)₁₉-CP-3′, indicating that in this step, the nucleic acid engages the weak DNA-binding subsite of the polymerase and assumes the bent structure (eq. 12). The second step in eq. 12 is hidden in the first step of the simpler mechanism, determined using the etheno-derivatives (eq. 7) and only reflected by the accompanying large changes of the fluorescence of the nucleic acids (Table 1). Thus, the combined kinetic data using the fluorescence emission of the etheno-derivatives, or the sensitized emission of 5′Fl-dT(pT)₁₉-CP-3′ indicate that the binding of the ssDNA, which engages the total DNA-binding site of the polymerase, includes the initial association with the strong DNA-binding subsite and is then followed by the fast association of the DNA with the weak subsite, without an intervening protein structural change.

Association of DNA with ASFV Pol X Proceeds Through Steps Characterized by Dramatically Different Dynamics and Energetics

Intermediates in the ssDNA association with the ASFV pol X dramatically differ in the dynamics and energetics of their formation, both for the association with the total DNA-binding site, as well as the strong DNA-binding subsite. In the studies using the sensitized emission of 5′Fl-dT(pT)₁₉-CP-3′, the first bimolecular step, ASFV pol X + ssDNA <-> (P-ssDNA)₁ (eq. 12), is beyond detection in the stopped-flow experiments. That would require the relaxation time, characterizing this binding step, to be ≥1000 s, at the applied protein concentrations [26–35,38]. Because the relaxation time mainly reflects the rate constant, k₋₁, the value of k₋₁ must be at least ≥1000 s⁻¹ for the initial binding to the strong subsite [26–35,53].

The second transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, (eq, 12) detected only by the sensitized emission of 5′Fl-dT(pT)₁₉-CP-3′, is fast, although significantly slower than the first step, with k₂ ≈ 1250 s⁻¹ and k₋₂ ≈ 10 s⁻¹. The dramatic drop in the rate of the second reaction step indicates a change in the nature of the formed intermediate. A large increase of the sensitized emission of the DNA indicates a strong bending of the nucleic acid and the dynamics of the (P-ssDNA)₂ formation reflects the fast engagement of the weak DNA-binding subsite of the polymerase in interactions with the DNA (see above). The transition, (P-ssDNA)₁ <-> (P-ssDNA)₂, is energetically favorable with K₂ ≈ 125, as expected for the engagement of the additional DNA-binding subsite. In the case of dεA(pεA)₉, this step is not present, as the oligomer exclusively binds to the strong subsite and the observed second step in eq. 7 corresponds to the final conformational transition of the complex (see below). The observed large difference between the values of K₁ for dεAp(εA)₉ and dεAp(εA)₁₉, respectively, whose kinetic mechanism of binding is described by the apparently simpler mechanism (eq. 7), results from the fact that the 10-mer cannot access the weak subsite (Table 1).

The rates of the slowest final transition, (P-ssDNA)₂ <-> (P-ssDNA)₃, are within experimental accuracy, the same for all examined etheno-derivatives and 5′Fl-dT(pT)₁₉-CP-3′, i.e., the transition is present in the case of the exclusive binding to the strong DNA-binding site as well as the binding to the total DNA-binding site and is detected by the fluorescence emission of etheno-adenosines, and the sensitized emission. These data strongly suggest that this step reflects, not a large conformational change of the bound DNA, but a conformational transition of the protein - nucleic acid complex. On the other hand, the different dynamics of the final step, observed for the short versus the long oligomers, indicate that shorter oligomers can enter the last intermediate faster the longer nucleic acids. Moreover, the step contributes favorably to the overall ΔG°, only for the oligomers, which bind exclusively to the strong subsite, or inefficiently engage the weak subsite (Table 1).

Different Apparent Enthalpy and Entropy Changes Characterizing Formations of Different Intermediates as a Function of the ssDNA Length Reflects Gradual Engagement of the Weak DNA-Binding Subsite in Interactions With the Nucleic Acid

Temperature effect on binding the etheno-derivatives of the ssDNA to the ASFV pol X provides an additional, strong indication of the different nature of the formed intermediates. For the 10-mer, formation of (P-ssDNA)₁ (eq. 7) is characterized by the small apparent positive enthalpy and entropy changes (Table 1). It must include the fast association of the nucleic acid and the fast local rearrangement of the DNA in the strong subsite, as indicated by the large fluorescence change of the nucleic acid. Thus, the intrinsic DNA-binding process to the strong DNA-binding subsite of the ASFV pol X apparently is an entropy-driven process (see below). As the length of the nucleic acid increases, the positive enthalpy and entropy changes for the first binding step (eq. 7) increase, reaching the values of ~14.4 kcal/mol and ~80 cal/(mol deg) for the 20-mer (Table 1). Such large increases of the ΔH°₁ and ΔS°₁ indicate a dramatic change in the nature of the formed intermediate. In other words, in the case of the longer nucleic acids, the binding step in eq. 7 includes the gradual engagement of the weak DNA-binding subsite, as detected using the sensitized emission only (see above). The following transition, (P-ssDNA) ₁ <-> (H-ssDNA)₂ (eq. 7) is very different. It is characterized by very low enthalpy and entropy changes (Table 1). Such different behavior corroborates the conclusion that the final relaxation step reflects the protein conformational change in the complex, without profound changes of the engagement of the DNA-binding subsites of the enzyme in interactions with the nucleic acid.

Association of the ssDNA with the Total DNA-Binding Site and the Strong DNA-Binding Subsite of the ASFV Pol X Is Accompanied By the Release of Water Molecules, Which Occurs in the Intrinsic Binding Steps of the Reaction

Thermodynamic studies indicate that binding of the ssDNA to the total DNA-binding site and the strong DNA-binding subsite is accompanied by the release of large and substantially different numbers of water molecules (see accompanying paper). The log-log plots of the partial equilibrium constants, K₁ and K₂, obtained for the 10-mer, dεAp(εA)₉, indicate that water molecules are release only in the binding step of the reaction, but not in the following conformational transition of the complex. Recall, the 10-mer does not engage the weak subsite on the N-terminal domain of the protein [20–22]. Therefore, the value of ∂LogK₁/∂Log[H₂O] ≈ −11 reflects the number of water molecules release in the first binding step to the strong subsite (Figure 5a). Because the oligomers, which engage the total DNA-binding site, also initially associate only the strong subsite (see above), the data indicate that ~11 water molecules are released in the association of all examined nucleic acids with the strong subsite.

In the case of the 20-mer, dεAp(εA)₁₉, the value of ∂LogK₁/∂Log[H₂O] ≈ −21 is twice as large as that observed for the 10-mer (Figure 5b). However, for the 20-mer, the first step in the simpler mechanism, defined by eq. 7, contains the step that is only resolved using the sensitized emission (eq. 12), i.e., it contains the engagement of the weak DNA-binding subsite of the enzyme in interactions with the nucleic acid. Thus, the value of ∂LogK₁/∂Log[H₂O] ≈ −21 reflects the number of water molecules released in the first binding step to the strong subsite and the water molecules released as a result of association with the weak subsite. The data strongly suggest that a very similar number of water molecules, ~10, accompanies the nucleic acid association with both the strong and the weak subsite. Notice, the obtained numbers of the released water molecules in the binding steps of the reaction corroborate the analogous numbers determined in equilibrium studies (see accompanying paper). Moreover, the kinetic data indicate that the final conformational transition of the protein does not contribute to the observed release of the water molecules, neither for the oligomer that exclusively associates with the strong DNA-binding subsite, nor with the total DNA-binding site.

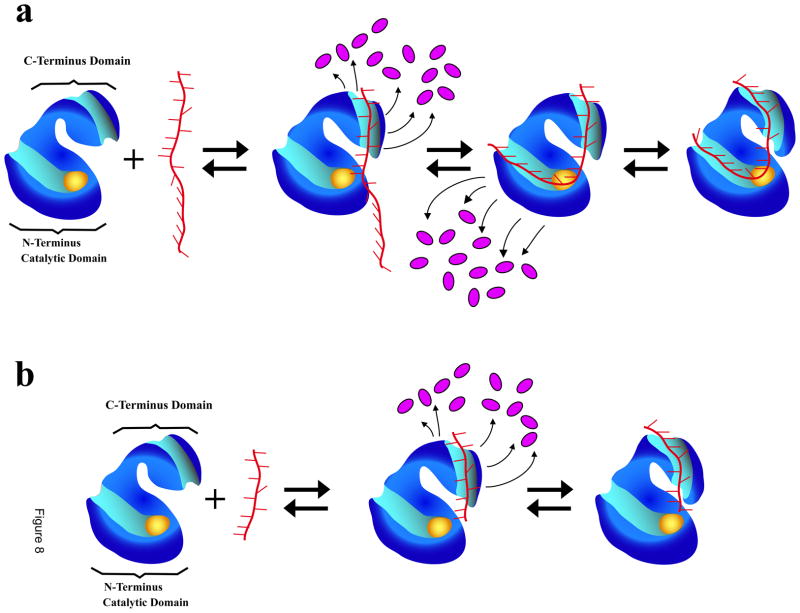
Schematic model of the ssDNA binding to the total DNA-binding site of the ASFV pol X, based on the data obtained in this work, is shown in Figure 8a. Initially, The nucleic acid binds to the strong DNA-binding subsite of the polymerase on the C-terminal domain, forming the initial complex, (P-ssDNA)₁ (eq. 12). In the intermediate, local conformational transition of the complex strongly immobilizes the bases in direct interactions with the binding subsite. Moreover, the association is accompanied by the release of water molecules and the initial step provides the major part of the overall free energy of binding. Formation of the next intermediate, (P-ssDNA)₂, is also energetically favorable and the DNA engages the weak DNA-binding subsite on the catalytic N-terminal domain of the protein. The nucleic acid is now strongly bent in the complex with the polymerase (see above). This binding step is also accompanied by the release of a very similar number of water molecules, as in the association with the strong subsite. In the final intermediate, (P-ssDNA)₃, the protein - DNA complex undergoes a conformational transition, which is not energetically favorable and without significantly affecting the global topology of the DNA, and without releasing additional water molecules. In the case of the ssDNA oligomer, which exclusively binds to the strong DNA-binding subsite, only the formation of the intermediate (P-ssDNA)₁, is accompanied by the release of water molecules (Figure 8b, eq. 7). The final intermediate, (P-ssDNA) ₂, is a conformational transition without any release of water molecules.

Figure 8.

a. Schematic model of the ssDNA binding to the total DNA-binding site the ASFV pol X. The nucleic acid makes the first contact with the strong DNA-binding subsite of the polymerase on the C-terminal domain, forming the (P-ssDNA)₁ intermediate (eq. 12). In the intermediate, the local conformational transition of the complex strongly immobilizes the bases, which are in direct interactions with the binding subsite and the association is accompanied by the release of water molecules (magenta ovals). In the next intermediate, (P-ssDNA)₂, the DNA engages the weak DNA-binding subsite on the catalytic N-terminal domain of the protein, also a reaction accompanied by the release of a similar number of water molecules, as in the association with the strong subsite. In the final intermediate, (P-ssDNA)₃, the protein - nucleic acid complex undergoes a conformational transition, without significantly affecting the global topology of the bound DNA and without releasing additional water molecules. The nucleic acid remains strongly bent in the complex with the polymerase (details in text). The yellow oval indicates the location of the active site. b. Analogous schematic model of the ssDNA binding exclusively to the strong DNA-binding subsite on the C-terminal domain of the ASFV pol X. The nucleic acid makes the first contact with the strong subsite forming (P-ssDNA)₁ (eq. 7). The local conformational transition of the complex strongly immobilizes the bases directly engaged in interactions with the binding subsite and the association is accompanied by the release of water molecules (magenta ovals). The nucleic acid does not engage the weak DNA-binding subsite on the N-terminal domain. In the final intermediate, (P-ssDNA)₂, the protein - nucleic acid complex undergoes a conformational transition without releasing additional water molecules (details in text).

On the basis of equilibrium studies, we previously indicated that, when the ASFV pol X engages the total DNA-binding site, the polymerase - DNA complex exists in equilibrium between two states, though the state with both the strong and the weak DNA-binding subsite engaged in interactions with the nucleic acid, dominates the equilibrium complex [20]. Kinetic data described in this work support this conclusion and indicate that the dominating state exists in an additional equilibrium, (P-ssDNA)₂ <-> (P-ssDNA)₃, with another conformational state of the polymerase - ssDNA complex (Figure 7). Moreover, the transition rates are fast and equilibrium is established prior the catalysis [5,6]. Engagement of the weak DNA-binding subsite is absolutely necessary for the catalytic activity of the enzyme, as the ssDNA constitutes the template of the newly synthesized DNA. The catalytic activity of the final (P-ssDNA)₃ intermediate is unknown. However, the existence of such additional and fast-established equilibrium complexes indicates that the mechanism of the catalysis is more complex than previously thought and is, most probably, one of the factors behind the observed low processivity and very modest fidelity of the ASFV pol X [5,6].

Abbreviations

ASFV

African Swine Fever Virus

DTT

dithiothreitol

ssDNA

single-stranded DNA

dsDNA

double-stranded DNA

εA

etheno-adenosine

CP

7-Diethylamino-3-(4′-maleimidylphenyl)-4-methylcoumarin

FRET

fluorescence resonance energy transfer