Shear elastic modulus estimation from indentation and SDUV on gelatin phantoms

Abstract

Tissue mechanical properties such as elasticity are linked to tissue pathology state. Several groups have proposed shear wave propagation speed to quantify tissue mechanical properties. It is well known that biological tissues are viscoelastic materials; therefore velocity dispersion resulting from material viscoelasticity is expected. A method called Shearwave Dispersion Ultrasound Vibrometry (SDUV) can be used to quantify tissue viscoelasticity by measuring dispersion of shear wave propagation speed. However, there is not a gold standard method for validation. In this study we present an independent validation method of shear elastic modulus estimation by SDUV in 3 gelatin phantoms of differing stiffness. In addition, the indentation measurements are compared to estimates of elasticity derived from shear wave group velocities. The shear elastic moduli from indentation were 1.16, 3.40 and 5.6 kPa for a 7, 10 and 15% gelatin phantom respectively. SDUV measurements were 1.61, 3.57 and 5.37 kPa for the gelatin phantoms respectively. Shear elastic moduli derived from shear wave group velocities were 1.78, 5.2 and 7.18 kPa for the gelatin phantoms respectively. The shear elastic modulus estimated from the SDUV, matched the elastic modulus measured by indentation. On the other hand, shear elastic modulus estimated by group velocity did not agree with indentation test estimations. These results suggest that shear elastic modulus estimation by group velocity will be bias when the medium being investigated is dispersive. Therefore a rheological model should be used in order to estimate mechanical properties of viscoelastic materials.

I. Introduction

Noninvasive measurement of tissue mechanical properties as an estimator for tissue pathology is an emerging field of medical imaging [1–8]. In principle, all elasticity imaging methods introduce mechanical excitation to tissue and then monitor the tissue response with conventional imaging methods. The first proposed elasticity imaging methods either excite tissue externally, as in ultrasound elastography [9], or use focused ultrasound to produce acoustic radiation force to push tissue as in acoustic radiation force impulse (ARFI) imaging [3]. While elastography and ARFI are useful approaches, they do not provide a quantitative measure of tissue stiffness; both methods typically form a 2D image providing a relative map of tissue stiffness. Shear wave propagation speed methods, such as magnetic resonance elastography (MRE) [1], shear wave elasticity imaging (SWEI) [7], Transient elastography (TE) [2] and supersonic shear imaging (SSI) [10], have been proposed to quantify tissue mechanical properties. Most of these methods consider a pure elastic medium to describe the tissue mechanical properties, therefore only tissue elasticity is quantified.

Shear wave speed, c_s, in a pure elastic medium is related to the shear modulus, G, and density, ρ, by

$$c_s=\sqrt{\frac{G}{\rho }}$$ (1)

The wave speed in a given medium can be defined by the velocity of a single frequency component (phase velocity) or the velocity of the wave packet (group velocity). In a non-dispersive medium, phase velocity is the same as group velocity. In such circumstance, the wave velocity is independent of frequency. In contrast, in a dispersive medium, the wave speed is dependent on frequency; therefore phase velocity is not the same as group velocity in a dispersive medium. Dispersion can be caused by both tissue geometry and material properties.

It has been established that soft biological tissues exhibit a combination of elastic and viscous behavior [11]. A material subject to periodic oscillations exhibits a complex modulus M(ω) described by [12]

$$M(\omega )=M_1(\omega )+{jM}_2(\omega )$$ (2)

where the real part M₁(ω) is the elastic or storage modulus, and the imaginary part M₂(ω) is the loss or viscous modulus. The most common rheological models are the Voigt and the Maxwell model. The Voigt model has been shown to be appropriate for describing viscoelastic properties of tissue in the low frequency range (50–500 Hz) [13–16]. The complex shear modulus for the Voigt model is given by M₁(ω) = μ₁ and M₂(ω) = ωμ₂, where μ₁ is shear elastic modulus and μ₂ is viscosity [13].

A few elasticity imaging methods take advantage of the dispersive nature of soft tissue and can quantitatively solve for both tissue elasticity and viscosity [10, 17–21]. Even though sonoelastography [8] and supersonic shear imaging (SSI) [10] can provide maps of shear modulus and viscosity, specialized hardware is necessary to implement both methods.

A method called Shearwave Dispersion Ultrasound Vibrometry (SDUV) can be used to quantify both tissue shear elasticity and viscosity by evaluating dispersion of shear wave propagation speed over a certain bandwidth [20, 22]. It is desirable to have an inexpensive, reproducible tool to validate SDUV measurements. Mechanical testing is usually regarded as the gold standard method, but mechanical testing devices are usually very expensive.

Chen, et al., have reported a quantitative model for a sphere vibrated by two ultrasound beams in a homogeneous viscoelastic medium [22]. In this study, a Doppler laser vibrometer was used to measure the mechanical frequency response of the sphere. Although this method can estimate material properties in an independent manner, its main disadvantage is that the medium around the target must be optically clear. To overcome this problem, a single element ultrasound transducer can be used to measure the sphere time-domain response [23, 24], which was then fit using a model to obtain estimates of the shear elasticity and viscosity. However, these methods are not suitable for tissue mechanical properties characterization since a sphere must be embedded within a homogeneous tissue. Therefore, a more comprehensive study is needed to validate SDUV.

Several methods to measure tissue mechanical properties such as stress-relaxation, quasi-static and dynamic test have been used on biological tissues [11]. Mechanical tests had been used to evaluate the accuracy of elasticity methods such as MRE, ARFI and TE. MRE measurements have been compared to compression tests and dynamic tests on tissue like gelatin phantoms of varying elasticity [25, 26]. An integrated indentation and ARFI imaging has been used to characterize soft tissue stiffness [27]. TE measurements have been compared to tensile tests and dynamic test on a tissue like polymers [28, 29]. Cross-validation between MRE and ultrasound-based transient elastography had been made in homogeneous tissue mimicking phantoms [30, 31]. Dynamic tests allow estimation of the change in tissue property parameters versus frequency, but the material needs to be characterized one frequency at a time. Quasi-static methods include compression tests, tensile tests and indentation tests. Compared to the others, indentation tests have been widely used to assess the mechanical properties of tissues. Their main advantage is that they can be applied both ex vivo and in vivo [11, 32–40]. The indentation test is considered a gold standard test to assess elastic mechanical properties. Furthermore, it is attractive because of its widespread use and ease of implementation, with its only requirement is to have a surface for indenter contact application.

The purpose of this study is to validate linearity and phase velocity assumptions of SDUV estimations of shear elastic modulus with quasi-static indentation measurements of elastic modulus on gelatin phantoms of differing stiffness. In addition, the indentation measurements are compared to estimates of elasticity derived from shear wave group velocities.

II. Methods

A. Indentation test

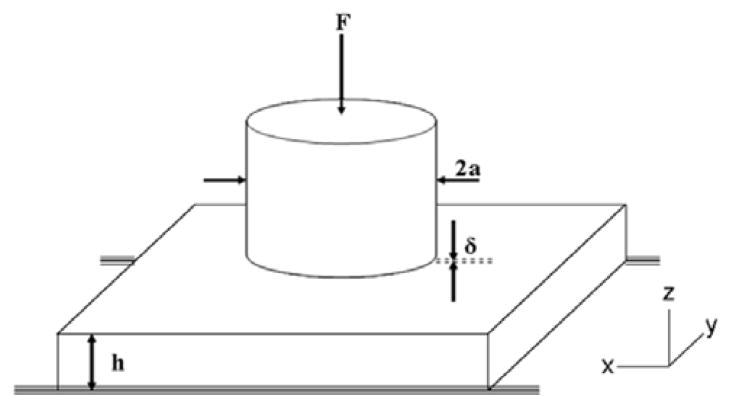
Soft tissue indentation based on a Hayes model [41] was used in this study. Fig. 1 illustrates a lateral infinite isotropic elastic material with a finite thickness resting on a rigid half-space. The material deforms under the action of a rigid axisymmetric indenter pressed normal to the surface by an axial force F.

Fig. 1.

Experimental set up, where F is the indentation force, Δ is the indentation depth, a is the indenter radius, and h is the material thickness.

Shear tractions between indenter and material are assumed negligible and the material is assumed to adhere to the half-space rigid surface. For a flat-end cylindrical indenter, the effective shear elastic modulus G is:

$$G=\frac{(1-\nu )}{4a\kappa (\nu ,a/h)}·\frac{F}{\delta }$$ (3)

where ν is the Poisson ratio, F is the indentation force, Δ is the indentation depth, a is the indenter radius, h is the material thickness and κ is a geometry factor. Values of κ for a range of a/h and ν have been estimated by Hayes, et al [41].

B. Principles of SDUV

Shearwave Dispersion Ultrasound Vibrometry (SDUV) applies a focused ultrasound beam to generate harmonic shear waves or impulse shear waves that propagate outward from the vibration center [19, 20]. Chen, et al., originally reported using modulated ultrasound to create harmonic shear waves to characterize the viscoelastic properties of gelatin phantoms using shear wave dispersion [19, 20]. A limitation of this method was that the modulation frequency had to be changed multiple times to evaluate the dispersion over a significant bandwidth. This method was advanced to make faster measurements by transmitting repeated tonebursts of ultrasound [20]. A single toneburst could be used to generate shear wave dispersion but the signal-to-noise ratio at high frequencies may be poor. Although repeated tonebursts require more acquisition time compared to a single toneburst, the advantage of using repeated tonebursts is that shear waves are created that have motion amplitudes with high signal-to-noise ratio at harmonics of the repetition frequency [20, 42].

For an isotropic, viscoelastic, homogenous material modeled using the Voigt model the shear wave propagation speed, c_s, depends on the frequency of shear wave, ω_s [13]

$$c_s({\omega }_s)=\sqrt{\frac{2({\mu }_1^2+{\omega }_s^2{\mu }_2^2)}{\rho \left({\mu }_1+\sqrt{{\mu }_1^2+{\omega }_s^2{\mu }_2^2}\right)}}$$ (4)

where ρ, μ₁ and μ₂ are the density, shear elastic modulus and viscosity of the medium, respectively.

The shear wave speed is estimated from its phase measured at least at 2 locations separated by Δr along its traveling path:

$$c_s({\omega }_s)={\omega }_s\mathrm{\Delta }r/\mathrm{\Delta }{\phi }_s$$ (5)

where Δφ_s = φ₁ − φ₂ is the phase change over the traveled distance Δr. Generally, a regression is made on the phase versus distance over an extended region in order to improve wave speed estimation.

The shear wave speed is then estimated with (5). Dispersion measurements at fundamental frequency of 50 Hz and its harmonics of 100 Hz, 150 Hz, 200 Hz, etc. are fit by (4) to solve for shear elastic modulus and viscosity.

III. Experiments

A. Gelatin phantom characterization

Three sets of gelatin phantoms were made to compare shear elastic modulus values from indentation tests and SDUV. Gelatin phantoms were made using 300 Bloom gelatin (Sigma-Aldrich, St. Louis, MO) and glycerol (Sigma-Aldrich, St. Louis, MO) with a concentration of 7, 10, and 15% by volume to achieve different values of the shear elastic modulus. A preservative of potassium sorbate (Sigma-Aldrich, St. Louis, MO) was added with a concentration of 7, 10, and 15% by volume. Cellulose particles (Sigma-Aldrich, St. Louis, MO) with size 20 μm were also added with a concentration of 0.5% by volume to provide adequate ultrasonic scattering.

To evaluate the suitability of Hayes’ model, two different samples (cylindrical shape) thicknesses were used. Similarly, the impact of sample diameter was evaluated by using three different sample diameters (four samples of each type) and two flat-end cylindrical indenter sizes, a 3 mm indenter diameter and a 2 mm indenter diameter. Table I summarizes the sample characterization.

Table I.

Sample characterization for mechanical test. Four samples of each type were made.

7% gelatin phantom
Sample type	Thickness (mm)	Diameter (mm)
1	7.98	35
2	17.44	35.3
3	7.98	13.8
10% gelatin phantom
Sample type	Thickness (mm)	Diameter (mm)
1	7.88	35
2	17	35.3
3	7.88	13.8
15% gelatin phantom
Sample type	Thickness (mm)	Diameter (mm)
1	7.3	35
2	19	35.3
3	7.3	13.8

Additionally, a block of gelatin (15 × 15 × 4 cm) was made from the same batch of each gelatin solution preparation for use in SDUV experiments.

B. Indentation test

Quasi-static unconfined uniaxial indentation experiments were performed using a mechanical testing machine (Enduratec, ElectroForce® 3200). A 50 gram load cell was used to record load as the flat-end cylindrical indenter was moved at a rate of 0.1 mm/sec. The sampling frequency was 20 kHz. The noise floor of the system was about 0.15 mN. The linear region of the force-displacement curve was defined as described by Zhai, et al., [27]. The absolute difference from the raw data and the fit was calculated. A threshold equal to 3 times the system’s floor noise was set. A data window of approximately 20 samples (5% of indenter diameter) was linearly fit. The data window was increased until the absolute difference or error was just below the threshold. Each sample was compressed four times.

C. SDUV

Fig. 2 illustrates the experimental setup. The ‘Push Transducer’ (custom made with piezo crystals from Boston Piezo-Optics, Inc., Bellingham, MA) has a diameter of 44 mm, a center frequency of 3 MHz and a focal length of 70 mm. Shear waves generated at the transducer focal point propagate through gelatin phantom and vibration was detected by a single element transducer (Harisonic 13-0508-R, Staveley Sensors Inc.) with a diameter of 12.7 mm, a center frequency of 5 MHz and a 50 mm focus length (‘Detect Transducer’). The ‘Push Transducer’ and ‘Detect Transducer’ were aligned confocally with a pulse echo technique using a small sphere as a point target. The force was localized 5 mm deep into the gelatin phantom surface.

Fig. 2.

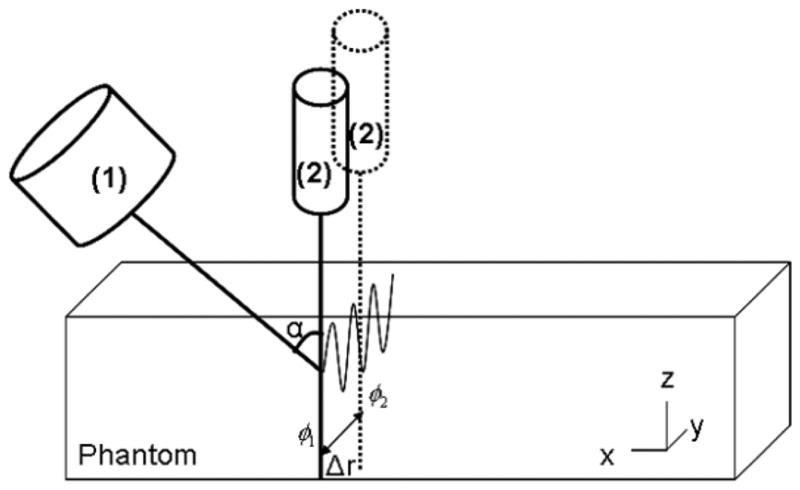
Illustration of the experimental set up. SDUV applies a localized force generated by a ‘Push Transducer’ (1) coupled to the phantom, transmitting repeated tonebursts of ultrasound. A separated transducer acts as the detector, ‘Detect Transducer’ (2).

The pulse repetition frequency of the push tonebursts was 50 Hz and the toneburst length was 300 μs. The propagation of the shear wave was tracked by the single element transducer in pulse-echo mode over a lateral range of 10 mm. The pulse repetition frequency of the ‘Detect Transducer’ was 1.6 kHz for the 7% and 10%. Because the 15% gelatin phantom was expected to be stiffer, thus shear waves travel faster, compared to the 7% and 10% gelatin phantoms, the pulse repetition frequency of the ‘Detect transducer’ for the 15% gelatin phantom was 3.2 kHz.

The ultrasound echoes were digitized at 100 MHz and processed by the cross-spectrum analysis previously described [43] to estimate the shear phase gradient. The shear wave propagation speed was calculated by (5) and dispersion measurements from 50 to 400 Hz were fit by (4) to solve for shear elastic modulus and viscosity. The group velocity for each phantom was calculated by evaluating the time shifts in the shear waves versus position and using

$$c_g=\mathrm{\Delta }r/\mathrm{\Delta }t$$ (6)

where c_g is the group velocity, and Δt is the time shift measured over a distance Δr.

During each experiment, the single element transducer was moved by 1 mm intervals 11 times on y-axis (refer to Fig. 2). This acquisition sequence was repeated 4 times in each of the regions of interest (ROI). Additionally, SDUV measurements were repeated at 4 different regions.

IV. Results

A. Indentation test

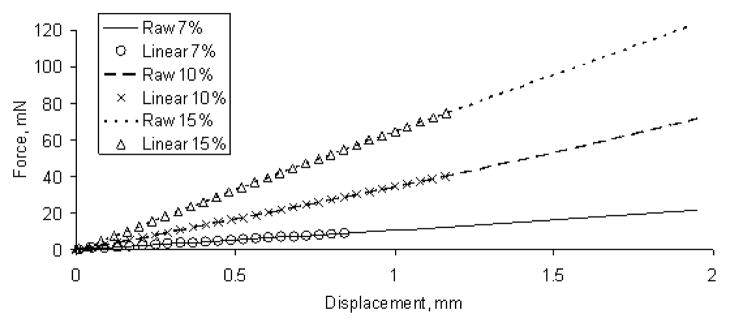
The force-displacement raw data for one sample (Sample type 1, refer to Table I) of 7%, 10% and 15% gel phantom with a 2 mm indenter diameter is shown in Figure 3.

Fig. 3.

Force-displacement data for one sample of each gelatin phantom (Sample type 1, refer to Table I). The three symbols represent the linear region for the three gelatin phantoms. The three line types represent the raw data for the three gelatin phantoms.

All three phantom samples showed a linear response up to approximately 1 mm compression. The maximum force for each linear region was 9 mN, 40 mN and 63 mN for 7, 10 and 15% phantoms respectively.

Table II shows the influence of sample thickness and sample diameter on the Hayes model for the 7%, 10% and 15% gelatin phantoms. The sample thickness was approximately 5.3, 8, 11.3 and 17 times the indenter radii. Similarly, the sample diameter was approximately 9.2, 13.8, 23.3 and 35 times the indenter radii. Because the geometry factor κ is not very sensitive to Poisson’s ratio ν from 0.45 to 0.5 for a/h ratio range from 0.05 to 0.20, the Poisson’s ratio ν was set to 0.475.

Table II.

Shear elastic modulus (kPa) for different sample diameter (d), indenter diameter (2a) and sample thickness.

7% gelatin phantom
Thickness (mm)	2a= 2 mm	2a= 3 mm	2a= 2 mm	2a= 3 mm
	D= 35 mm	D= 35 mm	D= 13.8 mm	D= 13.8 mm
7.98	1.35 ± 0.06	1.36 ± 0.01	1.29 ± 0.19	1.22 ± 0.20
17.44	1.16 ± 0.01	1.29 ± 0.04	-	-
10% gelatin phantom
Thickness (mm)	2a= 2 mm	2a= 3 mm	2a= 2 mm	2a= 3 mm
	D= 35 mm	D= 35 mm	D= 13.8 mm	D= 13.8 mm
7.88	3.65 ± 0.21	3.63 ± 0.14	3.54 ± 0.09	3.51 ± 0.12
17	3.40 ± 0.05	3.28 ± 0.09	-	-
15% gelatin phantom
Thickness (mm)	2a= 2 mm	2a= 3 mm	2a= 2 mm	2a= 3 mm
	D= 35 mm	D= 35 mm	D= 13.8 mm	D= 13.8 mm
7.3	4.68 ± 0.03	4.67 ± 0.1	4.76 ± 0.1	4.63 ± 0.05
19	5.60 ± 0.06	5.00 ± 0.01	-	-

mean ± SD, n = 4

B. SDUV

The displacement amplitude estimates over 50 ms for 7% gelatin phantom are shown in Figure 4 and as calculated by the cross-spectrum method [43]. The peak displacement amplitude was approximately 18 μm, 16 μm and 12 μm at 4, 6 and 8 mm away from the vibration center.

Fig. 4.

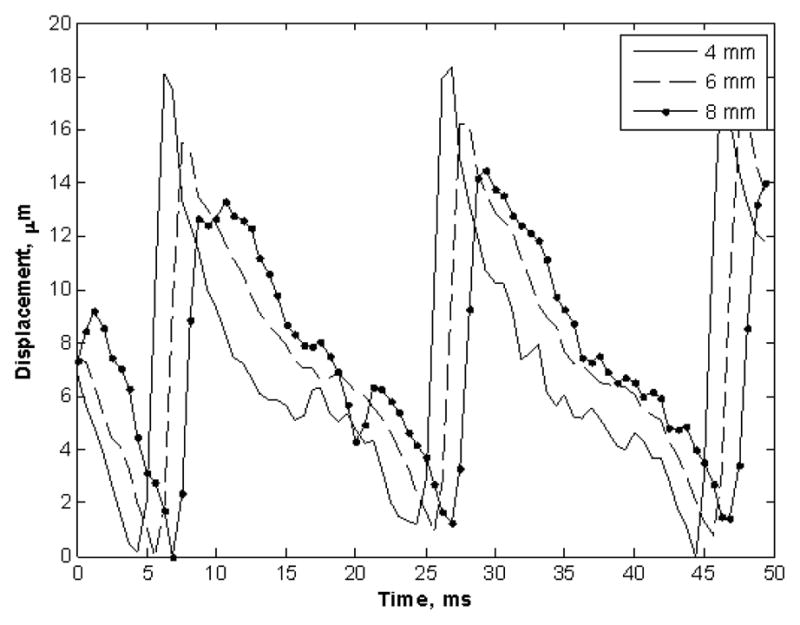
Displacement amplitude estimates over 50 ms for 7% gelatin phantom. The three symbols represent three sets of the measured amplitude for 4, 6 and 8 mm away from the vibration center.

The magnitude spectra of the velocity signal for the 7%, 10% and 15% gelatin phantoms over 200 ms are shown in Figure 5. The frequency at which the amplitude is highest, or the center frequency of broadband signal, is denoted as ω_p. The center frequencies of the SDUV response, from 0 ms to 200 ms, were 100 Hz for 7% phantom, 350 Hz for 10% phantom and 100 Hz for the 15% phantom. The group velocity, is described by Morse and Ingard as the “velocity of progress of the ‘center of gravity’ of a group of waves that differ somewhat in frequency [44]”. The center of gravity was calculated by [45]

Fig. 5.

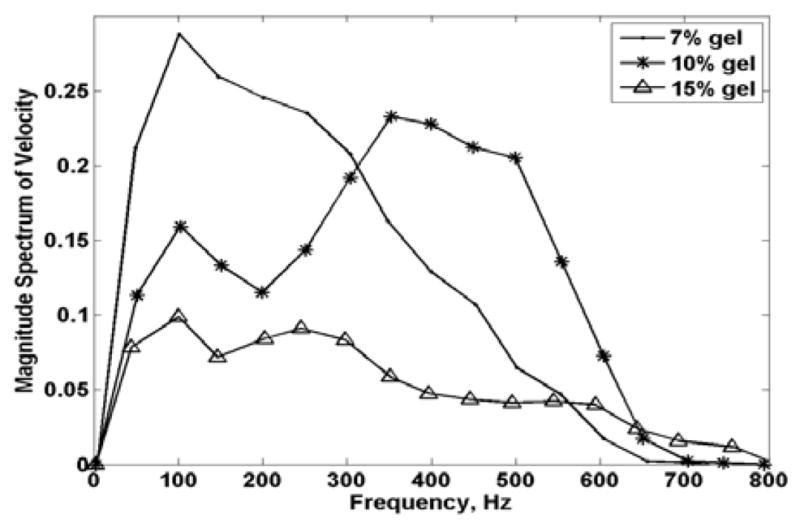
Magnitude spectra of the velocity signals over 200 msec. The three symbols represent 7, 10 and 15% gelatin phantoms.

$${\omega }_c=\sum \omega ·{\mid V(\omega )\mid }^2/\sum {\mid V(\omega )\mid }^2$$ (7)

where V(ω) is the complex spectrum of the velocity signal and ω is the frequency. The center of gravity of the magnitude spectrum of the velocity signal for each gelatin phantom was 200, 350 and 250 Hz for the 7, 10 and 15% gelatin phantoms.

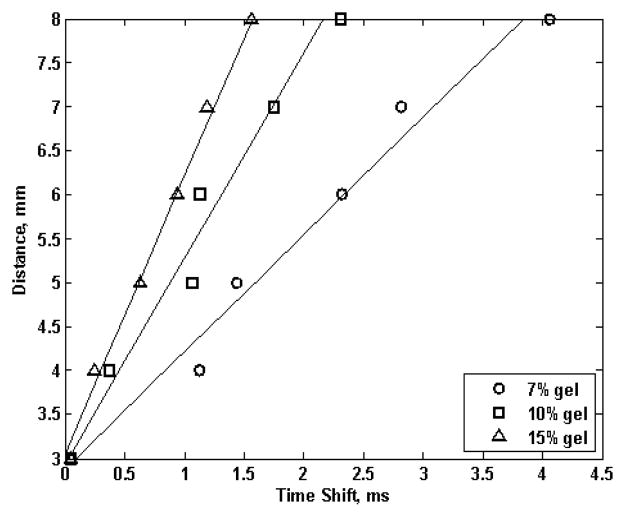
Figure 6 shows the distance from the vibration center versus time shift for 7%, 10% and 15% gel phantoms over 5 mm. The time shifts were calculated by cross-correlation method [46]. The solids lines are linear regression for the time shifts. The group velocity was calculated from (6).

Fig. 6.

Time shift estimates for the gelatin phantoms over 3 to 8 mm away from the vibration center. The three symbols represent 7, 10 and 15% gelatin phantoms. The solid line represents linear regression.

The group velocity (slope of solid lines in Fig. 6) for each gelatin phantom was 1.33, 2.35 and 3.15 m/s for 7, 10 and 15% respectively. By assuming a non-dispersive medium, in other words, by setting μ₂ = 0 in (4), and also assuming a linear elastic material, where group velocity is same as the phase velocity for all frequencies, the shear elastic modulus by (1) for the 7, 10 and 15% gelatin phantom was 1.77, 5.52 and 9.92 kPa respectively.

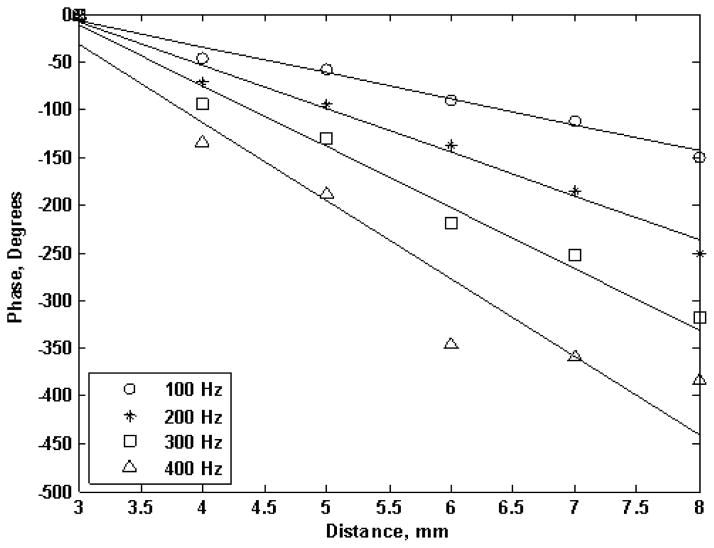
The phase of shear waves at frequencies 50 to 400 Hz was estimated by Kalman filter [47]. Figure 7 illustrates the phase of shear wave at frequencies 100 to 400 Hz for the 7% gel phantom. There is a linear relation between shear wave phase and propagation distance. The solid lines are linear regressions for the phase estimates. The coefficients of determination, R², of the linear regressions were greater than 0.95, 0.97 and 0.96 for the 7%, 10% and 15% gelatin phantom respectively. This indicates that the linear assumption of (5) is appropriate.

Fig. 7.

Phase estimates for the 7% gelatin phantom over 3 to 8 mm away from the vibration center. The four symbols represent four sets of estimated phase changes over the distance for four vibrations with frequencies from 100 Hz to 400 Hz. The solid line represents linear regression.

Figure 8 shows shear wave propagation speed as a function of frequency.

Fig. 8.

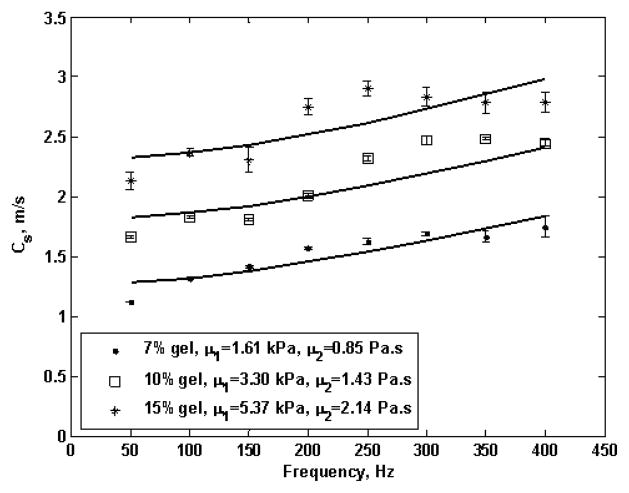
Shear wave speed measured from 50 Hz to 400 Hz. The three symbols represent 7, 10 and 15% gelatin phantoms. The solid lines are fits from the Voigt dispersion model, which gives estimates of shear elastic modulus (μ₁) and viscosity (μ₂) shown at the bottom of this figure.

The symbols represent the mean shear wave speed of four repetitions for each gelatin phantom. Error bars represent the standard deviation of the measured shear wave speed at each particular frequency four times. The solid lines are the least mean square (LMS) fits from (4) that give a shear elastic modulus of μ₁ = 1.61, 3.30 and 5.37 kPa and viscosity of μ₂ = 0.85, 1.43 and 2.14 Pa·s for 7%, 10% and 15% gelatin phantoms, respectively. The median absolute error, that is, the median of the absolute difference between the Voigt model fit and experimental data, was 0.09, 0.14 and 0.23 m/s for 7, 10 and 15% gelatin phantom respectively.

V. Discussion

The use of Hayes’ model is suitable for describing small deformation indentation on lateral infinite isotropic elastic media. Even though this model takes the sample thickness into account, it is important to satisfy its assumed boundary conditions. Shear elastic modulus was slightly underestimated when the sample diameter was decreased, particularly on the softer phantom. This is caused by the violation of the assumption of lateral infinite geometry. Not surprisingly, there was not a significant variation of shear elastic moduli for different sample thickness (Refer to Table 2) for the 7% and 10% gelatin phantom. However, shear elastic modulus was slightly different for the 15% gelatin phantom for different sample thickness. These observations agree with FEM simulations described by Zhai et al [27], suggesting that a sample with 5 kPa of Young’s modulus is large enough when its thickness and diameter are over 15 times of the indenter radii. Therefore, the shear elastic modulus for the 7, 10 and 15 gelatin phantoms were 1.16, 3.40 and 5.60 kPa respectively (refer to Table II). However, a more suitable model should include both sample thickness and sample diameter in consideration.

The peak displacement amplitude estimated by SDUV was approximately 18 μm, which is considered a small displacement and therefore within a linear region of a force-displacement curve. Tissue response to a harmonic excitation using different voltage amplitudes on the ‘Push transducer’ has shown a fairly independent relationship between shear wave speed and excitation voltage, which is equivalent to a linear relationship between force and displacement [48]. Similarly, the force-displacement curve from the indentation experiments was linear for up to 1 mm. Although force-displacement curves of gelatin phantoms were nonlinear for large displacements (larger than 1 mm), indentation can be used to assess elastic components of mechanical properties of viscoelastic materials under small deformation.

The phase estimates at high frequencies showed more variation compared to lower frequencies (refer to Fig. 7). This was consistent in all 3 phantoms. Because the displacement amplitude is decreased at high frequencies, the error of the phase estimates is expected to increase at high frequencies [49]. However, the coefficients of determination, R², of the linear regressions were high in all 3 phantoms.

Table III shows a comparison between group velocity (c_g), phase velocity evaluated at center of gravity (c_s(ω_c))and phase velocity evaluated at center frequency (c_s(ω_p)). Both phase velocities calculations were close to group velocities for the 7 and 10% gelatin phantom. The magnitude spectrum of the velocity signal for the 15% phantom (Refer to Fig. 5) was broader compared to the other phantoms. This could be a reason why the group velocity for the 15% gelatin phantom was rather different than the phase velocities. In theory, the group velocity should be identical or close to the phase velocity c_s evaluated at ω_c.

Table III.

Group velocity, phase velocity evaluated at center of gravity and phase velocity evaluated at center frequency

	7% gelatin phantom	10% gelatin phantom	15% gelatin phantom
Group Velocity, cg	1.33 m/s	2.35 m/s	3.15 m/s
Phase Velocity at ωc, cs(ωc)	1.57 m/s	2.49 m/s	2.83 m/s
Phase Velocity at ωp, cs(ωp)	1.32 m/s	2.49 m/s	2.38 m/s

The shear wave speed versus frequency results in Figure 8 fits well with the Voigt model, particularly for the softer phantom. Stiffer phantoms seem to have peaks at certain frequencies that deviate from the ideal Voigt model, however the absolute error between the Voigt model fit and experimental data was not significantly large. Shear wave estimation may be affected by tissue geometry depending on the type of wave that is being excited. For instance, mathematical models for shear wave dispersion of anti-symmetric Lamb and Rayleigh suggest that shear wave speed is affected by material thickness mostly at lower frequencies when the material thickness is larger than one to two wavelengths of the wave [50]. Although the largest wavelength, about 42 mm for the 15% gelatin phantom at 50 Hz, was approximately equal to the phantom thickness, substantial errors for measurement of the shear wave speed related to phantom thickness are not expected. SDUV generates pure shear waves, that is, a shear wave propagating in an infinite medium, therefore SDUV assumes there are no reflections from boundaries. In addition, the phase gradient in equation (5) assumes that there is only one wave traveling one direction. Therefore, reflections from the surface may cause variations in the phase and cause errors in the speed measurements.

The SDUV method assumes a viscoelastic material by implying a complex shear elastic modulus. The compression rate for the indentation test was 0.1 mm/sec and each gelatin showed a linear response up to 1 mm compression, therefore the excitation frequency for indentation test was approximately 0.1 Hz. Because the excitation frequency from the indentation test is close to zero, the shear elastic modulus estimation by indentation test should be the same or close to the real component of the shear complex modulus on the Voigt model.

Figure 9 provides a summary of the shear elastic modulus estimated from group velocity (linear elastic medium), phase velocity (viscoelastic medium, Voigt model) and indentation test. Error bars represent the standard deviation of the measured shear elastic modulus for each particular phantom at four different locations.

Fig. 9.

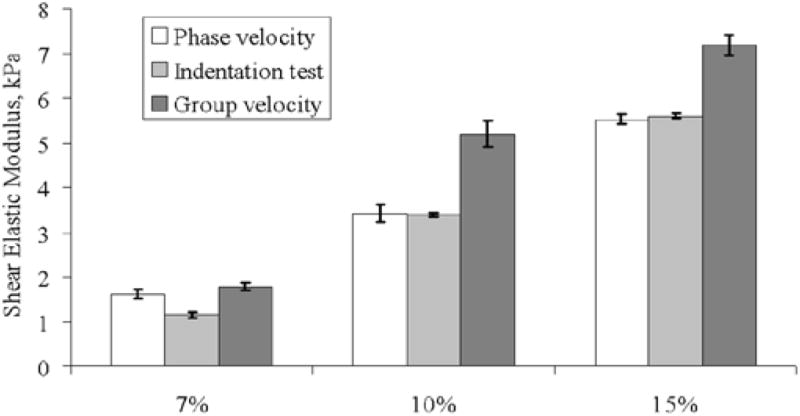
Shear elastic modulus comparison between phase velocity, indentation test and group velocity. Mean ± SD, n=4

The shear elastic modulus estimated from group velocity measurements can definitively differentiate the three phantoms. However, these values do not agree well with both the indentation experiment results and phase velocity results, especially when the phantom is stiffer. This disagreement could be attributed to the fact that gelatin phantoms are dispersive [13, 16, 19]; therefore the wave speed is dependent on frequency. Shear elastic modulus estimation from the indentation test and phase velocity for the 7% phantom were slightly different. This could be due to inhomogeneities on gelatin samples. The cellulose component, introduced for ultrasound scattering, did tend to settle down in the sample molds while the gelatin was liquid. Because the 7% gelatin is less viscous, the cellulose distribution was probably different compared to the other phantoms.

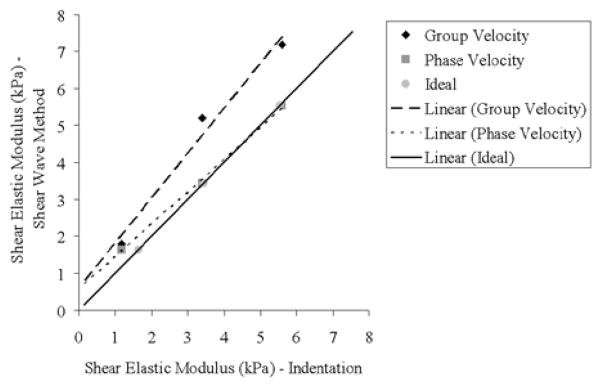
A linear correlation comparing shear elastic modulus from indentation test with group velocity and SDUV phase velocity is shown in Figure 10. The correlation coefficients were 0.98 for the group velocity and 0.99 for the SDUV phase velocity method. Although the correlation coefficients are similar and large, most likely because the number of gelatin phantoms is small, the shear elastic modulus correlation between SDUV phase velocity method and indentation test is closer to the ideal correlation (continuos line on Fig. 10). On the other hand, the shear elastic modulus correlation between group velocity and indentation test seem considerably different from the ideal correlation, suggesting that shear elastic modulus estimation by group velocity will be bias when the medium being investigated is dispersive. Therefore a rheological model should be used in order to estimate mechanical properties of viscoelastic materials. Because tissues are more viscous than these phantoms [16, 19, 20], this would be the case for tissues as well. This study shows acceptable agreement of shear elastic moduli estimates from SDUV phase velocity method and indentation test on gelatin phantoms.

Fig. 10.

Linear correlation comparing indentation test with group velocity (diamonds and dashed line) and SDUV phase velocity (squares and dotted line). The continuous line represents an ideal correlation.

VI. Conclusion

In this paper, we present an independent validation method of elastic modulus estimation by SDUV in gelatin phantoms. The shear elastic modulus, estimated from the SDUV phase velocity method, matched the elastic modulus measured by the indentation method. The shear elastic modulus estimated by group velocity did not agree with indentation test estimations. These results suggest that a rheological model for linear viscoelastic material must be used to estimate elastic modulus on gelatin phantoms and soft tissue.

Biographies

Carolina Amador (IEEE/S’09) was born in Medellin, Colombia on April 14, 1984. She received the B.S. degree in biomedical engineering at Escuela de Ingenieria de Antioquia, Medellin, Colombia, in 2006. She is currently a graduate student in the biomedical engineering PhD program at the Mayo Clinic College of Medicine in Rochester, MN, USA. She has been a visiting undergraduate student at the Biomedical Imaging Resource at Mayo Clinic, Rochester, MN, USA. Her research interest is noninvasive evaluation of mechanical properties of soft tissue.

Matthew W. Urban (IEEE/S’02, M’07) was born in Sioux Falls, SD in on February 25, 1980. He received the B.S. degree in electrical engineering at South Dakota State University, Brookings, SD in 2002 and the Ph.D. in biomedical engineering at the Mayo Clinic College of Medicine in Rochester, MN in 2007. He is currently an Assistant Professor in the Department of Biomedical Engineering, Mayo Clinic College of Medicine. He has been a Summer Undergraduate Fellow at the Mayo Clinic Biomechanics laboratory. His current research interests are ultrasonic signal and image processing, vibro-acoustography, and vibrometry applications. Dr. Urban is a member of Eta Kappa Nu, Tau Beta Pi, IEEE, and the Acoustical Society of America.

Shigao Chen (M’02) received the B.S. and M.S. degrees in biomedical engineering from Tsinghua University, China, in 1995 and 1997 respectively, and the Ph.D. degree in biomedical imaging from the Mayo Graduate School, Rochester, MN in 2002. He is currently Assistant Professor of Mayo Graduate School, and Associate Consultant, Department of Biomedical Engineering, Mayo Clinic College of Medicine. His research interest is noninvasive quantification of viscoelastic properties of soft tissue using ultrasound.

Qingshan Chen received his M.S. in Biomedical Engineering in Memphis, TN in 2001.

He is a research engineer at the Orthopedic Biomechanics Laboratory at the Mayo Clinic in Rochester, MN, and Assistant Professor of Bioengineering, Mayo Medical School. He has co-authored more than 50 scientific articles and book chapters, most being in peer-reviewed journals.

Mr. Chen’s research interests include tissue biomechanics, biomaterials, orthopedics and magnetic resonance elastography. He has received several awards from various societies.

Kai-Nan An received his Ph.D. in mechanical engineering and applied mechanics in 1975 from Lehigh University in Bethlehem, PA.

He is the Director (1993-present) of the Orthopedic Biomechanics Laboratory at the Mayo Clinic in Rochester, MN, and Professor of Bioengineering, Mayo Medical School. He was named the John and Posy Krehbiel Professor of Orthopedics, Mayo Medical School, in 1993. He has co-authored more than 700 scientific articles and book chapters, most being in peer-reviewed journals. Dr. An’s research interests include biomechanics, biomaterials, orthopedics and rehabilitation. He has received several awards from various societies, including being named as a Fellow of the ASME in 2007. He is a founding member of the American Institute for Medical and Biological Engineering, and serves as advisor to graduate students and research fellows, as well as various medical and engineering organizations.

James F. Greenleaf (M’73–SM’84–F’88) was born in Salt Lake City, UT, on February 10, 1942. He received the B.S. degree in electrical engineering from the University of Utah, Salt Lake City, in 1964, the M.S. degree in engineering science from Purdue University, Lafayette, IN, in 1968, and the Ph.D. degree in engineering science from the Mayo Graduate School of Medicine, Rochester, MN, and Purdue University in 1970. He is currently Professor of Biomedical Engineering and Associate Professor of Medicine, Mayo Medical School, and Consultant, Department of Physiology, Biophysics, and Cardiovascular Disease and Medicine, Mayo Foundation.

He has served on the IEEE Technical Committee for the Ultrasonics Symposium for seven years. He served on the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society (UFFC-S) Subcommittee on Ultrasonics in Medicine/IEEE Measurement Guide Editors, and on the IEEE Medical Ultrasound Committee. Doctor Greenleaf was President of the UFFC-S in 1991 and Vice President for Ultrasonics in 1992 to 2003.

Dr. Greenleaf has 12 patents and is a recipient of the 1986 J. Holmes Pioneer Award and the 1998 William J. Fry Memorial Lecture Award from the American Institute of Ultrasound in Medicine, and is a Fellow of IEEE, American Institute of Ultrasound in Medicine, and American Institute for Medical and Biological Engineering. Dr. Greenleaf was the Distinguished Lecturer for IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society (1990/1991). His special field of interest is ultrasonic biomedical science, and he has published more than 237 peer-reviewed articles and edited or authored five books in the field.