A Geometric and Electrostatic Study of the [4Fe-4S] Cluster of Adenosine-5´-Phosphosulfate Reductase from Broken Symmetry Density Functional Calculations and Extended X-ray Absorption Fine Structure Spectroscopy

Abstract

Adenosine-5’-phosphosulfate reductase (APSR) is an iron-sulfur protein that catalyses the reduction of adenosine-5’-phosphosulfate (APS) to sulfite. APSR coordinates to a [4Fe-4S] cluster via a conserved CC-X_~80-CXXC motif and the cluster is essential for catalysis. Despite extensive functional, structural and spectroscopic studies, the exact role of the iron-sulfur cluster in APS reduction remains unknown. To gain an understanding into the role of the cluster, density functional theory (DFT) analysis and extended X-ray fine structure spectroscopy (EXAFS) have been performed to reveal insights into the coordination, geometry and electrostatics of the [4Fe-4S] cluster. XANES data confirms that the cluster is in the [4Fe-4S]²⁺ state in both native and substrate-bound APSR while EXAFS data recorded at ~0.1 Å resolution indicates that there is no significant change in the structure of the [4Fe-4S] cluster between the native and substrate-bound forms of the protein. On the other hand, DFT calculations provide an insight into the subtle differences between the geometry of the cluster in the native and APS-bound forms of APSR. A comparison between models with and without the tandem cysteine pair coordination of the cluster suggests a role for the unique coordination in facilitating a compact geometric structure and ‘fine-tuning’ the electronic structure to prevent reduction of the cluster. Further, calculations using models in which residue Lys144 is mutated to Ala confirm the finding that Lys144 serves as a crucial link in the interactions involving the [4Fe-4S] cluster and APS.

1. Introduction

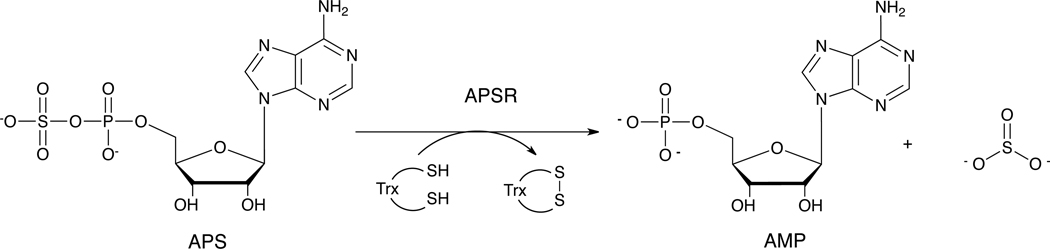
In plants and many species of bacteria such as Mycobacterium tuberculosis (Mt) and Pseudomonas aeruginosa (Pa), de-novo synthesis of cysteine occurs via the sulfate assimilation pathway.¹ In this pathway, inorganic sulfate is activated to form adenosine-5′-phosphosulfate (APS), which is subsequently reduced to sulfite and then sulfide, and incorporated into cysteine.^2,3 The first committed step in sulfate assimilation is carried out by the enzyme, adenosine-5′-phosphosulfate reductase (APSR), which catalyzes the reduction of APS to sulfite and adenosine-5′-monophosphate (AMP) (Scheme 1) using reducing equivalents from thioredoxin (Trx), a protein cofactor.^1,4–6 APSR has been shown to be essential for survival of bacteria in the latent phase of tuberculosis infection⁷ and since there is no human homolog of APSR, it represents a promising drug target for antibacterial therapy.⁸

Scheme 1.

Reaction catalyzed by APSR.

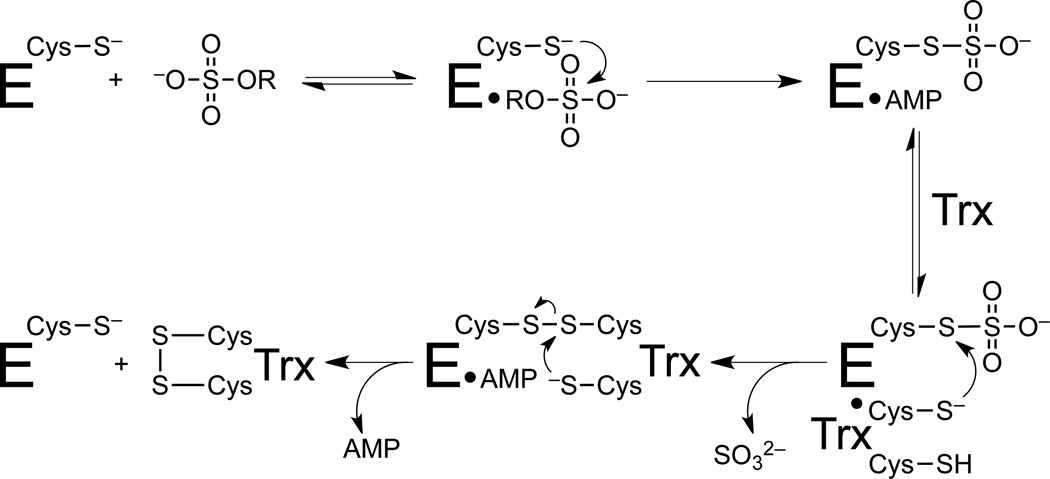
APSRs from M. tuberculosis (Mt-APSR) and P. aeruginosa (Pa-APSR) are related by high sequence homology (27.2% of sequence identity and 41.4% of sequence similarity, Supplementary Fig. S1), particularly in the residues that line the active site.⁹ The mechanism of APSR involves a nucleophilic attack by the catalytic Cys256 (residue numbers throughout manuscript correspond to the Pa-APSR sequence) in the C-terminal tail of APSR on APS to form an enzyme S-sulfocysteine intermediate, E-Cys−S_γ−SO₃⁻, which is then reduced to sulfite and AMP through intermolecular thiol−disulfide exchange with Trx (Figure 1).⁴ It is likely that in the initial Michaelis complex APS binds to other residues, changing their resulting mobility within the substrate-binding pocket; this could have important mechanistic implications.

Figure 1.

Proposed mechanism of APSR. APSR reduces adenosine 5’-phosphosulfate (APS) to sulfite and adenosine 5’-monosulfate (AMP) using reducing equivalents from the protein cofactor, thioredoxin (Trx).

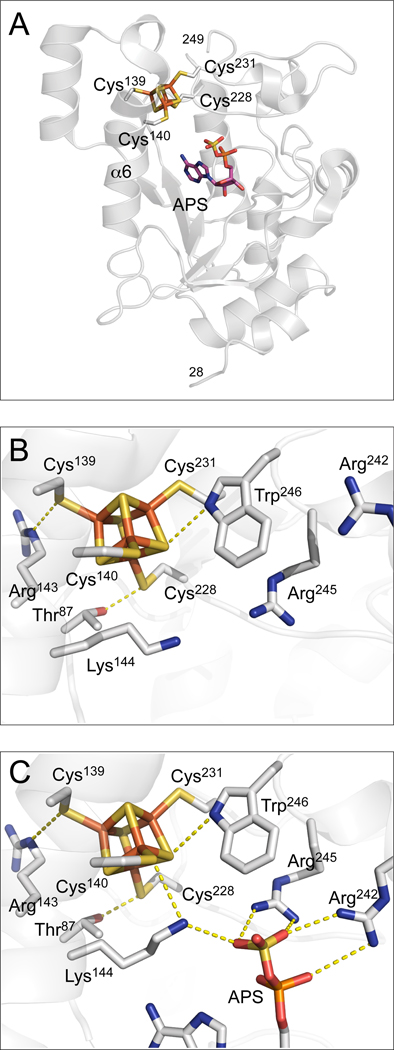
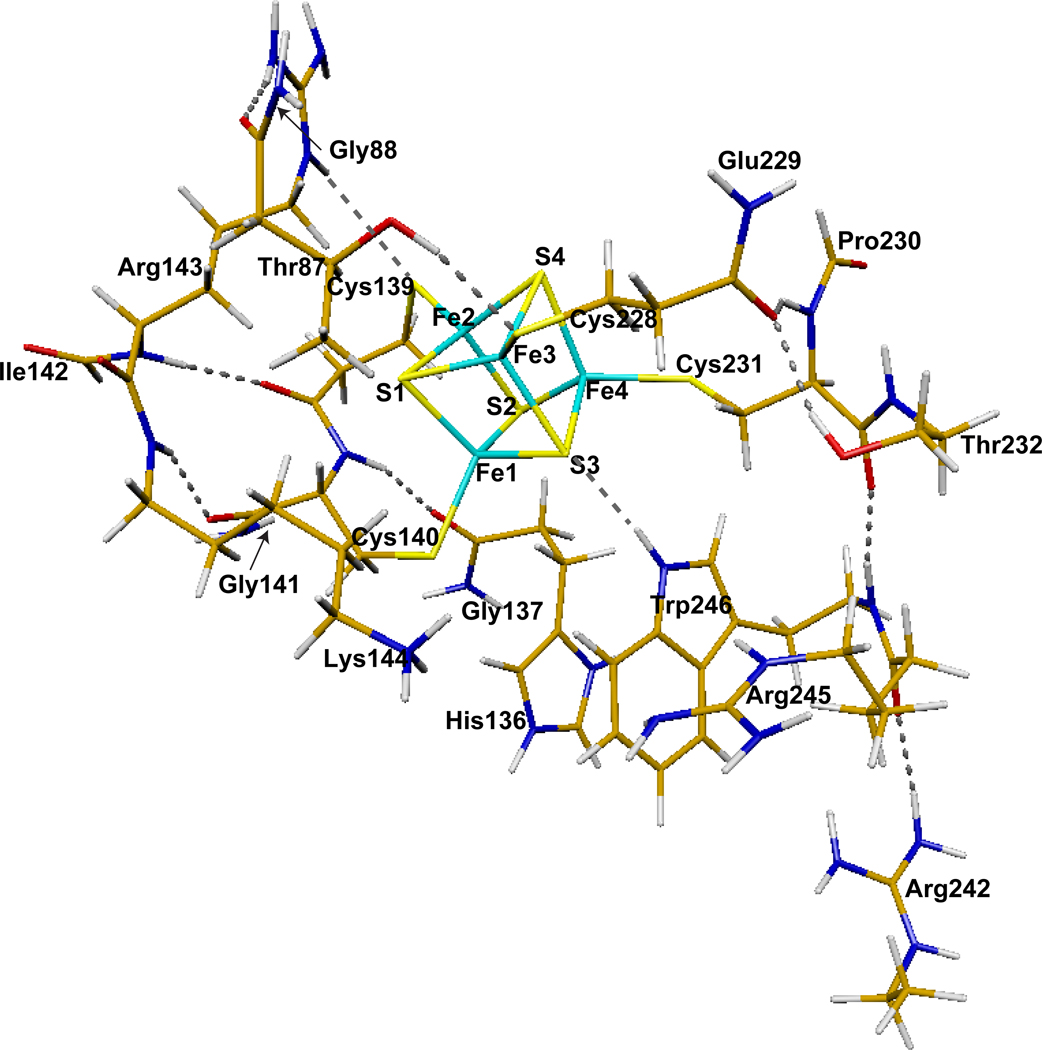
From a structural perspective, APSR is an iron-sulfur protein with a conserved CC-X_~80-CXXC motif, correlated with the presence of a [4Fe-4S] cluster. The cluster has been shown to be essential for catalytic activity in both plant and bacterial APSRs,^3,10–12 but the exact role of the cluster in APS reduction remains unknown. Interestingly, studies by Carroll et al. have shown that the [4Fe-4S]²⁺ cluster in APSR does not undergo redox changes during the catalytic cycle.⁴ The 2.7 Å crystal structure of Pa-APSR bound to substrate¹³ shows the iron-sulfur cluster coordinated by Cys228 and Cys231, positioned at the tip of a β-loop, and a special tandem pair, Cys139 and Cys140 within a kinked helix, α₆ (Figure 2A). Helix α₆ is kinked where Lys144 is oriented into the active site. Amongst interactions of the cluster, there are four charged and/or polar NH⋯S or OH⋯S hydrogen bonds involving side chains of absolutely conserved residues (Figure 2B and C). The CysCys motif interacts with a pair of basic residues, Arg143 and Lys144. In addition, Cys140 hydrogen bonds to His136. Other interactions with the iron-sulfur cluster involve the side chains of Thr87 and Trp246. The phosphosulfate group of APS is positioned at a distance of approximately 7 Å to the iron site, which coordinates to S_γ-Cys140, and as such, the sulfate moiety is not in direct contact with the [4Fe-4S] cluster. Interestingly, however, both cluster and substrate interact with Lys144 (Figure 2C).

Figure 2.

The environment of the [4Fe-4S] cluster in Pa-APSR.¹⁸ A. The structure of Pa-APSR bound to substrate APS (subunit B or chain-B). The [4Fe-4S] cluster is ligated by four cysteine residues at positions 139, 140, 228 and 231. PDB code: 2GOY. B. Three conserved residues participate in charged or polar NH⋯S or OH⋯S hydrogen bonds to inorganic S or cysteine S_γ atoms; Thr87, Arg143, Lys144 and Trp246 (yellow dashes). PDB code: 2GOY, chain A. C. Conserved basic residues Lys144, Arg242 and Arg245 in the active site interact with the phosphate and sulfate groups of APS (yellow dashes). In the presence of APS, Lys144 makes a NH⋯S hydrogen bond to the Cys140-S_γ atom. Residues that also interact with APS, but are not depicted in this figure are Arg171 and His259; these residues interact with the α-phosphate group. The shortest distance between a sulfate oxygen atom and a cysteine sulfur atom coordinated to the [4Fe-4S] cluster is 6.0 Å. PDB code: 2GOY, chain B.

Coordination by sequential cysteines is highly unusual for [4Fe-4S] clusters and has been characterized in only one other crystal structure – the NuoB subunit of respiratory complex I.¹⁴ The tandem cysteines also reside within an α-helix and the subunit of NuoB exhibits substrate-induced conformational changes.¹⁵ In APSR, constraints imposed by the tandem cysteine coordination do not affect the tetrahedral symmetry of the cluster, but the side chain of Cys140 is distorted, resulting in steric clashes between the C_α proton and an inorganic sulfur atom of the cluster.¹³

In addition to the structural information available, based on differences in cysteine reactivity and cluster stability, biochemical and mass spectrometric studies with Mt-APSR have suggested a structural rearrangement in the S-sulfocysteine complex and AMP-bound enzyme relative to free enzyme.¹⁶ In fact, solution kinetics and mass spectrometric studies of Mt-APSR performed with APS (at concentrations exceeding the K_d of APS and AMP), have shown that the subsequent formation of the stable E-Cys−S_γ−SO₃⁻ intermediate with AMP-bound and C-terminal tail docked in the active site, prevents cluster degradation and loss of APSR activity.^4,9,16 Furthermore, a comparison of Resonance Raman spectra of Pa-APSR in the native form and in the S-sulfocysteine form (with AMP bound and the C-terminal tail docked in the active site of the enzyme) shows an enhancement in Fe-S_γ(Cys) stretching modes centered near 355 and 369 cm⁻¹.¹⁷ Recently, we demonstrated that APS binding induced an increase in intensity and resolution of the EPR signal of reduced Mt-APSR that was not observed among a panel of substrate analogs, including adenosine 5′-diphosphate. Additionally, through kinetic and EPR studies, Lys144 was identified as a key link between APS and the iron-sulfur cluster.¹⁸ Mössbauer analyses of native Mt-APSR confirmed the presence of a [4Fe-4S]²⁺ cluster, however, no change was observed in the Mössbauer spectra of Mt-APSR comparing samples with and without substrate-binding. Spectroscopic data taken together with known structural and functional information, implicate the iron-sulfur cluster in the catalytic mechanism of APS reduction.

The goal of this study is to determine high-resolution geometric and electronic structures of the [4Fe-4S] cluster in APSR. Although the crystal structure of Pa-APSR is a significant advance in the characterization of this enzyme, the resolution of the structure (2.7 Å) is close to the Fe-Fe distance within a [4Fe-4S] cluster,¹⁹ placing a significant limit on the structural features that can be visualized in electron density maps calculated using the X-ray data. Given the unique coordination of the [4Fe-4S] cluster by two consecutive cysteines, it is important to obtain direct confirmation of the apparent structure. In particular, the X-ray structure shows that torsion angles of the Cys139 and Cys140 side chains are significantly strained, which could affect details of Fe-Fe and Fe-S-(S_γ) distances in various states of the catalytic cycle.¹³ EPR studies on one-electron reduced Mt-APSR demonstrate mid-range electrostatic interactions involving the cluster, Lys144 and the substrate that implicate the cluster in catalysis.¹⁸ However, changes in the geometric and electronic structure of the cluster during catalysis have not been determined by any structure determination technique. Determining these high-resolution structures will ultimately further our understanding of the role of the iron-sulfur cluster in APS reduction.

The work described here combines Fe K-edge x-ray absorption spectroscopy investigations (both extended X-ray absorption fine structure, EXAFS, and X-ray absorption near-edge structure, XANES) with density functional theory (DFT) calculations to determine the local geometric structure, spin states, electrostatic potential charges, and ⁵⁷Fe Mössbauer properties of the [4Fe-4S] cluster of APSR. XANES data confirms that the cluster is in the [4Fe-4S]²⁺ state in native Mt-APSR (Figure 3A) and that there is no detectable change in structure when APS binds. EXAFS data recorded at ~0.1 Å resolution (k = 17 Å⁻¹) (Figure 3B) indicates that there is no significant change in the average Fe-S and Fe-Fe bond lengths of the [4Fe-4S] cluster between the native and substrate-bound forms of the protein (see Supplementary Figure 2 for comparison spectra). Since the EXAFS structure reflects the average over all four irons in the cluster, it is insensitive to changes at individual sites (e.g., a decrease in one Fe-Fe distance that is compensated by an increase in a second Fe-Fe distance). To explore these changes, DFT calculations starting from the experimental X-ray structure of Pa-APSR¹³ were used to provide insight into the subtle changes within the geometric and electronic structure of the cluster and how they relate to the role of the [4Fe-4S] cluster in the mechanism of APS reduction.

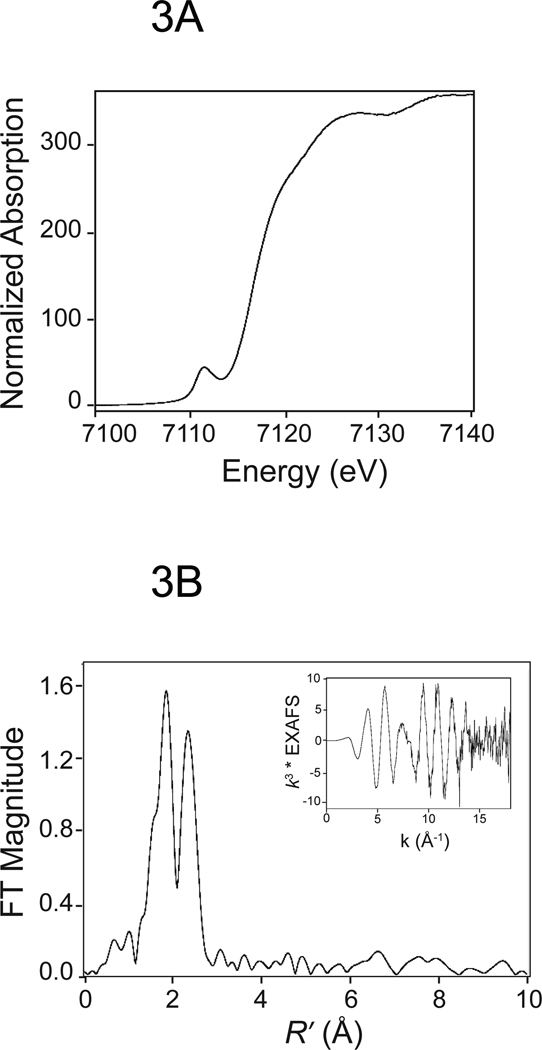
Figure 3.

EXAFS analysis of Mt-APSR. A. Iron K-edge XANES spectrum. B. k³ weighted EXAFS (inset) and Fourier transform calculated over a range of k = 2.35 ~ 17 Å⁻¹.

2. Experimental Materials and Methods

Materials

E. coli BL21(DE3) used for expression was obtained from Novagen (Bad Soden, Germany). APS was purchased from Biolog Life Sciences Institute, ≥95% (Bremen, Germany). AMP and reagents for the buffer were obtained from Sigma-Aldrich (St. Louis, MO) and were of the highest purity available.

Preparation of Mt-APSR Samples for EXAFS Spectroscopy

Mt-APSR was purified as detailed in Ref. 18, concentrated using 10,000 MWCO Amicon Ultra-4 centrifugal filter devices (Millipore Corporation, Billerica, MA) and used at a final concentration of 1 mM in buffer containing 50 mM Tris–HCl, 150 mM NaCl (pH 8.5 at 4 °C) and 10% (v/v) glycerol. Protein concentrations were determined using the extinction coefficient, ε₂₈₀=36,815 M⁻¹ cm⁻¹, obtained by quantitative amino acid analysis. Analysis of iron content by inductively coupled plasma (ICP) mass spectrometry for Mt-APSR indicated that each mole of protein contained 3.5 ± 0.4 mol of iron, as expected for a [4Fe-4S] cluster. The iron and sulfur content of APSR is consistent with the incorporation of four irons and four inorganic sulfides per mol of protein.^4,20 The specific activity of the purified enzyme was 5.2 µM min⁻¹ mg protein⁻¹ as determined by an assay using ³⁵S-APS described in Ref. 9 and consistent with the previously reported value.⁴ For samples with ligand, 1 mM enzyme was incubated with 3 mM ligand for 15 min at room temperature, prior to loading. All samples were loaded in 1 mm Lucite cells with 37 µm Kapton windows for X-ray absorption studies, immediately frozen in liquid nitrogen, and maintained under liquid nitrogen conditions until data were collected.

EXAFS Measurements and Data Analysis

X-ray absorption spectra were recorded at the Stanford Synchrotron Radiation Laboratory (beam line 9–3) under dedicated conditions as fluorescence excitation spectra, using a solid-state Ge detector array equipped with a Mn filter and Soller slits focused on the sample. All channels of each scan were examined for glitches, and the good channels were averaged for each sample (two independent samples for each protein composition, with or without ligand) to give the final spectrum. During data collection, samples were maintained at a temperature of approximately −263 °C using a liquid-helium flow cryostat. As a measure of sample integrity, XANES spectra measured for the first and last scan of each sample were compared. No changes were observed over the course of the data collection. Data were measured with an integration time of 1 second through the edge, and between 1 and 25 seconds in the post-edge region. For each sample, between 5 and 10 35-min scans were accumulated, and each sample was measured in duplicate. The useful fluorescence count rate per channel was ~10⁴ counts/second, giving a total of ~6 × 10⁶ counts/scan at k = 17 Å⁻¹. For energy calibration, the absorption spectrum of an iron metal foil was measured simultaneously by transmittance, and the energy was calibrated with reference to the lowest-energy inflection points of the foil standard, which was assumed to be 7111.3 eV for iron. EXAFSPAK²¹ was used to extract and analyze EXAFS data, using ab initio phase and amplitude parameters calculated using FEFF version 7.02.^22,23 with the initial threshold energy E₀ defined as 7130 eV. Non-linear least squares fits of the data used 4 variable parameters (R and σ² for each shell) with the amplitude correction factor and ΔE₀ set to 0.9 and −11 eV respectively based on fits to model Fe/S clusters., XANES data were normalized to tabulated absorption coefficients²⁴ using MBACK.²⁵ The area of the 1s → 3d transition in the XANES region was calculated by fitting the pre-edge region (7107–7118 eV) using the sum of a Gaussian and an arctan function; for comparison with previously published data, the fitted Gausian area was normalized to the K-edge jump for Fe (3.556 × 10² cm²/g).

3. Quantum Cluster Models for DFT Calculations

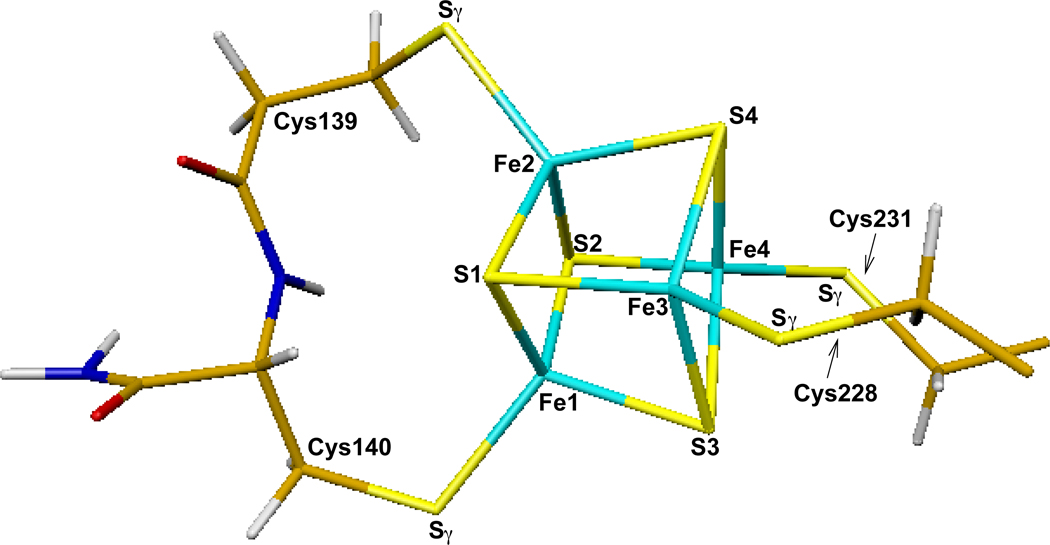
3.1. Wild-Type Models with and without Substrate

The initial geometries for DFT calculations of the wild type APSR active site models including the [4Fe-4S] cluster were taken from the X-ray crystal structure (2GOY.pdb, 2.7 Å resolution) of Pa-APSR.¹³ Pa-APSR was serendipitously crystallized such that density for APS was observed in two of the four monomeric subunits. Thus the differentially occupied subunits could be used to compare the geometry and electronic structure of the [4Fe-4S] cluster in the free and substrate-bound forms of the protein. The cluster without APS was taken from subunit A (or chain-A) of the crystal structure (Figure 4). A closer look at the [4Fe-4S-4Cys] center is shown in Figure 5. The quantum cluster of the active site with APS was taken from chain-B of the crystal structure (Figure 6). The main or side chains of Cys139, Cys140, Cys228, Cys231, Thr87, His136, Arg143, Lys144, Arg242, Arg245, and Trp246 were also included in the quantum models. To facilitate calculations by minimizing the number of atoms in the model, some changes were made to the residues, including cleavage of certain bonds, addition of link-H atoms²⁶ and partial inclusion of neighboring residues to have closed valence. Explicitly, for Thr87, Cys139, His136 and Cys228, C_α-NH was replaced with C_α-H. Since the electron density map shows δ⁺ density on His136, the His136 side chain was protonated in our calculations. For Gly88, Gly137, Gly141, and Glu229, HN-C_α was included into the quantum cluster and C_α was replaced with H. For Ile142 and Pro230, C_α-C=O was included in the cluster and C_α was replaced with H. For Lys144 and Thr232, C_α-C=O was replaced with C_α-H. For Arg242 and Arg245, C_γ-C_β was replaced with C_γ-H. Finally for Trp246, HN-C_α-C=O was replaced with H-C_α-H.

Figure 4.

DFT optimized quantum cluster model of the [4Fe-4S] center in APSR without APS. Initial geometry was taken from chain-A of the X-ray crystal structure (PDB code: 2GOY).¹³

Figure 5.

A closer look of the [4Fe-4S] center and the atom labels with the four cysteine side chains.

Figure 6.

DFT optimized quantum cluster model of the [4Fe-4S] center in APSR with APS. Initial geometry was taken from chain-B of the X-ray crystal structure (PDB code: 2GOY).¹³

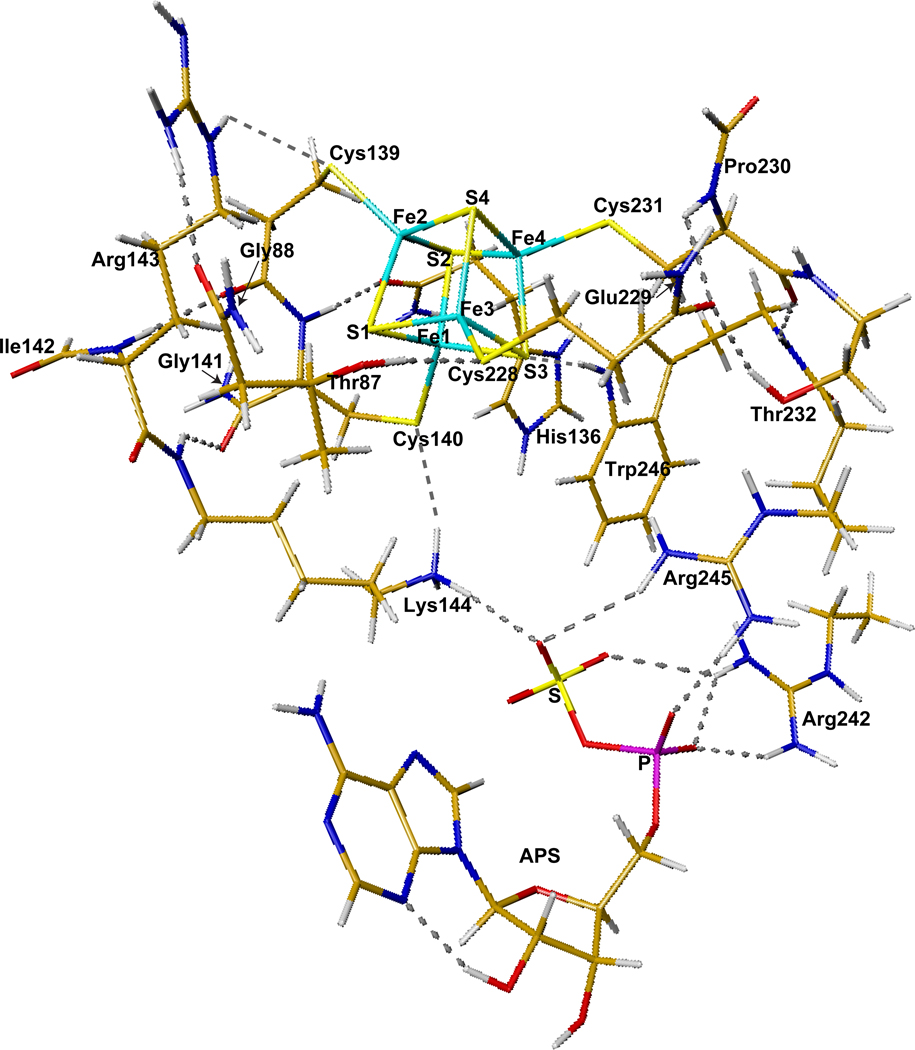
The following three H-bonds are found in the crystal structure between the inorganic S’s and S_γ’s of the [4Fe-4S-4Cys] cluster and the protein residues in both chain-A and chain-B: S3⋯HN_ε1-Trp246, Cys139-S_γ⋯HN_ε-Arg143, and Cys228-S_γ⋯HO_γ1-Thr87. In chain-B where APS is bound, the side chain of Lys144 H-bonds with both S_γ-Cys140 and O from the sulfate group of APS. Model cluster for chain-A (Figure 4) has eleven H-bonds and a total of 211 atoms. By contrast, model cluster for chain-B (Figure 6) has eighteen H-bonds (of which, 7 involve the substrate) and a total of 250 atoms.

Without APS, the Arg242 side chain H-bonds with the main chain −C=O group of Arg245 (chain-A, Figure 4). In the presence of APS, Arg242 rotates to form H-bonds with the phosphate and sulfate groups of APS. Arg245 also H-bonds with APS (chain-B, Figure 6).

3.2. No-Tandem Models

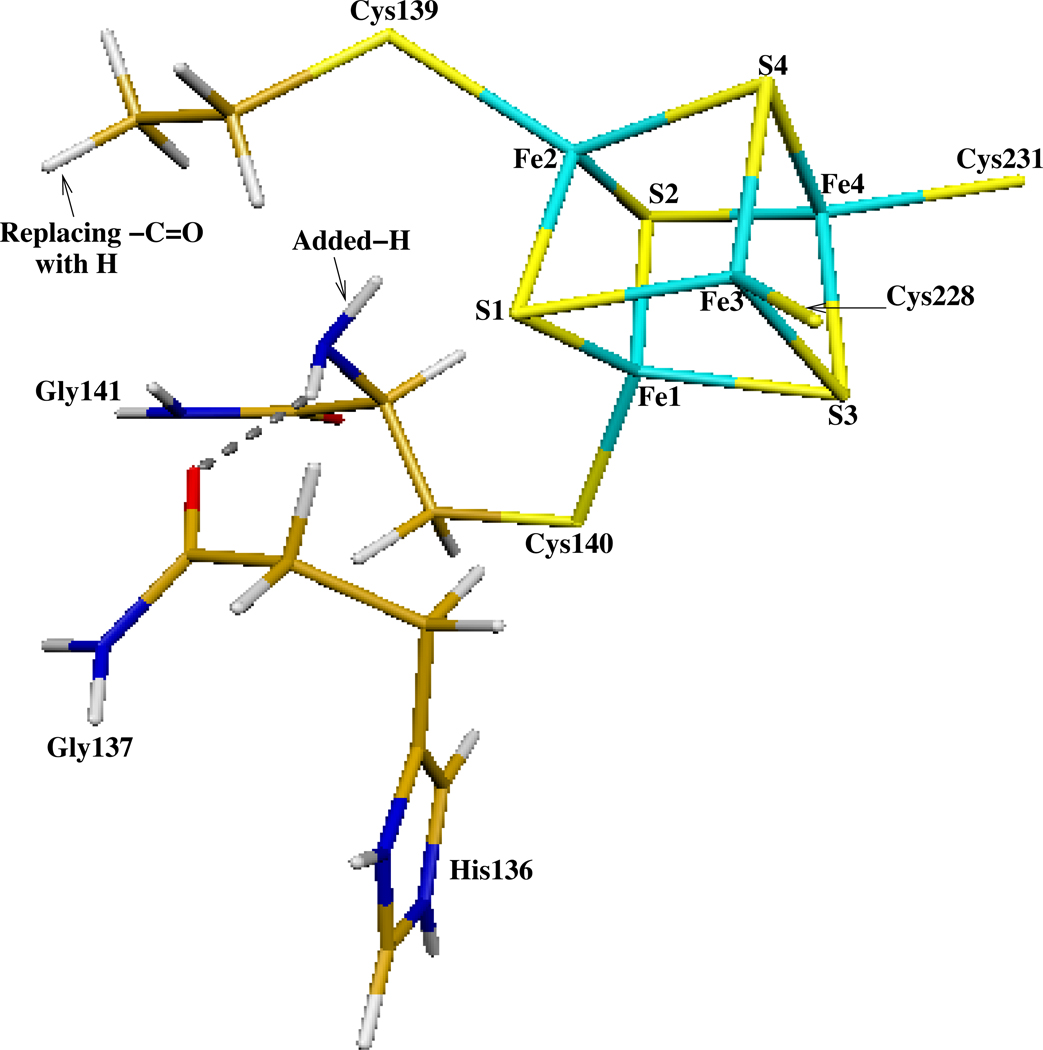
Since coordination by sequential cysteines in Pa-APSR is highly unusual for [4Fe-4S] clusters, it is valuable to determine what changes would occur in the geometric and electronic structure of the cluster if we break the linkage between Cys139 and Cys140. For this purpose, two “no-tandem” computational models were constructed by breaking the HN-CO peptide bond between Cys139 and Cys140 in both chain-A (without APS) and chain-B (with APS). The – C=O group of Cys139 was replaced by a hydrogen (Figure 7), meanwhile a hydrogen was added to the –NH group of Cys140 to fill the open valence. In the absence of the peptide bond, the number of atoms in each of the model clusters remained constant.

Figure 7.

The HN-CO peptide bond between Cys139 and Cys140 was cut in order to study the “no-tandem” structures in both chain-A (without substrate) and chain-B (with substrate). The -CO group of Cys139 was replaced by a hydrogen, meanwhile a hydrogen was added to the -NH group of Cys140 to fill the open valence.

3.3. K144A Models

As previously mentioned, there is biochemical and spectroscopic evidence to show that the stability and microenvironment of the cluster in APSR changes upon substrate binding.^4,16,27 This indicates that APS does interact with the [4Fe-4S] cluster, not by direct contact, but via a network of electrostatic interactions. Lys144, Arg242, and Arg245 all have H-bonding interactions with APS, of which Lys144 is positioned between the [4Fe-4S] cluster and APS. Therefore we constructed the K144A models (for both chain-A and chain-B) by replacing Lys144 with Ala in order to investigate changes in the properties of the [4Fe-4S] cluster without Lys144. Explicitly, the C_β-C_γ bond of Lys144 was cut and a proton was added to C_β to close valence, resulting in a total of 199 and 238 atoms in the chain-A and chain-B models respectively.

4. Computational Methodology

All density functional spin-unrestricted calculations were performed using the Amsterdam Density Functional (ADF) package^28–30 with the OLYP functional. OLYP is the combination of Handy’s optimized exchange (OPTX)³¹ and LYP correlation.³² Swart et al. have tested different functionals in calculating the atomization energies for the G2-set of up to 148 molecules, six reaction barriers of S_N2 reactions, geometry optimizations of 19 small molecules and 4 metallocenes, and zero-point vibrational energies for 13 small molecules.³³ Their examination shows that the OPTX containing functionals perform better than the regular general gradient approximation functionals (GGAs) like PBE,^34,35 BLYP,^32,36 and BP.^36–38 For organic systems, OLYP has been shown to function as well as the hybrid functional B3LYP.^33,39 Very recently, Hopmann et al. reported that for ⁵⁷Fe Mössbauer isomer shift calculations, the OLYP potential performs comparably well for iron nitrosyls and for iron complexes in general.⁴⁰

The resting state of the [4Fe-4S] core in APSR has +2 charge, [Fe₄S₄]²⁺. The core plus the four Cys side chains has a net charge of −2, [Fe₄S₄(S_γ-Cys)₄]²⁻. Therefore each of the four equivalent iron sites has a 2.5+ oxidation state.^19,41 The antiferromagnetically (AF) coupled S_total = 0 ground state requires two mixed valence iron pairs with opposite spins. The combinations of the spin states can be: {Fe1^↓Fe2^↓Fe3^↑Fe4^↑}, {Fe1^↑Fe2^↓Fe3^↓Fe4^↑}, and {Fe1^↑Fe2^↓Fe3^↑Fe4^↓}, where “^↑” and “^↓” represent spin up and down, respectively. As in previous work, we perform “broken-symmetry” (BS)^42–44 calculations to represent the AF-coupled spin states. First we construct a ferromagnetically (F) spin-coupled (S_total = 18/2) determinant, where the spins on the four irons are aligned in a parallel fashion. Then we rotate the spin vector located on two of the iron sites by interchanging the α and β fit density blocks on the two sites from the output file TAPE21 created by this F-coupled calculation in ADF to get the starting spin density for the S_total = 0 state. These BS states are not pure S_total = 0 states. Instead, these states (and their energies) are weighted averages of the pure spin states, strongly weighted toward the lower S_total states based on the spin coupling algebra.^19,41–44 We have not included spin projection corrections in the current work since we have estimated that these will make very small differences in the DFT calculated relative energies of different states.

4.1. Geometry Optimization

To determine which one of the three spin states of the [4Fe-4S] cluster in APSR has the lowest energy and is geometrically closest to the X-ray crystal structure, we geometry optimized the active site clusters taken from chain-A (without substrate binding) and chain-B (with substrate binding) in the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑}, {Fe1^↑Fe2^↓Fe3^↓Fe4^↑}, and {Fe1^↑Fe2^↓Fe3^↑Fe4^↓} three BS spin states. All calculations were performed within the conductor-like screening (COSMO)^45–48 solvation model with dielectric constant ε = 20. In COSMO, the quantum cluster is embedded in a molecular shaped cavity surrounded by a continuum dielectric medium. There is no universal dielectric constant for COSMO-like solvation calculations. Although the dielectric value ε = 4 is commonly used for the protein interior, since this is the value for the dielectric constants of crystalline and polymeric amides⁴⁹ and dry protein and peptide powders,^50–53 many studies show that higher effective dielectric constant values (4–30) for protein interiors are needed in reproducing the pK_a values of certain internal ionizable groups.^53–60 For the current study, since many charged groups are in the quantum cluster, a larger dielectric constant (ε = 20) was chosen for the COSMO calculations. The van der Waals radii for atoms Fe, C, S, P, O, N, and H were taken as 1.5, 1.7, 1.8, 1.8, 1.4, 1.55, and 1.2 Å, respectively.^61,62 The probe radius for the contact surface between the cluster and solvent was set to 2.0 Å. The triple-ζ (TZP) (for Fe and S) and double-ζ (DZP) (for other atoms) polarization Slater-type basis sets with frozen cores (C(1s), N(1s), O(1s), S(1s,2s,2p), P(1s,2s,2p), and Fe(1s,2s,2p) are frozen) were applied for geometry optimizations. To partially apply the strain from the protein environment, C_α atoms on Lys144, Thr232, Arg245, and Trp246, C_γ of Arg242, and the link-H atoms on Thr87, Gly88, His136, Gly137, Cys139, Gly141, Ile142, Lys144, Cys228, Glu229, Pro230, Thr232, Arg242, Arg245, and Trp246, were fixed during geometry optimizations. The broken-symmetry state energies obtained after COSMO geometry optimizations were used to compare the relative energies in Section 6.

4.2. Mössbauer Isomer Shift and Quadrupole Splitting Calculations

For all models, we applied single-point Mössbauer isomer shift and quadruple splitting calculations at the optimized geometries using all-electron (i.e. without frozen core approximation) all TZP Slater-type basis sets. First, a high-spin F-coupled single-point energy calculation was performed at the BS optimized geometry. Its TAPE21 file was then modified accordingly by interchanging the α and β fit density blocks on two of the iron sites. Starting from the modified TAPE21, a BS state single-point energy calculation in COSMO again with all-electron TZP Slater-type basis sets was performed to obtain the electron density (ρ(0)) and the electric field gradient (EFG) at the Fe nucleus.

The Mössbauer isomer shifts δ were calculated based on ρ(0):

$$\mathrm{\delta }=\mathrm{\alpha }(\mathrm{\rho }(0)-A)+C$$ (1)

where A = 11877 is a constant. Our previous isomer shift fit based on 19 Fe^{2.5+,3+,3.5+,4+} complexes (30 distinct iron sites) using OLYP/all-electron-TZP method (with INTEGRATION = 4.0) yielded: α = −0.307 and C = 0.385 mm s⁻¹.⁶³ The numerical integration accuracy parameter INTEGRATION = 4.0 is also used for the current calculations.

For calculating the Mössbauer quadrupole splittings (ΔE_Q), the EFG tensors V were diagonalized and the eigenvalues were reordered so that |V_zz| ≥ |V_xx| ≥ |V_yy|. The asymmetry parameter η is defined as

$$\mathrm{\eta }=|(V_{\mathrm{x}\mathrm{x}}-V_{\mathrm{y}\mathrm{y}})/V_{\mathrm{z}\mathrm{z}}|$$ (2)

Then the ΔE_Q for ⁵⁷Fe of the nuclear excited state (I = 3/2) can be calculated as

$$\mathrm{\Delta }{E}_{\mathrm{Q}}=(½)eQ{V}_{\mathrm{z}\mathrm{z}}{\left(1+{\mathrm{\eta }}^2/3\right)}^{½}$$ (3)

where e is the electrical charge of a positive electron, Q is the nuclear quadrupole moment of Fe. We had used eQ = 0.15 electron-barn⁶⁴ in our previous publications. For the current study, we applied a slightly different eQ = 0.158 electron-barn taken from the careful quantum chemical calculations (non-relativistic) by Neese’s group.⁶⁵

4.3. Fitting Atomic Charges from Electrostatic Potentials (ESP)

A modified version of CHELPG code^41,66 was used to fit the atomic point charges from the molecular electrostatic potentials (ESP) obtained from the final all-electron all-TZP single-point energy calculations. The singular value decomposition (SVD) method⁴¹ was introduced into the code to minimize the uncertainties in the fitting procedure. The total net charge and the three Cartesian dipole moment components of each cluster were used as constraint conditions for the fit. The fitted points lay on a cubic grid between the van der Waals radius and the outer atomic radius with a grid spacing of 0.2 Å. The outer atomic radius (5.0 Å here for all atoms) defines the outer boundary of the electrostatic potential that was used in the charge fitting. The same van der Waals radii were used as in COSMO calculations.

5. X-ray Absorption Spectroscopy (XAS) Results and Discussion

To probe the coordination and geometry of the [4Fe-4S] cluster in APSR we examined Mt-APSR by XAS. To facilitate EXAFS analyses, monomeric Mt-APSR was used instead of Pa-APSR since Pa-APSR purifies as a tetramer. In order to determine the effect of APS binding on Fe-site structure, Mt-APSR was incubated with a 3-fold stoichiometric excess of APS, at a concentration exceeding the k_d of APS and AMP (0.2 μM and 5.4 μM respectively⁹). Therefore, the form of Mt-APSR in EXAFS experiments was the S-sulfocysteine state with AMP bound and the C-terminal docked in the active site (closed state). By contrast, for crystallization of Pa-APSR, ~60-fold excess of APS over enzyme was added and the stable form that crystallized was formed with the C-terminal tail out of the active site (open state) (see Figure 6C in ref 13)

5.1. Fe K-Edge XAS

The normalized Fe K-edge XANES spectrum of APSR is shown in Figure 3. This region of the XAS spectra (1s → 3d transitions) provides valuable information about metal ion coordination number and oxidation state.⁶⁷ The Fe pre-edge area calculated for APSR (~18 × 10⁻² eV) is consistent with a four-coordinate Fe species. This conclusion is supported by Mössbauer studies for native Mt-APSR which confirm the presence of a [4Fe-4S]²⁺ cluster.¹⁸ The pre-edge feature observed at ~7112 eV occurs due to an electronic dipole-forbidden quadrupole-allowed transition from the Fe 1s orbital to valence orbitals with significant Fe 3d character.^67,68 The increase in intensity of this formally forbidden transition is a result of mixing of Fe 4p-3d orbitals caused by deviation of the absorbing Fe center from centrosymmetry.⁶⁹ To investigate changes in cluster geometry and coordination during catalysis, Mt-APSR was incubated with APS to form the S-sulfocysteine intermediate with AMP bound in the active site and XAS was recorded for this stable conformation of the enzyme (Table 1, Supplementary Figure 2). No shift in position or intensity of the pre-edge energy was observed for the Mt-APSR S-sulfocysteine intermediate, indicating that the level of 4p mixing is identical to native Mt-APSR. Since the 1s → 3d transition is very sensitive to local Fe-site structure, this is a sensitive indication that not only is there no change in oxidation state or coordination number, but there is unlikely to be more than a very small change in geometry of the Fe in the [4Fe-4S] cluster between the native and S-sulfocysteine intermediate forms of Mt-APSR.

Table 1.

Extended X-ray Absorption Fine Structure (EXAFS) Curve-Fitting Parameters for Fe K-edge. Coordination Number (N), Interatomic Distances (R), Mean-Square Deviations in Interatomic Distance (σ², Ų), Fit-Error Function (F) is Defined as <{Σk⁶ (χ_calc* – χ_expt)² / Σχ²_expt}^1/2>. For Mt-APSR the k Range was 2.35 ~ 17 (Filtered R = 1.2 ~ 3); for Mt-APSR + APS the k Range was 2.15 ~ 17 (Filtered R = 1.2 ~ 3); giving resolution ~ 0. 1 Å and ~17 independent degrees of freedom. Fits are shown both for fixed (marked with *) and variable N

Sample	Interaction	N	R (Å)	σ2 × 103	F
Mt-APSR	Fe-S	4*	2.297	3.9	1.93
sample 1	Fe-Fe	3*	2.726	2.4
	Fe-S	3.9	2.297	3.8	1.92
	Fe-Fe	2.1	2.726	2.7
Mt-APSR	Fe-S	4*	2.294	3.9	1.92
sample 2	Fe-Fe	3*	2.729	2.0
	Fe-S	3.7	2.294	3.4	1.86
	Fe-Fe	1.7	2.729	1.3
Mt-APSR + APS a	Fe-S	4*	2.298	3.9	1.28
sample 1	Fe-Fe	3*	2.728	2.2
	Fe-S	3.8	2.298	3.6	0.93
	Fe-Fe	2.0	2.728	2.2
Mt-APSR + APS a	Fe-S	4*	2.297	3.8	1.48
sample 2	Fe-Fe	3*	2.730	2.5
	Fe-S	3.6	2.297	3.4	1.44
	Fe-Fe	1.8	2.730	2.0

^aThe enzyme was in the S-sulfocysteine state with AMP bound and the C-terminal docked in the active site.

5.2. EXAFS

The EXAFS data for Mt-APSR, reported at high-resolution to k ~ 17 Å⁻¹ was shown in Figure 3 (inset). . The pattern in the data reflects the fact that there are at least two shells of scatterers, sulfur and iron, significantly contributing to the EXAFS spectrum. The Fourier transform (FT) of Mt-APSR (Figure 3, Table 1) shows an intense first-shell Fe-S interaction at 2.3 Å and a slightly less intense second-shell Fe-Fe interaction at 2.73 Å. For this k range, resolution in R space is ~0.1 Å, meaning that if the Fe-Fe or Fe-S distances differed by > 0.1 Å they should, in principle, be resolvable, and that if the distances differ by > ~0.12 Å they should be readily resolvable into two different shells of scatterers (Two Fe-Fe distances that differed by 0.12 Å would show a “beat” in the EXAFS at ~k = 13 Å⁻¹ which would be readily detectable). No improvement was seen for multiple shell fits. It is possible, of course, that there are not two, but up to six different Fe-Fe distances (Note that if there were significant disorder, with multiple forms of the Fe/S cluster, this could increase further the number of Fe-Fe distances. This is ruled out by the absence of disorder in the Mossbauer spectra). In this case, individual Fe-Fe distances might not be resolvable. However, if this were the case, there would be an increase in the Debye-Waller factor. However, the observed Debye-Waller factors are small, indicating that there is, at most a very small (< 0.12 Å) spread in Fe-Fe distance, consistent with the spread in Fe-Fe distances that is found in the DFT calculations (Tables 2 and 3).

Table 2.

Fe-Fe and Fe-ligand Bond Lengths (Å), Broken-Symmetry State Energies (E, eV), Fe Net Spin Populations (NSP), and Mössbauer Properties (Isomer shifts δ, Quadrupole Splittings ΔE_Q, mm s⁻¹, and η) of the Resting State [Fe₄S₄(S_γ-Cys)₄]²⁻ Cluster in Wild-Type Pa-APSR without Substrate Binding: Comparison between Calculations and Experiments (Exp).

	Calculated Chain-A without APS			Expa
	Fe1↓Fe2↓Fe3↑Fe4↑	Fe1↑Fe2↓Fe3↓Fe4↑	Fe1↑Fe2↓Fe3↑Fe4↓
Fe1-Fe2	2.685	2.700	2.651	2.7
Fe1-Fe3	2.657	2.687	2.662	2.7
Fe1-Fe4	2.707	2.742	2.724	2.7
Fe2-Fe3	2.758	2.963	2.767	2.7
Fe2-Fe4	2.684	2.711	2.750	2.8
Fe3-Fe4	2.646	2.671	2.663	2.8
Fe1-S1	2.309	2.219	2.291	2.2
Fe1-S2	2.323	2.305	2.222	2.2
Fe1-S3	2.232	2.299	2.300	2.2
Fe2-S1	2.339	2.349	2.259	2.3
Fe2-S2	2.293	2.191	2.290	2.3
Fe2-S4	2.269	2.341	2.335	2.2
Fe3-S1	2.211	2.293	2.286	2.3
Fe3-S3	2.313	2.229	2.309	2.3
Fe3-S4	2.330	2.345	2.255	2.3
Fe4-S2	2.201	2.267	2.287	2.3
Fe4-S3	2.314	2.306	2.238	2.3
Fe4-S4	2.322	2.247	2.321	2.3
Fe1-Sγ-Cys140	2.249	2.270	2.333	2.3
Fe2-Sγ-Cys139	2.311	2.312	2.267	2.3
Fe3-Sγ-Cys228	2.301	2.325	2.292	2.3
Fe4-Sγ-Cys231	2.277	2.298	2.324	2.3
E	−1193.735	−1193.369	−1193.532
NSP(Fe1, Fe2, Fe3, Fe4)	−3.11, −3.18, 3.16, 3.11)	(3.12, −3.17, −3.17, 3.14)	(3.10, −3.18, 3.20, −3.15)
δ(Fe1, Fe2, Fe3, Fe4)	(0.43, 0.48, 0.45, 0.44)	(0.42, 0.46, 0.46, 0.44)	(0.39. 0.46, 0.43, 0.43)	0.45 18
Average δ	0.45	0.45	0.43
ΔEQ(Fe1, Fe2, Fe3, Fe4)	(1.17, 1.01, 0.80, −1.01)	(0.95, 1.20, 1.20, 0.78)	(0.91, 0.99, 1.04, 1.32)	1.09 18
Average |ΔEQ|	1.00	1.03	1.07
η(Fe1, Fe2, Fe3, Fe4)	(0.48, 0.62, 0.65, 0.92)	(1.00, 0.31, 0.24, 0.77)	(0.96, 0.46, 0.55, 0.35)

^aThe crystal structure of Pa-APSR was at 2.7 Å resolution, PDB code: 2GOY.¹³ Distances are taken from chain-A without substrate binding.

Table 3.

Fe-Fe and Fe-ligand Bond Lengths (Å), Broken-Symmetry State Energies (E, eV), Fe Net Spin Populations (NSP), and Mössbauer Properties (Isomer shifts δ, Quadrupole Splittings ΔE_Q, mm s⁻¹, and η) of the Resting State [Fe₄S₄(S_γ-Cys)₄]²⁻ Cluster in Wild-Type Pa-APSR with Substrate Binding: Comparison between Calculations and Experiments (Exp).

	Calculated Chain-B with APS			Exp a
	Fe1↓Fe2↓Fe3↑Fe4↑	Fe1↑Fe2↓Fe3↓Fe4↑	Fe1↑Fe2↓Fe3↑Fe4↓
Fe1-Fe2	2.741	2.718	2.669	2.7
Fe1-Fe3	2.683	2.690	2.717	2.7
Fe1-Fe4	2.727	2.813	2.742	2.7
Fe2-Fe3	2.732	2.863	2.750	2.7
Fe2-Fe4	2.680	2.708	2.792	2.7
Fe3-Fe4	2.728	2.670	2.678	2.7
Fe1-S1	2.304	2.205	2.303	2.3
Fe1-S2	2.333	2.308	2.227	2.3
Fe1-S3	2.209	2.310	2.314	2.3
Fe2-S1	2.313	2.308	2.221	2.3
Fe2-S2	2.267	2.183	2.274	2.2
Fe2-S4	2.247	2.343	2.338	2.3
Fe3-S1	2.178	2.267	2.271	2.2
Fe3-S3	2.310	2.222	2.308	2.2
Fe3-S4	2.305	2.293	2.217	2.2
Fe4-S2	2.193	2.273	2.285	2.3
Fe4-S3	2.290	2.284	2.202	2.3
Fe4-S4	2.310	2.230	2.302	2.3
Fe1-Sγ-Cys140	2.304	2.329	2.326	2.3
Fe2-Sγ-Cys139	2.293	2.325	2.315	2.3
Fe3-Sγ-Cys228	2.290	2.306	2.306	2.3
Fe4-Sγ-Cys231	2.257	2.289	2.276	2.3
E	−1446.545	−1446.291	−1446.501
NSP(Fe1, Fe2, Fe3, Fe4)	(−3.13, −3.11, 3.12, 3.07)	(3.14, −3.16, −3.12, 3.13)	(3.14, −3.14, 3.17, −3.13)
δ(Fe1, Fe2, Fe3, Fe4)	(0.45, 0.45, 0.43, 0.42)	(0.46, 0.45, 0.43, 0.43)	(0.47, 0.46, 0.44, 0.43)	0.45 18
Average δ	0.44	0.44	0.45
ΔEQ(Fe1, Fe2, Fe3, Fe4)	(1.08, 0.95, 0.79, −1.03)	(0.87, 1.24, 1.15, 0.70)	(0.85, 1.04, 0.87, 1.23)	1.12 18
Average |ΔEQ|	0.96	0.99	1.00
η(Fe1, Fe2, Fe3, Fe4)	(0.33, 0.65, 0.53, 0.88)	(0.78, 0.34, 0.29, 0.62)	(0.89, 0.64, 0.42, 0.33)

^aThe crystal structure was at 2.7 Å resolution, PDB code: 2GOY.¹³ Distances are taken from chain-B with substrate binding.

If the experimental Fe-Fe σ² value of ~2.5×10⁻³ Ų is attributed solely to static disorder and if the most asymmetric possible distribution of Fe-Fe distances is assumed (i.e., 5 short and 1 long distance), the spread in distances is the spread in Fe-Fe distances is ~ $\sqrt{6}$ σ = 0.12 Å. A more reasonable estimate would recognize that the experimental σ² is the sum of σ²_vib and σ²_static, The former can be estimated from the fitted σ² value for Pyrococcus furiousus ferredoxin, 2.0 ×10⁻³ Ų. If this is attributed to vibrational motion, the apparent σ²_static is 5.0 ×10⁻⁴ Ų, suggesting a spread in Fe-Fe distances of ~0.05 Å. While the true spread in Fe-Fe distances will depend on details of the distribution in Fe-Fe distances and the vibrational contribution to σ², it should be between these limits.

Coordination numbers were initially constrained to the chemically correct values (4 Fe-S and 3 Fe-Fe). These gave excellent fits. Modest improvement in fit quality was possible if the coordination number was allowed to vary; this improvement is consistent with that expected for a 50% increase in variable parameters. To confirm that these data are consistent with a [4Fe-4S] cluster, we compared the EXAFS and FT of Mt-APSR with those previously reported data for Pyrococcus furiosus ferredoxin containing either an [3Fe-4S] cluster or a [4Fe-4S] clusters (data provided by Prof. G.N. George, University of Saskatoon). Supplementary Figure 3 unambiguously shows that the EXAFS spectrum for Mt-APSR is in good agreement with the spectrum for the [4Fe-4S] cluster in ferredoxin, albeit with a slightly less intense Fe-Fe peak, suggesting somewhat larger disorder in the Fe-Fe scattering in Mt-APSR, consistent with the fitting results..

The EXAFS spectrum and FT of the Mt-APSR S-sulfocysteine intermediate are identical to those of native Mt-APSR, and the Fe-S and Fe-Fe bond lengths remain consistent (Table 1, Supplementary Figs. 2B and 2C). Although the accuracy of EXAFS bond-lengths is generally taken as ~0.02 Å, the precision is much better. We have found previously that the precision of biological EXAFS data is ~0.003 Ų;²⁴ this is reflected in the excellent reproducibility of the duplicate samples in Table 1. This precision, together with the invariance seen in Table 1, indicates that the average core structure of the [4Fe-4S] cluster in Mt-APSR is unaffected in the S-sulfocysteine conformation of the protein. Since XAS spectra reflect bond-lengths that are averaged over all the atoms in the cluster, it is in principle possible that small changes at one site could be compensated by equal but opposite changes at another site, such that the average distances remain the same. To probe these changes at high resolution, density functional theory calculations were undertaken.

6. DFT Calculation Results and Discussion

6.1. Calculating Results for Wild-Type [Fe₄S₄(S_γ-Cys)₄]²⁻ Models

The main calculated properties for different spin states of the wild-type [4Fe-4S] cluster without and with the substrate are given in Tables 2 and 3, respectively. The calculated Fe-Fe and Fe-S distances and ⁵⁷Fe Mössbauer isomer shifts and quadrupole splittings are compared with available experimental results.¹⁸

As previously reported,⁴¹ each of the optimized [Fe₄S₄(S_γ-Cys)₄]²⁻ clusters has a compression structure with four “short” (~2.2 Å) and eight “long” (~2.3 Å) Fe-S distances. The two irons with the same spin direction are in an Fe₂S₂ rhomb distorted butterfly “plane” with four “long” Fe-S distances, and the four Fe-S bonds between the two “planes” have “short” distances. Taking the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} state in Table 2 (without APS binding) as an example, Fe1 and Fe2 (spin down) are on the plane containing Fe1-S1-Fe2-S2, and Fe3 and Fe4 (spin up) are on the plane with Fe3-S3-Fe4-S4. As a result, the eight Fe-S bond lengths on the two planes are long (in average 2.32 Å), and the four Fe1-S3, Fe2-S4, Fe3-S1, and Fe4-S2 bonds between the two planes are shorter (in average 2.23 Å). Overall, the spread of the DFT calculated Fe-S (2.20−2.34 Å) and Fe-Fe (2.65−2.76 Å) distances agree with the EXAFS’s results of ~2.3±0.1 Å and ~2.7 ±0.1 Å, respectively. Since the Pa-APSR crystal structure was solved at 2.7 Å resolution,¹³ the compression structure for the [4Fe-4S] cluster is not obvious in either chain-A (without APS binding) or chain-B (with APS binding). It is also not reliable to determine the spin state of the cluster based on the comparison between the calculated geometries and the crystal structure. Since the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} state yields the lowest broken-symmetry energy in both chain-A and chain-B, it is likely that the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster of Pa-APSR is in the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} state before and after substrate binding.

In the presence of APS, the calculated distances of Fe1-Fe2 and Fe3-Fe4 are increased by 0.06 Å; the four “short” distances (Fe1-S3, Fe2-S4, Fe3-S1, and Fe4-S2) between the two planes “Fe1-S1-Fe2-S2” and “Fe3-S3-Fe4-S4” are shortened by 0.02 Å on average. Since the thiolate of Cys140 now has a direct H-bonding interaction with the Lys144 side chain (Figure 6), the Fe1-S_γ-Cys140 bond is increased by 0.06 Å, and it becomes the longest among the four Fe-S_γ-Cys bonds. The elongation of the Fe1-S_γ-Cys140 distance may explain the marked change in Fe-S_γ stretching modes observed in the Resonance Raman spectra of Pa-APSR upon APS binding.¹⁷

The net spin populations (NSP) from Mulliken population analysis are the main indication of the high-spin or intermediate-spin character of the metal sites. In the ideal ionic limit, the net unpaired spin populations are 5 and 4 for the high-spin Fe³⁺ (five d-electrons) and Fe²⁺ (six d-electrons) sites, respectively. Therefore, for the delocalized spins between the high-spin Fe³⁺ and Fe²⁺ sites, one should expect the average net spin of 4.5. However, because of the Fe-ligand covalency, our previous calculations show that the calculated net spin magnitude for a high-spin Fe³⁺/Fe²⁺ site is normally by about 1 e⁻ smaller than the ionic limit.^{19,41,70–73} The current calculated net spins on the four Fe sites in both chain-A and chain-B are 3.1 ~ 3.2 (Tables 2 and 3), about 1.3 ~ 1.4 e⁻ smaller than 4.5, indicative of the high spin Fe^2.5+ sites with substantial Fe-S covalency. The opposite signs for the spin densities indicate the AF-coupling.

Experimentally derived ⁵⁷Fe Mössbauer parameters were almost identical for the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster for native APSR and for the S-sulfocysteine intermediate form with AMP bound and C-terminal tail docked in the active site. Note that the Mössbauer analyses on Mt-APSR¹⁸ were performed by incubating the enzyme with a 2-fold stoichiometric excess of APS at a concentration well above the K_d of APS or AMP, similar to the current EXAFS study. Our calculations show the subtle differences of the Mössbauer isomer shifts and quadrupole splittings for each Fe site in different spin states, with or without substrate. However the predicted isomer shifts are all around 0.45 mm s⁻¹, in excellent agreement with the experiment. The average predicted quadrupole splitting values (~1 mm s⁻¹) also agree well with the experimental values (Tables 2 and 3).

To understand how APS binding influences the charge distributions of the [4Fe-4S] cluster, we calculated the ESP atomic charges of the [Fe₄S₄(S_γ-Cys)₄]²⁻ clusters in chain-A and chain-B in the Fe1^↓Fe2^↓Fe3^↑Fe4^↑ spin state. The ESP charges are given in Table 4 under the “Wild-type” columns.

Table 4.

Comparing the Calculated ESP Atomic Charges of the [Fe₄S₄(S_γ-Cys)₄]²⁻ Quantum Cluster in the Fe1^↓Fe2^↓Fe3^↑Fe4^↑ Spin State in Different Models.

	Chain-A without APS			Chain-B with APS
	Wild-type	No-tandem	K144A	Wild-type	No-tandem	K144A
Fe1	0.43	0.43	0.47	0.45	0.42	0.50
Fe2	0.58	0.58	0.60	0.61	0.59	0.61
Fe3	0.62	0.63	0.63	0.61	0.65	0.61
Fe4	0.62	0.60	0.63	0.62	0.61	0.64
S1	−0.44	−0.46	−0.48	−0.44	−0.48	−0.46
S2	−0.45	−0.44	−0.44	−0.44	−0.43	−0.46
S3	−0.47	−0.46	−0.53	−0.48	−0.49	−0.54
S4	−0.70	−0.68	−0.70	−0.70	−0.67	−0.71
Sγ-Cys140	−0.41	−0.40	−0.54	−0.45	−0.39	−0.59
Sγ-Cys139	−0.63	−0.68	−0.59	−0.64	−0.67	−0.66
Sγ-Cys228	−0.61	−0.60	−0.66	−0.70	−0.70	−0.70
Sγ-Cys231	−0.65	−0.67	−0.67	−0.63	−0.66	−0.68
Σtotal	−2.11	−2.15	−2.28	−2.19	−2.22	−2.44

In chain-A without APS, Fe1 has the least positive charge (0.43), which is approximately 0.2 charge units less than Fe3 and Fe4. In addition, the Cys140 thiolate which coordinates to Fe1 has the least negative charge (−0.41), which is also by 0.2 charge units in magnitude less than the other three Cys residues. This shows the charge transfer from the Cys140 thiolate to the nearby cationic group of Lys144 side chain. In chain-B (Figure 6), Lys144 is in between Cys140 and APS. The distances between S_γ-Cys140 and N-Lys144, and between N-Lys144 and O-APS are 3.16 Å (3.56 Å) and 3.19 Å (3.03 Å), respectively, in the X-ray (DFT optimized) structure of chain-B. The charge transfer from Cys140 to Lys144 is decreased in the presence of APS. As a result, S_γ-Cys140 becomes more negative from −0.41 (chain-A) to −0.45 (chain-B), and the ESP charge on Fe1 is slightly increased from 0.43 (chain-A) to 0.45 (chain-B). The repulsion between APS and Cys228 also increases the magnitude of the negative charge on S_γ-Cys228 from −0.61 (chain-A) to −0.70 (chain-B). These changes result in a subtle increase in the total negative ESP charge of the entire [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster from −2.11 (Chain-A) to −2.19 (Chain-B).

Even though APS does not have a direct interaction with the [4Fe-4S] cluster, the mid-range electrostatic interactions between the two species indeed influence the charge distribution and the detailed geometry within the [4Fe-4S] cluster, although the geometric changes are not large enough to be observed in EXAFS and Mössbauer experiments.

6.2. Calculating Results for No-Tandem [Fe₄S₄(S_γ-Cys)₄]²⁻ Models

The main Fe-Fe and Fe-S distances of the optimized no-tandem models in the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} state with and without APS are shown in Table 5, in the columns under “No-tandem”. After breaking the peptide bond between Cys139 and Cys140 (Figure 7), the [4Fe-4S]²⁺ core in both chain-A and chain-B expands. For chain-A without APS, the Fe1-Fe2 distance is increased by 0.08 Å compared to wild-type (Table 2). Fe1-Fe3, Fe1-Fe4, and Fe3-Fe4 are also increased by 0.03, 0.04 and 0.02 Å, respectively. Except for Fe2-S2, Fe2-S4, and Fe2-S_γ-Cys139, which are decreased by 0.01 Å, all other Fe-S distances are increased by 0 ~ 0.03 Å. The RMSD of the Fe-Fe and Fe-S distances between the calculated no-tandem model and the wild-type optimized cluster of chain-A is 0.022 Å. The angles ∠Fe1-S_γ-C_β-Cys140 and ∠Fe2-S_γ-C_β-Cys139 are widened from 112.6° and 109.6° to 117.3° and 112.4°, respectively. Meanwhile the distance between (S_γ-Cys140) and (S_γ-Cys139) is enlarged from 6.19 Å to 6.43 Å.

Table 5.

Calculated Fe-Fe and Fe-ligand Bond Lengths (Å) and Fe Net Spin Populations (NSP) for the [Fe₄S₄(S_γ-Cys)₄]²⁻ Quantum Cluster in Fe1^↓Fe2^↓Fe3^↑Fe4^↑ Spin State with Substrate and without Substrate Binding in No-tandem and K144A Models.

	Chain-A without APS		Chain-B with APS
	No-tandem	K144A	No-tandem	K144A
Fe1-Fe2	2.755	2.710	2.819	2.720
Fe1-Fe3	2.683	2.661	2.700	2.676
Fe1-Fe4	2.745	2.716	2.761	2.733
Fe2-Fe3	2.742	2.754	2.735	2.731
Fe2-Fe4	2.680	2.694	2.649	2.696
Fe3-Fe4	2.662	2.689	2.705	2.727
Fe1-S1	2.317	2.311	2.306	2.303
Fe1-S2	2.340	2.323	2.326	2.317
Fe1-S3	2.238	2.224	2.218	2.208
Fe2-S1	2.349	2.340	2.311	2.317
Fe2-S2	2.284	2.298	2.272	2.276
Fe2-S4	2.253	2.262	2.242	2.251
Fe3-S1	2.218	2.203	2.210	2.175
Fe3-S3	2.325	2.340	2.308	2.317
Fe3-S4	2.333	2.340	2.298	2.302
Fe4-S2	2.208	2.203	2.199	2.201
Fe4-S3	2.326	2.335	2.296	2.296
Fe4-S4	2.332	2.341	2.310	2.318
Fe1-Sγ-Cys140	2.279	2.254	2.323	2.270
Fe2-Sγ-Cys139	2.303	2.313	2.281	2.298
Fe3-Sγ-Cys228	2.325	2.303	2.293	2.284
Fe4-Sγ-Cys231	2.288	2.284	2.257	2.276
RMSD a	0.022	0.014	0.022	0.012
NSP(Fe1)	−3.15	−3.12	−3.13	−3.11
NSP(Fe2)	−3.16	−3.19	−3.11	−3.13
NSP(Fe3)	3.18	3.18	3.12	3.12
NSP(Fe4)	3.14	3.14	3.07	3.10

^aRoot mean squares difference of the calculated Fe-Fe and Fe-S distances between the current modified models and the optimized wild-type models (in Fe1^↓Fe2^↓Fe3^↑Fe4^↑ state) given in Table 2 (for chain-A) and Table 3 (for chain-B).

From chain-A to chain-B for the no-tandem models, the Fe1-Fe2 distance is further increased by 0.06 Å, and reaches 2.82 Å, which is the longest Fe-Fe distance for the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} state of the [4Fe-4S] cluster in the current study. For chain-B with APS, the RMSD of the Fe-Fe and Fe-S distances between the no-tandem model and the optimized wild-type cluster is also 0.022 Å.

Thus, the unique tandem pair Cys139 and Cys140 in Pa-APSR keeps the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster more compact, which works to prevent the cluster from being reduced. It is known that, once the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster is reduced (net charge of the cluster would be −3), the repulsion among the S⋯S atoms would be stronger, forcing the expansion of the overall cluster.⁴¹ The tandem structure in Pa-APSR makes the expansion of the [4Fe-4S] energetically unfavorable, which explains why it is difficult to reduce the cluster.¹⁸ After several attempts, we were able to reduce the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster in Mt-APSR but the reduction efficiency was at most 44% of the total protein.¹⁸

The calculated ESP atomic charges for the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster in the no-tandem models in both chain-A and chain-B are given in Table 4 in the columns under “No-tandem”. In both chain-A and chain-B, Fe1 still holds the least positive ESP charge. Overall, the calculated ESP charges of the no-tandem models are similar to the corresponding wild-type results. The total ESP charges (Σ_total) of the no-tandem models are a little more negative than those of the wild-type cluster, which increases the possibility of one-electron oxidation of the [4Fe-4S] cluster in the no-tandem form. The propensity and rate of cluster degradation after oxidation is a complex multi-step problem, and would be expected to involve both the covalent Cys linkages and H-bonding interactions with surrounding residues.

The function that, the unique tandem pair Cys139 and Cys140 in Pa-APSR is to protect the [4Fe-4S] cluster from reduction, will be examined by redox potential calculations in Section 6.4. Note that our current method to construct the no-tandem models is the simplest, but may not represent the best approach. An alternative possibility would be to insert one or more residues between the Cys139 and Cys140 pair. However, this would cause large conformational change and increase the size of the clusters, which currently contain 211 (in chain-A) and 250 (in chain-B) atoms, and approach the reasonable limit of DFT/COSMO calculations. This issue could be examined in future studies, ostensibly starting with a smaller overall cluster size.

6.3. Calculating Results for K144A [Fe₄S₄(S_γ-Cys)₄]²⁻ Models

The calculated Fe-Fe and Fe-S distances of the optimized K144A models in the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} spin state with and without APS binding are shown in Table 5, in the columns under “K144A”. The calculated ESP atomic charges for the [Fe₄S₄(S_γ-Cys)₄]²⁻ portion of the K144A models in both chain-A and chain-B have also been shown in Table 4 in the columns under “K144A”.

There is marked anisotropy in the change of charge distribution and bond lengths when Lys144 is mutated to Ala. In particular, without charge transfer to Lys144, the negative ESP charge on S_γ-Cys140 changes significantly from −0.41 (and −0.45) in the wild type to −0.54 (and −0.59) in the K144A model of chain-A (and chain-B) (Table 4). This influences the charge on Fe1 such that Fe1 is more positive and in turn, the charge on S3 is more negative in both models of K144A, compared to the respective wild type model. Overall the total charge of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster becomes more negative from −2.11 in the wild type to −2.28 in the K144A models for chain-A, and from −2.19 to −2.44 for chain-B, respectively (Table 4). The increase of the negative charge of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster, in combination with the electrostatic interaction of the negatively charged cluster with the Lys144⁺ vs. neutral Ala144, explains why the Fe-S cluster is even more difficult to reduce in K144A mutant as observed in EPR experiments.¹⁸ The reduction potential of the K144A clusters will also be examined in Section 6.4.

In chain-B, loss of the H-bonding interaction between S_γ-Cys140 and Lys144 decreases the Fe1-S_γ-Cys140 bond length by 0.03 Å, which is greater than the other corresponding Fe-S_γ-Cys distance changes. In general, the RMSD of the calculated Fe-Fe and Fe-S distances between the K144A model and the optimized wild-type cluster is 0.014 Å for chain-A and 0.012 Å for chain-B. The cluster is more compact in the wild type protein than in the K144A model. For instance, in chain-A without APS binding, except for Fe2-Fe3, Fe1-S2, Fe1-S3, Fe2-S4, and Fe3-S1, which either remain unchanged or are decreased by less than 0.01 Å, all other Fe-Fe and Fe-S distances are increased by 0–0.04 Å from the wild-type cluster to the K144A model. Overall the cluster in K144A expands compared to the wild-type optimized cluster, which is consistent with the increasing of the electron density over the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster, and the increasing lability of the cluster in K144A as observed in EPR experiments.¹⁸

Additionally, a comparison between ESP charges for APS in the wild-type and K144A models shows that the overall charge on APS becomes more negative changing from −1.75 in wild type to −1.84 in the K144A model (data not shown). As indicated above, without charge transfer to Lys144⁺, the calculated total ESP charge of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster also becomes more negative from −2.19 in wild-type to −2.44 in K144A (chain-B). This supports the crucial role of Lys144 such that in the absence of the positive charge, the H-bonding interactions are lost and the negative charges on both the cluster and APS are more localized making the cluster and APS more negative in the K144A model. This would result in a strong repulsion between the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster and APS that is detrimental to substrate binding in the mutant protein. In fact, kinetic studies show that there is a 400-fold decrease in the K_d of APS for Lys144Ala Mt-APSR and consequently, a decrease in the catalytic efficiency of the mutant protein by almost 63,000-fold as compared to wild type Mt-APSR.¹⁸

Compared to wild-type chain-B, the calculated distances of (S-APS)⋯(S_γ-Cys140), (S-APS)⋯Fe1, and (S-APS)⋯Fe2 increase from 6.79, 8.20, and 10.84 Å, respectively in the wild type to 7.29, 8.57, and 11.15 Å, respectively in the K144A model. Therefore, without Lys144 bridging between APS and Cys140, repulsion causes APS and the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster to move away from each other.

6.4. Calculated [Fe₄S₄(S_γ-Cys)₄]³⁻ Clusters and the Reduction potentials of [Fe₄S₄(S_γ-Cys)₄]²⁻ + e⁻ → [Fe₄S₄(S_γ-Cys)₄]³⁻ in Different Models

If an electron is transferred to the resting state of the [4Fe-4S]²⁺ core in APSR, the core will change to [4Fe-4S]¹⁺, and the core plus the four Cys side chains will have a net charge of −3, [Fe₄S₄(S_γ-Cys)₄]³⁻. Since the [4Fe-4S]²⁺ core is likely to be in the {Fe1^↓Fe2^↓Fe3^↑Fe4^↑} spin state, the added electron then either goes to the pair {Fe1,Fe2} to form the {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} state, or goes to (Fe3,Fe4} to form the {Fe1^2.5+↓Fe2^2.5+↓Fe3^2+↑Fe4^2+↑} state. Our geometry optimizations show that these two states yield very similar broken-symmetry energies (less than 2 kcal mol⁻¹ difference) for all the cluster models. And for most of the models (only wild-type chain-A is an exception), the {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} state is slightly lower in energy than the corresponding {Fe1^2.5+↓Fe2^2.5+↓Fe3^2+↑Fe4^2+↑} state. Therefore, here we only present the geometries (Tables 6 and 7) and energies (Table 7) of the {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} state for all the cluster models.

Table 6.

Calculated Fe-Fe and Fe-ligand Bond Lengths (Å) and Fe Net Spin Populations (NSP) for the [Fe₄S₄(S_γ-Cys)₄]³⁻ Quantum Cluster in {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} State with Substrate and without Substrate Binding in Wild-type, No-tandem and K144A Models.

	Chain-A without APS			Chain-B with APS
	Wild-type	No-tandem	K144A	Wild-type	No-tandem	K144A
Fe1-Fe2	2.704	2.788	2.706	2.755	2.809	2.683
Fe1-Fe3	2.661	2.700	2.663	2.676	2.708	2.685
Fe1-Fe4	2.694	2.730	2.700	2.731	2.749	2.740
Fe2-Fe3	2.761	2.735	2.750	2.746	2.719	2.725
Fe2-Fe4	2.729	2.718	2.737	2.723	2.705	2.729
Fe3-Fe4	2.635	2.636	2.634	2.676	2.655	2.672
Fe1-S1	2.325	2.327	2.321	2.319	2.307	2.306
Fe1-S2	2.305	2.321	2.301	2.281	2.301	2.297
Fe1-S3	2.270	2.294	2.276	2.263	2.263	2.265
Fe2-S1	2.318	2.324	2.317	2.296	2.300	2.291
Fe2-S2	2.299	2.295	2.300	2.271	2.276	2.279
Fe2-S4	2.317	2.292	2.319	2.298	2.274	2.317
Fe3-S1	2.213	2.226	2.206	2.192	2.219	2.184
Fe3-S3	2.357	2.348	2.370	2.345	2.340	2.348
Fe3-S4	2.373	2.358	2.363	2.323	2.315	2.321
Fe4-S2	2.211	2.221	2.211	2.204	2.212	2.203
Fe4-S3	2.333	2.332	2.368	2.296	2.300	2.308
Fe4-S4	2.364	2.358	2.340	2.331	2.323	2.338
Fe1-Sγ-Cys140	2.296	2.336	2.296	2.329	2.387	2.313
Fe2-Sγ-Cys139	2.347	2.329	2.339	2.330	2.309	2.324
Fe3-Sγ-Cys228	2.349	2.350	2.351	2.329	2.337	2.318
Fe4-Sγ-Cys231	2.338	2.349	2.331	2.319	2.318	2.322
NSP(Fe1)	−2.93	−3.01	−2.92	−2.92	−2.99	−2.94
NSP(Fe2)	−3.00	−2.94	−3.01	−2.97	−2.92	−2.94
NSP(Fe3)	3.26	3.27	3.25	3.23	3.23	3.21
NSP(Fe4)	3.22	3.24	3.23	3.19	3.20	3.21

Table 7.

Averages (avg) of the Calculated Fe-Fe and Fe-ligand Bond Lengths (Å), Broken-Symmetry State Energies (E, eV), and Reduction Potentials of the [Fe₄S₄(S_γ-Cys)₄]²⁻/[Fe₄S₄(S_γ-Cys)₄]³⁻ (2−/3−) Quantum Clusters with Substrate and without Substrate Binding in Wild-type, No-tandem and K144A Models.

	Chain-A without APS
	Wild-type		No-tandem		K144A
	2−	3−	2−	3−	2−	3−
6(Fe-Fe)avg	2.690	2.697	2.711	2.718	2.704	2.698
4(Fe-S)avg a	2.228	2.253	2.229	2.258	2.223	2.253
8(Fe-S)avg b	2.318	2.334	2.326	2.333	2.329	2.335
4(Fe-Sγ)avg	2.285	2.333	2.299	2.341	2.289	2.329
E	−1193.735	−1196.724	−1185.564	−1188.659	−1135.356	−1138.287
E0	−1.35		−1.25		−1.41
	Chain-B with APS
	Wild-type		No-tandem		K144A
	2−	3−	2−	3−	2−	3−
6(Fe-Fe)avg	2.715	2.718	2.728	2.724	2.714	2.706
4(Fe-S)avg a	2.207	2.239	2.217	2.242	2.209	2.242
8(Fe-S)avg b	2.304	2.308	2.303	2.308	2.306	2.311
4(Fe-Sγ)avg	2.286	2.327	2.289	2.338	2.282	2.319
E	−1446.545	−1449.460	−1438.362	−1441.410	−1387.923	−1390.710
Eo	−1.43		−1.29		−1.55

^aThe average of the following four Fe-S distances: Fe1-S3, Fe2-S4, Fe3-S1, and Fe4-S2 (see Figure 5).

^bThe average of the following eight Fe-Fe distances: Fe1-S1, Fe1-S2, Fe2-S1, Fe2-S2, Fe3-S3, Fe3-S4, Fe4-S3, and Fe4-S4.

The formal net spin population of a high-spin Fe²⁺ ion is 4. Our calculated magnitudes of the net spins (2.92 ~ 3.01) of Fe1 and Fe2 in all the {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} state [Fe₄S₄(S_γ-Cys)₄]³⁻ clusters are about 1 e⁻ smaller than 4 (Table 6). The calculated net spin values for Fe3 and Fe4 in the [Fe₄S₄(S_γ-Cys)₄]³⁻ clusters (Table 6) are about 0.1 larger than the corresponding ones in the [Fe₄S₄(S_γ-Cys)₄]²⁻ clusters (Tables 2, 3, and 5). One measure of the metal-ligand covalency is the ratio of the calculated to the formal site spin population (spin population ratio), and lower percentages represent greater covalency. In wild-type chain-A, the spin population ratios of the four iron sites change from (69%, 71%, 70%, 69%) in the {Fe1^2.5+↓Fe2^2.5+↓Fe3^2.5+↑Fe4^2.5+↑} state [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster to (73%, 75%, 72%, 72%) in the {Fe1^2+↓Fe2^2+↓Fe3^2.5+↑Fe4^2.5+↑} state [Fe₄S₄(S_γ-Cys)₄]³⁻ cluster. Very similar percentage changes are also obtained for other model clusters. Therefore, with an additional electron, the [4Fe-4S]¹⁺ core of the [Fe₄S₄(S_γ-Cys)₄]³⁻ cluster in general has less covalency (larger spin population ratio) than the [4Fe-4S]²⁺ core of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster. As a result, upon 1e⁻ reduction, the [4Fe-4S] core expands. This is seen relatively easier by comparing the average (avg) Fe-Fe and Fe-S distances (Table 7). Especially for the wild-type chain-A model, where upon 1e⁻ reduction, the (Fe-Fe)_avg elongates from 2.690 Å to 2.697 Å, the average of the four Fe-S distances of Fe1-S3, Fe2-S4, Fe3-S1, and Fe4-S2 is increased from 2.228 Å to 2.253 Å, and the average distance of the eight Fe-S bonds on the ‘Fe1-S1-Fe2-S2’ and ‘Fe3-S3-Fe4-S4’ planes is also increased from 2.318 Å to 2.334 Å.

Based on the OLYP/COSMO calculated broken-symmetry state energies (E), we have calculated the reduction potentials (E⁰) of [Fe₄S₄(S_γ-Cys)₄]²⁻ + e⁻ → [Fe₄S₄(S_γ-Cys)₄]³⁻ for all the cluster models according to:

$$E^0=E\left\{{\left[{\text{Fe}}_4{\mathrm{S}}_4{({\mathrm{S}}_{\mathrm{\gamma }}-\text{Cys})}_4\right]}^{2-}\right\}-E\left\{{\left[{\text{Fe}}_4{\mathrm{S}}_4{({\mathrm{S}}_{\mathrm{\gamma }}-\text{Cys})}_4\right]}^{3-}\right\}+\mathrm{\Delta }\text{SHE}$$ (4)

where ΔSHE is the standard hydrogen electrode potential. Here we use ΔSHE = −4.34 V, obtained from Lewis et al’s calculations based solely on experimental data plus our electron energy threshold correction.^74–76 The calculated reduction potentials for all the model clusters are given in Table 7.

The measured 2−/3− reduction potentials of the [4Fe-4S] clusters in ferredoxins are from −0.28 to −0.45.^77–79 So far, reduction of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster in Pa-APSR has not been successful. In our recent EPR experiment, we could photo reduce the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster in Mt-APSR in the presence of deazaflavin/oxalate with at most 44% reduction efficiency.¹⁸ It is likely that the 2−/3− reduction potential of the [4Fe-4S] cluster in APSR is much more negative than ferredoxins, because of the tandem Cys pair and less H-bonding interactions around the [4Fe-4S] in APSR. There are 10 H-bonding interactions around the [4Fe-4S] active site in ferredoxins.¹⁹ These H-bonds are expected to stabilize the negative charges of the [Fe₄S₄(S_γ-Cys)₄]³⁻ cluster, making the 1e⁻ reduction easier. By contrast, there are only three H-bonding interactions with S or S_γ in the crystal structure of Pa-APSR (Figure 4).

It is still a big challenge to accurately predict the redox potentials for the Fe-S systems. The redox potentials obtained from quantum mechanical calculations within a solvation model vary with the dielectric constant of the solvent and the probe radius for the contact surface between the quantum cluster and solvent.^19,41 In general, the larger the dielectric constant and the smaller the radius, the reduced state is more stabilized, and the reduction potential is more positive (or less negative).^19,41 Our previous calculations also show that the DFT/solvation calculations systematically predict the redox potentials of the Fe-S systems by 0 ~ 0.5 V more negative than the measured values.^19,41 Our current predicted reduction potentials for the [4Fe-4S] cluster models in Pa-APSR are also very negative, ranging from −1.25 to −1.55 V. Since the experimental reduction potential of Pa-APSR is not available, we do not have a clear picture if or how much our calculations overestimate (more negative) these reduction potentials. Therefore we will focus on the relative values of the predicted E⁰’s to see how the APS binding, the breaking of the Cys tandem pair, and the K144A mutation will change the reduction potential of Pa-APSR.

From wild-type chain-A to wild-type chain-B, E⁰ is more negative by 0.08 V (from −1.35 V to −1.43 V). With APS²⁻ nearby, the negatively charged [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster is then even more difficult to accept an electron from outside, and therefore is more difficult to be reduced.

From wild-type to no-tandem model, E⁰ becomes more positive by 0.1 V and 0.14 V in chain-A and chain-B, respectively. Therefore, the no-tandem cluster of [Fe₄S₄(S_γ-Cys)₄]²⁻ is easier to be reduced than the wild-type. This is consistent with our conclusion in Section 6.2 that the function of the unique tandem pair Cys139/Cys140 in Pa-APSR is to keep the [4Fe-4S] cluster more compact and protect the cluster from reduction.

In chain-A, the calculated E⁰ of K144A is more negative than the wild-type by 0.06 V. In chain-B with APS, the K144A model yields the most negative E⁰ (−1.55 V) among all the model clusters. Upon the Lys144 → Ala144 mutation, there is no more negative charge transfer from the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster to Lys144, the cluster is therefore more difficult to be reduced, and the reduction becomes even more difficult when APS²⁻ is present, as proposed in Section 6.3.

7. Conclusion

In order to understand the role of [4Fe-4S] cluster in APS reduction, we have examined the coordination and geometry of the native and APS-bound forms of the enzyme by XAS. Results from the XANES and EXAFS analysis were valuable in indicating that there is no change in coordination and overall geometry of the [4Fe-4S] cluster between both forms of the enzyme. However, in terms of resolving subtle changes in the geometry and electrostatics DFT calculations were employed. Taken together, the EXAFS and DFT analyses provide a complete picture of the coordination, geometry and electrostatic environment of the [4Fe-4S] cluster in APSR. This is the first report of the application of both of these techniques to APSR and thereby contributes to the characterization of the cluster in APSR with a view to gaining insight into the function of the cluster in APS reduction.

Fe K-edge EXAFS analysis confirms the presence of the [4Fe-4S] cluster and a comparison of samples of Mt-APSR in the native and substrate-bound forms suggests that the core of the cluster is essentially unaffected during catalysis. This is supported by biochemical evidence, which shows that the cluster in APSR has no redox activity during the catalytic cycle⁴ and hence we do not expect any change in the oxidation state of the cluster in Mt-APSR with and without APS.

DFT geometry optimizations have been performed on the [4Fe-4S] clusters of the wild-type, no-tandem, and K144A models constructed starting from the Pa-APSR X-ray crystal structures.¹³ Both substrate-free and substrate-binding forms for each type of the models were studied. Calculations show that substrate binding influences the geometric and electronic structures of the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster, in agreement with the resonance Raman and EPR spectra experiments.^11,18 However, the geometric changes of the [4Fe-4S] core are not large enough to be observed in EXAFS and Mössbauer experiments.

Calculations with the ‘no-tandem’ models show that the coordinating tandem Cys139-Cys140 pair in Pa-APSR keeps the [4Fe-4S] cluster more compact and prevents it from reduction. The tandem pair also leads to a strain in the geometry of the cysteine side chains. Conformations of the cysteinyl ligands of an iron-sulfur cluster can result in differences in redox energies of ~100 mV that can directly influence the redox properties of the cluster.⁸⁰

Additionally, the replacement of Lys144⁺ by Ala in our calculations has a two-fold effect: (1) Loss of the bridging charged H-bonding interactions of Lys144 with S_γ-Cys140 and the terminal sulfate moiety of APS destabilizes the Fe-S cluster as the overall charge of the cluster becomes more negative. The calculated reduction potentials of the clusters in K144A models are by 0.06 ~ 0.12 V more negative than the wild-type clusters. In fact, the lability of the cluster and difficulty in reduction have been observed in EPR experiments in which reduction of the cluster in the K144A mutant resulted in a 6-fold decrease of signal intensity and the appearance of an additional signal corresponding to free Fe³⁺ formed due to cluster degradation, compared to wild type APSR.¹⁸ (2) Loss of the bridging Lys144 cation increases the repulsion between the negatively charged APS²⁻ and the [Fe₄S₄(S_γ-Cys)₄]²⁻ cluster. This explains why the Lys144Ala mutation is detrimental to APS-binding and catalysis.¹⁸

The importance of Lys144 in stabilizing the sulfate moiety of APS is analogous to the role of a conserved Lys residue in sulfotransferases which acts as a catalytic acid, stabilizing the transition state of the substrate, phosphoadenosine phosphosulfate (PAPS), by interacting with the SO₃ moiety that is being transferred.⁸¹ Conversely, we could glean a role for the [4Fe-4S] cluster in positioning Lys144 in the active site such that it can interact favorably with the incoming substrate. In addition to Lys144, other conserved positively charged residues such as Arg242 and Arg245, and Arg171 (present in a flexible ‘Arg-loop’) also play crucial roles in substrate binding.⁹ Lysines and arginines are cations with long, flexible and mobile side chains. They often function as “molecular guidewires” as found in other sulfate and phosphate transfer enzymes.^82–87 The cationic side chains electrostatically screen the bound anions during group transfer, facilitating covalent bond formation.

It should also be noted that the current Pa-APSR crystal structure is missing the disordered C-terminal segment of residues 250–267, which carry the catalytically essential Cys256.¹³ When the missing segment was modeled into the active site of Pa-APSR using the structure of S. cerevisiae APSR, it was observed that Cys256 is proximal to the sulfate moiety of APS, and the side chains of Cys140 and Lys144.¹⁸ Thus with the addition of the negatively charged, nucleophilic thiolate in the transition state, the optimum positioning of Lys144 and other cationic side chains to make key H-bonding interactions with APS, is required to maintain an energetically favorable charge balance within the active site.

In summary, our study characterizes the [4Fe-4S] cluster in APSR by EXAFS spectroscopy and by findings from our DFT calculations which substantiate (1) modulation of the redox potential of the cluster brought about by the constrained tandem cysteine coordination, (2) the role of Lys144 as a critical link between the [4Fe-4S] cluster and APS, and finally, (3) a role for the Fe-S cluster in contributing to stabilization of the transition state via positioning of Lys144 and maintaining charge balance in the active site during catalysis. In order to gain further insights into the mechanism of APS reduction, efforts to determine the structure of APSR with the intact C-terminal segment are currently underway.