Electrostatic Selectivity in Protein–nanoparticle Interactions

Abstract

The binding of bovine serum albumin (BSA) and β-lactoglobulin (BLG) to TTMA (a cationic gold nanoparticle coupled to 3, 6, 9, 12-Tetraoxatricosan-1-Aminium, 23-mercapto-N, N, N-TriMethyl)- was studied by high-resolution turbidimetry (to observe a critical pH for binding), dynamic light scattering (to monitor particle growth), and isothermal titration calorimetry (to measure binding energetics), all as a function of pH and ionic strength. Distinctively higher affinities observed for BLG vs. BSA, despite the lower pI of the latter, were explained in terms of their different charge anisotropies, namely the negative charge patch of BLG. To confirm this effect, we studied two isoforms of BLG that differ in only two amino acids. Significantly stronger binding to BLGA could be attributed to the presence of the additional aspartates in that negative charge domain for dimer, best portrayed in DelPhi. This selectivity decreases with ionic strength, for which both isoforms bind well below pI, but increases with ionic strength for BLG vs. BSA which binds above pI. This result points to the diminished role of long-range repulsions for binding above pI. Dynamic light scattering reveals a tendency for higher-order aggregation for TTMA–BSA at pH above the pI of BSA, due to its ability to bridge nanoparticles, whereas soluble BLG–TTMA complexes were stable over a range of pH because the charge anisotropy of this protein at pH < pI makes it unable to bridge nanoparticles. Finally, isothermal titration calorimetry shows endoenthalpic binding for all proteins; the higher affinity of TTMA for BLGA vs. BLGB comes from a difference in the dominant entropy term.

Introduction

The association of proteins with macroions has been the foundation for many applications of these complexes in food science, biosensors, drug delivery and tissue engineering.^1,2 In this paper, we consider two types of macroions, linear polyelectrolytes and highly charged nanoparticles, both of which complex with proteins primarily via electrostatics. In principle these interactions can be stronger and more versatile with nanoparticles due to their higher charge densities and increased specificity arising from facile synthetic modifications. Nevertheless, the body of literature for protein–polyelectrolyte complexes,^1,3–5 both applied^6,7 and fundamental,^8–15 is much more extensive.

Evidence for the electrostatic nature of protein–polyelectrolyte interactions comes from the observed influences of polyelectrolyte linear charge density ξ (usually controlled by synthesis), solution pH (which controls the protein net charge Z), and ionic strength I (which screens the interaction). If any two of these three variables are fixed, variation in the third can produce a transition, leading to soluble complex formation or phase separation. “pH_c” or “pH_ϕ” (at fixed I and ξ) are used to designate, respectively, the transition from non-interacting solution to soluble complex, or from soluble complex to phase separation.^11,13,16 While pH_ϕ is subject to the effects of polymer molecular weight and macromolecular concentrations, pH_c, as a local phenomenon, does not depend on these variables,¹⁷ but is sensitive to polyelectrolyte chain stiffness¹⁶ and hydrophobic constituents.¹² Short-range attraction based on hydrophobic interactions are evident when the hydrophobic group on the polyelectrolyte can access a hydrophobic domain on the protein.¹⁸ On the other hand, short-range electrostatic attraction is not limited in this way. However, when Z, the net protein charge, is of the same sign as ξ, any attractive force must be balanced by long-range protein–polyelectrolyte repulsion, resulting in a maximum in polyelectrolyte–protein affinity with ionic strength, i.e. short-range attraction/long-range repulsion.¹³ This polyelectrolyte-binding “on the wrong side” of the isoelectric point,^11,15,19 is an indication of protein “charge patch”.^3,10,13,20 Surface charge anisotropy is very protein specific as observed long ago by Tanford,²¹ who found that BSA binds to Cl⁻ but not K⁺, while BLG binds to K⁺ not Cl⁻, consequences of a positive local electrostatic potential for BSA, and a negative site for BLG.¹³ The same reverse anisotropies for these two proteins can be seen in their interactions with a polycation, which binds BLG more strongly than BSA.²² Thus, to understand the interaction of proteins with either polyelectrolytes or charged nanoparticles, quantitative visualization of the “charge patch” is essential.

DelPhi (Molecular Simulations, San Diego, CA) is a powerful tool to visualize the charge patches around proteins readily revealing the above-mentioned reverse anisotropies¹³ of BLG and BSA. DelPhi solves the Poisson-Boltzmann equation leading to values for the electrostatic potential ψ everywhere in space around a protein. Contour maps (equipotential surfaces) at properly chosen values of ψ effectively represent the protein “as seen by” the polyelectrolyte, allowing for semi-quantitative comparison with experiment. As an example, Grymonpré⁸ et al. modeled the binding of hyaluronic acid (HA) to BSA at pH_c for different ionic strengths. It was possible to identify a single ψ = 2.3 mV HA binding domain on BSA capable of binding a segment of HA with a net charge of 10, corresponding to an interaction energy of 10 × 0.1 kT/e, consistent with the expectation of a binding energy close to thermal energy at the onset of binding. Other protein phenomena explained semi-quantitatively by DelPhi included the size of the heparin binding site on BSA,⁸ the local maximum in binding affinity in the ionic strength range 10–50 mM for a number of protein–polyelectrolyte pairs,¹³ the effects of pH and ionic strength on the rate of aggregation of BLG,²³ the difference in the polycation binding affinity of the two isoforms of BLG^22,24 and the pH-dependence of the uptake of BLG and BSA on an absorbed polycation surface.²⁵ Quantitative aspects of visualization in DelPhi enhance its ability to explain and predict protein electrostatic interactions.

Surface-charged nanoparticles can, like polyelectrolytes, also bind to proteins via electrostatic interactions. Gold-based nanoparticles contain a solid core which contributes little to interaction with proteins, while covalently coupled ligands yield surface groups with apparent competence for electrostatic, hydrophobic or hydrogen bonding. For the first, nanoparticle charge density is easily manipulated by the degree of coupling. Such nanoparticles have been studied in the context of applications for biosensors,²⁶ diagnostics,²⁷ bionanomaterials,²⁸ etc. An important objective in these studies has been selective binding of proteins. The lock-and-key model of short-range complementarity has been assumed, following the established paradigm of specificity as the source of such selectivity. However, electrostatic interactions, unlike hydrophobic and hydrogen bonding interactions, are essentially unlimited with respect to distance (here we refer to screened Coulomb forces as opposed to salt-bridges – the pairing of uncompensated charges within low-dielectric and largely anhydrous protein domains) and in that regard, long-range. It is therefore assumed that screened Coulomb forces while contributing to interaction energy cannot of themselves provide selectivity, so that nanoparticle surfaces must proffer functional groups susceptible to short-range interactions in order to bind proteins differentially.

A number of attempts have been made to systematically address the separate contributions of electrostatic and hydrophobic effects. Dubin and Gao¹⁸ studied electrostatically-dominated (pH-induced) interaction between a polyacid and two proteins (BSA and BLG), while varying the length of an alkyl group on each repeat unit. They found that at least 3–4 methylenes for alkyl chain length are required to obtain significant hydrophobic interactions. Seyrek et al¹³ measured the ionic strength dependence for the binding of BSA to hydrophobically modified polyacids. They found that the non-monotonic ionic strength dependence mentioned above was completely preserved, regardless of polymer hydrophobicity, but that binding was strongly elevated by the alkyl group length. This amplification by the hydrophobic contribution indeed magnified the electrostatic effect, meaning in this case that the hydrophobic interaction actually increased the electrostatically-driven sensitivity to protein charge anisotropy. Similar phenomena were observed by Rotello and coworkers^29,30 who enhanced the selectivity of an anionic nanoparticle for Cytochrome C vs. Cytochrome C peroxidase, by the addition of a hydrophobic phenyl ring to the nanoparticle.

While it is useful to study the effects of systematic changes in nanoparticle or polyelectrolyte structure on selective protein binding, the great variations among proteins can make it difficult to verify the mechanism of that selectivity. Systematic variations in protein structure can address this problem, and even identify the site of the interaction controlling selectivity. In this work, we first compare the binding of a cationic nanoparticle “TTMA” to two proteins, BLG and BSA, with similar pI (5.2 and 4.9, respectively) but different charge anisotropies i.e. “charge patch” of opposite sign. To confirm that the greater affinity of TTMA for BLG arises from its negative domain, we turn to alleles of BLG which differ with respect to only two amino acids, namely Val118 (BLGA)→ Ala (BLGB) and Asp64 (BLGA)→Gly (BLGB). The latter corresponds to the BLG negative domain.³¹ This leads, in the BLGA dimer -- the stable form at near physiological conditions -- to an additional two nearby negative charges in that “charge patch”. This results in a slightly lower pI for BLGA compared to BLGB (reported values are 5.1and 5.2, respectively).³² The presence of Asp64 as will be shown is significant even at pH well below the pI. We test the hypothesis that the difference in affinity for these two variants is due to electrostatics and involves a protein “charge patch” by (1) comparing the selective binding of the nanoparticle to that of a polycation (PDADMAC) of lower charge density, (2) examining the effect of ionic strength.

Experimental section

1. Materials

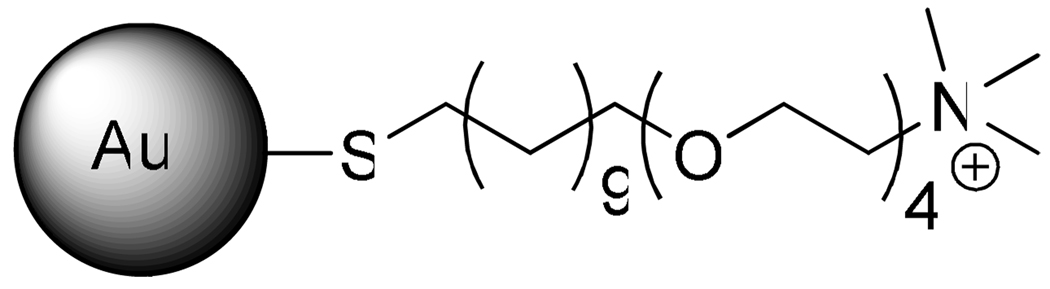
The PDADMAC described here (gift from W. Jaeger, Fraunhoffer Inst., Golm) was prepared from diallydimethylammonium chloride by free radical polymerization and characterized after dialysis and lyophilization by membrane osmometry (M_n = 141 kDa) and light scattering (M_w = 219 kDa).³³ Fatty acid-free bovine serum albumin fraction V (BSA, M_w = 68.0 kDa, pI = 4.9) was Calbiochem lot B31232. Bovine β-lactoglobulin (BLG, M_w = 18.3 kDa, pI = 5.2) was a gift from C. Schmitt (Nestle, Lausanne, JE 001-1-922). BLG variants (BLGA, BLGB) were Sigma-Aldrich Company lots 097K7010 and 048K7003, respectively (note that “BLG” without the “A” or “B” designation always refers to “native BLG” with a ratio of the two isoforms typically found in bovine milk, the standard source for all commercial and research grade β-lactoglobulin). TTMA nanoparticle was prepared based on published process.²⁶ TTMA is abbreviation of the end group of ligand attached to gold nanoparticle, means Tetra-ethylene glycol-Tri-Methyl-Amine. The bare gold core size is 2 nm and the overall size is ~10 nm with cationic ligand outside. The number of ligands attached to gold core is around 100. The chemical structure of the ligand is shown in Figure 1. Molecular weight of TTMA is ~100 kDa. NaCl, standard NaOH, and HCl solutions were purchased from Fisher Scientific. Milli-Q water was used through the experiments.

Figure 1.

Chemical structure of the ligand on cationic gold nanoparticle TTMA.

2. Turbidimetric Titration

Turbidimetric titrations were carried out for solutions containing protein and nanoparticle in order to determine the point of complex formation (pH_c). The methodology for observing and the rationale for identifying pH_c as the point of incipient complexation has been described for a number of protein–polyelectrolyte pairs in which the latter component was anionic³⁴ or cationic,^19,35 and synthetic¹² or natural.⁸ pH_c has been similarly identified for systems involving pH-dependent micelles,³⁶ pH-dependent polymers¹⁰ and pH-dependent dendrimers.⁷ In the present case, the measurement of transmittance is complicated by the absorbance of the nanoparticle at 420 nm, the wavelength chosen for evaluation of the turbidity. The extinction coefficient of gold nanoparticles was found to be independent of pH.³⁷ A constant value of %T = 40 was subtracted from all measurements as a blank correction, and the blank corrected values are shown for all titrations involving nanoparticles. Temperature was controlled at 23~25°C within which no temperature effect could be seen.

Protein (BSA, BLG, BLGA, and BLGB) solutions (1.2 µM for BSA, and 3.2 µM for BLG, BLGA, and BLGB) were prepared in 5 mM phosphate buffer at pH ~2.5, and then filtered (0.20 µm Millipore). In order to get stoichiometries both for BSA and BLG, the concentration of BLG was slightly larger than for BSA. TTMA nanoparticle stock solutions with concentration of 40 µM were diluted to 0.4 µM by adding 5 mM phosphate buffer with pH 5.5. The concentration of proteins and nanoparticles were obtained by UV extinction coefficients of 4.69 × 10⁴ M⁻¹ cm⁻¹ and 1.76 × 10⁴ M⁻¹ cm⁻¹ for BSA³⁸ and BLG³⁹ (A or B) at 280 nm, and 4.92 × 10⁵ M⁻¹ cm⁻¹ for TTMA at 506 nm.³⁷ The final solution was prepared by mixing 5 mL of protein and 5 mL of nanoparticle solutions. Final ionic strength (55 mM, 80 mM, and 105 mM) was adjusted with NaCl. High-resolution pH-turbidimetric titration⁴⁰ was carried out with a Corning 240 pH meter, and a Brinkmann PC 800 colorimeter equipped with a 10 mm path length fiber optics probe and a 420 nm filter. Equilibrium of colorimeter for 90 min was sufficient to reduce instrument drift to less than 0.15 transmittance unit/h. Precise increments of 0.1 N or 1N NaOH were added to the 10 mL sample corresponding to increments of about 0.1 pH unit with stirring speed of nominal 1000 rpm. Each value of transmittance and pH, recorded every minute, represents the average of 5 readings. The instrument error is less than ± 0.1 transmittance unit and ± 0.01 in pH.

3. Dynamic Light Scattering

Dynamic light scattering (DLS) was carried out at 25°C with a Malvern Zetasizer Nano ZS instrument, measurement duration was 60 seconds per measurement. The measurement angle was 173° (backscatter). For data processing, the analysis model was “multiple narrow modes (high resolution)”, which is based on Non-Negative-constrained Least Squares (NNLS). The other Malvern mode for DLS data analysis “general purpose (normal resolution)” based on CONTIN was not applied here. Volume particle size distribution (PSD) was chosen for plotting, in order to avoid a dominant effect of large aggregates. 0.4 mL samples at desired pH values were taken from turbidimetric titration and allowed to equilibrate for 10 min. Average and standard deviations for apparent sizes from 5 duplicates were given as final data.

4. Isothermal Titration Calorimetry

Isothermal titration calorimetry (ITC) was carried out with a Microcal VP-ITC calorimeter. BLGA (or BLGB) solutions were prepared at 20 µM in 5 mM phosphate buffer as described above and stirred and degassed, to avoid bubbles, for 10 min at 0.5°C lower than the reaction temperature of 25°C.

The reference cell was filled with 5 mM phosphate buffer. In order to obtain high signal to noise ratio, TTMA solutions (8 µM) were titrated into BLGA/B solution (20 µM) in the sample cell. By automatic addition of 5 µL increments of titrant with an interval time 300 s, continued for 55 injections. Acquisition time between two data points was set to 2 s. For BLGA/B and TTMA blank titrations, 5 mM phosphate buffer was titrated to sample cell with BLGA/B solution, or TTMA titrants were titrated into 5 mM phosphate buffer in the sample cell. ITC data were fitted by Origin 7.0 program (Microcal, Northampton, MA, USA). As will be discussed below, analysis of the raw data is not trivial when the definition of “ligand” and “substrate” is complicated by similarities in size of the two reactants.

5. DelPhi Modeling

Computer modeling allows visualization of the electrostatic potential around the protein as a function of pH and ionic strength. In DelPhi V98.0 (Molecular Simulations Inc.), the electrostatic potential around the protein is calculated by nonlinear solution of the Poisson–Boltzmann equation.⁴³ HSA with identification 1N5U.pdb and BLG 1BEB.pdb were downloaded from RCSB Protein Data Bank (http://www.rscb.org). However, the deposited structure 1BEB.pdb had A variant Val at position 118, and B variant Gly at 64, which in fact corresponds neither to BLGA (Asp64, Val118) nor to BLGB (Gly64, Ala118). In order to rectify this incorrect amino acid sequence, the charge file used for the electrostatic calculations was modified by replacing Gly64 with Asp64 to mimic a BLGA dimer. The amino acid charges were determined using the spherical-smeared-charged model put forward by Tanford⁴¹ utilizing the protein titration curve of BLG²¹ as explained in detail elsewhere.¹⁰ Further details of the modeling parameters can be found in refs 8, 13, 23 and 25.

Results and Discussion

1. BSA vs. BLG for TTMA and PDADMAC

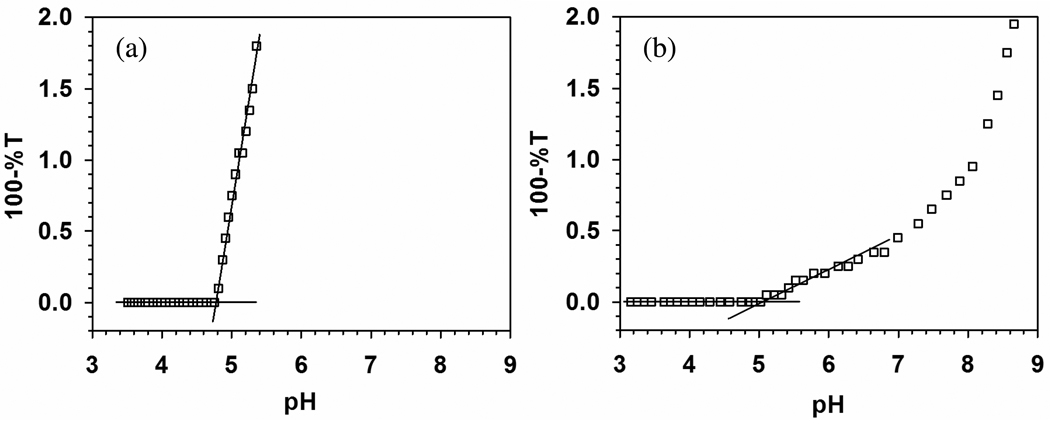
Polyelectrolyte–protein (PE–protein) systems exhibit a well-defined pH-induced transition from non-interacting solution to soluble complexes, known as pH_c which depends only on ionic strength. High-resolution turbidimetry allows this point of incipient complexation to be operationally identified as a transition to a non-zero slope from a “baseline” region of negligibly small d(100-%T)/d(pH). In applying this method to both the nanoparticle–protein (NP–protein) and the PE–protein systems (Figure 2a), we assume it signifies a similar transition, and conclude that the difference in pH_c for PDADMAC–BSA vs. NP–BSA, ΔpH_c = 0.30 ± 0.11 (5.1 ± 0.10 – 4.8 ± 0.01), indicates somewhat stronger binding for TTMA, in spite of the fact that both are very near the pI of BSA although the absence of binding at pH<4.9 (“on the wrong side of pI”) removes the need to define a unique polycation-binding domain on BSA (negative “charge patch”), the charge anisotropy of BSA still leads to a discontinuity in the ionic strength dependence of pH_c at pH near 5.2,¹³ telling us that binding takes place at negative domain(s) compared to the near-neutral global charge of the protein. The presence of both negative and positive domains leads to a combination of short-range attraction and long-range repulsion.¹³ Comparison of the relative contributions of these two forces for TTMA vs. PDADMAC is complicated by differences in geometry (surface vs. linear charge, respectively) but leads, as will be shown, to different influences of ionic strength on protein affinity. Features of the PDADMAC–BSA system at 5 < pH < 8 have been described in terms of the formation of a soluble intra-polymer complex, thence a soluble aggregate, and finally phase separation.¹⁹ The marked difference between this and Figure 2a points to a different process, to be described below.

Figure 2.

(a) Turbidimetric titration of BSA–TTMA (expanded scale): [BSA] = 0.6 µM (0.04 g/L), [TTMA] = 0.2 µM (0.02 g/L), in 5 mM phosphate buffer. pH_c = 4.80 ± 0.01. (b) Turbidimetric titration of BSA–PDADMAC. [BSA] = 0.6 g/L, [PDADMAC] = 0.12 g/L, 5 mM NaCl, pH_c = 5.1 ± 0.1. Published with permission from Ref. 22. Copyright 2011 American Chemical Society. Standard deviations were smaller than the symbols here and in Figures 3, 5, 10 and 14.

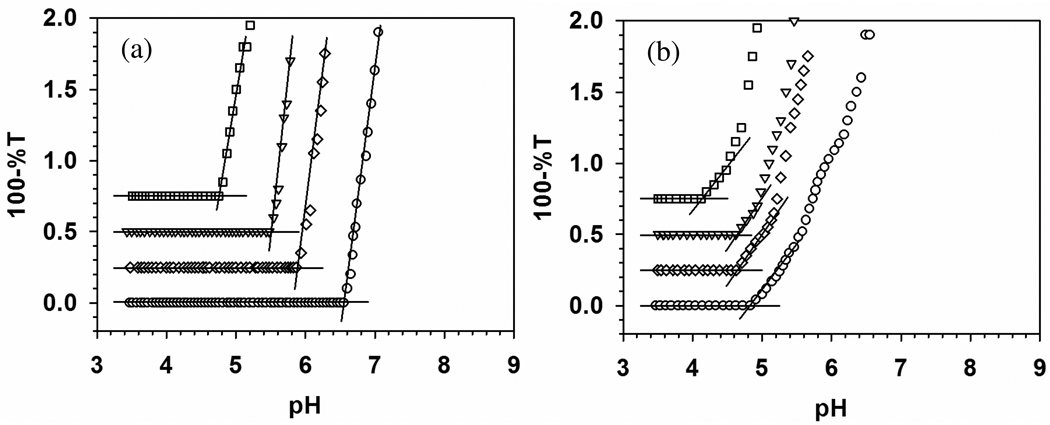
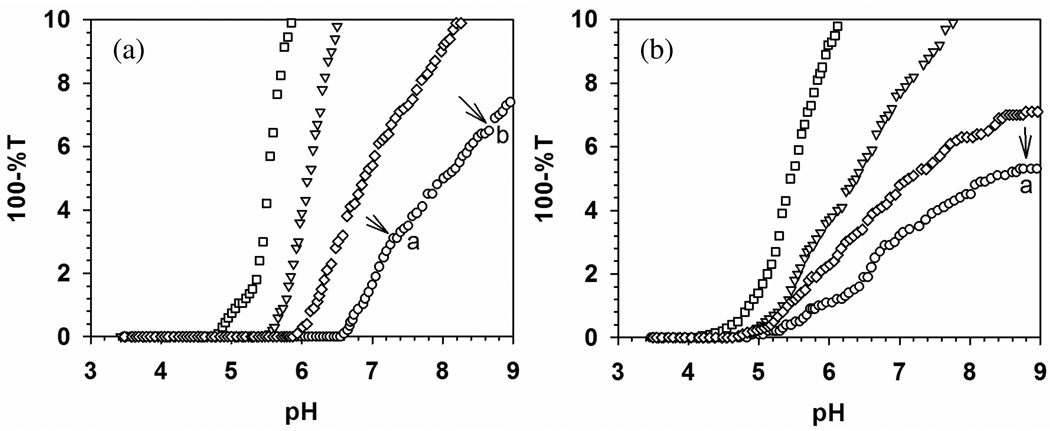
Turbidimetric titrations for TTMA with (a) BSA and (b) BLG, at ionic strengths from 5 to 105 mM, are shown in Figure 3 with expanded scale. BLG shows a stronger binding to TTMA at all ionic strengths and less ionic strength dependence than BSA (stronger binding of BLG corresponding to lower pH_c can be visualized its earlier binding when a mixture of both proteins with TTMA is titrated with base). Precise definition of pH_c is facilitated by remarkably high signal to noise ratio for both BSA and BLG data, and the resultant pH_c values are plotted as a function of I in Figure 4. In contrast to BSA, BLG does exhibit “binding on the wrong side of pI”. Such effects have been ascribed to “charge regulation”, essentially shifts in protein pK’s induced by the electrical field of the polymer.^42,43 pH titrations of BSA in the presence and absence of PDADMAC showed that such effects were limited to pH > 6 and low ionic strength,⁴⁴ but the high charge density of TTMA could have a substantially more pronounced effect of this type on the relevant Asp units of BLG.

Figure 3.

Turbidimetric titrations of (a) BSA–TTMA and (b) BLG–TTMA at different ionic strength. [BSA] = 0.6 µM, [BLG] = 1.6 µM, [TTMA] = 0.2 µM. Key: (□) 5 mM, (▽) 55 mM, (◇) 80 mM, (○) 105 mM. Both of the Y axes were expanded to make pH_c clear.

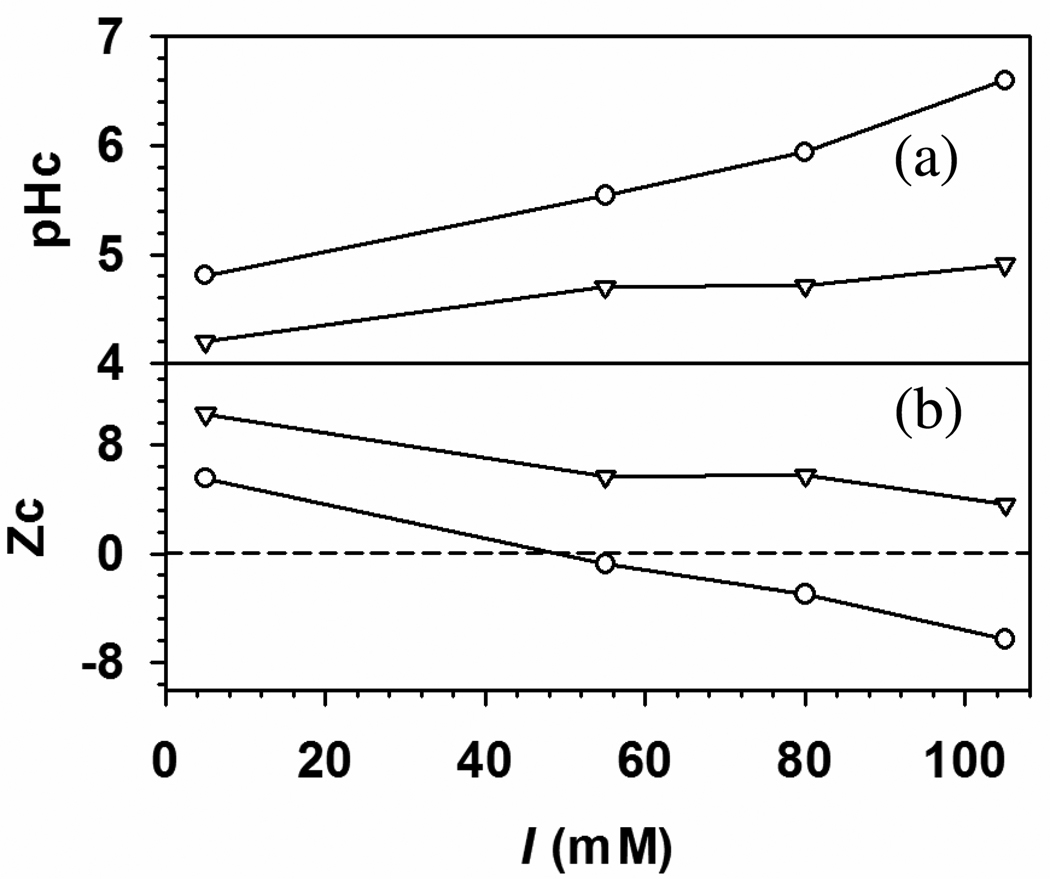
Figure 4.

pH_c (a) and critical net protein charge, Z_c (b) versus I for (○) BSA–TTMA and (▽) BLG–TTMA complex. Z_c of BSA⁴⁵ and BLG²¹ at different ionic strength were obtained by pH titration. At low I (5mM), TTMA binds to both BSA and BLG with positive net charge.

While “charge regulation” is not particularly falsifiable, the difference in the curves for BSA and BLG is best attributed to their different charge anisotropies. The binding of both BSA and BLG to TTMA at pH < pI can be explained by “charge patch” on these two proteins,¹¹ Figure 4a also shows that the addition of base to a low-pH mixture of BSA and BLG at any ionic strength would lead first to binding of the latter, i.e. stronger binding of BLG. Another consequence of this stronger binding, seen in Figure 4b, is that binding “on the wrong side of pI” persists at all I’s for BLG, because its negative domain retains its unity at pH < pI, whereas that of BSA becomes fragmented (see Figure 7 below). The effect of I is also different: the curves of Figure 4b for the two proteins diverge at high I because the slope d|Z_c|/dI is larger for BSA. Thus, for BSA, weakening the interaction by an increase in I from 5 mM to 105 mM requires compensation by an additional −12 charges, but only an additional −7 charges for BLG. The greater influence of negative charges for BLG signifies the concentration of those charges at the TTMA-binding site, clearly visible in the DelPhi images to be presented below. In contrast, as noted above, negative domains in BSA are more dispersed. A similar argument was made for the opposite case of polyanion binding by BSA, to explain the higher effectiveness of positive charges in the high pH range.¹⁶

Figure 7.

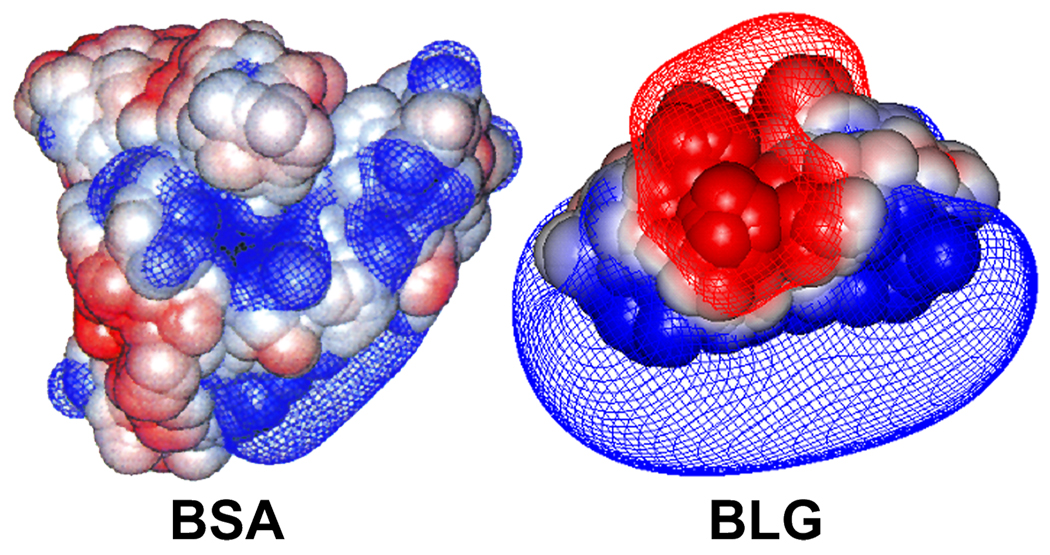
Potential surfaces (−0.5 kT/e (red) and +0.5 kT/e (blue)) around BSA and BLG at pH 5.6 for BSA and 5.0 for BLG, both of I = 5 mM. This visualization more realistically reflects the significances of electrostatic interactions at distances exceeding that of several water molecules.

As pH progresses beyond pH_c (Figure 5), the increase in turbidity indicates an increase in the size of scattering species and/or their number. The region between pH_c and pH_ϕ (5.0–8.0 in Figure 2b) for BSA–PADAMAC corresponds to sequential formation of soluble complexes and their aggregates, followed by liquid-liquid phase separation (coacervation), an effect related to charge neutralization of polycation by globally negative protein. This may be the case also for BSA–TTMA, for which Figure 5a shows steeper curves in the region 4.5 < pH < 6.5 (seen most dramatically in the transition from the zero slope region in Figure 2a), followed by the appearance of visible turbidity at pH > 7.5. In contrast, BLG binds to TTMA at pH < pI, so that repulsion among positively charged complexes hinders further aggregation and the solutions retain optical clarity up to pH 8.8, beyond which macroscopic particles begin to appear. The clarity of the BLG solution is consistent with the low rates of aggregation under these conditions seen by Majhi et al.²³ Finally, for BSA, there is a large effect of salt on pH_c (Figure 5a), compared to little effect of salt on pH_c for BLG (Figure 5b). In contrast, salt has a larger effect on turbidity in the aggregation region for BLG.

Figure 5.

Turbidimetric titrations of (a) BSA–TTMA and (b) BLG–TTMA at different ionic strength. [BSA] = 0.6 µM, [BLG] = 1.6 µM, [TTMA] = 0.2 µM. Key: (□) 5 mM, (▽) 55 mM, (◇) 80 mM, (○) 105 mM. Point “a” indicates the onset of turbidity and “b” indicates observation of macroscopic particles.

In order to examine the process of aggregation more closely, DLS was carried out as a function of pH for TTMA–BSA and TTMA–BLG at I = 105 mM, this ionic strength was chosen because it corresponded to the largest difference in NP–protein affinity for the two proteins, as judged by ΔpH_c.

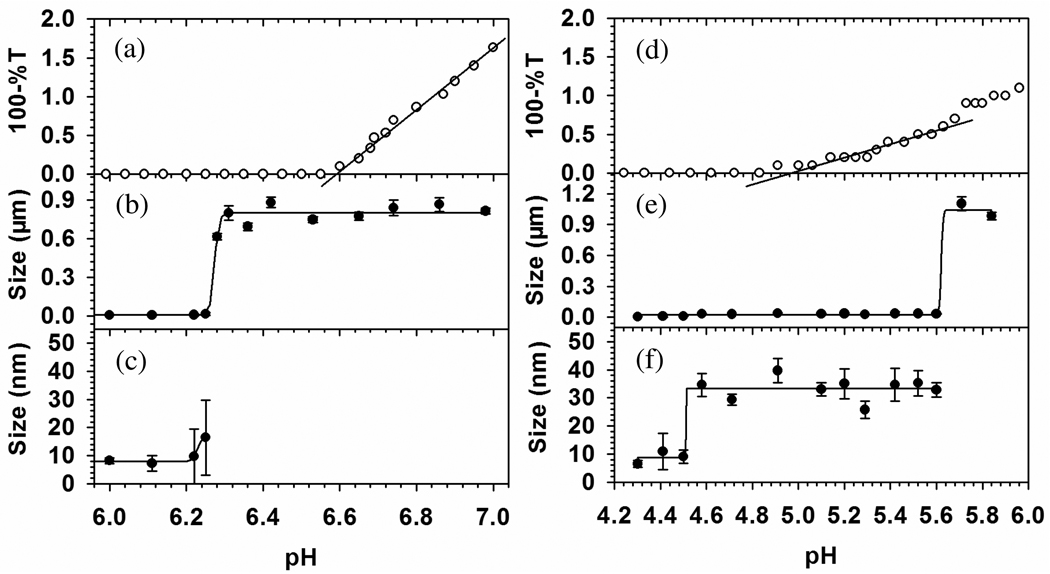
The results in Figure 6b for BSA–TTMA show a dramatic increase in particle diameter, d, from 10 to 800 nm at pH 6.25 ± 0.03. The virtual absence of particles of intermediate size indicates the absence of conventional soluble complexes. In contrast, results for BLG–TTMA (Figure 6f) clearly show stable soluble complexes, d = 33 ± 4 nm, over a range of an entire pH unit, with micron-size particles appearing only at pH > 5.6, and BLG self-aggregation is suppressed by TTMA near pH 5.2. The relationship between the turbidimetric pH_c and the transition seen by DLS is also very different for BSA–TTMA vs. BLG–TTMA. This is seen from the difference between Figure 6a and 6b, compared to the difference between Figure 6d and 6e. For BSA–TTMA, particles appear at pH = 6.25 (0.3 unit below the turbidimetric pH_c); for BLG–TTMA, soluble complexes form at pH = 4.50 (0.7 pH unit below the turbidimetric pH_c). DLS results indicate binding of BLG and BSA at pH 4.5 and 6.3, respectively, and this much higher affinity for BLG is qualitatively confirmed by its low critical pH (pH_c) corresponding to the initial binding between protein and TTMA. The onset of complexation is detected differently by DLS and turbidity because the DLS signal is a complex result of the refractive index increment of the large particles, and interference effects which may diminish the signal for particles with much above λ/20 in the backscatter optical design of the Malvern. Nevertheless, the difference between turbidimetry and DLS indicates the need for more attention to what happens at “pH_c”, i.e. to consider the nature of the product formed as a result of binding. The interaction of TTMA with BLG, which begins at pH 4.5, well below the pI of 5.2, leads to stable 33 nm (diameter) complexes that persist up to pH 5.6, before the formation of micro-size particles; the interaction with BSA, which begins at pH 6.2, well above the pI of 4.9, immediately leads to large particles. The preferential binding of BLG at pH < pI must be related to its negative “charge patch”, absent for BSA -- as described elsewhere^22,23 -- and as seen in Figure 7.

Figure 6.

Turbidimetric titration (a) for BSA–TTMA and (d) for BLG–TTMA, and DLS (b, c) for BSA–TTMA and (e, f) for BLG–TTMA both with I = 105 mM at selected pH near pH_c. 10 ml mixed solution containing 0.6 µM BSA or 1.6 µM BLG and 0.2 µM TTMA was titrated with 0.1 N NaOH to increase pH. Average and standard deviation of apparent diameter were given here from 5 duplicates.

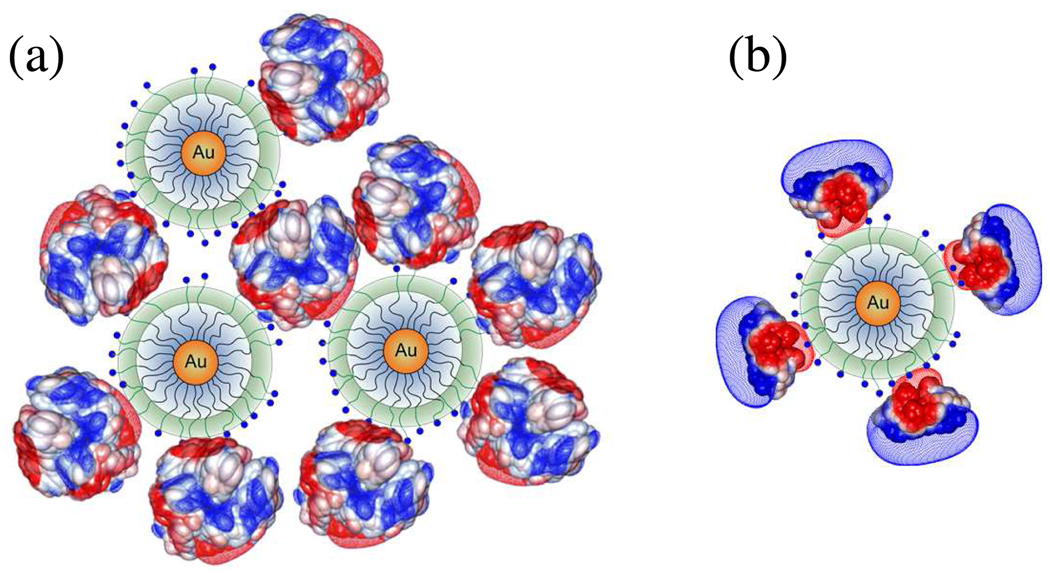
The charge anisotropy of BSA and BLG can be also helpful to explain the absence of stable complexes for BSA (the data point with the large error bar in Figure 6c may indicate an instability at pH 6.25). While the net charge of BSA is negative at pH > 4.9, these widely distributed charges are evidently ineffective at binding TTMA, and interaction only appears with the formation of negative domains at pH > 6.25. Assuming BSA and TTMA as spherical particles, the maximum number of BSA bound to TTMA could be calculated by N_max = π((R+r)/r)², where R is the radius of TTMA (5 nm) and r is the radius of BSA (4.2 nm). Geometric considerations suggest a maximum of N_max = 15 for BSA and 26 for BLG dimer (r = 2.7 nm). It is not sufficient to neutralize TTMA charge at this pH. Since the solution stoichiometry is such that TTMA is in excess on a mole basis (bulk charge stoichiometry [+]/[−] = 3) the nanoparticles cannot be saturated with or neutralized by BSA. Instead, we propose that the micro-stoichiometry of the complexes n (the number of proteins bound per TTMA) varies widely. Even though all complexes may be net positive at this pH, some may possess a distal layer of negative protein, which will interact favorably with other complexes of smaller n. Disproportionation and polarization can thus create BSA-poor regions in one complex, available for short-range coulombic interaction with the BSA-rich domain of another. In other words, BSA can function as a negative “sticker” binding together two or more TTMA particles (Figure 8a). Nevertheless, the resultant aggregates always exhibit a positive net charge, and coulomb blocking⁴⁶ limits the size of aggregates to ~0.9µm.

Figure 8.

Depiction of aggregation for (a) BSA–TTMA (pH 6.3–6.8) and for (b) BLG–TTMA (pH 4.6–5.6). Diameters (DLS): BSA, 7.4 nm; BLG dimer, 5.4 nm; TTMA, 10 nm. Multiple negative charge patches of BSA interact with several TTMA and form large complex aggregates; single negative patch of BLG binds to TTMA yielding an effectively positive complex. See Figure 6.

Turning to BLG, its binding to TTMA “on the wrong side of pI” is evidence for charge anisotropy, i.e. a negative charge patch. One consequence of this, in addition to binding at pI-pH = +0.7, is the formation of a positively charge protein “layer” around TTMA, which stabilizes the resultant ~30 nm complexes (Figure 8b). Even when pH approaches pI, the negative domain of BLG remains proximal and the outer layer is positive. As pH exceeds pI, the orientation of BLG on TTMA can become more variable allowing for inter-complex association. As the pH approaches 6, the net charge on aggregates can be small if the number of BLG bound per TTMA is large. The lower complex charge and diminished coulomb blocking might explain the larger aggregate size (~1.0 µm) for BLG–TTMA.

The instability of the DLS measurement of d~20 nm for BSA–TTMA at pH 6.28 (see Figure 6) suggests a kinetically controlled process. This condition, just beyond the point of initial binding at pH 6.2, arises from the initial formation of complexes in which one TTMA binds one or a few proteins with charge −9. Such complexes are inherently unstable with a strong tendency to associate, since the Debye length of 1 nm allows for strong interaction between such proteins and another TTMA (either similar or protein-free), while screening the repulsive interaction between two NP’s separated by distances corresponding to one or more proteins. Like multifunctional monomers subject to step-growth polymerization, the three-dimensional growth of these aggregates is limited only by kinetics and coulomb blocking. The result is a small number of very large particles, which at pH 6.4 dominate the DLS signal, so that complexation is first signaled by DLS. As their number increases, they contribute to the turbidity, which then becomes linear with pH at pH > 6.5, corresponding to an increase in number particles of constant mass. The formation of these particles is subject to a binding isotherm that describes the equilibrium between free and TTMA-bound BSA, with an equilibrium constant very sensitive to pH. Evidence of complexation appearing first by DLS is also observed for BLG. However, in contrast to BSA–TTMA, turbidity reflects a continuous increase in the number of soluble complexes with d~35 nm (see Figure 6). The gradual increase in the number of these small particles corresponds to the low slope of the turbidity vs. pH in the range of 5.0–5.3 (slightly above the pI). At pH > 5.3 the size of aggregates depends on the appearance of negative domains on BLG apart from the primary negative patch.

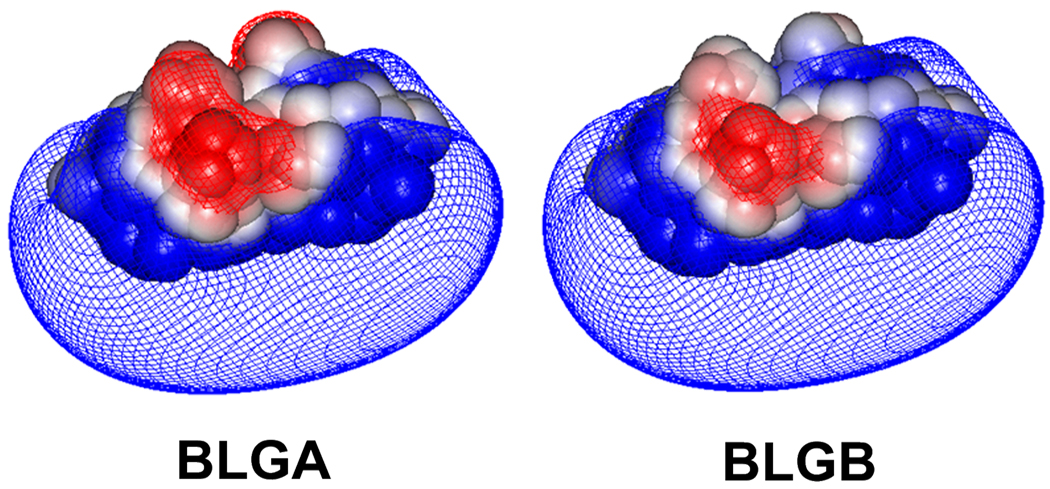
Although the different charge anisotropies of BSA and BLG are obvious, other differences between these two proteins (size, hydrophobicity) might be invoked to account for these results. To avoid these complications and to limit differences to a charged domain alone, we used the two isoforms of BLG. A dramatic effect on aggregation seen when the neutral amino acids in BLGB are replaced with acidic ones in BLGA, has been discussed in terms of alteration of the negative patch,²³ and a similar effect on binding to PDADMAC was also observed.²² For BLGA, Asp replaces Gly in position 64, which is located near two Glu’s at the dimer interface (near the CD loop) to form a more negative cluster for BLGA (Figure 9). It was expected that the high charge density of TTMA might lead to even more dramatic results of this substitution than was seen with PDADMAC.

Figure 9.

Electrostatic potential contours (−0.5 kT/e (red) and +0.5 kT/e (blue)) for dimers of BLGA (left) and BLGB (right), in 100 mM salt at pH 4.82.

2. BLGA vs. BLGB

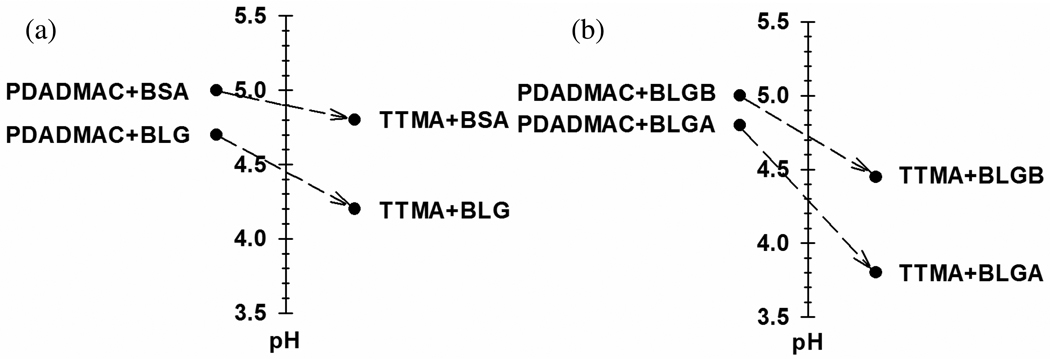
The aim for choosing BLG vs. BSA is different from the aim for choosing BLGA vs. BLGB. We chose BLG because despite an isoelectric point (5.2) very similar to BSA (4.9), it is very different; this allowed us to introduce the “charge patch”. In contrast only two amino acids differed between BLGA and BLGB, the basis of “electrostatic selectivity”. Figure 10 presents results the binding of TTMA to BLG isoforms, along with comparable data for PDADMAC²². The values for pH_c at I= 5 mM are also presented by Figure 11, a format that facilitates the following comparisons. First, for both proteins, we observe stronger binding (lower pH_c) for TTMA vs. PDADMAC. However, the enhanced BLGA/BLGB selectivity of TTMA occurs because this effect is larger for BLGA than for BLGB (Figure 11a). Second, if we take ΔpH_c (= pH_c^B − pH_c^A) as a measure of selectivity, comparison of the data for TTMA in Figure 11a and 11b, shows that TTMA “recognizes” the difference between BLGA and BLGB (ΔpH_c = 0.65) about as effectively as the difference between BLG and BSA (ΔpH_c = 0.60) – a remarkable result given the subtle differences between the isoforms. On the other hand, PDADMAC distinguishes between BLG and BSA (ΔpH_c = 0.30) better than between BLGA and BLGB (0.20). These effects can be explained on the basis of the larger charge density of TTMA, which leads to its strong orientation towards the negative charge patch of BLG. This binding is strong enough to lead to pH_c well below pI. In contrast, the interaction of PDADMAC with this charge patch is not strong enough to bind to proteins with strong global positive charge (pH > pI + 0.5). Binding occurs only when other negative domains appear. The electrostatic recognition of proteins by PDADMAC is thus more global (including its configurational flexibility to minimize repulsion and maximize attraction). In summary, polyelectrolytes can distinguish between proteins based on both global and local interactions, but recognition of similar proteins might always be more effective for the locally binding nanoparticles. This generalization clearly needs to be validated with other proteins.

Figure 10.

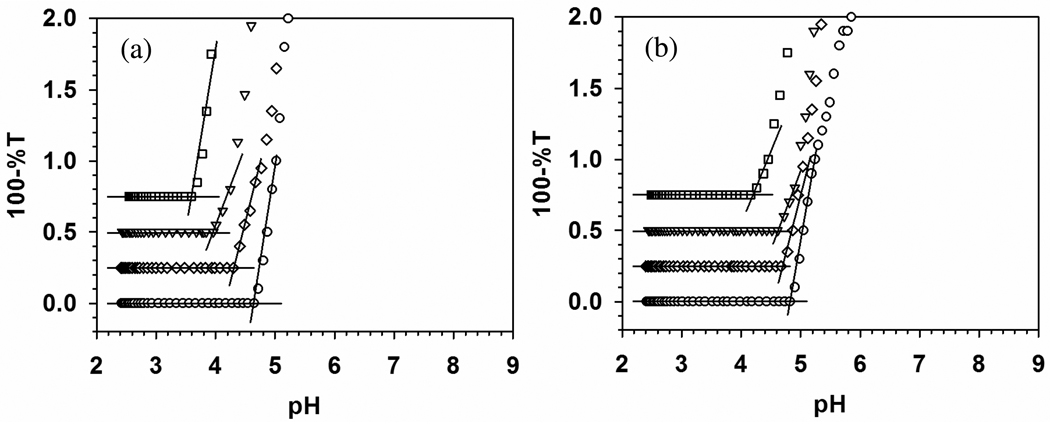
Turbidimetric titrations of (a) BLGA–TTMA and (b) BLGB–TTMA at different ionic strengths. [BLGA] = 1.6 µM, [BLGB] = 1.6 µM, [TTMA] = 0.2 µM. Key: (□) 5 mM, (▽) 55 mM, (◇) 80 mM, (○) 105 mM.

Figure 11.

Difference in pH_c, at I = 5 mM, for PDADMAC (ref 22) vs. TTMA with (a) BSA and BLG and (b) BLGA and BLGB.

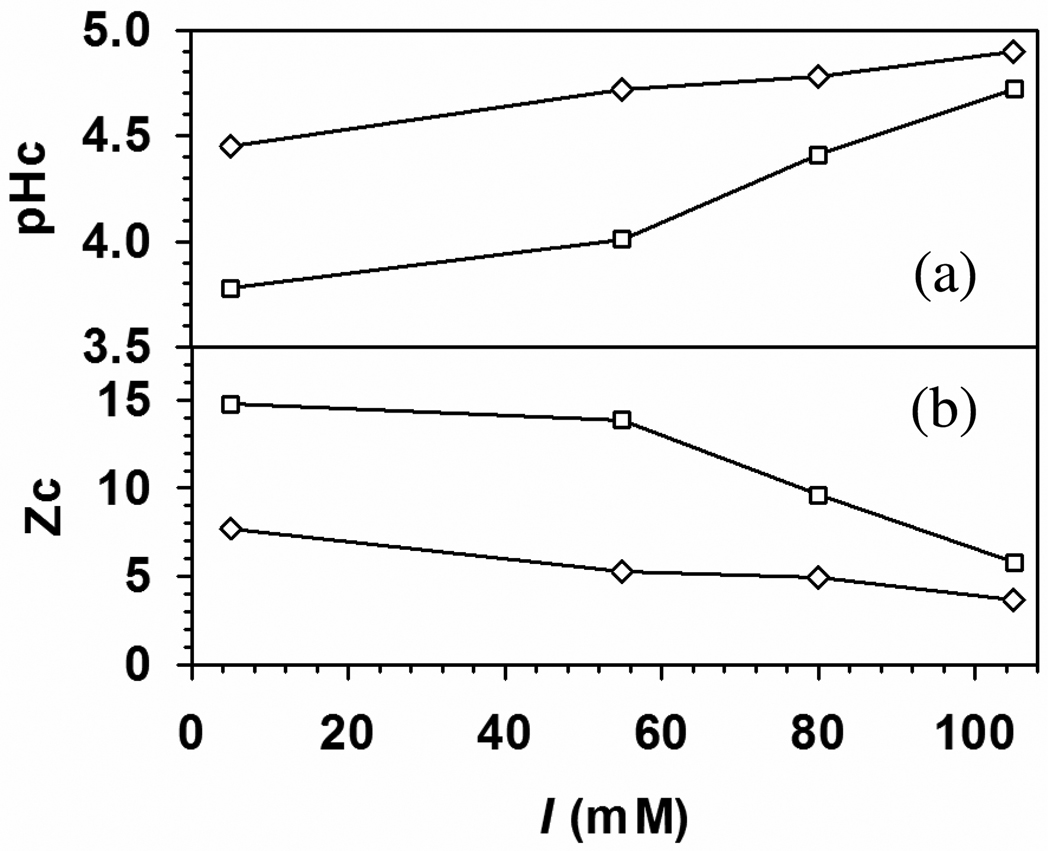
The difference between global and local electrostatics should lead to different ionic strength dependences for protein binding by TTMA and PDADMAC, shown in Figure 12. As reflected by the range of pH over which complexation occurs, the protein affinity of the nanoparticle is larger than that of the polyelectrolyte for all proteins studied. This is a result of the high surface positive charge density of the NP and its stronger Coulomb interaction with the negative domain of the protein, thus particularly significant for BLG. The behavior of BLGB is typical: additional screening at high salt requires compensation by higher pH (more negative net protein charge). With pH_c always below the pI (5.2), “patch binding” is dominant, but ΔpH_c diminishes strongly at higher salt (Figure 12a), indicating a diminution of the role of the “patch”. As global charge becomes more significant, recognition of the difference between BLGA and BLGB diminishes. The influence of the additional aspartate residues on binding to a cationic surface is also evidenced by the later retention of BLGA (v. B) on an anion-exchange column.²⁴ Then, the orientation of protein in the TTMA complex may be less controlled by its electrostatic dipole.¹³

Figure 12.

pH_c (a) and critical net protein charge, Z_c (b) versus I for (□) BLGA–TTMA and (◇) BLGB–TTMA complex.

ΔpH_c in Figure 11 shows conditions for separation but does not show energetics: the stronger binding to BLGA at any pH > pH_c is not quantified. For proteins binding to polyelectrolytes, ITC data can be converted to binding isotherms, and hence to binding constants through a proper binding model, the most rational being that of McGhee and von Hippel.^{9,10,22,47–49} However, as seen from the schematic of Figure 8, any distinction between host and guest (the former binding multiple units of the latter) is likely to be subjective. Although titration of BLGA and BLGB into PDADMAC clearly showed the stronger (more endothermic) binding of BLGA,²² thermograms obtained by titrating BLG into TTMA displayed uninterpretable maxima. We therefore chose TTMA as titrant, leading to the thermograms in Figure 13. We chose an ionic strength of 5 mM because of (1) the larger value of ΔpH_c at low ionic strength (Figure 12), and (2) reports that the enthalpy of nanoparticle–protein interactions becomes larger with decrease in I (regardless of sign).^50,51 The stronger binding for BLGA is qualitatively evident in Figure 13 from the incremental heat absorbed for the first TTMA additions, and from the total area under the curve (corresponding to the completion of protein binding). For a more quantitative analysis, it is necessary to consider the binding process for the titration carried out in this way.

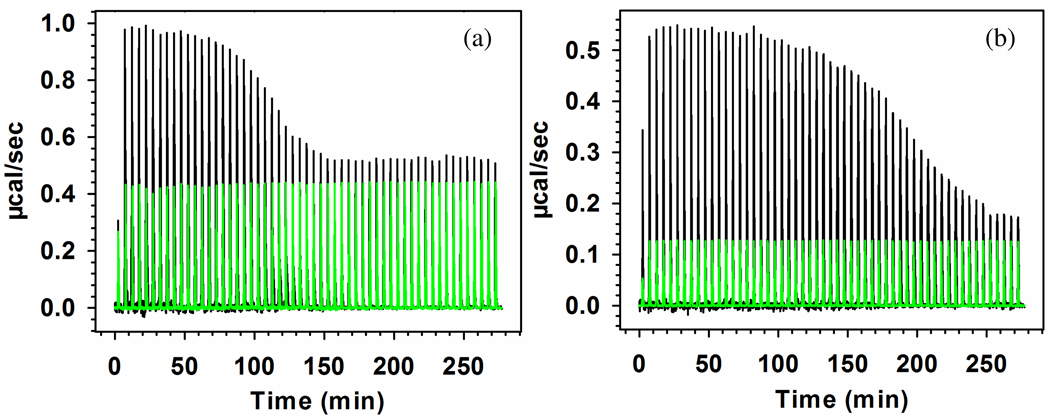
Figure 13.

ITC raw data for the interaction of (a) BLGA–TTMA and (b) BLGB–TTMA at pH 5.5 and I = 5 mM. Green lines mean a control experiment in which BLGA/B was diluted by buffer under the same condition. No correction made for dilution of TTMA for which the enthalpy change is negligible.

A more detailed analysis of the thermograms requires certain assumptions about the BLGA/B–TTMA interactions. Figure 6f at I = 105 mM indicates that soluble complexes, d ≈ 30 nm, are stable at 4.5 < pH < 5.6; the comparable values of turbidity in this pH range for all I’s in Figure 10 suggests that stable complexes are also formed in the conditions of Figure 13. This is also supported by the observation of optical clarity after completion of the ITC experiment. Uniformity of complexation leads us to propose a model in which the binding of every BLG to TTMA produces the same ΔH, regardless of the overall extent of binding, i.e. TTMA as depicted in Figure 8, has n identical and independent binding sites, unchanged by the overall degree of binding. Considerations of 3D geometry and charge neutrality suggest that n might be in the range of 40–50. Regardless, n can be established as a fitting parameter, starting with the assumption that every binding event is subject to the same equilibrium:

$$\mathit{\text{site}}+\mathit{\text{protein}}\stackrel{K_b}{\leftrightarrow }\mathit{\text{complex}}$$ (1)

in which “complex” stands for an occupied binding site on TTMA. The total heat change (Q) absorbed at any point in the titration is assumed to be proportional to the concentration of the complex, i.e. Q = a[complex]. The molar concentration of total binding sites is n[TTMA]_tot. For equivalent, independent sites, a is constant, leading to eq 2 in which the denominator contains the concentrations of free sites and free protein,

$$K_b=\frac{[\mathit{\text{complex}}]}{[\mathit{\text{site}}][\mathit{\text{protein}}]}\text{=}\frac{Q/a}{{([\mathit{\text{site}}]}_{\mathit{\text{tot}}}-Q/a)({[\mathit{\text{protein}}]}_{\mathit{\text{tot}}}-Q/a)}$$ (2)

Solving for Q,

$$Q=\frac{a}{2}\left\{\left({[\mathit{\text{protein}}]}_{\mathit{\text{tot}}}+n{[\mathit{\text{TTMA}}]}_{\mathit{\text{tot}}}+\frac{1}{K_b}\right)-\sqrt{{\left({[\mathit{\text{protein}}]}_{\mathit{\text{tot}}}+n{[\mathit{\text{TTMA}}]}_{\mathit{\text{tot}}}+\frac{1}{K_b}\right)}^2-4n{[\mathit{\text{protein}}]}_{\mathit{\text{tot}}}{[\mathit{\text{TTMA}}]}_{\mathit{\text{tot}}}}\right\}$$ (3)

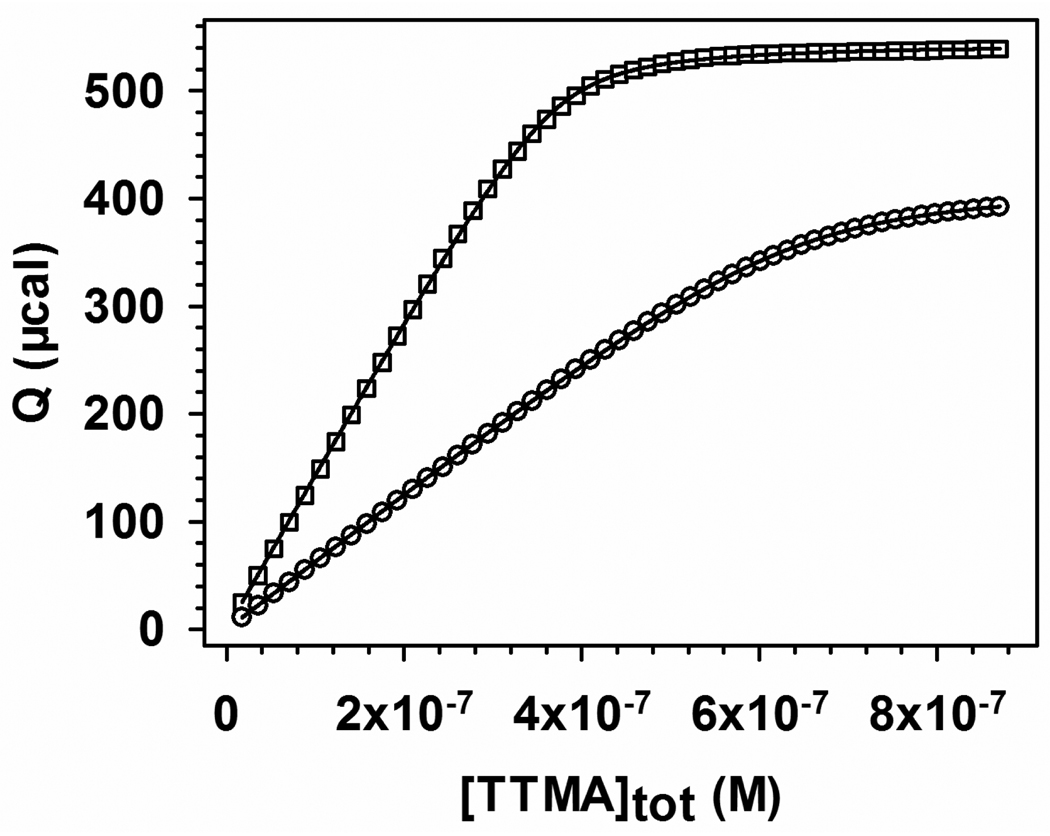
The integrated heat Q obtained from Figure 13 is plotted for BLGA and BLGB vs. [TTMA]_tot in Figure 14. Values of K_b and n are obtained by fitting (Origin 7.0) to eq 3 are given in Table 1, along with ΔG = −RTlnK_b, and TΔS = ΔH − ΔG. ΔH was derived from the heat adsorption in the first injection.

Figure 14.

Binding isotherms for (□) BLGA–TTMA and (○) BLGB–TTMA from integration of the curves in Figure 13. These values have been corrected for the heat change from protein dilution (see Figure 13). Solid lines are fitting via eq 3, see text.

Table 1.

Thermodynamic parameters obtained from equivalent, independent site-binding model for BLGA/B–TTMA.

	n	Kb/M−1	ΔG/kcal mol−1	ΔH/kcal mol−1		TΔS/kcal mol−1
				First	Total3
TTMA–BLGA	54	3.8×106	−9.1	261	19	35
TTMA–BLGB	31	2.1×106	−8.7	201	14	29
PDADMAC–BLGA4	32	1500	−4.4	3.52	2.5	7.9
PDADMAC–BLGB4	24	730	−4.0	2.72	1.5	6.7

¹Heat absorbed in first injection divided by moles of TTMA added, and multiplied by n.

²Heat absorbed in first injection divided by moles of protein added.

³Total heat absorbed during titration divided by initial number of moles of protein.

⁴From ref 22.

From Table 1 we observe: (1) both TTMA and PDADMAC bind endothermically to BLG; the binding is entropy-driven (as is the case for the interaction of BSA with TTMA,⁵² or of PDADMAC with BLGA or BLGB²²). (2) By any measurement, TTMA binds more strongly to BLGA; ΔG_TTMA is more negative (binding constants larger by a factor of 3000) not because of any relative decrease in ΔH or increase in TΔS ({ΔH_TTMA/ΔH_PDADMAC} ≈ {ΔS_TTMA/ΔS_PDADMAC}) but simply because entropy is the dominant term. Further comparisons are complicated by the difference in methodology; here TTMA was used as titrant, while protein was the titrant for PDADMAC experiments. While the enthalpy for the first injection in ITC is generally considered to provide the heat for a single ligand binding, ΔH, in the case of TTMA, it is the heat for binding n ligands (BLGA/B) to a known number of TTMA molecules. Since n can only be determined from the model-dependent binding isotherm, estimates of ΔH obtained by dividing the overall heat change during the titration by the (constant) number of moles of proteins are also reported for the PDADMAC results. The differences between these ΔH_first and ΔH_total in Table 1 for TTMA might point to the sensitivity of ΔH to the fitted values of n (which are surprisingly different for the two isoforms), and caution against an overinterpretation of other thermodynamic quantities in Table 1. Nevertheless, we find that the ratios of ΔH for BLGA vs. BLGB are not affected by the method of obtaining ΔH, and thus may provide a better foundation for comparing TTMA results with those for PDADMAC, since these must be determined under different pH and I conditions in order to correspond to the soluble complex region. In the case of PDADMAC, ΔH is not dependent on n, but agreement between ΔH_first and ΔH_total is poor because ITC in ref 22 was terminated short of completion. The effect of this on the values of K_b, ΔG and ΔS in Table 1 arise from possible errors in the binding isotherm. Truncation of the binding isotherm is considered to have relatively minor influence on the relative (A/B) values in Table 2.

Table 2.

Comparison of ΔpH_c and for TTMA vs. PDADMAC using relative (BLGA/BLGB) quantities.

	ΔpHc1	δKb2	δΔG2	δΔH2		δTΔS2
				First	Total
TTMA	0.6	1.8	1.0	1.3	1.4	1.2
PDADMAC	0.2	2.1	1.1	1.3	1.7	1.2

¹From Figure 11.

²Relative values, for example, δK_b=K_b^BLGA/K_b^BLGB

Table 2 uses relative values (BLGA vs. BLGB) to compare the present results to PDADMAC results in ref 22. The critical pH values for binding visualized in Figure 11 indicate higher BLGA/BLGB selectivity for TTMA, but there is surprisingly little difference in any of the relative values (or for that matter in δΔG = ΔG^A − ΔG^B) for PDADMAC vs. TTMA. Either such relative values do not correlate with selectivity, or ΔpH_c is simply not relevant as a thermodynamic quantity. Indeed ΔpH_c = {(pH-pH_c)_A − (pH-pH_c)_B}, while an indication of the separability of the two proteins at some given pH, is only qualitatively related to the binding constant; in other words, the correlation of ΔpH_c with e.g. ΔK_b is unknown since (∂ΔG/∂pH) is not known; and a large value of K_b^A /K_b^B might correspond to small ΔpH_c depending on the ∂pH/∂K_b.

Conclusions

Protein affinity, as evaluated by the width of the pH range in which complexation occurs, was found to be larger for cationic nanoparticle than for a linear polycation. This effect, true for both BSA and “native” BLG, over a range of ionic strengths, is presumably due to the higher positive charge density of the nanoparticle, and particularly for BLG which interacts with nanoparticle via its positive domain (patch). The binding of BLG to the cationic nanoparticle TTMA at pH well below pI is indicative of the importance of the BLG negative charge patch: Selective binding of BLGA vs. BLGB arises from the enhancement of this negative domain for BLGA. Binding proceeds by a complex mechanism with higher-order aggregation likely arising from charge neutralization. The charge of the protein-nanoparticle complex ([+]/[−])_micro depends on the charges of the two macroions, the bulk charge stoichiometry ([+]/[−])_macro, and the stoichiometry (combining ratio) of the complex. This last term is influenced by both protein MW and charge anisotropy. Calorimetry confirms that both isoforms bind more strongly to TTMA than to the soluble polycation PDADAMC, but relative values of thermodynamic parameters (X_A ÷ X_B) do not particularly correlate with binding affinity. This suggests that both particulate and linear polycations are subject to similar short-range attraction/long-range repulsion effects. Consequently, maximum binding and selectivity might be achieved with a macroion whose “electrostatic epitope” is spatially surrounded by neutral moieties.