Non-experts' Recognition of Structure in Personal Network Data

Abstract

Network-based interventions are gaining prominence in the treatment of chronic illnesses; however, little is known about what aspects of network structure are easily identified by non-experts when shown network visualizations. This study examines which structural features are recognizable by non-experts. Nineteen non-experts were asked to pile-sort 68 network diagrams. Results were analyzed using multidimensional scaling, discriminant analysis, cluster analysis, and PROFIT analysis. Participants tended to sort networks along the dimensions of isolates and size of largest component, suggesting that interventions aimed at helping individuals understand and change their social environments could benefit from incorporating visualizations of social networks.

INTRODUCTION

Interest in social networks has grown exponentially in the social sciences over the past decade (Borgatti et al., 2009). One of the most active areas of research into social relationships has been the study of network influences on positive and negative health behaviors (Valente & Fosados, 2006). For example, some recent studies of social networks and health have highlighted the influence of networks on obesity, smoking, and mental health (Christakis & Fowler, 2007, 2008; Fowler & Christakis, 2008). Social relationships have also been studied to explore how they influence help-seeking for health problems and coping with a wide variety of (especially chronic) illnesses (Heaney & Israel, 2002). These studies of social relationships, however, tend to focus on measures of functional support embedded in social networks (Sherbourne & Stewart, 1991).

More recent research is focused on the relationship between social network structure and health. Researchers now recognize that in addition to their total social support, people are embedded within networks of social relationships that influence their health behavior and resources for seeking help (Valente & Fosados, 2006). Recent studies have suggested that social networks have emergent properties that influence health and health care and transcend the sum of the characteristics of the individuals in the network (Christakis, 2004).

Increasingly, health interventions are incorporating a focus on social network structure (Heaney & Israel, 2002), targeting changes in the structure of networks to influence better health behaviors, reduce negative health behaviors, and improve social support and help seeking (Gottlieb & Coppartd, 1987). Studies of network-based interventions have described the potential health benefits of changing network size through the addition or elimination of network members, or strengthening existing networks by increasing multiplexity, reciprocity, density and reducing isolates. For example, Costenbader et al. (2006) found that IDUs who increased the number of their non-drug-using social network ties engaged in fewer HIV risk behaviors. Biegel et al. (1994) describes how mental health case workers can help their clients by targeting their natural support networks through building new network ties and maintaining and strengthening existing network ties. Pinto (2006) discusses how people with severe mental illnesses tend to have small, dense, and non-reciprocal and non-multiplex networks, increasing the likelihood of hospitalization and describes intervention techniques for adding network size, diversity, and reciprocity.

Family health clinicians and researchers in health interventions have described how visualizations of family and social relationships can be helpful in health interventions (Rempel et al., 2007). In these interventions, visualizations of social networks are co-created by individuals and caregivers during qualitative interviews to help them come to a shared understanding of their social environment. Visualizations are helpful tools that condense a large amount of information about many social relationships into one visual representation. The visualizations help facilitate conversations about abstract concepts, such as relationships, into conversations about concrete visual representation of these relationships.

For example, a technique called an “ecomap” helps people understand their social environment and can be used to assess changes in social networks over time with repeated interviews (Rempel et al., 2007). Ecomaps visually represent key individuals in families, such as caregivers, along with qualitatively generated information about the focal person’s relationships. They have been used with people from a wide variety of backgrounds to convey information about social networks and health, identify supportive and non-supportive members of a network and facilitate discussions about how those network members may affect health behaviors. Another social network technique used in social work is the “Social Network Map” (Tracy & Whittaker, 1990). This visual tool helps clients and therapists identify different types of social network members (household members, relatives, friends, people from work, school, clubs, etc.) and assess network members in these categories on different functional aspects (e.g., closeness, criticalness, reciprocity). This tool has helped clients identify latent support in some of their relationships as well as realizing that some of their relationships were exploitive and lacked reciprocation (Tracy & Whittaker, 1990).

Although tools such as ecomaps and the Social Network Map convey information about social networks in health interventions visually, they do not convey information about network structure. Ecomaps contain information about a set of dyadic social relationships but not about the set of relationships among these social network members. Social Network Maps convey information about types of network members and visually reveal associations between types of relationships and function. Yet both tools lack information about structural properties of the network of relationships, such as isolates, density, or components. For example, the Social Network Map has been helpful for women in abusive relationships to realize the lack of support they were receiving from their relationship with an abusive partner (Tracy & Whittaker, 1990), but does not reveal the relationships this partner has with other network members. Ending a relationship with an abusive partner who is not connected to any other network members (i.e., an isolate) would be much different than ending a relationship with an abusive partner who has a close relationship with the majority of other network members (i.e., high degree centrality).

Tools such as the Ecomap or the Social Network Map could be modified to include structure by incorporating existing techniques for depicting network structure used in studies of personal networks. These studies focus on network ties around an independent sample of focal individuals who provide information about their perception of their own networks (McCarty, 2002). Personal networks can be thought of as perceived/cognitive network neighborhoods. Therefore, they are very similar to the types of networks analyzed with ecomaps and the Social Network Map in clinical practice.

Augmenting existing social network based clinical tools with information about network structure would allow therapists and clients to target structural weaknesses in networks in addition to compositional weaknesses. However, it is unclear how well non-experts in social network analysis (SNA) might understand a visual presentation of the structure in their networks. While individuals who view personal networks often find them interesting and intuitive (Hogan et al., 2007; McCarty et al., 2007), it is not known whether non-experts can identify particular aspects of network structure to understand areas of potential change. It is also not known how well non-experts can identify structure in network diagrams that are not their own, which may be relevant to interventions that incorporate descriptions or diagrams of desirable network structures. For example, if increasing a client’s network density is an intervention goal, the client may be shown an example of a network with a healthier amount of density in contrast to the client’s low density network.

The goal of this study is to better understand non-experts’ perceptions of network diagrams and identify which, if any, structural features were salient to a sample of individuals who were non-experts in SNA. Further, we explore these data to determine if network diagrams are consistently categorized into discrete types or if they are sorted according to continuous dimensions based on structural characteristics.

METHODS

We explored non-experts’ perceptions of structure in personal networks by asking 19 participants to sort 68 personal network diagrams from two studies of the homeless in Los Angeles County, California. One study examined 28 personal networks of homeless women (Tucker et al., 2009) and the other examined 40 personal networks of homeless youth (both male and female) (Wenzel et al., 2009). Personal network data were collected in face-to-face interviews in which respondents were asked to name 25 people they know (“alters”) and how often each unique combination of alters interacted (never, rarely, sometimes, often). We produced graphs of each network using the spring embedding algorithm and defined a tie as a relationship between two alters who interacted with each other “often.” Our initial analyses of these graphs indicated that they depicted a wide range of different types of networks and had a wide range of values of key measures typically used in studies of personal networks, such as: number of isolates (range: 0 to 25), dyads (range: 0 to 4), and components (0 to 5); number in largest component (range: 0 to 25); density (range: 0 to .93); and centralization (range: 0 to .64), Because this set of networks came from a sample of personal networks collected with the same data collection methods and represented a wide range of types of networks, we decided it would be a useful sample for an exploration of the structural perceptions of non-experts in network analysis.

We printed each network on a sheet of paper (see Figure 1 for examples) and asked a convenience sample of non-experts to view the 68 personal network diagrams and sort them into piles according to which diagrams looked similar (Weller & Romney, 1988). We told participants that the diagrams represented pictures of the people that one person knows and explained that nodes (circles) represented people and lines represented two people who had contact with each other. We conducted two rounds of sorts with two different groups of non-experts (e.g., administrative staff, research assistants; n = 9 and 10). Sorters were asked to sort the graphs into as many piles as they thought necessary to represent the patterns they identified in the graphs.

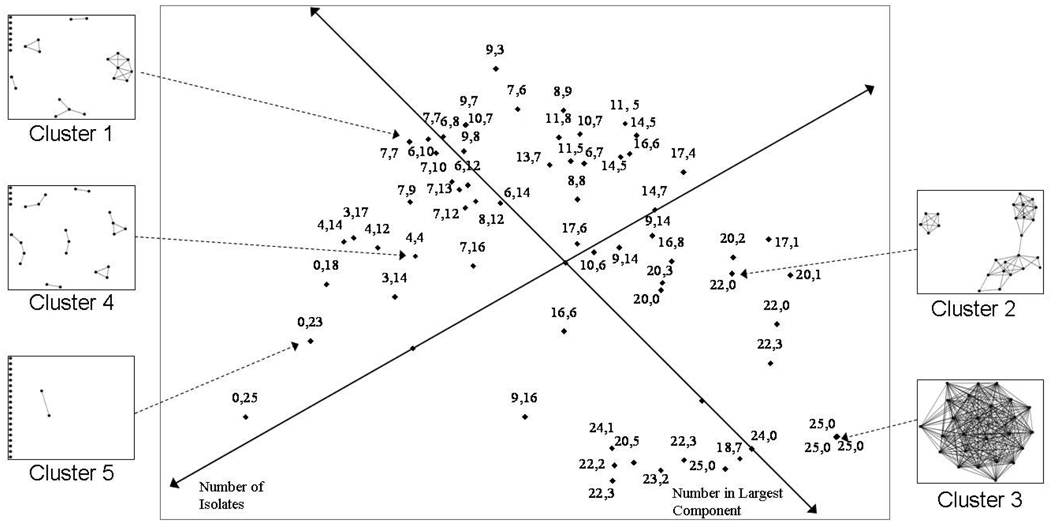
Figure 1.

Multidimensional scaling (MDS) and PROFIT analysis output of pile sort data. Points in MDS represent graphs from pile sort. The two primary structural dimensions identified by PROFIT analysis are indicated by solid arrows with dimension labels: “Number in Largest Component” and “Number of Isolates”. Dashed arrows link images of five example graphs and their corresponding points on the MDS. These graphs are also examples from each of the five clusters. Points are labeled with values of the two primary PROFIT dimensions separated by a comma: Number in Largest Component, Number of Isolates.

We also collected qualitative data about the sorting process. In the pile sorting instructions, we asked participants to “write a description of each pile” to understand the characteristics of the graphs they were using to create the piles. We made this question open-ended to explore how salient structural characteristics of the graphs were in the pile sorting decisions. We also conducted interviews with several sorters to better understand what they were thinking as they evaluated the similarities and differences among graphs.

Analysis

We conducted two stages of analysis. First, we analyzed the sort data to determine if sorters tended to group graphs with similar structural properties together and might have used structural characteristics when deciding how to put graphs into piles. We used cluster analysis to test whether discrete groups of graphs emerged from the pile sort data. We conducted discriminant analysis on the clusters to test the extent that structural characteristics might have influenced the pile sorting. See Table 1 for details of cluster analysis and discriminant analysis procedures.

Table 1.

Detailed pile sort analysis procedures

Procedure	Data Source	Goal	Software	Analytic Details
Create Distance Matrix	Pile sort data	Transform raw pile sort data into an item by item distance matrix	ANTHROPAC; UCINET	Entered pile sort data into the software Anthropac (Borgatti, 1996a) and produced an item by item aggregate proximity matrix which was then transformed into a distance matrix
Cluster Analysis	Distance Matrix produced with UCINET;	Determine optimal number of clusters and cluster membership	MATLAB Cluster Analysis Toolbox	1) Identified the best-fitting Anti-Robinson form and reordered the rows and columns of the distance matrix; 2) determined cluster membership and calculated objective functions using maximum-link clustering for all possible clusters (2 to 67); 3) graphed objective function values corresponding to all possible partitions and used this scree plot to identify the optimal number of clusters; 4) determined greatest change in the objective function values and used this information to validate the choice of the optimal number of clusters.
Discriminant Analysis	Cluster membership from MATLAB toolbox and network structural measures from UCINET	To determine what graph structural characteristics are associated with placement in piles and clusters	UCINET; SPSS 17	1) Produced structural measures of 68 graphs: a) density, b) number of ties, c) centralization, d) number of components, e) size of largest component, f) number of dyads, g) number of isolates; 2) completed discriminant analyses and ran “leaveone-out validation” procedure with structural measures as predictors of cluster membership
Multi-dimensional Scaling (MDS) analysis	Item by item aggregate proximity matrix	To produce visual representation of pile sort data and explore continuous dimensions of graphs	ANTHROPAC	1) Ran the non-metric MDS procedure in 2 dimensions; 2) inspected stress output
PROFIT Analysis	Two dimensional coordinates from MDS; coordinates of lines representing dimensions of MDS output	To test the strength of different structural characteristics of graphs as predictors of MDS dimensions	UCINET; ANTHROPAC, Excel (PROFIT plot)	1) Produced coordinates of lines that indicated dimensions for each structural measure; 2) plotted lines on top of MDS scatter plot; 3) inspected output of strength of prediction for structural features; 4) labeled points on MDS plot with values of two strongest structural measures for visual inspection
Qualitative Data Analysis	Text describing piles graph sorters created	To identify descriptions of structural features in non-technical language	Excel	1) Read through pile description text for each sorter; 2) highlighted words and phrases that potentially indicated structural characteristics; 3) visually inspected graphs to confirm structural correspondence or uncover connection between non-technical explanation and structural characteristic

Next, we analyzed the sort data to determine if participants were sorting graphs along continuous dimensions of structural features (i.e., more or less of certain structural characteristics, such as density) rather than into discrete groups of graphs with Multi-dimensional Scaling (MDS) and Property Fitting (PROFIT) Analysis. MDS produces a set of points in k-dimensional space to visually approximate the similarities among a set of items (Weller & Romney, 1988). These plots allow for identification of discrete clusters or underlying dimensions that explain the similarity of a set of items (Borgatti, 1996b). PROFIT analysis allows us to evaluate the correspondence between one or more attributes of the networks and their location in multidimensional space and test the hypothesis that the items’ placement on the MDS is driven by an attribute of the items (Borgatti, 1996b). We ran non-metric MDS in 2 dimensions using Anthropac on the item by item pile sort proximity data. We used PROFIT analysis in UCINET on the MDS output (x and y dimensions) with structural network measures as predictors of dimensions in the MDS layout.

To give context to the results, we analyzed qualitative data collected from the 19 participants. We entered text from the pile descriptions into a spreadsheet and compared the descriptions to the visualizations to link descriptions and structural features. We identified words, phrases and sentences that matched structural characteristics of the graphs as well as words, phrases, and sentences that did not. We then coded the text for these structural features and sorted the text to explore how non-experts described what they saw in the networks. See Table 1 for detailed analytic procedures and software.

Measures

We selected commonly used measures of network structure with reasonably apparent visual characteristics. We developed a list of structural measures a priori and modified this list based on feedback from qualitative interviews with sorters. We used these structural measures in the cluster analyses and the PROFIT/MDS analyses. The structural measures included 1) density, 2) centralization, 3) number of components, 4) size of largest component, 5) number of dyads, and 6) number of isolates. These measures are correlated but not identical and have distinctive visual characteristics. Density is the number of alters who interacted with each other “often” divided by the number of possible ties, indicating the level of connectedness among network alters. Centralization measures the extent that the network is dominated by a few alters. Number of components indicates how many completely separate groups of three or more alters are formed where alters are either directly or indirectly tied together; the size of the largest component is the number of alters in the component with the most alters. The number of dyads indicates the numbers of pairs of alters who were connected to each other but no other alters in the networks. The number of isolates indicates the number of alters who had no connections to any other alters in the network. (See Wasserman and Faust (1994) for formal definitions of these measures.)

RESULTS

Objective functions from cluster analyses and examination of an R² scree plot suggested that network diagrams might fall into five main clusters. Table 2 provides overall and within-cluster descriptive statistics for the structural variables used in the discriminant analysis. The five clusters are illustrated by the five graphs in Figure 1. We conducted ANOVAs to determine which structural measures might distinguish among the five clusters. As shown in Table 2, significant differences were found between clusters for all structural measures investigated (p < .001).

Table 2.

Structural characteristics of graphs (overall and by cluster), and results of ANOVAs

	Overall	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	ANOVA RESULTS
	Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)	F	Df	p
Network density	0.16	0.08	0.10	0.14	0.31	0.00	6.19	(4, 63)	<0.001
	(0.18)	(0.04)	(0.03)	(0.13)	(0.26)	(0.00)
Components	1.76	2.20	1.42	2.14	1.35	0.00	5.42	(4, 63)	0.001
	(0.98)	(0.68)	(0.90)	(1.3)	(0.61)	(0.00)
N in largest component	12.38	9.67	17.50	5.64	21.35	0.00	78.35	(4, 63)	<0.001
	(7.46)	(2.82)	(4.25)	(2.70)	(3.16)	(0.00)
Number of dyads	0.97	0.80	0.83	1.82	0.24	0.00	8.61	(4, 63)	<0.001
	(1.08)	(0.77)	(1.19)	(1.04)	(0.56)	(0.00)
Centralization	0.21	0.19	0.24	0.13	0.34	0.00	13.31	(4, 63)	<0.001
	(0.13)	(0.08)	(0.08)	(0.07)	(0.16)	(0.00)
Number of Isolates	7.59	7.93	5.33	11.55	1.71	25.00	30.16	(4, 63)	<0.001
	(6.03)	(3.45)	(3.87)	(4.47)	(2.31)	(0.00)

Note: N of graphs: Overall = 68; Cluster 1: 15; Cluster 2: 12; Cluster 3; 22; Cluster 4: 17; Cluster 5: 2. We experimented with other structural measures (transitivity and clustering coefficient) that did not have obvious visual characteristics and found none to be significant predictors of any clusters. A small number of graphs had fewer (24) or more (26) nodes because of an error in data collection.

Stepwise discriminant analysis of the entire sample of 68 network diagrams, using F-tests to determine significant predictors, revealed that the important discriminating variables were size of largest component (F=30.72), and number of isolates (F=7.05). Wilk’s Lambda for the first discriminant function was 0.12 (df=8, p<0.001), which accounted for 91.8% of the variance in the model. Size of largest component was correlated at 0.996 with this function, suggesting that the first separation among these networks is how large their main components were. The second discriminant function had a Wilk’s Lambda of 0.692 (df = 3, p<0.001) and accounted for the remaining 8.2% of the variance in the model. Number of isolates was correlated at 0.82 with the second discrminant function, suggesting that number of isolates is most likely to separate the networks after they have been separated by the size of their largest component.

Cross validation and leave-one-out cross-validation revealed only 66.2% of cases were correctly classified for the five cluster solution (22 errors in classification, an improvement of 46.2% over chance). Subsequent discriminant analyses explored four, three, and two cluster solutions, finding that the same variables (i.e., size of largest component, number of isolates, and--with the fewest clusters--density) emerged as significant predictors of cluster membership across analyses. However, classification success improved with fewer clusters (4 clusters: classification success = 75%, a 50% improvement over chance; 3 clusters: classification success = 78%, a 45% improvement over chance; 2 clusters: classification success = 90%, a 40% improvement over chance). Leave-one-out validation was 66.2% for the five-cluster solution, 72.1% for four clusters, 76.5% for three clusters, and 88.2% for two clusters.

Figure 1 presents the results of an MDS and PROFIT analysis of the sort data. The two structural measures that explained most of the variance were the size of the largest component and the number of isolates. The R² for the number in the largest component measure is .865 while the number of isolates has an R² of .667. This suggests that these two structural characteristics were the dominant features used by sorters to group the graphs. The next highest R² was centralization (.427) followed by the number of components (.358), the number of dyads (.334), and density (.157). Each of these measures had a p-value <.001 suggesting that it is highly unlikely that participants were not considering (either implicitly or explicitly) these structural features when sorting the graphs. Figure 1 visually demonstrates both the MDS output and the two dominant dimensions found in the PROFIT analysis. The MDS represents the graph by graph similarity data in two- dimensional space. The points on the MDS represent each of the 68 graphs. Two points close together indicate that these two graphs were frequently judged to be similar by sorters. The stress for the MDS is .113 which indicates that the MDS is a good representation of the data (Sturrock & Rocha, 2000). The MDS does not show any clearly identified clusters of points indicating the lack of discrete groups of graphs (also indicated by the improved classification success with fewer clusters in the discriminant analyses). However, the MDS does demonstrate the dimensions explained by the PROFIT analysis, indicating continuous differences among the graphs. The MDS points are labeled with their measures on the two dominant dimensions: number in largest component and number of isolates. The PROFIT analysis produces two points on the graph for each predictor that can be used to draw an arrow to indicate the direction of dimensionality in the two-dimensional space. In Figure 1, arrows representing the ‘number in the largest component’ and ‘number of isolates’ dimensions are overlaid on top of the MDS output.

Table 3 presents the results of an analysis of the qualitative descriptions participants gave to their piles. Our readings of the text descriptions and comparisons between the text and the network diagrams revealed many descriptions of network structure, albeit in non-technical language. The text descriptions of the piles fell into six different structural categories: number of isolates, size of largest component, size and density of largest component, number of components, dyads, and triads. Table 3 gives examples of the raw text coded for references to structural features of the graphs. Table 3 also gives examples of pile descriptions that did not indicate structural characteristics. These descriptions focused mainly on the shape of the components and the similarities of these shapes to other objects, such as kites, pentacles or constellations.

Table 3.

Descriptions of graph piles and their correspondence to structural characteristics

Structural Measure	Examples of Qualitative Descriptions of Piles
Number of isolates	“Graphs with no networks” “Lots of singles (single dots on left)”	“Graphs that are blank” “Nobody knows anyone”
Size of largest component	“Large”/”small” “groups”/”networks” “Small, loose, scattered clusters” “Graphs with…very large clusters”	“Dominated by a large, dense cluster” “Contains multiple people knowing 5 or more other people that know each other”
Size and density of largest component	“Large dense clusters” “Large dense clusters and small groups” “Large sparse cluster with none to many small groups”	“Each member seems to know at least 18 or more other people, thus making the graphs look very condensed, like black stars or very thick tangles of spider webs”
Number of Components	“Small, loose, scattered clusters” “One dominant cluster”	“Graphs with scattered networks”
Dyads	“Straight lines” “Only one person knows one other person”	“Contains people that know one or two other people (straight lines)” “Graphs with single lines”
Triads	“Knows two people that know each other and another common person (triangles)”	“Graphs with a lot of triangles”
Non-structural descriptions	“Graphs trying to form a sphere” “Graphs that have diamonds” “Graphs trying to form asterisks” “Graphs with squares” “Reminded me of a kite or astrological image”	“interlocking pentacle-like shapes” “resemble constellations” “kite-shapes featured with simple 2-point lines and simple pentacles.” “Shapes that remind me of birds flying or of fish jumping.”

DISCUSSION

This study demonstrated that a group of non-experts in SNA sorted network graphs with consistency. Through discriminant and PROFIT analysis, we found associations between structural characteristics of the graphs and the pattern in how graphs were placed in piles. Qualitative analysis provided additional insight into the ways that non-experts distinguish network graphs according to their structural features. The results of the discrete category analysis and the continuous dimension analysis suggests that, though they likely used structural features to sort graphs, respondents sorted graphs along a multi-dimensional continuum rather than discrete sets.

Though the discriminant analysis suggested that a discrete solution may not be the best when considering this set of 68 network diagrams, both the discriminant analysis and the PROFIT analysis showed that size of largest component and the number of isolates were highly salient to this sample of non-experts in their evaluations of the graphs. Additionally, other structural properties, such as dyads/triads, number of components and density emerged as salient concepts to these non-experts.

Graphs are often used by network researchers to search for patterns in data that they may not have identified using other analytic techniques (Wasserman & Faust, 1994). Experts in SNA certainly have training that helps them identify structural features in network graphs that are not intuitive to non-experts (McGrath et al., 1997). Our findings suggest that it is feasible to introduce non-experts to structural features of network diagrams in interventions. Our findings also suggest that non-experts can identify clear patterns of structural characteristics across a group of network graphs. Viewing network diagrams comes easily to non-experts in part because of the growing popularity of network concepts and network diagrams in many different settings (Borgatti et al., 2009).

Limitations

Our study examined a limited number of structural variables. Other variables may have yielded additional insights. Also, the network diagrams we used came from two studies on homeless people in Los Angeles. There may be differences between these networks and networks from other populations. However, we have no reason to think that using these types of networks in this sort exercise produced data that are much different than we would have received if participants had sorted network graphs from respondents with different backgrounds. The network diagrams we included in our sort procedures represented the full range of network structural characteristics, from completely disconnected networks to completely connected networks, and a broad range of network types in between. However, the possibility remains that some unknown influence biased our findings.

The non-experts we selected for this study were not selected at random. Therefore, we are unable to determine if a similar characteristic of these participants contributed to the similarity of their sorts. For example, our participants may be more highly educated than a target population of some interventions and this experience may contribute to the similarity in the types of structural features they saw in the networks. Thus, though we demonstrated that our non-expert respondents can identify structural characteristics of network graphs, we do not know how much we can generalize these findings to other communities of non-experts. There are also some limitations due to our approach to the pile-sort task. The graphs included two types of networks that were extreme: completely disconnected networks with all isolates and completely connected networks with no isolates and high density. Although these are common forms of network types in personal network studies, a pile sort task with fewer extremes may have yielded results with different structural features emphasized by sorters.

Conclusion

These analyses strengthen the assumption that non-experts can be shown network graphs and that they will be able to intuitively identify structural characteristics of those networks. We believe our findings suggest that there is an untapped field of inquiry into what types of structural characteristics non-experts see in network graphs and what circumstances determine which structural features they identify (e.g., the background characteristics of non-experts viewing the graphs, the visualization technique for producing graphs, etc.). We also believe these findings suggest that there are many possibilities for inclusion of visualizations of social network characteristics into interventions that attempt to make individuals aware of the social environment they are embedded so that they can make changes to this environment.

We believe these findings suggest that many interventions that guide participants to change structural aspects of their networks could include network visualizations as part of their procedures. Our results indicate that non-experts are able to view network diagrams and intuitively identify structural features. Visualizations of networks may enhance their understanding of abstract network concepts. However, we recommend that interventionists incorporating network visualizations first conduct pilot tests using procedures similar to those reported here with participants similar to their target population to explore what participants detect in the visualizations. A pilot test with a small sample of intervention recipients will help identify strengths and weaknesses associated with using network diagrams to illustrate characteristics of social networks.

We also recommend additional sorts using different sorting procedures than the ones we used in this study. For example, it is likely that different sort procedures would help identify additional structural measures obvious to non-experts but not as obvious as the number of isolates or the size of the largest component. We may have been able to detect these other structural dimensions if we asked another set of participants to sort graphs that were not at the extremes of these two dimensions. Also, pile sorts of graphs that include and do not include ego might provide richer information regarding which structural features are being used in the sorting task, especially if a primary goal is to understand how ego could actively influence the network through affecting resource or information exchange (Wutich & McCarty, 2005). Additional pile sort exercises with different graphs, different special arrangements other than spring embedding, or other forms of comparison, such as successive pile sorts or triadic comparisons – asking respondents to view three items at a time and pick the one item that is most different than the other two items (see Weller & Romney, 1988) -- would help to explore this further.

In particular, we recommend an experimental design such as that used by McGrath and colleagues (McGrath et al., 1997) to identify how non-experts cognitively process different types of network graphs. This work demonstrated that the judgment of viewers of network graphs was altered with different spatial arrangements of the same graphs. An experimental design in which sorters were presented with a set of graphs that only varied a single feature (e.g., number of cliques or size of largest component) but kept all other features as constant as possible would be useful in identifying and isolating salient network features.

These recommendations are only a few possible extensions of this research. We believe there are many other possible techniques for collecting and analyzing data to explore the use of network visualizations in interventions with participants who do not have expertise in network data analysis. However, we believe it is unnecessary for additional research to take place before interventions targeting change in social networks can pilot test the incorporation of visualizations. We believe that these findings suggest that clinical encounters of many different types could be enhanced through the use of visual aids. Visualizations of social networks would help both patients and clinicians come to a mutual understanding of the social context in which a patient is experiencing illness and treatment. Incorporating structure into these visualizations may be important in many ways. For example, personal network visualizations could reveal how the negative health effects of certain stigmatizing or stress-causing network members are amplified through a high number of connections throughout the network. Also, for individuals requiring extensive social support from their networks, visualizations incorporating structure can illustrate barriers to the flow of information throughout the patient’s support network. Visualizations of network composition have already contributed to successful health interventions and we believe that adding visual depictions of structural characteristics of these networks will enhance participants understanding of their networks and may help to achieve improved health.