Tracking the Temporal Evolution of a Perceptual Judgment Using a Compelled-Response Task

Abstract

Choice behavior and its neural correlates have been intensely studied with tasks in which a subject makes a perceptual judgment and indicates the result with a motor action. Yet a question crucial for relating behavior to neural activity remains unresolved: what fraction of a subject's reaction time (RT) is devoted to the perceptual evaluation step, as opposed to executing the motor report? Making such timing measurements accurately is complicated because RTs reflect both sensory and motor processing, and because speed and accuracy may be traded. To overcome these problems, we designed the compelled-saccade task, a two-alternative forced-choice task in which the instruction to initiate a saccade precedes the appearance of the relevant sensory information. With this paradigm, it is possible to track perceptual performance as a function of the amount of time during which sensory information is available to influence a subject's choice. The result—the tachometric curve—directly reveals a subject's perceptual processing capacity independently of motor demands. Psychophysical data, together with modeling and computer-simulation results, reveal that task performance depends on three separable components: the timing of the motor responses, the speed of the perceptual evaluation, and additional cognitive factors. Each can vary quickly, from one trial to the next, or can show stable, longer-term changes. This novel dissociation between sensory and motor processes yields a precise metric of how perceptual capacity varies under various experimental conditions and serves to interpret choice-related neuronal activity as perceptual, motor, or both.

Introduction

Making a choice on the basis of a perceptual judgment can be difficult in two fundamentally different ways. First, the sensory signal may be weak or noisy relative to the sensitivity of the sensory apparatus. For instance, when driving in search of an address in a heavy downpour, discerning the street names and deciding where to turn is difficult, even when driving very slowly. Second, even if the signal is strong, the system may not be able to process it fast enough. Such is the case when a tennis player tries to return a 130 mph serve and must decide whether to hit a forehand or a backhand; now, although the ball is clearly visible, the decision must be made extremely quickly.

Psychophysical and neurophysiological experiments have focused on the former situation (Shadlen and Newsome, 2001; Ernst and Banks, 2002; de Lafuente and Romo, 2005; Gu et al., 2008) much more than on the latter (Bergen and Julesz, 1983; Ratcliff and Rouder, 2000; Kiani et al., 2008), possibly because for fast perceptual judgments, the time that the brain needs to process a relevant sensory signal is difficult to determine reliably. The core of the problem is the high variability of the reaction time (RT), a key psychophysical quantity that depends not only on sensory and motor components of a response but also on their trade-off (Welford, 1980; Luce, 1986; Sanders, 1998). As a result, it has not been possible to precisely dissociate the time courses of the perceptual and motor processes that contribute to a choice.

This issue may be crucial for understanding the neural basis of perceptual decision making, because task-related activity often correlates with both sensory and motor events associated with making a choice (Thompson et al., 1996; Gold and Shadlen, 2000; Shadlen and Newsome, 2001; McPeek and Keller, 2002, 2004). Many single-unit studies have attempted to circumvent this problem with tasks designed specifically to disrupt the natural tendency to rapidly select a sensory goal and immediately respond to it (Murthy et al., 2001; Sato and Schall, 2003; Arai et al., 2004; Carello and Krauzlis, 2004; Horwitz et al., 2004; Camalier et al., 2007). Although such studies have revealed neuronal activity that discriminates sensory events (e.g., a target stimulus versus competing distracters), its interpretation requires numerous assumptions. For example, the transition from perceptual evaluation to saccadic selection is assumed to occur the moment the neural discrimination reaches an arbitrary criterion level; but then, does the degree of discrimination at any given point in time reflect the current state of the perceptual decision process, the motor plan, or some combination of the two? This cannot be answered definitively with current choice tasks because they do not provide an independent behavioral measure of the covert perceptual evaluation process that is assumed to precede the motor report.

Here, we present data from five monkeys trained to perform a novel task whereby the perceptual capability of a subject can be reliably isolated and quantified during fast choices (Stanford et al., 2010). We investigate how motor timing and perceptual capacity interact to determine a subject's behavioral performance during color discrimination, and how these processes are modified by motivation and experience. We find that perceptual discrimination is very fast (25–50 ms) and that both the onset of the discrimination process and its speed may vary substantially from one trial to the next. These results provide important benchmarks for interpreting neuronal activity as related to perceptual performance, motor execution, or both.

Materials and Methods

Data were collected from five monkeys, G, F, R, Q, and S. One data set from monkey G and another from monkey S were presented previously (Stanford et al., 2010) and are included in this study (see Fig. 2) for comparison purposes. The rest of the data have not been used in any previous studies.

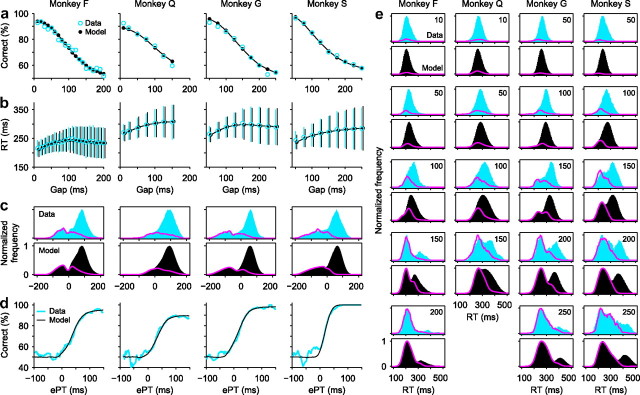
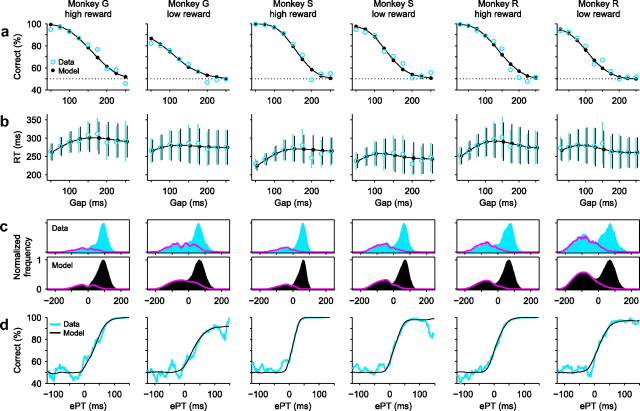
Figure 2.

Psychophysical performance of four monkeys in the CS task. a, Percentage of correct responses as a function of gap (psychometric curve). b, RT as a function of gap (chronometric curve). Data points are mean values, which include both correct and incorrect trials at each gap; error bars indicate ±1 SD. c, Distributions of ePT values for correct (blue and black bars) and incorrect (magenta traces) trials. Bin size, 20 ms. A value of 1 corresponds to the maximum number of observations in correct trials. d, Percentage of correct responses as a function of ePT (tachometric curve). Bin size, 20 ms. e, Distributions of RT values in correct (blue and black bars) and incorrect (magenta traces) trials at specific gaps. Gap values are indicated on top right corners. Bin size, 40 ms. For each monkey, the same model parameters were used in all panels (Table 1). Experimental results are based on a total of 7935, 5609, 6676, and 5231 trials for monkeys F, Q, G, and S (set 1), respectively.

Behavior.

All experimental protocols complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, United States Department of Agriculture regulations, and the policies set forth by the Wake Forest University School of Medicine Animal Care and Use Committee. For each monkey, before behavioral training, an MRI-compatible titanium post was attached to the skull under general anesthesia. During subsequent training and data collection sessions, the post served to restrain the monkey's head. Eye movements were monitored either with an implanted eye coil (monkeys F, S, and Q), which provided an analog signal of eye position at a rate of 500 Hz, or with an infrared tracking device [an EyeLink1000 (SR Research) for monkey G and an ISCAN system for monkey R] with a sampling rate of 1000 Hz.

Stimuli were colored spots presented either on a monitor (ViewSonic P815 for monkey R) or through a custom-made array of tricolor light-emitting diodes, or LEDs (for all other monkeys). In all cases, pairs of saccade targets were placed at various positions and orientations around the central fixation spot, and were separated by 10–20° of visual angle. The difficulty of the task was controlled through the time interval referred to as the gap. This parameter varied between 10 and 250 ms. RT was measured as the amount of time from the go signal until the velocity of the saccade reached a cutoff value of 50°/s. Monkeys were allowed to initiate a response up to 600 ms after the go signal; responses that took longer caused the trial to be aborted. Correct saccades were rewarded with a drop of water (0.1–0.7 ml). During the motivational bias sessions, for monkeys G and S large rewards were three times larger than small rewards (3:1 ratio), whereas for monkey R the reward ratio was 2:1. The high-reward color was kept constant for a block of 150–250 trials and was then switched. In all conditions, standard and biased, red and green targets were presented with equal probability at all target locations.

Data analysis.

We define the raw processing time (rPT) as follows:

where the gap is a temporal delay that is under the experimenter's control (see below). The rPT is the maximum amount of time that, in principle, is available for processing the sensory cue in a trial. The effective processing time (ePT) is as follows:

where the constant T_ND is the total nondecision time. This constant can be thought of as the time consumed by all the processes not specifically related to the perceptual judgment and the associated oculomotor report, averaged over trials. In the race-to-threshold model, it represents the sum of the afferent and efferent delays of a circuit that generates a saccadic choice (see below). The tachometric curve is the percentage of correct responses plotted as a function of either rPT or ePT. Because T_ND is a constant, the choice of rPT or ePT simply sets the origin of the plot differently; the shape of the curve does not change.

Tachometric curves were constructed by calculating the percentage of correct responses for all the trials within a rPT (or ePT) bin. For all curves, bin size was 20 ms and bin centers were spaced every 2 ms. To assess the positions of the tachometric curves along the time axis, as well as their steepness, we fitted each curve with the following Weibull cumulative function, as follows:

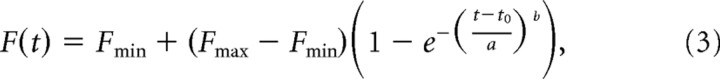where the time t is rPT or ePT, F_min and F_max are the minimum and maximum percentage correct values, and a, b, and t₀ are free parameters. Optimal values for the free parameters were found by nonlinear least-squares regression, using the Matlab function nlinfit. We refer to the time at which the curve is halfway between F_min and F_max as its center point; for instance, when F_min = 50% and F_max = 100%, it is equal to the time at which F reaches 75%. Given the parameters of a curve, the center point is equal to

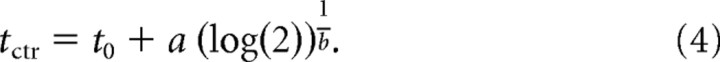To quantify the steepness of the curve, we use the rise time, which is given by

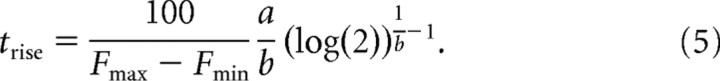The rise time is the time that it would take for the curve to go from 50 to 100% correct if its slope were always equal to the slope at the center point. Thus, steeper curves have shorter rise times. In summary, the center point and the rise time of a tachometric curve are obtained by fitting the curve to a Weibull function and applying the two expressions above.

Bootstrapping techniques (Efron, 1982; Davison and Hinkley, 2006) were used to quantify differences between tachometric curves; specifically, differences in their center points and rise times. Two analyses were performed. First, we estimated the joint distributions of those two characteristic parameters. For each tachometric curve, this was done by (1) generating 2000 new curves by resampling with replacement the original set of experimental trials, (2) fitting each new curve with a Weibull function, and (3) calculating the corresponding center points and rise times using Equations 4 and 5. The resulting distributions indicate the likely spread of t_ctr and t_rise for the original curve (see Figs. 6b,d,f, 7b, 9b).

Figure 6.

Comparison of perceptual performance in high- versus low-reward trials. a, Percentage of correct responses as a function of rPT (tachometric curve) for high-reward (purple trace) and low-reward (orange trace) trials performed by monkey G. The black lines are best Weibull fits. The vertical dotted lines mark the time points at which the percentage correct is halfway between the minimum and maximum values (i.e., t_ctr). The experimental data are the same as in Figure 5d, except with rPT (=RT − gap) on the x-axis. b, Joint distributions of center points (t_ctr) and rise times (t_rise) obtained from bootstrapping of monkey G's data. For clarity, only 1000 points per set are shown. The crosses mark the t_ctr and t_rise values of the original fits shown in a. Histograms at the top and on the right show the corresponding marginal distributions, based on 2000 resamplings per set. c–f, As in a and b, but for monkeys S and R.

Figure 7.

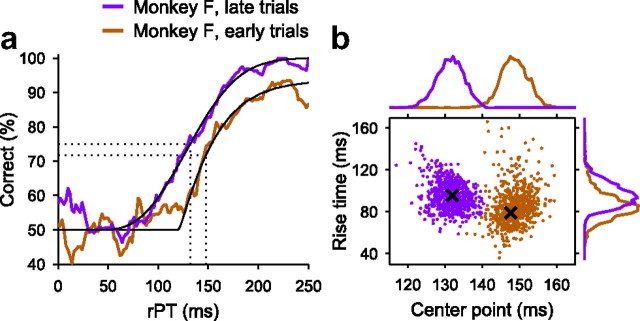
Comparison of the perceptual performance of monkey F during early and late trials. a, Tachometric curves based on 2632 early and 2599 late trials. b, Joint distributions of center points and rise times obtained from bootstrapping. The format is the same as in Figure 6.

Figure 9.

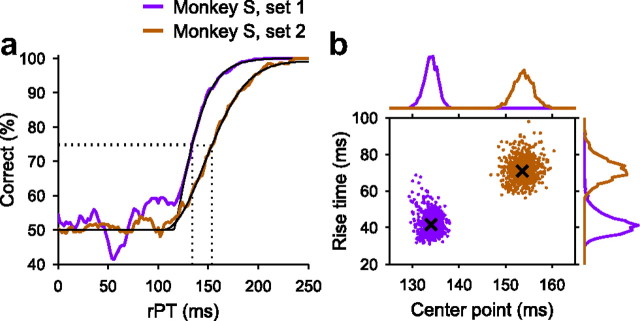
Comparison of the perceptual performance of monkey S in data set 1 versus data set 2. a, Tachometric curves. b, Joint distributions of center points and rise times obtained from bootstrapping. The format is the same as in Figure 6.

The second analysis was applied to pairs of tachometric curves and was specifically designed for calculating the significance of the differences between them. For example, suppose that curves A and B were obtained with N_A and N_B trials, that the difference in center points was Δt_ctr, and that the difference in rise times was Δt_rise (computed so that they are positive). The significance of these differences was computed by (1) combining all the trials into one set of N_A + N_B trials, (2) shuffling those N_A + N_B trials 10,000 times, (3) generating 10,000 new pairs of tachometric curves by splitting each shuffled set into two sets of N_A and N_B trials, (4) fitting Weibull functions for each new pair of curves and computing the corresponding differences in center points and rise times, exactly as done with the original data, and (5) calculating the fraction of repetitions (of 10,000) in which the difference between center points was ≥Δt_ctr and the fraction of repetitions in which the difference between rise times was ≥Δt_rise. These numbers give the probability of having observed the measured differences Δt_ctr and Δt_rise or larger ones just by chance, when there was actually no difference between the two data sets.

When plotting a tachometric curve as a function of ePT, another useful quantity is the time required to reach 75% correct, or t₇₅. This quantity was read directly from the experimental curves, using linear interpolation if necessary. The variability in t₇₅ was quantified in two ways: (1) by bootstrapping, as described above; that is, the original data were resampled with replacement 2000 times, and from the resulting 2000 curves, the SD of the t₇₅ values was obtained; (2) by running the race-to-threshold model 2000 times with parameter values that best replicated the experimental data, each time simulating the same numbers of trials per gap as in the data. A distribution of t₇₅ values was obtained from the simulated tachometric curves, and an SD was computed from it. The SD values obtained with these two methods were typically within 1 ms of each other (and were similar to the SD of t_ctr as well). In Results, we quote the largest of the two.

Accelerated race-to-threshold model.

All model simulations were performed using Matlab (The Mathworks). The code is available from the authors on request.

The race model was the same as used in a previous report (Stanford et al., 2010) (see also Salinas et al., 2010) except for one minor difference described below. The model consists of two competing variables, x_L and x_R, that represent the population activity of neurons triggering movements to the left and to the right, respectively. Each race corresponds to a behavioral trial in which a saccadic response is produced. In each race, both variables start with a value of 0, and the winner is the first one to climb to a threshold of 1000 units, at which point the race is over. The outcome of the race is considered to be a movement to the left if x_L wins, or a movement to the right if x_R wins.

Each race has two parts: a first, precue stage during which the relevant sensory information is not yet available, and so the competition is random, and a second stage during which this information is accessible and influences the competing variables. Crucially, the sensory cue acts by favoring a movement toward the target side, such that if the target is on the right and the distracter on the left, then x_R increases toward threshold more rapidly than x_L; and vice versa, if the target is on the left, then x_L speeds up and x_R slows down.

Each simulated trial proceeds as follows. The go signal is given at t = 0 and the race starts as soon as this signal reaches the model oculomotor circuit, which happens after an afferent delay T_A. During this first stage, the rates at which x_L and x_R change—the buildup rates—are constant and random; they are drawn from a two-dimensional Gaussian distribution with mean r_G (same for both variables), SD σ_G (same for both variables) and correlation coefficient ρ_G. Negative values of ρ_G, as found in all fits, indicate that the competing variables are anticorrelated; when one increases at a high rate, the other increases at a much lower rate or even decreases. During this stage, x_L and x_R evolve as follows:

where r_L⁰ and r_R⁰ are the buildup rates drawn initially. In races in which one of the variables reaches threshold during this stage, the outcome is a coin toss, because the buildup rates were sampled randomly from a symmetric distribution. Otherwise, the two oculomotor plans keep changing as prescribed by the above equations until the cue information arrives. The cue is revealed gap milliseconds after the go signal, at t = gap, so it reaches the model circuit at t = gap + T_A. At this time, the competing variables start accelerating according to the locations of the target and distracter. If the target is on the right side, then the buildup rate of x_R approaches a large, positive value r_T (for target) and the buildup rate of x_L approaches a small or negative value r_D (for distracter). The corresponding equations are as follows:

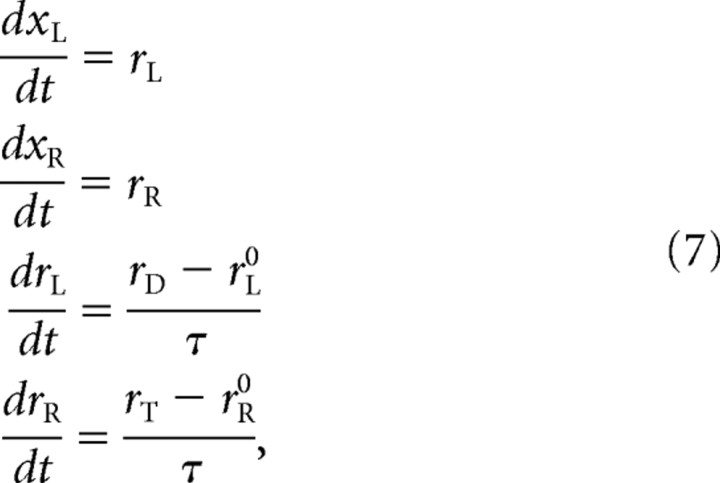with the added rule that, once the buildup rates reach their new target values—that is, once r_L is equal to r_D and r_R is equal to r_T—they stop changing, so the last two derivatives become zero. In this way, the acceleration is constant but lasts a finite amount of time, which is precisely equal to τ, and r_T is the maximum possible buildup rate for the variable that generates a movement toward the target. The assumption that the acceleration remains constant (while it occurs) is not only simple but also computationally convenient because it means that the time to threshold can be computed analytically.

In the converse situation, when the target is to the left of fixation, the roles of x_R and x_L are reversed: when the sensory information arrives, r_L increases toward the high rate r_T and r_R decreases toward the low rate r_D, so

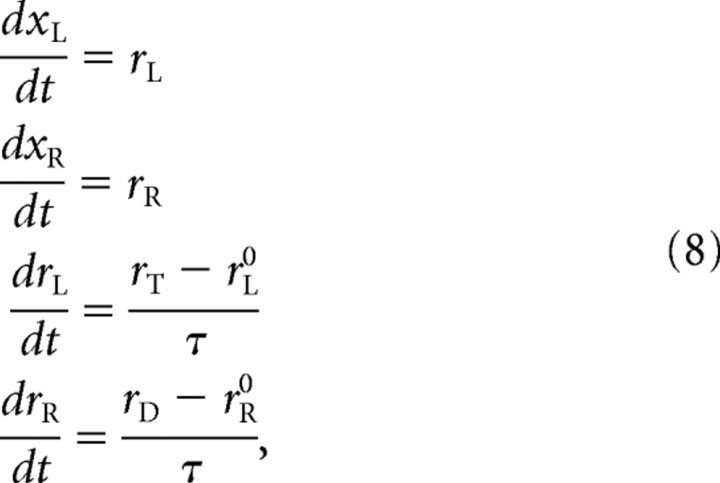in this case, again applying the rule that the last two derivatives become zero once the equilibrium values are reached. This integration process continues until x_R or x_L reaches threshold, and a saccade is assumed to occur a short efferent delay T_E after that. The outcome (saccade direction) and RT are then recorded for the trial.

Apart from this basic description, there are three additional aspects of the model that are important. First, we observed that the monkeys occasionally made mistakes at long ePTs, when they should have had enough time to make an accurate color discrimination. To account for such lapses, in each simulated trial there is a small probability p_e of making an incorrect assignment; that is, of associating the target and distracter rates r_T and r_D with the wrong (i.e., reversed) locations. This amounts to exchanging Equations 7 and 8 in a fraction p_e of the trials chosen randomly. In practice, within the range of behaviors explored here, the parameter p_e uniquely sets the maximum value of the tachometric function.

Second, we assume that the afferent delay varies across trials and independently for the go and cue signals. This variability is Gaussian with a SD σ_A, but such that negative delays are not allowed.

Third—and this implementation is slightly different from in the original version of the model (Stanford et al., 2010)—the rise to threshold is interrupted between t = I₁ and t = I₂. During this interval, neither the buildup rates nor x_L and x_R change. This interruption was included to account for a dip that is often seen in the ePT distributions of the monkeys near ePT = 0; its effect on the rest of the curves was generally modest. The onset and offset times I₁ and I₂ are constant and are given with respect to the point in time when the cue information reaches the circuit. So, if I₁ = −10 and I₂ = 5, for instance, the interruption starts 10 ms before the cue information arrives and lasts 15 ms.

It may seem strange that such interruption can occur before the cue information arrives at the circuit, but there are two possible explanations for this. First, the interruption could be effected by other circuits that receive the cue information earlier than the model oculomotor circuit. And second, although the race itself requires color-specific information, the interruption does not; that is, the interruption could be attributable to the detection of the cue (“colors changed”) occurring before its content (“red on the left, green on the right”) is determined. This is consistent with the general finding that reaction times for detection are generally shorter than for discrimination (Luce, 1986; Sanders, 1998).

In all, the race model has 11 free parameters that were adjusted to match each monkey's data (Table 1). The model does not distinguish between the afferent and efferent delays; it is only their sum, the total nondecision time, that matters. The total nondecision time varies across trials because it inherits the variability of T_A. The single parameter T_ND represents its mean value averaged across trials. The model produces different outcomes and RTs from one trial to another primarily because different initial buildup rates (r_L⁰, r_R⁰) are drawn for each trial; the variability of T_A, which is the only other independent quantity that also changes in every trial, has a more modest influence on the results.

Table 1.

Model parameter values for each data set

Monkey	rG	σG2	ρG	rT	rD	τ	TND	σA	I1	I2	pe
F	5.6	13	−0.6	150	−140	1600	91	10	−16	3	0.048
Q	4.2	16	−0.7	34	−23	310	150	13	−8	−4	0.105
G	4.5	17	−0.8	340	−220	1600	139	20	−40	−10	0.02
S, set 1	3.8	20	−0.6	43	−23	190	116	8	−5	0	0
S, set 2	6.4	34	−0.7	16	−8	180	106	8	−10	−5	0
G, high reward	4.1	4	−0.95	160	−120	1800	104	14	−15	6	0
G, low reward	5.3	11	−0.8	130	−110	900	136	23	−7	9	0.085
S, high reward	4.7	5	−0.9	20	−12	85	102	11	−16	−3	0
S, low reward	5.7	8	−0.7	17	−14	90	106	16	−16	6	0.02
R, high reward	5.2	14	−0.8	40	−37	180	142	23	−25	5	0
R, low reward	7.0	20	−0.6	22	−31	140	155	26	−20	5	0.03

Model fitting.

For each experimental data set, the free parameters of the race-to-threshold model were optimized to minimize the mean absolute error between the simulated and the monkey data. Six psychophysical curves were used to fit each data set: the psychometric (percentage correct vs gap), chronometric (mean RT vs gap and SD of the RT vs gap), and tachometric (percentage correct vs rPT) curves, and the rPT distributions for correct and error trials. Thus, the error function had the following form:

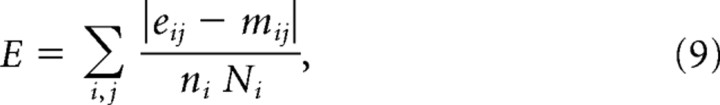where e and m are experimental and model values, respectively; the index i = 1, 2, … 6 identifies each of the six psychophysical curves; the index j runs through each point in a curve; the factor n_i is the number of points in curve i; and N_i normalizes the contribution of each curve according to its range of values. For example, suppose that curve 1 consists of nine points that vary between 0.4 and 1.0; then n₁ = 9 and N₁ = 0.6. In this way, the error contributed by each curve is expressed as a fraction between 0 and 1.

Best-fitting parameter values were found by exhaustive search; that is, by establishing a multidimensional grid where each point is a different combination of parameters, running the model with each combination, and selecting the one that minimized the above error. For each data set, a coarse grid covering a wide parameter range was used initially, and progressively finer grids were used afterward. Separate parameter optimizations run with different initial conditions typically converged on nearly identical results. In general, changes in the responses of the model (and in E) became appreciable when each single parameter varied by ∼10%, but two quantities were sensitive to even smaller changes: p_e, which determines quite precisely the maximum value of the simulated tachometric curve, and T_ND, which determines the position of this curve along the x-axis; typically, noticeable changes in the error were produced when T_ND deviated by 2 ms or more from its optimal value. Compared with such sensitivity (≤10%), the range of variation of the optimal parameter values found across all monkeys and conditions (Table 1) was much larger, suggesting that there was little redundancy in their effects.

Minimal functional model.

Given the task design, the psychometric, chronometric, and tachometric curves are not independent of each other. In particular, knowing the latter two is sufficient to determine the former. This statistical relationship is independent of the race model or any other mechanistic framework. Thus, the minimal functional model is just a straightforward sampling procedure for inferring the psychometric curve given Equation 1, the subject's perceptual capacity (tachometric curve), and his overall motor performance (chronometric curve). It runs as follows.

We assume that the tachometric and chronometric curves are known. Then a series of trials are performed, each consisting of four steps: (1) a gap is selected and a RT is drawn from the given RT distribution for that gap, (2) the rPT is calculated by subtracting RT − gap (Eq. 1), (3) the probability of a correct response for that rPT is read out from the given tachometric curve, and (4) the outcome of the trial, correct or incorrect, is set according to that probability. In this way, by averaging over many trials, one obtains the percentage of correct responses as a function of gap—the psychometric curve.

The advantage of this reduced model is that it allows us to systematically explore how different features of the chronometric and tachometric curves determine a subject's choice accuracy in the task regardless of the underlying neural mechanisms. It tells us how observed changes in choice accuracy correlate with changes in perceptual and motor speed.

Results

The compelled-response paradigm

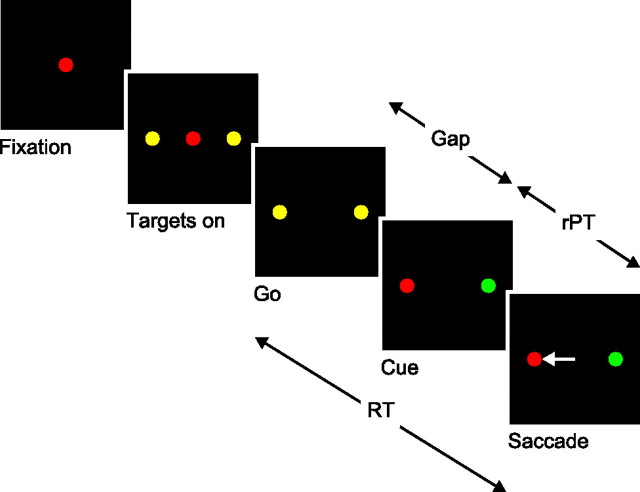
The sequence of events in the compelled-saccade (CS) task is shown in Figure 1. First, the subject fixates on a central spot and its color, red or green, indicates the color of the target. Then two yellow spots appear, separated by 10–20°. These are the potential saccadic targets. Next, the fixation spot disappears; this is the go signal that instructs the subject to initiate a saccade to one of the peripheral spots, although at this point both are still yellow. The identities of the target and distracter are revealed later, after a time gap that varies between 10 and 250 ms in duration, at the point marked “cue.” At the cue, one yellow spot turns red, and the other, green. Finally, once the saccade is executed, if the response is correct, a drop of liquid is given as a reward. The RT is measured between the onset of the go signal and the onset of the saccade, and the key parameter under the experimenter's control is the gap duration, which determines the amount of time that the crucial information is withheld.

Figure 1.

Schematic of the CS task. In each trial, the subject must make an eye movement to the peripheral spot that matches the color of the fixation point (red, in this example). However, the instruction to make the saccade (Go) is given first, before the identities of the target and distracter are revealed (Cue). Task difficulty is controlled according to the time gap between the go and the cue (10–250 ms). In each trial, the maximum amount of time available for viewing the cue is the rPT.

The objective of the CS task is to decouple the perceptual-evaluation and motor-planning stages of the task by triggering all saccades in the same way but varying their success rate according to the amount of sensory information that is presented later, while the oculomotor plan develops. That is, the go signal is always given first, so once the perceptual information becomes available, it influences a saccadic choice process that is already ongoing. The situation is analogous to that faced by players in tennis and other sports in which a judgment about the trajectory of the ball must be made extremely fast: to be able to strike the ball, the player typically starts his or her motion early, before seeing the ball (Abernethy, 1990; Land and McLeod, 2000; Yarrow et al., 2009). Note that the version of the task that we have implemented is based on eye movements, but this is not essential; the same design could be used with other motor actions instead.

The task and the psychophysical results that follow can be understood intuitively by recognizing that performance should vary continuously between two extremes. At very short gaps (e.g., zero), the subject has enough time to view the red and green stimuli and find the target, so performance is expected to be near 100% correct. In contrast, at very long gaps (e.g., infinite), the motor response must be executed before the cue is revealed, so the subject must guess the target location. Performance is expected to be near 50% correct in this case. Because gap values are pseudorandomly interleaved across trials, the timing of the cue is unpredictable, and the subject's choices throughout an experimental session are combinations of guesses and informed discriminations.

Quantifying perceptual performance

Figure 2 illustrates the behavior of four monkeys trained to perform the CS task. The psychometric curves (Fig. 2a) show that performance is >90% correct at short gaps, when the subjects have a relatively long time to differentiate target from distracter, and as the gap becomes longer, performance drops to chance levels, near 50% correct. Meanwhile, mean RTs show relatively little variation, particularly considering the large spread in RT at each gap (Fig. 2b) (error bars indicate ±1 SD). Therefore, in the compelled-response condition, large changes in performance are relatively decoupled from systematic changes in RT.

Although performance clearly varies as a function of gap, the gap is a period of time during which the relevant sensory information is absent from the visual display. What is most important is the complement of the gap, the interval of time during which the cue information is available for viewing. The maximum possible length of this complementary interval in any given trial is equal to the RT minus the gap. We call this quantity the raw processing time, or rPT (Eq. 1, Fig. 1). Note, however, that in each trial there may be other intervals beside the gap period during which the cue information is either unavailable or not being processed. For instance, any transmission delays between the retina and the circuits that generate the saccadic choice should also be subtracted from the rPT. We refer to the effective processing time, or ePT, as the rPT minus the total time T_ND consumed by any nondecision processes (Eq. 2). We will explain in a moment how, through a model, T_ND may be estimated.

The ePT is the crucial quantity that determines performance in the CS task because it corresponds to the amount of time that the subject effectively has for viewing and analyzing the relevant sensory information in each trial. Indeed, when plotted as a function of ePT, performance varies much more sharply than as a function of gap (Fig. 2, compare a, d, noting difference in timescale). We refer to the resulting curve (Fig. 2d) as a “tachometric curve” because it directly reveals the speed of a subject's perceptual processing. For instance, monkeys F and Q required 50 ± 3 ms (±1 SE, from bootstrap) (see Materials and Methods) and 46 ± 3 ms, respectively, to go from chance to 75% correct. In contrast, monkeys G and S, whose data were reported previously (Stanford et al., 2010), had somewhat sharper tachometric curves and so discriminated faster: they reached 75% correct in 42 ± 2 and 26 ± 2 ms, respectively.

The distributions of ePT values for correct and error trials also have distinctive features that are consistent with the constraints of the task (Fig. 2c). For ePT <0, the distributions of correct and error responses are practically identical. This is to be expected because a negative ePT corresponds to a trial in which the subject had no time to view the red and green stimuli, and so was forced to guess. In contrast, longer, positive ePTs mean that the subject had time to view the stimuli and hence made an informed decision. So, the proportion of correct versus incorrect responses increases sharply after ePT = 0 (in fact, if one plots the rPT distributions, which are identical except for a shift along the x-axis, the point at which the error and correct distributions split from each other is always within a few milliseconds of the T_ND value inferred from the model, which represents the time at which the sensory information starts to have an effect on performance). The tachometric curve is closely related to the distributions in Figure 2c: it is obtained by dividing (pointwise) the curve for correct trials by the total number of trials at each point (i.e., by the sum of the curves for error and correct trials).

The data in Figure 2 extend our previous observations (Stanford et al., 2010) and show that behavior in the task is consistent across subjects.

A race-to-threshold model of the CS task

The interplay that takes place in the CS task between making an informed decision (at short gaps/long ePTs) and guessing (at long gaps/negative ePTs) can be easily understood with a simple phenomenological model (for details, see Materials and Methods). In the model, a saccadic choice is conceived as a competition between two variables, x_L and x_R, that represent the activities of two populations of oculomotor neurons. An eye movement is generated when one of the variables reaches a threshold, as in previous accounts of saccadic response generation (Carpenter and Williams, 1995; Hanes and Schall, 1996; Roitman and Shadlen, 2002; Smith and Ratcliff, 2004; Palmer et al., 2005; Hanks et al., 2006; Lo and Wang, 2006; Wong and Wang, 2006; Boucher et al., 2007; Ratcliff and McKoon, 2008). Importantly, however, these developing oculomotor plans are also informed by sensory input (Horwitz and Newsome, 1999; Gold and Shadlen, 2000; Shadlen and Newsome, 2001; Churchland et al., 2008). Here, the essential idea is that, when the sensory information becomes available to the oculomotor circuit, its effect is to speed up the developing saccadic plan toward the target and slow down the plan toward the distracter. In this way, the model produces both random choices (guesses) and accurate choices, depending on when that information arrives; that is, on the gap.

In each simulated trial, the model generates an outcome, left or right, and a RT. When x_L reaches threshold first, a movement to the left spot is produced; and vice versa, when x_R reaches threshold first, the response is to the right. Figure 3 shows various examples of simulated trials in which x_L and x_R correspond to green and red traces, respectively. All the races start in the same way: a short period after the go signal (afferent delay, 60 ms in the examples of Fig. 3), the two variables start increasing with constant rates. These initial buildup rates are drawn randomly from a distribution, because the identities of the target and distracter are initially unknown. The rates are anticorrelated (ρ_G < 0), so when x_R starts rising very fast x_L tends to rise much more slowly or may even decrease, and vice versa. Then, once the gap period of the circuit has elapsed, the buildup rates begin changing according to the target and distracter locations [the gap period of the circuit has the same duration as the gap but occurs later because of the afferent delay; it is the period during which the oculomotor plan proceeds without guidance from the cue (Fig. 3, area marked in gray)]. So, if the target is, say, on the right, as is the case in all the shown examples, then the buildup rate of x_R increases and that of x_L decreases. That is what happens in Figure 3, a–c, f, and g. Most of those trials are correct because the variable representing the target side typically reaches threshold first, even if it rises more slowly at the beginning, before the cue information is available (as in Fig. 3b,g). The only exception is Figure 3c, where x_L increases so fast initially, that it reaches threshold before x_R can catch up, resulting in an error. In contrast, in Figure 3, d, e, h–j, the race is over before the end of the gap period of the circuit, so the winner is determined randomly. Trials like those, which end before the cue information becomes available, typically occur at long gaps.

Figure 3.

Ten trials of the race-to-threshold model. Each panel shows the competing variables x_L (green traces) and x_R (red traces) as functions of time. In these examples, the target was always red and located to the right of fixation, so trials in which the red trace (x_R) crosses threshold (dotted lines) first are correct and trials in which the green trace (x_L) crosses threshold first are errors. The black triangles and black vertical lines mark when the go signal is given (Go) and when the saccade is initiated (Sac); the interval between them is the RT. In these examples, each race starts 60 ms (afferent delay) after the go, and a saccade is produced 30 ms (efferent delay) after threshold crossing, so T_ND = 90 ms. The gray shadows mark the gap period of the circuit. a–c, Three trials with a 50 ms gap. d–g, Four trials with a 150 ms gap. h–j, Three trials with a 250 ms gap. The blue bars indicate the ePT period; numbers below are ePT values. Positive ePTS (dark blue) correspond to races influenced by the sensory cue (a–c, f, g). Negative ePTs (light blue) correspond to races that end before the cue information is available and thus have random outcomes (d, e, h–j).

This model is useful in three ways. First, in it the ePT is perfectly well defined: it is the time between the end of the gap period of the circuit and the threshold crossing (Fig. 3, blue bars and ePT values shown below). Second, the nondecision time is also well defined and is equal to the afferent plus the efferent delays (note, however, that what matters for the model is their sum, so T_ND is indeed a single parameter). The mean nondecision time T_ND for a particular data set can be estimated by fitting the model to those data. For monkeys F and Q, T_ND was equal to 91 ms (the smallest in all data sets we have analyzed) and 150 ms (the second largest in all data sets we have analyzed), respectively, which is consistent with the relatively large difference in mean RT between the two animals (Fig. 2b). And third, the model provides an intuitive and quantitative understanding of the mixture of informed decisions and guesses that subjects execute during the CS task. As can be seen in Figure 2, with the correct parameter values the model can replicate a monkey's behavior quite accurately (compare data vs model). In particular, examine the RT distributions for correct and error trials that are found at each gap (Fig. 2e). For correct responses, the RT distribution transitions from unimodal to bimodal, whereas for incorrect trials, the peak of the RT distribution typically remains at the same point and coincides with the early peak of the correct-trial distribution. The model captured this progression quite accurately in all the data sets from the five monkeys.

An important feature of the tachometric curve that should be kept in mind is that its shape does not depend on the set of gap values used in the experiment. According to the model, for a given perceptual task, the tachometric curve is an intrinsic property of the subject. Therefore, the gaps are chosen experimentally to generate a range of ePT values that is large enough to yield the full tachometric curve (and to prevent the subjects from predicting the cue onset), but as long as the resulting ePT distribution is wide enough, the specific gap values do not matter. This is manifest in Figure 2. There, the tachometric curves for monkeys F and Q are fairly similar, although they were obtained with quite different sets of gaps (Fig. 2a).

Performance as a result of perceptual and motor processes

Successful performance in the CS task depends both on the speed of the color discrimination, which is revealed by the tachometric curve, and on the speed of the motor report. It is precisely the ability to independently assess the relative contributions of perceptual and motor processing that is a key feature of the CS task. To better understand how these two factors can interact to determine performance, Figure 4 shows how various forms of chronometric (i.e., RT vs gap), tachometric, and psychometric curves relate to each other, as predicted by a minimal functional model. This is a highly simplified framework, entirely separate from the race-to-threshold model, that describes the functional relationships between the three curves (see Materials and Methods). This figure serves as a road map for understanding the various effects that may be observed when varying the conditions of a compelled-response experiment.

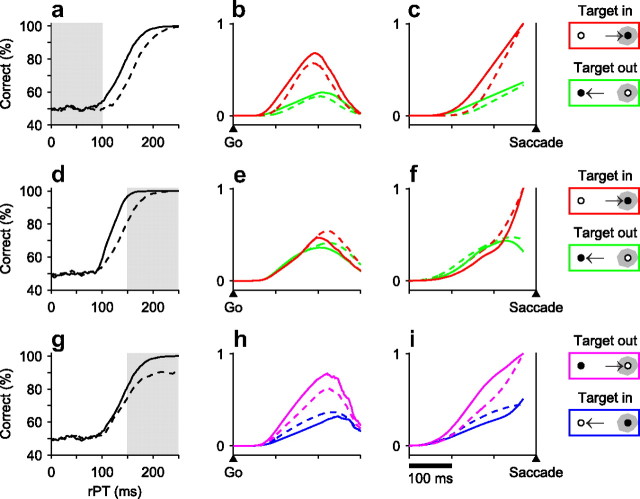
Figure 4.

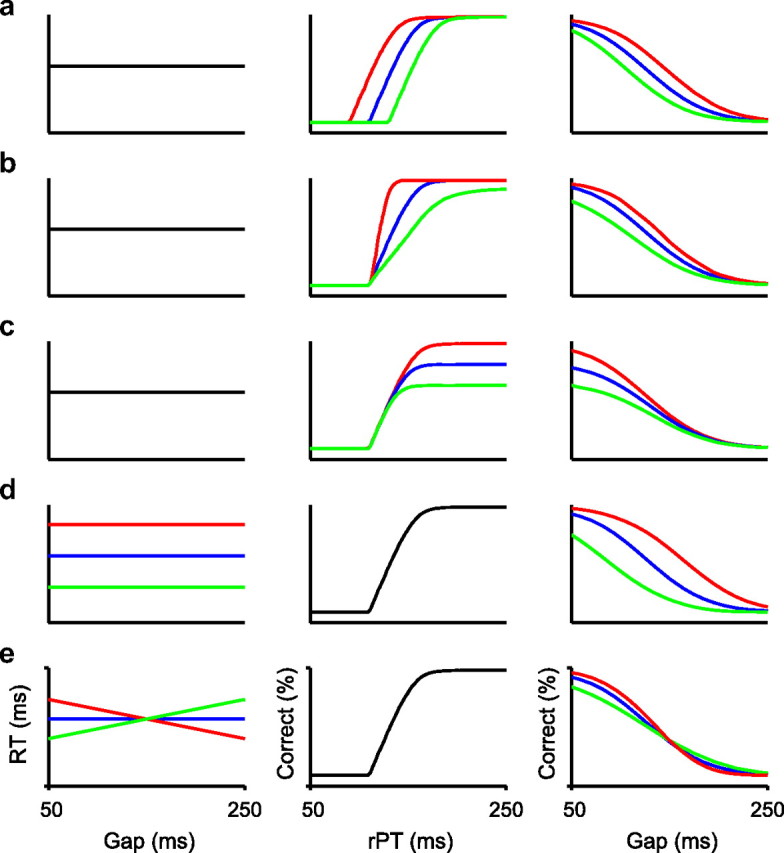
Overall performance in the CS task depends on motor timing and perceptual discrimination. Each row shows one or more hypothetical chronometric curves (left column), one or more hypothetical tachometric curves (middle column), and the resulting psychometric curves (right column) obtained from the minimal functional model. Only mean RTs are shown, but full distributions were used. a–c, Variations in performance caused by variations in the onset of perceptual discrimination (a), in the speed of perceptual discrimination (b), or in the maximum perceptual accuracy (c). d, e, Variations in performance caused by variations in RT.

The basis of this minimal functional model is that performance in the CS task is fully determined by the subject's tachometric and chronometric curves: the former specifies how much viewing time is needed to achieve a particular success rate and the latter specifies how much total time is needed to respond given a particular gap, so by combining them one can derive the success rate as a function of gap—the psychometric curve. Figure 4 was created by generating hypothetical chronometric (Fig. 4, left column) and tachometric (Fig. 4, middle column) curves and applying the minimal functional model to infer the corresponding psychometric curve (Fig. 4, right column).

Figure 4a–c illustrates the consequence on performance of altering the tachometric curve in different ways while the distributions of RTs remain constant. Similarly, Figure 4, d and e, shows the opposite case, when the tachometric curve does not change but the RT distributions do. It is easy to see that overall performance in the CS task can improve through a combination of four mechanisms: (1) by shifting the tachometric curve to the left, which means that the discrimination process starts earlier in the trial (Fig. 4a); (2) by increasing the steepness of the tachometric curve, which means that, once begun, the perceptual discrimination progresses more rapidly (Fig. 4b); (3) by bringing the percentage correct at long viewing times as close to 100% as possible (Fig. 4c); and (4) by increasing the RT, in which case the subject has more time to view the stimuli (Fig. 4d). It is also worth noting that the slope of the chronometric curve partially determines the steepness of the psychometric curve (Fig. 4e).

The minimum functional model provides a statistical description of the task, not a mechanistic one like the race-to-threshold model. Because of this, the basic effects shown in Figure 4 do not necessarily correspond to changes in single parameters of the race model. There are, nonetheless, important regularities: mechanism 1 (Fig. 4a) corresponds most closely to changes in T_ND, the mean nondecision time; mechanism 2 (Fig. 4b) corresponds primarily to changes in the acceleration parameters, r_T, r_D, and τ, which convey the influence of the sensory cue; mechanism 3 (Fig. 4c) corresponds exactly to changes in p_e for the range of behaviors explored here; and mechanisms 4 and 5 (Fig. 4d,e) correspond mostly to changes in r_G, σ_G, and ρ_G, which determine the oculomotor activity that develops initially, although practically all other parameters contribute to some degree as well.

Given this catalog of possible effects, we performed experimental variations of the CS task and diverse types of data analyses to determine whether the expected relationships between psychometric, chronometric, and tachometric curves were actually observed. If these are indeed the basic psychophysical effects that a subject may exhibit in a compelled-response situation, such would provide strong evidence that motor and perceptual contributions to changes in behavioral performance can be clearly dissociated.

Motivation modulates performance through multiple mechanisms

To generate changes in the subject's RTs and performance levels, we implemented a variant of the task in which the monkey knew at the beginning of each trial, via the color of the fixation point, whether a large or a small reward was at stake. In this condition, correct movements to, say, the red target yielded a high reward, whereas correct movements to the green target yielded a lower reward. The association between colors and reward amounts was kept constant for blocks of 150–250 trials and then the high- and low-reward colors were reversed. In this experiment, the target color is revealed at the beginning of each trial, when the fixation spot appears, so the subject always knows whether the current trial can lead to a large or a small reward. Thus, the incentive to perform the task correctly varies across trials and is set at the start of each one.

Initially, data in this “motivational bias” experiment were collected from monkeys G and S. Their behaviors, however, were somewhat different, so to try to gain some additional insight as to which effect was more common, a third monkey, monkey R, was subsequently trained. This third subject displayed an effect similar to that of monkey G. The results of this experiment are shown in Table 2 and Figure 5; for ease of comparison, all results are displayed separately for high- and low-reward trials, although these were interleaved during task performance.

Table 2.

Behavioral performance in the motivational bias experiment

	Monkey G		Monkey S		Monkey R
	High reward	Low reward	High reward	Low reward	High reward	Low reward
Trials	2394	2421	4728	4538	2742	2834
Correct (%)	81	67	81	72	73	67
p (binomial)	10−15		10−10		10−3
RT ± 1 SD (ms)	288 ± 39	276 ± 43	258 ± 35	249 ± 39	279 ± 44	270 ± 43
p (Wilcoxon)	10−23		10−39		10−13
trise ± 1 SE (ms)	91 ± 9	98 ± 13	40 ± 6	60 ± 7	68 ± 10	68 ± 8
p (bootstrap)	0.26		0.0061		0.50
tctr ± 1 SE (ms)	139 ± 5	170 ± 5	115 ± 2	123 ± 3	151 ± 3	170 ± 3
p (bootstrap)	0		0.0015		0

Percentage correct and RT data are averages over all gaps. Significance values from bootstrap are based on 10,000 resamplings.

Figure 5.

Psychophysical performance of monkeys G, S, and R during the motivational bias experiment. At the beginning of each trial, the monkey knew whether a correct response would result in a small or a large reward. a, Psychometric curves. b, Chronometric curves. c, Distribution of ePT values. d, Tachometric curves. Data are shown separately for high- and low-reward trials, as indicated. The format is the same as in Figure 2. See Table 2.

The psychometric and chronometric curves (Fig. 5a,b) show that, when working for a small reward, monkeys performed worse and initiated their responses sooner (Table 2). Consistent with the hypothetical curves of Figure 4d, the slight but significant increase in overall RT observed in large-reward trials was accompanied by an increase in choice accuracy. Perhaps more importantly, there were differences in the corresponding tachometric curves too (Fig. 5d), but these were not identical for the three subjects: as explained below, in monkeys G and R the dominant effect was a change in the onset of the discrimination process, whereas in monkey S there was a significant difference in perceptual processing speed.

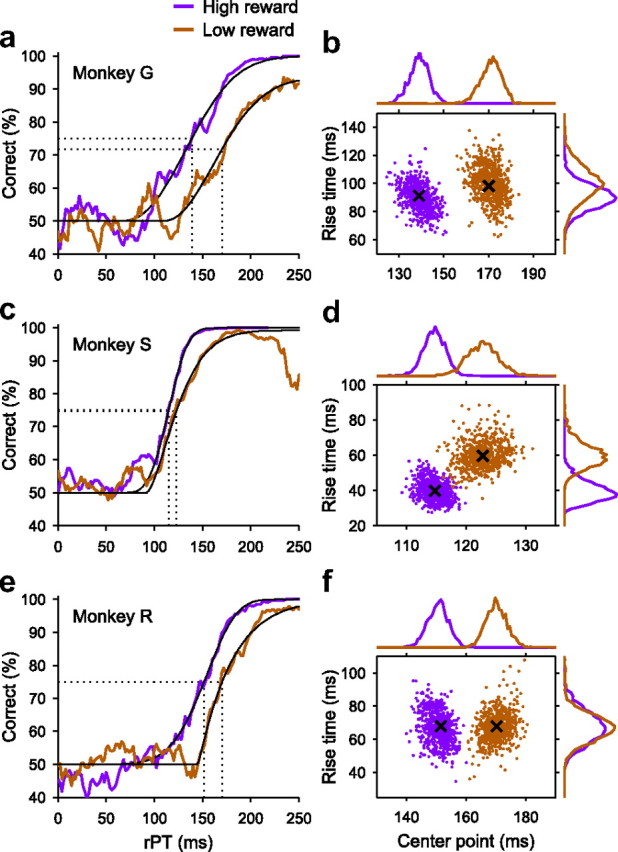
To compare the low-reward and high-reward tachometric curves of each monkey more carefully and, in particular, to determine whether they differed significantly in steepness, we performed the analysis shown in Figure 6 (see Materials and Methods). Here, the tachometric curves obtained in high- and low-reward trials are replotted using rPT on the x-axis. In this way, the values on the y-axis are the same as before, with ePT, but the original relative timing is preserved, and more importantly, because T_ND is taken out of the calculation, the analysis becomes insensitive to any error in T_ND. The thin black lines superimposed on the purple and orange traces are the cumulative Weibull functions that best fitted the data. To characterize each tachometric curve, we considered two quantities that were derived from the respective Weibull fits: the center point and the rise time (see Materials and Methods). The center point t_ctr is the rPT at which performance reaches the midpoint between the minimum and the maximum percentage correct (Fig. 6a,c, vertical dotted lines). The rise time t_rise is inversely related to the steepness of the curve; it is the time that it would take for performance to go from 50 to 100% correct if the slope were constant and equal to the slope at t_ctr.

The crosses in Figure 6b indicate the values of t_ctr and t_rise for the two tachometric curves of monkey G, and the surrounding clouds of dots show the values obtained by bootstrapping; that is, by repeatedly resampling with replacement the original trials and recomputing the fits (see Materials and Methods). The distributions of likely center point values (Fig. 6b, histograms at the top) and rise time values (Fig. 6b, histograms on the right) were obtained from these clouds of points, and their overlap indicates whether these parameters are significantly different when compared across the two conditions. Note, however, that the corresponding p values were actually obtained through a second resampling analysis specifically designed for evaluating the significance level (see Materials and Methods).

In the case of monkey G, there are three notable results. First, the tachometric curves are shifted relative to each other by ∼30 ms (Table 2) and the shift is highly significant, as is apparent by the lack of overlap in the distributions of t_ctr values in Figure 6b (top histograms). This means that the decision-making process starts ∼30 ms later in low- than in high-reward trials. This effect is precisely the one shown in Figure 4a, and it is consistent with more accurate performance in high- than in low-reward trials, as expected.

The second result to be noted in Figure 6, a and b, is that the steepness of the two curves was statistically identical. The tachometric curve for high-reward trials had a slightly shorter rise time (Table 2), but in this case the distributions of likely values obtained from bootstrapping were highly overlapping (Fig. 6b, histograms on the right), and the difference was not significant (Table 2). Therefore, for monkey G, the speed of the perceptual process remained essentially constant across the two conditions.

Finally, the third result for monkey G is that the maximum percentage correct reached by the two curves in Figure 6a was not the same: the asymptotic performance values were 99% correct for high- and 90% correct for low-reward trials (p = 10⁻⁷, binomial test). This is very much as in Figure 4c. Thus, for trials that could lead to a large reward, the monkey rarely made a mistake when provided ample time to view the stimuli, whereas for trials that could only lead to a small reward, the monkey made significantly more “careless” mistakes, errors that could not be attributed to insufficient viewing time.

In summary, then, in high-reward trials monkey G responded slightly but significantly more slowly, shifted his tachometric curve to the left, and made fewer mistakes at long processing times. Therefore, three of the mechanisms in Figure 4 were operating simultaneously (Fig. 4a, c, d), all in favor of better performance when a high reward was at stake. Importantly, the steepness of the tachometric curve remained constant, which we take to mean that monkey G's perceptual processing speed did not change.

Now consider the behavior of monkey S, as depicted in Figure 6, c and d. In this case, the percentage of correct responses at long viewing times was again close to the maximum in high-reward trials (99%) but not in low-reward trials (97%), as with monkey G. The difference was small but highly significant (p = 10⁻⁶, binomial test). However, the results for this monkey differed in a conspicuous way: the tachometric curve for high-reward trials was significantly steeper than for low-reward trials (Table 2). Such an increase in steepness also leads to higher accuracy (Fig. 4b), so this effect again implies better accuracy given the potential for a large reward. Although the tachometric curves of monkey S had different center points (Table 2), this did not result from a pure shift along the x-axis, as with monkey G, but rather was a consequence of the change in slope. Consistent with this, the difference in T_ND values for the two curves was only 4 ms (Table 1).

We want to stress that the most direct interpretation of a change in steepness in the tachometric curve is that it reveals a true change in perceptual processing speed. Alternatively, however, the steepness of the curve could also depend on the rule that links the outcome of the perceptual discrimination with the correct motor response as dictated by the design of the task. This possibility is elaborated in Discussion. In any case, an increase in steepness reflects an effective increase in sensory processing speed, which, in turn, leads to more accurate performance, as demonstrated in Figure 4b.

Monkeys G and S behaved somewhat differently in this experiment; the former showed a shift in the tachometric curve, and the latter, a change in steepness. To get a better sense for the predominance of these effects, a third monkey was trained in the CS task and a motivational bias was induced (Fig. 5, monkey R). The success rate of this subject, monkey R, was again higher when a high reward was at stake than when a low reward was at stake, and again the higher performance was accompanied by slower RTs (Table 2). Overall, the tachometric curves in this case were similar to those of monkey G (Fig. 6e,f): there was a significant shift to the left of ∼20 ms in high-reward trials, no significant difference in rise time across conditions, and a small but significant difference in the maximum probability correct at long viewing times (99 and 97% correct in high-and low-reward trials, respectively; p = 0.01, binomial test).

In conclusion, the increased motivation caused by the possibility of collecting a larger reward resulted in a higher fraction of correct choices through a combination of four mechanisms: a slight increase in mean RT (three monkeys) (Fig. 4d), a higher efficiency in using the available sensory information, possibly because of better attentional control (three monkeys) (Fig. 4c), an earlier onset of the perceptual discrimination process (monkeys G and R) (Fig. 4a), and an effective increase in sensory processing speed (monkey S) (Fig. 4b). Importantly, because high- and low-reward trials were interleaved in this experiment, the results demonstrate that these mechanisms can vary on a relatively short timescale, from one trial to the next.

As can be seen from Table 1, the best-fitting parameters found by the race-to-threshold model in the two reward conditions changed in a highly consistent manner across monkeys. For instance, the nondecision times T_ND were always larger in the low-reward condition, in agreement with the observation that the tachometric curves in that case were shifted to the right (Fig. 6). Similarly, the initial buildup rates, as determined by r_G, were always higher in low-reward trials, consistent with the shorter RTs observed in those trials. Other parameters that produce less intuitive effects also changed in the same direction for the three monkeys. For example, the spread in the initial buildup rates, given by σ_G, was always larger in low- than in high-reward trials, whereas the variability in the afferent delays, given by σ_A, was consistently larger in low-reward trials too. This suggests that the differences in the behavior of the three monkeys were attributable to quantitative differences in how various perceptual and motor mechanisms adapted to the reward contingencies, rather than to the deployment of qualitatively separate mechanisms across individuals.

Training-related changes in discrimination timing

As shown hypothetically in Figure 4, a and b, and empirically in Figure 6, a change in effective perceptual performance may be manifest as a shift (timing) and/or a change in the slope (speed) of the tachometric curve. To determine whether training history might lead to a change in either of these two variables, for each monkey we performed a post hoc comparison of two subsets of the data, one from the beginning and one from the end of the data collection period. We found that over the course of the training period, which typically spanned a few months, the psychophysical performance of monkeys G, S, Q, and R was highly stable, but that for monkey F demonstrated important changes.

From the full data set of monkey F, the results of which were shown in Figure 2, we compared the first third and the last third of the trials. The resulting psychometric and chronometric curves were similar to those in Figure 2 (data not shown). The difference in overall percentage correct was small but revealed a significantly higher accuracy in the later trials (on average, 69% correct in n = 2632 early trials vs 75% correct in n = 2599 late trials; p = 0.0008, binomial test). RTs also decreased by a few milliseconds after training (on average, 237 ± 48 ms in n = 2632 early trials vs 231 ± 40 ms in n = 2599 late trials; mean ± SD; p = 0.0001, Wilcoxon's rank sum). However, the most pronounced difference was that between the tachometric curves for early versus late trials, as illustrated in Figure 7.

As can be seen from this figure, the perceptual performance of monkey F before and after several weeks of practice in the CS task showed three prominent characteristics. First, the two curves were shifted along the x-axis, in this case by ∼16 ms (t_ctr = 132 ± 4 ms in late trials and t_ctr = 148 ± 4 ms in early trials). This shift was again highly significant, as can be seen by the very small overlap in the likely t_ctr values (Fig. 7b, top histograms) (p = 0.0008, 8 of 10,000 resamplings). Second, the steepness of the two curves was statistically identical (Fig. 7b, histograms on the right) (t_rise = 96 ± 13 ms in late trials; t_rise = 79 ± 17 ms in early trials; p = 0.56; 5571 of 10,000 resamplings). And third, the maximum percentage correct reached by the two curves in Figure 7a was again different, so that the outcome of a long viewing period was more reliable in the later experimental sessions (asymptotic performance was 90 and 96% correct for early and late trials, respectively; p = 0.00014, binomial test). Therefore, this analysis revealed the same combination of psychophysical effects exhibited by monkey G in the motivational bias experiment (Fig. 6), although they may have arisen from different sources (see Discussion).

Long-term changes in discrimination speed

Whereas monkey F demonstrated improved performance, presumably as a result of practice, a post hoc comparison of two separate data sets from monkey S revealed diminished perceptual performance after a prolonged period of inactivity. The first data set from monkey S comprises trials collected over a period of ∼3 months; before this data collection period, the monkey had been performing the CS task continuously for several months. In contrast, the second data set was also collected over a 3 month period, ∼1 year later, but after the monkey had been inactive, not working in any laboratory tasks, for ∼4 months.

The results are shown in Figure 8. As is apparent from the plots (Fig. 8d), the tachometric curve for data set 1 is quite steeper than the curve for data set 2, reflecting more rapid discriminations, but there were other large differences across sets. Judging from the psychometric curves (Fig. 8a), it is clear that performance during set 2 was much worse than during set 1 (on average, 75% correct, n = 5231 trials in set 1 vs 59% correct, n = 8010 trials in set 2; p = 0, binomial test). The RTs were also much shorter in set 2 (Fig. 8b) (270 ± 56 ms; n = 5231 in set 1 vs 217 ± 49 ms, n = 8010 in set 2; mean RT ± SD; p = 0, Wilcoxon's rank sum). Interestingly, although the tachometric curve for set 2 is less steep than for set 1 (Fig. 8d), the difference is not nearly as dramatic as are the differences in the psychometric and chronometric curves. In this case, the large change in performance is primarily accounted for by the decrease in RT, that is, by the mechanism shown in Figure 4d.

Figure 8.

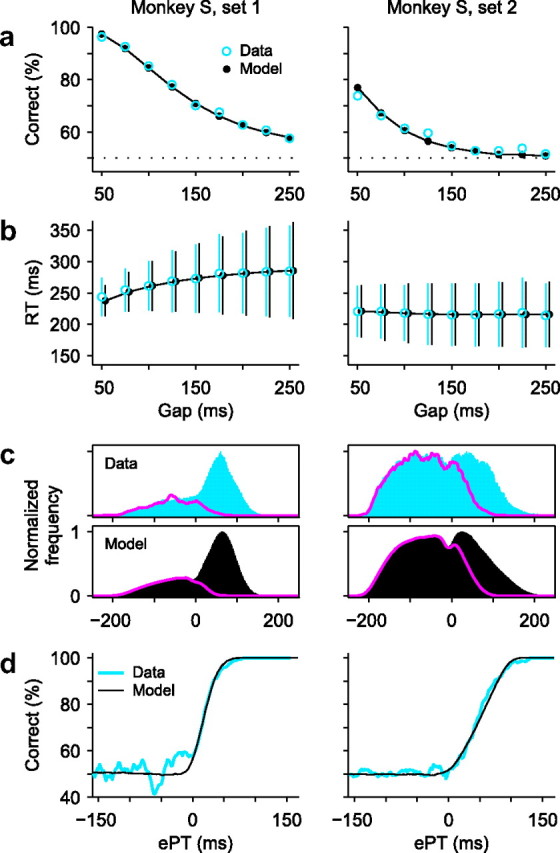
Psychophysical performance of monkey S during two separate data collection periods, which resulted in data sets 1 (left column, same data shown in Fig. 2) and 2 (right column). In all, sets 1 and 2 included 5231 and 8010 trials, respectively.

The tachometric curves from data sets 1 and 2 are replotted in Figure 9a using rPT on the x-axis, as in previous figures. When superimposed in this way, the curve from set 1 is clearly steeper than that from set 2. Crucially, the likely distributions of rise times were almost completely non-overlapping, indicating that this parameter was indeed significantly different when compared across the two data sets (t_rise = 42 ± 6 ms for set 1; t_rise = 71 ± 6 ms for set 2; p < 0.0001; 0 of 10,000 resamplings).

The reason for these results could be the amount of practice leading to each data collection period. The pattern could not be explained by differences in other task parameters across the two data sets, such as the proportions of left and right choices, reward amounts, target eccentricities, or the relative probabilities of red and green targets; all of these factors were statistically the same in the two conditions. However, even if other causes were responsible, the results are interesting because they confirm that the behavioral curves characterizing a subject's performance in the task are plastic, that changes in performance can occur through combinations of the perceptual and motor mechanisms identified earlier (Fig. 4), and that these changes can remain stable over timescales on the order of months.

Reliability of the tachometric curve

The tachometric curve is a powerful diagnostic of perceptual ability because a subject's choice accuracy in the CS task varies much more sharply with processing time than with gap or RT individually; it is their difference that correlates most strongly with correct discrimination, as can be easily understood from the race-to-threshold model. However, it is also important to consider the sources of error or uncertainty to which the tachometric curve may be subject. We investigated five such potential sources through model simulations.

First, in the race-to-threshold model, transmission delays contribute an average of T_ND milliseconds to the total RT in any trial. This parameter may also include the time consumed by other processes that do not directly impact the developing oculomotor choice. Either way, the model assumes that there is variability in T_ND, and the consequence of this variability is that the inferred tachometric curve becomes less sharp, particularly near ePT = 0, where it starts increasing. This is shown in Figure 10b. With a SD σ_A = 10 ms, the effect is small. With σ_A = 20 ms, the broadening is more noticeable, although still relatively modest given such a high variability.

Figure 10.

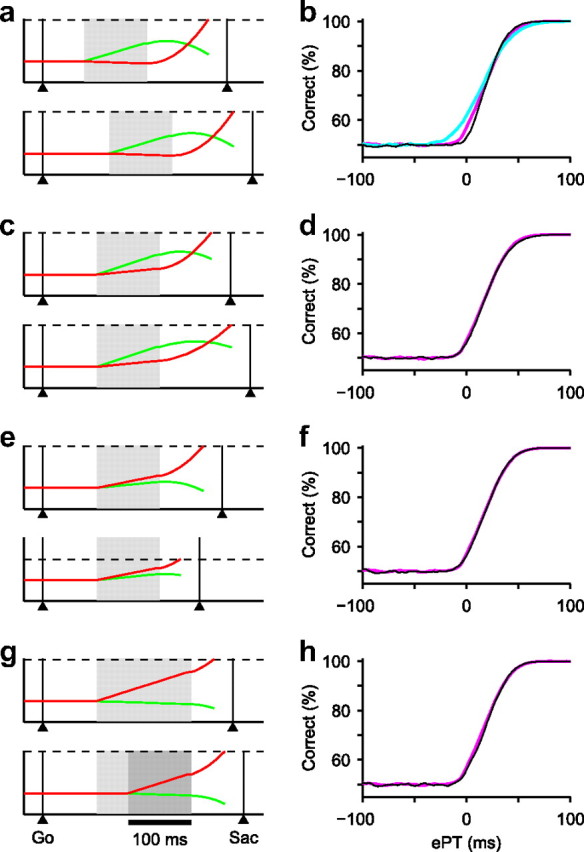
Possible sources of error in the tachometric curve. Simulations with a standard set of fixed parameters (monkey S, set 1) (Table 1) are compared with simulations that included various amounts of intertrial variability in some of those parameters. a, Two simulated trials in which T_ND varied by 40 ms. The format is the same as in Figure 3. b, Tachometric curves obtained with different amounts of variability in T_ND; σ_A = 0 (black), 10 (magenta), and 20 ms (blue). Deviations in T_ND were normally distributed. c, Two simulated trials in which parameters r_T and r_D varied by 50%. d, Tachometric curves obtained with no variability in r_T and r_D (magenta) or with Gaussian intertrial variability (black). The SD of r_T and r_D was equal to 25% of their standard values. e, Two simulated trials in which threshold varied by 50%. f, Tachometric curves obtained with no variability in the threshold (magenta) or with Gaussian intertrial variability (black). The SD of the threshold was equal to 25% of its standard value. g, Two simulated trials, one in which the subject does not wait (ΔT_W = 0; top), and another in which the subject waits (ΔT_W = 50 ms; bottom). The applied gap was 150 ms in both trials (light gray); the effective gap was reduced by ΔT_W in the bottom trial (dark gray). h, Tachometric curves obtained with no waiting (magenta) and with waiting (black). In each waiting trial, ΔT_W was initially drawn from an exponential distribution with a mean of 75 ms, but then could not exceed the applied gap. The magenta curve in b, d, f, and h is the same.

To appreciate this result, it is important to recall that the simulated tachometric curves were obtained in the same way as with the experimental data; that is, without knowledge of the time delays in individual trials. The result is thus different from the horizontal shift that would be observed just with a change in the mean onset time (i.e., in T_ND): the fluctuations in the duration of the processes that are not directly related to the saccadic choice “smear” the tachometric curve. Thus, the fact that the percentage correct rises above chance at ePT = 0 is an artifact caused by the smearing, which also tends to increase the experimentally measured discrimination time (t₇₅). Another way to think about this is that the variability in T_ND causes uncertainty in each measured rPT value. With enough data and careful analysis of onset times, it may be possible to estimate σ_A based on recorded oculomotor activity associated with the subject's choices.

Second, across trials, there are large variations in the initial oculomotor activity triggered by the go signal, which develops during the first, precue stage of each saccadic choice. Such variations are an intrinsic part of the model; in fact, they represent its main source of variability and are most responsible for generating different outcomes across trials. They do not need to be considered further.

Third, the influence of the sensory cue could also vary from one trial to another, and we have explored this scenario too (Fig. 10c, d). In our model, the parameters r_T, r_D, and τ, which effect the influence of the cue, normally remain constant for a given monkey or a given experimental condition. For this simulated experiment, however, r_T and r_D varied randomly and independently across trials; their SDs were set equal to 25% of their original values listed in Table 1 (monkey S, set 1). This amount of variability is quite high, but as can be seen in Figure 10d, this manipulation had a negligible impact on the tachometric curve, and the same was true for the chronometric and psychometric curves, and for simulations involving variability in τ. Thus, the measures of psychophysical performance we have used, which are based on averages over trials, are highly insensitive to fluctuations in the flow of cue information across trials, at least as far as we can tell with the model.

Fourth, in the model, the circuit is committed to a specific motor response when activity reaches a threshold. This is consistent with neurophysiological evidence (Hanes and Schall, 1996; Roitman and Shadlen, 2002; Hanks et al., 2006; Kiani et al., 2008) and is a feature of most accounts of perceptual decision making (Wang, 2002; Smith and Ratcliff, 2004; Palmer et al., 2005; Wong and Wang, 2006; Boucher et al., 2007; Ratcliff and McKoon, 2008; Cisek et al., 2009). Interestingly, Reddi and Carpenter (2000) showed that changes in threshold in their model were consistent with changes in the speed–accuracy trade-off of subjects making saccades to single, low-visibility targets. This suggests that the threshold may be adjusted according to task demands, and therefore that it may vary across trials. To investigate the impact of possible variations in threshold, first we increased its value by 50% and found that performance became better but slower—both the psychometric and chronometric curves shifted upward by large amounts—and the opposite changes were seen when the threshold was decreased by 50% relative to the standard value. This agrees with the speed–accuracy trade-off reported previously (Reddi and Carpenter, 2000). Most importantly, however, neither of these manipulations had a discernible effect on the tachometric curve. To confirm this, we performed additional simulations in which the threshold changed in every trial (Fig. 10e,f). In this case, the psychometric and chronometric curves changed minimally, but more importantly, again there was no observable effect on the tachometric curve, even though the fluctuations were quite large (Fig. 10f).

Finally, the monkey's behavioral strategy is another factor that might seem as a potential source of uncertainty in the tachometric curve. In particular, what happens if a monkey tries to wait for the cue? That is, suppose that, instead of reacting as soon as he detects the disappearance of the fixation point, the subject waits a certain amount of time ΔT_W before initiating his response selection; would not this strategy bias the estimate of processing time and thus the resulting tachometric curve?

To answer this question, one must define exactly what is meant by waiting, or how exactly such a waiting strategy is implemented, but in general waiting is not a cause for concern, particularly when the subject's psychometric performance ranges from nearly 100% correct to near chance (Salinas et al., 2010). If waiting leads to a simple delay in responding but the cue signal is still able to inform the ongoing oculomotor plan, then it is harmless, as we pointed out previously (Salinas et al., 2010; Stanford et al., 2010). The example shown in Figure 10g illustrates why. Two things happen when the subject delays the response: (1) the nondecision period is extended by an amount ΔT_W, and (2) the “true” gap is effectively shortened by the same amount. Therefore, when calculating the difference RT − gap using the nominal gap value, the result is, on average, the same as if the subject had not waited. Over many trials, the effect of ΔT_W is simply equivalent to having performed the experiment with shorter gaps (and no waiting), and although this may have an evident impact on the psychometric and chronometric curves (data not shown) (Salinas et al., 2010), it has virtually no consequence on the tachometric curve (Fig. 10h). We have also explored other, more complex waiting mechanisms, but none of them were consistent with the empirical data obtained in the task (Salinas et al., 2010).

In summary, then, as far as we have observed in the model, the dominant source of uncertainty in the tachometric curves, and likely in our calculations of perceptual processing speed, is the variability in T_ND, which reflects the internal variability of neural processes that take place during each trial but are unrelated to the decision-making steps. This factor tends to widen the tachometric curve, so it leads to processing speeds that underestimate the true values. Thus, sensory processing during a red/green discrimination of high-contrast stimuli may be even slightly faster than we have inferred. Other than this, the tachometric curve is extremely resilient to various forms of variability.

Expected neural correlates of psychophysical changes

We used the race model to explore some of the possible neural correlates of the psychophysical phenomena observed during performance of the compelled-saccade task. That is, given the various possible changes in the tachometric curve, we analyzed simulated neuronal responses to predict the corresponding changes in neuronal activity that should be expected during actual neurophysiological recordings. To generate such predictions, for each experimental condition, several thousand trials were run using parameters that fitted or approximated that condition, and the simulated motor plans (i.e., the trajectories of the x_L and x_R variables) were saved for all trials. Then, average traces were computed for the motor plans in the preferred direction of the neurons and for the plans in the opposite direction. These average traces were calculated with all trials synchronized either on the go signal or on the saccade. Also, because the rPT is a crucial variable in the task, separate averages were generated for trials with long and with short rPTs. The idea was to replicate the standard procedures used for analyzing extracellular recordings from oculomotor cells (Thompson et al., 1996; Port and Wurtz, 2009; Stanford et al., 2010).

The results are shown in Figure 11, which plots the expected mean oculomotor responses (colored traces) that correspond to each of the three major effects on the tachometric curve that were found. According to the race model, a shift of the tachometric curve along the horizontal axis (Fig. 11a) will manifest as a shift in the evoked neuronal activity in the same temporal direction, both when the responses are synchronized on the go signal (Fig. 11b) and when synchronized on the saccade (Fig. 11c). The latter case is not expected to appear as a pure shift, however, because the level of activity immediately preceding saccade onset should be constant (Hanes and Schall, 1996; Roitman and Shadlen, 2002; Stanford et al., 2010). Importantly, although the predictions for this case are shown for short-rPT trials, similar shifts are also predicted for long-rPT trials. So, a rightward shift of the tachometric curve should be accompanied by rightward shifts in the evoked oculomotor activity at all rPTs.

Figure 11.

Neurophysiological predictions of the race-to-threshold model. For each condition (tachometric curve), 16,000 trials were simulated and sorted according to rPT and movement direction. The model responses x_L and x_R in each group were aligned either on the go signal (middle column) or on the saccade (rightmost column) and were then averaged. a, Simulated rightward shift in the tachometric curve. The model parameters are as in Figure 5d (monkey G), except with p_e = 0 in both cases, for clarity. The gray area indicates short rPTs. b, c, Average neural activity predicted by the model during correct trials with short rPTs. The continuous and dashed traces are from the same runs as the corresponding curves in a. The red and green lines are for correct eye movements into and away from the motor field of the neuron, as indicated. The y-axes correspond to normalized firing rate. d, Simulated decrease in slope of the tachometric curve. The continuous and dashed traces differ by a factor of 2 in the parameter τ. The dashed trace is the same as the continuous trace in a. The gray area indicates long rPTs. e, f, Average neural activity predicted by the model during correct trials with long rPTs for the two conditions in d, indicated by continuous and dashed traces. g, Simulated decrease in the maximum percentage correct of the tachometric curve. The continuous trace is the same as in a, and the dashed trace was obtained by setting p_e = 0.1. h, i, Average neural activity predicted by the model during error trials with long rPTs for the two conditions in g, indicated by continuous and dashed traces.

In contrast, when the slope of the tachometric curve decreases (Fig. 11d), a shift in the opposite temporal direction is expected; this effect should be clearer for the data aligned on the saccade (Fig. 11f) and should only be observed for long rPTs, not for short ones (data not shown). For the data synchronized on the go signal (Fig. 11e), the difference is expected to be small, and to arise only at a relatively high level of activity at long rPTs. So, a shallower tachometric curve, which moves just part of the curve to the right, should be accompanied primarily by a partial shift to the left in the evoked oculomotor activity aligned on saccade onset, and this shift should be seen at long rPTs only.

Finally, according to the model, a decrease in the maximum percentage correct of the tachometric curve (Fig. 11g) will not have any impact on the responses evoked during correct trials (data not shown). Rather, such a change should only be manifest in the activity levels observed during error trials, and furthermore, only for those trials with long rPTs (Fig. 11h, i).

It should be quite feasible to test these predictions in future neurophysiological experiments using single-neuron recordings. This is because the three types psychophysical effect discussed, shifts, changes in slope, and changes in maximum percentage correct, should lead to characteristic changes in activity that are specific for temporal direction (earlier vs later), rPT interval (short vs long), and outcome type (correct vs error).

Discussion

We have described the behavior of five monkeys trained to perform the CS task, a task that, to a large extent, dissociates the codependence between RT and behavioral performance that is typically observed in sensory discrimination paradigms. With this design, it is possible to track the temporal evolution of a perceptual judgment with little contamination caused by variability in motor execution, which typically plagues this type of calculation.

Estimating sensory processing times

Previous psychophysical studies based on choice tasks have estimated sensory-integration time windows in the ∼100 ms range (Ludwig et al., 2005; Ghose, 2006). In contrast, our results imply that two highly discriminable colors can be perceptually differentiated much faster, approximately within 25–50 ms, depending on the subject and the desired criterion level. In fact, our findings are consistent with estimates of sensory processing times based on rapid alternation of colored gratings, according to which color discrimination in humans requires ∼25 ms (Holcombe and Cavanagh, 2001; Bodelón et al., 2007). This number probably reflects pure sensory identification, whereas our task also requires that the output of the sensory discrimination be associated with the correct motor action on the fly. Here, the sensory-motor rule is simple (“move to the spot that matches the color of the fixation point”), and likely contributes little, but other more complex rules (e.g., “move to the spot that is different from the color of the fixation spot”) might require additional processing time. Hence, the temporal resolution of the tachometric curve may be close to that of the rapid-grating-alternation method. Crucially, however, the tachometric curve generates much more than a single number (perceptual speed): it characterizes the perceptual capacity of a subject and allows us to pinpoint how various psychophysical mechanisms contribute to the observed choice accuracy (Fig. 4).

Learning and perceptual optimization

The tachometric curve of monkey S was significantly steeper after several months of practice than after several months of inactivity (Fig. 9). This may appear analogous to perceptual learning experiments, whereby extensive practice increases the performance of a basic perceptual task, such as contrast detection (Fiorentini and Berardi, 1980; Li et al., 2009), orientation discrimination (Vogels and Orban, 1985; Yang and Maunsell, 2004), or line alignment (Li et al., 2004; Gilbert et al., 2009). However, even if we were certain that it was a consequence of training, the present result is fundamentally different because it reveals a change in processing speed.

Previous studies in perceptual learning have documented changes in the effective sensitivity of subjects after repeated exposure to specific sensory stimuli, and have explained those results in terms of signal and noise components. In some cases, the behavioral changes have identifiable neural correlates, such as sharpening of tuning functions (Jenkins et al., 1990; Recanzone et al., 1993; Yang and Maunsell, 2004). However, in the current implementation of the CS task, the red and green spots are bright and easily discriminable, so color sensitivity is unlikely to be a performance-limiting factor. Consequently, changes in color tuning are probably unrelated to the behavioral effects reported here. Rather, the variation in processing speed displayed by monkey S suggests that, with training, the neural circuits that process sensory evidence and weigh the two motor alternatives are able to work faster. It is not clear what neural mechanisms account for such dynamic changes, but it should be possible to explore them with a more biophysically realistic version of the race-to-threshold model (Wang, 2002; Beck et al., 2008; Furman and Wang, 2008; Lo et al., 2009) and additional experiments.

Variability in the onset of perceptual discrimination

A shift in the tachometric curve along the time axis, particularly when it results from presumptive changes in motivation (Fig. 6), indicates that the onset of the perceptual discrimination process can change by at least a few tens of milliseconds from one trial to the next. This shift is thus relatively large, considering that the perceptual discrimination itself has a timescale on the order of 25–50 ms (to reach 75% correct).

This result is intriguing. On one hand, the effect suggests that sensory information required different amounts of time to travel from the retina to the relevant decision-making circuits. And indeed, to replicate tachometric curve shifts associated with large and small rewards, the model required different T_ND values; for instance, 104 and 136 ms in the case of monkey G (Table 1). But given that the sensory inputs were identical, it is unclear how to account for a ∼30 ms difference in T_ND in biophysical terms. Whatever the underlying mechanism, our finding that the onset of the perceptual analysis can vary to such a degree is novel and suggests a new specific way in which neuronal activity can be linked to context-dependent changes in choice performance.

RTs, reward, and performance

In the motivational bias experiment, larger rewards were associated not only with better performance but also with slightly longer RTs (Fig. 5a,b). At first, this seems counter to previous studies in which the availability of larger rewards was typically associated with significantly shorter RTs (Takikawa et al., 2002; Watanabe et al., 2003a). However, such reward-dependent decreases in RT require a reliable association between reward value and stimulus location/movement vector. Indeed, when such an association exists, analogous reward-related RT effects are also obtained in the context of the CS task (Stanford et al., 2010). In the present study, there was no such correspondence between reward and location; the position of the highly rewarded target varied randomly, and success always required an accurate color discrimination. Also, all else being equal, in the CS task longer RTs lead directly to higher success rates (Fig. 4d). Therefore, the increases in RT displayed by our subjects were consistent with higher motivation, better performance, and the availability of a larger reward. In future neurophysiological experiments, it will be interesting to explore how reward affects oculomotor activity under this condition, in contrast to previous tasks in which the typical inverse relationship between RT and reward is observed (Kobayashi et al., 2002, 2007; Lauwereyns et al., 2002; Watanabe et al., 2003b).

Sensory information influences a developing motor plan

Our model shares several features with “bounded integrator” or “drift-diffusion” models of choice tasks: neural activity ramps up until one of two competing alternatives crosses a threshold, at which point a particular response is produced (Ratcliff and Rouder, 2000; Usher and McClelland, 2001; Wang, 2002; Smith and Ratcliff, 2004; Palmer et al., 2005; Wong and Wang, 2006). In many such models, sensory-evoked activity is directly integrated, so reaching a threshold is interpreted as reaching a particular amount of accumulated sensory evidence, or a particular level of certainty (Carpenter and Williams, 1995; Reddi and Carpenter, 2000; Gold and Shadlen, 2002; Beck et al., 2008; Brown and Heathcote, 2008).

Our model is different, more conservative, because (1) its dynamical variables represent developing motor plans, (2) its primary source of variability is the initial state of those variables rather than noise in the sensory input (Drugowitsch and Pouget, 2010) (see also Brown and Heathcote, 2008), (3) the integration process does not accumulate sensory evidence, but rather directly advances the motor plans, and (4) reaching a threshold means that the system has committed to generating a motor action that can no longer be cancelled, which is consistent with neurophysiological data (Hanes and Schall, 1996; Roitman and Shadlen, 2002; Lo and Wang, 2006; Boucher et al., 2007). Our race model is thus more akin to that of Cisek et al. (2009), in which sensory information modulates a growing signal that represents the urgency to make a response. However, we propose that the cue information influences the ongoing saccadic choice through a specific mechanism—by accelerating and decelerating the neural discharges that trigger eye movements to the target and distracter locations, respectively—which is consistent with recordings from oculomotor cortical neurons (Stanford et al., 2010).

Implications for interpreting neuronal activity

A crucial issue for understanding the neural basis of perceptual decision making is determining whether task-related activity reflects the sensory or motor processes associated with making a choice (Thompson et al., 1996; Gold and Shadlen, 2000, 2007; Shadlen and Newsome, 2001; Lovejoy and Krauzlis, 2010). However, distinguishing an evolving perceptual discrimination from a developing motor plan is complicated by the conjunction of two factors: first, as noted in Introduction, there has been no behavioral measure that thoroughly decouples perceptual performance from motor performance; and second, because many of the same neurons respond to both sensory and motor events, parsing their respective neural correlates is very difficult (Thompson et al., 1996; Wyder et al., 2004; Port and Wurtz, 2009).

The CS task provides two new handles on these problems: a reliable time stamp marking the moment at which the cue information starts influencing a choice, and a temporal profile of the subject's percept. Thus, single-neuron activity and behavior can be correlated through time to investigate how such activity relates to the perceptual discrimination, the motor plan, or both. Moreover, the precision with which such correlates may be temporally localized provides a unique opportunity to assess the relative position of structures (Pasupathy and Miller, 2005) like the superior colliculus, the frontal eye fields, and others within a functional hierarchy of visuomotor control.