Abstract
This paper introduces new longitudinal network data from the “Promoting School-Community-University Partnerships to Enhance Resilience” or “PROSPER” peers project. In 28 communities, grade-level sociometric friendship nominations were collected from two cohorts of middle school students as they moved from 6th, to 9th grade. As an illustration and description of these longitudinal network data, this paper describes the school popularity structure, changes in popularity position, and suggests linkages between popularity trajectory and substance use. In the cross-section, we find that the network is consistent with a hierarchical social organization, but exhibits considerable relational change in both particular friends and position at the individual level. We find that both the base level of popularity and the variability of popularity trajectories effect substance use.
Introduction
At least since Hollingshead (1949) and Coleman (1961), school settings have been effectively conceptualized as youth status systems. These networks are often seen as semi-autonomous, with a structure unto themselves that creates distinct youth norms and practices. But these “adolescent societies” are also dynamic: new students enter, old students leave, current students rise in status while others fall (Bukowski & Newcomb 1984, Hallinan 1978, Dunphy 1963). Such dynamism raises fundamental questions about the stability of school network systems and their effectiveness for transmitting norms, values and practices. If school networks are a significant source shaping social behavior, how effective can they be in the face of dramatic turnover?
Like many complex network systems (Barabasi 2003; Newman 2003), schools have very skewed popularity distributions, where some kids receive many more nominations than others. This inequality is (likely) noticed by youth and youth commentators, and which can plausibly affect behavior. Coleman (1961) popularized this idea for adolescent networks as a “leading crowd” – a collection of youth admired by others who set the social and behavioral agenda for a school.2 In a dynamic network, if social status is gained, maintained, and signaled through involvement in particular behaviors, then changes in one’s status should affect behavior. So long as kids adopt “leading crowd” behaviors in a (never completely successful) attempt to gain status and reject (or lose access to) such behaviors at lower positions of the status structure, a general correlation between status and behavior can be created even with dramatic changes in individual popularity. Moreover, if adolescents perceive a link between behavior and popularity, any change in popularity may affect behaviors such as smoking, as students attempt to (re)gain status by adopting behaviors they think confer status.
Such ideas are often difficult to test, however, since they require fully dynamic data on a large and varied sample of networks, which is rare. The data used here, collected as part of the PROSPER project, make such analyses possible. We have multiple cohorts observed across hundreds of schools with 5 waves of data collected over 4 years. This paper describes the basic popularity dynamics evident in this rich network data, providing a portrait of adolescent social systems that is rarely observable. While there are many ways that the youth network affects (and is affected by) behavior (Snijders et al 2010), here we explore a simple trajectory idea: That the history of one’s position in the network status system may have a unique affect on ultimate substance use. This is the sort of question that one can only ask if you have detailed network data collected over multiple time points, and thus nicely illustrates the potential of such data collection. Other approaches, including joint peer influence and selection models (Snijders et al 2007), will be explored in future work.
Background & Prior work
During adolescence, time spent outside of the household increases, as adolescents spend more time engaged in school activities, work, and in the community (Aquilino 1997; Furstenberg 2000). Thus, adolescents tend to spend more time with friends and less time with family members, and parental supervision declines over time (Baumrind 1991; Bryant & Zick, 1996; Bulcroft, et al. 1996; Furstenberg 2000; Osgood et al 1996). These features are reflected in the peer structure and likely relate to deviance. Research typically describes hierarchical patterns in these structures, with high status students influencing lower status peers (Killeya-Jones et al. 2007).
Status in youth networks is linked to popularity, which has been measured in two distinct ways: sociometric popularity (“Who do you like the most?”) and perceived popularity (”Who is the most popular?”). Though correlated, the overlap can be low (Cillessen & Rose 2005, Parkhurst & Hopmeyer, 1998) and the two measures seem to have distinct relationships with behavior (Cillessen & Rose 2005, McElhaney et al. 2008). For example, sociometrically popular (i.e., well-liked) youth are typically characterized by high levels of prosocial behavior and low levels of aggressive behavior; whereas a substantial subset of students with high levels of perceived popularity are characterized by elevated levels of aggressive (or “tough”) behavior (Rodkin, Farmer, Pearl & van Acker, 2000). Given that friendships are essentially “liking” relationships (Hartup, 1996), our data on youths’ self-reported friendships allow us to measure sociometric popularity (hereafter simply “popularity”), which we feel nicely captures intuitive notions of system-level social status. If the network system serves as the foundation for normative behavior, then we would expect position in this system to directly affect behavior.
Since social status likely changes over time, we also expect change itself may affect behavior. The stability of sociometric status has been assessed as moderate to high, although data are much more extensive for classroom-based networks in elementary school than for networks in middle school or high school (Jiang & Cillessen, 2005). Nonetheless, considerable stability in social status has been observed in a number of networks of youth followed across the transition from elementary school to middle school (Berndt & Hoyle, 1985; Bukowski and Newcomb, 1984), with extreme swings in popularity occurring infrequently (Coie & Dodge, 1983). In an examination of peer relations among high school girls, Eder (1985) found a system of social stratifications develop around a stable hierarchy of cliques by the 8th grade. She describes a “cycle of popularity”, where popular girls tended to avoid associating with lower status students. The foundations of stability within a network are typically related to homophily and social balance. Relations among those who are similar (homophily) or who have many friends in common (socially balanced) tend to be more stable (Hallinan & Hutchins 1980; Carley 1991; Hallinan and Williams 1987; Wellman, Wong, Tindall, and Nazer 1997).
Sociometric popularity has been associated with prosocial behavior (e.g., cooperative, helpful), assertive but nonaggressive leadership, academic competence and low levels of aggression (Asher & McDonald, 2009). Popularity is also associated with being in a racial majority (Urberg, et al. 1995) in the cross-section and stability over time with gender and grade (Bowker 2004; Berndt & Hoyle 1985). Hardy, et al. (2002) found gender differences in stability, with girls experiencing less stability in reciprocated friendships than boys. While both girls and boys had similar numbers of reciprocated friendships, girls were more likely to nominate new peers over time. Bowker (2004) similarly finds differences in relational strategies by gender. Stability appears negatively associated with the amount of time between survey interviews and positively associated with age, which hints at the possibility of an important age effect (Santor et al. 1999; Jiang & Cillessen, 2005). While suggestive, the evidence for these patterns is rarely based on data with as extensive coverage as we explore here, typically making use of either small case studies or short windows for dynamics. One of the key advantages of the PROSPER peers project is the ability to trace these patterns across many schools and long time scales.
Developmental data are limited, but the behavioral correlates of sociometric popularity appear to shift over time, with the negative association between aggression and popularity dissipating with age (Asher & McDonald, 2009; Rubin, Bukowski & Parker, 2006) and even “flipping” to a positive association in some settings (Light & Dishion, 2007). This is consistent with research on substance use in adolescence, in which high popularity appears to be associated with smoking cigarettes and/or marijuana and drinking alcohol (Santor et al. 1999; Alexander, et al. 2001; Diego, et al. 2003) in cross sectional studies, though there can be significant contextual effects (Alexander, et al. 2001). Recent longitudinal studies have found that regular substance abusers were more likely to be popular and maintain their social standing over time (Killeya-Jones et al. 2007) and that popular adolescents were more likely to engage in behaviors that receive peer approval (Allen et al., 2005), highlighting the interdependence of status and behavior.
This work leads us to explore the dynamics of popularity and substance use at both the network and individual levels, and use the unique opportunity afforded by the PROSPER data to provide a basic descriptive portrait of sociometric popularity dynamics. At the network level, we examine the popularity structure for stability across settings and over time. Based on the long ethnographic and case-study history, we expect to find a consistent network form reflecting hierarchy in any cross-section. This will be indicated jointly by a long-tailed popularity distribution and a hierarchical ordering of peer groups. At the individual level, we ask how position in the status structure changes over time: how fluid are relations at the dyad level and how does this translate into popularity stability?
We are also interested in exploring the links between substance use and popularity. Our expectations turn on the suggested status-conferring effects of substance use. First, since substance use is a form of minor rebellion that signals adult-like behavior and the transition through middle school marks a cultural break with childhood; substance use should be positively associated with popularity. However, precisely because substance use is a signal for higher status, youth experiencing greater popularity change over time will also have higher levels of substance use. This could work for both gains and losses in popularity. Those with strongly declining status may use more in an attempt to regain lost popularity. But, those rapidly increasing will likely also use more, since use reinforces their new, and thus seemingly unstable, status gains. Note these are sequenced behaviors that are likely self-reinforcing, making distinctions between cause and effect difficult to tease out empirically, and we are not claiming cause in these examinations.
Data, Measures, & Methods
Our data are from the PROSPER project, a program designed to evaluate substance use interventions. The project focused on 28 rural school districts, 14 each in Iowa and Pennsylvania. To insure the inclusion of families at significant risk, the sample was limited to districts where at least 15% of families are eligible for free or reduced cost school lunches. The selected school districts all have at least 95% English-speaking enrollments. As is typical of much non-metropolitan America, all are predominantly white (range: 97% to 61%)
The sample consists of two grade cohorts followed over 4 years. Cohort 1 students were enrolled during the 2002–2003 school year, Cohort 2 students a year later. In-school assessments were conducted in fall of the 6th grade, then again in the spring following the PROSPER intervention, and every spring there after through the 9th grade, for 5 waves total.3 There are approximately 6 months separating wave 1 from wave 2 and approximately a year separating every other wave. Within each district every school with a 6th grade was selected. Compiled over 5 waves and 2 cohorts this yields 368 distinct in-grade networks, these networks overlap in time (as members age).4 Participation rates ranged from 86% to 90% for all eligible students with an average of 87.2%. In total, over 16,000 students filled out at least one school questionnaire and over 61,000 total surveys were returned, with about 12,000 students responding each wave. Over-time participation is naturally lower. Of the 12,245 wave-1 respondents, 90% completed 3 waves, 85% completed 4 and 71% completed all 5 waves. Since enrollment is open, new students are added at each wave, targeting a full census for each network cross-section. For network-level indices, we thus use all responses collected for each wave. For individual behavior models, we use all cases with network data when evaluating contemporaneous models or descriptive statistics. We restrict the sample to those with valid data in the first and last waves (1 and 5) who also have non-missing data on no more than 1 other wave (approximately 65%) when evaluating trajectory models.
Network data were collected using an open name generator. Students named friends in response to the question “Who are your best and closest friends in your grade?” with two names allowed for best friends and 5 names allowed for “other close friends.” Students wrote the first and last names of each friend on the survey form and we matched those names to student rosters.5
Network Measures
Popularity is measured as the sum of all nominations received (“in-degree”). We convert this to percentile rank within the school network as the primary measure of popularity. In-degree captures sociometric popularity directly, and is also amongst the most stable measures in the face of incomplete or missing data (Borgatti et al, 2006). Macro-level status structures are measured in two ways. The primary indicator is the popularity distribution, where we focus on the inequality of the distribution. Since a skewed degree distribution is consistent with many underlying topologies, we augment this measure with scores tailored to test for hierarchy based on the distribution of triads (Wasserman and Faust 1994; Johnsen 1985, 1986). The distribution of popularity captures inequality in the extent to which people are well-liked by others. In general, the more unequally distributed popularity is (i.e. longer-tailed producing high skew), the more a small number of people are sociometric stars.6
While an unequal popularity distribution is a clear indicator of hierarchical structure, it is not sufficient. The key to hierarchy is that clusters of youth with similar status jointly nominate higher status alters. Such structures are ideally measured through a blockmodel, where we would directly identify equivalence classes of students and identify how those groups are related to each other. While useful for small numbers of networks, it is intractable to blockmodel all of the networks examined here. Thus, we seek a simpler general measure of the network shape, to confirm that the degree distribution likely corresponds to an overall network hierarchy.
One strategy for assessing the level of hierarchy is to see if the distribution of triads in the network is consistent with a particular hierarchical macro structure. The triad census of a directed network is the summary count of the 16 possible isomorphic classes of 3 node sub-graphs in each network. Network theorists have shown a necessary link between the triad distribution and the network macro-structure (Cartwright and Harary 1956; Johnsen 1985; 1986). For example, if we hypothesize a triad distribution allowing only complete triads (a←→b, b←→c, a←→c), the only possible corresponding macro structure is a completely connected clique (Cartwright and Harary 1956). If we were to allow only directed transitive triads (a→b, b→c, a→c) the resulting macro-structure must form a completely ordered hierarchy, with one node receiving nominations from everyone, another receiving ties from all but the most popular and so forth. There are numerous other possible models (Johnsen, 1985; 1986) including some sorts of clustered hierarchies that describe patterns we might see in a school network.
Since the triad models are based on distributions over a 16 element vector, we need a summary statistic to test for correspondence between the hypothetical and observed distributions. The tau statistic (Wasserman and Faust 1994:594), provides this. Substantively, the tau statistic compares the observed distribution of triads in a network to the distribution expected in a random network. The tau statistic is calculated as in eq 1 below:
| (1) |
Where T is the 16-element vector of observed triad counts, l is a weight vector specifying the hypothesized macro-model, μ is the expected count and ∑T is the variance/covariance matrix of the random-graph triad counts. The random network we compare to here is the uniform random conditional on the number of mutual, asymmetric and null dyads (known as the U|MAN distribution, see Wasserman 1977).7 The numerator is thus the difference between the observed allowed count (l’T) and the expected-at-random count (l’ μT), divided by a term for the standard deviation of the linear combination of counts and are effectively t-values where 0 would indicate the observed graph were no different than a random one. Higher values indicate a greater difference from expectation, and thus can be used very roughly as a comparative index favoring one model over another, though maximum values for a “perfect” fit are unknown.8
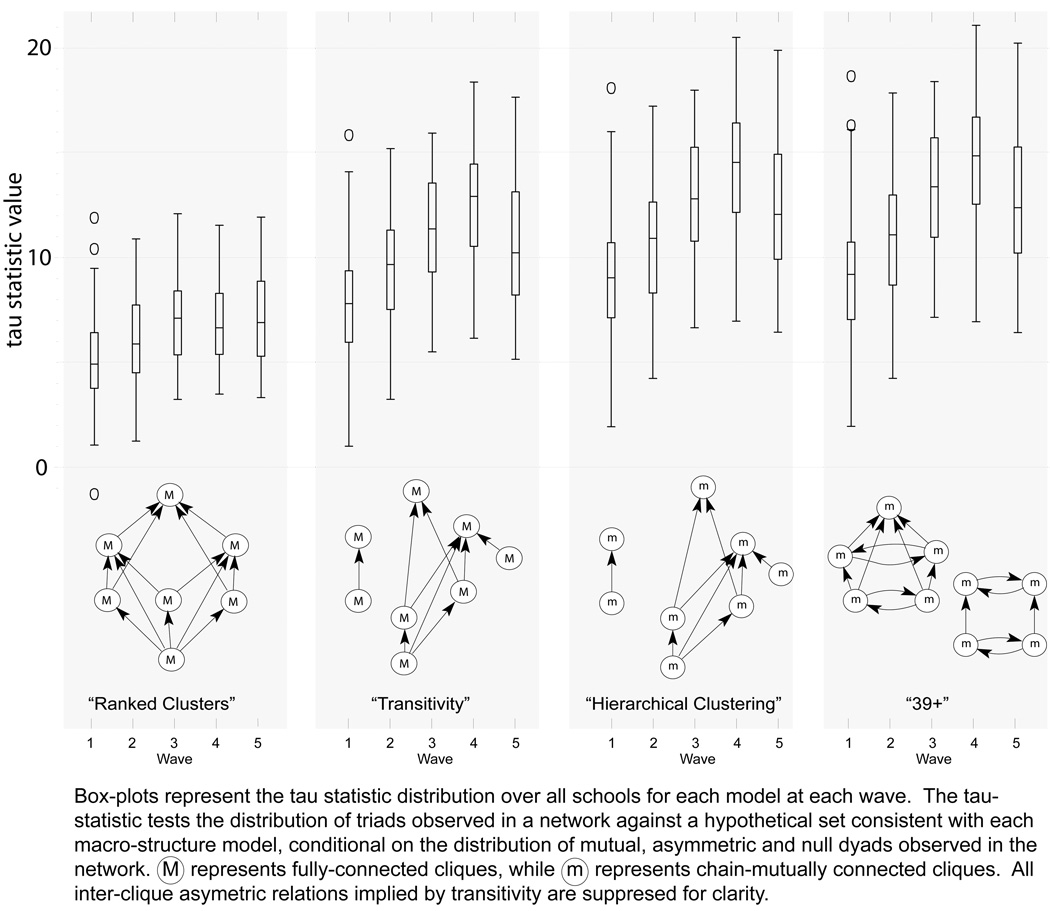
All triad micro models specify a set of allowed triads that, if observed, determine a particular macro-structure. It is important to note that these reflect form only. So, for example, under the strict balance model, the relative size of the two cliques is not at issue, just that there are only 2. Johnsen (1985, 1986) summarizes a number of different triad-based models that we test here (see figure 3 for details). First, the “Ranked Clusters” model9 describes a system with completely connected cliques ordered in a single hierarchy. The system admits to clear rank-levels which may contain multiple cliques, but cliques within a level have no ties to other cliques on the same level. Asymmetric ties only flow between levels in the hierarchy and these ties are transitive. The “Transitivity” model10 also describes a system of completely connected cliques, but these cliques need not organize around a single hierarchy, nor are there necessarily strict rank-levels. Instead, every clique is partially ordered by between-group asymmetric ties. The next two models relax the assumption of completely-connected cliques. Instead, these models are built around “chain-mutually connected” sets, where a chain of mutual ties connects everyone in the set (referred to here as m-cliques). All asymmetric ties within the m-clique are ordered transitively. The “Hierarchical Clusters” model11 mirrors the transitivity macro-structure, but based on chain-mutual cliques instead of complete cliques. The final model12, named “39+” by Johnsen in reference to the size of the networks where this model was discovered, consists of multiple “super-clusters” of hierarchically ordered m-cliques. Within each super-cluster, m-cliques at different levels will be partially ordered by asymmetric ties, while those at similar rank-levels exchange asymmetric ties (again, the number of levels and size of m-cliques is not constrained).
Figure 3.
Triad macro-structure model results for PROSPER school networks.
Substance Use
The dependent variable in our substance use models is an item-response adjusted score based on frequencies of 3 types of substance use over the month preceding the interview: smoking tobacco, drinking alcohol, and smoking marijuana. The IRT methodology (see Osgood, McMorriz and Potenza (2002)) translates discrete categories of the response scale to a shared dimension that is continuous and has an equal-interval metric. We used Samejima’s (1969) graded response model, which uses the full ordinal information for every item. The resulting score has a mean of 0.32 (sd=0.77) and a ranges from −0.07 to 3.47.
Results
Global Network Structure: Evidence for hierarchy
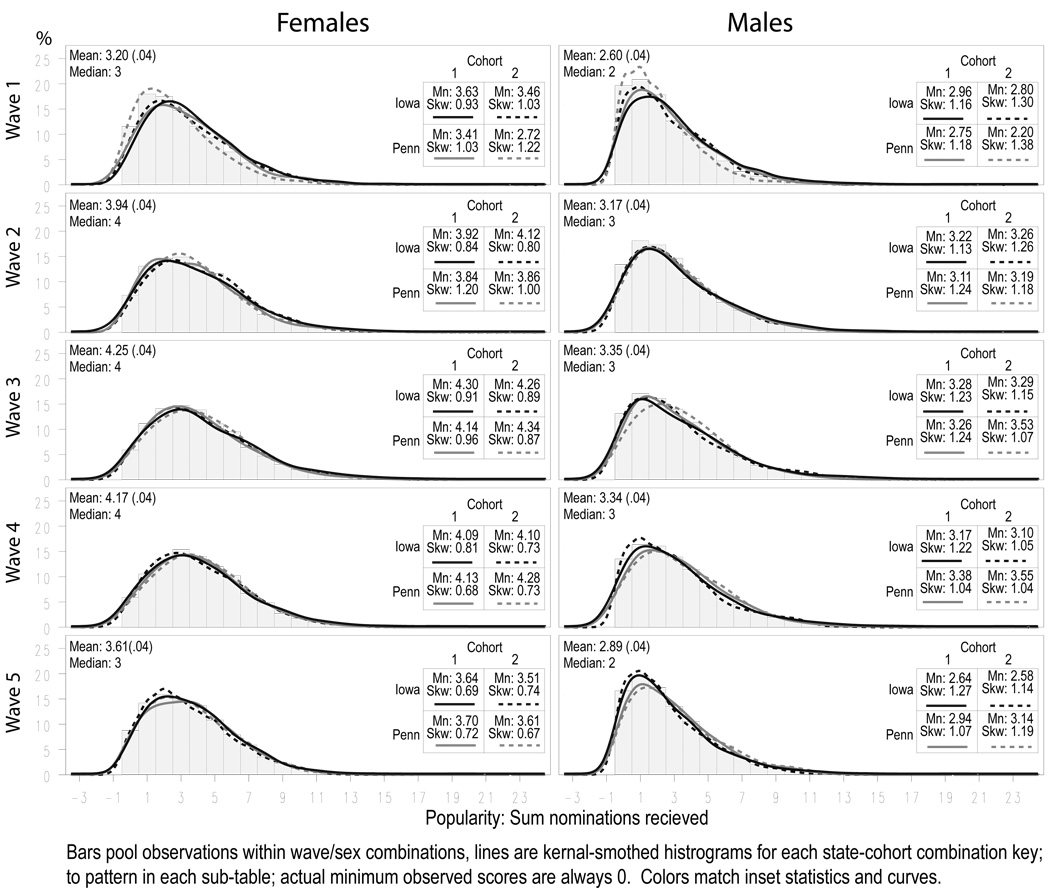
Figure 1 presents histograms of the popularity distributions by sex, wave, state and cohort.
Figure 1.
Popularity Distributions
By sex, wave, and setting
Males are more likely to receive zero nominations than females, leading to a consistently lower average popularity. In-degree is higher in the middle 3 waves, peaking in wave 3 for all groups. While mean degree simply reflects tie volume, the shape of the in-degree distribution better reflects structure. The shapes of the distributions are remarkably similar, with each histogram aligning similarly over time. The skewness of a distribution measures the asymmetry of the variable around the mean. In our context, where the distribution is limited to zero on the low end, differences in skewness reflect differences in the relative length of the high-popularity tail, which nicely captures an intuitive notion of unequal popularity. An alternative measure of degree inequality is network centralization, which is given in the third column of figure 1.13 Skewness is somewhat higher for males than for females. Since the maximum and top-quintile scores (not shown) are higher for females than males, most of differences in skewness appear due to the higher number of males receiving zero nominations.
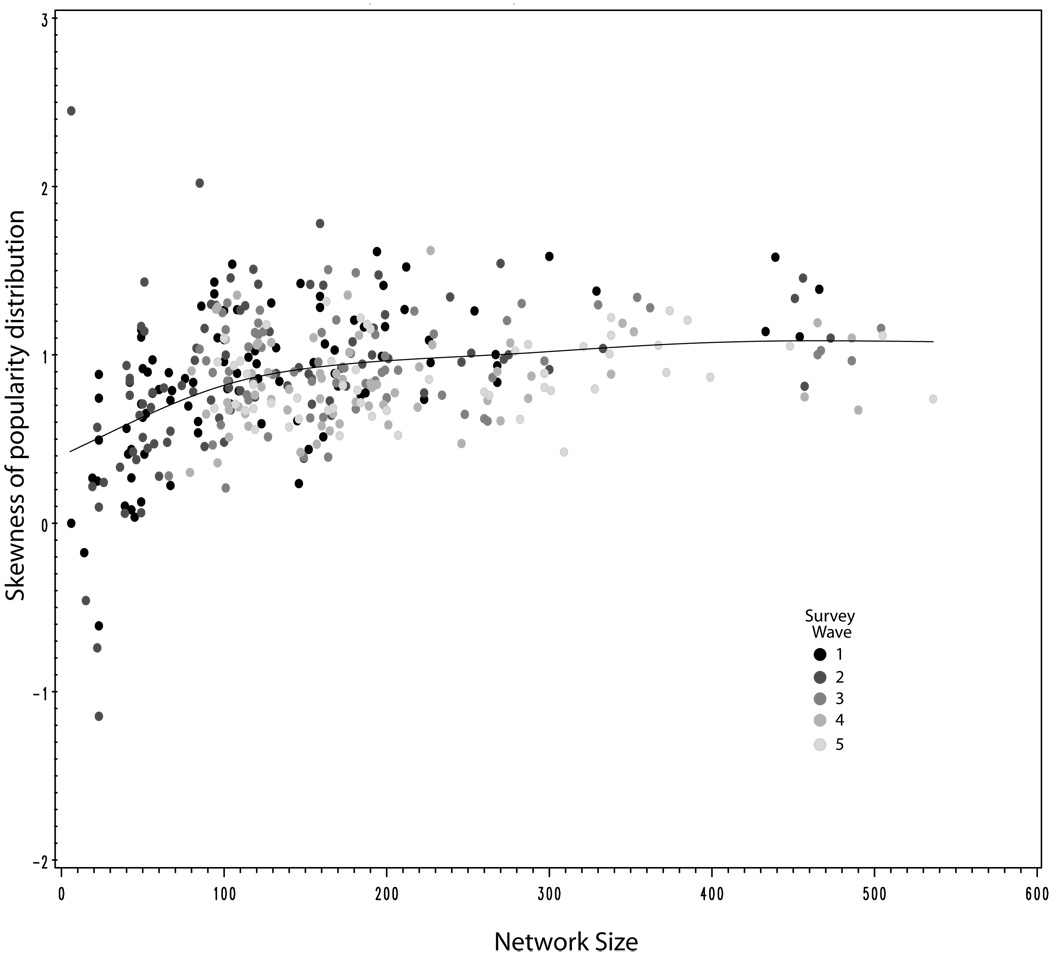
While figure 1 pools individual-level popularity across networks, a similar story emerges if we look at each network. Figure 2 plots the popularity skewness scores by network size. While the heterogeneity in skewness is larger for small networks (<100 nodes), the overall distribution of popularity is remarkably similar across networks of very different sizes.14 The earlier waves (6th graders) are typically smaller, with network size increasing across waves.
Figure 2.
Network popularity skewness by size
Figure 3 presents the distribution of the tau-statistics across waves, along with a graphical sketch of the implied macro-structural form implied by each model. All models fit better than random (0 line), with the hierarchical clustering and “39+” models fitting slightly better than the others, though such differences are likely marginal. The consistency across the different models – all showing much different distributions than a random graph – confirms that these settings are hierarchically ordered.
The models that require fully-connected cliques have slightly lower scores that those resting on chain-connected cliques, and the disconnected arrangements implied by the 39+ and hierarchical clustering models do a little better than the fully connected ranked-cluster model (though these are likely statistically indistinguishable). If these distinctions are real, while it is impossible to know for sure from just the tau statistics, any macro-level split into multiple groups likely implies that there are multiple hierarchies within the setting, which may be organized around some large-scale division. Given the age-range observed here, this is likely gender.
The distribution of both popularity and triads in these networks are consistent with a hierarchically ordered macro structure. This basic structure is common across settings and over time, though the extent varies across settings (based on the wide box-plots). Within networks, the extent of hierarchy tends to be stable over time, with a cross-wave correlation for the 39+ model tau statistic averaging just over 0.6 (not shown). This suggests that students are likely to face a similar network patterns throughout their time in middle school. Note this does not imply that the same people or groups are populating the hierarchy: groups may be changing members and/or position over time. But, the resulting structure always appears to take a hierarchical form.
Local Network Patterns
How are students positioned within these hierarchical networks and how stable are the relations that compose them? Table 1 shows us the proportion of nominations made at the row wave that were retained through the column wave.
Table 1.
Proportion of nominations matching across waves.
| Wave 2 | Wave 3 | Wave 4 | Wave 5 | |
|---|---|---|---|---|
| Wave 1 | 0.49 | 0.26 | 0.19 | 0.14 |
| Wave 2 | 0.29 | 0.20 | 0.14 | |
| Wave 3 | 0.32 | 0.21 | ||
| Wave 4 | 0.29 |
Not surprisingly, the greatest stability is between waves 1 and 2, showing that 49% of nominations made at wave 1 were repeated 6 months later. Only about a quarter of wave-1 nominations last a year, and only 1 in 7 relations last all 4 years. These figures suggest a very volatile relational structure.
Does this change reflect similar changes in status, or are “popular kids” consistently popular over time? We can test this by examining popularity mobility and popularity trajectories. Popularity mobility refers to the change in one’s position in the popularity distribution. Here we calculate popularity as percentile rank within the network, and then look at changes in that rank over time.
To disentangle changes in the size of the marginal distribution from movement within the table, we standardize the cell values so that both the rows and columns sum to 100 using the Mosteller (1968) transformation. In general, marginal distributions will be pretty equal when the table is based on percentiles, differing only due to ties, which is most common at 0 or 1 nominations. Substantively the Mosteller transformation is the same as normalizing by the expected value under row-column independence models. We also provide the simple correlation between popularity rank at each wave.
The data suggest a moderate level of popularity mobility that, not surprisingly, is more pronounced over longer periods. The shortest time-span is between wave 1 and wave 2, where we see a correlation of 0.62 in popularity rank. This stability is strongest at the top and bottom of the distribution, with nearly half of cases stable. As the examined time frame lengthens, the correlation with status decreases and the surface becomes more smooth, with a slowly decreasing probability of movement as you move from stability (diagonal) to the off-diagonal cells. This suggests a core element of popularity that remains stable, as people either cycle around a base rank level or smoothly move between nearby levels.
Of course, these mobility tables are bivariate comparisons, not trajectories, which can mask significant variability over the observation period. What does the 4 year experience as a whole look like? First, consider dividing the population into those whose popularity “stays low” (25th percentile or below), “stays medium” (between 30th and 70th percentile) and “stays high” (above 75th percentile) consistently across all 5 waves. Doing so shows that only about 3.5% are consistently low, 2.8% are consistently middle and 5.6% are consistently high. The remaining students cross these bounds at least once over the 5 waves, and examinations of the trajectories show remarkable variability (see below). Strong upward or downward mobility (moving from lowest quartile at time 1 to top quartile at time 2 or vice-versa) is rare (2.3 & 2.9% respectively).
As further indications of these trajectories, consider table 2, which cross-classifies number of times a person has been in the top quintile against the number of times they have been in the bottom quintile.
Table 2.
Popularity trajectories. Number of times a student spent in the bottom (row) and top (column) quintile.
| Times in top quintile | ||||||||
|---|---|---|---|---|---|---|---|---|
| Times in bottom quintile | 0 | 1 | 2 | 3 | 4 | 5 | Total | |
| 0 | 16.3 | 13.2 | 10.0 | 7.8 | 5.9 | 3.9 | 57.1 | |
| 1 | 13.8 | 4.8 | 1.8 | 0.5 | 0.2 | 21.2 | ||
| 2 | 9.1 | 1.2 | 0.2 | 0.0* | 10.5 | |||
| 3 | 5.7 | 0.3 | 0.0* | 5.9 | ||||
| 4 | 3.3 | 0.0 | 3.4 | |||||
| 5 | 1.9 | 1.9 | ||||||
| Total | 50.1 | 19.6 | 12.0 | 8.4 | 6.0 | 3.9 | 100 | |
Since the sum of row/column cannot exceed 5 some cells are undefined, indicated by shading.
rounds to zero. N=8936
About 1.9% of students were in the bottom quintile over all 5 waves while 3.9% were steadily at the top. But nearly 43% of the students spent at least 1 wave in the bottom quintile (49% in top); while 22% of the sample has been in the bottom quintile 2 or more times (30% in the top 2 times or more).
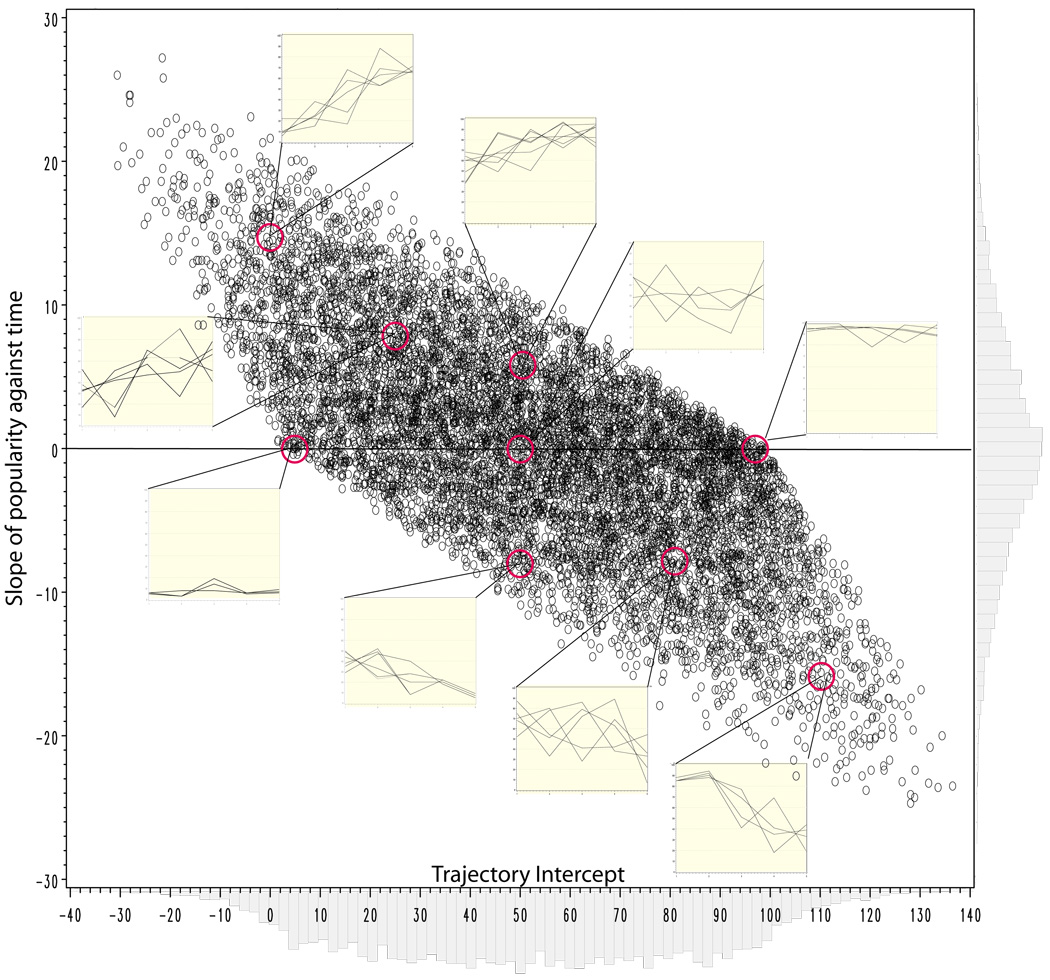
Another way to summarize the trajectories is to regress popularity against wave within persons. The slope and intercept of this regression then summarizes the (linear) movement in popularity over time.15 If you plot the slope against the intercept, you get a "space" of trajectories, which is given in figure 5 below. There is a necessary constraint to the space; since the intercept will be negatively correlated with the slope. Any person with a slope above zero is getting more popular over time, anyone with a slope below zero is getting less popular. We've picked some relevant points (3 along slope=0, 3 at increasing and 3 at decreasing) in the space and plotted sample trajectories from those points to help illustrate what the two coefficients capture: thus in the upper left of the space we find students who achieved the greatest level of upward mobility, moving from low popularity to high, while those in the lower-right started very popular and end unpopular. The histograms on the axis provide summary of the slope and intercept coefficient distributions.
Figure 5.
Sample popularity trajectories across the trajectory space
The space itself is remarkably smooth, reflecting the diversity of trajectories. The sampled points are more homogeneous, since we take them from small points of the space to illustrate the general tendencies, but the key here is that there are no “clumps” in the trajectory space, and thus models based on clustering the trajectory history (such as sequence analysis (Abbott & Hyrack 1990) will have great difficulty identifying clear trajectory clusters.
Thus, the lived-experience of popularity in middle schools indicates something of a muddle characterized by high levels of trajectory heterogeneity. There is clear evidence of latent stability, reflected in the bivariate correlation over time, suggesting that youth are likely to move short distances over time. But, these moderate correlations admit to a great deal of variation across actors. Very few respondents are consistently popular or unpopular, with many youths spending at least some time at either end of the popularity distribution. To strike a balance between this potential underlying “latent” popularity and the evident temporal variability, we use both the average popularity in prior waves and the variability in popularity (measured as the standard deviation) in trajectory models below. Variability captures the sheer amount of change, so it will be high for kids at either extreme of the trajectories given in figure 5 above, as well as for those with high variability but stable mean. However, to examine effects of the trajectory direction itself, we also use the coefficients defining the space in figure 5 in models predicting substance use.
Substance Use and Popularity
These data are remarkable not only for their rich dynamic networks, but also for the behavioral data we can link to network change. Can we find any hints in these data of a link between one’s popularity history and youth substance use? While a full treatment of the causes of substance among adolescents is beyond the scope of this paper, which is primarily concerned with describing the network context, we want to assess whether there is any potential linkage between position in the network and behavior.16 To do this, we first estimate repeated measures HLM models for substance use as a function of popularity, controlling for gender, race, wave, cohort and state. These models allow for multiple measures (one at each wave) within individuals over time. We also distinguish popularity rank from an indicator for social isolation, to ensure that the results do not depend on a single part of the distribution since, particularly for males, there is an over-representation of isolates that could confound the effect of popularity rank. These models are 3-level models, nesting time within individuals within network settings (settings are the unique combination of school and cohort). Since half of the schools received substance use interventions, the models protect against a (likely) school-level effect of the treatment program.17 The intra-class correlation for the IRT substance use score suggests that 12% of the variability in substance use is between network settings.
Our dependent variable is an IRT score of smoking, alcohol and marijuana use in the month preceding the interview. The reported rate of any use in the prior month as well as the IRT mean score by wave and gender is given in table 3.
Table 3.
Percent of students reporting any use of substances in prior month, by sex.
| Smoking | Drinking | Marijuana | Any of the 3 | Mean IRT Score | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Wave | Male | Female | Male | Female | Male | Female | Male | Female | Male | Female |
| 1 | 4.1 | 2.9 | 9.6 | 7.1 | 1.0 | 0.4 | 11.6 | 8.6 | 0.10 | 0.05 |
| (5372) | (5508) | (5367) | (5506) | (5360) | (5507) | (5354) | (5498) | [0.49] | [0.40] | |
| (5360) | (5506) | |||||||||
| 2 | 5.3 | 4.9 | 12.9 | 10.5 | 2.1 | 0.9 | 15.4 | 12.6 | 0.17 | 0.11 |
| (5060) | (5210) | (5060) | (5202) | (5063) | (5202) | (5051) | (5195) | [0.58] | [0.51] | |
| (5063) | (5205) | |||||||||
| 3 | 8.0 | 9.8 | 17.5 | 17.1 | 4.2 | 2.7 | 20.5 | 20.8 | 0.27 | 0.26 |
| (5382) | (5566) | (5382) | (5568) | (5375) | (5565) | (5360) | (5556) | [0.71] | [0.68] | |
| (5380) | (5570) | |||||||||
| 4 | 11.2 | 15.0 | 25.2 | 27.3 | 7.7 | 6.6 | 29.2 | 32.2 | 0.45 | 0.47 |
| (5362) | (5537) | (5350) | (5523) | (5324) | (5514) | (5295) | (5487) | [0.87] | [0.84] | |
| (5353) | (5534) | |||||||||
| 5 | 16.1 | 20.1 | 34.0 | 37.8 | 12.6 | 11.3 | 38.9 | 43.4 | 0.68 | 0.73 |
| (5266) | (5481) | (5260) | (5476) | (5259) | (5476) | (5245) | (5457) | [1.02] | [1.01] | |
| (5262) | (5480) | |||||||||
Standard deviation for IRT score in brackets, N for each cell in parentheses.
We find that use increases steadily over the 5 waves. Use is extremely rare early in 6th grade, but increases to just over a third of students reporting using at least one of these substances once in the prior month.
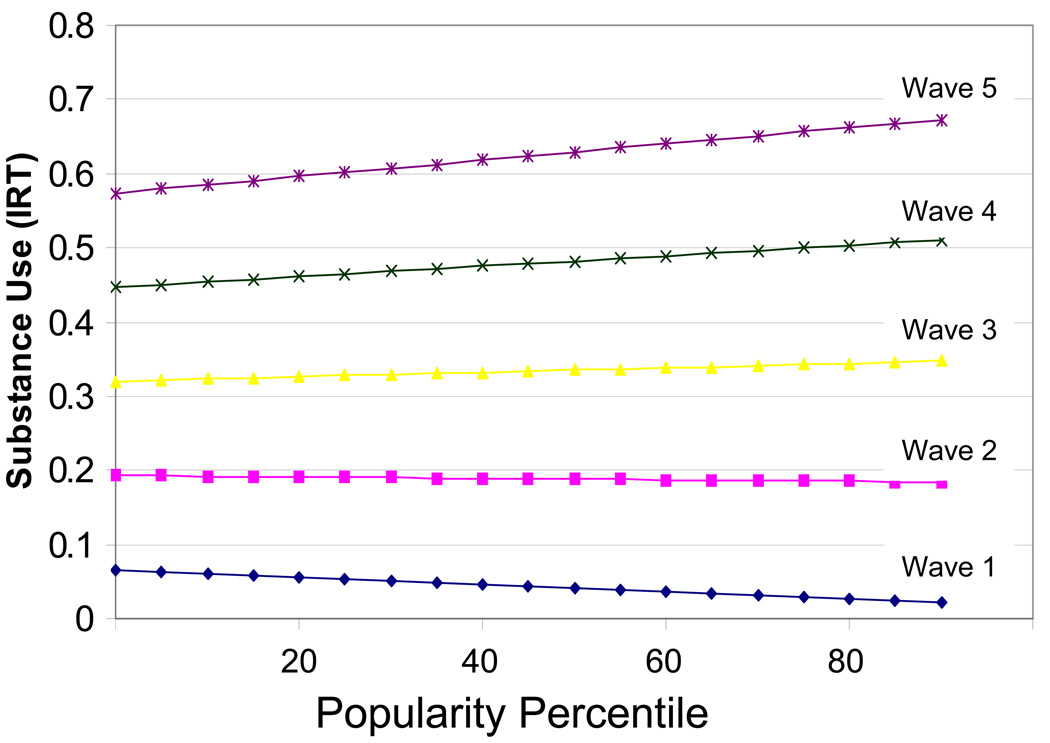
Turning to the relation between substance use and popularity, table 4 suggests a consistent relation between popularity and substance use that depends on time, as made clear by the significant positive interaction between popularity and wave. If we plot this predicted result as in figure 6, we find that for youth in wave 1 or 2 the more popular kids are either less likely to use substances or no more likely than their less-popular classmates.
Table 4.
Repeated measures models of contemporaneous popularity on substance use, with individuals nested in network settings and measures repeated within individuals over time. Standard errors in parentheses.
| Model 1 | Model 2 | |||
|---|---|---|---|---|
| Intercept | −0.031 | ** | 0.036 | ** |
| (0.019) | (0.020) | |||
| −.009 | *** | −0.008 | *** | |
| 0.003) | (0.002) | |||
| Isolated | 0.018 | |||
| (0.016) | ||||
| Wave | 0.127 | *** | 0.128 | *** |
| (0.004) | (0.04) | |||
| Male | 0.003 | 0.002 | ||
| (0.09) | (0.008) | |||
| Popularity × Wave | 0.004 | 0.004 | ||
| (0.001) | (0.001) | |||
| White | −0.054 | *** | −0.054 | *** |
| (0.011) | (0.011) | |||
| Cohort 1 | 0.076 | *** | 0.076 | *** |
| (0.009) | (0.009) | |||
| Iowa | −0.055 | *** | −0.055 | *** |
| (0.009) | (0.009) | |||
| Individuals | 52,195 | 52,195 | ||
| Network settings | 158 | 158 | ||
| Waves (repeated n) | 5 | 5 | ||
| −2 Res Log L | 110,984 | 116,072 | ||
p≤ 0.05;
≤ 0.01
≤ 0.001
Figure 6.
Substance use by wave & popularity
The slope of the effects is modest substantively, though consistent across multiple model specifications and estimation procedures.18 The effect of popularity is not due simply to lower use among isolated students.
We next turn to trajectory directly by modeling use in waves 4 and 5 as a function of popularity level and trajectory variability in prior waves. We restrict the analyses to these last two waves because we need multiple prior waves to build the trajectory score. However, we don’t want the results to depend on a single wave, so choosing the last 2 time points seems prudent. As above, these are random intercepts models with students nested in networks. We measure overall popularity as the respondent’s mean popularity across waves and variability as the standard deviation. Higher standard deviation scores on popularity reflect greater popularity change over time. The extent of increasing or decreasing popularity over time is captured with the slope coefficients for popularity trajectory.
The first two models of table 5 explore the effect of mean and variability in popularity trajectories, the last two of the trajectory direction based on the slope & intercepts of figure 5. Within the two sets, the models differ only in the inclusion of a lagged dependent variable, which while having a large effect, does not suppress the network structure effect. Looking to the simpler models of mean and variability, the effect of average prior popularity remains statistically significant and the value is substantively stronger than in the cross-section: a 10 percentile increase in average popularity increases the substance use by 0.022, about double that estimated in the cross section. This indicates a moderate relation between popularity level and substance use. The popularity stability measure suggests that larger variance in popularity over time increases substance use. The average value for popularity variability is 17.2, with a standard deviation of 8.8, so a 1–standard deviation change in popularity variability increases substance use by 0.026. So, again, the effects are substantively modest, but also similarly robust to model specification and estimation techniques.19
Table 5.
Trajectory models with setting-level random intercepts. Standard errors in parentheses.
| Model 1 | Model 2 | Model 3 | Model 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Intercept | 0.286 | *** | 0.175 | *** | 0.303 | *** | 0.178 | *** |
| (0.041) | (0.031) | (0.04) | (0.035) | |||||
| Mean Popularity (div by 10) | 0.034 | *** | 0.022 | *** | ||||
| (0.003) | (0.003) | |||||||
| Standard Deviation of Popularity | 0.005 | *** | 0.003 | *** | 0.005 | *** | 0.002 | *** |
| (0.001) | (0.001) | (0.001) | (0.000) | |||||
| Popularity Trend Slope | 0.003 | *** | 0.004 | *** | ||||
| (0.001) | (0.001) | |||||||
| Popularity Trend | 0.003 | *** | 0.002 | *** | ||||
| Intercept | (0.000) | (0.000) | ||||||
| Lagged Substance Use | 0.640 | *** | 0.639 | |||||
| Score | (0.008) | (0.009) | ||||||
| Wave 5 | 0.234 | *** | 0.126 | *** | 0.243 | *** | 0.130 | *** |
| (0.023) | (0.017) | (0.023) | (0.018) | |||||
| Male | −0.013 | −0.016 | −0.042 | ** | −0.040 | ** | ||
| (0.014) | (0.012) | (0.015) | (0.013) | |||||
| White | −0.100 | *** | −0.048 | ** | −0.101 | *** | −0.047 | ** |
| (0.018) | (0.016) | (0.020) | (0.018) | |||||
| Cohort 1 | 0.011 | *** | 0.053 | *** | 0.114 | *** | 0.055 | ** |
| (0.029) | (0.020) | (0.029) | (0.021) | |||||
| Iowa | −0.086 | ** | −0.029 | −0.074 | *** | −0.026 | ||
| (0.029) | (0.020) | (0.029) | (0.021) | |||||
| Level 1 N : 109 | ||||||||
| Level 2 N: 17,393 | ||||||||
| −2 Log L | 52,335 | 40980 | 41264 | 33090 | ||||
p≤ 0.05;
≤ 0.01
≤ 0.001
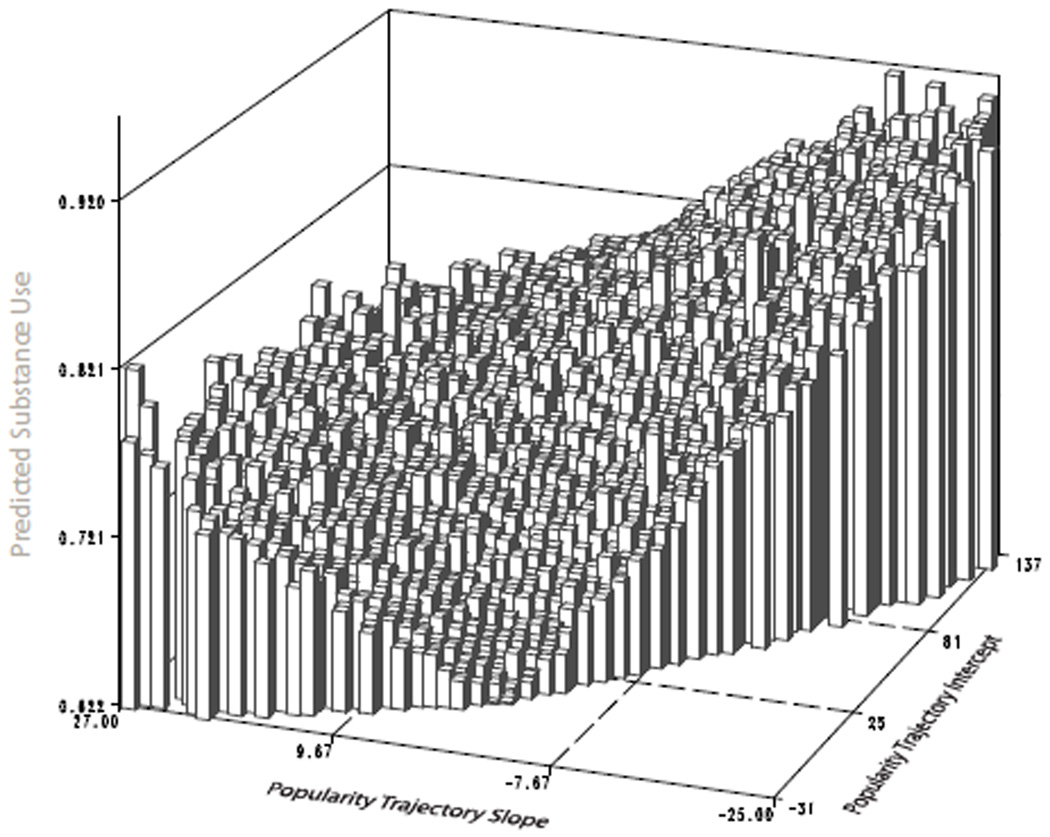
Popularity variability is high both when popularity is increasing and when it is decreasing, so a strong trend in either direction will generate a high level of trajectory variance. Since both trend directions create high variability, we want to know whether there is a significant effect of direction per se. In the last two models, we add the slope and intercept scores to summarize trajectory direction. Because of the necessary interaction between absolute value of slope and the standard deviation of popularity, it is simpler to interpret this model by examining the predicted values produced by the model. Figure 7 plots the mean predicted levels of substance use for each region of the trajectory space.20
Figure 7.
Predicted Effect of Popularity Trajectory on Substance Use
The important features to draw from figure 6 are the shape and relative height (absolute height would shift based on race, gender or setting). We find a “tilted-saddle” shape in the level of use across the trajectory space.21 The highest ends are where popularity trajectories are steep – either increasing or decreasing. The model predicts a somewhat higher effect for decreasing popularity than for increasing. The upward slope to the surface as you move across the intercept dimension captures the base increase in drinking due to mean popularity. So, we see those kids who are consistently unpopular, having a slope and intercept approaching zero, are the least likely to use substances. In contrast, substance use increases for those who are steadily popular (slope about 0 but positive intercept). However, from this base level of consistent popularity, those who are increasing in popularity and those decreasing are both more likely to use substances than those who remain steady at similar starting points. Thus we see a fairly complex relation between the number of ties received and substance use. In general, popularity level is associated with high use, but the trend matters. Those with either strongly increasing or decreasing popularity (as well as those with highly variable but non-trending popularity) are more likely to use substances.
How to interpret this pattern of findings? If use is driven by diffusion, particularly of the “any of my friends do it” type, then popular kids will be exposed to more users and thus be more likely to use themselves. But such a model cannot explain a consistent effect of variability, since once exposed we’d expect continued action. However, a status model fits both the mean and variability finding: if using confers some status, then those who are popular will use more (main effect), and attempts to maintain status will drive use when popularity is unstable. An alternative specification based on directly on peer influence, such as from within the Siena framework (Snijders et al 2010), would be needed to fully test this competing model. But, the current effects are suggestive of a status seeking effect on use.
Summary & Conclusions
This paper provides an initial description of the popularity structure and dynamics of a new sample of longitudinal networks. The results suggest that these networks are hierarchically organized across settings and over time, with a small number of students named as friends significantly more often than others. The distribution of microstructures in the network is consistent with a multiple-rank hierarchical macrostructure that appears stable over time. This form remains stable in spite of significant change at the micro level. Particular dyads are very unstable, with less than 1- in-7 remaining over the study period and nearly half changing within a year. Consistent with a 5-year longitudinal study of social status among younger children (Coie & Dodge, 1983), individual position within the network is moderately correlated over time. A significant popularity correlation suggests that at some students remain in similar positions and that students tend to make incremental changes in their position over time. The variability around this latent level is high, however, and examinations of individual trajectories suggest that students often move in and out of even the most extreme ends of the popularity distribution.
While the simple passing of time is the strongest predictor of substance use, which is consistent with much of the developmental literature, position in the popularity structure has consistent, if modest, effects on substance use. Students with higher popularity levels are more likely to use, even controlling for past use, and this appears more true in later periods than in earlier waves. Moreover, sheer instability in popularity over time contributes to greater substance use. Those who have moved widely across the popularity distribution are more likely to use substances, controlling for prior use and mean popularity.
These results are consistent with a status-seeking model of substance use, though we would need to take both substance use opportunity and peer-behavior into account to fully exclude alternate peer-influence readings of these results. To the extent that substance signals high-status, students with highly variable popularity may increase substance use to re-gain or reinforce past status. However, if students with high status variability are more likely to have access to substances (perhaps due to learning from former popular friends), then they may be carrying a learned behavior from earlier times forward, though this possibility is lowered somewhat by controls for earlier use. One of the key advantages of these data is that we can use the time-order to help disentangle such features, and future work will contrast the pure status effects proposed here against peer behavior and selection (Snijders et al 2007)
We have not yet examined the determinates of popularity variability itself, leaving this to future work. The determinates of popularity should follow from at least four sources: stable characteristics of the person (such as attractiveness or personality traits (Fowler et. al 2009), the cultural salience of which could potentially change over time), variable traits of the individual (like substance use or school performance), changes in the setting that make some people more visible than others (tracking or extracurricular involvement patterns) and the dynamics of internal friendship processes that lead to cascades in nomination patterns. Thus, if a popular person becomes friends with an unpopular person, many others may wish to become friends with him or her as well, leading to a nomination cascade. These data should be very useful for answering such questions, and more generally identifying how peer relations form and evolve over time. Particularly if middle school and early high-school are moments when students just begin to build their self identity, we anxiously look forward to having future data on a longer time span to see if the networks converge on a more stable structure.
The possibility of such effects makes clear the need for full network data to understand peer effects: events that look individual (such as smoking) may rest on cascading network effects initiated at a point far distant from the individual. This finding is a clear example of a “positional” network effect, which contrasts sharply with the standard “connectionist” diffusion models (Burt 1987). While much of the work on substance use focuses on the diffusion of non-normative behavior, focusing on the network position itself as providing a context for behavior holds much promise (Ennet & Bauman 1993). Here we’ve expanded the notion of “position” here to include change over time; treating the trajectory itself as a positional effect. This is a common strategy in work on sequence analysis (Abbott and Hyrack 1990), but rarely used in network modeling. The basic premise of this sort of work is that the meaning of occupying a given network position depends crucially on how one arrived at that position over time. If adolescents are actively orienting toward the network structure, feeling its effects and anticipating its dynamics (Coleman 1961), then the relational work they engage in likely encompasses behaviors of interest to health and education scholars.
Identifying a consistent network effect of popularity trajectory is only possible because the fine-grained dynamic data collected by PROSPER allow us to disentangle current position from an overall average with a variable trajectory. This is among the simplest of analyses made possible by a large, long-series longitudinal data source. The experimental intervention design underlying the PROSPER project is a key element of these data that we have only minimally controlled for here by using random-effects models. Future work will examine how the intervention affects peer network structure and the size of peer effects on substance use. These data will thus be extremely important for building our understanding of youth contexts, social development, experimental social health programs, and peer effects.
Figure 4.
Popularity Mobility Tables
Marginal Normalized; by wave.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
This project is funded by NSF/HSD: 0624158, W. T. Grant Foundation 8316 & NIDA 1R01DA018225-01. Thanks to Sonja Siennick, Jeff Smith, and Dan McFarland for comments and discussion related to these ideas. Prior versions of this paper were presented at the Sunbelt Social Networks Conference, The Duke University Networks Reading group, and the UNC Population Center.
While Coleman’s focus was on the collective effect of a clearly defined “crowd” of culture-setting students, we focus here on individual position within the overall network for both theoretical and practical reasons. Theoretically, we want to start with the simplest expression of status, which turns on individual popularity. Practically, identifying a “leading crowd” in a way that is estimable and consistent across multiple dynamic networks is a non-trivial challenge deserving of a paper in its own right.
The data were actually collected through the 12th grade, but have yet to be coded. Future work will extend these data through the entire high-school career. The uneven spacing of observations in the first year implies a shorter window for change between waves 1 & 2 than between waves 3 to 5.
This number excludes a small number of very small schools (less than 10 students). Note that multiple elementary schools can feed into the same high school in a given community, so there are unbalanced numbers of schools across districts.
Names were matched to in-class rosters 83% of the time. Of the remaining 17% of names, 15.1% were names that coders concluded matched none of the names on the class roster, while only 1.9% of nominations had duplicate plausible matches/unknown. These percentages imply that we succeeded in matching over 97% of the friendship choices of our frame (same-grade friends in the school).
Note there is no attempt here to account for the status of nominators. Future work will focus on centrality measures sensitive to the status of nominators. In-degree is useful as a starting point, however, since it is commonly used by other studies and easily interpreted.
One can condition on other features. For example, the PAJEK software provides expected values for the simple Erdos random graph, and formulas have been developed for conditioning on the in or out degree. One could also fit a Tau-statistic like term from within the Exponential Random Graph Modeling (ERGM) framework (Handcock et al 2003), allowing a much more flexible set of conditioning factors (but requiring MCMC estimation rather than closed-form solutions). We do not extend this exercise here, as by conditioning on U|MAN we capture much of the local (density & dyad) features responsible for structure in the triad census (See Faust 2009), and the implementation and model-fit task related to fitting an ERGM to over 300 networks is beyond the scope of this paper.
This comparison is not a formal statistical test; but merely a simple summary way to compare the triad distributions across models. We would not recommend using the tau scores to compare closely-matched models or think they justify drawing strong conclusions if the values are close to the statistical boundary. But in the absence of any reasonable summary score for identifying hierarchical topology in networks, this is a reasonable way to move forward. Ideally, we would have margin-free statistics comparable to centralization for each form of hierarchy; but currently none exist.
Triads are named by the number of Mutual, Asymmetric and Null arcs in each, with an additional indicator for direction of the asymmetric arcs if the counts are not unique. For the ranked clusters of M-cliques model, the allowed triad set is: {300, 102, 003, 120D, 120U, 030T, 021D, 021U}.
Allowed triad set: {300, 102, 003, 120D, 120U, 030T, 021D, 021U, 012}
Allowed triad set: {300, 102, 003, 120D, 120U, 030T, 021D, 021U, 012, 210}
Allowed triad set: {300, 102, 120D, 120U, 030T, 021D, 021U, 012, 210, 120C}
Note that these measures operate on a different level of analysis. Skewness is a property of the degree distribution while centralization is a property of the network. Figure 1 pools observations within the panels, combining networks. In random networks of the same size and density, skewness and centralization are highly correlated. But, this correlation lessens when size and density vary; and centralization scores are more sensitive to density than skewness. This likely turns on the fact that centralization scores are normalized to have a maximum in a star-like network, which is harder to reach in large networks.
Results are substantively similar if you use maximum as well. The number of nominations received by the most popular kids rises steadily from a low value in the smallest of schools, then stabilizes around 14 in networks with over 100 nodes.
This is a regression based on 5 points: the observed popularity score at each wave. To the extent that these points are error-prone, the resulting trajectory slope will be unstable. Such error could be due to at least two sources. First, there is within-sample error, where the observed in-degree might change were we to have some change in the data collection for that day. In general, in-degree is amongst the most robust statistics to such error (Borgatti et al 2006). Second, having more assessments of popularity – by increasing the number of waves within year for example – would likely provide a smoother estimate of change as we’d expect people to make small changes over shorter time periods. While we would always prefer more data, that both the tie-level & popularity correlations behave as-expected with distance in time suggests that the overall trend captured here is likely representative.
Note there are two sorts of questions being asked here. First, we use repeated measures HLM model to see if there is any effect of popularity per se on one’s smoking behavior. This is a fairly standard question asked of network data, and could be further expanded to multiple equation models and Siena models (Snijders et al 2009) to create a dual-dependent variable model where popularity affects substance use which, in turn, affects popularity. The other question, which we ask in the last set of models, asks if there is any relation between the history of popularity and smoking. Thus, we are not asking in these models if youth at a particular level of popularity are likely to smoke, but if having traversed a particular sequence of popularity affects behavior. The difference in the two questions is clear when you imagine how arriving at the same popularity level at time t might mean different things if it implied upward or downward mobility from some state in t-1.
The school-level treatment effect may also affect the slope of the relation between popularity, popularity variability and substance use. This falls outside our current scope, but other work explores the experimental treatment effects on network properties.
The size of this effect is difficult to judge, and thus figure 6 gives a better overall sense of magnitude. In standardized coefficient terms for simple popularity effect (without the interaction term), the effect size is similar to the difference between whites and nonwhites. Expressed as a logistic model on use above the mean or not, a 10-percentile change in popularity makes you about 3% more likely to use substances more than average. A similar result is found if one logs the dependent variable to correct for skew. Models controlling for other network features (out-degree, reciprocity, transitivity) show no substantive change in the effect of popularity. Thus while substantively modest, the effect is consistent and persistent across model specifications and estimation techniques.
We find similar results in spite of controls for alternative network measures, logging the dependent variable or estimating logistic regressions modeling heavier-than-average use.
This figure is produces as follows. First, calculate the predicted level of substance use based on slope, intercept and variability measures for each point in figure 5, holding constant race, gender and setting. This allows us to map the observed level of trajectory variability onto the xy coordinates of the trajectory space. Then measure the mean predicted value at each 1-unit wide point, and plot it here as a surface.
Alternative specifications with a curved term for intercept are significant, suggesting an even sharper bow to the shape; but the global fit statistics are weaker so we use the linear term.
Contributor Information
James Moody, Duke Sociology.
Wendy D. Brynildsen, Duke Sociology
D. Wayne Osgood, Penn State Sociology.
Mark E. Feinberg, Penn State Prevention Research
Scott Gest, Penn State.
References
- Andrew Abbott, Hyrcak Alexandra. Measuring Resemblance in Social Sequences. American Journal of Sociology. 1990;96:144–185. [Google Scholar]
- Alexander C, Piazza M, Mekos D, Valente T. Peers, schools, and adolescent cigarette smoking. Journal of Adolescent Health. 2001;29:22–30. doi: 10.1016/s1054-139x(01)00210-5. [DOI] [PubMed] [Google Scholar]
- Allen J, Porter M, McFarland FC, Marsh P, McElhaney K. The two faces of adolescents’ success with peers: Adolescent popularity, social adaptation, and deviant behavior. Child Development. 2005;76(3):747–760. doi: 10.1111/j.1467-8624.2005.00875.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aquilino WS. From adolescent to young adult: A prospective study of parent-child relations during the transition to adulthood. Journal of Marriage and Family. 1997;59:670–686. [Google Scholar]
- Asher SR, McDonald KL. The behavioral basis of acceptance, rejection and perceived popularity. In: Rubin KH, Bukowski William R, Laursen Brett, editors. Handbook of Peer Interactions, Relationships and Groups. New York: Guilford Press; 2009. [Google Scholar]
- Baumrind D. Parenting styles and adolescent development. In: Lerner RM, Petersen AC, Brooks-Gunn J, editors. Encyclopedia of Adolescence. New York: Garland; 1991. [Google Scholar]
- Berndt T, Hoyle S. Stability and change in childhood and adolescent friendships. Developmental Psychology. 1985;21(6):1007–1015. [Google Scholar]
- Berndt TJ, Hawkins JA, Hoyle SG. Changes in friendship during a school year: Effects on children’s and adolescents’ impressions of friendship and sharing with friends. Child Development. 1986;57:1284–1297. [Google Scholar]
- Bowker A. Predicting friendship stability during early adolescence. Journal of Early Adolescence. 2004;24(2):85–112. [Google Scholar]
- Bryant WK, Zick CD. An examination of parent-child shared time. Journal of Marriage and Family. 1996;58:227–237. [Google Scholar]
- Bukowski W, Newcomb A. Stability and determinants of sociometric status and friendship choice: A longitudinal perspective. Developmental Psychology. 1984;20(5):941–952. [Google Scholar]
- Bulcroft RA, Carmody DC, Bulcroft KA. Patterns of parental independence giving to adolescents: Variations by race, age, and gender of child. Journal of Marriage and Family. 1996;58:866–883. [Google Scholar]
- Burt Ronald S. Social Contagion and Innovation: Cohesion versus Structural Equivalence. American Journal of Sociology. 1987;92:1287–1335. [Google Scholar]
- Carley KM. A Theory of Group Stability. American Sociological Review. 1991;56:331–354. [Google Scholar]
- Cartwright D, Harary F. Structural Balance: A Generalization of Heider’s Theory. Psychological Review. 1956;63:277–293. doi: 10.1037/h0046049. [DOI] [PubMed] [Google Scholar]
- Cillessen A, Rose A. Understanding Popularity in the Peer System. Current Directions in Psychological Science. 14:102–105. [Google Scholar]
- Coie JD, Dodge KA. Continuities and changes in children’s social status: A five-year longitudinal study. Merrill-Palmer Quarterly. 1983;29:261–282. [Google Scholar]
- James Coleman. The Adolescent Society. New York: The Free Press of Glencoe; 1961. [Google Scholar]
- Degirmenciogui SM, Urberg KA, Tolson JM, Richard P. Adolescent friendship networks: Continuity and change over the school year. Merrill-Palmer Quarterly. 1998;44:313–337. [Google Scholar]
- Diego M, Field T, Sanders C. Academic performance, popularity, and depression predictor adolescent substance use. Adolescence. 2003;38:35–42. [PubMed] [Google Scholar]
- Dunphy DC. The Social Structure of Urban Adolescent Peer Groups. Sociometry. 1963;26:230–246. [Google Scholar]
- Eder D. The cycle of popularity: Interpersonal relations among female adolescents. American Sociological Association. 1985;58(3):154–165. [Google Scholar]
- Ennett Susan T, Bauman Karl E. Peer group structure and adolescent cigarette smoking: A social network analysis. Journal of Health & Social Behavior. 1993;34:226–236. [PubMed] [Google Scholar]
- Fowler JH, Dawes CT, Christakis NA. Model of genetic variation in human social networks. Proceedings of the National Academy of Sciences. 2009 doi: 10.1073/pnas.0806746106. published online before print January 26, 2009. doi:10.1073/pnas.0806746106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furstenberg F. The sociology of adolescence and youth in the 1990’s: A critical commentary. Journal of Marriage and the Family. 2000;62(4):896–910. [Google Scholar]
- Hallinan Maureen T. The Structure of Positive Sentiment. The Netherlands: Elsevier Scientific Publishing Company; 1974. [Google Scholar]
- Hallinan Maureen T. The Process of Friendship Formation. Social Networks. 1978;1:193–210. [Google Scholar]
- Hallinan Maureen T, Hutchins E. Structural Effects on Dyadic Change. Social Forces. 1980;59(1):225–245. [Google Scholar]
- Hallinan Maureen T, Williams R. The Stability of Students’ Interracial Friendships. American Sociological Review. 1987;52(5):653–664. [Google Scholar]
- Hallinan Maureen T, Kubitschek W. The Formation of Intransitive Friendships. Social Forces. 1990;69(2):505–519. [Google Scholar]
- Handcock Mark S, Hunter David R, Butts Carter T, Goodreau Steven M, Morris Martina. Statnet: Software tools for the Statistical Modeling of Network Data. 2003 doi: 10.18637/jss.v024.i01. http://statnetproject.org. [DOI] [PMC free article] [PubMed]
- Hardy C, Bukowski W, Sippola L. Stability and change in peer relationships during the transition to middle-level school. Journal of Early Adolescence. 2002;22(2):117–142. [Google Scholar]
- Hartup WW. The company they keep: Friendships and their developmental significance. Child Development. 1996;67:1–13. [PubMed] [Google Scholar]
- Horrocks J, Buker A. A study of friendship fluctuations of preadolescents. Journal of Genetic Psychology. 1951;78:131–144. doi: 10.1080/08856559.1951.10533571. [DOI] [PubMed] [Google Scholar]
- Jiang X, Cillessen A. Stability of continuous measures of sociometric status: A meta-analysis. Developmental Review. 2005;25:1–25. [Google Scholar]
- Johnsen EC. Network Macrostructure Models for the Davis-Leinhardt Set of Empirical Sociomatrices. Social Networks. 1985;7:203–224. [Google Scholar]
- Johnsen EC. Structure and Process: Agreement Models for Friendship Formation. Social Networks. 1986;8:257–306. [Google Scholar]
- Killeya-Jones L, Nakajima R, Costanzo P. Peer standing and substance use in early adolescent grade-level network: A short-term longitudinal study. Prev Sci. 2007;8:11–23. doi: 10.1007/s11121-006-0053-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Light JM, Dishion TJ. Early adolescent antisocial behavior and peer rejection: A dynamic test of a developmental process. In: Rodkin P, Hanish L, editors. New Directions for Child and Adolescent Development, Special Issue: Social Network Analysis and Children’s Peer Relationships. San Francisco: Jossey-Bass; 2007. pp. 77–89. [DOI] [PubMed] [Google Scholar]
- McElhaney K, Antonishak J, Allen J. “They like me, they like me not”: Popularity and adolescents’ perceptions of acceptance predicting social functioning over time. Child Development. 2008;79(3):720–731. doi: 10.1111/j.1467-8624.2008.01153.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosteller F. Association and Estimation in Contingency Tables. Journal of the American Statistical Association. 1968;63:1–28. [Google Scholar]
- Newman MEJ. The Structure and Function of Networks. SIAM Review. 2003;45:167–256. [Google Scholar]
- Osgood D Wayne, Wilson Janet K, Bachman Jerald G, O'Malley Patrick M, Johnston Lloyd D. Routine Activities and Individual Deviant Behavior. American Sociological Review. 1996;61:635–655. [Google Scholar]
- Osgood Wayne D, Barbara J McMorris, Potenza Maria T. Analyzing Multipleitem Measures of Crime and Deviance I: Item Response Theory Scaling. Journal of Quantitative Criminology. 2002;18(3):267–296. [Google Scholar]
- Oh W, Rubin K, Bowker J, Booth-LaForce C, Rose-Krasnor L, Laursen B. Trajectories of Social Withdrawal from Middle Childhood to Early Adolescence. Journal of Abnormal Child Psychology. 2008;36(4):553–566. doi: 10.1007/s10802-007-9199-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodkin PC, Farmer TW, Pearl W, van Acker R. Heterogeneity of popular boys: Antisocial and prosocial configurations. Developmental Psychology. 2000;36:14–24. doi: 10.1037//0012-1649.36.1.14. [DOI] [PubMed] [Google Scholar]
- Rubin KH, Bukowski W, Parker JG. Peer interactions, relationships, and groups. In: Damon W, Lerner RM, Eisenberg N, editors. Handbook of child psychology: Vol. 3. Social, emotional, and personality development. 6th ed. New York: Wiley; 2006. pp. 571–645. (Series Eds.) (Vol. Ed.) [Google Scholar]
- Santor D, Messervey D, Kusumakar V. Measuring peer pressure, and conformity in adolescent boys and girls: Predicting school performance, sexual attitudes, and substance abuse. Journal of Youth and Adolescence. 2000;29(2):163–182. [Google Scholar]
- Snijders TAB, Steglich CEG, van de Bunt GG. Introduction to actor-based models for network dynamics. Social Networks. 2010;32:44–60. [Google Scholar]
- Snijders Tom AB, Steglich Christian EG, Schweinberger Michael. In: Modeling the co-evolution of networks and behavior in Longitudinal models in the behavioral and related sciences. van Montfort Kees, Oud Han, Satorra Albert., editors. Lawrence Erlbaum; 2007. pp. 41–71. [Google Scholar]
- Urberg K, Degirmencioglu S, Tolson J, Halliday-Scher The structure of adolescent peer networks. Developmental Psychology. 1995;31(4):540–547. [Google Scholar]
- Wasserman S. Random Directed Graph Distributions and the Triad Census in Social Networks. Journal of Mathematical Sociology. 1977;5:61–86. [Google Scholar]
- Wasserman S, Faust K. Social Network Analysis. Cambridge: Cambridge University Press; 1994. [Google Scholar]
- Wellman B, Wong RY, Tindall D, Nazer N. A Decade of Network Change: Turnover, Persistence and Stability in Personal Communities. Social Networks. 1997;19(1):27–50. [Google Scholar]