Rethinking motor learning and savings in adaptation paradigms: model-free memory for successful actions combines with internal models

Abstract

Although motor learning is likely to involve multiple processes, phenomena observed in error-based motor learning paradigms tend to be conceptualized in terms of only a single process – adaptation, which occurs through updating an internal model. Here we argue that fundamental phenomena like movement direction biases, savings (faster relearning) and interference do not relate to adaptation but instead are attributable to two additional learning processes that can be characterized as model-free: use-dependent plasticity and operant reinforcement. Although usually “hidden” behind adaptation, we demonstrate, with modified visuomotor rotation paradigms, that these distinct model-based and model-free processes combine to learn an error-based motor task: (1) Adaptation of an internal model channels movements toward successful error reduction in visual space. (2) Repetition of the newly adapted movement induces directional biases towards the repeated movement. (3) Operant reinforcement through association of the adapted movement with successful error reduction is responsible for savings.

Introduction

Skilled motor behaviors outside the laboratory setting require the operation of multiple cognitive processes, all of which are likely to improve through learning (Wulf et al., 2010; Yarrow et al., 2009). Several simple laboratory-based tasks have been developed in an attempt to make the complex problem of motor learning more tractable. For example, error-based paradigms have been used extensively to study motor learning in the context of reaching movements (Debicki and Gribble, 2004; Flanagan et al., 2003; Held and Rekosh, 1963; Imamizu et al., 1995; Krakauer et al., 1999; Lackner and Dizio, 1994; Malfait et al., 2005; Miall et al., 2004; Pine et al., 1996; Scheidt et al., 2001; Shadmehr and Mussa-Ivaldi, 1994). In these paradigms, subjects experience a systematic perturbation, either as a deviation of the visual representation of their movements, or as a deflecting force on the arm, both of which induce reaching errors. Subjects then gradually correct these errors to return behavioral performance to pre-perturbation levels.

Error reduction in perturbation paradigms is generally thought to occur via adaptation: learning of an internal model that predicts the consequences of outgoing motor commands. When acting in a perturbing environment, the internal model is incrementally updated to reflect the dynamics of the new environment. Improvements in performance are usually assumed to directly reflect improvements in the internal model. This learning process can be mathematically modeled in terms of an iterative update of the parameters of a forward model (a mapping from motor commands to predicted sensory consequences) by gradient descent on the squared prediction error (Thoroughman and Shadmehr, 2000), which also can be interpreted as iterative Bayesian estimation of the movement dynamics (Korenberg and Ghahramani, 2002). This basic learning rule can be combined with the notion that what is learned in one direction partially generalizes to neighboring movement directions (Gandolfo etal 1996; Pine et al., 1996), leading to the so-called state space model (SSM) of motor adaptation (Donchin et al., 2003; Thoroughman and Shadmehr, 2000). Despite its apparent simplicity, the SSM framework fits trial-to-trial perturbation data extremely well (Ethier et al., 2008; Huang and Shadmehr, 2007; Scheidt et al., 2001; Smith et al., 2006; Tanaka et al., 2009). In addition, parameter estimates from state-space model fits also predict many effects that occur after initial adaptation such as retention (Joiner and Smith, 2008) and anterograde interference (Sing and Smith, 2010).

The success of the SSM framework has led to the prevailing view that the brain solves the control problem in a fundamentally model-based way: in the face of a perturbation, control is recovered by updating an appropriate internal model, which is then used to guide movement. An alternative view is that a new control policy might be learned directly through trial and error until successful motor commands are found. No explicit model of the perturbation is necessary in this approach and thus it can be described as model-free. This distinction between model-free and model-based learning originates from the theory of reinforcement learning (Kaelbling et al., 1996; Sutton and Barto, 1998). However, the dichotomy is applicable in any scenario where a control policy must be learned from experience and not just when explicit rewards are given. If learning in perturbation paradigms were purely model-free one would expect substantial trial-to-trial variability in movements. However such trial-and-error behavior is not usually observed; in fact it is only seen if subjects receive nothing but binary feedback about success or failure of their movements (Izawa and Shadmehr, 2011).

Despite the success of SSMs in explaining initial reduction of errors, there are phenomena in adaptation tasks that these models have difficulty accounting for. In particular, relearning of a given perturbation for a second time is faster than initial learning – a phenomenon known as savings (Ebbinghaus, 1913; Kojima et al., 2004; Krakauer et al., 2005; Smith et al., 2006; Zarahn et al., 2008) – whereas a basic single-timescale SSM predicts that learning should always occur at the same rate, regardless of past experience (Zarahn et al., 2008). Although SSM variants that include multiple timescales of learning (Kording et al., 2007; Smith et al., 2006) are able to explain savings over short timescales, this approach fails to predict the fact that savings still occurs following a prolonged period of washout of initial learning (Krakauer et al., 2005; Zarahn et al., 2008). Beyond SSMs, there are other potential ways to explain savings and still remain within the framework of internal models. For example, more complex neural network formulations of internal model learning can exhibit savings despite extensive washout (Ajemian et al., 2010), owing to redundancies in how a particular internal model can be represented. Another possible explanation is that rather than updating a single internal model, savings could occur by concurrent learning and switching between multiple internal models, with apparent faster relearning occurring because of a switch to a previously learned model (Haruno et al., 2001; Lee and Schweighofer, 2009). The core idea in all of these models is that savings is the result of either faster re-acquisition or re-expression of a previously learned internal model; i.e., they all explain savings within a model-based learning framework.

An entirely different idea is that savings does not emerge from internal model acquisition but instead is attributable to a qualitatively different form of learning that operates independently. We hypothesize that savings reflects the recall of a motor memory formed through a model-free learning process that occurs via reinforcement of those actions that lead to success, regardless of the state of the internal model. This idea is consistent with the suggestion that the brain recruits multiple anatomically and computationally distinct learning processes that combine to accomplish a task goal (Doya, 1999). We posit an operant process whereby the movement on which adaptation converges in hand space is reinforced because it is associated with successful target attainment in the context of a perturbation; this operant memory should not be affected by washout of an internal model. In this formulation, savings would result from accelerated recall of the reinforced action rather than of an internal model.

Support for the idea that a memory for actions exists independently of internal models comes from experiments in which repetition of a particular action leads future movements to be biased towards that action (Arce et al., 2009; Classen et al., 1998; Jax and Rosenbaum, 2007; Verstynen and Sabes, 2008). Since these experiments do not entail any change in the dynamics of the environment, these biases cannot be explained in terms of the framework of internal models. Instead, they reflect a form of model-free motor learning. More recently it has been shown that biases can be observed in parallel with acquisition of an internal model along the task-irrelevant dimension in a redundant task (Diedrichsen et al., 2010). The term that has been used for these repetition-induced biases is use-dependent plasticity (Butefisch et al., 2000; Classen et al., 1998; Diedrichsen et al., 2010; Krutky and Perreault, 2007; Ziemann et al., 2001). Here we will argue that the process underlying savings is also model-free but distinct from use-dependent plasticity.

We hypothesized that multiple learning processes can combine along the task-relevant dimension of an adaptation task. We sought to dissociate model-based (adaptation) and model-free (use-dependent plasticity and operant reinforcement) learning processes using variants of a visuomotor rotation paradigm that either eliminated or exaggerated movement repetition in the setting of adaptation. Our prediction was that, following adaptation in the absence of repetition, model-free learning processes would not be engaged and subjects would exhibit neither savings nor biases in execution of subsequent movements. Conversely, we predicted that both savings and movement biases would be more prominent when repetition is exaggerated in the context of error reduction.

Results

Experiment 1: Movement repetition caused by adaptation induced large directional biases

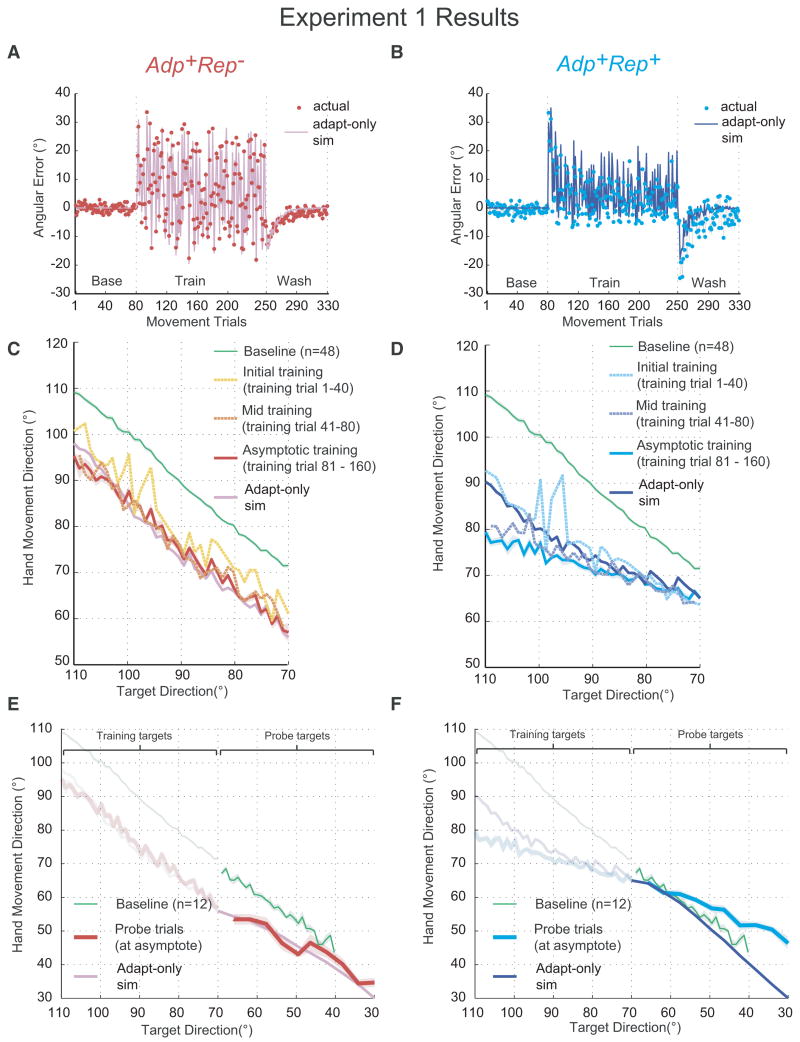
We first sought to test the hypothesis that biases can be induced along the task-relevant dimension (movement direction) of a visuomotor rotation task in the setting of adaptation (Fig. 1A). We compared two groups of subjects that were exposed to identical, uniform distributions of counter-clockwise (“+”) visuomotor rotations (mean=+20°, range=[0°, +40°]) (Fig. S1B). The protocol for the first group was predicated on the idea that adaptation itself, by converging on a single movement direction that is then repeated, can induce directional biases. We wished to exaggerate this purported asymptotic process in order to unmask it by designing an adaptation protocol for which the adapted solution in hand-space would be the same for all visual target directions (Fig. 1A). Specifically we introduced a target-dependent structure to the sequence of rotations such that the ideal movement in hand space was always in the 70° direction. In other words, cursor feedback of a movement made toward a target at θ was rotated by +(θ − 70)° (Fig. 1B). We named this group Adp⁺Rep⁺ and refer to the 70° movement direction in hand space as the “repeated direction” (Fig. 1A). It should be noted that although adaptation is not a prerequisite for biases to occur (Diedrichsen et al., 2010; Verstynen and Sabes, 2008), here the idea was to exploit adaptation to induce repetition of a particular movement direction.

Figure 1.

Protocols for Experiment 1. A. Adapted movement directions in hand space are represented by solid “pointing hand” arrows, corresponding cursor movement directions in visual space are represented by dotted arrows in the same color. For Adp⁺Rep⁻ training, cursor feedback was rotated by random, counter-clockwise angles sampled from a uniform distribution ranging from 0° to +40°. For Adp⁺Rep⁺ training, cursor feedback was rotated by a target-specific angle, sampled from the same uniform distribution as Adp⁺Rep⁻, such that the hand always had to move in the 70° direction for the cursor to hit the target (repeated direction in hand space). In probe trials subjects had to move to targets shown clockwise from the training targets without cursor feedback. Numbers and locations of targets are schematic and not to scale. B. In Adp⁺Rep⁻, the imposed rotation was randomly selected every time the subject visited each target. In Adp⁺Rep⁺, the rotations were structured so that the adapted hand movement was always toward the 70° direction in hand space.

In the second group, Adp⁺Rep⁻ (i.e., adaptation-only), which served as a control, we sought to induce pure adaptation without the possibility of repetition-induced biases, which was accomplished by sampling from the same perturbation distribution and randomly varying the rotations at each target so that the solution in hand space was never repeated for any given target (Fig. 1A, B). Subjects in Adp⁺Rep⁻ were expected to counter-rotate by -20° on average (Scheidt et al., 2001), making 70° movements in hand space on average for all visual targets as the result of adaptation alone.

The imposed rotations resulted in reaching errors that drove both Adp⁺Rep⁻ and Adp⁺Rep⁺ to adapt (Fig. 2A, B). State-space models have been used extensively in adaptation studies and have shown good fits to trial-to-trial data (Donchin et al., 2003; Huang and Shadmehr, 2007; Scheidt et al., 2001; Smith et al., 2006; Tanaka et al., 2009; Thoroughman and Shadmehr, 2000). We reasoned that if we had succeeded in creating a condition that only allowed adaptation, Adp⁺Rep⁻, then a state-space model that describes the process of internal model acquisition would simulate the empirical data well. In contrast, in Adp⁺Rep⁺, we predicted that we would obtain a good state-space model fit during initial leaning but that subsequently subjects' performance would be better than predicted because of the presence of additional model-free learning processes that become engaged through repetition of the same movement. We obtained rotation learning parameters and the directional generalization function width from our previously published data (Tanaka et al., 2009) and used these to generate simulated hand directions for the target sequences presented in Adp⁺Rep⁺ and Adp⁺Rep⁻ during training (Fig. 2C, D, “Adapt-only sim”). The state-space model was an excellent predictor of the empirical data for Adp⁺Rep⁻ (r²=0.968, Fig. 2C), which supports our assumption that asymptotic performance in Adp⁺Rep⁻ can be completely accounted for by error-based learning of an internal model alone; subjects rotated their hand movement by an average of --13.97±1.41° (mean±s.d.) (the vertical displacement from the naïve line in Fig. 2C), or about 70% adaptation on average for all targets.

Figure 2.

Group average results for Experiment 1. Left column: Adp⁺Rep⁻; right column: Adp⁺Rep⁺. A, B. Time courses for empirical trial-to-trial data (dots) and adaptation (state-space) model simulations (lines). Errors were computed as the angular separation between cursor and target direction (shadings indicate s.e.m). C, D. Hand-movement direction versus displayed target direction for the initial, middle and asymptotic phases of training: both data and simulation at asymptote shown. For comparison, baseline data from all subjects are also plotted (green line). Shading indicates s.e.m. The two “peaks” in initial training line show that the performance of the first two trials in training was close to naïve performance. E, F. Hand-movement direction versus target direction for generalization probes: both data and simulation shown. Panels from C and D are re-plotted in faded colors. Baseline performance to the probe target directions for a separate group of subjects is plotted (green) for comparison. Shading indicates s.e.m.

For Adp⁺Rep⁺, the adaptation model was able to predict hand directions relatively well in the early phase of training (r²=0.753) but then began to fail as subjects developed a directional bias beyond what was expected from adaptation alone (r²=-0.502) (Fig. 2D, asymptotic training). This suggests that errors were first reduced through adaptation but then were further reduced through mechanisms other than adaptation.

The divergence between the data and the model in Adp⁺Rep⁺ had a particular structure: a bias towards the repeated direction. Indeed, at training asymptote, movement directions in hand space for Adp⁺Rep⁺ were more tightly distributed around the repeated direction (mean s.d.=4.9±0.4°, mean±s.e.m) when compared to Adp⁺Rep⁻ (mean s.d.=11.7±0.45°, t(14)=-11.95, p<0.001). This tight distribution of hand movements at asymptote constituted our key step for induction of use-dependent learning (distribution shown in supplementary Fig. S1D), which we posited would manifest as a movement bias toward the mean of the hand movement distribution at the end of training (i.e., toward the repeated direction). The mean movement direction at the end of training across subjects was 76.0±2.1° (mean±s.d.) for Adp⁺Rep⁻ (supplementary Fig. S1D) and the mean movement direction at the end of training was 71.6±1.3° (mean±s.d.) for Adp⁺Rep⁺.

We tested for generalization in a mirror subset of untrained probe targets arrayed evenly and clockwise of the repeated direction (Fig 1A, Block 3). No cursor feedback was provided in these trials. Our previous work has demonstrated that generalization for adaptation alone falls off as a function of angular separation away from the training direction (Donchin et al., 2003; Gandolfo et al 1996; Krakauer et al., 2000; Pine et al., 1996; Tanaka et al., 2009); subjects return to their default 0° mapping once they are 45° from the training direction. Within this range, the direction of movements in hand space should always be opposite to the rotation in visual space. In other words, since all the imposed rotations were counter-clockwise, all movements toward the probes in hand space should rotate clockwise relative to the target direction. As expected for generalization of adaptation, hand directions in Adp⁺Rep⁻ were clockwise and gradually converged to naïve performance and this was predicted well by the state-space model (Fig. 2E). However, if we were correct in surmising that the Adp⁺Rep⁺ protocol induced biased movements towards the repeated direction then this would predict a similar pattern of directional biases at the probe targets. Adp⁺Rep⁺ crossed and began to show an increasing bias away from naive directions as the probe directions moved further away from the repeated direction in hand space (Fig. 2F); this is the opposite of the expectation for adaptation but entirely consistent with a bias toward the repeated direction (Verstynen and Sabes, 2008).

Interestingly, the bias generated during Adp⁺Rep⁺, which can be plotted as the dependent relationship between displayed targets and hand movement direction, was also apparent during learning, with a slope of 0.32 (±0.03) for the trained targets that was comparable to the slope for the probe targets (0.42±0.04). To summarize Experiment 1, adaptation to a target sequence that led to movements distributed around the repeated direction in hand space led to a bias towards the repeated direction that was comparable for trained and untrained targets, with increasing absolute size of bias for farther away targets in both directions. These results are opposite of what would be predicted if the observed behavior were solely due to adaptation of an internal model and show that a model-free process based on repeated actions is in operation in Adp⁺Rep⁺ but not Adp⁺Rep⁻.

Experiment 2: Savings occurred following adaptation-induced repetition but not with either adaptation or repetition alone

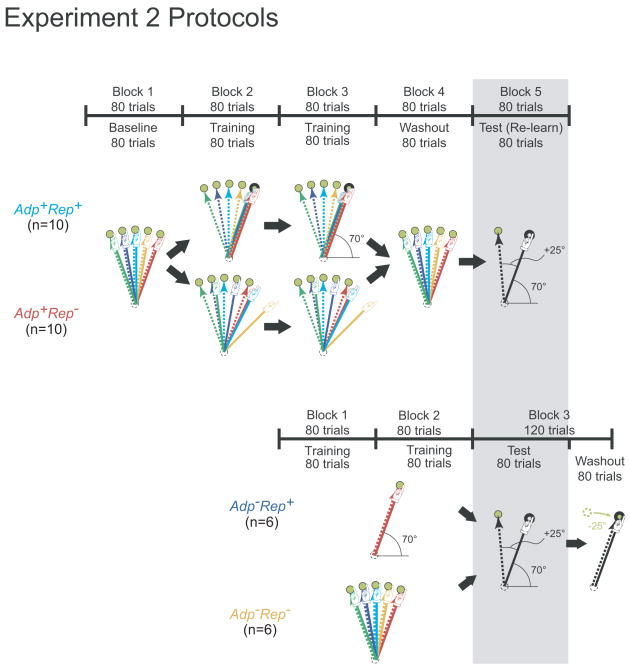
The results of Experiment 1, which showed directional biases in the Adp⁺Rep⁺ group, suggested a possible mechanism for savings: subjects in Adp⁺Rep⁺ learned to associate the repeated 70° direction movement in hand space with successful adaptation to all targets, i.e., a particular movement in hand space was associated with successful cancellation of errors in the setting of a directional perturbation at all targets. This led us to hypothesize that savings may, at least in part, be attributable to recall of the movement direction that was reinforced at or near asymptote during initial adaptation. The idea is that as re-adaptation proceeds it will bring subjects within the vicinity of the movement direction that they have previously experienced and associated with successful adaptation, they will therefore retrieve this direction before adaptation alone would be expected to converge on it. Therefore, the prediction would be that post-washout re-exposure to a rotation at a single target would lead to savings for Adp⁺Rep⁺ when the re-adapted solution in hand space is the previous repeated direction, but there would be no savings for Adp⁺Rep⁻. Also no savings would be predicted after repetition alone (Adp⁻Rep⁺) because it would not be associated with (previously successful) adaptation. Finally, a naïve group practiced movements in all directions in the absence of a rotation (Adp⁻Rep⁻); this group had no error to adapt to and movements to multiple directions would prevent repetition-related directional biases. Thus Adp⁻Rep⁻ served as a control for the other 3 groups.

We therefore studied four new groups of subjects who each underwent one of four different kinds of initial training (Adp⁺Rep⁺, Adp⁺Rep⁻, Adp⁻Rep⁺, Adp⁻Rep⁻). The two Adp⁺ groups had a washout block after training and all four groups were tested with a +25° rotation at the 95° target (Fig. 3). That is, the movement solution in hand space for the test session was again the 70° direction. We chose a +25° rather than a +20° rotation in order to increase the dynamic range available to demonstrate savings and because reinforcement should be rotation angle invariant as it is the adaptation-guided direction in hand space that matters. We fit a single exponential function to each subject's data to estimate the rate of error-reduction, expressed as the inverse of the time constant (in units of trial^-1). Savings would be indicated by a faster error-reduction rate for relearning when compared to naïve learning.

Figure 3.

Adp⁺Rep⁻,Adp⁺Rep⁺,Adp⁻Rep⁺ and Adp⁻Rep⁻ protocols for Experiment 2, illustrated in the same format as Figure 1A. The Adp⁺ groups initially trained with counter-clockwise rotations drawn from a uniform distribution ranged from 0° to +40°. The Adp⁻ groups initially trained without rotation. The test block is shown with a gray box background: in all four groups, every subject was tested at the 95° target with a counter-clockwise 25° rotation.

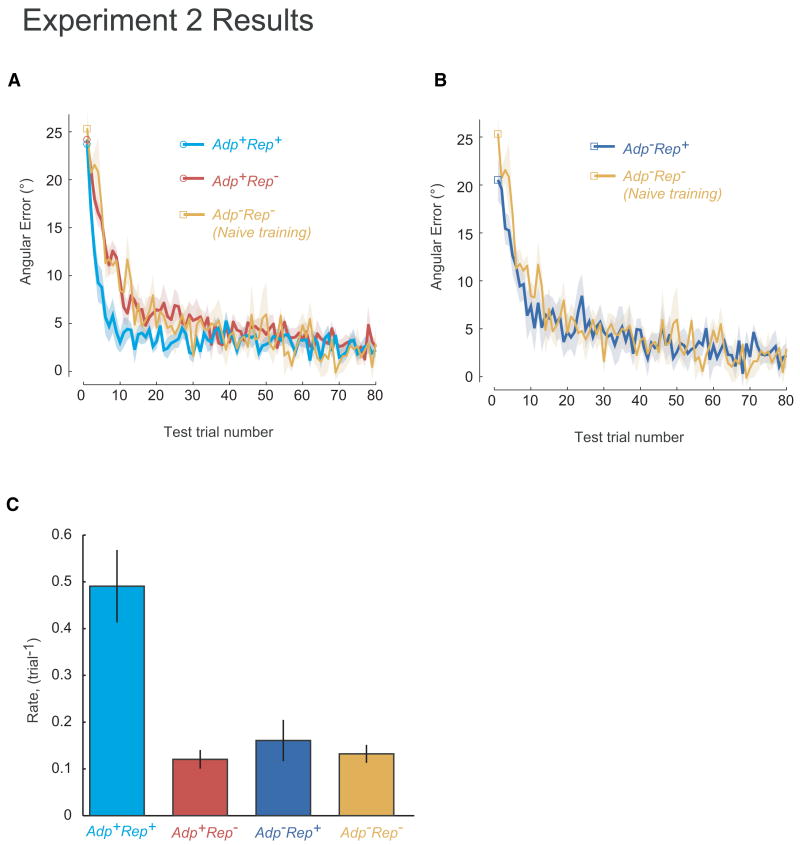
We first tested for savings in Adp⁺Rep⁺ and Adp⁺Rep⁻. On the first test trial after washout, both Adp⁺Rep⁺and Adp⁺Rep⁻, produced errors close to 25°, which indicated that washout was complete (Adp⁺Rep⁺: 23.73±1.18° (mean±s.e.m.); Adp⁺Rep⁻, 24.20±2.37, t(18)=-0.340, p=0.738) (Fig. 4A). We fit a single exponential function to each subject's data to estimate the rate of error reduction (Fig. 4C). In support of our hypothesis, Adp⁺Rep⁺ showed significant savings (0.49±0.08 trial^-1, mean±sem) when compared to the naïve training group Adp⁻Rep⁻ (0.13±0.02 trial^-1) (two-tailed t-test, t(14)=3.495, p=0.004). In contrast, Adp⁺Rep⁻ (0.12±0.02 trial^-1) were no faster than the naïve training control and showed no savings (t(14)=-0.39, p=0.70)(Fig. 4A,C). An alternative analysis using repeated-measure ANOVA yielded the same result (not shown). Indeed, Adp⁺Rep⁺ had a faster rate of relearning rate than Adp⁺Rep⁻, (t(18)=4.62, p<0.001). We had power of 0.8 (see Methods) and thus the negative results are likely true negatives. The effect size we saw for savings is comparable to that in previous studies conducted in our and other laboratories. The time constants are similar to our previous report of savings (Zarahn et al., 2008). While savings is defined as faster relearning rate, it has been measured in various ways in published studies; therefore we converted reported values in the literature to a percentage increase (e.g., [amount of error reduced in relearning - amount of error reduced in naïve] / amount of error reduced in naïve). The degree of savings reported in the literature is quite variable. For example, we have previously reported a 20% increase for a 30° visuomotor rotation (Krakauer et al., 2005). For force field adaptation, an estimated 23% increase has been reported (Arce et al., 2010). In Experiment 2, we found a 35% increase in the average amount of error reduced in Adp⁺Rep⁺ over the first 20 trials when compared to naïve (Adp⁻Rep⁻) (two-tailed, t(14)=-4.175, p=0.001). Thus we saw a marked savings effect for a +25° rotation for Adp⁺Rep⁺, but no savings at all for Adp⁺Rep⁻. This suggests that adaptation alone is insufficient to induce savings.

Figure 4.

Group average results for Experiment 2. A. Test block learning curves for Adp⁺Rep⁻, Adp⁺Rep⁺, and, Adp⁻Rep⁻. Square and circular markers show the average errors for the first test trial. Errors were computed as the angular separation between cursor and target direction. B. Test block learning curves for Adp⁻Rep⁺ and Adp⁻Rep⁻. Square markers show the average errors for the first test trial. Errors were computed as the angular separation between cursor and target direction. S.e.m. was omitted for clarity. C. Estimated error reduction rates for all four groups during the test block (means of the time constant of a single exponential fit to individual subject data). Error bars indicate s.e.m.

There are, however, two potential concerns with the interpretation of experiment 2. First, the difference between Adp⁺Rep⁺ and Adp⁺Rep⁻ might be attributable to the fact that subjects in these two groups might not have adapted to the exactly the same degree to the 95° target direction during initial training, although the difference was small (approximately 6°). Second, subjects in Adp⁺Rep⁻ were exposed to a 20° rotation but were then tested on 25°, i.e, a larger angle than they adapted to on average, although it has been shown that adaptation to smaller rotation facilitates subsequent adaptation to a larger rotation (Abeele and Bock, 2001). Therefore we also tested for savings in two additional groups with a +20° rotation in the 90° direction, where the two groups showed comparable degrees of initial adaptation (Adp⁺Rep⁻: 17.3±0.8°, Adp⁺Rep⁺: 18.51±0.9°, t(14)=-1.047, p=0.31)(supplementary Fig. S1A, E). Again, Adp⁺Rep⁺ had a significantly greater savings than the Adp⁺Rep⁻ (0.15±0.01 trial^-1 versus 0.08±0.02 trial^-1, t(14)=3.06, p=0.009) (supplementary Fig. S1F).

In contrast, no savings was observed for the repetition-only group, Adp⁻Rep⁺ (Fig. 4B); indeed the learning rate was not significantly different from naïve training in Adp⁻Rep⁻ (0.16±0.04 trial^-1 v.s. 0.13±0.02 trial^-1, two-tailed t-test, t(10)=0.594, p=0.565) (Fig. 4C). Of note, there was a small bias at the beginning of the test session for Adp⁻Rep⁺, which suggests the development of use-dependent plasticity as the result of single direction training; the imposed rotation was 25° but they started with an initial error of 20.54±2.23° (mean±s.e.m.) whereas the naïve control group started at the expected value of 25.36±1.93°.

To summarize Experiment 2, an adaptation protocol with movement repetition led to clear savings whereas neither adaptation alone nor repetition alone led to any savings. These results suggest that the association of movement repetition with successful adaptation is necessary and sufficient for savings.

Experiment 3: Savings occurs for oppositely signed rotations if they share the same hand-space solution

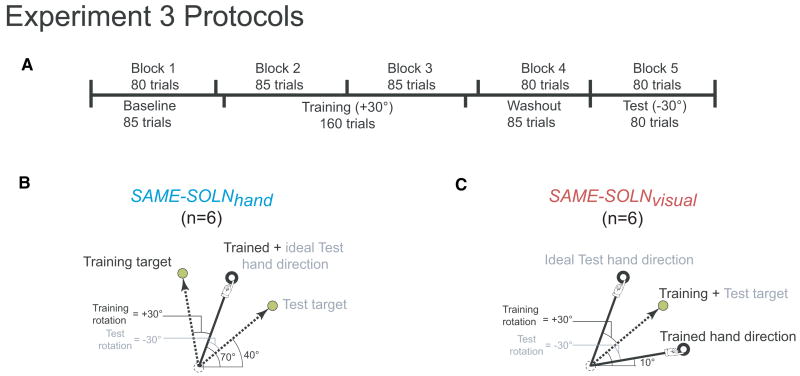
The results of Experiment 2 support the idea that savings is dependent on recall of a repeated solution in hand space. Experiment 2 was designed to exaggerate the presence of model-free reinforcement learning, a process that we argue is present even when the solution in hand-space does not map onto multiple directions in visual space. To show that reinforcement also occurs in the more common scenario of one hand space solution for one visual target, we took advantage of the observation that when rotations of opposite sign are learned sequentially using the popular A-B-A paradigm (where A and B designate opposite rotations in sign) there is no transfer of savings between A and B, nor subsequent savings when A is relearned (Bock et al., 2001; Brashers-Krug et al., 1996; Krakauer et al., 2005; Krakauer et al., 1999; Tong et al., 2002; Wigmore et al., 2002). A surprising prediction of our reinforcement hypothesis is that savings should be seen for B after A if the required hand direction is the same for both A and B, even if the two rotations are opposite in sign and learning effects of A are washed out by a intervening block of baseline trials before exposing subjects to B. In this framework, interference (or no savings) in the A-B-A paradigm is attributable to a conflict between the hand space solutions associated with success for the A and B rotations and not because A and B are opposite in sign in visual space.

Two groups were studied to test the prediction that savings would be seen for a counter-rotation after learning a rotation if they shared the same solution in hand space (SAME-SOLN_hand) but not if they only shared the same solution in visual space (SAME-SOLN_visual) (Fig. 5). The SAME-SOLN_hand subjects first trained in one target direction (100° target) with a +30° rotation and then, after a washout block, tested in another target direction (40° target) with a counter-rotation of -30°. The two different target directions were chosen so that the adapted solution to the two oppositely-signed rotations would be the same direction in hand space (70°) and so that target separation was sufficient to minimize generalization effects (Tanaka et al., 2009) (Fig. 5B). In the SAME-SOLN_visual group, subjects first trained in one target direction (40° target) with a +30° rotation and then, after a washout block, tested in the same target direction with a -30° rotation. Thus in this case, the adapted solution for the two rotations was the same direction in visual space, which led to different adapted solutions in hand space (Fig. 5C). Baseline and washouts blocks contained equally spaced targets between the 100° and 40° target directions.

Figure 5.

Protocol for Experiment 3. A. SAME-SOLN_hand and SAME-SOLN_visual were first trained on a +30° rotation then tested on a -30° rotation. B. Illustrations of ideal solution in hand space and in visual (cursor) space for SAME-SOLN_hand. The adapted movement in hand space was the same for both the +30° and -30° rotations. Black labels indicate the imposed rotation, the displayed target, and the adapted hand movement direction for initial training with the +30° rotation. Gray labels indicate the imposed rotation, the displayed target, and the ideal hand movement direction for the -30° rotation. C. Illustrations of ideal solution in hand space and in visual (cursor) space for SAME-SOLN_visual. The adapted movement in visual (cursor) space was the same for both the +30° and -30° rotations.

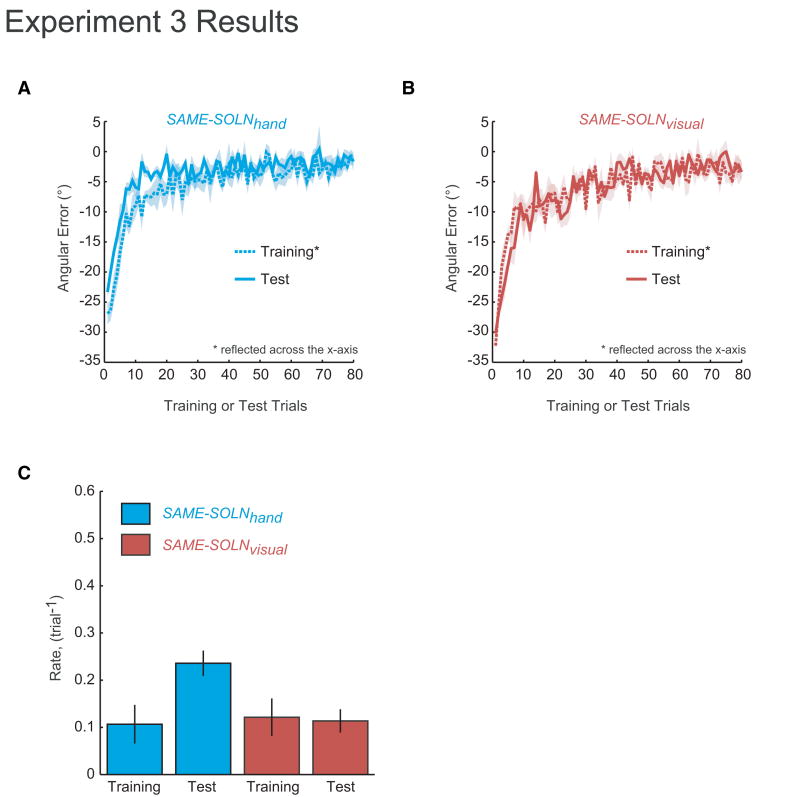
The two groups exhibited similar behaviors during initial training (Fig. 6). During initial training on +30° rotation, SAME-SOLN_hand had a learning rate of 0.11±0.04 trial^-1 (mean±s.e.m.) and SAME-SOLN_visual had a rate of 0.12±0.04 trial^-1 (Fig. 6C). Consistent with the prediction of operant reinforcement, SAME-SOLN_hand showed savings for the -30° rotation after training on +30° (Fig. 6A); the relearning rate during test (0.23±0.03 trial^-1) was significantly faster than initial learning (Fig. 6C) (paired one-tailed t(5)=-2.371, p=0.03). In contrast, no savings were seen for SAME-SOLN_visual which had a relearning rate of 0.11±0.02 trial^-1 during test (Fig. 6B) (paired one-tailed t(5)=0.238, p=0.411).

Figure 6.

Group average results for experiment 3. A. Learning curves for initial training and test sessions for SAME-SOLN_hand. Shading indicates s.e.m. B. Learning curves for initial training and test sessions for SAME-SOLN_visual. C. Estimated learning rates for training and test (means of the time constant of a single exponential fit to individual subject data). Error bars indicate s.e.m.

Interestingly, in the first test trial of the -30° rotation, SAME-SOLN_hand had an average error that was less than the -30° (-23.34±0.88°, one-tailed t(5)=7.56, p<0.001) while SAME-SOLN_visual had an error not significantly different from -30° (t(5)=-0.2, p=0.849) (Fig. 6B). This is consistent with the bias seen in experiment 1. In summary, the results of Experiment 3 suggest that savings is attributable a model-free operant memory for actions and not to faster re-learning or re-expression of a previously learned internal model.

Discussion

We sought to unmask two model-free learning processes, use-dependent plasticity and operant reinforcement, which we posited go unnoticed in conventional motor adaptation experiments because their behavioral effects are hidden behind adaptation. We found evidence for use-dependent plasticity in the form of a bias towards the repeated direction (i.e., the direction in hand space converged upon by adaptation) for both trained and untrained targets. We found evidence for operant reinforcement in the form of savings – subjects showed faster relearning when rotations of either sign (clockwise or counter-clockwise) required an adapted solution that coincided with a previously successful hand movement direction.

Use-dependent plasticity

We designed our Adp⁺Rep⁺ protocol so that adaptation itself would create a narrow distribution of hand movements centered on a particular direction, with the prediction that this would lead to a directional bias via use-dependent plasticity. Adp⁺Rep⁺, as expected, did induce a bias toward the mean of the hand movements at asymptote. The hand direction versus target direction relationship was well described with a single linear fit (0 < slope ≪ 1) that had a close fit to both training and probe targets. These results are consistent with a recent study by Verstynen and Sabes (Verstynen and Sabes, 2008), which showed that repetition alone leads to directional bias. Interestingly, the biases we observed here in the setting of adaptation appear to be larger compared to those induced by repetition alone, which suggests that repetition in the context of reducing errors in response to a perturbation may in itself generate reward that modulates use-dependent plasticity.

Support for our contention that use-dependent plasticity can be induced during adaptation comes from a force-field adaptation study by Diedrichsen et al (Diedrichsen et al., 2010), in which they demonstrated the existence of use-dependent learning in a redundant-task design. In this study, a force channel restricting lateral movements of the hand gradually redirected subjects' hand paths by 8° laterally. However, this had no effect on success in the task because the task-relevant error only related to movement amplitude. Crucially, use-dependent learning occurred in a direction that was orthogonal to the task-relevant dimension, which is why it could be separately identified. Another important result in the study by Diedrichsen and colleagues is that adaptation, pushing in the direction opposite to the channel, occurred in parallel to use-dependent plasticity so that the latter only became apparent after washout of adaptation. The critical difference between our study and that by Diedrichsen and colleagues is that we reasoned that adaptation itself can act like a channel but in the task-relevant dimension – it not only reduces visual error but also guides subjects' hand towards a new path in hand space. Analogously to washing out adaptation in the Diedrichsen et al. study in order to show use-dependent plasticity (Diedrichsen et al., 2010), we probed for use-dependent plasticity beyond the range of the expected generalization function for adaptation and found a strong bias towards the repeated direction in hand space.

Savings

Savings is a form of procedural and motor memory that manifests as faster relearning compared with initial learning (Ebbinghaus, 1913; Smith et al., 2006; Zarahn et al., 2008). We reasoned that the reward landscape is not flat during adaptation but rather is increasingly rewarding as the prediction error decreases, i.e., the hand movement that is induced by the adaptation process will be reinforced through increasing success (decreasing error). Our current results suggest that subjects on second exposure recall the hand direction that was reinforced during the first exposure to the perturbation. Adp⁺Rep⁺ showed marked savings whereas Adp⁺Rep⁻showed no savings, even though they adapted to the same mean rotation. We conclude from Experiment 2 that a reinforcement process was necessary and sufficient for savings, and that use-dependent plasticity is not sufficient for savings.

A set of previously puzzling results reported in visuomotor rotation studies may also be more easily interpreted as arising from an operant model-free mechanism. Savings for a given rotation is disrupted if subjects train with a counter-rotation even at prolonged time-intervals after initial training and when aftereffects have decayed away (Krakauer et al., 2005; Krakauer et al., 1999). We propose that persistent interference effects occur because successful cancellation of rotations of opposite sign is associated with different movements in hand space even if the movement of the cursor into the target is the same in visual space. That is, the corresponding motor commands to the same target are distinctly different for oppositely signed rotations. Thus the association of the same target with different commands in a serial manner, as is done with A-B-A paradigms, could lead to interference as is seen with other forms of paired-associative paradigms. In such paradigms, interference occurs through retrieval inhibition (Adams and Dickinson, 1981; Anderson et al., 2000; MacLeod and Macrae, 2001; Wixted, 2004). Complementary to this explanation for interference, we can predict that there should be facilitation, i.e., savings, for two rotations of opposite sign if they are both associated with the same commands or movements in hand space. This was exactly what we found in Experiment 3: learning a +30° counter-clockwise rotation facilitated learning of a -30° clockwise rotation when both rotations required the same directional solution in hand space. This supports the idea that an operant reinforcement process underlies savings and interference effects in adaptation experiments. Furthermore, results from Experiment 3 showed that the directional solution in hand space need not be associated with multiple targets, as in Experiment 1 and 2, for reinforcement to occur; success at a single target, as in Experiment 3 (and in most conventional error-based motor learning paradigms), is sufficient for savings.

Numerous studies suggest that adaptation is dependent on the cerebellum (Martin et al., 1996a, b; Smith and Shadmehr, 2005; Tseng et al., 2007), a structure unaffected in Parkinson's disease (PD), and therefore initial learning in patients with PD would be expected to proceed as in controls – as indeed was recently demonstrated (Bedard and Sanes, 2011; Marinelli et al., 2009). Operant learning is, however, known to be impaired in PD (Avila et al., 2009; Frank et al., 2004; Rushworth et al., 1998; Rutledge et al., 2009; Shohamy et al., 2005). Thus, our contention that initial learning of a rotation occurs through adaptation but savings results from operant learning predicts that patients with PD would show a selective savings deficit in an error-based motor learning paradigm. This is exactly what has been found: patients with PD were able to adapt to initial rotation as well as control subjects but they did not show savings (Bedard and Sanes, 2011; Marinelli et al., 2009). Thus our framework of multiple learning processes can explain this otherwise puzzling result. A prediction would be that PD patients would show no difference in learning rates between Adp⁺Rep⁻ and Adp⁺Rep⁺ protocols, because only adaptation would occur.

Adaptation as model-based learning

Prevailing theories of motor learning in adaptation paradigms are fundamentally model-based: they posit that the brain maintains an explicit internal model of its environment and/or motor apparatus that is directly used for planning of movements. When faced with a perturbation, this model is updated based on movement errors and execution of subsequent movements reflects this updated model (Shadmehr et al., 2010). We wish to define adaptation as precisely this model-based mechanism for updating a control policy in response to a perturbation. Adaptation does not invariably result in better task performance. For example, in a previous study we showed that adaptation to rotation occurs despite conflicting with explicit task goals (Mazzoni and Krakauer, 2006). In the current study, hyper- or over-adaptation occurred to some targets due to unwanted generalization – this was why the steady-state predicted by the state-space model for Adp⁺Rep⁺ showed that subjects adapted past the 70° target for near targets and insufficiently adapted for far targets (Fig. 2D). Diedrichsen and colleagues also showed that force-field adaptation occurs at the same rate with or without concomitant use-dependent learning (Diedrichsen et al., 2010). It appears, therefore, that adaptation is “automatic” – it is an obligate, perhaps reward-indifferent (Mazzoni and Krakauer, 2006), cerebellar-based (Martin et al., 1996a, b; Smith and Shadmehr, 2005; Tseng et al., 2007) learning process that will attempt to reduce prediction errors whenever they occur, even if this is in conflict with task goals.

In spite of the fact that most behavior in error-based motor learning paradigms is well described by adaptation, we argue here that there are phenomena in perturbation paradigms that cannot be explained in terms of adaptation alone. Instead, additional learning mechanisms must be present which are model-free in the sense that they are associated with a memory for action independently of an internal model and are likely to be driven directly by task success (i.e. reward). We posit that there at least two distinct forms of model-free learning processes: use-dependent plasticity, which gives rise to movement biases towards a previously repeated action, and operant reinforcement, which leads to savings when model-based adaptation leads behavior towards a previously successful repeated action.

Combining model-based and model-free learning

In the theory of reinforcement learning, the general problem to be solved is to use experience to identify a suitable control policy in an unknown or changing environment (Sutton and Barto, 1998). All motor learning can be conceptualized within this framework; even if there is no explicit reward structure, any task implicitly carries some notion of success or failure that can be encapsulated mathematically through a cost (reward) function.

There are two broad categories of solution methods for such a problem. In a model-based approach, an explicit model of the dynamics of the environment is built from experience and this is then used to compute the best possible course of action through standard methods of optimal control theory such as dynamic programming. Note that, in general, model-based control can also entail building a model of the reward structure of the task. In the case of motor control, however, we assume that the reward structure is unambiguous: success is achieved by the cursor reaching the target. In model-free control, by contrast, no such model of the task dynamics is built and instead the value of executing a given action in a given state is learned directly from experience based on subsequent success or failure. While a model-based learning strategy requires significantly less experience to obtain proficient control in an environment and offers greater flexibility (particularly in terms of the ability to generalize knowledge to other tasks), model-free approaches have the advantage of computational simplicity and are not susceptible to problems associated with learning inaccurate or imprecise models (Daw et al., 2005; Dayan, 2009). Therefore each approach can be advantageous in different circumstances. In sequential discrete decision-making tasks, the brain utilizes both model-based and model-free strategies in parallel (Daw et al., 2011; Daw et al., 2005; Fermin et al., 2010; Glascher et al., 2010). Theoretical treatments have argued that competition between these two mechanisms enables the benefits of each to be combined to maximum effect (Daw et al., 2005).

Our results suggest that a similar scenario of model-based and model-free learning processes acting in parallel also occurs in the context of motor learning. Adaptation is the model-based component, while model-free components include use-dependent plasticity and operant reinforcement. It is important to note that although the terminology of model-free and model-based learning arises from the theory of reinforcement learning, this does not imply that adaptation is directly sensitive to reward. On the contrary, we believe that adaptation is indifferent to reward outcomes on individual trials, and is purely sensitive to errors in the predicted state of the hand or cursor.

Unlike what has been suggested in the case of sequential decision-making tasks, we believe that under normal circumstances model-based and model-free learning are more cooperative than competitive. In continuous and high-dimensional action spaces, pure model-free learning is unfeasible, especially if a detailed feedback control policy must be acquired. We speculate that during initial learning of a visuomotor rotation, adaptation guides exploration of potential actions towards a suitable solution in hand space, at which point model-free learning becomes more prominent: the asymptotic solution induces use-dependent plasticity through repetition and is reinforced through its operant association with successful adaptation to a perturbation.

Success in a reaching task may not be all-or-nothing, i.e. hitting or missing the target. In fact we argue that adaptation to errors without actually hitting the target is itself rewarding because it is indicative of imminent success. This idea of the value of “near-misses” has been argued for in reinforcement algorithms that assign value to near-misses even when actual reinforcement is not given on such trials (MacLin et al., 2007). The rewarding/motivating nature of “near misses” has been reported for gambling where they increase the desire to play (Clark et al., 2009; Daw et al., 2006; Kakade and Dayan, 2002). Thus we would argue that movements driven by adaptation are reinforced in hand space because the process of incremental error reduction is the process of ever-closer near misses. Neither repetition alone nor adaptation alone led to savings, which suggests that it is the association of the two that is critical. The novel idea we wish to put forth here is that the association of successful adaptation with a particular movement creates an attractor centered on the movement in hand-space. Re-experiencing the same task with the same or even opposite rotational perturbations induces the learner to initially reduce error through pure adaptation but when their movements come within range of the attractor, savings occurs. Furthermore, we conjecture that errors need not be consciously experienced during adaptation in order for the association between the repeated movement and success to occur; all that is required is that adaptation be in operation. There is a precedent for such unconscious reward-based learning in the perceptual learning literature, and the reward can be internal – it does not need to be explicitly provided by the experimenter (Seitz et al., 2009).

Multiple Timescales of Learning

A recent motor learning model has been conceptualized in terms of the existence of fast and slow error-based processes (Kording et al., 2007; Smith et al., 2006). We would argue that skill learning is better conceptualized as cooperation between two qualitatively different kinds of learning: fast model-based adaptation followed by slower improvement through model-free reinforcement. Our previous study of active learning (Huang et al., 2008) in which subjects were allowed to select their own practice sequence to eight targets, each associated with errors of different sizes, can serve as an example of this re-conceptualization. We found that subjects repeated successful movements more frequently than error-based learning would predict; from a pure error-based learning perspective, such behavior is sub-optimal as it competes with time that could be spent on practice to target directions still associated with large errors – why revisit targets that you have already solved? This behavior is less surprising in our framework, which provides a possible explanation for this apparently sub-optimal behavior; namely that repeating a successful movement is a way to reinforce it. Indeed there are data from other areas of cognitive neuroscience that demonstrate that repeating something that you have successfully learned is the best way to remember it (Chiviacowsky and Wulf, 2007; Karpicke and Roediger, 2008; Wulf and Shea, 2002). We propose that motor skills are acquired through the combination of fast adaptive processes and slower reinforcement processes.

Conclusions

We have shown that use-dependent plasticity and operant reinforcement both occur along with adaptation. Based on our results, we argue that heretofore unexplained, or perhaps erroneously explained, phenomena in adaptation experiments result from the fact that most such experiments inadvertently lie somewhere between our adaptation-only protocol and our adaptation-plus-repetition protocol, with the result that three distinct forms of learning – adaptation, use-dependent plasticity, and operant reinforcement – are unintentionally lumped together. Future work will need to further dissect these processes and formally model them. The existence of separate learning processes may indicate an underlying anatomical separation. Error-based learning is likely to be cerebellar-dependent (Martin et al., 1996a, b; Smith and Shadmehr, 2005; Tseng et al., 2007). Use-dependent learning may occur through Hebbian changes in motor cortex (Orban de Xivry et al., 2010; Verstynen and Sabes, 2008). The presence of dopamine receptors on cells in primary motor cortex (Huntley et al., 1992; Luft and Schwarz, 2009; Ziemann et al., 1997) could provide a candidate mechanism for reward-based modulation of such use-dependent plasticity (Hosp et al., 2011). Our suggestion of an interplay between a model-based process in the cerebellum and a model-free retention process in primary motor cortex is supported by the results of a recent non-invasive brain stimulation study of rotation adaptation; adaptation was accelerated by stimulation of the cerebellum, while stimulation of primary motor cortex led to longer retention (Galea et al., 2010). Finally, operant reinforcement may require dopaminergic projections to the striatum (Wachter et al., 2010). If we are right in our assertion that motor learning studied with error-based paradigms results from the combination of model-free and model-based learning processes then these paradigms may be well suited to study how the brain modularly assembles complex motor abilities.

Experimental Procedures

The set-up

Subjects were seated with their hand and forearm firmly strapped in a splint using padded Velcro bands. The splint was attached to a light-weight frame over a horizontal glass surface. A system of air jets lifted the frame supporting the arm 1 mm above the glass surface, eliminating friction during hand movements. Subjects rested their forehead above the work surface, with their hand and arm hidden from view by a mirror. Targets (green circles) and hand position (indicated, when specified by the task, by a small round cursor) were projected onto the plane of the hand and forearm using a mirror. The arrangement of the mirror, halfway between the hand's workspace and the image formed by the projector, made the virtual images of cursor and targets appear in the same plane as the hand. The workspace was calibrated so that the image of the cursor indicating hand position fell exactly on the unseen tip of the middle finger's location (i.e., veridical display) (Mazzoni et al., 2007).

Hand position was recorded using a pair of 6 degree of freedom magnetic sensors (Flock of Birds, Ascension Technologies, Burlington, VT) placed on the arm and forearm, which transmitted hand position and arm configuration data to the computer at 120 Hz. Custom software recorded hand and arm position in real time and displayed hand position as a cursor on the computer screen. The same software also controlled the display of visual targets.

Subjects

A total of 60 healthy, right-handed subjects participated in the study (mean age=24.7±4.9, 25 males). All subjects were naïve to the purpose of the study and gave informed consent in compliance to guidelines set forth by the Columbia University Medical Center Institutional Review Board. They were randomly assigned to groups in each experiment.

The arm shooting task

Subjects were asked to make fast, straight and planar movements through a small circular target presented on a veridical display composed of a monitor and a mirror (Huang and Shadmehr, 2009; Huang et al., 2008). At the start of a trial, subjects were asked to move the cursor to a starting circle (2.5 mm radius) situated directly in front of them. Once the cursor was in the starting circle, a green, circular target (2.5 mm radius) appeared 6 cm away from the starting circle and the computer played a short, random-pitch tone, prompting subjects to move. If applicable for the trial, a rotation centered at the starting circle was imposed on the cursor feedback. As soon as the cursor was 6 cm away from the starting circle, a small white dot appeared at the cursor position at that time and remained there for the rest of the trial. Thus, the position of the white dot indicated the angular error the subject made in that trial. Subjects were then asked to return the overshot cursor to the target. The cursor disappeared briefly at this point. Subjects were given feedback regarding movement speed and target accuracy in order to keep these movement variables uniform across individuals. In addition, subjects were verbally encouraged to move faster at the end of a trial if the peak movement speed was less than 80 cm/s. The cursor then reappeared, and subjects brought it back to the starting circle ready for the next trial. All subjects were asked to complete a questionnaire asking them to identify any explicit strategies they might have used during the session.

Experiment 1

Adp⁺Rep⁻ group

Adp⁺Rep⁻ subjects (n=8) performed the reaching task in four types of trial: baseline, training, probe, and washout (Fig. 1A). In baseline trials, subjects made movements without additional manipulations to their visual feedback. Targets were randomly chosen from a uniform distribution of directions ranging from 70° to 110° (measured from the positive x-axis) totaling 40 possible locations. In training trials, the cursor was rotated counter-clockwise (CCW or “+”) by a magnitude randomly drawn from a uniform distribution ranging +0° to +40° (Fig. S1B). Ten probe trials were interspersed between the 81^st and the 160^th training trials. These probes were to 10 novel targets evenly distributed between 30° to 70° from the positive x-axis (Fig. 1A). In probe trials, the cursor vanished as soon as it left the starting circle. The washout trials were identical to baseline trials.

Subjects performed these trials in four consecutive blocks with short (1 to 2 minutes) breaks between blocks. Block 1 consisted of 80 baseline trials and Block 2, 80 training trials. Block 3 started with 10 probe trials interspersed within 80 training trials and ended with 10 washout trials. Block 4 had 70 washout trials.

Adp⁺Rep⁺ group

The Adp⁺Rep⁺ protocol (n=8) was identical to Adp⁺Rep⁻ except for the order of the imposed rotations in the training trials (Fig. 1A). In Adp⁺Rep⁺ training trials, cursor movements were also rotated by a magnitude drawn from the same distribution as of Adp⁺Rep⁻ training trials (Fig. S1B). In Adp⁺Rep⁺, however, the optimal movement to cancel out the rotation was always toward the 70° direction (i.e., the repeated direction) in hand space (Fig 1A). For example, the cursor was rotated by +40° when the 110° target was displayed, the rotation was +20° for the 90° target, and +5° for the 75° target, etc (Fig. 1B).

Experiment 2

Adp⁺Rep⁻ and Adp⁺Rep⁺ groups

Adp⁺Rep⁻ (n=10) and Adp⁺Rep⁺ (n=10) participated in Experiment 2. The initial training and washout blocks for Adp⁺Rep⁻ and Adp⁺Rep⁺ in Experiment 2 were identical to their counterparts in Experiment 1 except that training was done without probe trials, and after the washout block, subjects underwent an additional test (relearning) block where they were exposed to a +25° rotation at the 95° target for another 80 trials (Fig. 3).

Adp⁻Rep⁻ and Adp⁻Rep⁺ groups

Adp⁻Rep⁻ (n=6) and Adp⁻Rep⁺ (n=6) performed the shooting task in three consecutive blocks. In the each of the 160 training trials spanning Block 1 and 2, Adp⁻Rep⁻ aimed for a random target between 70° to 110° without any cursor rotation. In contrast, Adp⁻Rep⁺ was given only the 70° target in all 160 training trials, also without cursor rotation (Fig. 3). Block 3 started with 80 test trials in which both groups were given only the 95° target and their cursor movements were rotated by +25°. Forty washout trials immediately followed training with the target relocated to the 70° position and movements were made without cursor rotation.

Experiment 3

SAME-SOLN_hand and SAME-SOLN_visual groups

SAME-SOLN_hand (n=6) and SAME-SOLN_visual (n=6) groups performed the task in four types of trial: baseline, training, washout, and test trials (Fig. 5A). These two groups performed the task in five consecutive blocks. Block 1 consisted of 80 baseline trials. Block 2 started with 5 baseline trials then followed with 80 training trials. Block 3 began with 80 training trials and finish with 5 baseline trials. Block 4 was a washout block and had 80 baseline trials. Block 4 consisted of 80 test trials (Fig. 5A). Baseline and washout trials were the same for both groups and consisted of targets uniformly dispersed between 40° to 100° with no rotation. In training trials, a +30° rotation was imposed on a single target. In test trials a -30° rotation was imposed on a single target (Fig 5B, C).

In SAME-SOLN_hand, the solution in hand space was the same for both training and test trials – arbitrarily chosen to be the movement to the 70° direction in hand space (Fig. 5B). Thus subjects first trained in one target direction (the 100° target) with a +30° rotation and then, after a washout block, trained in another target direction (the 40° target) with a counter-rotation of -30°.

In SAME-SOLN_visual, the solution in visual/cursor space was the same for both training and test trials (40°) while solutions in hand space were different (Fig. 5C). Thus subjects first trained in one target direction (the 40° target) with a +30° rotation and then, after a washout block, trained to the same target with a -30° rotation.

Data Analysis

Data analysis was performed using Matlab (version R2007a, The Mathworks Inc., Natick, MA). Statistical analysis was performed using SPSS 11.5 (SPSS Inc, Chicago, IL). Unless otherwise specified, t- and p- values were reported using independent-sample 2-tailed t-tests. Angular error was calculated as the angular difference between the displayed target center and the white feedback dot. The error reduction rate (i.e., learning and relearning rate) was defined as the time constant obtained by fitting the error time-series with a single decaying exponential function of the form y = C₁ exp(-rate * x) +C₀, where C₁ and C₀ are constants, y is the error and x the trial number.

We simulated trial-to-trial hand movement directions in response to the visuomotor rotations as a result of adaptation alone using a single-state state-space model (Donchin et al., 2003; Tanaka et al., 2009). The model equations took the following form:

$$\begin{array}{l}{\text{y}}^{(\text{n})}={\text{R}}^{(\text{n})}-\text{K}({\text{T}}^{(\text{n})}){\mathbf{\text{z}}}^{(\text{n})}\\ {\mathbf{\text{z}}}^{(\text{n}+1)}=\text{A}{\mathbf{\text{z}}}^{(\text{n})}+\mathbf{\text{B}}{\text{y}}^{(\text{n})}.\end{array}$$

The k by 1 vector z⁽ⁿ⁾, is the state of the learner that represents the estimated visuomotor mapping (rotation) associated with each of the k targets in trial n. K(T⁽ⁿ⁾) is the selector matrix that selects the corresponding element in z⁽ⁿ⁾ for the target T⁽ⁿ⁾. At each trial, K(T⁽ⁿ⁾) z⁽ⁿ⁾ represents the hand movement direction. The variable R⁽ⁿ⁾ represents the rotation that was imposed; thus, y⁽ⁿ⁾, computed as the difference between R and z, represents the error in the visuomotor mapping (i.e., cursor error). The visuomotor mapping / states of the learner are updated by a generalization function B of size k by 1 that determines how much errors in one target direction affects mapping estimations in neighboring directions. In addition, the visuomotor mapping / states of the learner slowly forget at a rate determined by the scalar A.

To limit the number of parameters in the simulations, we grouped targets in bins with 5° width. Thus k=16, including all training and probe targets. According to recently published estimations (Tanaka et al., 2009), we interpolated that B, a function of target-to-target angular difference, decreased its gain linearly from 0.09 to 0 within 9 target bins (i.e., a 45° directional window) and that A had a value of 0.98. The motor performance prediction by adaptation alone was simulated deterministically using these parameter values.

Power analysis

We computed minimum sample sizes on assumed effect sizes for savings based on previously reported data (Zarahn et al., 2008). For an independent samples t-test using a two-tailed alpha of 0.05 and power of 0.8, and assuming an effect size d = 1.9375 (computed based on previously reported group means and standard deviation; time constant = 0.47 for savings and 0.16 for naïve, with s.d. = 0.16), the minimum sample size is 6 subjects per group.

Article Highlights.

1. Internal models are not sufficient to explain results in adaptation paradigms

2. Repetition of adapted movements leads to use-dependent movement biases

3. Operant association between adapted movements and success enables savings

4. Motor tasks are learned by combining model-based and model-free processes