Relationship between Genomic Distance-Based Regression and Kernel Machine Regression for Multi-marker Association Testing

Abstract

To detect genetic association with common and complex diseases, two powerful yet quite different multi-marker association tests have been proposed, genomic distance-based regression (GDBR) (Wessel and Schork 2006, AJHG 79:821-833) and kernel-machine regression (KMR) (Kwee et al 2008, AJHG 82:386-397; Wu et al 2010, AJHG 86:929-942). GDBR is based on relating a multi-marker similarity metric for a group of subjects to variation in their trait values, while KMR is based on nonparametric estimates of the effects of the multiple markers on the trait through a kernel function or kernel matrix. Since the two approaches are both powerful and general, but appear quite different, it is important to know their specific relationships. In this report, we show that, under the condition that there is no other covariate, there is a striking correspondence between the two approaches for a quantitative or a binary trait: if the same positive semi-definite matrix is used as the centered similarity matrix in GDBR and as the kernel matrix in KMR, the F-test statistic in GDBR and the score test statistic in KMR are equal (up to some ignorable constants). The result is based on the connections of both methods to linear or logistic (random-effects) regression models.

Large-scale genetic association studies have been successful in identifying genetic variants associated with complex disease and traits, as evidenced by recent achievements in genome-wide association studies (GWAS) (Altshuler et al 2008). However, in spite of many identified susceptibility loci, they can explain only a small fraction of heritability (Maher 2008). One possible reason is due to typically small effect sizes of genetic variants on complex disease and traits, while often only single-marker tests with limited power are applied. Hence, in spite of many existing statistical analysis tools, it remains critical to develop and apply more powerful multi-marker tests to existing and incoming genetic data. Two novel and powerful multi-marker methods are genomic distance-based regression (GDBR) (Wessel and Schork 2006) and kernel machine regression (Kwee et al 2008; Wu et al 2010). An interesting feature of GDBR is its approach to capturing genotype or haplotype information across multiple loci through a similarity measure between any two subjects. Many possible similarity measures can be used. A suitable similarity measure may be able to characterize some complex effects of multiple loci on a phenotype, e.g. epistasis, which may be ignored by other more commonly used and simpler models (e.g. main-effects logistic regression models, possibly with some low-order interaction terms), leading to reduced power. GDBR is unique in its regression analysis relating variation in the measure of genomic similarity to variation in their trait values. A recent study by Lin and Schaid (2009) demonstrated the high power of GDBR and its superiority over several commonly used tests across a wide range of realistic scenarios. In addition, Lin and Schaid (2009) showed that GDBR is closely related to the class of haplotype similarity tests (Tzeng et al 2003a,b; Yuan et al 2006; Sha et al 2007; Klei and Roeder 2007). Finally, GDBR is general with its applicability to other high-dimensional data, such as microarray gene expression data (Zapala and Schork 2006) and next-generation sequencing data (Wessel and Schork 2006). On the other hand, Kwee et al (2008) proposed a linear KMR method for quantitative traits while Wu et al (2010) proposed a logistic KMR methodology for binary traits, showing the high power and general applicability of KMR. In particular, the numerical studies of Wu et al (2010) provided evidence that logistic KMR was more powerful than GDBR under some simulation set-ups. KMR is similar to typical linear or logistic regression in regressing a phenotype on genotypes (and possibly other covariates); a distinguishing feature is its nonparametric modeling of the effects of genotypes on a phenotype through a kernel function or kernel matrix; the kernel function provides a similarity measure on genotypes between any two subjects. In spite of their dramatic differences at the first glance, since both GDBR and KMR depend on the use of a similarity/kernel matrix to measure the similarity between any two subjects based on theor genotypes, the two methods, along with some other similarity-based nonparametric methods (Schaid et al 2005; Wei et al 2008; Tzeng and Zhang 2007; Tzeng et al 2009; Mukhopadhyay et al 2010), are being recognized to be somewhat related, though their specific relationships are still unknown (Schaid 2010a,b). Our main reasoning in connecting GDBR and KMR is based on the following observation. It has been shown that GDBR for binary traits can be formulated as a logistic regression problem (Han and Pan 2010), while KMR is equivalent to fitting a random-effects generalized linear model (Liu et al 2008), hence the two methods are related through their common connection to a logistic regression model for binary traits. Nonetheless, it is still unclear what specific relationship exists between the two methods. For example, is one method more powerful than the other, as shown by Wu et al (2010)? In this short report, we show that, if a common positive semi-definite matrix is used as the (centered) similarity matrix in GDBR and as the kernel matrix in KMR, then there is a striking correspondence between the two methods: their test statistics are equal (up to some ignorable constants).

First we need some notation. Given n independent observations (Y_i,X_i) with Y_i as phenotype and X_i = (X_i1, …, X_ik)’ as genotype scores at k SNPs for subjecti = 1, …, n, we would like to test for any possible association between the phenotype and genotypes. The k SNPs are possibly in linkage disequilibrium (LD), as drawn from a candidate region or an LD block.

We summarize the GDBR procedure as the following:

• Step 1. Calculate an n × n distance matrix for all pairs of subjects by D = (D_ij) = (1 – S_ij) with 0 ≤ S_ij ≤ 1 as an initial similarity measure between subjects i and j;

• Step 2. Calculate $A=(-D_{ij}^2∕2)$;

• Step 3. Obtain a centered similarity matrix G = (I – 11′/n)A(I – 11′/n);

• Step 4. Denote y as the n × 1 vector of centered phenotypes with elements $y_i=Y_i-\stackrel{‒}{Y}=Y_i-{\sum }_{j=1}^n{Y}_j∕n$;

• Step 5. Calculate the projection matrix H = y(y’y)⁻¹y’;

• Step 6. Calculate the F-statistic as

  $$F=\frac{tr\left(HGH\right)}{tr{\left[(I-H)G(I-H)\right]}^{\prime }}$$

  where tr(A) is the trace of matrix A.

Since the (asymptotic) distribution of F is unknown, to obtain a p-value, we recourse to permutations by shuffling y. If G is an outer product matrix, e.g. when the distance matrix D is Euclidean, the above F-test reduces to the usual F-test in multivariate analysis of variance (MANOVA); otherwise, it is an extension of MANOVA with any given distance matrix D. As discussed by McArdle and Anderson (2001), if G is an outer product matrix, say G = ZZ’ with an n × p matrix Z, the above F-test is simply testing $H_0^{\prime }:B=0$ in a multivariate linear model

$$Z=1\mu +yB+∊,$$ (1)

where 1 is an n × 1 vector of all 1’s, μ is a 1 × p vector of unknown intercepts, y is an n × 1 vector of centered phenotypes with elements y_i, B is a 1 × p vector of unknown regression coefficients, and ∊ is an n × p matrix of random errors. Since y is the vector of centered phenotypes, we have 1’y = 0, and thus the least squares estimates are

$$\widehat{\mu }=\stackrel{‒}{Z}=\sum _{i=1}^n{Z}_{i.}∕n,\widehat{B}={\left(y^{\prime }y\right)}^{-1}{y}^{\prime }Z$$

If G is positive and semi-definite (psd), by Theorem 14.2.1 of Mardia et al (1979, p.397), $Z=(I-\frac{1}{n}{11}^{\prime })Z_0$ for some matrix Z₀; that is, the sum of each column of Z is 0. Hence, we have $\widehat{\mu }=\stackrel{‒}{Z}=0$; that is, we do not need the intercept term in (1). With the corresponding fitted values $\widehat{Z}=1\stackrel{‒}{Z}+y\widehat{B}$ and residuals $R=Z-\widehat{Z}=(I-H)Z$, the total sum of squares and cross-product (SSCP) matrix can be partitioned into: $Z^{\prime }Z={\widehat{Z}}^{\prime }\widehat{Z}+R^{\prime }R$. Then it is easy to verify that

$$\begin{array}{cc}\hfill F=& \frac{tr\left(HGH\right)}{tr\left[(I-H)G(I-H)\right]}=\frac{tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)}{tr\left(R^{\prime }R\right)}=\frac{1}{tr\left(R^{\prime }R\right)∕tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)}\hfill \\ \hfill \propto & \frac{1}{[tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)+tr\left(R^{\prime }R\right)]∕tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)}=\frac{tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)}{tr\left(Z^{\prime }Z\right)}.\hfill \end{array}$$

Since permutations are used to obtain the p-value for the F-statistic while tr(Z’Z) is fixed as a constant across all permutations, the inclusion of exclusion of term tr(Z’Z) would not have any effect on the p-value. Hence tr(Z’Z) can be ignored from the F-statistic, leading to

$$F\propto tr\left({\widehat{Z}}^{\prime }\widehat{Z}\right)=tr\left({\left(y^{\prime }y\right)}^{-1}{Z}^{\prime }y{y}^{\prime }Z\right)\propto tr\left(Z^{\prime }y{y}^{\prime }Z\right),$$ (2)

in which, since y’y is fixed and invariant under permutations, it can be ignored.

To assess possible association between genotype Z and phenotype y (or equivalently, Y ), rather than regressing Z on y as in GDBR, following Han and Pan (2010), we regress Y on Z via a linear model for quantitative traits:

$$E\left(Y\right)={\beta }_0+Z\beta ,$$ (3)

or via a logistic model for binary traits:

$$\mathrm{Logit}\mathrm{Pr}(Y=1)={\beta }_0+Z\beta ,$$ (4)

where the assessment of possible association can be accomplished by testing on the unknown p × 1 vector of unknown regression coefficients in null hypothesis H₀ : β = 0. The score vector, as shown by Clayton et al (2004) for logistic regression, is

$$U=Z^{\prime }(Y-\stackrel{‒}{Y}1)=Z^{\prime }y,$$

and thus the SSU test statistic (Pan 2009) is

$$T_{SSU}=U^{\prime }U=tr\left(U^{\prime }U\right)=tr\left(U^{\prime }U\right)=tr\left(Z^{\prime }y{y}^{\prime }Z\right).$$ (5)

Comparing (2) and (5), we see that the F-statistic and SSU-statistic are equivalent. We emphasize that the SSU test here is being applied to model (3) or (4) with genotype information coded in Z derived from the centered similarity matrix G, not the usual genotype score X.

Note that the above derivation extends the result of Han and Pan (2010) in two aspects. First, the result holds for both quantitative and binary traits, not just for binary traits as for the case-control design in GWAS. Second, we do not require the condition of equal numbers of cases and controls for binary traits. The reason of such a requirement in Han and Pan (2010) is due to the use of a non-centered phenotype vector y, as originally used in McArdle and Anderson (2001) and others.

For quantitative traits, Kwee et al (2008) proposed linear kernel-machine regression (KMR) with a semi-parametric linear model:

$$E\left(Y_i\right)={\beta }_0+h(X_{i1},\dots ,X_{ik}),$$ (6)

while for binary traits, Wu et al (2010) proposed logistic KMR with a semi-parametric logistic model:

$$\mathrm{Logit}\mathrm{Pr}(Y_i=1)={\beta }_0+h(X_{i1},\dots ,X_{ik}),$$ (7)

where h(.) is an unknown function to be estimated, which offers the flexibility in modeling the effects of the SNPs on Y_i. The form of h(.) is determined by a user-specified positive and semi-definite (psd) kernel function K(., .): by the representer theorem (Kimeldorf and Wahba 1971), $h_i=h\left(X_i\right)={\sum }_{j=1}^n{\gamma }_{j}K(X_i,X_j)$ with some γ₁,…,γ_n. To test the null hypothesis of no association between the phenotype and SNPs, one can test H₀: h = (h₁(X₁), …, h_n(X_n))’ = 0. Denote K as the n × n matrix with the (i, j)th element as K(X_i,X_j) and γ = (γ₁, …, γ_n)’, then we have h = Kγ. Treating h as subject-specific random effects with mean 0 and covariance matrix τK, testing H₀: h = 0 for no SNP effects is equivalent to testing H₀: τ = 0. The corresponding variance component score test statistic is (proportional to)

$$Q={(Y-\stackrel{‒}{Y}1)}^{\prime }K(Y-\stackrel{‒}{Y}1).$$

(For quantitative traits, there is a factor $1∕{\widehat{\sigma }}^2$ in Q as used by Kwee et al (2008), which however can be omitted from Q since it is treated as non-random and fixed, and can be absorbed into the variance term of Q, which is to be applied to standardize the distribution of Q, as for binary traits shown by Wu et al (2010).) Since K is psd, we can decompose K = ZZ’ (Magnus and Neudecker 1999, p.21), and have

$$Q={(Y-\stackrel{‒}{Y}1)}^{\prime }Z{Z}^{\prime }(Y-\stackrel{‒}{Y}1)=T_{SSU},$$

which is the SSU test statistic for linear model (3) and logistic model (4). By the earlier result on the equivalence between the F-statistic in GDBR and the SSU statistic, we establish a striking correspondence between the F-test in GDBR and the score test in KMR.

The above correspondence result can be also viewed from another angle. As shown by Pan (2009), the SSU test is equivalent to Goeman’s (2006) test, which is derived as a variance component score test for logistic regression. Specifically, in model (4), if we assume β as random effects from a distribution with E(β) = 0 and Cov(β) = τI, then the permutation-based score test on H₀: τ = 0 is equivalent to the SSU test. Note that, if we rewrite h = Zβ, then model (6) and (7) are equivalent to model (3) and (4), respectively, since their distributional assumptions are equivalent:

$$E\left(h\right)=0\iff E\left(\beta \right)=0,Cov\left(h\right)=\tau K\iff Cov\left(\beta \right)=\tau I.$$

In summary, there is a correspondence between the F-test in GDBR and the score test in KMR if the same psd matrix is used as the kernel matrix K in KMR and as the centered similarity matrix G in GDBR. We emphasize that we require (centered) K = G, not K = S, the initial similarity matrix in GDBR. We also note that, centering K (to facilitate its use as G) does not change the result for KMR:

$$K_c=(I-{11}^{\prime }∕n)K(I-{11}^{\prime }∕n),Q_c={(Y-\stackrel{‒}{Y}1)}^{\prime }{K}_c(Y-\stackrel{‒}{Y}1)={(Y-\stackrel{‒}{Y}1)}^{\prime }K(Y-\stackrel{‒}{Y}1)=Q,$$

since ${(Y-\stackrel{‒}{Y}1)}^{\prime }1=0$. If K is not centered, we center it and use G = K_c in GDBR to achieve the same result of KMR.

We did a numerical study to verify the above analytical result. We simulated genotype data by discretizing some latent multivariate normal variates with an AR1(0.8) correlation structure (Wang and Elston 2007; Pan 2009). There were 11 SNPs in LD, in which the center one was the causal SNP. The minor allele frequency (MAF) for the causal SNP was fixed as 0.2 while the MAFs for others were randomly chosen between 0.2 and 0.5. A binary outcome (i.e. disease status) was generated according to the logistic model:

$$\mathrm{Logit}\mathrm{Pr}(Y=1)={\beta }_0+\log \left(OR\right)X_0,$$

where X₀ is the number of the minor alleles at the causal SNP, β₀ = log(0.2/0.8) was chosen to yield a background disease prevalence of 0.2, and OR = 1 or OR = 2 was used for the scenarios of no or strong genetic association. For each simulated dataset, we generated 100 cases and 100 controls; only the outcome and the 10 SNPs after excluding the causal SNP were available in each dataset.

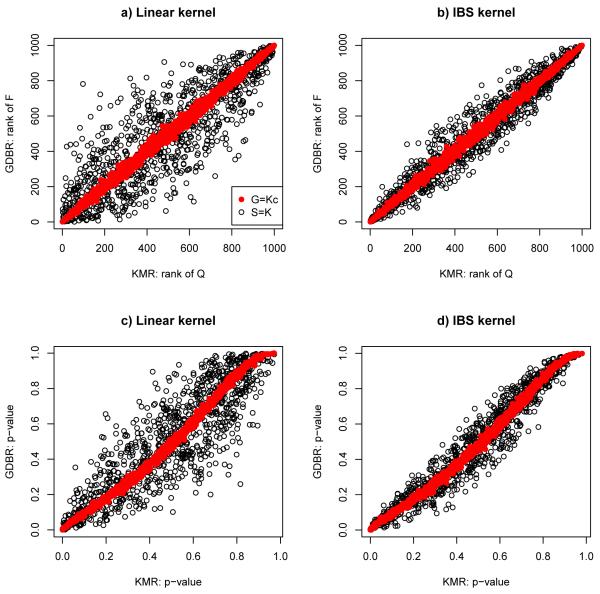
For each dataset, we applied KMR and GDBR with one of the four kernels: linear, quadratic, identity-by-state (IBS) or weighted IBS (wIBS) kernel. We used the R function implementing logistic KMR by Wu et al (2010), and implemented GDBR in R as outlined in the GDBR procedure with B = 1000 permutations. To implement GDBR that was equivalent to KMR, we centered a kernel matrix K in KMR as K_c, and took K_cas the centered matrix G; the GDBR procedure was modified to run through Steps 4 to 6. In addition, as a comparison, we also took the kernel matrix K as the initial similarity matrix S, which was not expected to be equivalent to KMR. The Type I error rates (for OR=1) and power (for OR=2) estimated from 1000 simulated datasets are shown in Table 1. It can be seen that KMR and GDBR with the same kernel matrix and centered similarity matrix (i.e. G = K_c) gave essentially the same results. Although the results for KMR and GDBR with S = K were also close, the former could be much more powerful than the latter as for the case with a quadratic kernel, which was also shown by Wu et al (2010). It is noted that, even if G = K_c, since the p-value of a score test in KMR and that of the F-test in GDBR were obtained from the asymptotic distribution and permutation distribution respectively, their Type I error rates and power would not be exactly the same. For a further examination, The Pearson correlation coefficients of the test statistics (i.e., Q-statistic in KMR and F-statistic in GDBR) and p-values between the two methods are shown in Table 2. We also compared the ranks of the F-statistics in GDBR and Q-statistics in KMR in Figure 1. It is confirmed that, if G = K_c, KMR and GDBR gave essentially the same results. For the p-values, the minor discrepancy between the two methods was due to their use of the asymptotic distribution and permutation distribution respectively. For the test statistics, note that when we derived their correspondence, we ignored some fixed constants (i.e. Z’Z and y’y) in the F-statistic; these fixed terms are invariant to permutations and thus ignorable for a given dataset, but are not fixed across different datasets, causing some minor ranking differences across datasets between the F- and Q-statistics. The unusually strong agreement between the two methods cannot be explained as purely coincident. In contrast, if S = K (and thus G ≠ K_c, though they might be close), the two method gave similar but more different results.

Table 1.

Empirical Type I error rates (for OR=1) and power (for OR=2) at the nominal level α = 0.05 for KMR and GDBR based on 1000 simulations. In GDBR, we took the (centered) kernel matrix K as the initial similarity matrix S or as the centered similarity matrix G

		Kernel matrix K
OR	Method	Linear	Quadratic	IBS	wIBS
1	KMR	.046	.053	.049	.048
	GDBR, G = Kc	.048	.053	.052	.046
	GDBR, S = K	.053	.058	.054	.052
2	KMR	.714	.719	.714	.714
	GDBR, G = Kc	.712	.725	.708	.714
	GDBR, S = K	.717	.638	.675	.677

Table 2.

Pearson’s correlations of the test statistics (Stat) or p-values (P) between KMR and GDBR based on 1000 simulations. In GDBR, we took the (centered) kernel matrix K as the initial similarity matrix S or as the centered similarity matrix G

		Linear		Quadratic		IBS		wIBS
OR	GDBR	Stat	P	Stat	P	Stat	P	Stat	P
1	G = Kc	.998	.995	.992	.992	.999	.995	.999	.995
	S = K	.903	.865	.903	.866	.969	.969	.969	.969
2	G = Kc	.996	.995	.989	.994	.998	.995	.998	.995
	S = K	.960	.922	.952	.927	.992	.980	.993	.981

Figure 1.

Comparison of the test statistics and p-values from KMR and GDBR with linear or IBS kernel for OR=1.

A major difference between the GDBR and KMR is that GDBR does not require its similarity matrix to be psd while KMR requires its kernel matrix to be psd. From the operational aspect, since it is not always guaranteed that a chosen similarity or distance metric would result in a psd matrix, GDBR is attractive in this aspect. However, it is not clear what are the implications for performance from using a non-psd similarity matrix. In particular, GDBR was originally proposed as an extension of the usual F-statistic implying the use of a psd similarity matrix, though its ability to use a non-psd matrix was argued to be advantageous (McArdle and Anderson 2001). Schaid (2010a) also commented on the conceptual appeals of having a psd similarity or kernel matrix. Here we did some simple experiments to see the effects of using a psd matrix derived from a non-psd similarity matrix. The simulated data were generated in the same way as before, but we modified a kernel matrix in two practical ways. First, we randomly chose 0 to 5 SNPs to be missing for any individual, and then calculated the IBS and wIBS kernels, which might not be psd (Schaid 2010b). Second, for an IBS or wIBS kernel from complete genotype data, we added a noise, randomly generated from a uniform distribution between −0.2 and 0.2, to each non-diagonal element of the kernel matrix, reflecting a scenario of having measurement errors for kernels. we applied the GDBR with these non-psd kernels. Alternatively, we used only the positive eigen values and their corresponding eigen vectors of a non-psd kernel K to construct a new psd kernel K⁺, which was then supplied to GDBR. The simulation results were shown in Table 3. It can be seen that there was barely any power difference between using non-psd K and using psd K⁺, though further studies are needed. It is again confirmed that using G = K_c in GDBR had a slight edge over using S = K. More importantly, using an un-centered G = K led to a dramatic loss of power; Schaid (2010a) discussed the importance of centering a similarity matrix G in GDBR. Table 4 shows the distributions of the positive and negative eigen values of non-psd kernel matrix K, indicating a substantial proportion of negative eigen values of K.

Table 3.

Empirical power of GDBR with various similarity matrices G or S from 500 simulations. In each of the two cases, the original kernel matrix K was not psd, and a psd K⁺ was derived based on K

		non-psd			psd
Case	K	G = Kc	S = K	G = K	$G=K_c^{+}$	S = K+	G = K+
1	IBS	.684	.640	.148	.676	.662	.154
	wIBS	.674	.664	.140	.684	.666	.152
2	IBS	.676	.652	.162	.688	.664	.158
	wIBS	.684	.658	.140	.698	.682	.144

Table 4.

The mean number and sum of the positive or negative eigen values (EVs) of the kernel matrix K

	K: IBS				K: wIBS
	Positive EVs		Negative EVs		Positive EVs		Negative EVs
Case	Number	Sum	Number	Sum	Number	Sum	Number	Sum
1	88.1	237.8	111.9	−37.8	88.1	476.1	111.9	−76.1
2	105.1	327.6	94.9	−127.6	106.7	524.7	93.3	−124.7

In spite of the correspondence of the GDBR and KMR approaches in the case without covariates, there are some differences between them, as discussed by Wu et al (2010). First, it is easy to incorporate other covariates into KMR, while it is difficult for the original F-test in GDBR. though it is straightforward to do so in some extensions of GDBR (Li et al 2009; Han and Pan 2010). The importance of incorporating covariates to improve power, or adjust for population stratification, is well recognized. Second, the F-test in GDBR uses permutations to calculate p-values, while the score test in KMR (or an extension of GDBR, Han and Pan 2010) is based on its asymptotic distribution. Since permutation can be computationally demanding for GWAS while we found that the asymptotic distribution of KMR was accurate even for small samples as shown in our simulations, it seems that KMR is easier to apply.

In summary, when the kernel or similarity matrix is psd, both methods can be formulated as a (random-effects) linear or logistic regression model, in which genotype or haplotype information is derived from a similarity or kernel matrix. In particular, the two methods are expected to give essentially the same p-values when a comparable kernel or centered similarity matrix is used. This correspondence suggests that, rather than exploring differences between the two methods, it may be more productive to focus more on the design and choice of suitable similarity or kernel matrices (Schaid 2010b).