Multi-pathway sequences for MR thermometry

Abstract

MR-based thermometry is a valuable adjunct to thermal ablation therapies as it helps to determine when lethal doses are reached at the target and whether surrounding tissues are safe from damage. When the targeted lesion is mobile, MR data can further be used for motion-tracking purposes. The present work introduces pulse sequence modifications that enable significant improvements both in terms of temperature-to-noise-ratio (TNR) properties and target-tracking abilities.

Instead of sampling a single magnetization pathway as in typical MR thermometry sequences, the pulse-sequence design introduced here involves sampling at least one additional pathway. Image reconstruction changes associated with the proposed sampling scheme are also described. The method was implemented on two commonly used MR thermometry sequences: the gradient-echo and the interleaved echo-planar imaging (EPI) sequences. Data from the extra pathway enabled TNR improvements by up to 35%, without increasing scan time. Potentially of greater significance is that the sampled pathways featured very different contrast for blood vessels, facilitating their detection and use as internal landmarks for tracking purposes. Through improved TNR and lesion-tracking abilities, the proposed pulse-sequence design may facilitate the use of MR-monitored thermal ablations as an effective treatment option even in mobile organs such as the liver and kidneys.

Introduction

Initially proposed over 2 decades ago [1, 2], MR thermometry has proven to be particularly well-suited for monitoring thermal ablations, based on its ability to accurately detect temperature changes in a non-invasive manner. Several MR parameters are temperature sensitive such as the tissue bulk magnetization [3], T₁ relaxation time [2], the diffusion coefficient of water molecules [4] and the proton-resonant frequency (PRF) of water protons [5, 6]. The PRF approach has been shown to be the most practical in terms of providing fairly accurate maps of temperature changes in a wide range of tissues [7, 8] and has become the most widely used MR thermometry method. The pulse sequence of choice in most current PRF thermometry applications is typically a simple gradient-echo sequence with long TE.

Successful clinical applications of MR thermometry have been achieved in situations where little or no motion is present, e.g., for thermometry in the brain [9] or for the treatment of uterine fibroids [10]. However, MR monitoring in mobile organs such as the liver or kidneys still remains a significant challenge. Especially in the context of focused ultrasound ablation, where there is no device or needle inserted into the body, the task of accurately targeting in the presence of motion relies entirely on imaging data. As a consequence, the acquired images must fulfill two separate purposes: temperature monitoring and target tracking. To achieve a temporal resolution sufficient to resolve respiratory motion, fast interleaved echo-planar imaging (EPI) sequences can be employed [11, 12].

The present work aims to significantly improve the performance of pulse sequences currently used for PRF thermometry, both in terms of temperature-to-noise-ratio (TNR) properties and target-tracking abilities. Instead of sampling a single magnetization pathway, we propose sampling at least one additional pathway as well [13–15]. Typical MR thermometry sequences sample a single magnetization pathway with maximum temperature sensitivity at the end of the TR period and leave the early-TR period non- or ill-utilized. In contrast, other magnetization pathways may feature maximum temperature sensitivity at the beginning of the TR period and, for this reason, sampling one pathway early and a different pathway late during the TR period would seem to make perfect sense in terms of TNR. We show results where the data associated with a second pathway gave TNR improvements of up to 35%, without any increase in imaging time. Such TNR improvements may prove particularly beneficial in conjunction with fast imaging sequences, as employed in mobile-organ applications, where SNR and TNR tend to be low. The exact amount of TNR that may be gained depends on the relative signal strength of the pathways being sampled, which in turn depends on many different factors such as relaxation, diffusion and acquisition parameters.

Of potentially greater importance, the availability of data from one or more extra pathway can also greatly facilitate the task of tracking lesions. As an organ moves and deforms, tracking its vascular bed may be the best way of tracking lesions embedded in it [16]. Different pathways are characterized by different flow properties, and sampling more than one can allow blood vessels to be detected. There are two different mechanisms responsible for this. First, because some pathways are more similar to spin echoes than to gradient echoes, signal losses are expected to occur in flowing materials for these spin echo-like pathways [17] because moving spins may miss the excitation or refocusing RF pulse. Second, intravoxel dephasing in blood vessels should be greater for pathways that involve greater amounts of time spent in the transverse plane because gradient imbalances from one TR to the next act like separate lobes of a flow-encoding gradient waveform [18]. Due to both these effects, blood signal is expected to be stronger in some pathways than in others.

We propose here the use of multi-pathway sequences for MR thermometry, for improved TNR properties and improved lesion-tracking abilities. While the present work mostly consists of pulse sequence developments, modifications to current reconstruction algorithms for handling multi-pathway datasets are also described. The proposed modifications have been implemented and tested on the two most-commonly used PRF sequences, the gradient-echo and interleaved-EPI sequences, in phantoms (with heating) and in vivo (without heating). By improving TNR properties and lesion-tracking abilities, the present work may contribute to the emergence of MR-monitored thermal ablations as an effective treatment for lesions in mobile organs such as the liver and kidneys.

Theory

1. Phase diagrams and basic types of gradient-echo sequences considered here

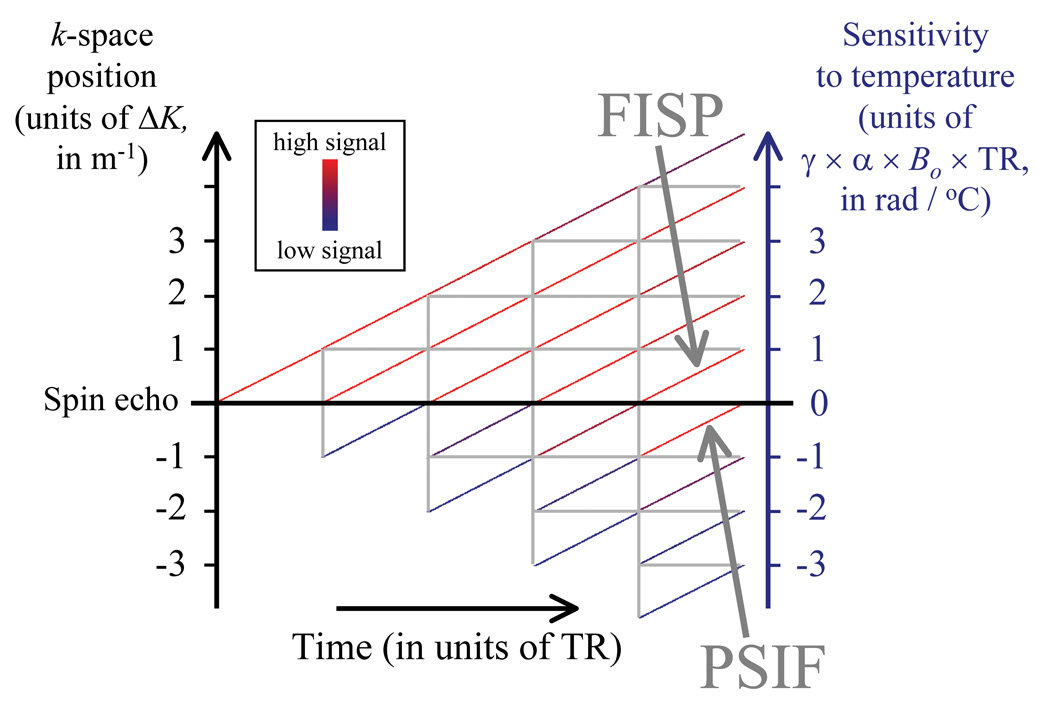
Assuming an RF pulse with flip angle φ_RF is applied every TR, then the signal evolution over the TR periods can be represented using a modified phase diagram [19, 20] as shown in Fig. 1 for the first five such TR periods. This diagram will be used throughout the Theory section to help explain how magnetization and temperature sensitivity evolve. In Fig. 1, vertical gray lines are used to represent when RF pulses occur. Gradient-echo sequences often include a strong spoiler gradient pulse and this non-zero gradient area effectively displaces magnetization by ΔK in k-space, as shown on the left vertical axis. The diagonal lines in Fig. 1 represent individual magnetization pathways whose strength is color-coded (for acquisition and relaxation parameters as listed in the caption). When pathways cross the central ‘spin echo’ horizontal black line, all temperature-induced phase offsets have been completely re-phased, resulting in zero temperature sensitivity. A pathway of particular importance is the 0^th pathway, which is often referred to as the FISP (for ‘fast imaging with steady state precession’) and is found in the [0,1] interval in Fig. 1. Also of importance is the −1^st pathway, which is often called ‘inverted FISP’ or PSIF and is found in the [−1,0] interval.

Fig. 1.

A graphical tool based on so-called phase-diagrams was developed to help guide pulse sequence developments in PRF thermometry. As an RF pulse is applied on each TR, different magnetization pathways develop, shown here as colored diagonal segments. The FISP (in the [0,1] interval) and the PSIF (in the [−1,0] interval) are of particular importance. The displayed signal levels were obtained with T₁ = 800 ms, T₂ = 35 ms and T₂^* = 20 ms (relaxation times typical for liver tissues at 3 T), along with TR = 5 ms and φ_RF = 30°. While only a few TR periods could be displayed here, many more TR periods are necessary to reach a steady-state signal.

The pulse sequences that are considered here to be useful for multi-pathway temperature mapping have a non-zero gradient area during any given TR (i.e., ΔK is non-zero in Fig. 1), and no RF spoiling [19]. This type of sequence will be referred as ‘unbalanced steady-state free precession’ (ub-SSFP) below. Note that all gradient waveforms in the balanced SSFP (b-SSFP) sequence have zero area over any given TR period (i.e., ΔK = 0), thus, the left vertical axis in Fig. 1 collapses and temperature information mostly cancels out. This is because pathways with positive and negative temperature sensitivities overlap. While measuring temperature with a b-SSFP sequence is possible [21], a non-zero ΔK is preferred in this work so that pathways do not overlap and can be individually sampled instead. Unlike spoiled sequences, steady-state sequences (both ub-SSFP and b-SSFP) feature strong signal at short TR settings, even for relatively long T₁ species. Spoiled sequences [19] are also excluded from consideration, as spoiling is aimed at destroying the signal pathways we wish here to exploit.

2. Sampling individual pathways

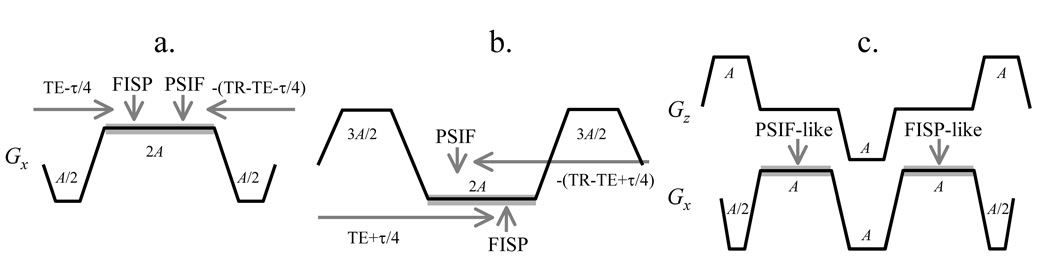
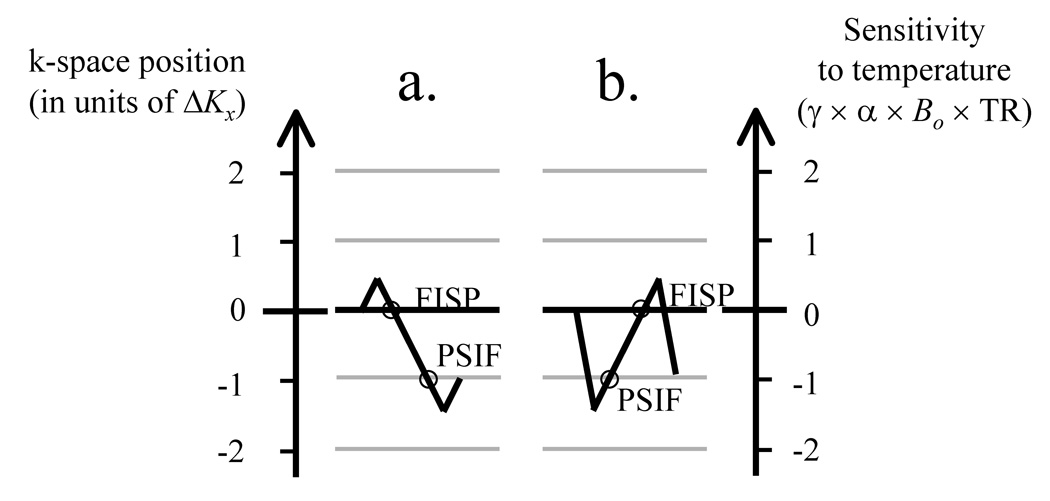
Sequences that sample more than one magnetization pathway are not new [22]. For example, in a case where the y and z gradient waveforms are balanced but not the x waveform, then ΔK in Fig. 1 becomes ΔK_x and one can move from one pathway to the next using the readout x gradient. Figure 2a depicts the readout gradient waveform for a sequence that samples both the FISP and PSIF pathways (similar to the ‘dual echo in the steady state’ or DESS sequence from Siemens). Looking at the horizontal lines in Fig. 1 and with ΔK oriented along k_x, the dephaser lobe, G_x, in Fig. 2a moves the acquisition process from a 0 to a 0.5ΔK location along the vertical axis in Fig. 1. The middle gradient lobe (the readout) then causes a move from location 0.5ΔK to −1.5ΔK and samples the 0^th (FISP) and −1^st (PSIF) pathways along the way. Finally, the rephaser lobe brings us back to the −ΔK location (where by definition the TR period must end). This particular trajectory is depicted in Fig. 3a. Note that with stronger/longer gradient lobes, in principle, readout waveforms could be designed to sample any number of desired pathways, so long as they end at the −ΔK location in representations such as Figs 1 and 3.

Fig. 2.

Examples of x gradient waveforms that can be used to sample both a FISP and a PSIF echo. Data-sampling windows are shown as thick gray lines along the G_x(t) waveform. a) Both the so-called ‘FISP’ and ‘PSIF’ echoes are sensitive to temperature, and this sensitivity is proportional to the length of the horizontal gray arrows, TE-τ/4 and TR-TE-τ/4. τ is the readout duration, and A is the gradient area corresponding to a k-space offset of ΔK (Fig. 1). b) While the FISP was sampled first in (a), here the PSIF is sampled first for improved temperature sensitivity, as seen from the longer horizontal gray arrows. c) A gradient waveform with non-zero total area is associated with flow sensitivity. For example, such sensitivity could be a problem if oriented in the S/I direction, as most organs move mostly along S/I during breathing. In contrast, it can be useful if oriented along the R/L direction, to help detect vessels oriented along R/L. Unlike for the sequence in (b), the sequence in (c) has a gradient imbalance along z (rather than x), showing that the flow-sensitized direction can be rotated.

Fig. 3.

a) Effects of the readout waveforms from Fig. 2a are further described here. The gradient lobes in Fig. 2a cause a move along the ‘k-space position’ axis from 0 to +0.5ΔK, then to −1.5ΔK, and then to −1.0ΔK. A displacement of ΔK corresponds to at least the full width of a k-space matrix, to avoid signal overlap between consecutive pathways. The trajectory finishes at a position −1.0ΔK, and samples the FISP at 0 and then the PSIF at −ΔK along the way. b) The waveform in Fig. 2b causes a move from 0 to −1.5ΔK, then to +0.5ΔK, and finally at −ΔK. Note that, in this case, The PSIF is sampled first. At least in principle, waveforms that sample any number of desired pathways could be designed.

For reasons further explained below, we are interested in sampling first the PSIF and then the FISP, rather than the other way around. This can be accomplished as shown in Fig. 2b, and also depicted in Fig. 3b. The initial lobe in Fig. 2b moves the acquisition process from 0 to −1.5ΔK. The central readout lobe then causes a move from −1.5ΔK to 0.5ΔK capturing the PSIF and the FISP echoes along the way, and the last lobe brings us finally to −ΔK.

An alternative is shown in Fig. 2c, where ΔK is oriented along k_z rather that k_x, meaning that the x and y gradient waveforms are balanced but not z gradient. ‘Superblips’ along the z gradient are used to move from one pathway to the next. The first superblip brings the acquisition from 0 to −ΔK so a PSIF echo can be sampled. The second superblip brings us back to 0 for a FISP echo, and the final one ensures TR ends at −ΔK. As in Fig. 2b, the waveform in Fig. 2c allows a PSIF followed by a FISP to be acquired, but in Fig. 2c the flow sensitivity associated with unbalanced gradients has now been moved along the z direction instead of x.

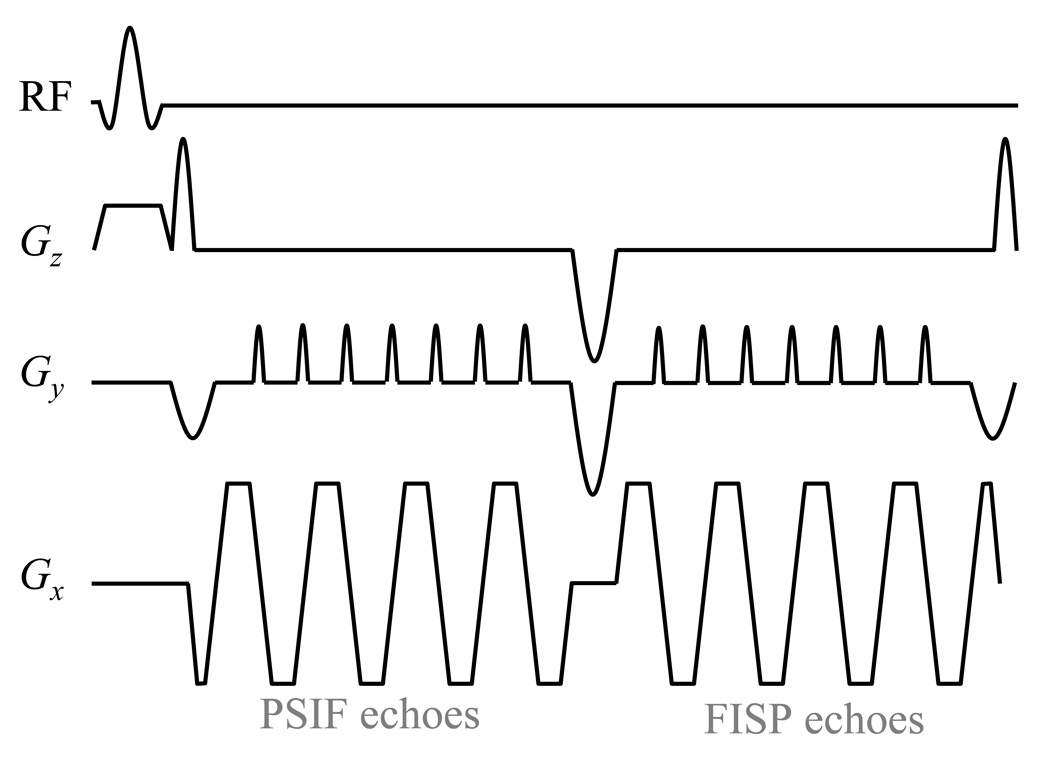
For any given pathway, whether FISP of PSIF, k-space can be sampled with a single or with multiple readouts. Sampling a single k-space line every TR leads to good image quality and minimum susceptibility-induced distortion, and fast imaging can still be achieved if TR is short. On the other hand, longer TR values that would allow a TE about equal to T₂^* (around 15 to 20 ms in liver) are preferable in terms of TNR [8]. Also, with longer TR one can employ an EPI readout to sample each pathway, as shown in Fig. 4, to enable faster imaging. It may be pointed out that the temperature-sensitivity considerations described below are not dependent on how k-space is covered, except for the fact that the echo time, TE, may be more readily defined with sampling schemes such as ub-SSFP as compared with others, such as EPI.

Fig. 4.

The gradient-echo EPI version of the pulse sequence design proposed here is depicted. The readout scheme from Fig. 2c is modified so that single-line readouts are replaced by EPI readouts instead. As in Fig. 2c, ‘superblips’ along the G_z(t) waveform allow PSIF echoes to be acquired first, followed by FISP echoes. Note that the first and last superblips are smaller than the middle one because they were merged with the negative rephaser and dephaser lobes associated with the slice-selective excitation pulse. Because the phantom imaged here was water-based and featured no fat signals, a regular RF pulse was employed, although, for in vivo imaging, it should be replaced with a spectral-spatial pulse.

3. Temperature sensitivity for sampled pathways

The color-coded diagonal lines in Fig. 1 are associated with the right vertical axis, and show that the sensitivity to temperature changes during TR. More specifically, the temperature sensitivity for any given pathway is given by:

$${\mathrm{\Lambda }}_p=\left(\gamma \alpha B_o\right)\times (\mathit{\text{pTR}}+{\mathit{\text{TE}}}_p),$$ [1]

where p is the pathway index (e.g., 0 for FISP and −1 for PSIF pathways), γ is the gyromagnetic ratio for hydrogen (2π × 42.58 MHz/T) and α is the PRF change coefficient (−0.01 ppm/°C). For example, for the FISP (p = 0) pathway the right-hand side of Eq. 1 reduces to γαB₀TE₀, which is the proportionality constant traditionally used for converting phase shifts into temperature measurements [8]. From Eq. 1, it may be noted that negative (p < 0) and positive (p ≥ 0) pathways lead to different polarities for the temperature sensitivity, Λ_p, and that for negative pathways the absolute value of the (pTR + TE_p) term is maximized when TE_p is made as small as possible while, for positive pathways, it is maximized when TE_p is as large as possible. This behavior can be understood by considering, as an example, the spin-echo-like PSIF (p = −1) pathway and the gradient-echo-like FISP (p = 0) pathway. The PSIF echo is sampled while magnetization is rephasing, with a spin-echo-like event occurring at the end of the TR interval. The further away from the end of the TR interval, the shorter TE₋₁ becomes, and the greater temperature-induced phase shifts can be. In contrast, the FISP magnetization is sampled while magnetization is dephasing, and greater temperature-induced phase shifts are obtained for greater values of TE₀. The difference in polarity for Λ_p comes from the fact that negative (p < 0) pathways are sampled while they are rephasing toward a ‘spin-echo-like’ event, while positive (p ≥ 0) pathways are dephasing away from an excitation event. This difference in the polarity of Λ _p means that temperature-induced phase shifts measured from a positive and a negative pathway are expected to have opposite signs. For negative pathways, greater TNR can be expected when a short echo time is employed, while for positive pathways a longer echo time would be preferable. The validity of Eq. 1 was confirmed through simulations (see Results section).

4. TNR-optimum reconstruction

Using N_c coil elements and sampling N_p different magnetization pathways, N_c × N_p independent complex images I_p,c are obtained for each time frame, where p and c represent the pathway and coil index, respectively. While the phase-sensitive combination of data from different coil elements has been studied in detail [23], combining temperature data from different pathways is novel. The task of combining different pathway data is somewhat simplified by the fact that, unlike coil elements, there is no noise correlation between pathways. Different pathways are sampled at different times, in different sampling windows, leading to uncorrelated thermal noise.

The temperature-induced phase shift, Δϕ_p (r⃗, t), is obtained for each pathway, p, by combining the complex signal from all available coil elements in a phase-sensitive manner. The proper procedure has been described by Bernstein et al. [23] and requires sensitivity maps for all coil elements. Equations are presented in the Appendix whereby the signals from all available pathways are employed toward generating the required sensitivity maps. Once phase information from all coils has been combined, Δϕ_p (r⃗, t) may be obtained using a simple phase difference with respect to a pre-heating reference or, alternately, by using a more elaborate multi-baseline or referenceless algorithm [24–26].

The term Δϕ_p/Λ_p represents the temperature measurement obtained from pathway, p, and Eq. 2 below shows how temperature measurements from all N_p pathways may be combined in a TNR-optimum fashion. The combination is a weighted sum, whereby the weights account for the fact that temperature information may be noisier for some pathways than for others:

$$T(\overrightarrow{r},t)=\frac{{\displaystyle \sum _p\left(\left|{\mathrm{\Lambda }}_p\right|A_p(\overrightarrow{r},t)W_p\left(\raisebox{1ex}{$\mathrm{\Delta }{\varphi }_p(\overrightarrow{r},t)$}\!\left/ \!\raisebox{-1ex}{${\mathrm{\Lambda }}_p$}\right.\right)\right)}}{{\displaystyle \sum _p(\left|{\mathrm{\Lambda }}_p\right|A_p(\overrightarrow{r},t)W_p)+\epsilon }};A_p(\overrightarrow{r},t)=\sqrt{{\displaystyle \sum _c|I_{p,c}(\overrightarrow{r},t){|}^2}}$$ [2]

where |Λ_p|A_p (r⃗, t)W_p is the weight. The denominator as a whole represents a normalization factor and ε is an arbitrarily-small positive number to ensure the denominator is not zero. The factors A_p (r⃗, t) and Λ_p account for the fact that TNR is proportional to both the signal amplitude and the size of the phase shift, respectively. The dimensionless factor, W_p, is meant to handle cases where different noise levels might be expected from different pathways, for example, if a different readout duration or bandwidth is used. In the present work, and as depicted in Figs 2 and 4, all pathways are sampled similarly and, thus, W_p = 1.

5. TNR improvement

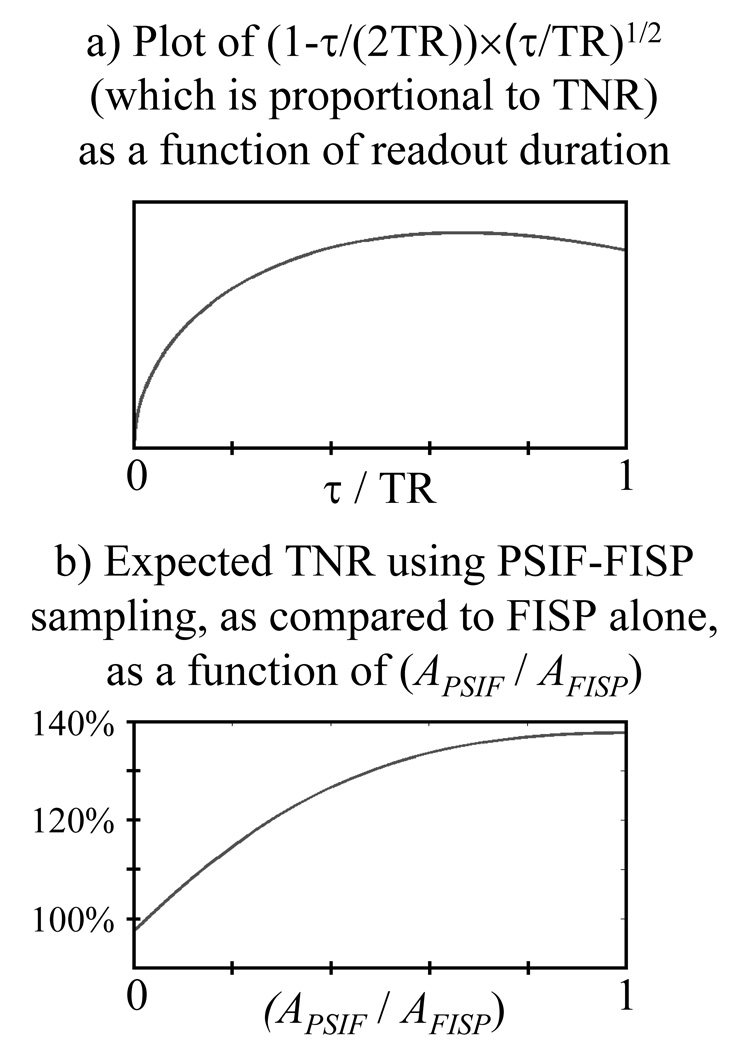
With the typical sequences used for MR temperature mapping, where a single pathway is sampled, the early part of the TR interval cannot be effectively exploited toward improving TNR. With τ the readout duration, and with (TR-τ/2) the maximum TE value, TNR is roughly proportional to (TR-τ/2) ×τ^1/2, neglecting relaxation. This expression is normalized by TR^3/2 to make it a function of (τ/TR), f_TNR(τ/TR) = (τ/TR)^1/2 − (τ/TR)^3/2 / 2 = (1−τ/(2TR)) × (τ/TR)^1/2, as plotted in Fig. 5a. By differentiating with respect to (τ/TR), one finds this function (and, therefore, the TNR) is optimized when τ/TR = 2/3, leaving roughly the first third of TR unused.

Fig. 5.

a) Expected TNR as a function of normalized readout time (τ/TR) is plotted here. While for a single pathway an optimum value τ/TR = 2/3 could be used, when sampling two pathways no more than half of TR can be allocated to each pathway. The TNR penalty associated with such reduction in τ is very small, as the value for τ/TR = 1/2 is 97.4% of the maximum value. b) If one further takes into account the TNR benefits of having data from a second pathway (see Eq. 3), a clear TNR improvement is expected as compared to sampling the FISP pathway alone. Note that even for a PSIF signal with half the strength of the FISP signal (i.e., A_PSIF / A_FISP = 0.5), a 31% TNR improvement would still be obtained. In comparison, for A_PSIF / A_FISP = 1.0, an improvement of $(0.974\sqrt{2}-100\%)=38\%$ would be obtained instead.

Now consider a case where the PSIF and the FISP are sampled (rather than just the FISP as is normally done). No more than half of TR might be allotted to each, meaning that a very modest TNR penalty on the FISP signal is incurred by a factor of about f_TNR(1/2) / f_TNR(2/3) = 0.974. On the other hand, the availability of the PSIF signal can help boost TNR as we shall see.

If we assume that the bandwidth is the same for both echoes, then TE_PSIF ≈ TR/4 and TE_FISP ≈ 3×TR/4, leading to |Λ_PSIF| ≈ |Λ_FISP| in Eq. 1 and 2. With W_p = 1 and, because noise variance adds in quadrature, the averaging of signals as expressed in Eq. 2 reduces noise by a factor of $\sqrt{{A_{\mathit{\text{PSIF}}}}^2+{A_{\mathit{\text{FISP}}}}^2}/\left(A_{\mathit{\text{PSIF}}}+A_{\mathit{\text{FISP}}}\right)$. Combining all effects discussed here, the expected TNR obtained by sampling the PSIF pathway in addition to the FISP, as compared to sampling the FISP alone, is roughly given by:

$$B_{\mathit{\text{TNR}}}(A_{\mathit{\text{PSIF}}}/A_{\mathit{\text{FISP}}})=\frac{0.974\times \left(\left(A_{\mathit{\text{PSIF}}}/A_{\mathit{\text{FISP}}}\right)+1\right)}{\sqrt{{\left(A_{\mathit{\text{PSIF}}}/A_{\mathit{\text{FISP}}}\right)}^2+1}}.$$ [3]

This function is plotted in Fig. 5b. Note that the PSIF signal is expected to be weaker than the FISP signal because the PSIF sustains greater diffusion-related and relaxation-related losses. But even in a case where the PSIF signal is only half the FISP signal, i.e., (A_PSIF / A_FISP) = 0.5 in Fig. 5b, a TNR improvement by as much a 31% may still be obtained.

Materials and Methods

1. Simulations

All simulations were performed in Matlab (The MathWorks, Natick, MA), and involved applying rotations and decays/recovery to a 1D row of magnetization vectors. From one simulated TR to the next, the simulation involved applying RF pulses, gradient pulses, relaxation and temperature-induced frequency shifts to the simulated object, as well as sampling the signal. Given that the 1D simulated object was homogeneous with arbitrarily fine spatial resolution, and that different pathways are separated in k-space (see Fig. 1), magnetization from different pathways could be obtained by a simple FFT of the simulated object. Simulations similar to that from Fig. 1 were performed over a range of flip angles [1°, 90°] and TR values [5 ms, 40 ms], and run through as many as 150 TR periods to ensure steady-state magnetization was reached. The amount of signal in each pathway could then be computed.

TNR analyses performed as part of the present work, both on simulated data (present section) and on experimental data (next section), involved relative TNR as opposed to absolute TNR measurements. Relative TNR values can capture how TNR varies from one method to the next or from one set of imaging parameters to the next. In contrast, absolute TNR measurements tend to be more anecdotal in nature, as they are determined in part by how much heating happens to be present in a particular experiment. Assuming all other parameters such as noise, equilibrium magnetization M₀ and coil sensitivity to be constant, the amount of simulated signal could be converted into a measure of relative TNR. For any given combination of pathway, p, flip angle and TR value, the amount of simulated signal was multiplied by the temperature sensitivity, Λ_p, to obtain a number proportional to TNR. Relative TNR measurements were then obtained by normalizing with the maximum value found over all pathways, flip angle and TR values.

The validity of Eq. 1 was tested through a second set of simulations. As each pathway consists of a superposition of signals, each with its own history of RF excitation, refocusing and relaxation, it is not obvious a priori that the phase of the composite signal should remain linear with temperature. While any given signal in the simulated transverse plane during any given TR period receives a frequency shift that is directly proportional to temperature, the echoes that get sampled consist of a superposition of many such signals. The simulation program was used to test whether the phase of such composite echoes may still be considered linearly proportional to temperature, despite the fact they consist of a sum of many individual signals having different histories. Linearity between temperature, T, and phase shift, Δϕ_p, was tested for the −1^st (PSIF) and 0^th (FISP) pathways, as well as for pathways −2, 1 and 2, over the range from 0 to 100 °C. According to Eq. 1, the temperature sensitivity, Λ_p, is the proportionality constant that relates Δϕ_p to T. Data were computed using the same TE value for all pathways (i.e., TE_p = TE) and a linear fit was performed on these data to test the predictions of Eq. 1.

2. Experimental data

All imaging was performed on a 3.0 T MR system (GE Signa HDxt Twin Speed, Milwaukee, WI, 40 mT/m, 150 T/m/s). The ability to capture blood vessels was tested in free-breathing in vivo human liver imaging experiments without heating. Most of the respiratory-induced motion is expected to occur along the S/I direction, and motion in the A/P and L/R directions, although present, is expected to be much less significant. Sagittal in vivo 2D images were obtained using the acquisition scheme from Fig. 2c, with the through-slice z direction oriented in the R/L direction (FOV = 24×24 cm, matrix size = 128×96, slice thickness = 5 mm, TR = 6.4 ms, TE₋₁ = 1.67 ms, TE₀ = 4.73 ms, bandwidth = 62.5 kHz, flip angle = 35°, 50 time frames). All in vivo images were obtained during free breathing using a product 8-element abdominal array, with informed consent obtained according to an IRB-approved protocol.

Phantom experiments were also performed, with heating, using three different pulse sequences: A dual-pathway unbalanced SSFP (ub-SSFP) sequence as shown in Fig. 2c, a regular (single-pathway) ub-SSFP sequence and a dual-pathway multi-shot gradient-echo EPI sequence as shown in Fig. 4. The phantom consisted of a tissue-mimicking gel phantom (T₁ = 955±75 ms, T₂ = 128±2 ms) placed in an acrylic tank filled with degassed and de-ionized water within a GE 8-channel head coil. Five equivalent datasets were acquired with each sequence, to evaluate reproducibility. The same sagittal slice was imaged in all cases (FOV = 24×24 cm, matrix size = 128×96, slice thickness = 5 mm). All ub-SSFP datasets were acquired with TR = 6.4 ms, TE₋₁ = 1.67 ms, TE₀ = 4.73 ms, bandwidth = 62.5 kHz, flip angle = 35°, 200 time frames, and temporal resolution = 96×6.4 ms = 0.614 s. EPI datasets were acquired with TR = 34 ms, TE₋₁ = 12.7 ms, TE₀ = 24.5 ms, echo-train length = 12, 8 shots, bandwidth = 250 kHz, ramp sampling, flip angle = 30°, 220 time frames and temporal resolution = 8×34 ms = 0.272 s. Especially when using longer TE and TR values, phase unwrapping along the temporal dimension may be needed to avoid temperature aliasing [27]. Once unwrapped, temperature increments as high as 16 °C and 83 °C from one time frame to the next can be handled in the EPI and ub-SSFP implementations, respectively.

Temperature noise was measured as the standard deviation along the time axis, averaged spatially over a non-heated ROI, and averaged over all five repeat-datasets. More specifically, consecutive temperature time frames were subtracted two-by-two to remove any trend and the de-trended data were divided by $\sqrt{2}$ to cancel out the noise increase that occurred with the subtraction. The standard deviation was calculated along the time axis, and averaging was then performed over the spatial ROI and all repeat datasets. The measured temperature-noise values could then be used toward calculating relative-TNR values. Given that all tested methods provide accurate temperature readings, as extensively tested in the Results section, relative TNR depends only on temperature noise and not on temperature itself. Temperature-noise ratios were thus obtained and interpreted as relative-TNR measurements.

Focused ultrasound heating was generated using a single-element, spherically-curved, piezoelectric transducer with a resonance frequency of 1.5 MHz (radius of curvature = 100 mm and diameter = 100 mm). The transducer was driven by a function generator (Model 396, Fluke, Everett, WA) and RF amplifier (model 240L, E and I, Rochester, NY), and monitored using a power meter (model 438A, Hewlett Packard, Palo Alto, CA) and dual directional coupler (model C1373, Werlatone, Brewster, NY). Continuous wave, 30 s 10–20 W acoustic power sonications were delivered to the phantom material.

Results

1. Simulations

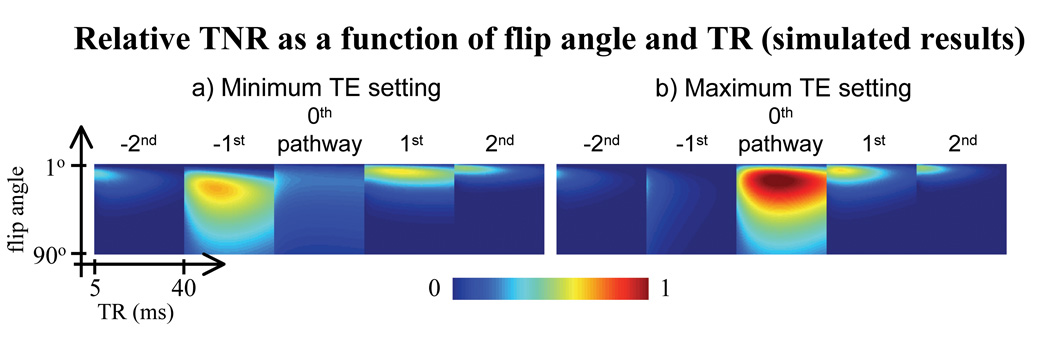
Fig. 6 displays the TNR available from each pathway, from −2^nd to 2^nd, over a range of flip angles and TR values. Results in Fig. 6a represent a case with minimum TE setting (TE = 2 ms), while those in Fig. 6b represents a case with maximum TE setting (TE = TR - 2 ms). It should be noted that the −1^st pathway has maximum TNR for short TE, while the 0^th pathway has maximum TNR for long TE.

Fig. 6.

Relative TNR, as compared to the maximum TNR case, is shown as a function of TR and flip angle. a) For short TE values, the −1^st (PSIF) pathway offers much better TNR than the 0^th (FISP) pathway. b) For long TE values, the situation is reversed. For this reason, the preferred multi-pathway sequence involves sampling two pathways, first the PSIF early during the TR period (short TE₋₁), and the FISP later during TR (long TE₀). Other higher-order pathways have less-advantageous TNR properties. Relaxation times consistent with liver imaging were used here (T₁ = 800 ms, T₂ = 35 ms, T₂^* = 20 ms).

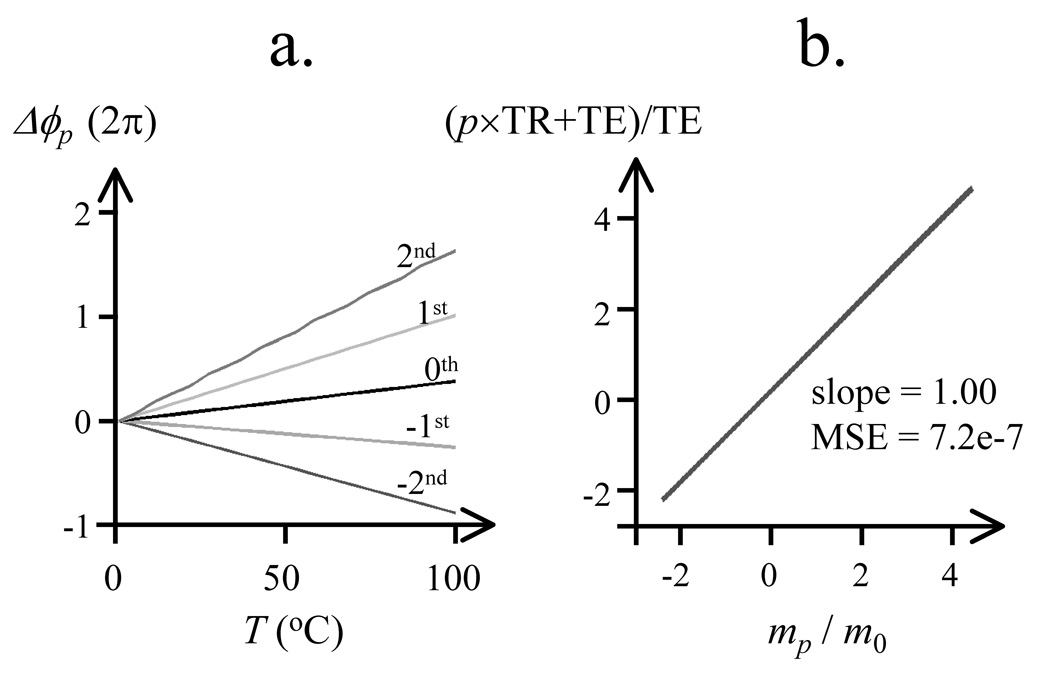
Results of the simulations to test the validity of Eq. 1 are shown in Fig. 7a, for pathways, p, from −2 to 2. From linear fitting on these data, the mean square error for each pathway was: 1.12e-6 (p = −2), 1.29e-13 (p = −1), 8.76e-12 (p = 0), 7.64e-7 (p = 1), 3.51e-3 (p = 2). The best (i.e., most linear) relationships were obtained for i = −1 (PSIF) and i =0 (FISP) pathways, with intermediate values for i = 1 and i = −2. The fitted values for the slope are plotted in Fig. 7b, after normalization by m₀ (i.e., by the fitted slope value for the 0^th pathway). Based on Eq. 1, equating the slope values to Λ_p implies that the ratio m_p/m₀ should correspond to (p×TR+TE)/TE. Figure 7b tends to confirm Eq. 1, as it shows a linear relationship with slope 1.00 is obtained when plotting (p×TR+TE)/TE against m_p/m₀.

Fig. 7.

Simulations were performed to validate Eq. 1. The linearity of the relationship between temperature and phase shift was tested in (a) for pathways from −2 to 2. The value of the proportionality constant in these linear relationships was tested in (b), as compared to expected values from Eq. 1. See text for more details.

In terms of which pathways should be sampled in practice, our decision was dictated mostly by TNR considerations and flow contrast properties. The −1^st and 0^th pathway were chosen here because they offer the best TNR (Fig. 6), good linearity (Fig. 7a), significantly different blood-vessel contrast (shown below), and that they have their best temperature sensitivity for very different TE values (Fig. 6).

2. In vivo imaging (without heating)

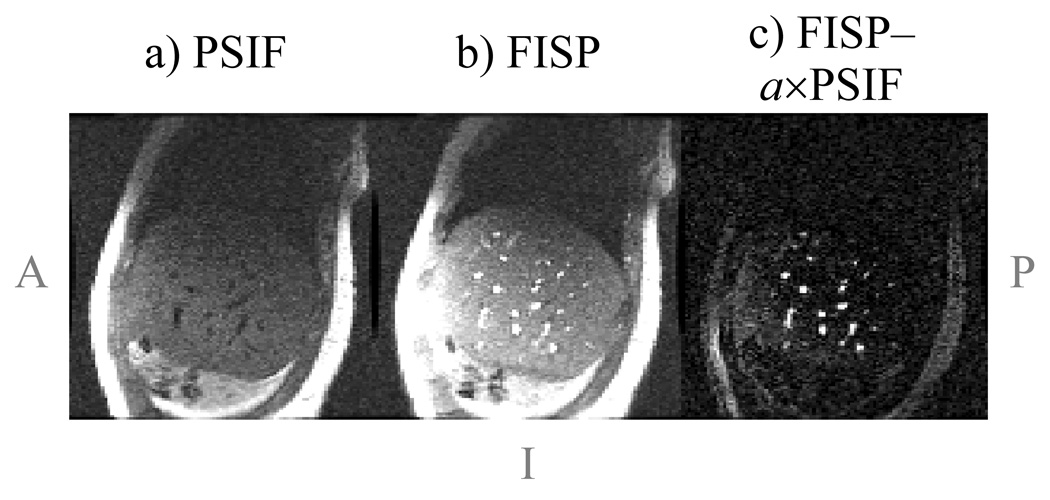
Figure 8 shows results from the free-breathing liver imaging experiments. One time frame for one of five acquired sagittal slices is displayed in Fig. 8a,b. Notice that blood vessels tend to appear bright in the FISP image and dark in the PSIF image, as opposed for example to fat, which appears bright in both images. In this acquisition, the inherent flow sensitivity of the sequence was oriented along the z direction to help detect vessels that run in the R/L direction, which are expected to provide particularly good landmarks toward tracking S/I and A/P motion. While such velocity sensitization might be harmful in the S/I direction and possibly lead to signal losses in liver tissues, velocity sensitization along the R/L direction may help detect vessels with R/L flow. Although velocity sensitization along the R/L direction could lead to image degradation in the presence of (unexpected) significant motion along R/L, the free-breathing results in Fig. 8 suggest this is not likely to be a significant problem.

Fig. 8.

a,b) Liver images were acquired during free breathing using the sequence from Fig. 2c (sagittal plane, 5 slices, 5 mm thick, 128×96, 24×24 cm, TR = 6.4 ms, temporal resolution = 96×6.4 = 614 ms). Because blood vessels tend to appear dark in the PSIF images due to flow effects, acquiring both the FISP and PSIF magnetization pathways as in Fig. 2c greatly facilitates the task of localizing blood vessels for target-tracking purposes. c) A simple subtraction between FISP and PSIF images, using a scalar weight, a, to maximize signal cancellation (a = 1.4 here), yields images of mostly just blood vessels. When viewed in a movie loop, the blood-vessel images clearly capture the (in-plane) changes in liver position and shape caused by breathing. Notice that non-flowing materials such as fat or liver parenchyma have more similar contrast in both images, and appear to be suppressed in (c).

In post-processing, blood-vessel images were obtained from the dual echo images as I_vessels = |I_FISP| − a×|I_PSIF|, where a is a scalar that minimizes the spatial integral of |I_vessels|². A value of a = 1.4 was found here, meaning that the FISP signal was about 40% stronger than the PSIF signal. Given that the noise level is the same in both cases, the SNR differed by 40% as well. The blood-vessel image, computed from the images in Fig. 8a and Fig. 8b, is shown in Fig. 8c. Even using such a simple post-processing algorithm, images like Fig. 8c can be obtained that clearly highlight blood vessels.

3. Phantom results

Data from the first (out of five) repeat-datasets from the heating experiments are presented in Fig. 9 for each sequence. Temperature maps are shown for the moment of maximum heating, about 30 s into the imaging experiment. Temperature-noise measurements for each imaging sequence, obtained over the non-heated ROI shown in blue, are presented in the upper-left corner of each image in Fig. 9a. It is also worth noting that temporal resolution was more than two-fold higher for EPI results (0.272 s) than for ub-SSFP results (0.614 s).

Fig. 9.

Phantom data with FUS heating were acquired using three different 2D pulse sequences: the dual-pathway unbalanced SSFP sequence from Fig. 2c, a regular gradient-echo sequence (i.e., FISP only), and the dual pathway interleaved-EPI sequence from Fig. 4. Temporal resolution was more than two-fold better for EPI than for the ub-SSFP sequence (272 compared to 614 ms). a) Temperature maps are shown for the time frame with maximum heating (about 8 °C at focus). To evaluate temperature noise, the standard deviation was calculated along the time axis for each pixel in the non-heated ROI (shown in blue). Results for all the pixels in this ROI were then averaged and the resulting value is displayed in the upper-left corner of each image in (a). Notice that the dual-pathway ub-SSFP implementation (top row) provides about a 35% improvement in TNR compared to its single-pathway counterpart (middle row), as 0.27 °C / 0.20 °C = 1.35. b) The magnitude component of data employed to generate the images in (a) is also displayed here. Notice that although the EPI implementation (bottom row) provides superior TNR and higher frame rates, the ub-SSFP short-TR implementation (top row) also has value, as it provides better anatomical images with less geometric distortion for potentially superior motion tracking. c) The temperature information from (a) is displayed as an overlay onto the magnitude information from (b). Throughout this figure, the same windowing settings were used whenever comparing results from different sequences or pathways.

Figure 9b shows the magnitude information that corresponds with the data from Fig. 9a. While PSIF and FISP phase images were combined (through Eq. 2) into a single temperature map in Fig. 9a, their magnitude images are shown separately in Fig. 9b (using identical windowing). Notice that the PSIF images are quite significant in terms of intensity as compared to FISP images, even in the EPI case where TR is longer. It should also be noted from Fig. 9b that, as expected, image quality and geometric fidelity tends to be much higher in the ub-SSFP images than in the EPI images. In Fig. 9c, the temperature information from Fig. 9a is shown as an overlay on the magnitude information from Fig. 9b. Whenever available, the PSIF magnitude image was combined in quadrature with the FISP image to generate the magnitude background for the overlay. Throughout Fig. 9, identical window settings were used whenever comparing different sequences or different magnetization pathways.

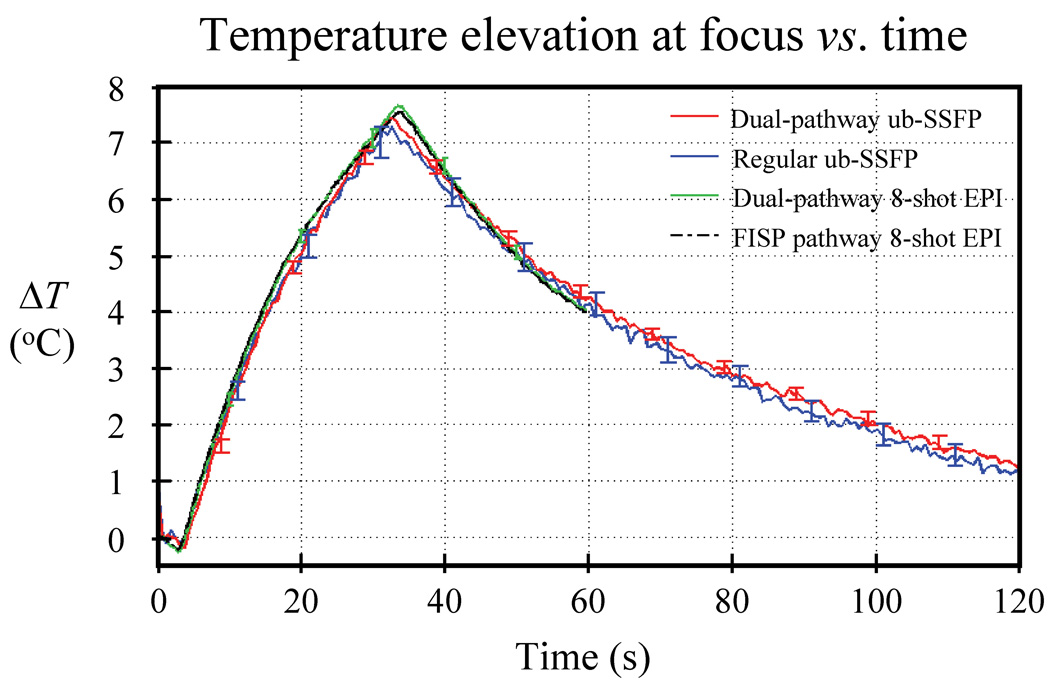
Figure 10 shows the temperature curves associated with data from Fig. 9. The pixel location at the focus of maximum heating was identified, and a 3×3 ROI was placed and centered at this location. While pixels at identical locations in the image matrix were used for both ub-SSFP datasets, the focus location was not exactly the same in EPI images due to geometric distortions. The focus in the EPI datasets was found to be about 4 pixels away from that in the ub-SSFP datasets, mostly in the phase-encoded direction, as expected. The temperature averaged over all five repeat-datasets is plotted in Fig. 10, where the standard deviation over repeat-datasets was used to generate the error bars. Strictly speaking, the standard deviation of a distribution is itself a random number, which converges toward its correct value σ only when the number of samples approaches infinity. With only five samples, the standard deviation was very noisy here. A more accurate estimate was obtained by averaging all standard deviation values obtained over 10 s windows and, for this reason, error bars in Fig. 10 are displayed only every 10 s along the time axis. Close agreement can be seen among the three imaging sequences, as the curves plotted in Fig. 10 differ from each other by no more than 0.21 °C on average.

Fig. 10.

Temperature curves are shown for all three types of sequences from Fig. 9, as averaged over a 3×3 pixel ROI located at focus. Five repeat-datasets were acquired with each sequence, the average value among repeats was plotted and the standard deviation among repeats was used to generate error bars. Very close temperature agreement was obtained between all three imaging sequences (dual pathway ub-SSFP, regular ub-SSFP and dual-pathway EPI). On average, the curves plotted here differed from each other by only 0.21 °C or less. As a reference, temperature measurements from the usual (FISP) pathway of the dual-pathway EPI sequence are also shown, averaged over all five repeats.

All compared methods provided equivalent temperature measurements (see Fig. 10), but different temperature-noise levels (see Fig. 9a). Accordingly, ratios of temperature-noise measurements (Fig. 9a) could be used to evaluate relative TNR. Comparing the two top rows in Fig. 9a, it can be seen that the dual-pathway scheme improved TNR by 35% (0.27 °C / 0.20 °C = 1.35), and that the longer-TR, longer-TE EPI sequence had significant TNR advantages over the short-TR short-TE ub-SSFP sequence (0.20 °C compared to 0.075 °C noise levels).

Discussion

A multi-pathway pulse sequence design was proposed here for PRF imaging in order to provide improved TNR properties and contrast characteristics over what is available with current temperature mapping sequences. While a large number of possible pathways could in principle be sampled, all with different temperature sensitivity and image contrast properties, we verified that the FISP and the PSIF pathways offer desirable TNR and contrast properties.

In terms of TNR, we noted that usual (FISP-based) PRF thermometry sequences tend to leave the beginning of the TR period un-utilized or ill-utilized. Exploiting the early part of the TR period to sample the PSIF magnetization makes perfect sense in terms of TNR, as the PSIF has maximum temperature sensitivity early within TR. For example, a 35% improvement in TNR was obtained in the ub-SSFP implementation by sampling both pathways instead of only the FISP (see Fig. 9).

In terms of contrast, we noted that signals from different pathways offer very different flow properties, facilitating the detection of blood vessels (e.g., see Fig. 8). As lesions may move during treatment, their displacements need to be tracked, and the vascular bed may represent an ideal internal landmark to do so [16]. By focusing on a limited number of landmarks rather than having to consider all voxels in the imaged volume, a displacement map could be generated very rapidly using landmark-based (also called feature-based) registration [28–30]. As latency should be kept to a minimum, only a fraction of a second may be available for registration, and blood-vessel images obtained as described here could allow fast, non-rigid, landmark-based registration for motion tracking purposes.

Limitations of the current study include the use of a single-element FUS transducer and off-line reconstruction. To make good use of tracking information, one would ultimately use a large 2D matrix transducer array with beam steering capability and a real-time reconstruction platform, to make the FUS focus location track the location of the moving anatomy in real time. Furthermore, the regular RF pulses used here should be replaced with spectral-spatial pulses, to allow for fat suppression. Indeed, fat protons do not undergo hydrogen bonds like water protons and are mostly immune to temperature-induced frequency shifts and, for this reason, their signal, if not suppressed, may corrupt temperature measurements [31–35]. Spectral-spatial pulses tend to have a longer duration than regular RF pulses, reducing the amount of time available for sampling the PSIF signal [36]. For simplicity, the estimates of TNR improvement presented in Eq. 3 and Fig. 5b assumed the entire TR duration to be available for readout but, in reality, the RF excitation and several non-readout gradient pulses do require some time. Depending on pulse sequence parameters and implementation details, the actual amount of time available for sampling a PSIF and the associated TNR boost that can be achieved may be lower than those predicted by Eq. 3 and Fig. 5. This may be especially true if long-duration RF pulses occupy a large portion of the TR interval.

One type of sequence tested here featured single-line readouts and short TR values (6.4 ms), while a second type featured EPI readouts and longer TR values (34 ms). Single-line readouts lead to good quality images with minimum susceptibility-induced distortion, while EPI readouts allow improved temperature sensitivity and temporal resolution. The anatomical images from ub-SSFP were clearly superior to those from EPI. However, if one ignores geometric distortion and anatomical image quality while considering only TNR and temporal resolution, the temperature maps from EPI were clearly superior to those from ub-SSFP. While the better TNR and temporal resolution of EPI shown here may be very advantageous for thermometry in moving organs, the greater image quality and geometric fidelity of ub-SSFP that has been demonstrated might prove particularly valuable when spatially-accurate motion tracking is considered to be critical. With shorter echo-train lengths, both the advantages and disadvantages of EPI would become subtler. In any case, independent of the chosen readout strategy (single-line, EPI or other), the present work shows that sampling the PSIF magnetization in the early part of TR is expected to bring significant added value over sampling only the FISP, in terms of both TNR and contrast.

Conclusions

There is significant added value in terms of TNR and image contrast in sampling the PSIF magnetization early within TR, while still sampling the FISP magnetization as usual in later parts of the TR interval. This statement is expected to remain true regardless of the type of readout being used, whether single-line, EPI or other.

Appendix

When using multiple coil elements, c, to sample multiple magnetization pathways, p, signal from all pathways can be used toward calculating the sensitivity maps, S_c (r⃗). The sensitivity maps are preferably time-independent here because otherwise temperature-induced phase changes could be mistaken for sensitivity-induced phase changes. Separating the magnitude and phase information, S_c (r⃗) = |S_c (r⃗)|e^iθ_c(r⃗), the magnitude is obtained in two steps: 1) Image data from all pathways are combined through a weighted sum whereby the image magnitude is used as its own weight, and 2) as usual, the root-sum-of-squares of data from all coils is used as a normalization factor for the sensitivity maps:

$$D_c(\overrightarrow{r})=\frac{{\displaystyle \sum _p|R_{p,c}(\overrightarrow{r}){|}^2}}{{\displaystyle \sum _p|R_{p,c}(\overrightarrow{r})|}};\left|S_c(\overrightarrow{r})\right|=\frac{D_c(\overrightarrow{r})}{\sqrt{{\displaystyle \sum _c{D}_c{(\overrightarrow{r})}^2}}},$$ [A1]

where R_p,c is the image data available for sensitivity-mapping purposes, e.g., an average of a few or all time frames from the full dataset, I_p,c (r⃗, t).

The sensitivity phase difference, Δθ_ji (r⃗), between coil j and coil l is expected to be the same regardless of which pathway, p, is used in the measurement and, accordingly, information from all pathways can be employed:

$$\Delta {\theta }_{\mathit{\text{jl}}}(\overrightarrow{r})=\angle \left\{{\displaystyle \sum _p\left(\left|R_{p,j}(\overrightarrow{r})R_{p,l}(\overrightarrow{r})\right|e^{i\left(\angle \left\{R_{p,l}(\overrightarrow{r})\right\}-\angle \left\{R_{p,j}(\overrightarrow{r})\right\}\right)}\right)}\right\},$$ [A2]

where ∠{ } returns the phase of a complex number. Because all MRI data arise from the product of coil sensitivity and object magnetization, there is always a one-degree of freedom ambiguity about phase at any given pixel location, i.e., any arbitrary canceling phase shift could be attributed to both sensitivity maps and object. This ambiguity is lifted here using θ₁ (r⃗) = ∠{R_0,1 (r⃗)}, where it is assumed that the FISP (p = 0) pathway is sampled. Phase for other coil elements is found from θ₁ (r⃗) through Eq. A2, and combined with amplitude values from Eq. A1 to generate the sensitivity maps, S_c (r⃗).