Estimating the Term Structure With a Semiparametric Bayesian Hierarchical Model: An Application to Corporate Bonds

Abstract

The term structure of interest rates is used to price defaultable bonds and credit derivatives, as well as to infer the quality of bonds for risk management purposes. We introduce a model that jointly estimates term structures by means of a Bayesian hierarchical model with a prior probability model based on Dirichlet process mixtures. The modeling methodology borrows strength across term structures for purposes of estimation. The main advantage of our framework is its ability to produce reliable estimators at the company level even when there are only a few bonds per company. After describing the proposed model, we discuss an empirical application in which the term structure of 197 individual companies is estimated. The sample of 197 consists of 143 companies with only one or two bonds. In-sample and out-of-sample tests are used to quantify the improvement in accuracy that results from approximating the term structure of corporate bonds with estimators by company rather than by credit rating, the latter being a popular choice in the financial literature. A complete description of a Markov chain Monte Carlo (MCMC) scheme for the proposed model is available as Supplementary Material.

1 Introduction

The term structure of interest rates, also called the zero-coupon yield curve, refers to the relationship between the interest rate of zero-coupon bonds and their time to maturity. The term structure can be estimated for government or corporate bonds. In both cases the resulting estimators have important practical applications. The term structure of government bonds–also referred to as risk-free term structure–contains information about macroeconomic conditions and expectations of market agents about the future of the economy (Anderson and Breedon 1996). On the other hand, the term structure of corporate bonds is an essential input for pricing defaultable bonds and credit derivatives (Jarrow and Turnbull 1995), inferring the credit quality of bonds for risk management purposes (Saunders and Allen 2002), and assessing the risk of derivative products (Hull and White 1995; Duffee 1996).

This paper focuses on corporate debt. The rest of this section introduces the single-curve approach for estimating corporate term structures, describes why having small samples of bonds is a limitation for improving the single-curve estimators, and explains how the characteristics of the proposed model make it suitable to cope with such a limitation.

A popular approach for estimating the term structure of corporate bonds is the single-curve approach which consists of grouping the bonds by credit rating level, and then estimating the term structure of each class by using methods similar to those developed for government bonds (Schwartz 1998). Such methods include the use of splines (McCulloch 1971) and exponential polynomials (Nelson and Siegel 1987; Svensson 1994). An improvement on the single-curve approach consists of jointly modeling both corporate and government bonds (Houweling et al. 2001; Jankowitsch and Pichler 2004). The joint-model has the advantage of producing, for each rating class, estimators of credit spread curves that are smoother as a function of time to maturity than those produced with the single-curve approach; credit spreads are defined as the difference between term structures of corporate bonds and those of treasuries.

The single-curve approach uses credit ratings as a metric to define groups of bonds. Although ratings are accepted in practice as a sufficient metric to define homogeneous groups, it has been reported that there are other bond characteristics that influence their term structure: default risk, liquidity, tax liability, recovery rate and bond age (Elton et al. 2004). A natural approach for incorporating these factors into the single-curve approach would be to use them as metrics for defining bond classes. However, such an alternative is not feasible in practice given the current estimation methods because, as Elton et al. (2004) pointed out, this would result in classifications with too few bonds within each group to estimate term structures with any accuracy.

Another criterion for grouping corporate bonds that has been considered in the literature is the issuer company. This classification is relevant because the resulting estimators approximate the term structure of individual firms, and consequently, they reflect the uniqueness of a firm’s credit risk. Jarrow et al. (2004) proposed a spline-based model that describes the term structure of corporate debt as the sum of the risk-free term structure and a spread curve. A Bayesian version of Jarrow’s model is described in Li and Yu (2005). A similar approach was used in Krishnan et al. (2009) with the difference that the spread curves were modeled with exponential polynomials following the parameterization introduced by Diebold and Li (2006).

An important constraint, however, for estimating the term structure of individual companies is that most of the companies only issue a handful of bonds. As a result, empirical studies use monthly data and consider only companies with a large number of outstanding bonds to support estimation. Jarrow et al. (2004) and Li and Yu (2005), for example, applied their method to a data set consisting of bonds issued by AT&T that included, on average, 4.3 bonds per month. Krishnan et al. (2009) applied their method to companies having transaction prices for at least 5 bonds per month and with maturities that span at least 7 years. In practice, however, it is common to find companies for which there are fewer bonds available. For example, the data set described in Section 4, which includes daily information for 2009, shows that the average number of bonds per company is as small as 2.1.

It follows from the discussion above that the estimation of corporate term structures could be improved if we had estimation methods capable of producing reliable estimators based on small samples. Specifically, such methods will allow us to use different criteria for defining homogeneous groups of bonds as well as to estimate the term structure of single companies using daily data and without having to filter out companies with a small number of outstanding bonds. In this paper we introduce one such estimation method.

The key feature of our approach is to compensate for the small number of bonds per group/company by jointly modeling their term structures. Unlike Houweling et al. (2001) or Jarrow et al. (2004), however, we do not focus on the relationship between corporate and government term structures, instead we propose to pool information and borrow strength across the groups of corporate bonds. We achieve this by using a Bayesian hierarchical model which is defined as follows. First, each group of corporate bonds is modeled as a subject with its term structure being determined by a four-dimensional vector of parameters corresponding to the functional form proposed by Nelson and Siegel (1987). Next, we pool information among the subjects by setting a prior distribution that represent the subject-specific parameters as a sample from a common distribution. Since our goal is to perform estimation when only a small sample is available, the use of a hierarchical model is a natural choice because this type of model is known to perform well in situations when there are more parameters than data points per subject (Gelman et al. 2004).

The prior distribution in our model should be flexible enough to capture the heterogeneity across the subject-specific parameters, including outliers, over-dispersion, and multimodality. Such a flexibility is achieved by using a mixture prior distribution in which the number of components and their corresponding parameters are random. Specifically, the weights and the location parameters of the components in the mixture are both modeled via a Dirichlet process (DP). The use of a DP prior is a popular modeling approach among the so-called Bayesian nonparametric methods (Müller and Quintana 2004). It has been used in many applications including pharmacokinetics (Rosner and Müller 1997), stochastic frontier models (Griffin and Steel 2004), spatial modeling (Gelfand et al. 2005), density estimation (Dunson et al. 2007), and survival analysis (De Iorio et al. 2009).

The proposed model is illustrated with an empirical analysis in which the term structures of individual companies are estimated. This empirical analysis also quantifies the improvement in performance that results of using estimators by company–produced with the proposed model–versus those obtained when the bonds are grouped by credit rating. The performance is measured in terms of price residuals; the residual of each bond is defined as its observed price minus its theoretical price implied by the estimated term structure. We consider in this paper price residuals corresponding to both in-sample and out-of-sample tests, with the latter being computed via cross-validation. Using a sample of 599 U.S. bonds traded on June 15, 2009, we found that the estimators by company show price residuals smaller than those of estimators by credit rating; the reduction in terms of in-sample price residuals is 80% while for out-of-sample price residuals is on average 61%.

Our empirical analysis uses only corporate bonds–treasuries are not included– and it uses the same sample of bonds to perform estimation at both the company and rating level. These features are favored because we are interested in, on the one hand, showing the positive effect of modeling the information shared among corporate bonds (producing reliable estimators with small samples), and on the other, quantifying the improvement in accuracy that results of analyzing a given sample of bonds at the firm rather than the rating level. Because of the goals just described, our empirical analysis does not include a comparison to the estimation methods introduced by Jarrow et al. (2004) and Krishnan et al. (2009), respectively. These two approaches combine corporate and government bonds and, as explained earlier, their implementation has been limited to monthly data and companies with a large number of outstanding bonds to support estimation.

This rest of this paper is organized as follows. Section 2 introduces the discounted cash flow principle and shows how it is used for estimating the term structure. Our proposed model is described in Section 3. The details of the empirical application are given in Section 4. And finally, conclusions and discussion appear in Section 5.

2 Estimation of the Term Structure

Since most of the corporate and government bonds have a positive coupon, their term structures are not observable and they have to be estimated from market prices using statistical techniques. In this paper we consider estimation methods that are based on the discounted cash flow (DCF) principle. This section defines the DCF principle and explains how it has been used to estimate term structures.

Before introducing the DCF principle, we discuss equivalent representations of the term structure. One representation is the zero-coupon yield curve, y(T), which describes the relationship between spot rates of zero-coupon bonds and their time to maturity, T. Two other representations of the term structure are the discount curve, D(T), and the forward rate curve, f(T). The representations y(T), D(T) and f(T) are all equivalent since they satisfy the following relationships:

$$D(T)=\mathit{\text{exp}}\{-\mathit{\text{Ty}}(T)\}=\mathit{\text{exp}}\left\{-{\displaystyle {\int }_0^T}f(s)\mathit{\text{ds}}\right\}.$$ (1)

In this manuscript we will refer to the term structure using any of these equivalent representations.

In order to estimate the term structure, the discounted cash flow (DCF) can be used to link bond prices to the discount curve. A bond is a debt in favor of the bondholder, who receives in return a cash flow composed of interest (coupon) and the payment of the principal at the set maturity date. The DCF principle states that an investor is willing to pay for a given bond, b, the sum of the present value of the remaining payments in the cash flow:

$$P_{\mathit{\text{DCF}},b}={\displaystyle \sum _{j=1}^{m_b}}{\mathbf{\text{CF}}}_b(j)*D(t_{b,j}),$$ (2)

where P_DCF,b denotes the DCF bond price, CF_b is the cash flow vector including the m_b remaining payments, and D(·) is the discount curve evaluated at the time t_b,j when the jth cash flow is paid. The discount function reflects the time value of money as well as a risk premium. Although equation (2) express P_DCF,b in terms of the discount function, the relationships in (1) allow us to write P_DCF,b in terms of any of the equivalent representations of the term structure. For example, using the zero-coupon yield curve, y(·), $P_{\mathit{\text{DCF}},b}={\displaystyle {\sum }_{j=1}^{m_b}}{\mathbf{\text{CF}}}_b(j)*\mathit{\text{exp}}\{-t_{b,j}y(t_{b,j})\}$.

Based on the DCF principle, we can estimate the term structure as follows. First, any of the equivalent representations of the term structure is approximated using a parametric function; we denote its parameters as θ. Such a parametric function is called an approximating function. Two popular functional forms are splines (McCulloch 1971) and exponential polynomials (Nelson and Siegel 1987). Next, the discount function is written in terms of the approximating function by using the relationships (1) and is used to compute the DCF bond price which now is a function of θ. Finally, θ is estimated by comparing the DCF price to the observed price of each bond in the sample; observed prices, also referred to as dirty prices, incorporate any interest accrued. The basic estimation problem is to find a discount curve with optimal explanatory power, that is, a discount curve that minimizes pricing errors with respect to a given norm. For example, using a quadratic loss function as the norm and approximating the zero-coupon yield curve with a parametric function, the details of the estimation problem are as follows. The yield curve is now a function of both time, t, and a vector of parameters, θ, corresponding to the functional form being used: y(t, θ). Using (1), the discount function is given by D(t, θ) = exp {−t y(t, θ))} and the DCF bond price is equal to

$$P_{\mathit{\text{DCF}},b}(\mathit{\theta })={\displaystyle \sum _{j=1}^{m_b}}{\mathbf{\text{CF}}}_b(j)*D(t_{b,j},\mathit{\theta }).$$ (3)

The estimated term structure corresponds to θ that minimizes

$$L(\mathit{\theta })={\displaystyle \sum _b}{\omega }_b{(P_b-P_{\mathit{\text{DCF}},b}(\mathit{\theta }))}^2,$$ (4)

where P_b is the observed price of the bond b, and each bond weight, ω_b, can be set based, for example, on the duration of the bond.

The estimation procedure just described can be applied to both government and corporate bonds, respectively. Unlike government bonds, however, we cannot assume that all corporate bonds have the same term structure because they are associated with different default risk levels. It is common practice to split the corporate bonds into homogeneous groups based on some criterion and estimate the term structure for each group using the DCF principle. A popular criterion used in practice for defining groups is the credit rating level of the bonds. We follow Houweling et al. (2001) and refer to this case as the single-curve approach.

In our hierarchical model, the DCF principle is used to define the likelihood. The details are shown in the following section.

3 A Semiparametric Bayesian Hierarchical Model

Consider n term structures to be estimated. For example, when working with corporate bonds those term structures could correspond to rating classes or individual firms, depending on the criterion used for grouping the bonds. Let θ_i be the vector of parameters characterizing the ith term structure. In this section, we introduce a Bayesian hierarchical model for jointly estimating {θ₁, θ₂, …, θ_n}.

Let P_ib be the logarithm of the price of the bth bond corresponding to the ith term structure, the proposed Bayesian hierarchical model includes the following three main components:

$$\begin{array}{ccc}p(P_{\mathit{\text{ib}}}|{\mathit{\theta }}_i),\hfill & p({\mathit{\theta }}_i|\varphi ),\hfill & p(\varphi ),\hfill \end{array}$$ (5)

where the likelihood p(P_ib|θ_i) links bond prices and term structures via a non-linear regression model, p(θ_i|ϕ) is the prior for the vector of parameters θ_i, and p(ϕ) denotes the probability model of the hyperparameters ϕ.

The following sections describe the distributional assumptions for each component in (5). The likelihood p(P_ib|θ_i) is set in Section 3.1 while the distribution p(θ_i|ϕ) and p(ϕ) are introduced in Section 3.2. We explain how to incorporate bond weights into the model in Section 3.3. And finally, the sampling scheme for the posterior distribution is discussed in Section 3.4.

3.1 Non-linear Regression Model

The likelihood in our model is given by a non-linear regression based on the discounted cash flow (DCF) principle. Using the indexes ib to denote the data of the bond b with term structure i, observed bond prices are modeled as

$$P_{\mathit{\text{ib}}}=\mathrm{\Psi }({\mathit{\theta }}_i,{\mathbf{\text{CF}}}_{\mathit{\text{ib}}})+{\epsilon }_{\mathit{\text{ib}}},$$ (6)

where Ψ(θ_i, CF_ib) is equal to the DCF price (see equation (3)) computed with the cash flow vector CF_ib, that is,

$$\mathrm{\Psi }({\mathit{\theta }}_i,{\mathbf{\text{CF}}}_{\mathit{\text{ib}}})={\displaystyle \sum _{j=1}^{m_{\mathit{\text{ib}}}}}{\mathbf{\text{CF}}}_{\mathit{\text{ib}}}(j)*D(t_{\mathit{\text{ib}},j},{\mathit{\theta }}_i),$$

and ε_ib is an error term with ε_ib ~ N(0, τ⁻¹), where τ is the precision (inverse variance). The use of an error term is necessary because the exact equality between observed and DCF prices does not hold in practice due to market imperfections (Bliss 1997; Houweling et al. 2001). By using normal errors we can easily introduce bond weights into the model (see Section 3.3).

To complete the specification of Ψ(θ_i, CF_ib), we need to set a parametric function to approximate the discount function D(t, θ_i), or any of its equivalent representations: yield curve or forward curve. We model the yield curve with the functional form:

$$y(t,[{\beta }_0,\alpha ,{\beta }_{2,}\gamma ])={\beta }_0\left(1-\frac{1-\text{exp}(-t/\gamma )}{t/\gamma }\right)+\alpha \left(\frac{1-\text{exp}(-t/\gamma )}{t/\gamma }\right)+{\beta }_2\left(\frac{1-\text{exp}(-t/\gamma )}{t/\gamma }-\text{exp}\left(-\frac{t}{\gamma }\right)\right),$$ (7)

where t > 0 denotes time, and the parameters satisfy β₀, α, γ > 0 and β₂ ∈ R.

The approximating function (7) and the functional form introduced by Nelson and Siegel (1987) are equivalent, but in the former the only condition on the parameters, if any, is to be strictly positive. Because of that feature, we can compute the logarithm of the parameters β, α and γ and use the parameterization θ = [k₀ log(β₀), k₀ log(α), 10 k₀ β₂, k₀ log(γ)], where k₀ is a positive integer. The coordinates of θ have infinite support, which is necessary because, as described in Section 3.2, we use a mixture of multivariate normal distributions to model the parameters of the yield curve. The integer k₀ increases the scale of the coordinates of θ, providing numerical stability. When k₀ = 1 the covariance matrix of θ shows a small determinant that leads to numerical errors when modeling its inverse (see the hyperprior for S⁻¹ in Section (3.2)). In our experience, a value of k₀ = 50 is adequate to avoid the numerical problem described above.

Although splines are a popular alternative for modeling the term structure, we define (7) based on the Nelson-Siegel (N-S) functional because it provides a flexible representation that is able to generate a wide range of shapes found in practice including humps, S shapes, and monotonic curves (Nelson and Siegel 1987). In addition, the (N-S) form is a parsimonious representation of the term structure which is completely determined by only four parameters. In contrast, setting a spline-based functional is more complicated because this would require us to choose a specific family of splines as well as the number and position of the corresponding knots. Finally, based on an empirical application, Ioannides (2003) argued that parsimonious representations of the term structure–similar to (7)–perform better than those based on splines because the latter tend to overfit the data.

The approximating function given in equation (7) is used to describe each one of the n term structures being estimated. Therefore, each term structure is characterized by a four-dimensional vector θ_i.

3.2 Prior Distribution: Dirichlet Process Mixture

In order to produce reliable estimators based on small samples, we propose to borrow strength across the n individual regression models defined in Section 3.1. We achieve this by using a Bayesian hierarchical model with a prior distribution in which the parameters θ_i are modeled as a sample from a common population distribution. We use a mixture prior for such a common distribution so that our model can accommodate heterogeneity such as outliers, over-dispersion, multiple modes and skewness. Outliers can appear, for example, if the term structure of investment-grade firms is being estimated and some of the companies are digressing to junk status–and consequently, the observed prices of their bonds will show low prices–before the ratings of its bonds change. The details on the mixture prior are as follows.

The multivariate distribution of term structure parameters, p(θ_i|ϕ), is modeled with a mixture of normals with weights w_h, locations μ_h, and common covariance matrix S, that is,

$$\begin{array}{ccc}{\mathit{\theta }}_i\stackrel{\mathit{\text{iid}}}{~}M(\mathit{\theta })\hfill & \text{with}\hfill & M(\mathit{\theta })={\displaystyle \sum _{h=1}^{\mathrm{\infty }}}{w}_{h}N({\mathit{\mu }}_h,\mathbf{S}).\hfill \end{array}$$ (8)

Although the mixture in equation (8) is infinite, the hyperprior that we introduce below implies that most of the weight is assigned to only a few components. The use of a normal kernel in the mixture allows for computationally efficient implementation of the full posterior inference. A common covariance matrix across the components is assumed, thereby reducing the number of model parameters.

The mixture in equation (8) is equivalent to

$$\begin{array}{c}{\mathit{\theta }}_i~N({\mathit{\mu }}_i,\mathbf{S})\hfill \\ {\mathit{\mu }}_i~G={\displaystyle {\sum }_{h=1}^{\mathrm{\infty }}}{w}_h\delta ({\mathit{\mu }}_h),\hfill \end{array}$$ (9)

where the function δ (x) assigns probability 1 to the value of x and 0 elsewhere and G is a discrete distribution on μ with possible values μ_h and probabilities w_h, for h = 1, …, ∞. With the notation as in (9), the parameters of the prior mixture are written as {G, S}. Because of the lack of information about the underlying distribution of θ_i, we treat the hyperparameters {G, S} as random.

We model G as a random measure generated from a Dirichlet Process (DP) with base measure G₀ and total mass parameter M, that is, G ~ DP(G₀, M). The mean of the random measure G is given by G₀, while M is a scaling factor that determines the variance of G around G₀ (Ferguson 1973). For a review of models using a DP prior on the random mixing measure see, for example, West et al. (1994) or Escobar and West (1995). Regarding S, we adopt the usual conjugate inverse Wishart prior S⁻¹ ~ Wishart(r, (rR)⁻¹) with r degrees of freedom and mean r(rR)⁻¹ = R⁻¹. The mixing measure, G₀, as well as the covariance matrix, S, are common to all the parameters θ_i. Thus, the posterior inference will take advantage of the information shared across the term structures. The hyperprior distribution described above is similar to that used in Müller and Rosner (1997), where a hierarchical model for a pharmacokinetic study is discussed.

To complete our model we specify a hyperprior on {M, G₀}. Considering these parameters as random allows us to reduce the chance of impacting the posterior results due to inappropriate selection fixed values. Unfortunately, this approach increases the complexity of the model. As a compromise between flexibility and complexity, we use hyperpriors that allow for an efficient implementation of the model. Specifically, M is given a gamma distribution and G₀ a multivariate normal: M ~ Ga(a_m, b_m) and G₀ ~ N(b, B). The moments b and B are chosen to be conjugate to the kernel of the mixture: b ~ N(b₀, B₀) and B⁻¹ ~ Wishart (w, (wW)⁻¹). And finally, the precision τ at the top level of the hierarchical model (see equation 6) is modeled with a gamma hyperprior: τ ~ G(a_τ, b_τ).

3.3 Bond Weights

The maturity of a bond affects the amount of information available to infer the term structure. The shorter the maturity the more reliable the bond prices. Estimation procedures usually incorporate this information by using weights defined as function of duration. We use such an approach; the weights scale the variance of the error terms in equation (6) as follows:

$$P_{\mathit{\text{ib}}}~N(\mathrm{\Psi }({\mathit{\theta }}_i,{\mathbf{\text{CF}}}_{\mathit{\text{ib}}}),{(\tau {\omega }_{\mathit{\text{ib}}})}^{-1}),$$ (10)

where ω_ib is the weight of the bond b corresponding to the term structure i. Under this approach, the effect of the weights is similar to that in equation (4) because maximizing the induced likelihood is equivalent to minimizing the weighted non-linear least square criterion. In this paper, we define the bond weights as

$$w_{\mathit{\text{ib}}}=\frac{\frac{1}{d_{\mathit{\text{ib}}}}}{{\displaystyle {\sum }_b}\frac{1}{d_{\mathit{\text{ib}}}}},$$ (11)

where d_ib is equal to the Macaulay duration of the bond. The duration is a weighted average of the maturity of a bond using the present value of its cash flow as weights. Thus, in a set of bonds, the weights will tend to be higher for those bonds with short time to maturity.

3.4 Posterior Inference

The posterior distribution of the proposed model does not have a closed form. Thus, we use a Markov chain Monte Carlo (MCMC) scheme to sample from the posterior distribution. A general description of such a scheme is provided below.

Conditional on currently imputed values for θ, the full conditional distributions on the parameters have closed forms, thus they all can be updated by a Gibbs sampling algorithm. In particular, since the kernel of the mixture and the base measure G₀ are both normally distributed, updating the parameters μ_i, which follow a DP hyperprior, can be easily accomplished by using the sampling algorithm for conjugate models described in MacEachern and Müller (1998). A review of sampling methods for DP in mixture models with extensions to non-conjugate models is provided in Neal (2000). Resampling M is done by introducing a latent beta-distributed variable as described in Escobar and West (1995).

For updating θ_i, however, we cannot use a Gibbs sampling scheme because the full conditional does not have a closed form due to the non-linearity in the likelihood of the model. An alternative is to use a Metropolis-Hasting algorithm which requires the specification of a proposal distribution. When the sample size is small, however, it is difficult to find good approximations to the posterior which could be used to set the parameters of the proposal distribution. To overcome this difficulty, we use the adaptive Metropolis (AM) algorithm introduced by Haario et al. (2001). The proposal distribution in the AM algorithm is a Gaussian distribution centered on the current state and with covariance matrix calculated using all the previous states after a given burning period. The adaptation provided by the AM algorithm allows us to produce accurate estimators, even though it starts with a rough initial covariance matrix for the proposal distribution.

The Supplementary Material includes the details about the implementation of the MCMC algorithm: a complete description of the sampling scheme and rules for setting both initial values and hyperparameters. It also discusses the sensitivity of the proposed model to the hyperprior on the precision parameter, M, of the Dirichlet process. Although, as suggested in (Dorazio 2009), the hyperprior on M strongly influence the number of components in the mixture, its effect is far more limited on the shape and performance of the resulting estimators (for details see the Supplementary Material).

4 Application of Term Structure Modeling

This section presents the results of applying the proposed methodology to estimate the term structure of corporate bonds. As previously noted, the proposed model described in Section 3 allows estimation to take place at the individual company level, where only a handful of bonds may be issued. Approximating the term structure of corporate bonds with term structures of companies is an alternative to the popular procedure of using estimators of rating classes. As we will demonstrate, grouping bonds by firm increases the accuracy of the estimators due to the fact that the resulting classification is more homogeneous than the classification based on credit ratings. This section includes a comparison of estimators produced under the two alternative criteria, credit rating and issuer company.

4.1 Data

A sample of U.S. corporate bonds were obtained by combining information from two databases: the Trade Reporting and Compliance Engine (TRACE) introduced by the Financial Industry Regulatory Authority, and The Mergent Fixed Income Securities Database (Mergent-FISD) for academia. Both databases were accessed through the Wharton Research Data Services (http://wrds.wharton.upenn.edu/). The database TRACE, introduced in July of 2002, consolidates transaction data on 100 percent of over-the-counter activity representing over 99 percent of total U.S. corporate bond market activity in over 30,000 securities. TRACE provides, for a given trading day, a list of the bonds traded and their prices. However, other characteristics of those bonds, their time to maturity, coupon, payment frequency, issuer, etc., are not available in TRACE. We obtained such information in Mergent-FISD, a comprehensive database of publicly-offered U.S. bonds that provides details on debt issues and the issuers on over 140,000 securities.

For illustration, we consider U.S. corporate bonds traded on June 15, 2009. The characteristics per bond in our data set include issuer company, maturity date, coupon, face value, payment frequency, clean prices, and Moody’s credit ratings. Our sample includes fixed coupon, non-callable, non-putable, investment grade bonds (AAA, AA, A, BBB), with maturity between 1 and 20 years. We exclude all bonds with a negative yield, since this may indicate poor liquidity. Our final sample contains 599 bonds. Two criteria will be considered for splitting those bonds into groups: credit rating and issuer company. The resulting classification greatly differ in terms of the number of bonds per group. The classification based on credit ratings includes 4 groups corresponding to the levels AAA, AA, A, and BBB; each of those groups include 31, 117, 306 and 145 bonds, respectively. In contrast, the classification determined by issuer includes 197 groups, 114 (58%) of them have only one bond (see Table 1).

Table 1.

Distribution of companies by number of bonds. The table refers to U.S. corporate bonds with information for June 15, 2009. Percentages do not add up to 100% due to rounding

	Number of Bonds
	1	2	3	4	5	≥ 6
# Companies	114 (58%)	33 (17%)	17 (9%)	5 (3%)	10 (5%)	18 (9%)

4.2 Implementation

The proposed Bayesian model includes an MCMC scheme to produce a sample from its posterior distribution. The implementation of such a sampling algorithm is written in the programming language C. The parameters of the ith term structure are estimated as the posterior mean of the vector of parameters θ_i; the posterior mean is approximated by averaging the posterior sample. Regarding the single-curve method, it estimates the term structure of credit rating classes using the DCF principle. The computations are performed using the package “termstrc,” which is written in the R system for statistical computing (Ferstl and Hayden 2008). The functional form proposed by Nelson and Siegel (1987) is used as approximating function of the discount function. The parameters are estimated by minimizing the weighted squared errors in (4), the weights are defined as in (11), and the optimization problem is solved numerically with the optimiser nlminb() available in R.

The performance of term structure estimation methods are compared through both in-sample and out-of-sample metrics. The in-sample goodness of fit is measured in terms of price residuals, also called price errors, which are equal to the market price minus the theoretical DCF bond price (see equation 3) calculated using the estimated discount curve. Comparing price residuals is appropriate because term structure models should be able to explain market prices accurately since interest rates are the main determinants of bond prices. The term structure model with the lowest price errors provides the best fit.

Out-of-sample measures (Bliss 1997) are obtained using cross-validation. One round of cross-validation starts by partitioning the dataset into complementary subsets: a training set and a test set. The training set is used to fit term structures that are used to compute the theoretical DCF price for each bond in the test set and residual of the DCF price from the market prices is obtained. To summarize these residuals, we compute the root mean square prediction error (RMSPE) and the mean absolute prediction error (MAPE) for the test set.

4.3 Estimators by Rating Class

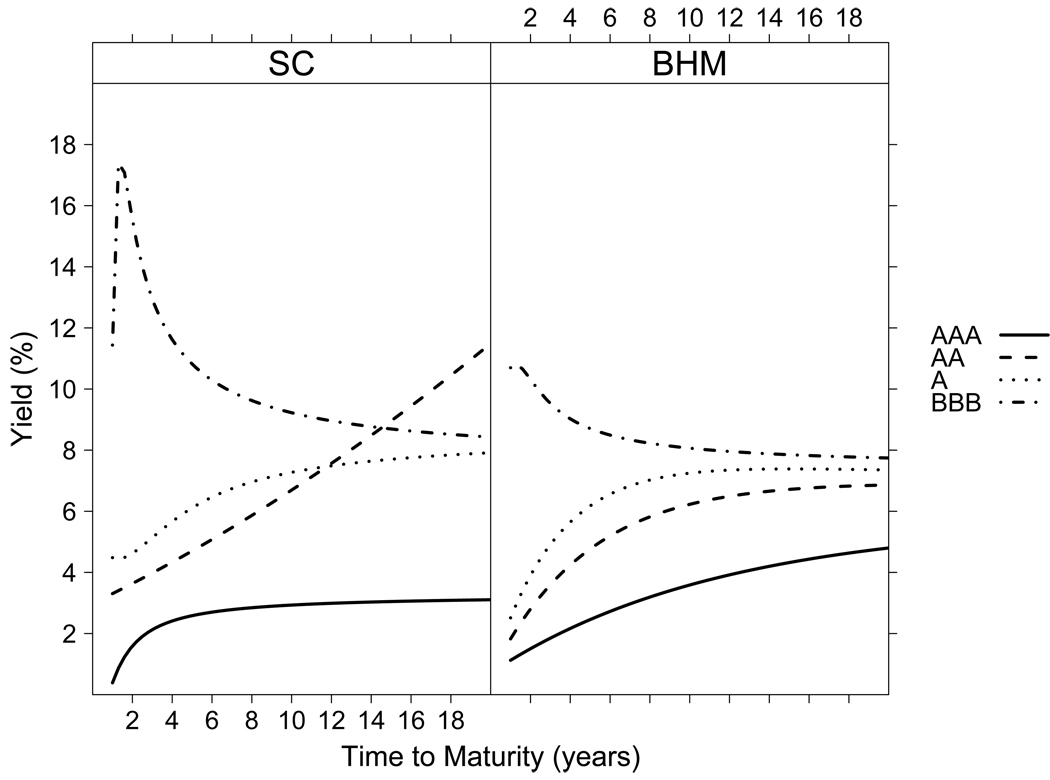
Term structures by credit rating class are estimated using both methods: the proposed Bayesian model and the single-curve approach (see Figure 1). The yield curves produced with the proposed Bayesian model show the expected relationship between credit risk and yield: the lower the credit rating, the higher the yield. In contrast, the curves estimated using the single-curve method fail to show such a pattern for maturities higher than 10 years, even though all rating classes except the AAA include bonds with time to maturity in the range (10, 20] (see Table 2).

Figure 1.

Yield curves by rating class. The estimators produced with the proposed Bayesian hierarchical model (BHM) are in line with the theory in terms of their “order.” In contrast, the single-curve estimators (SC) cross each other.

Table 2.

Distribution of bonds by maturity (columns) and rating class (rows). This table shows that the number of bonds decrease for long maturities. In particular, there are 394 bonds with maturity between 1 and 5 years that account for 66% of the bonds in the sample.

	(1–5]	(5–10]	(10–15]	(15–20]	ALL
AAA	31	0	0	0	31
AA	69	44	3	1	117
A	201	83	8	14	306
BBB	93	26	15	11	145
Total	394	153	26	26	599

The estimated parameters are reported in Table 3. In all rating classes, The methods produce different parameter estimates, especially in rating class AA. Since the estimators in the single-curve approach are produced by numerically solving a minimization problem, the user needs to provide an initial value to start the search for the minimum. Using alternative initial values, the estimated parameters were in all cases consistent with those reported in Table 3.

Table 3.

Estimated parameters for term structures of rating classes by method. To allow comparison, the estimators are expressed in term of the original parameterization introduced by Nelson and Siegel (1987). For estimators obtained with the proposed Bayesian hierarchical model (BHM), 90% probability intervals are reported in parenthesis.

		Estimated Parameters
Method	Rating	β0	β1	β2	τ
SC
	AAA	0.03	−0.06	0.00	0.6
	AA	53.28	−53.25	−50.87	378.17
	A	0.09	−0.03	−0.09	1.10
	BBB	0.08	−22.43	23.27	0.19
BHM
	AAA	0.06 (0.04,0.08)	−0.05 (−0.07, −0.03)	0.06 (−0.02, 0.15)	11.79 (8.24, 18.12)
	AA	0.07 (0.04, 0.1)	−0.06 (−0.08, −0.04)	0.08 (0.00, 0.15)	5.2 (3.98,7.02)
	A	0.07 (0.05,0.10)	−0.06 (−0.08,−0.05)	0.08 (−0.01,0.15)	3.46 (2.66,4.47)
	BBB	0.07 (0.07,0.08)	−0.07 (−0.08,−0.07)	0.21 (0.16,0.27)	0.49 (0.25,0.73)

The hierarchical Bayesian model and the single curve estimator demonstrate similar performance of in-sample metrics as seen in the boxplots of figure 2 and the summary statistics in Table 4. A key advantage of the hierarchical Bayesian method applied at the level of rating class is that the yield curves produced via the hierarchical Bayesian method are in line with economic theory. The single curve estimators can be improved by removing outliers; a bond is considered to be an outlier based on the size of its pricing error. Filter rules reported in the literature include single thresholds and iterative algorithms that continue until no outliers are identified. An example of the former is Elton et al. (2004) who removed all bonds having a price error greater than 5 dollars, while (Schwartz 1998) illustrate iterative rules. In our case study, removing bonds from the sample improves the shape of the single curve estimators: it eliminates the hump in the estimated BBB yield curve (for details, see the Supplementary Material). The hierarchical Bayesian method is not overly influenced by the presence of the outliers: its DP prior allows the outliers to have their own cluster and, thereby, leave the central mass alone. By keeping all bonds in the sample, we avoid introducing bias.

Figure 2.

Boxplots for in-sample absolute price errors by method and rating. The labels “AAA”, “AA”,“A”, “BBB” refer to credit rating levels while “ALL” indicates that all the residuals are being considered. The estimation approaches considered are: the single-curve approach that produces estimators by rating class (SC-rating), and the proposed Bayesian hierarchical model with estimators by rating class (BHM-rating) and firm (BHM-firm)

Table 4.

Summary statistics of absolute price errors. Statistics are reported by method (rows) and rating level (columns). “SC-rating” corresponds to the single-curve approach producing estimators by rating class. “BHM-rating” and “BHM-firm” refers to the estimators produced with the Bayesian hierarchical model by rating and by firm, respectively. The median absolute price residuals of estimators by firm are smaller than those obtained by rating class. Both median and interquartile range (IQR) increase for low credit rating classes.

Method	Statistic	ALL	AAA	AA	A	BBB
SC-rating
	Median	2.80	0.18	1.52	2.63	9.31
	IQR	5.63	0.20	2.41	4.65	9.47
BHM-rating
	Median	2.98	0.45	1.20	2.70	8.89
	IQR	6.08	0.41	2.44	4.19	7.02
BHM-firm
	Median	0.56	0.15	0.66	0.57	0.53
	IQR	1.22	0.12	1.37	1.10	1.54

4.4 Estimators by Company

The primary reason for introducing the hierarchical Bayesian model to this problem is to capitalize on the ability to estimate the term structure at the issuer level by borrowing strength from similarities across issuers. In this section we demonstrate the superior performance obtained through estimation at the issuer level, justifying the large increase in number of model parameters necessary for this approach.

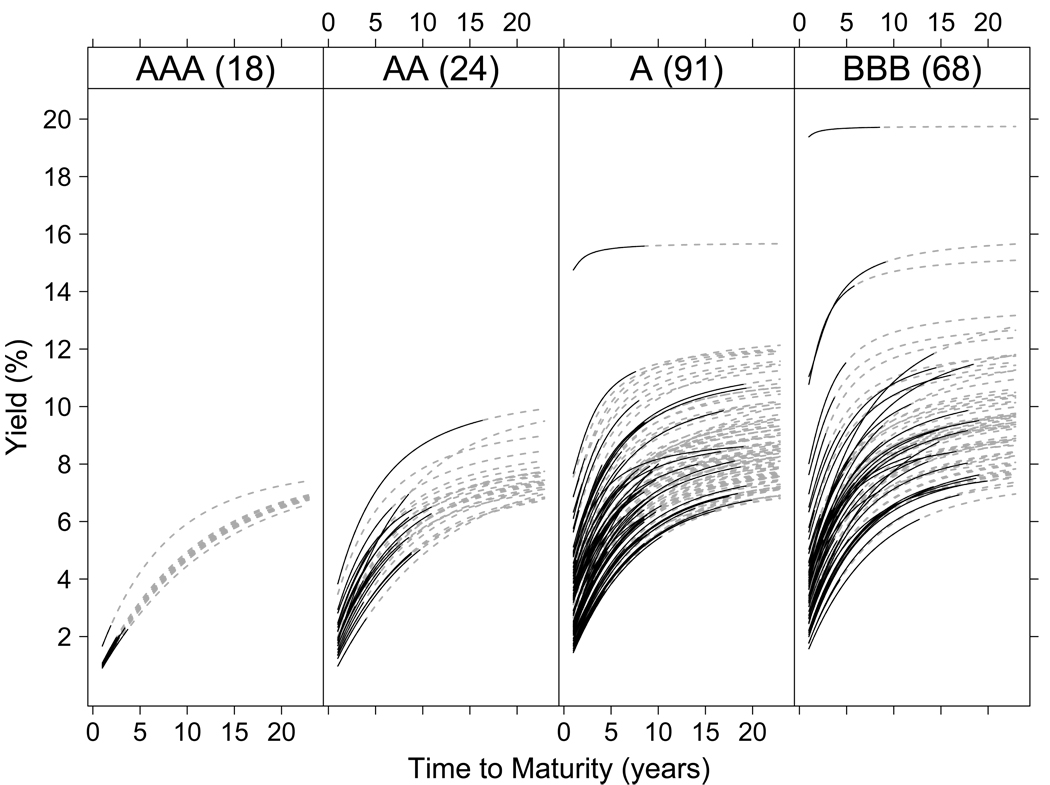
The Bayesian hierarchical model is used to jointly estimate the term structure of 197 individual firms. The estimated yield curves are smooth and reflect the inherent heterogeneity among companies whose outstanding bonds have a low credit rating (see Figure 3). The median in-sample absolute price residual of estimators by firm and those produced with the single-curve approach are 0.56 and 2.80, respectively. A relative difference of −80% (see Table 4).

Figure 3.

Yield curves by company obtained with the Bayesian hierarchical model. Each panel includes the yield curve of companies that have at least one outstanding bond with a given rating level. Since four companies in our data set include bonds with different rating levels, four yield curves appear more than once. The number of curves in each panel is indicated in parenthesis. For each company, a segment of its yield curve is displayed with a solid line, the right extreme in the x-axis of such a segment is equal to the longest time to maturity of the bonds issued by the given company. Thus, the solid segment reflects the range in which bond data is available.

As expected, the out-of-sample metrics also demonstrate improved performance for the Bayesian hierarchical model applied at the issuer level. In this comparison, the test set is defined by randomly selecting one bond from any company having more than one outstanding bond, while the training set includes the rest of the bonds in the sample. Consequently, any company with x number of bonds in the original sample, where x > 1, will become a company with x − 1 bonds in the training set. Since 83 of the companies in the original sample have more than one outstanding bond, then the test set includes 83 bonds. We generate 30 random partitions of test and training sets. For each partition, we compute the out-of-sample measures of the estimators by firm obtained with the proposed Bayesian model, and the estimators by rating class produced with the single-curve approach. That is, the bonds in the training set are grouped based on the appropriate criterion (issuer company or credit rating), term structures are estimated for each group, and finally, the RMSPE and MAPE are computed based on the prediction errors of the bonds in the test set. The average RMSPE and MAPE over the 30 partitions are reported in Table 5. The estimators by firm show the best performance; their RMSPE and MAPE are, respectively, 62% and 61% smaller than those of estimators by rating class.

Table 5.

Average of the root mean squared predition error (RMSPE) and mean absolute prediction error (MAPE) over 30 partitions by method. The out-of-sample statistics of the Bayesian hierarchical model (BHM-firm) that estimates term structures by firm are 60% smaller than those by rating class obtained with the single-curve approach (SC-rating).

	RMSPE	MAPE
BHM-firm	3.20	2.14
SC-rating	8.34	5.46
Relative Difference	−62%	−61%

5 Discussion

We introduced a Bayesian hierarchical model for jointly estimating, across all firms in our sample, the term structures of interest rates for corporate bonds. A hierarchical approach provides the opportunity to produce reliable estimators based on small samples of bonds, a necessary feature for estimating term structures of firms. Due to the heterogeneous nature of term structure at the credit rating level, we see significant improvements from term structure estimation at the issuer level. In addition, the hierarchical Bayesian methodology applied at the level of credit rating resulted in term structure estimators demonstrating improved consistency with economic theory than estimating a single discount curve function through non-linear weighted least squares to each credit rating class.

The methodology developed provides additional advantages of estimation of term structures. The methodology is easily adapted to fit term structures of corporate bonds grouped by other criteria, and even consider other types of bonds. For example, combinations of corporate and/or government bonds and estimation of credit spreads, i.e., the difference between government and corporate yield curves, can be implemented through this methodology. Computing credit spreads based on the estimators produced with our model are likely to be accurate because of the good performance of our model in identifying the underlying term structure of corporate bonds, along with the fact that there are usually enough government bonds to accurately estimate the risk-free term structure. Another possible application is the estimation of spreads between bonds from different countries. In this case we would consider each country as a subject, jointly estimate their term structures, and take the difference of the estimated curves by pairs to obtain the spreads.

Regarding the practical implementation of the proposed model, our experience suggests that it does not require excessive tuning. Sensible results have always been obtained by using the formulas described in the Supplementary Material for defining initial values and setting fixed hyperparameters.

In summary, the term structure estimation model described in this paper is able to produce accurate estimators of the term structure when only a handful of bonds are available. Furthermore, it is a flexible model that is not restricted to a specific type of bond and it can be easily implemented in practice since no excessive tuning of its parameters is required.

Appendix

Supplementary Material - includes: a complete description of the MCMC, rules for setting initial values and hyperparameters, a sensitivity analysis on the hyperprior for the precision parameter of the Dirichlet process, and a discussion on the shape of the term structure estimators corresponding to the BBB rating class.