Abstract
The mechanosensitive channel of small conductance (MscS) is a bacterial tension-driven osmolyte release valve with homologues in many walled eukaryotic organisms. When stimulated by steps of tension in excised patches, Escherichia coli MscS exhibits transient opening followed by reversible adaptation and then complete inactivation. Here, we study properties of the inactivation transition, which renders MscS nonconductive and tension insensitive. Using special pressure protocols we demonstrate that adaptation and inactivation are sequential processes with opposite tension dependencies. In contrast to many eukaryotic channels, which inactivate from the open state, MscS inactivates primarily from the closed state because full openings by preconditioning pulses do not influence the degree of inactivation, and saturating tensions keeping channels open prevent inactivation. The easily opened A98S mutant lacks inactivation completely, whereas the L111S mutant with a right-shifted activation curve inactivates silently before reaching the threshold for opening. This suggests that opening and inactivation are two independent tension-driven pathways, both starting from the closed state. Analysis of tension dependencies for inactivation and recovery rates estimated the in-plane expansion (ΔA) associated with inactivation as 8.5 nm2, which is about half of the area change for opening. Given that the interhelical contact between the outer TM1–TM2 pairs and the core TM3s is the force-transmitting path from the periphery to the gate, the determined ΔA now can be used as a constraining parameter for the models of the inactivated state in which the lipid-facing TM1–TM2 pairs are displaced and uncoupled from the gate.
INTRODUCTION
The mechanosensitive channel of small conductance (MscS) is a ubiquitous osmolyte release valve present in all phyla of walled cells, from bacteria to higher plants (Pivetti et al., 2003; Balleza and Gómez-Lagunas, 2009). In bacteria, MscS and three other mechanosensitive channels (MscM, MscK, and MscL) comprise a membrane tension–driven osmolyte efflux system adjusting turgor in a wide range of osmotic downshifts. Among them, MscS mediates the bulk of osmolyte efflux opening at moderate tensions (5–8 mN/m), which is above the threshold for MscM (Schumann et al., 2010) but considerably below nearly lytic tensions (10–14 mN/m) that open MscL (Sukharev et al., 1999; Moe and Blount, 2005; Belyy et al., 2010b). Responding generally in nonemergency situations, MscS exhibits intricate adaptive behavior. In patch clamp experiments, MscS readily responds to abrupt pulses of tension, but under slow ramps, only a fraction of channel population opens (Akitake et al., 2005, 2007). Analysis of responses to prolonged pressure steps revealed that in excised patches, MscS first undergoes reversible adaptation, and then enters a tension-insensitive inactivated state (Akitake et al., 2005, 2007). Adaptation is a gradual shift of the activation curve midpoint toward higher tensions (by 10–20%) ascribed to mechanical stress redistribution in inside-out patches, which is not observed in whole spheroplast mode (Belyy et al., 2010b). Adapted channels can be reactivated by stronger tension. Inactivation, in contrast, renders channels completely tension insensitive; it is present in all recording modes and appears to be an intrinsic property of the channel. Our recent data showed that inactivation occurring in wild-type (WT) MscS with a relatively slow (∼30 s) kinetics provides substantial advantage to bacteria in terms of osmotic survival under different regimes of osmotic shock in vivo when compared with noninactivating or fast inactivating mutants (Boer et al., 2011). This further suggested that MscS inactivation observed in electrophysiology is not an artifact of patch clamp recording, but rather a functional trait excluding unnecessary activity and leakage under persisting but not threatening tensions. Although previous data suggested that inactivation occurs at tensions above the activating threshold from the closed-adapted state (Akitake et al., 2005, 2007), it was unclear whether closed-state inactivation is the only mechanism or it can also occur from the open state as in many voltage-gated channels (Aldrich and Stevens, 1983; Patlak, 1991; Armstrong, 2006).
Most previous studies addressed the mechanism of tension-driven activation of MscS, in which the crystal structures of WT (Steinbacher et al., 2007) or A106V MscS (Wang et al., 2008) were used to model the resting and/or conductive states. Electron paramagnetic resonance–derived constraints (Vásquez et al., 2008a,b), or unitary conductance and thermodynamically estimated in-plane protein expansion (Akitake et al., 2007; Anishkin et al., 2008a,b), combined with computational techniques were used to envision the opening transition. The tension- and voltage-dependent mechanisms of inactivation (Koprowski and Kubalski, 1998; Vásquez and Perozo, 2004; Akitake et al., 2005), however, were not fully addressed in structural terms. Inactivation was linked to formation of the crystallographic kink at G113 in TM3 (Akitake et al., 2007) and strongly facilitated by mutations that hydrophilize the reconstructed hydrophobic interface between TM2 and the gate region on TM3 (Belyy et al., 2010a). The latter study suggested that inactivation may be caused by some displacement of TM1–TM2 pairs from the gate, although the spatial scale of this tension-driven transition has never been estimated. The tension dependence of the recovery process (reverse of inactivation) has not been characterized either.
Here, we study MscS inactivation with a special set of pressure protocols including preconditioning pressure steps and saturating test pulses and show that opening does not enhance, but rather excludes, inactivation. Analysis of “soft” and “stiff” mutants with different opening thresholds illustrates that the opening and inactivation are two competing transition pathways from the same closed state. Tension dependencies of both inactivation and recovery rates suggest the spatial scale of the inactivating transition, which guides the modeling of the inactivated state.
MATERIALS AND METHODS
WT Escherichia coli MscS was expressed from the pB10b vector (Okada et al., 2002) in MJF465 (ΔkefA, ΔmscS, and ΔmscL) E. coli cells (Levina et al., 1999) or PB113 E. coli strain, which is a ΔrecA variant of MJF429 (ΔmscS and ΔmscK) (Levina et al., 1999; Li et al., 2002) carrying the chromosomal copy of mscL. Preparation of giant E. coli spheroplasts and patch-clamping procedures were conducted as described previously (Blount et al., 1999; Akitake et al., 2005). Population channel recordings were conducted at +30 mV (pipette) on excised inside-out patches in symmetrical buffers containing 200 mM KCl, 10 mM CaCl2, 40 mM MgCl2, and 10 mM HEPES, pH 7.4. The bath solution differed only in the addition of 400 mM sucrose. Traces were recorded under programmed pressure stimuli delivered from an HSPC-1 pressure clamp machine (ALA Scientific Instruments) using the Clampex 10.2 software (Molecular Devices). After seal formation and excision, each patch was tested with a saturating 1-s pressure ramp to determine the activation midpoint (p0.5). p0.5 was then used as a subsaturating pressure stimulus in step protocols and as a reference point for pressure normalization (Fig. 1).
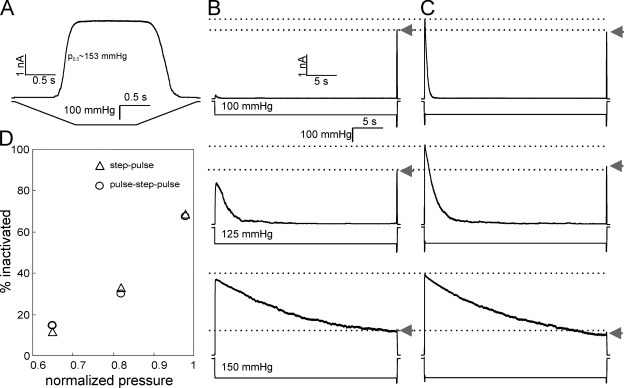
Figure 1.
Dependence of MscS inactivation on the preconditioning saturating pulse at different tensions. (A) Ramp responses of channel population in a patch characterized by the midpoint of 153 mmHg and saturating pressure of 180 mmHg. Responses to the step pulse protocol with the increasing amplitude of a 30-s step (B). (C) Responses of the same patch to pulse-step-pulse stimuli, where the first short pulse opens the entire MscS population, and the pulse at the end reveals the part of the population remaining active in both protocols (arrows). Inactivated fractions of channel population plotted as a function of normalized pressure during the 30-s step (D) are similar regardless of the presence of the first pulse. The data were collected on a single representative patch and were qualitatively reproduced on four separate patches. In D, pressures are normalized to the ramp response midpoint p0.5 (A).
Here, we further developed protocols that allowed us to separate the kinetically intertwined processes of adaptation and inactivation. In these protocols, the channel populations were subjected to prolonged subsaturating pressure steps with interspersed short test pulses of saturating pressure (Fig. 3 A and legend). The current observed during the steps reflected adaptation, and test pulses monitored the noninactivated population of channels. Segments of traces reflecting different stimuli (step vs. pulse) were digitized and fitted in Mathcad 13 using analytical solutions of the standard set of differential equations (Houston, 2001) describing a three-state kinetic model (O→CA→I):
where k1 and k2 are the rate constants for the sequential transitions O→CA and CA→I, respectively. The discretization of the traces and isolation of the open (O), closed-adapted (CA), and inactivated (I) populations are illustrated in Fig. 4 (A–C).
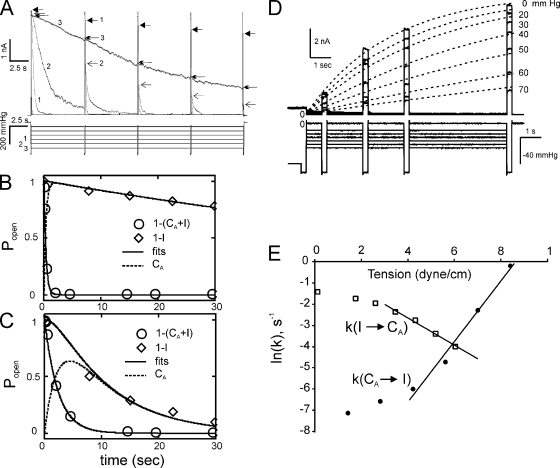
Figure 3.
The dependencies of the rates of MscS inactivation and recovery on tension in excised patches. (A) The current traces and the stimulus protocols that involve 30-s steps to varied amplitude (from 25 to 150 mmHg in 25-mmHg increments) with interspersed short saturating (180-mmHg) pulses testing for the availability of channels. The numbers 1, 2, and 3 correspond to the pressure steps of 100, 125, and 150 mmHg, respectively. The tips of current responses to test pulses are marked with different arrows. The activation midpoint for this patch determined using 1-s ramp was 140 mmHg. (B) Fitting of MscS transition kinetics recorded at a 100-mmHg pressure step to the three-state model: O→CA→I. Normalization dictates that O + CA + I = 1. The circles designate the position of the continuous trace (A) representing open population (O), the diamonds represent noninactivated population (O + CA), and the intermediate closed-adapted (CA) fraction (dashed line) is calculated by fitting the two other populations to the model (see Materials and methods). (C) A similar fit of the trace obtained at higher background tension (125 mmHg) showing slower adaptation but faster inactivation rate. (D) Membrane tension slows down MscS recovery from inactivation. MscS population was inactivated by a 60-s conditioning step (the last second is shown), and the degree of inactivation was tested by the short saturating test pulse at the end of the step. The pressure was then dropped to different levels, and four saturating test pulses were applied at different time points. The current responses, reflecting the recovered fraction of the population, were then fitted with monoexponential functions. (E) The rates of inactivation and recovery plotted against membrane tension. The slopes dlnk/dγ = ΔA/kT gave estimations of ΔAC→B = 4.6 nm2 and ΔAI→B = 2.6 nm2; the protein area changes from the bottoms of the closed (C) or inactivated (I) well to the transition barrier (B). The values averaged over three independent experiments and their sum representing total protein expansion associated with the CA→I transition are given in Results.
Figure 4.
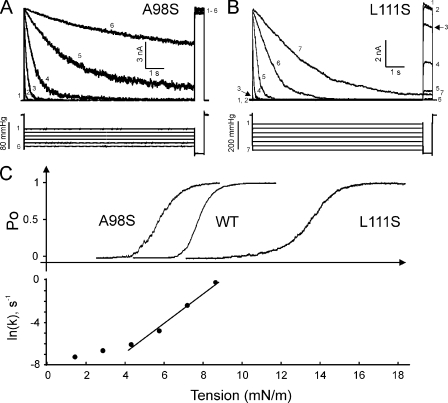
The comparison of activation and inactivation thresholds for WT MscS, soft A98S, and stiff L111S mutants. (A) A series of traces obtained in response to step pulse protocol shows that the soft A98S MscS mutant does not inactivate. (B) The stiff L111S mutant partially inactivates silently without opening, as illustrated by trace 3 (arrows). (C) Positions of activation curves for A98S (γ0.5 = 5.8 mN/m), WT (γ0.5 = 7.8 mN/m), and L111S (γ0.5 = 13.4 mN/m), and the tension dependence of the inactivation rate of WT MscS (data from Fig. 3 E) on the tension scale.
RESULTS
Activation of MscS antagonizes inactivation
Fig. 1 A shows a typical response to a trapezoidal stimulus that we used to calibrate the pressure sensitivity of the MscS population in a particular patch, which in this case exhibits a midpoint of p0.5 = 153 mmHg. Two protocols are then used: (1) a prolonged (30-s) conditioning step, and then short saturating pulse testing for channel availability (Fig. 1 B); and (2) a short saturating pulse that opens the entire population, and then a conditioning step and a short test pulse again (Fig. 1 C). We studied the degree of inactivation at different amplitudes of the conditioning step, which were chosen to be slightly below p0.5. As indicated by the level of population current to the saturating test pulse at the end of the first protocol (Fig. 1 B, arrow), MscS progressively inactivates. Responses of the same patch to the second protocol with the same amplitude of steps are shown in Fig. 1 C. In the first protocol, the conditioning step activates only a fraction of channels, whereas in the latter case, the first saturating pulse obligatorily opens the entire MscS population. In both cases, the population gradually closes with a characteristic time that depends on the amplitude of the step. The second protocol forces the entire population through the opening cycle (O→C→O), yet the fraction of inactivated channels is equal in both protocols (Fig. 1 D), indicating that opening does not aid inactivation.
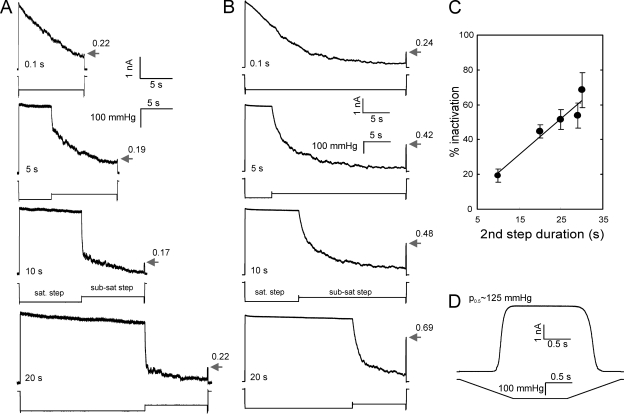
The data presented in Fig. 2 show that dwelling in the open state actually precludes inactivation. Each of the two pressure protocols includes a saturating step that keeps the population open, an intermediate step at which the channels are given a chance to close, and a final saturating test pulse probing for the remaining active part of the population. In experiments presented in Fig. 2 A, the length of the saturating step varied, whereas the second sub-saturating step was kept constant (10 s). As shown by arrows, the responses to the test pulse at the end are the same with an accuracy of 15%, indicating that the degree of MscS inactivation is independent of the open period. In Fig. 2 B, the total duration of the stimulus was kept constant, and the length of each step varied reciprocally. When the first step is short (0.1 s), the population is allowed to close gradually under moderate pressure for the entire ∼30-s duration of the second step, and the inactivation was profound (76%). Extending the length of the first saturating step from 0.1 to 20 s and reducing the time of the second step from ∼30 to 10 s, respectively, increased the number of active channels. The fraction of inactivated channels progressively decreased with the decrease of time spent at sub-saturating pressure when the channels had time to close. The inactivated fraction plotted as a function of sub-saturating step duration shows a nearly linear dependence (Fig. 2 C). Fig. 2 D shows the calibration ramp response for that specific patch. The experiment was repeated four times on different patches, and the error bars in Fig. 2 C represent the standard deviation. The protocol demonstrates that opening does not help inactivation, but rather locks MscS in a state from which it cannot inactivate.
Figure 2.
The degree of MscS inactivation is independent of the open period but increases with the time spent in the closed-adapted state. (A) Current responses to a double-step protocol in which the first saturating step (105 mmHg) of varied length is followed by a 10-s subsaturating step (75 mmHg). The responses to the short test pulse at the end indicate the fraction of active channels (numbers by the arrows). (B) The 30-s stimulus includes saturating (160 mmHg) and subsaturating (125 mmHg) pressure steps of reciprocally varying duration. The percentage of inactivation averaged over four patches studied with this protocol is shown in C (bars represent SD). The test ramp experiment (D) indicated the midpoint of 125 mmHg for the patch examined in B.
The conclusion above is consistent with our previous results obtained with two-step protocols where the channels were first exposed to a prolonged conditioning step above the threshold, and then the population was tested with a saturating pulse at the end. During the prolonged step, the rate of adaptive current decline decreases monotonously as tension increases. The fraction of channels remaining active at the end of the step exhibits a nonmonotonous tension dependence with a minimum at the pressure corresponding to the activation midpoint on 1-s saturating ramp (Akitake et al., 2005; see Fig. S4 B in Belyy et al., 2010a). Pressures below p0.5 are not strong enough to elicit full MscS inactivation, whereas above p0.5, MscS undergoes very slow adaptive closure being trapped in the open state. Thus, initially tension facilitates inactivation, but once the population of open channels increases, the inactivated fraction declines (Akitake et al., 2005, 2007; Belyy et al., 2010a).
Tension dependencies for the rates and the spatial scale of inactivation
The above data suggests that only nonconductive (closed or closed-adapted) channels can inactivate. Previous study (Belyy et al., 2010b) has shown that adaptation of MscS and MscL in excised patches is a consequence of tension redistribution in the membrane, which is essentially the adaptation of the stimulus. Thus, the adaptive current decline should be considered as closure. Under moderate supra-threshold stimuli, when most of the open channels undergo adaptive closure and finally inactivate, the entire process can be presented as a linear three-state scheme: O→CA→I. The pressure protocol we used here is a prolonged (30-s) pressure step with short saturating test pulses interspersed evenly from the beginning to the end (Fig. 3 A). The initial test pulse preconditions the entire population to the O state. The pressure-dependent rate of the following current relaxation, reflecting closure O→CA, can be directly obtained by fitting the time course of current decay (Kamaraju and Sukharev, 2008). In Fig. 3 (B and C), the remaining open fraction (O) is designated by open circles. The current spikes in response to saturating test pulses reveal the fraction of channels that remain active (noninactivated), both open and closed (O+CA). This combined fraction, complementary to the inactivated fraction (I = 1−(O+CA)), is shown with diamonds for two different conditioning steps (Fig. 3, B and C). The intermediate closed-adapted fraction (CA) can be calculated from the analytical solutions of the standard system of differential equations describing two sequential reactions (see Materials and methods). Fig. 3 B shows the trace-fitting quality obtained at relatively low pressure featuring fast current decay and slow inactivation, and at intermediate pressure (C), at which the adaptation and inactivation rates become comparable. Fitting a series of such traces allowed us to extract the tension dependence of the inactivation rate plotted in Fig. 3 E (filled circles). The inactivation rate becomes appreciable at tensions near 5 mN/m and increases with the slope corresponding to the area of 6.1 ± 1.5 (n = 3) nm2. This area can be interpreted as the area from the bottom of the closed-state well to the top of the rate-limiting barrier separating the closed (C) and inactivated (I) states (ΔAC→B).
To find the remaining part of the expansion on the other side of the barrier separating C and I states, we measured the recovery rate from inactivation at different tensions. The protocol combined a long 60-s step driving the entire population into the inactivated state, followed by a drop to a desired subthreshold pressure with a series of test pulses monitoring the return of the population. The latter part of it is shown in Fig. 3 D. The current values at the tips of the test pulse responses were plotted against time and fitted with monoexponential functions. The rates of MscS recovery were then plotted as a function of tension in semi-logarithmic scale (Fig. 3 E, squares). The slope of the decreasing recovery rate consistently indicated ΔAB→I = 2.5 ± 0.1 nm2 (n = 3). In the simplifying assumption of a single rate-limiting barrier separating the closed and inactivated states (because both inactivation and recovery kinetics are close to monoexponential), the two area estimates added together suggest that the total protein in-plane expansion of 8.5 ± 1.6 nm2 is associated with the process of inactivation. This area is smaller than the area change associated with the opening transition (13–15 nm2; Akitake et al., 2005; Belyy et al., 2010b; Kamaraju et al., 2010). The slight deviation from the monoexponential kinetics (Fig. 3 D) can be a result of noise in a population of ∼200 channels. It can also be a consequence of non-uniformity of the population (Chiang et al., 2004) because individual channels may reside in a slightly different environment in the patch.
The larger spatial scale of the C→O transition as compared with C→I makes the open state more stable under high tension where the channels are “trapped” with no tendency to inactivate. On the other hand, from Fig. 3 (D and E) it is clear that tension also strongly stabilizes the inactivated state. Note that these estimations of area changes were made under the assumption that the tension midpoint for MscS γ0.5 = 7.8 mN/cm, as recently measured in whole spheroplast experiments (Belyy et al., 2010b). If we use γ0.5 = 5.5 mN/cm as previously measured for MscS in liposomes (Sukharev, 2002), the area estimates are slightly larger, ΔAC→B = 8.6 ± 2.2 nm2 and ΔAC→B = 3.5 ± 0.2 nm2, totaling 12.1 nm2, which becomes comparable to the expansion area associated with opening.
The gain- and loss-of-function mutants exhibit opposite propensities toward inactivation
Previous data have indicated that 10-s steps of pressure at p0.5 (as determined on ramp test) typically cause full transient activation of ∼90% of MscS population, which adapts and simultaneously inactivates by ∼50% (Akitake et al., 2005; Belyy et al., 2010a). Fig. 4 A shows the response of the soft (gain-of-function) A98S mutant to a series of 10-s pressure steps ending with a 0.5-s saturating test pulse. The test pulse–invoked currents invariably show maximal activity indicative of no inactivation. The stiff (loss-of-function) L111S mutant shows complete inactivation at pressures considerably below its midpoint, but also substantial inactivation just below the activation threshold (see trace 3 in Fig. 4 B). In other words, L111S MscS inactivates silently, bypassing the opening–closing cycle. WT MscS and the two mutants were expressed in PB113 cells carrying native MscL used as an internal “gauge” to calibrate their activation midpoints (p0.5) as described previously (Akitake et al., 2007; Belyy et al., 2010a). The A98S p0.5 was estimated to be 0.75 WT p0.5, and the L111S p0.5 was 1.72 WT p0.5. The top panel in Fig. 4 C shows the three activation curves, and the bottom panel presents the inactivation rate for WT MscS plotted on the same tension scale. Under the assumption that the A98S and L111S mutations affect primarily the threshold and midpoint for activation but not the process of inactivation, the layout of the curves suggests a simple interpretation of the data. The soft A98S mutant opens completely before the inactivation rate becomes appreciable, and the population becomes “locked” in the open state with no ability to inactivate. We found it practically impossible to even estimate the rate of inactivation for this mutant, as inactivation was undetectable in the entire range of tensions. L111S, in contrast, becomes active at tensions where inactivation rate reaches maximal measurable values, and even before that it quickly inactivates without opening. We have attempted determination of the inactivation rates for L111S, but the extremely high threshold for this mutant made the patches prohibitively unstable under saturating pulses.
DISCUSSION
The data presented above show that (a) WT MscS inactivates from the closed (resting) state, whereas opening prevents inactivation; (b) inactivation, as activation, is also driven by tension and is accompanied by ∼8.5-nm2 in-plane protein expansion; and (c) it appears that gain- or loss-of-function mutations that alter the position of the activation curve influence inactivation indirectly, simply by shifting the activation and inactivation curves relative to one another, thus either abolishing inactivation or producing “silent” inactivation without activation.
The experiments presented in Figs. 1 and 2 A illustrate that full opening of the MscS population does not increase the fraction of inactivated channels at the end of the pressure protocol. With the increase of the duration of the saturating step and reciprocal shortening of the subsaturating step in the fixed-length protocol (Fig. 2 B), the degree of inactivation diminishes. Inactivation increases when the channels are given a chance to close and spend more time at moderate tensions. Applying pressure step protocols with interspersed saturating test pulses delivered from a computer-driven pressure clamp machine critically helped us to characterize the processes of adaptation, inactivation, and recovery. Fig. 3 shows that the kinetically intertwined processes of adaptation and inactivation are separable and have opposite tension dependencies. Adaptation, previously called “desensitization” (Akitake et al., 2005), slows down with tension, whereas the inactivation rate increases. Thus, at higher conditioning tensions, when more channels tend to be open, fewer channels are recruited into the inactivation path, but the rate of inactivation increases. Recovery from inactivation, as illustrated in Fig. 3 (D and E), has an opposite tension dependence from the inactivation process, although with a lower slope. In the simplifying assumptions that recovery is inactivation in reverse and the closed or adapted (C and CA) and inactivated (I) states are separated by a single rate-limiting barrier (B), the sum of ΔAC→B and ΔAB→I calculated from the slopes of respective tension dependencies predicts the total expansion of ∼8.5 nm2 accompanying the C→I transition. Therefore, both processes of opening and inactivation originate in the closed or closed-adapted states, with essentially coinciding thresholds (Akitake et al., 2005). However, larger expansion associated with opening (12–15 nm2) and correspondingly steeper dependence on tension sets a higher rate and probability for opening at higher tensions that permits a transient response. The schemes illustrating possible transitions between main functional states in WT MscS are presented in Fig. 5, with the explanation of the sequence of events in the legend. The major feature is the presence of the adapted closed state (CA) in excised patches, from where inactivation occurs. The CA state may be a result of some pre-expansion of the channel complex under asymmetrically distributed tension in the surrounding membrane because of relaxation of the inner leaflet not attached to the pipette (Belyy et al., 2010b).
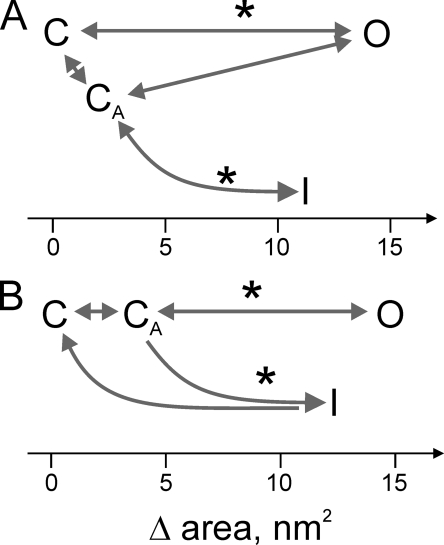
Figure 5.
The possible branching pathways connecting main functional states visited by MscS in excised inside-out patches. (A) The channel undergoes a direct C→O transition, adaptive closure (O→CA) because of midpoint shift, from where the channels inactivate in a tension-dependent manner. Upon tension release, the channels obligatorily go to the CA state first and then recover completely. (B) Under tension, especially gradually imposed, channels first adapt (C→CA) and then open (CA→O). Channels remaining in the CA state (not open) gradually escape to the I state. Further adaptive shift of activation curve will add to the CA population from the O state (O→CA). Because the recovery rate is strongly tension dependent and channels refuse to recover unless tension is very low, it is conceivable that there is more preferential return to the C state as opposed to the CA state. Note that the CA state may not be just a pre-stressed state of the channel by tension, but rather a state of the surrounding membrane with a distorted tension profile (Belyy et al., 2010b). The positions of the state wells on the expansion coordinate are shown by letters (C, CA, O, and I), and the approximate positions of rate-limiting barriers are designated by asterisks. The area change for the opening transition is taken from Belyy et al. (2010b).
The estimated in-plane expansion associated with the C→I transition provides guidance for the modeling of the inactivated state. Our previous studies have shown that the two nonconductive states are likely characterized by different conformations of TM3 helices predicted to be bent either at G121 in the resting state or at G113 (crystallographic kink) in the inactivated state (Akitake et al., 2007). In both conformations, the TM3 bundle is predicted to be relatively narrow, with a tightly closed dehydrated gate. The estimated 8.5-nm2 expansion suggests that it is probably not the TM3s but rather the lipid-facing TM1–TM2 pairs that change their orientation from a compact TM3-aligned position (Anishkin et al., 2008a; Belyy et al., 2010a) to a wider conformation, taking more space in the bilayer. In this wider state, the lipid-facing helices no longer convey force sufficient to separate the closed dehydrated gate (Anishkin and Sukharev, 2004). Our recent study suggests that it is unlikely that the TM1–TM2 pairs assume a wide splayed crystal-like conformation in the inactivated state, as the TM2–TM3 crevices do not seem to be hydrated in any state, yet there must be a mechanism of disengagement of the peripheral lipid-facing helices from the gate. The presence of flexible points in TM1 (Gly41) and TM2 (Gly76) suggests that there might be a bending/twisting motion of the TM1–TM2 pairs that would disjoin the critical F68 (TM2) from L111 and L115 (TM3), thus uncoupling the gate from the stimulus. Our preliminary data already suggest that the G76A mutant lacks inactivation (unpublished data), supporting the idea of TM1–TM2 twisting, which will be a topic of separate publication. The estimated in-plane area increase will constrain the mutual positions of the transmembrane helices and the degree of twisting.
The inactivation path in MscS starting from the closed state may have its own biological meaning. Most of the ion-permeation mechanisms that carry a signaling function, such as Na+- or Ca2+-based action potentials, are strictly transient, and intrinsic inactivation in these channels sets limits for the duration of the spike (Hille, 2001). Inactivation mechanisms are diverse and often involve not only special inactivation gates (Hoshi et al., 1990; Yellen, 1998; Panyi and Deutsch, 2006) but also selectivity filters (Ogielska and Aldrich, 1999; Cordero-Morales et al., 2007; Cuello et al., 2010). Both open-state and closed-state mechanisms of inactivation have been well documented, including the “slippage” mechanism in which the same gate that produces activation becomes uncoupled from the voltage-sensing domains (Shin et al., 2004; Bähring and Covarrubias, 2011). It appears that MscS inactivates through a similar mechanism of gate uncoupling from the peripheral stimulus-receiving domains (Akitake et al., 2005, 2007; Belyy et al., 2010a). Why is it important that MscS inactivates from the closed but not open state? MscS does not seem to be involved in signaling, but acts as a relatively large (∼1-nS) nonselective osmolyte release valve in a rather small bacterial cell with internal volume of only ∼0.04 µm3 (Loferer-Krössbacher et al., 1998). When the cell is subjected to an abrupt osmotic downshock, and the population of MscS channels opens, it takes ∼100 ms for the osmotic equilibration to complete (Boer et al., 2011). If the cell remains in a hypoosmotic medium for an extended period of time, residual tension may persist, and because the activation threshold is not high (4–5 mN/m), MscS would constantly flicker, dissipating vital gradients and preventing recovery. Inactivation thus ensures that under constant nonthreatening tension, MscS is silent and the cell is allowed to function. The mechanism that prevents inactivation from the open state ensures that MscS will not shut as long as tension is close to saturating and the channel will fulfill its protective role. The requirement of closing before inactivation implies that tension must drop to a level below or near the threshold, from where the channel can be safely disengaged. Return of the cell to a normal or hyperosmotic medium would release tension completely and permit fast recovery to the resting “ready-to-fire” state.
Acknowledgments
The authors thank Drs. Ian Booth and Paul Blount for the strains used in this work.
This work was supported by the National Institutes of Health (grant GM075225 to S. Sukharev) and a Howard Hughes Medical Institute undergraduate research fellowship provided through the University of Maryland to V. Belyy.
Christopher Miller served as editor.
Footnotes
Abbreviations used in this paper:
- MscS
- mechanosensitive channel of small conductance
- WT
- wild type
References
- Akitake B., Anishkin A., Sukharev S. 2005. The “dashpot” mechanism of stretch-dependent gating in MscS. J. Gen. Physiol. 125:143–154 10.1085/jgp.200409198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akitake B., Anishkin A., Liu N., Sukharev S. 2007. Straightening and sequential buckling of the pore-lining helices define the gating cycle of MscS. Nat. Struct. Mol. Biol. 14:1141–1149 10.1038/nsmb1341 [DOI] [PubMed] [Google Scholar]
- Aldrich R.W., Stevens C.F. 1983. Inactivation of open and closed sodium channels determined separately. Cold Spring Harb. Symp. Quant. Biol. 48:147–153 [DOI] [PubMed] [Google Scholar]
- Anishkin A., Sukharev S. 2004. Water dynamics and dewetting transitions in the small mechanosensitive channel MscS. Biophys. J. 86:2883–2895 10.1016/S0006-3495(04)74340-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anishkin A., Akitake B., Sukharev S. 2008a. Characterization of the resting MscS: modeling and analysis of the closed bacterial mechanosensitive channel of small conductance. Biophys. J. 94:1252–1266 10.1529/biophysj.107.110171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anishkin A., Kamaraju K., Sukharev S. 2008b. Mechanosensitive channel MscS in the open state: modeling of the transition, explicit simulations, and experimental measurements of conductance. J. Gen. Physiol. 132:67–83 10.1085/jgp.200810000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong C.M. 2006. Na channel inactivation from open and closed states. Proc. Natl. Acad. Sci. USA. 103:17991–17996 10.1073/pnas.0607603103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bähring R., Covarrubias M. 2011. Mechanisms of closed-state inactivation in voltage-gated ion channels. J. Physiol. 589:461–479 10.1113/jphysiol.2010.191965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleza D., Gómez-Lagunas F. 2009. Conserved motifs in mechanosensitive channels MscL and MscS. Eur. Biophys. J. 38:1013–1027 10.1007/s00249-009-0460-y [DOI] [PubMed] [Google Scholar]
- Belyy V., Anishkin A., Kamaraju K., Liu N., Sukharev S. 2010a. The tension-transmitting ‘clutch’ in the mechanosensitive channel MscS. Nat. Struct. Mol. Biol. 17:451–458 10.1038/nsmb.1775 [DOI] [PubMed] [Google Scholar]
- Belyy V., Kamaraju K., Akitake B., Anishkin A., Sukharev S. 2010b. Adaptive behavior of bacterial mechanosensitive channels is coupled to membrane mechanics. J. Gen. Physiol. 135:641–652 10.1085/jgp.200910371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blount P., Sukharev S.I., Moe P.C., Martinac B., Kung C. 1999. Mechanosensitive channels of bacteria. Methods Enzymol. 294:458–482 10.1016/S0076-6879(99)94027-2 [DOI] [PubMed] [Google Scholar]
- Boer M.S., Anishkin A., Sukharev S. 2011. Adaptive MscS gating in the osmotic permeability response in E. coli: the question of time. Biochemistry. 50:4087–4096 10.1021/bi1019435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang C.S., Anishkin A., Sukharev S. 2004. Gating of the large mechanosensitive channel in situ: estimation of the spatial scale of the transition from channel population responses. Biophys. J. 86:2846–2861 10.1016/S0006-3495(04)74337-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero-Morales J.F., Jogini V., Lewis A., Vásquez V., Cortes D.M., Roux B., Perozo E. 2007. Molecular driving forces determining potassium channel slow inactivation. Nat. Struct. Mol. Biol. 14:1062–1069 10.1038/nsmb1309 [DOI] [PubMed] [Google Scholar]
- Cuello L.G., Jogini V., Cortes D.M., Pan A.C., Gagnon D.G., Dalmas O., Cordero-Morales J.F., Chakrapani S., Roux B., Perozo E. 2010. Structural basis for the coupling between activation and inactivation gates in K(+) channels. Nature. 466:272–275 10.1038/nature09136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. 2001. Ionic Channels of Excitable Membranes. Third edition. Sinauer Asssociates, Inc., Sunderland, MA: 814 pp [Google Scholar]
- Hoshi T., Zagotta W.N., Aldrich R.W. 1990. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 250:533–538 10.1126/science.2122519 [DOI] [PubMed] [Google Scholar]
- Houston P.L. 2001. Chemical Kinetics and Reaction Dynamics. Dover, Mineola, NY: 352 pp [Google Scholar]
- Kamaraju K., Sukharev S. 2008. The membrane lateral pressure-perturbing capacity of parabens and their effects on the mechanosensitive channel directly correlate with hydrophobicity. Biochemistry. 47:10540–10550 10.1021/bi801092g [DOI] [PubMed] [Google Scholar]
- Kamaraju K., Gottlieb P.A., Sachs F., Sukharev S. 2010. Effects of GsMTx4 on bacterial mechanosensitive channels in inside-out patches from giant spheroplasts. Biophys. J. 99:2870–2878 10.1016/j.bpj.2010.09.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koprowski P., Kubalski A. 1998. Voltage-independent adaptation of mechanosensitive channels in Escherichia coli protoplasts. J. Membr. Biol. 164:253–262 10.1007/s002329900410 [DOI] [PubMed] [Google Scholar]
- Levina N., Tötemeyer S., Stokes N.R., Louis P., Jones M.A., Booth I.R. 1999. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: identification of genes required for MscS activity. EMBO J. 18:1730–1737 10.1093/emboj/18.7.1730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Moe P.C., Chandrasekaran S., Booth I.R., Blount P. 2002. Ionic regulation of MscK, a mechanosensitive channel from Escherichia coli. EMBO J. 21:5323–5330 10.1093/emboj/cdf537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loferer-Krössbacher M., Klima J., Psenner R. 1998. Determination of bacterial cell dry mass by transmission electron microscopy and densitometric image analysis. Appl. Environ. Microbiol. 64:688–694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moe P., Blount P. 2005. Assessment of potential stimuli for mechano-dependent gating of MscL: effects of pressure, tension, and lipid headgroups. Biochemistry. 44:12239–12244 10.1021/bi0509649 [DOI] [PubMed] [Google Scholar]
- Ogielska E.M., Aldrich R.W. 1999. Functional consequences of a decreased potassium affinity in a potassium channel pore. Ion interactions and C-type inactivation. J. Gen. Physiol. 113:347–358 10.1085/jgp.113.2.347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada K., Moe P.C., Blount P. 2002. Functional design of bacterial mechanosensitive channels. Comparisons and contrasts illuminated by random mutagenesis. J. Biol. Chem. 277:27682–27688 10.1074/jbc.M202497200 [DOI] [PubMed] [Google Scholar]
- Panyi G., Deutsch C. 2006. Cross talk between activation and slow inactivation gates of Shaker potassium channels. J. Gen. Physiol. 128:547–559 10.1085/jgp.200609644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak J. 1991. Molecular kinetics of voltage-dependent Na+ channels. Physiol. Rev. 71:1047–1080 [DOI] [PubMed] [Google Scholar]
- Pivetti C.D., Yen M.R., Miller S., Busch W., Tseng Y.H., Booth I.R., Saier M.H., Jr 2003. Two families of mechanosensitive channel proteins. Microbiol. Mol. Biol. Rev. 67:66–85 10.1128/MMBR.67.1.66-85.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumann U., Edwards M.D., Rasmussen T., Bartlett W., van West P., Booth I.R. 2010. YbdG in Escherichia coli is a threshold-setting mechanosensitive channel with MscM activity. Proc. Natl. Acad. Sci. USA. 107:12664–12669 10.1073/pnas.1001405107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin K.S., Maertens C., Proenza C., Rothberg B.S., Yellen G. 2004. Inactivation in HCN channels results from reclosure of the activation gate: desensitization to voltage. Neuron. 41:737–744 10.1016/S0896-6273(04)00083-2 [DOI] [PubMed] [Google Scholar]
- Steinbacher S., Bass R., Strop P., Rees D.C. 2007. Structures of the prokaryotic mechanosensitive channels MscL and MscS. Current Topics in Mechanosensitive Ion Channels, Part A. 58:1–24 10.1016/S1063-5823(06)58001-9 [DOI] [Google Scholar]
- Sukharev S. 2002. Purification of the small mechanosensitive channel of Escherichia coli (MscS): the subunit structure, conduction, and gating characteristics in liposomes. Biophys. J. 83:290–298 10.1016/S0006-3495(02)75169-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukharev S.I., Sigurdson W.J., Kung C., Sachs F. 1999. Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel, MscL. J. Gen. Physiol. 113:525–540 10.1085/jgp.113.4.525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vásquez V., Perozo E. 2004. Voltage dependent gating in MscS. Biophys. J. 86:545A [Google Scholar]
- Vásquez V., Sotomayor M., Cordero-Morales J., Schulten K., Perozo E. 2008a. A structural mechanism for MscS gating in lipid bilayers. Science. 321:1210–1214 10.1126/science.1159674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vásquez V., Sotomayor M., Cortes D.M., Roux B., Schulten K., Perozo E. 2008b. Three-dimensional architecture of membrane-embedded MscS in the closed conformation. J. Mol. Biol. 378:55–70 10.1016/j.jmb.2007.10.086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., Black S.S., Edwards M.D., Miller S., Morrison E.L., Bartlett W., Dong C., Naismith J.H., Booth I.R. 2008. The structure of an open form of an E. coli mechanosensitive channel at 3.45 A resolution. Science. 321:1179–1183 10.1126/science.1159262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen G. 1998. The moving parts of voltage-gated ion channels. Q. Rev. Biophys. 31:239–295 10.1017/S0033583598003448 [DOI] [PubMed] [Google Scholar]