Energy scaling of mode-locked fiber lasers with chirally-coupled core fiber

Abstract

We report a mode-locked dissipative soliton laser based on large-mode-area chirally-coupled-core Yb-doped fiber. This demonstrates scaling of a fiber oscillator to large mode area in a format that directly holds the lowest-order mode and that is also compatible with standard fiber integration. With an all-normal-dispersion cavity design, chirped pulse energies above 40 nJ are obtained with dechirped durations below 200 fs. Using a shorter fiber, dechirped durations close to 100 fs are achieved at pump-limited energies. The achievement of correct energy scaling is evidence of single-transverse-mode operation, which is confirmed by beam-quality and spectral-interference measurements.

1. Introduction

Ultrafast science has long been dominated by solid-state sources, mainly Ti:sapphire lasers [1]. Despite their high energy and tunability, these lasers are limited by the power available from high beam quality visible laser pumps. Rare-earth doped fiber lasers offer the potential for integrated air-cooled sources driven by low cost diode pumps. Thanks to advances in understanding of nonlinear pulse evolution, as well as developments in large mode-area fiber technology, fiber lasers are emerging as competitive sources of ultrashort light pulses.

The performance of modelocked fiber lasers is mainly limited by nonlinear phase accumulation. Net-normal dispersion cavities provide the highest pulse energies by enabling chirped-pulse evolutions such as in the self-similar [2] and the all-normal dispersion (ANDi) lasers [3]. In particular, the ANDi laser uses spectral filtering of a chirped pulse to achieve dispersion-compensation-free self-consistent pulse shaping. This flexible pulse shaping mechanism supports a wide variety of spectral shapes [4], and is well-modeled by dissipative solitons of the cubic-quintic Ginzburg Landau equation (CQGLE) [5].

A larger effective mode area scales the peak power supported by a given pulse evolution at constant nonlinear phase shift [6]. So far, the most successful technology for scaling to large single mode cores has been photonic crystal fibers (PCF) and rods [7]. Oscillators that reach the megawatt peak powers have been reported based on this approach [8, 9]. Despite their impressive performance, lasers based on PCF have found little practical application; integration into fiber devices is hindered by incompatibility with fusion splicing and sensitivity to bend loss. Large mode-area step-index fibers offer superior integration potential. Amplifiers based on multimode fiber have been demonstrated with close to single-mode beam quality. This is achieved using fundamental-mode excitation and higher-order mode (HOM) suppression, usually through selective bend loss [10]. There is a brief and isolated report of a modelocked soliton laser based on multimode fiber [11]. A recent systematic investigation of modelocking under multimode conditions finds that conventional step-index fibers cannot suppress HOMs sufficiently to allow stable modelocking at high single-pulse energies [12]. Small amounts of energy in HOMs cause multi-pulsing at energies well below those expected from mode-area scaling. There is thus a need for a distributed transverse mode filtering mechanism that is robust enough for an application as sensitive as ultrafast modelocking, yet retains the integration potential of all-glass fibers. Leaky waveguides that selectively couple out HOMs while maintaining low losses on the fundamental mode provide such a mechanism. Examples include leakage channel fibers [13], as well as Bragg fiber for which a mode-locked oscillator was recently demonstrated [14]. Another implementation of selective leakage is chirally-coupled core (CCC) fiber, which use a secondary core wound around a large central core to create a distributed and integrated HOM filtering mechanism [15]. Using no external mode-filtering or mode-matching methods, CCC fiber systems have shown effectively single-mode performance. Although a continuous-wave (CW) laser based on Yb-doped CCC fiber has been demonstrated [16], an application as sensitive as ultrafast modelocked lasers has yet to be investigated.

In this work, we present a dissipative soliton laser based on Yb-doped large mode-area CCC fiber. This is the first mode-locked laser to use CCC fiber, and demonstrates its ability to scale the pulse energy of ultrafast fiber lasers in a solid glass package with low bend sensitivity and compatibility with fiber fusion technology. The performance matches simulations of dissipative soliton pulse evolution, as well as pulse energies expected from scaling of single-mode ANDi fiber lasers. Beam quality, spectral interference and a high single-pulsing limit demonstrate effectively single-mode operation. The oscillator provides chirped pulses of energies greater than 40 nJ, which dechirp to below 200 fs. With a shorter fiber, pulse durations close to 100 fs are achieved at chirped pulse energies of 22 nJ, limited by the available pump power.

2. Design and numerical simulations

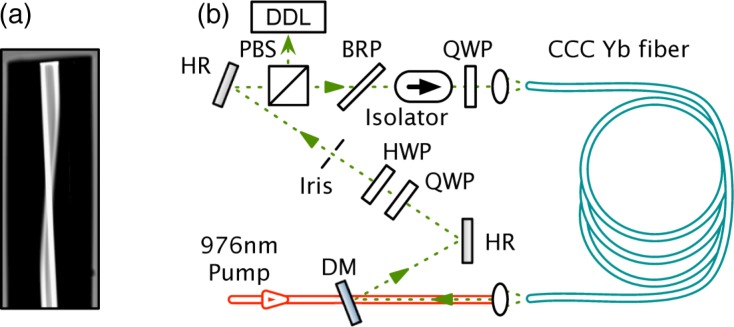
The central component of the oscillator is an Yb-doped CCC fiber. It has a core diameter of 33.5 μm and a numerical aperture (NA) of 0.06, which yields an effective area of ∼ 350 μm² and a V = 6.1. This core nominally supports six modes. To suppress these HOMs, a secondary leaky side core is wrapped in a helix in optical proximity around the main core, as can be seen in Fig. 1(a). Central modes can be coupled into the secondary core selectively through quasi-phase-matched interactions that involve the optical angular momentum of each mode in this helically symmetric structure. By properly choosing the diameter and the NA of the secondary core as well as the helix properties, the HOMs with azimuthal numbers l ≥ 1 can be coupled out while keeping the l = 0 fundamental mode off-resonance [15].

Fig. 1.

(a) Side view of angle-cleaved CCC fiber. (b) CCC fiber oscillator design: DM, dichroic mirror; PBS, polarizing beamsplitter; DDL, dispersive delay line; BRP, birefringent plate; QWP and HWP, quarter- and half-waveplate; HR, dielectric mirror.

We built a ring laser based on the ANDi design, as shown in Fig. 1(b). The cladding of the fiber has a diameter of 250 μm, and a low-index coating provides a cladding NA of 0.46. The absorption at wavelengths around 975 nm is 5 dB/m. We used 3.9 m of Yb CCC fiber to obtain efficient pump absorption. The fiber was loosely coiled with a 30-cm diameter to avoid bend loss and external HOM filtering. The light from a fiber-coupled diode bar that provides up to 35 W at 976 nm is coupled through a dichroic mirror into the cladding of the fiber. An isolator ensures unidirectional operation. The nonlinear polarization evolution (NPE) in the fiber is converted into amplitude modulation by three wave plates and a polarizing beamsplitter. This NPE port also functions as a variable output coupler. A quartz plate placed in front of the input polarizer of the isolator creates a birefringent spectral filter. An iris placed before the output coupler filters out residual cladding light. An external grating compressor compensates the chirp of the output pulses. The present cavity uses free-space coupling of pump and signal given the novel nature of CCC fiber. However, the solid glass nature of such fibers is compatible with the development of fused components such as pump/signal combiners.

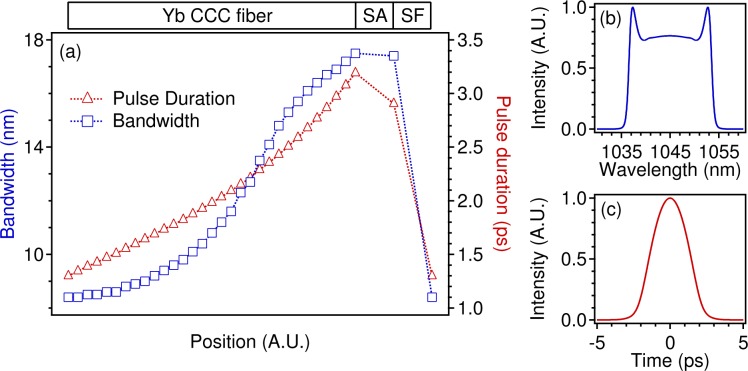
To verify that the cavity supports dissipative solitons, we performed split-step Fourier simulations of the non-linear Schrödinger equation, as in [4]. The group-velocity dispersion is β₂ = 23 ps²/km and the Kerr non-linearity is γ = 0.40 (W km)⁻¹. The small signal gain is ∼ 30 dB and we use a saturation energy E_sat = 38 nJ. An output coupling of 0.92 is followed by an instantaneous saturable absorber and an 80% linear loss. A stable solution starting from white noise and using a filter bandwidth of 8 nm is shown in Fig. 2. The chirped pulse duration and spectral bandwidth increase in the CCC fiber, and the spectral filter shapes the chirped pulse to self-consistency with large temporal and spectral breathing. The solution taken after the saturable absorber has a pulse energy of 40 nJ and a transform-limited duration of 170 fs.

Fig. 2.

(a) Simulated pulse evolution: SA, saturable absorber; SF, spectral filter. Output pulse (b) spectrum and (c) chirped time profile.

3. Experiments

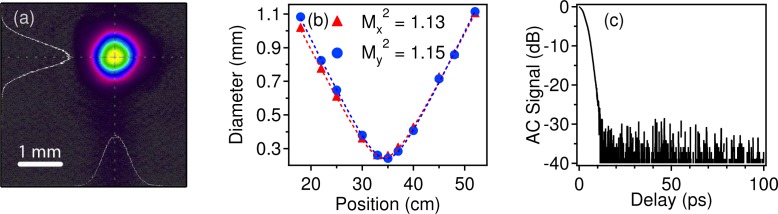
Experimentally, a variety of self-starting mode-locked states are obtained by adjusting the wave plates. The laser outputs a stable pulse train at 53 MHz, which was monitored using a sampling oscilloscope with 30-ps resolution, and single-pulsing was checked with an autocorrelator with up to 60-ps delay. Beam quality measurements are shown in Fig. 3. The beam profile is gaussian. In both CW and mode-locked operation at 2.5 W and 1.9 W output power respectively, we measured M² ∼ 1.10 – 1.15, consistent with M² ≤ 1.1 we measured from single-mode sources. A similar oscillator using fibers with 20 μm core diameter and 0.07 NA yielded M² ∼ 1.3 – 1.7 [12]. Combined with the absence of any secondary pulse on the long-range autocorrelation (AC) in Fig. 3(c), this confirms robust filtering of the higher-order modes by the CCC fiber.

Fig. 3.

Mode-locked beam characteristics around 2 W output power: (a) beam profile, (b) M² measurement and (c) long-range AC.

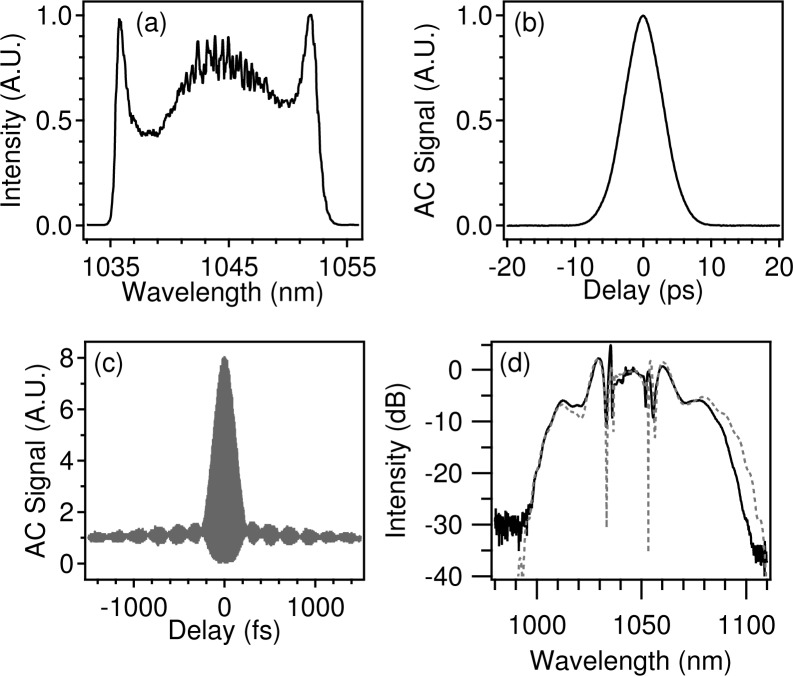
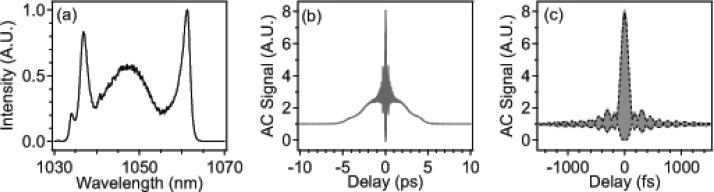
Data from a representative mode-locked state using an 8-nm filter are presented in Fig. 4. This state is sustained over hours, and equivalent states have been reproduced over several weeks. With about 15 W of coupled pump power, the average output power is 2.3 W, which corresponds to a chirped pulse energy of 43 nJ, in agreement with simulations. The dechirped pulse duration is 195 fs. This is within 10% of the transform-limited pulse duration inferred from the zero-phase Fourier transform of the power spectrum. Our compressor yields 28 nJ of dechirped energy, corresponding to more than 125 kW of peak power. Stable pulse energies of up to 47 nJ were obtained, but the pulses had larger wings, extending out to ∼ 1 ps from the peak. Increasing the pump power further results in a multipulsing instability. The spectrum displays modulations that we attribute to spectral interference with a small amount of HOM content. From the amplitude of the spectral modulation, we infer that the HOMs carry on the order of 0.1% of the energy, consistent with the absence of any secondary pulse on the long-range AC as previously shown. No measurable increase in secondary mode content is thus obsverved over the operating range of the laser.

Fig. 4.

Experimental mode-locked pulse from 3.9 m cavity at 2.3 W output power: (a) spectrum (0.1 nm res.), (b) chirped AC, (c) dechirped interferometric AC. (d) Spectrum after propagation trough 1 m of SMF (solid) compared to simulation (dashed).

To verify the peak power, we launched 2-nJ dechirped pulses into 1 m of single-mode fiber (SMF) with a 5 μm core diameter and NA of 0.14. The self-phase modulation (SPM)-induced spectral broadening is shown in Fig. 4(d). We compare the spectrum with a split-step simulation starting from a simulated pulse as in Fig. 2. The calculation accounts for dispersion up to the third order, SPM, intrapulse Raman scattering and small under-compensation of chirp from the grating compressor. The simulation reproduces the complex spectrum of the measured pulse quite accurately, which confirms that the energy is indeed located in the main pulse.

Although the current results do not set new performance records for fiber lasers, we can verify that the performance of CCC fiber scales correctly with mode area. We make a controlled comparison between this laser and an SMF-based ANDi laser with similar cavity dispersion, spectral filtering and output bandwidth. With an effective area of ∼ 30 μm², such a cavity reaches pulse energies of 4 – 5 nJ as shown in Fig.12–13 of [4]. This scales by a factor of ∼ 10 from the CCC results as expected, demonstrating sufficient higher-order mode suppression for high energy mode-locking [12]. With the correct pulse energy scaling demonstrated, the general trends of ANDi lasers should apply. There are indications that such lasers can be optimized for short pulses or high energy using lower or higher net dispersion respectively [17, 18]. As a preliminary example, results from a cavity using 1.8 m of CCC gain fiber and a 15-nm spectral filter are shown in Fig. 5. The pulse dechirps to 105-fs duration, very close to the transform limit. The chirped pulse energy is pump-limited to 22 nJ at 88-MHz repetition rate.

Fig. 5.

Experimental pulse from 1.8 m cavity: (a) spectrum, (b) chirped and (c) dechirped interferometric AC (solid grey) compared to calculated transform limited AC (dashed).

4. Conclusion

To summarize, we have demonstrated the energy scaling of modelocked fiber lasers by use of a chirally-coupled core fiber. The performance of a dissipative-soliton laser agree well with simulations that assume single-mode propagation, and scales correctly with mode area from equivalent SMF lasers. Self-starting pulse trains are obtained, with chirped pulse energies above 40 nJ and dechirped durations below 200 fs. A lower-dispersion cavity yields pulses as short as 100 fs, as expected from previous results. Although the current design uses free-space optics for pump and signal coupling, the solid glass design of CCC fiber is compatible with integration into monolithic fused fiber components. Development of pump combiners and pigtailed isolators is underway. Having demonstrated sufficient higher-order mode suppression and effective core size scaling for an application as exacting as femtosecond mode-locked oscillators, we anticipate that CCC fiber can enable robust, integrated and high power ultrafast sources.