Abstract
The present work evaluates the use of species distribution model (SDM) algorithms to classify high density of small container Aedes mosquitoes at a fine scale, in the Bermuda islands. Weekly ovitrap data collected by the Health Department of Bermuda (UK) for the years 2006 and 2007 were used for the models. The models evaluated included the following algorithms: Bioclim, Domain, GARP, logistic regression, and MaxEnt. Models were evaluated according to performance and robustness. The area Receiver Operating Characteristic (ROC) curve was used to evaluate each model’s performance, and robustness was assessed considering the spatial correlation between classification risks for the two datasets. Relative to the other algorithms, logistic regression was the best model for classifying high risk areas, and the maximum entropy approach (MaxEnt) presented the second best performance. We report the importance of covariables for these two models, and discuss the utility of SDMs for vector control efforts and the potential for the development of scripts that automate the task of creating risk assessment maps.
Keywords: Aedes, species distribution models, SDM, risk prediction, Bermuda Islands
Introduction
Considering that Aedes mosquitoes (Diptera: Culicidae) are important vectors of human arboviruses (e.g., Beaty & Aitken, 1979; Dohm et al., 1995; Mitchell, 1995), the accurate detection and determination, at multiple scales, of areas that are prone to breed high mosquito densities is critical to develop control and mitigation strategies. Public health officers in many countries conduct surveys and sampling programs that allow them to direct their resources efficiently to protect the public. Different types of traps and collection devices, designed to collect mosquitoes at different life stages, provide information regarding species presence and densities. Additional methods that detect the presence of specific human pathogens in mosquito populations (such as PRC based technologies, e.g., Porter et al., 1993; Hadfield et al., 2001; Shi et al., 2001) could be combined to provide critical public health information.
Ovitrap sampling allows the collection of eggs from small container breeding mosquitoes and has been commonly used to monitor Aedes (e.g., Evans & Bevier, 1969; Lee, 1992; Dhang et al., 2005; Morato et al., 2005, Kaplan et al., 2010). Data obtained with this sampling scheme are often used as proxy estimators of presence, activity, or size of mosquito populations in the trap’s vicinity. This methodological approach allows the collection of large amounts of data with relatively low efforts. However, several sources of error can remain, including inhibition of oviposition in presence of chemical clues in the water, habitat selection (including attraction to preferable habitats near the trap), or multiple ovitrap oviposition events. The data obtained with ovitraps, as with any other sampling procedure, are subject to stochastic variation and could make the production of a comprehensive risk assessment map a challenge.
Several different Species Distribution Models (SDMs) are commonly used to produce coarse scale risk prediction maps (i.e., considering continental, national, and state or provincial scales), and an extensive list of examples can be found in the literature. For example, Benedict et al. (2007) used an ecological modeling algorithm (GARP, see below) to predict worldwide Aedes albopictus risk, while Foley et al. (2010) used two different algorithms to predict the distribution of Anopheles spp. in the Republic of Korea. SDMs use presence, presence/absence, or quantitative data for the species of interest to produce predictions based on a combination of geographically referenced climatic, biological, demographic, and/or physical data. Similar procedures are seldom used to produce comparable predictions at a very fine scale (i.e., considering pixel sizes smaller than 100m), and small study areas (i.e., considering areas smaller than 100km2), perhaps due to scarce availability of environmental variables at those fine scales, their small variability over short distances, and the absence of species information at a very fine scale that could successfully account for microhabitat variation.
Two of the most commonly used presence only data algorithms, MaxEnt (Maximum Entropy, Phillip et al., 2004) and GARP (Genetic Algorithm for Rule-set Prediction, Stockwell & Peters, 1999), have often shown accurate prediction capabilities in simulations and evaluations, outperforming classical modeling approaches, such as Domain, Bioclim, and logistic regression (see Phillip et al., 2004; Hijmans & Graham, 2006; Phillip & Dudík, 2008; but also see Stockman et al., 2006). These algorithms differ in their rationales and procedures. Briefly, MaxEnt finds the maximum entropy probability distribution that agrees with the provided presence data based on environmental data; a large literature describes in detail the underlying MaxEnt algorithms and rationale (e.g., Phillip et al., 2004; Phillip et al., 2006). In contrast, GARP includes multiple, non-deterministic iterative procedures that incorporate various model distribution methods such as logistic regression and range envelopes, producing with each run predicted binary maps of presences and absences. Multiple optimal models are produced for each data set, which can be converted into presence likelihoods. The three additional algorithms mentioned above, Domain (multivariate distance metric algorithm), Bioclim (envelop algorithm), and logistic regression (considering both presences and absences) are less complex than the former two, and often perform poorly in simulations (e.g., Phillip et al., 2004; Wisz et al., 2008). Different algorithms produce different outputs, but in general convey presence probabilities, or some arbitrary value that could be interpreted in similar fashion.
The Bermuda Islands (UK), an archipelago located in the Atlantic Ocean off the east coast of the USA (32° 14′ – 32° 24′ N, 64° 39′ – 64° 53′ W), have a subtropical climate, with mild winters and hot, humid summers which provides suitable conditions for Aedes mosquitoes. Historically, these mosquitoes were responsible of extensive outbreaks of yellow and dengue fever. No vector borne diseases have been recently reported, despite the presence of Aedes mosquitoes in the area. However, the Health Department of Bermuda maintains an aggressive mosquito monitoring and control program to prevent potential health risks found in comparable places and to reduce the biting nuisance that may affect the local economy.
In this study, we aim to assess the performance of commonly used species distribution model algorithms (SDMs) to classify areas prone to breed high densities of small container breeding mosquitoes. Specifically, we aim initially to evaluate the performance of Bioclim, Domain, GARP, logistic regression, and MaxEnt algorithms at a very fine scale in the Bermuda Islands. Subsequently, we aim to identify environmental covariates that contribute to high mosquito prevalence at this fine scale.
Material and methods
The small size of the Bermuda islands (< 54km2) makes the application of species distribution models for the generation of risk maps a challenging task, as typical bioclimatic variables cannot be used due to the lack of spatial variability in that region. On the other hand, the region seems suitable for the empirical determination of infestation risk, considering: a) the presence of an extensive weekly ovitrap program (see Kaplan, 2006, for a comprehensive description of the sampling program); b) the almost exclusive presence of a single small container breeding mosquito species, Aedes albopictus (Skuse), with marginal and occasional presence of Aedes aegypti (L.), see Kaplan et al. (2010); and c) the availability of two consecutive years of mosquito records in which the population appears to remain constant (see below), allowing the comparisons of areas’ classifications between datasets as a measure of the algorithms’ robustness.
Selection of environmental data layers was based on availability and a priori expectation of influences in the mosquito population. Distance to buildings, distance to roads, and human population density were selected as proxies of human influence on the mosquito population, considering that human activities provide both breeding habitats (artificial containers and other breeding grounds) and dispersal opportunities (movement of containers colonized by eggs or larvae). Elevation and slope were selected in consideration of their influence on water accumulation. Slope was also presumed to influence access of cleaning crews to steep areas. Distance to shore was selected to consider sea water effects, such as salt spray, or wind exposure. Aspect was selected to consider effects of solar irradiation, wind incidence, and its potential effect on egg desiccation. Some variables that are commonly used with SDMs, including primary productivity, temperature, precipitation, or moisture were not used in our study. There is low variation in these variables due to the small size of the islands (see above).
The same ovitrap data and environmental variables were used in all models (elevation, slope, aspect, distance to buildings, distance to shore, distance to roads, human population). The Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) with a spatial resolution of 90m was used for elevation data; the DEM was resampled based on a bilinear interpolation in order to match the 45m resolution of the remaining layers. Slope and aspect layers were derived from the DEM. Aspect was rescaled to an index of southwestness, using the function cos(aspect degrees-225°) (Franklin et al., 2000), where values range from 1 (representing southwest) to −1 (representing northeast). This measure was considered appropriate considering the islands’ general orientation along a southwest to northeast axis. Layers representing distance to buildings, distance to roads, and distance to shore, as well as human population following public vote registration records, were also included as variables. All GIS processing to obtain the above mentioned layers was performed using IDRISI v16.05 “Taiga Edition” (Eastman, 2010).
Weekly presence data for 292 ovitraps from 2006 and 2007 were used in all models. The prevalence values (frequency of positive ovitraps; 2006: 0.12 ± 0.02SE, 2007: 0.11 ± 0.02SE) of Aedes eggs for these years appeared stable and were found not significantly different by Kaplan et al. (2010). In order to classify ovitraps as high density, we selected those that presented values higher than the mean (i.e., disturbance criterion). Ovitraps were scored as positive (presence data point for the SDMs) for high mosquito density if eggs were detected in six or more weeks throughout each year, which represents values higher than the mean for both datasets (mean number of positive weeks, 2006: 5.89 ± 0.03SE, 2007: 5.79 ± 0.03SE). Ovitraps with lower values were considered negative and included as absences for logistic regression and ROC calculations (see below).
The 292 ovitraps used in this study were deployed by the Bermuda Ministry of Health. In order to perform statistical comparisons and validations, data were partitioned into a training set consisting of 75% of the observations (used to developed the prediction models) and testing sets consisting of 25% of the data (used to evaluate the accuracy of the results). The process was performed in DIVA-GIS v.5.2.0.2 (Hijmans et al., 2001) with 30 repetitions in order to obtain 30 training-testing subsamples for each dataset. Each modeling algorithm was run independently with each of the 30 subsamples. The algorithms used were Bioclim (Nix & Busby, 1986), as implemented in GIS-DIVA, Domain, as implemented in GIS-DIVA, GARP v.1.1.6 (Stockwell & Peters, 1999), logistic regression, as implemented in IDRISI v.16.05 module LOGREG (Eastman, 2010), and MaxEnt v.3.3.1 (Phillip et al., 2004).
MaxEnt was run using linear, quadratic, product, threshold, and hinge features, with output set to logistic (see Phillip & Dudik, 2008). GARP was run with optimization parameters set to 100 runs with a convergence limit of 0.005 and a maximum of 1000 iterations. All four rule types (atomic, range, negated range, and logistic regression) were used. The best subset option was enabled to select the 10 best models (omission threshold = 20%, commission threshold = 50 % and 20 total models under hard omission threshold). The 10 best models were imported into IDRISI v.16.05 and converted into probabilities. Bioclim and Domain were run using the default 0.025 percentile cut-off level. The logistic regression algorithm also requires absence values (i.e., negative presence points) and those were included in its input file.
Considering that many algorithms produce dimensionally different output, the outputs from each run were rescaled to values from 0 to 1 by dividing each pixel by the maximum pixel value. The performance of each model predicting yearly presences was evaluated using the area under the Receiver Operating Characteristic (ROC) curve, using the online tool JLABROC4 (Eng, n.d.; http://www.jrocfit.org). The Area Under the ROC Curve (AUC) can range from 0 to 1, where a value of 1 indicates perfect model agreement, a value of 0.5 indicates agreement equal to chance, and 0 indicates complete disagreement. Differences among AUC values obtained for each subsample with each algorithm were tested by ANOVA, and a subsequent Tukey-Kramer HSD procedure was used to assess pairwise differences. The AUC values obtained for the 2007 dataset failed a normality goodness of fit test (Shapiro-Wilk W=0.98, p<0.05) and were transformed (y’=−1/y) to achieve normality. In order to check algorithms’ robustness, a spatial correlation for each subsample between the classification prediction for 2006 and 2007 for each algorithm was performed using IDRISI (REGRESS module). The obtained statistic failed the normality goodness of fit test (Shapiro-Wilk W=0.88, p<0.05) and no satisfactory transformation for normality was found. For pairwise comparisons, bootstrap procedures were used to produce 95% confidence intervals after 10,000 replicates using S-plus v.8.0.4 (Insightful Corp, 2007). Non-overlapping confidence intervals were considered statistically different. Unless stated otherwise, statistical analyses were performed using JMP v.7.0 (SAS Institute, 2007).
To obtain classification risk maps, we used the complete dataset for both years and used the AUC values as goodness-of-fit indicators for the two models that performed better using the AUC criterion as described above. We compare the overall performance of the algorithms based on classification risk maps and AUCs.
Results
Model performance
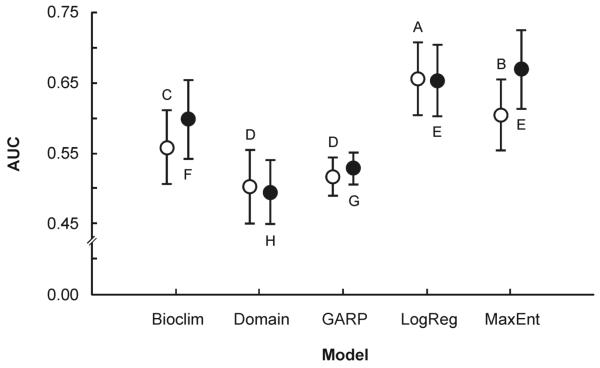
The five models performed differently with both datasets based on the 30 subsamples (ANOVA for the 2006 dataset, F149=49.9, p<0.001; for the 2007 dataset, F149=75.5, p<0.001). Considering the overall performance of the algorithms in each dataset, two models surpass the rest, logistic regression and MaxEnt. For the 2006 dataset, logistic regression performed best, followed by MaxEnt. For the 2007 dataset, both logistic regression and MaxEnt performed better than any other model. For both datasets, Bioclim presented an intermediate performance, while GARP and Domain presented consistently low performances. Fig. 1 shows the overall performance and pairwise statistical differences for all models for both datasets. Examination of the best performance among the 30 subsamples for each algorithm presented a similar pattern: logistic regression and MaxEnt ranked among the highest AUC values. Table 1 summarizes performance of each model.
Fig. 1.
Performance (AUC) of the five algorithms evaluated (MaxEnt, logistic regression, GARP, Domain, and Bioclim) with the two different datasets based on the 30 training-testing subsamples. Circles indicate mean values and error bars one standard deviation. Open markers represent 2006 and filled ones 2007 values. Markers not connected by same letter are significantly different (Tukey-Kramer HSD test, α=0.05).
Table 1.
Algorithm performance with the 30 training-testing subsamples for the two datasets, based on AUC (Area Under the ROC Curve). AUC value of 1 indicates a perfect model agreement, a value of 0.5 indicates agreement equal to chance, and 0 indicates complete disagreement
| Mean AUC | Median AUC | Best model AUC | ||||
|---|---|---|---|---|---|---|
| Model | 2006 | 2007 | 2006 | 2007 | 2006 | 2007 |
| Bioclim | 0.56 | 0.60 | 0.57 | 0.60 | 0.68 | 0.69 |
| Domain | 0.50 | 0.49 | 0.51 | 0.49 | 0.58 | 0.58 |
| GARP | 0.52 | 0.53 | 0.53 | 0.53 | 0.56 | 0.60 |
| Logistic Regression | 0.66 | 0.65 | 0.76 | 0.65 | 0.81 | 0.75 |
| MaxEnt | 0.61 | 0.67 | 0.76 | 0.68 | 0.75 | 0.76 |
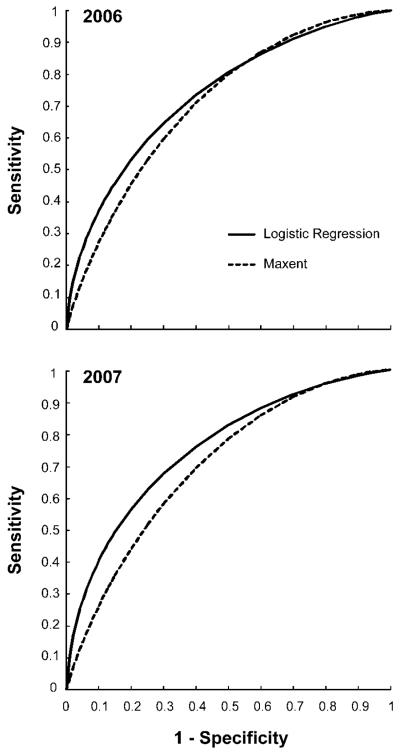
Using both complete datasets, the goodness-of-fit for each of the two best models, logistic regression and MaxEnt, indicated acceptable performances for each dataset (Fig. 2).
Fig. 2.
Goodness-of-fit of the two best performing models using the complete dataset for year 2006 and 2007: logistic regression (AUC 2006 = 0.71; 2007 = 0.70) and MaxEnt (AUC 2006 = 0.74; 2007 = 0.76).
Model robustness
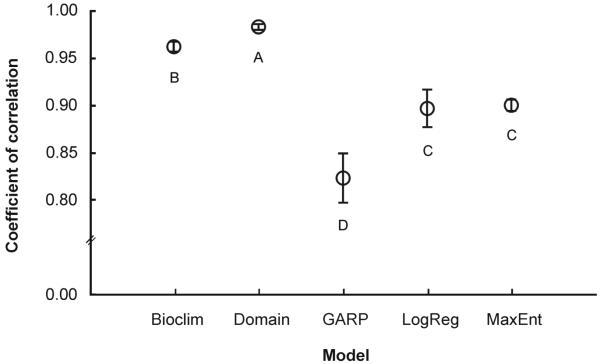
The algorithms showed high robustness (all algorithms presented mean coefficients of correlation above 82%), which is consistent with high spatial correlation between the predicted risk for the two consecutive years. Bioclim and Domain presented the highest agreement between risk classifications across the years, with values of coefficient of regression between the two datasets above 0.96. Interestingly, the two algorithms that performed better according to the AUC criterion, MaxEnt and the logistic regression approach, showed lower robustness values than Bioclim and Domain, being GARP the model with the lowest robustness across dates (Fig. 3). This suggests that the predicted risk surfaces produced with these algorithms were slightly different for each yearly dataset.
Fig. 3.
Coefficients of correlation between the risk classifications of the five algorithms evaluated (MaxEnt, logistic regression, GARP, Domain, and Bioclim) with the two different datasets based on the 30 training-testing subsamples. Circles indicate mean values and bars the 95% bootstrap confidence intervals for 10,000 replicates. Symbols marked by same letter indicate overlapping confidence intervals.
Variables importance
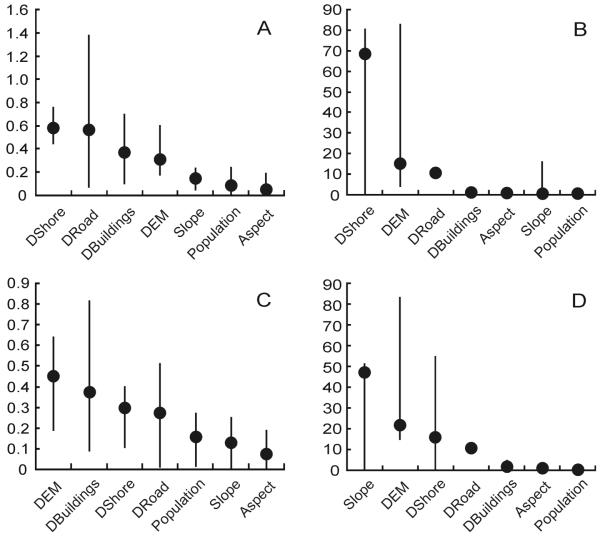
For the logistic regression algorithm, four variables stand as the most important for both datasets: distance to shore, distance to roads, distance to buildings, and elevation. However, these predictions have wide ranges across the different subsamples (Fig. 4A, C). For MaxEnt, the identification of variables’ importance is more difficult. For the 2006 dataset, distance to shore is the variable that contributes the most to the model (Fig. 4B), while slope has the highest contribution in the 2007 dataset (Fig. 4D). MaxEnt calculation of variable contribution is sensitive to correlation between variables. If two variables are important, MaxEnt will assign a large contribution to one of them and a low contribution to the other one. This characteristic of MaxEnt can cause the observed variability between 2006 and 2007 contributions. Although the correlation between distance to shores and slope is low (r=−0.18), it seems large enough to affect MaxEnt determination of weights. This can be corroborated by observing the individual importance of each variable to the model (MaxEnt jackknife approach, Table 2); the variables that contribute the most by themselves (when run with that variable alone) are elevation, distance to shore, slope, and distance to buildings. However, they all have redundant information (model gain does not vary when the variable is excluded), and therefore those variables contribute quite diversely across models. Distance to roads has the less redundant information and, if excluded, is the variable that affects model performance the most. On the other hand, this variable is not important when used alone, suggesting the presence of interactions between distance to roads and other variables that improve model performance.
Fig. 4.
Importance of environmental variables (covariates) for the two best models: logistic regression and MaxEnt. (A) Logistic regression for the 2006 dataset; (B) MaxEnt for the 2006 dataset; (C) Logistic regression for the 2007 dataset; (D) MaxEnt for the 2007 dataset. For logistic regression, importance is expressed in terms of regression coefficients. For MaxEnt, importance is expressed as percentage. Circles represent median values and lines range values. DEM: elevation; DBuildings: distance to buildings; DShore: distance to shore; DRoad: distance to roads.
Table 2.
MaxEnt Jackknife of variable importance. The values represent the training gains when the variable is used in isolation (“with only”) and when the variable is excluded (“without”). Gain represents the fit between MaxEnt’s probability distribution and the distribution of the sample observation data. A variable that contributes useful information to the model would have a high gain when used in isolation. A variable that contributes unique information will have the gain reduced when it is excluded from the model. Gain with all variables equals 2.58 for 2006 and 2.61 for 2007
| 2006 | 2007 | |||
|---|---|---|---|---|
| With only | Without | With only | Without | |
| DShore | 2.00 | 2.39 | 1.91 | 2.46 |
| DEM | 1.99 | 2.42 | 2.00 | 2.44 |
| Slope | 1.82 | 2.45 | 1.86 | 2.44 |
| DBuildings | 1.62 | 2.43 | 1.81 | 2.44 |
| Aspect | 1.43 | 2.44 | 1.44 | 2.45 |
| Population | 0.50 | 2.45 | 0.56 | 2.47 |
| DRoad | 0.01 | 2.16 | 0.01 | 2.17 |
Overall, three variables (distance to shore, elevation, and slope) vary in their contribution among the different subsamples, having high importance values in some, but not in others. In contrast, aspect and population consistently have very low importance (Fig. 4).
Risk assessment
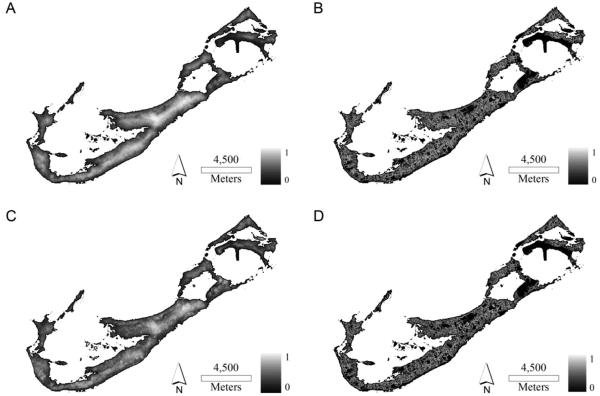
The risk maps produced from all the points with the two better performing models, logistic regression and MaxEnt, differ in their classification of risk areas. Both models agreed in the classification of some areas as low risk (dark areas in Fig. 5); these areas included the airport, a large nature reserve, or small islands. Interestingly, these areas share some general characteristics: closeness to shore, low elevation, low slope, and low population, in addition to low prevalence of human related features such as roads or buildings.
Fig. 5.
Relative risk prediction maps produced by logistic regression (panels A and C) and MaxEnt (panels B and D) for year 2006 (A and B) and 2007 (C and D). Lighter pixels indicate higher risks.
Discussion
Several modeling strategies are often used to produce vector risk maps, but generally these approaches are implemented at a much coarser scale than the one used here (e.g., Benedict et al., 2007; Moffett et al., 2007; Foley et al., 2010). In this study, we explored a similar approach (i.e., probability of mosquito presence) at a very fine scale, which allowed the modeling of risk in specific, restricted local areas. This modeling approach could produce especially advantageous results in the case of mosquitoes breeding in small containers, considering that breeding habitats are indeed very small and thus well below the resolution of satellite images that could be used with other vector mosquitoes, such as marsh breeders.
Most algorithms analyzed here produced better-than-random classifications (Table 1, Fig. 1), and some algorithms perform better than others, especially logistic regression. However, the overall classification performance of the algorithms could be considered low, which could stem from the ecological situation. The ovitrap data reflect the stochasticity in females’ oviposition events in discrete time intervals. Remarkably, two of the algorithms that produced low predictions (Bioclim and Domain) are the ones that presented extremely high robustness values (>96%). Possibly, those algorithms closely follow independent variables that only partially explain the dependent variable and thus provide highly correlated predictions that fail to predict accurately the risk areas for container mosquitoes.
The differences in classification performance across dates detected in most models is puzzling and unexpected; no a priori observation or descriptive statistic suggested any significant difference between these two datasets. Nevertheless, the difference allows two interesting conclusions: first, that any modeling approach should use multiple datasets when possible; second, the logistic regression approach was much less sensitive to this variation, presenting similar classification performance values according to the AUC criterion (Table 1, Fig. 1). However, some authors (Peterson et al., 2007) have recently raised concerns about the extensively used AUC to assess accuracy of ecological models, as two very different ROC curves can produce similar areas and consequently, two very spatially different models could result in similar AUCs. Nevertheless, it has been pointed out that the criterion remains extremely useful for comparing relative performances of different models (Wisz et al., 2008); further evaluations, beyond the scope of this work, would be necessary to address this issue.
All factors considered, the logistic regression, as implemented in IDRISI, provides the best modeling approach for mapping risk areas of mosquito infestation in Bermuda. Logistic regression presented the higher AUC values for both datasets, with high consistency among years, considering both the visual examination (Fig. 5B, D) and the correlation between the classification areas (Fig. 3). Moreover, a comparison of the areas classified as high density prone with the closest competing model, MaxEnt, suggests that the logistic regression algorithm produces a more realistic classification. The MaxEnt classification appears to be biased by the presence of roads. Interestingly, distance to roads does not have high covariance in Maxent runs, nor an ample range among replicates (Fig. 4) i.e., distance to roads does not have high contribution in MaxEnt models, however the Jackknife analysis of variable importance suggests the possible presence of interactions between distance to roads and other variables as mentioned above.
The algorithms evaluated in this study were selected for simplicity and feasibility for use by mosquito control officials; most of these algorithms are available in stand-alone packages that require minimal data preparation once the environmental variables are produced. Some recent or more elaborate algorithms, such as GAM, GMB and MARS, have not been evaluated here, because they require more complex scripting and the use of advanced statistical languages, or because they had not been released for public use at the time evaluations were performed, as in the cases of OM-GARP or LIVES (for details see Elith et al., 2006; Wisz et al., 2008). It seems feasible to implement an automatic script within IDRISI (i.e., using the macro functionality) that could take data obtained by control agencies’ monitoring programs at any point in the season and immediately produce risk maps. Such a procedure may allow quicker responses and a more efficient use of vector control and prevention resources.
Taking a critical point of view, none of the algorithms presented here are able to produce extremely accurate classifications (Table 1), but this evaluation could help to promote the development or improvement of specific algorithms suited for this task. The only dynamic variables (i.e., those that change over time) used in the models were distance to roads, distance to buildings, and population. Because these variables contributed the least to the models, we can consider that our results are static representations of risk, and therefore of limited used in analyses of future risk. Other dynamic variables that could influence risk at this fine scale, such as canopy density and evapotranspiration, micro-climate conditions, or areas with abundant discarded small containers were not included in the analyses due to absence of this information at the spatial scale of this research. If spatially detailed micro habitat variables were available for the Bermuda islands, the empirical models of best accuracy (logistic regression in this work) could be used to model future mosquito risk. There exist, however, limitations in the application of empirical species distribution models to predict future risk. Because the main purpose of the mathematical formulations of empirical models is to describe the distribution of the observations and not the underlying ‘cause-effect’ (Guisan & Zimmerman, 2000), these models may decrease their performance when projecting species distributions under future conditions. Decreased prediction accuracy can arise from the dependence of inferred relationships on current conditions and sample data, as a model could be trained under a combination of environmental conditions that does not exist in the future, or the species could be adapted to combinations of variables that currently do not exist (Hijmans & Graham, 2006). Moreover, if sample data used is spatially biased (e.g., due to accessibility), the relationships could be taken only on part of the species niche and therefore the accuracy both current and future projections could be affected. Mechanistic models are considered superior for understanding the effect of climate on species distribution under the assumption of universal dispersal and absence of competition (Hijmans & Graham, 2006). This is because mechanistic models are based on the knowledge of the physiology of the species, and thus, do not depend on sampling schemes. Although detailed physiological data are required to parameterize mechanistic models, they could produce better representations of future risk. Their applicability in the context of fine-scale container breeding mosquito risk prediction should be evaluated in future research, as they could provide useful tools for controlling and eradicating Aedes populations.
Acknowledgments
We thank Ross Furbert and other personnel of the Vector Control staff at the Bermuda Ministry of Health for their efforts in monitoring traps that produced the data for this study. The National Institutes of Health (Grant R15 AI062712-01 to TPL) and the Keck Foundation provided support for this project. We thank two anonymous reviewers for helpful comments..
References
- Beaty J, Aitken THG. In vitro transmission of yellow fever virus by geographic strains of Aedes aegypti. Mosquito News. 1979;39:232–238. [Google Scholar]
- Benedict MQ, Levine RS, Hawley WA, Lounibos LP. Spread of the tiger: global risk of invasion by the mosquito Aedes albopictus. Vector-Borne Zoonotic Diseases. 2007;7:76–85. doi: 10.1089/vbz.2006.0562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhang CC, Benjamin S, Saranum MM, Fook CY, Lim LH, Ahmad NW, Sofian-Azirun M. Dengue vector surveillance in urban residential and settlement areas in Selangor, Malaysia. Tropical Biomedicine. 2005;22:39–43. [PubMed] [Google Scholar]
- Dohm DJ, Logan TM, Barth JF, Turell MJ. Laboratory transmission of Sindbis virus by Aedes albopictus, Ae. aegypti, and Culex pipiens (Diptera: Culicidae) Journal of Medical Entomology. 1995;32:818–821. doi: 10.1093/jmedent/32.6.818. [DOI] [PubMed] [Google Scholar]
- Elith J, Grahm CH, Anderson RP, Dudík M, Ferrier S, Guisan A, Hijmans RJ, Huettmann F, Leathwick JR, Lehmann A, Li J, Lohmann LG, Loiselle BA, Manion G, Moritz C, Nakamura M, Nakazawa Y, Overtone JM, Peterson AT, Phillips SJ, Richardson K, Scachetti-Pereira R, Schapire RE, Soberon J, Williams S, Wisz MS, Zimmermann NE. Novel methods improve prediction of species’ distribution from occurrence data. Ecography. 2006;29:129–151. [Google Scholar]
- Eastman R. IDRISI Taiga version 16.05. Clark Labs; Worcester, MA: 2010. [Google Scholar]
- Eng J. ROC analysis: web-based calculator for ROC curves. n.d. URL http://www.jrocfit.org [Retrieved December 2009]
- Evans BR, Bevier GA. Measurement of field populations of Aedes aegypti with the ovitrap in 1968. Mosquito News. 1969;29:347–53. [Google Scholar]
- Foley DH, Klein TA, Kim HC, Brown T, Wilkerson RC, Rueda LM. Validation of Ecological Niche Models for Potential Malaria Vectors in the Republic of Korea. Journal of the American Mosquito Control Association. 2010;26:210–213. doi: 10.2987/09-5939.1. [DOI] [PubMed] [Google Scholar]
- Franklin J, McCullough T, Gray C. Terrain variables used for predictive mapping of vegetation communities in Southern California. In: Wilson J, Gallant J, editors. Terrain analysis: principles and applications. Willey; New York: 2000. pp. 331–3553. [Google Scholar]
- Guisan A, Zimmermann NE. Predictive habitat distribution models in ecology. Ecological Modelling. 2000;135:147–186. [Google Scholar]
- Hadfield TL, Turell M, Dempsey MP, David J, Park EJ. Detection of West Nile virus in mosquitoes by RT-PCR. Molecular Cellular Probes. 2001;15:147–150. doi: 10.1006/mcpr.2001.0353. [DOI] [PubMed] [Google Scholar]
- Hijmans RJ, Guarino L, Cruz M, Rojas E. Computer tools for spatial analysis of plant genetic resources data: 1. DIVA-GIS. Plant Genetic Research News. 2001;127:15–19. [Google Scholar]
- Hijmans RJ, Graham CH. The ability of climate envelope models to predict the effect of climate change on species distributions. Global Change Biology. 2006;12:1–10. [Google Scholar]
- Insightful Corp. S-plus version 8.0.4. Insightful Corporation; Palo Alto, CA: 2007. [Google Scholar]
- Kaplan L. M.S. Thesis. Clark University; Worcester, MA: 2006. Aedes aegypti and Aedes albopictus in Bermuda: The spatial and temporal distribution from 2000-2005. [Google Scholar]
- Kaplan L, Kendell D, Robertson D, Livdahl T, Khatchikian C. Aedes aegypti and Aedes albopictus in Bermuda: extinction, invasion, invasion and extinction. Biological Invasions. 2010;12:3277–3288. [Google Scholar]
- Lee HL. Aedes ovitrap and larval survey in several suburban communities in Selangor, Malaysia. Mosquito-Borne Diseases Bulletin. 1992;9:9–15. [Google Scholar]
- Mitchell CJ. The role of Aedes albopictus as an arbovirus vector. Parasitology. 1995;37:109–113. [PubMed] [Google Scholar]
- Moffett A, Shackelford N, Sarkar S. Malaria in Africa: vector species’ niche models and relative risk maps. PLoS ONE. 2007:e824. doi: 10.1371/journal.pone.0000824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morato VCG, Teixeira MG, Gomes AC, Bergamaschi DP, Barreto ML. Infestation of Aedes aegypti estimated by oviposition traps in Brazil. Revista Saúde Pública. 2005;39:553–558. doi: 10.1590/s0034-89102005000400006. [DOI] [PubMed] [Google Scholar]
- Nix HA, Busby JR. BIOCLIM: a bioclimate analysis and prediction system. Division of Water and Land Resources. Canberra: 1986. Research Report No. 1983-85. [Google Scholar]
- Peterson AT, Papes M, Eaton M. Transferability and model evaluation in ecological niche modeling: a comparison of GARP & Maxent. Ecography. 2007;30:550–560. [Google Scholar]
- Phillip SJ, Dudík M, Schapire RE. A maximum entropy approach to species distribution modeling; Proceedings of the 21st International Conference of Machine Learning, Banff, Canada. ACM International Conference Proceedings Series; New York, NY. 2004.p. 8. [Google Scholar]
- Phillip SJ, Anderson RP, Schapire RE. Maximum entropy modeling of species geographic distribution. Ecological Modeling. 2006;190:231–259. [Google Scholar]
- Phillip SJ, Dudík M. Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography. 2008;31:161–175. [Google Scholar]
- Porter KR, Summers PL, Dubois D, Puri B, Nelson W, Henchal E, Oprandy JJ, Hayes CG. Detection of West Nile virus by the polymerase chain reaction and analysis of nucleotide sequence variation. American Journal of Tropical Medicine and Hygiene. 1993;48:440–446. doi: 10.4269/ajtmh.1993.48.440. [DOI] [PubMed] [Google Scholar]
- SAS Institute . JMP version 7.0. SAS Institute Incorporated; Cary, NC: 2007. [Google Scholar]
- Shi P, Kauffman EB, Ren P, Felton A, Tai JH, Dupuis AP, II, Jones SA, Ngo KA, Nicholas DC, Maffei J, Ebel GD, Bernard KA, Kramer LD. High-Throughput Detection of West Nile Virus RNA. Journal of Clinical Microbiology. 2001;39:1264–1271. doi: 10.1128/JCM.39.4.1264-1271.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockman AK, Beamer DA, Bond JE. An evaluation of a GARP model as an approach to predicting the spatial distribution of non-vagile invertebrate species. Diversity and Distributions. 2006;12:81–89. [Google Scholar]
- Stockwell D, Peters D. The GARP modeling system: problems and solutions to automated spatial prediction. International Journal of Geographic Information Sciences. 1999;13:143–158. [Google Scholar]
- Wishart E. Adult mosquito (Diptera: Culicidae) and virus survey in metropolitan Melbourne and surrounding areas. Australian Journal of Entomology. 1999;38:310–313. [Google Scholar]
- Wisz MS, Hijman RJ, Li J, Peterson AT, Graham CH, Guisan A, et al. Effects of sample size on the performance of species distribution models. Diversity and Distributions. 2008;14:763–773. [Google Scholar]