Abstract
How numerical representation is encoded in the adult human brain is important for a basic understanding of human brain organization, its typical and atypical development, its evolutionary precursors, cognitive architectures, education, and rehabilitation. Previous studies have shown that numerical processing activates the same intraparietal regions irrespective of the presentation format (e.g., symbolic digits or non-symbolic dot arrays). This has led to claims that there is a single format-independent, numerical representation. In the current study we used a functional magnetic resonance adaptation paradigm, and effective connectivity analysis to re-examine whether numerical processing in the intraparietal sulci is dependent or independent on the format of the stimuli. We obtained two novel results. First, the whole brain analysis revealed that format change (e.g., from dots to digits), in the absence of a change in magnitude, activated the same intraparietal regions as magnitude change, but to a greater degree. Second, using dynamic causal modeling as a tool to disentangle neuronal specialization across regions that are commonly activated, we found that the connectivity between the left and right intraparietal sulci is format-dependent. Together, this line of results supports the idea that numerical representation is subserved by multiple mechanisms within the same parietal regions.
Keywords: parietal lobes, numbers, cortical specialization, functional magnetic resonance imaging, adaptation, effective connectivity
Introduction
Numerical understanding is not confined to numerate humans. Infants (Starkey et al., 1983), animals (Beran, 2008), and innumerate indigenous tribes (Pica et al., 2004; Butterworth et al., 2008) are able to process numerical magnitude when they appear in non-symbolic formats (e.g., dot arrays). It has been suggested that these non-symbolic numerical abilities serve as the foundation for later, symbolic, numerical representation, by mapping spoken and written numerals onto the non-symbolic core representation (Butterworth, 1999). Another, somewhat complementary idea, is that the link between symbolic (e.g., digits) and non-symbolic numerals is subserved by a single, format-independent, neuronal population in the intraparietal sulcus (IPS), the core area for numerical representation (Dehaene et al., 2003; Cohen Kadosh and Walsh, 2009). Since the 1980’s the idea that numbers are represented by a single mechanism has served as the dominant view in numerical cognition (McCloskey et al., 1985; Cohen Kadosh and Walsh, 2009). This idea impacts not only on the field of numerical cognition and our understanding of information processing in the human brain, but also on education and rehabilitation programs. For example, some intervention programs intended to help children with developmental dyscalculia are (Wilson et al., 2006a,b) based on the idea of an abstract, and single representation. Therefore, it is assumed that training on non-symbolic numerosity will improve the numerical computation with digits (but see Rousselle and Noel, 2007).
Recently the conclusion that there is a single numerical representation has been questioned (Cohen Kadosh and Walsh, 2009). First, neuronal activation in the IPS that has been attributed to numerical representation might have resulted from response selection that served as a bottleneck, and activated the same brain structure (Goebel et al., 2004). Second, claims for a single numerical representation have been based on lack of evidence for differences in parietal activation for different numerical formats in functional magnetic resonance imaging (fMRI) studies. These null effects may have resulted from a relative lack of spatial resolution (cf, Cohen Kadosh and Walsh, 2009), because each activated mm3 voxel in the parietal lobe in an fMRI experiment contains about 1.25 million neurons (Pakkenberg and Gundersen, 1997). Therefore, observing similar activations at the voxel-level for different formats (Pinel et al., 2001), does not necessarily indicate a single representation. This theoretical point is gaining experimental support from single-cell neurophysiology in monkeys which found that most of the neurons in the left and right IPS were selective to one numerical format or to another, as they showed high selectivity specific to dots or digits (Diester and Nieder, 2007). Human fMRI studies have also shown that numerical processing in the right parietal lobe is more responsive to digits than verbal numbers (Cohen Kadosh et al., 2007a).
In the current study, we used an fMR adaptation (fMRA) paradigm, and effective connectivity analysis to test the hypothesis that neuronal responses within the human IPS area that responds to magnitude are specialized to represent different numerical formats. fMRA has been used to examine neuronal specialization in the ventral stream in the case of object and face recognition (Kourtzi and Kanwisher, 2000), for a recent review see Kanwisher (2010). The logic of this technique is based on the reduction in neural responses to repeated presentation of the same stimulus characteristic (to which the neurons are tuned) relative to presentation of a different stimulus characteristic. These neural adaptation effects are believed to cause a corresponding decrease in the blood-oxygenation-level-dependent (BOLD) signal as recorded by fMRI (Grill-Spector and Malach, 2001) and these activation decreases have been associated with an increase in the accuracy with which the stimulus can be predicted (Friston et al., 2006). Numerical information is processed automatically (Henik and Tzelgov, 1982; Pavese and Umilta, 1998) and this is reflected in changes in the BOLD signal (Kaufmann et al., 2005; Tang et al., 2006; Cohen Kadosh et al., 2007b; Piazza et al., 2007; Wood et al., 2009). Therefore, passive viewing is sufficient to modulate IPS activation without response selection components.
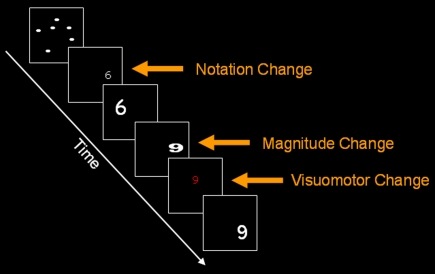
In order to assess the properties of the neuronal populations coding numerical representations, we changed the numerical magnitude after repeating a constant magnitude within a given format, while the subjects preformed a color-detection task (Figure 1). This magnitude change should modulate the BOLD signal associated with numerical representations. For example, several repetitions of the digit 6 were followed by a deviant digit (e.g., 9) with perceptual change controlled by varying the size, location and font on a trial to trial basis. In the dot condition the same deviant and repeating values appeared in dots. Repetitive exposure to the multiple instances of same format and numerosity causes adaptation in the neuronal population representing the stimulus (Li et al., 1993) and this reduces the BOLD signal (Grill-Spector et al., 2006). Conversely, when repetition of the same representation is followed by a deviant stimulus (i.e., format or numerosity) adaptation is released and a rise in BOLD signal is expected. This rationale allowed us to compare the effect of magnitude change within dots and within digits. The standard model of single, format-independent representation predicts a main effect of magnitude change in IPS irrespective of the format (dots or digits). However, common activation in the same voxels for both formats does not indicate whether magnitude change is format-dependent or format-independent within a given voxel. The same logic has been applied in studies of perception (Grill-Spector and Malach, 2001; Kanwisher, 2010), attention (Schafer and Moore, 2007), including numerical cognition (Cohen Kadosh et al., 2008).
Figure 1.
An example of notation change, magnitude change and visuomotor change in the current paradigm for digit format. Similar conditions were used for dots. The current figure is only for illustrative purposes.
To identify evidence for distinguishing between the single numerical representation and multiple numerical representations within voxels, we investigated several other factors:
-
(1)
We measured activation change in response to a change in format while the magnitude was held constant. For instance, the number 6 in dot format appeared after a repetition train of the number 6 in various fonts and sizes in digit format. According to the single representation hypothesis, the same neuronal population in IPS should code magnitude irrespective of format: this population should not show any release from adaptation upon changing from 6 dots to number 6. In contrast, according to the multiple representations hypothesis, magnitude related release from adaptation will be observed in IPS upon a format change because a specialized subpopulations of neurons within each IPS voxel code magnitude in different numerical formats (Figure 2), even when the magnitude of the representation is the same in both formats (Piazza et al., 2007; Jacob and Nieder, 2009). Alternatively, a common effect of magnitude change and format change might be a consequence of changes in visual attention induced by the mismatch between the new stimulus and top-down expectation established during the repetition phase (Friston et al., 2006; Gilbert and Sigman, 2007). To exclude this possibility, we correlated IPS activation with the degree of magnitude change. (e.g., a change of five units in 1,1,1,1,6 vs. a change of eight units in 1,1,1,1,9). Such a relationship ensured that the effects of magnitude change or notation change were observed in areas associated with magnitude, rather than non-perceptual number processing.
-
(2)
We used an effective connectivity analysis as a complementary and independent analysis to examine, for the first time, whether the communication between the left and right parietal lobes depends on the numerical format, in other words whether it is format-independent or format-dependent (Figure 3). This analysis tests the plausibility of a causal and directional influence of information processing by estimating how activity in one brain region could have influenced the activity in another brain area. If the modulation of activation in the IPS were due to visual attention, or some other general mechanism induced by the mismatch between the new stimulus and top-down expectation established during the repetition phase, the communication between the left and right IPS should not be modulated by type of change. To find the best functional connectivity account of our data, we used family level inference because this removes uncertainty about irrelevant aspects of the model structure when there are many models to compare (Penny et al., 2010).
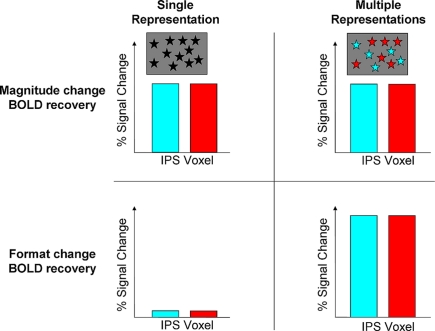
Figure 2.
Predictions of the recovery for magnitude and format change by the abstract and multiple representations. In this 2 × 2 matrix, the recovery for magnitude change is predicted to be similar for both hypotheses. This can be due to a single abstract representation in an IPS voxel (black asterisks), or because of multiple but overlapped representations due to developmental principles of human brain organization [turquoise (digits) and red (dots) asterisks]. Both hypotheses differ in the predictions for BOLD signal recovery during format change. The single representation predicts that although the format has been changed no recovery will be obtained as the same quantity is being presented. In contrast, the multiple representations hypothesis posits that during format change a full recovery will be obtained in the same areas that showed recovery for magnitude change. This recovery should be comparable or even stronger, but not weaker, compared to magnitude change, as a new representation comes into play (e.g., separate neuronal substrates for dots and digits, e.g., for 6 dots vs. the digit 6). In contrast, compared to format change, the recovery for magnitude change is only partial as neurons for a given quantity also code other similar magnitudes to some degree (Nieder and Miller, 2003; Cohen Kadosh et al., 2010).
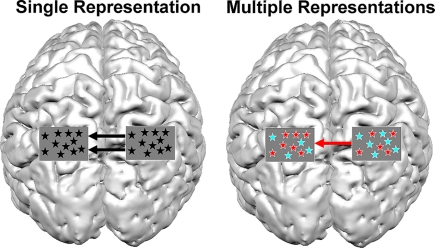
Figure 3.
Possible scenarios for brain connectivity under the assumption of single representation and multiple representations. A picture of a brain is shown from a top view. The rectangles over parietal lobes represent a magnification of voxels in the IPS and the type of representation within them. In the case of a single representation, format-independent representation exists in the IPS (black asterisks). In such a case the communication between the left and right IPS should be independent of format (i.e., digits or dots). In this example, the activation in the right IPS modulates the activation in the contralateral IPS. In contrast, the multiple representations hypothesis predicts that if different representations exist in the IPS, the activation between both IPS should be format-dependent. In the current example, the right IPS modulates the activity in the left IPS for dots (red asterisks), but not for digits (turquoise asterisks). The current figure is only an example, and is a simplified version of possible connectivity that can occur between the hemispheres, and does not discuss possible connectivity that can occur within a hemisphere.
In summary, we investigated whether release from adaptation in the IPS during numerical processing was format-independent, as predicated by a single numerical representation model, or format-dependent, as predicted by the multiple numerical representations (Cohen Kadosh and Walsh, 2009). Our focus was centered around the areas identified in a meta-analysis (Cohen Kadosh et al., 2008) of magnitude and numerical representations (x = −31, y = −53, z = 49; and x = 36, y = −49, z = 45). Support for the hypothesis that the numerical representation in IPS is single would be observed if (a) IPS release from adaptation was sensitive to a change in magnitude but not to a change in format and (b) processing interactions between the left and right IPS magnitude areas was format-independent. Alternatively support for the hypothesis that numerical representations in IPS are multiple would be observed if (a) IPS release from adaptation was sensitive to both magnitude change (independent of format change) and format change (independent of magnitude change) and (b) the processing interactions between the left and right IPS magnitude areas were format-dependent.
Materials and Methods
Participants
Nineteen participants (average age: 26.26 years, SD = 4.1, 12 females) were recruited from an academic environment, and received £15 for participating in the experiment. None of the participants had a history of neurological or psychiatric disorders. All participants had normal or corrected-to-normal vision and gave informed consent to participate in the study. The study was approved by the UCL ethics committee and informed consent was obtained from each participant.
Stimuli
As it is debatable whether the basic representation for numbers includes two-digit numbers (Nuerk et al., 2001; Wood et al., 2006) the numbers 1, 4, 6, or 9, in symbolic (digit) or non-symbolic (dots) format were used and presented in white on a black background. As in previous studies (Nieder et al., 2002), a number of steps were taken to minimize the impact of low-level perceptual attributes of stimuli on numerosity processing: (1) dots were pseudo-randomly varied in circumference, luminance, configuration, density and total surface area. (2) Digits were presented in four different fonts (Arial, Times New Roman, Impact, or Verdana; Cohen Kadosh et al., 2007a), and varied from trial to trial such that, for every digit presentation, position, luminance, and total surface area were matched to a matching dot trial of the same numerosity (that would appear at some other randomly assigned trial in the experiment). To control for the total surface area, total luminance and inter-item density of the dots, the total surface area for each trial (visual angle squared) was either 15, 30, 45, or 60. The individual item size for each trial was the total surface area (covered by the dots) divided by the number of items assigned to those trials. Overall, about 32 dot stimuli were generated corresponding to each combination of total surface area and magnitude. To control for local (between-item) density in the displays with four, six, or nine items randomly dispersed on the screen, the visual angle of the center-to-center distance between every pair of items was held constant (5–7 degrees).
Variation of these physical properties within format and maintaining a match (for the common attributes) between formats was meant to provide as close a control as possible changes in physical properties during magnitude and format change. Moreover, perceptual processing changes could not explain the correlation between IPS activation and the degree of magnitude change.
Experimental procedures and stimulus presentation were controlled using Cogent toolbox (http://www.vislab.ucl.ac.uk/cogent.php) for Matlab (Mathworks, MA, USA).
Experimental procedure
The participants were required to fixate on a cross in the middle of the screen, and to detect, via a button press, when the stimulus changed color. In order to make use of the fMRA technique, the stimulus on the screen was changed randomly in only one dimension at a time: (1) numerical magnitude, (2) numerical format, or (3) color, which led to a button press, and is therefore referred to as a visuomotor change. Thus, we had a 3 × 2 factorial design with change (magnitude, format, and visuomotor) and format (symbolic, non-symbolic), as within-subject factors. Please note that although “format” appears as one of the levels in the factor change, and as a factor itself, both are orthogonal. Namely, the level format in the factor change indicates the transition from one format (e.g., symbolic) to another (e.g., non-symbolic). The factor format, however, reflects the format that is being presented (symbolic or non-symbolic) on every trial, whether it includes a change or a repetition. We did not include trials that involve simultaneous change in magnitude and format as this condition is difficult to interpret (Piazza et al., 2007; Cohen Kadosh and Walsh, 2009) and would have necessitated reducing the number of trials in our conditions of interest. Moreover, in the case of support of the multiple representations, which we aimed to detect in the current study, such a result would have to be based on a null result. Each stimulus was presented for 200 ms, in order to avoid eye-movements or counting, with an inter-stimulus interval of 1 s. The minimum time for change duration of a train of repetition was 6 s and the maximum was 10.8 s. Each participant took part in four runs each of which lasted between 10 min and 3 s and 11 min and 50 s.
For the 3 × 2 factorial design with change and format there were 150 events of each format, on average there were 55 events with format change, 55 with magnitude change (range 54–57 for both) and about 40 (range 38–41) with visuomotor change.
fMRI acquisition and analysis
Data were acquired using a 3T Allegra MRI scanner (Siemens Medical Systems). Four runs of 244–281 volumes were collected per participant (38 axial slices; TR = 2.47 s; TE = 50 ms; flip angle = 90°; field-of-view = 192 mm × 192 mm; resolution 3 mm3). A T1-weighted structural image (1 mm3 resolution) was acquired to allow coregistration of functional data with the individual participants’ structural scans, and to ensure a healthy neurological status.
We analyzed fMRI data using SPM5 (Wellcome Department of Imaging Neuroscience, London; http://www.fil.ion.ucl.ac.uk/spm). The first five images of each run were discarded to allow for T1 equilibration. The remaining volumes were spatially realigned, coregistered to the individual participants’ structural scans, normalized to the Montreal Neurological Institute (MNI) standard space, and spatially smoothed with a Gaussian kernel of 6 mm full-width half-maximum.
Statistical analysis was performed in two stages. In the first stage, we computed a General Linear Model (GLM) with eight regressors, one for each condition in the factorial design (3 change × 2 format), plus two that modeled the quantity on a trial by trial basis for each format, as effects of no interest. Thus, the six regressors of interest explained the variance for the change conditions over and above variance that occurred during the adaptation trials. Each regressor was convolved with a canonical hemodynamic response function. Voxel-wise parameter estimates for these regressors were obtained by restricted maximum-likelihood estimation (ReML), using a temporal high-pass filter (cut-off 128 s) to remove low-frequency drift, and modeling temporal autocorrelation across scans with an AR(1) process. To examine whether magnitude change affected the activation of the parietal lobes in a parametric fashion we further examined whether the parietal lobes were modulated by the degree of the numerical change by running another SPM analysis. In this analysis instead of magnitude change we included a regressor that included the parametric modulation of the numerical change in every magnitude change event (Wood et al., 2008).
fMR adaptation
In the second stage, images of these parameter estimates comprised the data for a second GLM that treated participants as the only random effect. This GLM included only the six conditions of interest, using a single pooled error estimate, whose nonsphericity was estimated using ReML (Friston et al., 2002). The statistical threshold was p < 0.05 (FWE corrected for multiple comparisons across the whole brain) at the height or cluster-level when the voxel-level was thresholded at p < 0.001 (uncorrected). When we used inclusive masking the threshold of the masking condition(s) was set to p < 0.001, uncorrected, voxel-level. For the region of interest analysis of different types of change in the medial IPS (mIPS) we used a small volume correction for multiple comparisons centered on the coordinates of in a meta-analysis (Cohen Kadosh et al., 2008) of magnitude and numerical representations (x = −31, y = −53, z = 49; and x = 36, y = −49, z = 45).
To examine the effect of the degree of magnitude change with the activation in the mIPS we entered the level of magnitude change by calculating the numerical distance between the two deviant numerical magnitudes, which yielded the values of two, three, five, and eight.
Connectivity analysis
We extracted subject-specific time series of local fMRI activity from the left and the right mIPS voxels that were activated irrespective of condition. Specifically, to ensure the effects were not biased toward magnitude change, the time-series were extracted from the peak coordinates of the conjunction of magnitude change, format change and visuo-motor change in the group analysis (x = −33, y = −54, z = 48; x = 36, y = −51, z = 48). In each subject, peak activation was extracted from data prior to spatial smoothing and within 4 mm of the group local maxima coordinates (see Table 1 for details of these effects in each individual).
Table 1.
ROI for each participant of the closest activation to the coordinates in the group mean from the conjunction analysis (x = -33, y = -54, z = 48; x = 36, y = -51, z = 48) used for the dynamic causal modeling analysis.
| Participant | Left IPS | Right IPS | ||||
|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |
| 1 | −30 | −54 | 48 | 39 | −51 | 51 |
| 2 | −33 | −54 | 48 | 36 | −48 | 48 |
| 3 | −33 | −54 | 48 | 36 | −48 | 48 |
| 4 | −33 | −54 | 48 | 36 | −51 | 48 |
| 5 | −30 | −54 | 48 | 36 | −51 | 48 |
| 6 | −33 | −54 | 48 | 36 | −51 | 48 |
| 7 | −33 | −57 | 48 | 36 | −48 | 51 |
| 8 | −33 | −54 | 48 | 36 | −51 | 48 |
| 9 | −33 | −54 | 48 | 36 | −51 | 48 |
| 10 | −33 | −54 | 48 | 36 | −51 | 48 |
| 11 | −33 | −54 | 48 | 36 | −51 | 48 |
| 12 | −30 | −54 | 48 | 33 | −54 | 39 |
| 13 | −33 | −54 | 45 | 36 | −51 | 45 |
| 14 | −33 | −51 | 45 | 33 | −54 | 48 |
| 15 | −30 | −54 | 45 | 36 | −51 | 48 |
| 16 | −33 | −54 | 48 | 36 | −51 | 48 |
| 17 | −36 | −51 | 51 | 39 | −48 | 51 |
| 18 | −33 | −51 | 48 | 33 | −54 | 45 |
| 19 | −33 | −54 | 51 | 36 | −48 | 48 |
| Mean | −32.52 | −53.68 | 47.84 | 35.84 | −50.68 | 47.68 |
| SD | 1.50 | 1.37 | 1.57 | 1.57 | 1.97 | 2.62 |
In all models, the exogenous (driving) inputs to both left and right mIPS were format and change independent. The only factor that we varied was the inter-hemispheric connections, which could vary as a function of change or format.
We used random effects analysis (RFX) and partitioned our hypothesis-driven model-space into several families of models, depending on the question of interest. Bayesian Model Averaging (BMA) is then conducted within a family, and provides a summary of the parameters of that family, while avoiding assumptions about any one model.
In the first analysis we examined whether the modulation (connectivity) between the left and right mIPS is affected by the type of change. As we had seven different combinations of change, they were represented by seven families.
Family 1: Change-dependent models. Modulation only for magnitude
Family 2: Change-dependent models. Modulation only for color
Family 3: Change-dependent models. Modulation only for format
Family 4: Change-dependent models. Modulation only for magnitude and color
Family 5: Change-dependent models. Modulation only for magnitude and format
Family 6: Change-dependent models. Modulation only for color and format
Family 7: Change-independent models. Modulation for format, magnitude, and color
While the seventh family reflects change-independent modulation, as in the case of attentional-related modulation, the rest of the models assumed modulation related to magnitude, format, color or a combination of these changes.
In the second analysis we examined whether the modulation (connectivity) between the left and right mIPS was affected by the type of format. We constructed four families.
Family 1: Format-dependent models. Modulation only for digits
Family 2: Format-dependent models. Modulation only for dots
Family 3: Format-dependent models (Mixed modulation of digits and dots; e.g., modulation of left mIPS to right mIPS for digits and in the opposite direction for dots)
Family 4: Format-independent models. Modulation of the left and right mIPS occurs independently of format (both dots and digits).
While the first family reflects single representation, the rest of the families reflect multiple representations.
Note that not all families consisted of the same number of models (e.g., in the last family comparison, family 1–3 consisted of 21 models each, while family 4 consisted of 28 models). This does not affect the outcome of the family level inference (Penny et al., 2010).
Results
Response times
The reaction times for detecting color change were the same for dots (583 ms, SD = 59.2) and digits (583 ms, SD = 55.9) and did not differ significantly [t(18) = 0.1, p = 0.92]. The average accuracy was high (0.94) but due to a programming failure it was not possible to compare the error rates for digits and dots. This should not affect the interpretation of our data, as the accuracy of response only related to the detection of color change, which was incidental to the effects of interest (i.e., magnitude change and format change).
fMR adaptation
Details of the whole brain analysis are presented in the Supplementary material (Tables S1–S3). Here we focus on the regions of interest from prior studies of numerical magnitude (Cohen Kadosh et al., 2008). As predicted, an effect of magnitude change was observed for both dots and digits in the horizontal segment of the mIPS (left mIPS, Z = 3.7, PFWE-Corr < 0.001; right mIPS, Z = 3.55, PFWE-Corr < 0.001). This effect was observed when the format (dots or digits) was held constant and can not be explained by differences in visual input.
Activation in the same left and right mIPS voxels was also influenced by format change (left mIPS, PFWE-Corr < 0.001; right mIPS, PFWE-Corr < 0.001) and visuomotor (color) change (left mIPS, PFWE-Corr < 0.001; right mIPS, PFWE-Corr < 0.001, see Figure 4, for MNI coordinates and Z scores see Table 2). The effect of format change did not depend on the direction of the change (dots to digits or digits to dots) as might be expected if the response was due to perceptual changes. When we directly contrasted magnitude change and visuomotor change, there were no significant differences in mIPS activation (visuomotor change > magnitude change: left mIPS, Z = 1.91; right mIPS, Z = 2.14; p > 0.01, uncorrected).
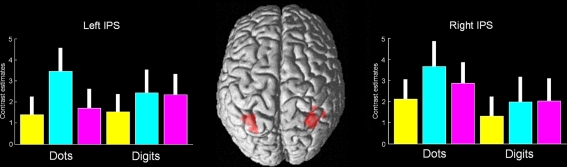
Figure 4.
Conjunction analysis of magnitude change, format change, and visuomotor change. The only significant activation was found in the bilateral middle IPS (p < 0.001, uncorrected, the peak was significant at p < 0.05 corrected). This activation falls within the coordinates of a recent meta-analysis of magnitude and numerical representation (Cohen Kadosh et al., 2008). Magnitude change appears in yellow, format change in turquoise, and visuomotor change in magenta. Error bars represent 90% confidence intervals.
Table 2.
Effects of change within the mIPS.
| Effect | x | y | z | Z score |
|---|---|---|---|---|
| Magnitude change | −30 | −54 | 48 | 3.7 |
| (dots and digits) | 36 | −48 | 45 | 3.55 |
| Notation change | −30 | −51 | 48 | 5.62 |
| (dots and digits) | 36 | −48 | 48 | 4.42 |
| Visuomotor change | −33 | −54 | 48 | 4.47 |
| (dots and digits) | 39 | −48 | 45 | 4.96 |
| Notation change vs. | −33 | −51 | 48 | 4.55 |
| Magnitude change | 33 | −48 | 38 | 3.44 |
| Notation change vs. | −33 | −51 | 48 | 3.14 |
| Visuomotor and magnitude change | 33 | −45 | 51 | 3.17 |
| Magnitude sensitive | −30 | −54 | 51 | 5.28 |
| (parametric modulation) | 36 | −51 | 45 | 3.17 |
Critically, the effect of format change for both digits and dots was greater than the effect of magnitude change in both the left mIPS (PFWE-Corr < 0.001) and in the right mIPS (PFWE-Corr < 0.01; Table 2). This finding is not consistent with the single representation hypothesis, rather, it fits with the multiple representations hypothesis. We excluded the possibility that it was explained by non-numerical processing that is shared by all types of changes (e.g., attention changes) by conducting two analyses: First, the effect of format change for both digits and dots was greater than the effect of visuomotor and magnitude change in both the left and right mIPS (in both cases PFWE-Corr < 0.001; Table 2). Second, because a correlation analysis confirmed that activation in both the left and right mIPS was sensitive to the size of magnitude change, irrespective of whether the stimuli were dots or digits: A conjunction analysis of the parametric modulation of magnitude change for (i) dots and (ii) digits was significant in both left mIPS (PFWE-Corr < 0.001) and right mIPS, (PFWE-Corr = 0.005), with no significant differences between the parametric effects in the symbolic and non-symbolic conditions under the current threshold, and also no hemispheric differences (Table 2). This correlation indicates mIPS sensitivity to a non-perceptual level of numerical processing that is difficult to explain in terms of visual attention. The results from the connectivity analysis, as detailed below, provide further support for this conclusion.
Connectivity analyses
The results reported above suggest that the same IPS voxels are sensitive to magnitude change, format change and visuomotor change. If these common effects are driven by a single general type of process (e.g., visual attention), then we would expect that inter-hemispheric connectivity between the left and right mIPS would be invariant across all three types of changes. To test this prediction we used connectivity analyses [Dynamic Causal Modeling (DCM)] to investigate whether the inter-hemispheric effective connectivity between left and right mIPS depended on the type of change (magnitude, format, or visuomotor).
We compared the evidence for different patterns of inter-hemispheric interactions using the Free Energy, F(m), as an approximation to the log-evidence, to choose the pattern that represents the optimal balance between data fit and model complexity. Each DCM describes a hypothetical model (e.g., format-dependent, format-independent) that describes how variations in the experimental factors modulated the network dynamics between the left and right mIPS.
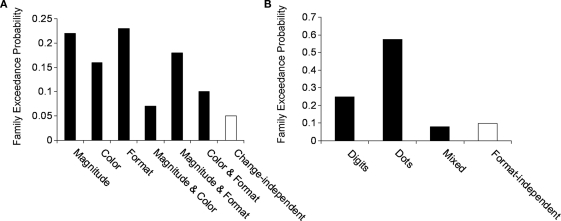
The results indicated that effective connectivity between the left and right mIPS depended on the type of change (magnitude, format or color). Namely, the family of models that assumed change-independent modulation, as suggested by a general mechanism that was involved in the detection of change, yielded a poor performance of exceedance probability of 0.05. On the other hand, the families of models that assumed change-dependent connectivity yielded an aggregated exceedance probability of 0.95 (Figure 5A).
Figure 5.
Family exceedance probability for (A) change-dependent and –independent families and (B) format-dependent and -independent families. Black bars indicate change- and format-dependent families, while white bars indicate change- and format-independent families. As can be seen in both cases the extrinsic modulation of the IPS was dominated by change-dependent and format-dependent families. In line with Penny et al. (2010) we grouped the families which shared a feature of interest, in this case extrinsic-dependent modulation. The aggregated evidence for these families has yielded exceedance probabilities above 0.9 for change-dependent and format-dependent families.
We further examined whether the effective connectivity between left and right mIPS was characterized by single or multiple representations of magnitude. The family that assumed format-independent modulation (dots and digits), as predicted by a single numerical representation yielded a poor performance of 0.09. In contrast, the families of models that assumed format-dependent modulation (e.g., dots or digits), yielded an exceedance probability of 0.91 [relative contribution of dots, 0.58; digits, 0.25; mixed (e.g., dots from left to right, digits from right to left), 0.08; Figure 5B].
Discussion
In the current study we examined whether the left and right mIPS process magnitude in a format-dependent or format-independent fashion. Evidence for format-independent processing would be consistent with a single numerical representation (McCloskey et al., 1985; Cohen Kadosh and Walsh, 2009). In contrast, evidence for format-dependent processing would be in line with multiple numerical representations (McCloskey et al., 1985; Cohen Kadosh and Walsh, 2009). Our results provide clear evidence for format-dependence, which is in line with the existence of multiple numerical representations. First, the whole brain analysis revealed that the same bilateral mIPS areas responded to format change, in the absence of a change in magnitude. However, based on these results alone, one might suggest that the same region/neuronal population responds independently to magnitude change and format change. One way to test the independence of these effects, in future experiments, would be to examine whether the change in format was greater when there was also a change in magnitude. In the current experiment, we used dynamic causal modeling to test the notion of format specific numerical processing further. In this analysis, there were no assumptions about the format of the inputs. The observation that the modulatory effect of magnitude change varied with the format therefore confirmed our hypothesis that the inter-hemispheric interactions between left and right mIPS during magnitude processing were format-dependent. In other words, using DCM, we showed that the connectivity between the left and right mIPS depends on the stimulus format and the type of change. As explained in the introduction these findings are in line with the multiple representations hypothesis (Figures 2 and 3).
We also demonstrated that the left and right mIPS responded to color change as well as magnitude and format change. This is consistent with prior studies illustrating that IPS responses are not specific to numerical computation (Goebel et al., 2004; Shuman and Kanwisher, 2004). Nevertheless, we considered the possibility that the mIPS responses to magnitude, format, and color change were driven by a common response to perceptual or attentional change. However, a generic explanation in terms of low-level processing cannot explain why (a) both left and right mIPS areas were sensitive to the size of magnitude change; and (b) the regional interactions between left and right mIPS depended on the type of stimulus (dots or digits) and the type of change (magnitude, format, or color). Our findings are also incompatible with a generic explanation of mIPS function in terms of response selection (Goebel et al., 2004) because, in our experiment, only the color change prompted a response change. Thus, the left and right mIPS were involved in several different functions including numerical representation for dots, numerical representation of digits, the degree of magnitude change, and the sensori-motor processing required in response to color change.
The current results provide evidence convergent with the single-cell neurophysiological study which found that the majority of the recorded neurons in the monkey IPS are format-dependent (Diester and Nieder, 2007). In this study, following several months of training, rhesus monkeys (Macaca mulatta) learned to associate each digit with its respective numerosity. It was found that only 2% of the recorded neurons in the IPS showed a preference for the numerical value independent of format. The authors suggested that following a longer training period the parietal lobe neurons might evolve into a format-independent representation. Although human neuroimaging does not have resolution at the neuronal level because a single voxel in the parietal lobe includes ∼1.25 million neurons (Pakkenberg and Gundersen, 1997; Cohen Kadosh and Walsh, 2009), our fMRA design and DCM analyses revealed that, as in monkey IPS, numerical processing of dots and digits in adult IPS can be format-dependent.
The finding of format-dependent representation in this study shows that numerical magnitude is coded in the mIPS by multiple representations. Previous studies have argued that the default numerical representation might be subserved by both multiple numerical representations and single numerical representations side-by-side. It may therefore be possible, as in monkey IPS (Diester and Nieder, 2007), that a small subset of neurons in human IPS code numbers in a format-independent fashion (Pesenti and Andres, 2009). This is consistent with observations that the left and right mIPS regions are involved in multiple levels of processing. More broadly, both left and right mIPS respond to visuomotor-related processes, including goal-directed behavior, planning and movement execution, information processing from both somatosensory and visual stimuli, perceptual change, response selection, and non-numerical processing (Walsh, 2003; Goebel et al., 2004; Shuman and Kanwisher, 2004; Cohen Kadosh et al., 2008; Basten et al., 2010; Cappelletti et al., 2010).
An intriguing question that can shed light on the origin of numerical understanding is why the mIPS is involved in numerical processing? Developmental studies have suggested increased involvement of the parietal lobe and decreased involvement of the prefrontal cortex as a function of age (Rivera et al., 2005; Ansari and Dhital, 2006; Cantlon et al., 2006; Houde et al., 2010).
The eventual involvement of the mIPS in numerical representation might be due to gradual specialization of neuronal populations that are initially involved in visuomotor functions (Johnson, 2001; Cohen Kadosh, 2011). According to this developmental theory, the establishment of specialized neuronal substrates results from an initial general neuronal assembly, say in the mIPS, interacting with other brain areas that subserve cognitive processes needed for the development of numerical concepts, such as the prefrontal cortex (Johnson, 2001; Cohen Kadosh, 2011). If the prefrontal cortex served as a comparator mechanism (Basten et al., 2010), a coarse understanding of numbers such as small/large could emerge during the early developmental stages. The human mIPS could then become more involved as numerical understanding increases, which occurs with education and age in Western cultures (Ansari, 2008). Therefore, it seems that the mIPS is able to accumulate the information in the environment based on numerical information to guide decision and action. This idea is in line with previous studies, which have used non-numerical information (Basten et al., 2010).
The current results indicate that in numbers do not need to be processed intentionally in order to modulate the mIPS activation, as we observed that non-intentional processing of numerical magnitude modulate the mIPS as well. In this light, the involvement of the mIPS in intentional and non-intentional numerical processing (as in the current study; Cohen Kadosh and Walsh, 2009) might relate to the idea that numbers are tightly linked to visuomotor transformation and action planning or to the attribution of numerical representations to sensorimotor grounding (i.e., embodiment) of semantic processing (Walsh, 2003; Andres et al., 2004; Lindemann et al., 2007; Brozzoli et al., 2008; Fischer and Campens, 2008).
The current results also suggest that some intervention programs designed to help children with developmental dyscalculia (Wilson et al., 2006a,b) should be revised. Namely, as the mIPS responds to numerical representations in a format-dependent fashion then training for improving numerical abilities (and assuming also their neural correlates) should be based on the format that it aims to impact the most, which in most cultures, is Arabic digits. Therefore, training on non-symbolic numerosity in order to improve the numerical computation or arithmetic with digits, might not be the most beneficial strategy.
In conclusion, we have found that the left and right mIPS respond to numerical representations in a format-dependent fashion. Specifically, we showed here for the first time that both the left and right mIPS respond to non-symbolic and symbolic numbers in a format-dependent fashion. Future studies are required to further examine how and at what developmental stage different neuronal populations within the mIPS are involved in different functions, and how the function of the mIPS depends on other areas that it is interacting with (Verguts and Fias, 2004). Together, the findings will enable a better understanding of numerical processing in the typical brain and have important implications for the intervention and rehabilitation of numerical disabilities.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/human_neuroscience/10.3389/fnhum.2011.00062/abstract
Acknowledgments
We would like to thank Dr Mohamed Seghier for helping with the DCM analysis. This work was supported by The Wellcome Trust (Wellcome Trust Centre for Neuroimaging, Institute of Neurology, University College London). Roi Cohen Kadosh was supported by a Marie Curie Intra European Fellowship and is supported by the Wellcome Trust (WT88378).
References
- Andres M., Davare M., Pesenti M., Olivier E., Seron X. (2004). Number magnitude and grip aperture interaction. NeuroReport 15, 2773–2777 [PubMed] [Google Scholar]
- Ansari D. (2008). Effects of development and enculturation on number representation in the brain. Nat. Rev. Neurosci. 9, 278–291 10.1038/nrn2334 [DOI] [PubMed] [Google Scholar]
- Ansari D., Dhital B. (2006). Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. J. Cogn. Neurosci. 18, 1820–1828 10.1162/jocn.2006.18.11.1820 [DOI] [PubMed] [Google Scholar]
- Basten U., Biele G., Heekeren H. R., Fiebach C. J. (2010). How the brain integrates costs and benefits during decision making. Proc. Natl. Acad. Sci. U.S.A. 107, 21767–21772 10.1073/pnas.0908104107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beran M. J. (2008). The evolutionary and developmental foundations of mathematics. PLoS Biol. 6, e19. 10.1371/journal.pbio.0060019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brozzoli C., Ishihara M., Goebel S. M., Salemme R., Rossetti Y., Farne A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. U.S.A. 105, 5644–5648 10.1073/pnas.0708414105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterworth B. (1999). The Mathematical Brain. London: Macmillan [Google Scholar]
- Butterworth B., Reeve R., Reynolds F., Lloyd D. (2008). Numerical thought with and without words: evidence from indigenous Australian children. Proc. Natl. Acad. Sci. U.S.A. 105, 13179–13184 10.1073/pnas.0806045105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon J. F., Brannon E. M., Carter E. J., Pelphrey K. A. (2006). Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biol. 4, e125. 10.1371/journal.pbio.0040125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M., Lee H. L., Freedman D. J., Price C. J. (2010). The role of right and left parietal lobes in the conceptual processing of numbers. J. Cogn. Neurosci. 22, 331–446 10.1162/jocn.2009.21246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh K. (2011). What can emerging cortical face networks tell us about mature brain organisation? Dev. Cogn. Neurosci. 1, 246–255 10.1016/j.dcn.2011.02.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R., Cohen Kadosh K., Kaas A., Henik A., Goebel R. (2007a). Notation-dependent and -independent representations of numbers in the parietal lobes. Neuron 53, 307–314 10.1016/j.neuron.2006.12.025 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Cohen Kadosh K., Linden D. E. J., Gevers W., Berger A., Henik A. (2007b). The brain locus of interaction between number and size: a combined functional magnetic resonance imaging and event-related potential study. J. Cogn. Neurosci. 19, 957–970 10.1162/jocn.2007.19.12.2050 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Lammertyn J., Izard V. (2008). Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog. Neurobiol. 84, 132–147 10.1016/j.pneurobio.2007.11.001 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Muggleton N., Silvanto J., Walsh V. (2010). Double dissociation of format-dependent and number-specific neurons in human parietal cortex. Cereb. Cortex 20, 2166–2171 10.1093/cercor/bhp273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R., Walsh V. (2009). Numerical representation in the parietal lobes: abstract or not abstract? Behav. Brain Sci. 32, 313–373 10.1017/S0140525X09990938 [DOI] [PubMed] [Google Scholar]
- Dehaene S., Piazza M., Pinel P., Cohen L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506 10.1080/02643290244000239 [DOI] [PubMed] [Google Scholar]
- Diester I., Nieder A. (2007). Semantic associations between signs and numerical categories in the prefrontal cortex. PLoS Biol. 5, e294. 10.1371/journal.pbio.0050294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer M. H., Campens H. (2008). Pointing to numbers and grasping magnitudes. Exp. Brain Res. 192, 149–153 10.1007/s00221-008-1622-3 [DOI] [PubMed] [Google Scholar]
- Friston K. J., Kilner J., Harrison L. (2006). A free energy principle for the brain. J. Physiol. 100, 70–87 [DOI] [PubMed] [Google Scholar]
- Friston K. J., Penny W. D., Phillips C., Kiebel S., Hinton G., Ashburner J. (2002). Classical and bayesian inference in neuroimaging: theory. NeuroImage 16, 465–483 10.1006/nimg.2002.1091 [DOI] [PubMed] [Google Scholar]
- Gilbert C. D., Sigman M. (2007). Brain states: top-down influences in sensory processing. Neuron 54, 677–696 10.1016/j.neuron.2007.05.019 [DOI] [PubMed] [Google Scholar]
- Goebel S. M., Johansen-Berg H., Behrens T., Rushworth M. F. S. (2004). Response-selection-related parietal activation during number comparison. J. Cognitive Neurosci. 16, 1536–1551 10.1162/0898929042568442 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K., Henson R., Martin A. (2006). Repetition and the brain: neural models of stimulus-specific effects. Trends Cogn. Sci. 10, 14–23 10.1016/j.tics.2005.11.006 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K., Malach R. (2001). FMR-adaptation: a tool for studying the functional properties of human cortical neurons. Acta Psychol. 107, 293–321 10.1016/S0001-6918(01)00019-1 [DOI] [PubMed] [Google Scholar]
- Henik A., Tzelgov J. (1982). Is three greater than five: the relation between physical and semantic size in comparison tasks. Mem. Cogn. 10, 389–395 10.3758/BF03202431 [DOI] [PubMed] [Google Scholar]
- Houde O., Rossi S., Lubin A., Joliot M. (2010). Mapping numerical processing, reading, and executive functions in the developing brain: an fMRI meta-analysis of 52 studies including 842 children. Dev. Sci. 13, 876–885 10.1111/j.1467-7687.2009.00938.x [DOI] [PubMed] [Google Scholar]
- Jacob S. N., Nieder A. (2009). Notation-independent representation of fractions in the human parietal cortex. J. Neurosci. 29, 4652–4657 10.1523/JNEUROSCI.0651-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M. H. (2001). Functional brain development in humans. Nat. Rev. Neurosci. 2, 475–483 10.1038/35081509 [DOI] [PubMed] [Google Scholar]
- Kanwisher N. (2010). Functional specificity in the human brain: a window into the functional architecture of the mind. Proc. Natl. Acad. Sci. U.S.A. 107, 11163–11170 10.1073/pnas.1005062107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L., Koppelstaetter F., Delazer M., Siedentopf C., Rhomberg P., Golaszewski S., Felber S., Ischebeck A. (2005). Neural correlates of distance and congruity effects in a numerical Stroop task: an event-related fMRI study. NeuroImage 25, 888–898 10.1016/j.neuroimage.2004.12.041 [DOI] [PubMed] [Google Scholar]
- Kourtzi Z., Kanwisher N. (2000). Cortical regions involved in perceiving object shape. J. Neurosci. 20, 3310–3318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L., Miller E. K., Desimone R. (1993). The representation of stimulus familiarity in anterior inferior temporal cortex. J. Neurophysiol. 69, 1918–1929 [DOI] [PubMed] [Google Scholar]
- Lindemann O., Abolafia J. M., Girardi G., Bekkering H. (2007). Getting a grip on numbers: numerical magnitude priming in object grasping. J. Exp. Psychol. Hum. Percep. Perform. 33, 1400–1409 10.1037/0096-1523.33.6.1400 [DOI] [PubMed] [Google Scholar]
- McCloskey M., Caramazza A., Basili A. (1985). Cognitive mechanisms in number processing and calculation: evidence from dyscalculia. Brain Cogn. 4, 171–196 10.1016/0278-2626(85)90069-7 [DOI] [PubMed] [Google Scholar]
- Nieder A., Freedman D. J., Miller E. K. (2002). Representation of the quantity of visual items in the primate prefrontal cortex. Science 297, 1708–1711 10.1126/science.1072493 [DOI] [PubMed] [Google Scholar]
- Nieder A., Miller E. K. (2003). Coding of cognitive magnitude: compressed scaling of numerical information in the primate prefrontal cortex. Neuron 37, 149–157 10.1016/S0896-6273(02)01144-3 [DOI] [PubMed] [Google Scholar]
- Nuerk H.-C., Weger U., Willmes K. (2001). Decade breaks in the mental number line? Putting the tens and units back in different bins. Cognition 82, B25–B33 10.1016/S0010-0277(01)00142-1 [DOI] [PubMed] [Google Scholar]
- Pakkenberg B., Gundersen H. J. G. (1997). Neocortical neuron number in humans: effect of sex and age. J. Comp. Neurol. 384, 312–320 [DOI] [PubMed] [Google Scholar]
- Pavese A., Umilta C. (1998). Symbolic distance between numerosity and identity modulates Stroop interference. J. Exp. Psychol. Hum. Percept. Perform. 24, 1535–1545 10.1037/0096-1523.24.5.1535 [DOI] [PubMed] [Google Scholar]
- Penny W. D., Stephan K. E., Daunizeau J., Rosa M. J., Friston K. J., Leff A. P. (2010). Comparing families of dynamic causal models. PLoS Comput. Biol. 6, e1000709. 10.1371/journal.pcbi.1000709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesenti M., Andres M. (2009). Common mistakes about numerical representations. Behav. Brain Sci. 32, 346–347 10.1017/S0140525X09990835 [DOI] [Google Scholar]
- Piazza M., Pinel P., Le Bihan D., Dehaene S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305 10.1016/j.neuron.2006.11.022 [DOI] [PubMed] [Google Scholar]
- Pica P., Lemer C., Izard V., Dehaene S. (2004). Exact and approximate arithmetic in Amazonian indigene group. Science 306, 499–503 10.1126/science.1102085 [DOI] [PubMed] [Google Scholar]
- Pinel P., Dehaene S., Rivie're D., LeBihan D. (2001). Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage 14, 1013–1026 10.1006/nimg.2001.0913 [DOI] [PubMed] [Google Scholar]
- Rivera S. M., Reiss A. L., Eckert M. A., Menon V. (2005). Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cortex 25, 1779–1790 10.1093/cercor/bhi055 [DOI] [PubMed] [Google Scholar]
- Rousselle L., Noel M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs non-symbolic number magnitude processing. Cognition 102, 361–395 10.1016/j.cognition.2006.01.005 [DOI] [PubMed] [Google Scholar]
- Schafer R. J., Moore T. (2007). Attention governs action in the primate frontal eye field. Neuron 56, 541–551 10.1016/j.neuron.2007.09.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shuman M., Kanwisher N. (2004). Numerical magnitude in the human parietal lobe: tests of representational generality and domain specificity. Neuron 44, 557–569 10.1016/j.neuron.2004.10.008 [DOI] [PubMed] [Google Scholar]
- Starkey P., Spelke E. S., Gelman R. (1983). Detection of intermodal numerical correspondences by human infants. Science 222, 179–181 10.1126/science.6623069 [DOI] [PubMed] [Google Scholar]
- Tang J., Critchley H. D., Glaser D., Dolan R. J., Butterworth B. (2006). Imaging informational conflict: a functional magnetic resonance imaging study of numerical Stroop. J. Cogn. Neurosci. 18, 2049–2062 10.1162/jocn.2006.18.12.2049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verguts T., Fias W. (2004). Representation of number in animals and humans: a neural model. J. Cogn. Neurosci. 16, 1493–1504 10.1162/0898929042568497 [DOI] [PubMed] [Google Scholar]
- Walsh V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. 7, 483–488 10.1016/j.tics.2003.09.002 [DOI] [PubMed] [Google Scholar]
- Wilson A. J., Dehaene S., Pinel P., Revkin S. K., Cohen L., Cohen D. (2006a). Principles underlying the design of “The Number Race”, an adaptive computer game for remediation of dyscalculia. Behav. Brain Funct. 2, 19. 10.1186/1744-9081-2-20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson A. J., Revkin S. K., Cohen D., Cohen L., Dehaene S. (2006b). An open trial assessment of “The Number Race”, an adaptive computer game for remediation of dyscalculia. Behav. Brain Funct. 2, 20. 10.1186/1744-9081-2-20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood G., Ischebeck A., Koppelstaetter F., Gotwald T., Kaufmann L. (2009). Developmental trajectories of magnitude processing and interference control: an fMRI study. Cereb. Cortex 19, 2755–2765 10.1093/cercor/bhp056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood G., Nuerk H.-C., Sturm D., Willmes K. (2008). Using parametric regressors to disentangle properties of multi-feature processes. Behav. Brain Funct. 4, 38. 10.1186/1744-9081-4-38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood G., Nuerk H.-C., Willmes K. (2006). Neural representations of two-digit numbers: a parametric fMRI study. NeuroImage 29, 358–367 10.1016/j.neuroimage.2005.07.056 [DOI] [PubMed] [Google Scholar]