QT/RR Coupling and Gender Differences

Abstract

Data provided by THEW was used to test QT gender differences. Three QT/RR models were used during analysis: a transfer function model (TRF), a model based on exponential weighting of RR intervals (EXP), and an EXP model with additive direct coupling with RR intervals (EXPDC). Data from 81 men and 73 women was analyzed.

Women have a significantly higher QTc (p<10⁻⁶), steeper Gain_L (QT/RR slope, gain for slow RR variability, p<0.01), faster τ (QT adaptation, p<0.05), higher Gain_F (gain for fast RR variability, immediate change of QT, p<0.05) and higher QT random variability (p<0.05).

The higher prevalence of arrhythmias in women, given by longer QTc, is compensated to some extent by a higher level of Gain_F and faster τ. The proarrhythmic influence of drugs may originate in a change of Gain_L, Gain_F or τ without any change in QTc.

1. Introduction

The gender dependency of ventricular repolarization is well known. The QTc interval is longer in women than in men, Torsades de Pointes associated with long QT syndrome is more common in women, and women have more drug-induced proarrhythmias compared to men [1–3]. Some analysis has been done [1–3] concerning static repolarization parameters, as malignant arrhythmias are associated with prolonged cardiac repolarization. Arrhythmias are, however, frequently triggered by a sudden change in heart rate (RR interval) [4]. For this reason, analysis of dynamic properties is of equal importance to analysis of static properties. The gender dependency of QT dynamic properties may help to better understand why cardiac arrhythmias and drug-induced Torsades de Pointes are more prevalent in women.

2. Methods

Data provided by the Telemetric and Holter ECG Warehouse of the University of Rochester (THEW), NY, the Normal database [http://thew-project.org/index.htm] was used to test gender differences. ECG signals from 81 men and 73 women were extracted from the database. Two records, about 30 min. in length, were extracted for each subject. The first record was a.m., the second p.m. The applied criteria for the extracted records were: i) Sufficient RR changes in signal; ii) Good quality of the ECG signal to detect the majority of QT intervals.

Sometimes it was not possible to fulfill both criteria, the parts of the ECG signals with RR changes were distorted. Such records were excluded during QT detection.

Singular value decomposition (SVD) was used as preprocessing. The three-dimensional signal from the database was reduced to a one-dimensional signal:

$$S(t)=\sqrt{{ev}_1^2+{ev}_2^2}$$

where ev1 and ev2 are eigenvectors [5]. The S(t) signal was analyzed with our custom-designed software ScopeWin to obtain a continuous series of RR and QT intervals. The QT interval duration was determined from the onset of the QRS wave to the end of the T wave, defined as the crossing between the isoelectric line and the tangent to the descending T wave. A semiautomatic method of QT detection was used. If there was any doubt about proper detection or if accurate detection was not deemed possible, the corresponding beats were marked as non-detectable QT intervals.

Subsequently, the results of detection were compared with corresponding annotations records from the THEW database. All disagreements were visually controlled. Beats that were annotated as not normal were marked as QT not detectable.

Records in which the QT variability, connected with RR variability, was not remarkable were excluded from the following analysis. Such records have low signal to noise ratio and the resulting parameters are inaccurate. Following exclusion of all bad records, we analyzed 154 records from men and 126 records from women.

2.1. QT/RR dynamic models

The dynamic parameters of QT have not yet been standardized. They are based on a supposed QT/RR model and their validity depends on the validity of the used model. Three dynamic models of QT/RR coupling were used in the test of gender differences:

1. Transfer function model (TRF) [6, 7];

2. Exponential weighted model (EXP) [9];

3. Exponential weighted model with added direct coupling between QT and RR (EXPDC) [8]).

These models have a different basis and parameters, see [8, 7] for detailed description. The basis in the TRF model is the control system theory, in EXP and EXPDC the basis is the assumption about the shape of QT step response. The fitting of the model parameters is used in QT analysis to achieve the best agreement between modeled QT and detected QT.

The QT dynamic parameters of physiological significance are determined by QT step response, computed from fitted parameters [8]. The shapes of QT step responses differ according to the used model and the value of the corresponding parameters differ in the same way. The following QT parameters were tested:

1. Gain_L: The QT/RR slope, i.e. the amplitude of QT change that is achieved in the steady state, i.e. the gain of QT/RR coupling for slow variability of RR.

2. Gain_F: The gain of QT/RR coupling for fast variability of RR, i.e. the amplitude of QT change immediately following the change of RR. This parameter is missing in the EXP model.

3. τ The time constant of QT adaptation to RR change. In the TRF model τ represents the number of heartbeats after which the step response has achieved 90 % of the change needed to attain the new steady state value. τ is the number of beats used during exponential weighting in the EXP or EXPDC model.

The QTc and QT variability independent of RR (QTvar) were tested together with the parameters Gain_L, Gain_F and τ. QTvar was defined as the rms of the resulting error signal given by fitting, i.e. of the difference between modeled QT and detected QT. QTc computing was based on a tested model.

2.2. Nonlinear static model and QT averaging

Currently many QT analyses are based on a subject-specific, nonlinear static model. We tested one static model, which assumed the following relation between RR and QT intervals:

$$\mathit{QTm}(j)=\alpha +\beta \times RR{(j)}^{\gamma }$$

where α, β, and γ are fitted parameters and QTm(j) and RR(j) are the level of j-th beats or the moving average over 10 or 40 beats.

The limited accuracy of QT detection still poses a limitation on QT analysis. A suggestion has been made to use some representative level of QT in a 10 sec. area [9], instead of the exact level of QT. Such averaging must limit the QT dynamic parameters, and to test this limitation the moving mean level of QT intervals over 10 beats was also used in the analysis.

3. Results

The QT parameters for the tested models are given in Tab. 1 and 2. The detected QT intervals were used during the analysis in Tab. 1. The moving average of QT intervals over 10 beats was used for the analysis in Tab. 2. RR intervals were used without averaging in both cases.

Table 1.

QT parameters. QT intervals without averaging were used in the analysis. m – men, w – women. Statistical significance of gender differences:

Model		TRF	EXP	EXPDC
RMS [ms]	m	5.6±3*	6.0±2.9*	5.5±3*
	w	6.7±4.8	7.0±4.8	6.7±4.8
QTc [ms]	m	376±24†	373±20†	374±20†
	w	392±28	388±27	390±27
GainL	m	0.169±0.07**	0.150±0.05**	0.157±0.05**
	w	0.194±0.08	0.174±0.08	0.187±0.08
GainF	m	0.028±0.013*	0	0.028±0.014*
	w	0.033±0.019	0	0.034±0.022
τ [beats]	m	184±123*	166±64**	198±60**
	w	157±84	145±70	177±68

^*p<0.05,

^**p<0.01,

^†p<0.0000001

Table 2.

The moving average of QT intervals over 10 beats was used in the analysis. m – men, w – women. Statistical significance of gender differences:

Model		TRF	EXP	EXPDC
RMS [ms]	m	4.3±1.8	4.5±1.7	4.2±1.8
	w	4.8±3	5.0±3	4.8±3
QTc [ms]	m	376±24†	373±20†	373±20†
	w	391±29	389±27	389±28
GainL	m	0.163±0.07 **	0.148±0.04 ***	0.153±0.04 ***
	w	0.192±0.09	0.174±0.08	0.182±0.08
GainF	m	0.021±0.012 *	0	0.020±0.012 **
	w	0.026±0.017	0	0.027±0.020
τ [beats]	m	176±118	169±61**	189±60**
	w	162±101	149±66	173±63

^*p<0.05,

^**p<0.01,

^***p<0.001,

^†p<0.0000001.

Only RMS and QTc were analyzed on a nonlinear static model. Different averaging (no averaging, averaging over 10 and 40 beats) of QT and RR intervals was used, Tab. 3.

Table 3.

QTc and RMS given by a nonlinear static model. QT1: no averaging was used. QT10 and QT40: averaged RR and QT intervals over 10 or 40 beats were analyzed. m – men, w – women. Statistical significance of gender differences:

Parameters		QT1	QT10	QT40
RMS [ms]	m	8.1±3.5	4.9±2.3	4.9±2.3
	w	8.7±5	4.8±2.3	4.8±2.3
QTc [ms]	m	365±27	370±24*	370±24*
	w	370±28	378±25	377±25

^*p<0.05,

^**p<0.01.

4. Discussion

Statistically significant gender differences exist in all QT parameters given by dynamic models. Women have longer QTc, a steeper QT/RR slope (Gain_L), faster QT adaptation to RR changes (τ), higher level of Gain_F and higher QT random variability (RMS).

If averaged QT intervals are used, the resulting RMS is significantly lower (self evident change) and not gender dependent. Gain_F is also significantly lower, but the gender dependency remains significant. The changes of QTc and Gain_L are minimal and depend primarily on the signal-to-noise ratio (SNR) of the analyzed data.

We conclude that QT averaging is deceptive. With averaging, the QT dynamic parameters are distorted. Moreover, if multiple QT intervals are used in analysis, this increases SNR in the same way as the use of a lower number of averaged QT intervals.

The longer QTc and steeper Gain_L in women are well known [1]. According to these two parameters, the sex differences in the QT interval are more apparent at slower heart rates. At higher heart rates, the differences in QT are minimized owing to the steeper Gain_L in women. This is valid in a steady state heart rate, when the QT interval is already adapted to RR. Such analysis cannot explain the higher prevalence of cardiac arrhythmias in women.

It is well known that abrupt changes in the level of arousal or physical activity are a well-established trigger for malignant ventricular arrhythmia in patients with repolarization abnormalities [4]. We therefore hypothesized that the significant differences in the QT interval during early excitation relative to the steady state may assist our understanding of why there is a higher prevalence of malignant arrhythmia in certain situations. Such dynamic differences of QT intervals during sudden change of RR are directly proportional to the level of Gain_L and τ, and indirectly proportional to the level of Gain_F. According to this hypothesis, the higher prevalence of cardiac arrhythmias in women, given by the longer QTc and steeper QT/RR slope, is compensated to some extent by the slightly faster adaptation of QT and higher level of Gain_F.

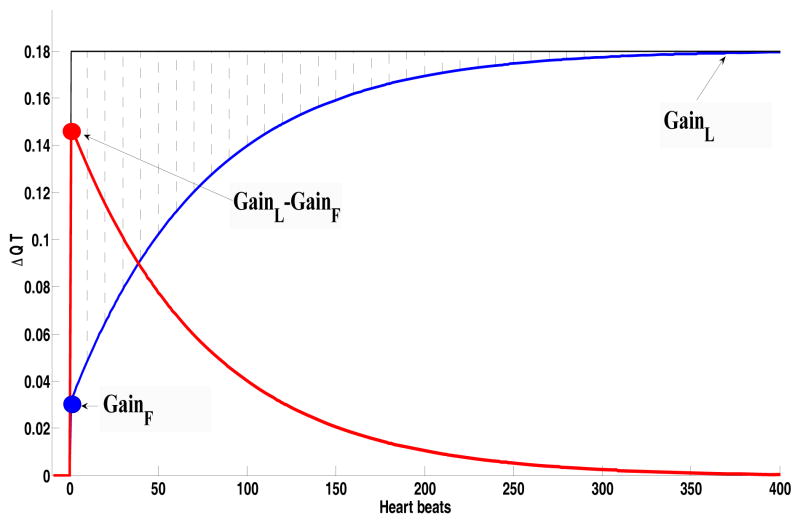
The QT behavior on a sudden change of RR, relative to steady state, is demonstrated in Fig. 1. The QT step response is given by the blue line, the QT steady state level by the black line. The QT difference is given by the red line, and corresponds to the dotted area between the step response and the steady state level of QT. The maximal amplitude of difference is seen at the time of RR change, and its level is (Gain_L - Gain_F )* ΔRR. The duration of QT difference depends on the time constant τ.

Fig. 1.

The QT difference from steady state on a sudden change of RR. The QT step response is given by the blue line; the QT steady state level is given by the black line. The QT difference, given by delayed QT adaptation, is given by the red line; this corresponds to the dotted area between step response and steady state level.

Thus, the dynamic aspects of QT interval coupling are likely to describe the clinical behavior of cardiac repolarization during the onset and offset of excitation, which in turn may assist our understanding of why “Torsades de Pointes” initiates in some circumstances and not others, despite comparable levels of activity or rest. Further, the testing of drug effects on QT dynamic parameters may elaborate why gender and certain specific physical states are more associated with drug-induced proarrhythmia. The proarrhythmic influence of drugs may originate in a change of Gain_L, Gain_F or τ without any change in QTc.

4.1. QT/RR models

The nonlinear static model has significantly higher RMS, QTc is underestimated, the gender differences in QTc exist with averaging only and are not so statistical significant as with dynamic models, and no QT dynamic parameters may be achieved by this model. The model was presented as something of a historical method, but is often still used. In our opinion, firstly the dynamic properties must be analyzed, and after their elimination any possible nonlinearity may be analyzed.

Three dynamic models were tested. The detailed comparison of a model may be based on mathematical properties (RMS, stability) or on physiological properties. The physiology of QT/RR coupling is at present not clear. The shape of the QT step response is known from measurements by Franz and Padrini [10, 11]. The step response has two parts – sudden change and slow adaptation. The physiological origin of these two parts is at present not known. The shapes of step responses in the TRF model agree very well with these previous measurements. The TRF model is the only possibility for measuring QT step response in healthy subjects. The shape is not merely an assumption; it is the result of analysis based on control system theory [6]. The models EXP and EXPDC are based on the assumed shape of QT step response. In model EXP, the important parameter Gain_F is missing. Such a parameter exists physiologically [10, 11] and its arrhythmic influence may be significant.

Mathematical comparison of the model is given primarily by RMS. The RMS in the EXP model is significantly higher than the RMS in the TRF or EXPDC models. Comparing the number of optimized parameters, EXP has 3, EXPDC 4 and TRF 3 or 4 (if the QT mean level is optimized). It may be supposed that the higher level of RMS in EXP is given by a missing parameter. But if some other parameter is added to the EXP model, for example nonlinearity [8], the RMS remains significantly higher. The importance of Gain_F is, therefore, also given mathematically.

The model EXPDC has somewhat lower RMS than the TRF model. The TRF model is a feedback system (IIR system), with higher sensitivity on irregular beats. EXPDC represents direct coupling and its stability is significantly higher. These differences manifest themselves primarily if the SNR of the analyzed signals is low.

5. Conclusion

Statistically significant gender differences exist in all tested parameters. Women have longer QTc, steeper slope Gain_L, faster adaptation τ, higher level of gain Gain_F, and higher level of RMS. We hypothesize that all these parameters are important in drugs tests. These parameters describe the QT behavior in the steady state and during sudden change of RR. The proarrhythmic influence of drugs may originate in a change to any of these parameters without any change to QTc.