Theoretical Study of the Mechanism of Oxoiron(IV) Formation from H₂O₂ and a Nonheme Iron(II) Complex: O–O Cleavage Involving Proton-Coupled Electron Transfer

Abstract

It has recently been shown that the nonheme oxoiron(IV) species supported by the 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane ligand (TMC) can be generated in near-quantitative yield by reacting [Fe^II(TMC)(OTf)₂] with a stoichiometric amount of H₂O₂ in CH₃CN in the presence of 2,6-lutidine (Li, F.; England, J.; Que L., Jr. J. Am. Chem. Soc. 2010, 132, 2134–2135). This finding has major implications for O–O bond cleavage events in both Fenton chemistry and nonheme iron enzymes. To understand the mechanism of this process, especially the intimate details of the O–O bond cleavage step, a series of density functional theory (DFT) calculations and analyses have been carried out. Two distinct reaction paths (A and B) were identified. Path A consists of two principal steps: (1) coordination of H₂O₂ to Fe(II) and (2) a combination of partial homolytic O–O bond cleavage and proton-coupled electron transfer (PCET). The latter combination renders the rate-limiting O–O cleavage effectively a heterolytic process. Path B proceeds via a simultaneous homolytic O–O bond cleavage of H₂O₂ and Fe–O bond formation. This is followed by H-abstraction from the resultant Fe(III)–OH species by an •OH radical. Calculations suggest that path B is plausible in the absence of base. However, once 2,6-lutidine is added to the reacting system, the reaction barrier is lowered and more importantly the mechanistic path switches to path A, where 2,6-lutidine plays an essential role as an acid-base catalyst in a manner similar to how the distal histidine or glutamate residue assists in Compound I formation in heme peroxidases. The reaction was found to proceed predominantly on the quintet spin state surface, and a transition to the triplet state, the experimentally known ground state for the TMC-oxoiron(IV) species, occurs in the last stage of the oxoiron(IV) formation process.

1. Introduction

The importance of a high-valent oxoiron(IV) (Fe(IV)=O) unit is well appreciated in the mechanisms of heme and nonheme iron enzymes, where Fe(IV)=O intermediates are often invoked as reactive species that are responsible for substrate oxidation steps including, among others, C-H bond cleavage.^1–3 The powerful oxidative properties of Fe(IV)=O intermediates of iron enzymes have inspired synthetic efforts to prepare complexes having such Fe(IV)=O units.⁴ 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane (TMC)^5a and its pendant thiolate analog^5b were among the first ligands (L) that allowed nonheme Fe(IV)=O complexes to be generated and characterized. Several complexes of the TMC series have also been shown to exhibit intriguing reactivity trends.^6,7

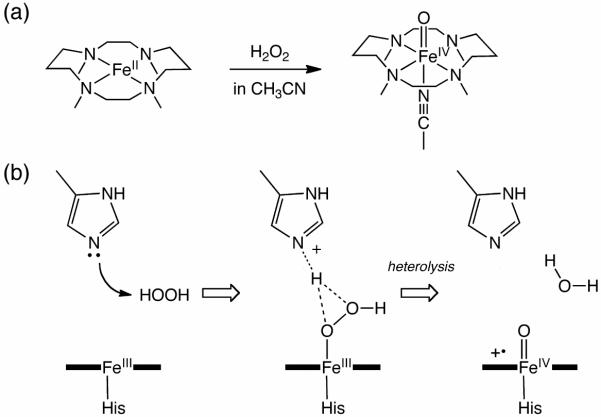
The rational design and further improvement of these synthetic Fe(IV)=O complexes necessarily require a detailed mechanistic understanding. However, it is difficult to unequivocally establish the mechanism for Fe(IV)=O formation experimentally, because it involves unstable and/or short-lived intermediates and transition states that are difficult to detect with conventional experimental techniques. For the characterization of such transient species, one may consider density functional theory (DFT) calculations, which can provide insights into both structural and electronic details, regardless of whether they are experimentally detectable. The reaction of [Fe^II(TMC)(NCCH₃)]²⁺ with H₂O₂ serves as an intriguing model for such computational studies. This reaction was recently shown by Li et al. to generate the [Fe^IV(O)(TMC)(NCCH₃)]²⁺ complex in near-quantitative yield from stoichiometric H₂O₂ (Scheme 1a) in the presence of 2,6-lutidine (2,6-dimethylpyridine).⁸ This observation excludes participation of an Fe(III)-level intermediate that can accumulate and strongly argues for a heterolytic O–O bond cleavage mechanism for the corresponding Fe(II)-H₂O₂ adduct to directly afford the experimentally observed Fe(IV)=O complex. In order to obtain a deeper molecular level understanding of the steps constituting the O–O bond cleavage itself that is not accessible by experimental approaches, DFT calculations have been carried out, to shed further light on this intriguing transformation.

Scheme 1.

(a) Fe(IV)=O formation in the synthetic system. (b) Likely mechanism for Cpd I formation in heme peroxidases.

Interestingly, it has also been shown experimentally that 2,6-lutidine enhances both the rate and yield of Fe(IV)=O formation, probably by acting as an acid-base catalyst.⁸ This proposed catalytic role of 2,6-lutidine is reminiscent of that played by a histidine or glutamate residue in the formation of an oxoiron(IV) porphyrin π-cation radical species (Compound I or Cpd I) in heme peroxidases (Scheme 1b).⁹ Further validation of the roles played by 2,6-lutidine can supplement the current mechanistic understanding of the O–O bond cleavage events in enzymatic as well as biomimetic systems. Therefore, the role of 2,6-lutidine as an acid-base catalyst is also examined theoretically.

The [Fe^II(TMC)(NCCH₃)]²⁺/H₂O₂ system is also an attractive model for our computational study with respect to the potential implications for Fenton chemistry. The mechanism for the reaction between Fe(II) and H₂O₂ has long been a subject of debate, as it is not clear whether the initial step involves homolytic or heterolytic O–O bond cleavage. The computational characterization of the Fe(TMC) reaction mechanism may provide useful insights into this experimentally challenging problem. In this study, DFT calculations have been applied to two reaction models of the TMC complex. Particular attention is focused on the mode of O–O cleavage and the role of the acid-base catalyst. Our computational study suggests that the initial phase of O–O bond cleavage in the presence of 2,6-lutidine has homolytic character. This phase is immediately followed by a partial proton-coupled electron transfer (PCET) step that results in an overall heterolytic O–O bond cleavage.

2. Methods

DFT calculations were performed using the Gaussian 09 program.¹⁰ Both quintet and triplet spin states were considered. The B3LYP¹¹ DFT functional was used in conjunction with two basis sets, B1 and B2. B1 is a combination of the SDD effective core potential basis set¹² for Fe and the 6-31G* basis set¹³ for all other atoms, and this was used for geometry optimizations. Vibrational analyses at the B3LYP/B1 stationary points confirmed their nature, and were used for zero-point energy (ZPE) calculations. B2 employed the TZVP basis set¹⁴ for all atoms, and was used for single point calculations to improve energetics. The effect of the acetonitrile solvent was modeled by the self-consistent reaction field (SCRF) method,¹⁵ as implemented in Gaussian 09. Molecular geometries were drawn with VMD software.¹⁶ Mulliken and natural-population-analysis (NPA)¹⁷ charges were calculated for some species to understand their intramolecular charge distributions.

Two different reaction models were considered. Model-1 can be regarded as an archetypal model, in which [Fe^II(TMC)(NCCH₃)]²⁺ reacts with H₂O₂ in the presence of 2,6-lutidine, which is thought to act as an acid-base catalyst. In Model-2, acetonitrile, in place of 2,6-lutidine, is assumed to act as an acid-base catalyst. This corresponds to the case where 2,6-lutidine is not present in the reacting system, and one of the solvent acetonitrile molecules approaches the reaction center and serves as a catalyst. For path A (see Scheme 2) of Model-1, geometry optimization was done in both the gas phase and solvent to understand the effect of solvation. However, to reduce the computational cost, only solution-phase geometry optimization was done for the other reaction paths. We follow an atomic nomenclature system as described in Scheme 2, to refer to some specific atoms in what follows.

Scheme 2.

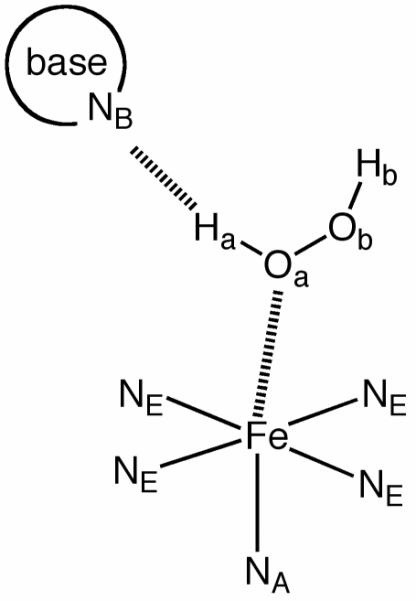
Labels for key atoms.

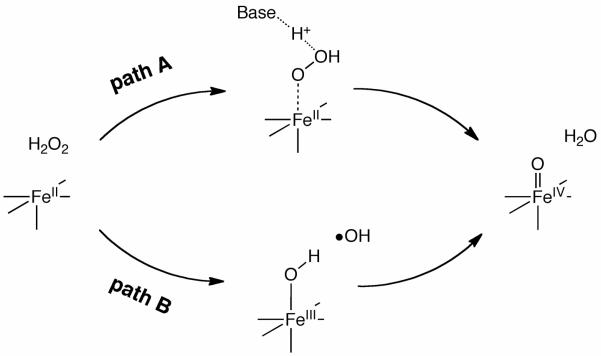
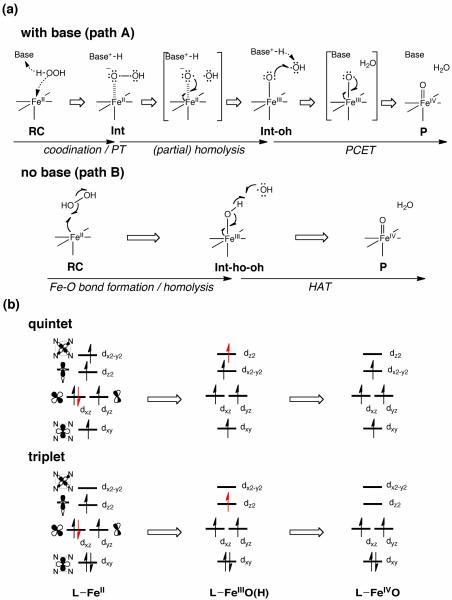
We examined two possible mechanisms for Fe(IV)=O formation from the reaction of the TMC-Fe(II) complex with H₂O₂ (paths A and B), which are presented in Scheme 3. Path A involves proton migration from the proximal oxygen to the distal oxygen within the coordinating H₂O₂ ligand. This proton migration is facilitated by a nearby base molecule and the subsequent O–O bond cleavage generates an Fe(IV)=O species, as well as a water molecule. On the other hand, path B involves the initial homolytic O–O bond cleavage of hydrogen peroxide at the ferrous center. This cleavage step enables the proximal OH radical of hydrogen peroxide to form a covalent bond with Fe, resulting in an increase in the oxidation state of iron to +3. The distal OH radical fragment then abstracts a hydrogen atom from the Fe(III)–OH moiety, to afford Fe(IV)=O and a water molecule.

Scheme 3.

Schematic representation of two reaction paths considered in this study.

3. Results and Discussion

3.1. Mechanism for Model-1

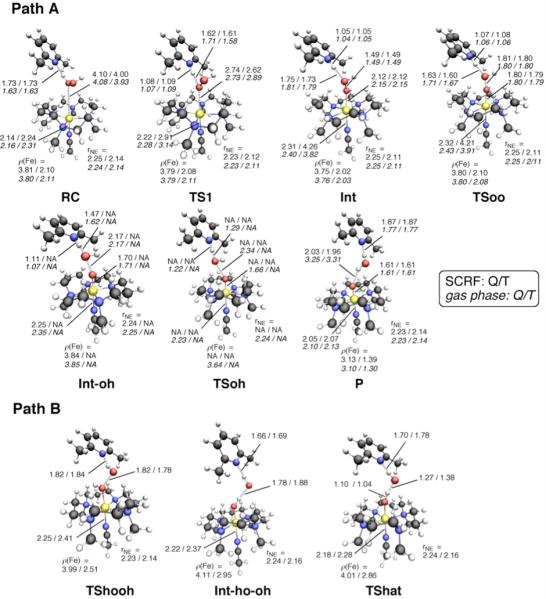
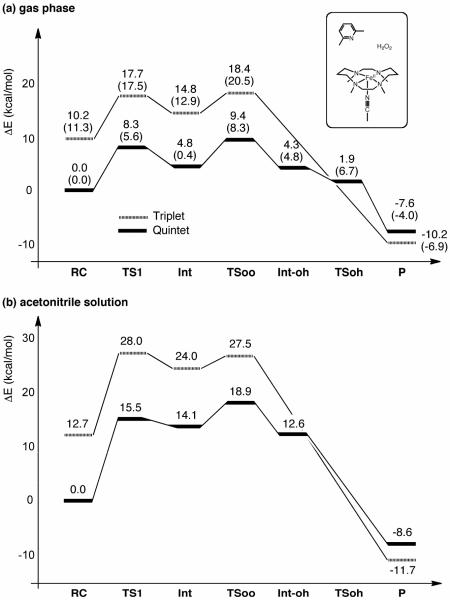
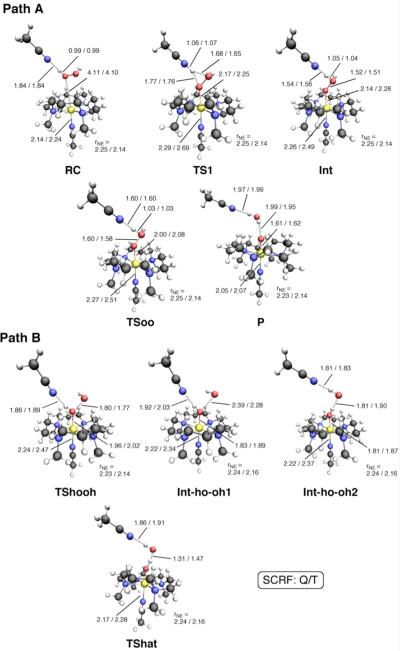
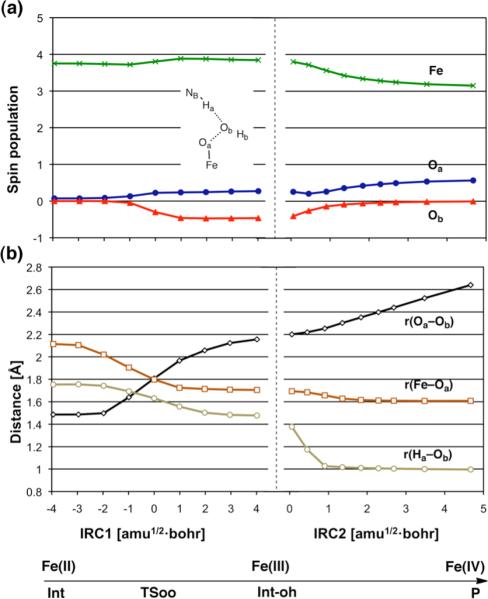
Our DFT calculations revealed reaction paths A and B for Model-1 (Scheme 3) for the formation of Fe(IV)=O from Fe(II) and H₂O₂. Several intermediates and transition states (TSs) were identified for each path. Figure 1 summarizes the optimized geometries of all key states. On path A, the reaction begins with the formation of a reaction cluster (RC), in which all separate molecular fragments interact attractively, but weakly with one another. At this stage, the distance between Fe and O_a (see Scheme 2) can be as long as c.a. 4 Å; thus, [Fe^II(TMC)(NCCH₃)]²⁺ remains nearly intact. There are four equatorial nitrogen (N_E) atoms coordinating to Fe, with an average Fe–N distance ($r_{\mathrm{NE}}={\stackrel{‒}{r}}_{\mathrm{Fe}-{\mathrm{N}}_{\mathrm{E}}}$) that is longer in the quintet state than in the triplet state by approximately 0.1 Å. This geometric difference is attributed to the occupation of the in-plane σ* orbital only in the quintet state, but not in the triplet state (see also section 3.5).^7a In the initial phase of the reaction, one oxygen atom of H₂O₂ (O_a) approaches the Fe center, while at the same time, the proton (H_a) on O_a migrates to the nitrogen atom of 2,6-lutidine (N_B). This step requires an energy barrier to be overcome, and the corresponding TS can be located as TS1, which has an Fe–O_a distance of 2.6 – 2.9 Å, depending on the spin state and the reaction environment. As the reaction progresses further, the Fe–O_a distance decreases to 2.12 Å in acetonitrile, to form an Fe(II)OOH-type intermediate (Int). At this point, the transferred proton (H_a) shifts its H-bonding target to the distal oxygen (O_b). The reaction process up to this point can be viewed as a H₂O₂ coordination step that involves proton transfer from H₂O₂ to the base. Although the formal oxidation state of Fe (+2) does not change in going from RC to Int, there is an increase in the Fe–N_A distance, which occurs in response to H₂O₂ coordination along that axis. As H₂O₂ approaches the iron center, the ligand field in that direction will increase, meaning that the energy levels of occupied anti-bonding d_z2-, d_xz- and d_yz-type orbitals will be raised and the system will become destabilized. This results in temporary dissociation of the acetonitrile ligand from Fe to alleviate the destabilization. In the second step of path A, the O_a–O_b bond in the Fe(II)OOH-type intermediate is cleaved. The O_a–O_b distance, which is calculated to be 1.49 Å in Int, elongates to 1.8 Å, leading to a TS for O–O cleavage (TSoo). Interestingly, further elongation of the O_a–O_b bond yields a local energy-minimum state, Int-oh, but only on the quintet surface. The H₂O₂ hydrogen (H_a) that was temporarily donated to N_B in Int and Int-oh is donated back to O_b to provide the final product (P). This back-donation of a proton, in the quintet, is found to involve a transition state (TSoh), but only for the gas-phase calculation without zero-point energy (ZPE) correction. Finally, the product complex P is obtained, which is composed of weakly interacting [Fe^IVO(TMC)(CH₃CN)]²⁺, H₂O, and 2,6-lutidine.

Figure 1.

Geometries (bond distances in Å) and spin population ρ(Fe) values for key species for Model-1 (paths A and B) in which acetonitrile is the axial ligand and 2,6-lutidine is the catalyst. Optimization was done at the B3LYP/B1 level in acetonitrile solution (plain) and in the gas phase (italic) for the quintet (Q) and triplet (T) states.

Path B was also found for Model-1. On this path, 2,6-lutidine forms a H-bond with the distal OH of hydrogen peroxide during the reaction. Attempts to find path B, assuming a H-bond between 2,6-lutidine and the proximal OH, failed, suggesting that this path does not exist. The first transition state for path B (TShooh) is associated with the homolytic O–O bond cleavage of hydrogen peroxide at the iron center. Upon completion, the proximal OH group reorients in a manner such that H_a becomes H-bonded to O_b. As a result, the intermediate Int-ho-oh is formed. Similar combinations of homolytic O–O cleavage and subsequent OH reorientation were proposed for Fe(III)-HOOH species in a catalase mimic,¹⁸ NOS,¹⁹ and CPO.²⁰ The reoriented hydrogen (H_a) is then abstracted by the distal OH radical, to form the final Fe(IV)=O product (P).

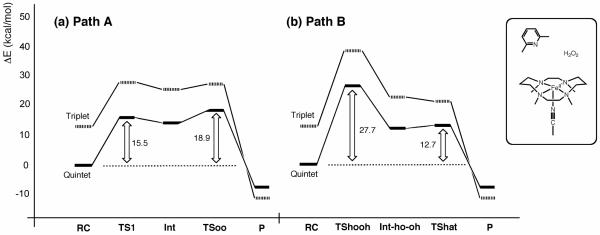
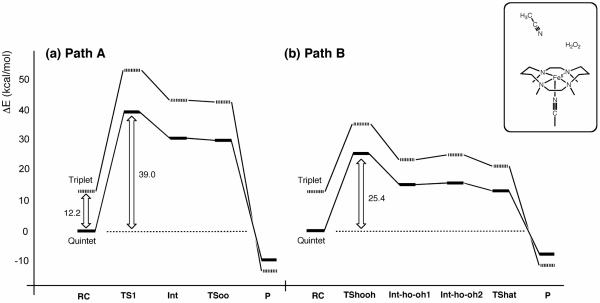
Figure 2 compares the reaction energy profiles for paths A and B of Model-1. In both mechanisms, the reaction primarily proceeds on the quintet-state energy surface. The profile for path A shows that the O–O bond cleavage step (second step) has a higher barrier than the first step, which involves H₂O₂ coordination to Fe(II) assisted by proton transfer from the O_a of H₂O₂ to 2,6-lutidine. This means that O–O cleavage is the rate-limiting step, and the overall reaction barrier is 18.9 kcal/mol. O–O cleavage is also the rate-limiting step for path B, but it represents the first step for this path, and the second step involves H-abstraction from the proximal OH group by the distal OH radical or H-transfer (HAT) from the proximal to the distal OH group. The overall reaction barrier for path B is 27.7 kcal/mol. These calculations suggest that path A is favored over path B in the reaction of Model-1.

Figure 2.

Comparison of the energy profiles in acetonitrile solution for Model-1, (a) path A and (b) path B, as obtained at the B3LYP(SCRF)/B2//B3LYP(SCRF)/B1+ZPE level.

3.2. Effect of solvent

The first step of path A of Model-1 is a H₂O₂-coordination step involving proton transfer from H₂O₂ to the base. As shown in Figure 1, at Int, the Fe–O_a distance decreases to 2.12 Å (in acetonitrile solution) or 2.15 Å (in the gas phase). Thus, no significant solvent effects on geometries are observed. The reaction energy profiles for Model-1, both in the gas phase and in solution at the B3LYP/B2//B1 level, are given in Figure 3. At the RC state, the quintet state is more stable than the triplet state by 10.2 and 12.7 kcal/mol in the gas phase and in solution, respectively. Therefore, it is proposed that the reaction starts exclusively in the quintet state. In the gas phase, the barrier for the first step, in the quintet state, is calculated to be 8.3 kcal/mol, and the barrier for the second step is 9.4 kcal/mol. These barrier heights for the two steps are comparable in the gas phase, with the latter being slightly higher. By comparison, the barriers are calculated to be higher in solution; the barrier for the first and second steps are 15.5 and 18.9 kcal/mol, respectively. Thus, the latter is higher in solution by 3.4 kcal/mol, suggesting that the O–O cleavage should be the rate-limiting step.

Figure 3.

Reaction energy profiles for Model-1, with acetonitrile as an axial ligand and 2,6-lutidine as catalyst, (a) in the gas phase, and (b) in acetonitrile, at the B3LYP/B2 level, with geometries optimized at the B3LYP/B1 level. ZPE at the B3LYP/B1 level, in either the gas phase or solution phase, was included. The values in parentheses indicate the relative energies obtained at the B3LYP/B1 level without ZPE correction.

In the B3LYP/B1 gas-phase calculation, the O–O cleavage in the Fe(II)OOH unit leads to an intermediate involving an •OH radical, ⁵Int-oh, and the subsequent proton transfer has a finite energy barrier (1.8 kcal/mol). This barrier is eliminated when a ZPE correction is included (Figure 3a). In solution, ⁵Int-oh is observed, but the subsequent 5TSoh could not be found because the PES is flat in this region. Therefore, the ⁵Int-oh state can be considered as a shoulder-type energy minimum on the potential energy surface in solution. The theoretically observed labile species, formed upon O–O cleavage, is reminiscent of analogous species suggested for other enzymes including tetrahydrobiopterin-dependent amino acid hydroxylases,^21a clavaminic acid synthase (CAS),^21b isopenicillin N synthase (IPNS),^21c cytochrome c oxidase (CcO),^22a and nitric oxide synthase (NOS).^22b With regard to the mechanism of O–O cleavage, previous theoretical studies showed that, after homolytic O–O cleavage of an Fe(III)OOH species, the distal OH radical undergoes a so-called “somersault” action. This allows the O–H bond to realign itself and form a H-bond between H_a and O_a.^23–25 Notably, however, because there is some remaining O–O bond character in Int-oh, which forbids the OH moiety from proceeding via the somersault mechanism. A similar scenario was reported in a computational study of CcO.^22a

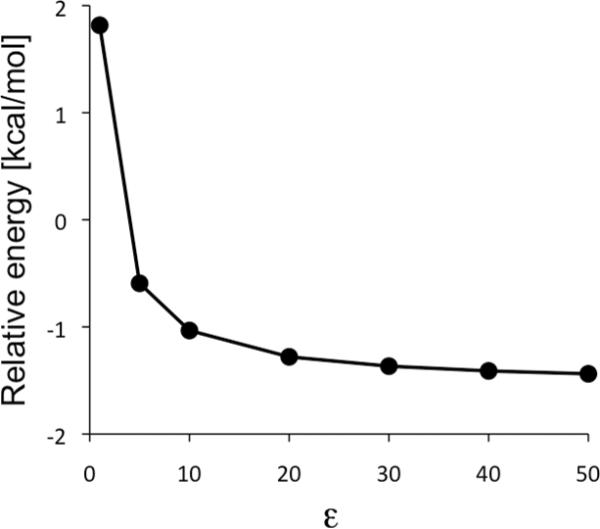
We checked the influence of solvents with varying dielectric constants on the formation of a free OH radical by performing a series of single-point energy calculations on the gas-phase geometries of ⁵Int-oh and ⁵TSoh, at the B3LYP(SCRF)/B1 level. Figure 4 presents the energy of ⁵TSoh relative to 5Int-oh, as a function of dielectric constant (ε). At the gas-phase B3LYP/B1 level (ε = 1), ⁵TSoh is higher in energy than ⁵Int-oh by 1.8 kcal/mol. It is apparent that ⁵TSoh becomes increasingly stabilized with increasing polarity. This indicates that solvents, including acetonitrile (ε~35.7), make the generation of a free radical more unlikely.

Figure 4.

Plot of energies for ⁵TSoh, relative to ⁵Int-oh as a function of solvent dielectric constant of solvent. The data were obtained at the B3LYP(SCRF)/B1//B3LYP(gas-phase)/B1 level.

It seems likely, from the energy profiles, that the reaction proceeds on the quintet-state energy surface up to this point. However, it is experimentally established that [Fe^IVO(TMC)(CH₃CN)]²⁺ has a triplet ground state.⁵ Consistent with this, at the stage of the product complex P, which involves [Fe^IVO(TMC)(CH₃CN)]²⁺, the triplet state is in fact calculated to be the ground state. Thus, as the energy profile in solution (Figures 2 and 3) suggests, a quintet-triplet spin conversion must occur in the final phase of the reaction. Whilst high-spin states are favored in ferrous and ferric states, the lower-spin triplet state is significantly stabilized in Fe(IV)=O because the decrease in the number of electrons occupying the d-type orbitals diminishes the exchange stabilization that can be gained by a high-spin configuration. This explains the preference for the quintet at early stages, and the very late spin crossover.

3.3. Effect of the base

The specific role of the base in the conversion of [Fe^II(TMC)(CH₃CN)]²⁺ to [Fe^IVO(TMC)(CH₃CN)]²⁺ can be discerned by comparing Model-1 with Model-2. Figure 5 depicts the stationary-point geometries for Model-2, as optimized for the reaction that employs acetonitrile as the axial ligand, catalyst, and solvent. As with Model-1 (Figure 1), RC is a loosely bound complex of the reactant components. However, a comparison between the two models reveals a few remarkable geometric differences in the subsequent steps, especially for path A. First, the Fe–O_a distance in TS1 is shorter for Model-2 (~2.2 Å) than that for Model-1 (~2.7 Å). In addition, the H₂O₂ proton (H_a), which is transferred to N_B, interacts mainly with O_a in TS1 for Model-1, interacts in Model-2 almost equally with both O_a and O_b. TS1 in Model-1 is associated with H₂O₂ coordination onto Fe, as triggered by the deprotonation of H₂O₂. However, the calculated geometries for TS1 in Model-2 suggest that it can be better characterized as a transition state for the proton migration from O_a to O_b. In contrast to the H_a proton in Model-1, where the H_a proton is bound to N_B and H-bonded to Ob in Int, the proton in Model-2 is instead bound to O_b and H-bonded to N_B at Int. Therefore, Int in Model-2 can be considered as an Fe(II)-OOH₂-type intermediate. This results from the low basicity of the acetonitrile base, compared with 2,6-lutidine. A slight increase in the O–O bond distance in the Fe(II)-OOH₂-type intermediate, leads to a TS (TSoo), and a further increase results in the formation of product complex P, which is composed of 2_TMC-an, H₂O, and acetonitrile. In Model-2, Int-oh is not observed.

Figure 5.

Geometries (bond distances in Å) for key species, for Model-2 (acetonitrile as the axial ligand, catalyst and solvent), at the B3LYP/B1 level, for the quintet (Q) and triplet (T) states.

Path B of Model-2 is similar to path B of Model-1. However, H-bonding between the acetonitrile base and the proximal OH is favorable for the first step of path B of Model-2. The first step of path B involves simultaneous Fe–O bond formation and homolytic O–O bond cleavage via a transition state, TShooh. In fact, the Fe–O bond in TShooh is much shorter (1.96 Å in the quintet) than the Fe–O distance (4.11 Å) in RC, and the O–O bond of H₂O₂ is significantly elongated (1.80 Å). The O–O cleavage is completed at intermediate Int-ho-oh1 where the Fe–O and O–O distances are 1.83 and 2.39 Å, respectively, in the quintet state. The system then undergoes reorganization of the H-bond network, so the H_a in the Fe(III)–OH moiety aligns itself with the •OH fragment. The OH radical then abstracts a hydrogen atom from the Fe(III)–OH moiety, to yield H₂O and a TMC-Fe(IV)=O species (P) via TShat.

Figure 6 compares the energy profiles for the two Model-2 reaction pathways, at the B3LYP(SCRF)/B2//B3LYP(SCRF)/B1+ZPE(B1) level. As discussed earlier, the rate-limiting step in path A for Model-1 is the O–O bond cleavage step with a barrier height of 18.9 kcal/mol. Interestingly, the rate-limiting step in path A for Model-2 is not the O–O bond cleavage step, but is instead the preceding proton migration step. The barrier for proton migration is as high as 39 kcal/mol in the quintet state (Figure 6a). Although ⁵TSoo is calculated as a saddle point, at the B3LYP(SCRF)/B1 level, the energy maximum disappears with ZPE corrections (Table S5). Hence, the calculations predict that, contrary to Model-1, the first step is the rate-limiting step in path A for Model-2. The high energy barrier required in path A for Model-2 is attributed to the low basicity of acetonitrile, which renders the peroxidase-like proton migration unachievable. This high barrier leads us to conclude that path A can be ruled out as a possibility.

Figure 6.

Comparison of energy profiles in acetonitrile for Model-2, (a) path A and (b) path B, as obtained at the B3LYP(SCRF)/B2//B3LYP(SCRF)/B1+ZPE level.

The rate-limiting step in path B for Model-2 is the homolytic O–O bond cleavage, with a barrier height of 25.4 kcal/mol (Figure 6b). This barrier is much lower than that for path A, and contrary to Model-1, the reaction with Model-2 proceeds via path B. It is noteworthy that this lower barrier for Model-2 is still higher than that for Model-1, which is consistent with the experimental observation that 2,6-lutidine enhances the reaction rate. Calculations with B1 suggest that Int-ho-oh2, involving an •OH free radical, is metastable, but the subsequent barrier is eliminated in B2 calculations. Therefore, the formation of a free radical does not seem plausible for Model-2. We note, however, that whereas the barrier after a •OH-involving intermediate in Model-1 (i.e. Int-oh) is zero at the B3LYP(SCRF)/B1 level, that in Model-2 (i.e. Int-ho-oh2) has a finite barrier (3.5 and 1.0 kcal/mol without and with ZPE corrections, respectively) at that theoretical level (Tables S3 and S5). This implies that Model-2 has a greater tendency to form metastable •OH than Model-1.²⁶ Thus, it might still be possible that a metastable •OH radical is formed at Int-ho-oh2 in Model-2. The •OH free radical might then easily dissociate from the Fe(III)-OH moiety or be scavenged or converted to other forms by the solvent or other molecules present in the system. Such side reactions could explain the lower yield of Fe(IV)=O in the absence of base (~70%), as compared with the ~90% yield in the presence of 2,6-lutidine,⁸ Further exploration of the role of •OH in the reactions of synthetic iron complexes is beyond the scope of this study but constitutes an interesting research topic. An important insight obtained from our calculations is that 2,6-lutidine is utilized not merely to lower the O–O cleavage barrier, but also to switch the favorable path to path A for more efficient Fe(IV)=O formation.

3.4. Proton-coupled electron transfer in the O–O cleavage step in Path A

The process described in Scheme 1a involves a change in the formal oxidation state for Fe, from +2 to +4. Since the coordination step in Model-1 (from RC to Int in path A) does not change the oxidation state of Fe, the change must occur in the second step. This somewhat complicated electronic process is discussed here. The process from Int to P involves a shoulder-type intermediate (Int-oh) in Model-1, as shown in Figure 3b. Therefore, a forward intrinsic reaction coordinate (IRC)²⁷ calculation, from TSoo terminates at Int-oh and does not reach P. Thus, it was not possible to trace the whole process from Int to P, using a single set of IRC calculations starting from TSoo. To analyze the reaction path from Int-oh to P, we performed geometry optimization that fixed the H_a–O_b distance at1.4 Å, to get a state slightly after Int-oh on the reaction path. The reaction path was then traced by allowing the resultant geometry to proceed downhill on the potential energy surface. This was done using the keyword “IRC=downhill” in Gaussian 09. The IRCs from Int to Int-oh, and from Int-oh to P, are henceforth called IRC1 and IRC2, respectively. Note that the reaction paths are traced using IRC calculations in mass-weighted Cartesian coordinates. The units of IRC are [amu^1/2•bohr], where amu is an atomic mass unit and bohr is a unit of distance. Figure 7a plots the key atomic spin population values along the reaction coordinates in acetonitrile solvent, and Figure 7b depicts the variations in a few key distances along the IRCs. Below the horizontal axis of Figure 7b, changes in Fe oxidation state are shown schematically. Initially (⁵Int), the spin population on Fe (ρ(Fe)) is 3.75. After IRC1 = 0 amu^1/2•bohr (i.e. around ⁵TSoo), this value increases slightly to c.a. 3.85. where r(O_a–O_b) ~ 1.8 Å. Along IRC2, the ρ(Fe) value gradually decreases to 3.1. These changes in the spin distribution are accompanied by changes in the Fe–O_a bond distance (Figure 7b). To further characterize the intermediates with differing electronic and geometric features, and Fe-O distances, in different Fe oxidation states were evaluated for a series of simple TMC complexes. The results are shown in Table 1 and suggest that the spin population values are similar in magnitude for the same Fe oxidation states.²⁸ More specifically, the ρ(Fe) value is 3.7–3.8 for the quintet TMC-Fe(II) complex, 3.9–4.2 for Fe(III) for the sextet TMC-Fe(III) complex, and 3.1 for the quintet TMC-Fe(IV) complex. Note, however, that comparisons of different species having the identical oxidation state show that the ρ(Fe) values are not perfectly identical, but vary with the ligand coordination environment. It should also be noted that the ρ(Fe) values are not always identical to the number of unpaired electrons. For example, the high-spin quintet Fe(II) case has one doubly occupied and four singly occupied d-type orbitals, and the ρ(Fe) value is close to 4. However, in the cases of the sextet Fe(III) and the quintet Fe(IV) species, there is significant d-orbital delocalization toward the oxygen ligand. As a result, the ρ(Fe) values are much smaller than the ideal values, namely, 5 for Fe(III) and 4 for Fe(IV). As for the Fe–O_a distance, there is a range of values for the Fe(III) oxidation state, as the distance depends strongly on the bonding nature of the Fe–O moiety. Nevertheless, a comparison between two species composed of the same atoms but differing in the oxidation state (e.g., [Fe^IIOOH(TMC)(CH₃CN)]¹⁺ vs. [Fe^IIIOOH(TMC)(CH₃CN)]²⁺) reveals that the distance is shorter in higher oxidation states.

Figure 7.

Variations in (a) key atomic spin populations and (b) Fe–O distance, as the reaction proceeds from Int through Int-oh to P. The values were obtained for path A (Model-1) in the quintet state, in acetonitrile solution. The data are from B3LYP(SCRF)/B1 calculations. Note that IRC2 = 0 corresponds to the state in which the geometry is optimized by fixing the H_a–O_b distance at 1.4 Å.

Table 1.

Mulliken atomic spin populations and Fe–O distances (in Å) for key species having various oxidation states for Fe calculated at the B3LYP(SCRF)/B1 level in acetonitrile solvent

species	ρ(Fe)	ρ(Oa)/ρ(Ob)	r(Fe–Oa)
[FeII(TMC)(CH3CN)]2+	3.81	−/−	–
[FeIIOOH(TMC)(CH3CN)]1+	3.73	0.10/0.00	2.04
[FeIIIO(TMC)(CH3CN)]1+	3.91	0.80/−	1.73
[FeIIIOH(TMC)(CH3CN)]1+	4.14	0.34/−	1.84
[FeIIIOOH(TMC)(CH3CN)]2+	4.06	0.38/0.10	1.89
[FeIVO(TMC)(CH3CN)]2+	3.12	0.59/−	1.61

Based on the results of Table 1, we now analyze the changes in spin density and geometry in going from ⁵Int to 5P in Figure 7. The ρ(Fe) value of 3.75 and the Fe–O_a distance of 2.12 Å at ⁵Int suggest that this state is characterized as [Fe^IIOOH(TMC)(CH₃CN)]¹⁺. Up to ⁵Int, the oxidation state of Fe does not change from +2. The small increase in ρ(Fe) at around r(O_a–O_b) = 1.8 Å suggests that the Fe oxidation state has changed to +3. This is verified by the fact that the ρ(Fe) value of 3.85 and the r(Fe–O_b) distance of 1.7 Å in ⁵Int-oh are similar to those for [Fe^IIIO(TMC)(CH₃CN)]¹⁺. The decreased ρ(Fe) value of ~3.1 in IRC2 suggests that the oxidation state of Fe has changed from +3 to +4 here. The Fe–O distance of 1.61 Å in P is also consistent with the typical value for Fe(IV)=O species (Table 1). Overall, our analysis shows that the Fe oxidation state changes from +2 via +3 to +4, in the conversion of [Fe^II(TMC)(CH₃CN)]²⁺ to [Fe^IVO(TMC)(CH₃CN)]²⁺ (Figure 7c).

Let us now turn our attention to the oxygen atoms (O_a and O_b) from H₂O₂. At the stage of ⁵Int (Figure 7a), neither of the oxygen atoms has a significant spin population, because the two oxygen atoms are covalently bonded in the [OOH]⁻ moiety. However, the departing oxygen (O_b) begins to accumulate a large negative spin population at around IRC1 = 0 amu^1/2•bohr. In the ⁵Int-oh state, this value amounts to −0.46. This non-zero spin population on O_b suggests that the O–O bond cleavage bears some homolytic character. It is unclear whether or not the ρ(O_b) value of −0.46 reflects the dissociating distal OH moiety gaining some extra electrons from the O_a part. Therefore, we further analyzed the group charge on the O_bH_b moiety in the ⁵Int-oh state. The calculated charges were negative: −0.26 (Mulliken) and −0.33 (NPA) at the B3LYP(SCRF)/B1 level, but the neutral •OH should have a zero charge. Therefore, the O_bH_b moiety must accept some extra electrons from the Fe–O_a part. This means that the O–O cleavage is not purely homolytic, but bears some heterolytic character. The group charge on the [2,6-lutidine---H_a⁺] moiety in the ⁵Int-oh state was calculated to be 0.80 (Mulliken) and 0.84 (NPA). This reflects some electron delocalization from the O_bH_b moiety to the [2,6-lutidine---H⁺] moiety. It is estimated that in total, 0.46–0.49 extra electrons are shifted from Fe–O_a to O_bH_b.

The ρ(O_b) value changes to zero when the oxidation state of Fe changes from +3 to +4, at around IRC2 = 1.0 amu^1/2•bohr. At this point, the OH moiety loses its radical character and is transformed into a water molecule. This water formation process involves two simultaneous, but distinct, steps. One is the transfer of a proton (H_a) from the base nitrogen to O_b, and the other is the transfer of an electron from Fe–O_a to O_b. This eliminates the radical character of the O_bH_b moiety. This event is therefore best described as a proton-coupled electron transfer (PCET) step, in which a proton and an electron are transferred simultaneously, but along different pathways.²⁹ After the PCET step, H_b becomes realigned to form a H-bond with O_a (see Figure S1 in the Supporting Information).

The spin population on O_a increases with increasing the oxidation state on Fe along IRC2 (Figure 7a). This is inconsistent with the ideal oxygen spin populations of 0.80 and 0.59 in ⁶[Fe^IIIO(TMC)(CH₃CN)]¹⁺ and ⁵[Fe^IVO(TMC)(CH₃CN)]²⁺, respectively (Table 1). Thus, the Fe(IV) state should have a smaller ρ(O_a) value than the Fe(III) state. However, this inconsistency comes from the partial heterolytic character of the O–O bond cleavage. The O_a of ⁶[Fe^IIIO(TMC)(CH₃CN)]¹⁺ is supposed to have a spin population value of 0.80, but when the O–O bond is cleaved, some electron density is shifted from the Fe–O_a moiety to the dissociating O_bH_b moiety. As a result, the number of electrons that the Fe–O_a moiety holds in ⁵Int-oh is smaller than that in the corresponding moiety in the isolated ⁶[Fe^IIIO(TMC)(CH₃CN)]¹⁺. This makes ρ(O_a) in the Fe(III) state small (0.27), in comparison to the ideal value of 0.80. The ρ(O_b) value of −0.46 and the ρ(O_a) value of 0.27 in ⁵Int, together with the above-described results from the atomic charge analysis, lead us to conclude that the two electrons that make up the O–O bond are shared unevenly (about 1.5 on O_b and about 0.5 on O_a), upon cleavage of the O–O bond.

3.5. Electron reorganization during the entire process

The overall electron reorganization process is schematically illustrated in Scheme 4. The first step of the reaction in the presence of 2,6-lutidine (path A from RC to Int) is associated with the coordination of H₂O₂ to Fe. This step also involves proton transfer from O_a to the base in the vicinity of the reaction center. However, this step does not involve a change in the formal oxidation state of Fe. In the following step, from Int to Int-oh, the O–O bond is cleaved. As discussed earlier, this cleavage has both homolytic and heterolytic character. For simplicity, we depict this cleavage, as purely homolytic in Scheme 4a. This results in an increase of the Fe oxidation state to +3, as a new Fe–O bond is formed. Subsequently, in going from Int-oh to P, the proton (H_a) originally on O_a is donated from the base back to O_b. At the same time, an electron (the number of electrons actually being smaller than 1) is donated to O_b. This PCET process creates a molecule of water. Also, a double bond is formed between Fe and O_a, and the Fe oxidation state is increased to +4.

Scheme 4.

Schematic illustration of (a) the electron reorganization process and (b) the change in d-orbital electron occupancy. The electron ejected in the subsequent step is colored red.

Whilst the O–O bond cleavage in the Fe(II)OOH intermediate in path A of Model-1 has partial heterolytic character, the cleavage is purely homolytic in path B. This can be seen from the ρ(O_b) value of −1.02 for ⁵Int-ho-oh of Model-1. The second step in path B is described as H-abstraction from Fe(III)–OH by •OH. Hence, the electron reorganization process for path B can be described by the second scheme in Scheme 4a. The H₂O₂ ligand in path B has essentially equivalent electronic distribution on the two oxygen atoms, and O–O cleavage occurs homolytically. In contrast, O–O bond cleavage in path A takes place at the Fe(II)OOH stage. Pure homolytic O–O bond cleavage of this species would generate an OH radical and an unstable Fe(III)–O species; therefore, the O–O cleavage in Model-1 has some heterolytic character, which is assisted by the nearby protonated base.

The oxidation-state change implies that the d-MOs of TMC-Fe(II) must lose two electrons upon Fe(IV)=O formation. Scheme 4b describes in more detail which electrons are lost. When the oxidation state of Fe changes from +2 to +3, the down-spin electron in the d_xz-type MO is removed to make an Fe-O bond. When the oxidation state changes from +3 to +4, the up-spin electron in the d_z2-type MO is then lost to make another bond. It is noteworthy that in a previous study the Fe(II) state of [Fe^II(TMC)(NCCH₃)]²⁺ has been calculated to have the occupation pattern as described in Scheme 4b.^7a This is somewhat different from the cases reported for other complexes bearing different ligands (e.g., N4Py), where the d_xy-type MO, instead of the d_xz-type MO, is doubly occupied. This double occupation of the d_xz-type MO in the case of TMC-Fe(II) may be attributed to a weaker ligand field in the axial direction vs. in the equatorial direction. The occupancy in [Fe^II(TMC)(NCCH₃)]²⁺ may have a beneficial effect on the O–O scission process, since both the d_xz- and d_z2-type MOs, from which the electrons are ejected, favorably overlap with the oxygen orbitals.

3.6. Fenton chemistry

For more than 100 years, it has been known that the combination of hydrogen peroxide and an iron(II) salt, referred to as Fenton's reagent,³⁰ affords a powerful oxidant. However, it is not yet entirely clear if the oxidant is generated via a homolytic cleavage of the O–O bond of H₂O₂, which yields a free OH• radical (eq. 1),³¹ or via a heterolytic cleavage, which yields an oxoiron(IV) species (eq. 2).³²

$${\mathrm{Fe}}^{2+}{\mathrm{H}}_2{\mathrm{O}}_2\to {\mathrm{Fe}}^{3+}+\mathrm{OH}•+{\mathrm{OH}}^{-}$$ (1)

$${\mathrm{Fe}}^{2+}{\mathrm{H}}_2{\mathrm{O}}_2\to {\mathrm{FeO}}^{2+}+{\mathrm{H}}_2\mathrm{O}$$ (2)

The reaction achieved using the TMC ligand by Li et al.⁸ (Scheme 1a) is interesting in view of the elusive nature of the actual oxidant in Fenton's reagent. Baerends and coworkers have investigated the reaction of an Fe(II) ion and H₂O₂ in aqueous solution using DFT and Car-Parrinello molecular dynamics³³ and demonstrated that [Fe^IVO(H₂O)₅)]²⁺ species can be produced from [Fe^II(H₂O)₅(H₂O₂)]²⁺ via an [Fe^IV(H₂O)₄(OH)₂]²⁺ intermediate. The molecular events associated with O–O cleavage were described as follows. After the coordination of H₂O₂ molecule to Fe(II) center, the O–O bond undergoes homolysis. The nascent •OH from O–O bond scission can then rapidly abstract a hydrogen from an adjacent H₂O ligand to afford the [Fe^IV(H₂O)₄(OH)₂]²⁺ intermediate. Notably, they found the mechanism producing a free •OH to be energetically unfavorable. In our current theoretical investigation, path B, involving a homolytic O–O bond cleavage followed by HAT, bears a strong resemblance to the Fenton chemistry mechanism of Baerends. While Fe(IV)=O species are generated as the final product in both our system and in the Baerends mechanism for Fenton chemistry, the particular proton donors for the HAT step are found to be different. In our case, it is the nascent Fe^III-OH molecule, while the proton derives from another coordinating water molecule (HOH) in the Baerends mechanism for Fenton chemistry. As we discussed in section 3.3, 2,6-lutidine may have the effect of switching the reaction trajectory from path B to path A and lowering the reaction barrier at the same time. Lastly, we note that, as far as the mode of O–O cleavage is concerned, paths A and B of the TMC case can be approximately viewed as corresponding to eqs. 2 and 1, respectively. However, both of the two reaction paths examined in this study lead to Fe(IV)=O. Therefore, it appears that overall the reaction in the TMC system is better described as eq. 2.

3.7 Similarities and differences in Fe(IV)=O formation between the non-heme TMC complex and enzymes

For the reaction of Fe(II)TMC and H₂O₂, the key step of the base-catalyzed Fe(IV)=O formation (Model-1, path A) is the O–O bond cleavage of an Fe^II-hydroperoxide-type intermediate, Int. The insights we have derived from this DFT study may have great relevance to the mechanisms of Fe(IV)=O formation by several non-heme iron enzymes, for which an Fe(II)OOH or Fe(II)OOR intermediate has been proposed.^21a,c,d,,34 There is a particularly strong similarity in the mechanistic notions related to Fe(IV)=O formation between the non-heme TMC complex and the enzyme isopenicillin N synthase (IPNS) for which an Fe(II)OOH intermediate has been proposed,^21c Both systems involve an initial O–O cleavage with some homolytic character followed by a PCET process. However, it was suggested for IPNS that, an iron-coordinated water molecule acts as a proton source that facilitates O–O bond cleavage of the Fe(II)OOH intermediate.³⁵ Although water molecules are likely to be present in the TMC reaction mixture,⁸ it is not likely here that water can serve as an efficient catalyst, as it is not coordinated to the iron center, and thus is not acidic enough to assist in heterolytic O–O cleavage.

The Fe(IV)=O formation mechanism, especially that involving H₂O₂, has been more extensively studied computationally for heme enzymes.³⁶ Therefore it is also useful to compare the present non-heme complex to heme enzymes. Our calculations suggest that the role of 2,6-lutidine is to promote the heterolytic O–O bond cleavage, as an acid-base catalyst. This role is quite similar to that played by a histidine residue in horseradish peroxidase (HRP)³⁷ and a glutamate residue in chloroperoxidase (CPO).²⁰ For both the synthetic TMC complex and these heme enzymes, the catalytic iron complex needs to undergo two-electron oxidation, for the Fe(IV)=O formation. However, it should be noted that the Fe(IV)=O formation reactions for these different systems operate via different iron oxidation states. For the heme peroxidases, Cpd I formation begins with coordination of H₂O₂ onto the iron in the ferric state (Fe(III)). The subsequent two-electron oxidation does not generate an Fe(V) species, but an oxoiron(IV) porphyrin π-cation radical species (Cpd I) instead. In contrast, the reaction of [Fe^II(TMC)(NCCH₃)]²⁺ with H₂O₂ involves coordination to the ferrous center (Fe(II)), and the two-electron oxidation occurs exclusively at the iron center (Scheme 4b).

The different oxidation states of the iron centers also lead to somewhat different modes of H₂O₂ coordination. The H₂O₂ coordination is more facile for the heme enzymes, as the ferric center is more Lewis acidic than the ferrous center of TMC-Fe(II). While previous theoretical calculations on heme enzyme systems did not reveal any difficulty for H₂O₂ to coordinate to the ferric center,^20,36,37, the ferrous state of [Fe^II(TMC)(NCCH₃)]²⁺ has much less affinity for H₂O₂, as can be seen from the long Fe-O distance in RC (Figure 1). Shortening the Fe-O distance of RC leads to Int, but the process involves a finite barrier. The inefficient H₂O₂ coordination observed for the TMC complex may also be partly attributed to the electron occupation of the d_z2-type orbital.

4. Conclusion

Previously reported experimental results provided strong evidence that the reaction of TMC-Fe(II) with stoichiometric H₂O₂ afforded a near-quantitative yield of [Fe^IV(O)(TMC)(NCCH₃)]²⁺ complex in the presence of 2,6-lutidine via an O–O bond heterolysis mechanism where the added base plays a key role as an acid-base catalyst. DFT studies on the mechanism of this transformation have been carried out and have provided additional insight into this O–O bond cleavage step. The results demonstrate that the reaction proceeds primarily on the quintet spin-state potential surface. In the absence of added base, O–O bond cleavage occurs via a homolysis pathway (path B in Scheme 3). Interestingly, addition of the base stabilizes an alternative peroxidase-like pathway (path A in Scheme 3). O–O cleavage via Path A consists of two components: (1) an initial O–O bond cleavage phase that bears partial homolysis and heterolysis character and (2) a (partial) PCET step. Despite this partial homolysis of the O–O bond that generates a transient Fe(III) state, formation of a free •OH radical having a finite lifetime is avoided due to the efficiency of the subsequent PCET step. This combination makes the O–O cleavage effectively an overall heterolytic process.