Short-Term Memory Scanning Viewed as Exemplar-Based Categorization

Abstract

Exemplar-similarity models such as the exemplar-based random-walk (EBRW) model (Nosofsky & Palmeri, 1997a) were designed to provide a formal account of multidimensional classification choice probabilities and response times (RTs). At the same time, a recurring theme has been to use exemplar models to account for old-new item recognition and to explain relations between classification and recognition. However, a major gap in research is that the models have not been tested on their ability to provide a theoretical account of RTs and other aspects of performance in the classic Sternberg (1966) short-term memory-scanning paradigm, perhaps the most venerable of all recognition-RT tasks. The present research fills that gap by demonstrating that the EBRW model accounts in natural fashion for a wide variety of phenomena involving diverse forms of short-term memory scanning. The upshot is that similar cognitive operating principles may underlie the domains of multidimensional classification and short-term, old-new recognition.

According to exemplar models of classification, people represent categories by storing individual exemplars in memory, and they classify objects on the basis of their similarity to the stored exemplars (Hintzman, 1986; Medin & Schaffer, 1978). A well known representative from the class of exemplar models is the generalized context model (GCM; Nosofsky, 1986). In the GCM, exemplars are represented as points in a multidimensional psychological space, and similarity between exemplars is a decreasing function of their distance in the space (Shepard, 1987). An important achievement of the GCM is that it allows for the prediction of fine-grained differences in classification probabilities for individual items, based on their fine-grained similarities to exemplars in the multidimensional space.

A central goal of exemplar models such as the GCM is to account not only for categorization, but to explain relations between categorization and other fundamental cognitive processes, such as old-new recognition memory (Estes, 1994; Hintzman, 1988; Nosofsky, 1988, 1991). When applied to item recognition¹ the GCM assumes that each member of a study list is stored as a distinct exemplar in memory. At time of test, the observer is presumed to sum the similarity of each test item to these stored study exemplars. The greater the summed similarity, the more “familiar” is the test item, so the greater is the probability with which the observer responds “old”. Indeed, the GCM can be considered a member of the class of “global matching” models that have been applied successfully in the domain of old-new recognition (e.g., Clark & Gronlund, 1996; Eich, 1982; Gillund & Shiffrin, 1984; Hintzman, 1988; Murdock, 1982; Shiffrin & Steyvers, 1997). Within this broad class, an important achievement of the GCM is that, just as is the case for categorization, the model predicts fine-grained differences in recognition probabilities for individual test items, based on their fine-grained similarities to the studied exemplars (Nosofsky, 1988, 1991; Nosofsky & Zaki, 2003).

A more recent development in the application of the GCM to categorization and recognition data involves extensions of the model to predicting categorization and recognition response times (RTs; Cohen & Nosofsky, 2003; Lamberts, 1995, 1998, 2000; Nosofsky & Palmeri, 1997a,b). This direction is important, because RT data often provide insights into categorization and memory processes that would not be evident based on the analysis of choice-probability data alone (Kahana & Loftus, 1999). Nosofsky and Palmeri’s (1997a) exemplar-based random-walk (EBRW) model adopts the same fundamental representational assumptions as does the GCM. However, it specifies a random-walk decision process, driven by the retrieval of stored exemplars, which allows the model to predict the time course of categorization and recognition judgments. Nosofsky and Palmeri (1997a) and Nosofsky and Stanton (2005) showed that, in perceptual categorization tasks, the EBRW model accurately predicted mean RTs and choice probabilities for individual stimuli as a function of their position in multidimensional similarity space, and as a function of variables such as individual item frequency, probabilistic feedback, and overall practice in the tasks. Analogously, Nosofsky and Stanton (2006) showed that, when applied to forms of long-term, perceptual old-new recognition, the model also achieved accurate predictions of mean RTs and choice probabilities (for closely related work, see Lamberts, Brockdorff, & Heit, 2003). These accurate predictions were obtained at the level of individual subjects and individual stimuli, thereby providing rigorous tests of the modeling ideas.

To date, however, a major gap in the tests of the EBRW model (and familiarity-based exemplar models more generally) is that researchers have not considered its predictions for the fundamental Sternberg memory-scanning paradigm, perhaps the most venerable of all old-new recognition RT tasks (Sternberg, 1966, 1969, 1975). In the Sternberg paradigm, observers are presented on each trial with a short list of items (the memory set), followed by a test item (or probe). They are required to judge, as rapidly as possible, while minimizing errors, whether the probe occurred on the study list. As is well known, highly regular sets of RT results are observed in the core version of the paradigm and in important variants of the paradigm (see below). Indeed, it forms a fundamental test-bed for a wide variety of formal models of recognition RT that aim to explain the nature of memory-based information processing.

From one perspective, the Sternberg paradigm may seem outside the intended scope of models such as the GCM and EBRW. After all, it involves forms of short-term memory access, and the processes that govern short-term recognition may be quite different from those that operate when people form categories or make long-term recognition judgments. Nevertheless, the central aim of the present work is to begin an investigation of the performance of the EBRW model in this fundamental paradigm and to fill this major gap in research. To the extent that the EBRW model can provide a natural and convincing account of the data, it would suggest the possibility that the seemingly disparate processes of “short-term memory scanning” and category representation and decision making may reflect the same underlying cognitive principles. Furthermore, detailed analysis of the recognition RT and accuracy data within the framework of the model also has the potential to provide important insights into the nature of people’s short-term memory representations and retrieval processes. For example, the patterns of parameter estimates derived from fits of the model to data may reveal interesting characteristics of those representations and processes.

Although one aim of the present work will be to consider the EBRW’s account of performance in the “standard” Sternberg paradigm, the goals are more far-reaching, because we will also consider its applications to important variants and extensions of the standard paradigm. For example, in the standard paradigm, the to-be-recognized items are generally highly discrete entities, such as alphanumeric characters. Because such items are highly discriminable in memory and because the to-be-remembered lists are short, accuracy is usually close to ceiling in the standard paradigm. Therefore, in modeling performance in the standard Sternberg paradigm, the central focus is usually on the RTs. By way of comparison, in a modern variant of the paradigm, Kahana, Sekuler and their colleagues have tested short-term recognition of visual patterns embedded in a continuous-dimension similarity space (e.g., Kahana & Sekuler, 2002; Kahana, Zhou, Geller, & Sekuler, 2007; Sekuler & Kahana, 2007; Viswanathan, Perl, Visscher, Kahana, & Sekuler, 2010). In this case, the stimuli are highly confusable, and highly structured sets of error data are collected. Indeed, the challenge to fitting the error data is so extreme that researchers have gone in the opposite direction, thus far focusing on only the error data, without formal consideration of the RTs. A major goal of the present work is to use the EBRW model to account jointly for the RTs and accuracies in this continuous-dimension, similarity-based variant of the Sternberg paradigm. As will be seen, in this extended version of the paradigm, the model will be applied to predicting mean RTs and accuracies at the level of individual lists with fine-grained differences in their similarity structure.

In addition to predicting mean RTs and accuracies in both the similarity-based and standard versions of the Sternberg paradigm, the model will be applied to predict: i) performance patterns in a category-based variant of the paradigm, ii) how accuracy grows with processing time in a response-signal version of the standard paradigm, and iii) detailed RT distribution data from the standard paradigm observed at the level of individual subjects and types of lists. Before turning to these diverse tests and applications, we first provide an overview of the formal model.

The EBRW Model of Old-New Recognition

In this section we provide an overview of the EBRW model as applied to old-new recognition RTs and accuracies. We start by describing the model in a generic form. Specializations of the model appropriate for the individual variants of the Sternberg paradigm are then described in the context of the individual applications. In general, in the variants of the Sternberg paradigm that we will consider, the fundamental independent variables that are manipulated include: 1) the size of the memory set, 2) whether the test probe is old or new, 3) the serial position of an old test probe within the memory set, 4) the similarity structure of the memory set, and 5) the similarity of the test probe to individual members of the memory set. The free parameters of the EBRW model may depend systematically on the manipulations of some of these independent variables. In this section we preview some ideas along these lines. More detailed assumptions are stated when fitting the EBRW model to the results from the specific experiments.

The EBRW model assumes that each item of a study list is stored as a unique exemplar in memory. The exemplars are represented as points in a multidimensional psychological space. In the baseline model, the distance between exemplars i and j is given by

$$d_{ij}={\left[\sum _{k=1}^K{w}_k{\mid x_{ik}-x_{jk}\mid }^{\rho }\right]}^{\frac{1}{\rho }},$$ (1)

where x_ik is the value of exemplar i on psychological dimension k; K is the number of dimensions that define the space; ρ defines the distance metric of the space; and w_k (0 < w_k, ∑w_k = 1) is the weight given to dimension k in computing distance. In situations involving the recognition of holistic or integral-dimension stimuli (Garner, 1974), which will be the main focus of the present work, ρ is set equal to 2, which yields the familiar Euclidean distance metric. The dimension weights w_k are free parameters that reflect the degree of “attention” that subjects give to each dimension in making their recognition judgments. In situations in which some dimensions are far more relevant than others in allowing subjects to discriminate between old versus new items, the attention-weight parameters may play a significant role (e.g., Nosofsky, 1991). In the experimental situations considered in the present work, however, all dimensions tend to be relevant and the attention weights will turn out to play a minor role.

The similarity of test item i to exemplar j is an exponentially decreasing function of their psychological distance (Shepard, 1987),

$$s_{ij}=\exp \left(-c_j{d}_{ij}\right),$$ (2)

where c_j is the sensitivity associated with exemplar j. The sensitivity governs the rate at which similarity declines with distance in the space. When sensitivity is high, the similarity gradient is steep, so even objects that are close together in the space may be highly discriminable. By contrast, when sensitivity is low, the similarity gradient is shallow, and objects are hard to discriminate. In most previous tests of the EBRW model, a single global level of sensitivity was assumed that applied to all exemplar traces stored in long-term memory. In application to the present short-term recognition paradigms, however, it seems almost certain that allowance needs to be made for forms of exemplar-specific sensitivity. For example, in situations involving high-similarity stimuli, an observer’s ability to discriminate between test item i and exemplar-trace j will almost certainly depend on the recency with which exemplar j was presented: Discrimination is presumably much easier if an exemplar was just presented, rather than if it was presented earlier on the study list (due to factors such as interference and decay). We state the detailed assumptions involving the exemplar-specific sensitivity parameters in the context of the modeling for each individual experiment.

Each exemplar j from the memory set is stored in memory with memory-strength m_j. As is the case for the sensitivities, the memory-strengths are exemplar-specific (with the detailed assumptions stated later). Almost certainly, for example, exemplars presented more recently will have greater strengths.

When applied to old-new recognition, the EBRW model presumes that background (or criterion) elements are part of the cognitive system. The strength of the background elements, which we hypothesize is at least partially under the control of the observer, helps guide the decision about whether to respond “old” or “new”. In particular, as will be explained below, the strength setting of these elements acts as a criterion for influencing the direction and rate of drift of the exemplar-based random-walk process. Other well known sequential-sampling models include analogous criterion-related parameters for generating drift rates, although the conceptual underpinnings of the models are different from those in the EBRW model (e.g., Ratcliff, 1985, pp. 215-216; Ratcliff, Van Zandt, & McKoon, 1999, p. 289).²

Presentation of a test item causes the old exemplars and the background elements to be activated. The degree of activation for exemplar j, given presentation of test item i, is given by

$$a_{ij}=m_j{s}_{ij},$$ (3)

Thus, the exemplars that are most strongly activated are those with high memory strengths and that are highly similar to test item i. The degree of activation of the background elements (B) is independent of the test item that is presented. Instead, background-element activation functions as a fixed criterion against which exemplar-based activation can be evaluated. As discussed later in this article, however, background-element activation may be influenced by factors such as the size and structure of the memory set, because observers may adjust their criterion settings when such factors are varied.

Upon presentation of the test item, the activated stored exemplars and background elements race to be retrieved (Logan, 1988). The greater the degree of activation, the faster the rate at which the individual races take place. On each step, the exemplar (or background element) that wins the race is retrieved. Whereas in Logan’s (1988) model the response is based on only the first retrieved exemplar, in the EBRW model the retrieved exemplars drive a random-walk process. First, there is a random-walk counter with initial setting zero. The observer establishes response thresholds, +OLD and −NEW, that determine that amount of evidence needed for making each decision. On each step of the process, if an old exemplar is retrieved, then the random-walk counter is incremented by unit value towards the +OLD threshold; whereas if a background element is retrieved, the counter is decremented by unit value towards the −NEW threshold. If either threshold is reached, then the appropriate recognition response is made. Otherwise, a new race is initiated, another exemplar or background element is retrieved (possibly the same one as on the previous step), and the process continues. The recognition decision time is determined by the total number of steps required to complete the random walk. It should be noted that the concept of a “criterion” appears in two different locations in the model. First, as explained above, the strength setting of the background elements influences the direction and rate of drift of the random walk. Second, the magnitude of the +OLD and−NEW thresholds determine how much evidence is needed before an old or a new response is made. Again, other well known sequential-sampling models include analogous criterion-related parameters at these same two locations (for extensive discussion, see, e.g., Ratcliff, 1985).

Given the detailed assumptions in the EBRW model regarding the race process (see Nosofsky & Palmeri, 1997a, p. 268), it turns out that, on each step of the random walk, the probability (p) that the counter is incremented towards the +OLD threshold is given by

$$p_i=\frac{A_i}{(A_i+B)},$$ (4)

where A_i is the summed activation of all of the old exemplars (given presentation of item i), and B is the activation of the background elements. (The probability that the random walk steps toward the −NEW threshold is given by q_i = 1− p_i.) In general, therefore, test items that match recently presented exemplars (with high memory strengths) will cause high exemplar-based activations, leading the random walk to march quickly to the +OLD threshold and resulting in fast OLD RTs. By contrast, test items that are highly dissimilar to the memory-set items will not activate the stored exemplars, so only background elements will be retrieved. In this case, the random walk will march quickly to the −NEW threshold, leading to fast NEW RTs. Through experience in the task, the observer is presumed to learn an appropriate setting of background-element activation (B) such that summed activation (A_i) tends to exceed B when the test probe is old, but tends to be less than B when the test probe is new. In this way, the random walk will tend to drift to the appropriate response thresholds for old versus new lists, respectively.

Given these processing assumptions and the computed values of p_i, it is then straightforward to derive analytic predictions of recognition choice probabilities and mean RTs for any given test probe and memory set. The relevant equations are summarized by Nosofsky and Palmeri (1997a, pp. 269-270, 291-292). Simulation methods, described later in this article, are used when the model is applied to predict fine-grained RT-distribution data.

In sum, having outlined the general form of the model, we now apply specific versions of it to predicting RTs and accuracies in different variants of the Sternberg memory-scanning paradigm

Experiment 1: Continuous-Dimension Sternberg Paradigm

In Experiment 1, we conduct the Kahana-Sekuler extension of the Sternberg paradigm (e.g., Kahana & Sekuler, 2002), in which subjects make recognition judgments for stimuli that are embedded in a continuous, multidimensional similarity space. All past applications of the Kahana-Sekuler paradigm, however, have involved the modeling of only choice-probability data. By contrast, the goal in the present experiment is to collect both accuracy and RT data and to test the EBRW model on its ability to simultaneously fit both forms of data. Furthermore, the goal is to predict these data at the level of individual lists.

In our experiment, the stimuli are a set of 27 Munsell colors varying along the dimensions of hue, brightness, and saturation (3 values along each dimension, combined factorially to yield the total set). These stimuli are classic examples of “integral-dimension” stimuli (Garner, 1974). Such stimuli appear to be encoded in holistic fashion and are well conceptualized as occupying points in a multidimensional similarity space (Lockhead, 1972), thereby allowing for straightforward application of the EBRW model. We conducted a multidimensional scaling study to precisely locate the colors in the space (see Appendix A for details). This form of detailed similarity-scaling information is needed to allow for the quantitative prediction of RTs and choice probabilities at the level of individual memory sets and test probes.

The design of the experiment involved a broad sampling of different list structures in order to provide a comprehensive test of the model. There were 360 lists in total. The size of the memory set varied from 1 to 4 unique items (with an equal number of lists at each memory-set size). For each memory-set size, half of the test probes were old and half were new. For old lists, for each memory-set size, the member of the memory set that matched the probe occupied each serial position an equal number of times. To create the lists, items were sampled randomly from the complete stimulus set, subject to the constraints described above.

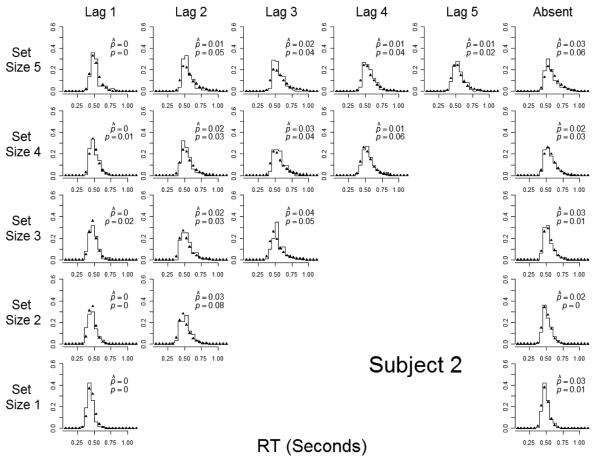
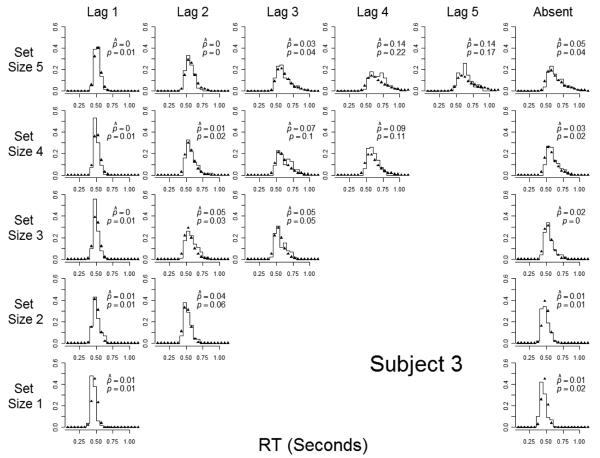
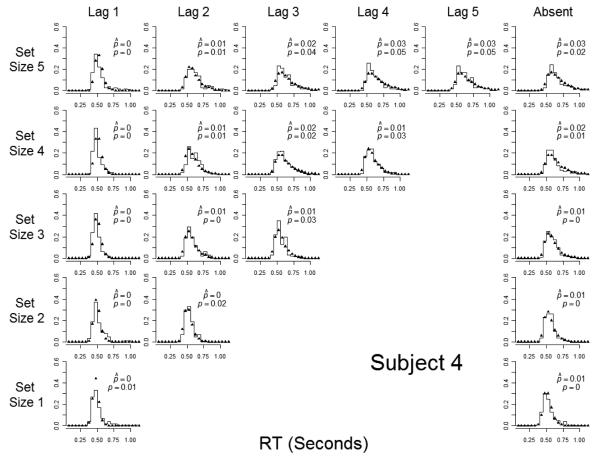
Because the goal was to predict performance at the individual-subject level, we tested three subjects for an extended period (approximately 20 one-hour sessions for each individual subject). As it turned out, each subject showed extremely similar patterns of performance and the pattern of best-fitting parameter estimates from the EBRW model was the same across the subjects. Therefore, for simplicity in the presentation, and to reduce noise in the data, we report the results from the averaged-subject data. The individual-subject data sets and fits to the individual-subject data are available from the authors upon request.

Method

Subjects

The subjects were three female graduate students at Indiana University with normal or corrected-to-normal vision and who reported having normal color vision. The subjects were paid for their participation ($8 per session plus a $3 bonus per session for good performance). The subjects were unaware of the issues being investigated in the study.

Stimuli

The stimuli were 27 computer-generated colors from the Munsell system. The original Munsell colors varied along the dimensions of hue (7.5 purple-blue, 2.5 purple-blue, and 7.5 blue), brightness (values 4, 5, and 6) and saturation (chromas 6, 8, and 10). The orthogonal variation of these values produced the 3 × 3 × 3 stimulus set. We used the Munsell color conversion program (WallkillColor, Version 6.5.1; Van Aken, 2006) to calculate each color’s RGB value. The red-green-blue (RGB) values for the 27 stimulus colors are reported in Appendix A. Each color occupied a 2 × 2 inch square (144 × 144 pixels) presented in the center of an LCD computer screen, displayed against a white background. The display resolution was set to 1024 × 768 pixels. Each stimulus subtended a visual angle of approximately 9.6 degrees.

Procedure

The structure of the 360 lists was as described in the introduction to this experiment. The same 360 lists were used for all of the subjects. Each list was presented once per day (session) of testing, with the order of presentation randomized for each individual subject on each individual session. Subjects 2 and 3 participated in 20 sessions and Subject 1 participated in 21 sessions. To enable the subjects to keep track of their progress, each trial was preceded by the trial number, displayed in the center of the screen for 1 s. The screen was then blank for 1 s, after which list presentation began. Each list item was presented for 1 s, with a blank 1-s interstimulus interval separating the items. Following the final list item, there was a presentation of a central fixation point (“x”) for 1140 ms. In addition, 440 ms after the onset of the fixation point, a high-pitch tone was sounded for 700 ms. Then the test probe appeared with the question, “Was this color on the preceding list?” The subject’s task was to respond by pressing either the left (“yes”) or right (“no) mouse button, using the left or right index finger. The test probe remained visible until the subject’s response was recorded. The subject received immediate feedback (“Correct” or “Wrong”, displayed for 1 s) following each response. Twenty practice lists were presented at the start of the experiment, and there were short rest breaks following every 90 trials.

For each subject-list combination, we removed from the analysis RTs greater than three standard deviations above the mean and also RTs of less than 100 ms. This procedure led to dropping 1.24% of the trials (1.65% for Subject 1, 0.75% for Subject 2, 1.32% for Subject 3).

Model-Fitting Procedure and Results

Multidimensional-Scaling Analysis

To fit the EBRW model to the recognition data, we make use of an MDS solution for the colors that is derived from the similarity-ratings data. The details of the MDS procedure are described in Appendix A. The main summary result is that a three-dimensional scaling solution for the colors provided a very good fit to the similarity data. Although there were some local distortions, the derived psychological structure of the stimuli reflected fairly closely the 3×3×3 Munsell coordinate structure. This derived three-dimensional scaling solution is used in combination with the EBRW model to fit the recognition data.

Fitting the EBRW Model to the Recognition Data

We fitted different versions of the EBRW model to the old-new recognition data by varying systematically which parameters were freely estimated and which parameters were constrained at default values. In this section, we describe what we view as the “core” version of the model. The core version achieved reasonably good fits to the mean RTs and accuracies associated with the 360 individual lists. Importantly, as will be seen, it also accounted for the major qualitative trends in the data, to be described below. Following presentation of the fits of the core version of the model, we then describe in more detail the role of the free parameters in achieving these fits.

First, as explained above, the psychological coordinate values of the stimuli (the x_ik values in Equation 1) were given by the three-dimensional scaling solution derived from the similarity ratings. These coordinate values are held fixed in all of the fits to the recognition data. However, the w_k attention weights in Equation 1 were allowed to vary as free parameters, in case subjects allocated attention to the dimensions differently for purposes of recognition than for purposes of making similarity judgments (Nosofsky, 1987, 1991). Because the weights vary between 0 and 1 and are constrained to sum to 1, there were two free attention-weight parameters.

With an exception to be described below, the exemplar-specific sensitivities (the c_j values in Equation 2) and the memory strengths (the m_j values in Equation 3) were assumed to depend on lag only, where lag is counted backwards from the presentation of the test probe to the memory-set exemplar. For example, for the case in which memory set-size is equal to 4, the exemplar in the fourth serial position has lag 1, the exemplar in the third serial position has lag 2, and so forth. Presumably, the more recently an exemplar was presented (i.e., the lower its lag), the greater will be the exemplar’s memory strength and its level of sensitivity. Note that memory-set size has no direct influence on the settings of the memory-strength and sensitivity parameters. Instead, memory-set size influences those parameter settings indirectly: The greater the memory-set size, the more exemplars there will be that have greater lags (cf. Murdock, 1971, 1985). The lag-based memory-strength parameters are denoted M₁ through M₄, and the lag-based sensitivities are denotedθ₁ through θ₄ (where the subscript indicates the lag). Without loss of generality, the value M₄ can be held fixed at 1, so there are three freely varying lag-based memory-strength parameters and four freely varying lag-based sensitivity parameters.

In addition, based on inspection of the data and on preliminary model fitting, provision was made for a modulating effect of primacy on memory strength and sensitivity (cf., Murdock, 1985). The memory strength for the exemplar that occupied the first serial position of each list was given by m = M_lag × P_M, where P_M is a primacy-based memory-strength multiplier and where M_lag is the lag-based memory-strength parameter defined previously. Analogously, the sensitivity for the exemplar that occupied the first serial position was given by c = θ_lag × P_θ. The special status of the exemplar in the first serial position most likely reflects that subjects tend to devote greater attention and rehearsal to it than to the other memory-set exemplars (cf. Atkinson & Shiffrin, 1968). For example, when it is first presented, there are no other memory-set exemplars that are competing with it for attention and rehearsal time.³

The strength of the background elements (B in Equation 4) was assumed to be linearly related to memory-set size S,

$$B=u+v\cdot S,$$ (5)

where u and v are freely estimated parameters. All other things equal, as memory-set size grows, summed activation (A_i in Equation 4) will also grow, because the sum is taking place over a larger number of stored exemplars. Allowing for increases in B with increases in memory set size is intended to reflect the possibility that the observer may establish a higher criterion for assessing the amount of summed activation that tends to be associated with longer lists. Otherwise, if B remains fixed, then as study lists become arbitrarily long, summed activation (A_i in Equation 4) would eventually always exceed B and the random walk would always drift toward the OLD response threshold, regardless of whether the probe is old or new.

Fitting the EBRW model also requires estimation of the random-walk response-threshold parameters, +OLD and −NEW. Just as is the case for the background-element strength, it is conceivable that the observer might adjust the magnitude of the threshold parameters depending on the properties of each studied list. Nevertheless, in fitting the core version of the model, we assumed for simplicity that single values of +OLD and −NEW operated for all lists.⁴

Finally, a scaling parameter κ was estimated for translating the number of steps in the random walk into ms; and a residual parameter μ was estimated that represented the mean of all processing times not associated with the random-walk decision-making stage (e.g., encoding and response-execution times).

In sum, the core version of the model uses 17 free parameters (2 attention weights, 4 lag-based sensitivities, 3 lag-based memory strengths, 2 primacy-related parameters, 2 background-strength parameters, 2 random-walk thresholds, 1 scaling constant, 1 mean residual time) for simultaneously fitting the mean RTs and choice probabilities associated with the 360 lists (a total of 720 freely varying data points). As will be seen, some of these free parameters can be set at default values with little effect on the quality of fit. Others will be seen to vary in highly systematic and psychologically meaningful ways.

Model-Fitting Approach

In many of the applications in the present article, the plan is to use the EBRW model to provide a joint account of both mean-RT and choice-probability data. It is unclear how best to combine these separate data sets into a composite fit index. Our general goal is simply to establish that the EBRW model is a serious contender by demonstrating that it accounts for the major qualitative trends in performance across diverse paradigms involving short-term memory scanning. Thus, for each paradigm, we choose heuristic fit indexes that seem to yield sensible results involving the joint prediction of the mean RTs and choice probabilities and that satisfy our general goal of demonstrating the utility of the model. Later in our article, we collect and analyze detailed RT-distribution data, which allows for the application of more rigorous and principled maximum-likelihood methods for jointly fitting the RTs and choice probabilities.

For the present paradigm, the criterion of fit was to maximize the average percentage of variance accounted for across the mean RTs and the “old” recognition probabilities. That is, for any given set of parameters, we used the model to derive the predictions of the “old” recognition probabilities for the 360 lists; and the predicted mean RTs of the 360 lists. Given these predictions, we computed the percentage of variance accounted for in the old recognition probabilities, and the percentage of variance accounted for in the mean RTs. The overall fit was the average of these two quantities. Here and throughout the rest of the article we used a computer-search routine (a modified version of Hooke and Jeeves, 1961) to locate the best-fitting parameters. In an effort to avoid local minima, 100 different random starting configurations were used in the parameter searches.

Model-Fit Results

The summary fits of the core version of the model are reported in the top row of Table 1. As shown in the left columns of the table, the model accounted for 96.5% of the variance in the “old” recognition probabilities, and for 83.4% of the variance in the mean RTs. A more detailed breakdown is provided in the right columns of the table, which report the summary fits for the “old” and “new” lists considered separately. Naturally, because the separate list types generally involve vastly reduced ranges of the dependent variables (especially the probability of responding “old”), the percent-variance summary statistics for the separate list types are smaller than for the aggregate data. As will be seen, considering the summary statistics for the old and the new lists separately provides diagnostic information for helping to evaluate different versions of the model.

Table 1.

Experiment 1: Summary Fits (Percentage of Variance Accounted For) of Different Versions of the EBRW Model to the Choice Probability and Mean Response-Time Data.

			Separate List Types
	Aggregated		Old		New
Model	P(Old)	RT	P(Old )	RT	P(Old)	RT
Core Version	96.5	83.4	72.3	86.7	79.0	80.9
Constant Sensitivity	95.5	59.5	73.6	75.3	69.9	47.4
Constant Memory Strength	94.8	78.2	69.4	76.2	65.3	79.6
Constant Sensitivity and  Memory Strength	93.7	51.4	43.2	52.0	65.2	50.7
Constant Background Strength	96.6	82.0	69.4	84.6	80.9	79.9
Binary Distance	87.3	67.8	59.0	84.3	5.1	55.1

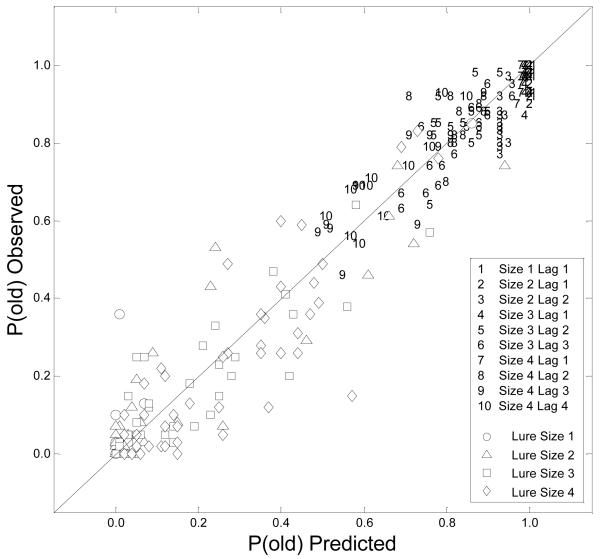
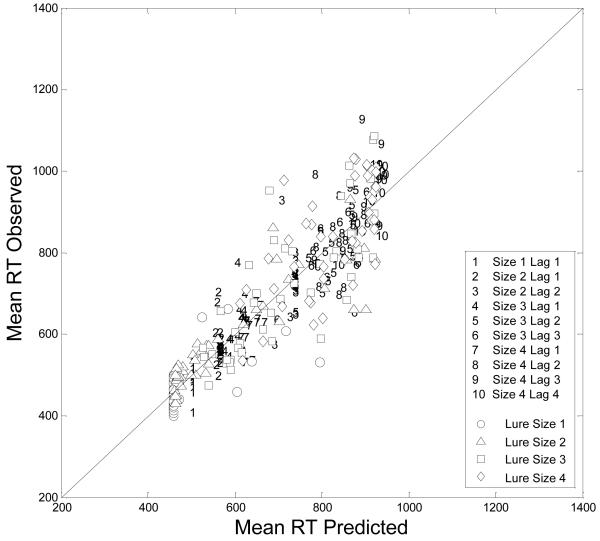
The performance of the core model is illustrated graphically in Figures 1 and 2. Figure 1 plots the observed recognition probabilities for the 360 lists against the predicted recognition probabilities. Figure 2 plots the observed mean RTs against the predicted mean RTs. Separate symbols are used to denote the size of each list; whether the test probe was old or new; and, if old, the test probe’s lag. To aid visual inspection, old lists are denoted by numeric symbols, whereas new lists are denoted by shape symbols. Inspection of the scatterplots suggests that, although there are occasional outliers, the model is providing a good overall quantitative account of the complete sets of choice-probability and mean-RT data. Furthermore, inspection of the scatterplots and the summary-fit statistics in Table 1 indicates that the model captures a substantial proportion of variance for the old and new lists considered separately.

Figure 1.

Experiment 1, individual list predictions. Old recognition probabilities for the 360 lists plotted against the predicted probabilities from the EBRW model.

Figure 2.

Experiment 1, individual list predictions. Overall mean response times for the 360 lists plotted against the predicted mean response times from the EBRW model.

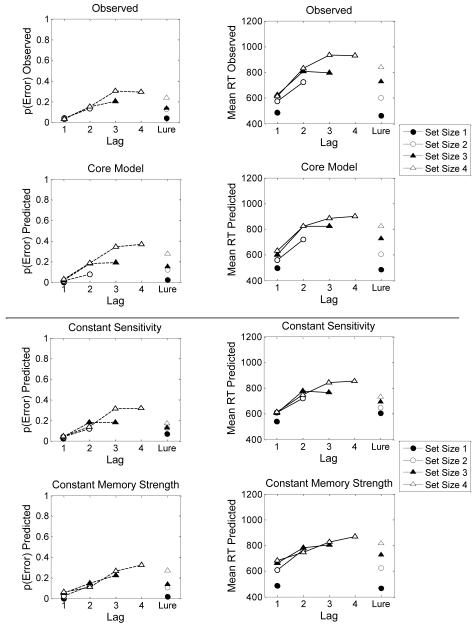
To help evaluate any systematic departures between observed and predicted data values, and to summarize key trends in the data, Figure 3 displays the observed (top row) and predicted (second row) results averaged across tokens of the main types of lists. Specifically, the left panels plot the observed and predicted error probabilities as a function of memory set size, type of test probe (old or new), and lag, averaged across the individual tokens of these main types of lists. The right panels do the same for the mean RTs. Inspection of these plots suggests that the model is doing an outstanding job of capturing the main patterns in the data. For both the error-probability and the mean RT data, there is a dramatic effect of lag: For each memory-set size, more recent items (with lower lags) have lower error probabilities and faster mean RTs than do less recent items. (As discussed later in this article, this same basic pattern is often observed in tests of the standard Sternberg paradigm.) Once one takes lag into account, there is little additional effect of memory-set size per se, i.e., the curves corresponding to old lists of varying set sizes are nearly overlapping. The main exception is a fairly consistent primacy effect: In general, for each memory-set size, the item with the longest lag is “pulled down” with a faster mean RT and, usually, a somewhat reduced error rate. The data also show a big effect of memory-set-size on the error rates and mean RTs of the new test probes (i.e., the lures): The greater the memory-set size, the greater is the mean false-alarm probability and the slower is the overall mean RT. As can be seen in Figure 3 (second-row panels), the core version of the EBRW model accounts for all of these qualitative trends and does so with high quantitative precision.

Figure 3.

Experiment 1, Observed summary trends and EBRW-predicted summary trends. Left panels: average error probabilities plotted as a function of lag, set size, and type of probe. Right panels: average mean RTs plotted as a function of lag, set size, and type of probe. Top row = observed, second row = core model, third row = constant-sensitivity special-case model, fourth row = constant memory-strength special-case model..

Beyond accounting for the main effects of lag, memory set size, and type of probe, inspection of the detailed, individual-list scatterplots in Figures 1 and 2 reveals that the model accounts well for effects of the fine-grained similarity structure of the lists. For example, consider lists of memory-set-size 4 in which the test probe is new (Lure Size 4). As can be seen in the scatterplots, there is huge variability in performance across different tokens of these lists. Some are associated with extremely high false alarm rates and others have very low false alarm rates. Likewise, some tokens of these types of lists have very slow mean RTs, whereas others have moderately fast ones. The model captures well this variability in performance across different tokens of the Lure-Size-4 lists. To understand why, note, for example, that false alarm rates will be high when the lure is highly similar to one or more exemplars of the memory set. By contrast, false alarm rates will be low when the lure is dissimilar to all of the memory-set members. In addition, in the latter case, the model predicts correctly that there will be fast correct-rejection RTs, because only background elements will be retrieved, leading the random walk to march rapidly to the NEW threshold.

Best-Fitting Parameters and Special-Case Versions of the Model

The best-fitting parameters from the model are reported in Table 2. First, note that the attention-weight parameters (i.e., the w_k’s) hover around their default values of 1/3, indicating that subjects gave roughly the same degree of attention to each of the individual stimulus dimensions in making their recognition judgments. The freely estimated weights are not doing much work in terms of allowing the model to achieve its good fits in the present situation.

Table 2.

Experiment 1: Best-fitting parameters for the EBRW model.

w 1	.329
w 2	.344
w 3	[.326]
M1	3.181
M2	1.415
M3	1.202
M4	[1.000]
θ 1	4.745
θ 2	1.361
θ 3	0.944
θ 4	0.711
PM	1.053
Pθ	1.470
u	0.000
v	0.377
OLD	3.464
NEW	3.513
μ	261.441
κ	55.391

Note: Parameter values in brackets are not free to vary. w_j = attention-weight for dimension j; M_j = lag-j memory strength; θ_j = lag-j sensitivity; P_M, P_θ = primacy multipliers on memory-strength and sensitivity; u, v = background-element strength constants; OLD, NEW = response threshold magnitudes; μ = mean residual RT; κ = random-walk time-scaling constant.

More importantly, there are systematic effects of lag on the values of the memory-strength and exemplar-specific sensitivity parameters. More recently presented exemplars have both greater memory strengths and greater sensitivities than do less recently presented exemplars. This pattern seems highly plausible from a psychological point of view. Presumably, the more recently an exemplar was presented, the greater should be the strength of its memory trace. (The implication is that a positive probe activates its own memory trace to a greater degree if it was just recently presented on the study list.) At the same time, the more recently an exemplar was presented, the better should subjects be at discriminating between that exemplar and test lures, so the pattern of estimated lag-related sensitivities seems sensible as well. Also, as expected from inspection of the data, there was a primacy effect on both the estimated memory strength and sensitivity, with the exemplar in the first serial position receiving a slight boost.

To assess the importance of the lag-specific sensitivity parameters, we fitted a constrained version of the EBRW model in which the sensitivity parameters were held fixed at a constant value. As shown in Table 1, the fit of this constrained model is dramatically worse than that of the core version, particularly with respect to the RTs associated with the new lists. The predictions of the summary trends from the constant-sensitivity version of the model are shown in the third-row panels of Figure 3. It is evident from inspection that this special-case model fails to predict correctly the lure RTs. In particular, the predicted range of RTs as a function of set size is vastly smaller than what is seen in the observed data.⁵

We also fitted a constrained version of the model in which the memory-strength parameters were held fixed at a constant value. Compared to the core version, this special-case model suffers with respect to the old RTs (see Table 1, right columns). The summary-trend predictions from the constant-memory-strength model are shown in the fourth-row panels of Figure 3. The model fails to predict sufficient separation between the old-RT functions associated with different set sizes and, in general, predicts too little overall variation in the old RTs. For completeness, we also fitted a special-case version of the model that assumed both constant sensitivity and constant memory strength. As can be seen in Table 1, this special-case model provides extremely poor fits to the data.

In sum, the estimated memory-strength and sensitivity parameters vary in systematic and psychologically meaningful ways and they make unique contributions to the fit of the EBRW model. Nevertheless, it is important to acknowledge that the values of these lag-related parameters are strongly correlated, suggesting also that some common psychological mechanism may underlie them.

It is interesting to note that the choice-probability data display set-size-based “mirror effects” (Glanzer & Adams, 1990) -- see Figure 3. Averaged across lags, hit rates get smaller and false alarm rates get larger as set size increases. The model predicts this mirror effect even if the background-parameter B is held fixed across the different set-size conditions. As shown in Table 1, for the present data set, there is little change in the fit of the model if B is held fixed; also, although not illustrated in Figure 3, when B is held fixed, the predictions of the summary trends are virtually identical to those of the core model. The reason the model predicts decreasing hit rates with increasing set size is because the lag for the positive probes tends to grow larger as set size increases. (With increasing lag, the positive probe activates its own memory trace to a lesser extent, and this self-activation is the dominant term in the summed-activation equation.) By contrast, the model predicts increasing false alarm rates with increasing set size for two reasons. First, all other things equal, as set size increases, summed activation for negative probes will tend to increase because the sum is taking place over a larger number of stored exemplars. Second, the larger the set size, the greater are the chances that the memory set will include at least one exemplar that is highly similar to the negative probe.

Similarity Assumptions

To assess the importance of the MDS-based similarity representation of the exemplars, we fitted other versions of the EBRW model as well. In one version, we made allowance for only a binary-valued distance relation between exemplars: The distance between an exemplar and itself was set equal to zero, whereas the distance between any two distinct exemplars was set equal to a free parameter D. With the exception of the attention-weight parameters (which contributed negligibly to the fit of the core model), the free parameters in this binary-distance model were the same as those in the core version of the model. The fits of the binary-distance model, reported in Table 1, are dramatically worse than those of the core model. (For example, the binary-distance model accounts for only 5.1% of the variance in the recognition probabilities associated with new lists.) Clearly, for the present paradigm, the graded similarity representation is a crucial component of the EBRW-modeling approach.

As acknowledged earlier, however, the core model makes clear mis-predictions for some of the lists as well, so there is room for improvement. At least part of the reason for some of the mis-predictions is that, despite its great utility, the derived MDS representation does not of course provide a perfect representation of the similarity relations among the exemplars. First, the representation was derived in an independent task, and the precise form of “similarity” that underlies peoples’ ratings may differ from the similarity that underlies their recognition judgments. Second, each individual subject will have a slightly differently calibrated perceptual system, so the group representation derived from the similarity ratings can provide only an approximation to each individual’s similarity space. Furthermore, because of the nonlinear relation between similarity and distance, even small errors in represented distance can sometimes lead to large errors in predicted recognition confusions and RT.⁶ Most likely, the ability of the EBRW model to predict the recognition choice-probability and RT data would improve with still more sophisticated approaches to deriving each individual’s similarity representation for the exemplars.

List Homogeneity Effects

In their previous work involving the continuous-dimension Sternberg paradigm, Kahana, Sekuler and their colleagues have provided convincing model-based evidence for a role of list homogeneity on old-new recognition judgments (e.g., Kahana & Sekuler, 2002; Kahana, et al., 2007; Sekuler & Kahana, 2007; Viswanathan et al., 2010; see also Nosofsky & Kantner, 2006). The general effect is that humans appear to set a stricter criterion for responding “old” when they study high-homogeneity lists compared to low-homogeneity ones. These effects are compatible with extended versions of the EBRW model that make allowance for criterion settings to depend on the degree of study-list homogeneity. We conducted extensive analyses similar to those of Kahana and Sekuler for the present data set. As it turned out, list homogeneity per se seemed to play only a limited role in the present case, so we present these analyses in Appendix B. In our judgment, the hypothesis that study-list homogeneity may sometimes exert a powerful influence on old-new recognition decisions is almost certainly true. However, future research is needed to understand the precise experimental conditions in which such list-homogeneity effects arise.

Summary

In summary, the EBRW model provides a good overall quantitative account of the mean RT data and old recognition probabilities associated with the 360 individual lists (Figures 1 and 2). It also accounts well for the major qualitative patterns of results involving memory set size, lag, and probe type (summarized in Figure 3), and accounts for effects of fine-grained similarity structure within these main list types. Finally, the best-fitting parameters from the model vary in systematic and easy-to-interpret ways. Taken together, this initial test suggests that the EBRW model is an excellent candidate model for explaining both choice probability and RTs in this continuous-dimension version of the Sternberg paradigm.

The Standard Sternberg Paradigm: Application to Monsell’s (1978) Data

Thus far, the focus in this article has been on the continuous-dimension extension of the Sternberg paradigm. A natural question, however, is how the EBRW model might fare in the standard version of the paradigm, in which highly discrete alphanumeric characters are used. To the extent that things work out in a simple, natural fashion, the applications of the EBRW model to the standard paradigm should be essentially the same as in the just-presented application, except they would involve a highly simplified model of similarity. That is, instead of incorporating detailed assumptions about similarity relations in a continuous multidimensional space, we apply a simplified version of the EBRW that is appropriate for highly discriminable, discrete stimuli.

Specifically, in the simplified model, we assume that the similarity between an item and itself is equal to one; whereas the similarity between two distinct items is equal to a free parameter s (0 < s < 1). (This model is a special case of the binary-distance model fitted to the Experiment-1 data.) Presumably, the best-fitting value of s will be small, because the discrete alphanumeric characters used in the standard paradigm are not highly confusable with one another. Note that the simplified model makes no use of the dimensional attention-weight parameters, lag-dependent sensitivity parameters, nor the primacy-based sensitivity parameter. In addition, in the experimental data that we will consider, the primacy effects were small, so we will not estimate a primacy-based memory-strength parameter. All other aspects of the model are the same, so we need to estimate the lag-dependent memory-strengths, random walk thresholds, and background-element parameters.

Here, we apply the simplified EBRW model to a well known data set collected by Monsell (1978; Experiment 1, immediate condition). In brief, Monsell (1978) tested 8 subjects for an extended period in the standard Sternberg paradigm, using visually presented consonants as stimuli. The design was basically the same as the one that we used in Experiment 1 of this article, except that the similarity structure of the lists was not varied. A key aspect of his design was that individual stimulus presentations were fairly rapid, and the test probe was presented either immediately or with brief delay. Critically, the purpose of this procedure was to discourage subjects from rehearsing the individual consonants of the memory set. If rehearsal takes place, then the psychological recency of the individual memory-set items is unknown, because it will vary depending on each subject’s rehearsal strategy. By discouraging rehearsal, the psychological recency of each memory set item should be a systematic function of its lag. Another important aspect of Monsell’s design is that he varied whether or not lures were presented on recent lists (i.e., lists immediately prior to the current one). Lures presented on recent lists are referred to as recent-negatives, whereas lures not presented on recent lists are referred to as novel-negatives. For starting purposes, we ignore this aspect of the procedure in describing and modeling the data, but then consider its impact in a subsequent discussion.

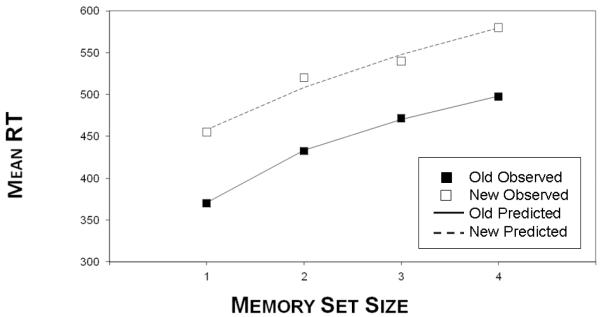
The mean RTs and error rates observed by Monsell (1978) in the immediate condition are reproduced in the top panel of Figure 4. (The results obtained in the brief-delay condition showed a similar pattern.) Following Monsell’s (1978, Figure 4) presentation, the data for the lures are averaged across the recent-negative and novel-negative conditions. Inspection of Monsell’s RT data reveals a pattern that is very similar to the one we observed in our Experiment 1 after averaging across the individual tokens of the main types of lists (i.e., compare to the observed-RT panel of Figure 3). In particular, the mean old RTs vary systematically as a function of lag, with faster RTs associated with more recently presented probes. Once lag is taken into account, there is little if any remaining influence of memory-set-size on old-item RTs. For new items, however, there is a big effect of memory-set-size on mean RT, with slower RTs associated with larger set sizes. Because of the non-confusable nature of the consonant stimuli, error rates are very low; however, what errors there are tend to mirror the RTs. Another perspective on the observed data is provided in Figure 5, which plots mean RTs for old and new items as a function of memory-set-size, with the old RTs averaged across the differing lags. This plot shows roughly linear increases in mean RTs as a function of memory-set-size, with the positive and negative functions being roughly parallel to one another. The main exception to that overall pattern is the fast mean RT associated with positive probes to 1-item lists. This overall pattern shown in Figure 5 is, of course, extremely commonly observed in the Sternberg memory-scanning paradigm.

Figure 4.

Observed (top panel) and EBRW-predicted data (bottom panel) for Monsell (1978, Experiment 1). Mean RTs and error rates plotted as a function of lag, memory set size, and type of probe. Observed data are estimates from Monsell’s (1978) Figures 3 and 4.

Figure 5.

Observed and EBRW-predicted set-size functions, averaged across different lags, for Monsell (1978, Experiment 1). Observed data are based on estimates from Monsell’s (1978) Figures 3 and 4.

We fitted the EBRW model to the Figure-4 data by using a weighted least-squares criterion. Specifically, we conducted a computer search for the values of the free parameters that minimized the quantity

$$\mathit{SSD}\left(\text{Total}\right)=\mathit{SSD}\left(\mathit{RT}\right)+W\cdot \mathit{SSD}\left(\text{Error}\right)$$ (6)

where SSD(RT) is the sum of squared deviations between the predicted and observed mean RTs, SSD(Error) is the sum of squared deviations between the predicted and observed error proportions, and W is the weight given to SSD(Error). Sensible-looking fits (i.e., ones for which the model yielded predictions that were simultaneously in the ballpark of the RT and error data) were obtained with W set equal to 100,000.

The predicted mean RTs and error probabilities from the EBRW model are shown graphically in the bottom panel of Figure 4. Comparison of the top and bottom panels of the figure reveals that the EBRW model does an excellent job of capturing the performance patterns in Monsell’s (1978) tests of the standard Sternberg paradigm. Mean RTs for old patterns get systematically slower with increasing lag, and there is little further effect of memory-set-size once lag is taken into account. Mean RTs for lures are predicted correctly to get slower with increases in memory-set size. (The model is also in the right ballpark for the error proportions, although in most conditions the errors are near floor.) Figure 5 shows the EBRW model’s predictions of mean RTs for both old and new probes as a function of memory-set size (averaged across differing lags), and the model captures the data from this perspective as well. Beyond accounting for the major qualitative trends in performance, the EBRW model provides an excellent quantitative fit to the complete set of data.

The best-fitting parameters from the model are reported in Table 3. As expected, the memory-strength parameters decrease systematically with lag, reproducing the pattern seen in the fits to our detailed Experiment 1 data. The best-fitting value of the similarity-mismatch parameter (s = .050) reflects the low confusability of the consonant stimuli from Monsell’s experiment.

Table 3.

Best-fitting parameters for the EBRW model applied to Monsell’s (1978) Experiment 1 data.

M1	2.157
M2	1.183
M3	1.065
M4	[1.000]
s	.050
u	0.529
v	0.044
OLD	2.750
NEW	4.500
μ	139.107
κ	49.253

Note: Parameter values in brackets are not free to vary.

As noted earlier, Monsell (1978) manipulated whether or not lures were presented on recent lists. One purpose of this manipulation was to test between different explanations of lag effects on mean RTs. In terms of the present modeling, old items with short lags have greater memory strengths, leading to more efficient memory retrievals and a speeded random-walk decision process. A potential alternative explanation, however, is that old items with short lags are encoded more rapidly when presented as test probes; that is, the explanation for the speeded RTs lies in the residual stages of processing and not in the memory-retrieval stage. Monsell’s manipulation of lure recency addresses this issue. If the sole explanation of the lag effects is that more recently presented items are encoded more rapidly, then recent-negatives should have faster RTs than do novel-negatives. The data, however, went decidedly in the opposite direction, with recent-negatives having slower RTs. This general pattern seems compatible with the EBRW-modeling ideas, simply by assuming that items on recently presented lists are still stored in memory, albeit with greatly reduced memory strengths (see Ratcliff, 1978, for a similar conceptual argument). Thus, if a recent-negative is presented as a test probe, it may occasionally retrieve its memory trace from previous trials, slowing the march of the random walk to the NEW threshold.

In sum, without embellishment, the EBRW model appears to provide a natural account of the major patterns of performance in the standard version of the Sternberg paradigm, at least in cases in which the procedure discourages rehearsal and where item recency exerts a major impact.

A Category-Based Version of the Sternberg Paradigm

Omohundro and Homa (1981) collected response-time data in paradigms that can be described as category-based versions of the Sternberg task. In these paradigms, instead of the stimuli being discrete alphanumeric characters, or arbitrary items randomly sampled from a continuous-dimension similarity space, the study lists were composed of members of categories. In their Experiment 1, Omohundro and Homa (1981) tested an individual-item recognition design similar to the ones described earlier in our article, with categorized lists that varied in memory-set size. In general, as expected, recognition RTs for both positive and negative probes increased with memory-set size, and the EBRW’s account of those data is similar to the ones that we provided earlier. Therefore, in this section we focus instead on their Experiment 2, which involved an alternative procedure in which subjects were tested on category-membership verification rather than on individual-item recognition. Importantly, although the task goals differ for recognition versus category verification, from the perspective of the EBRW model the underlying processes are the same. Furthermore, addressing the category-verification results is of particular interest because Omohundro and Homa (1981) argued that they were problematic for exemplar models.

In particular, Omohundro and Homa (1981; Experiment 2) used the classic prototype-distortion paradigm (Posner & Keele, 1968, 1970) to create categories and memory sets. In their paradigm, each category was defined around a polygon prototype. Statistical-distortion procedures were used to create low, medium, and high distortions of each prototype. In a preliminary training phase, subjects learned to classify the stimuli into three categories: a size-3 category, a size-6 category, and a size-9 category. There were equal numbers of low, medium, and high distortions within each category.

Following the training phase, subjects participated in a speeded-verification test of category membership. They were re-presented with the members of each category set, one at a time, and then presented with test probes. Half of the test probes were new members of the category (i.e., new statistical distortions of the category prototype). These test items were the positive probes. The remaining half of the test items were random patterns, i.e., negative probes. Among the new category members (positive probes), there was an equal number of low, medium, and high distortions. Subjects were asked to judge, as rapidly as possible without making errors, whether each test item was a member of the studied category.

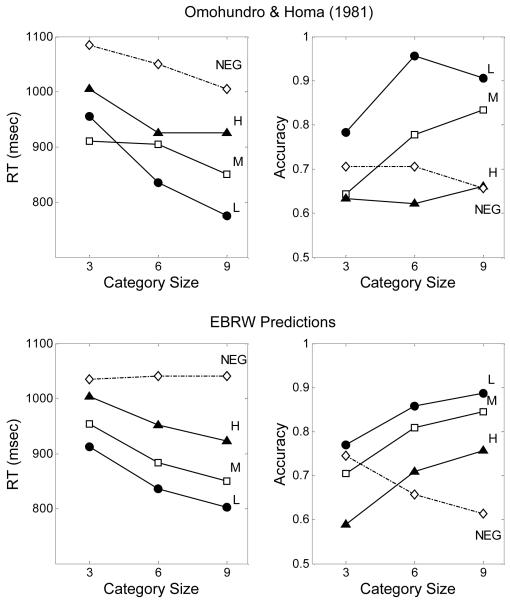
The RT and accuracy results from Omohundro and Homa (1981) are displayed in the top panels of Figure 6. The figure plots the mean RTs and accuracies as a function of category size and item type (low, medium, high distortion; or negative probe). As can be seen, for the positive probes, as category size increased, mean RTs got systematically faster and accuracies increased. (Note that this pattern is opposite of what is generally observed in individual-item recognition tasks.) In addition, subjects were fastest and most accurate on the low- distortion positive probes, intermediate on the medium-level probes, and slowest and least accurate on the high-distortion probes. Although there appear to be effects of category size on performance for the negative probes, Omohundro and Homa (1981) report that these changes were not statistically significant. (Note also that, for the negative probes, the RT and accuracy results go in opposite directions, with faster RTs for the size-9 category, but lower accuracy for the size-9 category.)

Figure 6.

Observed and EBRW-predicted data for Omohundro and Homa (1981, Experiment 2). Top panels: observed mean RTs and accuracies plotted as a function of category size and type of test probe. (Data are estimated from Omohundro and Homa’s Figure 4.) Bottom panels: EBRW-predicted mean RTs and accuracies. L = low distortion, M = medium distortion, H = high distortion, NEG = negative probe.

Omohundro and Homa (1981) interpreted their data as problematic for exemplar models of categorization and memory verification. In particular, they argued that “…if the comparison process is between the test probe and the individual category members, then the matching process should be slowed by increasing the number of exemplars used to define the category” (p. 279). Although Omohundro and Homa’s data may challenge certain versions of exemplar-matching and exemplar-search models, we argue below that the EBRW model provides a natural account of the results.

The EBRW model can be readily applied to the results from the Omohundro-Homa paradigm. First, we define parameters s_L, s_M, and s_H representing the average similarity of the low, medium, and high distortions to the category training patterns. (In general, the low distortions will tend to have the greatest average similarity to the training patterns, whereas the high distortions will tend to have the least.) Likewise, we define a free parameter s_N that represents the average similarity of the negative probes to the category members. (The value s_N should have the lowest magnitude among all of the similarity parameters.) For simplicity, we assume that the summed similarity of a test probe to the category exemplars is given by the category size times the average similarity.⁷ For example, for the size-3 category, the summed similarity for a low-distortion probe is simply 3*s_L. The remaining free parameters for the model are the same as in all previous applications in this article. Thus, we assume that the strength of the background elements (B) is linearly related to category size (S), B = u + v·S. Likewise, we need to estimate the random-walk threshold parameters +OLD and −NEW, the mean residual time μ, and a scaling parameter κ for translating the number of steps in the random walk into ms. Although the magnitude of the random-walk thresholds might conceivably vary as a function of category size (especially because the category-verification tests were conducted in a between-blocks fashion), for simplicity we hold those parameters constant across category size.

As in our applications to the standard Sternberg paradigm, we fitted the EBRW model to the Figure-6 data by searching for the values of the free parameters that minimized SSD(Total) in Equation 6. Again, we obtained reasonable-looking results with the weight on SSD(Error) set to W=100,000. The predicted mean RTs and accuracies are displayed graphically in the bottom panels of Figure 6, with the best-fitting parameters and summary fits reported in Table 4. As can be seen, this baseline version of the EBRW model provides a reasonably good account of the results. It predicts correctly that RTs for positive probes get faster (and accuracy increases) as category size increases and as the distortion level of the test probes gets smaller. The reason is that both factors lead to increasing summed similarity of the test probes to the stored exemplars, which increases the rate of drift toward the +OLD (i.e., category-member) response threshold. A possible limitation of the model is that, with the present parameter settings, it predicts a flat RT function for the negative probes, whereas the observed negative-probe RT appears to decrease with category size. Recall, however, that the observed RT changes for the negative probes were not statistically significant, so this limitation may not be a serious one. Finally, inspection of Table 4 reveals a sensible pattern of parameter estimates, with measured similarity decreasing regularly across the low, medium and high distortions and the negative probes.

Table 4.

Best-fitting parameters for the EBRW model applied to Omohundro and Homa’s (1981) category-verification task.

s L	.718
s M	.586
s H	.426
s N	.151
u	[1.000]
v	0.243
OLD	1.000
NEW	2.281
μ	100.00
κ	376.32

Note: The parameters s_L, s_M, s_H, s_N, u and v can be multiplied by any fixed positive constant without changing the predictions from the model. Here, the background-noise intercept u is set arbitrarily at 1.0, as indicated by placing that parameter value in brackets. The magnitude of the other parameters is measured relative to this setting.

In summary, without embellishment, the EBRW model accounts in natural fashion for the overall pattern of performance in the category-based version of the Sternberg paradigm tested by Omohundro and Homa (1981). An interesting direction for future research would be to conduct item-recognition and category-verification versions of the memory-scanning task in which all factors are held constant across conditions except for the task goal (i.e., recognition versus categorization). According to the present theory, the EBRW model should account simultaneously for the data across both conditions, while allowing only certain parameters to vary. For example, observers might learn to set a lower value on the background-element strength parameter in the categorization condition than in the item-recognition condition, because recognizing an item requires an exact match, whereas categorizing requires only a sufficient degree of match to the items on the study list.

Modeling Speed-Accuracy-Tradeoff Curves in the Response-Signal Paradigm

Another major perspective on the process of short-term memory recognition is obtained through use of the response-signal procedure (e.g., McElree & Dosher, 1989; Reed, 1973). In this procedure, rather than allowing the subject to respond freely, the subject is trained to make a response as soon as a signal is given. By varying the onset of the response signal, one can map out speed-accuracy-tradeoff (SAT) curves that show how accuracy changes as a function of processing time.

McElree and Dosher (1989) conducted an extremely rigorous and influential set of studies that applied the response-signal procedure to the Sternberg paradigm. In this section we briefly describe the results from their Experiment 1 and consider applications of the EBRW model to their data. In their Experiment 1, the stimuli were sets of words, and subjects were presented with lists of set-size 3 or 5. Within each set size, positive probes occurred equally often at each serial position. (Negative probes occurred equally often as did positive probes.) As was the case in Monsell’s (1978) study described earlier in this article, stimulus-presentation parameters were arranged to minimize rehearsal, so that psychological recency of the study-list items was determined by their lag. Following onset of the test probe, a response signal was presented at one of eight times: 100, 200, 300, 400, 550, 900, 1300 or 1800 msec.

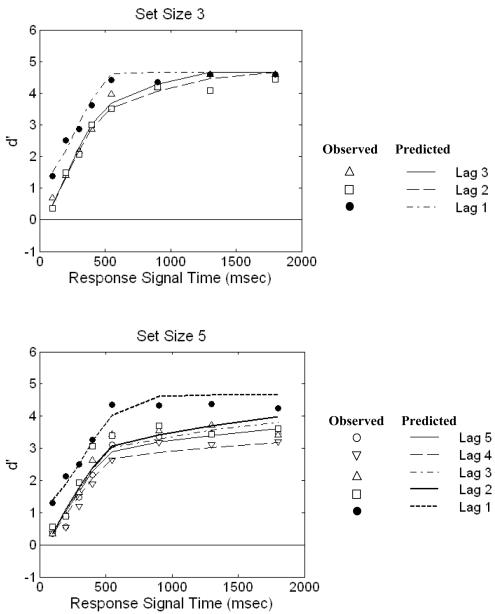
McElree and Dosher computed d’ as a function of set size, lag, and response-signal time and plotted the resulting SAT curves. The data averaged across subjects are re-presented in our Figure 7, where each SAT curve corresponds to a distinct combination of set size and lag. (Our plots differ slightly from those of McElree and Dosher because we do not include the mean RT associated with each response-signal delay.) To characterize the data, McElree and Dosher fitted exponential growth functions to the SAT curves, of the form

$$d^{\prime }\left(t\right)=\lambda \left\{1-\exp \left(-\beta \left[t-\delta \right]\right)\right\},t>\delta ,\text{else}0,$$ (7)

where d’(t) is the value of d’ at processing-time t; λ is the asymptote of the exponential-growth function; δ is the intercept where the curve starts to rise; and β is the rate at which the curve rises toward asymptote. In particular, they fitted different families of exponential curves to the data by placing different types of constraints on the free parameters (λ, δ and β) and reported the results from the family that provided the most parsimonious fit. The fit was evaluated using the proportion of variance accounted for (corrected by the number of free parameters):

$$r^2=1-\left[\sum {\left(d_i-{\widehat{d}}_i\right)}^2/(n-P)\right]/\left[\sum {\left(d_i-\stackrel{‒}{d}\right)}^2/(n-1)\right],$$ (8)

where d_i and ${\widehat{d}}_i$ are the observed and predicted d’ values, respectively; d̄ is the mean observed d’ value; n is the number of data points; and P is the number of free parameters.

Figure 7.

Observed and EBRW-predicted speed-accuracy tradeoff curves for McElree and Dosher (1989, Experiment 1). Top panel: set-size 3, bottom panel: set-size 5.

The main summary statement from these formal analyses was that a distinct asymptote (λ) was associated with each individual SAT curve. However, except for the lag-1 curves, the “dynamics” of the curves were the same, in the sense that they had nearly invariant intercepts and rates of rise toward asymptote. However, the best fits to the data required that a faster rate parameter be estimated for the lag-1 curves. In sum, this best-fitting exponential family used 8 distinct asymptote parameters, 2 rate parameters, and an intercept parameter. This descriptive model accounted for .956 of the (corrected) variance in the observed d’ data and provides a challenging benchmark against which to assess the fit of process-oriented models.

McElree and Dosher noted that a variety of formal models of short-term recognition failed to predict these general characteristics of the observed SAT curves. For example, they noted that serial exhaustive scanning models predicted curves with markedly different rate parameters, in marked contrast to the observed data. They noted as well that a general version of Ratcliff’s (1978) diffusion model with suitably chosen drift-rate parameters could capture the data, although they did not assess the quantitative fits of more specific, constrained versions of that process model.

We fitted different versions of the EBRW model to McElree and Dosher’s response-signal data by simulating the model and adopting the following assumptions. In the first version, we assumed that there is a log-normally distributed encoding stage (with location parameter μ_E and scale parameter σ_E) in which the observer first encodes the test probe.⁸ The random-walk decision process does not get started until the test probe is encoded. The difference between the processing time determined by the response signal and the simulated encoding time (DIFF) determines the amount of time that the exemplar-based random-walk process can operate. Recall that the EBRW model has a scaling parameter (κ) for translating number of steps of the random walk into ms. Thus, on a given simulated trial, the random walk will take int(DIFF/κ) steps, where int truncates any number down to the nearest integer. On any given step, the probability that the random-walk steps toward the OLD threshold is computed in the same manner as described previously for the standard Sternberg paradigm. Thus, we need to estimate the lag-related memory strength parameters M₁-M₅, the background-element parameters u and v, and the similarity-mismatch parameter s. (Without loss of generality, M₅ can be held fixed at 1, so there are 4 freely varying memory strengths.) To account for small primacy effects in McElree and Dosher’s data,⁹ we also estimate the primacy-based memory-strength multiplier P_M.

Note that in the present version of the model, estimates of the random-walk thresholds +OLD and −NEW are not needed to fit the data. Instead, we assume simply that, upon presentation of the response signal, if the random walk has taken a greater number of steps towards the OLD threshold than towards the NEW threshold that the observer responds “old”; else, the observer responds “new”. Finally, a technical assumption was needed to prevent undefined or exploding values of d’ at the very longest response-signal times. For simplicity, we set the maximum hit rate in any given condition to .99 and the minimum false alarm rate to .01. This technical assumption can be justified by positing the influence of a secondary process on performance. For example, there may always be some small probability of a response-execution error regardless of the outcome of the random-walk decision-making process.

Following McElree and Dosher, we conducted a computer search for the values of the free parameters that maximized the corrected r² value (Equation 8).¹⁰ The best-fitting version of the baseline model described above yielded r² = .941, a fit that is already in the same ballpark as the one achieved by the descriptive exponential-growth curves. In agreement with McElree and Dosher’s exponential growth-curve analysis, the main limitation of the baseline model was that it failed to account for the early rapid rise of the lag-1 functions at both set sizes 3 and 5. As noted by McElree and Dosher, the lag-1 curves correspond to a case of immediate repetition of a study item by the test probe. Immediate repetition may influence various components of the information-processing sequence. To accommodate the finding, we followed McElree and Dosher by allowing a separate free parameter unique to these curves. In particular, we estimated a separate encoding-time parameter (μ_E1) for the lag-1 curves to allow them to get off to a more rapid start. This elaborated model accounted for .962 of the corrected variance in the data, which is essentially the same as the fit achieved by the descriptive exponential growth curves from McElree and Dosher.

The fit of this version of EBRW model is shown along with the observed data in Figure 7. Inspection of the figure suggests that the EBRW model is providing a good quantitative account of the complete set of SAT curves. The best-fitting free parameters are reported in Table 5. As in our previous applications, the pattern of best-fitting free parameters seems easily interpretable and psychologically meaningful. For example, memory-strength declines systemically with lag of presentation, with a small residual primacy effect associated with the item in the first serial position. In addition, the estimated similarity between distinct items is s = .097; this low estimated value of similarity seems reasonable for the distinctive word stimuli used in the McElree and Dosher experiments.

Table 5.

Best-fitting parameters for the EBRW model applied to the response-signal data of McElree and Dosher (1989).

M1	1.821
M2	1.237
M3	1.211
M4	1.005
M5	[1.000]
PM	1.116
s	.097
u	0.667
v	0.159
μ E	4.922
μ E1	4.405
σ E	0.399
κ	11.249

Note: Parameter values in brackets are not free to vary. Given the best-fitting location and scale parameters of the log-normal encoding distribution (μ_E, μ_E1, and σ_E), the mean encoding time for the lag-2 through lag-5 serial positions is 148.7, whereas the mean encoding time for the lag-1 serial position is 88.6. The standard deviation of the encoding time for lag-2 through lag-5 is 61.8, whereas for lag-1 it is 36.8.

The version of the EBRW model described above assumed that partial information (i.e., whether the state of the random walk is positive or negative) is always available to the observer. Sophisticated techniques have been developed to evaluate whether this assumption is tenable and the issue has been debated in the literature (e.g., Meyer, Irwin, Osman, & Kounios, 1988; Ratcliff, 1988). An alternative approach to modeling response-signal data is to assume that response thresholds are still involved (e.g., Hintzman, Caulton, & Curran, 1994; Ratcliff, 2006). If one of the response thresholds has been reached by the time of the response signal, then the observer emits the appropriate response; otherwise, the observer guesses randomly. We also fitted this version of the EBRW model to McElree and Dosher’s (1989) data. It used the same free parameters as did the first version that we described above, but also estimated values for the response thresholds (+OLD and −NEW) and a response-threshold variability parameter (for details, see Extended EBRW Model section in Experiment 2). This alternative EBRW version accounted for an even higher corrected-proportion-of-variance (r² = ..968) in McElree and Dosher’s data than did the first version, albeit at the expense of an extra three free parameters.

In sum, regardless of whether or not one assumes that the observer has access to partial information, the EBRW model accounts in natural fashion for the growth in accuracy that is observed as a function of processing time in the response-signal paradigm of short-term recognition.

Predicting the Shapes of RT Distributions

If the EBRW model is to be considered a viable candidate for explaining short-term memory scanning, then it must also predict correctly the shapes of RT distributions observed in the task. In this section we provide an initial investigation of this issue. Then, in the following section, we provide rigorous tests of the model by fitting it to detailed RT distributions obtained in a new experiment.

One of the major approaches to characterizing the shapes of RT distributions is a method in which the “ex-Gaussian” distribution is fitted to the data (e.g., Heathcote, Popiel, & Mewhort, 1991; Hockley, 1984; Hockley & Corballis, 1982; Ratcliff & Murdock, 1976). The ex-Gaussian is a convolution of a normal and an exponential distribution. The normal component has two parameters, the mean (μ) and standard deviation (σ); whereas the exponential component has a rate parameter (τ). Although not intended as a process model (Matzke & Wagenmakers, 2009), the ex-Gaussian generally provides an excellent description of observed RT distributions. Furthermore, its best-fitting parameter estimates allow one to characterize the shapes of the distributions observed in a task and how the shapes change across experimental conditions. To a good first approximation, μ and σ reflect the leading edge of the distribution (i.e., the minimum RTs), whereas the ratio τ/ σ reflects the extent to which the distribution tails out and is positively skewed.

Hockley (1984) conducted a systematic investigation of how the ex-Gaussian parameters varied across different cognitive tasks. Included in his investigation was an examination of the standard Sternberg paradigm, with the key question of interest being how the shapes of the RT distributions changed as a function of memory set size. He reported clear-cut results (see Hockley, 1984, p. 603, Figure 4) in which τ increased markedly with memory set size; σ was constant; and μ increased very slightly. This same pattern was observed for both positive and negative probes. The bottom-line conclusion, corroborated by visual inspection of the observed RT distributions (see Hockley, 1984, p. 604, Figure 5), was that the leading edge of the RT distributions was nearly invariant with increases in memory set size; however, as set-size increased, the distributions tailed out and grew more positively skewed. Such results pose extreme challenges, for example, to serial-exhaustive scanning models, which predict large changes in the leading edge of the distributions as a function of set size. In addition, owing to implications of the central limit theorem, it seems that the most natural prediction from such models is that the distributions associated with large set sizes should tend to be more bell-shaped rather than more positively skewed.

Unfortunately, we cannot directly fit Hockley’s data with the EBRW model. The reason is that, in his results, mean RT did not vary with the serial position of the probe on the study list. In Hockley’s experimental procedure, a long retention interval was used, so subjects almost surely rehearsed the items on the study list. Therefore, the psychological recency of the individual items would not correspond in a direct way to their serial position. Because RT did not vary with serial position, we cannot estimate how memory strength varied with lag in Hockley’s experiment, so the EBRW model cannot be directly applied to his data.

Nevertheless, we can still examine what is the a priori pattern of qualitative predictions made by the EBRW model with respect to how the shapes of RT distributions should change with memory set size. To do so, we used as representative parameter settings (with one exception explained below) the best-fitting parameter estimates obtained from our fits of the EBRW model to Monsell’s (1978) memory-scanning data (see our Table 3). Then, using these parameter estimates, we simulated the EBRW model to generate its predicted RT distribution for each memory set size and each type of probe (positive and negative). Finally, we fitted the ex-Gaussian distribution to the simulated RT distributions to characterize how their shapes changed with increases in memory set size. Note that, although Hockley did not observe serial-position effects on RT, our analysis is still of theoretical relevance to his data. Our assumption is that his RT distributions were produced by averaging across trials in which memory strengths varied for given serial positions depending on how rehearsal operated on each trial. Flat serial position curves in the averaged data could be produced by numerous different rehearsal strategies, including random-order ones.

To generate plausible RT distributions from the EBRW model, however, we needed to make an additional assumption. Specifically, because we had fitted only mean RTs in our applications of the EBRW model to Monsell’s (1978) data, we had made use of only a mean residual-time parameter. The residual stages of encoding and response execution, however, are obviously variable, and will contribute to the overall variability and shape of the entire RT distribution. Therefore, as part of the simulations, we included variable encoding-time and response-execution-time components. For simplicity, we assumed that the encoding-time distribution was the one that we estimated by fitting the EBRW model to McElree and Dosher’s (1989) response-signal data, i.e., a log-normal distribution with mean 148.7 ms and standard deviation 61.8 ms. In the absence of any information about the time course of response-execution, we assumed for simplicity that response-execution times had this same distribution. (The encoding and response-execution times were assumed to be independent.)

Thus, on any given simulated trial, we made random draws from the encoding-time and response-execution-time distributions, and then simulated the EBRW process. The total RT on each simulated trial was the sum of these three components. We conducted 10,000 such simulations for each probe type and memory set size. For positive probes, for each memory set size, we conducted an equal number of simulations with the probe at each serial position of the study list. Finally, we fitted the ex-Gaussian distribution to each simulated distribution to obtain the best-fitting values of μ, σ, and τ. (These fits made use of the software package developed and made available by Heathcote et al., 1991.)

The results from these analyses are displayed in Figure 8, which plots the estimated values of μ, σ, and τ as a function of set size, separately for the positive and negative probes. The results are highly reminiscent of the ones observed by Hockley in the analysis of his empirical data (compare to Hockley, 1984, Figure 4). That is, for both positive and negative probes, the parameter τ increases markedly with increases in set size, whereas μ and σ are nearly flat. (Hockley’s set sizes varied from 3 to 6, whereas our simulations based on Monsell’s data consider set sizes that vary from 1 to 4, but the qualitative match between the plots is still clear.) Although we made no attempt to fit Hockley’s data, it is also worth noting that the quantitative values of the derived parameter values are remarkably close as well (for matching set sizes).

Figure 8.

Estimates of μ, σ, and τ obtained by fitting the ex-Gaussian distribution to the simulated RT distributions from the EBRW model. Left panel: results for negative probes; Right panel: results for positive probes.

Finally, in Figure 9 we plot the actual RT distributions that were generated from our simulations of the EBRW model, together with the best-fitting ex-Gaussian distributions. A separate plot is provided for each combination of type of probe and set size. Inspection of the plots reveals that the ex-Gaussian provides an excellent fit to the simulated RT distributions. Because Hockley showed that the ex-Gaussian describes well the shapes of empirical RT distributions in the Sternberg task, this result provides further support for the EBRW model as a viable candidate for explaining performance in the task. Furthermore, inspection of the plots reveals that the leading edge of the RT distributions is nearly invariant with increases in memory set size, while the positive skew increases systematically with increases in set size. Again, the plots are highly reminiscent of the empirical RT distributions reported by Hockley and mirror closely how the shapes of the empirical distributions changed with increases in memory set size in his experiment (compare to Hockley, 1984, Figure 5).

Figure 9.

Simulated RT distributions from the EBRW model (open-bar histograms) along with the best-fitting ex-Gaussian distributions (solid diamonds). The left panels are for negative probes and the right panels are for positive probes. The rows correspond to set-sizes 1 through 4.

Perhaps the main limitation of the model is that it predicts that μ should be flat, whereas Hockley (1984) did observe very slight (but statistically significant) increases in μ as set size increased. In the following part of the article we report a new experiment in which we collect our own RT-distribution data in the Sternberg task. As will be seen, under our experimental conditions, we observe large increases in μ with increases in set size, a result that the core model fails to account for. An extended version of the model, however, that allows for increases in the magnitude of the random-walk response thresholds with increases in set size, provides a good account of the detailed shapes of the RT-distribution data.

Experiment 2

The purpose of this experiment was to collect detailed RT-distribution data in the Sternberg task at the level of individual subjects and to test the EBRW model on its ability to account quantitatively for the data. We followed the general procedures of Monsell (1978) and McElree and Dosher (1984) by using rapid presentations of the memory-set items and a short retention interval. Again, this procedure was intended to minimize rehearsal. Thus, our expectation was that, unlike Hockley (1984), we would observe strong serial position effects in the data. In addition, we used two main designs for collecting the data. The first was the more typical design in which each set size was tested an equal number of times. In the second design, we instead tested each set-size/lag combination an equal number of times. The reason for also testing the latter design was that our goal was to model the RT distributions for each individual set-size/lag combination. A disadvantage of the first design is that the sample sizes are relatively small for the individual set-size/lag combinations in which set size is large. For example, in the case in which set size is equal to 5, then the total number of observations is divided across 5 different lag conditions. This problem is remedied by the second design. Nevertheless, a disadvantage of the second design is that trials involving small set sizes are relatively infrequent. Because each design has its own advantages and disadvantages, we decided to test both.

Method

Subjects

There were four subjects (1 male and 1 female in each of two designs). The subjects were all members of the Indiana University community with normal or corrected-to-normal vision. Subject 3 was the third author of this article. With the exception of Subject 3, the subjects were unaware of the issues under investigation in the research and they were paid for their participation ($9 per session plus a $3 bonus per session for good performance). Subjects 1 and 2 participated in Design 1, and Subjects 3 and 4 participated in Design 2.

Stimuli

The stimuli were the set of uppercase English consonants except for the letter “Y”. The stimuli were presented visually and sequentially. Each stimulus was presented in the center of the screen and subtended a visual angle of approximately 3 degrees.

Procedure

In both designs, memory-set-size varied from 1 to 5. On each trial, a study list was created by sampling randomly without replacement from the full set of stimuli. On negative-probe trials, the probe was selected randomly from the remaining stimuli in the full set. In Design 1, each memory-set-size was tested an equal number of times. Each subject participated in nine sessions (days) of testing, with 10 blocks per session and 50 trials per block. Within each block, there were 10 trials of each set size, half with positive probes and half with negative probes. On positive-probe trials, the serial position of the target was chosen randomly. In Design 2, each set-size/lag combination was tested an equal number of times. Each subject participated in 16 sessions of testing, with 10 blocks per session and 30 trials per block. Within each block, each set-size/lag combination was presented once. Half the trials had positive probes and half had negative probes. In both designs, the order of presentation of the trials within each block was random.

Each trial began with the presentation of a fixation cross, centered on the screen, for 500 ms. Each study item was then presented for 500 ms with a 100 ms break between stimuli. Following presentation of the last study item, an asterisk was presented for 400 ms. The asterisk signaled the presentation of the test probe, which remained on the screen until a response was made. Feedback was then provided for 1000 ms, followed by a blank screen for 1500 ms.

Subjects were instructed to respond as rapidly as possible without making errors. They were instructed that they would receive a $3 bonus in each session if they averaged less than one second per response and over 90% accuracy across all trials. Subjects made their responses by pressing the “F” key for OLD and the “J” key for NEW. They were instructed to rest their left and right index fingers on these keys throughout the testing session.

For each subject/list-type combination (where a list type refers to the combination of set size and lag), we removed from the analysis RTs greater than three standard deviations above the mean and also RTs of less than 150 ms. This procedure led to removing 1.57%. 1.40%, 1.50%, and 1.98% of the trials for Subjects 1-4, respectively.

Results and Model-Fitting Analyses

Mean Correct RTs

The mean correct RTs for the individual subjects are displayed as a function of experimental conditions in the left panels of Figure 10. (With a couple of exceptions to be described later, error rates were low and mirrored the RTs, so we focus first on the mean RT data.) Inspection of Figure 10 reveals that, for the most part, these individual-subject performance patterns are similar to the previous results that we have reported (e.g., compare to Figures 3 and 4). In general, mean RTs for the old lists get slower with increasing lag; however, there is usually a primacy effect in which the item with the greatest lag for each set size is “pulled down.” Mean RTs for the new lists get systematically slower with increases in set size. One difference from the previous performance patterns is that, for the old lists, the set-size functions do not overlap as much as before. That is, there are many cases in which, holding lag constant, set size exerts its own effect on RT, with larger set sizes generally leading to slower mean RTs. Two seemingly idiosyncratic results (which we will not attempt to model) are that: i) at Lag 1, Subject 4 shows slower mean RTs for set-size-1 lists than for some of the other lists; and ii) Subject 2 shows a nearly flat lag-RT function for set-size 5 (but not for any of the other set sizes).

Figure 10.

Experiment 2: Mean RTs plotted as a function of conditions for each of the four subjects. Left panels = observed, right panels = EBRW predicted.

Ex-Gaussian Analyses

We fitted the ex-Gaussian to the RT distributions observed for each individual subject in each set-size condition, with the data aggregated across lags. The best-fitting ex-Gaussian parameters are displayed for each subject as a function of set size and type of probe in Figure 11. In general, as was observed by Hockley (1984), the σ parameter is flat across the different set-size conditions; whereas τ increases markedly as a function of set size. (An exception arises for Subject 4, where τ is surprisingly large in the set-size-1 condition; this result coincides with the subject’s relatively slow mean RT in that condition.) The main difference from Hockley’s (1984) results is that we also observe large increases in μ as a function of set size. The large increase in μ suggests that the leading edges of the RT distributions increase as a function of set size under our experimental conditions.

Figure 11.

Experiment 2: Ex-Gaussian parameter estimates for the RT distributions corresponding to the different set sizes and probe types. m = μ, s = σ, t = τ are the ex-Gaussian parameter estimates derived from the observed RT distributions. Dashed lines show the ex-Gaussian parameter estimates derived from the predicted RT distributions.

From the perspective of the EBRW model, this systematic increase in the leading edge suggests that subjects may be increasing the magnitude of the random-walk thresholds (+OLD and −NEW) as set size increases. Intuitively, if the thresholds remain constant, then, regardless of the drift rate, the fastest RTs in each condition (i.e., the leading edge of the distributions) should be roughly the same. The reason is that, in some proportion of the cases, each step in the random walk will move in a consistent direction toward one or the other threshold, producing the same fastest RTs across the different set-size conditions. By contrast, if the thresholds increase as a function of set size, then the minimum number of steps required to complete the random walk increases as well. Note that the assumption of a response-threshold shift also has the potential to explain why the mean RT functions associated with different set sizes are not fully overlapping (see Figure 10). The drift rate for positive probes in the EBRW model is determined mainly by the probes’ lag. However, assuming a fixed lag and drift rate, the mean number of steps required to complete the random walk will increase as the threshold settings are increased, so mean RTs will increase with set size even if lag is held fixed.

Armed with this information regarding both the pattern of mean RTs and the leading edges of the RT distributions, we decided to extend the core version of the EBRW model by making allowance for threshold shifts with increases in set size.

Extended EBRW Model

Fitting the EBRW model to the RT-distribution data will require methods in which the random-walk process is simulated. In the discrete random walk, the threshold settings on each simulated trial are integer valued. To allow for “continuous-like” increases in the magnitude of the integer-valued threshold settings as a function of set size, we used the following mechanisms. First, we extended the EBRW model by explicitly incorporating threshold variability across trials (e.g., Brown & Heathcote, 2005; Ratcliff, van Zandt, & McKoon, 1999). In the simulations, a location parameter L and a range parameter R defined a uniform distribution from which the threshold was sampled on each given trial; the lower limit of the uniform distribution was given by L − R/2 and the upper limit by L + R/2. For set-size-1, the location parameters for the OLD and NEW thresholds were simply the parameters +OLD and −NEW; the same range parameter R was assumed for both the OLD and NEW thresholds. Next, for any given trial, a random sample was drawn from each uniform distribution. The integer-valued threshold magnitude for that simulated trial was then defined by truncating the randomly drawn sample to its integer-valued magnitude (e.g., the sampled value −3.6 would be truncated to −3). Finally, the magnitude of the location parameters that defined the uniform distributions were allowed to increase linearly as a function of set size. So, for example, for the old threshold, the location parameter for set-size S was given by L = OLD + δ·(S−1), where δ is the slope of the linear function. This extension adds the free parameters R and δ to what was the core version of the model. In a nutshell, the extended model defines integer-valued threshold settings that operate on each individual simulated trial, but allows for continuous-like increases in the locations of the distributions from which the threshold settings are sampled.

Finally, based on inspection of the data and preliminary model-fitting results, we made special provision for the modeling of Subject 3’s data. As will be seen in the next section, Subject 3 had high error rates in a couple of the conditions involving old lists with large set sizes and lags. The threshold-shift model described above failed to account for these high error rates. At the same time, the model predicted mean RTs in those conditions that were too slow. A salient hypothesis stemming from those combined mis-predictions was that Subject 3 occasionally “short-circuited” the memory-comparison process in cases in which it was dragging on for too long. To model this pattern, we assumed that the subject adopted a variable deadline time, and responded “new” whenever the deadline was exceeded. On each simulated trial, the deadline was randomly selected from a normal distribution with mean μ_d and standard deviation σ_d.

Model-Fitting Approach

For each subject, the correct RT data for each list type (i.e., each set-size/lag combination, plus the new lists) were divided into 50-ms bins, ranging from 150 ms to 1350 ms. In addition, a final bin defined the total number of errors for each list type. Because error rates were generally very low, we did not attempt to fit error-RT distributions. However, the error data still strongly constrain the model, because it is required to simultaneously fit both the correct-RT distributions and the overall error rates for each list type. In particular, the fit of the model to the data was evaluated using the multinomial log-likelihood function:

$$\ln L=\sum _{i=1}^n\ln \left(N_i!\right)-\sum _{i=1}^n\sum _{j=1}^{m+1}\ln \left(f_{ij}!\right)+\sum _{i=1}^n\sum _{j=1}^{m+1}{f}_{ij}\cdot \ln \left(p_{ij}\right)$$ (9)

where N_i is the number of observations of list type i (i = 1, n); f_ij is the frequency with which list-type i had a correct RT in the j’th bin (j = 1,m) or was associated with an error response (j = m+1); and p_ij (which is a function of the model parameters) is the predicted probability that list-type i had a correct RT in the j’th bin or was associated with an error response. The log-likelihood values were then transformed to account for the number of free parameters used by the model. In particular, we used the Bayesian Information Criterion (BIC; Schwarz, 1978), which penalizes the log-likelihood based on the number of free parameters and the size of the sample being fit:

$$\mathit{BIC}=-2\ln L+n_p\ln \left(M\right)$$ (10)

where n_p is the number of free parameters in the model and M is the total number of observations in the data set. The BIC will be useful for comparing the fit of the extended threshold-shift version of the EBRW model to the core version.

Quantitative predictions of the RT-distribution and error-probability data were generated using 10,000 simulations for each list type (200,000 simulations for the entire set). We used a modified Hooke and Jeeves (1961) parameter-search procedure starting from 100 different random starting configurations to find the set of best-fitting parameters for each individual subject.

Model-Fitting Results

The predicted RT distributions are shown along with the observed RT distributions for each individual list type in Panels A-D of Figure 12. (Each individual plot also reports the predicted and observed error rates for that list type.) The spatial layout of the plots is such that the rows correspond to the differing set sizes and the columns correspond to the differing lags. Visual inspection of these plots suggests that, besides predicting correctly the overall locations of the individual-list RT distributions, the model is providing a good account of their detailed shapes. As an example, note that, for each subject, the lag-1 distributions tend to have peaked shapes with only slight positive skew. As lag increases, the distributions begin to flatten out and exhibit greater positive skew. This pattern of changing shapes is well captured by the model. As a second example, consider the RT distributions for the lures (far right column of each figure). As one moves from set-size-1 through set-size-5, two changes can be observed. First, the leading edge of the distributions moves farther to the right; second, the shapes of the distributions change from peaked to flatter and more positively skewed. These patterns too are well captured by the model. Finally, although error rates tend to be low, the model is usually in the right ballpark for the error data.

Figure 12.

Experiment 2: RT distributions corresponding to each individual list type. Open bars = observed distributions, solid diamonds = predicted distributions. The figure also lists, within each panel, the predicted and observed error rates for that list type.

To gain some additional perspective on the performance of the model, in the right panels of Figure 10 we plot the predicted mean RTs as a function of conditions. Although no attempt was made to directly fit the observed mean RTs, visual inspection of the figure indicates that the model does quite well at reflecting the overall performance patterns. (Not surprisingly, it fails to predict the slow mean RT exhibited by Subject 4 in the size-1/lag-1 condition; and it fails to predict the flat lag-RT function for Subject 2 in the set-size-5 condition.)

To gauge the extent to which the model is accurately predicting the shapes of the distributions, we conducted ex-Gaussian analyses on the predicted RT distributions. In Figure 11 we plot the best-fitting predicted ex-Gaussian parameters as dashed lines for comparison with the observed parameters. These plots show that, in general, the parameters derived from the predicted distributions track very closely the parameters derived from the observed ones. The major exception occurs for Subject 4 in the set-size-1 conditions, where the model vastly under-estimates the observed value of τ.

In Table 6 we report the BIC fit of the model for each subject. For purposes of comparison, we also report the BIC fits of a constrained version of the model in which the response thresholds were assumed to remain fixed across the different set sizes (i.e., δ = 0). In all cases, the constrained model fits worse than does the extended one, sometimes dramatically so. The worse fit of the fixed-threshold model is not surprising in view of the previous qualitative evidence that suggested that threshold shifts occurred.

Table 6.

Experiment 2: BIC Fits of the EBRW Model to the Individual-Subject RT-Distribution and Error Data.

Subject	Threshold-Shift Model	Fixed-Threshold Model
1	1258.0	1470.8
2	1365.0	1494.5
3	1284.1	1684.6
4	1671.7	1729.5

Best-Fitting Parameters

The best-fitting EBRW parameters for each of the subjects are reported in Table 7. In general, the patterns of parameter estimates are similar to what we reported previously in fitting the core version of the model to the other data sets. For example, the memory strengths tend to decline with increasing lag. Note, however, that for S1 and S2, at very long lags the memory strengths begin to “wrap around” and slightly grow. Conceivably, for the set-size-5 lists, these subjects made efforts to rehearse and reactivate the initial members of the memory set. Such a process would help to explain the nearly flat lag-RT function observed for S2 in the set-size-5 condition.¹¹

Table 7.

Experiment 2: Best-fitting parameters for extended EBRW model.

	S1	S2	S3	S4
M1	4.254	1.757	4.290	3.441
M2	0.880	0.833	2.149	1.741
M3	0.782	0.734	1.699	1.372
M4	0.979	0.931	1.226	1.321
M5	[1.000]	[1.000]	[1.000]	[1.000]
PM	1.150	0.987	1.390	1.303
s	0.014	0.026	0.201	0.102
u	0.398	0.333	2.715	0.995
v	0.000	0.012	0.000	0.090
OLD	1.750	2.109	2.749	6.000
NEW	2.497	3.500	3.968	7.014
μ R	273.144	349.380	390.539	367.602
σ R	27.383	38.901	32.863	36.852
κ	30.634	20.438	1.876	6.000
R	0.937	1.417	1.315	1.023
δ	0.213	0.388	2.306	0.602

Note. For Subject 3, μ_d = 841.7, σ_d = 60.8. Parameter values in brackets are not free to vary.

Discussion

In sum, overall, the EBRW model provides a good account of the detailed shapes of the RT distributions observed in the Sternberg task. These good predictions are observed at the level of individual subjects and types of lists. However, to achieve these good fits, we needed to make allowance for the idea that subjects increased the magnitude of their random-walk response thresholds as memory set-size increased. Still, this assumption involved the estimation of only a single additional free parameter, and the model was required to fit extremely rich data sets. It is an open question what are the conditions that lead subjects to vary the magnitude of their random-walk thresholds across different set sizes. The subjects in the present experiment were highly experienced, having participated in the task for between 9-16 days of testing. Possibly, the between-list shifts in the random-walk thresholds were related to this extensive experience that the subjects had in performing the task.

Although the EBRW model provided a good overall account of the observed performance patterns, there were a couple of results that were outside its scope. Perhaps the most obvious example was the relatively slow mean RT displayed by Subject 4 on the size-1 lists. In the design in which Subject 4 participated, set-size-1 lists were rare. Possibly, some type of “surprise” factor may have contributed to the subject’s slow RTs on those trials. That particular result is likely to present a major challenge to virtually all reasonably constrained models of short-term memory scanning.

The Extralist Feature Effect on Short-Term Recognition

In our final application, we acknowledge an important limit on the EBRW’s account of short-term recognition and sketch some preliminary ideas that may remedy the problem. The limit involves a robust effect reported by Mewhort and Johns (2000; 2005; Johns & Mewhort, 2002) in which subjects make use of extralist feature information as a basis for correctly rejecting negative probes. As indicated in our introduction, the EBRW model is a member of the class of global-matching models, which assume that subjects judge a test probe to be “old” if there is sufficient positive match between the test probe and the items stored in memory. In contrast to this principle, Mewhort and Johns provide convincing evidence that there are situations in which subjects make use of individual features of test probes to provide negative evidence that the test probe must be new.

To illustrate, the structure of Mewhort and Johns’s (2000) Experiments 1-3 is shown schematically in Table 8. The study set consisted of colored shapes. In the table, each uppercase letter to the left denotes a shape, whereas each lowercase letter to the right denotes a color. Thus, Aa might denote square/red, Bb might denote circle/blue, and Ab would then denote square/blue. The critical manipulation in the experiment involved the types of negative probes presented at time of test. The features that composed the negative probes either came from the study set or instead were extralist features. For example, if the study colors included blue, green, and red, then an extralist color might be yellow. In the notation in Table 8, an uppercase X to the left denotes an extralist shape and a lowercase x to the right denotes an extralist color. Across Experiments 1-3, there were four main types of negative probes, denoted by the number of times that each of its features occurred in the study set. In particular, for a 0:0 probe, both features occurred zero times in the study set, i.e., both were extralist features (Xx). For a 1:0 probe, one feature occurred once in the study set and one feature was an extralist feature (e.g., Xa in Experiment 2). For a 2:0 probe, one feature occurred twice in the study set and the other feature was an extralist feature (e.g., Ax in Experiment 2). And for a 1:1 probe, each feature occurred once in the study set (e.g., Ba in Experiment 3).

Table 8.

Schematic design of Mewhort and Johns’s (2000) Experiments 1-3.

Experiment 1					Probe Type	Example Probe
					0:0	Xx
					1:0	Ax
Study Set:	Aa	Bb	Cc		1:1	Ba
Experiment 2					Probe Type	Example Probe
					0:0	Xx
					1:0	Xa
Study Set:	Aa	Ab	Bc	Cc	2:0	Ax
Experiment 3					Probe Type	Example Probe
					2:0	Ax
Study Set:	Aa	Ab	Bc	Cc	1:1	Ba

Perhaps the key result obtained by Mewhort and Johns was that 2:0 probes had much faster correct rejection RTs than did 1:1 probes, despite the fact that traditional global-matching models predict that they have the same degree of global match or familiarity to the items in the study set. To illustrate, consider an application of the EBRW model. When applied to separable-dimension stimuli (Shepard, 1964) composed of two discrete features, the model assumes that the similarity between items i and j is given by

$$s_{ij}={\alpha }_1{\alpha }_2$$ (11)

where α_k = 1 if objects i and j match on feature k; and α_k is set equal to a free parameter s (0 < s < 1) if the items mismatch on that feature (Medin & Schaffer, 1978; Nosofsky, 1984). (As discussed by Nosofsky [1984, 1986], this multiplicative-similarity rule entails the assumption that distances between separable-dimension stimuli are computed on a city-block metric, with similarity being an exponential-decay function of distance.) For example, the similarity of Ab to Ac would be equal to s, and the similarity of Ab to Cc would be equal to s². Thus, the reader may verify that, in Mewhort and Johns’s Experiment-3 design, the summed similarity of the 2:0 probe and the 1:1 probe to the study-set items is identically equal to 2s + 2s², so the model predicts they should have identical correct-rejection RTs, in marked contrast to the observed data.

Moreover, beyond this fundamental qualitative effect, Mewhort and Johns showed that the overall pattern of correct-rejection RTs across their Experiments 1-3 could be predicted reasonably well simply in terms of the number of a probe’s features that had occurred in the study set. (For example, in Experiment 3, one of the features of probe 2:0 occurred in the study set, whereas two of the features of probe 1:1 occurred in the study set.) This relation is shown in the top panel of our Figure 13 (adapted from Mewhort and Johns’s [2000] Figure 3). As can be seen in the figure, the greater the number of a probe’s features that had occurred in the study set, the slower was the mean correct-rejection RT. This result was among the sources of evidence that led Mewhort and Johns to suggest that the features of a probe are compared to a composite memory of features and items from the study set. Once an observer verifies that a given test feature was not in the study set, there is already sufficient evidence to reject the test probe as a new item. Furthermore, the greater the number of such extralist features, the faster on average can such negative evidence be found.

Figure 13.

Top panel: Mean RTs plotted as a function of number of a probe’s features in the study set across Experiments 1-3 of Mewhort and Johns (2000). (Adapted from Mewhort and Johns, 2000, Figure 3, bottom panel.) Bottom panel: Mean RTs plotted as a function of the EBRW model’s computation of summed similarity across Experiments 1-3 of Mewhort and Johns (2000).

Here, we sketch a couple of possible extensions of the EBRW model that might serve as starting points for candidate models to handle the effects. The first extension stays close to the standard EBRW model. In considering the applications of global-matching models to their experimental designs, Mewhort and Johns made an eminently reasonable assumption that we will term the fixed-similarity assumption. This assumption is that the similarity between two mismatching features that occurred on the study list (e.g., A and B in Experiment 1) is the same as the similarity between an extralist feature and a study feature (e.g., X and B in Experiment 1). This assumption is reasonable because the features that served as study-list features or extralist features were randomly chosen on each trial. Nevertheless, here we propose the alternative idea that an extralist feature may be psychologically less similar (on average) to a given study-list feature than are two study-list features to one another. This proposal draws upon an important idea from the psychological literature that inter-item similarity is not a fixed and invariant relation but rather a highly context-dependent one (Medin & Schaffer, 1978; Nosofsky, 1984, 1986; Tversky, 1977). For example, in the GCM and the EBRW model, the similarity between two items depends on the attention weights given to the features, and those weights are hypothesized to vary systematically depending on the structure of the categories or the study lists to be learned (Nosofsky, 1986, 1991). Thus, the overall global structure of a set of study items may influence inter-item similarity. Likewise, we think it is plausible that individual-feature similarity may be influenced by the context in which the features are embedded. A highly novel feature that is completely unique to a study set may become psychologically less similar to the study-set features than the study-set features are to one another.

Although future research is needed to test the idea, it is worth considering the implications of the assumption for the extralist feature results. Thus, we extend the EBRW model by assuming that although the similarity between two study-list features is given by s, the similarity between an extralist feature and a study-list feature is given by x < s. So, for example, the reader may verify that, in Mewhort and Johns’s Experiment 3 (see our Table 8), whereas the summed similarity of probe 1:1 to the study-list items is equal to 2s + 2s², the summed similarity of probe 2:0 is equal to 2x + 2sx. We considered the ability of this extended EBRW model to handle the general pattern of data in Mewhort and Johns’s Experiments 1-3 by plotting the correct rejection RTs against summed similarity (computed with feature-mismatch parameters s and x). We set s = .30 and then conducted a computer search for the value of x that maximized the correlation between summed similarity and the correct-rejection RTs. The results with x = .12 are shown in the bottom panel of Figure 13, which demonstrates that the model can capture very well the general pattern of correct-rejection RTs across the experiments. (Across a wide range of EBRW-parameter values, the same pattern is observed if the summed-similarity values are transformed to predicted RTs via the EBRW equations.) Similar results are obtained across a very wide range of settings of s for suitably chosen values of x. It remains to be seen if this type of extended model can capture other aspects of extralist feature effects observed in Mewhort and Johns’s experiments.

Finally, we sketch briefly an alternative possible extension of the EBRW model to account for extralist feature effects. This alternative extension is in keeping with Mewhort and Johns’s general proposal that, upon presentation of the study list, the observer stores a composite memory of both individual items and individual features. This composite form of memory representation seems particularly plausible in situations in which the to-be-remembered items consist of highly separable components, such as the colored shapes used in Mewhort and Johns’s (2000) Experiments 1-3. In the extended model, instead of decision-making being governed by a single-channel random walk process, as in the EBRW, we imagine that three separate random walks take place: one tuned to shape, one tuned to color, and the third to the items (i.e., the shape-color combinations). If any one of the random walks makes a “new” decision, then the observer can terminate the comparisons and conclude that the test probe must be new. An “old” decision is made only if the item-based random walk reaches its OLD threshold. Assuming that the individual-feature random walks operate more quickly than the item-based random walk, such a model would capture the general pattern of results observed in the studies. Negative probes with extralist features would lead to fast “new” decisions on the feature-based random walks. Negative probes without extralist features would need to rely on the slower item-based random walk to enable a correct rejection. Furthermore, the greater the number of extralist features in a probe, the faster on average would one of the feature-based random walks reach its response threshold, so the faster on average would be the correct-rejection RT. We have presented only the general outline of such a model in this section because a fully specified version would likely require more free parameters than there are data points to be fit. Nevertheless, in our view, such an extension seems promising, and merits careful investigation in future experiments.

General Discussion

Summary

Exemplar-similarity models such as the GCM were originally conceived as models of multidimensional stimulus classification. Extended versions of the originally formulated models, such as the exemplar-based random-walk (EBRW) model, have accounted well not only for choice-probability data, but also for classification RTs. A recurring theme in the literature has been to use exemplar-similarity models of classification to also explain old-new recognition performance. Moreover, just as is the case for the applications to classification, the goal is to model not only old-new recognition choice probabilities, but also recognition RTs. Recent work reported by Lamberts et al. (2003) and Nosofsky and Stanton (2006) showed that exemplar-similarity models accounted successfully for long-term recognition RTs and choice probabilities at the individual-subject and individual-stimulus levels, and that fine-grained differences in recognition RTs could be predicted on the basis of the precise location of test items in multidimensional similarity space. Taken together, these previous lines of research have suggested that exemplar-similarity models may provide a unified account of the processes of multidimensional classification and old-new recognition.

To date, however, a major gap in research is that the RT predictions of exemplar-similarity models such as the EBRW model have not been examined in the variants of the Sternberg paradigm, perhaps the most venerable of all recognition-RT tasks. The primary aim of the present work was to fill that gap, and to conduct a systematic investigation of the performance of the EBRW model in that paradigm. In our view, our reported tests of the model were largely successful, and the model appears to account in natural fashion for a wide array of results involving short-term memory scanning. The successful applications include natural accounts of: 1) mean RTs and choice probabilities associated with individual lists in the continuous-dimension, similarity-based version of the paradigm; 2) mean RTs as a function of memory-set size, serial position, and probe type in the standard version of the paradigm that uses discrete alphanumeric characters; 3) mean RTs and error rates in category-based versions of the paradigm; 4) detailed speed-accuracy trade-off curves observed in the response-signal method for assessing short-term recognition performance; and 5) the shapes of RT distributions observed in short-term memory scanning tasks. We also outlined extensions of the model that may provide viable accounts of extra-list feature effects on short-term recognition performance. Beyond accounting in natural fashion for these diverse forms of short-term recognition RT, the best-fitting parameters from the model varied in easy-to-interpret and psychologically meaningful ways.

In sum, these initial tests suggest that the EBRW model is indeed a promising candidate model for understanding performance in the many variants of the Sternberg paradigm. In our view, these preliminary successes are highly intriguing. To reiterate, exemplar-similarity models such as the GCM and EBRW model were originally conceptualized as models of multidimensional perceptual classification and have been highly successful in that domain. It is far from obvious that the types of processes that underlie perceptual classification may also underlie short-term, old-new recognition. Yet, the current successful tests suggest the very real possibility that the processes of multidimensional classification and short-term old-new recognition may be governed by common operating principles.

Other Memory-Scanning Phenomena and Issues

Despite the broad application of the EBRW model to the diverse paradigms considered in this article, many issues remain for future research and investigation. We briefly consider some of these issues in this section.

Automaticity in Consistent-Mapping Paradigms

The focus of the present research was on the version of the Sternberg (1966) paradigm that involved the “varied-set” procedure, in which the set of stimuli associated with positive responses changes from trial to trial. Sternberg (1966) also investigated a “fixed-set” procedure, in which the same positive set is tested for many trials. Sternberg (1966) observed the same set-size functions in the varied-set and fixed-set procedures. However, Shiffrin and Schneider (1977) found that in search paradigms involving fixed sets that receive “consistent mappings,” in which one set of items always receives positive responses and a second set always receives negative responses, there are eventually qualitative changes in the set-size functions. In particular, following extended practice, the RT set-size functions tend to flatten out, suggesting that some type of automatic detection of targets occurs. Shiffrin and Schneider (1977, p. 171) posited that Sternberg’s (1966) subjects in the fixed-set procedure were given too little training for the automatic-detection process to develop. The EBRW model presented here predicts flat set-size functions when: i) the memory strengths do not vary with set size or serial position; ii) similarity between distinct stimuli approaches zero, and iii) the random-walk thresholds do not increase with set size. Because subjects receive extensive practice searching for the same items under consistent-mapping conditions, it seems plausible that the memory strengths may reach asymptotic long-term levels and will not be dependent on set size or on their serial position in the study list presented on each specific trial. Furthermore, in cases involving highly discriminable stimuli, such as alphanumeric characters, it seems reasonable that a variety of learning processes might drive measured similarity between distinct items down to near-zero levels. Finally, under such conditions, it would be maladaptive for subjects to change their random-walk thesholds based on set size. Thus, the EBRW model may offer a viable account of the processes that are involved when subjects learn automatic-detection responses under consistent-mapping conditions.

Multiple Strategies of Short-Term Recognition

In providing perspective on the history of research involving the paradigm, Sternberg (1975, pp. 12-13) noted that, depending on experimental conditions, alternative processing strategies may come into play. Our focus in this article was on versions of the paradigm that used rapid presentation of the memory-set items and a short retention interval between study and test. Our rationale was that such conditions discourage complex rehearsal strategies and so psychological recency might be systematically related to lag of presentation. By contrast, in Sternberg’s seminal studies, slower presentation rates were used and there was a long retention interval. Furthermore, following the old-new recognition judgment, subjects attempted to recall the memory-set items in their order of presentation. Conceivably, subjects might adopt familiarity-based recognition strategies under conditions involving rapid presentations and short retention intervals, but adopt serial-search strategies under conditions such as those used by Sternberg (1966). One problem with applying the EBRW model under Sternberg’s (1966) conditions is that subjects’ manner of rehearsal is unknown. Possibly, future research might investigate performance with the stimulus-presentation and retention-interval parameters used by Sternberg (1966), yet develop procedures in which the manner of rehearsal is brought to light. For example, subjects might be required to rehearse overtly, or might be provided with specific instructions on the strategy of rehearsal to use. It is an open question whether or not suitable versions of the EBRW would continue to capture performance under these alternative experimental conditions.

Error Versus Correct RTs

A limitation of the work reported in this article is that we made no attempt to account for error RTs, which often show complex patterns and can be highly diagnostic for distinguishing between alternative classes of models. To take just one example, in their continuous-dimension version of the Sternberg paradigm, Huang, Kahana, and Sekuler (2009, Figures 5A and 5B) report an interesting pattern involving relations between false alarm probabilities and false-alarm RTs. Although false-alarm probabilities were (marginally) greater for high-similarity lures compared to a low-similarity lure (as would be expected), there was a case in which the mean false-alarm RT was marginally faster for the low-similarity lure than for the high-similarity ones. Intuitively, one might expect the RT results to go in the opposite direction, because the same processes that lead to high false-alarm probabilities might also induce fast false-alarm RTs. Possibly, the Huang et al. result could involve certain types of selection effects. In particular, subjects might be more likely to false-alarm to the low-similarity lure on trials in which the random-walk thresholds are not set at stringent values, thereby leading to faster RTs. More generally, for the EBRW model to provide a complete account of the detailed patterns of results involving error and correct RTs, detailed assumptions would need to be introduced involving both threshold and drift-rate variability across trials. We leave this important direction as one of our goals for future research.

Fixed Number of Slots in Visual Working Memory

We do not claim that the cognitive and neural systems that govern short-term and long-term memory are necessarily the same. Rather, given the success of the EBRW model in accounting for both short-term and longer-term recognition RTs, our claim is only that similar operating principles may underlie performance across these domains. Does our research have anything to say about the claim that visual working memory is limited by a fixed number of slots (e.g., Awh, Barton, & Vogel, 2005; Luck & Vogel, 1997; Rouder, Morey, Cowan, Zwilling, Morey, & Pratte, 2008)? In our view, the relation between the fixed-slots literature and the current work on short-term memory scanning is unclear. Much of the evidence for a fixed number of slots in visual working memory resides in the change-detection paradigm, in which subjects are presented with multiobject simultaneous visual displays. By contrast, in the Sternberg paradigm, we are concerned with the storage and retrieval of a sequentially presented list of items. We agree with the recent analysis of Öztekin, Davachi, and McElree (2010, p. 1131) that the change-detection experiments may measure capacity limits associated with encoding of simultaneous displays. Different processes may be involved when subjects attempt to encode and store in memory individual objects one at a time and then later attempt to recognize and retrieve them. Although the EBRW modeling is silent on the question of whether fundamentally different systems underlie working memory and long-term memory, it might serve as a useful analytic tool to help investigate that question. For example, suppose that subjects are presented with long lists of to-be-remembered items under conditions in which rehearsal is prevented, and are probed with items at varying serial positions on the list. Analysis of the RT and accuracy data within the framework of the EBRW model might reveal a sharp discontinuity between the magnitude of the memory-strength and sensitivity parameters associated with the final 3-4 items on the list and with the earlier items. Such a result would support the proposal of a specialized working memory system with a fixed number of slots.

Contrasting the EBRW Model with Alternative Accounts

The current exemplar-based account of short-term old-new recognition differs in important conceptual ways from the dominant past approaches in the field. The classic accounts of short-term memory recognition tend to posit forms of processing that involve access to individual items in memory. In some cases, the recognition RT might be based on the strength of an individually accessed item (e.g., Murdock, 1985). Other models assume that the subject engages in a serial-exhaustive scan of the memory set to check if a match to an individual item has been found (Sternberg, 1966, 1969). And, in perhaps the most successful and comprehensive past approach, discussed in more detail below, the assumption is that the subject engages in a parallel search of the items in the memory set, which self-terminates if matching access to any individual item is achieved (Ratcliff, 1978). By contrast, the conception in the EBRW model is that short-term old-new recognition is based on a global match of the test probe to the memory-set items, not on individual access to any single item. This global match is formalized in terms of the summed activation of the all of the memory-set items that is yielded by the presentation of the test probe.

To amplify on the conceptual distinction above, we consider in greater detail Ratcliff’s (1978) seminal multiple-channel diffusion model as applied to short-term recognition. According to the model, presentation of a test probe evokes a set of parallel diffusion processes (i.e. continuous-time random walks), with a separate diffusion process corresponding to each individual item in the memory set. The drift rate of each individual diffusion process corresponds to the degree of relatedness of the test probe to each individual memory-set item. If any individual diffusion process reaches the criterion for responding OLD, then the observer emits an OLD response, and the process self terminates. The observer emits a NEW response only if all of the individual item-diffusion processes reach their respective NEW criteria, which entails exhaustive processing of the memory-set items. Ratcliff’s (1978) application of the model to the Sternberg paradigm involved only the standard case in which the stimuli were discrete alphanumeric characters. However, it would likely be straightforward to extend the model to the continuous similarity-based and category-based versions of the paradigm by allowing the drift rates of the individual diffusion processes to be functionally related to the degree of similarity between the test probe and the individual memory-set items.

Despite the close relation between Ratcliff’s (1978) multiple-channel diffusion model and the present EBRW approach, the models are conceptually different. The Ratcliff (1978) model says that an OLD response is made if any individual diffusion process reaches its OLD criterion, i.e., it assumes a form of individual-item access. By contrast, the idea in the present EBRW model is that the exemplar-based information feeds into a single random-walk process, driven by the overall global match of the probe to all of the items in the memory set.

It remains an open question if sufficiently diagnostic experimental paradigms can be devised to tease apart the alternative conceptions. (For approaches that have been used to try to distinguish between multiple-channel and pooled single-channel random-walk models in the domain of multidimensional categorization, see, e.g., Fific, Little, & Nosofsky, 2010; Little, Nosofsky, & Denton, in press.) Certainly, the question of whether recognition is achieved via access to individual items or via global-matching processes is among the most fundamental ones in memory and cognition. Therefore, despite the close relation between the models, the research direction of trying to distinguish between them is an extremely important one to pursue.

Appendix A. Multidimensional Scaling Method and Analysis for Experiment 1

Method

Subjects

The subjects were 88 undergraduate students from Indiana University. The subjects received credit toward an introductory psychology course requirement and also received a small monetary bonus for good performance.

Stimuli

The stimuli were the same 27 color squares used in the memory experiment. The colors were presented in pairs in the center of the computer screen against a white background. Each color occupied 2 × 2 in. square, and members of the pair were separated by approximately 25 pixels.

Procedure

In the main part of the experiment, each subject was presented with all 351 distinct pairs of the 27 stimuli. On each trial, they rated the similarity of the members of a given pair on a scale from 1 (not similar) to 9 (very similar). The order of presentation of the pairs, as well as the left-right placement of the members of each pair, was randomized for each subject. Prior to this main phase, subjects received 25 practice trials, with pairs drawn randomly from the complete set.

Analysis

We computed the averaged similarity rating for each pair of stimuli and derived a three-dimensional scaling solution for the stimuli by fitting these averaged ratings. The scaling model assumed a linear relation between the ratings and the Euclidean distances between stimuli in the space. We conducted computer searches for the MDS-coordinate parameters that minimized the sum-of-squared deviations between the predicted and observed ratings. (Extremely similar solutions were derived using alternative ordinal, “non-metric” scaling methods that minimized stress.) The parameter search routine was a modified version of Hooke and Jeeves (1961). Alternative starting configurations based on the Munsell coordinate structure and on the best-fitting non-metric configuration led to identical solutions for the parameter-search routine. The derived three-dimensional scaling solution accounted for 97.4% of the variance in the averaged ratings. The solution is illustrated in Figure A1, and the individual-stimulus coordinates are listed in Table A1. Although there are some local distortions, inspection of Figure A1 confirms that the psychological structure of the stimuli reflects fairly closely the 3×3×3 Munsell coordinate structure. Use of a higher number of dimensions led to minuscule improvements in the fit of the scaling model to the similarity data; furthermore, the extra dimensions were not interpretable. Use of fewer than three dimensions led to dramatically worse fits.

Figure A1.

MDS solution for the colors. Top panel: plot of Dimension 1 (hue) against Dimension 2 (brightness). Bottom panel: plot of Dimension 1 (hue) against Dimension 3 (saturation). Hue dimension-values 1, 2, and 3 (both panels) are represented by open, gray, and solid symbols. Brightness dimension-values 1, 2, and 3 (top panel) are represented by circles, squares, and triangles. Saturation dimension-values 1, 2, and 3 (bottom panel) are represented by circles, squares, and triangles.

Table A1.

Multidimensional scaling coordinates for the colors used in Experiment 1.

Color	1	2	3
1	1.164	0.969	0.888
2	1.258	0.952	1.322
3	1.409	0.940	1.718
4	1.081	1.724	0.887
5	1.136	1.702	1.397
6	1.275	1.708	1.823
7	1.049	2.579	0.904
8	1.141	2.621	1.305
9	1.286	2.693	1.591
10	3.120	0.688	0.768
11	3.577	0.649	1.562
12	3.915	0.713	2.118
13	3.066	1.607	0.404
14	3.630	1.621	1.639
15	4.057	1.730	2.312
16	3.135	2.763	0.486
17	3.595	2.923	1.550
18	4.081	2.845	2.150
19	3.932	0.681	0.450
20	4.026	0.736	1.383
21	3.997	0.831	1.823
22	4.101	1.721	0.301
23	4.457	1.788	1.518
24	4.352	1.866	1.997
25	4.119	2.828	0.59
26	4.498	2.830	1.584
27	4.535	2.840	2.161

Table A2.

RGB values for the computer-generated colors used in Experiment 1.

Color	Hue	Brightness	Saturation	R	G	B
1	7.5 PB	4	6	88	94	136
2	7.5 PB	4	8	85	93	149
3	7.5 PB	4	10	81	91	162
4	7.5 PB	5	6	112	119	162
5	7.5 PB	5	8	109	118	175
6	7.5 PB	5	10	105	117	188
7	7.5 PB	6	6	137	145	188
8	7.5 PB	6	8	133	144	201
9	7.5 PB	6	10	129	143	215
10	2.5 PB	4	6	63	100	136
11	2.5 PB	4	8	42	101	150
12	2.5 PB	4	10	0	102	162
13	2.5 PB	5	6	88	125	161
14	2.5 PB	5	8	72	126	175
15	2.5 PB	5	10	46	127	189
16	2.5 PB	6	6	114	151	187
17	2.5 PB	6	8	99	152	202
18	2.5 PB	6	10	78	153	216
19	7.5B	4	6	38	104	132
20	7.5B	4	8	0	106	145
21	7.5B	4	10	0	107	157
22	7.5B	5	6	66	129	157
23	7.5B	5	8	15	131	170
24	7.5B	5	10	0	133	183
25	7.5B	6	6	91	156	183
26	7.5B	6	8	59	158	197
27	7.5B	6	10	0	160	210

Appendix B. List-Homogeneity Analyses Involving NEMO and the EBRW Model

In analyzing performance in the continuous-dimension Sternberg paradigm, Kahana and Sekuler (2002; Sekuler & Kahana, 2007) have used a model known as the noisy exemplar model (NEMO). NEMO has been applied to the prediction of choice-probability data only, and would need to be extended to account for recognition RTs.

NEMO is closely related to the GCM and EBRW model. It borrows from those models the assumptions of an exemplar-based memory representation and that the exemplars are embedded as points in a multidimensional similarity space. Furthermore, it uses the same functions for computing the similarity of a test probe to the memory-set exemplars. Likewise, it assumes that recognition decisions are based on summing the similarity of a test probe to the stored exemplars.

There are two main differences between NEMO and these other exemplar models. The first is that NEMO introduces noise into the recognition judgments in a different manner than does the GCM and the EBRW. In NEMO, it is assumed that there is noise in the exact locations of the exemplars in the space. Thus, the summed similarity of a test probe to the stored exemplars is noisy. If the noisy summed similarity exceeds a criterion value, then the observer responds “old”, whereas if the summed similarity fails to exceed the criterion, then the observer responds “new”. By contrast, in the GCM and the EBRW model, the exemplars occupy fixed points in the multidimensional similarity space. Responding is probabilistic because of a noisy decision rule (in the GCM) or a noisy retrieval process (in the EBRW).

The second difference is that Kahana, Sekuler and colleagues (e.g., Kahana & Sekuler, 2002; Kahana, et al., 2007; Sekuler & Kahana, 2007; Viswanathan, et al., 2010) have argued convincingly for the importance of including a list-homogeneity parameter within the framework of summed-similarity exemplar models (see also Nosofsky & Kantner, 2006). When the memory-set items are highly similar to one another, creating high-homogeneity lists, the parameter acts to subtract from the total summed similarity of a probe to the memory-set items. The degree of subtraction is related in continuous fashion to the degree of list homogeneity. As noted by Nosofsky and Kantner (2006), one way of interpreting the role of the list-homogeneity parameter is that the observer adjusts his or her criterion for responding “old” based on the homogeneity of the memory-set exemplars (see Viswanathan et al, 2010, for evidence in favor of this interpretation). When there is high homogeneity, the observer sets a higher criterion for responding “old”. That is, if the list items are highly similar to one another, then people require more evidence from a probe before they respond “old”.

To date, the major evidence for the role of list homogeneity in influencing recognition judgments is that NEMO provides far better fits to the individual-list choice-probability data when the parameter is included than when it is not included. In view of this evidence, we conducted extensive model-fitting analyses of the present data (and of data from Nosofsky & Kantner, 2006) to further investigate the possible role of list homogeneity.

We fitted NEMO to both the present Experiment 1 choice-probability data as well as to a previous data set collected by Nosofsky and Kantner (2006). The Nosofsky and Kantner experiment was closely related to the present one, using a similar stimulus set and design. The main difference was that Nosofsky and Kantner did not collect or attempt to model RTs, which is the focus of the present work. Nosofsky and Kantner previously fitted NEMO to their data, but used a maximum-likelihood statistic as a criterion of fit. To improve comparability between studies, we refitted the model here, using minimum SSD as the criterion of fit.

Because extensive descriptions of NEMO have been provided in previous articles, we do not repeat that presentation here. As explained above, the key issue is whether one makes use of the homogeneity parameter in the model. As a source of comparison, we also report fits of different versions of the EBRW model to both the present Experiment 1 data and to the Nosofsky and Kantner data. The fits to the present Experiment 1 data were constrained by also requiring the EBRW model to simultaneously fit the mean RT data of the individual lists.

The minimum-SSD fits of NEMO and the EBRW model are reported in Table B1. For NEMO, we show the fits of both the full version of the model (with the homogeneity parameter included) and the reduced version (with the homogeneity parameter held fixed at zero). We also fitted an extended version of NEMO that made allowance for position-specific sensitivity parameters and for the criterion parameter to increase linearly with memory-set-size (analogous to assumptions in the core version of the EBRW model). The fits of the analogous versions of the EBRW model are reported as well. (We did not include the primacy parameters in the reduced EBRW model fits.)

As can be seen in the table, for the Nosofsky-Kantner (2006) data, the fit of NEMO improves considerably when it makes use of the homogeneity parameter. However, it fails to provide a better fit than does the EBRW model, which makes no reference to list homogeneity. The fits of both NEMO and the EBRW improve slightly when allowance is made for the position-specific sensitivity parameters, but the EBRW model (without homogeneity) continues to perform as well as does NEMO (with homogeneity). Table B1 also shows that, for the present Experiment 1 data, the fit of standard NEMO is only slightly better than for its reduced version, and adding position-specific sensitivity parameters leads to only minor improvements in fit. Regardless of which version of NEMO is assumed, the EBRW model yields markedly better fits to the data, without introducing any assumptions about an extra role of list homogeneity.

Finally, we explored different approaches to adding a homogeneity parameter to the EBRW model. For example, one approach was to assume that the background-element strength was influenced by homogeneity. However, we did not find any versions that improved substantially the EBRW model’s fits to either data set.

Table B1.

Fits of NEMO and the EBRW Model to the choice-probability data from Experiment 1 and from Nosofsky and Kantner (2006).

Experiment 1
Model	# Free Parameters	SSD	Percent V ariance Accounted For
Standard NEMO (H)	11	3.56	94.0
Standard NEMO (no H)	10	3.67	93.8
Extended NEMO (H)	16	3.51	94.1
Extended NEMO (no H)	15	3.53	94.1
Reduced EBRW	9	2.78	95.3
Core-Version EBRW	15	2.23	96.5
Nosofsky & Kantner (2006)
Model	# Free Parameters	SSD	Percent V ariance A ccounted For
Standard NEMO (H)	11	2.63	92.5
Standard NEMO (no H)	10	3.35	90.4
Extended NEMO (H)	16	2.62	92.5
Extended NEMO (no H)	15	3.30	90.5
Reduced EBRW	9	2.58	92.6
Core-Version EBRW	15	2.46	92.9

Notes: NEMO = noisy exemplar model, Standard NEMO = version of NEMO fitted by Kahana and Sekuler (2002), Extended NEMO = NEMO with additional free parameters for position-specific sensitivity and set-size dependent decision-criterion setting, H = homogeneity parameter included, no H = homogeneity parameter not included.

Reduced EBRW = special case of the core version without position-specific sensitivity parameters, primacy parameters, or set-size dependent background-element strength.

The count of the # of free parameters for the EBRW model does not include those parameters that contribute to only the RT predictions.