Strategies for locating the female gamete: the importance of measuring sperm trajectories in three spatial dimensions

Abstract

The spermatozoon must find its female gamete partner and deliver its genetic material to generate a new individual. This requires that the spermatozoon be motile and endowed with sophisticated swimming strategies to locate the oocyte. A common strategy is chemotaxis, in which spermatozoa detect and follow a gradient of chemical signals released by the egg and its associated structures. Decoding the female gamete’s positional information is a process that spermatozoa undergo in a three-dimensional (3D) space; however, due to their speed and small size, this process has been studied almost exclusively in spermatozoa restricted to swimming in two dimensions (2D). This review examines the relationship between the mechanics of sperm propulsion and the physiological function of these cells in 3D. It also considers whether it is possible to derive all the 3D sperm swimming characteristics by extrapolating from 2D measurements. It is concluded that full insight into flagellar beat dynamics, swimming paths and chemotaxis under physiological conditions will eventually require quantitative imaging of flagellar form, ion flux changes, cell trajectories and modelling of free-swimming spermatozoa in 3D.

Introduction

The singular purpose of the sperm cell is to find the female gamete of its species and deliver its genetic material. Spermatozoa often display sophisticated swimming strategies in fulfilling this role. In many species, including mammals, spermatozoa locate female gametes by recognizing chemical signals released from the gametes themselves or from their associated structures—a mechanism known as chemotaxis (Publicover et al., 2007; Darszon et al., 2008; Kaupp et al., 2008; Chang and Suarez, 2010; Guerrero et al., 2010b). Spawning marine animals are commonly exploited to study sperm swimming strategies, as they provide a vast number of gametes from each individual, their physiological milieu is easy to reproduce in the laboratory and, in many instances, their sperm swim in circles close to surfaces (Miller, 1985; Cosson et al., 2003; Woolley, 2003; Elgeti et al., 2010)—an ideal characteristic for imaging studies (Darszon et al., 2008, Kaupp et al., 2008). When exposed to a chemoattractant, their sperm often redirect their swimming paths towards its source through stereotypical sequences of turns interspersed by periods of straighter swimming. Sperm redirect their trajectory by alternately increasing flagellar beating asymmetry during turns, and decreasing flagellar asymmetry during straighter swimming episodes.

Technological difficulties related to the speed (30–200 µm s⁻¹) and small size (≈4 µm head diameter) of sperm have determined that their swimming has mostly been studied in two dimensions (2D). Nevertheless, their physiological functions are performed in three-dimensional (3D) environments, and any attempt to fully characterize their function must take such considerations into account. The first report to describe how sperm swim in 3D was by Jennings (1901), whose observations indicated that sperm qualitatively display a helical trajectory in 3D. Thereafter, in 1978, Hiramoto and Baba compared the speed and diameter of 2D sperm paths when focusing a microscope at two different depths (close to the microscope slide and 300 µm above). They observed that the speed and curvature of the trajectories was significantly different between cells swimming close to surface, and free in a volume without border effects.

In this review, we will summarize current knowledge of how sperm swim in 3D, why they do so with a helical type trajectory and why it is not possible to derive all the 3D sperm swimming characteristics from 2D measurements.

How do flagella propel sperm?

Swimming strategies employed by organisms that operate at high Reynolds number Re¹ such as fish, birds or insects are ineffective at the micro-organism scale (the ‘world’ of low Re), where—given their typical sizes and velocities—their inertia is negligible and viscous effects dominate. This means that persistent movement requires the continuous action of a force, and if this force vanishes, the movement halts almost instantaneously. This is in sharp contrast with our daily experience in which continuous application of force leads to increase in velocity (Stokes, 1851; Reynolds, 1883; Purcell, 1977; Lauga and Powers, 2009). Imagining a person swimming through molasses is often cited as a way to intuitively grasp strange microscale worlds.

The locomotive properties of micro-organisms have been analyzed under different perspectives (Stokes, 1851; Reynolds, 1883; Purcell, 1977; Lauga and Powers, 2009). In general, the proposed models indicate that micro-organisms undergo a series of periodic deformations of their cilium(a)/flagellum(a), such that the reaction against the fluid propels them. Early efforts to understand how flagellated micro-organisms move had been derived from the waving propulsion of long, thin animals such as snakes (Taylor, 1951, 1952; Gray, 1953). In these kinds of models, the propagation of bending waves along the length of the tail pushes laterally against its surroundings, propelling the micro-organism (Gray, 1953). Gray and Hancock estimated the total propulsion of the spermatozoon based on the analysis of the forces exerted by the fluid over each small section of its flagellum (Gray, 1953; Gray and Hancock, 1955). They proposed that the direction of propulsion is related to the drag coefficients perpendicular to a tail segment and parallel to it ; if the waving of the flagellum propels the micro-organism (Fig. 1). The resistive-force model has been used to analyze the control of flagellar bending and sperm propulsion by several research groups (Gray and Hancock, 1955; Rikmenspoel et al., 1960; Brokaw, 1970; Yundt et al., 1975; Friedrich et al., 2010). Separate calculations of the drag anisotropy ratio () for the sperm flagellum beating in a plane are in the range of 1.5–1.8 for different species (Gray and Hancock, 1955; Rikmenspoel et al., 1960; Brokaw, 1970; Cox, 1971; Shack et al., 1974; Yundt et al., 1975; Brennen and Winet, 1977; Friedrich et al., 2010). It has been observed that environmental alterations usually produce minimal change in this ratio (Lighthill, 1976). More refined models that consider three-dimensional flow and beating have been proposed (Chwang and Wu, 1971; Fauci and McDonald, 1995; Brokaw, 2002, 2003, 2009; Lauga and Powers, 2009; Smith et al., 2009a; Elgeti et al., 2010), and some of them also integrate additional factors such as the interaction between flagella and other spermatozoa or with boundaries (Katz et al., 1975; Fauci and McDonald, 1995; Yang et al., 2008; Lauga and Powers, 2009; Elgeti et al., 2010). Nevertheless only a few models consider the molecular mechanism that controls the dynamic tail behavior involved in the generation and propagation of the bending waves.

Figure 1.

A section of a flagellum shown at two points, (i) and (ii), during bend propagation from left-to-right. The velocity, , of each segment i of the flagellum can be decomposed into a longitudinal component, 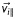, and a normal component, . The force exerted by the fluid over the segment is given by , where and are constants related to the resistance to the movement. When , the total force propels the spermatozoon in the opposite direction of bend propagation. For a very long thin filament, the drag anisotropy ratio is (Burgers and van Wetenschappen, 1938; Taylor, 1952).

Cilia and flagella are structurally closely-related organelles that act as motors to propel swimming micro-organisms; this propulsion is generated by the repetitive propagation of bends along the length of the flagellum, with the thrust aligning more or less along the long axis of the organelle (Gray, 1955; Gray and Hancock, 1955). Within the flagellum, there is a core arrangement of 9 pairs of microtubules arrayed around a central microtubule pair, also known as the axoneme (Fig. 2) (Gibbons, 1981; Lindemann and Lesich, 2010). The outer doublet microtubules are arranged cylindrically, and interconnect via nexin links and dynein arms, with radial spokes linking the outer doublets to the central pair. The shear force-generating components of the axoneme are the dynein ATPases that slide the outer doublet microtubules relative to one another (Gibbons and Rowe, 1965; Brokaw, 1989; Porter and Sale, 2000). Dyneins extending across an n doublet transiently interact with the surface on the adjacent doublet n + 1. The shear forces provided by ATP hydrolysis push the doublet n towards the basal end of the axoneme and concomitantly push the doublet n + 1 towards the distal end of the axoneme (Sale and Satir, 1977; Vale and Toyoshima, 1988). When viewed from base to the tip, the dynein arms always extend in a clockwise direction towards the adjacent doublet (Gibbons, 1961). As a consequence of this chiral distribution, the activity of the dynein arms should alternate cyclically to promote periodic bending in alternate directions that shape the flagellar beat. Due to the presence of constraints such as the nexin links, radial spokes and the basal anchor, this shear force bends the axoneme (Brokaw, 1971, 1972a,b). If dynein activity is regulated such that shear force is generated in an alternating pattern on opposite sides of the axoneme, the result will be cyclical bend generation and propagation of the bend along the length of the flagellum. The bend generation in the flagellum may regulate the activity of the dyneins therein (Okuno and Hiramoto, 1976; Hayashibe et al., 1997; Ishikawa and Shingyoji, 2007), which could initiate a self-regulatory feedback loop for coordinating microtubule sliding through the bend generation cycle (Nakano et al., 2003; Morita and Shingyoji, 2004; Hayashi and Shingyoji, 2008). Competing proposals to explain the dynein switch mechanism are currently under investigation (Riedel-Kruse et al., 2007; Brokaw, 2009; Lindemann and Lesich, 2010), and detailed discussion of each is beyond the scope of this review.

Figure 2.

Schematic 3D diagram of the sperm axoneme in cross-section. Except for nexin links and the 5–6 bridge, all structures were reconstructed based on cryo-electron microscope tomographies of the sea urchin axoneme obtained by Nicastro et al. 2006. DRC: dynein regulatory complex; CPC: central pair complex. 3D reconstruction created by A.G. with blender v2.49b.

Why is flagellar beating quasi-planar?

The axoneme seems ideally designed for generating helical bending waves. Computational models indicate that when the shear generated by the displacement of each of the nine outer doublets is identical, helical bending waves would result (Brokaw, 2002). However, most metazoan sperm flagella beat with almost planar bending waves. Theoretical models and computer simulations indicate that planar bending can produce faster swimming than helical bending (Chwang and Wu, 1971), suggesting that planar bending is a selected trait for rapid swimming. Structurally there is evidence that the ‘central pair’ of microtubules and associated structures in the axoneme interior play a key role in regulating planar bending (Omoto et al., 1999), as sperm that lack the central pair complex produce helical bending waves (Gibbons et al., 1985). For example, spermatozoa of Asian horseshoe crabs, in which the central flagellar pair is absent, produce helical bending waves; while sperm flagella of the American species possessing the central pair produce planar bending waves (Ishijima et al., 1988).

To make a planar bend, dynein arms of the doublet on the two ‘sides’ (with respect to the beat plane) of the central-pair complex play major roles (Shingyoji et al., 1977; Brokaw, 1989; Holwill and Satir, 1994; Nakano et al., 2003) (Fig. 2). The dyneins on the one side of the axoneme, associated with microtubule doublets 1 × 4, bend the flagellum in one direction of the beat cycle, and the dyneins on the opposite side (doublets 6–9) contribute to bending in the opposite direction (Fig. 2). Alternating activation of the two opposing dynein bridge cohorts determines the beat shape through switching of one set ‘on’ and the other set ‘off’ at appropriate mechanical set points (Satir, 1985; Satir and Matsuoka, 1989). In many flagella and cilia, the central pair is positioned perpendicularl to the major plane of the beat (Afzelius, 1961; Gibbons, 1961), and is thought to act as a distributor of signals to regulate the activity of dynein arms according to their position in the axoneme and the beating phase (Lindemann et al., 1992; Omoto et al., 1999; Bannai et al., 2000; Nakano et al., 2003). Also, both the material associated with the central pair of microtubules and the radial spokes display bilateral symmetry to the beat plane (Smith and Yang, 2004; Nicastro et al., 2005), then favouring the generation of planar bends, and the microtubule doublets numbered 5 and 6 are found frequently linked to one another and cannot slide relative to each other (Afzelius, 1959; Fig. 2).

The planar beat pattern can be described by two flexible incompressible rods linked by elastic structural elements (e.g. nexin links) and active force generators (dyneins). The relative displacement of the two rods produces shearing forces that bend the whole structure (Fig. 3). In this simplified representation, the shearing forces generated by the movement of one rod correspond to those forces created by the sliding of doublets 1–4. In the same way, the shearing forces generated by the movement of the opposite rod simulate the forces generated by the sliding of doublets 6–8.

Figure 3.

Relationship between shear and bending in a simple flagellar model consisting of two flexible inextensible filaments. Filaments are drawn as a series of alternating black and grey articulated rods to illustrate their sliding relative to each other. The basal body is resistant to sliding (A). Along the axoneme, the points of maximum shear are those found at the bending inflexion when the curvature is null (e.g. B and D), while the points of maximum bending curvature either positive or negative have no shear (e.g. C).

Given its morphology, the flagellar axoneme possesses an intrinsic asymmetry that results in unequal bending resistance that promotes twisting and, as consequence, the generation of local deflections out of the major bending plane (Chwang and Wu, 1971; Woolley and Vernon, 2001; Cosson et al., 2003; Woolley, 2003; Smith et al., 2009a). Since Gray (1955), it has been understood that if there is both asymmetry of the bending pattern and torsion of the swimming path, the sperm will swim in a 3D helix, and will thus become ‘trapped’ in the proximity of a surface (Gray, 1955).

How the torsional component of flagellar bending is generated is an open question that has at its root the asymmetric distribution of the axoneme components that generate and regulate the flagellar bending. Twisting could result from unequally distributed thrusts generated by successive adjacent pairs of doublets sliding out of register to one another or by local loosening of axonemal structures, or both (Gibbons, 1975; Woolley and Vernon, 2001; Woolley, 2003; Cosson et al., 2003). Steady-state activity of the dyneins can also generate a twist of the flagellum (Hines and Blum, 1985). In the case of echinoderm spermatozoa, flagella beat in a quasi-planar manner at viscosities close to that of sea water, yet increasing the viscosity to around 1.5 Pa induces a planar-to-helical transition in the flagellar beating pattern (Brokaw, 1966; Woolley and Vernon, 2001). Further viscosity increases (∼4 Pa) result in a return to pseudo-planar flagellar bending waves (Woolley and Vernon, 2001). Mouse and rat sperm flagella maintain 2D wave forms in viscous saline solutions (1.5–4 Pa, methyl cellulose); yet in unmodified saline solution, their flagella beat pattern displays more complex 3D components (Woolley, 2003). It is noteworthy that progressive swimming of mammalian sperm is influenced by additional flagellar elements such as the dense fibres and the outer sheath; in the midpiece a medial 3 - central - 8 partition of microtubule doublets is attached to the outer dense fibres 3 and 8 and in the principal piece to the fibrous sheath, providing differential stiffness in a plane orthogonal to the main beat plane (Lindemann et al., 1992).

In summary, the propulsion of spermatozoa is a result of the imbalance of the shear forces created by the alternate sliding of the microtubules in opposite sides of the axoneme. This creates local defections of the main flagellar beat plane that are responsible for the quasi-helical swimming behavior. The bending generated within the axoneme is counterbalanced by the viscosity of the external media, and the overall flagellar beat pattern is a product of the dynamic interplay between these parameters (Brokaw, 1988; Smith et al., 2009b).

Why are sperm confined to a curved trajectory near a surface?

Motile spermatozoa tend to accumulate at surfaces while remaining free-swimming (Rothschild, 1963; Fauci and McDonald, 1995; Woolley and Vernon, 2001; Cosson et al., 2003; Woolley, 2003; Smith et al., 2009a; Elgeti et al., 2010). Two factors play a role in this confinement: the asymmetric bending of the flagellum that generates a thrust component perpendicular to the surface (Woolley and Vernon, 2001; Cosson et al., 2003; Woolley, 2003), and a surface boundary effect (Rothschild, 1963; Fauci and McDonald, 1995; Smith et al., 2009a; Elgeti et al., 2010).

For an asymmetrically bending flagellum, the region of greater bending is known as the principal bend (P-bend) and the bend in the opposite orientation is the reverse bend (R-bend). A thrust component directed towards the surface arises if the bending resistance is unequal on opposite sides of the axoneme that are perpendicular to the plane of the flagellar beat plane (Cosson et al., 2003). In this case, the sliding of microtubules in the inter-bend regions promotes a twisting of the flagellum, which alters the planarity of the beat (Fig. 4). There is experimental evidence to support this idea, namely that small sperm flagella subregions move slightly out of focus when they are beating near to a surface (Chwang and Wu, 1971; Woolley and Vernon, 2001; Cosson et al., 2003; Woolley, 2003; Smith et al., 2009a). In echinoderm spermatozoa, the blurred subregions are the points of highest flagellar curvature, where the microtubule shear or displacement is practically zero (Brokaw, 1972b; Gibbons, 1982; Cosson et al., 2003). These subregional deviations are associated with both P and R bends, and their effect is cumulative on the strength of the thrust perpendicular to the flagellar plane. This behavior is not due to electrostatic interactions between the flagellar membrane and the surface, as the same effect is seen in demembranated sperm flagella (Cosson et al., 2003); nor is it due to the asymmetry of the flagella aligned to the beat plane, as the confinement also occurs when spermatozoa swim with a relatively straight trajectory (Cosson et al., 2003). For mammalian sperm, at least two mechanisms for the surface trapping effect have been proposed (Chwang and Wu, 1971; Woolley, 2003; Smith et al., 2009a). In the first, the flagellar beat of some mammalian sperm types exhibits a conical envelope due to the rolling of the cell while swimming forward. When they approach the boundaries, one edge of the conical flagellar envelope aligns with the surface; hence, the forward thrust vector has a component that points toward the surface. Alternatively, or in addition, some spermatozoa exhibit planar beating close to the surface with the plane of beating tilted relative to the plane of flattening of the head, resulting in a potential hydrofoil effect.

Figure 4.

Schematic 3D comparison between a planar beat versus a ‘quasi-planar’ beat. 3D visualizations of two spermatozoa intersecting a plane coplanar with their beat plane. Note the out-of-plane deviations of the spermatozoa displaying a quasi-planar beat of sea urchin (red) or mammals (yellow, a ‘human spermatozoon’). The sea urchin spermatozoon has a greater portion of its flagellum ion one side of the beat plane (compare A with B and C with D) that create an anisotropic thrust perpendicular to the beat plane that is in part responsible for the chiral surface confinement. (E, F) Projections showing the succession of right- and left-handed spirals of sea urchin spermatozoa that gave an eight shape when viewed from the head to the tail (E) (Cosson et al., 2003). Note that in some mammals (rodent, ramp and perhaps human) spermatozoa exhibit helical beating (yellow) (Chwang and Wu, 1971; Woolley and Vernon, 2001; Brokaw, 2003; Cosson et al., 2003; Woolley, 2003;). 3D reconstructions created by A.G. with blender v2.49b based on the micrographies ‘2a’ and ‘3d’ of (Cosson et al., 2003) ‘2a’ and ‘7a’ of (Smith et al., 2009b), and Fig. 11 of (Smith et al., 2009a). For illustrative purposes the human spermatozoon has been scaled to the sea urchin sperm length which is ∼2× shorter.

The bending resistance due to the fluid viscosity is influenced by the proximity to surfaces. Computational models suggest that the propagation of the bending waves along the flagellum creates local flow fields characterized by a forward fluid drag by the head and a backward fluid drag in the direction of the wave propagation. This generates two vortex rings that create a region of low pressure near to the midpiece of the flagellum, that will stimulate influx of fluid around this region (Fauci and McDonald, 1995; Elgeti et al., 2010). As the spermatozoon begins to swim near to a surface, the fluid influx to the midpiece area becomes restricted (Fauci and McDonald, 1995; Elgeti et al., 2010). As a consequence, the movement of flow onto the midpiece from above the surface is higher than the flow coming from the surface vicinity (Fauci and McDonald, 1995; Elgeti et al., 2010). This creates a region of low pressure that attracts the midpiece of the spermatozoon toward the surface (Elgeti et al., 2010). Near the flagella tip, a flow field repels the tip from the boundary, which induces a tilt of the axis of the plane of the flagellar beat that thrusts the head toward the surface (Elgeti et al., 2010). Other factors that may play a role in confinement include a steric inhibition of rotation of the flagellar beat plane due to surface proximity (Cosson et al., 2003), the relative stiffness of the flagellum (an elastic flagellum being more susceptible to subject to hydrodynamic confinement) (Elgeti et al., 2010).

Whatever the mechanism, the physiological effect of confinement is the promotion of surface contact and further penetration of the egg investments.

How do sperm orient their swimming toward the source of chemoattractant in 2D?

Micro-organisms that swim at low Re must navigate along chemical gradients to find food and survive. Purcell calculated that to increase their food supply by 10% relative to standing still, bacteria would have to randomly explore their environment by swimming 20 times faster than the speed they can achieve, implying that a velocity increase is not a solution (Purcell, 1977). Bacteria can steer upwards along a chemoattractant gradient using a biased random walk controlled by a chemotactic signaling network that depends on the history of the stimulus (Berg, 1978; Segall et al., 1986).

For marine spermatozoa, the strategy is quite different; they swim in quasi-circular trajectories near surfaces and in quasi-helical trajectories in bulk fluid in order to sample the gradients created by diffusion of chemoattractants from egg investments. This swimming strategy has the advantage that they just need to sample a small area² to locate the egg position, but has the disadvantage that sperm chemotaxis only operates at short distances from the egg [(<2 egg diameters or ≤ 1 mm, reviewed in (Darszon et al., 2008)]. To overcome this problem, marine animals release billions of gametes in a concerted manner, enhancing the probability of sperm–egg interaction. In this section, we review current knowledge of sperm chemotaxis of marine spermatozoa in 2D [((Darszon et al., 2008; Kaupp et al., 2008; Guerrero et al., 2010b); mammalian sperm chemotaxis is reviewed in (Publicover et al., 2007; Kaupp et al., 2008; Chang and Suarez, 2010))].

Marine spermatozoa orient themselves by changing their swimming direction according to the direction of the chemoattractant gradient. As spermatozoa swim in a chemoattractant gradient, they continuously sample the concentration field. The intensity of the sampled stimulus I(t) depends on the shape of the chemical concentration gradient, on sperm velocity and the direction of movement relative to the gradient³ (the rate of the stimulus intensity is maximal when the direction of the spermatozoon velocity is collinear to the gradient , Fig. 5, left). At surfaces, spermatozoa orient their direction by changing their curvature κ = 1/r, increasing it when swimming down the gradient to turn and decreasing it when swimming up the chemoattractant gradient to swim straighter toward the source (Fig. 5, right) (Miller and Brokaw, 1970; Miller, 1985; Böhmer et al., 2005; Shiba et al., 2008; Guerrero et al., 2010a, b). Thus a spermatozoon exhibits a positive orientation if its curvature is inversely proportional to the stimulus intensity . Conversely it exhibits negative orientation if .

Figure 5.

Circular like swimming is an efficient orientation strategy. Left panel: Sperm orientation with respect to the chemical gradient. The solid lines indicate the direction of the translational velocity of the spermatozoon and the dashed lines indicate the direction of the chemical gradient. Note that when , then . Right panel: Trajectory described by a Lyctechinus pictus spermatozoon undergoing chemotaxis. The dashed line corresponds to the trajectory s before stimulation, and the solid line is the trajectory described after exposure to the chemical gradient (3.2 s). The source of the chemical gradient is the centre of the X and Y axes. During the turns the radius of the trajectory decreases (solid arrows), and increases during the straighter swimming episodes (dashed arrows). The swimming direction is counter-clockwise.

Sperm-activating peptides (SAPs) diffuse from the egg investments, establishing concentration gradients encoding the oocyte's positional information that modulates sea-urchin sperm motility (Suzuki, 1995). Speract, isolated from ‘Strongylocentrotus purpuratus’ sea urchins, was the first characterized and most widely studied member of the SAP family (Hansbrough and Garbers, 1981; Suzuki et al., 1981). This decapeptide binds to its receptor in the flagellar membrane and induces a train of [Ca²⁺]_i increases that promote a stereotypical motor response comprising turns interspersed by periods of straighter swimming [Fig 6A, reviewed in (Darszon et al., 2008)].

Figure 6.

Signaling events controlling sea urchin sperm chemotaxis. (A) Egg investments contain peptides (SAPs, sperm activating peptides) that regulate sperm motility (Suzuki, 1995). SAP binding activates a membrane guanylate cyclase (GC), increasing cGMP levels which hyperpolarize the cell by opening cGMP-regulated K⁺ channels (Strünker et al., 2006; Galindo et al., 2007; Bönigk et al., 2009). This hyperpolarization is thought to remove inactivation from voltage-dependent Ca²⁺ channels (CaVs), which subsequently open following a depolarization (Granados-Gonzalez et al., 2005; Strünker et al., 2006). Transient increases in flagellar [Ca²⁺]_i caused by CaV openings have been associated with transitory increases in flagellar bending that result in sperm turning events (Babcock et al., 1992; Kaupp et al., 2003; Wood et al., 2003; Böhmer et al., 2005; Shiba et al., 2008; Guerrero et al., 2010a, b). It has been proposed that the [Ca²⁺]_i increases could open Ca²⁺-regulated Cl⁻-channels (CaCC) and/or Ca²⁺-regulated K⁺-channels (CaKC), which then contribute to a further hyperpolarization event, removing inactivation from CaVs and opening of the HCN (Wood et al., 2007). This hyperpolarization also facilitates the Ca²⁺ extrusion activity of K⁺ - dependent Na⁺/Ca²⁺ exchangers. The previous mechanism is then cyclically repeated to generate a train of Ca²⁺ increases that produce repetitive increases in flagellar bending, which steer the cell along the chemical gradient to its source. (B) Left panel: As a spermatozoon undergoing chemotaxis swims up the chemoattractant gradient, the onset of [Ca²⁺]_i fluctuations is suppressed until it senses descending a gradient (red semicircle). After a ∼200 ms delay, the [Ca²⁺]_i increases just before reaching the gradient minima (white circles). Consequently, the spermatozoon experiences a turn - and - straight episode that promotes the steering towards the chemoattractant source (black arrow). (B) Right panel: Non-chemotactic spermatozoa are unable to suppress the [Ca²⁺]_i increases as they swim in an ascending chemoattractant gradient; therefore the turns interspersed by periods of straighter swimming episodes promote sperm re-localization but not a biased approach towards the chemoattractant source. (C) Model of the molecular mechanisms that drive chemotaxis. A chemotactic spermatozoon swimming in a chemoattractant gradient (background) undergoes cyclic changes in V_m from resting to a hyperpolarized state (Hyp, green shadow) and then to a depolarized state (Dep, blue shadow) that control CaV activity. The sperm trajectory is depicted as a black arrow. The pseudo-colour bar represents the kinetics of [Ca²⁺]_i changes in the flagella; red and gray indicate low and high [Ca²⁺]_i, respectively. Note that the straight swimming periods coincide with an interval of elevated [Ca²⁺]_i (see main text for details).

Ample evidence indicates that the Ca²⁺-dependent turning episodes are essential elements of a chemotactic motility response and that extracellular Ca²⁺ is strictly required for sperm chemotaxis, from bracken to mammals. The absence of external Ca²⁺ or blockade of certain permeable cation channels inhibits the turning events and consequently sperm chemotaxis (Yoshida et al., 2002; Kaupp et al., 2003; Wood et al., 2005, 2007; Guerrero et al., 2010a). Experiments with demembranated spermatozoa revealed that high concentrations (>10⁻⁶ M) induced an asymmetrical propagation of the flagellar beat, while lower concentrations generated a more symmetrical flagellar beat (Brokaw, 1979). Electronic microscopy studies and bending responses showed that high concentrations of Ca²⁺ inhibit the dynein activity of doublets 3 and/or 4 on the axoneme, without affecting the activity of the dynein arms on doublet 7 (Nakano et al., 2003). [Ca²⁺]_i elevation in the axoneme results in shear accumulation due to increased sliding of doublets 7 and 8. There are myriad accessory proteins that have Ca²⁺ binding domains associated with dyneins in the axoneme and/or to other structural elements that control the distribution of the sliding forces in the axoneme (DiPetrillo and Smith, 2009; King, 2010) (e.g. calaxin is a Ca²⁺-binding axonemal protein that binds the beta-dynein heavy chain of the outer arm dynein in the presence of Ca²⁺ (Mizuno et al., 2009)). How these Ca²⁺-stimulated motility responses are synchronized in time and space with the polarity of the chemoattractant gradient to produce chemotaxis has become a key question in the field of sperm motility.

Periodic sperm stimulation due to swimming in a chemoattractant gradient triggers the signaling network to generate the Ca²⁺-dependent turning events. For a chemotactic response, spermatozoa must synchronize the [Ca²⁺]_i fluctuations with the periodic chemoattractant concentration changes as they swim toward the egg (Böhmer et al., 2005; Shiba et al., 2008; Guerrero et al., 2010a;); lack of synchronization causes sperm to fail to reach the source of the chemoattractant [Fig. 6B, Right panel (Guerrero et al., 2010a, b)]. Recently, it was discovered that Lytechinus pictus (painted sea urchin) spermatozoa undergo chemotaxis in response to a gradient of the chemoattractant speract (Guerrero et al., 2010a). Notably, under tested experimental conditions, even though speract induces S. purpuratus spermatozoa to redirect their swimming paths with the stereotypical turns interspersed by periods of straighter swimming, it does not induce chemotaxis (Guerrero et al., 2010a). The [Ca²⁺]_i fluctuations experienced by L. pictus spermatozoa are biased to the descending phase of the speract gradient (Fig. 6, left panel). In contrast, S. purpuratus spermatozoa generate [Ca²⁺]_i fluctuations in both descending and ascending speract gradients with almost the same frequency (Fig. 6, right panel). This suggests that selective triggering of the Ca²⁺ - dependent turning events in descending chemoattractant gradients is a feature of chemotaxis.

Chemotactic spermatozoa are likely sensitive to the ascending-to-descending gradient inflection which, when crossed, triggers the signaling events leading to a flagellar [Ca²⁺]_i fluctuation and a chemotactic turn. Chemotactic spermatozoa are able to suppress the onset of [Ca²⁺]_i fluctuations while swimming in ascending chemoattractant gradients (Shiba et al., 2008; Guerrero et al., 2010a). After crossing the positive-to-negative gradient inversion point spermatozoa must initiate signaling steps required to open the Ca²⁺ entry pathways.

Cook et al. (1994) proposed that shallow or decreasing chemoattractant gradients increase [Ca²⁺]_i to generate chemotactic turns; however, [Ca²⁺]_i is maintained low by sufficiently steep increasing gradients, allowing linear swimming trajectories until the egg is reached. It was subsequently demonstrated that the path curvature does not strictly follow [Ca²⁺]_i dynamics. Only the fast initial [Ca²⁺]_i rise correlates with the increase of κ; thereafter the curvature decreases even though [Ca²⁺]_i levels remain elevated, indicating that the straighter swimming episodes are less directly related to [Ca²⁺]_i dynamics (Wood et al., 2005; Guerrero et al., 2010a; Darszon et al., 2008). The latter likely reflects the complex signaling network regulating [Ca²⁺]_i and its influence on dynein motor activity. Furthermore, it was proposed that once the spermatozoon enters a descending gradient, bound chemoattractants may dissociate from their receptors, resulting in a [Ca²⁺]_i increase (Cook et al., 1994; Miller, 1985). Since speract binding is essentially irreversible (k_off ∼ 10⁻⁴ to 10⁻⁶ s⁻¹; k_on ∼ 10⁷ M⁻¹ s⁻¹), receptor occupancy is practically unaltered while spermatozoa swim down gradient, thus making this proposal unlikely (Nishigaki and Darszon, 2000; Nishigaki et al., 2001). Marine spermatozoa can detect a wide range of chemoattractant concentrations (10⁻¹² to 10⁻⁶ M) before becoming saturated (Kaupp et al., 2003; Böhmer et al., 2005; Shiba et al., 2008; Guerrero et al., 2010a). Sea-urchin spermatozoa have seemingly evolved high chemoattractant receptor densities (10⁴–10⁶ receptors per cell, according to species) to prevent the saturation of the signal transduction mechanisms that drive chemotactic responses (Nishigaki and Darszon, 2000; Nishigaki et al., 2001; Kaupp et al., 2008). This indicates that marine spermatozoa register relative changes in chemoattractant concentrations.

We propose a unified mechanistic model for sperm chemotaxis in the heart of which lies a negative-feedback loop (Fig. 6C), where the activity of voltage-gated Ca²⁺-channels (CaVs) is regulated by alterations of the membrane potential that translate the state of the chemoattractant gradient through the rate of recruitment of chemoattractant receptors (the rate of the stimulus intensity) (Guerrero et al., 2010a, b). In an ascending chemical gradient, the incremental recruitment of chemoattractant receptors may lead to an extended hyperpolarization that suppresses the CaV channel opening and thus prevents the [Ca²⁺]_i increase (Fig. 6C (i)). The hyperpolarization reverses once spermatozoa swim down the gradient, which—after a typical ∼200 ms delay (red line)—leads to the generation of a chemotactic turn that reorients them toward the gradient source (Fig. 6C (ii)). This re-polarization may be due, in part, to the inactivation of guanylyl cyclase, reduction of cGMP levels by degradation, Na⁺ influx through HCN channels and other unknown depolarizing elements, and results in the opening of CaV channels, possibly of the T and L type (Wood et al., 2003, 2005; Granados-Gonzalez et al., 2005; Strünker et al., 2006) (Fig. 6C (ii)). At a certain time while swimming straighter in the ascending chemoattractant gradient, a hyperpolarized membrane potential is reestablished and extended by continuous speract receptor recruitment (Fig. 6C (iii)), which once again reverts to depolarized membrane potentials as spermatozoa leave the ascending gradient (Fig. 6C (iv)). This sets up a sequence of chemotactic turns, triggered by hyperpolarization/depolarization cycles that serve as the primary translators of the state of the chemoattractant gradient to the kinetics of [Ca²⁺]_i, and hence to the Ca²⁺ regulated axonemal components.

What do we know about sperm 3D swimming?

In previous sections, we have already revisited the main structural and dynamic properties of flagellar beating which explain how sperm swim in 3D. At low Re, viscosity and negligible inertia combine in such a way that cell movement requires continuous force application to periodically deform the cell. The periodic generation of bending waves and their propagation from the sperm head to the tip of the flagellum result in a linear force propelling the sperm forward. The asymmetry in the curvature of the P- and R-bends, plus the deflections out of the major beat plane, creates a torque responsible for rotating the sperm around itself.

Helical swimming paths are a common feature of cilia- or flagella-driven locomotion in a diverse array of micro-organisms from fungal and plant spores, invertebrate larvae, rotifers, and invertebrate and vertebrate spermatozoa (Bullington, 1925; Jennings, 1901, 1904). Theoretical analyses suggest that the helical motion is a sampling strategy to determine the direction of chemical gradients to which the micro-organism is sensitive. Crenshaw and others proposed that a spermatozoon can reorient itself by adjusting its motion components according to the intensity of an external stimulus (Brokaw, 1958; Crenshaw, 1989, 1990, 1993a,b; Crenshaw and Edelstein-Keshet, 1993; Friedrich and Jülicher, 2007, 2008, 2009). These models describe the spermatozoon trajectory by a helical parametric equation. A spermatozoon can adjust its movement by changing the direction of the principal axis of the helix; this can be done by modifying the angle α between its translational and rotational velocities, being α=arctan (2π r/p)=κ/|τ |, where r is the helix radius, p is the pitch (the distance traveled by the cell in the direction of the principal axis of the helix for every helix turn), κ is the curvature and τ is the torsion of the helix. The spermatozoon can point its movement toward the source of the chemoattractant gradient by making α smaller as the stimulus intensity I(t) increases and by making α larger as I(t) decreases. Thus, a spermatozoon exhibits positive orientation if . Conversely it exhibits negative orientation (Crenshaw, 1989, 1990, 1993b). It follows that orientation in a chemoattractant gradient can be achieved by changing the path curvature and/or the torsion accordingly the polarity of the chemical field. Whether a 3D chemotactic response involves changes in path torsion or simply depends on the variation of curvature as happens in 2D () needs to be clarified. Measurements of both κ and τ are required to quantify chemotactic in 3D and determine the extent to which chemotaxis in 3D can be explained by the 2D observations and experiments (see following section).

The recording of sperm trajectories in 3D has been precluded by their small size and speed with which these cells move [30–200 µm s⁻¹, mammals-equinoderms (Gray, 1955; Gray and Hancock, 1955; Miller, 1985)]. Hiramoto and Baba compared quantitatively for the first time the speed and diameter of 2D sperm paths when focusing the microscope at two different levels (near a flat surface, and 300 µm distant from any boundary layer) (Hiramoto and Baba, 1978). Later, Crenshaw reported the first system capable of tracking 3D trajectories of single sea urchin spermatozoa for quantitative analysis (Crenshaw, 1990). This was an adaptation of the technology developed by Berg (Berg, 1978) to track, in 3D, low-speed single micro-organisms by keeping them focused at the center of the microscope field. Crenshaw’s system consisted of two video cameras that were attached to two perpendicularly orientated microscopes (one camera giving the X, Z coordinates and the other one the Y, Z coordinates). Focusing the microscopes to the centre of a volume, images were recorded and analysed frame by frame to determine the screen coordinates. Qualitative 3D trajectories were presented in this work in which exposure to an attractant stimulated sperm swimming. Quantitative parameters such as speed, curvature and torsion were also presented as an example for a single sperm (Crenshaw, 1990). Corkidi et al. proposed a different approach to acquire 3D multi-tracking images of spermatozoa using a single ultra-fast camera and microscope (Corkidi et al., 2008). A piezoelectric device was mounted between a long working distance objective of a microscope and the turret. When stimulated by a triangular ramp, this device displaces the objective vertically at up to 70 cycles per second and the camera synchronously acquires images of free-swimming spermatozoa at a rate of 4200 images per second, capturing successive focal planes in a depth of 100 µm. This produces the necessary data for reconstructing their trajectories in 3D. The geometric characteristics of the trajectories in 3D are distinct from those they display in 2D. The tangential velocities of spermatozoa are 25% slower in 2D and their circular trajectories have 130% larger average radius of curvature than those swimming in 3D (Fig. 7A) (Corkidi et al., 2008). These results point out to the necessity of characterizing the chemotactic response of sperm in 3D.

Figure 7.

Geometric considerations relating 2D and 3D sperm swimming trajectories. (A) Samples of swimming trajectories by L. pictus spermatozoa constrained to the plane (red) and in 3D (blue). The series of circular 2D trajectories were ranked by increasing radius and the 3D trajectories were translated and rotated so that the mean z value is 100µm and the principal component is aligned along Y axes (unpublished data). (B–D) Modeling of the swimming trajectory in 2D and 3D based on an iterative map of geometric transformations. B. Motion is determined by propelling forces relative to the body axis of the spermatozoon (x, y, z). The trajectory can be reconstituted through a geometric transformation relative to the self-referential axes system (x, y, z) (left), composed of a translation (T) and the rotations around the three axes, respectively (red, right). C) Two stationary helical trajectories in the external observer reference axes (X, Y, Z) generated through transformations (1.0,π/24,π/24,π/12) (green) and (1.0,π/20,π/20,π/12) (blue) that correspond to the same circular trajectory once constrained to the plane (1,0,0,π/12) (red). D) A non-stationary circular-like trajectory in the plane (transformation (1,0,0,θ_t), red) and two corresponding 3D trajectories (green- transformation (1,0.5θ_t,0.5θ_t,θ_t), blue- transformation (1,0.3θ_t,0.3θ_t,θ_t)). θ_t = π/7 for 50 < t< 56, θ_t = π/60 for 56 ≤ 70 and θ_t = π/12 otherwise.

Can we predict how sperm swim in 3D from 2D information?

Hitherto most quantitative studies on sperm swimming were performed in 2D for experimental and imaging conveniences. How much information can be extrapolated from these studies? As discussed already, changes in medium viscosity have nonlinear effects on the bending pattern of the axoneme forcing for example a switch from (quasi-)planar to helical bending. Similarly, it is tempting to speculate that the special hydrodynamic conditions at the planar surfaces could qualitatively change the flagellar beating pattern. These putative qualitative changes in axoneme dynamics would obviously preclude predicting the 3D path from the properties of the planar trajectory. But there are even deeper difficulties in trying to extrapolate from the 2D information.

The helical trajectory of a sperm in the reference axes of an external observer (X, Y, Z) can be generated by translations and rotations in the sperm cell frame (x, y, z) (Fig. 7B–D). We arbitrarily set the x-axes, bf to the longitudinal (antero-posterior) axes of the spermatozoon and the plane xy to the plane defined by major component of the bends (Fig. 7B). If the P- and R-bends are symmetrical, the sperm would be translated forward but without any rotation, displaying a linear path. However, because these reciprocal bends are asymmetric, a rotation is generated. The main rotational component is around the z-axis that extends perpendicular to plane along the greatest component of the beating pattern (x, y). If the asymmetry of the bends is also present in the deformation out of this plane, as discussed in the previous section, then this will generate, at least potentially, rotations around axis y and x. Thus, the trajectory of a spermatozoon in 3D can be estimated by computing the geometric transformation of the body axes (x_t, y_t, z_t) through a translation T, and three rotations around these axis, respectively θ_x, θ_y and θ_z. We will refer to this transformation as (T, θ_x, θ_y, θ_z). The stationary trajectory is the solution of the following iterative map:

We know since Crenshaw (Crenshaw, 1989) that the parameters of this transformation cannot be inferred in general from those of the helical trajectory (linear velocity, angular velocity and pitch). Only under the special condition in which the components θ_x and θ_y are identical or proportional, losing one degree of freedom for the trajectory, one can derive the effective three parameters of the referential from the positional information on trajectory. For the sake of the present argument, let us not be deterred by this difficulty.

Consider the simplest possible scenario in which the only effect of swimming near a planar surface is the cancellation of the torque components leading to rotations around the body axes x and y, maintaining the magnitude of the translation and rotation around the z axis. In other words, a spermatozoon whose stationary trajectory in 3D would be given by the transformation (T, θ_x, θ_y, θ_z) would describe a circle in 2D determined by the transformation (T, 0, 0, θ_z). Examples of these trajectories in 3D and in 2D are illustrated in Fig. 7C. The most striking effect is that the radius of the helical trajectory is smaller (in general smaller or equal) to the corresponding circular trajectory in the plane, as it has been documented for the real spermatozoon (Fig. 7A) (Hiramoto and Baba, 1978; Corkidi et al., 2008). The larger the rotational components θ_x and θ_y, the larger the difference between the radius of the 3D helix and the planar circle. As a corollary, there is an infinite number of helical trajectories in 3D that lead to the same circular trajectory when constrained to planar swimming, by forcing the torque components around the x and y axes to vanish (Fig. 7C). These simple geometric considerations lead to a paramount conclusion: the mapping between the helical trajectory and the circular trajectory is not bijective. If one could (at least in principle) predict which circular trajectory in the plane would be expected from a known helical trajectory, one cannot infer which helical trajectory would be expected from an observed circular trajectory.

What about sperm non-stationary swimming trajectories followed in response to a chemotactic stimuli? Can the pattern of turns interspersed by periods of straighter swimming observed in the plane be somehow extrapolated to 3D? Following the previous considerations, it is safe to say that this extrapolation will not be possible in general. Notwithstanding this fact, it is interesting to consider an extreme scenario where the rotational components are all interdependent. This should be the case if the magnitude of the deformation of the flagellum out of the major plane, as illustrated in Fig. 4, is proportional to the bending curvature in this major plane. In this scenario, if one knew the proportionality constants relating the rotations θ_x, θ_y and θ_z, one could calculate the 3D pattern of turns interspersed by periods of straighter swimming. This is illustrated in Fig. 7D, where a planar ‘turn and straighter’ trajectory is mapped onto two very distinct 3D swimming trajectories using two alternative relationships between the rotations.

We need to measure sperm swimming and chemotactic responses in 3D.

Flagellar beating patterns in the plane can be measured by defocusing microscopy methodologies (Agero et al., 2003; Cosson et al., 2003), which could allow to infer the corresponding trajectory in 3D based on the resistive force model (Gray and Hancock, 1955; Friedrich et al., 2010). This solution, however, would only be possible if the flagellar beating pattern is not modified by interactions it makes with the surface (Fauci and McDonald, 1995; Elgeti et al., 2010).

As we have seen, the experimental observations by us and others (reviewed above) indicate that there are differences between the radius of the helical trajectory in 3D and radius of circle described by spermatozoa near a surface. The simple geometric description presented in Fig. 7 can potentially explain this difference based on the cancelling of some of the torque components by the surface itself. The obvious question is: are the trajectories described compatible with this simple explanation? The variance in the radius in 3D and 2D (Fig. 7A) is so large that one cannot reach a definitive conclusion based on the small sample size we have of 3D trajectories. However, the potential to answer the question exists through measuring the 3D trajectories, computing the corresponding trajectory constrained to a plane, and comparing with the actual measured circular paths. Eventual deviations would be taken as evidence for changes in the beating pattern caused by the special hydrodynamic environment near the surface.

In any case, it seems inescapable that gaining insight into the flagellar beating dynamics and swimming paths under real physiological conditions requires quantitative imaging and modeling of free swimming sperm in 3D. Furthermore, we will have to surmount the technological challenge of simultaneously recording 3D trajectories and the associated changes in [Ca²⁺]_i triggered by sperm chemoattractants to understand how spermatozoa find the female gamete and produce a new individual.

Author's roles

A.G. and A.D. conceptualized the project and participated in the design and drafting of the manuscript. A.G. and J.C. wrote the paper. A.P. and G.C. participated in the acquisition of 3D data and wrote that section. J.C. modeled the sperm trajectories. C.D.W., G.C. and A.P. supervised, provided advice and contributed to writing the paper. All authors approved the final manuscript.

Funding

This work was supported by Consejo Nacional de Ciencia y Tecnología (CONACyT) [grant number 49113 & 128566 (to A.D.), 99508 (to G.C.) and 132478 (to C.D.W.)], National Institutes of Health [grant number R01 HD038082-07A1 (to A.D.)], Programa de Apoyo a Proyectos de Investigación e Innovación Technológica (PAPIIT) [grant numbers, IN211809, IN109210 & DGAPA/IXTLI IX200910 (to A.D.), IN111909 (to G.C.) and IN223810 (to C.D.W.)] and Fundação para a Ciência e a Tecnologia [grant PTDC/SAL-OBD/69928/2006 (to J.C.)]. Funding to pay the Open Access publication charges for this article was provided by National Institutes of Health [grant number R01 HD038082-07A1, Programa de Apoyo a Proyectos de Investigacioon e Innovacioon Technolóogica (PAPIIT) [grant numbers, IN211809, IN109210 (to A.D.), IN111909 (to G.C.), and IN223810 (to C.D.W.), Fundacao para a Ciencia e a Tecnologia [grant PTDC/SAL-OBD/69928/2006 (to J.C.)], Consejo Nacional de Ciencia y Tecnología (CONACyT) [grant number 128566 (to A.D.).